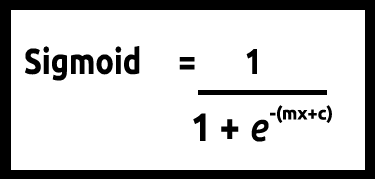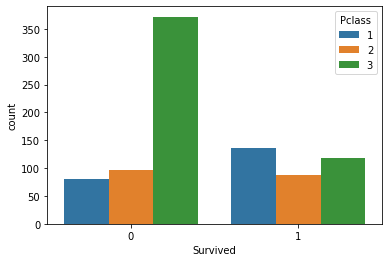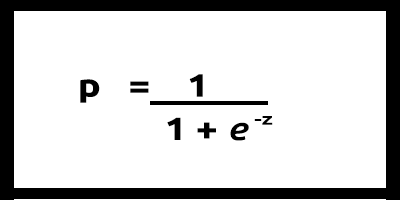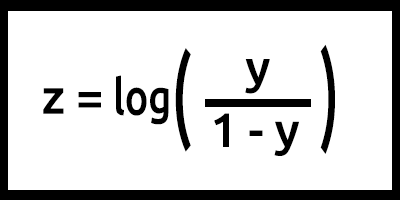
Машинное обучение и Data Science (Часть 02): Логистическая регрессия
В первой части мы говорили о линейной регрессии, сейчас же поговорим о логистической, которая представляет собой метод классификации, основанный на линейной регрессии.
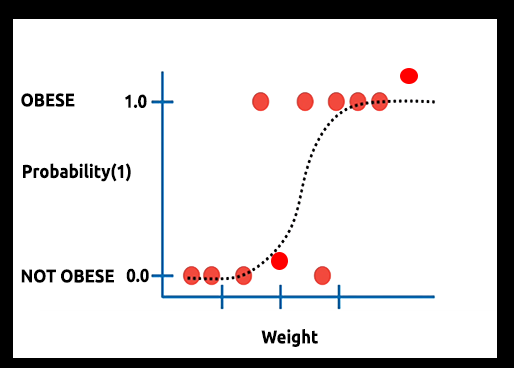
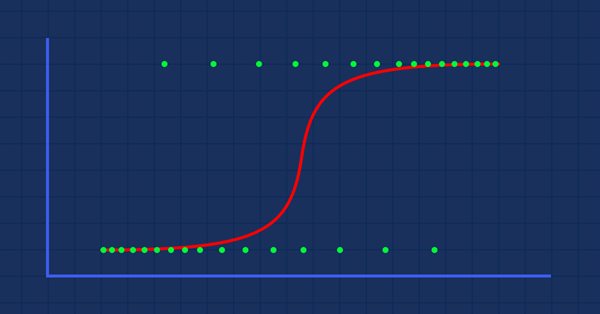
Теория. Предположим, мы построили график вероятности зависимости ожирения человека от его веса.
В этом случае нельзя использовать линейную модель. Будем использовать другую технику для преобразования этой линии в S-кривую, известную как сигмоид.
Поскольку логистическая регрессия дает результаты в двоичном формате, который используется для прогнозирования результата категориальной зависимой переменной, результат должен быть дискретным/категориальным, например:
- 0 или 1
- Да или нет
- Правда или ложь
- Максимум или минимум
- Покупка или продажа
В нашей библиотеке, которую будем создавать в этой статье, мы будем игнорировать другие дискретные значения. Сосредоточимся только на бинарных значениях (0,1).
Поскольку мы ожидаем значения y между 0 и 1, обрежем нашу линию, ограничив ее значениями 0 и 1. Это можно сделать с помощью следующей формулы:
После этого получим такой график
Линейная модель передается логистической функции (сигмоид/p) =1/1+е^t, где t является линейной моделью, результатом которой являются значения от 0 до 1. Так представлена вероятность того, что точка данных принадлежит классу.
Вместо использования y линейной модели в качестве зависимой, в качестве нее в функции используется p
p = 1/1+e^-(c+m1x1+m2x2+....+mnxn) при наличии нескольких значений
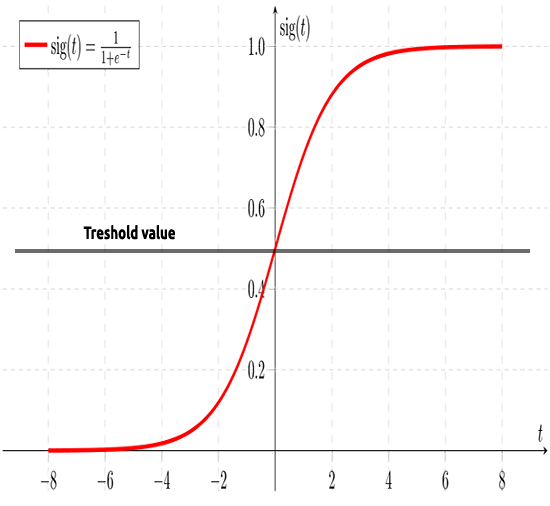
Как я писал ранее, сигмовидная кривая позволяет преобразовывать бесконечные значения в выходной двоичный формат (0 или 1). Но что, если есть точка данных, расположенная на 0,8? Как решить, что значение равно нулю или единице? Для этого будем использовать пороговые значения.
Порог указывает вероятность выигрыша или проигрыша, он находится на уровне 0,5 (посередине между 0 и 1).
Любое значение больше или равное 0,5 будет округлено до единицы и, следовательно, будет считаться выигрышным. Любое значение ниже 0,5 будет округлено до 0, следовательно, на данном этапе будет считаться проигрышем. Теперь давайте посмотрим, в чем же разница между линейной и логистической регрессией.
Линейная и логистическая регрессия
| Линейная регрессия | Логистическая регрессия |
|---|---|
| Непрерывная переменная | Категориальная переменная |
| Для решения задач регрессии | Для решения задач классификации |
| Модель имеет прямое уравнение | Модель имеет логистическое уравнение |
Прежде чем мы перейдем к детальному рассмотрению кодов и алгоритмов классификации данных, давайте реализуем несколько шагов, которые помогут понять данные и упростить построение нашей модели:
- Сбор и анализ данных
- Очистка данных
- Проверка точности
1. Сбор и анализ данных
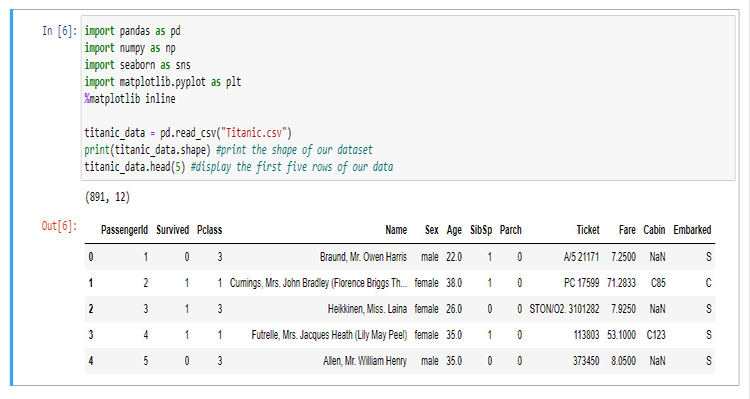
В этом разделе мы будем писать много кода на Python для визуализации наших данных. Для начала нужно импортировать библиотеки, которые мы будем использовать для извлечения и визуализации данных в блокноте Jupyter.
Для построения нашей библиотеки мы будем использовать данные о Титанике, том самом, который затонул в Северной Атлантике 15 апреля 1912 года после столкновения с айсбергом (если вдруг вы не слышали, подробности в Википедии). Все коды Python и наборы данных можно найти в моем GitHub по ссылке в конце статьи.
Поясню, что означают столбцы
survival - выживание (0 = нет; 1 = да)
class - пассажирский класс (1 = Первый; 2 = Второй; 3 = Третий)
name - имя
sex - пол
age - возраст
sibsp - количество сестер и братьев/супругов на борту
parch - количество родителей/детей на борту
ticket - номер билета
fare - пассажирский тариф
cabin - каюта
embarked - порт посадки (C = Шербур; Q = Квинстаун; S = Саутгемптон)
После сбора данных и сохранения их в переменной titanic_data приступим к визуализации данные в столбцах, начиная со столбца выживания.
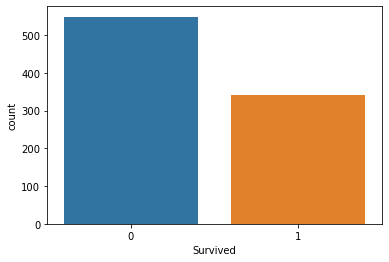
sns.countplot(x="Survived", data = titanic_data)
Выход
Он показывает, что в катастрофе выжило меньшинство пассажиров из всех, кто был на корабле. Большая же часть погибла.
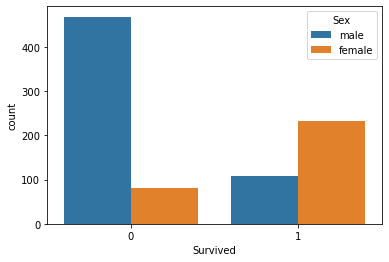
Далее визуализируем количество выживших в зависимости от пола
sns.countplot(x='Survived', hue='Sex', data=titanic_data)
Я не знаю, что случилось с мужчинами в тот день, но количество выживших женщин вдвое больше, чем мужчин.
Давайте теперь визуализируем число выживших в соответствии с классами пассажиров
sns.countplot(x='Survived', hue='Pclass', data=titanic_data)
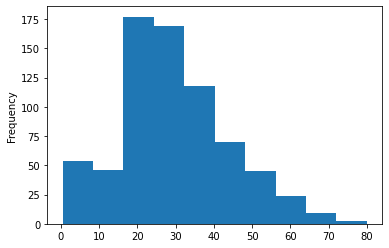
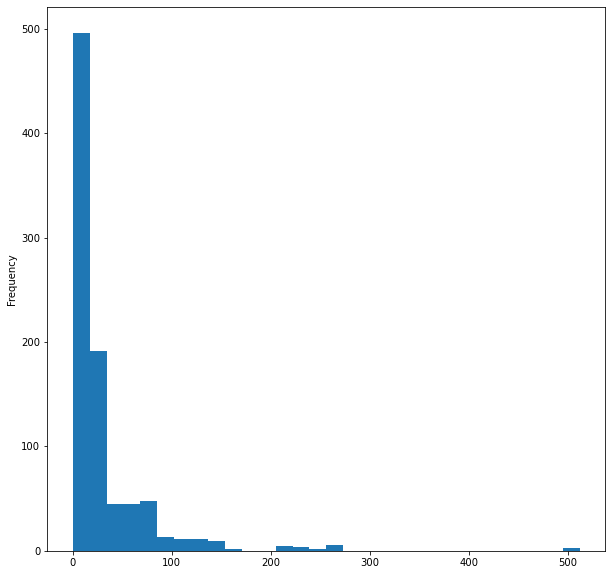
Построим гистограмму возрастных групп пассажиров, находившихся на корабле. Здесь не получится использовать Count-plot для визуализации данных, поскольку в нашем наборе данных есть много разных значений возраста, и они не организованы.
titanic_data['Age'].plot.hist()Результат:
Ни у последнее — пассажирский тариф на корабле
titanic_data['Fare'].plot.hist(bins=30, figsize=(10,10))
На этом закончим с визуализацией данных. Мы визуализировали только пять столбцов из 12 - самые важные данных. Теперь перейдем к очистке данных.
2. Очистка данных
Здесь очистим наши данные: удалим значения NaN (нет значений) и исключим ненужные столбцы из набора данных.
При использовании логистической регрессии нужно работать со значениями double и integer, а бессмысленные строковые значения надо исключить, поэтому в нашем случае мы игнорируем следующие столбцы:
- Столбец name (в имени нет значимой информации)
- Столбец ticket (не имеет никакого смысла для выживания в катастрофе)
- Столбец cabin (в нем слишком много пропущенных значений, это видно даже в первых 5 строках)
- Порт посадки (думаю, это не имеет значения)
Для этого откроем файл CSV в WPS office и вручную удалим столбцы. Вы можете использовать любую программу для работы с таблицами по выбору.
После удаления столбцов визуализируем новые данные.
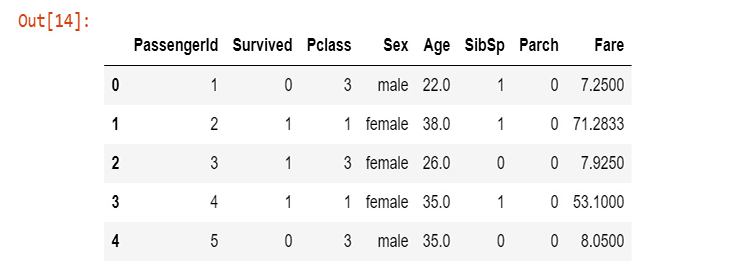
new_data = pd.read_csv(r'C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\titanic.csv') new_data.head(5)
Результат:
Мы очистили данные, хотя у нас все еще есть отсутствующие значения в столбце возраста, не говоря уже о том, что в столбце пола находятся строковые значения. Давайте исправим эти ошибки с помощью кода. Создадим label encoder для преобразования строковых значений male и female в 0 и 1, соответственно.
void CLogisticRegression::LabelEncoder(string &src[],int &EncodeTo[],string members="male,female") { string MembersArray[]; ushort separator = StringGetCharacter(m_delimiter,0); StringSplit(members,separator,MembersArray); //конвертируем список элементов в массив ArrayResize(EncodeTo,ArraySize(src)); //размер массива EncodeTo зададим равным размеру исходного массива int binary=0; for(int i=0;i<ArraySize(MembersArray);i++) // цикл по элементам массива { string val = MembersArray[i]; binary = i; //значения binary для элементов int label_counter = 0; for (int j=0; j<ArraySize(src); j++) { string source_val = src[j]; if (val == source_val) { EncodeTo[j] = binary; label_counter++; } } Print(MembersArray[binary]," total =",label_counter," Encoded To = ",binary); } }
Чтобы получить исходный массив с именем scr[] я также написал функцию для получения данных из определенного столбца в файле CSV, а затем поместил их в массив строковых значений MembersArray[]. Вот как получилось:
void CLogisticRegression::GetDatatoArray(int from_column_number, string &toArr[]) { int handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV|FILE_ANSI,m_delimiter); int counter=0; if (handle == INVALID_HANDLE) Print(__FUNCTION__," Invalid csv handle err=",GetLastError()); else { int column = 0, rows=0; while (!FileIsEnding(handle)) { string data = FileReadString(handle); column++; //--- if (column==from_column_number) //если столбец в цикле совпадает с искомым столбцом { if (rows>=1) //Исключаем первый столбец, который содержит заголовок { counter++; ArrayResize(toArr,counter); toArr[counter-1]=data; } } //--- if (FileIsLineEnding(handle)) { rows++; column=0; } } } FileClose(handle); }
Ниже показано, как правильно вызывать функции и инициализировать библиотеку внутри нашей программы testscript.mq5:
#include "LogisticRegressionLib.mqh"; CLogisticRegression Logreg; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- Logreg.Init("titanic.csv",","); string Sex[]; int SexEncoded[]; Logreg.GetDatatoArray(4,Sex); Logreg.LabelEncoder(Sex,SexEncoded,"male,female"); ArrayPrint(SexEncoded); }
После успешного выполнения скрипта будет выведена следующая информация
male total =577 Encoded To = 0
female total =314 Encoded To = 1
[ 0] 0 1 1 1 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 0 1 1 0 0 1 0 0 1 1 0 0 0 0 0 1 1 1 1 0 1 1 0 0 1 0 1 0 0 1 1 0 0 1 0 1 0 0 1 0 0 0 0 1 0 1 0 0 1 0 0 0
[ 75] 0 0 0 0 1 0 0 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0 0 1 1 1 0 0 0 0 1 0 0
... ... ... ...
... ... ... ...
[750] 1 0 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 1 1 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0
[825] 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 0 0 0 1 1 0 1 1 0 0 0 0 1 0 0 1 1 0 0 0 1 1 0 1 0 0 1 0 1 1 0 0
Перед тем как программировать значения обратите внимание на members="male,female" в аргументах функции. Первое значение в строке будет заменено на 0 — в данном случае первым идет столбец male, поэтому ему будет присвоен 0, а значению females будет присвоена 1. Однако функция не ограничивается двумя значениями, вы можете внести столько значений, сколько хотите.
Отсутствующие значения
Если вы обратите внимание на столбец Age, вы заметите, что в нем пропущены значения. Пропущенные значения в нашем наборе данных могут быть в основном связаны с одной причиной — смертью, в этом случае невозможно определить возраст человека. Эти пробелы можно выявить, изучив набор данных. Однако это может занять много времени, особенно для больших наборов данных. И поскольку мы используем pandas для визуализации данных, давайте так же найдем недостающие строки во всех столбцах
titanic_data.isnull().sum()
The output will be:
PassengerId 0
Survived 0
Pclass 0
Sex 0
Age 177
SibSp 0
Parch 0
Fare 0
dtype: int64
Из 891 строки в 177 строках в нашем столбце Age отсутствуют значения (NAN).
Давайте заменим отсутствующие значения в нашем столбце, заменив значения средним от всех возрастов.
void CLogisticRegression::FixMissingValues(double &Arr[]) { int counter=0; double mean=0, total=0; for (int i=0; i<ArraySize(Arr); i++) //первый шаг - найти среднее ненулевых значений { if (Arr[i]!=0) { counter++; total += Arr[i]; } } mean = total/counter; //все значения, поделенные на их количество Print("mean ",MathRound(mean)," before Arr"); ArrayPrint(Arr); for (int i=0; i<ArraySize(Arr); i++) { if (Arr[i]==0) { Arr[i] = MathRound(mean); //замена нулевых значений в массиве } } Print("After Arr"); ArrayPrint(Arr); }
Эта функция находит среднее значение всех ненулевых значений, а затем заменяет все нулевые значения в массиве средним значением.
Вот что покажет запуск скрипта. Как видите, все нулевые значения были заменены на 30.0 — средний возраст всех пассажиров Титаника.
mean 30.0 before Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 0.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 0.0 31.0 0.0 35.0 34.0 15.0 28.0 8.0 38.0 0.0 19.0 0.0 0.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 0.0 35.0 28.0 0.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 0.0 41.0 21.0 48.0 0.0 24.0 42.0 27.0 31.0 0.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 0.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 0.0 26.0 32.0
After Arr
[ 0] 22.0 38.0 26.0 35.0 35.0 30.0 54.0 2.0 27.0 14.0 4.0 58.0 20.0 39.0 14.0 55.0 2.0 30.0 31.0 30.0 35.0 34.0 15.0 28.0 8.0 38.0 30.0 19.0 30.0 30.0
… … … … … … … … …
[840] 20.0 16.0 30.0 34.5 17.0 42.0 30.0 35.0 28.0 30.0 4.0 74.0 9.0 16.0 44.0 18.0 45.0 51.0 24.0 30.0 41.0 21.0 48.0 30.0 24.0 42.0 27.0 31.0 30.0 4.0
[870] 26.0 47.0 33.0 47.0 28.0 15.0 20.0 19.0 30.0 56.0 25.0 33.0 22.0 28.0 25.0 39.0 27.0 19.0 30.0 26.0 32.0
Построение модели логистической регрессии
Для начала построим нашу логистическую регрессию, где у нас будет одна независимая переменная и одна зависимая переменная. А затем перейдем к модели полного решения проблемы.
Давайте построим модель на двух переменных Survived Versus Age, чтобы выяснить, каковы были шансы человека выжить в зависимости от его возраста.
Пока что мы знаем, что глубоко внутри логистической модели есть линейная модель. Начнем с написании функций, которые делают возможной линейную модель.
Coefficient_of_X() и y_intercept() — эти функции не новые, мы работали с ними в первой статье из этой серии. Рекомендую прочитать ее, чтобы узнать больше об этих функциях и линейной регрессии в целом.
double CLogisticRegression::y_intercept() { // c = y - mx return (y_mean-coefficient_of_X()*x_mean); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ double CLogisticRegression::coefficient_of_X() { double m=0; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<ArraySize(m_xvalues); i++) { x__x = m_xvalues[i] - x_mean; //правая часть числителя (сторона x) y__y = m_yvalues[i] - y_mean; //левая часть числителя (сторона y) numerator += x__x * y__y; //сумма произведений двух частей числителя denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
Теперь напишем код логистической модели по формуле.
Обратите внимание, что z здесь является логарифмом шансов (log-odds), потому что инверсия сигмоиды утверждает, что z можно определить как логарифм вероятности 1 (например, "выжил"), поделенной на вероятность 0 (например, "не выжил"):
Получается, y = mx+c (помним это из формулы линейной модели).
Переведя это в код, получим
double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1);
Обратите внимание, что мы сделали со значением z. Наша формула log(y/1-y), а в коде записано log(y_)-log(1-y_). Вспоминаете законы логарифмов из курса математики? Деление логарифмов с одинаковым основанием приводит к вычитанию степеней (ссылка).
Это основа нашей модели с запрограммированной формулой. Но внутри функции LogisticRegression() происходит многое. Вот что находится внутри функции:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { int arrsize = ArraySize(x); //размер входного массива double p_hat =0; //сохраним вероятность //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Обучаем модель в фоновом режиме double c = y_intercept(), m = coefficient_of_X(); //--- А вот и модель логистической регрессии int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //изменяем размер массива, чтобы он соответствовал размеру обучающего массива Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //округляем значения, чтобы получить фактические 0 или 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } //--- Тестируем модель if (train_size_split<1.0) //если есть возможность тестирования { ArrayRemove(m_xvalues,0,train_size); //очищаем массив ArrayRemove(m_yvalues,0,train_size); //очищаем массив от обучающих данных ArrayCopy(m_xvalues,x,0,train_size,test_size); //новые значения x начинаются там, где заканчивается обучение ArrayCopy(m_yvalues,y,0,train_size,test_size); //новые значения y начинаются там, где заканчивается тестирование Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //изменяем размер массива, чтобы он соответствовал размеру тестового массива for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); double odds_ratio = p_hat/(1-p_hat); TrainPredicted[i] = (int) round(p_hat); //округляем значения, чтобы получить фактические 0 или 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } }
Теперь давайте обучим и протестируем нашу модель в скрипте TestScript.mq5.
double Age[]; Logreg.GetDatatoArray(5,Age); Logreg.FixMissingValues(Age); double y_survival[]; int Predicted[]; Logreg.GetDatatoArray(2,y_survival); Logreg.LogisticRegression(Age,y_survival,Predicted);
The output of a successful script run will be:
Training starting..., train size=624
0 Age =22.00 survival_Predicted =0
1 Age =38.00 survival_Predicted =0
... .... ....
622 Age =20.00 survival_Predicted =0
623 Age =21.00 survival_Predicted =0
start testing...., test size=267
0 Age =21.00 survival_Predicted =0
1 Age =61.00 survival_Predicted =1
.... .... ....
265 Age =26.00 survival_Predicted =0
266 Age =32.00 survival_Predicted =0
Great. Теперь наша модель работает, и мы можем как минимум получить от нее результаты. Но делает ли модель хорошие прогнозы?
Нужно проверить ее на точность.
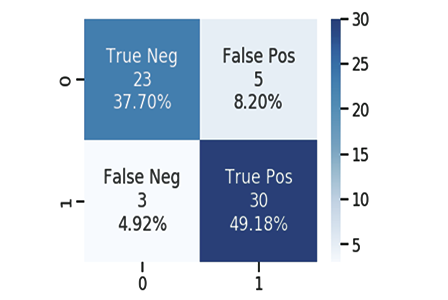
Матрица путаницы
Как мы знаем, каждая хорошая и плохая модель может делать предсказания. Я создал файл CSV с прогнозами, которая сделала наша модель, сопоставленными с оригинальными данными из тестирования выживаемости пассажиров. Все так же 1 означает, что пассажир выжил, а 0 означает, что не выжил.
Вот несколько столбцов:
| Оригинальные данные | Прогноз | |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 2 | 0 | 1 |
| 3 | 1 | 0 |
| 4 | 0 | 0 |
| 5 | 0 | 0 |
| 6 | 1 | 1 |
| 7 | 0 | 1 |
| 8 | 1 | 0 |
| 9 | 0 | 0 |
Вычисляем матрицу путаницы, используя:
- TP — истинно положительный
- TN — истинно отрицательный
- FP — ложноположительный
- FN — ложноотрицательный
Что означают эти значения?
TP (истинно положительный)
Это когда исходное значение положительное (1), и модель также дает положительное предсказание (1)
TN (истинный отрицательный результат)
Это когда исходное значение отрицательное (0), и модель также дает отрицательное предсказание (0)
FP — ложноположительный
Это когда исходное значение отрицательное (0), а модель дает положительное предсказание (1)
FN — ложноотрицательный
Это когда исходное значение положительное (1), а модель дает отрицательное предсказание (0)
Теперь давайте рассчитаем матрицу путаницы для приведенного выше примера.
| Оригинальные данные | Прогноз | TP/TN/FP/FN | |
|---|---|---|---|
| 0 | 0 | 0 | TN |
| 1 | 0 | 1 | FP |
| 2 | 0 | 1 | FP |
| 3 | 1 | 0 | FN |
| 4 | 0 | 0 | TN |
| 5 | 0 | 0 | TN |
| 6 | 1 | 1 | TP |
| 7 | 0 | 1 | FP |
| 8 | 1 | 0 | FN |
| 9 | 0 | 0 | TN |
Матрицу путаницы можно использовать для расчета точности нашей модели с использованием этой формулы.
Из нашей таблицы:
- TN = 4
- TP = 1
- FN = 2
- FP = 3
Точность = 1 + 5 / 4 + 1 + 2 + 3
Точность = 0,5
В нашем точность составляет 50% ( 0,5 * 100%)
Мы разобрались, как работает матрица путаницы 1X1. Пришло время преобразовать ее в код и проанализировать точность нашей модели на всем наборе данных.
void CLogisticRegression::ConfusionMatrix(double &y[], int &Predicted_y[], double& accuracy) { int TP=0, TN=0, FP=0, FN=0; for (int i=0; i<ArraySize(y); i++) { if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==1) TP++; if ((int)y[i]==Predicted_y[i] && Predicted_y[i]==0) TN++; if (Predicted_y[i]==1 && (int)y[i]==0) FP++; if (Predicted_y[i]==0 && (int)y[i]==1) FN++; } Print("Confusion Matrix \n ","[ ",TN," ",FP," ]","\n"," [ ",FN," ",TP," ] "); accuracy = (double)(TN+TP) / (double)(TP+TN+FP+FN); }
Вернемся к основной функции в нашем классе — LogisticRegression(). На этот раз мы превратим ее в двойную функцию, которая возвращает точность модели. Также я хочу уменьшить количество методов Print(), а вместо них использовать оператор if. По факту нам не нужно каждый раз выводить значения (если, конечно, это не отладка класса). Все изменения выделены синим цветом:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7) { double accuracy =0; //Точность обучения/тестовой модели int arrsize = ArraySize(x); //размер входного массива double p_hat =0; //сохраним вероятность //--- int train_size = (int)MathCeil(arrsize*train_size_split); int test_size = (int)MathFloor(arrsize*(1-train_size_split)); ArrayCopy(m_xvalues,x,0,0,train_size); ArrayCopy(m_yvalues,y,0,0,train_size); //--- y_mean = mean(m_yvalues); x_mean = mean(m_xvalues); // Обучаем модель в фоновом режиме double c = y_intercept(), m = coefficient_of_X(); //--- А вот и модель логистической регрессии int TrainPredicted[]; double sigmoid = 0; ArrayResize(TrainPredicted,train_size); //изменяем размер массива, чтобы он соответствовал размеру обучающего массива Print("Training starting..., train size=",train_size); for (int i=0; i<train_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //округляем значения, чтобы получить фактические 0 или 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d ",i,m_xvalues[i],TrainPredicted[i]); } ConfusionMatrix(m_yvalues,TrainPredicted,accuracy); //будьте осторожны, чтобы не перепутать массивы значений обучения printf("Train Model Accuracy =%.5f",accuracy); //--- Тестируем модель if (train_size_split<1.0) //если есть возможность тестирования { ArrayRemove(m_xvalues,0,train_size); //очищаем массив ArrayRemove(m_yvalues,0,train_size); //очищаем массив от обучающих данных ArrayCopy(m_xvalues,x,0,train_size,test_size); //новые значения x начинаются там, где заканчивается обучение ArrayCopy(m_yvalues,y,0,train_size,test_size); //новые значения y начинаются там, где заканчивается тестирование Print("start testing...., test size=",test_size); ArrayResize(Predicted,test_size); //изменяем размер массива, чтобы он соответствовал размеру тестового массива for (int i=0; i<test_size; i++) { double y_= (m*m_xvalues[i])+c; double z = log(y_)-log(1-y_); //log loss p_hat = 1.0/(MathPow(e,-z)+1); TrainPredicted[i] = (int) round(p_hat); //округляем значения, чтобы получить фактические 0 или 1 if (m_debug) PrintFormat("%d Age =%.2f survival_Predicted =%d , Original survival=%.1f ",i,m_xvalues[i],Predicted[i],m_yvalues[i]); } ConfusionMatrix(m_yvalues,Predicted,accuracy); printf("Testing Model Accuracy =%.5f",accuracy); } return (accuracy); //Наконец, вернем точность тестирования }
После исполнения скрипта получим такой результат:
Training starting..., train size=624
Confusion Matrix
[ 378 0 ]
[ 246 0 ]
Train Model Accuracy =0.60577
start testing...., test size=267
Confusion Matrix
[ 171 0 ]
[ 96 0 ]
Testing Model Accuracy =0.64045
Ура! Теперь мы можем определить, насколько хороша наша модель с помощью чисел. И хотя точность 64,045% на тестовых данных не такая уж хорошая, чтобы модель можно было использовать для прогнозирования (на мой взгляд), но у нас уже есть библиотека, которая может помочь нам классифицировать данные с помощью логистической регрессии.
Далее пояснения по основной функции:
double CLogisticRegression::LogisticRegression(double &x[],double &y[],int& Predicted[],double train_size_split = 0.7)
Входной параметр train_size_split позволяет разбить данные на учебную и тестовую выборку. По умолчанию набор делится так: 0,7 т.е. 70% данных будут использоваться для обучения, а оставшиеся 30% — для тестирования. Массив Predicted[] вернет прогнозируемые данные тестирования.
Двоичная перекрестная энтропия, или Функция потерь
Так же, как среднеквадратическая ошибка является функцией ошибки для линейной регрессии, двоичная перекрестная энтропия является функцией стоимости для логистической регрессии.
Теория:
Давайте посмотрим, как это работает в двух случаях использования логистической регрессии, например: когда фактический результат равен 0 и 1.
1. Когда фактический результат равен 1
Рассмотрим модель для двух входных выборок p1 = 0,4 и p2 = 0,6. Ожидается, что штраф на p1 должен быть больше, чем p2, потому что он дальше от 1, чем p1.
С математической точки зрения отрицательный логарифм малого числа есть большое число и наоборот.
Чтобы назначить входным данным штрафы, будем использовать следующую формулу
penalty = -log(p)
В этих двух случаях
- Штраф = -log(0.4)=0.4 т.е. штраф на p1 = 0.4
- Штраф = -log(0.6)=0.2 т.е. штраф на p2 = 0.2
2. Когда фактический результат равен 0
Рассмотрим выходные данные модели для двух входных выборок, p1 = 0,4 и p2 = 0,6 (как и в предыдущем случае). Ожидается, что p2 должен быть оштрафован больше, чем p1, потому что он дальше от 0, но не забывайте, что выход логистической модели — это вероятность того, что выборка будет положительной. Чтобы оштрафовать входные вероятности, нам нужно найти вероятность того, что выборка будет отрицательной. Это несложно. Вот формула:
Вероятность того, что выборка будет отрицательной = 1-вероятность того, что выборка будет положительной
Итак, чтобы найти штраф в этом случае, будем использовать формулу
penalty = -log(1-p)
В этих двух случаях
- Штраф = -log(1-p) = -log(1-0.4) =0.2, т.е. штраф равен 0.2
- Штраф = -log(1-p) = -log(1-0.6) =0.4, т.е. штраф равен 0.4
Штраф на p2 больше, чем на p1 (работает как положено). Отлично!
Теперь штраф для одной входной выборки, выход модели которой равен p, а истинное выходное значение равно y, можно рассчитать следующим образом.
if input sample is positive y=1:
penalty = -log(p)
else:
penalty = -log(1-p)
Однострочное уравнение, эквивалентное приведенному выше оператору блока if-else, может быть записано как
penalty = -( y*log(p) + (1-y)*log(1-p) )
где:
y = фактические значения в наборе данных
p = необработанная прогнозируемая вероятность модели (до округления)
Докажем, что это уравнение эквивалентно приведенному выше оператору if-else.
1. Когда выходные значения y = 1
штраф = -( 1*log(p) + (1-1)*log(1-p) ) = -log(p) следовательно, доказано
2. Когда выходные значения y = 0
штраф = -( 0*log(p) + (1-0)* log(1-p) ) = log(1-p) следовательно, доказано
Наконец, функция логарифмических потерь для N входных выборок выглядит так
Log-loss показывает, насколько близка вероятность предсказания к соответствующему фактическому/истинному значению (0 или 1 в случае бинарной классификации). Чем больше прогнозируемая вероятность отличается от фактического значения, тем выше значение логарифмической потери.
Функции стоимости, такие как log-loss (логарифмическая потеря) и многие другие, могут использоваться в качестве метрики того, насколько хороша модель. Но наибольшая польза — это оптимизация модели для достижения наилучших параметров с использованием градиентного спуска или других алгоритмов оптимизации (мы поговорим об этом в последующих сериях, так что следите за публикациями).
Если что-то можно измерить, это можно улучшить. Это основная цель функций затрат.
Из нашего набора данных для тестирования и обучения видно, что логарифмическая потеря составляет от 0,64 до 0,68, что не идеально (мягко говоря).
Обучающий набор данных
Logloss =0.6858006105398738
Тестовый набор данных
Logloss =0.6599503403665642
Вот как мы можем преобразовать нашу функцию log-loss в код
double CLogisticRegression::LogLoss(double &rawpredicted[]) { double log_loss =0; double penalty=0; for (int i=0; i<ArraySize(rawpredicted); i++ ) { penalty += -((m_yvalues[i]*log(rawpredicted[i])) + (1-m_yvalues[i]) * log(1-rawpredicted[i])); //сумма всех штрафов if (m_debug) printf("penalty =%.5f",penalty); } log_loss = penalty/ArraySize(rawpredicted); //все штрафы поделенные на их количество Print("Logloss =",log_loss); return(log_loss); }
Чтобы получить необработанный прогнозируемый результат, нужно вернуться к основному циклу тестирования и обучения и сохранить данные в необработанном прогнозируемом массиве непосредственно перед процессом округления вероятностей.
Задача множественной динамической логистической регрессии
Самая большая проблема, с которой я столкнулся при создании библиотек как линейной, так и логистической регрессии в этих двух статьях, — это функции множественной динамической регрессии, которые можно было бы использовать для множества столбцов данных без необходимости прописывать в коде все данные, добавляемые в модель. В предыдущей статье я написал две функции с одинаковыми именами, единственная разница между ними заключалась в количестве данных, с которыми могла работать каждая модель: одна могла работать с двумя независимыми переменными, другая с четырьмя соответственно:
void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]);
Но этот метод неудобный, кроме того, он нарушает правила чистого кода и принцип DRY (не повторяться) из ООП.
В отличие от Python с гибкими функциями, которые могут принимать большое количество аргументов с помощью *args и **kwargs, в MQL5, насколько я знаю, то же самое можно сделать, только если использовать строки. Думаю, это наша отправная точка.
void CMultipleLogisticRegression::MLRInit(string x_columns="3,4,5,6,7,8")
Входной параметр x_columns представляет все столбцы независимых переменных, которые мы будем использовать в нашей библиотеке. При этом для каждого столбца нужно было бы иметь отдельный массив, но создавать массивы динамически мы не можем, поэтому использование массивов здесь не подходит.
Мы могли бы динамически создавать файлы CSV и использовать их как массивы, но это сделает программы более дорогими в плане использования ресурсов компьютера по сравнению с использованием массивов. Особенно это будет заметно при работе с множеством данных, не говоря уже о циклах while, которые мы будем часто использовать для открытия файлов. Все это будет замедлять весь процесс. Но я не уверен в этом на 100%, так что поправьте меня, если я ошибаюсь.
Все же упомянутый способ можно использовать.
И я нашел способ использовать массивы — будем хранить все данные из всех столбцов в одном массиве, а затем использовать необходимые данные из этого единственного массива.
int start = 0; if (m_debug) //если режим отладки, выводим каждый массив против его строки for (int i=0; i<x_columns_total; i++) { ArrayCopy(EachXDataArray,m_AllDataArray,0,start,rows_total); start += rows_total; Print("Array Number =",i," From column number ",m_XColsArray[i]); ArrayPrint(EachXDataArray); }
Внутри цикла for проходим по данным и выполняем все необходимые вычисления для модели по всем столбцам. Я пробовал этот метод, но все еще не достиг успеха. Причина, по которой я рассказываю про эту гипотезу, — объяснить проблему читателям. Если у вас есть мнения насчет того, как можно написать код функции множественной динамической логистической регрессии, пожалуйста, делитесь ими в комментариях. Все, что я пытался сделать для создания этой библиотеки, можно посмотреть по этой ссылке: https://www.mql5.com/ru/code/38894.
Моя попытка не увенчалась успехом, но все не так безнадежно, и я считаю, что этим стоит поделиться.
Преимущества логистической регрессии
- Не предполагает распределения классов в пространстве признаков
- Легко расширяется до нескольких классов (полиномиальная регрессия)
- Естественно-вероятностный взгляд на предсказания классов
- Быстрое обучение
- Очень быстро классифицирует незнакомые данные
- Хорошая точность для многих простых наборов данных
- Устойчивость к подгонке
- Может интерпретировать коэффициенты модели как индикатор важности функции
Недостатки
- Строит линейные границы
Заключительные мысли
Это все, что касается этой статьи. Логистическая регрессия используется во многих областях реальной жизни, таких как классификация электронных писем как спам / не спам, и др.
Я понимаю, что нет прикладной цели в использовании алгоритмов логистической регрессии для классификации данных по Титанику, особенно в платформе MetaTrader 5, однако, как я уже говорил, набор данных использовался только ради построения библиотеки по сравнению с выводом, который был достигнут в python, ссылка: https://github.com/MegaJoctan/LogisticRegression-MQL5-and-python. В следующей статье мы увидим, как можно использовать логистические модели для прогнозирования падения фондового рынка.
Поскольку статья итак получилась слишком длинной, я оставляю задачу множественной регрессии в качестве домашнего задания для всех читателей.
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/10626
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Разработка торгового советника с нуля (Часть 16): Доступ к данным в Интернете (II)
Разработка торгового советника с нуля (Часть 16): Доступ к данным в Интернете (II)
 Разработка торгового советника с нуля (Часть 15): Доступ к данным в Интернете (I)
Разработка торгового советника с нуля (Часть 15): Доступ к данным в Интернете (I)
 Разработка торгового советника с нуля (Часть 14): Добавляем Volume at Price (II)
Разработка торгового советника с нуля (Часть 14): Добавляем Volume at Price (II)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования