Машинное обучение и Data Science (Часть 01): Линейная регрессия
Введение
"Искушение строить предварительные версии, основываясь на неполных данных, губительно в нашей профессии."
(Шерлок Холмс)
Data Science — наука о данных
Это практическая междисциплинарная сфера деятельности, которая использует научные методы, процессы, алгоритмы и системы для извлечения знаний и закономерностей из структурированных и неструктурированных данных и применения этих знаний и действенных закономерностей в широком диапазоне различных областей.
Специалист по Data science — это тот, кто создает программный код и сочетает его со статистическими знаниями для создания идей на основе данных.
Чего ожидать от этой серии статей?
- Теория (в математических уравнениях): теория наиболее важна в науке о данных. Надо иметь глубокое понимание алгоритмов и поведения модели, почему она ведет себя определенным образом. Понимать это намного сложнее, чем программировать сам алгоритм.
- Практические примеры на MQL5 и Python.
Линейная регрессия
Это модель зависимости переменной от одной или нескольких других переменных.
Линейная регрессия является одним из основных алгоритмов, который используется во многих других, таких как:
- Логистическая регрессия — модель, основанная на линейной регрессии
- Машины опорных векторов — семейство алгоритмов классификации на основе обучения с учителем, использующих линейное разделение пространства.
Что такое модель
Модель — это не что иное, как суффикс.
Теория
Каждая прямая, проходящая через график, имеет такое уравнение:
Откуда оно берется?
Предположим, у вас есть два набора данных с одинаковыми значениями x и y:
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
Наносим значения на график:
Поскольку y равно x, уравнение прямой будет y=x, так? Нет!
Хотя,
y = x математически то же самое, что y = 1x, это не так в науке о данных. Уравнение прямой будет y=1x, где 1 — это угол между прямой и осью x, также называется углом наклона линии
Но,
Угол наклона = изменение y / изменение x = m (называетсяm)
Таким образом, формула будет y = mx.
Наконец, нужно добавить в уравнение константу, то есть значение y при x равном нулю. Другими словами, значение y, когда линия пересекает ось y
Получается,
уравнение будет таким: y = mx + c (это не что иное, как модель в data science)
где c — это пересечение с осью y
Простая линейная регрессия
Простая линейная регрессия имеет одну зависимую переменную и одну независимую переменную. Это попытка понять зависимость между двумя переменными, например, как цена акции изменяется при изменении простой скользящей средней.
Сложные данные
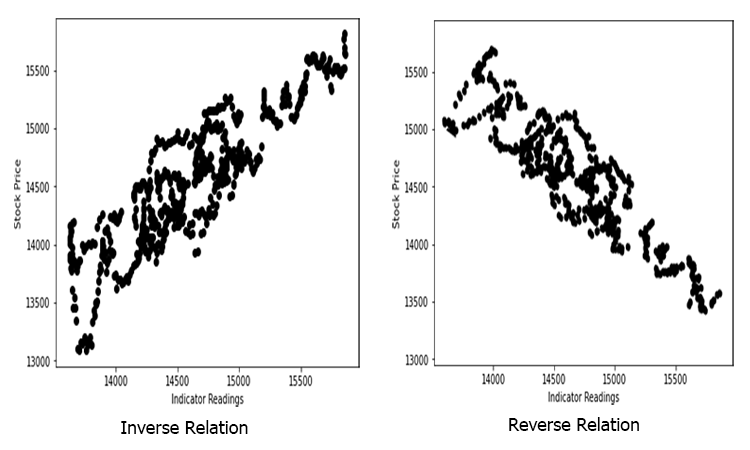
Предположим, есть случайные разбросанные значения индикатора на основе цены актива (обычная ситуация).
В этом случае наш Индикатор/независимая переменная может быть не очень хорошим предиктором цены актива/зависимой переменной.
Первый фильтр, который необходимо применить к набору данных, — это удалить все столбцы, которые не сильно коррелируют с вашей целью, чтобы не включать их в линейную модель.
Построение линейной модели с нелинейными связанными данными — огромная фундаментальная ошибка, поэтому необходимо внимательно к этому отнестись.
Связь не обязательно должна быть прямой, она может быть и обратной, но связь должна сильной для линейной модели.
Итак, как измерить силу между независимой переменной и нашей целью? Будем использовать показатель, известный как коэффициент корреляции.
Коэффициент корреляции
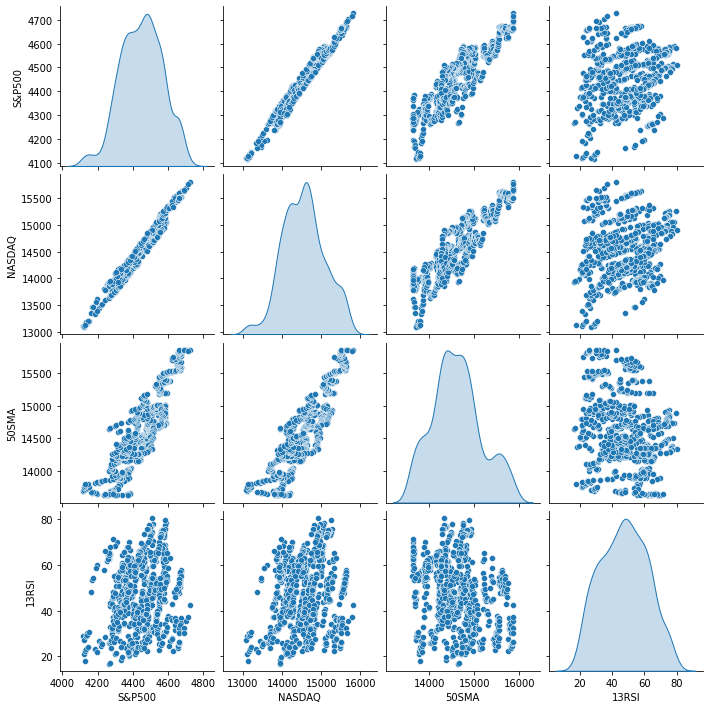
Напишем скрипт для создания набора данных, который будет использоваться в качестве основного примера для этой статьи. Будем находить предикторы NASDAQ.
input ENUM_TIMEFRAMES timeframe = PERIOD_H1; input int maperiod = 50; input int rsiperiod = 13; int total_data = 744; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { string file_name = "NASDAQ_DATA.csv"; string nasdaq_symbol = "#NQ100", s_p500_symbol ="#SP500"; //--- int handle = FileOpen(file_name,FILE_CSV|FILE_READ|FILE_WRITE,","); if (handle == INVALID_HANDLE) { Print("Данные для работы не найдены Err=",GetLastError()); } //--- MqlRates nasdaq[]; ArraySetAsSeries(nasdaq,true); CopyRates(nasdaq_symbol,timeframe,1,total_data,nasdaq); //--- MqlRates s_p[]; ArraySetAsSeries(s_p,true); CopyRates(s_p500_symbol,timeframe,1,total_data,s_p); //--- Данные скользящей средней int ma_handle = iMA(nasdaq_symbol,timeframe,maperiod,0,MODE_SMA,PRICE_CLOSE); double ma_values[]; ArraySetAsSeries(ma_values,true); CopyBuffer(ma_handle,0,1,total_data,ma_values); //--- Значения Rsi int rsi_handle = iRSI(nasdaq_symbol,timeframe,rsiperiod,PRICE_CLOSE); double rsi_values[]; ArraySetAsSeries(rsi_values,true); CopyBuffer(rsi_handle,0,1,total_data,rsi_values); //--- if (handle>0) { FileWrite(handle,"S&P500","NASDAQ","50SMA","13RSI"); for (int i=0; i<total_data; i++) { string str1 = DoubleToString(s_p[i].close,Digits()); string str2 = DoubleToString(nasdaq[i].close,Digits()); string str3 = DoubleToString(ma_values[i],Digits()); string str4 = DoubleToString(rsi_values[i],Digits()); FileWrite(handle,str1,str2,str3,str4); } } FileClose(handle); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
В скрипте мы собрали цены закрытия NASDAQ, значения 13-периодного RSI, S&P 500 и 50-периодную скользящую. Мы собрали данные в файл CSV, теперь будем их визуализировать в python. Будем работать с Anaconda в Jupyter. Если Anaconda у вас не установлена, для обработки данных код Python из этой статьи можно запускать в google colab.
Чтобы открыть CSV-файл, созданный тестовым скриптом, необходимо преобразовать его в кодировку UTF-8, чтобы Python мог его прочитать. Откройте файл CSV в notepad, сохраните его в кодировке UTF-8. Было бы неплохо скопировать файл во внешний каталог, чтобы python читал его отдельно по ссылке на этот каталог. В Pandas прочитаем файл CSV и сохраним его в переменной.
Результат выглядит так:
Из визуального представления данных уже можно заметить, что существует очень сильная корреляция между NASDAQ и S&P 500, а также сильная корреляция между NASDAQ и его 50-периодной скользящей средней. Как уже сказано, если данные разбросаны по всему графику, независимая переменная не будет хорошим предиктором, если мы ищем линейную корреляцию. Но давайте посмотрим, что числа говорят о корреляции, и сделаем вывод на основе чисел, а не визуально. Чтобы понять, как переменные коррелируют друг с другом, будем использовать коэффициент корреляции.
Коэффициент корреляции
Он используется для измерения силы между независимой переменной и целью.
Существует несколько типов коэффициентов корреляции, мы будем использовать самый популярный для линейной регрессии —коэффициент корреляции Пирсона (R), который колеблется между -1 и +1.
Корреляция экстремальных значений -1 и +1 означает соответственно идеальную отрицательную и положительную линейную зависимость между x и y, тогда как значение 0 означает отсутствие линейной корреляции.
Формула коэффициента корреляции/Коэффициент Пирсона (R).
Внутри основной библиотеки я создал файл linearRegressionLib.mqh. Давайте напишем функцию corrcoef().
Начнем с функции средней для значений: mean представляет собой сумму всех данных, поделенную на общее количество элементов.
double CSimpleLinearRegression::mean(double &data[]) { double x_y__bar=0; for (int i=0; i<ArraySize(data); i++) { x_y__bar += data[i]; // сумма всех значений } x_y__bar = x_y__bar/ArraySize(data); //сумма всех значений, поделенная на количество элементов return(x_y__bar); }Теперь напишем код для коэффициента Пирсона R
double CSimpleLinearRegression::corrcoef(double &x[],double &y[]) { double r=0; double numerator =0, denominator =0; double x__x =0, y__y=0; for(int i=0; i<ArraySize(x); i++) { numerator += (x[i]-mean(x))*(y[i]-mean(y)); x__x += MathPow((x[i]-mean(x)),2); //сумма значений x минус их среднеквадратичное значение y__y += MathPow((y[i]-mean(y)),2); //сумма значений y минус их среднеквадратичное значение } denominator = MathSqrt(x__x)*MathSqrt(y__y); //квадрат левой части x уравнения, умноженный на квадрат правой части уравнения r = numerator/denominator; return(r); }
При выводе сообщений в тестовом скрипте TestSript.mq5
Print("Correlation Coefficient NASDAQ vs S&P 500 = ",lr.corrcoef(s_p,y_nasdaq)); Print("Correlation Coefficient NASDAQ vs 50SMA = ",lr.corrcoef(ma,y_nasdaq)); Print("Correlation Coefficient NASDAQ Vs rsi = ",lr.corrcoef(rsi,y_nasdaq));
результат будет такой
Correlation Coefficient NASDAQ vs S&P 500 = 0.9807093773142763
Correlation Coefficient NASDAQ vs 50SMA = 0.8746579124626006
Correlation Coefficient NASDAQ Vs rsi = 0.24245225451004537
Как видите, у NASDAQ и S&P500 очень сильная корреляция по всем другим столбцам данных (потому что коэффициент корреляции очень близок к 1), поэтому нужно отбросить другие слабые столбцы при построении простой модели линейной регрессии.
Теперь у нас есть два столбца данных, на основе которых мы и будем строить нашу модель. Приступим к построению нашей модели.
Коэффициент X
Согласно определению, коэффициент x, также известный как уголь наклона (m) — отношение изменения Y к изменению X или, другими словами, крутизна линии
Формула:
Наклон = Изменение Y / Изменение X
Из алгебры помним, что наклон равен m в формуле
Y = M X + C
Наклон линейной регрессии m можно найти по формуле
Теперь мы знаем формулу и можем написать код наклона нашей модели.
double CSimpleLinearRegression::coefficient_of_X() { double m=0; double x_mean=mean(x_values); double y_mean=mean(y_values);; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<(ArraySize(x_values)+ArraySize(y_values))/2; i++) { x__x = x_values[i] - x_mean; //правая часть числителя (сторона x) y__y = y_values[i] - y_mean; //левая часть числителя (сторона y) numerator += x__x * y__y; //сумма произведений двух частей числителя denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
Обратите внимание на массивы y_values и x_values. Массивы инициализируются и копируются в функции Init() внутри класса CSimpleLinearRegression.
А вот функция CSimpleLinearRegression::Init():
void CSimpleLinearRegression::Init(double& x[], double& y[]) { ArrayCopy(x_values,x); ArrayCopy(y_values,y); //--- if (ArraySize(x_values)!=ArraySize(y_values)) Print(" Похоже, что массивы имеют разный размер. Это может привести к неточным вычислениям ",__FUNCTION__); int columns=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } columns++; if (FileIsLineEnding(m_handle)) { rows++; columns=0; } } m_rows = rows; m_columns = columns; FileClose(m_handle); //--- }
Мы написали код в части коэффициента X, перейдем к следующей части.
Y-Intercept
Y-intercept (пересечение Y) — это значение y при x равном нулю или значение y в котором линия пересекает ось y.

Находим y-intercept
В уравнении
Y = M X + C
переносим MX в левую часть уравнения, меняем местами, и получается вот такое уравнение x-intercept
C = Y - M X
где
Y = среднее значение всех значений y
x = среднее значение всех значений x
Теперь напишем функцию для поиска y-intercept
double CSimpleLinearRegression::y_intercept() { // c = y - mx return (mean(y_values)-coefficient_of_X()*mean(x_values)); }
Закончили с осью y, давайте теперь построим нашу модель линейной регрессии в основной функции LinearRegressionMain()
void CSimpleLinearRegression::LinearRegressionMain(double &predict_y[]) { double slope = coefficient_of_X(); double constant_y_intercept= y_intercept(); Print("The Linear Regression Model is "," Y =",DoubleToString(slope,2),"x+",DoubleToString(constant_y_intercept,2)); ArrayResize(predict_y,ArraySize(y_values)); for (int i=0; i<ArraySize(x_values); i++) predict_y[i] = coefficient_of_X()*x_values[i]+y_intercept(); //--- }
Модель также используется для прогноза значений y, это будет полезно в будущем, когда мы продолжим строить нашу модель и анализировать ее точность.
Далее вызовем функцию Onstart() внутри TestScript.mq5.
lr.LinearRegressionMain(y_nasdaq_predicted);
Результат вызова будет таким
2022.03.03 10:41:35.888 TestScript (#SP500,H1) The Linear Regression Model is Y =4.35241x+-4818.54986
void CSimpleLinearRegression::GetDataToArray(double &array[],string file_name,string delimiter,int column_number) { m_filename = file_name; m_delimiter = delimiter; int column=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } column++; //Получаем данные по каждому столбцу if (column==column_number) //если мы на определенном столбце, который нам нужен { ArrayResize(array,rows+1); if (rows==0) { if ((double(data))!=0) //на тот случай если в первой строке столбца в CSV указан заголовок столбца { array[rows]= NormalizeDouble((double)data,Digits()); } else { ArrayRemove(array,0,1); } } else { array[rows-1]= StringToDouble(data); } //Print("column ",column," "," Value ",(double)data); } //--- if (FileIsLineEnding(m_handle)) { rows++; column=0; } } FileClose(m_handle); }
Inside the void Function fileopen()
void CSimpleLinearRegression::fileopen(void) { m_handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV,m_delimiter); if (m_handle==INVALID_HANDLE) { Print("Данные для работы не найдены, Error = ",GetLastError()," ", __FUNCTION__); } //--- }
Теперь внутри TestScript для начала нужно объявить два массива
double s_p[]; //Массив для хранения значений S&P 500 double y_nasdaq[]; //Массив для хранения значений NASDAQ
Далее нужно передать эти массивы, чтобы получить ссылку на них из функции GetDataToArray() типа void
lr.GetDataToArray(s_p,file_name,",",1); lr.GetDataToArray(y_nasdaq,file_name,",",2);
Обратите внимание на номера столбцов, так как аргументы нашей функции выглядят так в public-части нашего класса.
void GetDataToArray(double& array[],string filename, string delimiter, int column_number);
Убедитесь, что вы ссылаетесь на правильный номер столбца. Вот так столбцы расположены в CSV-файле.
S&P500,NASDAQ,50SMA,13RSI 4377.5,14168.6,14121.1,59.3 4351.3,14053.2,14118.1,48.0 4342.6,14079.3,14117.0,50.9 4321.2,14038.1,14115.6,46.1 4331.8,14092.9,14114.6,52.5 4336.1,14110.2,14111.8,54.7 4331.5,14101.4,14109.4,53.8 4336.4,14096.8,14104.7,53.3 .....
После вызова функции GetDataToArray() можно вызывать функцию Init(), поскольку не имеет смысла инициализировать библиотеку без сбора и правильного хранения данных в соответствующих массивах. Вот таким будет правильный порядок вызова функции:
void OnStart() { string file_name = "NASDAQ_DATA.csv"; double s_p[]; double y_nasdaq[]; double y_nasdaq_predicted[]; lr.GetDataToArray(s_p,file_name,",",1); //Данные берутся из первого столбца и сохраняются в массиве s_p lr.GetDataToArray(y_nasdaq,file_name,",",2); //Данные берутся из второго столбца и сохраняются в массиве y_nasdaq //--- lr.Init(s_p,y_nasdaq); { lr.LinearRegressionMain(y_nasdaq_predicted); Print("slope of a line ",lr.coefficient_of_X()); } }
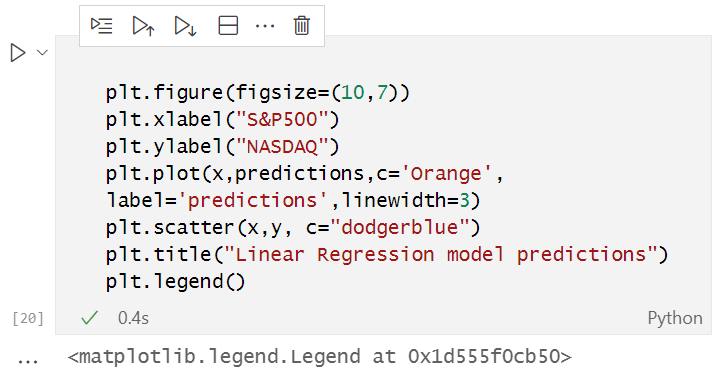
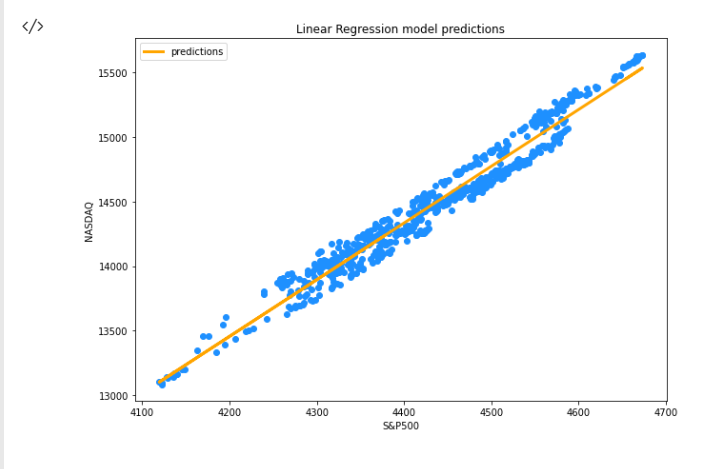
Мы получили прогнозные значения, которые хранятся в массиве y_nasdaq_predicted. Давайте теперь отобразим зависимую переменную (NASDAQ), независимую переменную(S&P500) и прогнозы на той же кривой.
Выполните код в блокноте Jupyter.
Полный код Python прилагается в конце статьи.
После запуска этого фрагмента кода вы должны увидеть вот такой график:
Теперь у нас в библиотеке есть модель и другие необходимые вещи. Что насчет точности нашей модели? Достаточно ли хороша наша модель, чтобы ее можно было где-то использовать?
Чтобы понять, насколько хорошо наша модель предсказывает целевую переменную, используем метрику, известную как коэффициент определителя, также называется R-квадрат.
R-квадрат
Это предположение о полной дисперсии y было объяснено моделью.
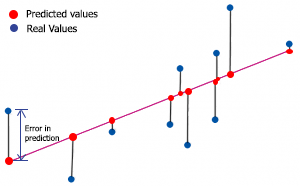
Чтобы найти r-квадрат, нужно понять ошибку в предсказании. Ошибка в предсказании — это разница между фактическим/реальным значением y и предсказанным значением y.
Математически
Ошибка = фактический Y - прогнозируемый Y
Формула R-квадрата
R-квадрат = 1 - (Сумма квадратов ошибок / Сумма квадратов остатков)
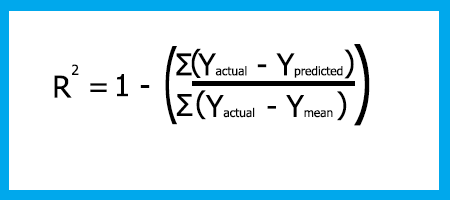
Почему используем квадрат ошибок?
- Ошибки могут быть положительными или отрицательными (выше или ниже линии), мы возводим их в квадрат, чтобы они все были положительными.
- Отрицательные значения могут уменьшать ошибку.
- Также возводим в квадрат ошибки, чтобы преувеличить большие ошибки.
Ноль означает, что модель не может объяснить любую дисперсию у, и указывает на то, что модель является наихудшей из возможных. Единица указывает на то, что модель способна объяснить всю дисперсию у в вашем наборе данных (такой модели не существует).
Результат r-квадрата можно рассматривать как процент, показывающий насколько хороша ваша модель. Ноль означает нулевую точность, а единица — 100-процентная точность модели.
Теперь давайте напишем код R-квадрата.
double CSimpleLinearRegression::r_squared() { double error=0; double numerator =0, denominator=0; double y_mean = mean(y_values); //--- if (ArraySize(m_ypredicted)==0) Print("Похоже, в массиве прогнозируемых значений нет данных. Вызовите основную функцию простой линейной регрессии перед использованием функции = ",__FUNCTION__); else { for (int i=0; i<ArraySize(y_values); i++) { numerator += MathPow((y_values[i]-m_ypredicted[i]),2); denominator += MathPow((y_values[i]-y_mean),2); } error = 1 - (numerator/denominator); } return(error); }
Внутри функции LinearRegressionMain, где мы сохранили прогнозные значения в массив predicted_y[], переданный по ссылке, нужно скопировать этот массив в массив глобальных переменных, объявленный в приватном разделе класса.
private: int m_handle; string m_filename; string m_delimiter; double m_ypredicted[]; double x_values[]; double y_values[];
В конец LinearRegressionMain я добавил строку для копирования этого массива в глобальный массив переменных m_ypredicted[].
//В конце функции LinearRegressionMain(double &predict_y[]) добавлена следующая строка: //Копируем прогнозные значения в m_ypredicted[], чтобы получить доступ внутри библиотеки ArrayCopy(m_ypredicted,predict_y);
Теперь выведем значение R-квадрата внутри TestScript
Print(" R_SQUARED = ",lr.r_squared());
The output will be:
2022.03.03 10:40:53.413 TestScript (#SP500,H1) R_SQUARED = 0.9590906984145334
Это все, что касается простой линейной регрессии. Теперь давайте посмотрим, как будет выглядеть множественная линейная регрессия.
Множественная линейная регрессия
Множественная линейная регрессия имеет одну независимую переменную и несколько зависимых.
Вот так выглядит формула модели множественной линейной регрессии:
Вот как выглядит наша библиотека после написания секций private и public нашего класса.
class CMultipleLinearRegression: public CSimpleLinearRegression { private: int m_independent_vars; public: CMultipleLinearRegression(void); ~CMultipleLinearRegression(void); double coefficient_of_X(double& x_arr[],double& y_arr[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[],double& C[],double& D[]); };
Поскольку мы будем работать с несколькими значениями, в этой части мы поиграем с большим количеством массивов с аргументами функций. Я не смог найти более короткую реализацию.
Создадим модель линейной регрессии для двух зависимых переменных с использованием этой функции.
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[]) { // Формула множественной регрессии = y = M1X1+M2X2+M3X3+...+C double constant_y_intercept=y_interceptforMultiple(Y,A,B); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); Print("Модель множественной регрессии ","Y="+DoubleToString(slope1,2)+"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(constant_y_intercept,2)); int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+constant_y_intercept; }
Переменная Y-intercept в данном варианте зависит от количества столбцов данных, с которыми мы решили поработать. После получения формулы из множественной линейной регрессии окончательная формула будет такой:
C = Y - M1 X1 - M2 X2
Так выглядит код
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[]) { //формула c=Y-M1X1-M2X2; return(mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)); }
При работе с тремя переменными нужно просто снова написать код функции, добавив еще одну переменную.
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[],double &C[],double &D[]) { double constant_y_intercept = y_interceptforMultiple(Y,A,B,C,D); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); double slope3 = coefficient_of_X(C,Y); double slope4 = coefficient_of_X(D,Y); //--- Print("Модель множественной регрессии ","Y="+DoubleToString(slope1,2),"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(slope3,2)+"C"+DoubleToString(slope4,2)+"D"+DoubleToString(constant_y_intercept,2)); //--- int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+slope3*C[i]+slope4*D[i]+constant_y_intercept; }
Для нашей множественной линейной регрессии Y-intercept будет такой.
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[],double &C[],double &D[]) { return (mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)-coefficient_of_X(C,Y)*mean(C)-coefficient_of_X(D,Y)*mean(D)); }
Допущения линейной регрессии
Модель линейной регрессии основана на наборе допущений. Если базовый набор данных не соответствует этим допущениям, возможно, данные придется преобразовать, иначе линейная модель может не подойти.
- Предположение о линейности. Предполагается линейная связь между зависимой/целевой переменной и независимыми/предикторными переменными.
- Предположение о нормальности распределения ошибок
- Должно быть нормальное распределение ошибок вместе с моделью
- Диаграмма разброса между фактическими значениями и прогнозируемыми значениями должна показывать данные, равномерно распределенные по модели.
Преимущества модели линейной регрессии
Простота реализации и интерпретации выходных данных и коэффициентов.
Недостатки
- Предполагается линейная связь между зависимыми и независимыми переменными, то есть предполагается, что между ними существует прямолинейная связь.
- Выбросы оказывают огромное влияние на регрессию
- Линейная регрессия предполагает независимость между атрибутами
- Линейная регрессия анализирует взаимосвязь между средним значением зависимой переменной и независимой переменной.
- Как среднее значение не является полным описанием одной переменной, линейная регрессия не является полным описанием взаимосвязей между переменными.
- Границы линейны
Заключительные мысли
Я думаю, что алгоритмы линейной регрессии могут быть очень полезны при создании торговых стратегий, основанных на корреляции пар и других вещах, таких как индикаторы, хотя наша библиотека далеко не закончена. Я не включал обучение и тестирование нашей модели и дальнейшее улучшение результатов. Это мы рассмотрим в следующей статье, так что следите за обновлениями. Поделюсь ссылкой на код на Python в моем Github-репозитории: ссылка. Любой вклад в библиотеку приветствуется, также не стесняйтесь делиться своими мыслями в комментариях.
До скорой встречи!
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/10459
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Разработка торгового советника с нуля (Часть 8): Концептуальный скачок (I)
Разработка торгового советника с нуля (Часть 8): Концептуальный скачок (I)
 Нейросети — это просто (Часть 15): Кластеризации данных средствами MQL5
Нейросети — это просто (Часть 15): Кластеризации данных средствами MQL5
 Индикаторы с интерактивным управлением на графике
Индикаторы с интерактивным управлением на графике
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования

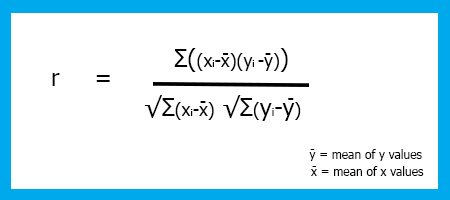
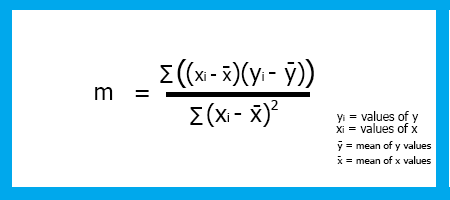
What is a Model
Модель - это не что иное, как суффикс.
Суффикс? Я не понимаю, что это значит.
Прежде чем открыть CSV-файл, созданный нашим тестовым скриптом, его нужно преобразовать в кодировку UTF-8, чтобы его мог прочитать python.
Зачем это нужно? Просто создайте файл данных в кодировке UTF-8 прямо из MQL.
Красное многоточие добавлено мной. Это неправильно, эта точка не является "y-интерцептом" и ее координаты не (0,-5).
Суффикс? Я не понимаю, что это значит.
Почему так? Просто создайте файл данных в формате UTF-8 прямо из MQL.
Красный эллипс добавлен мной. Это неправильно, эта точка не является "y-интерцептом" и ее координаты не (0,-5).
Под словом "суффикс" я подразумеваю математическое обозначение, например, y=mx+c - это модель.
Да, я понял, ошибся в изображении, другая точка должна была быть (-5,0), и она не является "y-intercept"
Здравствуйте, спасибо за краткую статью о линейной регрессии и ее возможностях.
Формула коэффициента Писсона имеет недостатки в знаменателе.
Здравствуйте, может он уже есть, просто я его не нашел, но где находится файл NASDAQ.csv, который используется в статье?