Адаптивные индикаторы

Введение

Наверное, каждый трейдер мечтал об индикаторе, который мог бы подстраиваться под текущую ситуацию на рынке. Чтобы он сам определял флэты и тренды, и мог бы учитывать актуальные изменения цены. В обычных технических индикаторах при обработке входного сигнала используются постоянные коэффициенты. И эти коэффициенты никак не зависят от характеристик входного сигнала и их изменений во времени.

Адаптивные индикаторы отличаются наличием обратной связи между значениями входных и выходного сигналов. Эта связь позволяет индикатору самостоятельно подстраиваться на оптимальную обработку значений финансового временного ряда. Если говорить совсем просто, то адаптивный индикатор – это обычный линейный индикатор, но его коэффициенты могут меняться со временем в зависимости от текущей рыночной ситуации.

Алгоритмы адаптации довольно разнообразны. Выбор конкретного алгоритма зависит от назначения индикатора. Но чаще всего, в основе этих алгоритмов лежат различные методы наименьших квадратов. Давайте на нескольких примерах посмотрим, как можно разработать адаптивный индикатор.

Первая попытка

Давайте попробуем создать адаптивный индикатор. Самый очевидный способ добиться адаптации индикатора – это тем или иным образом учитывать его последние ошибки. Давайте посмотрим, как это можно сделать.

Пусть, Indicator[i] – значение индикатора на i-ом баре. Тогда ошибка будет равна:  Error[i] = price[i] - Indicator[i].

Эту ошибку можно использовать для корректировки значений индикатора на следующем отсчете. Причем, мы можем обрабатывать ошибки по-разному. Например, можно взять среднее от нескольких последних ошибок, или применить к ним экспоненциальное сглаживание.

Давайте посмотрим, как такой подход будет выглядеть на графике. За основу возьмем шаблон из статьи про технические индикаторы. Но, внесем в него небольшие изменения. В первую очередь, зададим количество ошибок для

      double sum=0;
      for(int j=0; j<size; j++)
         sum=sum+coeff[j]*price[i+j];//Расчет значения индикатора

      if(i>0)
        {
        double cur_error=price[i]-sum;//Текущая ошибка
         if(NumErrors==0)
            cur_error=(error+cur_error)/2;
         if(NumErrors==1)
            error=cur_error/2;
         if(NumErrors>1)
           {
            for(int j=NumErrors-1; j>0; j--)
               errors[j]=errors[j-1];
            errors[0]=cur_error;

            cur_error=0;
            for(int j=0; j<NumErrors; j++)
               cur_error=cur_error+errors[j];
            error=cur_error/NumErrors;
           }
        }

      buffer[i]=sum+error;//Значение индикатора с учетом ошибки

Вот так будет выглядеть наш новый индикатор по сравнению с простой скользящей средней (красная линия).

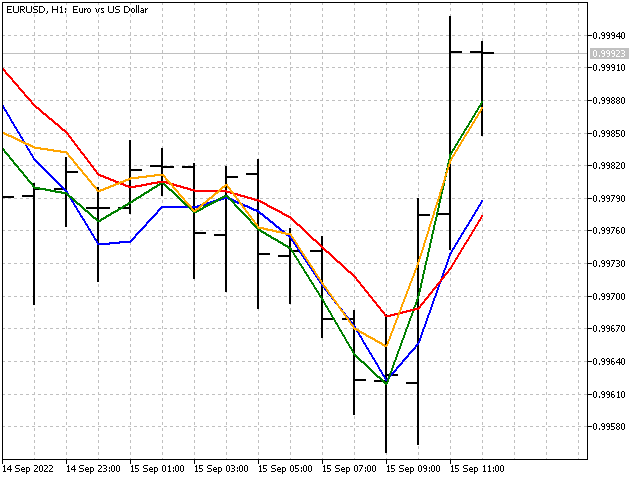
Картинка выглядит красиво, но является ли наш индикатор адаптирующимся? Ответ, увы, отрицательный. На самом деле у нас получился обычный линейный индикатор, но его весовые коэффициенты заданы неявным образом.

Возьмем для примера простую скользящую среднюю с периодом 3, и усреднением трех последних ошибок. Сначала рассчитаем ошибки:

Error[1] = price[1] - (price[1] + price[2] + price[3])/3

Error[2] = price[2] - (price[2] + price[3] + price[4])/3

Error[3] = price[3] - (price[3] + price[4] + price[5])/3

Тогда формула индикатора примет вид:

Indicator[0] = (price[0] + price[1] + price[2])/3+(Error[1] + Error[2] + Error[3])/3 =>

Indicator[0] = (3*price[0] + 5*price[1] + 4*price[2] + 0*price[3] - 2*price[4] - 1*price[5])/9

В результате мы получили обычный линейный индикатор. Из этого можно сделать простой вывод – только обработка ошибок не делает индикатор адаптивным.

Восход Солнца

Однажды Пьер-Симон Лаплас сформулировал задачу, которая стала известна как "проблема восхода солнца". Суть этой проблемы можно сформулировать так - если мы видели восход солнца в течение 1000 дней, то какова будет наша уверенность в том что солнце взойдет и в 1001 раз? Задача интересная и давайте посмотрим на неё с точки зрения трейдинга. Предположим, что вы совершили девять сделок, шесть из которых оказались прибыльными. Теперь, основываясь на этой информации попробуйте ответить на вопрос: какова вероятность прибыльной сделки?

Давайте рассуждать вместе. Как правило, вероятность определяется как отношение прибыльных сделок к их общему количеству:

В нашем примере вероятность в таком случае будет равна 6/9. Однако, мы сделаем шаг вперед – какова вероятность выигрыша для будущей сделки? Знаменатель дроби увеличится на единицу при любом исходе. А вот с числителем возможны два варианта – будущая сделка может оказаться и прибыльной, и убыточной. То есть, у нас есть два возможных варианта:

Возьмем среднее от этих значений. И тогда, наша оценка вероятности выигрыша у нас станет такой:

Что немного меньше первоначального значения в 6/9. Такой метод получил название "сглаживание Лапласа". Он может применяться для категориальных данных, когда переменные могут принимать несколько определенных значений ("успех – неудача" в нашем примере).

Давайте попробуем применить это сглаживание в индикаторе. Для этого мы сделаем одно небольшое допущение. Мы предположим, что в потоке цен есть еще одна скрытая цена (давайте назовем ее мнимой), которая будет так же влиять на показания индикатора.

Давайте посмотрим, как изменится формула индикатора в этом случае. Так выглядит формула простой скользящей средней:

А вот так будет выглядеть эта же средняя с мнимой ценой:

На первый взгляд всё выглядит прекрасно. Но, тут есть несколько неприятных моментов. Во-первых, сама мнимая цена будет неустойчивой:

Во-вторых, если мы переместим мнимую цену на следующий отсчет временного ряда, то наш индикатор упростится:

Это упрощение не помогло нам сделать индикатор устойчивым (коэффициент при price[1] равен 1). Однако, эта неудача может послужить основой для другого индикатора.

Сначала установим период индикатора iPeriod. Потом найдем значения SL для всех N со значениями от 1 до iPeriod. На следующем шаге нужно вычислить среднее от суммы всех SL. В результате у нас получится индикатор, показывающий устойчивое значение цены. Этот индикатор можно описать следующим образом: наивный прогноз (что было, то и будет), плюс немного ослабленный линейный тренд.

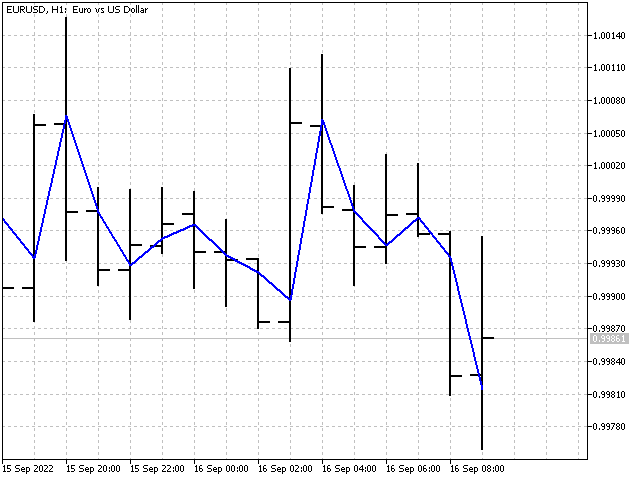
Что ж, индикатор у нас получился. Но, адаптации достичь так и не удалось. Еще одна попытка и снова фиаско. Давайте сделаем небольшой перерыв, а потом попытаемся все-таки создать адаптирующийся индикатор. Ну, или придется менять название статьи.

Закат Луны

Козьма Прутков однажды очень мудро заметил: "Если у тебя спрошено будет: что полезнее, солнце или месяц? – ответствуй: месяц. Ибо солнце светит днём, когда и без того светло; а месяц – ночью". Давайте посмотрим, как это изречение можно воплотить в мире трейдинга.

При сглаживании Лапласа мы использовали значения цен с одинаковыми весовыми коэффициентами. А что будет, если мы придадим ценам определенные веса? В оконных функциях весовые коэффициенты зависят от того, насколько далеко находится данный отсчет от весового центра индикатора. Сейчас мы поступим иначе. Сначала мы выберем определенное значение цены в качестве центрального. Оно будет иметь самый большой вес. Весовые коэффициенты остальных цен будут зависеть от того, насколько далеко находится цена от этого значения – чем дальше, тем меньше будет её вес. То есть, мы создадим оконную функцию не в области времени, а в области цены. Давайте посмотрим, как будет выглядеть такой алгоритм на практике.

      double value=price[i+center],//Значение цены в центре
             max=_Point;           //Максимальное отклонение
      for(int j=0; j<period; j++)//Считаем отклонения цен от центральной и макс. отклонение
        {
         weight[j]=MathAbs(value-price[i+j]);
         max=MathMax(max,weight[j]);
        }

      double width=(period+1)*max/period,//корректируем максимальное отклонение от центра, чтобы не было нолей на концах
             sum=0,
             denom=0;
      for(int j=0; j<period; j++)//рассчитаем весовые коэффициенты для каждой цены
        {
         if(Smoothing==Linear)//линейное сглаживание
            weight[j]=1-weight[j]/width;
         if(Smoothing==Quadratic)//степенное сглаживание
            weight[j]=1-MathPow(weight[j]/width,2);
         if(Smoothing==Exponential)//экспоненциальное сглаживание
            weight[j]=MathExp(-weight[j]/width);

         sum=sum+weight[j]*price[i+j];
         denom=denom+weight[j];
        }

      buffer[i]=sum/denom;//значение индикатора

Так выглядит наш индикатор на графике.

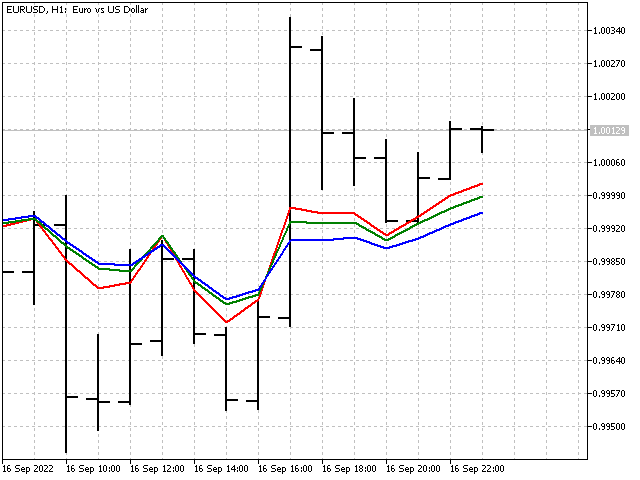
У этого индикатора весовые коэффициенты меняются. Но, назвать его адаптирующимся нельзя. Правильнее будет сказать, что этот индикатор подстраивается под текущую ситуацию на рынке. Адаптивный индикатор у нас не получился, но первый шаг к успеху мы сделали.

Вторая попытка

Возьмем за основу прямоугольную оконную функцию. Но, внесем в нее небольшие изменения – пусть коэффициенты в начале и в конце окна могут изменяться. Тогда формула индикатора будет выглядеть так:

Где, N – период индикатора, а C1 и C2 – адаптивные коэффициенты.

Предположим, что у нас уже есть значения этих коэффициентов. Появляется новое значение цены. И вместе с этим может измениться ошибка индикатора.

Для того чтобы уменьшить ошибку, нам нужно скорректировать каждый коэффициент на некоторую поправку R:

Само собой разумеется, что мы будем стремиться к тому, чтобы изменения коэффициентов свели ошибку индикатора к нулю. Но это будет не единственным условием. Давайте, дополнительно потребуем, чтобы поправки R также были небольшими. При соблюдении обоих условий мы можем надеяться на то, что значение адаптивных коэффициентов будут колебаться около некоторых оптимальных значений (если таковые имеются).

Итак, нам нужно найти решение следующей задачи:

Для нахождения поправок R мы воспользуемся методом наименьших квадратов. Тогда, вычисления можно сделать в несколько шагов. Сначала вычислим множитель сходимости:

Тогда, значения поправок будут равны: R = price*Error*M.

Соответственно, формулы для обновления коэффициентов будут такими:

Вот так будет выглядеть наш индикатор по сравнению с простой скользящей средней (красная линия).

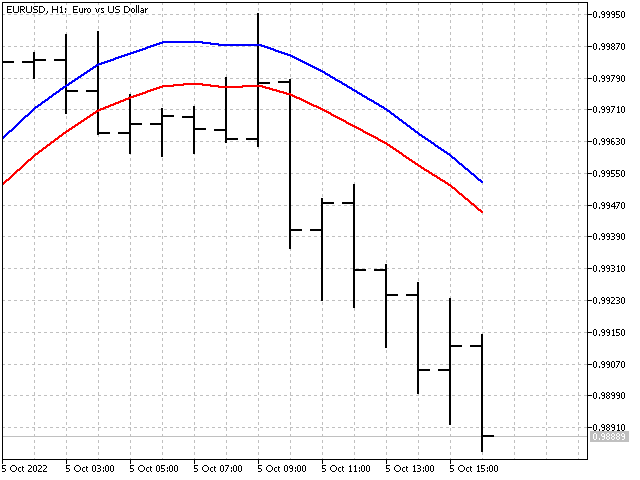
Адаптация

С двумя коэффициентами мы сумели справиться. А можно ли создать индикатор, у которого все коэффициенты будут адаптивными? Да, такой индикатор возможен. Расчеты коэффициентов такого индикатора похожи на те, что мы рассмотрели в предыдущем случае. Единственное отличие – расчет множителя сходимости:

Параметр P позволяет регулировать скорость изменения коэффициентов на каждом шаге. Его значение должно быть не меньше 1. При маленьком P коэффициенты индикатора очень быстро достигают оптимальных значений. Но, изменения коэффициентов индикатора могут оказаться чрезмерными. При большом значении P коэффициенты индикатора будут меняться медленно. То есть, чем больше P, тем более сглаженным будет индикатор. Например, так выглядят индикаторы с P = 1 и P = 1000.

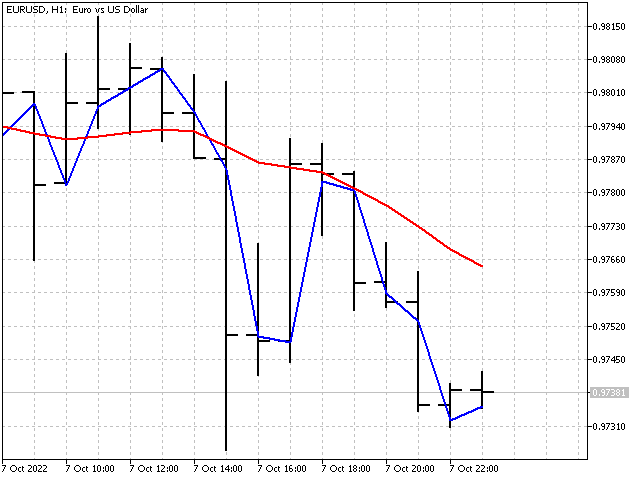
Общая рекомендация: сначала установите значение параметра равным периоду индикатора, а потом меняйте его в ту или другую сторону, пока не получите нужный результат.

Важной особенностью адаптивных индикаторов является их потенциальная неустойчивость. Сумма коэффициентов такого индикатора не равна единице, и может меняться в зависимости от входных данных. Возьмем для примера экспоненциальную среднюю. Классическая формула выглядит так:  .

А вот формула адаптивной EMA будет уже такой:  .

Причем, коэффициенты C1 и C2 не зависят друг от друга. Обновление коэффициентов происходит так же, как и в предыдущем индикаторе. Только при расчетах используются не только цены, но и предыдущие значения самого индикатора.

Тогда, обновленные коэффициенты будут равны:

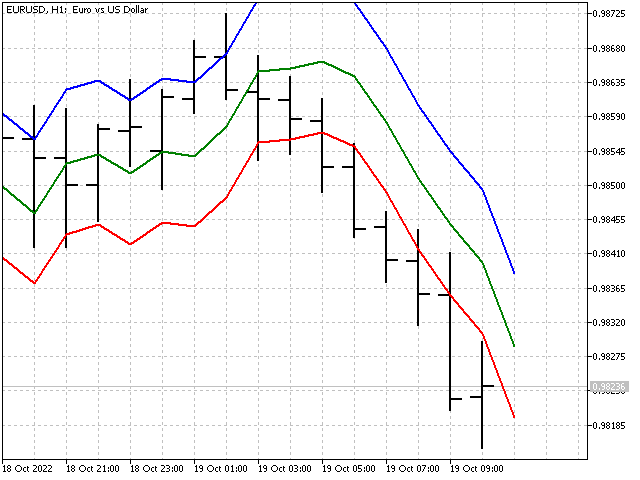
Сама адаптивная EMA с разными значениями параметра P выглядит так.

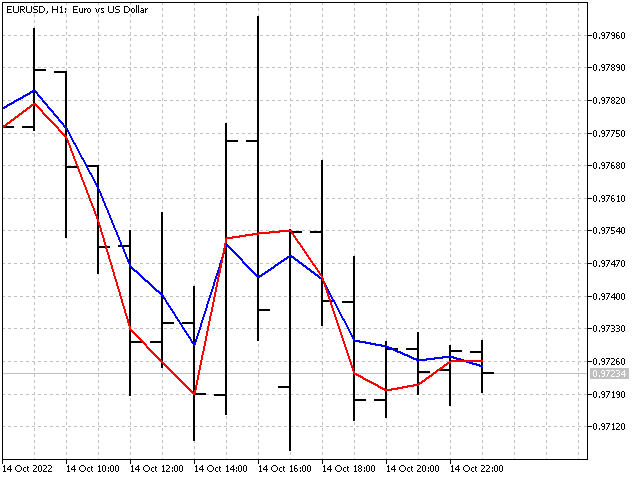
Алгоритмы адаптации можно применять и для оконных функций. Однако результат будет не таким впечатляющим, так как адаптация будет происходить за счёт изменения нормирующего коэффициента.

Возьмем за основу индикатор LWMA с периодом равным 5. Его формулу можно записать так:  .

Где, C – некоторый нормирующий коэффициент. В обычном случае значение этого коэффициента постоянно и его можно вычислить заранее. Сейчас же мы допустим возможность его изменения в ту или иную сторону.

Сначала нам нужно вычислить взвешенную сумму:  .

Тогда, уточненное значение нормирующего коэффициента можно найти по формуле:

Такой подход может оказаться полезным для индикаторов с маленьким периодом. При больших периодах влияние адаптации и параметра P будут практически незаметными.

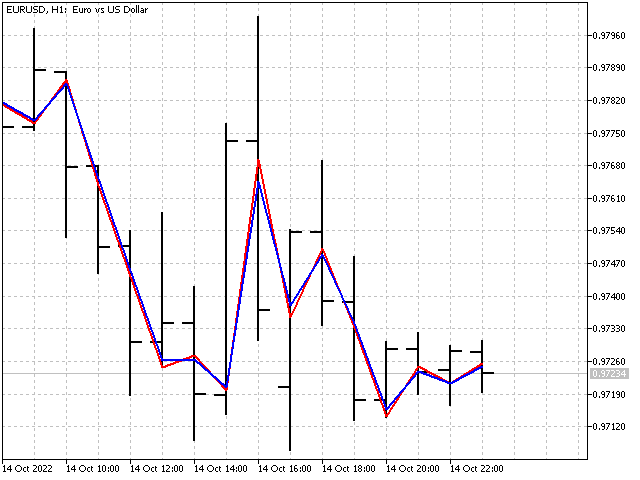
На основе адаптивных индикаторов можно создавать самые различные осцилляторы. Например, так выглядит адаптивный индикатор CCI.

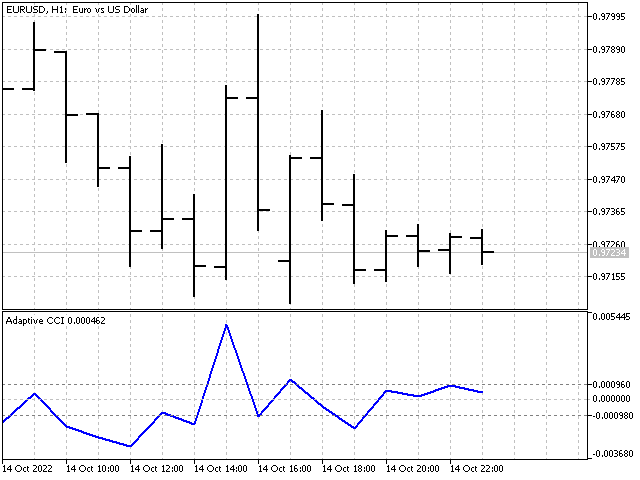
Линейное прогнозирование

Построение адаптивного индикатора во многом похоже на решение задачи линейного прогнозирования. Действительно, если в качестве ошибки мы будем использовать разность между значением индикатора и будущей (по отношению к самому индикатору) ценой, то адаптивный индикатор превратится в прогнозирующий.

Для примера возьмем цены open. Тогда формула индикатора и значение ошибки будут:

Все остальные вычисления выполняются по уже знакомым нам формулам. Единственное, что мы добавим в этот индикатор – вычисление средней ошибки прогноза. В результате мы получим прогнозное значение цены open для бара с индексом -1.

Линейное вероятностное прогнозирование

Задача линейного прогнозирования может быть выражена и через уравнение движения цены. В физическом мире всё выглядит довольно просто: если известно текущее положение точки, ее скорость и ускорение, то предсказать ее положение в следующий момент времени не составит большого труда. А вот с движением цены нам придется повозиться.

Значение цены нам известно. Скорость и ускорение – это, говоря языком математики, первая и вторая производные. Их мы заменим дискретным аналогом – разделенными разностями соответствующего порядка. Коэффициенты разделенных разностей можно взять из соответствующей строки треугольника Паскаля, нужно только попеременно менять знаки перед каждым коэффициентом. Так, мы получим:

1*open[0] -1*open[1] – дискретный аналог скорости;

1*open[0] -2*open[1] +1*open[2] – дискретный аналог ускорения.

Тогда уравнение движения цены можно выразить следующим образом:

open[0] + (open[0] – open[1]) + (open[0] – 2*open[1] + open[2]).

Добавим в это уравнение адаптивные коэффициенты и в итоге получим:

open[-1] = open[0] + c1*(open[0] – open[1]) + c2*(open[0] – 2*open[1] + open[2]).

Раскроем скобки и сгруппируем коэффициенты. Тогда, уравнение примет вид:

open[-1] = (1 + с1 + с2)*open[0] + (-c1 – 2*с2)*open[1] + c2*open[2].

Вспомним, что коэффициенты устойчивого индикатора должны лежать в пределах от -1 до +1. Тогда, нам нужно решить следующую систему неравенств:

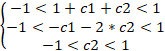
В результате мы получим три возможных варианта:

Теперь мы можем выбрать значения коэффициентов и использовать их в индикаторе.

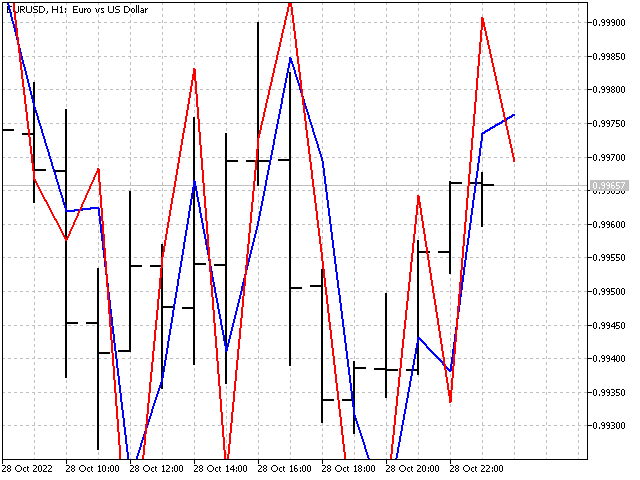
Конечно же, использование разностей более высоких порядков даст больше возможных вариантов и благоприятно отразится на внешнем виде индикатора.

Заключение

Применение алгоритмов адаптации позволяет получить довольно необычные индикаторы. Их главное преимущество - самостоятельная настройка под текущую рыночную ситуацию. А к недостаткам можно отнести увеличение числа управляющих параметров, подбор которых может потребовать некоторого времени. С другой стороны, адаптивные индикаторы могут изменяться в очень широком диапазоне, что может дать новые подходы в техническом анализе.