데이터 과학 및 기계 학습(파트 01): 선형 회귀
소개
불충분한 데이터로 성급한 이론을 만들려는 유혹은 우리의 골칫거리입니다.
"셜록 홈즈"
데이터 과학
은 과학적 방법, 프로세스, 알고리즘 및 시스템을 사용하여 정형 데이터와 비정형 데이터에서 지식과 통찰력을 추출하고 광범위한 영역에 걸쳐 데이터에서 해당 지식과 실행 가능한 통찰력을 적용하는 학제 간 분야입니다.
데이터 과학자는 프로그래밍 코드를 만들고 이를 통계적 지식과 결합하여 데이터에서 통찰력을 만드는 사람입니다.
이 기사 시리즈에서 무엇을 기대할 수 있을까요?
- 이론(수학 방정식에서와 같이): 이론은 데이터 과학에서 가장 중요합니다. 알고리즘을 심층적으로 알아야 하고 모델이 어떻게 작동하는지와 특정 방식으로 작동하는 이유를 알아야 합니다. 이를 이해하는 것이 알고리즘 자체를 코딩하는 것보다 훨씬 어렵습니다.
- MQL5 및 python의 실습 예제.
선형 회귀
종속 변수와 하나 이상의 독립 변수 간의 선형 관계를 찾는 데 사용되는 예측 모델입니다.
선형 회귀는 다음과 같은 많은 알고리즘에서 사용되는 핵심 알고리즘 중 하나입니다:
- 선형 회귀 기반 모델인 로지스틱 회귀
- Support Vector Machine, 이 유명한 데이터 과학 알고리즘은 선형 기반 모델입니다.
모델이란 무엇인가
모델은 접미사일 뿐입니다.
이론
그래프를 통과하는 모든 직선엔 방정식이 있습니다.
우리는 이 방정식을 어디서 얻을까요?
x와y 값이 같은 두 개의 데이터 세트가 있다고 가정합니다:
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
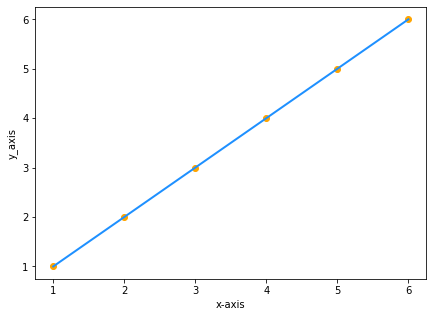
그래프에 값을 표시하면 다음과 같습니다:
y가 x와 같기 때문에 저 선의 방정식은y=x 가 될 것입니다. 맞지요? 틀립니다
그렇지만,
y = x는 수학적으로는 y = 1x와 동일합니다. 그러나 이것은 데이터 과학에서는 상당히 다른 것입니다. 선에 대한 공식은y=1x입니다. 여기서1은 선과 기울기라고도 하는x축사이에 형성된 각도입니다.
하지만,
기울기 = y의 변화 / x의 변화=m(m이라고 함)
이제 공식은 y = mx가 됩니다.
마지막으로 방정식에 상수, 즉 x가 0일 때 y값, 즉 선이 y축과 교차할 때 y 값을 추가해야 합니다.
그리고 마침내,
우리의 방정식은 y = mx + c가 될 것입니다(이것은 데이터 과학의 모델일 뿐입니다)
여기서 c는 y-절편입니다.
단순 선형 회귀
단순 선형 회귀에는 하나의 종속 변수와 하나의 독립 변수가 있습니다. 여기에서 우리는 예를 들어 단순 이동 평균의 변화에 따라 주가가 어떻게 변하는지와 같은 두 변수 간의 관계를 이해해보고자 합니다.
복잡한 데이터
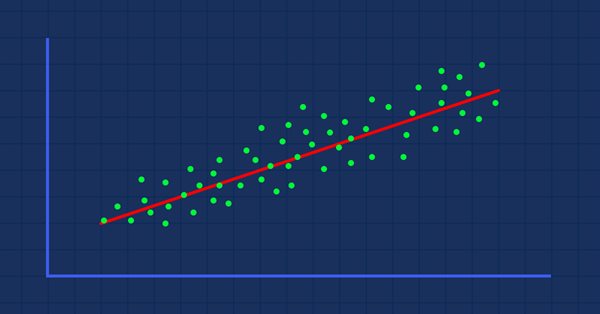
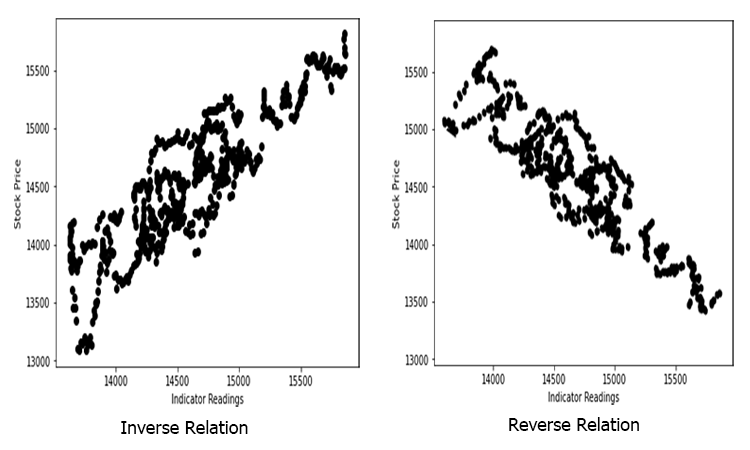
주가에 대해 그려질 때 무작위로 흩어져 있는 지표 값이 있다고 가정합니다(실생활에서 일어나는 일과 같이).
이 경우 지표/독립 변수는 주가/종속 변수에 대한 좋은 예측 변수가 아닐 수 있습니다.
데이터 세트에 적용해야 할 첫 번째 필터는 대상과 강하게 상관되지 않는 모든 열을 삭제하는 것입니다. 왜냐하면 이들은 선형 모델을 구축하는 것과 상관 없기 때문입니다
비선형 데이터로 선형 모델을 구축하는 것은 근본적으로 잘못된 실수입니다. 조심하세요!
관계는 역이 될 수 있지만 강력해야 합니다. 우리가 찾고자 하는 것은 선형 관계를 찾는 것이기 때문입니다.
그렇다면 독립변수와 목표 사이의 강도를 어떻게 측정해야 할까요? 우리는 상관 계수로 알려진 메트릭을 사용합니다.
상관 계수
이 기사에서 주요 예제로 사용할 데이터 세트를 생성하는 스크립트를 작성해 보겠습니다. 나스닥의 예측변수를 찾아봅시다.
input ENUM_TIMEFRAMES timeframe = PERIOD_H1; input int maperiod = 50; input int rsiperiod = 13; int total_data = 744; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { string file_name = "NASDAQ_DATA.csv"; string nasdaq_symbol = "#NQ100", s_p500_symbol ="#SP500"; //--- int handle = FileOpen(file_name,FILE_CSV|FILE_READ|FILE_WRITE,","); if (handle == INVALID_HANDLE) { Print("data to work with is nowhere to be found Err=",GetLastError()); } //--- MqlRates nasdaq[]; ArraySetAsSeries(nasdaq,true); CopyRates(nasdaq_symbol,timeframe,1,total_data,nasdaq); //--- MqlRates s_p[]; ArraySetAsSeries(s_p,true); CopyRates(s_p500_symbol,timeframe,1,total_data,s_p); //--- Moving Average Data int ma_handle = iMA(nasdaq_symbol,timeframe,maperiod,0,MODE_SMA,PRICE_CLOSE); double ma_values[]; ArraySetAsSeries(ma_values,true); CopyBuffer(ma_handle,0,1,total_data,ma_values); //--- Rsi values data int rsi_handle = iRSI(nasdaq_symbol,timeframe,rsiperiod,PRICE_CLOSE); double rsi_values[]; ArraySetAsSeries(rsi_values,true); CopyBuffer(rsi_handle,0,1,total_data,rsi_values); //--- if (handle>0) { FileWrite(handle,"S&P500","NASDAQ","50SMA","13RSI"); for (int i=0; i<total_data; i++) { string str1 = DoubleToString(s_p[i].close,Digits()); string str2 = DoubleToString(nasdaq[i].close,Digits()); string str3 = DoubleToString(ma_values[i],Digits()); string str4 = DoubleToString(rsi_values[i],Digits()); FileWrite(handle,str1,str2,str3,str4); } } FileClose(handle); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
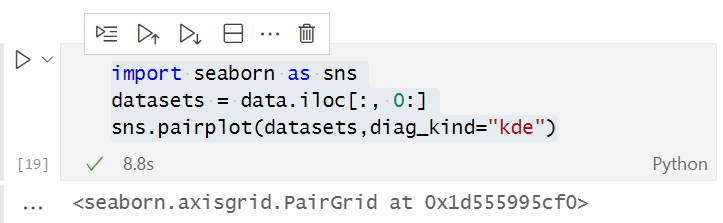
스크립트에서 우리는 NASDAQ 종가, 13 기간 RSI 값, S&P 500 및 50 기간의 이동 평균을 수집했습니다. CSV 파일로 데이터를 성공적으로 수집한 후 아나콘다가 설치되어 있지 않은 사용자를 위해 anaconda의 Jupyter 노트북에서 데이터를 파이썬으로 시각화해 보겠습니다.google colab에서 이 문서에 사용된 데이터 과학과 관련한 파이썬 코드를 실행할 수 있습니다.
테스트 스크립트로 생성된 CSV 파일을 열려면 먼저 UTF-8 인코딩으로 변환하여 파이썬에서 읽을 수 있도록 해야 합니다. 메모장으로 CSV 파일을 연 다음 인코딩을 UTF-8로 저장합니다. 해당 디렉토리에 연결할 때 python에서 별도로 읽을 수 있도록 외부 디렉토리에 파일을 복사하는 것이 좋습니다. pandas를 사용하여 CSV 파일을 읽고 데이터 변수에 저장해 보겠습니다.
csv 파일을 읽는 팬더
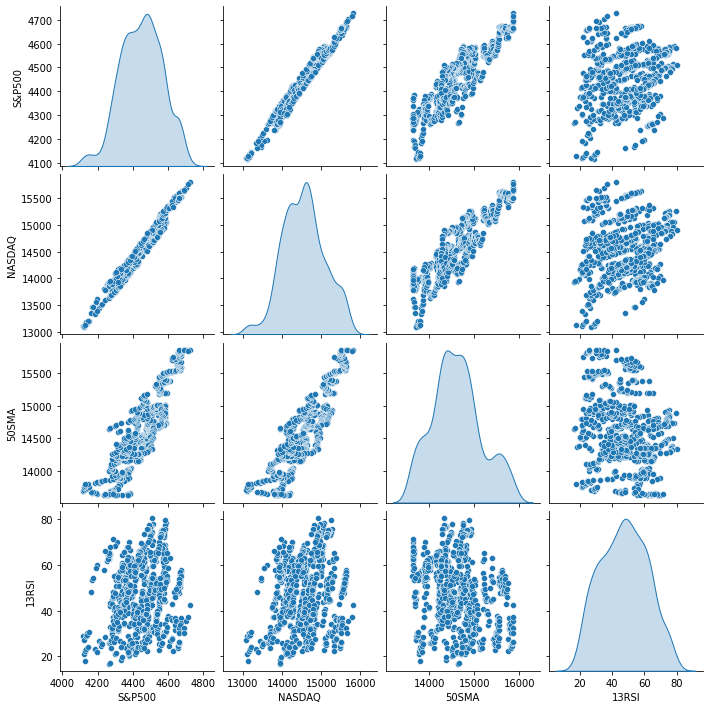
출력을 하면 다음과 같습니다:
데이터를 시각적으로 표현 했을때 우리는 이미 NASDAQ과 S&P 500 사이에 매우 강한 관계가 있고 NASDAQ과 50 기간 이동 평균 사이에 강한 관계가 있음을 알 수 있습니다. 앞서 말했듯이 선형 관계를 찾을 때 데이터가 그래프 전체에 흩어져 있으면 독립 변수는 타겟을 잘 예측하지 못할 수 있지만 숫자가 상관 관계에 대해 말헤 주는 것을 찾아 보고 숫자에 대한 결론을 도출하도록 해야 합니다. 변수가 서로 어떻게 상관 관계가 있는지 알아보기 위해 상관 계수라고 하는 메트릭을 사용합니다.
상관 계수
그렇다면 독립변수와 타겟 사이의 강도를 어떻게 측정할까요?
여러 유형의 상관 계수가 있지만 -1에서+1 사이의 범위를 가지며 Pearson의 상관 계수(R) 라고도 알려진 선형 회귀에 가장 널리 사용되는 상관 계수를 사용합니다.
-1과+1의 가능한 극한 값의 상관은 x와 y사이에 각각 완전한 음의 선형 및 완전한 양의 선형 관계를 나타내는 한편, 0(zero)의 상관은 선형 상관이 없음을 나타냅니다.
상관계수 공식/Pearson의 계수(R).
linearRegressionLib.mqh를 만들었습니다. 메인 라이브러리 안에corrcoef()함수를 코딩해 보겠습니다.
값과 관련한 평균 함수부터 시작해 보겠습니다. 평균은 모든 데이터의 합계를 해당 데이터의 총 요소 수로 나눈 것입니다.
double CSimpleLinearRegression::mean(double &data[]) { double x_y__bar=0; for (int i=0; i<ArraySize(data); i++) { x_y__bar += data[i]; // all values summation } x_y__bar = x_y__bar/ArraySize(data); //total value after summation divided by total number of elements return(x_y__bar); }이제 Pearson의 r 코드를 작성할 수 있습니다.
double CSimpleLinearRegression::corrcoef(double &x[],double &y[]) { double r=0; double numerator =0, denominator =0; double x__x =0, y__y=0; for(int i=0; i<ArraySize(x); i++) { numerator += (x[i]-mean(x))*(y[i]-mean(y)); x__x += MathPow((x[i]-mean(x)),2); //summation of x values minus it's mean squared y__y += MathPow((y[i]-mean(y)),2); //summation of y values minus it's mean squared } denominator = MathSqrt(x__x)*MathSqrt(y__y); //left x side of the equation squared times right side of the equation squared r = numerator/denominator; return(r); }
TestSript.mq5에서 결과를 프린트하면
Print("Correlation Coefficient NASDAQ vs S&P 500 = ",lr.corrcoef(s_p,y_nasdaq)); Print("Correlation Coefficient NASDAQ vs 50SMA = ",lr.corrcoef(ma,y_nasdaq)); Print("Correlation Coefficient NASDAQ Vs rsi = ",lr.corrcoef(rsi,y_nasdaq));
출력은 다음과 같을 것입니다.
상관 계수 NASDAQ vs S&P 500 = 0.9807093773142763
상관 계수 NASDAQ vs 50SMA = 0.8746579124626006
상관 계수 NASDAQ vs rsi = 0.24245225451004537
NASDAQ과 S&P500은 다른 모든 데이터 열과 매우 강한 상관 관계를 가지고 있음을 알 수 있습니다(상관 계수가 1에 매우 가깝기 때문에). 따라서 우리의 간단한 선형 회귀 모델을 만들어갈 때 다른 약한 열을 버려야 합니다.
이제 모델을 구축할 두 개의 데이터 열이 있습니다. 이제 모델 구축을 계속하겠습니다.
X 계수
기울기(m)라고도 하는 x 계수는 정의에 따라 Y의 변화와 X의 변화 비율, 즉 선의 기울기입니다.
공식:
기울기 = Y의 변화 / X의 변화
Algebra에서 기울기가 공식에서m임을 기억하십시오.
Y = M X + C
선형 회귀 기울기m을 찾으려면 공식은 다음과 같습니다.
이렇게 공식을 확인했습니다. 이제 모델의 기울기를 코딩해 봅시다.
double CSimpleLinearRegression::coefficient_of_X() { double m=0; double x_mean=mean(x_values); double y_mean=mean(y_values);; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<(ArraySize(x_values)+ArraySize(y_values))/2; i++) { x__x = x_values[i] - x_mean; //right side of the numerator (x-side) y__y = y_values[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
y_values및x_values배열에 주의하십시오. 이것은Init()함수 내부에서 초기화되고 복사된 배열입니다. 내부CSimpleLinearRegression.
다음은CSimpleLinearRegression::Init()함수입니다.
void CSimpleLinearRegression::Init(double& x[], double& y[]) { ArrayCopy(x_values,x); ArrayCopy(y_values,y); //--- if (ArraySize(x_values)!=ArraySize(y_values)) Print(" Two of your Arrays seems to vary In Size, This could lead to inaccurate calculations ",__FUNCTION__); int columns=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } columns++; if (FileIsLineEnding(m_handle)) { rows++; columns=0; } } m_rows = rows; m_columns = columns; FileClose(m_handle); //--- }
X 계수의 코딩을 완료했습니다. 이제 다음 부분으로 이동하겠습니다.
Y절편
앞에서 말했듯이 Y절편은 x의 값이 0일 때 y의 값입니다. 혹은 선이 y축을 자를 때 y의 값입니다.

y-절편 찾기
아래 방정식에서
Y = M X + C
MX를 방정식의 왼쪽으로 가져오고 방정식의 왼쪽과 오른쪽을 뒤집으면 x절편에 대한 최종 방정식은 다음과 같습니다.
C = Y - M X
여기서
Y = 모든 y 값의 평균
x = 모든 x 값의 평균
이제y절편을 찾는 함수의 코드를 작성해 보겠습니다.
double CSimpleLinearRegression::y_intercept() { // c = y - mx return (mean(y_values)-coefficient_of_X()*mean(x_values)); }
y-절편이 완료되었으므로 Main 함수LinearRegressionMain()에서 인쇄하여 선형 회귀 모델을 빌드해 보겠습니다.
void CSimpleLinearRegression::LinearRegressionMain(double &predict_y[]) { double slope = coefficient_of_X(); double constant_y_intercept= y_intercept(); Print("The Linear Regression Model is "," Y =",DoubleToString(slope,2),"x+",DoubleToString(constant_y_intercept,2)); ArrayResize(predict_y,ArraySize(y_values)); for (int i=0; i<ArraySize(x_values); i++) predict_y[i] = coefficient_of_X()*x_values[i]+y_intercept(); //--- }
우리는 또한 우리의 모델을 사용하여 예측된 y 값을 얻고 있습니다. 이는 나중에 모델을 계속 구축하고 정확성을 분석할 때 도움이 될 것입니다.
TestScript.mq5 내부의 Onstart()함수에서 함수를 호출해 보겠습니다.
lr.LinearRegressionMain(y_nasdaq_predicted);
출력을 하면 다음과 같을 것입니다.
2022.03.03 10:41:35.888 TestScript(#SP500,H1) 선형 회귀 모델은 Y =4.35241x+-4818.54986입니다.
void CSimpleLinearRegression::GetDataToArray(double &array[],string file_name,string delimiter,int column_number) { m_filename = file_name; m_delimiter = delimiter; int column=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } column++; //Get data by each Column if (column==column_number) //if we are on the specific column that we want { ArrayResize(array,rows+1); if (rows==0) { if ((double(data))!=0) //Just in case the first line of our CSV column has a name of the column { array[rows]= NormalizeDouble((double)data,Digits()); } else { ArrayRemove(array,0,1); } } else { array[rows-1]= StringToDouble(data); } //Print("column ",column," "," Value ",(double)data); } //--- if (FileIsLineEnding(m_handle)) { rows++; column=0; } } FileClose(m_handle); }
void함수fileopen()의 내부
void CSimpleLinearRegression::fileopen(void) { m_handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV,m_delimiter); if (m_handle==INVALID_HANDLE) { Print("Data to work with is nowhere to be found, Error = ",GetLastError()," ", __FUNCTION__); } //--- }
이제TestScript 에서 가장 먼저 해야 할 일은 두 개의 배열을 선언하는 것입니다.
double s_p[]; //Array for storing S&P 500 values double y_nasdaq[]; //Array for storing NASDAQ values
다음으로 해야 할 일은 해당 배열을 전달하여 GetDataToArray()void 함수에서 참조를 가져오는 것입니다.
lr.GetDataToArray(s_p,file_name,",",1); lr.GetDataToArray(y_nasdaq,file_name,",",2);
함수의 인수가 클래스의 퍼블릭 섹션에서 다음과 같이 표시되므로 열 번호에 주의하십시오.
void GetDataToArray(double& array[],string filename, string delimiter, int column_number);
올바른 열 번호를 참조하는지 확인하십시오. CSV 파일에서 열이 정렬되는 방식을 볼 수 있듯이
S&P500,NASDAQ,50SMA,13RSI 4377.5,14168.6,14121.1,59.3 4351.3,14053.2,14118.1,48.0 4342.6,14079.3,14117.0,50.9 4321.2,14038.1,14115.6,46.1 4331.8,14092.9,14114.6,52.5 4336.1,14110.2,14111.8,54.7 4331.5,14101.4,14109.4,53.8 4336.4,14096.8,14104.7,53.3 .....
GetDataToArray()함수를 호출한 후에는Init()함수를 호출해야 합니다. 데이터를 적절하게 수집하고 배열에 저장하지 않은 채 라이브러리를 초기화하는 것은 의미가 없기 때문입니다. 함수를 적절한 순서로 호출하면 다음과 같습니다.
void OnStart() { string file_name = "NASDAQ_DATA.csv"; double s_p[]; double y_nasdaq[]; double y_nasdaq_predicted[]; lr.GetDataToArray(s_p,file_name,",",1); //Data is taken from the first column and gets stored in the s_p Array lr.GetDataToArray(y_nasdaq,file_name,",",2); //Data is taken from the second column and gets stored in the y_nasdaq Array //--- lr.Init(s_p,y_nasdaq); { lr.LinearRegressionMain(y_nasdaq_predicted); Print("slope of a line ",lr.coefficient_of_X()); } }
이제 예측값이y_nasdaq_predicted배열에 저장되었으므로 종속변수(NASDAQ), 독립변수(S&P500) 및 동일한 곡선에 대한 prediction을 시각화해 보겠습니다.
Jupyter 노트북에서 다음 코드를 실행합니다.
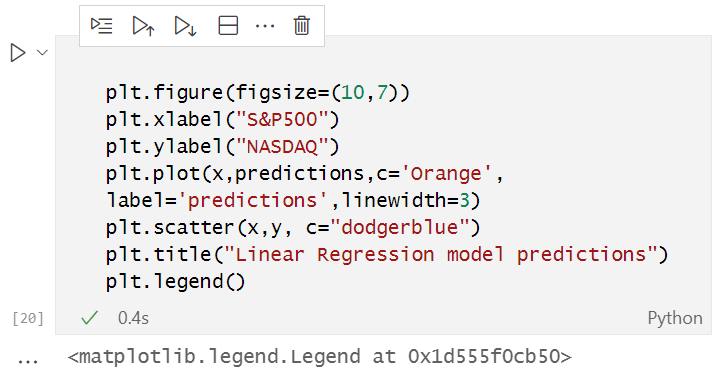
파이썬 코드의 전체는 기사의 끝에 첨부되어 있습니다.
위의 코드 조각을 성공적으로 실행하면 다음과 같은 그래프가 표시됩니다.
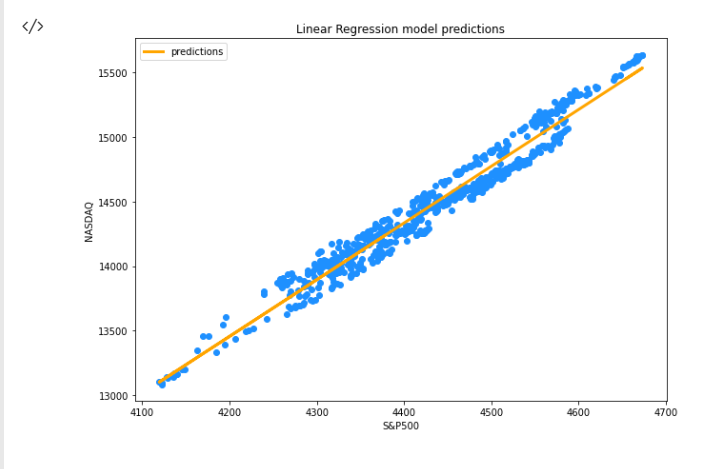
이제 모델이 라이브러리에서 진행 중입니다. 모델의 정확도는 어떻습니까? 우리의 모델이 의미가 있거나 사용하기에 충분히 좋은가요?
우리의 모델이 목표 변수를 얼마나 잘 예측하는지 이해하기 위해 R-제곱 이라고 하는결정 계수로알려진 메트릭을 사용합니다.
R-제곱
이것은 모델에 의해 설명된 y의 총 분산의 명제입니다.
r-제곱을 찾으려면 예측 오류를 이해해야 합니다. 예측 오차는 y의 사실상/실제 값과 y의 예측 값 간의 차이입니다.
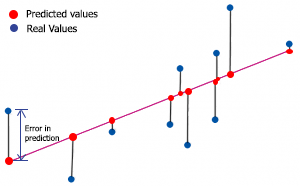
수학적으로,
오류 = 실제 Y - 예측 Y
R-제곱 공식은
Rsquared = 1 - (오차 제곱의 총합 / 잔차 제곱의 총합)
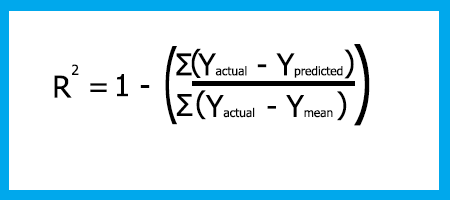
왜 제곱 오차일까요?
- 오류는 양수 또는 음수일 수 있습니다(선 위 또는 아래). 양수를 유지하기 위해 제곱합니다.
- 음수 값은 오류를 줄일 수 있습니다.
- 우리는 또한 오차를 제곱하여 큰 오차에 페널티를 부여하여 가능한 가장 잘 맞는 결과를 얻을 수 있습니다.
0은 모델이 가능한 최악의 모델임을 나타내며 y 의 분산을 설명할 수 없음을 의미하고 1 은 모델이 데이터 세트에서 y의 모든 분산을 설명할 수 있음을 나타냅니다. (이러한 모델은 존재하지 않습니다).
r-제곱 출력은 모델이 얼마나 좋은지를 나타내 주는 척도로 볼 수 있습니다. 백분율 0은 0 % 정확도를 의미하고1은 모델이 100% 정확함을 의미합니다.
이제 R 제곱을 코딩해 보겠습니다.
double CSimpleLinearRegression::r_squared() { double error=0; double numerator =0, denominator=0; double y_mean = mean(y_values); //--- if (ArraySize(m_ypredicted)==0) Print("The Predicted values Array seems to have no values, Call the main Simple Linear Regression Funtion before any use of this function = ",__FUNCTION__); else { for (int i=0; i<ArraySize(y_values); i++) { numerator += MathPow((y_values[i]-m_ypredicted[i]),2); denominator += MathPow((y_values[i]-y_mean),2); } error = 1 - (numerator/denominator); } return(error); }
참조로 전달된 predict_y[] 배열에 예측 값을 저장한 LinearRegressionMain 내부에서 해당 Array를 클래스의 private 섹션에 선언된 전역 변수 배열에 복사해야 합니다.
private: int m_handle; string m_filename; string m_delimiter; double m_ypredicted[]; double x_values[]; double y_values[];
LinearRegressionMain의 끝에 해당 배열을 전역 변수 배열 m_ypredicted[]에 복사하는 행을 추가했습니다.
//At the end of the function LinearRegressionMain(double &predict_y[]) I added the following line, // Copy the predicted values to m_ypredicted[], to be Accessed inside the library ArrayCopy(m_ypredicted,predict_y);
이제TestScript 내부에 R-제곱 값을 프린트해 보겠습니다.
Print(" R_SQUARED = ",lr.r_squared());
출력은 다음과 같습니다.
2022.03.03 10:40:53.413 TestScript (#SP500,H1) R_SQUARED = 0.9590906984145334
여기까지가 단순 선형 회귀입니다. 이제 다중 선형 회귀가 어떻게 생겼는지 살펴보겠습니다.
다중 선형 회귀
다중 선형 회귀에는 하나의 독립 변수와 둘 이상의 종속 변수가 있습니다.
다중 선형 회귀 모델의 공식은 다음과 같습니다.
이것이 우리의 라이브러리의 모양인데 클래스의 private 및 public 섹션을 하드 코딩한 후의 모양입니다.
class CMultipleLinearRegression: public CSimpleLinearRegression { private: int m_independent_vars; public: CMultipleLinearRegression(void); ~CMultipleLinearRegression(void); double coefficient_of_X(double& x_arr[],double& y_arr[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[],double& C[],double& D[]); };
우리는 여러 개의 값을 다룰 것이기 때문에 이 부분은 함수 Arguments의 많은 참조 배열을 다룰 부분이기도 합니다. 저는 이에 대한 지름길을 찾지 못했습니다.
두 개의 종속 변수에 대한 선형 회귀 모델을 생성하기 위해 우리는 이 함수를 사용할 것입니다.
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[]) { // Multiple regression formula = y = M1X1+M2X2+M3X3+...+C double constant_y_intercept=y_interceptforMultiple(Y,A,B); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2)+"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(constant_y_intercept,2)); int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+constant_y_intercept; }
이 인스턴스의 Y 절편은 작업하기로 결정한 데이터 열의 수를 기반으로 합니다. 다중 선형 회귀에서 공식을 유도한 후 최종 공식은 다음과 같을 것입니다:
C = Y - M1 X1 - M2 X2
코딩 후 모습입니다.
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[]) { //formula c=Y-M1X1-M2X2; return(mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)); }
변수가 3개인 경우 함수를 다시 하드 코딩하고 다른 변수를 추가하는 것이 문제라면 문제였습니다.
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[],double &C[],double &D[]) { double constant_y_intercept = y_interceptforMultiple(Y,A,B,C,D); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); double slope3 = coefficient_of_X(C,Y); double slope4 = coefficient_of_X(D,Y); //--- Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2),"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(slope3,2)+"C"+DoubleToString(slope4,2)+"D"+DoubleToString(constant_y_intercept,2)); //--- int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+slope3*C[i]+slope4*D[i]+constant_y_intercept; }
우리의 다중 선형 회귀에 대한 상수/Y 절편은 전에 말했듯이 다음과 같이 될 것입니다.
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[],double &C[],double &D[]) { return (mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)-coefficient_of_X(C,Y)*mean(C)-coefficient_of_X(D,Y)*mean(D)); }
선형 회귀 가정
선형 회귀 모델은 일련의 가정을 기반으로 합니다. 기본 데이터 세트가 이러한 가정을 충족하지 않으면 데이터를 변환해야 하거나 선형 모델이 적합하지 않을 수도 있습니다.
- 선형성 가정, 종속/목표 변수와 독립/예측 변수 간의 선형 관계를 가정합니다.
- 오차 분포의 정규성을 가정합니다.
- 오차는 모델을 따라 정규 분포를 따라야 합니다.
- 실제 값과 예측 값 사이의 산점도는 모델 전체에 균등하게 분포된 데이터를 보여야 합니다.
선형 회귀 모델의 장점
구현이 간단하고 출력과 계수를 더 쉽게 해석할 수 있습니다.
단점
- 종속 변수와 독립 변수 사이에 선형 관계를 가정합니다. 즉, 그들 사이에 직선 관계가 있다고 가정합니다.
- 이상치는 회귀에 큰 영향을 미칩니다.
- 선형 회귀는 속성 간의 독립성을 가정합니다.
- 선형 회귀는 종속 변수의 평균과 독립 변수 간의 관계를 중요시 합니다.
- 평균이 단일 변수에 대한 완전한 설명이 아닌 것처럼 선형 회귀는 변수 간의 관계에 대한 완전한 설명이 아닙니다.
- 경계는 선형입니다.
마침말
선형 회귀 알고리즘은 쌍의 상관 관계 및 지표와 같은 기타 항목을 기반으로 하는 트레이딩 전략을 만들 때 매우 유용할 수 있다고 생각합니다. 하지만 우리의 라이브러리는 완성된 라이브러리가 아닙니다. 우리 모델에 대한 추가적인 교육 및 테스트와 결과에 관한 추가적인 개선은 포함하지 않았습니다. 그 부분은 다음 기사에 있습니다. 계속 지켜봐 주십시오. 저의 Github 저장소에 파이썬 코드가 링크되어 있습니다. 무엇이든 라이브러리에 기여를 해 주신다면 감사하겠습니다. 또한 기사의 토론 섹션에서 자유롭게 생각을 공유 해 주시기 바랍니다.
다시 뵙겠습니다.
MetaQuotes 소프트웨어 사를 통해 영어가 번역됨
원본 기고글: https://www.mql5.com/en/articles/10459
경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.
이 글은 사이트 사용자가 작성했으며 개인의 견해를 반영합니다. Metaquotes Ltd는 제시된 정보의 정확성 또는 설명 된 솔루션, 전략 또는 권장 사항의 사용으로 인한 결과에 대해 책임을 지지 않습니다.
 스토캐스틱으로 거래 시스템 설계 하는 방법 알아보기
스토캐스틱으로 거래 시스템 설계 하는 방법 알아보기
 MACD을 기반으로 한 거래 시스템을 설계하는 방법 배우기
MACD을 기반으로 한 거래 시스템을 설계하는 방법 배우기
 데이터 과학 및 기계 학습(파트 02): 로지스틱 회귀
데이터 과학 및 기계 학습(파트 02): 로지스틱 회귀
 하나의 차트에 여러개의 지표 넣기(파트 06): MetaTrader 5를 RAD 시스템으로 전환하기(II)
하나의 차트에 여러개의 지표 넣기(파트 06): MetaTrader 5를 RAD 시스템으로 전환하기(II)

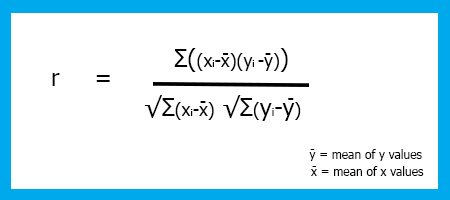
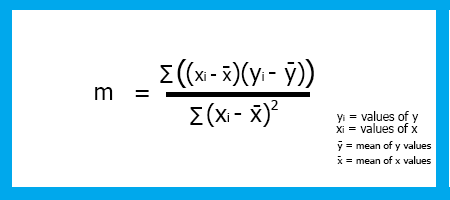
What is a Model
모델은 접미사에 불과합니다.
접미사라고요? 무슨 뜻인지 모르겠네요.
테스트 스크립트로 만든 CSV 파일을 열려면 먼저 파이썬에서 읽을 수 있도록 UTF-8 인코딩으로 변환해야 합니다.
왜 그럴까요? MQL에서 직접 UTF-8 데이터 파일을 만들기만 하면 됩니다.
제가 추가한 빨간색 타원입니다. 이 점은 "Y-절편"이 아니며 좌표가 (0,-5)가 아닙니다.
접미사? 무슨 뜻인지 모르겠네요.
왜 그럴까요? MQL에서 직접 UTF-8 데이터 파일을 만들면 됩니다.
제가 추가한 빨간색 타원입니다. 이 점은 "y-절편"이 아니며 좌표가 (0,-5)가 아닙니다.
접미사라는 단어는 수학적 표기법을 의미합니다. 예를 들어 y=mx+c 이것은 모델입니다.
네, 이미지에서 다른 점이 (-5,0)이어야 하는데 실수했고 "y-절편"이 아닙니다.
안녕하세요, 선형 회귀와 그 가능성에 대한 간결한 글에 감사드립니다.
피손 계수 공식은 분모에 결함이 있습니다.
안녕하세요, 아마 거기에 있을지도 모르지만 제가 찾지 못했을 뿐인데 기사에 사용된 NASDAQ.csv 파일은 어디에 있나요?