Возможности Мастера MQL5, которые вам нужно знать (Часть 45): Обучение с подкреплением с помощью метода Монте-Карло

Введение

Мы продолжаем рассматривать обучение с подкреплением. В этой статье мы рассмотрим алгоритм Монте-Карло. Алгоритм очень похож на Q-обучение и SARSA, поскольку он может как соответствовать политике (on-policy), так и быть вне ее (off-policy). Алгоритм отличается акцентом на эпизоды (episods). Это способ пакетирования обновлений циклов обучения с подкреплением, представленных в статье, чтобы обновление Q-значений Q-карты происходит реже.

При использовании алгоритма Монте-Карло Q-значения обновляются только после завершения эпизода. Эпизод — это серия циклов. В этой статье мы присвоили этому количеству циклов входной параметр m_episodes_size. Его можно оптимизировать или настраивать. Метод Монте-Карло считается достаточно устойчивым к изменчивости рынка, поскольку он может лучше моделировать широкий спектр возможных рыночных сценариев, позволяя трейдерам определять, как работают различные стратегии в различных условиях. Эта изменчивость помогает трейдерам понимать потенциальные компромиссы, риски и доходность, что позволяет им принимать более обоснованные решения.

Утверждается, что это преимущество обусловлено "долгосрочным пониманием эффективности", что контрастирует с традиционными методами, которые, как правило, фокусируются на краткосрочных результатах. Под этим подразумевается, что нечастые (один раз за эптзод) обновления, выполняемые моделированием Монте-Карло, позволяют избежать рыночного шума, с которым неизбежно сталкиваются Q-обучение и SARSA, поскольку в их случае обновления происходят чаще. Таким образом, метод Монте-Карло стремится достичь оценки долгосрочной эффективности торговых стратегий путем оценки накопленных с течением времени выгод. Анализируя многочисленные эпизоды, трейдеры могут получить представление об общей прибыльности и устойчивости своих стратегий.

Алгоритм Монте-Карло вычисляет оценки действия-ценности (action-value) на основе средней доходности пар состояние-действие (state-action) в течение нескольких циклов в пределах одного эпизода. Это позволяет трейдерам лучше оценить, какие действия (например, покупка или продажа) с наибольшей вероятностью принесут благоприятные результаты на основе исторических данных. Это обновление Q-значений обусловлено тем, что компонент вознаграждения этих Q-значений определяется следующим образом:

где:

• R t+1 , R t+2 ,…,R T — вознаграждения, полученные на каждом шаге после времени t.
• γ /гамма - это коэффициент дисконтирования (discount factor) (0 ≤ γ ≤ 1), который устанавливает, насколько будущие вознаграждения "дисконтируются" (оцениваются ниже, чем немедленные вознаграждения).
• T - временной шаг, на котором заканчивается эпизод (конечное состояние или размер эпизода в циклах).

Эти общие соображения о вознаграждении, вытекающие из обновления Q-значений, указанных выше, как правило, делают Монте-Карло более адаптируемым алгоритмом, как уже упоминалось выше. Эта способность к адаптации позволяет трейдерам корректировать свои стратегии в зависимости от меняющихся рыночных условий. Такая способность к адаптации имеет решающее значение на финансовых рынках, где тренды могут быстро меняться, а прошлые показатели не всегда могут предсказать будущие результаты. В последней статье об обучении с подкреплением, посвященной SARSA, мы рассматривали обучение с подкреплением как независимую модель, обученную прогнозировать поведение цен, а не просто помогать в обучении других моделей машинного обучения, как это было бы, если бы мы рассматривали его как третью форму обучения помимо обучения с учителем и без. В этой статье мы придерживаемся аналогичного подхода.

Таким образом, стратегии, которые можно было бы адаптировать в рамках метода Монте-Карло, во многом будут определяться выбором Q-карт и состояниями. В последней статье, поскольку алгоритм обучения с подкреплением также был основной моделью прогнозирования для советника посредством пользовательского класса сигналов, мы использовали 3 состояния среды, пересекающиеся через краткосрочный и долгосрочный горизонты, чтобы создать сетку/матрицу из 9 вариантов. Эти состояния отражали бычий, медвежий и флетовый настрой. Система довольно проста, но ее можно сделать более сложной и чувствительной к рынку не только за счет увеличения общих параметров, но и за счет добавления дополнительных факторов. Если объединить ее с Монте-Карло, то адаптивность повысится.

Обзор обучения с подкреплением (RL) в трейдинге

Обучение с подкреплением (reinforcement learning, RL) предназначено для работы в динамических средах, таких как финансовые рынки, где оно постоянно взаимодействует со своим "окружением", совершая действия (такие как покупка, продажа, удержание) на основе своего текущего состояния (где эти состояния определяются рыночными ценами или индикаторами и так далее). Каждое действие, предпринимаемое агентом, влияет на состояние окружающей среды, приводя к новым наблюдениям и потенциальным вознаграждениям.

Дополнительные примеры наборов состояний, которые могут быть приняты трейдерами для своих Q-карт, могут включать состояния на основе технических индикаторов. Они могут включать скользящие средние, где, если краткосрочная скользящая средняя больше долгосрочной, это означает бычье состояние, в то время как краткосрочная скользящая средняя ниже долгосрочной будет означать медвежье состояние, а равенство означает нейтральное состояние.

Поскольку мы объединили краткосрочные и долгосрочные прогнозы на одной оси, это означает, что теперь у нас есть возможность ввести еще одну ось, которая охватывает другие показатели, помимо показаний скользящей средней. Другим индикатором, который можно использовать для этой цели, является индекс относительной силы (RSI). При этом мы будем рассматривать состояние перекупленности (RSI > 70), которые потенциально могут быть сигналом к продаже, и состояние перепроданности (RSI < 30), которое потенциально может быть сигналом к покупке, а также дополнительное переходное состояние, которое не дает никакого сигнала.

Также в рамках состояний, основанных на индикаторах, мы могли бы рассмотреть полосы Боллинджера, где цена, находящаяся вблизи или выше верхней полосы, может быть медвежьим состоянием, в то время как цена на уровне или ниже нижней полосы может быть бычьим состоянием. Третье, нейтральное, состояние подразумевается для любой другой позиции.

Помимо состояний технических индикаторов, волатильность рынка также может представлять собой альтернативную ось матрицы состояний окружающей среды. При этом измерение будет основываться на таких индикаторах, как стандартное отклонение цены или ATR, и хотя можно будет использовать три возможных состояния: высокую волатильность, низкую волатильность и умеренную, можно будет добавить гораздо больше градаций, чтобы сделать алгоритм более чувствительным к рынкам. Эта настройка состояния (или ось) поможет агенту определить, следует ли торговать агрессивно или консервативно. Состояния на основе объема также можно рассматривать для акций с аналогичной градацией.

Помимо медвежьих и бычьих трендов в ценовом поведении, которые мы использовали в прошлых статьях и рассматриваем в качестве состояний для этой статьи, существуют и более конкретные модели ценового поведения, такие как прорывы уровней поддержки/сопротивления. В качестве альтернативы это может быть голова и плечи как для бычьих, так и для медвежьих сигналов, при этом любая другая модель будет пилой. Распознавание таких моделей в недавнем ценовом действии позволит агенту предвидеть продолжение или разворот.

Другой возможной осью состояний Q-карт могут быть состояния, основанные на времени. Напомним, эта ось затем будет сопряжена с другой осью, например, с осью ценового действия, указанной выше, или с упомянутыми техническими индикаторами, чтобы можно было сделать вывод о том, какое ценовое действие является более надежным в каждом периоде времени. Возможные временные состояния могут включать открытие/закрытие рынка, торговые сессии или даже дни недели. Состояния, основанные на настроениях, являются еще одной осью, которая может сформировать матрицу состояний среды. Измерение этих настроений будет зависеть от показаний календаря экономических новостей по конкретному индикатору, учитывая их разнообразие. Градация этих состояний должна варьироваться от положительного до нейтрального и отрицательного, с возможностью добавления внутренних состояний в зависимости от интересующей степени детализации. Включение настроений, особенно с помощью этих методов, может помочь агенту реагировать на внешние события, влияющие на рынок.

Аналогичным и альтернативным вариантом были бы состояния, основанные на экономических событиях. Однако есть нечто отличное от этих двух, что также можно было бы рассмотреть — это состояния на основе портфеля. Эта категория весьма применима за пределами форекса и представляет собой ряд потенциальных осей. Во-первых, это уровни подверженности риску, когда портфель оценивается по относительной подверженности риску, например, акций к облигациям. Градация может варьироваться от 90-10 на одном конце до 10-90 на другом конце соответственно. Такую ось можно связать со временем или любой другой, но связанной метрикой, так чтобы эффективность портфеля (которая будет соответствовать вознаграждениям агентов) могла направлять процесс обновления Q-значения.

Другим вариантом в состояниях на основе портфеля является уровень риска. Здесь может учитываться процентное распределение капитала для каждой инвестиции, при этом градации могут варьироваться от небольшой суммы < 0,5% до предельного значения, скажем, 10%. Опять же, сравнение или объединение этого показателя может осуществляться с другим показателем, характерным для портфеля, а оптимизация на основе приличного набора данных должна предоставить Q-карту, которая будет указывать, какие уровни риска и когда следует использовать. Другой альтернативой могли бы стать состояния просадки, и в целом эти состояния на основе портфеля позволили бы агенту учитывать более широкий финансовый контекст, а не только отдельные рыночные сигналы.

Я мог бы также упомянуть макротрендовые состояния. Принципы схожи, но, что более важно, примеры, представленные здесь, не являются исчерпывающими. Выбор состояний среды может иметь большое значение для определения стратегии и, следовательно, предоставления преимущества в зависимости от того, насколько она уникальна, а также от усилий, вложенных не только в тестирование, но и в ее перекрестную проверку.

Помимо состояний среды, сигналы вознаграждения после каждого действия предоставляют агенту обратную связь в форме, указывающей на успешность или неудачу его действия. Вознаграждения могут быть количественно оценены с точки зрения прибыли/убытка (как мы применяли до сих пор), доходности с поправкой на риск или любого другого соответствующего показателя эффективности, который может направить агента к более благоприятным действиям. Напомним, вознаграждения являются ключевым компонентом обновления Q-значений Q-карты.

RL, пожалуй, более известно тем, что при составлении прогнозов соблюдает баланс между исследованием и эксплуатацией. В теории агент часто применяет стратегии исследования для обнаружения новых действий, которые могут принести большее вознаграждение, одновременно используя известные действия, которые ранее оказались успешными. Баланс между исследованием и эксплуатацией, который контролируется входным параметром эпсилон, имеет решающее значение для того, чтобы агент мог избегать локальных оптимумов и продолжать совершенствовать процесс принятия решений с течением времени.

Таким образом, методом проб и ошибок, поскольку эпсилон-жадный подход к выбору подходящих действий включает случайный выбор, агент учится на своем опыте в окружающей среде и корректирует свою политику выбора действий, основываясь на прошлых результатах. С каждым опытом улучшается понимание агентом того, какие действия приводят к положительным вознаграждениям, что позволяет ему делать лучший выбор в аналогичных ситуациях в будущем.

Это улучшение стало возможным благодаря значениям Q-карт или политике агента. Карта представляет собой стратегию, которая связывает состояния с действиями и постоянно обновляет действия каждого состояния на основе наблюдаемых вознаграждений. Улучшение политики осуществляется с помощью алгоритмов обучения с подкреплением, цель которых — максимизировать кумулятивные вознаграждения с течением времени.

Это основные аспекты, которые мы рассмотрели в последних трех статьях об RL, однако в RL есть и более инновационные концепции. Одним из таких методов является оценка функции ценности, при которой агент часто оценивает функцию ценности, способной предсказать ожидаемую отдачу от заданного состояния или пары состояние-действие. Аппроксимируя функцию ценности, агент может оценить потенциальные долгосрочные выгоды различных действий, тем самым способствуя принятию более обоснованных решений.

Временное распределение вознаграждения (Temporal Credit Assignment) — еще одна концепция, в которой агент связывает действия, предпринятые в прошлом, с вознаграждениями, получаемыми в будущем. Такой подход в теории позволяет агенту понять, как его предыдущие действия влияют на будущие результаты, что может привести к лучшему планированию или упреждающей установке определенных политик, которые переопределяют пары "действие-состояние" по умолчанию.

Еще один пример — адаптируемые темпы обучения (adaptive learning rates), тема, которую мы рассматривали в одной из предыдущих статей, когда мы имели дело с многослойными перцептронами. Их также можно задействовать в качестве альфа-версии при обновлении Q-значений. Агент может использовать их, при этом они корректируются на основе неопределенности значений состояния и действия, что позволяет выполнять более агрессивные обновления, когда агент не уверен, и более консервативные обновления по мере обретения уверенности. Такая адаптивность может помочь агенту эффективно обучаться в меняющихся рыночных условиях.

Другие заслуживающие внимания идеи, связанные с RL, включают обобщение по всем состояниям (Generalization Across States) для повышения эффективности и разработки долгосрочной стратегии, которая выходит за рамки немедленных вознаграждений.

Алгоритм Монте-Карло

Подход к обучению, принятый в методах Монте-Карло, отличается от более ранних алгоритмов обучения с подкреплением, которые мы рассматривали, тем, что он обучается на основе полных эпизодов опыта, ожидая конца эпизода, чтобы "обучиться", но применяя целостный подход на основе множественных баллов вознаграждения, полученных за это время. Поэтому возникает необходимость в буферизации значений вознаграждений в течение нескольких периодов времени, чтобы по завершении эпизода все прошлые значения вознаграждений были доступны. Мы реализуем это в MQL5 следующим образом - из функции получения выходных данных нашего пользовательского класса сигнала:

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalMC::GetOutput(Cql *QL, vector &Rewards)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      for(int i = m_episode_cycles - 1; i > 0; i--)
      {  Rewards[i] = Rewards[i - 1];
      }
      Rewards[0] = QL.GetReward(_reward_max, _reward_min, _reward_float);
      QL.transition_act = 1;
      if(Rewards[m_episode_cycles - 1] != -1.0)
      {  double _reward = Rewards[m_episode_cycles - 1];
         for(int i = m_episode_cycles - 2; i >= 0; i--)
         {  _reward += pow(QL.THIS.gamma, m_episode_cycles - 1 - i) * Rewards[i];
         }
         if(m_policy)
         {  QL.SetOnPolicy(_reward, _in_e);
         }
         else if(!m_policy)
         {  QL.SetOffPolicy(_reward, _in_e);
         }
      }
   }
}

Q-обучение, напротив, использует метод обучения на основе временной разницы (temporal-difference, TD), который обновляет оценки значений после каждого выполненного действия (или после каждого цикла), используя самонастройку на основе последующих значений состояния-действия. Это похоже на SARSA, но здесь обновления оценок значений производятся с использованием действий, предпринимаемых в следующем состоянии, что обеспечивает подход к обучению в рамках политики.

Механизм обновления Монте-Карло основан на средней доходности, наблюдаемой после выполнения действий из состояния в течение нескольких циклов в эпизоде. Каждая пара "состояние-действие" обновляется только после завершения эпизода, чтобы отразить истинную долгосрочную доходность. Таким образом, значение вознаграждения, используемое в этом обновлении, представляет собой взвешенную сумму, как показано в уже приведенной выше формуле, а также в MQL5-коде в функции получения выходных данных выше.

Однако Q-обучение использует максимальное будущее вознаграждение из следующего состояния (вне политики) для обновления значения действия текущего состояния, что может привести к более агрессивному обучению, поскольку оно учитывает наилучший возможный результат на каждом этапе цикла в рамках эпизода. Аналогичным образом SARSA обновляет значение на основе фактических действий, предпринятых в следующем состоянии (в рамках политики), объединяя текущую политику агента с процессом обучения, что может привести к немного более консервативным обновлениям, чем Q-обучение, но все равно более агрессивным, чем Монте-Карло.

Метод Монте-Карло, как правило, полагается на полное исследование окружающей среды в ходе нескольких циклов в эпизоде для изучения оптимальных действий, что позволяет проводить тщательную выборку пар "состояние-действие" перед внесением обновлений. Это достигается с помощью ε-жадного подхода, который мы представили в нашей вводной статье о Q-обучении, где на обновления влияют действия, не предпринимаемые агентом.

SARSA также является ε-жадным в своем подходе к балансировке исследования и эксплуатации, однако он обновляет значения на основе действия, фактически предпринятого в следующем состоянии, что делает его более восприимчивым к текущей политике агента и выбору исследования. Отличие Монте-Карло от этих двух алгоритмов, помимо того, что обновления происходят только один раз за эпизод, заключается в том, что они могут быть как соответствующими политике, так и несоответствующими ей. С этой целью наш пользовательский класс сигналов для Монте-Карло имеет входной параметр m_on_policy, который является логическим и, как следует из его названия, определяет, используется ли он в рамках политики или вне ее.

Интерфейс класса для пользовательского класса сигнала представлен ниже:

//+------------------------------------------------------------------+
//| MCs CSignalMC.                                                   |
//| Purpose: MonteCarlo for Reinforcement-Learning.                  |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
class CSignalMC   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis
   int                           m_scale;             // Environments, row-to-col scale
   bool                          m_use_markov;        // Use Markov
   double                        m_epsilon;           // Epsilon
   bool                          m_policy;            // On Policy
   int                           m_episode_cycles;    // Episode Size

public:
   void                          CSignalMC(void);
   void                          ~CSignalMC(void);

   //--- methods of setting adjustable parameters
   void                          QL_Scale(int value)
   {  m_scale = value;
   }
   void                          QL_Markov(bool value)
   {  m_use_markov = value;
   }
   void                          QL_Epsilon(bool value)
   {  m_epsilon = value;
   }
   void                          QL_Policy(bool value)
   {  m_policy = value;
   }
   void                          QL_EpisodeCycles(int value)
   {  m_episode_cycles = value;
   }

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   void              GetOutput(Cql *QL, vector &Rewards);
   Sql               RL;
   Cql               *QL_BUY, *QL_SELL;
   vector            REWARDS_BUY, REWARDS_SELL;
};

Сходимость по методу Монте-Карло, как правило, происходит медленнее, поскольку для ее обновления требуются полные эпизоды, что не всегда эффективно в средах с длинными эпизодами или редкими вознаграждениями. Это контрастирует с алгоритмом Q-обучения, который в большинстве случаев сходится быстрее из-за своей природы самонастройки, однако неизбежно будет нестабильным, поскольку может колебаться или расходиться в средах с нестационарными вознаграждениями или высокой дисперсией. SARSA позиционируется как более стабильная технология, чем Q-обучение, в определенных ситуациях, поскольку она учитывает фактическую политику агента во время обновлений, что, как правило, приводит к более плавным кривым обучения.

Что касается эффективности выборки, метод Монте-Карло, как правило, менее эффективен из-за необходимости получения обновлений для полных эпизодов, что может стать серьезным недостатком в средах с большим пространством состояний и действий. Q-обучение более эффективно с точки зрения выборки, поскольку обновляет значения на каждом этапе, что позволяет быстрее вносить изменения на основе немедленной обратной связи. Фактически, можно утверждать, что оно даже более эффективно, чем SARSA, поскольку последний может потребовать больше образцов, чем Q-обучение, поскольку он чувствителен к текущей политике и используемой стратегии исследования.

Метод Монте-Карло хорошо подходит для сред, где эпизоды можно четко определить, а долгосрочная доходность, как правило, более важна, чем краткосрочные всплески, например, в торговых симуляциях. Это явно делает ее ключевой стратегией для ценовых или долгосрочных "трейдеров". Q-обучение эффективно в средах с четкой структурой вознаграждений и четко определенными переходами состояний, что делает его идеальным для таких задач, как внутридневная торговля. При этом SARSA полезен в ситуациях, когда обучение должно точно отражать политику агента, например, в динамичных или частично наблюдаемых средах, где адаптация имеет решающее значение, например, в свинговой торговле.

Реализация метода Монте-Карло в пользовательском классе сигналов

Мы реализуем наш собственный сигнал, который использует Монте-Карло RL в качестве корневой модели и генератора сигнала. Основные шаги по реализации уже описаны выше с интерфейсом класса и функцией получения выходных данных. Ниже приведены функции условий на покупку и продажу:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalMC::LongCondition(void)
{  int result = 0;
   GetOutput(QL_BUY, REWARDS_BUY);
   if(QL_BUY.transition_act == 0)
   {  result = 100;
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalMC::ShortCondition(void)
{  int result = 0;
   GetOutput(QL_SELL, REWARDS_SELL);
   if(QL_SELL.transition_act == 2)
   {  result = 100;//printf(__FUNCSIG__);
   }
   return(result);
}

Полный исходный код для этой реализации приложен внизу, а руководства по его использованию для сборки собранного советника можно найти здесь и здесь. Марковский процесс принятия решений является неотъемлемой частью использования Q-карт, тем не менее, существует входной параметр, который предоставляет возможность использовать весовые коэффициенты Маркова при обновлении Q-значений. Кроме того, мы можем решить, следует ли использовать политику или нет, указать размер эпсилон — нашего параметра, который определяет степень, в которой мы исследуем или эксплуатируем, а также определить количество циклов в эпизоде. Мы проводим оптимизационные прогоны по паре GBPUSD на 2022 год на часовом таймфрейме. Результаты ниже:

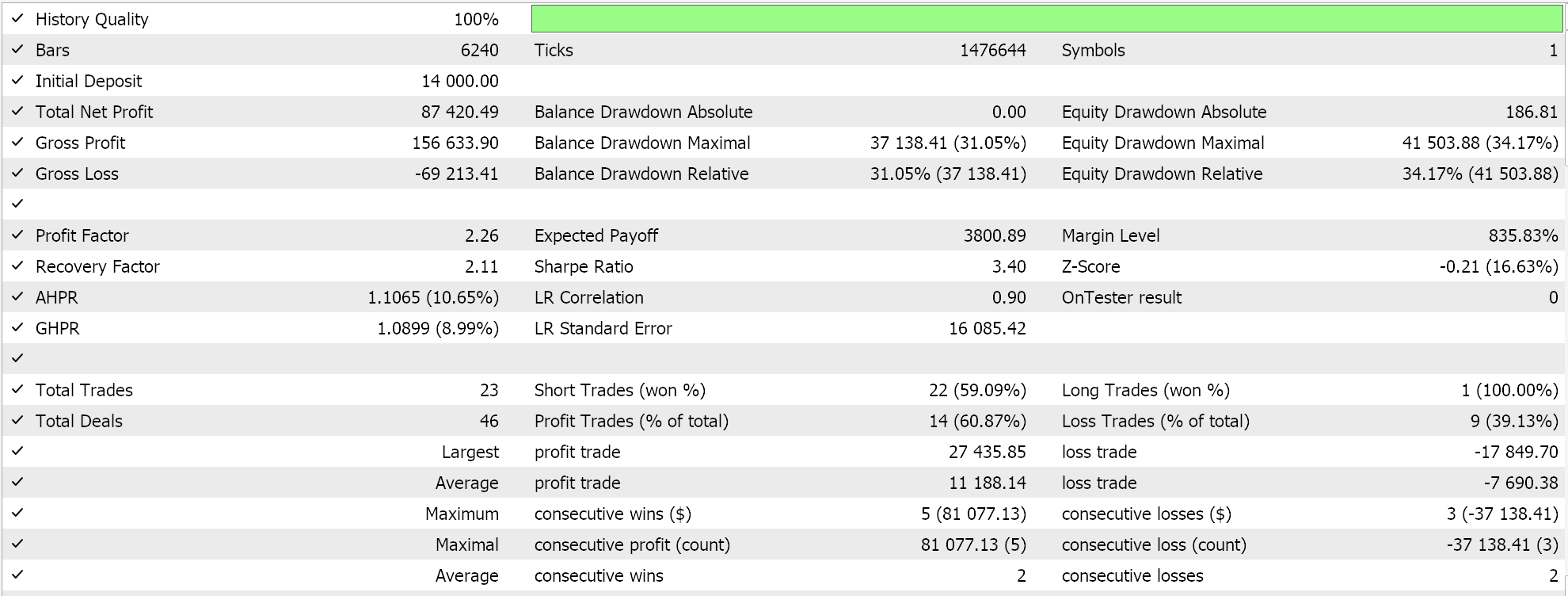
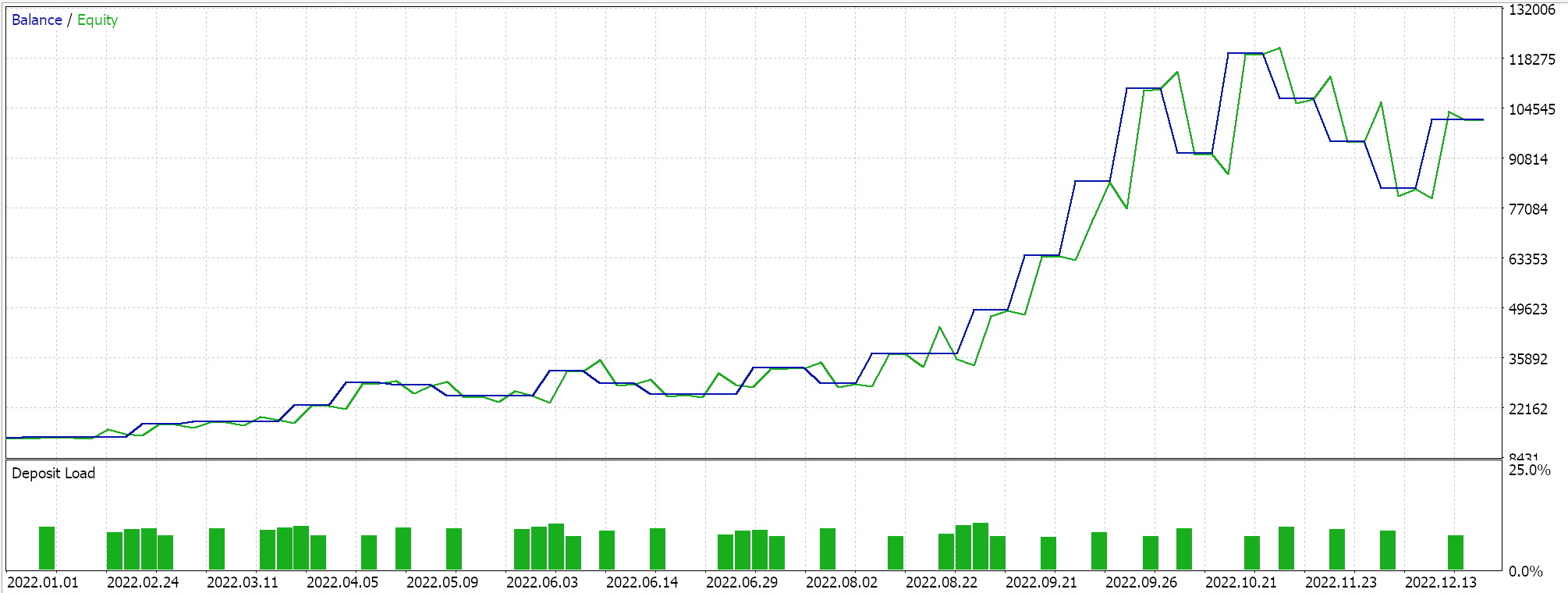
Заключение и дополнительные соображения

Мы рассмотрели алгоритм Монте-Карло в контексте обучения с подкреплением, который во многом заимствует черты из Q-обучения и SARSA - двух алгоритмов, которые мы уже рассматривали ранее здесь и здесь и представляет собой еще более динамичный и адаптивный способ обучения, который по-прежнему сосредоточен на долгосрочных чертах и атрибутах своей среды. Помимо использования более индивидуальной матрицы среды, как указано в некоторых альтернативах, перечисленных в этой статье, можно также использовать альтернативную шкалу действий с более чем тремя вариантами.

Метод Монте-Карло добивается компромисса между смещением и дисперсией при расчете вознаграждения за обновление. В случаях, когда количество циклов в эпизоде невелико, обычно наблюдается высокая степень смещения и низкая дисперсия, в то время как для более длительных эпизодов с большим количеством циклов характерна противоположная картина. В зависимости от целей, это следует учитывать при разработке Q-карты, поскольку высокое смещение, как правило, делает модель более адаптивной к краткосрочным действиям, в то время как высокая дисперсия лучше соответствует цели алгоритма по учету долгосрочных черт и атрибутов.

Более детальное исследование пространства "состояние-действие", которое обеспечивается за счет наличия нескольких вознаграждений из разных моментов времени при использовании нескольких возвратов в n шагов, означает, что путем изменения горизонтов возможных возвратов (которые в нашем пользовательском классе сигналов контролировались входным параметром m_episode_cycles) мы можем точно настраивать силу сигнала для торговых стратегий. Такая детализация приводит к принятию более взвешенных решений при определении точек входа и выхода, что позволяет оптимизировать обе точки и корректировать время и интенсивность их сигналов.