Science des données et Apprentissage Automatique (Partie 01) : Régression Linéaire
Introduction
La tentation de se forger des théories prématurées sur des données insuffisantes est le fléau de notre profession.
"Sherlock Holmes"
La science des données
est un domaine interdisciplinaire qui utilise des méthodes, des processus, des algorithmes et des systèmes scientifiques pour extraire des connaissances et des idées à partir de données bruyantes, structurées et non structurées. Elle applique ces connaissances et ces informations exploitables à partir de données dans un large éventail de domaines d'application.
Un data scientist est une personne qui écrit du code et le combine avec des connaissances statistiques pour créer des informations à partir des données.
À quoi devez-vous vous attendre de cette série d'articles ?
- La théorie (comme dans les équations mathématiques) : La théorie est la plus importante en Science des Données (data science). Vous devez connaître parfaitement les algorithmes, savoir comment un modèle se comporte, et pourquoi il se comporte d'une certaine manière. Comprendre cela est beaucoup plus difficile que de coder l'algorithme lui-même.
- Des exemples pratiques en MQL5 et en python.
Régression Linéaire
La régression linéaire est un modèle prédictif utilisé pour trouver la relation linéaire entre une variable dépendante et une ou plusieurs variables indépendantes.
La régression linéaire est l'un des algorithmes de base utilisés par de nombreux autres algorithmes, tels que :
- La régression logistique qui est un modèle basé sur la régression linéaire
- Le ’Support-Vector Machine’, ce célèbre algorithme en science des données est un modèle linéaire
Qu'est-ce qu'un Modèle ?
Un modèle n'est rien d'autre qu'un suffixe.
Théorie
Chaque ligne droite traversant le graphique correspond à une équation
Comment trouve-t-on cette équation ?
Supposons que nous ayons 2 ensembles de données avec les mêmes valeurs de xet de y :
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
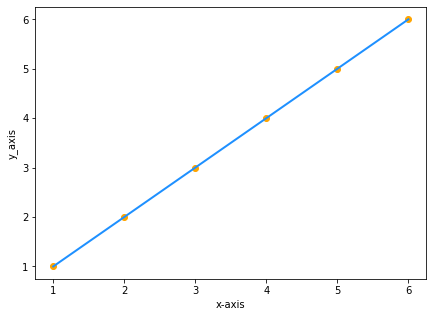
Le tracé des valeurs sur le graphique sera :
Puisque y est égal à x, l'équation de notre droite sera y=x , n’est-ce pas ? FAUX
Pourtant,
y = x est mathématiquement identique à y = 1x. En science des données, c’est un peu différent. La formule de la ligne sera y = 1x, où 1 est l'angle formé entre la ligne et l'axe des x, également connu sous le nom de pente de la ligne
Mais,
pente = changement de y / changement de x = m (appelé m)
Notre formule est maintenant y = mx.
Nous devons ensuite ajouter une constante à notre équation, c'est-à-dire une valeur de y lorsque x = 0. Autrement dit la valeur de y lorsque la ligne croisait l'axe des y.
Enfin,
notre équation sera y = mx + c (c’est un modèle en science des données)
où c est l'ordonnée à l'origine
Régression Linéaire Simple
La régression linéaire simple a une variable dépendante et une variable indépendante. Ici, nous essayons de comprendre la relation entre deux variables. Par exemple, comment le cours d'une action change avec le changement d'une moyenne mobile simple.
Données Complexes
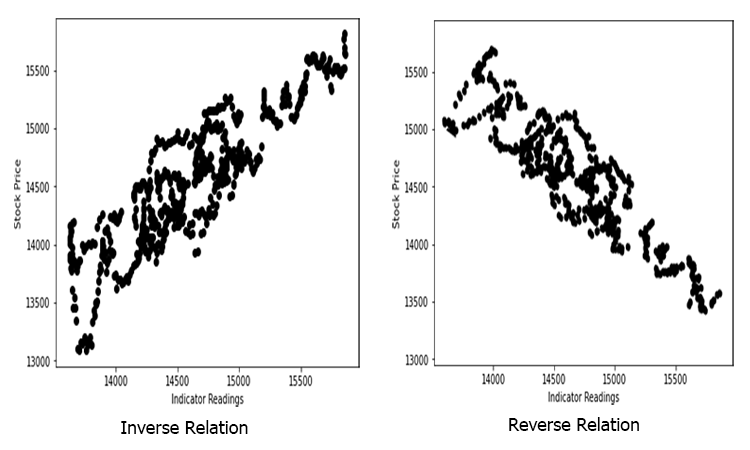
Supposons que nous ayons des valeurs dispersées aléatoires pour un indicateur lorsqu'elles sont prises par rapport au cours de l'action(ce qui se produit dans la vraie vie).
Dans ce cas, notre indicateur/variable indépendante peut ne pas être le bon prédicteur de notre prix de l'action/variable dépendante.
Le premier filtre que vous devez appliquer à vos ensembles de données consiste à supprimer toutes les colonnes qui ne sont pas fortement corrélées à votre cible, car vous n'allez pas construire votre modèle linéaire avec celles-ci.
Faites attention ! Construire un modèle linéaire avec des données liées non linéaires est une énorme erreur fondamentale !
La relation peut être inverse ou renversée, mais elle doit être forte. Et puisque nous recherchons des relations linéaires, c'est ce que vous voulez trouver.
Donc, comment mesurer la force entre la variable indépendante et la cible ? Nous utilisons une métrique connue sous le nom de coefficient de corrélation.
Coefficient de Corrélation
Codons un script pour créer un jeu de données à utiliser comme exemple principal de cet article. Trouvons les prédicteurs du NASDAQ :
input ENUM_TIMEFRAMES timeframe = PERIOD_H1; input int maperiod = 50; input int rsiperiod = 13; int total_data = 744; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { string file_name = "NASDAQ_DATA.csv"; string nasdaq_symbol = "#NQ100", s_p500_symbol ="#SP500"; //--- int handle = FileOpen(file_name,FILE_CSV|FILE_READ|FILE_WRITE,","); if (handle == INVALID_HANDLE) { Print("data to work with is nowhere to be found Err=",GetLastError()); } //--- MqlRates nasdaq[]; ArraySetAsSeries(nasdaq,true); CopyRates(nasdaq_symbol,timeframe,1,total_data,nasdaq); //--- MqlRates s_p[]; ArraySetAsSeries(s_p,true); CopyRates(s_p500_symbol,timeframe,1,total_data,s_p); //--- Moving Average Data int ma_handle = iMA(nasdaq_symbol,timeframe,maperiod,0,MODE_SMA,PRICE_CLOSE); double ma_values[]; ArraySetAsSeries(ma_values,true); CopyBuffer(ma_handle,0,1,total_data,ma_values); //--- Rsi values data int rsi_handle = iRSI(nasdaq_symbol,timeframe,rsiperiod,PRICE_CLOSE); double rsi_values[]; ArraySetAsSeries(rsi_values,true); CopyBuffer(rsi_handle,0,1,total_data,rsi_values); //--- if (handle>0) { FileWrite(handle,"S&P500","NASDAQ","50SMA","13RSI"); for (int i=0; i<total_data; i++) { string str1 = DoubleToString(s_p[i].close,Digits()); string str2 = DoubleToString(nasdaq[i].close,Digits()); string str3 = DoubleToString(ma_values[i],Digits()); string str4 = DoubleToString(rsi_values[i],Digits()); FileWrite(handle,str1,str2,str3,str4); } } FileClose(handle); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
Dans le script, nous avons rassemblé les prix de clôture du NASDAQ, les valeurs du RSI sur 13 périodes, du S&P 500 et de la moyenne mobile sur 50 périodes. Après la collecte des données dans un fichier CSV, visualisons les données en python sur le notebook Jupyter d’anaconda. Pour ceux qui n'ont pas installé anaconda sur leur machine, vous pouvez exécuter votre code python utilisé dans cet article sur google colab.
Avant de pouvoir ouvrir le fichier CSV créé par notre script de test, vous devez le convertir avec un encodage en UTF-8 afin qu'il puisse être lu par Python. Ouvrez le fichier CSV avec le bloc-notes puis enregistrez-le en l’encodant au format UTF-8. Ce sera une bonne chose de copier le fichier dans un répertoire externe afin qu'il soit lu séparément par python lorsque vous lirez ce répertoire avec pandas. Lisons le fichier CSV et stockons-le dans une variable.
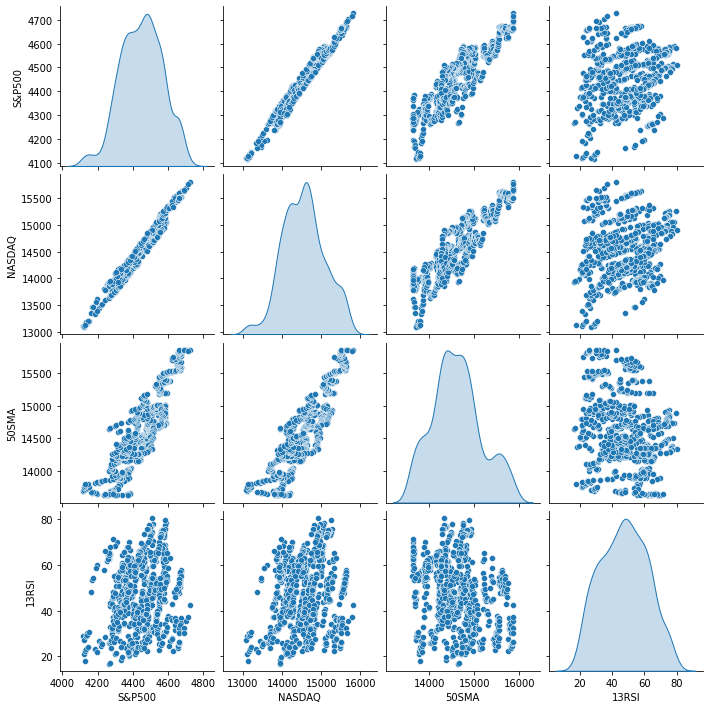
L’affichage est le suivant :
D'après la représentation visuelle des données, nous pouvons déjà voir qu'il existe une relation très forte entre le NASDAQ et le S&P 500, et qu’il existe une relation forte entre le NASDAQ et sa moyenne mobile sur 50 périodes. Comme dit précédemment, chaque fois que les données sont dispersées sur tout le graphique, la variable indépendante peut ne pas être un bon prédicteur de la cible lorsqu'il s'agit de trouver des relations linéaires. Mais voyons ce que les chiffres disent de leur corrélation et tirons une conclusion à partir des chiffres plutôt que selon nos yeux, pour trouver comment les variables sont corrélées les unes aux autres. Nous utiliserons pour cela la métrique connue sous le nom de Coefficient de Corrélation.
Coefficient de Corrélation
Il est utilisé pour mesurer la force entre la variable indépendante et la cible.
Il existe plusieurs types de coefficients de corrélation. Nous utiliserons le plus populaire, également connu sous le nom de coefficient de corrélationde Pearson (R) qui varie entre -1 et +1.
La corrélation des valeurs extrêmes possibles de -1 et +1 indique respectivement une relation linéaire négative parfaite et une relation linéaire positive parfaite entre x et y alors qu'une corrélation de 0 (zéro) indique l'absence de corrélation linéaire.
La formule du coefficient de corrélation de Pearson (R).
J'ai créé le fichier linearRegressionLib.mqh dans notre bibliothèque principale. Codons ensemble la fonction corrcoef().
Commençons par la fonction moyenne des valeurs. La moyenne est la somme de toutes les données, divisée par le nombre total d'éléments.
double CSimpleLinearRegression::mean(double &data[]) { double x_y__bar=0; for (int i=0; i<ArraySize(data); i++) { x_y__bar += data[i]; // all values summation } x_y__bar = x_y__bar/ArraySize(data); //total value after summation divided by total number of elements return(x_y__bar); }Codons maintenant le r de Pearson
double CSimpleLinearRegression::corrcoef(double &x[],double &y[]) { double r=0; double numerator =0, denominator =0; double x__x =0, y__y=0; for(int i=0; i<ArraySize(x); i++) { numerator += (x[i]-mean(x))*(y[i]-mean(y)); x__x += MathPow((x[i]-mean(x)),2); //summation of x values minus it's mean squared y__y += MathPow((y[i]-mean(y)),2); //summation of y values minus it's mean squared } denominator = MathSqrt(x__x)*MathSqrt(y__y); //left x side of the equation squared times right side of the equation squared r = numerator/denominator; return(r); }
L’affichage du résultat de TestSript.mq5 donne ceci :
Print("Correlation Coefficient NASDAQ vs S&P 500 = ",lr.corrcoef(s_p,y_nasdaq)); Print("Correlation Coefficient NASDAQ vs 50SMA = ",lr.corrcoef(ma,y_nasdaq)); Print("Correlation Coefficient NASDAQ Vs rsi = ",lr.corrcoef(rsi,y_nasdaq));
La sortie sera :
Coefficient de corrélation NASDAQ vs S&P 500 = 0,9807093773142763
Coefficient de corrélation NASDAQ vs SMA50 = 0,8746579124626006
Coefficient de corrélation NASDAQ Vs RSI = 0,24245225451004537
Comme vous pouvez le voir, le NASDAQ et le S&P500 ont une très forte corrélation de toutes les autres colonnes de données (son coefficient de corrélation est très proche de 1). Nous devons donc supprimer d'autres colonnes faibles lors de la construction de notre modèle de régression linéaire simple.
Nous avons maintenant deux colonnes de données sur lesquelles nous allons pouvoir construire notre modèle. Continuons à le faire.
Le Coefficient de X
Le coefficient de x, également connu sous le nom de pente (m), est, par définition, le rapport du changement de Y et de X, ou en d'autres termes, la pente de la ligne.
Formule :
pente = changement de y / changement de x
Rappelez-vous qu’en Algèbre, la pente est notée m dans la formule
Y = M X + C
Pour trouver la pente de régression linéaire m, la formule est la suivante :
Maintenant que nous avons vu la formule, codons pour la pente de notre modèle.
double CSimpleLinearRegression::coefficient_of_X() { double m=0; double x_mean=mean(x_values); double y_mean=mean(y_values);; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<(ArraySize(x_values)+ArraySize(y_values))/2; i++) { x__x = x_values[i] - x_mean; //right side of the numerator (x-side) y__y = y_values[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
Faites attention aux tableaux y_values et x_values. Ce sont des tableaux créées et copiés à l'intérieur de la fonction Init(), à l'intérieur de la classe CSimpleLinearRegression.
Voici la fonction CSimpleLinearRegression::Init() :
void CSimpleLinearRegression::Init(double& x[], double& y[]) { ArrayCopy(x_values,x); ArrayCopy(y_values,y); //--- if (ArraySize(x_values)!=ArraySize(y_values)) Print(" Two of your Arrays seems to vary In Size, This could lead to inaccurate calculations ",__FUNCTION__); int columns=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } columns++; if (FileIsLineEnding(m_handle)) { rows++; columns=0; } } m_rows = rows; m_columns = columns; FileClose(m_handle); //--- }
Nous avons fini de coder le coefficient de X. Nous pouvons passer maintenant à la partie suivante.
Ordonnée à l'Origine (Y-intercept)
Comme dit précédemment, l'Ordonnée à l'Origine (Y-intercept en anglais) est la valeur de y lorsque la valeur de x est 0, ou la valeur de y lorsque la ligne coupe l'axe des y.

Trouver l'Ordonnée à l'Origine
Avec l'équation
Y = M X + C
En prenant MX sur le côté gauche de l'équation et en retournant l'équation vers la droite, l'équation finale pour l'abscisse à l'origine sera :
C = Y - M X
avec
Y = moyenne de toutes les valeurs y
X = moyenne de toutes les valeurs x
Codons maintenant la fonction pour trouver l'Ordonnée à l'Origine.
double CSimpleLinearRegression::y_intercept() { // c = y - mx return (mean(y_values)-coefficient_of_X()*mean(x_values)); }
Nous en avons fini avec l'Ordonnée à l'Origine. Construisons maintenant notre modèle de régression linéaire en l'affichant dans notre fonction LinearRegressionMain() .
void CSimpleLinearRegression::LinearRegressionMain(double &predict_y[]) { double slope = coefficient_of_X(); double constant_y_intercept= y_intercept(); Print("The Linear Regression Model is "," Y =",DoubleToString(slope,2),"x+",DoubleToString(constant_y_intercept,2)); ArrayResize(predict_y,ArraySize(y_values)); for (int i=0; i<ArraySize(x_values); i++) predict_y[i] = coefficient_of_X()*x_values[i]+y_intercept(); //--- }
Nous utilisons également notre modèle pour obtenir les valeurs prédites de y qui nous utiles par la suite pour continuer à construire notre modèle et à analyser sa précision.
Appelons la fonction depuis la fonction Onstart() dans notre TestScript.mq5.
lr.LinearRegressionMain(y_nasdaq_predicted);
La sortie sera :
2022.03.03 10:41:35.888 TestScript (#SP500,H1) Le modèle de régression linéaire est Y =4.35241x+-4818.54986
void CSimpleLinearRegression::GetDataToArray(double &array[],string file_name,string delimiter,int column_number) { m_filename = file_name; m_delimiter = delimiter; int column=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } column++; //Get data by each Column if (column==column_number) //if we are on the specific column that we want { ArrayResize(array,rows+1); if (rows==0) { if ((double(data))!=0) //Just in case the first line of our CSV column has a name of the column { array[rows]= NormalizeDouble((double)data,Digits()); } else { ArrayRemove(array,0,1); } } else { array[rows-1]= StringToDouble(data); } //Print("column ",column," "," Value ",(double)data); } //--- if (FileIsLineEnding(m_handle)) { rows++; column=0; } } FileClose(m_handle); }
La fonction void fileopen()
void CSimpleLinearRegression::fileopen(void) { m_handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV,m_delimiter); if (m_handle==INVALID_HANDLE) { Print("Data to work with is nowhere to be found, Error = ",GetLastError()," ", __FUNCTION__); } //--- }
Dans notre TestScript, la première chose à faire est de déclarer 2 tableaux :
double s_p[]; //Array for storing S&P 500 values double y_nasdaq[]; //Array for storing NASDAQ values
Il suffit ensuite de passer ces tableaux pour obtenir leur référence à partir de notre fonction void GetDataToArray().
lr.GetDataToArray(s_p,file_name,",",1); lr.GetDataToArray(y_nasdaq,file_name,",",2);
Faites attention aux numéros de colonne puisque les arguments de la fonction ressemblent à ceci dans la section publique de notre classe :
void GetDataToArray(double& array[],string filename, string delimiter, int column_number);
Assurez-vous de vous référer au bon numéro de colonne. Voici comment sont disposées les colonnes dans notre fichier CSV :
S&P500,NASDAQ,50SMA,13RSI 4377.5,14168.6,14121.1,59.3 4351.3,14053.2,14118.1,48.0 4342.6,14079.3,14117.0,50.9 4321.2,14038.1,14115.6,46.1 4331.8,14092.9,14114.6,52.5 4336.1,14110.2,14111.8,54.7 4331.5,14101.4,14109.4,53.8 4336.4,14096.8,14104.7,53.3 .....
Après avoir appelé la fonction GetDataToArray(), il est temps d'appeler la fonction Init(), car cela n'a aucun sens d'initialiser la bibliothèque sans que les données soient correctement collectées et stockées dans leurs tableaux respectifs. L'appel des fonctions dans le bon ordre ressemble à ceci :
void OnStart() { string file_name = "NASDAQ_DATA.csv"; double s_p[]; double y_nasdaq[]; double y_nasdaq_predicted[]; lr.GetDataToArray(s_p,file_name,",",1); //Data is taken from the first column and gets stored in the s_p Array lr.GetDataToArray(y_nasdaq,file_name,",",2); //Data is taken from the second column and gets stored in the y_nasdaq Array //--- lr.Init(s_p,y_nasdaq); { lr.LinearRegressionMain(y_nasdaq_predicted); Print("slope of a line ",lr.coefficient_of_X()); } }
Maintenant que nous avons les valeurs prédites stockées dans le tableau y_nasdaq_predicted, nous pouvons visualiser la variable dépendante (NASDAQ), la variable indépendante (S&P500) et les prédictions sur la même courbe.
Exécutons le code suivant sur notre notebook Jupyter :
Le code python complet est joint à la fin de l'article.
Après avoir exécuté avec succès l'extrait de code ci-dessus, vous obtiendrez le graphique suivant :
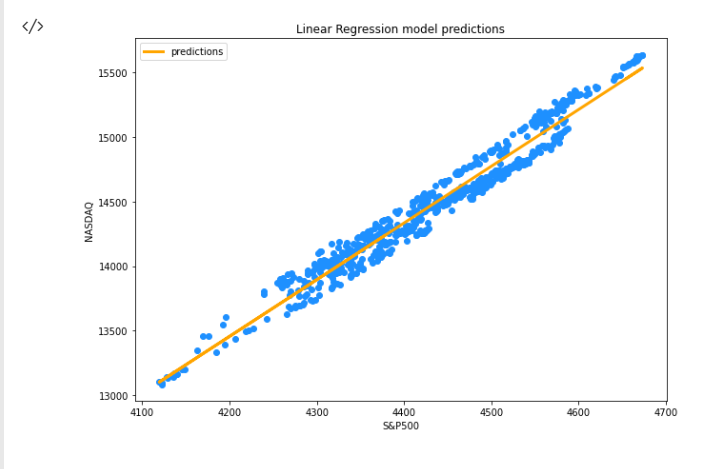
Nous avons maintenant notre modèle et d'autres choses en cours dans notre bibliothèque. Qu'en est-il de la précision de notre modèle ? Notre modèle est-il assez bon pour signifier quelque chose ou pour être utilisé dans quoi que ce soit ?
Pour comprendre à quel point notre modèle est efficace pour prédire la variable cible, nous utilisons une métrique connue sous le nom de Coefficient de Détermination appelée R-carré.
Coefficient de Détermination (R-carré)
C'est la proposition de variance totale de y qui a été expliquée par le modèle.
Pour trouver le R-carré, nous devons comprendre l'erreur de prédiction. L'erreur de prédiction est la différence entre la valeur actuelle/réelle de y et sa valeur prédite.
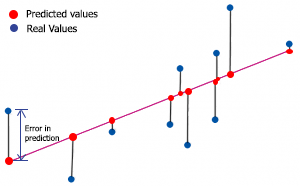
Mathématiquement :
Erreur = Y actuel - Y prédit
La formule R-carré est :
Rcarré = 1 - (Somme totale des erreurs au carré / Somme totale des résidus au carré)
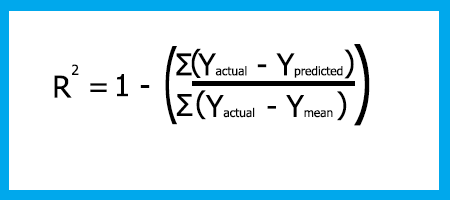
Pourquoi mettre les erreurs au carré ?
- Les erreurs peuvent être positives ou négatives (au-dessus ou en dessous de la ligne). Nous les mettons donc au carré pour les garder positives.
- Des valeurs négatives pourraient diminuer l'erreur.
- Nous corrigeons également les erreurs pour pénaliser les erreurs importantes afin d'obtenir un meilleur ajustement
0 signifie que le modèle n'est pas en mesure d'expliquer toute variance de y , indiquant que le modèle est le pire possible. 1 indique que le modèle est capable d'expliquer toute la variance de y dans votre ensemble de données (ce modèle n'existe pas).
Vous pouvez vous référer à la sortie R-carré comme étant le pourcentage de la qualité de votre modèle. 0 signifie une précision de 0% et 1 signifie que votre modèle est précis à 100%.
Codons maintenant le R-carré.
double CSimpleLinearRegression::r_squared() { double error=0; double numerator =0, denominator=0; double y_mean = mean(y_values); //--- if (ArraySize(m_ypredicted)==0) Print("The Predicted values Array seems to have no values, Call the main Simple Linear Regression Funtion before any use of this function = ",__FUNCTION__); else { for (int i=0; i<ArraySize(y_values); i++) { numerator += MathPow((y_values[i]-m_ypredicted[i]),2); denominator += MathPow((y_values[i]-y_mean),2); } error = 1 - (numerator/denominator); } return(error); }
Rappelez-vous que dans LinearRegressionMain où nous avons stocké les valeurs prédites dans le tableau predicted_y[] passé par référence, nous devons copier ce tableau dans un tableau de variables globales déclaré dans la section privée de notre classe.
private: int m_handle; string m_filename; string m_delimiter; double m_ypredicted[]; double x_values[]; double y_values[];
J’ai ajouté la ligne pour copier ce tableau dans la variable globale m_ypredicted[] à la fin de notre LinearRegressionMain.
//At the end of the function LinearRegressionMain(double &predict_y[]) I added the following line, // Copy the predicted values to m_ypredicted[], to be Accessed inside the library ArrayCopy(m_ypredicted,predict_y);
Imprimons maintenant la valeur R-carré dans notre TestScript.
Print(" R_SQUARED = ",lr.r_squared());
La sortie sera :
2022.03.03 10:40:53.413 TestScript (#SP500,H1) R_SQUARED = 0.9590906984145334
C'est tout pour la régression linéaire simple. Voyons maintenant à quoi ressemblerait une régression linéaire multiple.
Régression Linéaire Multiple
La régression linéaire multiple a une variable indépendante et plus d’une variable dépendantes.
La formule du modèle de régression linéaire multiple est la suivante :
Voici à quoi ressemble maintenant notre bibliothèque après avoir codé en dur les sections privées et publiques de notre classe :
class CMultipleLinearRegression: public CSimpleLinearRegression { private: int m_independent_vars; public: CMultipleLinearRegression(void); ~CMultipleLinearRegression(void); double coefficient_of_X(double& x_arr[],double& y_arr[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[],double& C[],double& D[]); };
Puisque nous utiliserons plusieurs valeurs, c'est la partie où nous jouerons avec de nombreux tableaux de référence de fonctions Arguments. Je n'ai pas trouvé une façon plus simple de l’implémenter.
Pour créer le modèle de régression linéaire pour 2 variables dépendantes, nous utiliserons cette fonction :
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[]) { // Multiple regression formula = y = M1X1+M2X2+M3X3+...+C double constant_y_intercept=y_interceptforMultiple(Y,A,B); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2)+"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(constant_y_intercept,2)); int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+constant_y_intercept; }
L'ordonnée à l'origine de cette instance sera basée sur le nombre de colonnes de données avec lesquelles nous avons décidé de travailler. Après avoir dérivé la formule de la régression linéaire multiple, la formule finale sera la suivante :
C = Y - M1 X1 - M2 X2
Voici à quoi cela ressemble après l'avoir codé :
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[]) { //formula c=Y-M1X1-M2X2; return(mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)); }
Dans le cas de 3 variables, il suffit de coder à nouveau la fonction en dur et d'ajouter une autre variable.
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[],double &C[],double &D[]) { double constant_y_intercept = y_interceptforMultiple(Y,A,B,C,D); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); double slope3 = coefficient_of_X(C,Y); double slope4 = coefficient_of_X(D,Y); //--- Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2),"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(slope3,2)+"C"+DoubleToString(slope4,2)+"D"+DoubleToString(constant_y_intercept,2)); //--- int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+slope3*C[i]+slope4*D[i]+constant_y_intercept; }
L'ordonnée à l'origine/Constant de notre régression linéaire multiple était comme dit précédemment.
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[],double &C[],double &D[]) { return (mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)-coefficient_of_X(C,Y)*mean(C)-coefficient_of_X(D,Y)*mean(D)); }
Hypothèses de Régression Linéaire
Le modèle de Régression Linéaire est basé sur un ensemble d'hypothèses. Si l'ensemble de données sous-jacent ne répond pas à ces hypothèses, les données peuvent devoir être transformées. Ou un modèle linéaire peut ne pas être alors le bon outil.
- Hypothèse de linéarité, suppose une relation linéaire entre la variable dépendante/cible et les variables indépendantes/prédictives
- Hypothèse de normalité de la distribution des erreurs
- Les erreurs doivent être distribuées de façon normale avec le modèle
- Un nuage de points entre les valeurs réelles et les valeurs prédites doit montrer les données réparties de manière égale dans le modèle
Avantages d'un Modèle de Régression Linéaire
Simple à mettre en œuvre et les sorties et les coefficients sont plus facile à interpréter.
Inconvénients
- Suppose une relation linéaire entre les variables dépendantes et indépendantes, c'est-à-dire qu'il doit exister une relation linéaire entre elles
- Une valeur aberrante a un effet énorme sur la régression
- La régression linéaire suppose l'indépendance des attributs
- La régression linéaire examine la relation entre la moyenne de la variable dépendante et la variable indépendante
- Tout comme la moyenne n'est pas la description complète d'une variable, la régression linéaire n'est pas une description complète des relations entre les variables
- Les frontières sont linéaires
Dernières pensées
Je pense que les algorithmes de régression linéaire peuvent être très utiles lors de la création de stratégies de trading basées sur la corrélation de paires et d'autres choses comme des indicateurs. Bien que notre bibliothèque soit loin d'être une bibliothèque finie, je n'ai pas inclus l’apprentissage et les tests de notre modèle, ainsi que d'autres améliorations des résultats. Cette partie sera dans le prochain article. Restez à l'écoute. Le code python est sur mon dépôt Github ici. Toute contribution à la bibliothèque sera appréciée. N'hésitez pas non plus à partager votre opinion dans les discussions de l'article.
À bientôt
Traduit de l’anglais par MetaQuotes Ltd.
Article original : https://www.mql5.com/en/articles/10459
Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.
Cet article a été rédigé par un utilisateur du site et reflète ses opinions personnelles. MetaQuotes Ltd n'est pas responsable de l'exactitude des informations présentées, ni des conséquences découlant de l'utilisation des solutions, stratégies ou recommandations décrites.
 Science des Données et Apprentissage Automatique (Partie 02) : Régression Logistique
Science des Données et Apprentissage Automatique (Partie 02) : Régression Logistique
 Ce qu’il est possible de faire avec les Moyennes Mobiles
Ce qu’il est possible de faire avec les Moyennes Mobiles
 Apprenez à concevoir un système de trading basé sur l’ADX
Apprenez à concevoir un système de trading basé sur l’ADX
 Apprenez à concevoir un système de trading basé sur le Stochastique
Apprenez à concevoir un système de trading basé sur le Stochastique
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation

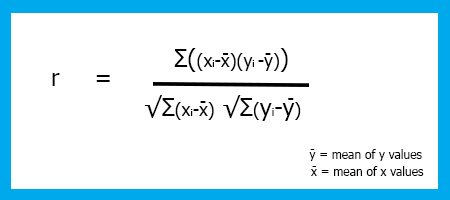
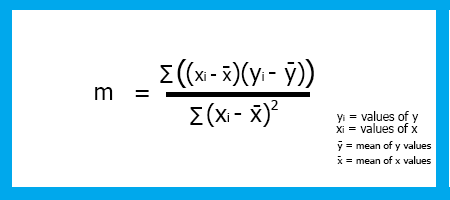
What is a Model
Un modèle n'est rien d'autre qu'un suffixe.
Un suffixe ? Je ne comprends pas ce que cela veut dire.
Avant de pouvoir ouvrir un fichier CSV créé par notre script de test, il faut le convertir en encodage UTF-8 pour qu'il puisse être lu par python.
Pourquoi ? Il suffit de créer un fichier de données UTF-8 directement à partir de MQL.
Ellipse rouge ajoutée par moi. C'est faux, ce point n'est pas une "ordonnée à l'origine" et ses coordonnées ne sont pas (0,-5).
Un suffixe ? Je ne comprends pas ce que cela signifie.
Pourquoi ? Il suffit de créer un fichier de données UTF-8 directement à partir de MQL.
Ellipse rouge ajoutée par moi. C'est faux, ce point n'est pas une "ordonnée à l'origine" et ses coordonnées ne sont pas (0,-5).
par le mot suffixe je veux dire une notation mathématique, comme y=mx+c c'est un modèle
Oui, j'ai compris, j'ai fait une erreur dans l'image, l'autre point était censé être (-5,0) et ce n'est pas une "ordonnée à l'origine".
Bonjour, merci pour cet article concis sur la régression linéaire et ses possibilités.
La formule du coefficient de Peasson présente des lacunes au niveau du dénominateur.
Bonjour, peut-être est-il là, mais je ne l'ai pas trouvé, mais où se trouve le fichier NASDAQ.csv utilisé dans l'article ?