Veri Bilimi ve Makine Öğrenimi (Bölüm 01): Lineer Regresyon
Giriş
Yetersiz verilere dayanarak erken teoriler oluşturmanın cazibesi mesleğimiz için ölümcüldür.
"Sherlock Holmes"
Veri Bilimi
Gürültülü, yapılandırılmış ve yapılandırılmamış verilerden bilgi ve kalıpları elde etmek ve bu bilgi ve eyleme dönüştürülebilir kalıpları çok çeşitli alanlarda uygulamak için bilimsel yöntemler, süreçler, algoritmalar ve sistemler kullanan disiplinler arası bir alandır.
Veri bilimcisi, programlama kodu oluşturan ve bunu istatistiksel bilgiyle birleştirerek verilerden kalıplar meydana getiren kişidir.
Bu makale serisinden ne beklemeliyiz?
- Teori (matematik denklemlerinde olduğu gibi): Veri biliminde en önemli şey teoridir. Algoritmaları derinlemesine bilmeniz ve modelin nasıl davrandığını, neden belirli bir şekilde davrandığını anlamanız gerekir, bunu anlamak algoritmanın kendisini kodlamaktan çok daha zordur.
- MQL5 ve Python'da uygulamalı örnekler.
Lineer Regresyon
Bir bağımlı değişken ile bir veya daha fazla bağımsız değişken arasındaki lineer ilişkiyi bulmak için kullanılan bir Öngörücü modeldir.
Lineer regresyon, şunlar gibi birçok algoritma tarafından kullanılan temel algoritmalardan biridir:
- Lineer regresyon tabanlı bir model olan lojistik regresyon
- Veri biliminde ünlü, lineer regresyon tabanlı bir model olan destek vektör makinesi
Model nedir?
Model bir son ekten başka bir şey değildir.
Teori
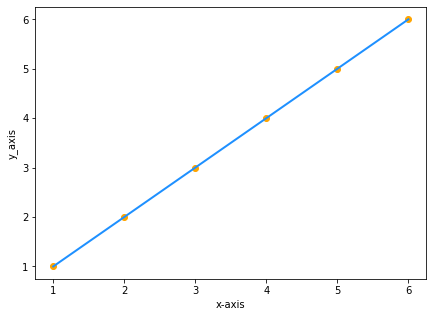
Grafikten geçen her doğrunun bir denklemi vardır:
Bu denklem nereden geliyor?
Aynı x ve y değerlerine sahip iki veri kümemiz olduğunu varsayalım:
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
Değerlerin grafikte çizilmesi şu şekilde olacaktır:
y, x'e eşit olduğu için doğrumuzun denklemi y=x olacaktır, değil mi? Değil!
Gerçek şu ki,
y=x matematiksel olarak y=1x ile aynıdır, veri biliminde ise bu oldukça farklıdır, doğrunun formülü y=1x olacaktır, burada 1, doğru ile x ekseni arasındaki açıdır, bu açı, doğrunun eğimi olarak da bilinir,
eğimi tanımlarsak,
eğim = y'deki değişim / x'deki değişim = m (eğim, m olarak ifade edilir).
Formülümüz şimdi y = mx olacaktır.
Son olarak, denklemimize bir sabit eklememiz gerekiyor, bu, x sıfır olduğundaki y'nin değeridir, diğer bir deyişle doğru y eksenini kestiğindeki y'nin değeridir.
Sonuç olarak,
denklemimiz y = mx + c olacaktır (bu, veri biliminde bir modelden başka bir şey değildir),
burada c, y-kesimidir.
Basit Lineer Regresyon
Basit lineer regresyon, bir bağımlı değişkene ve bir bağımsız değişkene sahiptir. Burada iki değişken arasındaki ilişkiyi anlamaya çalışıyoruz, örneğin bu, bir hisse senedi fiyatındaki değişimin SMA’daki değişimle olan ilişkisi olabilir.
Karmaşık Veriler
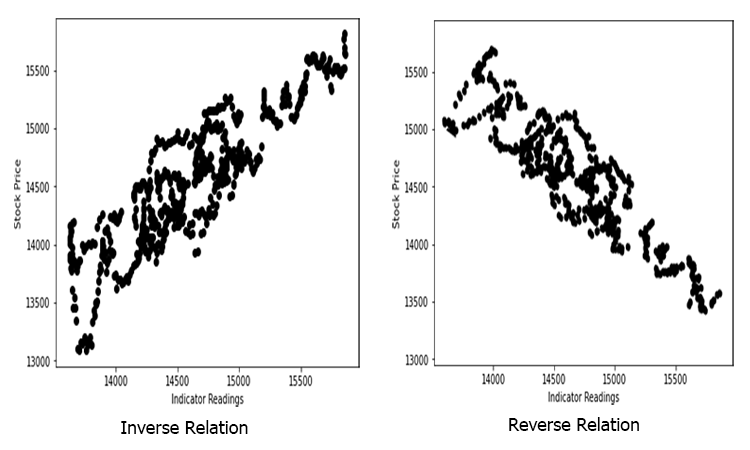
Hisse senedinin fiyatına göre gösterge değerlerini alıp grafikte çizdiğimizde aşağıdaki gibi rastgele dağılmış gösterge değerlerini elde ettiğimizi varsayalım (gerçek hayatta da durum böyledir).
Bu durumda, göstergemiz/bağımsız değişkenimiz hisse senedi fiyatımızın/bağımlı değişkenimizin iyi bir öngörücüsü olmayabilir.
Veri kümelerine uygulanması gereken ilk filtre, lineer modele dahil edilmemeleri adına hedefinizle yüksek düzeyde ilişkili olmayan tüm sütunları kaldırmaktır.
Lineer olmayan ilişkili verilerle lineer bir model oluşturmak büyük bir temel hatadır; dikkatli olun!
İlişki ters olabilir ancak güçlü olmalıdır ve lineer ilişkiler aradığımızdan dolayı, bulmak istediğiniz şey de budur.
Peki, bağımsız değişken ile hedefimiz arasındaki gücü nasıl ölçeceğiz? Bunun için, korelasyon katsayısı olarak bilinen bir metrik kullanıyoruz.
Korelasyon Katsayısı
Bu makalenin ana örneği olarak kullanılacak bir veri kümesi oluşturmak adına bir komut dosyası kodlayalım. NASDAQ için öngörücüleri bulalım.
input ENUM_TIMEFRAMES timeframe = PERIOD_H1; input int maperiod = 50; input int rsiperiod = 13; int total_data = 744; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { string file_name = "NASDAQ_DATA.csv"; string nasdaq_symbol = "#NQ100", s_p500_symbol ="#SP500"; //--- int handle = FileOpen(file_name,FILE_CSV|FILE_READ|FILE_WRITE,","); if (handle == INVALID_HANDLE) { Print("data to work with is nowhere to be found Err=",GetLastError()); } //--- MqlRates nasdaq[]; ArraySetAsSeries(nasdaq,true); CopyRates(nasdaq_symbol,timeframe,1,total_data,nasdaq); //--- MqlRates s_p[]; ArraySetAsSeries(s_p,true); CopyRates(s_p500_symbol,timeframe,1,total_data,s_p); //--- Moving Average Data int ma_handle = iMA(nasdaq_symbol,timeframe,maperiod,0,MODE_SMA,PRICE_CLOSE); double ma_values[]; ArraySetAsSeries(ma_values,true); CopyBuffer(ma_handle,0,1,total_data,ma_values); //--- Rsi values data int rsi_handle = iRSI(nasdaq_symbol,timeframe,rsiperiod,PRICE_CLOSE); double rsi_values[]; ArraySetAsSeries(rsi_values,true); CopyBuffer(rsi_handle,0,1,total_data,rsi_values); //--- if (handle>0) { FileWrite(handle,"S&P500","NASDAQ","50SMA","13RSI"); for (int i=0; i<total_data; i++) { string str1 = DoubleToString(s_p[i].close,Digits()); string str2 = DoubleToString(nasdaq[i].close,Digits()); string str3 = DoubleToString(ma_values[i],Digits()); string str4 = DoubleToString(rsi_values[i],Digits()); FileWrite(handle,str1,str2,str3,str4); } } FileClose(handle); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
Komut dosyasında NASDAQ ve S&P 500 kapanış fiyatlarını ve 50 periyotluk SMA, 13 periyotluk RSI değerlerini topladık. Verileri bir CSV dosyasında başarılı bir şekilde topladık, şimdi verileri Python'da Anaconda üzerinde Jupyter Notebook ile görselleştireceğiz. Makinelerinde Anaconda kurulu olmayanlar için bu yazıda kullanılan veri bilimi Python kodunu Google Colab'da çalıştırabilirsiniz.
Test komut dosyamız tarafından oluşturulan CSV dosyasını açmadan önce, Python tarafından okunabilmesi için onu UTF-8 kodlamasına dönüştürmeniz gerekir. CSV dosyasını not defteri ile açın ve UTF-8 kodlaması halinde kaydedin. Dosyayı dış dizine kopyalamak iyi bir şey olacaktır, böylece o dizine bağlanmak istediğinizde Python tarafından ayrı olarak okunacaktır, Pandas kullanarak CSV dosyasını okuyalım ve veri değişkeninde depolayalım.
Çıktı aşağıdaki gibidir:
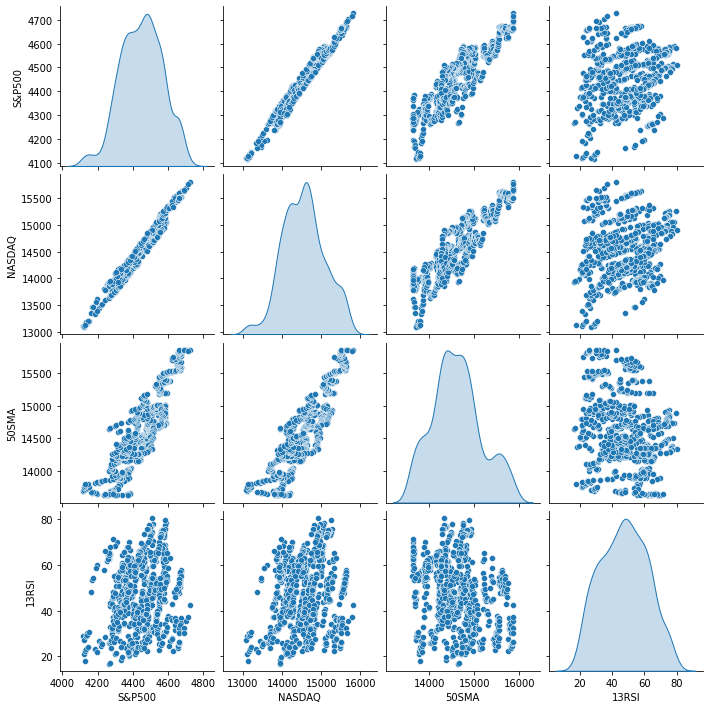
Verilerin görsel sunumundan, NASDAQ ile S&P 500 arasında çok güçlü bir ilişki olduğunu, NASDAQ ile 50 periyotluk SMA arasında da güçlü bir ilişki olduğunu görebiliyoruz. Daha önce de belirttiğimiz gibi, veriler grafiğin her tarafına dağıldığında, lineer ilişkiler bulmaya çalışıyorsak, bağımsız değişken hedefin iyi bir öngörücüsü olmayabilir. Ancak korelasyon konusunda sayıların söylediklerine bakalım, görsel olarak değil sayılara dayalı olarak sonuç çıkaralım. Değişkenlerin birbirleriyle nasıl ilişkili olduğunu anlamak adına korelasyon katsayısı olarak bilinen metriği kullanacağız.
Korelasyon katsayısı
Bağımsız değişken ile hedef arasındaki gücü ölçmek için kullanılır.
Çeşitli korelasyon katsayıları vardır, ancak biz lineer regresyon için olan en popüler korelasyon katsayısını kullanacağız: -1 ile +1 arasında değişen Pearson korelasyon katsayısı (r).
Korelasyonun katsayısının olası en uç değerler olan -1 ve +1 olması, x ve y arasında sırasıyla mükemmel negatif lineer ve mükemmel pozitif lineer ilişkiyi gösterirken, 0 olması lineer korelasyonun olmadığını gösterir.
Pearson korelasyon katsayısı (r) formülü:
Ana kütüphanemizin içerisinde linearRegressionLib.mqh oluşturdum, şimdi corrcoef() fonksiyonunu kodlayalım.
Değerler için mean fonksiyonuyla başlayalım: ortalama (mean), tüm verilerin toplamının toplam öğe sayısına bölünmesidir.
double CSimpleLinearRegression::mean(double &data[]) { double x_y__bar=0; for (int i=0; i<ArraySize(data); i++) { x_y__bar += data[i]; // all values summation } x_y__bar = x_y__bar/ArraySize(data); //total value after summation divided by total number of elements return(x_y__bar); }Şimdi Pearson korelasyon katsayısı için kodlama yapalım.
double CSimpleLinearRegression::corrcoef(double &x[],double &y[]) { double r=0; double numerator =0, denominator =0; double x__x =0, y__y=0; for(int i=0; i<ArraySize(x); i++) { numerator += (x[i]-mean(x))*(y[i]-mean(y)); x__x += MathPow((x[i]-mean(x)),2); //summation of x values minus it's mean squared y__y += MathPow((y[i]-mean(y)),2); //summation of y values minus it's mean squared } denominator = MathSqrt(x__x)*MathSqrt(y__y); //left x side of the equation squared times right side of the equation squared r = numerator/denominator; return(r); }
TestSript.mq5 dosyamızda sonucu yazdırdığımızda,
Print("Correlation Coefficient NASDAQ vs S&P 500 = ",lr.corrcoef(s_p,y_nasdaq)); Print("Correlation Coefficient NASDAQ vs 50SMA = ",lr.corrcoef(ma,y_nasdaq)); Print("Correlation Coefficient NASDAQ Vs rsi = ",lr.corrcoef(rsi,y_nasdaq));
çıktı şu şekilde olacaktır:
Correlation Coefficient NASDAQ vs S&P 500 = 0.9807093773142763
Correlation Coefficient NASDAQ vs 50SMA = 0.8746579124626006
Correlation Coefficient NASDAQ Vs rsi = 0.24245225451004537
Gördüğünüz gibi NASDAQ ve S&P500 diğer tüm veri sütunları arasında çok güçlü bir korelasyona sahiptir (çünkü korelasyon katsayısı 1'e çok yakındır), dolayısıyla basit lineer regresyon modelimizi oluşturmaya devam ederken diğer zayıf sütunları çıkarmamız gerekir.
Artık modelimizi üzerine inşa edeceğimiz iki veri sütunumuz var. Modelimizi oluşturmaya devam edelim.
x Katsayısı
Eğim (m) olarak da bilinen x katsayısı, tanımı gereği y'deki değişimin x'teki değişime oranı ya da başka bir deyişle doğrunun dikliğidir.
Formül:
eğim = y'deki değişim / x'deki değişim
Cebirden hatırlayacağınız şekilde, formülde eğim m olarak ifade edilir:
y = mx + c
Lineer regresyon eğimi m'yi bulmak için formül şöyledir:
Artık formülü biliyoruz, şimdi modelimizin eğimi için kodlama yapalım.
double CSimpleLinearRegression::coefficient_of_X() { double m=0; double x_mean=mean(x_values); double y_mean=mean(y_values);; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<(ArraySize(x_values)+ArraySize(y_values))/2; i++) { x__x = x_values[i] - x_mean; //right side of the numerator (x-side) y__y = y_values[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
y_values ve x_values dizilerine dikkat edin. Bu diziler CSimpleLinearRegression sınıfında Init() fonksiyonunda başlatılır ve kopyalanır.
İşte CSimpleLinearRegression::Init() fonksiyonu:
void CSimpleLinearRegression::Init(double& x[], double& y[]) { ArrayCopy(x_values,x); ArrayCopy(y_values,y); //--- if (ArraySize(x_values)!=ArraySize(y_values)) Print(" Two of your Arrays seems to vary In Size, This could lead to inaccurate calculations ",__FUNCTION__); int columns=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } columns++; if (FileIsLineEnding(m_handle)) { rows++; columns=0; } } m_rows = rows; m_columns = columns; FileClose(m_handle); //--- }
x katsayısını kodlamayı tamamladık, şimdi bir sonraki kısma geçelim.
y Kesimi
Daha önce de belirttiğimiz gibi y-kesimi, x değeri sıfır olduğundaki y değeridir veya doğru y eksenini kestiğindeki y değeridir.

y-kesimini bulma
Denklemden:
y = mx + c
mx'i denklemin sol tarafına alıp denklemi soldan sağa çevirdiğinizde, x-kesimi için nihai denklem şu şekilde olacaktır:
c = y - mx
Burada,
y = tüm y değerlerinin ortalaması
x = tüm x değerlerinin ortalaması
Şimdi, y-kesimini bulacak fonksiyon için kod yazalım.
double CSimpleLinearRegression::y_intercept() { // c = y - mx return (mean(y_values)-coefficient_of_X()*mean(x_values)); }
y-kesimi ile işimiz bitti, şimdi ise lineer regresyon modelimizi LinearRegressionMain() ana fonksiyonumuzda yazdırarak oluşturalım.
void CSimpleLinearRegression::LinearRegressionMain(double &predict_y[]) { double slope = coefficient_of_X(); double constant_y_intercept= y_intercept(); Print("The Linear Regression Model is "," Y =",DoubleToString(slope,2),"x+",DoubleToString(constant_y_intercept,2)); ArrayResize(predict_y,ArraySize(y_values)); for (int i=0; i<ArraySize(x_values); i++) predict_y[i] = coefficient_of_X()*x_values[i]+y_intercept(); //--- }
Modelimizi ayrıca y'nin öngörülen değerlerini elde etmek için de kullanıyoruz, bu bazen gelecekte modelimizi oluşturmaya devam ederken ve doğruluğunu analiz ederken yararlı olacaktır.
Fonksiyonu TestScript.mq5 içerisindeki Onstart() fonksiyonunda çağıralım.
lr.LinearRegressionMain(y_nasdaq_predicted);
Çıktı şu şekilde olacaktır:
2022.03.03 10:41:35.888 TestScript (#SP500,H1) The Linear Regression Model is Y =4.35241x+-4818.54986
void CSimpleLinearRegression::GetDataToArray(double &array[],string file_name,string delimiter,int column_number) { m_filename = file_name; m_delimiter = delimiter; int column=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } column++; //Get data by each Column if (column==column_number) //if we are on the specific column that we want { ArrayResize(array,rows+1); if (rows==0) { if ((double(data))!=0) //Just in case the first line of our CSV column has a name of the column { array[rows]= NormalizeDouble((double)data,Digits()); } else { ArrayRemove(array,0,1); } } else { array[rows-1]= StringToDouble(data); } //Print("column ",column," "," Value ",(double)data); } //--- if (FileIsLineEnding(m_handle)) { rows++; column=0; } } FileClose(m_handle); }
fileopen() void fonksiyonunda:
void CSimpleLinearRegression::fileopen(void) { m_handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV,m_delimiter); if (m_handle==INVALID_HANDLE) { Print("Data to work with is nowhere to be found, Error = ",GetLastError()," ", __FUNCTION__); } //--- }
Şimdi TestScript içerisinde, ilk olarak iki dizi bildirmemiz gerekiyor:
double s_p[]; //Array for storing S&P 500 values double y_nasdaq[]; //Array for storing NASDAQ values
Yapmamız gereken bir sonraki şey, GetDataToArray() void fonksiyonumuzdan referanslarını almak için bu dizileri iletmektir:
lr.GetDataToArray(s_p,file_name,",",1); lr.GetDataToArray(y_nasdaq,file_name,",",2);
Fonksiyon argümanlarımız sınıfımızın public bölümünde şu şekilde göründüğü için sütun numaralarına dikkat edin:
void GetDataToArray(double& array[],string filename, string delimiter, int column_number);
Doğru sütun numarasına başvurduğunuzdan emin olun. Sütunlar CSV dosyasında aşağıdaki gibi düzenlenir:
S&P500,NASDAQ,50SMA,13RSI 4377.5,14168.6,14121.1,59.3 4351.3,14053.2,14118.1,48.0 4342.6,14079.3,14117.0,50.9 4321.2,14038.1,14115.6,46.1 4331.8,14092.9,14114.6,52.5 4336.1,14110.2,14111.8,54.7 4331.5,14101.4,14109.4,53.8 4336.4,14096.8,14104.7,53.3 .....
GetDataToArray() fonksiyonunu çağırdıktan sonra, Init() fonksiyonunu çağırmanın zamanı gelmiştir, çünkü veriler düzgün bir şekilde toplanmadan ve dizilerinde depolanmadan kütüphaneyi başlatmak mantıklı değildir. Fonksiyonların doğru sırayla çağrılması şu şekilde olur:
void OnStart() { string file_name = "NASDAQ_DATA.csv"; double s_p[]; double y_nasdaq[]; double y_nasdaq_predicted[]; lr.GetDataToArray(s_p,file_name,",",1); //Data is taken from the first column and gets stored in the s_p Array lr.GetDataToArray(y_nasdaq,file_name,",",2); //Data is taken from the second column and gets stored in the y_nasdaq Array //--- lr.Init(s_p,y_nasdaq); { lr.LinearRegressionMain(y_nasdaq_predicted); Print("slope of a line ",lr.coefficient_of_X()); } }
Artık y_nasdaq_predicted dizisinde depolanan öngörü değerlerine sahibiz. Şimdi bağımlı değişkeni (NASDAQ), bağımsız değişkeni (S&P500) ve öngörüleri aynı eğri üzerinde görselleştirelim.
Jupyter not defterinizde aşağıdaki kodu çalıştırın:
Python kodunun tamamı makalenin sonuna eklenmiştir.
Yukarıdaki kod parçacığını başarıyla çalıştırdıktan sonra aşağıdaki grafiği elde edeceksiniz:
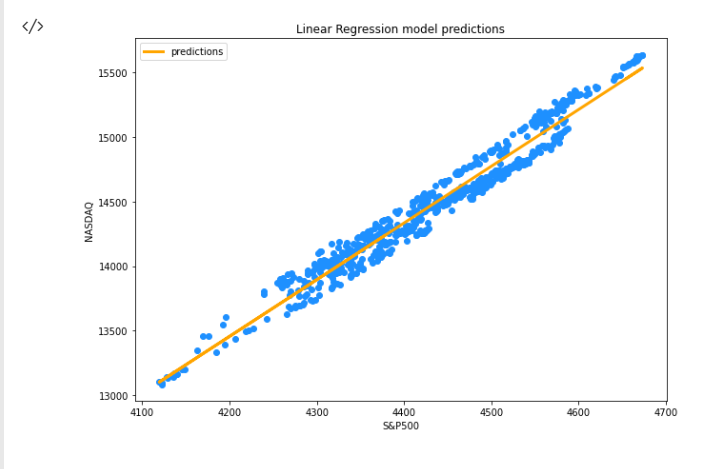
Şimdi, modelimize ve diğer gerekli şeylere sahibiz, peki ya modelimizin doğruluğu? Modelimiz herhangi bir şey ifade edecek ya da herhangi bir yerde kullanılacak kadar iyi mi?
Modelimizin hedef değişkeni öngörmede ne kadar iyi olduğunu anlamak adına r-kare olarak adlandırılan belirleyicilik katsayısı metriğini kullanırız.
r-kare
Bu, model tarafından açıklanan toplam y varyansının önermesidir.
r-kare değerini bulmak için öngörüdeki hatayı anlamamız gerekir. Öngörü hatası, y'nin gerçek değeri ile y'nin öngörülen değeri arasındaki farktır.
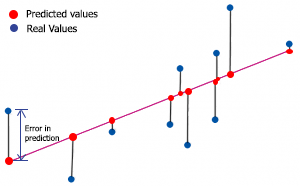
Matematiksel olarak,
Hata = y'nin gerçek değeri - y'nin öngörülen değeri
r-kare formülü ise şu şekildedir:
r-kare = 1 - (Karesel hataların toplamı / Karesel artıkların toplamı)
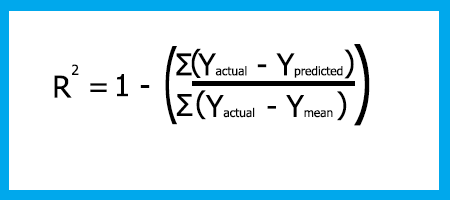
Neden karesel hataları kullanıyoruz?
- Hatalar pozitif veya negatif (çizginin üstünde veya altında) olabilir, onları pozitif tutmak için karelerini alıyoruz.
- Negatif değerler hatayı azaltabilir.
- Ayrıca, mümkün olan en iyi uyumu elde edebilmek için büyük hataları cezalandırmak amacıyla da hataların karesini alıyoruz.
Sıfır, modelin y'nin hiçbir varyansını açıklayamadığı anlamına gelir ve modelin mümkün olan en kötü model olduğunu gösterir. Bir ise modelin veri kümesindeki y'nin tüm varyansını açıklayabildiğini gösterir (böyle bir model mevcut değildir)
.
r-kare çıktısına modelin ne kadar iyi olduğunun yüzdesi olarak bakabilirsiniz. Sıfır, modelin yüzde sıfır doğru, bir ise modelin yüzde yüz doğru olduğu anlamına gelir.
Şimdi r-kare için kodlama yapalım.
double CSimpleLinearRegression::r_squared() { double error=0; double numerator =0, denominator=0; double y_mean = mean(y_values); //--- if (ArraySize(m_ypredicted)==0) Print("The Predicted values Array seems to have no values, Call the main Simple Linear Regression Funtion before any use of this function = ",__FUNCTION__); else { for (int i=0; i<ArraySize(y_values); i++) { numerator += MathPow((y_values[i]-m_ypredicted[i]),2); denominator += MathPow((y_values[i]-y_mean),2); } error = 1 - (numerator/denominator); } return(error); }
LinearRegressionMain içerisindeki, referans olarak iletilen predicted_y[] dizisini (öngörülen değerleri depoladığımız dizi) sınıfımızın private bölümünde bildirilen bir global değişken dizisine kopyalamamız gerekir.
private: int m_handle; string m_filename; string m_delimiter; double m_ypredicted[]; double x_values[]; double y_values[];
LinearRegressionMain'in sonuna, bu diziyi m_ypredicted[] global değişken dizisine kopyalamak için bir satır ekledim.
//At the end of the function LinearRegressionMain(double &predict_y[]) I added the following line, // Copy the predicted values to m_ypredicted[], to be Accessed inside the library ArrayCopy(m_ypredicted,predict_y);
Şimdi TestScript'imizin içerisinde r-kare değerini yazdıralım.
Print(" R_SQUARED = ",lr.r_squared());
Çıktı şu şekilde olacaktır:
2022.03.03 10:40:53.413 TestScript (#SP500,H1) R_SQUARED = 0.9590906984145334
Basit lineer regresyon için bu kadar, şimdi çoklu lineer regresyonun nasıl görüneceğine bakalım.
Çoklu Lineer Regresyon
Çoklu lineer regresyon bir bağımsız değişkene ve birden fazla bağımlı değişkene sahiptir.
Çoklu lineer regresyon modelinin formülü aşağıdaki gibidir:
Sınıfımızın private ve public bölümlerini kodladıktan sonra kütüphanemiz şu şekilde görünür.
class CMultipleLinearRegression: public CSimpleLinearRegression { private: int m_independent_vars; public: CMultipleLinearRegression(void); ~CMultipleLinearRegression(void); double coefficient_of_X(double& x_arr[],double& y_arr[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[],double& C[],double& D[]); };
Birden fazla değerle çalışacağımız için, bu, fonksiyon argümanlarının çok sayıda referans dizisiyle oynayacağımız kısımdır, uygulamak adına daha kısa bir yol bulamadım.
İki bağımlı değişken için lineer regresyon modeli oluşturmak adına şu fonksiyonu kullanacağız:
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[]) { // Multiple regression formula = y = M1X1+M2X2+M3X3+...+C double constant_y_intercept=y_interceptforMultiple(Y,A,B); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2)+"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(constant_y_intercept,2)); int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+constant_y_intercept; }
Bu örnek için y-kesimi, çalışmaya karar verilen veri sütunlarının sayısına bağlı olacaktır. Formülü çoklu lineer regresyondan türettikten sonra, nihai formül şu şekilde olacaktır:
c = y - m 1 x 1 - m 2 x 2
Kodladıktan sonra şu şekilde görünür:
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[]) { //formula c=Y-M1X1-M2X2; return(mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)); }
Üç değişken söz konusu olduğunda, bir değişken daha ekleyerek fonksiyonu yeniden kodlamak yeterlidir.
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[],double &C[],double &D[]) { double constant_y_intercept = y_interceptforMultiple(Y,A,B,C,D); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); double slope3 = coefficient_of_X(C,Y); double slope4 = coefficient_of_X(D,Y); //--- Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2),"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(slope3,2)+"C"+DoubleToString(slope4,2)+"D"+DoubleToString(constant_y_intercept,2)); //--- int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+slope3*C[i]+slope4*D[i]+constant_y_intercept; }
Çoklu lineer regresyonumuz için sabit/y-kesimi noktası ise şu şekilde olacaktır:
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[],double &C[],double &D[]) { return (mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)-coefficient_of_X(C,Y)*mean(C)-coefficient_of_X(D,Y)*mean(D)); }
Lineer Regresyon Varsayımları
Lineer regresyon modeli bir dizi varsayıma dayanır, eğer temel veri kümesi bu varsayımları karşılamıyorsa, verilerin dönüştürülmesi gerekebilir, aksi takdirde lineer model iyi bir uyum sağlamayabilir.
- Lineerlik varsayımı. Bağımlı/hedef değişken ile bağımsız/öngörücü değişkenler arasında lineer bir ilişki olduğunu varsayar.
- Hata dağılımının normalliği varsayımı.
- Hatalar modelle birlikte normal dağılım göstermelidir.
- Gerçek değerler ile öngörülen değerler arasındaki dağılım grafiği, verilerin modele eşit olarak dağıldığını göstermelidir.
Lineer Regresyon Modelinin Avantajları
Uygulaması basit ve çıktıları ve katsayıları yorumlaması daha kolay.
Dezavantajlar
- Bağımlı ve bağımsız değişkenler arasında lineer bir ilişki olduğunu varsayar.
- Uç değerlerin regresyon üzerinde büyük bir etkisi vardır.
- Lineer regresyon, özellikler arasında bağımsızlık olduğunu varsayar.
- Lineer regresyon, bağımlı değişkenin ortalaması ile bağımsız değişken arasındaki ilişkiye bakar.
- Ortalamanın tek bir değişkenin tam bir tanımı olmadığı gibi, lineer regresyon da değişkenler arasındaki ilişkilerin tam bir tanımı değildir.
- Sınırlar lineerdir.
Son Düşünceler
Kütüphanemiz tam olmaktan uzak olsa da, lineer regresyon algoritmalarının, enstrümanlar, göstergeler vb. arasındaki korelasyonlara dayalı ticaret stratejileri oluşturmada çok yararlı olabileceğini düşünüyorum. Bu makalede, modelimizi eğitme ve test etme ve böylece sonuçları daha da iyileştirme konusuna girmedim. Bunu bir sonraki makalede ele alacağız, takipte kalın. Github depomdaki Python koduna buradan ulaşabilirsiniz. Kütüphaneye her türlü katkınızı bekliyorum, ayrıca düşüncelerinizi makalenin tartışma bölümünde paylaşmaktan da çekinmeyin.
Yakında görüşmek üzere.
MetaQuotes Ltd tarafından İngilizceden çevrilmiştir.
Orijinal makale: https://www.mql5.com/en/articles/10459
Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.
Bu makale sitenin bir kullanıcısı tarafından yazılmıştır ve kendi kişisel görüşlerini yansıtmaktadır. MetaQuotes Ltd, sunulan bilgilerin doğruluğundan veya açıklanan çözümlerin, stratejilerin veya tavsiyelerin kullanımından kaynaklanan herhangi bir sonuçtan sorumlu değildir.
 Hareketli ortalamalar ile neler yapılabilir?
Hareketli ortalamalar ile neler yapılabilir?
 Stochastic Oscillator göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
Stochastic Oscillator göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
 Veri Bilimi ve Makine Öğrenimi (Bölüm 02): Lojistik Regresyon
Veri Bilimi ve Makine Öğrenimi (Bölüm 02): Lojistik Regresyon
 MACD göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
MACD göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz

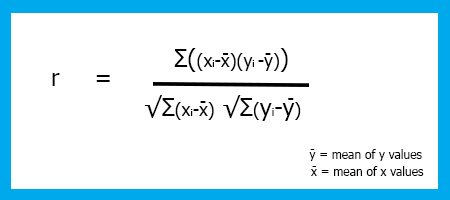
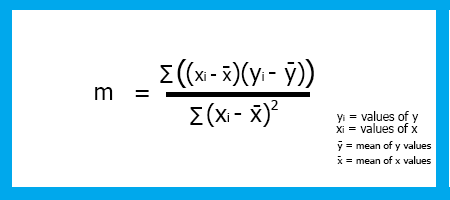
What is a Model
Model, bir sonekten başka bir şey değildir.
Son ek mi? Bunun ne anlama geldiğini anlamıyorum.
Test betiğimiz tarafından oluşturulan bir CSV dosyasını açmadan önce, python tarafından okunabilmesi için UTF-8 kodlamasına dönüştürmeniz gerekir.
Nedenmiş o? Sadece doğrudan MQL'den bir UTF-8 veri dosyası oluşturun.
Kırmızı elips benim tarafımdan eklenmiştir. Bu yanlış, bu nokta bir "y-intercept" değil ve koordinatları (0,-5) değil.
Son ek mi? Bunun ne anlama geldiğini anlamıyorum.
Neden böyle? Doğrudan MQL'den bir UTF-8 veri dosyası oluşturmanız yeterlidir.
Kırmızı elips benim tarafımdan eklenmiştir. Bu yanlış, bu nokta bir "y-kesişim noktası" değildir ve koordinatları (0,-5) değildir.
sonek kelimesi ile matematiksel bir gösterimi kastediyorum, örneğin y=mx+c bu bir modeldir
Evet anladım, resimde bir hata yaptım, diğer noktanın (-5,0) olması gerekiyordu ve bu bir "y-intercept" değil
Merhaba, doğrusal regresyon ve potansiyelleri hakkındaki özlü makale için teşekkürler.
Peasson katsayısı formülünün paydasında kusurlar var.
merhaba, belki de oradadır, sadece ben bulamadım, ama makalede kullanılan NASDAQ.csv dosyası nerede?