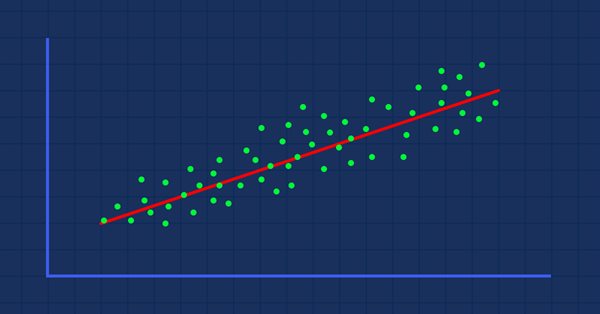
データサイエンスと機械学習(第01回):線形回帰
はじめに
不十分な資料で、早まった仮説なんか作りあげるのは、この職業には禁物ですからね。
- シャーロックホームズ
データサイエンス
データサイエンスは、科学的手法、プロセス、アルゴリズム、システムを用いて、ノイズの多いデータ、構造化データ、非構造化データから知識と洞察を抽出し、データからのその知識と実用的洞察を幅広い応用領域で適用する学際的分野です。
データサイエンティストとは、プログラミングコードを作成し、それを統計的な知識と組み合わせて、データから洞察を得る人のことです。
この連載に期待できること
- 理論(数学の方程式のようなもの):理論はデータサイエンスで最も重要なものです。アルゴリズムを深く理解し、モデルがどのように振る舞うのか、なぜそのように振る舞うのかを理解することは、アルゴリズムそのものをコーディングするよりもずっと難しいことです。
- MQL5とpythonによる実践的な例
線形回帰
従属変数と1つ以上の独立変数との間の直線相関を求めるために使用される予測モデルです。
線形回帰は、以下のような多くのアルゴリズムで使用されている中核的なアルゴリズムの1つです。
- ロジスティック回帰:線形回帰に基づくモデル
- サポートベクターマシン:データサイエンスで有名なアルゴリズムで、線形に基づいたモデル
モデルとは
モデルとは、接尾辞に過ぎません。
理論
グラフを通る直線にはすべて
という方程式があります。この方程式はどこから来るのでしょうか。
xとyが同じ値の2つのデータセットがあるとします。
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
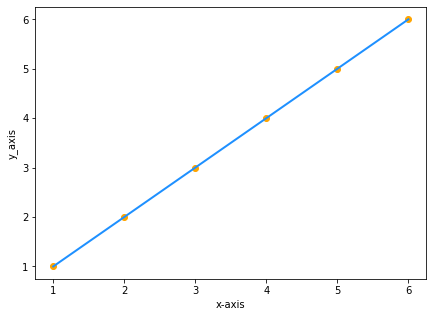
グラフに値をプロットすると、次のようになります。
yはxに等しいので、直線の方程式はy=xになりますね? 違います。
しかし、
y = xは数学的にはy = 1xと同じですが、これはデータサイエンスではかなり異なります。直線の式はy=1xとなり、ここで1は直線とx軸の成す角、または直線の傾きとして知られています。
ただし...
傾き = yの変化量/xの変化量 = m(以下mと表記)
これで、式はy = mxとなります。
最後に、方程式に定数を加える必要があります。これは、xがゼロのときのyの値、言い換えれば、線がy軸を横切るときのyの値です。
最終的に
方程式はy = mx + cとなります(これはデータサイエンスにおけるモデルに過ぎません)。
ここで、cはY切片です
単純線形回帰
単純線形回帰は、1つの従属変数と1つの独立変数を持っています。ここで理解しようとするのは、例えば単純移動平均の変化に対して株価がどのように変化するかなど、2つの変数の関係です。
複雑なデータ
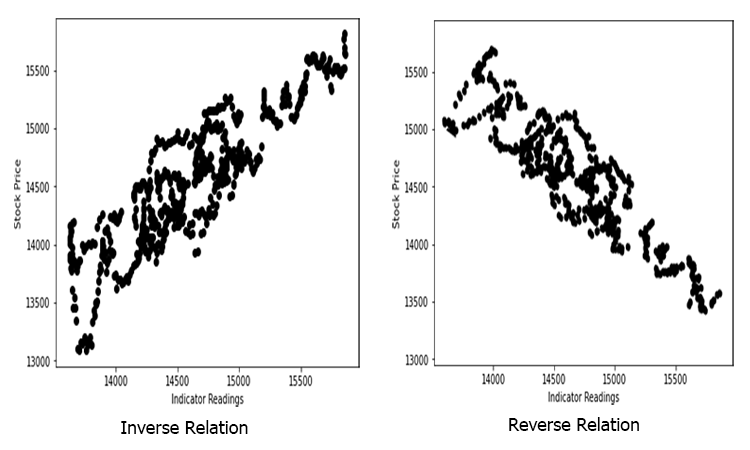
株価に対して描画したときに、ランダムに散らばる指標値があるとします(現実に起こることです)。
この場合、指標/独立変数が株価/独立変数の適切な予測因子でない可能性があります。
データセットに適用する最初のフィルターは、ターゲットと強く相関しない列をすべて削除することです。
非線形に関連するデータで線形モデルを構築するのは、基本的に大きな間違いなので、注意が必要です。
関係は逆(inverseまたはreverse)でもいいのですが、強くなければなりません。直線相関を探しているのですから、それを見つけるべきです。
では、独立変数とターゲットの関係性の強さは、どのように測ればよいのでしょうか。これには、相関係数と呼ばれる指標を使用します。
相関係数
この記事の主要な例として使用するデータセットを作成するスクリプトをコーディングしてみましょう。NASDAQの予測因子を探します。
input ENUM_TIMEFRAMES timeframe = PERIOD_H1; input int maperiod = 50; input int rsiperiod = 13; int total_data = 744; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { string file_name = "NASDAQ_DATA.csv"; string nasdaq_symbol = "#NQ100", s_p500_symbol ="#SP500"; //--- int handle = FileOpen(file_name,FILE_CSV|FILE_READ|FILE_WRITE,","); if (handle == INVALID_HANDLE) { Print("data to work with is nowhere to be found Err=",GetLastError()); } //--- MqlRates nasdaq[]; ArraySetAsSeries(nasdaq,true); CopyRates(nasdaq_symbol,timeframe,1,total_data,nasdaq); //--- MqlRates s_p[]; ArraySetAsSeries(s_p,true); CopyRates(s_p500_symbol,timeframe,1,total_data,s_p); //--- Moving Average Data int ma_handle = iMA(nasdaq_symbol,timeframe,maperiod,0,MODE_SMA,PRICE_CLOSE); double ma_values[]; ArraySetAsSeries(ma_values,true); CopyBuffer(ma_handle,0,1,total_data,ma_values); //--- Rsi values data int rsi_handle = iRSI(nasdaq_symbol,timeframe,rsiperiod,PRICE_CLOSE); double rsi_values[]; ArraySetAsSeries(rsi_values,true); CopyBuffer(rsi_handle,0,1,total_data,rsi_values); //--- if (handle>0) { FileWrite(handle,"S&P500","NASDAQ","50SMA","13RSI"); for (int i=0; i<total_data; i++) { string str1 = DoubleToString(s_p[i].close,Digits()); string str2 = DoubleToString(nasdaq[i].close,Digits()); string str3 = DoubleToString(ma_values[i],Digits()); string str4 = DoubleToString(rsi_values[i],Digits()); FileWrite(handle,str1,str2,str3,str4); } } FileClose(handle); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
スクリプトでは、NASDAQの終値、13期間のRSI値、S&P500、50期間の移動平均を収集しました。CSVファイルへのデータ収集が成功したら、データをAnacondaのJupyter NotebookのPythonで可視化してみましょう。マシンにAnacondaがインストールされていない場合は、この記事で使用されているデータサイエンスのPythonコードをgoogle colabで実行できます。
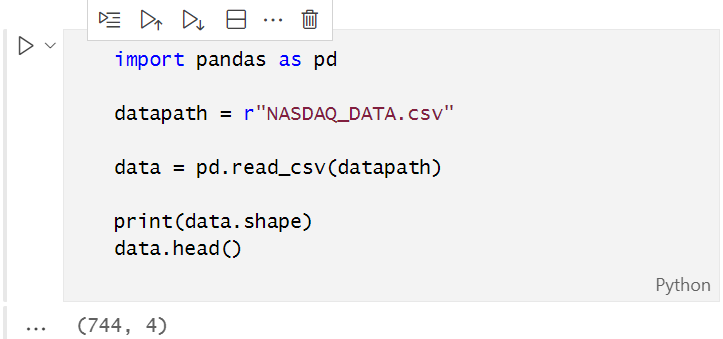
テストスクリプトで作成したCSVファイルを開く前に、Pythonで読めるようにUTF-8エンコーディングに変換する必要があります。CSVファイルをメモ帳で開き、UTF-8エンコーディングで保存します。pandasを使用して、外部ディレクトリにリンクしたときにPythonによって個別に読み取られるように、外部ディレクトリにファイルをコピーすることをお勧めします。pandasを使用して、CSVファイルを読み取り、データ変数に格納します。
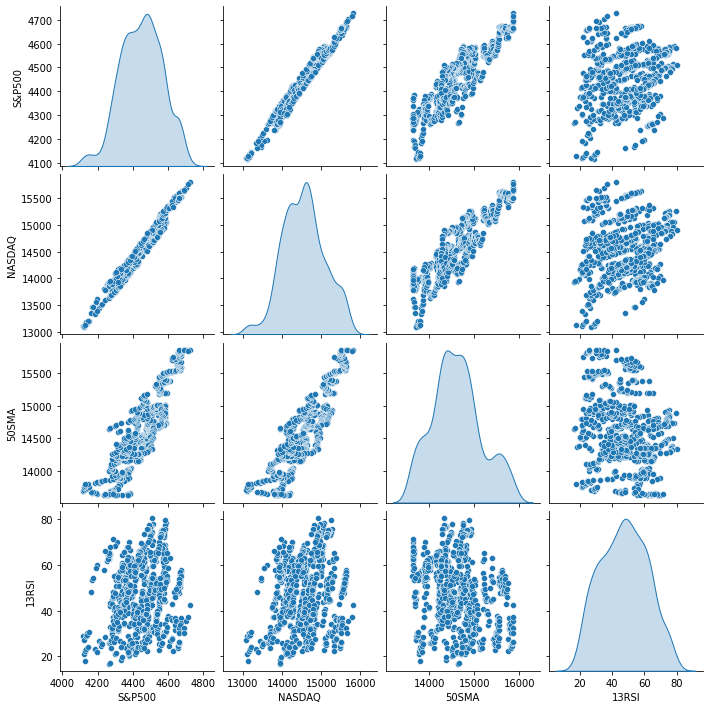
出力は以下の通りです。
データの視覚的表示から、NASDAQとS&P500の間に非常に強い関係があることと、NASDAQと50期間移動平均の間に強い関係があることがすでに見て取れます。先に述べたように、データがグラフ上に散らばっているときはいつでも、直線相関を見つけることになると、独立変数はターゲットの良い予測因子ではないかもしれません。ただし、数字がその相関について語るものを見て、目ではなく数字で結論を出しましょう。変数がお互いにどのように相関しているかを見つけるには、相関係数として知られる指標を使用します。
相関係数
相関係数は、独立変数と対象との間の強さを測定するために使用されます。
相関係数には何種類かありますが、ここでは線形回帰に最もよく使われる、-1から+1までの範囲を持つ、ピアソンの相関係数(R)を使用します。
相関が極端な-1と+1の場合はそれぞれxとyは完全な負/正の直線相関にあり、相関が0の場合は、直線相関がありません。
以下は、相関係数式/ピアソンの係数(R)です。
メインライブラリの中にlinearRegressionLib.mqhを作成しました。関数corrcoef()をコーディングしてみましょう。
まず、値の平均関数から見てみます。平均とは 、すべてのデータの総和を、それらの要素の総数で割ったものです。
double CSimpleLinearRegression::mean(double &data[]) { double x_y__bar=0; for (int i=0; i<ArraySize(data); i++) { x_y__bar += data[i]; // all values summation } x_y__bar = x_y__bar/ArraySize(data); //total value after summation divided by total number of elements return(x_y__bar); }次に、Pearsonのrをコーディングします。
double CSimpleLinearRegression::corrcoef(double &x[],double &y[]) { double r=0; double numerator =0, denominator =0; double x__x =0, y__y=0; for(int i=0; i<ArraySize(x); i++) { numerator += (x[i]-mean(x))*(y[i]-mean(y)); x__x += MathPow((x[i]-mean(x)),2); //summation of x values minus it's mean squared y__y += MathPow((y[i]-mean(y)),2); //summation of y values minus it's mean squared } denominator = MathSqrt(x__x)*MathSqrt(y__y); //left x side of the equation squared times right side of the equation squared r = numerator/denominator; return(r); }
TestSript.mq5で結果を表示します。
Print("Correlation Coefficient NASDAQ vs S&P 500 = ",lr.corrcoef(s_p,y_nasdaq)); Print("Correlation Coefficient NASDAQ vs 50SMA = ",lr.corrcoef(ma,y_nasdaq)); Print("Correlation Coefficient NASDAQ Vs rsi = ",lr.corrcoef(rsi,y_nasdaq));
出力は次のようになります。
Correlation Coefficient NASDAQ vs S&P 500 = 0.9807093773142763
Correlation Coefficient NASDAQ vs 50SMA = 0.8746579124626006
Correlation Coefficient NASDAQ Vs rsi = 0.24245225451004537
NASDAQとS&P500は他のデータ列と非常に強い相関があることがわかる(相関係数が1に非常に近いため)ので、単純線形回帰モデルを構築する際には、他の弱い列を削除する必要があります。
さて、モデルを構築するための2つのデータ列ができたので、モデルの構築を進めましょう。
Xの係数
Xの係数は傾き(m)とも呼ばれ、定義上、Yの変化とXの変化の比、言い換えれば直線の勾配です
式
傾き = Yの変化量/Xの変化量
代数学では、傾きは式の中のmであることを思い出してください。
Y = MX + C
線形回帰の傾きmを求める式は以下のようになります。
式を見たので、モデルの傾きをコーディングしてみましょう。
double CSimpleLinearRegression::coefficient_of_X() { double m=0; double x_mean=mean(x_values); double y_mean=mean(y_values);; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<(ArraySize(x_values)+ArraySize(y_values))/2; i++) { x__x = x_values[i] - x_mean; //right side of the numerator (x-side) y__y = y_values[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
y_values配列とx_values配列に注意を向けてください。これらは、CSimpleLinearRegressionクラスのInit()関数内で初期化されコピーされた配列です。
以下はCSimpleLinearRegression::Init()関数です。
void CSimpleLinearRegression::Init(double& x[], double& y[]) { ArrayCopy(x_values,x); ArrayCopy(y_values,y); //--- if (ArraySize(x_values)!=ArraySize(y_values)) Print(" Two of your Arrays seems to vary In Size, This could lead to inaccurate calculations ",__FUNCTION__); int columns=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } columns++; if (FileIsLineEnding(m_handle)) { rows++; columns=0; } } m_rows = rows; m_columns = columns; FileClose(m_handle); //--- }
Xの係数のコーディングが終わったので、次の部分に移りましょう。
Y切片
先に述べたように、Y切片とは、xの値がゼロのときのyの値、つまり直線がy軸を切ったときのyの値です。

Y切片の求め方
以下の式
Y = M X + C
より、MXを方程式の左辺に移し、方程式の左辺と右辺を交換すると、最終的にX切片の方程式は次のようになります。
C = Y - M X
ここで
Y = すべてのy値の平均
X = すべてのx値の平均
次に、Y切片を求める関数のコードを書いてみましょう。
double CSimpleLinearRegression::y_intercept() { // c = y - mx return (mean(y_values)-coefficient_of_X()*mean(x_values)); }
Y切片の計算が終わったので、主要関数LinearRegressionMain()で出力して線形回帰モデルを構築します。
void CSimpleLinearRegression::LinearRegressionMain(double &predict_y[]) { double slope = coefficient_of_X(); double constant_y_intercept= y_intercept(); Print("The Linear Regression Model is "," Y =",DoubleToString(slope,2),"x+",DoubleToString(constant_y_intercept,2)); ArrayResize(predict_y,ArraySize(y_values)); for (int i=0; i<ArraySize(x_values); i++) predict_y[i] = coefficient_of_X()*x_values[i]+y_intercept(); //--- }
また、このモデルを使ってyの予測値を求めていますが、これは将来、モデルの構築や精度の分析を継続する際に役立つことになります。
TestScript.mq5内のOnstart()関数で呼び出すことにしましょう。
lr.LinearRegressionMain(y_nasdaq_predicted);
出力は次のようになります。
2022.03.03 10:41:35.888 TestScript (#SP500,H1) The Linear Regression Model is Y =4.35241x+-4818.54986
void CSimpleLinearRegression::GetDataToArray(double &array[],string file_name,string delimiter,int column_number) { m_filename = file_name; m_delimiter = delimiter; int column=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } column++; //Get data by each Column if (column==column_number) //if we are on the specific column that we want { ArrayResize(array,rows+1); if (rows==0) { if ((double(data))!=0) //Just in case the first line of our CSV column has a name of the column { array[rows]= NormalizeDouble((double)data,Digits()); } else { ArrayRemove(array,0,1); } } else { array[rows-1]= StringToDouble(data); } //Print("column ",column," "," Value ",(double)data); } //--- if (FileIsLineEnding(m_handle)) { rows++; column=0; } } FileClose(m_handle); }
void関数fileopen()の内部
void CSimpleLinearRegression::fileopen(void) { m_handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV,m_delimiter); if (m_handle==INVALID_HANDLE) { Print("Data to work with is nowhere to be found, Error = ",GetLastError()," ", __FUNCTION__); } //--- }
TestScriptの中で、最初にしなければならないことは、2つの配列を宣言することです。
double s_p[]; //Array for storing S&P 500 values double y_nasdaq[]; //Array for storing NASDAQ values
次にすべきことは、これらの配列を渡して、GetDataToArray()void関数からその参照を取得することです。
lr.GetDataToArray(s_p,file_name,",",1); lr.GetDataToArray(y_nasdaq,file_name,",",2);
クラスのpublicセクションの関数では引数が次のようになるので、列番号に注意してください。
void GetDataToArray(double& array[],string filename, string delimiter, int column_number);
必ず正しい列番号を参照してください。CSVファイルでの列の配置をご覧ください。
S&P500,NASDAQ,50SMA,13RSI 4377.5,14168.6,14121.1,59.3 4351.3,14053.2,14118.1,48.0 4342.6,14079.3,14117.0,50.9 4321.2,14038.1,14115.6,46.1 4331.8,14092.9,14114.6,52.5 4336.1,14110.2,14111.8,54.7 4331.5,14101.4,14109.4,53.8 4336.4,14096.8,14104.7,53.3 .....
データが適切に収集されて配列に格納されていない状態でライブラリを初期化しても意味がないので、GetDataToArray()関数を呼び出したら、今度はInit()関数を呼び出す必要があります。次のように関数を正しい順序で呼び出します。
void OnStart() { string file_name = "NASDAQ_DATA.csv"; double s_p[]; double y_nasdaq[]; double y_nasdaq_predicted[]; lr.GetDataToArray(s_p,file_name,",",1); //Data is taken from the first column and gets stored in the s_p Array lr.GetDataToArray(y_nasdaq,file_name,",",2); //Data is taken from the second column and gets stored in the y_nasdaq Array //--- lr.Init(s_p,y_nasdaq); { lr.LinearRegressionMain(y_nasdaq_predicted); Print("slope of a line ",lr.coefficient_of_X()); } }
予測値が配列y_nasdaq_predictedに格納されたので、従属変数(NASDAQ)、独立変数(S&P500)、予測値を同じ曲線上に可視化してみましょう。
Jupyter Notebook上で次のコードを実行します。
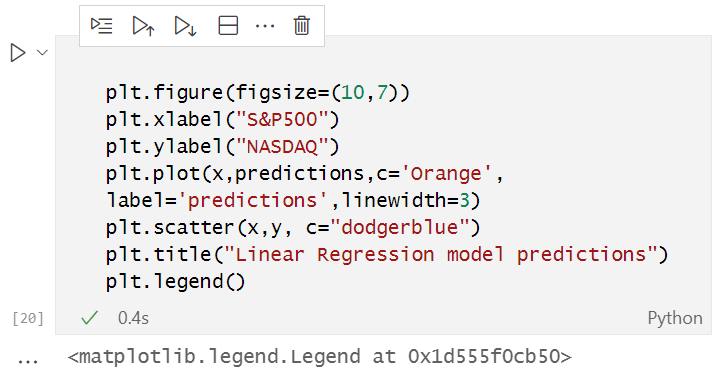
完全なPythonコードは記事の最後に添付してあります。
上記のコードが正常に実行されると、次のようなグラフが表示されます。
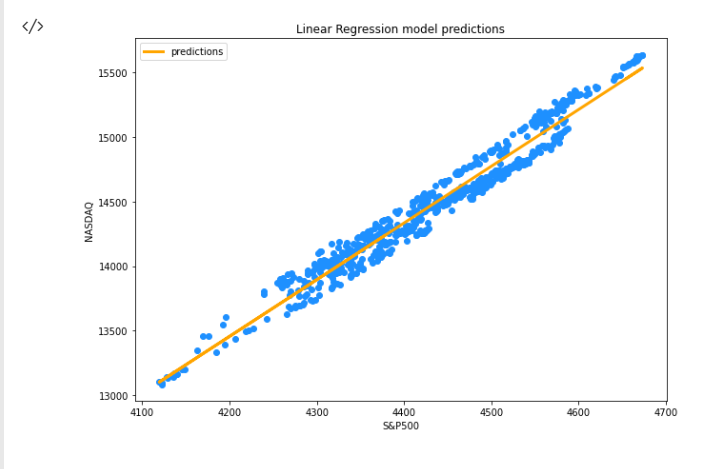
さて、モデルやその他のライブラリを作成しましたが、モデルの精度はどうでしょうか。私たちのモデルは、何かを意味し、何かに使われるのに十分なものなのでしょうか。
モデルがターゲット変数の予測にどれだけ優れているかを理解するために、R2乗と呼ばれ決定係数として知られる指標を使用します。
決定係数
これは、モデルによって説明されたyの全分散の命題です。
決定係数を求めるには、予測誤差を理解する必要があります。予測誤差とは、yの実績値とyの予測値の差のことです。
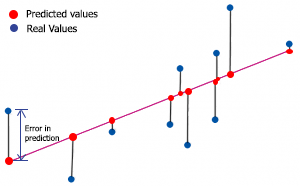
数学的には次のようになります。
誤差 = Y実績値 - Y予測値
線形回帰の式は次になります。
線形回帰 = 1 - (二乗誤差の総和/残差平方和)
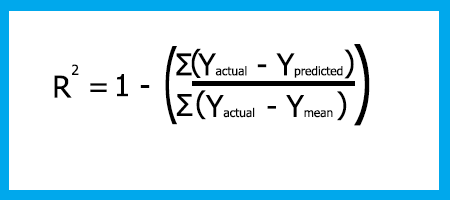
二乗誤差を使用するには次の理由があります。
- 誤差は正または負(線の上または下)になる可能性があるので、正に保つために二乗する
- 負の値が誤差を小さくする可能性がある
- また、誤差を二乗して大きな誤差にペナルティを課して、可能な限り最適なフィットを得られるようにする
0は 、モデルがyの分散を全く説明できないことを意味し、そのモデルが最悪のものであることを示します。1は、モデルがデータセットのyの分散をすべて説明できることを示します(そのようなモデルは存在し,ません)。
決定係数の出力は、モデルがどれだけ優れているかの割合として参照することができます。 0は0%精度、1はモデルが100%正確であることを意味します。
次に、決定係数のコードを書いてみましょう。
double CSimpleLinearRegression::r_squared() { double error=0; double numerator =0, denominator=0; double y_mean = mean(y_values); //--- if (ArraySize(m_ypredicted)==0) Print("The Predicted values Array seems to have no values, Call the main Simple Linear Regression Funtion before any use of this function = ",__FUNCTION__); else { for (int i=0; i<ArraySize(y_values); i++) { numerator += MathPow((y_values[i]-m_ypredicted[i]),2); denominator += MathPow((y_values[i]-y_mean),2); } error = 1 - (numerator/denominator); } return(error); }
LinearRegressionMainの内部では、予測値を参照渡しされるpredicted_y[]配列に格納していますが、その配列をクラスのprivateセクションで宣言されたグローバル変数配列にコピーしなければならないことを思い出してください。
private: int m_handle; string m_filename; string m_delimiter; double m_ypredicted[]; double x_values[]; double y_values[];
LinearRegressionMainの最後に、その配列をグローバル変数配列m_ypredicted[]にコピーする行を追加しました。
//At the end of the function LinearRegressionMain(double &predict_y[]) I added the following line, // Copy the predicted values to m_ypredicted[], to be Accessed inside the library ArrayCopy(m_ypredicted,predict_y);
では、TestScriptで決定係数の値を表示してみましょう。
Print(" R_SQUARED = ",lr.r_squared());
出力は次のようになります。
2022.03.03 10:40:53.413 TestScript (#SP500,H1) R_SQUARED = 0.9590906984145334
単純線形回帰は以上ですが、次は重回帰がどのようなものかを見てみましょう。
重回帰
重回帰は、1つの独立変数と複数の従属変数を持ちます。
重回帰のモデルの式は以下の通りです。
クラスのprivateとpublicの部分をハードコーディングすると、ライブラリは次のようになります。
class CMultipleLinearRegression: public CSimpleLinearRegression { private: int m_independent_vars; public: CMultipleLinearRegression(void); ~CMultipleLinearRegression(void); double coefficient_of_X(double& x_arr[],double& y_arr[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[],double& C[],double& D[]); };
複数の値を扱うため、関数の引数の参照配列をたくさん扱うことになります。実装の近道は見つかりませんでした。
2つの従属変数に対する線形回帰モデルを作成するために、次の関数を使用します。
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[]) { // Multiple regression formula = y = M1X1+M2X2+M3X3+...+C double constant_y_intercept=y_interceptforMultiple(Y,A,B); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2)+"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(constant_y_intercept,2)); int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+constant_y_intercept; }
この場合のY切片は、作業することにしたデータ列の数に基づいています。重回帰から式を導き出した後、最終的な式は次のようになります。
C = Y - M1 X1 - M2 X2
コーディングの後はこのようになります。
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[]) { //formula c=Y-M1X1-M2X2; return(mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)); }
変数が3つの場合は、関数をもう一度ハードコーディングして、別の変数を追加すればよいのです。
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[],double &C[],double &D[]) { double constant_y_intercept = y_interceptforMultiple(Y,A,B,C,D); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); double slope3 = coefficient_of_X(C,Y); double slope4 = coefficient_of_X(D,Y); //--- Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2),"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(slope3,2)+"C"+DoubleToString(slope4,2)+"D"+DoubleToString(constant_y_intercept,2)); //--- int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+slope3*C[i]+slope4*D[i]+constant_y_intercept; }
重回帰の定数/Y切片は先ほど言った通りで、次のようになります。
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[],double &C[],double &D[]) { return (mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)-coefficient_of_X(C,Y)*mean(C)-coefficient_of_X(D,Y)*mean(D)); }
線形回帰の仮定
線形回帰モデルは、一連の仮定に基づいています。基礎となるデータセットがこれらの仮定を満たしていない場合、データを変換しないと線形モデルがうまく適合しない可能性があります。
- 線形性の仮定:従属変数/ターゲット変数と独立変数/予測変数の間に直線相関を仮定する
- 誤差分布の正規性の仮定
- モデルの誤差は正規分布である必要があります
- 実際の値と予測値の散布図は、データがモデル全体に均等に分布していることを示している必要があります
線形回帰モデルの利点
実装が簡単で、出力や係数の解釈がしやすいです。
欠点
- 従属変数と独立変数の間に直線相関があると仮定します。
- 外れ値は回帰に大きな影響を与えます。
- 線形回帰では属性間の独立性が仮定されています。
- 線形回帰は、従属変数の平均値と独立変数の関係を見るものです。
- 平均が単一の変数の完全な記述でないのと同様に、線形回帰は変数間の関係の完全な記述ではありません。
- 境界が線的です。
最終的な考え
線形回帰アルゴリズムは、指標のようなペアや他のものの相関に基づいて取引戦略を作成する際に非常に有用であると思います。私たちのライブラリは、完成からはほど遠いもので、モデルの訓練とテストや結果のさらなる改善が含まれていません。これは次の記事になりますのでお楽しみに。PythonコードはGithubレポジトリでこちらにリンクしてあります。ライブラリへの貢献は歓迎です。また、記事のディスカッションセクションでご自分の考えを自由に共有してください。.
またすぐお会いしましょう。
MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/10459
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 単一チャート上の複数インジケータ(第06部):MetaTrader 5をRADシステムに変える(II)
単一チャート上の複数インジケータ(第06部):MetaTrader 5をRADシステムに変える(II)
 一からの取引エキスパートアドバイザーの開発(第7部):価格別出来高の追加(I)
一からの取引エキスパートアドバイザーの開発(第7部):価格別出来高の追加(I)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索

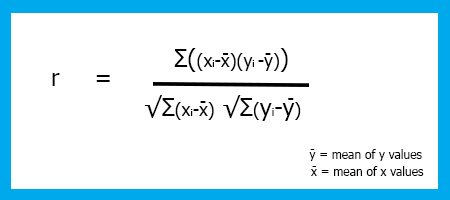
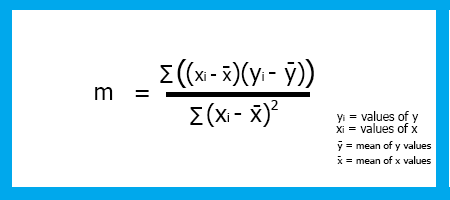

What is a Model
モデルは接尾辞にすぎない
接尾辞?意味がわかりません。
テストスクリプトで作成したCSVファイルを開く前に、pythonで読めるようにUTF-8エンコーディングに変換する必要があります。
なぜですか?MQLから直接UTF-8のデータファイルを作成すればいいのです。
赤い楕円は私がつけた。この点は "y切片 "ではないし、座標も(0,-5)ではない。
接尾辞?この意味がわからない。
なぜですか?MQLから直接UTF-8のデータファイルを作成すればいい。
私が追加した赤い楕円。この点は「y切片」ではないし、座標も(0,-5)ではない。
接尾辞というのは、y=mx+cのような数学的な表記法のことです。
もう一つの点は(-5,0)であるべきで、それは "y-切片 "ではない。
Peasson係数の公式は分母に欠陥がある。
もしかしたらあるかもしれませんが、私が見つけられなかっただけで、記事の中で使われているNASDAQ.csvファイルはどこにありますか?