Aprendizaje automático y Data Science (Parte 01): Regresión lineal
Introducción
“La tentación de construir versiones preliminares a partir de datos incompletos resulta fatal en nuestra profesión”.
(Sherlock Holmes)
Data Science
Es un campo práctico e interdisciplinario que usa métodos, procesos, algoritmos y sistemas científicos para extraer conocimientos y patrones de datos estructurados y no estructurados y aplicar dichos conocimientos y patrones procesables a una amplia gama de áreas diferentes.
Un especialista en Data Science es alguien que crea un código y lo combina con conocimiento estadístico para generar información a partir de los datos.
¿Qué podemos esperar de esta serie de artículos?
- Teoría (en ecuaciones matemáticas): la teoría es muy importante en la ciencia de datos. Uno debe tener una comprensión profunda de los algoritmos y el comportamiento del modelo, y también de las causas de dicho comportamiento. Entender esto resulta mucho más difícil que programar el propio algoritmo.
- Ejemplos prácticos en MQL5 y Python.
Regresión lineal
Es un modelo que muestra la dependencia de una variable respecto a una o más variables.
La regresión lineal es uno de los principales algoritmos utilizados en muchos otros como:
- La regresión logística, un modelo basado en la regresión lineal
- Las máquinas de vectores de soporte, una familia de algoritmos de clasificación supervisados que utilizan la partición lineal del espacio.
Qué es un modelo
El modelo no es más que un sufijo.
Teoría
Cada línea que pasa por el gráfico tiene la siguiente ecuación:
¿De dónde viene?
Digamos que tiene dos conjuntos de datos con los mismos valores de x e y:
| x | y |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
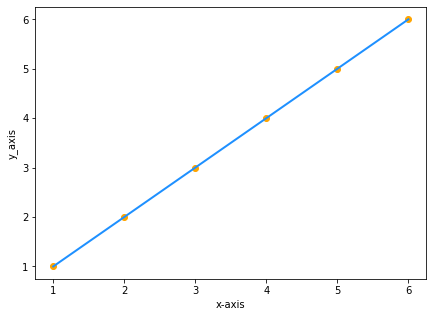
Trazamos los valores en el gráfico:
Dado que y es igual a x, la ecuación de la recta sería y=x, ¿verdad? ¡No!
Aunque
y = x es matemáticamente lo mismo que y = 1x, este no es el caso en la ciencia de datos. La ecuación de una línea recta sería y=1x, donde 1 es el ángulo entre la línea recta y el eje x, también llamado inclinación de la línea.
Pero
el ángulo de inclinación = el cambio de y / el cambio de x = m (llamado m)
Entonces la fórmula sería y = mx.
Finalmente, deberemos añadir una constante a la ecuación, es decir, el valor de y cuando x es igual a cero. En otras palabras, el valor de y cuando la línea cruza el eje y
Entonces
la ecuación será: y = mx + c (esto no es más que un modelo en ciencia de datos)
donde c es la intersección con el eje y
Regresión lineal simple
La regresión lineal simple tiene una variable dependiente y una variable independiente. Este es un intento de comprender la relación entre dos variables, por ejemplo, cómo cambia el precio de una acción al cambiar una media móvil simple.
Datos complejos
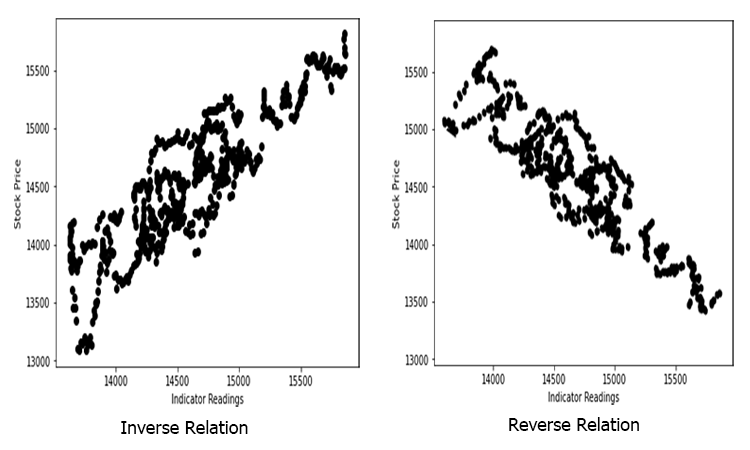
Supongamos que hay valores de indicadores dispersos aleatorios basados en el precio de un activo (situación habitual).
En este caso, nuestro indicador/variable independiente podría no ser un buen predictor del precio del activo/variable dependiente.
El primer filtro que se aplica al conjunto de datos es la eliminación de todas las columnas que no están muy correlacionadas con su objetivo para que no se incluyan en el modelo lineal.
La construcción de un modelo lineal con datos no lineales relacionados es un gran error fundamental, por lo que deberemos tener cuidado al respecto.
La relación no tiene que ser directa, puede ser inversa, pero la relación para el modelo lineal deberá ser fuerte.
Entonces, ¿cómo medimos la fuerza entre la variable independiente y nuestro objetivo? Usaremos una medida conocida como el coeficiente de correlación.
Coeficiente de correlación
Vamos a escribir un script para crear el conjunto de datos que se utilizará como ejemplo principal para este artículo. Buscaremos los predictores NASDAQ.
input ENUM_TIMEFRAMES timeframe = PERIOD_H1; input int maperiod = 50; input int rsiperiod = 13; int total_data = 744; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { string file_name = "NASDAQ_DATA.csv"; string nasdaq_symbol = "#NQ100", s_p500_symbol ="#SP500"; //--- int handle = FileOpen(file_name,FILE_CSV|FILE_READ|FILE_WRITE,","); if (handle == INVALID_HANDLE) { Print("data to work with is nowhere to be found Err=",GetLastError()); } //--- MqlRates nasdaq[]; ArraySetAsSeries(nasdaq,true); CopyRates(nasdaq_symbol,timeframe,1,total_data,nasdaq); //--- MqlRates s_p[]; ArraySetAsSeries(s_p,true); CopyRates(s_p500_symbol,timeframe,1,total_data,s_p); //--- Moving Average Data int ma_handle = iMA(nasdaq_symbol,timeframe,maperiod,0,MODE_SMA,PRICE_CLOSE); double ma_values[]; ArraySetAsSeries(ma_values,true); CopyBuffer(ma_handle,0,1,total_data,ma_values); //--- Rsi values data int rsi_handle = iRSI(nasdaq_symbol,timeframe,rsiperiod,PRICE_CLOSE); double rsi_values[]; ArraySetAsSeries(rsi_values,true); CopyBuffer(rsi_handle,0,1,total_data,rsi_values); //--- if (handle>0) { FileWrite(handle,"S&P500","NASDAQ","50SMA","13RSI"); for (int i=0; i<total_data; i++) { string str1 = DoubleToString(s_p[i].close,Digits()); string str2 = DoubleToString(nasdaq[i].close,Digits()); string str3 = DoubleToString(ma_values[i],Digits()); string str4 = DoubleToString(rsi_values[i],Digits()); FileWrite(handle,str1,str2,str3,str4); } } FileClose(handle); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+
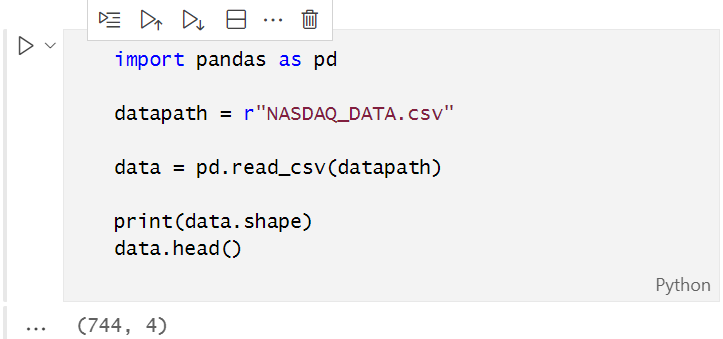
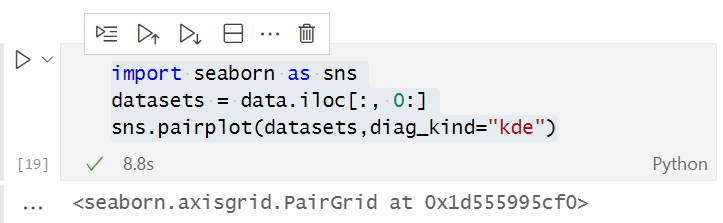
En el script, recopilaremos los precios de cierre de NASDAQ, un RSI de 13 periodos, S&P 500 y una media móvil de 50 periodos. Hemos recopilado los datos en un archivo CSV que visualizaremos ahora en python. Trabajaremos con Anaconda en Jupyter. Si no tiene instalado Anaconda, para procesar los datos, podrá ejecutar el código Python de este artículo en google colab.
Para abrir el archivo CSV generado por el script de prueba, deberá pasarlos a la codificación UTF-8 para que Python pueda leerlo. Abra el archivo CSV en el bloc de notas, y luego guárdelo en la codificación UTF-8. Estaría bien copiar el archivo en un directorio externo, para que Python lo lea por separado según el enlace de ese directorio. En Pandas, leemos el archivo CSV lo guardamos en una variable.
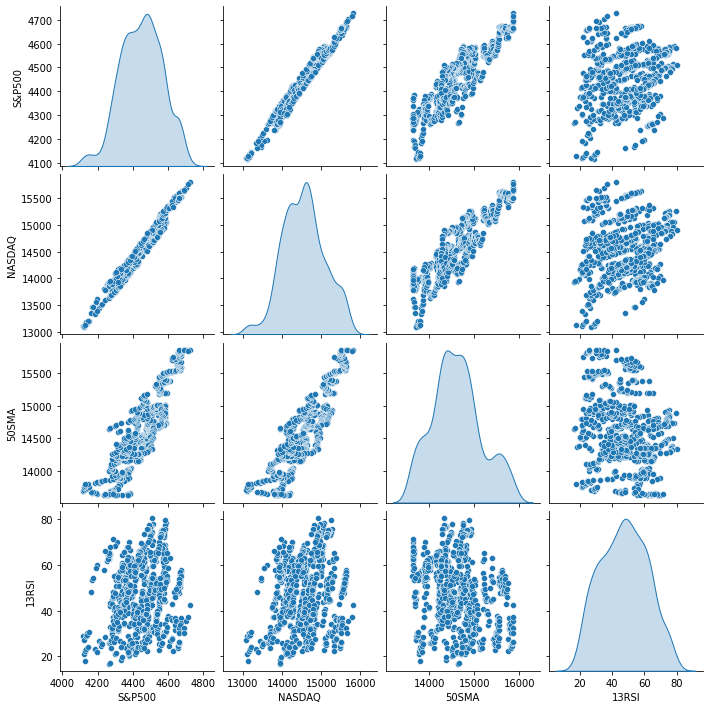
El resultado tendrá el aspecto siguiente:
Por la presentación visual de los datos, ya podemos ver que existe una correlación muy fuerte entre NASDAQ y S&P 500, así como una fuerte correlación entre NASDAQ y su media móvil de 50 periodos. Como ya hemos mencionado, si los datos están dispersos por todo el gráfico, la variable independiente no será un buen predictor al buscar una correlación lineal. Veamos, sin embargo, lo que dicen los números sobre la correlación y saquemos una conclusión basada en los números, no visual. Para comprender cómo se correlacionan las variables entre sí, usaremos el coeficiente de correlación.
Coeficiente de correlación
Se usa para medir la fuerza entre la variable independiente y el objetivo.
Hay varios tipos de coeficientes de correlación, usaremos el más popular para la regresión lineal:el coeficiente de correlación de Pearson (R), que fluctúa entre -1 y +1.
La correlación de los valores extremos -1 y +1 significa, respectivamente, una perfecta relación lineal negativa y positiva entre x e y, mientras que un valor de 0 significará que no existe correlación lineal.
Fórmula del coeficiente de correlación/coeficiente de Pearson (R).
Dentro de la biblioteca principal, hemos creado el archivo linearRegressionLib.mqh. Vamos a escribir la función corrcoef().
Comenzaremos con la función de promedio de los valores: la media es la suma de todos los datos dividida por el número total de elementos.
double CSimpleLinearRegression::mean(double &data[]) { double x_y__bar=0; for (int i=0; i<ArraySize(data); i++) { x_y__bar += data[i]; // all values summation } x_y__bar = x_y__bar/ArraySize(data); //total value after summation divided by total number of elements return(x_y__bar); }Ahora escribimos el código para el coeficiente de Pearson R
double CSimpleLinearRegression::corrcoef(double &x[],double &y[]) { double r=0; double numerator =0, denominator =0; double x__x =0, y__y=0; for(int i=0; i<ArraySize(x); i++) { numerator += (x[i]-mean(x))*(y[i]-mean(y)); x__x += MathPow((x[i]-mean(x)),2); //summation of x values minus it's mean squared y__y += MathPow((y[i]-mean(y)),2); //summation of y values minus it's mean squared } denominator = MathSqrt(x__x)*MathSqrt(y__y); //left x side of the equation squared times right side of the equation squared r = numerator/denominator; return(r); }
Al mostrar mensajes en el script de prueba TestSript.mq5,
Print("Correlation Coefficient NASDAQ vs S&P 500 = ",lr.corrcoef(s_p,y_nasdaq)); Print("Correlation Coefficient NASDAQ vs 50SMA = ",lr.corrcoef(ma,y_nasdaq)); Print("Correlation Coefficient NASDAQ Vs rsi = ",lr.corrcoef(rsi,y_nasdaq));
el resultado será el siguiente
Coeficiente de correlación NASDAQ vs S&P 500 = 0.9807093773142763
Coeficiente de correlación NASDAQ vs 50SMA = 0.8746579124626006
Coeficiente de correlación NASDAQ Vs rsi = 0.24245225451004537
Como podemos ver, NASDAQ y S&P500 tienen una correlación muy fuerte en todas las demás columnas de datos (porque el coeficiente de correlación es muy cercano a 1), por lo que deberemos descartar otras columnas débiles al construir un modelo de regresión lineal simple.
Ahora tenemos dos columnas de datos que utilizaremos para construir nuestro modelo. Vamos a construir nuestro modelo.
Coeficiente X
Por definición, el coeficiente x, también conocido como ángulo de inclinación (m), es la relación entre el cambio de Y y el cambio de X o, en otras palabras, la inclinación de la línea.
Fórmula:
Inclinación = Cambio de Y / Cambio de X
Por el álgebra, recordamos que la inclinación es igual a m en la fórmula
Y = M X + C
La inclinación de la regresión lineal m se puede encontrar a partir de la fórmula
Ahora conocemos la fórmula y podemos escribir el código de la inclinación para nuestro modelo.
double CSimpleLinearRegression::coefficient_of_X() { double m=0; double x_mean=mean(x_values); double y_mean=mean(y_values);; //--- { double x__x=0, y__y=0; double numerator=0, denominator=0; for (int i=0; i<(ArraySize(x_values)+ArraySize(y_values))/2; i++) { x__x = x_values[i] - x_mean; //right side of the numerator (x-side) y__y = y_values[i] - y_mean; //left side of the numerator (y-side) numerator += x__x * y__y; //summation of the product two sides of the numerator denominator += MathPow(x__x,2); } m = numerator/denominator; } return (m); }
Preste atención a las matrices y_values y x_values. Las matrices se inicializan y se copian en la función Init() dentro de la clase CSimpleLinearRegression.
Y aquí está la función CSimpleLinearRegression::Init():
void CSimpleLinearRegression::Init(double& x[], double& y[]) { ArrayCopy(x_values,x); ArrayCopy(y_values,y); //--- if (ArraySize(x_values)!=ArraySize(y_values)) Print(" Похоже, что массивы имеют разный размер. Это может привести к неточным вычислениям ",__FUNCTION__); int columns=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } columns++; if (FileIsLineEnding(m_handle)) { rows++; columns=0; } } m_rows = rows; m_columns = columns; FileClose(m_handle); //--- }
Ya hemos escrito el código en la parte del coeficiente X, vamos a pasar a la parte siguiente.
Y-Intercept
Y-intercept (intersección en Y) es el valor de y cuando x es cero, o el valor de y en el que la línea se cruza con el eje y.

Hallamos y-intercept
en la ecuación
Y = M X + C
trasladamos MX al lado izquierdo de la ecuación, cambiamos los lugares y obtenemos la siguiente ecuación de x-intercept
C = Y - M X
donde
Y = la media de todos los valores de y
x = la media de todos los valores de x
Ahora escribiremos la función para buscar y-intercept
double CSimpleLinearRegression::y_intercept() { // c = y - mx return (mean(y_values)-coefficient_of_X()*mean(x_values)); }
Ya hemos terminado con el eje y. Ahora construiremos nuestro modelo de regresión lineal en la función principal LinearRegressionMain()
void CSimpleLinearRegression::LinearRegressionMain(double &predict_y[]) { double slope = coefficient_of_X(); double constant_y_intercept= y_intercept(); Print("The Linear Regression Model is "," Y =",DoubleToString(slope,2),"x+",DoubleToString(constant_y_intercept,2)); ArrayResize(predict_y,ArraySize(y_values)); for (int i=0; i<ArraySize(x_values); i++) predict_y[i] = coefficient_of_X()*x_values[i]+y_intercept(); //--- }
El modelo también se usará para predecir los valores de y, esto será útil en el futuro a medida que continuamos construyendo nuestro modelo y analizando su precisión.
A continuación, llamaremos a la función Onstart() dentro de TestScript.mq5.
lr.LinearRegressionMain(y_nasdaq_predicted);
El resultado de la llamada será el siguiente
2022.03.03 10:41:35.888 TestScript (#SP500,H1) El modelo de regresión lineal es Y =4.35241x+-4818.54986
void CSimpleLinearRegression::GetDataToArray(double &array[],string file_name,string delimiter,int column_number) { m_filename = file_name; m_delimiter = delimiter; int column=0, columns_total=0; int rows=0; fileopen(); while (!FileIsEnding(m_handle)) { string data = FileReadString(m_handle); if (rows==0) { columns_total++; } column++; //Get data by each Column if (column==column_number) //if we are on the specific column that we want { ArrayResize(array,rows+1); if (rows==0) { if ((double(data))!=0) //Just in case the first line of our CSV column has a name of the column { array[rows]= NormalizeDouble((double)data,Digits()); } else { ArrayRemove(array,0,1); } } else { array[rows-1]= StringToDouble(data); } //Print("column ",column," "," Value ",(double)data); } //--- if (FileIsLineEnding(m_handle)) { rows++; column=0; } } FileClose(m_handle); }
Inside the void Function fileopen()
void CSimpleLinearRegression::fileopen(void) { m_handle = FileOpen(m_filename,FILE_READ|FILE_WRITE|FILE_CSV,m_delimiter); if (m_handle==INVALID_HANDLE) { Print("Data to work with is nowhere to be found, Error = ",GetLastError()," ", __FUNCTION__); } //--- }
Ahora, dentro de TestScript, primero deberemos declarar dos matrices
double s_p[]; //Array for storing S&P 500 values double y_nasdaq[]; //Array for storing NASDAQ values
A continuación, deberemos transmitir estas matrices para obtener un enlace a ellas desde la función GetDataToArray() de tipo void
lr.GetDataToArray(s_p,file_name,",",1); lr.GetDataToArray(y_nasdaq,file_name,",",2);
Preste atención a los números de la columna, ya que los argumentos de nuestra función se verán así en la parte pública de nuestra clase.
void GetDataToArray(double& array[],string filename, string delimiter, int column_number);
Asegúrese de que se está refiriendo al número de columna correcto. Así es como se organizan las columnas en el archivo CSV.
S&P500,NASDAQ,50SMA,13RSI 4377.5,14168.6,14121.1,59.3 4351.3,14053.2,14118.1,48.0 4342.6,14079.3,14117.0,50.9 4321.2,14038.1,14115.6,46.1 4331.8,14092.9,14114.6,52.5 4336.1,14110.2,14111.8,54.7 4331.5,14101.4,14109.4,53.8 4336.4,14096.8,14104.7,53.3 .....
Después de llamar a la función GetDataToArray(), podemos llamar a la función Init(), porque no tiene sentido inicializar la biblioteca sin recopilar y almacenar correctamente los datos en las matrices correspondientes. Este es el orden correcto para llamar a la función:
void OnStart() { string file_name = "NASDAQ_DATA.csv"; double s_p[]; double y_nasdaq[]; double y_nasdaq_predicted[]; lr.GetDataToArray(s_p,file_name,",",1); //Data is taken from the first column and gets stored in the s_p Array lr.GetDataToArray(y_nasdaq,file_name,",",2); //Data is taken from the second column and gets stored in the y_nasdaq Array //--- lr.Init(s_p,y_nasdaq); { lr.LinearRegressionMain(y_nasdaq_predicted); Print("slope of a line ",lr.coefficient_of_X()); } }
Hemos obtenido los valores predichos, que se almacenan en la matriz y_nasdaq_predicted. Ahora representaremos la variable dependiente (NASDAQ), la variable independiente (S&P500) y los pronósticos en la misma curva.
Ejecutamos el código en el bloc de notas Jupyter.
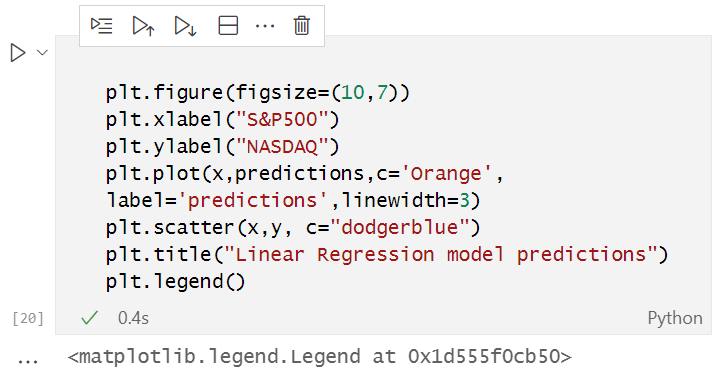 Visualizando
Visualizando
Adjuntamos el código Python completo al final del artículo.
Después de ejecutar este fragmento de código, deberíamos ver un gráfico como el siguiente:
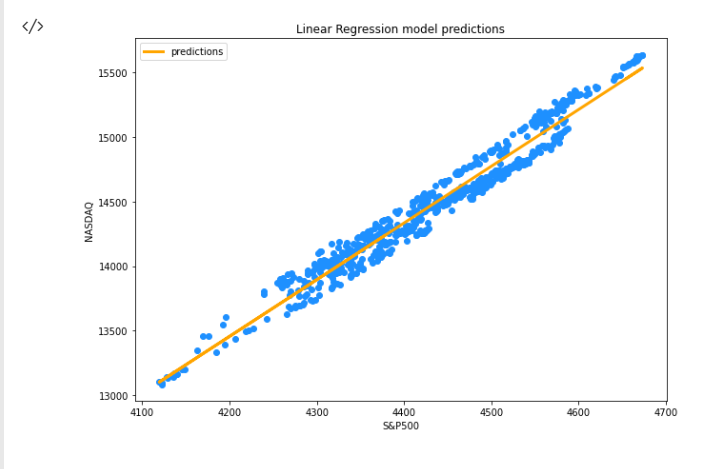
Ahora tenemos el modelo y otras cosas necesarias en la biblioteca. ¿Y qué ocurre con la precisión de nuestro modelo? ¿Es nuestro modelo lo suficientemente bueno para ser usado en alguna parte?
Para comprender cómo de bien predice nuestro modelo la variable objetivo, usaremos una métrica conocida como coeficiente de determinación, también llamado R-cuadrado.
R-cuadrado
Este supuesto sobre la varianza total de y ha sido explicado por el modelo.
Para encontrar R-cuadrado, deberemos entender el error en la predicción. El error de predicción es la diferencia entre el valor y factual/real y el valor y previsto.
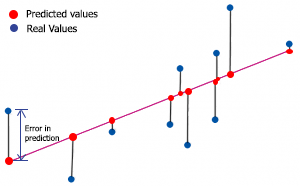
Matemáticamente
Error = Y factual - Y previsto
Fórmula de R-cuadrado
R-cuadrado = 1 - (Suma de los cuadrados de los errores / Suma de los cuadrados de los restos)
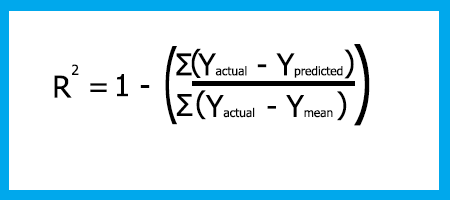
¿Por qué usar el cuadrado del error?
- Los errores pueden ser positivos o negativos (por encima o por debajo de la línea), los elevamos al cuadrado para que todos sean positivos.
- Los valores negativos pueden reducir el error.
- También elevaremos al cuadrado los errores para exagerar los errores grandes.
Cero significa que el modelo no puede explicar ninguna variación de y, e indica que el modelo es el peor posible. Uno indica que el modelo puede explicar toda la varianza de y en su conjunto de datos (no existe tal modelo).
El resultado de R-cuadrado se puede considerar como un porcentaje que indica como de bueno es nuestro modelo. Cero significa un precisión igual a cero y uno significa un 100% de precisión del modelo.
Ahora escribamos el código de R-cuadrado.
double CSimpleLinearRegression::r_squared() { double error=0; double numerator =0, denominator=0; double y_mean = mean(y_values); //--- if (ArraySize(m_ypredicted)==0) Print("Похоже, в массиве прогнозируемых значений нет данных. Вызовите основную функцию простой линейной регрессии перед использованием функции = ",__FUNCTION__); else { for (int i=0; i<ArraySize(y_values); i++) { numerator += MathPow((y_values[i]-m_ypredicted[i]),2); denominator += MathPow((y_values[i]-y_mean),2); } error = 1 - (numerator/denominator); } return(error); }
Dentro de la función LinearRegressionMain, donde guardamos los valores predichos en la matriz predicted_y[] transmitida por enlace, necesitaremos copiar esta matriz en la matriz de variables globales declaradas en la sección privada de la clase.
private: int m_handle; string m_filename; string m_delimiter; double m_ypredicted[]; double x_values[]; double y_values[];
Al final de LinearRegressionMain, hemos añadido una línea para copiar esta matriz en la matriz de variables globales m_ypredicted[].
//At the end of the function LinearRegressionMain(double &predict_y[]) I added the following line, // Copy the predicted values to m_ypredicted[], to be Accessed inside the library ArrayCopy(m_ypredicted,predict_y);
Ahora, generaremos el valor de R-cuadrado dentro de TestScript
Print(" R_SQUARED = ",lr.r_squared());
La salida será:
2022.03.03 10:40:53.413 TestScript (#SP500,H1) R_SQUARED = 0.9590906984145334
Eso es todo en cuanto a la regresión lineal simple. Ahora, vamos a echar un vistazo a cómo se vería una regresión lineal múltiple.
Regresión lineal múltiple
La regresión lineal múltiple tiene una variable independiente y varias dependientes.
Así es como se ve la fórmula para un modelo de regresión lineal múltiple:
Así es como se ve nuestra biblioteca después de escribir las secciones private y public de nuestra clase.
class CMultipleLinearRegression: public CSimpleLinearRegression { private: int m_independent_vars; public: CMultipleLinearRegression(void); ~CMultipleLinearRegression(void); double coefficient_of_X(double& x_arr[],double& y_arr[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[]); void MultipleRegressionMain(double& predicted_y[],double& Y[],double& A[],double& B[],double& C[],double& D[]); double y_interceptforMultiple(double& Y[],double& A[],double& B[],double& C[],double& D[]); };
Como trabajaremos con múltiples valores, en esta parte jugaremos con más matrices con argumentos de función. No hemos podido encontrar una implementación más corta.
Vamos a crear un modelo de regresión lineal para dos variables dependientes usando esta función.
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[]) { // Multiple regression formula = y = M1X1+M2X2+M3X3+...+C double constant_y_intercept=y_interceptforMultiple(Y,A,B); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2)+"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(constant_y_intercept,2)); int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+constant_y_intercept; }
La variable Y-intercept en esta variante depende del número de columnas de datos con las que decidamos trabajar. Después de obtener la fórmula de la regresión lineal múltiple, la fórmula final será:
C = Y - M1 X1 - M2 X2
Este será el aspecto del código
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[]) { //formula c=Y-M1X1-M2X2; return(mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)); }
Cuando trabajamos con tres variables, solo necesitamos escribir de nuevo el código de la función, añadiendo una variable más.
void CMultipleLinearRegression::MultipleRegressionMain(double &predicted_y[],double &Y[],double &A[],double &B[],double &C[],double &D[]) { double constant_y_intercept = y_interceptforMultiple(Y,A,B,C,D); double slope1 = coefficient_of_X(A,Y); double slope2 = coefficient_of_X(B,Y); double slope3 = coefficient_of_X(C,Y); double slope4 = coefficient_of_X(D,Y); //--- Print("Multiple Regression Model is ","Y="+DoubleToString(slope1,2),"A+"+DoubleToString(slope2,2)+"B+"+ DoubleToString(slope3,2)+"C"+DoubleToString(slope4,2)+"D"+DoubleToString(constant_y_intercept,2)); //--- int ArrSize = (ArraySize(A)+ArraySize(B))/2; ArrayResize(predicted_y,ArrSize); for (int i=0; i<ArrSize; i++) predicted_y[i] = slope1*A[i]+slope2*B[i]+slope3*C[i]+slope4*D[i]+constant_y_intercept; }
Para nuestra regresión lineal múltiple, Y-intercept será así.
double CMultipleLinearRegression::y_interceptforMultiple(double &Y[],double &A[],double &B[],double &C[],double &D[]) { return (mean(Y)-coefficient_of_X(A,Y)*mean(A)-coefficient_of_X(B,Y)*mean(B)-coefficient_of_X(C,Y)*mean(C)-coefficient_of_X(D,Y)*mean(D)); }
Supuestos de la regresión lineal
Un modelo de regresión lineal se basa en un conjunto de supuestos. Si el conjunto de datos subyacente no cumple con estos supuestos, es posible que sea necesario transformar los datos; de lo contrario, probablemente el modelo lineal no sea adecuado.
- Supuesto de linealidad. Se supone una relación lineal entre la variable dependiente/objetivo y las variables independientes/predictoras.
- Supuesto de distribución normal de errores
- Debe haber una distribución normal de errores junto con el modelo
- El diagrama de dispersión entre los valores reales y los valores pronosticados debe mostrar datos que se distribuyen uniformemente en todo el modelo.
Ventajas del modelo de regresión lineal
Facilidad de implementación e interpretación de los datos de salida y los coeficientes.
Desventajas
- Se supone una relación lineal entre las variables dependientes e independientes, es decir, se supone que existe una relación directa entre ellas.
- Los valores atípicos tienen un gran impacto en la regresión
- La regresión lineal presume la independencia entre los atributos
- La regresión lineal analiza la relación entre la media de la variable dependiente y la variable independiente.
- Así como la media no es una descripción completa de una sola variable, la regresión lineal no es una descripción completa de las relaciones entre variables.
- Los límites son lineales
Conclusiones finales
A nuestro juicio, los algoritmos de regresión lineal pueden resultar muy útiles para crear estrategias comerciales basadas en correlaciones de pares y otras cosas como los indicadores, aunque nuestra biblioteca está lejos de estar completa. No hemos incluido el entrenamiento y la prueba de nuestro modelo, ni la posterior mejora de los resultados. Abarcaremos esto en el próximo artículo, así que permanezca atento. Compartiremos un enlace al código de Python en nuestro repositorio de Github: enlace. Cualquier contribución a la biblioteca será bienvenida; siéntase igualente libre de compartir sus pensamientos en los comentarios.
¡Nos vemos pronto!
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/10459
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Aprendiendo a diseñar un sistema comercial basado en RSI
Aprendiendo a diseñar un sistema comercial basado en RSI
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso

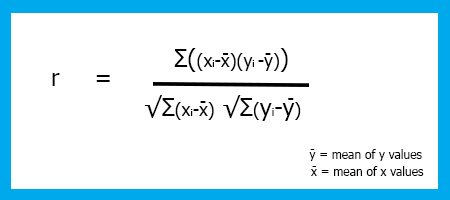
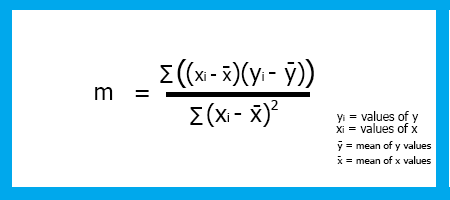
What is a Model
Un modelo no es más que un sufijo.
¿Un sufijo? No entiendo lo que esto significa.
Antes de poder abrir un archivo CSV que fue creado por nuestro script de prueba es necesario convertirlo en codificación UTF-8 para que pueda ser leído por python.
¿Por qué? Basta con crear un archivo de datos UTF-8 directamente desde MQL.
Elipse roja añadida por mí. Eso está mal, este punto no es un "y-intercepto" y sus coordenadas no es (0,-5).
¿Un sufijo? No entiendo lo que significa.
¿Por qué es eso? Basta con crear un archivo de datos UTF-8 directamente desde MQL.
Elipse roja añadida por mí. Eso está mal, este punto no es un "y-intercepto" y sus coordenadas no es (0,-5).
por la palabra sufijo me refiero a una notación matemática, como y=mx+c esto es un modelo
Sí lo entiendo, cometido un error en la imagen el otro punto se suponía que era (-5,0) y no es un "y-intercepto"
Hola, gracias por un artículo conciso sobre la regresión lineal y sus posibilidades.
La fórmula del coeficiente de Peasson tiene fallos en el denominador.
hola, tal vez está ahí, sólo que no lo encontré, pero ¿dónde está el archivo NASDAQ.csv utilizado en el artículo?