
Busca de padrões sazonais no mercado de Forex usando o algoritmo CatBoost
Introdução
Dois outros artigos dedicados à busca de padrões sazonais já foram publicados (1, 2). Eu queria saber como os algoritmos de aprendizado de máquina podem lidar com a tarefa de busca de padrões. Os sistemas de negociação nos artigos acima mencionados foram construídos com base em análises estatísticas. O fator humano pode ser eliminado agora simplesmente instruindo o modelo a negociar em uma determinada hora de um determinado dia da semana. A busca de padrões pode ser fornecida por um algoritmo separado.
Função de filtragem do tempo
A biblioteca pode ser facilmente ampliada adicionando uma função de filtro.
def time_filter(data, count): # filter by hour hours=[15] if data.index[count].hour not in hours: return False # filter by day of week days = [1] if data.index[count].dayofweek not in days: return False return True
A função verifica as condições especificadas dentro dela. Outras condições adicionais podem ser implementadas (não apenas filtros de tempo). Mas, como o artigo é dedicado aos padrões sazonais, eu usarei apenas os filtros de tempo. Se todas as condições forem atendidas, a função retorna True e a amostra apropriada é adicionada ao conjunto de treinamento. Por exemplo, neste caso específico, nós instruímos o modelo a abrir negociações apenas às 15:00 da terça-feira. As listas de 'horas' e 'dias' podem incluir outras horas e dias. Ao comentar todas as condições, você pode deixar o algoritmo funcionar sem as condições, da maneira como funcionou no artigo anterior.
A função add_labels agora recebe essa condição como uma entrada. Em Python, as funções são objetos de primeiro nível, portanto, você pode passá-los com segurança como argumentos para outras funções.
def add_labels(dataset, min, max, filter=time_filter): labels = [] for i in range(dataset.shape[0]-max): rand = random.randint(min, max) curr_pr = dataset['close'][i] future_pr = dataset['close'][i + rand] if filter(dataset, i): if future_pr + MARKUP < curr_pr: labels.append(1.0) elif future_pr - MARKUP > curr_pr: labels.append(0.0) else: labels.append(2.0) else: labels.append(2.0) dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop( dataset[dataset.labels == 2].index) return dataset
Assim que o filtro é passado para a função, ele pode ser usado para marcar as negociações de Compra ou Venda. O filtro recebe o conjunto de dados original e o índice da barra atual. Os índices no conjunto de dados são representados como 'datetime index' contendo a hora. O filtro procura a hora e o dia no 'datetime index' do dataframe pelo i-ésimo número e retorna False se não encontrar nada. Se a condição for atendida, a transação será marcada como 1 ou 0, caso contrário, como 2. Finalmente, todos os 2 são removidos do conjunto de dados de treinamento e, portanto, são deixados apenas os exemplos para os dias e horas específicos que foram determinados pelo filtro.
Um filtro também deve ser adicionado ao testador personalizado, para permitir a abertura de negociação em um momento específico (ou de acordo com qualquer outra condição definida por este filtro).
def tester(dataset, markup=0.0, plot=False, filter=time_filter): last_deal = int(2) last_price = 0.0 report = [0.0] for i in range(dataset.shape[0]): pred = dataset['labels'][i] ind = dataset.index[i].hour if last_deal == 2 and filter(dataset, i): last_price = dataset['close'][i] last_deal = 0 if pred <= 0.5 else 1 continue if last_deal == 0 and pred > 0.5: last_deal = 2 report.append(report[-1] - markup + (dataset['close'][i] - last_price)) continue if last_deal == 1 and pred < 0.5: last_deal = 2 report.append(report[-1] - markup + (last_price - dataset['close'][i])) y = np.array(report).reshape(-1, 1) X = np.arange(len(report)).reshape(-1, 1) lr = LinearRegression() lr.fit(X, y) l = lr.coef_ if l >= 0: l = 1 else: l = -1 if(plot): plt.plot(report) plt.plot(lr.predict(X)) plt.title("Strategy performance") plt.xlabel("the number of trades") plt.ylabel("cumulative profit in pips") plt.show() return lr.score(X, y) * l
Isso é implementado da seguinte maneira. O dígito 2 é usado quando não há posição aberta: last_deal = 2. Não há posições abertas antes do início do teste, portanto, definimos para 2. Iteramos por todo o conjunto de dados e verificamos se a condição do filtro é atendida. Se a condição for atendida, abrimos um negócio de Compra ou Venda. As condições do filtro não se aplicam ao fechamento do negócio, pois podem ser fechadas em outro horário ou dia da semana. Essas mudanças são suficientes para mais treinamento e testes corretos.
Análise exploratória para cada hora de negociação
Não é muito conveniente testar o modelo manualmente para cada condição individual (e para uma combinação de horas ou dias). Uma função especial foi escrita para este propósito, que permite a obtenção rápida de estatísticas resumidas para cada condição separadamente. A função pode levar algum tempo para ser concluída, mas gera os intervalos de tempo em que o modelo exibe um melhor desempenho.
def exploratory_analysis(): h = [x for x in range(24)] result = pd.DataFrame() for _h in h: global hours hours = [_h] pr = get_prices(START_DATE, STOP_DATE) pr = add_labels(pr, min=15, max=15, filter=time_filter) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] iterations = 10 for i in range(iterations): res.append(brute_force(10000, gmm)) print('Iteration: ', i, 'R^2: ', res[-1][0], ' hour= ', _h) r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h)) result = result.append(r) plt.scatter(result.index, result, c = result.index) plt.show() return result
Você pode definir na função uma lista de horas a serem verificadas. No meu exemplo, todas as 24 horas estão definidas. Para a pureza do experimento, eu desativei a amostragem definindo 'min' e 'max' (horizonte mínimo e máximo de uma posição em aberto) igual a 15. A variável 'iterations' é responsável pelo número de ciclos de retreinamento para cada hora. Uma estatística mais confiável pode ser obtida aumentando este parâmetro. Depois de concluir a operação, a função exibirá o seguinte gráfico:
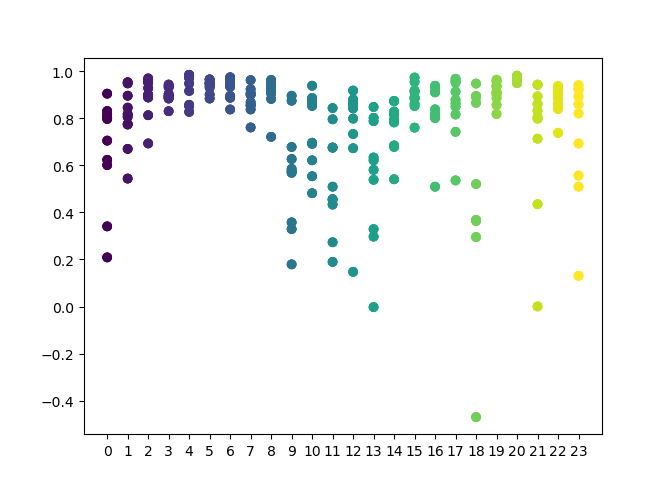
O eixo X apresenta os números ordinais das horas. O eixo Y representa os escores R^2 para cada iteração (foram usadas 10 iterações, significando um retreinamento do modelo para cada hora). Como você pode ver, os passes de 4, 5 e 6 horas estão mais próximos, o que dá mais confiança na qualidade do padrão encontrado. O princípio de seleção é simples — quanto mais alto a posição e a densidade dos pontos, melhor é o modelo. Por exemplo, no intervalo de 9-15, o gráfico mostra uma grande dispersão de pontos e a qualidade média dos modelos cai para 0.6. Você pode ainda selecionar as horas desejadas, treinar novamente o modelo e visualizar seus resultados no testador personalizado.
Testando os modelos selecionados
A análise exploratória foi realizada no par de moedas GBPUSD, com os seguintes parâmetros:
SYMBOL = 'GBPUSD' MARKUP = 0.00010 TIMEFRAME = mt5.TIMEFRAME_H1 START_DATE = datetime(2017, 1, 1) TSTART_DATE = datetime(2015, 1, 1) FULL_DATE = datetime(2015, 1, 1) STOP_DATE = datetime(2021, 1, 1)
Os mesmos parâmetros serão usados para teste. Para maior confiança, você pode alterar o valor FULL_DATE para ver como o modelo se saiu nos dados do histórico anterior.
Nós podemos distinguir visualmente um grupo de 3, 4, 5 e 6 horas. Pode-se presumir que as horas adjacentes têm padrões semelhantes, então o modelo pode ser treinado para toda essa hora.
hours = [3,4,5,6] # make dataset pr = get_prices(START_DATE, STOP_DATE) pr = add_labels(pr, min=15, max=15, filter=time_filter) tester(pr, MARKUP, plot=True, filter=time_filter) # perform GMM clasterizatin over dataset # gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] for i in range(10): res.append(brute_force(10000, gmm)) print('Iteration: ', i, 'R^2: ', res[-1][0]) # test best model res.sort() test_model(res[-1])
Nenhuma explicação adicional é necessária para o código restante, como foi explicado em detalhes nos artigos anteriores. Com a única exceção, em vez de um GMM simples, você pode usar um modelo bayesiano comentado, embora seja apenas uma ideia experimental.
Um modelo ideal após a amostragem de negócios seria assim:
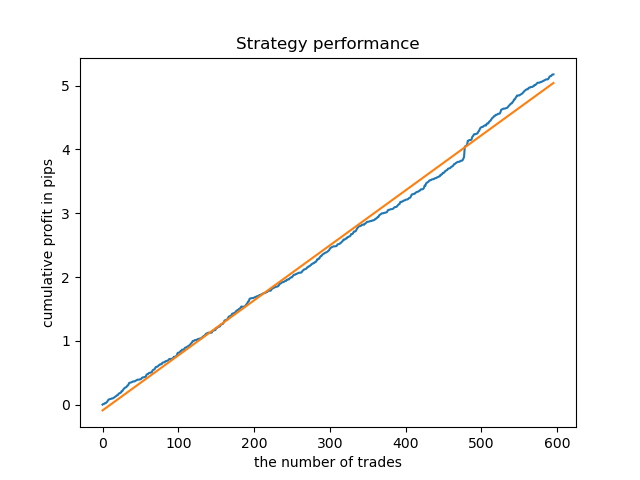
O modelo treinado (incluindo os dados de teste) mostra o seguinte desempenho:
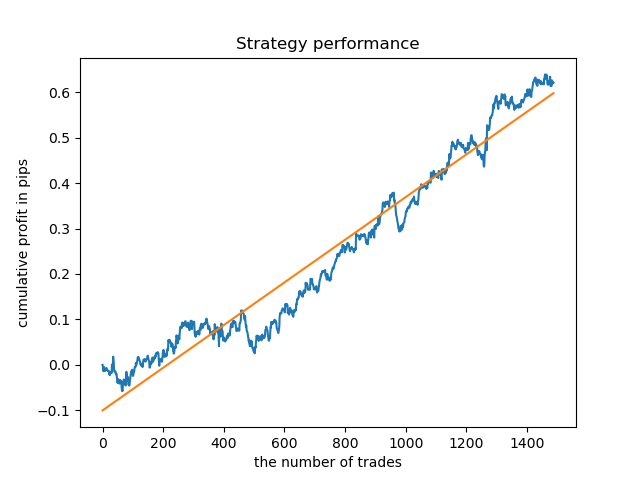
Modelos separados podem ser treinados para horas de alta densidade. Abaixo estão os gráficos de saldo para os modelos já treinados para as horas 5 e 20:
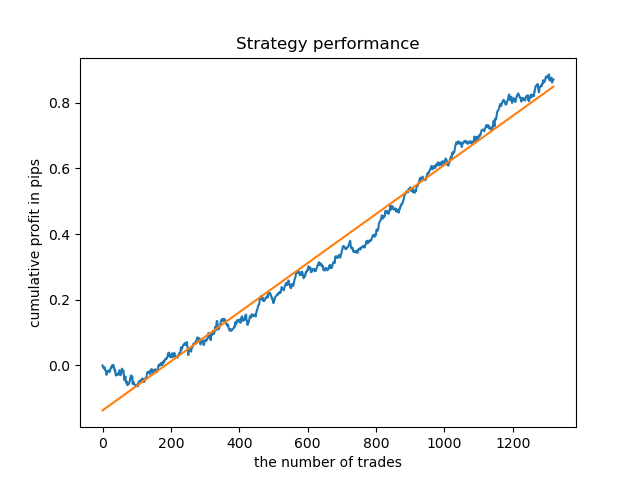
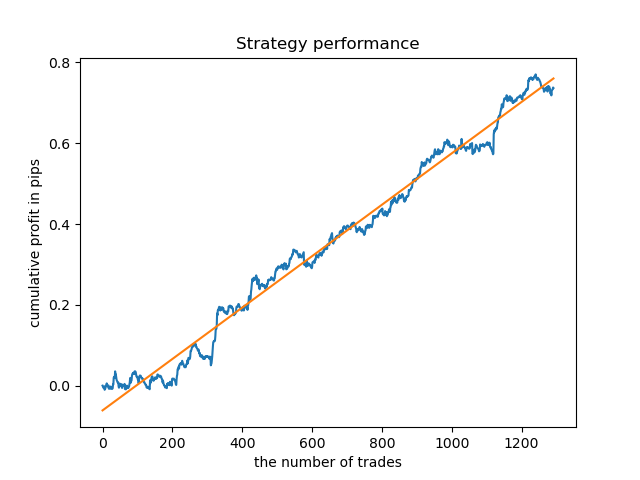
Agora, para comparação, você pode olhar para os modelos treinados em horas com maior variação. Veja as horas 9 e 11, por exemplo.
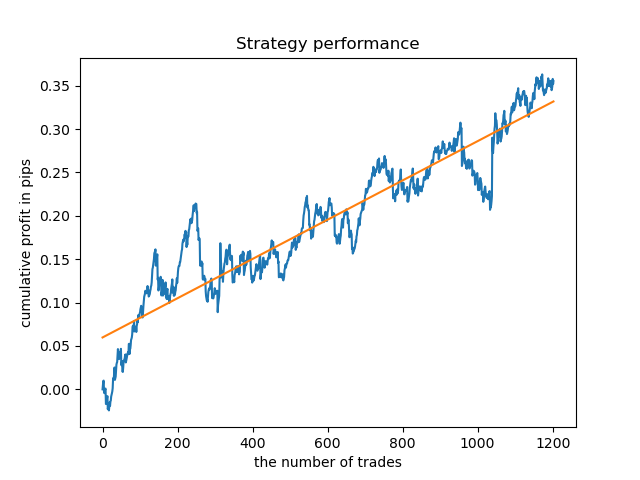

Os gráficos de saldo aqui mostram mais do que quaisquer comentários. Obviamente, ao treinar os modelos, uma atenção especial deve ser dada ao tempo.
Análise exploratória para cada dia de negociação
O filtro pode ser facilmente modificado para outros intervalos de tempo, como por exemplo dias da semana. Basta substituir a hora por um dia da semana.
def time_filter(data, count): # filter by day of week global hours if data.index[count].dayofweek not in hours: return False return True
Nesse caso, a iteração deve ser realizada no intervalo entre 0 e 5 (excluindo o 5º número ordinal, que é sábado).
def exploratory_analysis():
h = [x for x in range(5)]
Agora, executamos uma análise exploratória para o par de moedas GBPUSD. A frequência dos negócios, ou seu horizonte, é o mesmo (15 barras).
pr = add_labels(pr, min=15, max=15, filter=time_filter) O processo de treinamento é exibido no console, onde você pode visualizar instantaneamente as escore de R^2 para o período atual. Agora, a variável 'hour' não contém o número da hora, mas o número ordinal do dia da semana.
Iteration: 0 R^2: 0.5297625368835237 hour= 0 Iteration: 1 R^2: 0.8166096906047893 hour= 0 Iteration: 2 R^2: 0.9357674260125702 hour= 0 Iteration: 3 R^2: 0.8913802241811986 hour= 0 Iteration: 4 R^2: 0.8079720208707672 hour= 0 Iteration: 5 R^2: 0.8505663844866759 hour= 0 Iteration: 6 R^2: 0.2736870273207084 hour= 0 Iteration: 7 R^2: 0.9282442121644887 hour= 0 Iteration: 8 R^2: 0.8769775718602929 hour= 0 Iteration: 9 R^2: 0.7046666925774866 hour= 0 Iteration: 0 R^2: 0.7492883761480897 hour= 1 Iteration: 1 R^2: 0.6101962958733655 hour= 1 Iteration: 2 R^2: 0.6877652983219245 hour= 1 Iteration: 3 R^2: 0.8579669286548137 hour= 1 Iteration: 4 R^2: 0.3822441930760343 hour= 1 Iteration: 5 R^2: 0.5207801806491617 hour= 1 Iteration: 6 R^2: 0.6893157850263495 hour= 1 Iteration: 7 R^2: 0.5799059801202937 hour= 1 Iteration: 8 R^2: 0.8228326786957887 hour= 1 Iteration: 9 R^2: 0.8742262956151615 hour= 1 Iteration: 0 R^2: 0.9257707800422799 hour= 2 Iteration: 1 R^2: 0.9413981795880517 hour= 2 Iteration: 2 R^2: 0.9354221623113591 hour= 2 Iteration: 3 R^2: 0.8370429185837882 hour= 2 Iteration: 4 R^2: 0.9142875737195697 hour= 2 Iteration: 5 R^2: 0.9586871067966855 hour= 2 Iteration: 6 R^2: 0.8209392060391961 hour= 2 Iteration: 7 R^2: 0.9457287035542066 hour= 2 Iteration: 8 R^2: 0.9587372191281025 hour= 2 Iteration: 9 R^2: 0.9269140213952402 hour= 2 Iteration: 0 R^2: 0.9001009579436263 hour= 3 Iteration: 1 R^2: 0.8735623527502183 hour= 3 Iteration: 2 R^2: 0.9460714774572146 hour= 3 Iteration: 3 R^2: 0.7221720163838841 hour= 3 Iteration: 4 R^2: 0.9063579778744433 hour= 3 Iteration: 5 R^2: 0.9695391076372475 hour= 3 Iteration: 6 R^2: 0.9297881558889788 hour= 3 Iteration: 7 R^2: 0.9271590681844957 hour= 3 Iteration: 8 R^2: 0.8817985496711311 hour= 3 Iteration: 9 R^2: 0.915205007218742 hour= 3 Iteration: 0 R^2: 0.9378516360378022 hour= 4 Iteration: 1 R^2: 0.9210968481902528 hour= 4 Iteration: 2 R^2: 0.9072205941748894 hour= 4 Iteration: 3 R^2: 0.9408826184927528 hour= 4 Iteration: 4 R^2: 0.9671981453714584 hour= 4 Iteration: 5 R^2: 0.9625144032389237 hour= 4 Iteration: 6 R^2: 0.9759244293257822 hour= 4 Iteration: 7 R^2: 0.9461473783201281 hour= 4 Iteration: 8 R^2: 0.9190627222826241 hour= 4 Iteration: 9 R^2: 0.9130350931314233 hour= 4
Observe que todos os modelos foram treinados com os dados desde o início de 2017, enquanto os escores de R^2 também incluem o período de teste (dados adicionais a partir de 2015). A consistência de estimativas altas para cada dia fornece ainda mais confiança. Vamos ver o resultado final.
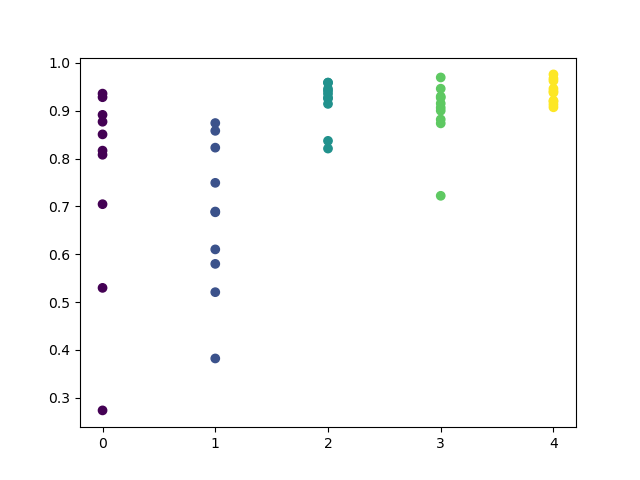
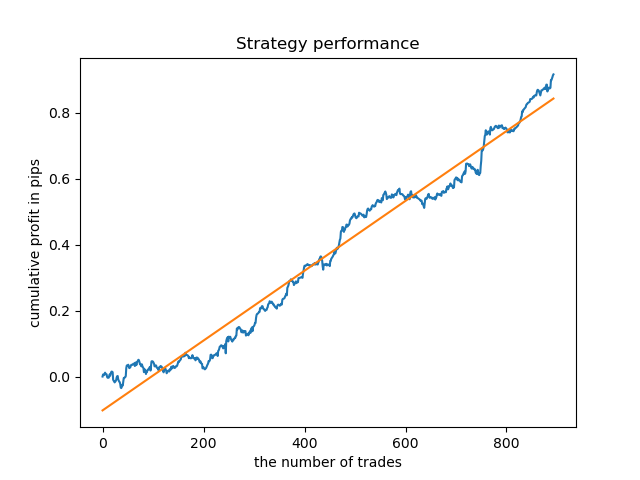
A análise exploratória mostrou que quarta e sexta-feira são os dias mais favoráveis para a negociação, especialmente a sexta-feira. O pior dia para negociação é terça-feira, pois tem uma grande variação de erros e um valor médio baixo. Vamos treinar o modelo para negociar apenas às sextas-feiras e ver o resultado.
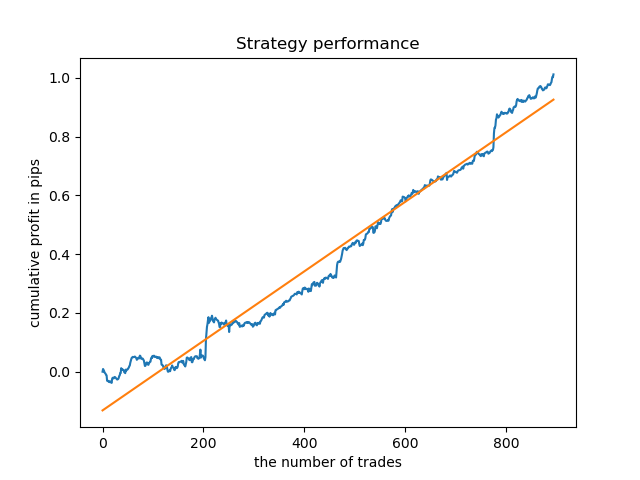
Da mesma forma, nós podemos obter um modelo de negociação às terças-feiras.
Uma duração fixa de negócios nem sempre é adequada, então vamos tentar expandir a janela de busca e aumentar o número de iterações da análise exploratória para 20.
pr = add_labels(pr, min=5, max=25, filter=time_filter) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] iterations = 20
A faixa de valores tornou-se maior, enquanto os melhores dias para negociação são quinta e sexta-feira.
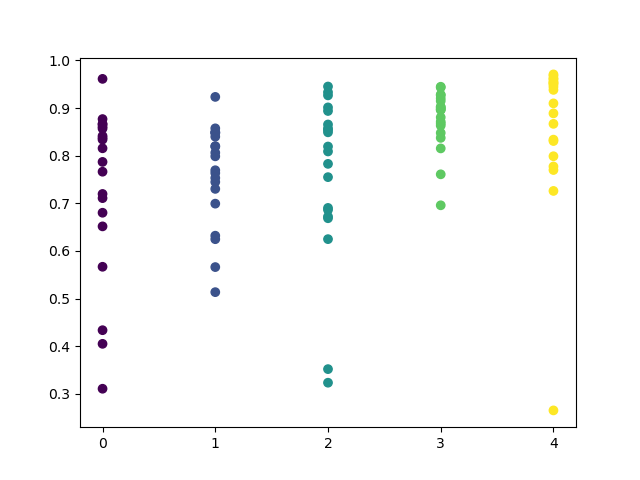
Vamos agora treinar um modelo de controle para a quinta-feira e ver o resultado. É assim que se parece o ciclo de aprendizagem (para quem não leu os artigos anteriores).
hours = [3]
# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=5, max=25, filter=time_filter)
tester(pr, MARKUP, plot=True, filter=time_filter)
# perform GMM clasterizatin over dataset
# gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X)
gmm = mixture.GaussianMixture(
n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])
# iterative learning
res = []
for i in range(10):
res.append(brute_force(10000, gmm))
print('Iteration: ', i, 'R^2: ', res[-1][0])
# test best model
res.sort()
test_model(res[-1])
O resultado é um pouco pior do que com uma duração fixa de negócios.
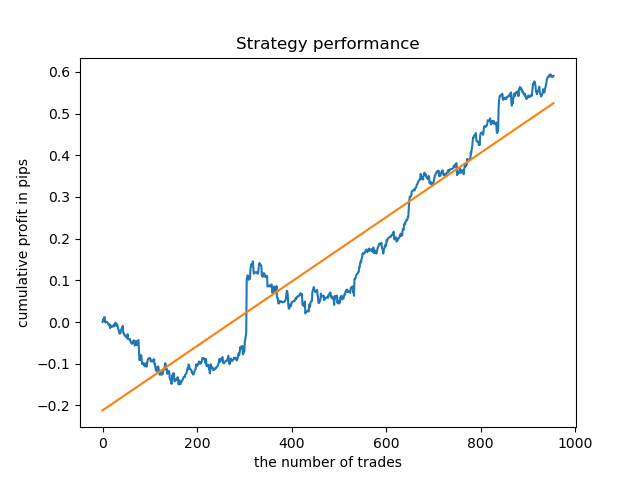
Obviamente, o parâmetro de frequência (horizonte) em períodos específicos é importante. A seguir, vamos iterar esses valores e verificar como eles afetam o resultado.
Avaliação da influência do tempo de vida do negócio na qualidade do modelo
Semelhante à função de análise exploratória para um critério selecionado (filtro), nós podemos criar uma função auxiliar que avaliará o desempenho do modelo dependendo do tempo de vida do negócio. Suponha que nós possamos definir um tempo de vida fixo para o negócio no intervalo de 1 a 50 barras (ou qualquer outro período), então a função terá a seguinte aparência.
def deals_frequency_analyzer(): freq = [x for x in range(1, 50)] result = pd.DataFrame() for _h in freq: pr = get_prices(START_DATE, STOP_DATE) pr = add_labels(pr, min=_h, max=_h, filter=time_filter) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] iterations = 5 for i in range(iterations): res.append(brute_force(10000, gmm)) print('Iteration: ', i, 'R^2: ', res[-1][0], ' deal lifetime = ', _h) r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h)) result = result.append(r) plt.scatter(result.index, result, c = result.index) plt.xticks(np.arange(0, len(freq)+1, 1)) plt.title("Performance by deals lifetime") plt.xlabel("deals frequency") plt.ylabel("R^2 estimation") plt.show() return result
A lista 'freq' contém os valores da duração do negócio para iterar. Eu executei esta iteração para a 5ª hora do par GBPUSD. Aqui está o resultado.
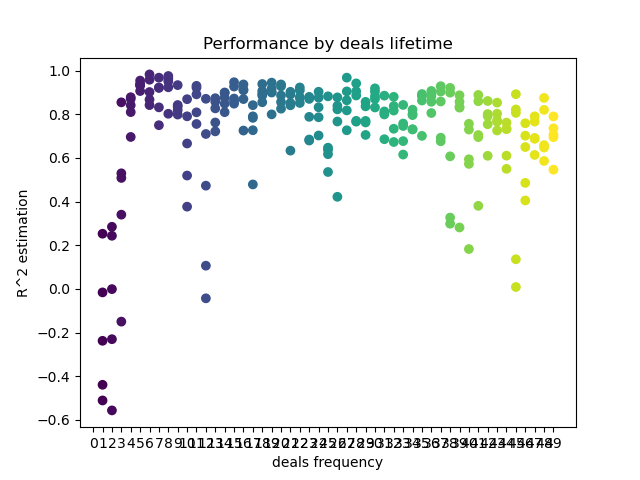
O eixo X mostra a frequência do negócio, ou melhor, sua duração em barras. O eixo Y representa o escore R^2 para cada um dos passes. Como você pode ver, negociações muito curtas de 0-5 barras têm um efeito negativo no desempenho do modelo, enquanto a duração de 15-23 barras é o ideal. Negociações mais longas (acima de 30 barras) pioram o resultado. Há um pequeno cluster com duração do negócio de 6-9 barras, que tem os escores mais altos. Vamos tentar treinar os modelos com esses valores de vida útil e comparar os resultados com outros clusters.
Eu selecionei a duração de 8 barras, para as quais o modelo foi testado desde 2013. Mas a curva do saldo não é tão uniforme quanto eu gostaria que fosse.
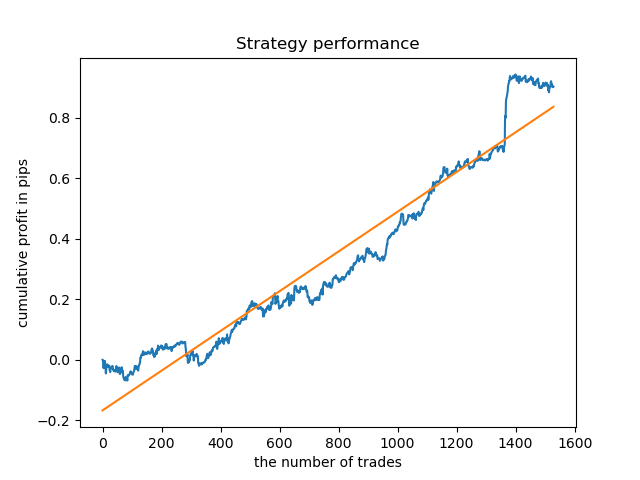
Para a duração do cluster com a densidade mais alta, o gráfico parece muito bom desde 2015, no entanto, o modelo tem um desempenho ruim em um intervalo do histórico anterior.
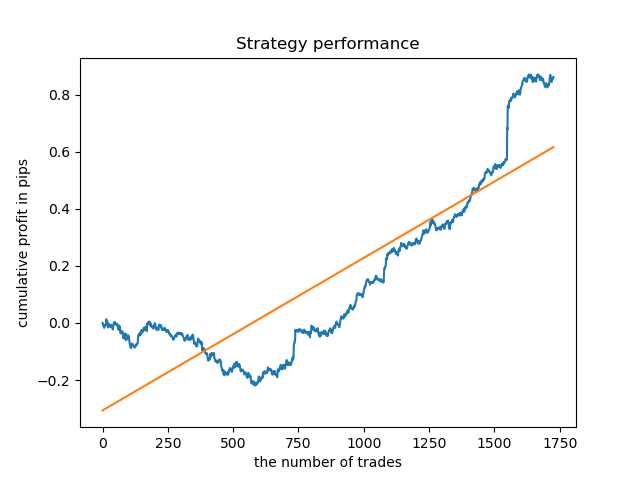
Finalmente, eu selecionei uma série dos melhores clusters 15-23 e retreinei o modelo várias vezes (uma vez que a amostragem da duração da negociação é aleatória).
pr = add_labels(pr, min=15, max=23, filter=time_filter)
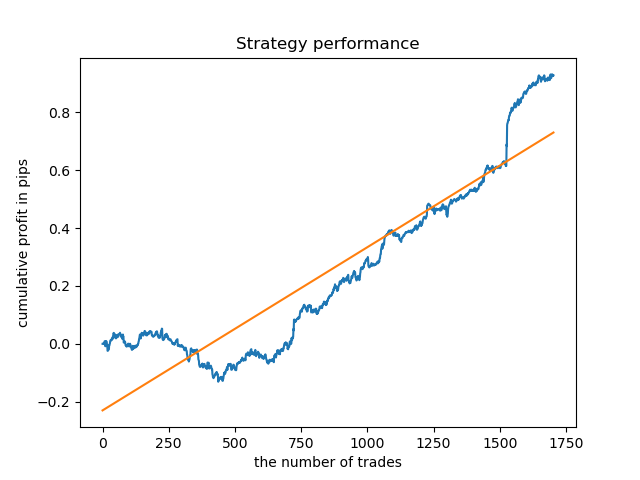
Um modelo baseado em tais padrões não mostra uma capacidade de sobrevivência em dados anteriores a 2015. Provavelmente, houve algumas mudanças fundamentais na estrutura do mercado. Um grande estudo separado é necessário para analisar esta situação. Após o modelo ter sido selecionado e sua estabilidade comprovada ao longo de um determinado intervalo de tempo, o treinamento pode ser realizado durante todo esse intervalo, incluindo uma amostra de teste. Este modelo pode então ser enviado para produção.
Testando em um histórico mais longo
E se nós verificarmos o modelo em um histórico mais longo? O modelo foi treinado em dados desde 2000 e testado usando os dados desde 1990. Os padrões são mal captados em um período histórico tão longo, o que pode ser visto na curva do saldo, mas o resultado ainda é positivo.
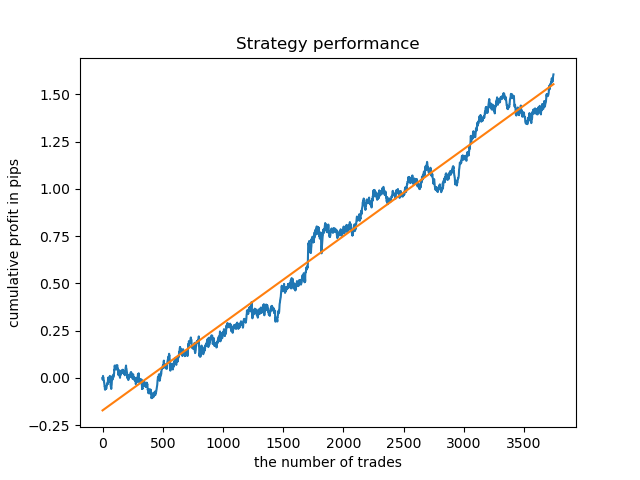
Conclusão
O artigo fornece uma descrição de uma ferramenta poderosa para encontrar padrões sazonais e criar sistemas de negociação. Você pode analisá-lo para diferentes instrumentos (além do FOREX), diferentes tempos gráficos e com diferentes filtros (não apenas os filtros de tempo). A gama de aplicações desta abordagem é muito ampla. Para revelar totalmente os seus recursos, nós precisaríamos de vários testes com filtros diferentes. Após conduzir a análise, você pode construir um robô de negociação usando a função de exportação do modelo descrito nos artigos anteriores.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/8863
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Algoritmo auto-adaptável (Parte III): evitando a otimização
Algoritmo auto-adaptável (Parte III): evitando a otimização
 O mercado e a física de seus padrões globais
O mercado e a física de seus padrões globais
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Você pode publicar um EA para esse mesmo modelo com cronogramas?
A resposta é a mesma do segundo artigo, mas no terminal você precisa adicionar a limitação de abertura de negociações por horário, e tudo o mais para os dias da semana e diferentes combinações.
O mesmo para os dias da semana e diferentes combinações. Além disso, no MT5, a contagem regressiva de horas é deslocada em 1 para a direita, ou seja, se no python for a 4ª hora, no MT será a 5ª hora
A resposta é a mesma do segundo artigo, mas no terminal você precisa adicionar a limitação de abertura de negociações por horário, e pronto
o mesmo para os dias da semana e diferentes combinações. Além disso, no MT5, a contagem regressiva das horas é deslocada em 1 para a direita, ou seja, se no Python for a 4ª hora, no MT será a 5ª
Obrigado.
Tópico interessante e próximo.
Seria muito curioso ver o patrimônio líquido final de um testador MT5 padrão em qualquer um dos instrumentos FORTS de sua escolha, obtido pela aplicação desse método.
Como feedback, estou pronto para postar o patrimônio líquido do meu algoritmo sazonal no instrumento selecionado :)