
Поиск сезонных закономерностей на валютном рынке с помощью алгоритма CatBoost
Введение
Поиску сезонных закономерностей уже были посвящены две статьи (1, 2). Мне было интересно посмотреть, насколько хорошо алгоритм машинного обучения может справиться с задачей обнаружения таких закономерностей. Если вспомнить подход из упомянутых статей, то торговые системы строились на основе статистического анализа. Теперь можно исключить человеческий фактор, просто сказав модели: "Хочу, чтобы ты торговала в определенный час определенного дня недели". А поиск закономерностей возложить на плечи алгоритма.
Функция фильтрации по времени
Библиотеку легко расширить, добавив дополнительную функцию-фильтр.
def time_filter(data, count): # filter by hour hours=[15] if data.index[count].hour not in hours: return False # filter by day of week days = [1] if data.index[count].dayofweek not in days: return False return True
Функция проверяет условия, заданные внутри неё. Можно добавлять дополнительные условия (необязательно только фильтры по времени). Но поскольку статья именно про сезонные закономерности, то я буду использовать только временные фильтры. Если все условия выполняются, то функция возвращает True и соответствующий семпл добавляется в обучающую выборку. Например, в данном конкретном случае мы говорим модели, что открывать сделки можно только в 15-м часу во вторник. Списки hours и days могут быть дополнены другими часами и днями. Если закомментировать все условия, то алгоритм будет работать без условий, как это было в предыдущей статье.
Функция add_labels теперь принимает на вход это условие. В языке Python функции являются объектами первого уровня, поэтому их смело можно передавать в качестве аргументов в другие функции.
def add_labels(dataset, min, max, filter=time_filter): labels = [] for i in range(dataset.shape[0]-max): rand = random.randint(min, max) curr_pr = dataset['close'][i] future_pr = dataset['close'][i + rand] if filter(dataset, i): if future_pr + MARKUP < curr_pr: labels.append(1.0) elif future_pr - MARKUP > curr_pr: labels.append(0.0) else: labels.append(2.0) else: labels.append(2.0) dataset = dataset.iloc[:len(labels)].copy() dataset['labels'] = labels dataset = dataset.dropna() dataset = dataset.drop( dataset[dataset.labels == 2].index) return dataset
После того, как фильтр передан в функцию, его можно использовать для маркировки сделок на покупку или продажу. Фильтр, в свою очередь, принимает исходный датасет и индекс текущего бара. Индексы в датасете представлены в виде datetime index, которые содержат время. Фильтр ищет час и день в datetime index'e датафрейма по i-тому порядковому номеру и возвращает False, если ничего не нашел. Если условие выполнено, то сделка помечается как 1 или 0, в противном случае как 2. В конце все двойки удаляются из обучающего датасета, таким образом остаются только примеры для конкретных дней и часов, определенных фильтром.
В кастомный тестер тоже необходимо добавить фильтр, чтобы сделки открывались в определенное время (или по любому другому условию, заложенному в фильтр).
def tester(dataset, markup=0.0, plot=False, filter=time_filter): last_deal = int(2) last_price = 0.0 report = [0.0] for i in range(dataset.shape[0]): pred = dataset['labels'][i] ind = dataset.index[i].hour if last_deal == 2 and filter(dataset, i): last_price = dataset['close'][i] last_deal = 0 if pred <= 0.5 else 1 continue if last_deal == 0 and pred > 0.5: last_deal = 2 report.append(report[-1] - markup + (dataset['close'][i] - last_price)) continue if last_deal == 1 and pred < 0.5: last_deal = 2 report.append(report[-1] - markup + (last_price - dataset['close'][i])) y = np.array(report).reshape(-1, 1) X = np.arange(len(report)).reshape(-1, 1) lr = LinearRegression() lr.fit(X, y) l = lr.coef_ if l >= 0: l = 1 else: l = -1 if(plot): plt.plot(report) plt.plot(lr.predict(X)) plt.title("Strategy performance") plt.xlabel("the number of trades") plt.ylabel("cumulative profit in pips") plt.show() return lr.score(X, y) * l
Реализовано это следующим образом. Отсутствие открытой позиции обозначается цифрой 2, то есть last_deal = 2. Перед началом тестирования нет никаких открытых позиций, поэтому ставим 2. Итеративно проходим по всему датасету и проверяем, выполнено ли условия фильтра. Если да, то открываем сделку на покупку или продажу. На закрытие сделок условия фильтра уже не действуют, поскольку они могут быть закрыты уже в другой час и даже день недели. Собственно, это все изменения, достаточные для корректного обучения и тестирования.
Разведочный анализ по каждому торговому часу
Тестировать модель вручную по каждому отдельному условию (будь то комбинация часов или дней) не очень удобно. Для этого была написана специальная функция, которая позволяет получить сводную статистику по каждому условию отдельно. Её работа может занять продолжительное время, зато на выходе сразу можно увидеть временные диапазоны, на которых модель работает наилучшим образом.
def exploratory_analysis(): h = [x for x in range(24)] result = pd.DataFrame() for _h in h: global hours hours = [_h] pr = get_prices(START_DATE, STOP_DATE) pr = add_labels(pr, min=15, max=15, filter=time_filter) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] iterations = 10 for i in range(iterations): res.append(brute_force(10000, gmm)) print('Iteration: ', i, 'R^2: ', res[-1][0], ' hour= ', _h) r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h)) result = result.append(r) plt.scatter(result.index, result, c = result.index) plt.show() return result
В функции можно задать список часов, которые необходимо проанализировать. Здесь заданы все 24 часа. Для чистоты эксперимента я выключил случайный семплинг, поставив min и max (минимальный и максимальный горизонт открытой позиции) равными 15. Переменная iterations отвечает за количество переобучений для каждого часа. Увеличив этот параметр, можно получить более достоверную статистику. После завершения работы, функция отобразит следующий график:
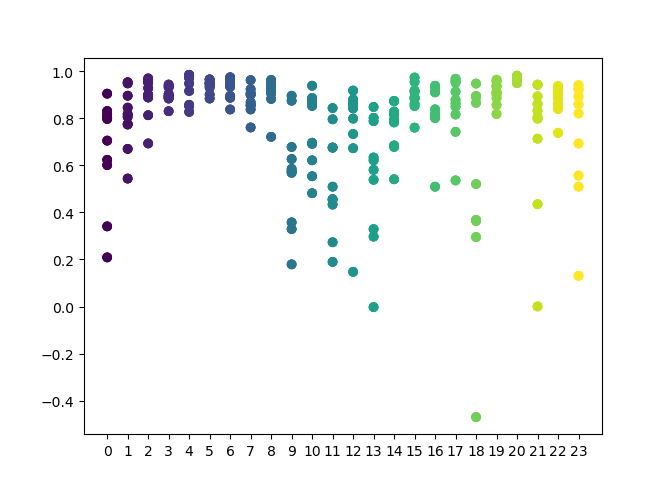
По оси X расположен порядковый номер часа. По оси Y представлены оценки R^2 для каждой итерации (было выбрано 10 итераций, то есть переобучений модели для каждого часа). Хорошо видно, что для 4,5,6 часов все проходы расположены кучнее, что придает больше уверенности в качестве найденной закономерности. Здесь принцип выбора достаточно простой — чем выше и кучнее точки, тем лучше модель. Например, на интервале 9-15 график показывает большой разброс, а среднее качество моделей опускается до уровня 0.6. Выбрав интересующие часы, можно заново переобучить модель и посмотреть её результаты в кастомном тестере.
Тестирование отобранных моделей
Разведочный анализ проводился на валютной паре GBPUSD со следующими параметрами:
SYMBOL = 'GBPUSD' MARKUP = 0.00010 TIMEFRAME = mt5.TIMEFRAME_H1 START_DATE = datetime(2017, 1, 1) TSTART_DATE = datetime(2015, 1, 1) FULL_DATE = datetime(2015, 1, 1) STOP_DATE = datetime(2021, 1, 1)
Соответственно, при тестировании буду использоваться они же. Для уверенности, можно изменить FULL_DATE, чтобы посмотреть как модель работала на более ранних исторических данных.
Хорошо вырисовывается кластер 3,4,5,6 часов. Можно предположить, что рядом идущие часы имеют схожие закономерности и обучить сразу на всех этих часах.
hours = [3,4,5,6] # make dataset pr = get_prices(START_DATE, STOP_DATE) pr = add_labels(pr, min=15, max=15, filter=time_filter) tester(pr, MARKUP, plot=True, filter=time_filter) # perform GMM clasterizatin over dataset # gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] for i in range(10): res.append(brute_force(10000, gmm)) print('Iteration: ', i, 'R^2: ', res[-1][0]) # test best model res.sort() test_model(res[-1])
Остальной код не нуждается в пояснениях, поскольку был хорошо разобран в предыдущих статьях. За тем исключением, что вместо простой GMM можно использовать закомментированную байесовскую, но это пока без комментариев и является экспериментальным.
Идеальная модель после семплинга сделок будет выглядеть следующим образом:
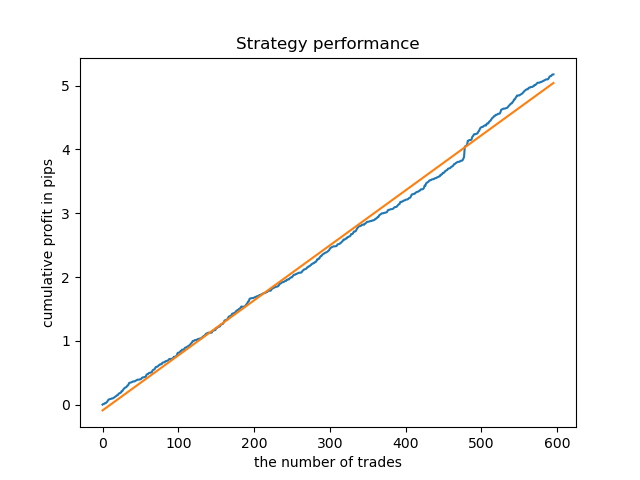
Обученная модель (включая тестовые данные) показывает такую производительность:
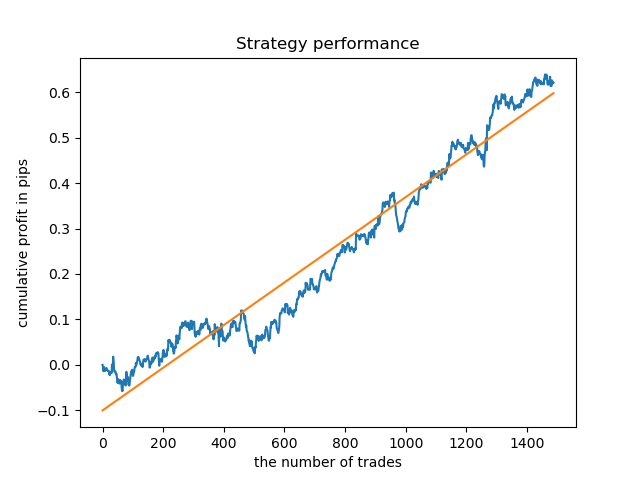
Можно обучить отдельные модели для самых "кучных" часов. Так выглядят график балансов уже обученных моделей для 5 и 20-го часов:
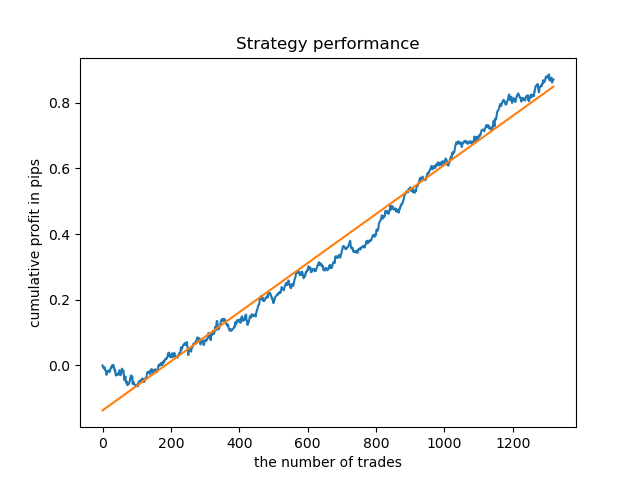
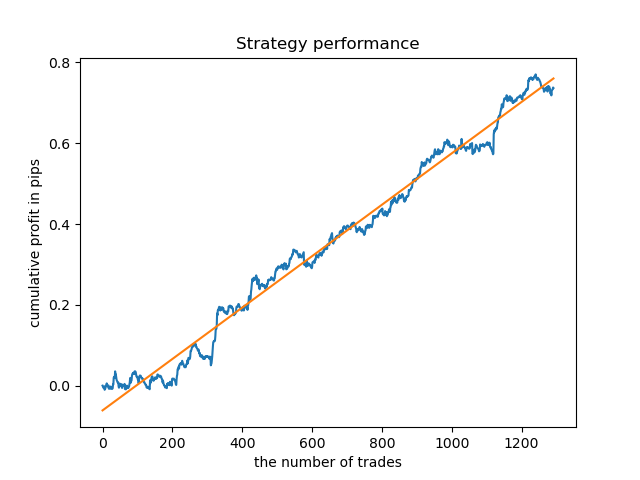
Теперь для сравнения можно посмотреть на модели, обученные на часах с большим разбросом. Возьмем, например, 9 и 11 часы.
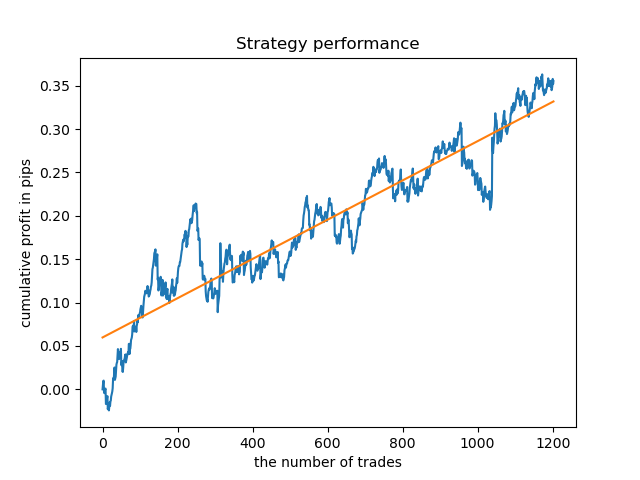

Графики балансов здесь будут многословнее любых комментариев к ним. Очевидно, что при обучении моделей особое внимание следует уделять их таймингу.
Разведочный анализ по каждому торговому дню
Можно легко модифицировать фильтр для других временных интервалов, например, для дней недели. Достаточно заменить проверку часа на день недели.
def time_filter(data, count): # filter by day of week global hours if data.index[count].dayofweek not in hours: return False return True
В таком случае, перебор следует делать в диапазоне от нуля до 5 (исключая 5-й порядковый номер, который является субботой).
def exploratory_analysis():
h = [x for x in range(5)] Теперь можно провести разведочный анализ для валютной пары GBPUSD. Частота сделок, вернее, их горизонт, остался прежним (15 баров).
pr = add_labels(pr, min=15, max=15, filter=time_filter) Процесс обучения отображается в консоли, где можно сразу посмотреть оценки R^2 для текущего периода. Здесь переменная hour теперь содержит не порядковый номер часа, но порядковый номер дня.
Iteration: 0 R^2: 0.5297625368835237 hour= 0 Iteration: 1 R^2: 0.8166096906047893 hour= 0 Iteration: 2 R^2: 0.9357674260125702 hour= 0 Iteration: 3 R^2: 0.8913802241811986 hour= 0 Iteration: 4 R^2: 0.8079720208707672 hour= 0 Iteration: 5 R^2: 0.8505663844866759 hour= 0 Iteration: 6 R^2: 0.2736870273207084 hour= 0 Iteration: 7 R^2: 0.9282442121644887 hour= 0 Iteration: 8 R^2: 0.8769775718602929 hour= 0 Iteration: 9 R^2: 0.7046666925774866 hour= 0 Iteration: 0 R^2: 0.7492883761480897 hour= 1 Iteration: 1 R^2: 0.6101962958733655 hour= 1 Iteration: 2 R^2: 0.6877652983219245 hour= 1 Iteration: 3 R^2: 0.8579669286548137 hour= 1 Iteration: 4 R^2: 0.3822441930760343 hour= 1 Iteration: 5 R^2: 0.5207801806491617 hour= 1 Iteration: 6 R^2: 0.6893157850263495 hour= 1 Iteration: 7 R^2: 0.5799059801202937 hour= 1 Iteration: 8 R^2: 0.8228326786957887 hour= 1 Iteration: 9 R^2: 0.8742262956151615 hour= 1 Iteration: 0 R^2: 0.9257707800422799 hour= 2 Iteration: 1 R^2: 0.9413981795880517 hour= 2 Iteration: 2 R^2: 0.9354221623113591 hour= 2 Iteration: 3 R^2: 0.8370429185837882 hour= 2 Iteration: 4 R^2: 0.9142875737195697 hour= 2 Iteration: 5 R^2: 0.9586871067966855 hour= 2 Iteration: 6 R^2: 0.8209392060391961 hour= 2 Iteration: 7 R^2: 0.9457287035542066 hour= 2 Iteration: 8 R^2: 0.9587372191281025 hour= 2 Iteration: 9 R^2: 0.9269140213952402 hour= 2 Iteration: 0 R^2: 0.9001009579436263 hour= 3 Iteration: 1 R^2: 0.8735623527502183 hour= 3 Iteration: 2 R^2: 0.9460714774572146 hour= 3 Iteration: 3 R^2: 0.7221720163838841 hour= 3 Iteration: 4 R^2: 0.9063579778744433 hour= 3 Iteration: 5 R^2: 0.9695391076372475 hour= 3 Iteration: 6 R^2: 0.9297881558889788 hour= 3 Iteration: 7 R^2: 0.9271590681844957 hour= 3 Iteration: 8 R^2: 0.8817985496711311 hour= 3 Iteration: 9 R^2: 0.915205007218742 hour= 3 Iteration: 0 R^2: 0.9378516360378022 hour= 4 Iteration: 1 R^2: 0.9210968481902528 hour= 4 Iteration: 2 R^2: 0.9072205941748894 hour= 4 Iteration: 3 R^2: 0.9408826184927528 hour= 4 Iteration: 4 R^2: 0.9671981453714584 hour= 4 Iteration: 5 R^2: 0.9625144032389237 hour= 4 Iteration: 6 R^2: 0.9759244293257822 hour= 4 Iteration: 7 R^2: 0.9461473783201281 hour= 4 Iteration: 8 R^2: 0.9190627222826241 hour= 4 Iteration: 9 R^2: 0.9130350931314233 hour= 4
Напомню, что все модели обучались с начала 2017 года, тогда как оценка R^2 делалась с учетом тестового участка (дополнительные данные, начиная с 2015 года). Дополнительную уверенность придает последовательность высоких оценок для каждого дня. Отобразим итоговый результат.
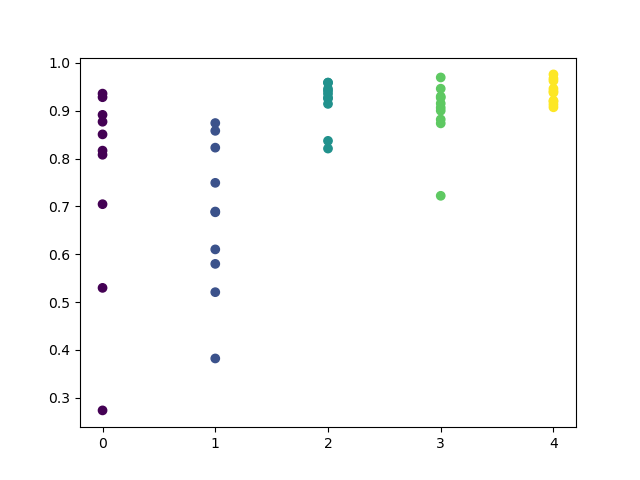
Разведочный анализ показал, что среда и пятница являются наиболее благоприятными днями для торговли, особенно пятница. Самым плохим днем оказался вторник, он имеет большой разброс ошибок и низкое их среднее значение. Давайте обучим модель торговать только в пятницу и посмотрим на результат.
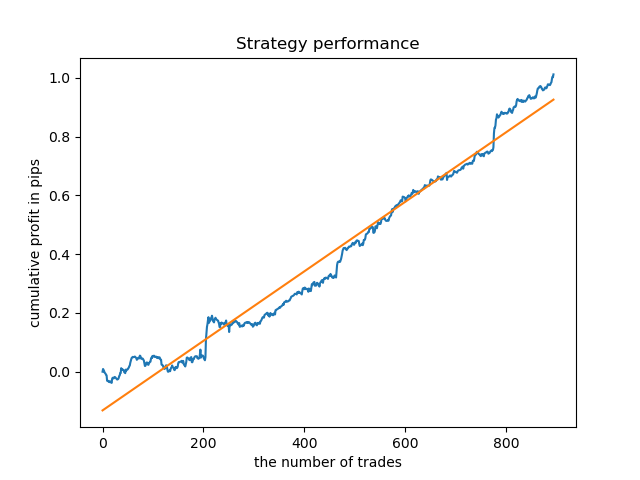
Таким же образом можно получить модель, торгующую только во вторник.
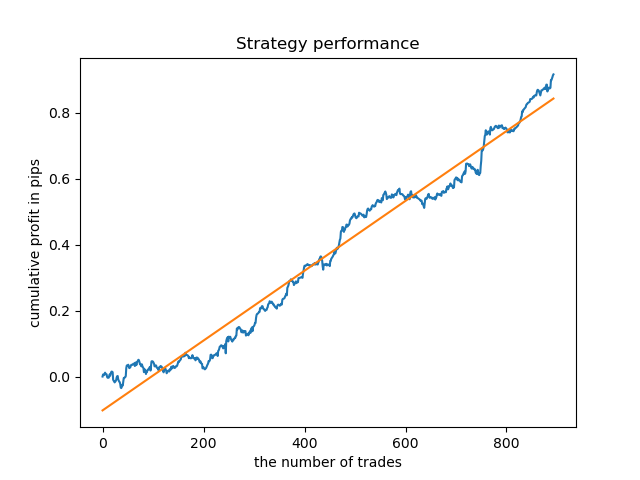
Фиксированная продолжительность сделок не всегда может быть оправданной, поэтому имеет смысл расширить окно поиска и увеличить количество итераций разведочного анализа до 20.
pr = add_labels(pr, min=5, max=25, filter=time_filter) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] iterations = 20
Разброс значений закономерно увеличился, наилучшими днями для торговли являются четверг и пятница.
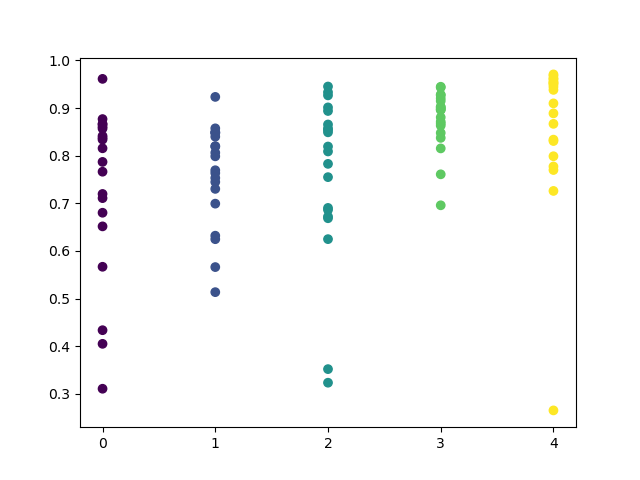
Давайте обучим контрольную модель для четверга, чтобы посмотреть на результат. Так выглядит цикл обучения (для тех, кто не читал предыдущие статьи).
hours = [3]
# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=5, max=25, filter=time_filter)
tester(pr, MARKUP, plot=True, filter=time_filter)
# perform GMM clasterizatin over dataset
# gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X)
gmm = mixture.GaussianMixture(
n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])
# iterative learning
res = []
for i in range(10):
res.append(brute_force(10000, gmm))
print('Iteration: ', i, 'R^2: ', res[-1][0])
# test best model
res.sort()
test_model(res[-1]) Результат получается несколько хуже, чем при фиксированной продолжительности сделок.
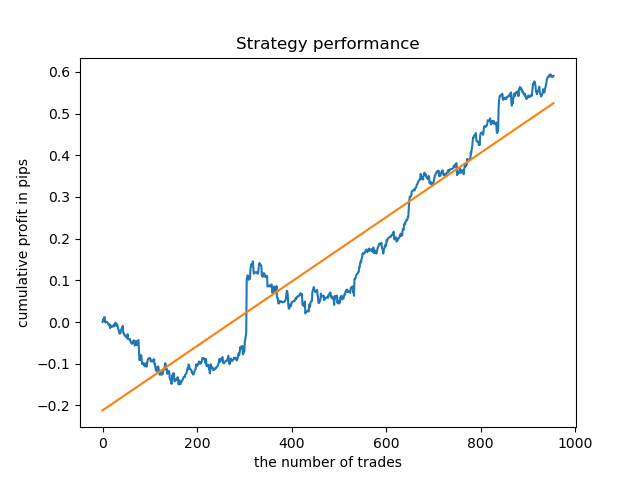
Очевидно, параметр частоты (горизонта) сделок при торговле в конкретные периоды имеет большое значение. Интересно было бы перебрать эти значения и посмотреть, как они влияют на результат.
Оценка влияния продолжительности сделок на качество моделей
По аналогии с функцией разведочного анализа по выбранному критерию (фильтру), можно написать вспомогательную функцию, которая будет оценивать производительность модели в зависимости от продолжительности сделок. Предположим, что можно сделать продолжительность сделок фиксированной на интервале от 1 до 50 баров (или любом другом интервале), тогда функция будет выглядеть следующим образом.
def deals_frequency_analyzer(): freq = [x for x in range(1, 50)] result = pd.DataFrame() for _h in freq: pr = get_prices(START_DATE, STOP_DATE) pr = add_labels(pr, min=_h, max=_h, filter=time_filter) gmm = mixture.GaussianMixture( n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]]) # iterative learning res = [] iterations = 5 for i in range(iterations): res.append(brute_force(10000, gmm)) print('Iteration: ', i, 'R^2: ', res[-1][0], ' deal lifetime = ', _h) r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h)) result = result.append(r) plt.scatter(result.index, result, c = result.index) plt.xticks(np.arange(0, len(freq)+1, 1)) plt.title("Performance by deals lifetime") plt.xlabel("deals frequency") plt.ylabel("R^2 estimation") plt.show() return result
Список freq содержит продолжительности сделок, которые перебираются. Я сделал такой перебор для 5-го часа валютной пары GBPUSD. Посмотрим на результат.
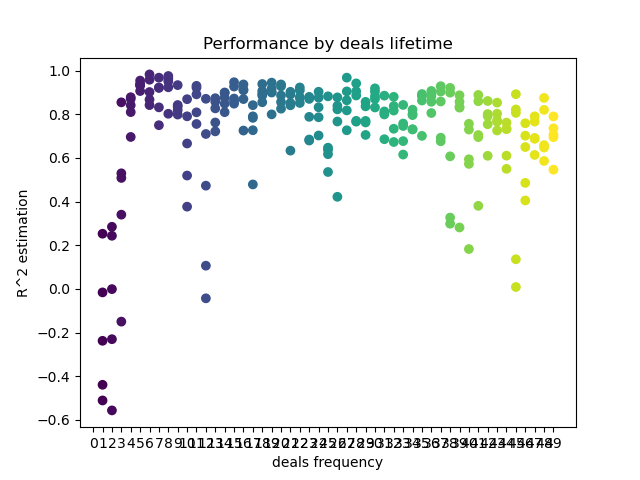
По оси X отображена частота сделок, вернее, их продолжительность, в барах. По оси Y оценка R^2 для каждого из проходов. Хорошо видно, что слишком короткие сделки в 0-5 баров плохо влияют на производительность модели, тогда как диапазон 15-23 является оптимальным. Увеличение продолжительности сделок свыше 30 баров начинает ухудшать результат. Есть небольшой кластер с продолжительностями сделок 6-9 баров, для которого оценки максимальны. Давайте попробуем обучить модели с такими продолжительностями и сравним результаты с другими кластерами.
Я выбрал продолжительность 8 баров, для которой модель прошла тест аж с 2013 года, но кривая баланса не такая ровная, как хотелось бы.
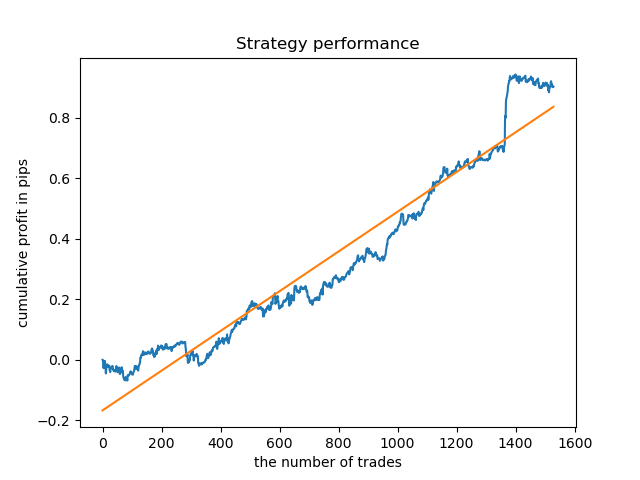
Для продолжительности из наиболее "кучного" кластера график выглядит очень хорошо с 2015 года, однако модель показывает плохой результат на более раннем участке истории.
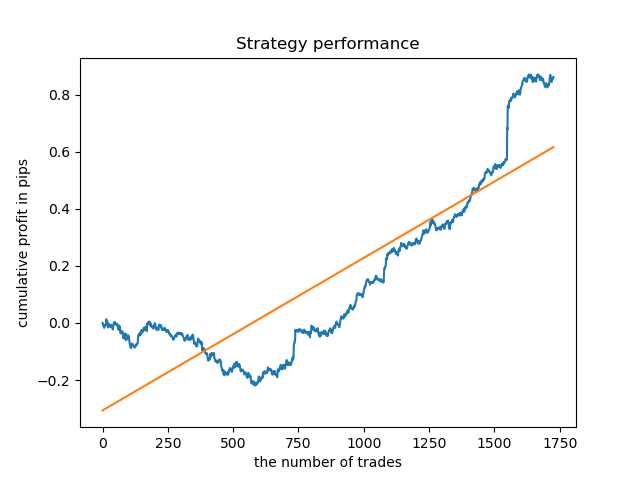
В завершение был выбран диапазон лучших кластеров 15-23 и модель была переобучена несколько раз (поскольку семплинг продолжительности сделок случайный).
pr = add_labels(pr, min=15, max=23, filter=time_filter)
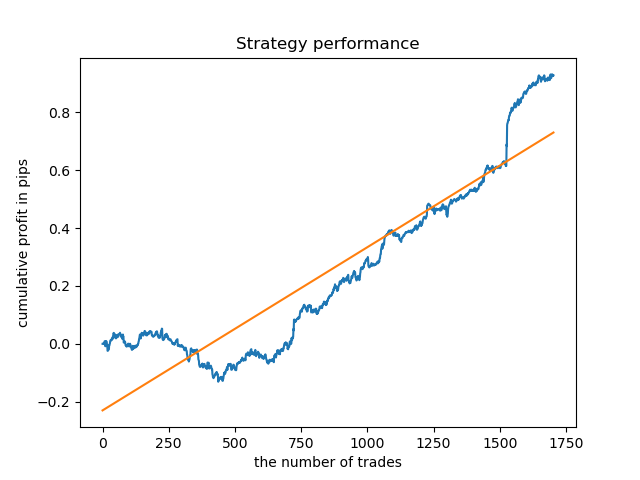
Модель на таких закономерностях в среднем отказывается жить на данных раньше 2015 года, что обусловлено какими-то кардинальными изменениями в структуре рынка. Для анализа этой ситуации требуется отдельное объемное исследование. После того, как модель отобрана и доказана ее устойчивость на определенном временном интервале, можно сделать обучение на всем этом интервале, включая тестовую выборку и отправить такую модель в продакшн.
Проверка на более длинной истории
Может возникнуть интерес проверить модель на более длинной истории. Модель была обучена на данных с 2000 года и протестирована на периоде с 1990г. На таком продолжительном участке истории закономерности улавливаются слабо, что отражено в неровной кривой баланса, но итог все равно положителен.
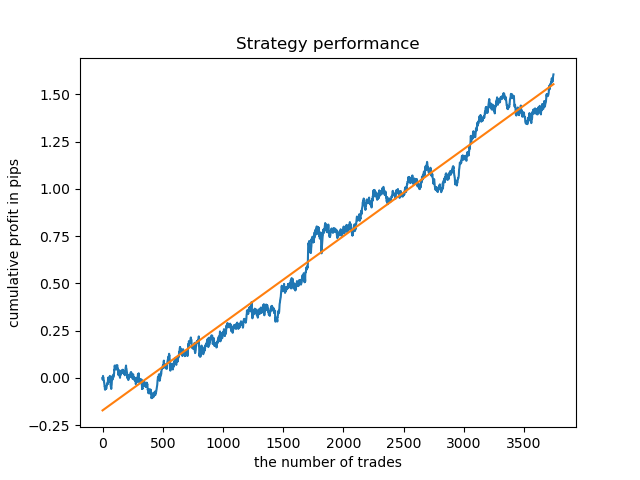
Заключение
В статье предложен мощный инструмент для поиска сезонных закономерностей и создания торговых систем. Вы можете проводить анализ для разных инструментов (не обязательно FOREX), разных таймфреймов и с различными фильтрами (не обязательно временными). Спектр применения такого подхода настолько широк, что для полного раскрытия его возможностей требуются множественные тесты с различными фильтрами. После проведенного анализа можно скомпоновать готового робота при помощи функции экспорта моделей, предложенной в предыдущих статьях.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Самоадаптирующийся алгоритм (Часть III): Отказываемся от оптимизации
Самоадаптирующийся алгоритм (Часть III): Отказываемся от оптимизации
 Нейросети — это просто (Часть 10): Multi-Head Attention (многоголовое внимание)
Нейросети — это просто (Часть 10): Multi-Head Attention (многоголовое внимание)
 Рынок и физика его глобальных закономерностей
Рынок и физика его глобальных закономерностей
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
а можете опубликовать советника для этой самой модели с таймингом?
Ответная часть такая же как во 2-й статье, но в терминал нужно добавить ограничение открытия сделок по времени, и все
то же самое для дней недели и разных комбинаций. Еще в МТ5 отсчет часов со сдвигом на 1 вправо, т.е. если в питоне 4-й час, то в МТ 5-й
Ответная часть такая же как во 2-й статье, но в терминал нужно добавить ограничение открытия сделок по времени, и все
то же самое для дней недели и разных комбинаций. Еще в МТ5 отсчет часов со сдвигом на 1 вправо, т.е. если в питоне 4-й час, то в МТ 5-й
спасибо.
Интересная и близкая тема.
Было бы очень любопытно посмотреть итоговую эквити стандартного тестера MT5 по любому из инструментов FORTS на выбор, полученную при применении данного метода.
В качестве обратной связи готов выложить эквити своего сезонного алгоритма по выбранному инструменту :)