利用 CatBoost 算法寻找外汇市场的季节性模式

介绍

另外两篇关于季节性模式搜索的文章已经发表（1，2）。我想知道机器学习算法如何处理模式搜索任务。上述文章中的交易系统是在统计分析的基础上构建的。现在，只要简单地指示模型在一周中某一天的某个时间进行交易，就可以消除人为因素。模式搜索可以由单独的算法提供。

时间过滤器函数

通过添加过滤函数，可以很容易地扩展开发库。

def time_filter(data, count):
    # filter by hour
    hours=[15]
    if data.index[count].hour not in hours:
        return False

    # filter by day of week
    days = [1]
    if data.index[count].dayofweek not in days:
        return False

    return True

函数检查其中指定的条件，可以实现其他附加条件（不仅仅是时间过滤器）。但由于本文专门讨论季节性模式，因此我将只使用时间过滤器。如果满足所有条件，函数将返回True，并将适当的样本添加到训练集中。例如，在这种特殊情况下，我们指示模型仅在周二15:00进行交易。“hours”和“days”列表可以包括其他小时和天。通过注释掉所有条件，您可以让算法无条件地工作，就像前一篇文章中的工作方式一样。 

add_labels 函数现在接收这个条件作为输入。在Python中，函数是一级对象，因此可以将它们作为参数安全地传递给其他函数。

def add_labels(dataset, min, max, filter=time_filter):
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'][i]
        future_pr = dataset['close'][i + rand]
        if filter(dataset, i):
            if future_pr + MARKUP < curr_pr:
                labels.append(1.0)
            elif future_pr - MARKUP > curr_pr:
                labels.append(0.0)
            else:
                labels.append(2.0)
        else:
            labels.append(2.0)
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2].index)

    return dataset

一旦过滤器被传递给函数，它就可以用来标记买入或卖出交易。过滤器接收原始数据集和当前柱的索引。数据集中的索引表示为包含时间的“datetime index”。过滤器按第i个数字在数据帧的“datetime index”中搜索小时和天，如果未找到任何内容，则返回 False。如果满足条件，则交易标记为1或0，否则标记为2。最后，从训练数据集中删除所有2，因此只留下由过滤器确定的特定天数和小时的示例。

还应向自定义测试仪添加一个过滤器，以在特定时间启用交易打开（或根据此过滤器设置的任何其他条件）。

def tester(dataset, markup=0.0, plot=False, filter=time_filter):
    last_deal = int(2)
    last_price = 0.0
    report = [0.0]
    for i in range(dataset.shape[0]):
        pred = dataset['labels'][i]
        ind = dataset.index[i].hour
        if last_deal == 2 and filter(dataset, i):
            last_price = dataset['close'][i]
            last_deal = 0 if pred <= 0.5 else 1
            continue
        if last_deal == 0 and pred > 0.5:
            last_deal = 2
            report.append(report[-1] - markup +
                          (dataset['close'][i] - last_price))
            continue
        if last_deal == 1 and pred < 0.5:
            last_deal = 2
            report.append(report[-1] - markup +
                          (last_price - dataset['close'][i]))

    y = np.array(report).reshape(-1, 1)
    X = np.arange(len(report)).reshape(-1, 1)
    lr = LinearRegression()
    lr.fit(X, y)

    l = lr.coef_
    if l >= 0:
        l = 1
    else:
        l = -1

    if(plot):
        plt.plot(report)
        plt.plot(lr.predict(X))
        plt.title("Strategy performance")
        plt.xlabel("the number of trades")
        plt.ylabel("cumulative profit in pips")
        plt.show()

    return lr.score(X, y) * l

具体实现如下:当没有未平仓时使用数字2：last_deal=2。测试开始前没有未平的仓位，因此设置2。遍历整个数据集并检查是否满足筛选条件。如果条件满足，就开始买卖交易。过滤条件不应用于交易结束，因为它们可以在一周的另一个小时或一天结束。这些变化足以进行进一步的正确训练和测试。 

每个交易小时的探索性分析

对于每个单独的条件（以及几个小时或几天的组合），手动测试模型不是很方便。为此编写了一个特殊函数，可以分别快速获取每个条件的汇总统计信息。该函数可能需要一些时间才能完成，但它会输出模型显示出更好性能的时间范围。

def exploratory_analysis():
    h = [x for x in range(24)]
    result = pd.DataFrame()
    for _h in h:
        global hours 
        hours = [_h]
        pr = get_prices(START_DATE, STOP_DATE)
        pr = add_labels(pr, min=15, max=15, filter=time_filter)
        gmm = mixture.GaussianMixture(
            n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

        # iterative learning
        res = []
        iterations = 10
        for i in range(iterations):
            res.append(brute_force(10000, gmm))
            print('Iteration: ', i, 'R^2: ', res[-1][0], ' hour= ', _h)
        
        r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h))
        result = result.append(r)

    plt.scatter(result.index, result, c = result.index)
    plt.show()
    return result

您可以在函数中设置要检查的小时数列表。在我的例子中，所有的24小时都设置好了。为了实验的纯度，我通过将“min”和“max”（开启仓位的最小和最大水平）设置为15来禁用采样。“iterations”变量负责每小时的再训练周期数。增加这个参数可以得到更可靠的统计数据。操作完成后，函数将显示下图：

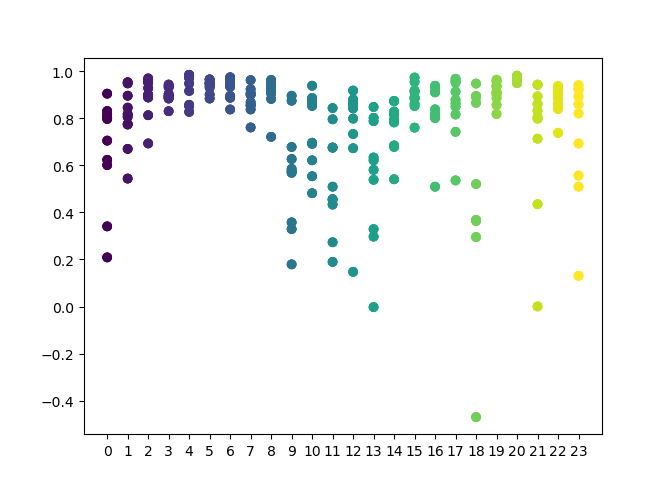
X轴以小时的序号为特征。Y轴表示每次迭代的R^2分数（使用10次迭代，这意味着每小时进行一次模型再培训）。如您所见，4小时、5小时和6小时的通行证位于更近的位置，这使您对找到的模式的质量更有信心。选择原则很简单 - 点的位置和密度越高，模型就越好。例如，在9-15点的时间间隔内，图中显示了大量的点分散，模型的平均质量下降到0.6。您可以进一步选择所需的小时数，重新训练模型并在自定义测试器中查看其结果。

测试选择的模型

对 GBPUSD 货币对进行了探索性分析，参数如下：

SYMBOL = 'GBPUSD'
MARKUP = 0.00010
TIMEFRAME = mt5.TIMEFRAME_H1
START_DATE = datetime(2017, 1, 1)
TSTART_DATE = datetime(2015, 1, 1)
FULL_DATE = datetime(2015, 1, 1)
STOP_DATE = datetime(2021, 1, 1)

相同的参数将用于测试。为了获得更大的可信度，您可以更改 FULL_DATE 值以查看模型在早期历史数据中的执行情况。

我们可以直观地分辨出3、4、5和6小时的一组。可以假设相邻的时间有相似的模式，所以模型可以针对所有的时间进行训练。

hours = [3,4,5,6]
# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=15, max=15, filter=time_filter)
tester(pr, MARKUP, plot=True, filter=time_filter)

# perform GMM clasterizatin over dataset
# gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X)
gmm = mixture.GaussianMixture(
    n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

# iterative learning
res = []

for i in range(10):
    res.append(brute_force(10000, gmm))
    print('Iteration: ', i, 'R^2: ', res[-1][0])

# test best model
res.sort()
test_model(res[-1])

其余的代码不需要额外的解释，因为在以前的文章中已经详细解释过。唯一的例外是，你可以使用注释贝叶斯模型来代替一个简单的GMM，尽管这只是一个实验性的想法。 

交易抽样后的理想模型如下所示：

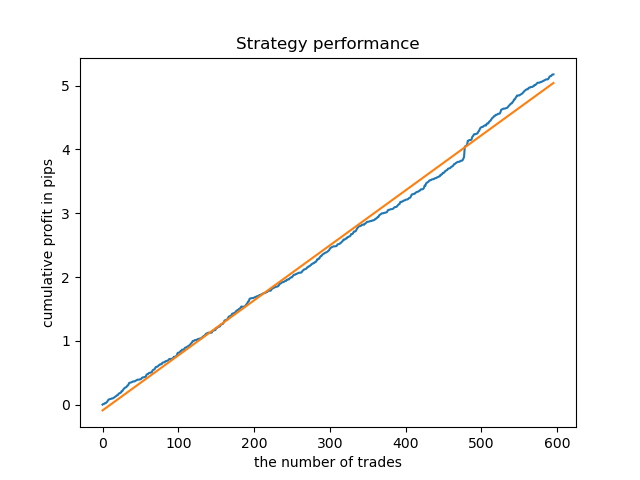
经过训练的模型（包括测试数据）显示了以下性能：

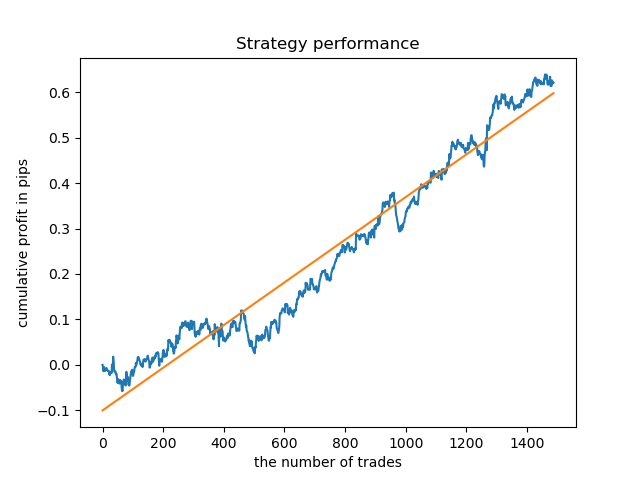
单独的模型可以进行高密度训练。下面是已经训练过的5小时和20小时模型的余额图：

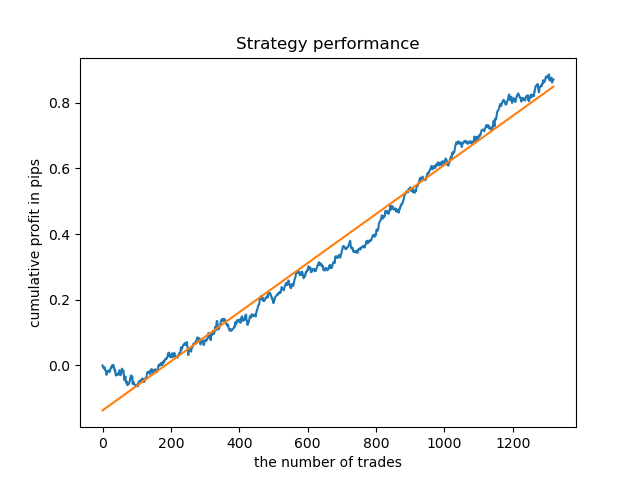
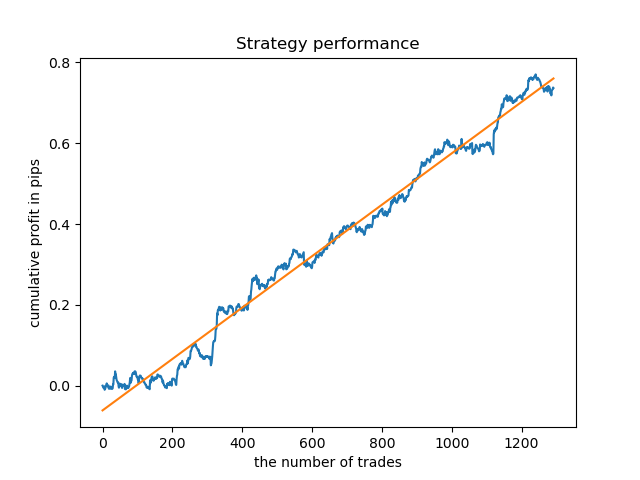
现在，为了进行比较，你可以看看那些训练时数变化较大的模型。例如查看第9和11小时。

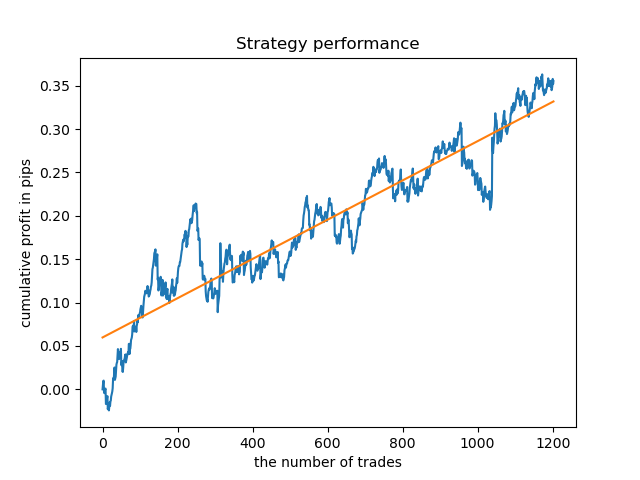
这里的余额图显示的比任何注释都多，显然，在训练模式时，要特别注意时机。 

每个交易日的探索性分析

对于其他时间间隔，例如一周中的几天，可以很容易地修改过滤器。您只需将小时替换为一周中的一天。

def time_filter(data, count):
    # filter by day of week
    global hours
    if data.index[count].dayofweek not in hours:
        return False
    return True

在这种情况下，迭代应该在0到5之间的范围内执行（不包括第5个序号，也就是星期六）。

def exploratory_analysis():
    h = [x for x in range(5)]

现在，对 GBPUSD 货币对进行探索性分析。交易的频率，或者说它们的范围，是相同的（15个柱）。

pr = add_labels(pr, min=15, max=15, filter=time_filter)

训练过程显示在控制台中，您可以立即查看当前期间的R^2分数。“hour”变量现在不包含小时数，而是一周中某一天的序号。

Iteration:  0 R^2:  0.5297625368835237  hour=  0
Iteration:  1 R^2:  0.8166096906047893  hour=  0
Iteration:  2 R^2:  0.9357674260125702  hour=  0
Iteration:  3 R^2:  0.8913802241811986  hour=  0
Iteration:  4 R^2:  0.8079720208707672  hour=  0
Iteration:  5 R^2:  0.8505663844866759  hour=  0
Iteration:  6 R^2:  0.2736870273207084  hour=  0
Iteration:  7 R^2:  0.9282442121644887  hour=  0
Iteration:  8 R^2:  0.8769775718602929  hour=  0
Iteration:  9 R^2:  0.7046666925774866  hour=  0
Iteration:  0 R^2:  0.7492883761480897  hour=  1
Iteration:  1 R^2:  0.6101962958733655  hour=  1
Iteration:  2 R^2:  0.6877652983219245  hour=  1
Iteration:  3 R^2:  0.8579669286548137  hour=  1
Iteration:  4 R^2:  0.3822441930760343  hour=  1
Iteration:  5 R^2:  0.5207801806491617  hour=  1
Iteration:  6 R^2:  0.6893157850263495  hour=  1
Iteration:  7 R^2:  0.5799059801202937  hour=  1
Iteration:  8 R^2:  0.8228326786957887  hour=  1
Iteration:  9 R^2:  0.8742262956151615  hour=  1
Iteration:  0 R^2:  0.9257707800422799  hour=  2
Iteration:  1 R^2:  0.9413981795880517  hour=  2
Iteration:  2 R^2:  0.9354221623113591  hour=  2
Iteration:  3 R^2:  0.8370429185837882  hour=  2
Iteration:  4 R^2:  0.9142875737195697  hour=  2
Iteration:  5 R^2:  0.9586871067966855  hour=  2
Iteration:  6 R^2:  0.8209392060391961  hour=  2
Iteration:  7 R^2:  0.9457287035542066  hour=  2
Iteration:  8 R^2:  0.9587372191281025  hour=  2
Iteration:  9 R^2:  0.9269140213952402  hour=  2
Iteration:  0 R^2:  0.9001009579436263  hour=  3
Iteration:  1 R^2:  0.8735623527502183  hour=  3
Iteration:  2 R^2:  0.9460714774572146  hour=  3
Iteration:  3 R^2:  0.7221720163838841  hour=  3
Iteration:  4 R^2:  0.9063579778744433  hour=  3
Iteration:  5 R^2:  0.9695391076372475  hour=  3
Iteration:  6 R^2:  0.9297881558889788  hour=  3
Iteration:  7 R^2:  0.9271590681844957  hour=  3
Iteration:  8 R^2:  0.8817985496711311  hour=  3
Iteration:  9 R^2:  0.915205007218742   hour=  3
Iteration:  0 R^2:  0.9378516360378022  hour=  4
Iteration:  1 R^2:  0.9210968481902528  hour=  4
Iteration:  2 R^2:  0.9072205941748894  hour=  4
Iteration:  3 R^2:  0.9408826184927528  hour=  4
Iteration:  4 R^2:  0.9671981453714584  hour=  4
Iteration:  5 R^2:  0.9625144032389237  hour=  4
Iteration:  6 R^2:  0.9759244293257822  hour=  4
Iteration:  7 R^2:  0.9461473783201281  hour=  4
Iteration:  8 R^2:  0.9190627222826241  hour=  4
Iteration:  9 R^2:  0.9130350931314233  hour=  4

请注意，所有模型都是使用2017年初以来的数据进行培训的，而R^2分数也包括测试期（从2015年开始的额外数据）。每天高估计值的一致性提供了更大的信心。让我们看看最后的结果。

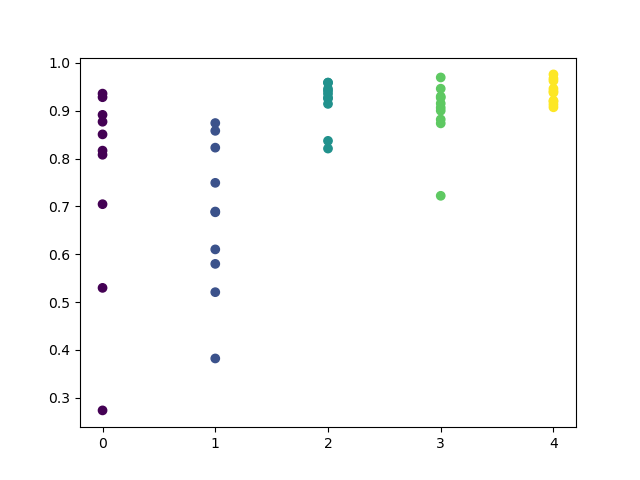
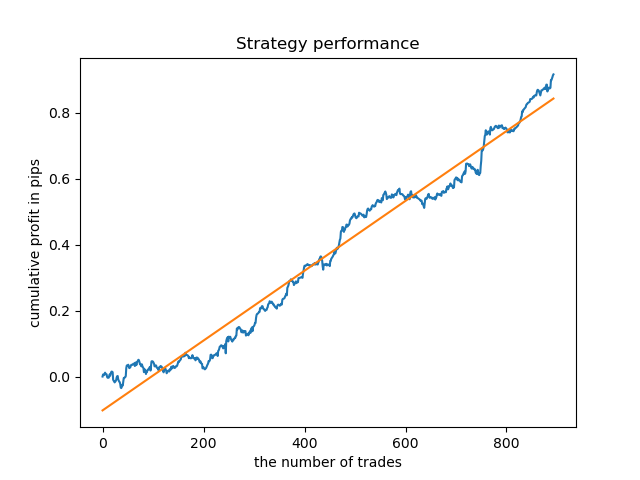
探索性分析表明，周三和周五是最有利的交易日，尤其是周五。周二是交易最糟糕的一天，因为它有很大的误差方差和较低的平均值。让我们训练模型只在星期五交易，看看结果。

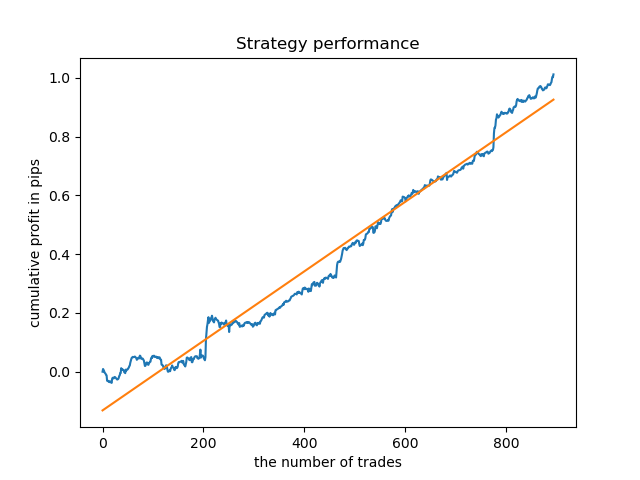
同样，我们可以在周二获得一个交易模型。

固定的交易时间段并不总是合适的，因此让我们尝试扩展搜索窗口，并将探索性分析迭代次数增加到20次。

pr = add_labels(pr, min=5, max=25, filter=time_filter)
        gmm = mixture.GaussianMixture(
            n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

        # iterative learning
        res = []
        iterations = 20

价值区间已经变大，而周四和周五是最好的交易日。

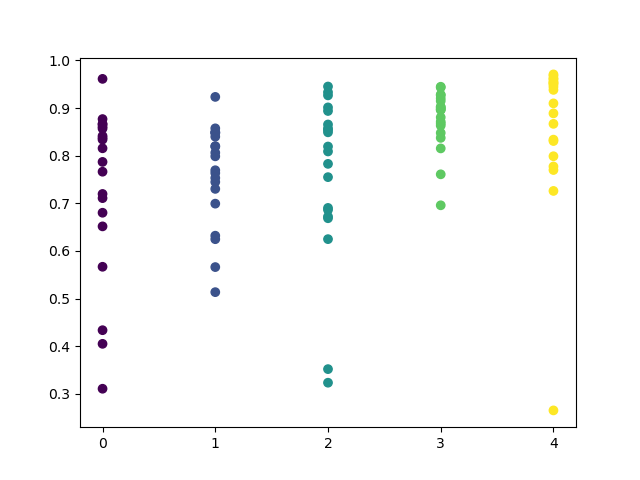
现在让我们为周四训练一个控制模型，看看结果。这就是学习周期的样子（对于那些没有读过之前文章的人来说）。

hours = [3]
# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=5, max=25, filter=time_filter)
tester(pr, MARKUP, plot=True, filter=time_filter)

# perform GMM clasterizatin over dataset
# gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X)
gmm = mixture.GaussianMixture(
    n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])


# iterative learning
res = []
for i in range(10):
    res.append(brute_force(10000, gmm))
    print('Iteration: ', i, 'R^2: ', res[-1][0])

# test best model
res.sort()
test_model(res[-1])

结果比固定交易期限的情况稍差。 

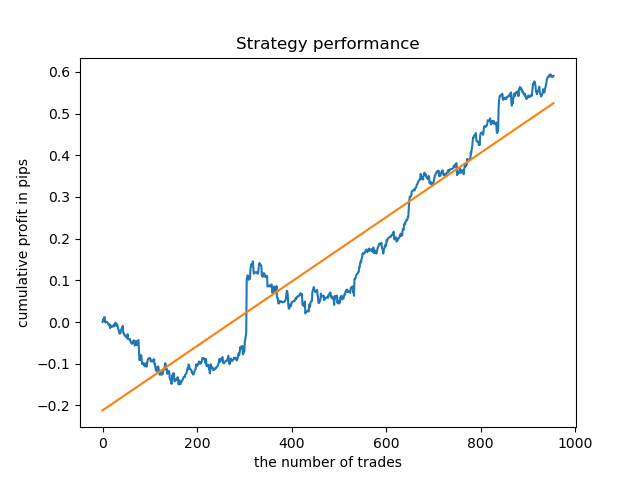
显然，特定时期的频率（水平）参数很重要。接下来，让我们迭代这些值并检查它们如何影响结果。

交易期间对模型质量影响的评估

与所选标准（过滤器）的探索性分析函数类似，我们可以创建一个辅助函数，该函数将根据交易期间评估模型性能。假设我们可以在1到50个柱（或任何其他时间段）的间隔内设置一个固定的事务生存期，那么函数将如下所示。

def deals_frequency_analyzer():
    freq = [x for x in range(1, 50)]
    result = pd.DataFrame()
    for _h in freq:
        pr = get_prices(START_DATE, STOP_DATE)
        pr = add_labels(pr, min=_h, max=_h, filter=time_filter)
        gmm = mixture.GaussianMixture(
            n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

        # iterative learning
        res = []
        iterations = 5
        for i in range(iterations):
            res.append(brute_force(10000, gmm))
            print('Iteration: ', i, 'R^2: ', res[-1][0], ' deal lifetime = ', _h)
        
        r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h))
        result = result.append(r)

    plt.scatter(result.index, result, c = result.index)
    plt.xticks(np.arange(0, len(freq)+1, 1))
    plt.title("Performance by deals lifetime")
    plt.xlabel("deals frequency")
    plt.ylabel("R^2 estimation")
    plt.show()
    return result

“freq”列表包含要迭代的交易时期的值。我在 GBPUSD 对的第5个小时执行了这个迭代，这是结果。

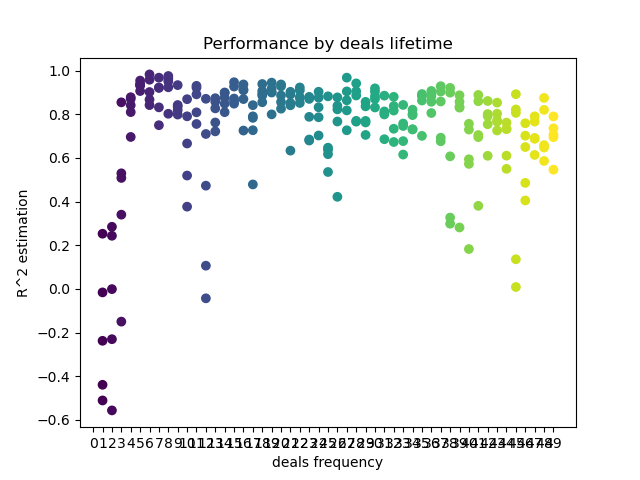
X轴显示交易频率，或者更确切地说，以柱数为单位显示其时间。Y轴表示每个过程的R^2分数。如您所见，0-5 个柱的太短交易对模型性能有负面影响，而15到23个柱的时间是最佳的。更长的交易（超过30个柱）会使结果变坏。有一个小集群，其交易时间为6-9个柱，得分最高。让我们尝试用这些生存期值来训练模型，并将结果与其他集群进行比较。

我选择了8个柱的时间，从2013年开始对模型进行了测试，但余额曲线并不像我希望的那样均匀。

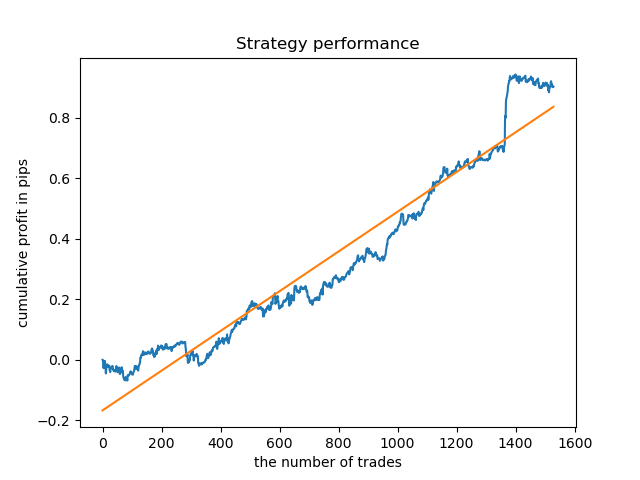
对于具有最高密度的集群的时间段，自2015年以来，该图看起来非常好，但是，该模型在较早的历史间隔中表现不佳。

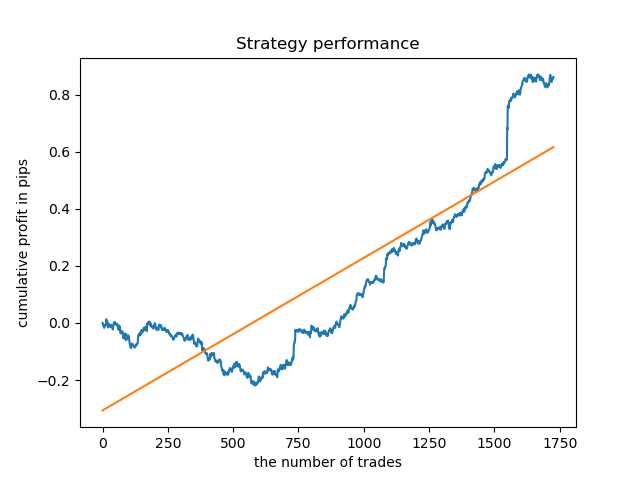
最后，我选择了一系列最好的聚类15-23，并对模型进行了多次重新训练（因为交易时间的抽样是随机的）。 

pr = add_labels(pr, min=15, max=23, filter=time_filter)

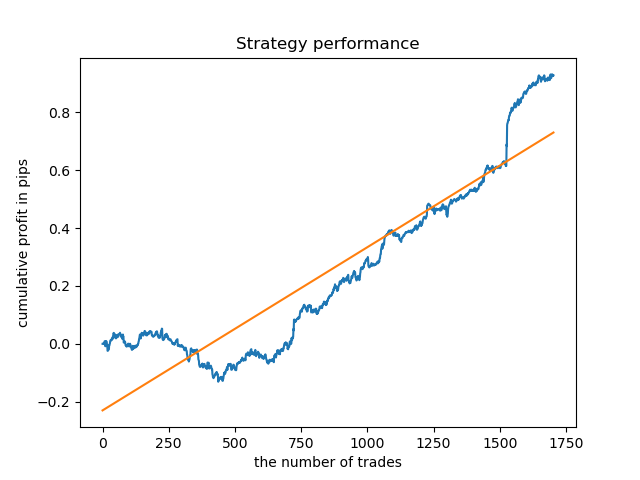
基于这种模式的模型在2015年之前并不能显示数据的生存能力。或许，市场结构发生了一些根本性的变化。需要一个单独的大型研究来分析这种情况。在选定模型并证明其在一定时间间隔内的稳定性之后，可以在整个时间间隔内执行训练，包括测试样本。然后这个模型就可以投入实际应用了。

在较长的历史上进行测试

如果我们在更长的历史上检查模型呢？该模型自2000年以来一直以数据为基础进行训练，并使用1990年以来的数据进行测试。从余额曲线上可以看出，在如此长的历史时期内，模式捕捉得很差，但结果仍然是正面的。

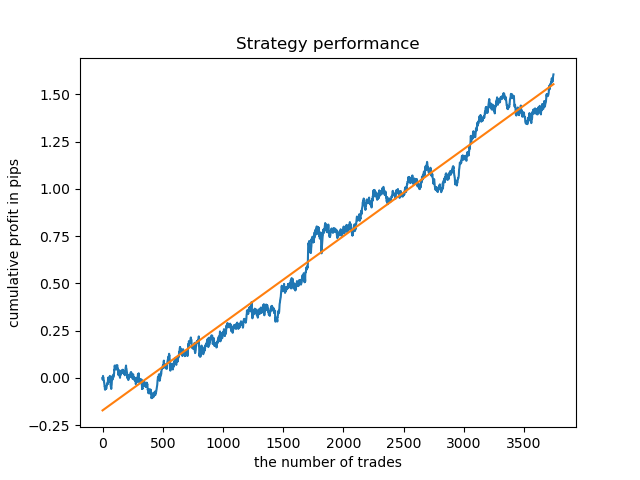
结论

这篇文章描述了一个寻找季节性模式和创建交易系统的强大工具。您可以针对不同的工具（外汇除外）、不同的时间段和不同的过滤器（不仅仅是时间过滤器）对其进行分析。这种方法的应用范围非常广泛。为了充分展示它的功能，我们需要使用不同的过滤器进行多个测试。在进行分析之后，您可以使用前面文章中描述的模型导出功能构建一个交易机器人。