Über das Finden von zeitlicher Mustern im Devisenmarkt mit dem CatBoost-Algorithmus

Einführung

Zwei weitere Artikel, die sich mit der zeitlichen Mustersuche beschäftigen, wurden bereits veröffentlicht (1, 2). Ich habe mich gefragt, wie maschinelle Lernalgorithmen die Aufgabe der Mustersuche bewältigen können. Die Handelssysteme in den oben erwähnten Artikeln wurden auf der Basis statistischer Analysen aufgebaut. Der menschliche Faktor kann nun eliminiert werden, indem das Modell einfach angewiesen wird, zu einer bestimmten Stunde an einem bestimmten Wochentag zu handeln. Die Mustersuche kann durch einen separaten Algorithmus bereitgestellt werden.

Filterfunktion der Zeit

Die Bibliothek kann durch Hinzufügen einer Filterfunktion leicht erweitert werden.

def time_filter(data, count):
    # filter by hour
    hours=[15]
    if data.index[count].hour not in hours:
        return False

    # filter by day of week
    days = [1]
    if data.index[count].dayofweek not in days:
        return False

    return True

Die Funktion prüft die in ihr angegebenen Bedingungen. Es können auch andere zusätzliche Bedingungen implementiert werden (nicht nur Zeitfilter). Da sich der Artikel aber mit zeitlichen Mustern befasst, werde ich nur Zeitfilter verwenden. Wenn alle Bedingungen erfüllt sind, gibt die Funktion "True" zurück und das entsprechende Muster wird dem Trainingssatz hinzugefügt. In diesem speziellen Fall weisen wir das Modell z. B. an, Positionen nur um 15:00 Uhr am Dienstag zu öffnen. Die Listen "Stunden" und "Tage" können auch andere Stunden und Tage enthalten. Wenn Sie alle Bedingungen auskommentieren, können Sie den Algorithmus ohne Bedingungen arbeiten lassen, so wie er im vorherigen Artikel gearbeitet hat. 

Die Funktion add_labels erhält nun diese Bedingung als Eingabe. In Python sind Funktionen Objekte der ersten Ebene, Sie können sie also gefahrlos als Argumente an andere Funktionen übergeben.

def add_labels(dataset, min, max, filter=time_filter):
    labels = []
    for i in range(dataset.shape[0]-max):
        rand = random.randint(min, max)
        curr_pr = dataset['close'][i]
        future_pr = dataset['close'][i + rand]
        if filter(dataset, i):
            if future_pr + MARKUP < curr_pr:
                labels.append(1.0)
            elif future_pr - MARKUP > curr_pr:
                labels.append(0.0)
            else:
                labels.append(2.0)
        else:
            labels.append(2.0)
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()
    dataset = dataset.drop(
        dataset[dataset.labels == 2].index)

    return dataset

Sobald der Filter der Funktion übergeben wird, kann er zum Markieren von Kauf- oder Verkaufsgeschäften verwendet werden. Der Filter erhält den Originaldatensatz und den Index des aktuellen Balkens. Die Indizes im Datensatz werden als 'datetime index' dargestellt, der die Uhrzeit enthält. Der Filter sucht die Stunde und den Tag im 'datetime index' des Datenrahmens um die i-te Zahl und gibt False zurück, wenn er nichts findet. Wenn die Bedingung erfüllt ist, wird die Position mit 1 oder 0 markiert, sonst mit 2. Schließlich werden alle Zweier aus dem Trainingsdatensatz entfernt, so dass nur noch Beispiele für bestimmte Tage und Stunden übrig bleiben, die durch den Filter bestimmt werden.

Dem nutzerdefinierten Tester sollte ebenfalls ein Filter hinzugefügt werden, um die Eröffnung von Geschäften zu einer bestimmten Uhrzeit (oder gemäß einer anderen durch diesen Filter festgelegten Bedingung) zu ermöglichen.

def tester(dataset, markup=0.0, plot=False, filter=time_filter):
    last_deal = int(2)
    last_price = 0.0
    report = [0.0]
    for i in range(dataset.shape[0]):
        pred = dataset['labels'][i]
        ind = dataset.index[i].hour
        if last_deal == 2 and filter(dataset, i):
            last_price = dataset['close'][i]
            last_deal = 0 if pred <= 0.5 else 1
            continue
        if last_deal == 0 and pred > 0.5:
            last_deal = 2
            report.append(report[-1] - markup +
                          (dataset['close'][i] - last_price))
            continue
        if last_deal == 1 and pred < 0.5:
            last_deal = 2
            report.append(report[-1] - markup +
                          (last_price - dataset['close'][i]))

    y = np.array(report).reshape(-1, 1)
    X = np.arange(len(report)).reshape(-1, 1)
    lr = LinearRegression()
    lr.fit(X, y)

    l = lr.coef_
    if l >= 0:
        l = 1
    else:
        l = -1

    if(plot):
        plt.plot(report)
        plt.plot(lr.predict(X))
        plt.title("Strategy performance")
        plt.xlabel("the number of trades")
        plt.ylabel("cumulative profit in pips")
        plt.show()

    return lr.score(X, y) * l

Dies ist wie folgt implementiert. Die Zahl 2 wird verwendet, wenn es keine offene Position gibt: last_deal = 2. Es gibt keine offenen Positionen vor Testbeginn, daher 2 setzen. Iterieren Sie durch den gesamten Datensatz und prüfen Sie, ob die Filterbedingung erfüllt ist. Wenn die Bedingung erfüllt ist, öffnen Sie einen Kauf- oder Verkaufsposition. Die Filterbedingungen gelten nicht für das Schließen von Positionen, da diese zu einer anderen Stunde oder an einem anderen Wochentag geschlossen werden können. Diese Änderungen reichen für weiteres korrektes Training und Testen aus. 

Explorative Analyse für jede Handelsstunde

Es ist nicht sehr bequem, das Modell manuell für jede einzelne Bedingung (und für eine Kombination von Stunden oder Tagen) zu testen. Für diesen Zweck wurde eine spezielle Funktion geschrieben, die es ermöglicht, schnell eine zusammenfassende Statistik für jede Bedingung separat zu erhalten. Die Funktion kann einige Zeit in Anspruch nehmen, aber sie gibt die Zeitbereiche aus, in denen das Modell eine bessere Leistung zeigt.

def exploratory_analysis():
    h = [x for x in range(24)]
    result = pd.DataFrame()
    for _h in h:
        global hours 
        hours = [_h]
        pr = get_prices(START_DATE, STOP_DATE)
        pr = add_labels(pr, min=15, max=15, filter=time_filter)
        gmm = mixture.GaussianMixture(
            n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

        # iterative learning
        res = []
        iterations = 10
        for i in range(iterations):
            res.append(brute_force(10000, gmm))
            print('Iteration: ', i, 'R^2: ', res[-1][0], ' hour= ', _h)
        
        r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h))
        result = result.append(r)

    plt.scatter(result.index, result, c = result.index)
    plt.show()
    return result

Sie können in der Funktion eine Liste der zu prüfenden Stunden einstellen. In meinem Beispiel sind alle 24 Stunden eingestellt. Für die Sauberkeit des Experiments habe ich das Sampling deaktiviert, indem ich 'min' und 'max' (minimaler und maximaler Horizont einer offenen Position) auf 15 gesetzt habe. Die Iterationsvariable ist für die Anzahl der Umschulungszyklen für jede Stunde verantwortlich. Eine zuverlässigere Statistik kann durch Erhöhen dieses Parameters erreicht werden. Nach Abschluss der Operation zeigt die Funktion die folgende Grafik an:

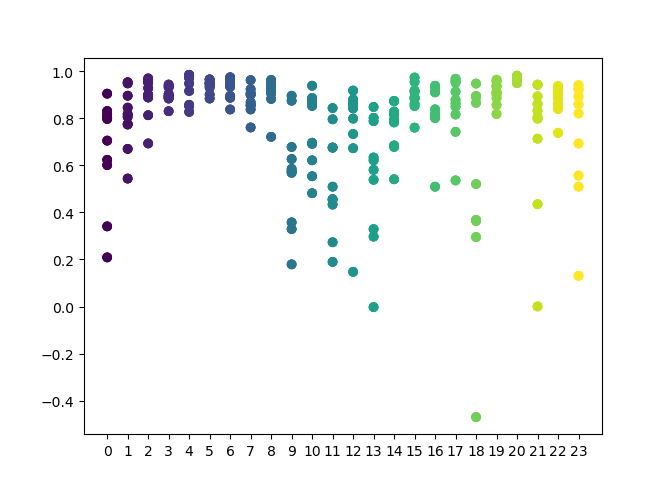
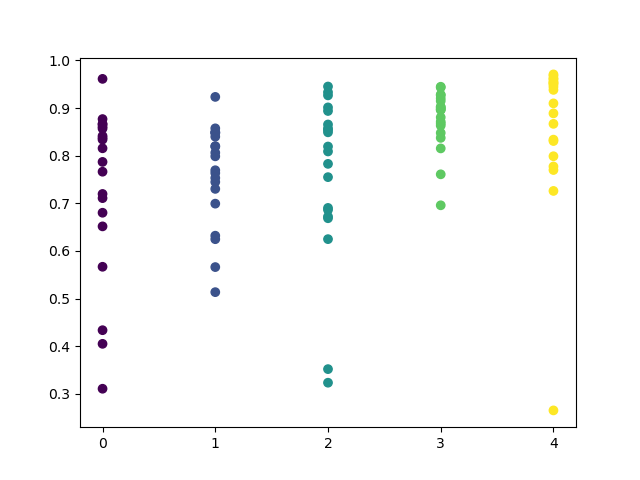
Die X-Achse weist die Ordnungszahlen der Stunden auf. Die Y-Achse stellt die R^2-Werte für jede Iteration dar (es wurden 10 Iterationen verwendet, was bedeutet, dass das Modell für jede Stunde neu trainiert wird). Wie Sie sehen können, liegen die Durchgänge für die Stunden 4, 5 und 6 näher beieinander, was mehr Vertrauen in die Qualität des gefundenen Musters gibt. Das Auswahlprinzip ist einfach - je höher die Position und Dichte der Punkte, desto besser das Modell. Zum Beispiel im Intervall von 9-15 zeigt das Diagramm eine große Streuung der Punkte, und die durchschnittliche Qualität der Modelle sinkt auf 0,6. Sie können weiterhin die gewünschten Stunden auswählen, das Modell neu trainieren und seine Ergebnisse im benutzerdefinierten Tester ansehen.

Testen ausgewählter Modelle

Die explorative Analyse wurde für das Währungspaar GBPUSD mit den folgenden Parametern durchgeführt:

SYMBOL = 'GBPUSD'
MARKUP = 0.00010
TIMEFRAME = mt5.TIMEFRAME_H1
START_DATE = datetime(2017, 1, 1)
TSTART_DATE = datetime(2015, 1, 1)
FULL_DATE = datetime(2015, 1, 1)
STOP_DATE = datetime(2021, 1, 1)

Zum Testen werden die gleichen Parameter verwendet. Um das Vertrauen zu erhöhen, können Sie den Wert FULL_DATE ändern, um zu sehen, wie das Modell in früheren historischen Daten abgeschnitten hat.

Wir können visuell ein Cluster der Stunden 3, 4, 5 und 6 unterscheiden. Es kann davon ausgegangen werden, dass benachbarte Stunden ähnliche Muster aufweisen, so dass das Modell für alle diese Stunden trainiert werden kann.

hours = [3,4,5,6]
# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=15, max=15, filter=time_filter)
tester(pr, MARKUP, plot=True, filter=time_filter)

# perform GMM clasterizatin over dataset
# gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X)
gmm = mixture.GaussianMixture(
    n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

# iterative learning
res = []

for i in range(10):
    res.append(brute_force(10000, gmm))
    print('Iteration: ', i, 'R^2: ', res[-1][0])

# test best model
res.sort()
test_model(res[-1])

Für den restlichen Code sind keine weiteren Erklärungen erforderlich, da er in früheren Artikeln ausführlich erläutert wurde. Mit der einzigen Ausnahme, dass Sie anstelle eines einfachen GMMs ein kommentiertes Bayes'sches Modell verwenden können, obwohl dies nur eine experimentelle Idee ist. 

Ein ideales Modell nach dem Sampling der Positionen würde wie folgt aussehen:

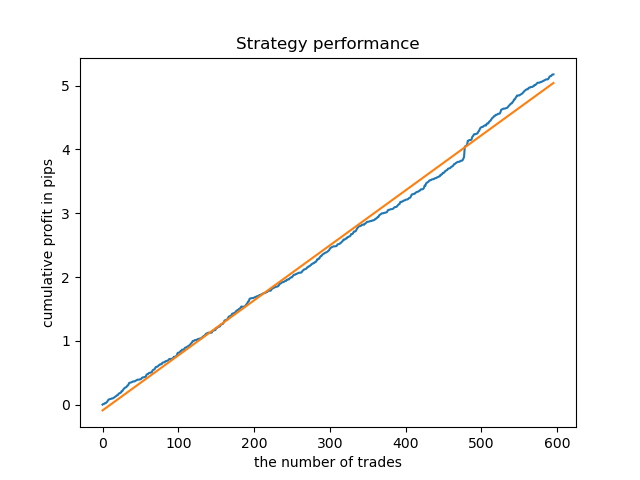
Das trainierte Modell (einschließlich Testdaten) zeigt die folgende Leistung:

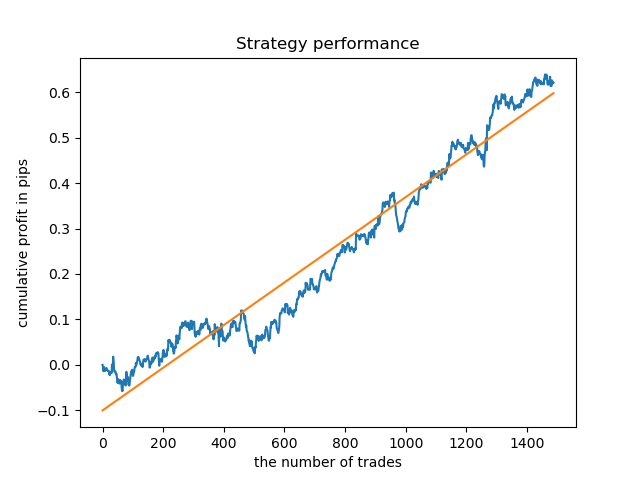
Separate Modelle können für Stunden mit hoher Dichte trainiert werden. Unten finden Sie Bilanzdiagramme für bereits trainierte Modelle für die Stunden 5 und 20:

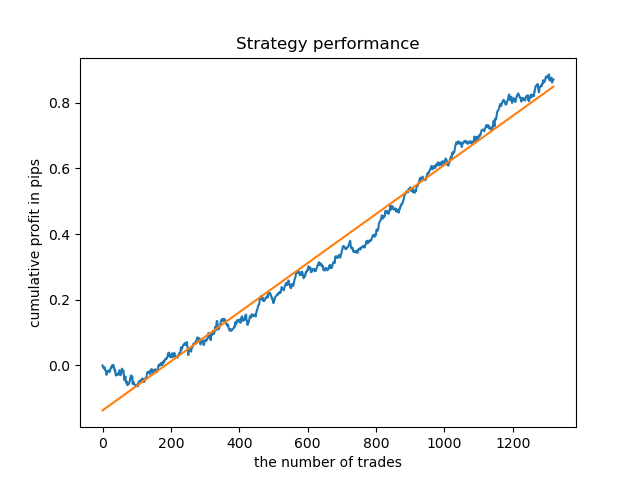
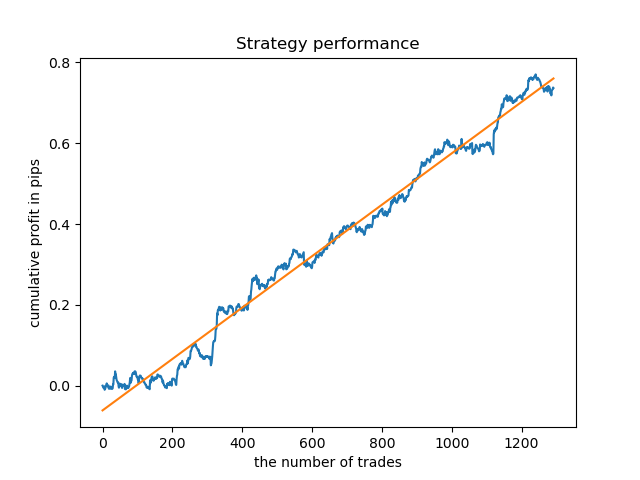
Zum Vergleich können Sie sich nun die Modelle ansehen, die für Stunden mit größerer Varianz trainiert wurden. Betrachten Sie zum Beispiel die Stunden 9 und 11.

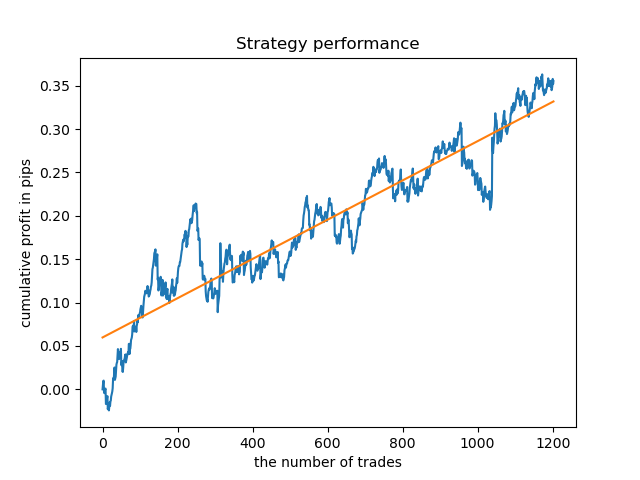
Die Saldenkurven hier zeigen mehr als alle Kommentare. Es ist offensichtlich, dass beim Trainieren von Modellen dem Timing besondere Aufmerksamkeit gewidmet werden sollte. 

Explorative Analyse für jeden Handelstag

Der Filter kann leicht für andere Zeitintervalle, wie z. B. Wochentage, modifiziert werden. Sie müssen lediglich die Stunde durch einen Wochentag ersetzen.

def time_filter(data, count):
    # filter by day of week
    global hours
    if data.index[count].dayofweek not in hours:
        return False
    return True

In diesem Fall sollte die Iteration im Bereich zwischen 0 und 5 durchgeführt werden (mit Ausnahme der 5. Ordnungszahl, die der Samstag ist).

def exploratory_analysis():
    h = [x for x in range(5)]

Führen Sie nun eine Sondierungsanalyse für das Währungspaar GBPUSD durch. Die Häufigkeit der Geschäfte, oder ihr Horizont, ist gleich (15 Balken).

pr = add_labels(pr, min=15, max=15, filter=time_filter)

Der Trainingsprozess wird in der Konsole angezeigt, wo Sie sofort die R^2-Werte für den aktuellen Zeitraum sehen können. Die Variable 'hour' enthält jetzt nicht die Stundenzahl, sondern die Ordnungszahl des Wochentages.

Iteration:  0 R^2:  0.5297625368835237  hour=  0
Iteration:  1 R^2:  0.8166096906047893  hour=  0
Iteration:  2 R^2:  0.9357674260125702  hour=  0
Iteration:  3 R^2:  0.8913802241811986  hour=  0
Iteration:  4 R^2:  0.8079720208707672  hour=  0
Iteration:  5 R^2:  0.8505663844866759  hour=  0
Iteration:  6 R^2:  0.2736870273207084  hour=  0
Iteration:  7 R^2:  0.9282442121644887  hour=  0
Iteration:  8 R^2:  0.8769775718602929  hour=  0
Iteration:  9 R^2:  0.7046666925774866  hour=  0
Iteration:  0 R^2:  0.7492883761480897  hour=  1
Iteration:  1 R^2:  0.6101962958733655  hour=  1
Iteration:  2 R^2:  0.6877652983219245  hour=  1
Iteration:  3 R^2:  0.8579669286548137  hour=  1
Iteration:  4 R^2:  0.3822441930760343  hour=  1
Iteration:  5 R^2:  0.5207801806491617  hour=  1
Iteration:  6 R^2:  0.6893157850263495  hour=  1
Iteration:  7 R^2:  0.5799059801202937  hour=  1
Iteration:  8 R^2:  0.8228326786957887  hour=  1
Iteration:  9 R^2:  0.8742262956151615  hour=  1
Iteration:  0 R^2:  0.9257707800422799  hour=  2
Iteration:  1 R^2:  0.9413981795880517  hour=  2
Iteration:  2 R^2:  0.9354221623113591  hour=  2
Iteration:  3 R^2:  0.8370429185837882  hour=  2
Iteration:  4 R^2:  0.9142875737195697  hour=  2
Iteration:  5 R^2:  0.9586871067966855  hour=  2
Iteration:  6 R^2:  0.8209392060391961  hour=  2
Iteration:  7 R^2:  0.9457287035542066  hour=  2
Iteration:  8 R^2:  0.9587372191281025  hour=  2
Iteration:  9 R^2:  0.9269140213952402  hour=  2
Iteration:  0 R^2:  0.9001009579436263  hour=  3
Iteration:  1 R^2:  0.8735623527502183  hour=  3
Iteration:  2 R^2:  0.9460714774572146  hour=  3
Iteration:  3 R^2:  0.7221720163838841  hour=  3
Iteration:  4 R^2:  0.9063579778744433  hour=  3
Iteration:  5 R^2:  0.9695391076372475  hour=  3
Iteration:  6 R^2:  0.9297881558889788  hour=  3
Iteration:  7 R^2:  0.9271590681844957  hour=  3
Iteration:  8 R^2:  0.8817985496711311  hour=  3
Iteration:  9 R^2:  0.915205007218742   hour=  3
Iteration:  0 R^2:  0.9378516360378022  hour=  4
Iteration:  1 R^2:  0.9210968481902528  hour=  4
Iteration:  2 R^2:  0.9072205941748894  hour=  4
Iteration:  3 R^2:  0.9408826184927528  hour=  4
Iteration:  4 R^2:  0.9671981453714584  hour=  4
Iteration:  5 R^2:  0.9625144032389237  hour=  4
Iteration:  6 R^2:  0.9759244293257822  hour=  4
Iteration:  7 R^2:  0.9461473783201281  hour=  4
Iteration:  8 R^2:  0.9190627222826241  hour=  4
Iteration:  9 R^2:  0.9130350931314233  hour=  4

Bitte beachten Sie, dass alle Modelle mit den Daten seit Anfang 2017 trainiert wurden, während die R^2-Werte auch den Testzeitraum (zusätzliche Daten ab 2015) beinhalten. Die Konsistenz der hohen Schätzungen für jeden Tag sorgt für noch mehr Vertrauen. Lassen Sie uns das Endergebnis betrachten.

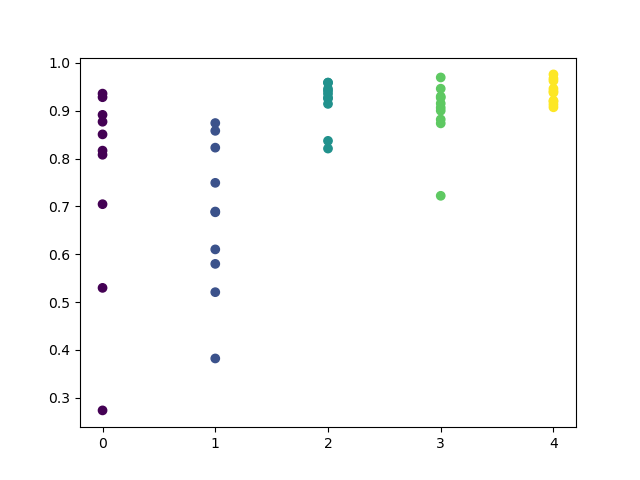
Die explorative Analyse hat gezeigt, dass Mittwoch und Freitag die günstigsten Tage für den Handel sind, besonders Freitag. Der schlechteste Tag für den Handel ist Dienstag, da er eine große Varianz der Fehler und einen niedrigen Durchschnittswert hat. Lassen Sie uns das Modell so trainieren, dass es nur an Freitagen handelt, und sehen Sie sich das Ergebnis an.

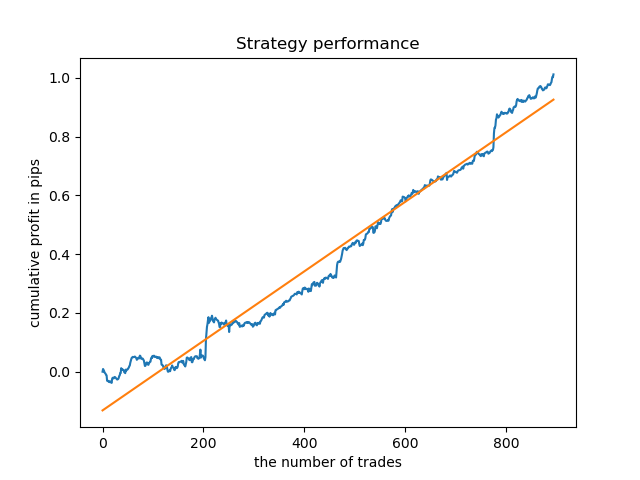
Auf ähnliche Weise können wir ein Modell erhalten, das an Dienstagen handelt.

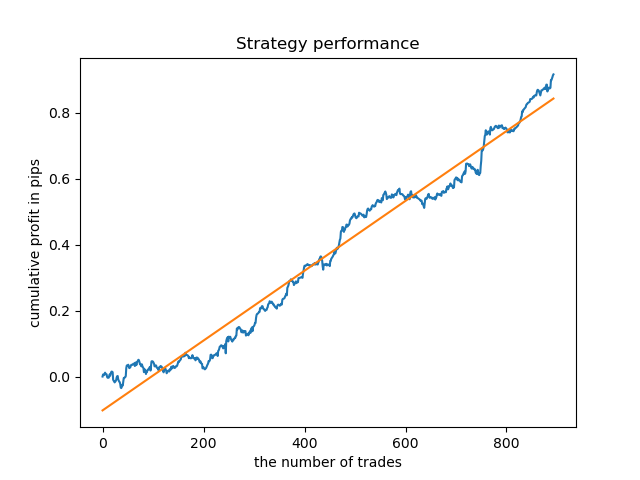
Eine feste Lebensdauer von Geschäften ist nicht immer geeignet, also lassen Sie uns versuchen, das Suchfenster zu erweitern und die Anzahl der Iterationen der explorativen Analyse auf 20 zu erhöhen.

pr = add_labels(pr, min=5, max=25, filter=time_filter)
        gmm = mixture.GaussianMixture(
            n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

        # iterative learning
        res = []
        iterations = 20

Die Spanne der Werte ist größer geworden, die besten Tage für den Handel sind Donnerstag und Freitag.

Lassen Sie uns nun ein Kontrollmodell für Donnerstag trainieren, um das Ergebnis zu sehen. So sieht der Lernzyklus aus (für diejenigen, die die vorherigen Artikel nicht gelesen haben).

hours = [3]
# make dataset
pr = get_prices(START_DATE, STOP_DATE)
pr = add_labels(pr, min=5, max=25, filter=time_filter)
tester(pr, MARKUP, plot=True, filter=time_filter)

# perform GMM clasterizatin over dataset
# gmm = mixture.BayesianGaussianMixture(n_components=n_compnents, covariance_type='full').fit(X)
gmm = mixture.GaussianMixture(
    n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])


# iterative learning
res = []
for i in range(10):
    res.append(brute_force(10000, gmm))
    print('Iteration: ', i, 'R^2: ', res[-1][0])

# test best model
res.sort()
test_model(res[-1])

Das Ergebnis ist etwas schlechter als bei einer festen Laufzeit der Positionen. 

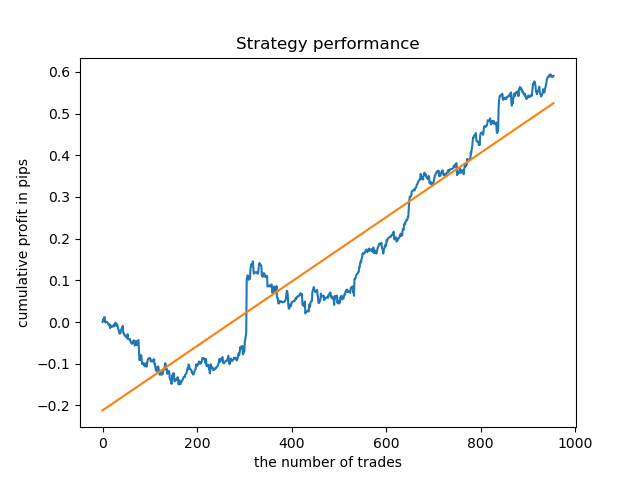
Offensichtlich ist der Parameter Häufigkeit (Horizont) in bestimmten Perioden wichtig. Als Nächstes wollen wir über diese Werte iterieren und prüfen, wie sie das Ergebnis beeinflussen.

Bewertung des Einflusses der Geschäftslebensdauer auf die Modellqualität

Ähnlich wie bei der explorativen Analysefunktion für ein ausgewähltes Kriterium (Filter) können wir eine Hilfsfunktion erstellen, die die Modellleistung in Abhängigkeit von der Geschäftsdauer bewertet. Angenommen, wir können eine feste Geschäftsdauer im Intervall von 1 bis 50 Takten (oder einem anderen Zeitraum) einstellen, dann sieht die Funktion wie folgt aus.

def deals_frequency_analyzer():
    freq = [x for x in range(1, 50)]
    result = pd.DataFrame()
    for _h in freq:
        pr = get_prices(START_DATE, STOP_DATE)
        pr = add_labels(pr, min=_h, max=_h, filter=time_filter)
        gmm = mixture.GaussianMixture(
            n_components=n_compnents, covariance_type='full', n_init=1).fit(pr[pr.columns[1:]])

        # iterative learning
        res = []
        iterations = 5
        for i in range(iterations):
            res.append(brute_force(10000, gmm))
            print('Iteration: ', i, 'R^2: ', res[-1][0], ' deal lifetime = ', _h)
        
        r = pd.DataFrame(np.array(res)[:, 0], np.full(iterations,_h))
        result = result.append(r)

    plt.scatter(result.index, result, c = result.index)
    plt.xticks(np.arange(0, len(freq)+1, 1))
    plt.title("Performance by deals lifetime")
    plt.xlabel("deals frequency")
    plt.ylabel("R^2 estimation")
    plt.show()
    return result

Die 'freq'-Liste enthält die Werte der Handelsdauer, über die iteriert werden soll. Ich habe diese Iteration für die 5. Stunde des GBPUSD-Paares durchgeführt. Hier ist das Ergebnis.

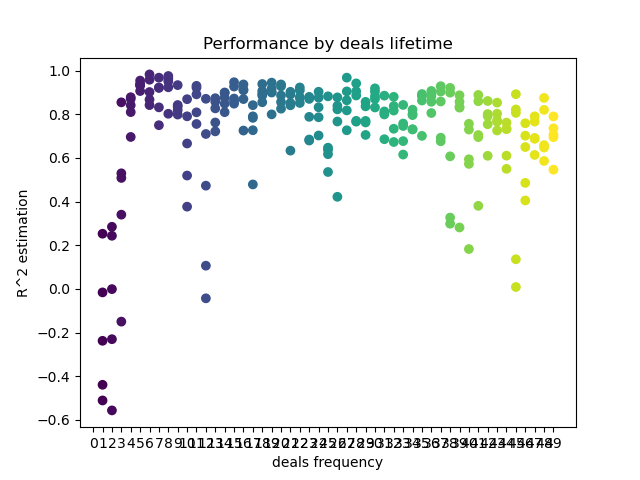
Die X-Achse zeigt die Häufigkeit bzw. deren Lebensdauer dr Positionen in Balken an. Die Y-Achse stellt den R^2-Score für jeden der Durchläufe dar. Wie Sie sehen können, wirken sich zu kurze Abschlüsse von 0-5 Takten negativ auf die Modellleistung aus, während die Lebensdauer von 15-23 optimal ist. Längere Abschlüsse (über 30 Balken) verschlechtern das Ergebnis. Es gibt ein kleines Cluster mit der Positions-Lebensdauer von 6-9 Balken, die die höchsten Scores haben. Lassen Sie uns versuchen, Modelle mit diesen Lebenszeitwerten zu trainieren und die Ergebnisse mit anderen Clustern zu vergleichen.

Ich habe die Lebensdauer von 8 Balken gewählt, für die das Modell seit 2013 getestet wurde. Aber die Gleichgewichtskurve ist nicht so gleichmäßig, wie ich es mir wünschen würde.

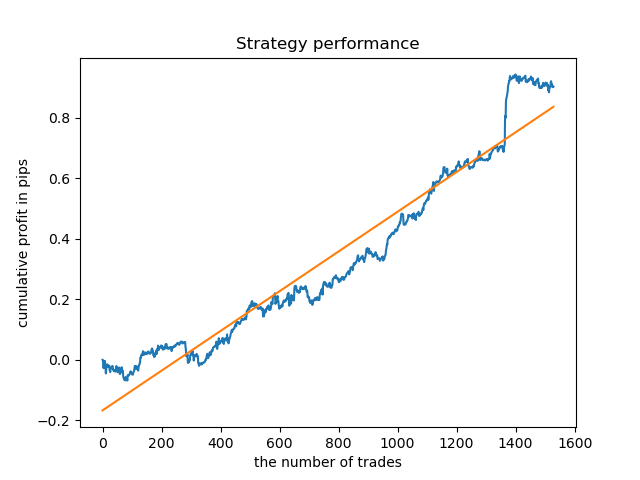
Für die Lebensdauer des Clusters mit der höchsten Dichte sieht die Kurve seit 2015 sehr gut aus, allerdings schneidet das Modell in einem früheren historischen Intervall schlecht ab.

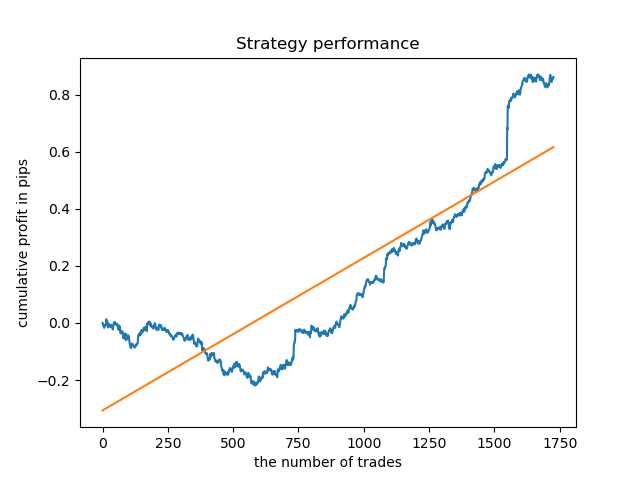
Schließlich habe ich einen Bereich mit den besten Clustern 15-23 ausgewählt und das Modell mehrmals neu trainiert (da die Stichprobenziehung für die Handelslebensdauer zufällig ist). 

pr = add_labels(pr, min=15, max=23, filter=time_filter)

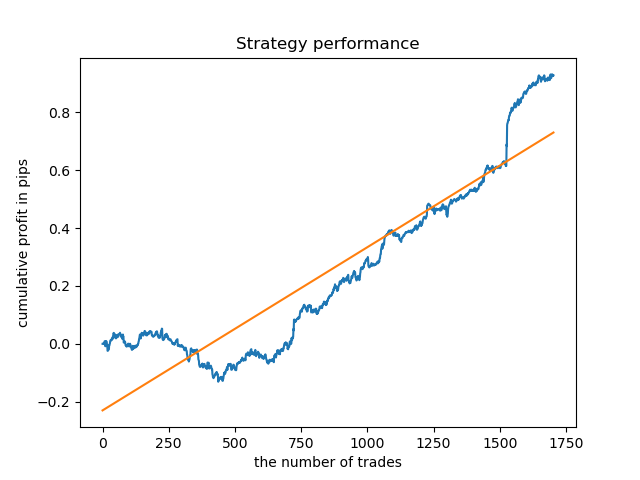
Ein Modell, das auf solchen Mustern basiert, zeigt keine Überlebensfähigkeit auf Daten vor 2015. Wahrscheinlich gab es einige kardinale Veränderungen in der Marktstruktur. Eine separate große Studie ist erforderlich, um diese Situation zu analysieren. Nachdem das Modell ausgewählt wurde und seine Stabilität über ein bestimmtes Zeitintervall bewiesen wurde, kann ein Training über dieses gesamte Intervall durchgeführt werden, einschließlich einer Teststichprobe. Dieses Modell kann dann in die Produktion geschickt werden.

Testen über eine längere Historie

Was ist, wenn wir das Modell mit einer längeren Historie prüfen? Das Modell wurde mit Daten seit 2000 trainiert und mit Daten seit 1990 getestet. Die Muster werden auf einem so langen historischen Zeitraum schlecht erfasst, was an der Saldenkurve zu erkennen ist, aber das Ergebnis ist immer noch positiv.

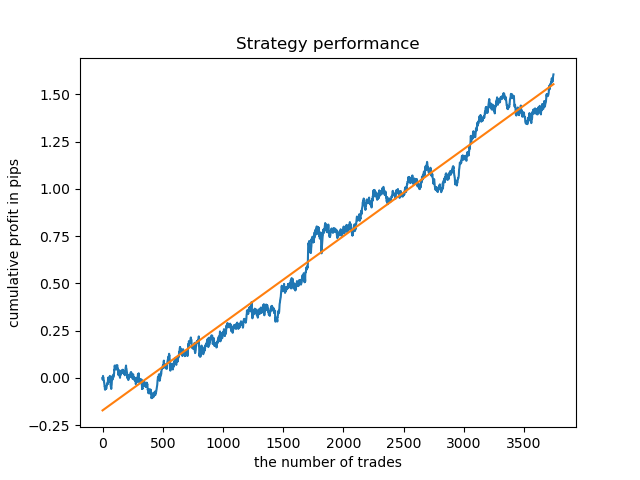
Schlussfolgerung

Der Artikel beschreibt ein leistungsfähiges Tool zum Auffinden von zeitlichen Mustern und zum Erstellen von Handelssystemen. Sie können es für verschiedene Instrumente (außer FOREX), verschiedene Zeitrahmen und mit verschiedenen Filtern (nicht nur Zeitfiltern) analysieren. Der Anwendungsbereich dieses Ansatzes ist sehr breit gefächert. Um seine Fähigkeiten vollständig zu enthüllen, wären mehrere Tests mit verschiedenen Filtern nötig. Nachdem Sie die Analyse durchgeführt haben, können Sie einen Handelsroboter mithilfe der in den vorherigen Artikeln beschriebenen Modellexportfunktion erstellen.