
Modelos ocultos de Markov em sistemas de trading com aprendizado de máquina
Conteúdo
- Introdução
- Algoritmos apresentados na biblioteca hmmlearn
- Descrição da classe hmm.GaussianHMM
- Descrição da classe hmm.GMMHMM
- Descrição da classe vhmm.VariationalGaussianHMM
- Comparação da eficiência dos modelos
- Métodos de definição de matrizes a priori
- Definição de regimes de mercado com o uso de HMM
- Criação de matrizes a priori
- Exportação de modelos para o MetaTrader 5
- Considerações finais
Introdução
Os modelos ocultos de Markov (HMM) representam uma classe poderosa de modelos probabilísticos, destinados à análise de dados sequenciais, nos quais os eventos observáveis dependem de alguma sequência de estados não observáveis (ocultos), que formam um processo de Markov.Os HMM são um processo estocástico duplo, caracterizado por um conjunto finito de estados ocultos e por uma sequência de eventos observáveis, cuja probabilidade depende do estado oculto atual.As principais suposições dos HMM incluem a propriedade de Markov para os estados ocultos, o que significa que a probabilidade de transição para o próximo estado depende apenas do estado atual, e a independência das observações, desde que o estado oculto atual seja conhecido.
Os modelos ocultos de Markov encontram ampla aplicação em diversas áreas, incluindo reconhecimento de fala e de padrões, processamento de linguagem natural, por exemplo, rotulação de classes gramaticais, bioinformática, análise de sequências de DNA e proteínas, e análise de séries temporais, como previsão e detecção de anomalias.A possibilidade de modelar sistemas cuja estrutura interna não é observada diretamente, mas exerce influência sobre os dados de saída observáveis, torna os HMM uma ferramenta valiosa para a análise de dependências temporais complexas. As observações em tais modelos são apenas um reflexo indireto dos processos ocultos, e a compreensão desses processos pode fornecer informações importantes sobre a dinâmica do sistema.
A biblioteca hmmlearn representa um conjunto de algoritmos na linguagem Python para aprendizado não supervisionado, isto é, de modelos ocultos de Markov (HMM). Ela foi desenvolvida para fornecer ferramentas simples e eficientes para trabalhar com HMM, seguindo a API da biblioteca scikit-learn, o que facilita a integração em projetos existentes de aprendizado de máquina e simplifica o processo de aprendizado para usuários familiarizados com o scikit-learn. O hmmlearn é construído com base em bibliotecas fundamentais do ecossistema científico do Python, como NumPy, SciPy e Matplotlib.
As principais funcionalidades do hmmlearn incluem a implementação de diferentes modelos de HMM com diversos tipos de distribuições de emissão, o treinamento dos parâmetros dos modelos a partir de dados observados, a inferência das sequências mais prováveis de estados ocultos, a geração de amostras a partir de modelos treinados, bem como a possibilidade de salvar e carregar modelos treinados. A diversidade de modelos implementados permite que os usuários escolham o tipo de distribuição de emissão mais adequado, dependendo da natureza de seus dados. O tipo de dado, contínuo, discreto ou de contagem, determina qual distribuição probabilística descreve melhor o processo de geração das observações em cada estado oculto.
Algoritmos apresentados na biblioteca hmmlearn
Na biblioteca hmmlearn, estão implementados os seguintes modelos principais de HMM:
- hmm.CategoricalHMM: para a modelagem de sequências de observações categóricas, isto é, discretas.
- hmm.GaussianHMM: para a modelagem de sequências de observações contínuas, assumindo uma distribuição gaussiana em cada estado oculto.
- hmm.GMMHMM: para a modelagem de sequências de observações contínuas, nas quais as emissões de cada estado oculto são descritas por uma mistura de distribuições gaussianas.
- hmm.MultinomialHMM: para a modelagem de sequências de observações discretas, nas quais cada estado possui uma distribuição de probabilidades sobre um conjunto fixo de símbolos.
- hmm.PoissonHMM: para a modelagem de sequências de dados que representam contadores de eventos, nas quais as emissões de cada estado oculto seguem uma distribuição de Poisson.
- vhmm.VariationalCategoricalHMM: versão variacional do CategoricalHMM, que utiliza métodos de inferência variacional para o treinamento.
- vhmm.VariationalGaussianHMM: versão variacional do GaussianHMM, destinada a observações contínuas distribuídas segundo uma distribuição normal multivariada, e treinada com o uso de inferência variacional.
Estamos interessados em algoritmos que trabalham com dados contínuos, portanto apenas esses serão considerados.
Descrição detalhada da classe hmm.GaussianHMM
A classe hmm.GaussianHMM na biblioteca hmmlearn implementa um modelo oculto de Markov com emissões gaussianas. Esse modelo é aplicado quando as variáveis observadas são contínuas e assume-se que, em cada estado oculto, elas seguem uma distribuição normal multivariada, isto é, gaussiana.
O GaussianHMM é amplamente utilizado para a modelagem de diversos tipos de séries temporais, como dados financeiros, por exemplo, preços de ações, leituras de diferentes sensores, bem como outros processos contínuos nos quais os valores observados podem ser descritos por uma distribuição gaussiana em cada um dos estados ocultos.
O construtor da classe hmm.GaussianHMM aceita os seguintes parâmetros:
- n_components (int, padrão 1): define o número de estados ocultos no modelo. Cada estado estará associado ao seu próprio conjunto de parâmetros de uma distribuição gaussiana.
- covariance_type ({"spherical", "diag", "full", "tied"}, padrão "diag"): especifica o tipo de matriz de covariância utilizada para cada estado. A escolha do tipo de covariância influencia diretamente a complexidade do modelo e o número de parâmetros a serem estimados.
- "spherical": cada estado utiliza a mesma variância para todas as características. A matriz de covariância é proporcional à matriz identidade.
- "diag": cada estado utiliza uma matriz de covariância diagonal, assumindo que as características dentro do estado são estatisticamente independentes, mas podem possuir variâncias diferentes.
- "full": cada estado utiliza uma matriz de covariância completa, sem restrições, o que permite modelar correlações entre as características dentro de cada estado. Essa opção é a mais flexível, porém requer uma maior quantidade de dados para estimativa e pode estar sujeita a sobreajuste.
- "tied": todos os estados ocultos compartilham a mesma matriz de covariância completa. Isso permite levar em conta correlações entre as características, mas assume que a estrutura dessas correlações é idêntica em todos os estados.
- min_covar (float, padrão 1e-3): define o valor mínimo para os elementos diagonais da matriz de covariância, a fim de evitar sua degeneração, por exemplo, variância zero, durante o treinamento e reduzir o risco de sobreajuste.
- startprob_prior (array, forma (n_components,), opcional): parâmetros da distribuição a priori de Dirichlet para as probabilidades iniciais startprob_, que determinam a probabilidade de início da sequência de observações em cada um dos estados ocultos.
- transmat_prior (array, forma (n_components, n_components), opcional): parâmetros da distribuição a priori de Dirichlet para cada linha da matriz de probabilidades de transição transmat_, que define a probabilidade de transição entre estados ocultos.
- means_prior (array, forma (n_components,), opcional): valor médio da distribuição normal a priori para os valores médios (means_) de cada estado oculto.
- means_weight (array, forma (n_components,), opcional): peso, isto é, precisão, o inverso da variância, da distribuição normal a priori para os valores médios (means_) de cada estado oculto.
- covars_prior (array, forma (n_components,), opcional): parâmetros da distribuição a priori para a matriz de covariância covars_. O tipo dessa distribuição depende do parâmetro covariance_type. Para "spherical" e "diag", são parâmetros da distribuição inversa gama, e para "full" e "tied", são parâmetros associados à distribuição inversa de Wishart.
- covars_weight (array, forma (n_components,), opcional): peso dos parâmetros da distribuição a priori para a matriz de covariância covars_. De forma análoga ao covars_prior, a interpretação depende de covariance_type, sendo parâmetros de escala para a distribuição inversa gama ou para a distribuição inversa de Wishart.
- algorithm ({"viterbi", "map"}, opcional): algoritmo utilizado para a decodificação, isto é, para encontrar a sequência mais provável de estados ocultos correspondente à sequência observada. "viterbi" implementa o algoritmo de Viterbi, enquanto "map", maximum a posteriori estimation, realiza o suavizamento, forward-backward, para determinar o estado mais provável em cada instante de tempo.
- random_state (RandomState ou int, opcional): objeto do gerador de números aleatórios ou um seed inteiro para a inicialização aleatória dos parâmetros do modelo, o que garante a reprodutibilidade dos resultados.
- n_iter (int, opcional): número máximo de iterações executadas pelo algoritmo Expectation-Maximization (EM) durante o treinamento do modelo. Por padrão, o valor é 10.
- tol (float, opcional): limiar de convergência do algoritmo EM. Se a variação da log-verossimilhança entre duas iterações consecutivas se tornar menor do que esse valor, o treinamento é interrompido. O valor padrão é 0.01.
- verbose (bool, opcional): se definido como True, informações sobre a convergência em cada iteração serão exibidas no fluxo padrão de erros. A convergência também pode ser acompanhada por meio do atributo monitor_.
- params (string, opcional): string que indica quais parâmetros do modelo serão atualizados durante o treinamento. Pode conter uma combinação dos símbolos: "s" para as probabilidades iniciais (startprob_), "t" para as probabilidades de transição (transmat_), "m" para as médias (means_) e "c" para as covariâncias (covars_). O padrão é "stmc", isto é, todos os parâmetros são atualizados.
- init_params (string, opcional): string que indica quais parâmetros do modelo serão inicializados antes do início do treinamento. Os símbolos possuem o mesmo significado que no parâmetro params. O padrão é "stmc", ou seja, todos os parâmetros são inicializados.
- implementation (string, opcional): define qual implementação do algoritmo forward-backward será utilizada, a logarítmica, "log", ou a baseada em escalonamento, "scaling". Por padrão, utiliza-se "log" para garantir compatibilidade retroativa; no entanto, a implementação "scaling" geralmente apresenta melhor desempenho.
A inicialização dos parâmetros do GaussianHMM ocorre antes do início do treinamento do modelo com o uso do algoritmo EM. Os parâmetros de inicialização definem o estado inicial do modelo. O parâmetro init_params controla quais parâmetros serão inicializados. Se algum parâmetro não estiver incluído em init_params, assume-se que seu valor já foi definido manualmente.
Os valores iniciais dos parâmetros podem ser definidos aleatoriamente ou calculados com base nos dados fornecidos. Uma inicialização adequada dos parâmetros pode influenciar de forma significativa a velocidade de convergência do algoritmo EM e a qualidade do modelo final, uma vez que o algoritmo EM pode ficar preso em ótimos locais.
A otimização dos parâmetros do GaussianHMM é realizada por meio do algoritmo iterativo Expectation-Maximization (EM). Esse algoritmo consiste em dois passos principais, executados iterativamente até que a convergência seja alcançada.
- Etapa E, Expectation: nessa etapa, com base nas estimativas atuais dos parâmetros do modelo e na sequência de dados observados, são calculadas as probabilidades a posteriori de que, em cada instante de tempo, o sistema estivesse em um determinado estado oculto. Isso normalmente é feito utilizando o algoritmo forward-backward.
- Etapa M, Maximization: nessa etapa, os parâmetros do modelo, probabilidades iniciais, probabilidades de transição entre estados, valores médios e covariâncias de cada estado, são atualizados de modo a maximizar a log-verossimilhança esperada dos dados observados, condicionada às probabilidades a posteriori calculadas na etapa E.
O processo é repetido até que a convergência seja atingida, o que é determinado είτε pelo alcance do número máximo de iterações definido pelo parâmetro n_iter, ou quando a variação da log-verossimilhança entre iterações consecutivas se torna menor do que o limiar especificado em tol. O algoritmo EM garante o aumento, ou a manutenção, da log-verossimilhança a cada iteração; entretanto, não garante a obtenção do máximo global, e o resultado final pode depender da inicialização inicial dos parâmetros.
A escolha do parâmetro covariance_type exerce influência direta sobre a estrutura da matriz de covariância utilizada para modelar as emissões em cada estado oculto.
- Ao selecionar "spherical", assume-se uma covariância isotrópica, isto é, a variância de todas as características em um determinado estado é a mesma, e a matriz de covariância é proporcional à matriz identidade.
- "diag" indica o uso de uma matriz de covariância diagonal, o que significa que as características em cada estado são consideradas estatisticamente independentes, embora possam apresentar variâncias distintas.
- "full" permite o uso de uma matriz de covariância completa, levando em conta as correlações entre diferentes características dentro de cada estado oculto.
- "tied" significa que todos os estados ocultos compartilham conjuntamente a mesma matriz de covariância completa. A escolha do tipo de covariância deve se basear em suposições sobre a estrutura dos dados em cada estado oculto. Tipos de covariância mais complexos, como "full", podem se ajustar melhor a dados que apresentam dependências complexas entre características, porém exigem um número maior de parâmetros a serem estimados, o que pode levar ao sobreajuste quando o volume de dados é insuficiente.
A flexibilidade proporcionada pelos diversos parâmetros do hmm.GaussianHMM permite que pesquisadores adaptem o modelo às características específicas das séries temporais financeiras. Em particular, o parâmetro covariance_type possibilita assumir diferentes hipóteses sobre as relações entre as características em cada estado oculto.
Ao configurar os parâmetros do hmm.GaussianHMM para séries temporais financeiras, deve-se levar em consideração suas características específicas, como volatilidade, saltos de preços e possíveis desvios das distribuições em relação à lei normal. O número de estados ocultos (n_components) deve ser escolhido com base no número esperado de regimes de mercado. Isso pode ser determinado a partir de conhecimento especializado ou com o uso de critérios de seleção de modelos, como AIC ou BIC.
Recomenda-se iniciar com um número pequeno de estados, por exemplo, 2 ou 3, e aumentá-lo conforme necessário, monitorando ao mesmo tempo o risco de sobreajuste. Para séries temporais financeiras unidimensionais, como retornos, podem ser suficientes os tipos de covariância "diag" ou "spherical". Para séries multidimensionais, como retornos de vários ativos ou características como preço e volume, o tipo "full" permite modelar correlações, mas aumenta a complexidade do modelo. O tipo de covariância "tied" assume uma estrutura de correlação idêntica para todos os estados.
O parâmetro min_covar ajuda a prevenir o sobreajuste, garantindo que as variâncias não se tornem excessivamente pequenas. O valor padrão 1e-3 costuma ser um bom ponto de partida. A definição de distribuições a priori informativas, por exemplo, com o uso de startprob_prior e transmat_prior para refletir concepções prévias sobre as probabilidades iniciais dos estados e as tendências de transição, pode ser útil, especialmente quando o volume de dados é limitado. Por exemplo, pode-se esperar certa persistência dos regimes de mercado, o que pode ser codificado na distribuição a priori da matriz de transição.
Os parâmetros n_iter e tol controlam o número máximo de iterações e o limiar de convergência do algoritmo EM. Um valor maior de n_iter pode levar a uma convergência melhor, mas também aumentará o tempo de treinamento. Um valor menor de tol resulta em critérios de convergência mais rigorosos.
O pré-processamento dos dados financeiros é de importância crucial. Recomenda-se utilizar retornos, isto é, variações percentuais, em vez de preços e, possivelmente, incluir indicadores técnicos, como médias móveis, medidas de volatilidade, por exemplo, a Média de Amplitude de Variação (ATR), e indicadores de volume, como características. A normalização ou padronização das características também é recomendada. As séries temporais financeiras frequentemente são não estacionárias. Deve-se considerar a possibilidade de diferenciar os dados ou utilizar uma janela deslizante para a estimativa dos parâmetros, a fim de se adaptar à dinâmica mutável do mercado.
Para encontrar a combinação ideal de hiperparâmetros para um conjunto de dados financeiros específico, devem ser utilizados métodos como busca em grade ou otimização bayesiana, por exemplo, com o auxílio do Optuna. A natureza não estacionária das séries temporais financeiras exige um pré-processamento cuidadoso e, possivelmente, o uso de métodos adaptativos, como o treinamento com janelas deslizantes. O ajuste de hiperparâmetros também é fundamental para garantir que o modelo GaussianHMM capture de forma eficaz a dinâmica subjacente do mercado, sem sobreajustar aos dados históricos.
Descrição detalhada da classe hmm.GMMHMM
A classe hmm.GMMHMM é destinada ao trabalho com emissões contínuas que são melhor representadas por uma mistura de várias distribuições gaussianas. Isso permite modelar padrões de emissão mais complexos em comparação com o uso de uma única distribuição gaussiana, o que é especialmente útil para dados que apresentam agrupamentos bem definidos dentro de cada estado oculto.
O hmm.GMMHMM pode ser útil quando a distribuição dos dados financeiros dentro de um determinado regime é multimodal ou difere significativamente da gaussiana. Por exemplo, os retornos em um regime de alta volatilidade podem apresentar características distintas dependendo da direção do movimento do preço. O hmm.GMMHMM amplia as capacidades do hmm.GaussianHMM, permitindo associar cada estado oculto a uma mistura de distribuições gaussianas. Isso é particularmente vantajoso para séries temporais financeiras, que podem apresentar um comportamento mais complexo e não normalmente distribuído em diferentes regimes de mercado.
- O construtor da classe hmm.GMMHMM inclui todos os parâmetros da classe hmm.GaussianHMM e adiciona o parâmetro n_mix, um inteiro com valor padrão 1, que define o número de componentes da mistura em cada estado, bem como as distribuições a priori associadas aos pesos da mistura.
- O parâmetro covariance_type no GMMHMM possui uma opção "tied" ligeiramente diferente: todos os componentes da mistura de cada estado utilizam a mesma matriz de covariância completa.
- Os parâmetros params e init_params também incluem o símbolo "w" para controlar os pesos da mistura do GMM.
- A principal diferença nos parâmetros está em n_mix e nas distribuições a priori associadas aos pesos da mistura, o que proporciona uma modelagem mais flexível das probabilidades de emissão em cada estado oculto. A opção mais refinada "tied" para a covariância no GMMHMM também oferece uma forma adicional de restringir o modelo.
Ao ajustar os parâmetros do hmm.GMMHMM para séries temporais financeiras, a escolha do número de componentes da mistura, n_mix, é um passo de importância crítica. O número de componentes da mistura deve representar da melhor forma possível a distribuição dos dados financeiros em cada estado oculto. Isso pode exigir experimentação. Recomenda-se começar com um número pequeno de componentes, por exemplo, 2 ou 3, e aumentá-lo caso o modelo apresente subajuste, evitando, contudo, o sobreajuste.
Para determinar o valor ideal de n_mix, podem ser utilizados critérios de informação, como AIC ou BIC. Os demais parâmetros podem ser ajustados de maneira semelhante aos parâmetros do hmm.GaussianHMM, levando em conta as características específicas dos dados financeiros. Por exemplo, a escolha de covariance_type influenciará a forma como a dispersão é modelada dentro de cada componente da mistura. A seleção do número ótimo de componentes da mistura, n_mix, é uma etapa fundamental para o uso eficaz do hmm.GMMHMM em séries temporais financeiras. Isso envolve equilibrar a capacidade do modelo de capturar distribuições de dados complexas com o risco de sobreajuste e pode exigir o uso de métodos como validação cruzada ou critérios de informação para obter estimativas robustas.
Descrição detalhada da classe vhmm.VariationalGaussianHMM
A classe vhmm.VariationalGaussianHMM representa um modelo oculto de Markov com emissões gaussianas multivariadas, cujo treinamento é realizado por meio de inferência variacional, e não pelo algoritmo Expectation-Maximization (EM) utilizado no hmm.GaussianHMM.
A inferência variacional tem como objetivo encontrar os parâmetros de uma distribuição que seja o mais próxima possível da verdadeira distribuição a posteriori das variáveis ocultas e dos parâmetros do modelo. Diferentemente do EM, que fornece estimativas pontuais dos parâmetros, a inferência variacional produz distribuições a posteriori para os parâmetros do modelo, o que pode ser útil para a avaliação da incerteza.
A principal diferença do vhmm.VariationalGaussianHMM reside no uso da inferência variacional para o treinamento. Essa abordagem bayesiana apresenta vantagens em relação à estimativa por máxima verossimilhança do hmm.GaussianHMM, especialmente no que diz respeito à disponibilização de medidas de incerteza por meio das distribuições a posteriori dos parâmetros do modelo.
- O construtor da classe vhmm.VariationalGaussianHMM inclui os parâmetros n_components, covariance_type, algorithm, random_state, n_iter, tol, verbose, params, init_params e implementation, que são análogos aos parâmetros do hmm.GaussianHMM.
- Os principais parâmetros adicionais, relacionados às distribuições a priori, são startprob_prior, transmat_prior, means_prior, beta_prior, dof_prior e scale_prior. Caso esses parâmetros tenham valor None, são utilizadas as distribuições a priori padrão. O parâmetro beta_prior está relacionado à precisão da distribuição normal a priori para os valores médios. Os parâmetros dof_prior e scale_prior definem a distribuição a priori da matriz de covariância, sendo a distribuição inversa de Wishart ou a distribuição inversa gama, dependendo do valor de covariance_type.
- A inicialização do vhmm.VariationalGaussianHMM exige a especificação das distribuições a priori para todos os parâmetros do modelo. Essas distribuições a priori desempenham um papel importante no processo de treinamento, especialmente quando o volume de dados é limitado, e permitem incorporar conhecimentos ou crenças prévias a respeito dos parâmetros.
Ao ajustar os parâmetros do vhmm.VariationalGaussianHMM para séries temporais financeiras, a escolha das distribuições a priori é de grande importância. As distribuições a priori atuam como uma forma de regularização, evitando o sobreajuste do modelo aos dados de treinamento. Elas também permitem incorporar conhecimentos existentes ou crenças prévias sobre os parâmetros do modelo.
Por exemplo, se houver razões para acreditar que a distribuição inicial dos estados (startprob_) deva ser relativamente uniforme, pode-se utilizar uma distribuição a priori de Dirichlet com parâmetros simétricos próximos de 1. De forma semelhante, crenças a respeito das probabilidades de transição (transmat_), dos valores médios (means_prior) ou das covariâncias (scale_prior, dof_prior) podem ser codificadas por meio de escolhas apropriadas de distribuições a priori.
A escolha das distribuições a priori influencia as distribuições a posteriori resultantes dos parâmetros do modelo após o treinamento com os dados. Distribuições a priori informativas, por exemplo, com pequena variância em torno de um determinado valor, exercerão uma influência mais forte, deslocando a distribuição a posteriori em direção à a priori. Distribuições a priori não informativas ou fracas, por exemplo, com grande variância ou distribuições uniformes, terão menor influência, permitindo que os dados dominem a distribuição a posteriori.
Comparação da eficiência dos modelos para séries temporais financeiras
O modelo hmm.GaussianHMM é um modelo básico que assume que os dados financeiros observados em cada estado oculto são distribuídos segundo uma lei gaussiana. Seu ponto forte é a simplicidade e a eficiência computacional, o que o torna adequado para grandes conjuntos de dados e para situações em que não há motivos para supor que as distribuições diferem significativamente da normal.
Entretanto, sua principal limitação é a suposição de normalidade das distribuições, que pode não se verificar para muitas séries temporais financeiras, caracterizadas por assimetria, curtose elevada e caudas pesadas. Em cenários nos quais os dados financeiros em cada regime são relativamente bem aproximados por uma distribuição normal, o hmm.GaussianHMM pode apresentar bons resultados, por exemplo, na modelagem de regimes de mercado principais em dados diários ou semanais. Por outro lado, ele pode apresentar desempenho inferior ao modelar dados de alta frequência ou dados sujeitos a saltos abruptos e distribuições não normais.
O modelo hmm.GMMHMM amplia as capacidades do hmm.GaussianHMM ao permitir o uso de uma mistura de distribuições gaussianas para modelar as emissões em cada estado oculto. Seu principal ponto forte é a capacidade de modelar distribuições mais complexas e multimodais, o que o torna mais adequado para dados financeiros que podem apresentar diferentes subpadrões dentro de um mesmo regime de mercado. Por exemplo, em períodos de alta volatilidade, os retornos podem se comportar de maneira distinta dependendo da direção do movimento do mercado.
O ponto fraco do hmm.GMMHMM é o aumento no número de parâmetros, o que pode levar ao sobreajuste, especialmente quando o volume de dados é limitado. Além disso, o treinamento pode ser mais custoso do ponto de vista computacional em comparação com o hmm.GaussianHMM.
O hmm.GMMHMM pode apresentar melhores resultados na modelagem de séries temporais financeiras em que as distribuições dentro dos regimes são não normais ou multimodais, por exemplo, na análise de dados intradiários ou de dados de volatilidade. Ele pode apresentar desempenho inferior na modelagem de regimes simples com distribuições aproximadamente normais ou em situações com volumes de dados muito pequenos, nas quais o risco de sobreajuste é elevado.
O modelo vhmm.VariationalGaussianHMM utiliza inferência variacional para o treinamento, o que constitui uma abordagem bayesiana. Seu principal ponto forte é a capacidade de fornecer distribuições a posteriori dos parâmetros, permitindo avaliar a incerteza do modelo. A abordagem bayesiana também pode ser vantajosa quando o volume de dados é limitado, graças ao uso de distribuições a priori, que podem regularizar o modelo e incorporar conhecimentos prévios.
A principal limitação do vhmm.VariationalGaussianHMM é a complexidade na definição das distribuições a priori, que pode influenciar de forma significativa os resultados. Além disso, a inferência variacional é um método aproximado, e a distribuição a posteriori obtida pode diferir da verdadeira distribuição a posteriori.
O vhmm.VariationalGaussianHMM pode apresentar melhores resultados na modelagem de séries temporais financeiras em que a avaliação da incerteza dos parâmetros é importante ou quando há poucos dados disponíveis e é necessário utilizar conhecimentos a priori. Ele pode apresentar desempenho inferior se as distribuições a priori forem escolhidas de forma inadequada ou se for necessária uma altíssima precisão na estimativa dos parâmetros, a qual pode ser alcançada pelo método de máxima verossimilhança quando há dados suficientes.
A escolha do modelo é influenciada por fatores como o volume de dados disponível, a complexidade da dinâmica do mercado e os requisitos de interpretabilidade do modelo. Com um grande volume de dados e uma dinâmica de mercado relativamente simples, o hmm.GaussianHMM pode ser suficiente e preferível devido à sua simplicidade e eficiência computacional. Em cenários de dinâmica mais complexa ou distribuições não normais, pode ser necessário recorrer ao hmm.GMMHMM. Se a avaliação da incerteza for importante ou se houver poucos dados disponíveis, deve-se considerar o vhmm.VariationalGaussianHMM.
Conclusão e recomendações
Para séries temporais financeiras, o modelo potencialmente melhor ou pior depende da tarefa específica e das características dos dados.
De modo geral, se os dados financeiros dentro dos regimes de mercado puderem ser razoavelmente aproximados por uma distribuição gaussiana, o hmm.GaussianHMM representa uma escolha simples e eficiente. Se as distribuições forem mais complexas ou multimodais, o hmm.GMMHMM pode proporcionar um melhor ajuste, porém exige uma configuração mais cuidadosa e pode ser mais propenso ao sobreajuste. O vhmm.VariationalGaussianHMM oferece uma abordagem bayesiana com a possibilidade de avaliar a incerteza, o que pode ser útil em determinados cenários, mas requer compreensão e escolha adequada das distribuições a priori.
É importante enfatizar que a escolha do modelo não pode ser feita exclusivamente com base em fundamentos teóricos. A validação empírica e o backtesting com dados financeiros reais são etapas necessárias para determinar qual modelo é mais adequado para uma tarefa específica. Diferentes métricas de desempenho, como log-verossimilhança, precisão de previsão e métricas específicas do domínio financeiro, por exemplo, MAPE e R^2, devem ser utilizadas para comparar o desempenho dos modelos e selecionar o mais apropriado para a resolução de um problema concreto de análise de séries temporais financeiras.
Métodos para determinar matrizes de covariância a priori para séries temporais na biblioteca hmmlearn
Um dos tipos mais comuns de HMM são os modelos com emissões gaussianas, nos quais se assume que os dados observados em cada estado oculto seguem uma distribuição normal multivariada. Os parâmetros dessa distribuição são o vetor de médias e a matriz de covariância, que define a forma, a orientação e o grau de dependência entre os componentes dos dados observados.
No treinamento de HMM gaussianos, especialmente ao utilizar abordagens bayesianas, como a inferência variacional, a definição das matrizes de covariância a priori desempenha um papel fundamental. Conhecimentos a priori sobre a estrutura de covariância de uma série temporal podem auxiliar de maneira significativa no processo de treinamento do modelo, sobretudo em situações em que o volume de dados disponíveis é limitado. A definição inadequada das informações a priori pode levar a resultados subótimos, a problemas de convergência dos algoritmos de treinamento ou ao sobreajuste do modelo.
A biblioteca hmmlearn em Python disponibiliza as classes hmm.GaussianHMM, assim como hmm.GMMHMM, e vhmm.VariationalGaussianHMM para trabalhar com HMM com emissões gaussianas. A classe hmm.GaussianHMM implementa o treinamento do modelo utilizando o algoritmo clássico Expectation-Maximization (EM), enquanto o vhmm.VariationalGaussianHMM oferece uma abordagem bayesiana baseada em inferência variacional.
Ambas as classes fornecem parâmetros para influenciar o processo de treinamento e a inicialização do modelo, incluindo a possibilidade de definir distribuições a priori para as matrizes de covariância. Em particular, o parâmetro covariance_type permite escolher o tipo de matriz de covariância, esférica, diagonal, completa ou compartilhada, enquanto os parâmetros covars_prior e covars_weight no hmm.GaussianHMM, assim como scale_prior e dof_prior no vhmm.VariationalGaussianHMM, possibilitam a definição de distribuições a priori para as covariâncias. O uso correto desses parâmetros exige a compreensão dos diferentes métodos de definição de matrizes de covariância a priori para séries temporais.
Métodos de definição de matrizes de covariância a priori para séries temporais
Existem diversas abordagens para a definição de matrizes de covariância a priori para séries temporais, cada uma baseada em diferentes suposições sobre os dados e sobre as informações prévias disponíveis.
Estimativa empírica. Um dos métodos mais diretos consiste em estimar a matriz de covariância diretamente a partir de dados previamente coletados da série temporal. A matriz de covariância amostral reflete a covariância entre diferentes componentes da série temporal, em que cada elemento (i, j) da matriz representa a covariância amostral entre o i-ésimo e o j-ésimo componentes, enquanto os elementos diagonais representam as variâncias amostrais.Para uma série temporal X de comprimento T e dimensionalidade p, a matriz de covariância amostral Σ̂ pode ser calculada pela fórmula padrão. No entanto, a aplicação da estimativa empírica a séries temporais apresenta algumas limitações.
Primeiro, pressupõe-se que a série temporal seja estacionária, isto é, que suas propriedades estatísticas, como média e covariância, não se alterem ao longo do tempo.
Segundo, para obter uma estimativa confiável, é necessário um volume de dados suficientemente grande em relação à dimensionalidade da série temporal.
Terceiro, quando o tamanho da amostra é pequeno em comparação com a dimensionalidade, pode surgir o problema da singularidade da matriz de covariância, tornando-a inadequada para uso em alguns algoritmos.
Apesar dessas limitações, a estimativa empírica pode servir como um ponto de partida razoável quando há uma quantidade suficiente de dados estacionários disponíveis.
Métodos de shrinkage. Em situações nas quais a estimativa empírica da matriz de covariância pode ser pouco confiável, devido ao volume limitado de dados ou à alta dimensionalidade, podem ser utilizados métodos de shrinkage. Esses métodos combinam a matriz de covariância amostral com uma determinada matriz alvo, utilizando um coeficiente de shrinkage para definir o peso de cada matriz.
A matriz alvo pode representar, por exemplo, a matriz identidade, assumindo independência entre os componentes, uma matriz diagonal, assumindo ausência de correlação entre os componentes, ou uma matriz de variância constante. A fórmula do shrinkage linear tem a forma Rα = (1 − α)S + αT, onde S é a matriz de covariância amostral, T é a matriz alvo e α ∈ é o coeficiente de shrinkage.
Os métodos de shrinkage são especialmente úteis quando o volume de dados é limitado, pois permitem reduzir o erro de estimativa da matriz de covariância, aumentar sua robustez e prevenir o sobreajuste do modelo. A escolha da estrutura alvo pressupõe a existência de alguma informação a priori sobre a natureza das dependências nos dados.
Uso de distribuições a priori informativas. Se houver conhecimento prévio sobre o domínio do problema ou sobre a estrutura de covariância da série temporal, esse conhecimento pode ser formalmente incorporado ao modelo por meio do uso de distribuições a priori informativas.
Para matrizes de covariância, é frequentemente utilizada a distribuição inversa de Wishart, que é a distribuição a priori conjugada para matrizes de covariância na distribuição normal multivariada. Os parâmetros da distribuição inversa de Wishart são a matriz de escala e os graus de liberdade.
A escolha dos parâmetros da distribuição a priori deve refletir as crenças prévias existentes sobre a estrutura de covariância. Distribuições a priori informativas podem ser formadas com base em resultados de estudos anteriores, conhecimento especializado ou análise de séries temporais semelhantes. O uso dessas informações a priori pode melhorar significativamente a qualidade do treinamento do modelo, especialmente quando há conhecimento prévio bem fundamentado.
Distribuições a priori não informativas. Em casos nos quais não existem crenças prévias fortes sobre a estrutura de covariância da série temporal, podem ser utilizadas distribuições a priori não informativas. O objetivo dessas distribuições a priori é minimizar sua influência sobre a distribuição a posteriori, permitindo que os dados tenham maior peso na determinação dos resultados do treinamento.
Um exemplo de distribuição a priori não informativa para a matriz de covariância é a distribuição de Jeffreys. Para matrizes de correlação, é frequentemente utilizado o prior LKJ, que fornece uma distribuição uniforme sobre o espaço das matrizes de correlação ou permite definir diferentes níveis de concentração em torno da correlação zero. No entanto, deve-se considerar que a definição de um a priori verdadeiramente não informativo pode ser uma tarefa complexa, e mesmo distribuições a priori fracamente informativas podem influenciar os resultados, especialmente quando o volume de dados é limitado.
Suposições estruturais sobre séries temporais. Se a série temporal apresenta propriedades conhecidas de autocorrelação, esse conhecimento pode ser utilizado para a construção de uma matriz de covariância a priori. Por exemplo, a análise da função de autocorrelação (ACF) e da função de autocorrelação parcial (PACF) pode ajudar a identificar a ordem de processos autorregressivos (AR) ou de média móvel (MA) que podem descrever a série temporal.
Com base nos parâmetros desses modelos, pode-se construir uma matriz de covariância a priori que reflita as dependências temporais conhecidas. Por exemplo, para um processo AR(1), a estrutura da matriz de covariância dependerá do parâmetro de autocorrelação. Essa abordagem pressupõe que a série temporal possa ser descrita adequadamente por algum modelo de séries temporais e que os parâmetros desse modelo possam ser estimados a partir de dados preliminares.
Aplicação dos métodos de definição de matrizes de covariância a priori no hmmlearn
A biblioteca hmmlearn oferece diversas possibilidades para a definição de matrizes de covariância a priori ao utilizar as classes hmm.GaussianHMM e vhmm.VariationalGaussianHMM.
A estimativa empírica da matriz de covariância, obtida com base em dados preliminares, pode ser utilizada para a inicialização direta do atributo covars_ tanto na classe hmm.GaussianHMM quanto na classe vhmm.VariationalGaussianHMM. De forma semelhante, os resultados da aplicação de métodos de shrinkage à matriz de covariância empírica podem ser utilizados para inicializar o atributo covars_.
Para a definição de distribuições a priori informativas, a classe hmm.GaussianHMM disponibiliza os parâmetros covars_prior e covars_weight. Esses parâmetros controlam os parâmetros da distribuição a priori da matriz de covariância covars_. O tipo de distribuição a priori depende do valor do parâmetro covariance_type. Se covariance_type estiver definido como "spherical" ou "diag", utiliza-se a distribuição inversa gama. Se covariance_type estiver definido como "full" ou "tied", utiliza-se a distribuição inversa de Wishart.
O parâmetro covars_prior é interpretado como o parâmetro de forma da distribuição inversa gama e está relacionado aos graus de liberdade da distribuição inversa de Wishart. O parâmetro covars_weight é o parâmetro de escala da distribuição inversa gama e está associado à matriz de escala da distribuição inversa de Wishart.
A classe vhmm.VariationalGaussianHMM também permite definir distribuições a priori informativas para as matrizes de covariância por meio dos parâmetros scale_prior e dof_prior. O parâmetro dof_prior define os graus de liberdade da distribuição de Wishart, para os casos "full" e "tied", ou da distribuição inversa gama, para os casos "spherical" e "diag". O parâmetro scale_prior define a matriz de escala da distribuição de Wishart, para "full" e "tied", ou o parâmetro de escala da distribuição inversa gama, para "spherical" e "diag". Esses parâmetros determinam as crenças a priori sobre a estrutura de covariância no modelo bayesiano implementado por meio de inferência variacional.
Para definir distribuições a priori não informativas, podem ser utilizados os parâmetros covars_prior, covars_weight, scale_prior e dof_prior, ajustando seus valores de forma que a distribuição a priori seja fraca ou difusa. Por exemplo, podem ser definidos valores muito pequenos para parâmetros associados à precisão ou ao inverso da escala, ou valores muito grandes para parâmetros associados à escala.
Por fim, suposições estruturais sobre séries temporais podem ser consideradas por meio da construção de uma matriz de covariância apropriada com base na análise de autocorrelações e do uso dessa matriz para inicializar o atributo covars_ em ambas as classes do hmmlearn.
Definição de regimes de mercado com o uso de HMM: passando à prática
Antes de prosseguir com a leitura desta seção, recomenda-se a leitura de dois artigos anteriores:
Nesses artigos, é descrito o princípio básico de construção de sistemas de trading que será utilizado. No entanto, em vez de inferência causal ou de clusterização de regimes de mercado, serão empregados modelos ocultos de Markov para a definição dos regimes de mercado. Dessa forma, será possível testar e comparar essas abordagens entre si e formar uma opinião própria sobre sua eficácia.
Antes de iniciar o trabalho, certifique-se de que os pacotes necessários estejam instalados.
import math import pandas as pd from datetime import datetime from catboost import CatBoostClassifier from sklearn.model_selection import train_test_split from sklearn.cluster import KMeans from hmmlearn import hmm, vhmm from bots.botlibs.labeling_lib import * from bots.botlibs.tester_lib import tester_one_direction from bots.botlibs.export_lib import export_model_to_ONNX
O algoritmo irá definir os regimes de mercado por meio do treinamento de modelos ocultos de Markov seguindo o mesmo princípio descrito nos artigos sobre clusterização de regimes de mercado. Portanto, as alterações no código estarão relacionadas apenas ao próprio processo de definição dos regimes de mercado.
A seguir é apresentada a função que define os regimes de mercado:
def markov_regime_switching(dataset, n_regimes: int, model_type="GMMHMM") -> pd.DataFrame: data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy() # Extract meta features meta_X = data.loc[:, data.columns.str.contains('meta_feature')] if meta_X.shape[1] > 0: # Format data for HMM (requires 2D array) X = meta_X.values # Features normalization before training from sklearn.preprocessing import StandardScaler scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # Create and train the HMM model if model_type == "HMM": model = hmm.GaussianHMM( n_components=n_regimes, covariance_type="spherical", n_iter=10, ) elif model_type == "GMMHMM": model = hmm.GMMHMM( n_components=n_regimes, covariance_type="spherical", n_iter=10, n_mix=3, ) elif model_type == "VARHMM": model = vhmm.VariationalGaussianHMM( n_components=n_regimes, covariance_type="spherical", n_iter=10, ) # Fit the model model.fit(X_scaled) # Predict the hidden states (regimes) hidden_states = model.predict(X_scaled) # Assign states to clusters data['clusters'] = hidden_states return data
No código são apresentados três modelos descritos na parte teórica, todos com parâmetros padrão. Primeiro, é necessário verificar se eles realmente funcionam e, em seguida, passar para o ajuste dos parâmetros. Você pode escolher um dos modelos ao chamar a função e testar imediatamente a qualidade da clusterização.
O ciclo de treinamento permaneceu o mesmo, com exceção da função de definição dos regimes de mercado:
for i in range(1): data = markov_regime_switching(dataset, n_regimes=hyper_params['n_clusters'], model_type="HMM") sorted_clusters = data['clusters'].unique() sorted_clusters.sort() for clust in sorted_clusters: clustered_data = data[data['clusters'] == clust].copy() if len(clustered_data) < 500: print('too few samples: {}'.format(len(clustered_data))) continue clustered_data = get_labels_one_direction(clustered_data, markup=hyper_params['markup'], min=1, max=15, direction=hyper_params['direction']) print(f'Iteration: {i}, Cluster: {clust}') clustered_data = clustered_data.drop(['close', 'clusters'], axis=1) meta_data = data.copy() meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0) models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1)))
Os hiperparâmetros de treinamento são definidos da seguinte forma:
hyper_params = {
'symbol': 'XAUUSD_H1',
'export_path': '/drive_c/Program Files/MetaTrader 5/MQL5/Include/Trend following/',
'model_number': 0,
'markup': 0.2,
'stop_loss': 10.000,
'take_profit': 5.000,
'periods': [i for i in range(5, 300, 30)],
'periods_meta': [5],
'backward': datetime(2000, 1, 1),
'forward': datetime(2024, 1, 1),
'full forward': datetime(2026, 1, 1),
'direction': 'buy',
'n_clusters': 5,
} - O período das características sobre as quais será realizado o treinamento dos modelos ocultos de Markov é igual a cinco.
- Direção de compra para o ouro.
- O número estimado de regimes é igual a cinco.
Todos os modelos serão testados utilizando os desvios padrão em uma janela deslizante, isto é, a volatilidade, como características:
def get_features(data: pd.DataFrame) -> pd.DataFrame: pFixed = data.copy() pFixedC = data.copy() count = 0 for i in hyper_params['periods']: pFixed[str(count)] = pFixedC.rolling(i).std() count += 1 for i in hyper_params['periods_meta']: pFixed[str(count)+'meta_feature'] = pFixedC.rolling(i).std() count += 1 return pFixed.dropna()
Resultados do treinamento com parâmetros padrão
- O algoritmo GaussianHMM com parâmetros padrão demonstrou a capacidade de encontrar estados ocultos, isto é, regimes, de forma eficaz, graças ao que a curva de saldo nos dados de teste apresenta um aspecto aceitável.
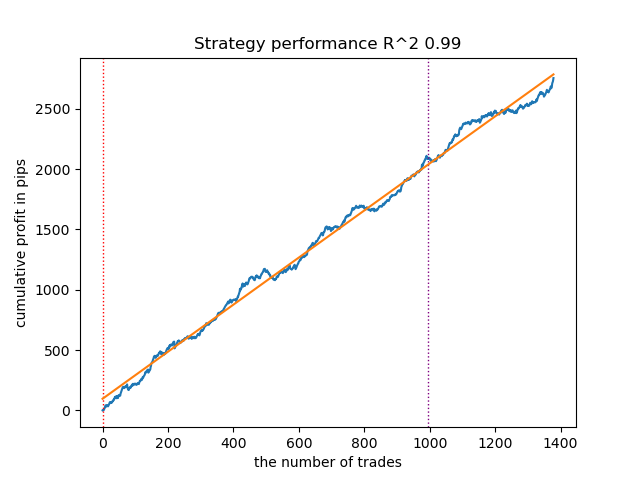
Fig. 1. Teste do GaussianHMM com configurações padrão
- O algoritmo GMMHMM também apresentou um desempenho razoável, não sendo observadas mudanças significativas na qualidade dos modelos.
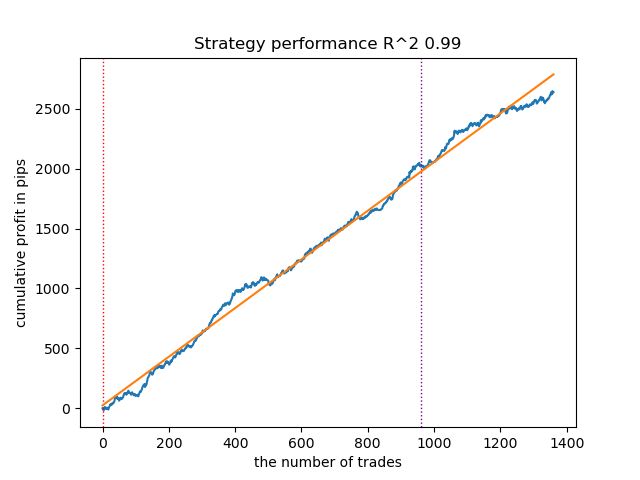
Fig. 2. Teste do GMMHMM com configurações padrão
- O algoritmo VariationalGaussianHMM pode parecer um outsider, porém, após algumas reotimizações, é possível obter curvas mais atraentes.
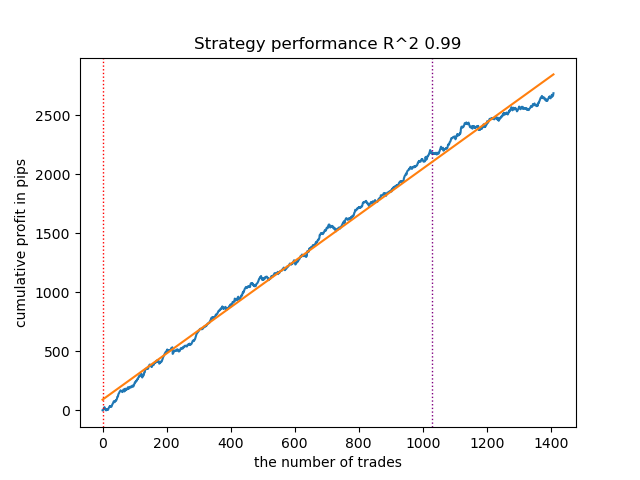
Fig. 3. Teste do VariationalGaussianHMM com configurações padrão
De modo geral, todos os algoritmos comprovaram sua funcionalidade, o que significa que é possível passar ao ajuste fino de seus parâmetros.
Aumento do número de iterações de treinamento (n_iter = 100)
Com o aumento do número de iterações de treinamento dos modelos de Markov, os resultados em novos dados melhoraram ligeiramente para todas as variações do algoritmo. Isso aparentemente está relacionado ao fato de que os algoritmos encontraram ótimos locais mais vantajosos. Em geral, nesta etapa, não foram observadas diferenças significativas na qualidade dos modelos obtidos para os diferentes algoritmos. No entanto, o GaussianHMM foi treinado um pouco mais rapidamente, devido à sua simplicidade.
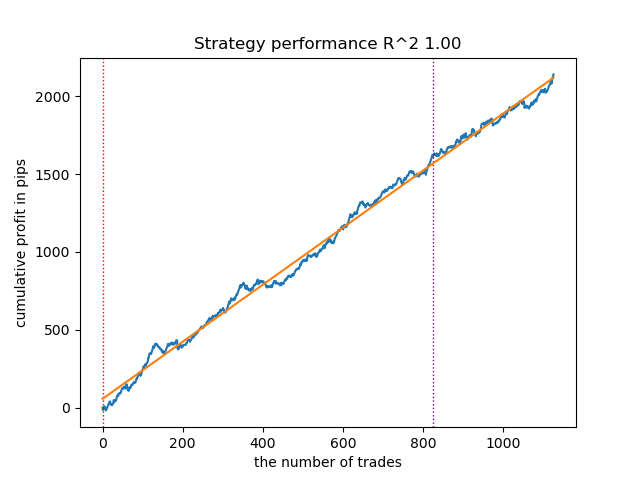
Fig. 4. Teste do GaussianHMM com n_iter = 100
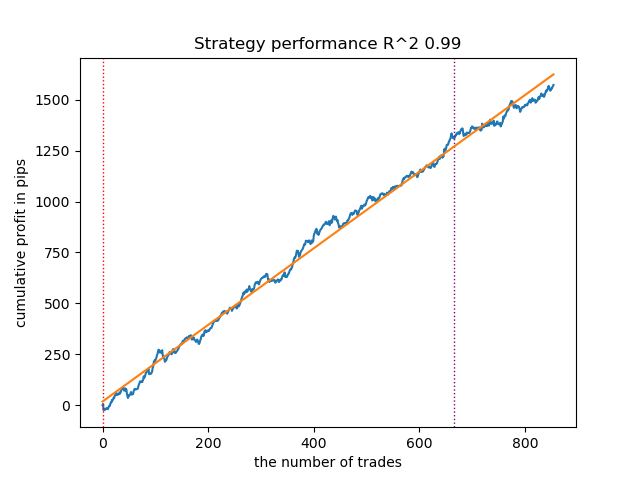
Fig. 5. Teste do GMMHMM com n_iter = 100
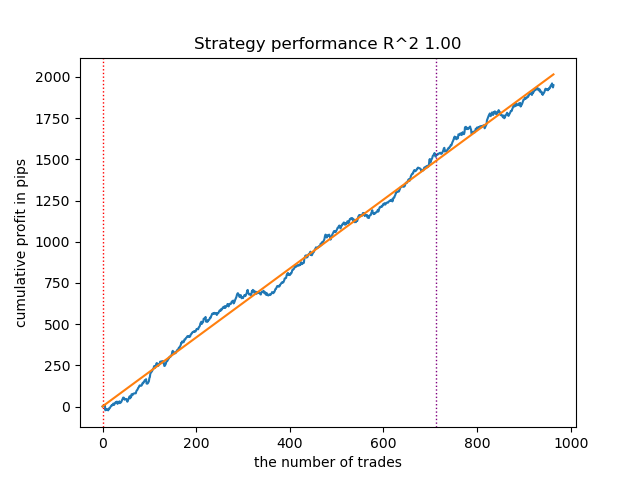
Fig. 6. Teste do VariationalGaussianHMM com n_iter = 100
Redução do número de regimes de mercado para três
O número de iterações influencia a qualidade dos modelos, portanto manteremos esse parâmetro em 100 iterações. Vamos tentar reduzir o número de regimes, isto é, os estados ocultos dos modelos, para três e observar os resultados.
hyper_params = {
'symbol': 'XAUUSD_H1',
'export_path': '/drive_c/Program Files/MetaTrader 5/MQL5/Include/Trend following/',
'model_number': 0,
'markup': 0.2,
'stop_loss': 10.000,
'take_profit': 5.000,
'periods': [i for i in range(5, 300, 30)],
'periods_meta': [5],
'backward': datetime(2000, 1, 1),
'forward': datetime(2024, 1, 1),
'full forward': datetime(2026, 1, 1),
'direction': 'buy',
'n_clusters': 3,
} GaussianHMM, GMMHMM e VariationalGaussianHMM demonstraram excelentes resultados na identificação de três regimes de mercado, porém, para o último foi necessário realizar algumas reinicializações do treinamento.
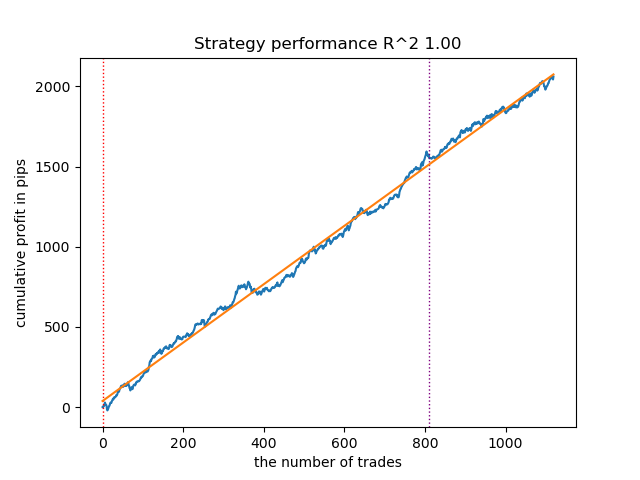
Fig. 7. Teste do VariationalHMM com n_iter = 100 e três regimes
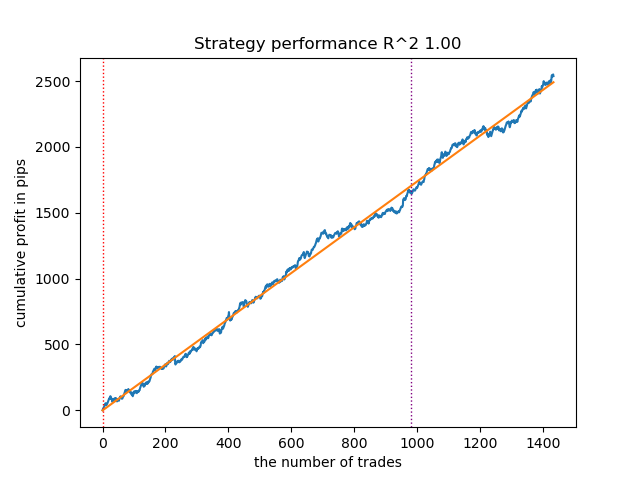
Fig. 8. Teste do GMMHMM com n_iter = 100 e três regimes
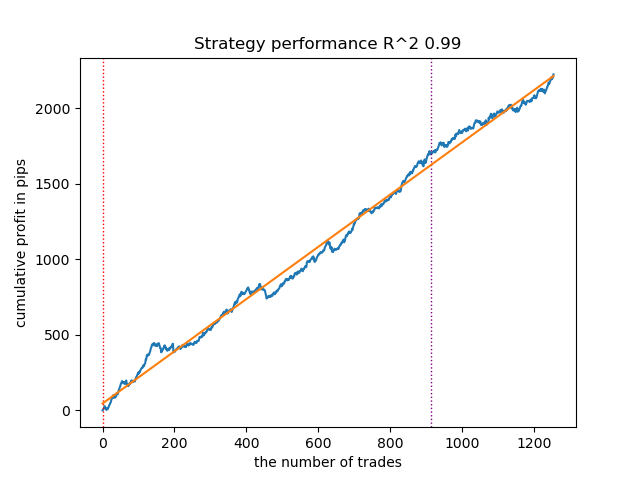
Fig. 9. Teste do VariationalGaussianHMM com n_iter = 100 e três regimes
Criação de matrizes de covariância a priori para modelos ocultos de Markov
Na parte teórica do artigo, foram analisados cinco métodos para a definição de matrizes de covariância a priori para séries temporais. Os métodos que mais se adequam ao nosso caso são o primeiro e o último, vamos relembrá-los:
- Estimativa empírica. Um dos métodos mais diretos consiste em estimar a matriz de covariância diretamente a partir de dados previamente coletados da série temporal. A matriz de covariância amostral reflete a covariância entre diferentes componentes da série temporal, em que cada elemento (i, j) da matriz representa a covariância amostral entre o i-ésimo e o j-ésimo componentes, enquanto os elementos diagonais representam as variâncias amostrais. Para uma série temporal X de comprimento T e dimensionalidade p, a matriz de covariância amostral Σ̂ pode ser calculada pela fórmula padrão. No entanto, a aplicação da estimativa empírica a séries temporais apresenta algumas limitações. Em primeiro lugar, assume-se que a série temporal seja estacionária, isto é, que suas propriedades estatísticas, como média e covariância, não se alterem ao longo do tempo. Em segundo lugar, para obter uma estimativa confiável, é necessário um volume de dados suficientemente grande em relação à dimensionalidade da série temporal. Em terceiro lugar, quando o tamanho da amostra é pequeno em comparação com a dimensionalidade, pode surgir o problema da singularidade da matriz de covariância, tornando-a inadequada para uso em alguns algoritmos. Apesar dessas limitações, a estimativa empírica pode servir como um ponto de partida razoável quando há uma quantidade suficiente de dados estacionários disponíveis.
- Suposições estruturais sobre séries temporais. Se a série temporal apresenta propriedades conhecidas de autocorrelação, esse conhecimento pode ser utilizado para a construção de uma matriz de covariância a priori. Por exemplo, a análise da função de autocorrelação (ACF) e da função de autocorrelação parcial (PACF) pode ajudar a identificar a ordem de processos autorregressivos (AR) ou de média móvel (MA) que podem descrever a série temporal. Com base nos parâmetros desses modelos, pode-se construir uma matriz de covariância a priori que reflita as dependências temporais conhecidas. Por exemplo, para um processo AR(1), a estrutura da matriz de covariância dependerá do parâmetro de autocorrelação. Essa abordagem pressupõe que a série temporal possa ser descrita adequadamente por algum modelo de séries temporais e que os parâmetros desse modelo possam ser estimados a partir de dados preliminares.
No entanto, não podemos afirmar com segurança que uma série temporal financeira possa ser descrita adequadamente por modelos tão simples. Os experimentos mostraram que tais priors nem sempre melhoram o resultado da identificação dos estados ocultos de Markov. Além disso, realizei experimentos com uma clusterização prévia por meio do k-means para inicializar as matrizes de transição com os valores obtidos. Isso levou ao fato de que os modelos ocultos de Markov passaram a produzir resultados semelhantes aos da artigo anterior, no qual foi realizada a clusterização dos regimes de mercado, melhorando apenas ligeiramente ou não melhorando a curva de saldo em novos dados.
Criação de priors com base em clusterização
No script de treinamento é apresentada uma função experimental para o cálculo prévio de priors por meio de clusterização e o posterior treinamento dos modelos ocultos de Markov.
def markov_regime_switching_prior(dataset, n_regimes: int, model_type="HMM", n_iter=100) -> pd.DataFrame: data = dataset[(dataset.index < hyper_params['forward']) & (dataset.index > hyper_params['backward'])].copy() # Extract meta features meta_X = data.loc[:, data.columns.str.contains('meta_feature')] if meta_X.shape[1] > 0: # Format data for HMM (requires 2D array) X = meta_X.values # Features normalization before training scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # Calculate priors from meta_features using k-means clustering from sklearn.cluster import KMeans # Use k-means to cluster the data into n_regimes groups kmeans = KMeans(n_clusters=n_regimes, n_init=10) cluster_labels = kmeans.fit_predict(X_scaled) # Calculate cluster-specific means and covariances to use as priors prior_means = kmeans.cluster_centers_ # Shape: (n_regimes, n_features) # Calculate empirical covariance for each cluster from sklearn.covariance import empirical_covariance prior_covs = [] for i in range(n_regimes): cluster_data = X_scaled[cluster_labels == i] if len(cluster_data) > 1: # Need at least 2 points for covariance cluster_cov = empirical_covariance(cluster_data) prior_covs.append(cluster_cov) else: # Fallback to overall covariance if cluster is too small prior_covs.append(empirical_covariance(X_scaled)) prior_covs = np.array(prior_covs) # Shape: (n_regimes, n_features, n_features) # Calculate initial state distribution from cluster proportions initial_probs = np.bincount(cluster_labels, minlength=n_regimes) / len(cluster_labels) # Calculate transition matrix based on cluster sequences trans_mat = np.zeros((n_regimes, n_regimes)) for t in range(1, len(cluster_labels)): trans_mat[cluster_labels[t-1], cluster_labels[t]] += 1 # Normalize rows to get probabilities row_sums = trans_mat.sum(axis=1, keepdims=True) # Avoid division by zero row_sums[row_sums == 0] = 1 trans_mat = trans_mat / row_sums # Initialize model parameters based on model type if model_type == "HMM": model_params = { 'n_components': n_regimes, 'covariance_type': "full", 'n_iter': n_iter, 'init_params': '' # Don't use default initialization } from hmmlearn import hmm model = hmm.GaussianHMM(**model_params) # Set the model parameters directly with our k-means derived priors model.startprob_ = initial_probs model.transmat_ = trans_mat model.means_ = prior_means model.covars_ = prior_covs # Fit the model model.fit(X_scaled) # Predict the hidden states (regimes) hidden_states = model.predict(X_scaled) # Assign states to clusters data['clusters'] = hidden_states return data return data
A preparação das distribuições a priori, no exemplo do modelo GaussianHMM, ocorre da seguinte forma:
- Normalização dos dados. As meta-características são escalonadas com o uso do StandardScaler para eliminar a influência da escala nos resultados da clusterização.
- Clusterização K-means. Determina os parâmetros iniciais para os estados ocultos, isto é, os regimes. Os dados são clusterizados em n_regimes clusters. As etiquetas de cluster obtidas, cluster_labels, são utilizadas para calcular os valores médios prior_means, os centros dos clusters, e as matrizes de covariância prior_covs, que correspondem à covariância empírica dentro dos clusters ou à covariância global, caso o cluster seja muito pequeno.
- Cálculo das probabilidades iniciais. A distribuição inicial initial_probs corresponde à proporção de pontos em cada cluster. Por exemplo, se 30% dos dados pertencem ao cluster 0, então initial_probs[0] = 0.3.
- Matriz de transição. É calculada contando-se com que frequência um cluster segue outro ao longo do tempo.
- Em seguida, o modelo oculto de Markov é inicializado com esses priors e treinado.
Os demais métodos fornecem suposições ainda mais fracas sobre as dependências e, por esse motivo, não foram considerados. Provavelmente, esta não é uma lista completa de todos os métodos possíveis para a definição de priors. Outros métodos podem ser utilizados, porém devem se basear em avaliações especializadas.
Testes de modelos ocultos de Markov com distribuições a priori
Foi observado que a dispersão dos resultados diminuiu. Os modelos passaram a ficar menos presos em mínimos locais, porém sua diversidade também foi reduzida. Além disso, para a definição de regimes de mercado por meio de modelos ocultos de Markov, normalmente é necessário um número menor de regimes, isto é, clusters, em comparação com o k-means.
Os resultados dos testes dos três modelos com priors definidos são apresentados a seguir:
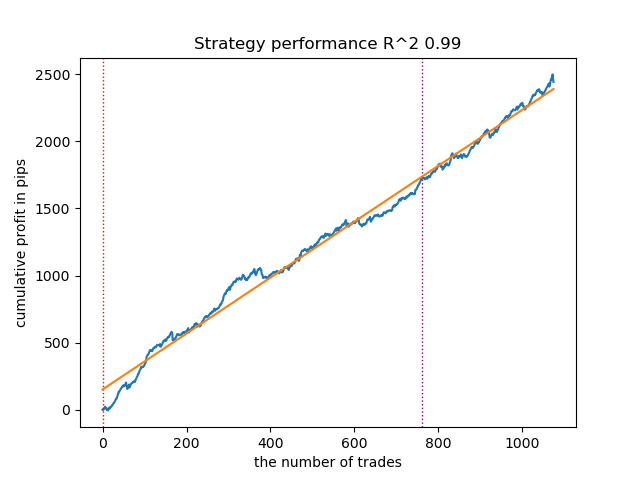
Fig. 10. Teste do GaussianHMM com distribuições a priori
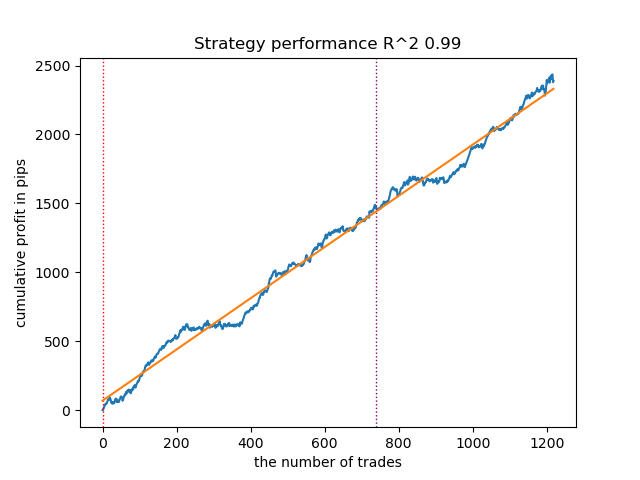
Fig. 11. Teste do GMMHMM com distribuições a priori
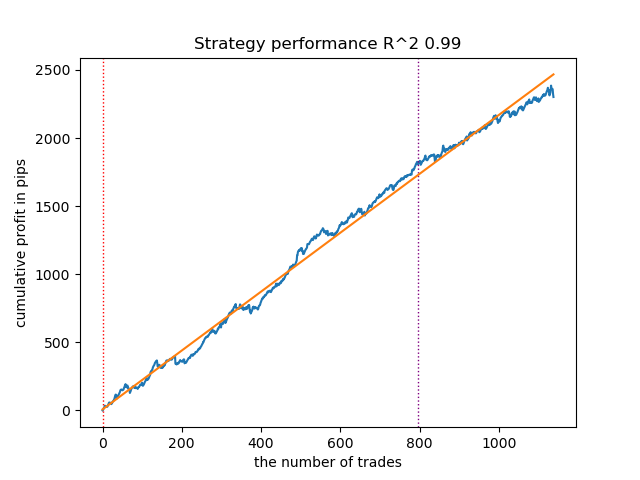
Fig. 12. Teste do VariationalGaussianHMM com distribuições a priori
Exportação dos modelos e compilação do robô para a plataforma Meta Trader 5
A exportação dos modelos ocorre exatamente da mesma forma que foi proposta nos artigos anteriores. O módulo de exportação está incluído no arquivo anexado.
Suponhamos que tenhamos selecionado o modelo utilizando um testador de estratégias customizado.
# TESTING & EXPORT models.sort(key=lambda x: x[0]) test_model_one_direction(models[-1][1:], hyper_params['stop_loss'], hyper_params['take_profit'], hyper_params['forward'], hyper_params['backward'], hyper_params['markup'], hyper_params['direction'], plt=True)
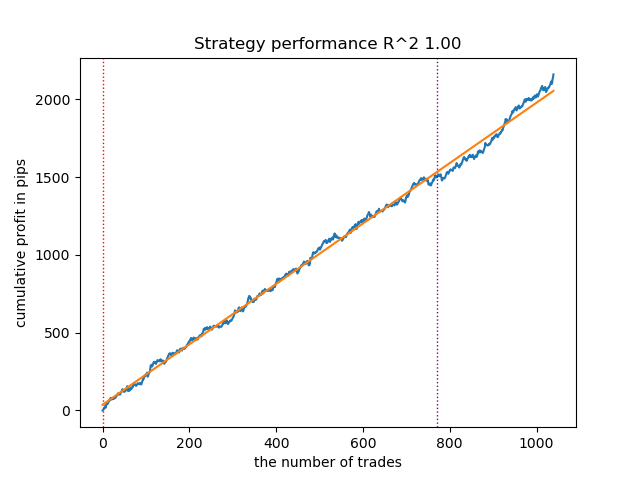
Fig. 13. Teste do melhor modelo com o uso do testador de estratégias customizado
Agora é necessário chamar a função de exportação, que salvará os modelos na pasta do terminal.
export_model_to_ONNX(model = models[-1], symbol = hyper_params['symbol'], periods = hyper_params['periods'], periods_meta = hyper_params['periods_meta'], model_number = hyper_params['model_number'], export_path = hyper_params['export_path'])
Em seguida, deve-se compilar o robô incluído ao final do artigo e testá-lo no testador do MetaTrader 5.
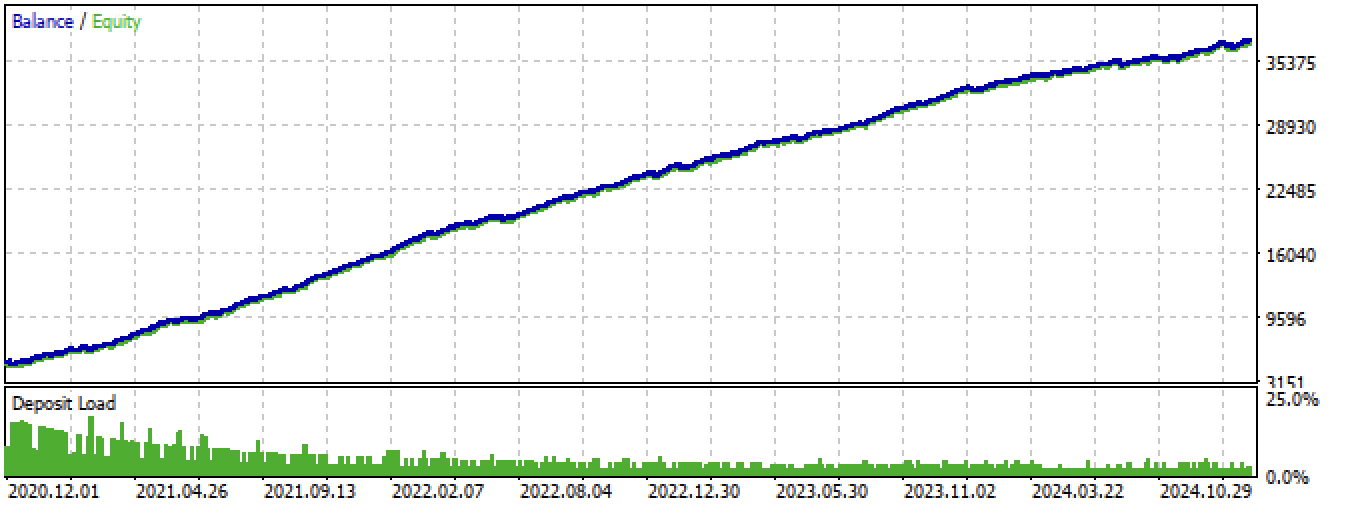
Fig. 14. Teste do melhor modelo no terminal Meta Trader 5 ao longo de todo o período
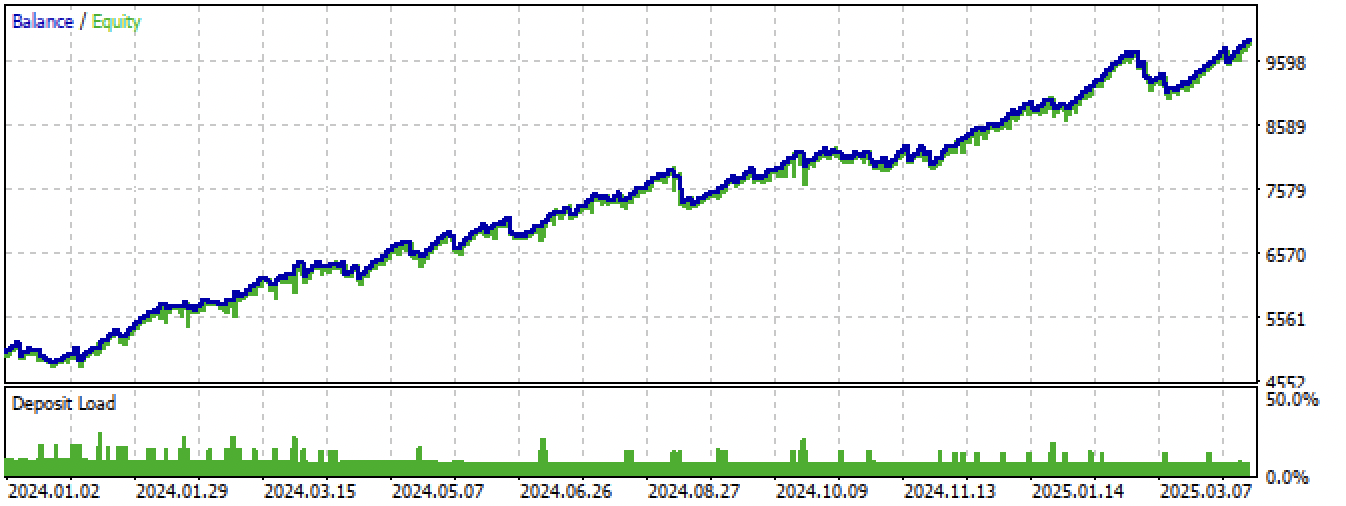
Fig. 15. Teste do melhor modelo no terminal Meta Trader 5 em novos dados
Considerações finais
Os modelos ocultos de Markov são um método interessante para a definição de regimes de mercado. Contudo, assim como todos os modelos de aprendizado de máquina, eles são propensos ao sobreajuste em séries temporais não estacionárias.
A definição adequada de matrizes a priori permite identificar regimes de mercado mais estáveis, que continuam funcionando em novos dados. Em geral, é necessário um número menor de regimes de mercado do que no caso da clusterização. Se, no primeiro caso, foram necessários 10 clusters, no segundo, muitas vezes é suficiente definir de 3 a 5 estados ocultos.
Não observei uma grande diferença no desempenho dos três algoritmos, todos apresentam resultados aproximadamente semelhantes. Portanto, pode-se utilizar o GaussianHMM como a opção mais simples e rápida. O GMMHMM, teoricamente, permite obter curvas de saldo mais suaves devido à presença de uma mistura de distribuições, o que ajuda a identificar subpadrões dentro de cada regime de mercado, porém, por esse mesmo motivo, pode estar mais sujeito ao sobreajuste. Para o VariationalGaussianHMM, é necessária uma definição mais cuidadosa dos priors; ao mesmo tempo, os parâmetros desse modelo são mais complexos de definir e interpretar.
Outro enfoque potencialmente útil pode ser a validação cruzada dos modelos por meio da avaliação dos parâmetros das distribuições dos regimes em diferentes folds, porém essa abordagem não foi considerada neste artigo.
O arquivo Python files.zip contém os seguintes arquivos para desenvolvimento no ambiente Python:
| Nome do arquivo | Descrição |
|---|---|
| one direction HMM.py | Script principal para o treinamento dos modelos |
| labeling_lib.py | Módulo atualizado com rotuladores de operações |
| tester_lib.py | Testador de estratégias customizado atualizado, baseado em aprendizado de máquina |
| export_lib.py | Módulo para exportação dos modelos para o terminal |
| XAUUSD_H1.csv | Arquivo com cotações exportadas do terminal MetaTrader 5 |
O arquivo MQL5 files.zip contém os arquivos para o terminal MetaTrader 5:
| Nome do arquivo | Descrição |
|---|---|
| one direction HMM.ex5 | Robô compilado desta artigo |
| one direction HMM.mq5 | Código-fonte do robô do artigo |
| pasta Include//Trend following | Contém os modelos ONNX e o arquivo de cabeçalho para conexão com o robô |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17917
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Construindo Expert Advisors Auto-Otimizáveis em MQL5 (Parte 4): Dimensionamento Dinâmico de Posição
Construindo Expert Advisors Auto-Otimizáveis em MQL5 (Parte 4): Dimensionamento Dinâmico de Posição
 Algoritmo baseado em fractais - Fractal-Based Algorithm (FBA)
Algoritmo baseado em fractais - Fractal-Based Algorithm (FBA)
 Dominando Registros de Log (Parte 4): Salvando logs em arquivos
Dominando Registros de Log (Parte 4): Salvando logs em arquivos
 Redefinindo os Indicadores MQL5 e MetaTrader 5
Redefinindo os Indicadores MQL5 e MetaTrader 5
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Затем, следует скомпилировать приложенного в конце статьи бота и протестировать его в тестере MetaTrader 5.
Fig. 14. Teste do melhor modelo no terminal MetaTrader 5 para todo o período
O arquivo MQL5 files.zip contém arquivos para o terminal MetaTrader 5
Por favor, torne padrão a publicação dos arquivos tst correspondentes aos resultados do backtest publicados nos artigos. Muito obrigado.
Por favor, torne padrão a publicação dos arquivos tst correspondentes dos resultados do backtest publicados nos artigos também. Muito obrigado.