Redes Neurais Profundas (Parte I). Preparando os Dados
3 957
0
A RNP são amplamente utilizadas e intensamente desenvolvidos em muitas áreas. Os exemplos mais comuns do uso das redes neurais no dia a dia são o reconhecimento de fala, imagem e a tradução automática de um idioma para o outro. As RNPs também são usadas na negociação. Dado o rápido desenvolvimento da negociação algorítmica, o estudo aprofundado das RNPs parece ser útil.
Ultimamente, os desenvolvedores trouxeram muitas novas ideias, métodos e abordagens para o uso da RNP, provando-a experimentalmente. Esta série de artigos considerará o estado e as principais direções do desenvolvimento da RNP. Muito espaço será dedicado a testar várias ideias e métodos usando experiências práticas ao lado de características qualitativas da RNP. Em nosso trabalho, nós usaremos apenas as redes multicamadas totalmente conectadas.
Os artigos terão quatro áreas de foco:
- Preparação, avaliação e amplificação dos dados de entrada por várias transformações.
- Novas capacidades do pacote de darch (v.0.12). Flexibilidade e funcionalidade estendida.
- O uso da amplificação de resultados de predição (otimização de hiperparâmetros da RNP e de conjuntos de redes neurais).
- Capacidades gráficas para controlar o funcionamento de um Expert Advisor durante a aprendizagem e o trabalho.
Este artigo considerará a preparação dos dados recebidos na plataforma de negociação para o uso da rede neural.
Conteúdo
- Introdução. A linguagem R
- 1. Criação dos dados iniciais (não processados)
- 2. Análise de dados exploratórios
- 3. Preparando os Dados
- Aplicação
- Links
Introdução
O desenvolvimento, treinamento e teste de uma rede neural profunda são realizados em estágios que possuem uma sequênciarigorosa. Semelhante a qualquer modelo de aprendizagem de máquina, o processo de criação de um RNP pode ser dividida em duas partes desiguais:
- preparação dos dados de entrada e saída para os experimentos;
- criação, treinamento, teste e otimização dos parâmetros da RNP.
A primeira etapa leva uma parte maior do tempo do projeto - cerca de 70%. O trabalho de uma RNP depende em grande parte do sucesso deste estágio. Afinal, lixo entra - lixo sai. É por isso que descreveremos detalhadamente a sequênciade ações nesta etapa.
Para repetir os experimentos, você precisará instalar o MRO 3.4.0 e o Rstudio. As instruções para instalar este software podem ser facilmente encontradas na internet. Os arquivos anexados a este artigo também contêm essas informações, portanto não vamos considerar isso em detalhes.
A linguagem R
Lembre-se de algumas coisas importantes sobre a R. Esta é uma linguagem de programação e um ambiente para computação gráfica e estatística. Ela foi desenvolvida em 1996 pelos cientistas neozelandeses Ross Ihaka e Robert Gentleman na Universidade de Auckland. R é um projeto GNU,ou seja, um software de código aberto. A abordagem de uso de software livre cai para os seguintes princípios (liberdades):
- a liberdade de lançar programas para qualquer propósito (liberdade 0);
- a liberdade de estudar como o programa funciona e adaptá-lo às necessidades do programador (liberdade 1);
- a liberdade de distribuir cópias para que você possa ajudar o seu vizinho (liberdade 2);
- a liberdade de melhorar o programa e distribuir a versão modificada para beneficiar toda a comunidade com a mudança.
Hoje a R está sendo melhorada e desenvolvida principalmente pela "R Development Core Team" e R Consortium fundado no ano passado. A lista dos membros do consórcio (IBM, Microsoft, Rstudio, Google, Mango, Oracle e outros) indica um bom suporte, interesse significativo e boas perspectivas da linguagem.
Vantagens da R:
- Hoje, R é o padrão em computação estatística.
- Ela possui suporte e é desenvolvida pela comunidade científica mundial.
- Um amplo conjunto de pacotes relativos a todas as direções avançadas na mineração de dados. Deve-se mencionar que o tempo entre uma publicação de uma nova ideia por parte dos cientistas e a implementação desta ideia em R não passa de duas semanas.
- E, por último, mas não menos importante, ela é absolutamente grátis.
1. Criação dos dados iniciais (não processados)
"Todos os movimentos de preços anteriores, atuais e futuros estão no próprio preço"
Existem muitos métodos (pacotes) projetados para preparação preliminar, avaliação e escolha dos preditores. A revisão desses métodos pode ser encontrada em [1]. Sua variedade é explicada pela diversidade de dados do mundo real. O tipo de dados em uso definirá os métodos de exploração e processamento.
Nós estamos explorando os dados financeiros. Estes são hierárquicos, séries temporais regulares que são infinitas e podem ser facilmente extraídos. A linha base é a cotação em OHLCV para o instrumento no tempo gráfico específico.
Todos as outras séries temporais provêm desta linha base:
- não paramétrica. Por exemplo, x^2, sqrt(abs(x)), x^3, -x^2 etc.
- funcional não paramétrica. Por exemplo, sin(2*n*x), ln(abs(x)), log(Pr(t)/Pr(t-1)) etc.
- paramétrica. Aqui temos uma série de indicadores, que são usados principalmente como preditores. Eles podem ser osciladores e diferentes tipos de filtros.
Os indicadores que geram sinais (fatores) ou uma sequência de declarações condicionais produzindo um sinal podem ser usados como uma variável objetivo.
1.1. Cotações
As cotações OHLC, Volume e tempo que recebemos do terminal como vetores (o, h, l, cl, v, d). Nós precisamos escrever uma função que se junte aos vetores recebidos do terminal no dataFrame. Para isso, nós mudaremos o formato da hora de início da barra para o formato POSIXct.
#---pr.OHLCV-------------------
pr.OHLCV <- function(d, o, h, l, cl, v){
# (d, o, h, l, cl, v)- vector
require('magrittr')
require('dplyr')
require('anytime')
price <- cbind(Data = rev(d),
Open = rev(o), High = rev(h),
Low = rev(l), Close = rev(cl),
Vol = rev(v)) %>% as.tibble()
price$Data %<>% anytime(., tz = "CET")
return(price)
}
Como os vetores da cotação foram carregados no ambiente env, vamos calcular o dataFrame pr e limpar o ambiente env de variáveis não utilizadas:
evalq({pr <- pr.OHLCV(Data, Open, High, Low, Close, Volume)
rm(list = c("Data", "Open", "High", "Low", "Close", "Volume"))
},
env)
Nós queremos ver como este dataFrame se parece no início:
> head(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-01-10 11:00:00 122.758 122.893 122.746 122.859 2 2017-01-10 11:15:00 122.860 122.924 122.818 122.848 3 2017-01-10 11:30:00 122.850 122.856 122.705 122.720 4 2017-01-10 11:45:00 122.721 122.737 122.654 122.693 5 2017-01-10 12:00:00 122.692 122.850 122.692 122.818 6 2017-01-10 12:15:00 122.820 122.937 122.785 122.920 # ... com 1 variável a mais: Vol <dbl>
e no final:
> tail(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-05-05 20:30:00 123.795 123.895 123.780 123.888 2 2017-05-05 20:45:00 123.889 123.893 123.813 123.831 3 2017-05-05 21:00:00 123.833 123.934 123.825 123.916 4 2017-05-05 21:15:00 123.914 123.938 123.851 123.858 5 2017-05-05 21:30:00 123.859 123.864 123.781 123.781 6 2017-05-05 21:45:00 123.779 123.864 123.781 123.781 # ... com 1 variável a mais: Vol <dbl>
Assim, existem 8000 barras com a data de início 10.01.2017 e a data final 05.05.2017. Vamos adicionar variações do preço para o dataframe pr — Preço Médio, Preço Típico e Preço Ponderado
evalq(pr %<>% mutate(., Med = (High + Low)/2, Typ = (High + Low + Close)/3, Wg = (High + Low + 2 * Close)/4, #CO = Close - Open, #HO = High - Open, #LO = Low - Open, dH = c(NA, diff(High)), dL = c(NA, diff(Low)) ), env)
1.2. Preditores
Nós vamos trabalhar com um conjunto de preditores simplificados. Os filtros digitais FATL, SATL, RFTL, RSTL desempenharão esse papel. Eles são descritos em detalhes no artigo de V. Kravchuk "New Adaptive Method of Following the Tendency and Market Cycles", que pode ser encontrado nos arquivos anexados a este artigo (veja o capítulo "New Tools of Technical Analysis and their Interpretation"). Eu vou listá-los aqui.
- FATL - Fast Adaptive Trend Line;
- SATL - Slow Adaptive Trend Line;
- RFTL - Reference Fast Trend Line;
- RSTL - Reference Slow Trend Line.
A taxa de variação do FATL e SATL podem ser monitoradas usando os indicadores FTLM - Fast Trend Line Momentum e STLM - Slow Trend Line Momentum.
Existem dois osciladores entre as ferramentas técnicas que nós precisaremos - os índices RBCI e PCCI. O índice RBCI (Range Bound Channel Index) é um índice de canal limitado pela largura da banda, que é calculado por meio de um filtro de canal. O filtro remove a tendência de baixa freqüência e o ruído de baixa freqüência. O índice PCCI (Perfect Commodity Channel Index) é um índice de canais de commodities perfeito.
A função que calcula os filtros digitais FATL, SATL, RFTL, RSTL é a seguinte:
#-----DigFiltr------------------------- DigFiltr <- function(X, type = 1){ # X - vector require(rowr) fatl <- c( +0.4360409450, +0.3658689069, +0.2460452079, +0.1104506886, -0.0054034585, -0.0760367731, -0.0933058722, -0.0670110374, -0.0190795053, +0.0259609206, +0.0502044896, +0.0477818607, +0.0249252327, -0.0047706151, -0.0272432537, -0.0338917071, -0.0244141482, -0.0055774838, +0.0128149838, +0.0226522218, +0.0208778257, +0.0100299086, -0.0036771622, -0.0136744850, -0.0160483392, -0.0108597376, -0.0016060704, +0.0069480557, +0.0110573605, +0.0095711419, +0.0040444064, -0.0023824623, -0.0067093714, -0.0072003400, -0.0047717710, 0.0005541115, 0.0007860160, 0.0130129076, 0.0040364019 ) rftl <- c(-0.0025097319, +0.0513007762 , +0.1142800493 , +0.1699342860 , +0.2025269304 , +0.2025269304, +0.1699342860 , +0.1142800493 , +0.0513007762 , -0.0025097319 , -0.0353166244, -0.0433375629 , -0.0311244617 , -0.0088618137 , +0.0120580088 , +0.0233183633, +0.0221931304 , +0.0115769653 , -0.0022157966 , -0.0126536111 , -0.0157416029, -0.0113395830 , -0.0025905610 , +0.0059521459 , +0.0105212252 , +0.0096970755, +0.0046585685 , -0.0017079230 , -0.0063513565 , -0.0074539350 , -0.0050439973, -0.0007459678 , +0.0032271474 , +0.0051357867 , +0.0044454862 , +0.0018784961, -0.0011065767 , -0.0031162862 , -0.0033443253 , -0.0022163335 , +0.0002573669, +0.0003650790 , +0.0060440751 , +0.0018747783) satl <- c(+0.0982862174, +0.0975682269 , +0.0961401078 , +0.0940230544, +0.0912437090 , +0.0878391006, +0.0838544303 , +0.0793406350 ,+0.0743569346 ,+0.0689666682 , +0.0632381578 ,+0.0572428925 , +0.0510534242,+0.0447468229, +0.0383959950, +0.0320735368, +0.0258537721 ,+0.0198005183 , +0.0139807863,+0.0084512448, +0.0032639979, -0.0015350359, -0.0059060082 ,-0.0098190256 , -0.0132507215, -0.0161875265, -0.0186164872, -0.0205446727, -0.0219739146 ,-0.0229204861 , -0.0234080863,-0.0234566315, -0.0231017777, -0.0223796900, -0.0213300463 ,-0.0199924534 , -0.0184126992,-0.0166377699, -0.0147139428, -0.0126796776, -0.0105938331 ,-0.0084736770 , -0.0063841850,-0.0043466731, -0.0023956944, -0.0005535180, +0.0011421469 ,+0.0026845693 , +0.0040471369,+0.0052380201, +0.0062194591, +0.0070340085, +0.0076266453 ,+0.0080376628 , +0.0083037666,+0.0083694798, +0.0082901022, +0.0080741359, +0.0077543820 ,+0.0073260526 , +0.0068163569,+0.0062325477, +0.0056078229, +0.0049516078, +0.0161380976 ) rstl <- c(-0.0074151919,-0.0060698985,-0.0044979052,-0.0027054278,-0.0007031702,+0.0014951741, +0.0038713513,+0.0064043271,+0.0090702334,+0.0118431116,+0.0146922652,+0.0175884606, +0.0204976517,+0.0233865835,+0.0262218588,+0.0289681736,+0.0315922931,+0.0340614696, +0.0363444061,+0.0384120882,+0.0402373884,+0.0417969735,+0.0430701377,+0.0440399188, +0.0446941124,+0.0450230100,+0.0450230100,+0.0446941124,+0.0440399188,+0.0430701377, +0.0417969735,+0.0402373884,+0.0384120882,+0.0363444061,+0.0340614696,+0.0315922931, +0.0289681736,+0.0262218588,+0.0233865835,+0.0204976517,+0.0175884606,+0.0146922652, +0.0118431116,+0.0090702334,+0.0064043271,+0.0038713513,+0.0014951741,-0.0007031702, -0.0027054278,-0.0044979052,-0.0060698985,-0.0074151919,-0.0085278517,-0.0094111161, -0.0100658241,-0.0104994302,-0.0107227904,-0.0107450280,-0.0105824763,-0.0102517019, -0.0097708805,-0.0091581551,-0.0084345004,-0.0076214397,-0.0067401718,-0.0058083144, -0.0048528295,-0.0038816271,-0.0029244713,-0.0019911267,-0.0010974211,-0.0002535559, +0.0005231953,+0.0012297491,+0.0018539149,+0.0023994354,+0.0028490136,+0.0032221429, +0.0034936183,+0.0036818974,+0.0038037944,+0.0038338964,+0.0037975350,+0.0036986051, +0.0035521320,+0.0033559226,+0.0031224409,+0.0028550092,+0.0025688349,+0.0022682355, +0.0073925495) if (type == 1) {k = fatl} if (type == 2) {k = rftl} if (type == 3) {k = satl} if (type == 4) {k = rstl} n <- length(k) m <- length(X) k <- rev(k) f <- rowr::rollApply(data = X, fun = function(x) {sum(x * k)}, window = n, minimum = n, align = "right") while (length(f) < m) { f <- c(NA,f)} return(f) }
Depois de terem sido calculados, adicione-os ao dataframe pr
evalq(pr %<>% mutate(., fatl = DigFiltr(Close, 1), rftl = DigFiltr(Close, 2), satl = DigFiltr(Close, 3), rstl = DigFiltr(Close, 4) ), env)
Adicionado os osciladores FTLM, STLM, RBCI, PCCI, suas primeiras diferenças e as primeiras diferenças dos filtros digitais no dataframe pr:
evalq(pr %<>% mutate(., ftlm = fatl - rftl, rbci = fatl - satl, stlm = satl - rstl, pcci = Close - fatl, v.fatl = c(NA, diff(fatl)), v.rftl = c(NA, diff(rftl)), v.satl = c(NA, diff(satl)), v.rstl = c(NA, diff(rstl)*10) ), env) evalq(pr %<>% mutate(., v.ftlm = c(NA, diff(ftlm)), v.stlm = c(NA, diff(stlm)), v.rbci = c(NA, diff(rbci)), v.pcci = c(NA, diff(pcci)) ), env)
1.3. Variável objetivo
O ZigZag() será usado como um indicador que gera a variável objetivo.
A função para o seu cálculo receberá as séries temporais e dois parâmetros: um comprimento mínimo de uma curva (int ou double) e o tipo do preço para cálculo (Close, Med, Typ, Wd, com (High, Low)).
#------ZZ----------------------------------- par <- c(25, 5) ZZ <- function(x, par) { # x - vector require(TTR) require(magrittr) ch = par[1] mode = par[2] if (ch > 1) ch <- ch/(10 ^ (Dig - 1)) switch(mode, xx <- x$Close, xx <- x$Med, xx <- x$Typ, xx <- x$Wd, xx <- x %>% select(High,Low)) zz <- ZigZag(xx, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]} return(zz) }
Calcule o ZigZag, a primeira diferença, o sinal da primeira diferença e adiciona-os ao dataframepr:
evalq(pr %<>% cbind(., zigz = ZZ(., par = par)), env) evalq(pr %<>% cbind(., dz = diff(pr$zigz) %>% c(NA, .)), env) evalq(pr %<>% cbind(., sig = sign(pr$dz)), env)
1.4.Conjunto inicial de dados
Vamos resumir os dados que devemos ter como resultado dos cálculos.
Nós recebemos do terminal os vetores OHLCV e uma marca temporária de início da barra no tempo gráfico M15 para o EURJPY. Esses dados formaram o dataframe pr. As variáveis FATL, SATL, RFTL, RSTL, FTLM, STLM, RBCI, PCCI e suas primeiras diferenças foram adicionadas a este dataframe. O ZigZag com uma alavancagem mínima de 25 pontos (4 casas decimais), sua primeira diferença e o sinal da primeira diferença (-1,1), que será usado como sinal, foram adicionados ao dataframe também.
Todos esses dados foram carregados não no ambiente global, mas em um novo ambiente filho env, onde todos os cálculos serão realizados. Esta divisão permitirá o uso de conjuntos de dados de diferentes símbolos ou tempos gráficos sem conflitos de nomes durante o cálculo.
A estrutura do conjunto de dados total pr é exibida abaixo. As variáveis, necessárias para os seguintes cálculos, podem ser facilmente extraídas deste.
str(env$pr) 'data.frame': 8000 obs. of 30 variables: $ Data : POSIXct, format: "2017-01-10 11:00:00" ... $ Open : num 123 123 123 123 123 ... $ High : num 123 123 123 123 123 ... $ Low : num 123 123 123 123 123 ... $ Close : num 123 123 123 123 123 ... $ Vol : num 3830 3360 3220 3241 3071 ... $ Med : num 123 123 123 123 123 ... $ Typ : num 123 123 123 123 123 ... $ Wg : num 123 123 123 123 123 ... $ dH : num NA 0.031 -0.068 -0.119 0.113 ... $ dL : num NA 0.072 -0.113 -0.051 0.038 ... $ fatl : num NA NA NA NA NA NA NA NA NA NA ... $ rftl : num NA NA NA NA NA NA NA NA NA NA ... $ satl : num NA NA NA NA NA NA NA NA NA NA ... $ rstl : num NA NA NA NA NA NA NA NA NA NA ... $ ftlm : num NA NA NA NA NA NA NA NA NA NA ... $ rbci : num NA NA NA NA NA NA NA NA NA NA ... $ stlm : num NA NA NA NA NA NA NA NA NA NA ... $ pcci : num NA NA NA NA NA NA NA NA NA NA ... $ v.fatl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rftl: num NA NA NA NA NA NA NA NA NA NA ... $ v.satl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rstl: num NA NA NA NA NA NA NA NA NA NA ... $ v.ftlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.stlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.rbci: num NA NA NA NA NA NA NA NA NA NA ... $ v.pcci: num NA NA NA NA NA NA NA NA NA NA ... $ zigz : num 123 123 123 123 123 ... $ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ... $ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
Selecione todos os preditores calculados anteriormente a partir do dataframe DataSet . Converte a variável objetivo sig em um fator e move uma barra para a frente (no futuro).
evalq(dataSet <- pr %>% tbl_df() %>%
dplyr::select(Data, ftlm, stlm, rbci, pcci,
v.fatl, v.satl, v.rftl, v.rstl,
v.ftlm, v.stlm, v.rbci, v.pcci, sig) %>%
dplyr::filter(., sig != 0) %>%
mutate(., Class = factor(sig, ordered = F) %>%
dplyr::lead()) %>%
dplyr::select(-sig),
env)
Visualizando a análise de dados
Desenha o gráfico OHLC usando o pacote ggplot2. Pega os dados nos últimos dois dias e desenha um gráfico de cotações em barras.
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + labs(title = "EURJPY Candlestick Chart", y = "Close Price", x = "") + theme_tq(), env)
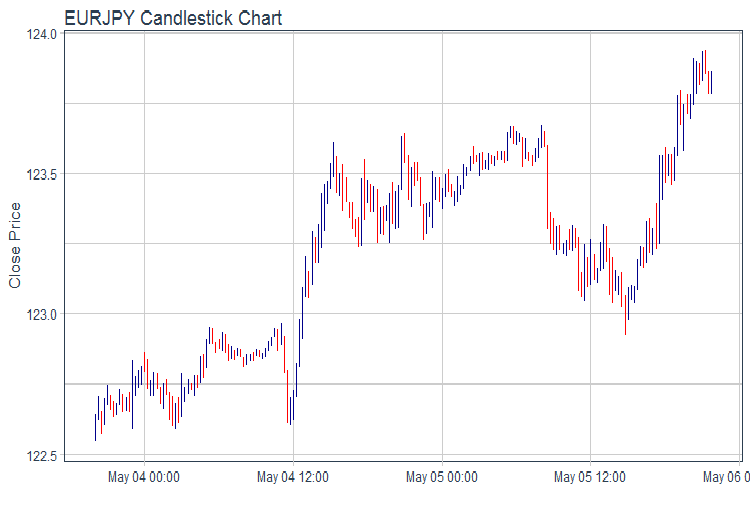
Fig.1. Gráfico de cotações
Desenha o FATL, SATL, RFTL, RSTL e ZZ:gráfico
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + geom_line(aes(Data, fatl), color = "steelblue", size = 1) + geom_line(aes(Data, rftl), color = "red", size = 1) + geom_line(aes(Data, satl), color = "gold", size = 1) + geom_line(aes(Data, rstl), color = "green", size = 1) + geom_line(aes(Data, zigz), color = "black", size = 1) + labs(title = "EURJPY Candlestick Chart", subtitle = "Combining Chart Geoms", y = "Close Price", x = "") + theme_tq(), env)
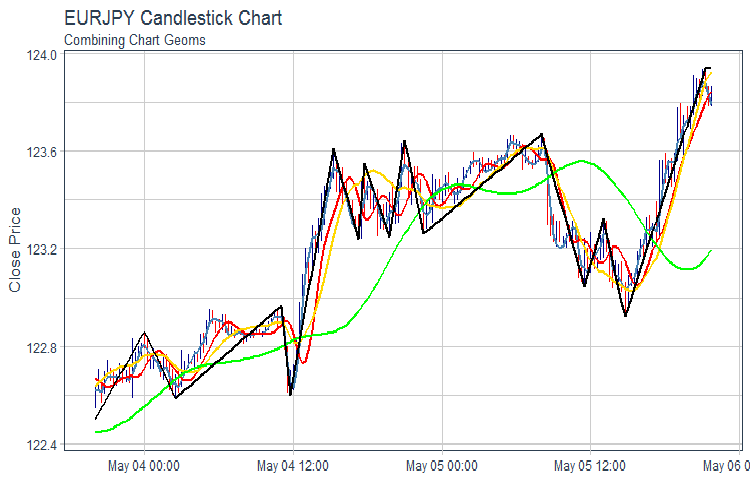
Fig.2. FATL, SATL, RFTL, RSTL e ZZ
Divide os osciladores em três grupos para uma representação mais conveniente.
require(dygraphs) evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, ftlm, stlm, rbci, pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator base") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "blue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
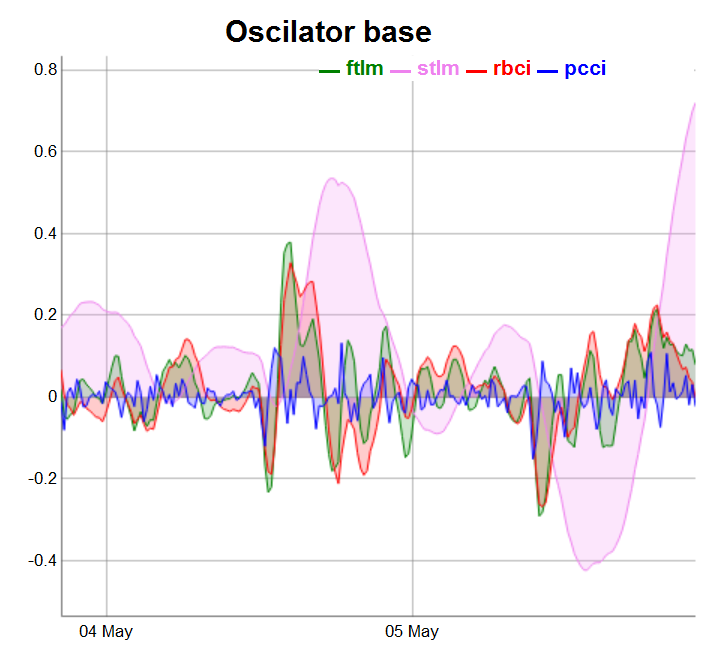
Fig.3. Base oscillators
evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, v.fatl, v.satl, v.rftl, v.rstl) %>% tk_xts() %>% dygraph(., main = "Oscilator 2") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
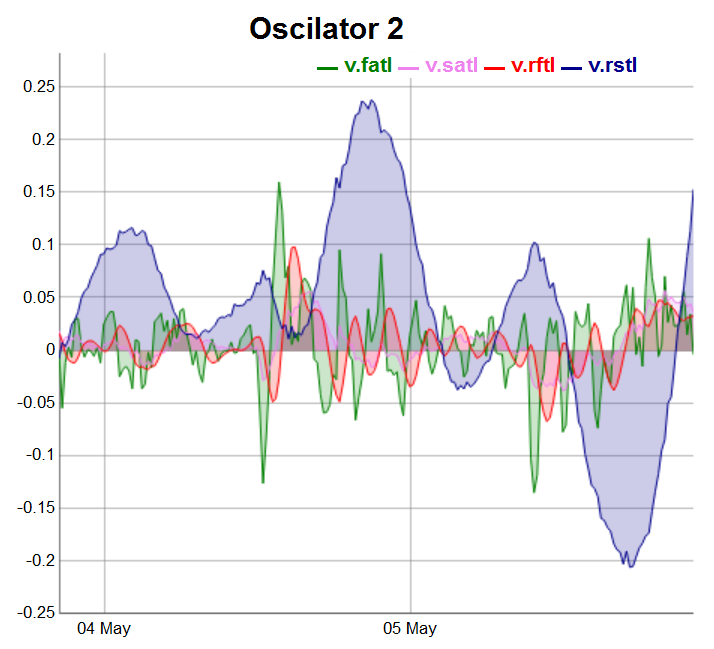
Fig.4. Osciladores do segundo grupo
Os osciladores do terceiro grupo serão desenhados nas últimas 100 barras:
evalq(dataSet %>% tail(., 100) %>% tk_tbl %>% select(Data, v.ftlm, v.stlm, v.rbci, v.pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator 3") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
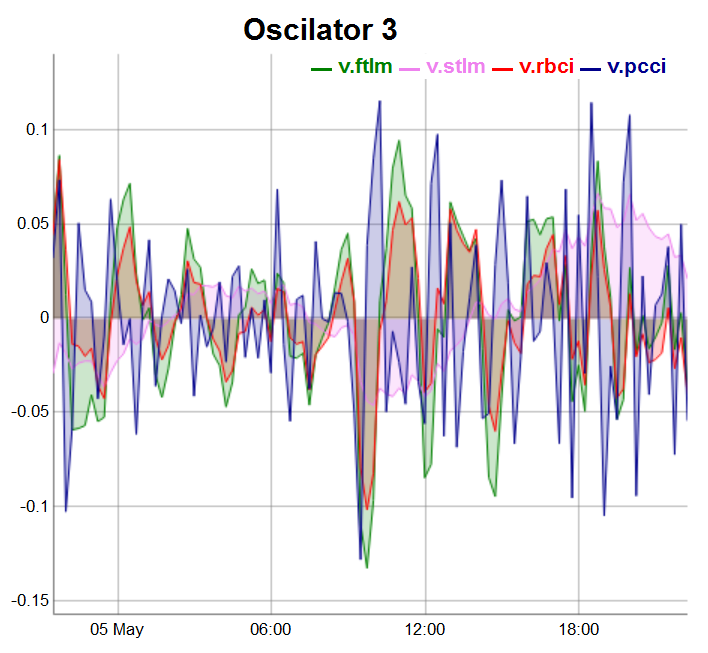
Fig.5. Osciladores do terceiro grupo
2.Exploração da análise de dados, EDA
"Não há questões estatísticas triviais, há procedimentos estatísticos duvidosos." - Sir David Cox
"Uma resposta aproximada ao problema certo vale muito mais do que uma resposta exata para um problema aproximado". — John Tukey
Nós estamos usando a EDA para desenvolver a compreensão dos dados em uso. A maneira mais simples de fazer isso é usar as perguntas como ferramenta de pesquisa. Quando fazemos uma pergunta, nós estamos focados em uma certa parte dos dados. Isso ajudará a decidir quais gráficos, modelos e transformações nós devemos usar.
A EDA é essencialmente um processo criativo. Semelhante aos processos mais criativos, a chave para fazer uma boa pergunta é criar ainda mais perguntas. É difícil fazer perguntas fundamentais no início da análise, pois não sabemos quais as conclusões que o conjunto de dados contém. Por outro lado, cada nova questão que perguntamos, é destacado um novo aspecto dos dados, aumentando nossas chances de fazer uma descoberta. Nós podemos rapidamente mudar para a parte mais interessante do conjunto de dados e esclarecer a situação fazendo perguntas sequenciais.
Não há regras para quais questões nós devemos pedir para estudar os dados. Dito isto, existem dois tipos de perguntas que serão úteis:
-
Qual tipo de alteração minhas variáveis estão passando?
- Que tipo de covariação está ocorrendo entre as variáveis?
Vamos definir o conceito principal.
Variações são a tendência que os valores de uma variável tem a mudar em diferentes medidas. Há muitos exemplos de variações na vida cotidiana. Se você medir qualquer variável contínua sete vezes, você terá sete valores diferentes. Isso é verdade mesmo para constantes, por exemplo, a velocidade da luz. Cada medida conterá pequenos erros que serão diferentes a cada vez. Variáveis do mesmo tipo também podem mudar. Por exemplo, a cor do olho de diferentes pessoas ou o nível de energia elétrica em diferentes momentos. Cada variável possui seu próprio caráter de variações que podem revelar informações interessantes. A melhor maneira de entender essa informação é visualizar a distribuição dos valores das variáveis. Este é um caso em que um diagrama é melhor do que mil palavras.
2.1.Estatísticas totais
A estatística total de uma série temporal é conveniente para rastrear usando a função table.Stats()::PerformenceAnalitics.
> table.Stats(env$dataSet %>% tk_xts()) Using column `Data` for date_var. ftlm stlm rbci pcci Observations 7955.0000 7908.0000 7934.0000 7960.0000 NAs 42.0000 89.0000 63.0000 37.0000 Minimum -0.7597 -1.0213 -0.9523 -0.5517 Quartile 1 -0.0556 -0.1602 -0.0636 -0.0245 Median -0.0001 0.0062 -0.0016 -0.0001 Arithmetic Mean 0.0007 0.0025 0.0007 0.0001 Geometric Mean -0.0062 NaN -0.0084 -0.0011 Quartile 3 0.0562 0.1539 0.0675 0.0241 Maximum 2.7505 3.0407 2.3872 1.8859 SE Mean 0.0014 0.0033 0.0015 0.0006 LCL Mean (0.95) -0.0020 -0.0040 -0.0022 -0.0010 UCL Mean (0.95) 0.0034 0.0090 0.0035 0.0012 Variance 0.0152 0.0858 0.0172 0.0026 Stdev 0.1231 0.2929 0.1311 0.0506 Skewness 4.2129 1.7842 2.3037 6.4718 Kurtosis 84.6116 16.7471 45.0133 247.4208 v.fatl v.satl v.rftl v.rstl Observations 7959.0000 7933.0000 7954.0000 7907.0000 NAs 38.0000 64.0000 43.0000 90.0000 Minimum -0.3967 -0.0871 -0.1882 -0.4719 Quartile 1 -0.0225 -0.0111 -0.0142 -0.0759 Median -0.0006 0.0003 0.0000 0.0024 Arithmetic Mean 0.0002 0.0002 0.0002 0.0011 Geometric Mean -0.0009 0.0000 -0.0003 -0.0078 Quartile 3 0.0220 0.0110 0.0138 0.0751 Maximum 1.4832 0.3579 0.6513 1.3093 SE Mean 0.0005 0.0002 0.0003 0.0015 LCL Mean (0.95) -0.0009 -0.0003 -0.0005 -0.0020 UCL Mean (0.95) 0.0012 0.0007 0.0009 0.0041 Variance 0.0023 0.0005 0.0009 0.0188 Stdev 0.0483 0.0219 0.0308 0.1372 Skewness 5.2643 2.6705 3.9472 1.5682 Kurtosis 145.8441 36.9378 74.4182 13.5724 v.ftlm v.stlm v.rbci v.pcci Observations 7954.0000 7907.0000 7933.0000 7959.0000 NAs 43.0000 90.0000 64.0000 38.0000 Minimum -0.9500 -0.2055 -0.6361 -1.4732 Quartile 1 -0.0280 -0.0136 -0.0209 -0.0277 Median -0.0002 -0.0001 -0.0004 -0.0002 Arithmetic Mean 0.0000 0.0001 0.0000 0.0000 Geometric Mean -0.0018 -0.0003 -0.0009 NaN Quartile 3 0.0273 0.0143 0.0207 0.0278 Maximum 1.4536 0.3852 1.1254 1.9978 SE Mean 0.0006 0.0003 0.0005 0.0006 LCL Mean (0.95) -0.0012 -0.0005 -0.0009 -0.0013 UCL Mean (0.95) 0.0013 0.0007 0.0009 0.0013 Variance 0.0032 0.0007 0.0018 0.0034 Stdev 0.0561 0.0264 0.0427 0.0579 Skewness 1.2051 0.8513 2.0643 3.0207 Kurtosis 86.2425 23.0651 86.3768 233.1964
Aqui está o que esta tabela nos diz:
- Todos os preditores têm um número relativamente pequeno de variáveis indefinidas NA.
- Todos os preditores têm uma pronunciada assimetria direita.
- Todos os preditores têm uma alta curtose.
2.2.Visualizando as estatísticas totais
"O maior valor de uma imagem é quando isso nos obriga a notar o que nunca esperamos ver". — John Tukey
Vejamos a variação e covariação entre as variáveis no conjunto de dados. Como o número de variáveis (14) não nos permite representá-las em um gráfico, eles terão que ser divididos em três grupos.
require(GGally) evalq(ggpairs(dataSet, columns = 2:6, mapping = aes(color = Class), title = "DigFilter1"), env)
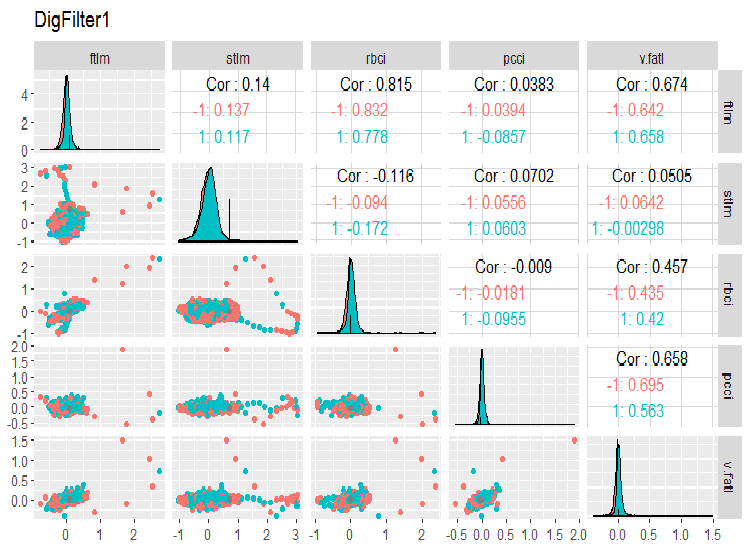
Fig. 6. Primeiro grupo de preditores
evalq(ggpairs(dataSet, columns = 7:10, mapping = aes(color = Class), title = "DigFilter2"), env)
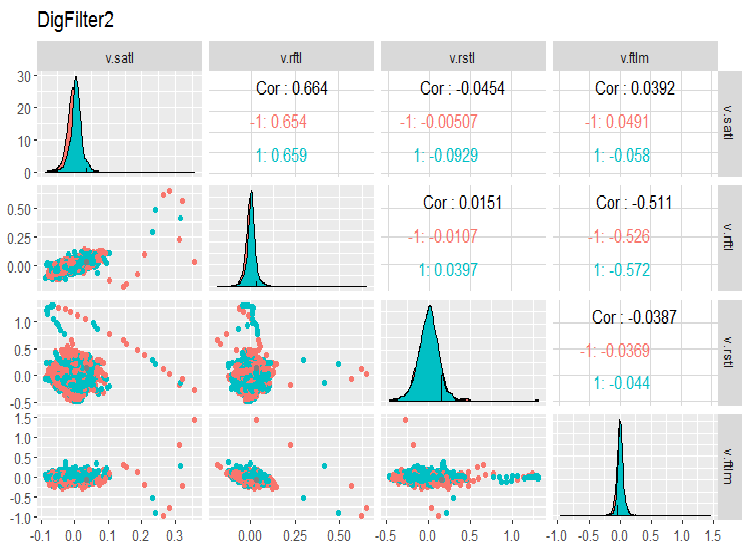
Fig. 7. Segundo grupo de preditores
evalq(ggpairs(dataSet, columns = 11:14, mapping = aes(color = Class), title = "DigFilter3"), env)
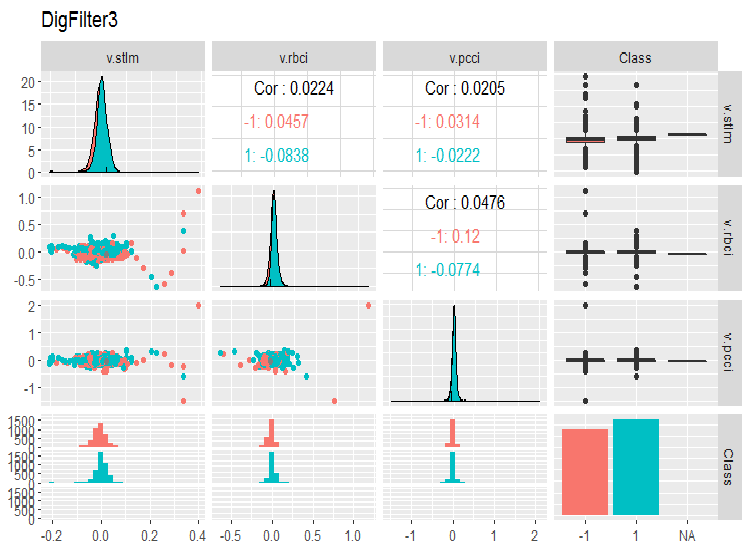
Fig. 8. Terceiro grupo de preditores
Isto é o que devemos ver nos gráficos:
- Todos os preditores têm a forma de distribuições próximas ao normal, embora haja uma assimetria direita bem pronunciada;
- Todos os preditores têm uma faixa interquartil muito estreita (IQR);
- Todos os preditores têm outliers proeminentes;
- o número de exemplos em dois níveis da variável objetivo "Class" tem uma pequena diferença.
3.Preparação dos dados
Normalmente, a preparação dos dados tem sete estágios:
- "Imputação" — remoção ou imputação de dados perdidos/indefinidos;
- "Variância" — remoção de variáveis com dispersão zero ou quase zero;
- "Dividir" — dividir o conjunto de dados nos subconjuntos train/valid/test;
- "Dimensionamento" — escalando o intervalo de variáveis;
- "Outliers" — remoção ou entrada de outliers;
- "Amostragem" — correção do desequilíbrio da classe;
- "Denoise" — remoção ou redefinição de ruído;
- "Seleção" — selecionando preditores irrelevantes.
3.1. Limpeza de dados
A primeira etapa da preparação dos dados brutos é a remoção ou imputação de valores indefinidos e lacunas nos dados. Embora muitos modelos permitam o uso de dados indefinidos (NA) e lacunas nos conjuntos de dados, é melhor excluí-los antes de iniciar as ações principais. Esta operação é realizada para o conjunto de dados completo, independentemente do modelo.
As estatísticas totais de nossos dados brutos indicaram que o conjunto de dados contém NA. Estes são artificiais A, que apareceram ao calcular os filtros digitais. Não há muitos deles para que eles possam ser excluídos. Nós já obtivemos a base de dados pronta para posterior processamento. Vamos limpá-la.
Em um caso geral, a limpeza significa as seguintes operações:
- remoção de preditores com uma dispersão zero ou quase zero (method = c(“zv”, “nzv”));
- remoção de variáveis altamente correlacionadas. Cabe ao usuário definir o limite para o coeficiente de correlação (method = “corr”). Seu valor padrão é igual a 0.9. Este estágio nem sempre é necessário. Depende dos seguintes métodos de transformação;
- remoção de preditores que possuem apenas um valor exclusivo em qualquer classe (method = “conditionalX”).
Todas essas operações são implementadas na função preProcess()::caret através dos métodos considerados acima. Essas operações são realizadas para a base de dados completa antes da divisão nos conjuntos de treinamento e teste.
require(caret)
evalq({preProClean <- preProcess(x = dataSet,method = c("zv", "nzv", "conditionalX", "corr"))
dataSetClean <- predict(preProClean, dataSet %>% na.omit)},
env)
Deixe-nos ver se há algum preditor excluído e o que temos após a limpeza:
> env$preProClean$method$remove #[1] "v.rbci" > dim(env$dataSetClean) [1] 7906 13 > colnames(env$dataSetClean) [1] "Data" "ftlm" "stlm" "rbci" "pcci" [6] "v.fatl" "v.satl" "v.rftl" "v.rstl" "v.ftlm" [11] "v.stlm" "v.pcci" "Class"
3.2. Identificando e processando os outliers
Problemas com a qualidade dos dados, tais como a assimetria e os valores atípicos (outliers), geralmente são interligados e interdependentes. Isso não só faz um processamento preliminar de dados que consome tempo, mas também dificulta a busca de correlações e tendências no conjunto de dados.
O que são outliers?
Vamos concordar que um outlier é uma observação muito distante de outras observações. Uma classificação detalhada de outliers, seus métodos de identificação e processamento são descritos em [2].
Tipos de outliers
Os outliers causam distorções significativas na distribuição de variáveis e treinam um modelo usando tais dados. Existem muitos métodos de identificação e processamento de valores atípicos. A escolha do método depende principalmente de identificarmos ou não o local a nível local ou global. Os outliers locais são valores atípicos de uma variável. Os outliers globais são valores atípicos em um espaço multidimensional definido por uma matriz ou um dataframe.
O que causa os outliers?
Os outliers podem ser divididos por origem:
Artificial
- erros de entrada de dados. Aqui pertencem os erros ocorridos durante a coleta, gravação e processamento de dados;
- erros experimentais;
- erros de amostragem.
Erros naturais causados pela natureza da variável.
Qual o impacto que os outliers possuem?
Os outliers podem arruinar os resultados da análise de dados e modelagem estatística. Isso aumenta a dispersão de erros e diminui o poder estatístico dos testes. Se os outliers não são distribuídos aleatoriamente, eles podem reduzir a normalidade. Os outliers também podem influenciar a assunção principal de análises de regressão e dispersão, juntamente com outros pressupostos estatísticos do modelo.
Como podemos identificar os valores atípicos locais?
Normalmente, os outliers podem ser revelados através da visualização de dados. Um dos métodos mais simples e amplamente utilizados é o boxplot. Vamos levar o preditor ftlm como um exemplo:
evalq(ggplot(dataSetClean, aes(x = factor(0),
y = ftlm,
color = 'red')) +
geom_boxplot() + xlab("") +
scale_x_discrete(breaks = NULL) +
coord_flip(),
env)
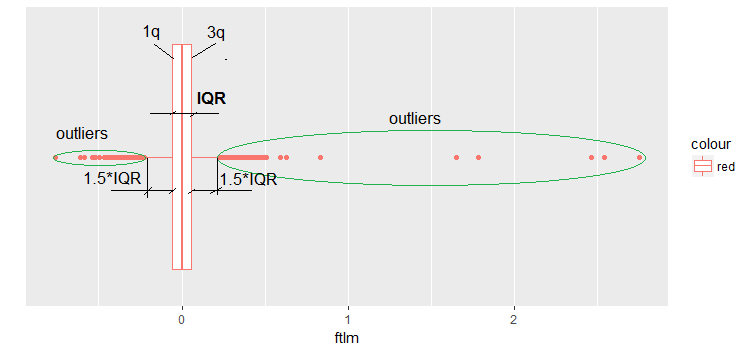
Fig.9. Boxplot ftlm
Alguns comentários ao diagrama:
IQR é a faixa interquartil ou a distância entre o primeiro e o terceiro quartil.
Desta forma, nós podemos definir os outliers de várias maneiras:
- Qualquer valor menor que -1.5*IQR e maior que +1.5*IQR é um valor atípico. Às vezes, o coeficiente é definido como 2 ou 3. Todos os valores entre 1.5*IQR e 3*IQR são chamados de outliers médios e os valores acima de3*IQR são chamados de outliers extremos.
- Qualquer valor que parece estar fora do 5º e 95º percentil pode ser considerado um valor atípico,
- Os pontos traçados três ou mais MSD longe são também outliers.
Avançando, nós vamos usar a primeira definição de outliers - através do IQR.
Como os outliers podem ser processados?
A maioria dos métodos de processamento de outliers são semelhantes aos métodos de processamento de NA - removendo as observações, transformando as observações, segmentando, imputando e outros.
- Remoção dos outliers. Nós removemos os valor atípicos se eles aparecem como resultado de um erro de entrada de dados ou se o número de outliers é muito pequeno. Nós também podemos cortar as extremidades da distribuição para remover os outliers. Por exemplo, nós podemos descartar 1% de cima e de baixo.
- Transformação e vinculação:
- a transformação de variáveis pode excluir os outliers (isto será analisado na próxima parte do artigo);
- o logaritmo natural diminui os casos de mudanças pelos valores extremos (isso também será discutido em detalhes na próxima parte do artigo);
- a discretização também é uma maneira de transformar uma variável (veja a próxima parte);
- nós também podemos usar a atribuição de peso para as observações (não discutiremos isso neste artigo).
Imputação. Os mesmos métodos que usamos para imputar valores indefinidos podem ser usados para imputar os outliers. Para isso, a média, a mediana e o modo podem ser usados. Antes de imputar os valores, é necessário estabelecer se o outlier é natural ou artificial. Se o outlier for artificial, ele pode ser imputado.
Se a amostra contiver um número significativo de outliers, elas devem ser analisadas separadamente em um modelo estatístico. Vamos discutir os métodos gerais utilizados para enfrentar os outliers. Eles são a remoção e a imputação.
Remoção dos outliers
Os outliers devem ser excluídos se forem causados pela entrada de dados, o processamento de dados ou se o número de outliers for muito pequeno (somente quando se identificam métricas de variáveis estatísticas).
Os dados de uma variável (ftlm, por exemplo) podem ser extraídos sem outliers da seguinte maneira:
evalq({dataSetClean$ftlm -> x
out.ftlm <- x[!x %in% boxplot.stats(x)$out]},
env)
Or:
evalq({dataSetClean$ftlm -> x
out.ftlm1 <- x[x > quantile(x, .25) - 1.5*IQR(x) &
x < quantile(x, .75) + 1.5*IQR(x)]},
env)
Eles são idênticos?
> evalq(all.equal(out.ftlm, out.ftlm1), env)
[1] TRUE
Quantos outliers existem no conjunto de dados?
> nrow(env$dataSetClean) - length(env$out.ftlm) [1] 402
Isto é o como o ftlm aparenta sem os outliers:
boxplot(env$out.ftlm, main = "ftlm without outliers", boxwex = 0.5)
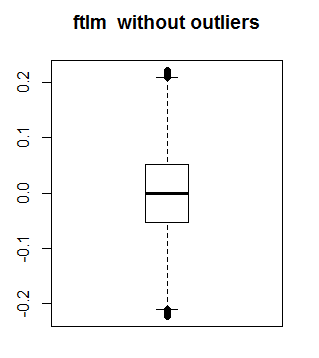
Fig. 10. ftlm sem outliers
O método descrito acima não é adequado para matrizes e matrizes de dados, pois cada variável em um dataframe pode ter um número diferente de valores atípicos. Um método de substituição de valores atípicos locais para NA seguido de métodos padrão de processamento de NA é adequado para tais amostras. A função que substituirá os outliers locais por NA é exibida abaixo:
#-------remove_outliers------------------------------- remove_outliers <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) y <- x y[x < (qnt[1] - H)] <- NA y[x > (qnt[2] + H)] <- NA y }
Vamos mudar dataSetClean em todas as variáveis, exceto em c(Data, Class), e os outliers para NA. Tendo feito isso, vamos ver como a distribuição do novo conjunto x.out:se altera.
evalq({
dataSetClean %>% select(-c(Data,Class)) %>% as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
remove_outliers(x[ ,i])
} -> x.out
colnames(x.out) <- colnames(x)
},
env)
par(mfrow = c(1, 1))
chart.Boxplot(env$x,
main = "x.out with outliers",
xlab = "")
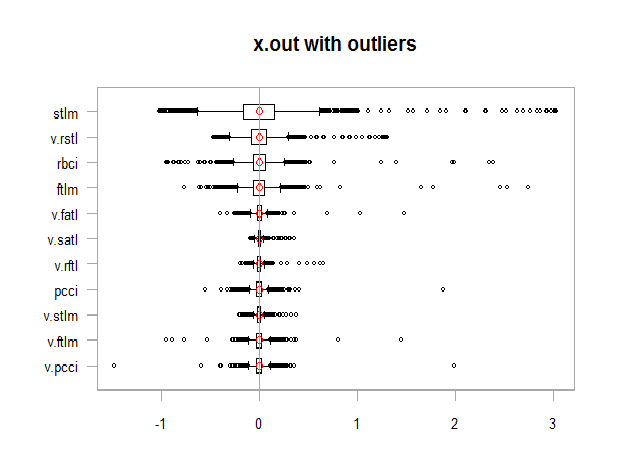
Fig. 11. Dados com outliers
chart.Boxplot(env$x.out, main = "x.out without outliers", xlab = "")
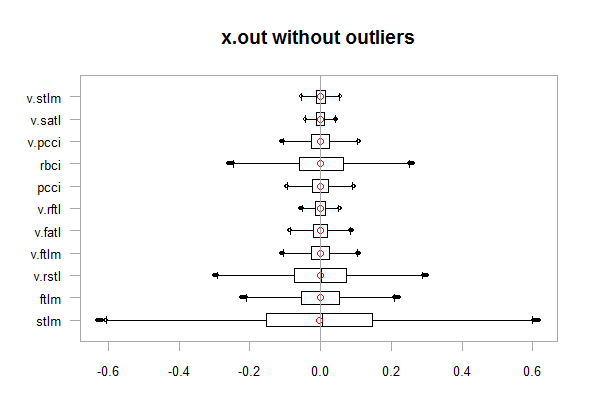
Fig.12. Dados sem outliers
Imputando o NA que apareceu em vez dos outliers
A imputação é uma substituição de valores que faltam, incorretos ou inválidos por outros valores. Os dados de entrada para treinamento do modelo devem conter apenas valores válidos. Você também pode:
- substituir NA pela média, mediana, mod (as características estatísticas do conjunto não mudarão)
- substituir os outliers superiores a 1,5*IQR por um percentil de 0,95 e os outliers menores que -1,5*IQR por um percentil de 0,05.
Vamos escrever uma função para executar a última versão da ação. Após a transformação ter sido feita, vamos dar uma olhada na distribuição:
#-------capping_outliers-------------------------------
capping_outliers <- function(x, na.rm = TRUE, ...) {
qnt <- quantile(x, probs = c(.25, .75),
na.rm = na.rm, ...)
caps <- quantile(x, probs = c(.05, .95),
na.rm = na.rm, ...)
H <- 1.5 * IQR(x, na.rm = na.rm)
y <- x
y[x < (qnt[1] - H)] <- caps[1]
y[x > (qnt[2] + H)] <- caps[2]
y
}
evalq({dataSetClean %>% select(-c(Data,Class)) %>%
as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
capping_outliers(x[ ,i])
} -> x.cap
colnames(x.cap) <- colnames(x)
},
env)
chart.Boxplot(env$x.cap,
main = "x.cap with capping outliers",
xlab = "")
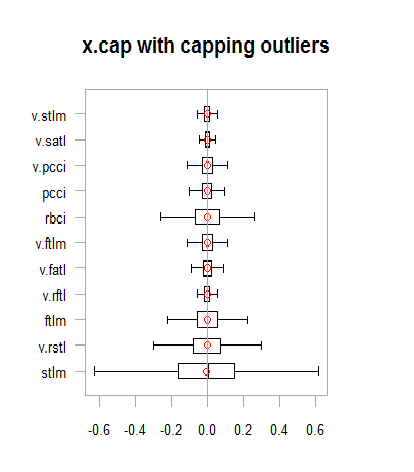
Fig.13. Conjunto de dados com outliers imputados
Consideremos a variação e covariação no tampão de DataSet. Isso é o mesmo que o dataSet, mas limpo e contendo outliers locais imputados. O número de variáveis (13) torna impossível colocá-las no mesmo gráfico, então elas devem ser divididas em dois grupos.
evalq(x.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetCap, env) require(GGally) evalq(ggpairs(dataSetCap, columns = 2:7, mapping = aes(color = Class), title = "PredCap1"), env)
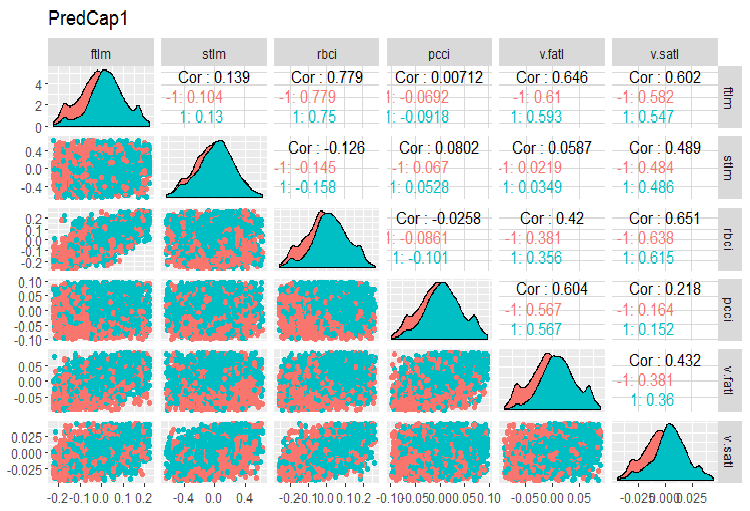
Fig.14. Variação e covariação da primeira parte do conjunto de dados com os outliers imputados.
E a segunda parte do conjunto:
evalq(ggpairs(dataSetCap, columns = 8:13, mapping = aes(color = Class), title = "PredCap2"), env)
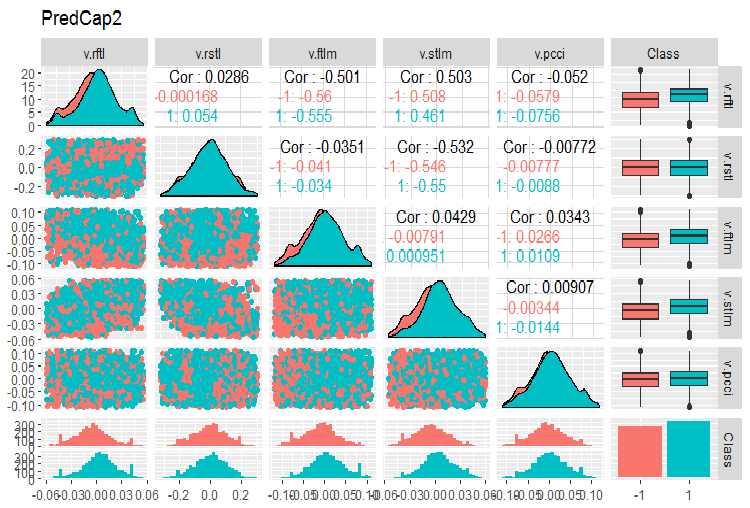
Fig.15. Variação e covariação da segunda parte do conjunto de dados com os outliers imputados
Como identificar os outliers globais?
Os outliers bidimensionais ou multidimensionais geralmente são identificados usando o índice de impacto ou proximidade. Várias distâncias são usadas para identificar os valores atípicos globais. Pacotes como DMwR, mvoutliers, Rlof podem ser usados para isso. Os outliers globais são avaliados com LOF (local outlier factor). Calcula e compara LOF para um conjunto com outliers x e um conjunto com outliers imputados x.cap.
##------DMwR2------------------- require(DMwR2) evalq(lof.x <- lofactor(x,10), env) evalq(lof.x.cap <- lofactor(x.cap,10), env) par(mfrow = c(1, 3)) boxplot(env$lof.x, main = "lof.x", boxwex = 0.5) boxplot(env$lof.x.cap, main = "lof.x.cap", boxwex = 0.5) hist(env$lof.x.cap, breaks = 20) par(mfrow = c(1, 1))
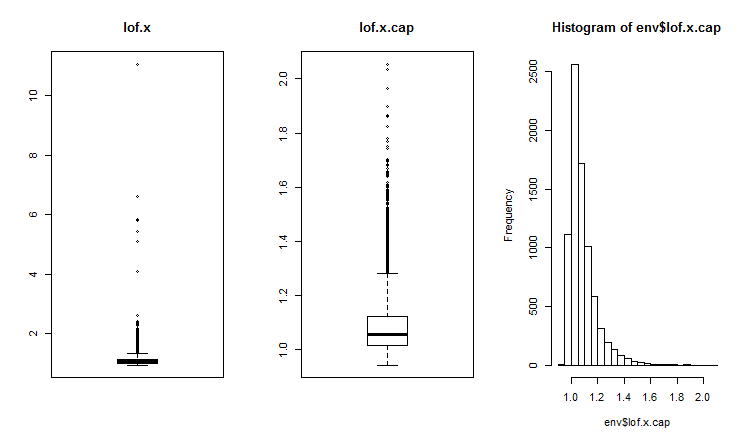
Fig.16. Fator outlier global para um conjunto de dados com outliers e um conjunto de dados com outliers imputados
A função lof() é implementada no pacote Rlof. ele encontra o fator outlier local [3] dos dados da matriz usando k vizinhos mais próximos. O fator outlier local (LOF) é a probabilidade de pertencer aos outliers que são calculados a cada observação. Com base nessa probabilidade, o usuário decide se a observação é um outlier.
O LOF leva em consideração a densidade local para identificar se a observação é um outlier. Esta é uma implementação mais eficiente do LOF usando outra estrutura de dados e funções de cálculo da distância para comparar com a função lofactor() disponível no pacote "dprep". Isto suportará vários valores de k que serão calculados simultaneamente, e várias medidas de distância além do padrão Euclidiano. Os cálculos são realizados simultaneamente em vários núcleos do processador. Vamos calcular o lofactor para os mesmos dois conjuntos (x e x.cap) para 5, 6, 7, 8, 9 e 10 vizinhos usando o método "minkowski" de cálculo da distância. Vamos desenhar os histogramas desses fatores.
require(Rlof) evalq(Rlof.x <- lof(x, c(5:10), cores = 2, method = 'minkowski'), env) evalq(Rlof.x.cap <- lof(x.cap, c(5:10), cores = 2, method = 'minkowski'), env) par(mfrow = c(2, 3)) hist(env$Rlof.x.cap[ ,6], breaks = 20) hist(env$Rlof.x.cap[ ,5], breaks = 20) hist(env$Rlof.x.cap[ ,4], breaks = 20) hist(env$Rlof.x.cap[ ,3], breaks = 20) hist(env$Rlof.x.cap[ ,2], breaks = 20) hist(env$Rlof.x.cap[ ,1], breaks = 20) par(mfrow = c(1, 1))
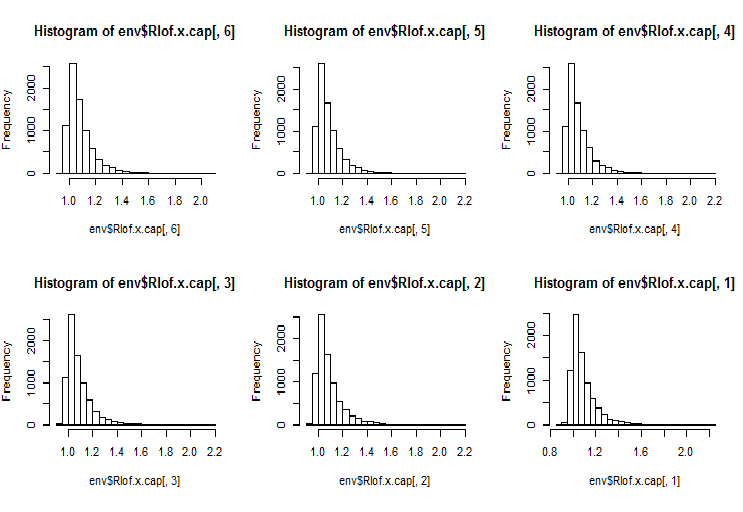
Fig.17. Fator outlier global para k vizinhos
Quase todas as observações estão dentro do alcance lofactor =1.6. Fora desta faixa:
> sum(env$Rlof.x.cap[ ,6] >= 1.6) [1] 32
Este é um número insignificante de valores aberrantes moderados para um conjunto desse tamanho.
Nota. Para identificar os limites de alcance, excedendo o que a observação será tratada como um outlier, deve-se usar um conjunto de dados de treinamento. O valor das variáveis do conjunto de dados de teste/validação é processado usando os parâmetros obtidos por meio do conjunto de treinamento. Quais parâmetros são estes? Estes são os limites upper = 1,5*IQR, lower = -1,5*IQR e cap = c (0,05, 0,95) percentil. Nós os usamos em nossos cálculos anteriores. Se fossem utilizados outros métodos de cálculo dos limites do intervalo e da imputação de outliers, eles devem ser definidos para o conjunto de dados de treinamento, guardados e armazenados para o processamento dos conjuntos de dados de validação e teste.
Vamos escrever a função que realizará os cálculos preliminares:
#-----prep.outlier-------------- prep.outlier <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) caps <- quantile(x, probs = c(.05, .95), na.rm = na.rm, ...) list(lower = qnt[1] - H, upper = qnt[2] + H, med = median(x), cap1 = caps[1], cap2 = caps[2]) }
Calcule os parâmetros necessários para identificar e imputar os outliers. Deixe o comprimento preliminar do conjunto de treinamento ser as primeiras 4000 barras e as seguintes 2000 barras serão usadas como o conjunto de dados de teste.
evalq(
{train <- x[1:4000, ]
foreach(i = 1:ncol(train), .combine = "cbind") %do% {
prep.outlier(train[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
#pre.outl %<>% t()
},
env)
Vejamos o resultado:
> env$pre.outl ftlm stlm rbci pcci lower.25% -0.2224942912 -0.59629203 -0.253231002 -9.902232e-02 upper.75% 0.2214486206 0.59242529 0.253529797 9.826936e-02 med -0.0001534451 0.00282525 -0.001184966 8.417127e-05 cap1.5% -0.1700418145 -0.40370452 -0.181326658 -6.892085e-02 cap2.95% 0.1676526431 0.39842675 0.183671973 6.853935e-02 v.fatl v.satl v.rftl v.rstl lower.25% -0.0900973332 -4.259328e-02 -0.0558921804 -0.2858430788 upper.75% 0.0888110249 4.178418e-02 0.0555115004 0.2889057397 med -0.0008581219 -2.130064e-05 -0.0001707447 -0.0001721546 cap1.5% -0.0658731640 -2.929586e-02 -0.0427927888 -0.1951978435 cap2.95% 0.0662353821 3.089833e-02 0.0411091859 0.1820803387 v.ftlm v.stlm v.pcci lower.25% -0.1115823754 -5.366875e-02 -0.1115905239 upper.75% 0.1108670403 5.367466e-02 0.1119495436 med -0.0003560178 -6.370034e-05 -0.0003173464 cap1.5% -0.0765431363 -3.686945e-02 -0.0765950814 cap2.95% 0.0789209957 3.614423e-02 0.0770439553
Como podemos ver, primeiro e terceiro quartis e mediana junto com o 5º e 95º percentil são definidos para cada variável no conjunto. Isso é tudo o que é necessário para identificar e processar os outliers.
Nós precisamos de uma função para processar os outliers de qualquer conjunto de dados usando os parâmetros previamente definidos. Possíveis formas de processamento: substituição de valores para NA, substituindo os outliers pela mediana e substituindo os outliers pelo percentil 5/95.
#---------treatOutlier--------------------------------- treatOutlier <- function(x, impute = TRUE, fill = FALSE, lower, upper, med, cap1, cap2){ if (impute) { x[x < lower] <- cap1 x[x > upper] <- cap2 return(x) } if (!fill) { x[x < lower | x > upper] <- NA return(x) } else { x[x < lower | x > upper] <- med return(x) } }
À medida que definimos os parâmetros necessários para o conjunto de treinamento, vamos processar os outliers do conjunto de treinamento, substituindo-os pelo 5º/95º percentil. Em seguida, processe os outliers do conjunto de dados de teste. Compare as distribuições nos conjuntos obtidos tendo desenhado três gráficos.
#------------
evalq(
{
foreach(i = 1:ncol(train), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = train[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> train.out
colnames(train.out) <- colnames(train)
},
env
)
#-------------
evalq(
{test <- x[4001:6000, ]
foreach(i = 1:ncol(test), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = test[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> test.out
colnames(test.out) <- colnames(test)
},
env
)
#---------------
evalq(boxplot(train, main = "train with outliers"), env)
evalq(boxplot(train.out, main = "train.out without outliers"), env)
evalq(boxplot(test.out, main = "test.out without outliers"), env)
#------------------------
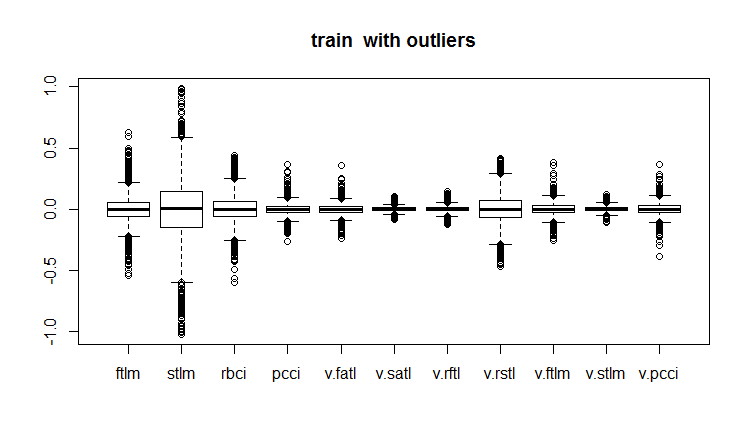
Fig.18. Conjunto de dados de treinamento com os outliers
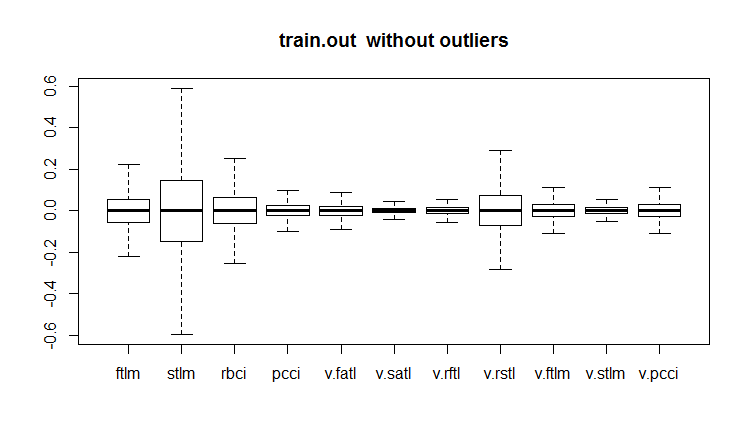
Fig.19. Conjunto de dados de treinamento com os outliers imputados
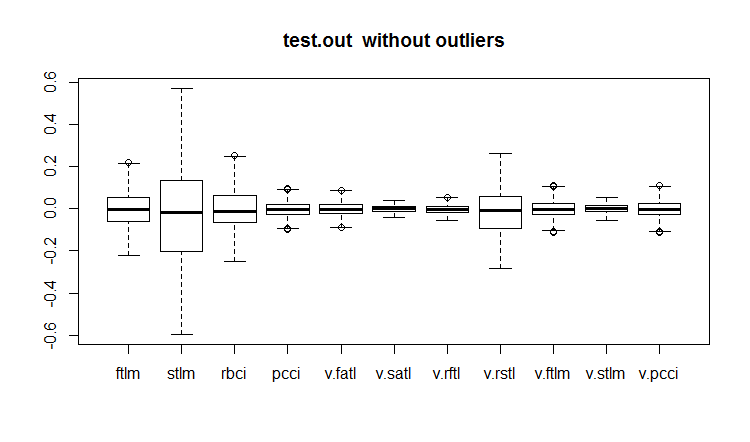
Fig.20. Conjunto de dados de teste com os outliers imputados
Nem todos os modelos são sensíveis aos outliers. Por exemplo, os modelos como a determinação de árvores (DT) e as florestas aleatórias (RF) são insensíveis a elas.
Ao definir e processar os outliers, alguns outros pacotes podem ser úteis. São eles: “univOutl”, “mvoutlier”, “outlier”, funModeling::prep.outlier().
3.3. Eliminação da assimetria
Skewness (assimetria) é a indicação da forma de distribuição. O cálculo do coeficiente de assimetria de uma variável é uma maneira geral de avaliar isso. Geralmente, a assimetria negativa mostra que a média é menor do que a mediana e a distribuição deixou a assimetria. Assimetria positiva indica que a média é maior do que a mediana e a distribuição tem uma assimetria correta.
Se a assimetria do preditor é 0, os dados são absolutamente simétricos.
Se a assimetria do preditor for menor que -1 ou superior a +1, os dados são significativamente distorcidos.
Se a assimetria do preditor estiver entre -1 e -1/2 ou +1 e +1/2, os dados são moderadamente distorcidos.
Se a assimetria do preditor for igual a -1/2 e +1/2, os dados são próximos de simétricos.
A afinidade certa pode ser corrigida tomando logaritmos e a assimetria esquerda usando a função exponencial.
Nós estabelecemos que as distorções assimétricas, outliers e outras estão conectadas. Vamos ver como o índice de assimetria mudou após a remoção e a imputação dos outliers.
evalq({
sk <- skewness(x)
sk.out <- skewness(x.out)
sk.cap <- skewness(x.cap)
},
env)
> env$sk
ftlm stlm rbci pcci v.fatl
Skewness 4.219857 1.785286 2.304655 6.491546 5.274871
v.satl v.rftl v.rstl v.ftlm v.stlm
Skewness 2.677162 3.954098 1.568675 1.207227 0.8516043
v.pcci
Skewness 3.031012
> env$sk.out
ftlm stlm rbci pcci
Skewness -0.04272076 -0.07893945 -0.02460354 0.01485785
v.fatl v.satl v.rftl v.rstl
Skewness 0.00780424 -0.02640635 -0.04663711 -0.04290957
v.ftlm v.stlm v.pcci
Skewness -0.0009597876 0.01997082 0.0007462494
> env$sk.cap
ftlm stlm rbci pcci
Skewness -0.03329392 -0.07911245 -0.02847851 0.01915228
v.fatl v.satl v.rftl v.rstl
Skewness 0.01412182 -0.02617518 -0.03412228 -0.04596505
v.ftlm v.stlm v.pcci
Skewness 0.008181183 0.009661169 0.002252508
Como você pode ver, tanto o conjunto com outliers removidos x.out e aquele com os outliers imputados x.cap são absolutamente simétricos e não requerem nenhuma correção.
Vamos avaliar a curtose também. A Curtose ou o coeficiente de pico é uma medida de pico de uma distribuição variável aleatória. A curtose de uma distribuição normal é 0. A curtose é positiva se o pico da distribuição em torno da expectativa matemática for acentuada e negativa se o pico for suave.
require(PerformanceAnalytics)
evalq({
k <- kurtosis(x)
k.out <- kurtosis(x.out)
k.cap <- kurtosis(x.cap)
},
env)
> env$k
ftlm stlm rbci pcci
Excess Kurtosis 84.61177 16.77141 45.01858 247.9795
v.fatl v.satl v.rftl v.rstl
Excess Kurtosis 145.9547 36.99944 74.4307 13.57613
v.ftlm v.stlm v.pcci
Excess Kurtosis 86.36448 23.06635 233.5408
> env$k.out
ftlm stlm rbci
Excess Kurtosis -0.003083449 -0.1668102 -0.1197043
pcci v.fatl v.satl
Excess Kurtosis -0.05113439 -0.02738558 -0.04341552
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.01219999 -0.1316499 -0.0287925
v.stlm v.pcci
Excess Kurtosis -0.1530424 -0.09950709
> env$k.cap
ftlm stlm rbci
Excess Kurtosis -0.2314336 -0.3075185 -0.2982044
pcci v.fatl v.satl
Excess Kurtosis -0.2452504 -0.2389486 -0.2331203
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.2438431 -0.2673441 -0.2180059
v.stlm v.pcci
Excess Kurtosis -0.2763058 -0.2698028
Os picos da distribuição no conjunto de dados inicial x são muito acentuados (a curtose é muito maior do que 0) no conjunto com os outliers removidos x.out, os picos são muito próximos do ponto normal de pico. O conjunto com outliers imputados possui picos mais suaves. Ambos os conjuntos de dados não requerem correções.
Aplicação
1. O arquivo DARCH12_1.zip contém os scripts para a primeira parte do artigo (dataRaw.R, PrepareData.R, FUNCTION.R) e um diagrama que representa a sessão Rstudio com os dados iniciais Cotir.RData. Carregue os dados no Rstudio e você poderá ver todos os scripts e trabalhar com eles. Você também pode fazer o download de Git /Part_I.
2. O arquivo ACTF.zip contém o artigo de V. Kravchuk "New Adaptive Method of Following the Tendency and Market Cycles"
3. O arquivo R_intro.zip contém materiais de referência em R.
Links
[1] A Systematic Approach on Data Pre-processing In Data Mining. COMPUSOFT, An international journal of advanced computer technology, 2 (11), November-2013 (Volume-II, Issue-XI)
[2] Outlier Detection Techniques.Hans-Peter Kriegel, Peer Kröger, Arthur Zimek. Ludwig-Maximilians-Universität München.Munich, Germany
[3] Breuning, M., Kriegel, H., Ng, R.T, and Sander. J. (2000). LOF: Identifying density-based local outliers. In Proceedings of the ACM SIGMOD International Conference on Management of Data.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/3486
Redes Neurais Profundas (Parte II). Desenvolvimento e seleção de preditores
Otimização Walk Forward em MetaTrader 5 feita com suas próprias mãos
Examinemos na prática o método adaptativo de acompanhamento do mercado
Classificador Bayesiano Ingênuo para sinais de um conjunto de indicadores
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso