
Tiefe neuronale Netzwerke (Teil I). Datenaufbereitung
DNN sind weit verbreitet und werden in verschiedenen Bereichen intensiv verwendet. Treffende Beispiele für die alltägliche Anwendung sind die Erkennung von Mustern, Spracherkennung und automatische Übersetzung. Die DNN werden auch im Trading verwendet, aus diesem Grund halte ich eine vertiefte Untersuchung von DNN vor dem Hintergrund einer schnellen Entwicklung des Algotradings für sehr nützlich und aussichtsreich.
In den letzten Jahren konnten Forscher viele neue Ideen, Methoden, Ansätze und Hypothesen hinsichtlich der Verwendung von DNN aufstellen und beweisen. In dieser Artikelserie werden der Entwicklungsstand und Hauptrichtungen des Themas betrachtet, verschiedene Ideen und Methoden werden anhand praktischer Experimente überprüft, darüber hinaus werden wir uns mit qualitativen Werten von DNN auseinandersetzen. In unserer Arbeit werden wir nur mehrschichtige voll verknüpfte neuronale Netze verwenden.
Die Artikelserie hat vier Schwerpunkte:
- Aufbereitung, Auswertung und Bestätigung von Inputdaten durch verschiedene Transformationen.
- Neue Möglichkeiten des Pakets darch (v.0.12). Flexibilität und erweiterte Möglichkeiten.
- Bestätigung der Ergebnisse der Prognose (Optimieren von Hyperparametern von DNN und Ensembles aus neuronalen Netzwerken).
- Grafische Möglichkeiten für die Kontrolle eines Expert Advisors sowohl während des Trainierens, als auch während der Arbeit.
Der vorliegende Artikel beschäftigt sich mit der Aufbereitung von Daten, die im Handelsterminal erhalten wurden, für die Verwendung im neuronalen Netzwerk.
Inhaltsverzeichnis
- Einleitung. Die Sprache R
- 1. Erstellung des Ausgangstadensatzes
- 2. Explorative Datenanalyse
- 3. Datenaufbereitung
- Anhang
- Links
Einleitung
Die Entwicklung, das Trainieren und Testen eines tiefen neuronalen Netzes besteht aus Schritten, die eine strenge Reihenfolge haben. Wie die Erstellung eines jeden Modells des Maschinellen Lernens kann die Erstellung eines DNN auch in zwei ungleiche Teile geteilt:
- Aufbereiten von Ein- und Ausgabedaten für Experimente;
- Erstellen, Trainieren, Testen und Optimieren von Parametern des Modells.
Die erste Phase nimmt die meiste Zeit der Umsetzung des Projekts in Anspruch: ca. 70%. Die Arbeitsergebnis des Modells hängt zu 80% von den Ergebnissen dieser Phase ab. Wie bekannt, "Garbage in, garbage out". Deswegen betrachten wir den Inhalt der Arbeit sehr ausführlich.
Um die Experimente zu wiederholen ist es notwendig, MRO 3.4.0 und Rstudio zu installieren. Wir werden auf die Installierung der Software nicht eingehen, weil es genug Informationen darüber im Internet und in den angehängten Dateien gibt.
Die Sprache R
Rufen wir uns einige wichtige Informationen über die Sprache R ins Gedächtnis. Das ist eine Programmiersprache sowie eine Umgebung für statistische Berechnungen und Zeichnen von Charts, die 1996 von neuseeländischen Wissenschaftlern Ross Ihaka und Robert Gentleman an der Universität Auckland entwickelt wurde. R ist ein GNU-Projekt, d.h. eine freie Software. Seine Philosophie läuft auf die folgenden Grundsätze (Freiheiten) hinaus:
- die Freiheit, Programme für jeden Zweck auszuführen (Freiheit 0);
- die Freiheit, die Funktionsweise eines Programms zu untersuchen, und es an seine Bedürfnisse anzupassen (Freiheit 1);
- die Freiheit, Kopien weiterzugeben und damit seinen Mitmenschen zu helfen (Freiheit 2);
- Freiheit, ein Programm zu verbessern, und die Verbesserungen an die Öffentlichkeit weiterzugeben, sodass die gesamte Gesellschaft profitiert.
Heute wird R hauptsächlich von "R Development Core Team" und dem im letzten Jahr gegründeten R Consortium verbessert und entwickelt. Die Liste der Mitglieder des Zusammenschlusses (IBM, Microsoft, Rstudio, Google, Mango, Oracle u.a.) zeugt von einer großen Unterstützung, einem starken Interesse an der Anwendung und von guten Aussichten der Sprache in der Zukunft.
Die Vorteile der Sprache R:
- Heutzutage ist die Sprache R de facto der Standard der statistischen Berechnungen.
- Die Sprache wird von der internationalen Wissenscahftsgemeinschaft entwickelt und unterstützt.
- Vielfältige Pakete hinsichtlich aller innovativen Richtungen des Data-Mining. Dabei vergehen zwischen der Veröffentlichung einer neuen Idee und deren Implementierung in R höchstens zwei Wochen.
- Zu guter Letzt ist seine Verwendung kostenlos.
1. Erstellung des Ausgangstadensatzes
"Die ganzen vorherigen, aktuellen und künftigen Preisbewegungen sind im Preis selbst enthalten"
Es gibt eine Vielzahl von Methoden (Paketen) für Aufbereitung, Auswertung und Auswahl von Prädiktoren. Eine Übersicht dieser Methoden ist in [1] angeführt. Ihre Vielfalt lässt sich durch die Vielfalt der Daten in der realen Welt erklären. Der verwendete Datentyp definiert die Methoden der Forschung und Verarbeitung.
Finanzdaten, die wir untersuchen, stellen hierarchische regelmäßige Zeitreihen dar, die "unendlich" und einfach zu extrahieren sind. Die Basis-Reihe — das sind OHLCV-Kurse für ein Symbols in einem konkreten Zeitrahmen.
Auf der Basis-Reihe beruhen alle weiteren Zeitreihen:
- nichtparametrische — zum Beispiel, x^2, sqrt(abs(x)), x^3, -x^2 usw.
- funktionell nichtparametrische — sin(2*n*x), ln(abs(x)), log(Pr(t)/Pr(t-1)) usw.
- parametrische — eine Vielzahl verschiedener Indikatoren, die hauptsächlich als Prädiktoren verwendet werden. Das können sowohl Oszillatoren als auch verschiedene Filter sein.
Als Zielvariable werden entweder Indikatoren, die Signale (Faktoren) erzeugen, oder eine Reihe von Bedingungen verwendet, deren Erfüllung ein Signal gibt.
1.1. Kurse
Die Kurse OHLC, Volume und time erhalten wir aus dem Terminal als Vektoren (o, h, l, cl, v, d). Schreiben wir eine Funktion, die die Vektoren vereinigt, die wir aus dem Terminal in dataFrame erhalten haben. Dabei ändern wir die Zeit des Anfangs des Balkens in POSIXct.
#---pr.OHLCV-------------------
pr.OHLCV <- function(d, o, h, l, cl, v){
# (d, o, h, l, cl, v)- vector
require('magrittr')
require('dplyr')
require('anytime')
price <- cbind(Data = rev(d),
Open = rev(o), High = rev(h),
Low = rev(l), Close = rev(cl),
Vol = rev(v)) %>% as.tibble()
price$Data %<>% anytime(., tz = "CET")
return(price)
}
Da wir die Vektoren der Kurse in die Umgebung env geladen haben, berechnen wir dataFrame pr und beseitigen unnötige Variablen aus der Umgebung env:
evalq({pr <- pr.OHLCV(Data, Open, High, Low, Close, Volume)
rm(list = c("Data", "Open", "High", "Low", "Close", "Volume"))
},
env)
Schauen wir, wie dataFrame am Anfang aussieht:
> head(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-01-10 11:00:00 122.758 122.893 122.746 122.859 2 2017-01-10 11:15:00 122.860 122.924 122.818 122.848 3 2017-01-10 11:30:00 122.850 122.856 122.705 122.720 4 2017-01-10 11:45:00 122.721 122.737 122.654 122.693 5 2017-01-10 12:00:00 122.692 122.850 122.692 122.818 6 2017-01-10 12:15:00 122.820 122.937 122.785 122.920 # ... with 1 more variables: Vol <dbl>
und am Ende:
> tail(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-05-05 20:30:00 123.795 123.895 123.780 123.888 2 2017-05-05 20:45:00 123.889 123.893 123.813 123.831 3 2017-05-05 21:00:00 123.833 123.934 123.825 123.916 4 2017-05-05 21:15:00 123.914 123.938 123.851 123.858 5 2017-05-05 21:30:00 123.859 123.864 123.781 123.781 6 2017-05-05 21:45:00 123.779 123.864 123.781 123.781 # ... with 1 more variables: Vol <dbl>
Wir haben also 8000 Balken von 10.01.2017 bis 05.05.2017. Fügen wir dem Datenrahmen pr abgeleitete Preise — Medium Price, Typical Price und Weighted Close hinzu.
evalq(pr %<>% mutate(., Med = (High + Low)/2, Typ = (High + Low + Close)/3, Wg = (High + Low + 2 * Close)/4, #CO = Close - Open, #HO = High - Open, #LO = Low - Open, dH = c(NA, diff(High)), dL = c(NA, diff(Low)) ), env)
1.2. Prädiktoren
Im Vergleich zu den vorherigen Experimenten, haben wir den Set von Prädiktoren vereinfacht. Ihre Rolle übernehmen die Zeitfilter FATL, SATL, RFTL, RSTL. Die Zeitfilter wurden im Artikel "New Adaptive Method of Following the Tendency and Market Cycles" von V. Kravchuk ausführlich beschrieben, den Sie im Anhang finden (s. das Kapitel "Neue Werkzeuge der technischen Analyse und deren Interpretation). Listen wir diese kurz auf.
- FATL — Fast Adaptive Trend Line;
- SATL — Slow Adaptive Trend Line;
- RFTL — Reference Fast Trend Line;
- RSTL — Reference Slow Trend Line.
Die Änderungsrate von FATL und SATL wird nach den Indikatoren FTLM (Fast Trend Line Momentum) und STLM (Slow Trend Line Momentum) überwacht.
Die weiteren benötigten technischen Werkzeuge sind zwei Oszillatoren — die Indexe RBCI und PCCI. Der Index RBCI, Range Bound Channel Index, ist ein Channel Index mit begrenzter Bandbreite, der mit einem Bandpassfilter berechnet wird (der Filter löscht einen tieffrequenten Trend und ein hochfrequentes Rauschen). Der Index PCCI — Perfect Commodity Channel Index.
Die Funktion, die die Zahlenfilter FATL, SATL, RFTL, RSTL, berechnet, sieht wie folgt aus:
#-----DigFiltr------------------------- DigFiltr <- function(X, type = 1){ # X - vector require(rowr) fatl <- c( +0.4360409450, +0.3658689069, +0.2460452079, +0.1104506886, -0.0054034585, -0.0760367731, -0.0933058722, -0.0670110374, -0.0190795053, +0.0259609206, +0.0502044896, +0.0477818607, +0.0249252327, -0.0047706151, -0.0272432537, -0.0338917071, -0.0244141482, -0.0055774838, +0.0128149838, +0.0226522218, +0.0208778257, +0.0100299086, -0.0036771622, -0.0136744850, -0.0160483392, -0.0108597376, -0.0016060704, +0.0069480557, +0.0110573605, +0.0095711419, +0.0040444064, -0.0023824623, -0.0067093714, -0.0072003400, -0.0047717710, 0.0005541115, 0.0007860160, 0.0130129076, 0.0040364019 ) rftl <- c(-0.0025097319, +0.0513007762 , +0.1142800493 , +0.1699342860 , +0.2025269304 , +0.2025269304, +0.1699342860 , +0.1142800493 , +0.0513007762 , -0.0025097319 , -0.0353166244, -0.0433375629 , -0.0311244617 , -0.0088618137 , +0.0120580088 , +0.0233183633, +0.0221931304 , +0.0115769653 , -0.0022157966 , -0.0126536111 , -0.0157416029, -0.0113395830 , -0.0025905610 , +0.0059521459 , +0.0105212252 , +0.0096970755, +0.0046585685 , -0.0017079230 , -0.0063513565 , -0.0074539350 , -0.0050439973, -0.0007459678 , +0.0032271474 , +0.0051357867 , +0.0044454862 , +0.0018784961, -0.0011065767 , -0.0031162862 , -0.0033443253 , -0.0022163335 , +0.0002573669, +0.0003650790 , +0.0060440751 , +0.0018747783) satl <- c(+0.0982862174, +0.0975682269 , +0.0961401078 , +0.0940230544, +0.0912437090 , +0.0878391006, +0.0838544303 , +0.0793406350 ,+0.0743569346 ,+0.0689666682 , +0.0632381578 ,+0.0572428925 , +0.0510534242,+0.0447468229, +0.0383959950, +0.0320735368, +0.0258537721 ,+0.0198005183 , +0.0139807863,+0.0084512448, +0.0032639979, -0.0015350359, -0.0059060082 ,-0.0098190256 , -0.0132507215, -0.0161875265, -0.0186164872, -0.0205446727, -0.0219739146 ,-0.0229204861 , -0.0234080863,-0.0234566315, -0.0231017777, -0.0223796900, -0.0213300463 ,-0.0199924534 , -0.0184126992,-0.0166377699, -0.0147139428, -0.0126796776, -0.0105938331 ,-0.0084736770 , -0.0063841850,-0.0043466731, -0.0023956944, -0.0005535180, +0.0011421469 ,+0.0026845693 , +0.0040471369,+0.0052380201, +0.0062194591, +0.0070340085, +0.0076266453 ,+0.0080376628 , +0.0083037666,+0.0083694798, +0.0082901022, +0.0080741359, +0.0077543820 ,+0.0073260526 , +0.0068163569,+0.0062325477, +0.0056078229, +0.0049516078, +0.0161380976 ) rstl <- c(-0.0074151919,-0.0060698985,-0.0044979052,-0.0027054278,-0.0007031702,+0.0014951741, +0.0038713513,+0.0064043271,+0.0090702334,+0.0118431116,+0.0146922652,+0.0175884606, +0.0204976517,+0.0233865835,+0.0262218588,+0.0289681736,+0.0315922931,+0.0340614696, +0.0363444061,+0.0384120882,+0.0402373884,+0.0417969735,+0.0430701377,+0.0440399188, +0.0446941124,+0.0450230100,+0.0450230100,+0.0446941124,+0.0440399188,+0.0430701377, +0.0417969735,+0.0402373884,+0.0384120882,+0.0363444061,+0.0340614696,+0.0315922931, +0.0289681736,+0.0262218588,+0.0233865835,+0.0204976517,+0.0175884606,+0.0146922652, +0.0118431116,+0.0090702334,+0.0064043271,+0.0038713513,+0.0014951741,-0.0007031702, -0.0027054278,-0.0044979052,-0.0060698985,-0.0074151919,-0.0085278517,-0.0094111161, -0.0100658241,-0.0104994302,-0.0107227904,-0.0107450280,-0.0105824763,-0.0102517019, -0.0097708805,-0.0091581551,-0.0084345004,-0.0076214397,-0.0067401718,-0.0058083144, -0.0048528295,-0.0038816271,-0.0029244713,-0.0019911267,-0.0010974211,-0.0002535559, +0.0005231953,+0.0012297491,+0.0018539149,+0.0023994354,+0.0028490136,+0.0032221429, +0.0034936183,+0.0036818974,+0.0038037944,+0.0038338964,+0.0037975350,+0.0036986051, +0.0035521320,+0.0033559226,+0.0031224409,+0.0028550092,+0.0025688349,+0.0022682355, +0.0073925495) if (type == 1) {k = fatl} if (type == 2) {k = rftl} if (type == 3) {k = satl} if (type == 4) {k = rstl} n <- length(k) m <- length(X) k <- rev(k) f <- rowr::rollApply(data = X, fun = function(x) {sum(x * k)}, window = n, minimum = n, align = "right") while (length(f) < m) { f <- c(NA,f)} return(f) }
Berechnen und fügen wir diese dem Datenrahmen pr hinzu
evalq(pr %<>% mutate(., fatl = DigFiltr(Close, 1), rftl = DigFiltr(Close, 2), satl = DigFiltr(Close, 3), rstl = DigFiltr(Close, 4) ), env)
Fügen wir die Oszillatoren FTLM, STLM, RBCI, PCCI, ihre ersten Differenzen und die ersten Differenzen zwischen den Zahlenfiltern dem Dataframe pr hinzu:
evalq(pr %<>% mutate(., ftlm = fatl - rftl, rbci = fatl - satl, stlm = satl - rstl, pcci = Close - fatl, v.fatl = c(NA, diff(fatl)), v.rftl = c(NA, diff(rftl)), v.satl = c(NA, diff(satl)), v.rstl = c(NA, diff(rstl)*10) ), env) evalq(pr %<>% mutate(., v.ftlm = c(NA, diff(ftlm)), v.stlm = c(NA, diff(stlm)), v.rbci = c(NA, diff(rbci)), v.pcci = c(NA, diff(pcci)) ), env)
1.3. Zielvariable
Als Indikator, der die Zielvariable erzeugt, werden wir den ZigZag() verwenden.
Die Funktion für dessen Berechnung erhält eine Zeitreihe und zwei Parameter: die minimale Länge einer Zigzag-Kurve (int oder double) und einen Preistyp für die Berechnung (Close, Med, Typ, Wd, mit (High, Low) ).
#------ZZ----------------------------------- par <- c(25, 5) ZZ <- function(x, par) { # x - vector require(TTR) require(magrittr) ch = par[1] mode = par[2] if (ch > 1) ch <- ch/(10 ^ (Dig - 1)) switch(mode, xx <- x$Close, xx <- x$Med, xx <- x$Typ, xx <- x$Wd, xx <- x %>% select(High,Low)) zz <- ZigZag(xx, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]} return(zz) }
Berechnen wir den ZigZag, die erste Differenz, das Vorzeichen der ersten Differenz und fügen wir diese dem Datenrahmen pr hinzu:
evalq(pr %<>% cbind(., zigz = ZZ(., par = par)), env) evalq(pr %<>% cbind(., dz = diff(pr$zigz) %>% c(NA, .)), env) evalq(pr %<>% cbind(., sig = sign(pr$dz)), env)
1.4. Ausgangsdatensatz
Fassen wir kurz zusammen, was und wie wir infolge der vorherigen Berechnungen erhalten haben.
Wir haben die Vektoren OHLCV und das Zeit-Label des Anfangs des Balkens auf М15 für EURJPY aus dem Terminal erhalten. Basierend auf diesen Daten wurde der Datenrahmen pr gebildet, zu welchem die Variablen FATL, SATL, RFTL, RSTL, FTLM, STLM, RBCI, PCCI und deren ersten Differenzen hinzugefügt wurden. Darüber hinaus wurde dem Datenrahmen der ZigZag mit der minimalen Länge der Zigzag-Kurve von 25 Punkten (4 Zeichen), seine erste Differenz und das Vorzeichen der ersten Differenz (-1,1), das als Signal verwendet wird.
Alle Daten wurden nicht in die globale Umgebung hochgeladen, sondern in die neue Umgebung env, in welcher wir alle weiteren Berechnungen durchführen werden. Solche Aufteilung erlaubt es, Datensätze verschiedener Symbole oder Zeitrahmen ohne Namenskonflikte bei der Berechnung zu verwenden.
Die Struktur des Datenrahmens pr ist unten angeführt. Die für die weiteren Berechnungen benötigten Variablen können da ausgewählt werden.
str(env$pr) 'data.frame': 8000 obs. of 30 variables: $ Data : POSIXct, format: "2017-01-10 11:00:00" ... $ Open : num 123 123 123 123 123 ... $ High : num 123 123 123 123 123 ... $ Low : num 123 123 123 123 123 ... $ Close : num 123 123 123 123 123 ... $ Vol : num 3830 3360 3220 3241 3071 ... $ Med : num 123 123 123 123 123 ... $ Typ : num 123 123 123 123 123 ... $ Wg : num 123 123 123 123 123 ... $ dH : num NA 0.031 -0.068 -0.119 0.113 ... $ dL : num NA 0.072 -0.113 -0.051 0.038 ... $ fatl : num NA NA NA NA NA NA NA NA NA NA ... $ rftl : num NA NA NA NA NA NA NA NA NA NA ... $ satl : num NA NA NA NA NA NA NA NA NA NA ... $ rstl : num NA NA NA NA NA NA NA NA NA NA ... $ ftlm : num NA NA NA NA NA NA NA NA NA NA ... $ rbci : num NA NA NA NA NA NA NA NA NA NA ... $ stlm : num NA NA NA NA NA NA NA NA NA NA ... $ pcci : num NA NA NA NA NA NA NA NA NA NA ... $ v.fatl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rftl: num NA NA NA NA NA NA NA NA NA NA ... $ v.satl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rstl: num NA NA NA NA NA NA NA NA NA NA ... $ v.ftlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.stlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.rbci: num NA NA NA NA NA NA NA NA NA NA ... $ v.pcci: num NA NA NA NA NA NA NA NA NA NA ... $ zigz : num 123 123 123 123 123 ... $ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ... $ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
Wählen wir alle vorher berechneten Prädiktoren in dataSet aus. Die Zielvariable sig wandeln wir in einen Faktor um und verschieben um einen Balken in die Zukunft.
evalq(dataSet <- pr %>% tbl_df() %>%
dplyr::select(Data, ftlm, stlm, rbci, pcci,
v.fatl, v.satl, v.rftl, v.rstl,
v.ftlm, v.stlm, v.rbci, v.pcci, sig) %>%
dplyr::filter(., sig != 0) %>%
mutate(., Class = factor(sig, ordered = F) %>%
dplyr::lead()) %>%
dplyr::select(-sig),
env)
Visuelle Datenanalyse
Zeichnen wir einen OHLC-Chart unter Verwendung des Pakets ggplot2. Nehmen wir die Daten für die letzten zwei Tage und zeichnen wir den Kurschart in Balken.
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + labs(title = "EURJPY Candlestick Chart", y = "Close Price", x = "") + theme_tq(), env)
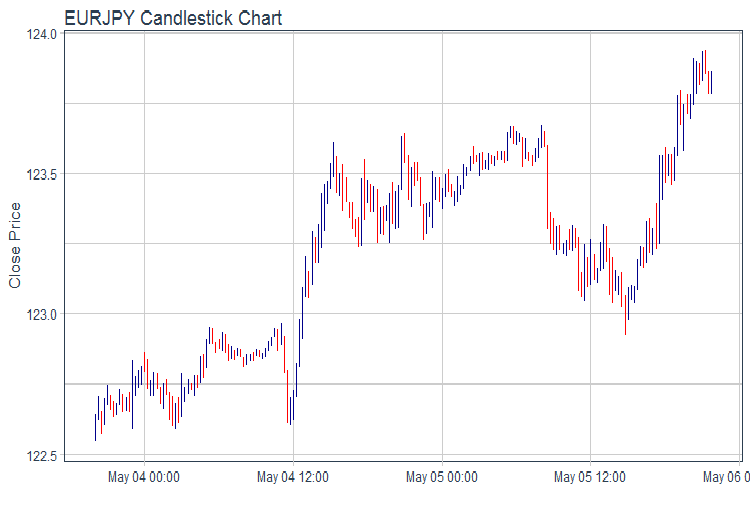
Abb.1. Kurschart
Zeichnen wir einen Chart von FATL, SATL, RFTL, RSTL und ZZ:
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + geom_line(aes(Data, fatl), color = "steelblue", size = 1) + geom_line(aes(Data, rftl), color = "red", size = 1) + geom_line(aes(Data, satl), color = "gold", size = 1) + geom_line(aes(Data, rstl), color = "green", size = 1) + geom_line(aes(Data, zigz), color = "black", size = 1) + labs(title = "EURJPY Candlestick Chart", subtitle = "Combining Chart Geoms", y = "Close Price", x = "") + theme_tq(), env)
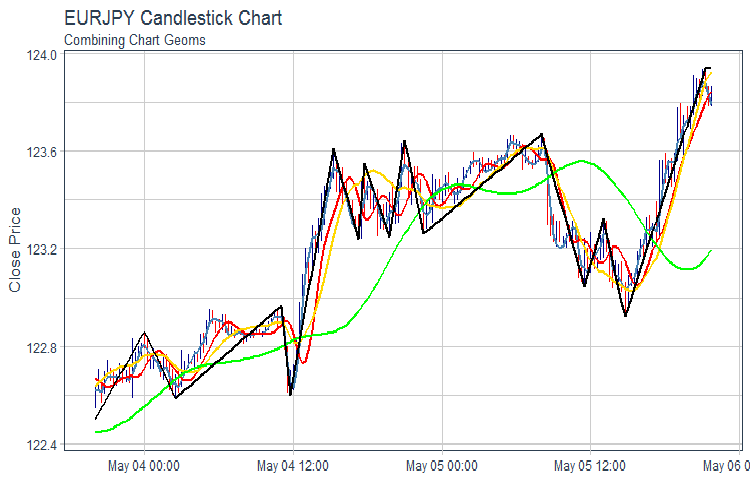
Abb.2. FATL, SATL, RFTL, RSTL und ZZ
Teilen wir die Oszillatoren in drei Gruppen für eine einfachere Anzeige auf.
require(dygraphs) evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, ftlm, stlm, rbci, pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator base") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "blue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
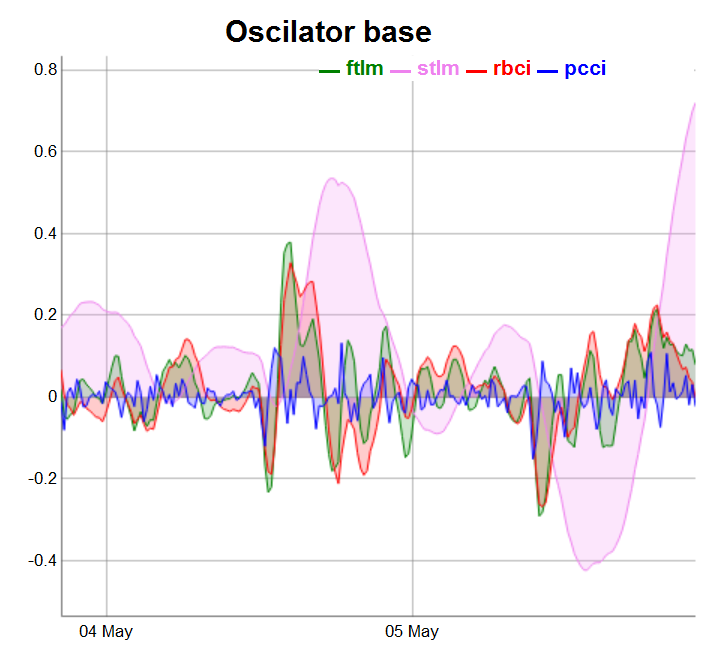
Abb.3. Basis-Oszillatoren
evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, v.fatl, v.satl, v.rftl, v.rstl) %>% tk_xts() %>% dygraph(., main = "Oscilator 2") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
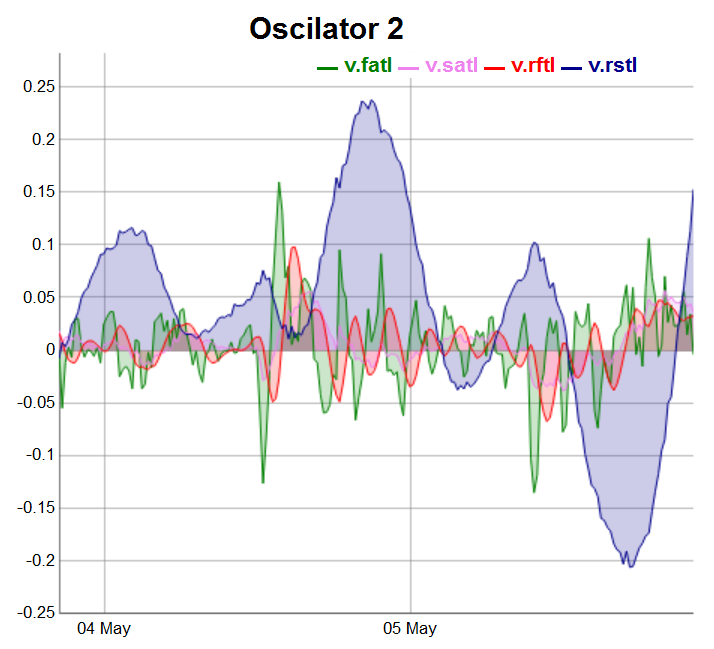
Abb.4. Oszillatoren der 2. Gruppe
Die Oszillatoren der dritten Gruppe werden auf den letzten 100 Balken eingezeichnet:
evalq(dataSet %>% tail(., 100) %>% tk_tbl %>% select(Data, v.ftlm, v.stlm, v.rbci, v.pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator 3") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
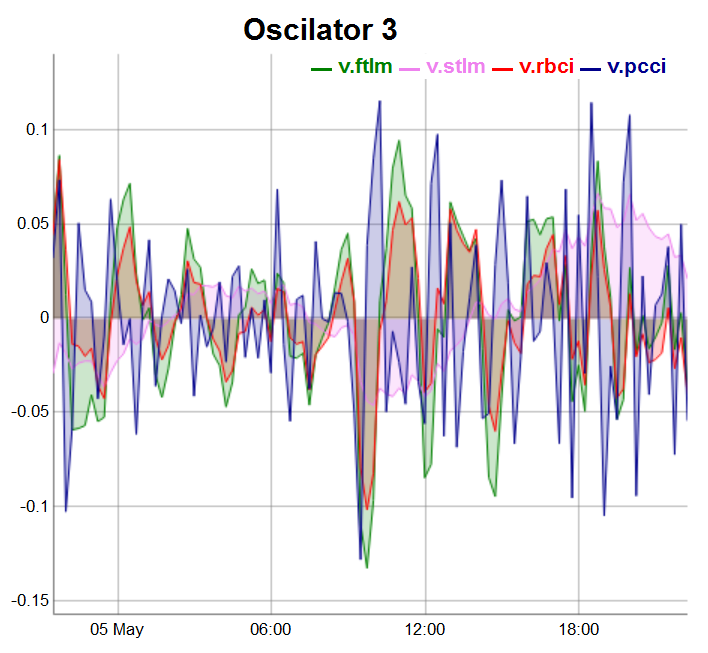
Abb.5. Oszillatoren der 3 Gruppe
2. Explorative Datenanalyse (EDA)
"There are no routine statistical questions, only questionable statistical routines." - Sir David R. Cox
“Viel besser eine ungefähre Antwort auf die richtige Frage, die oft vage ist, als eine exakte Antwort auf eine falsche Frage, die immer genauer formuliert werden kann.” — John Tukey
Wir verwenden die explorative Datenanalyse um, das Verständnis unserer Daten zu entwickeln. Die einfachste Methode ist Fragen als Werkzeug der Untersuchung zu verwenden. Wenn wir eine Frage stellen, konzentrieren wir uns auf einem bestimmten Datenteil. Dies hilft uns zu entscheiden, welche Charts, Modelle oder Transformationen wir verwenden sollten.
EDA ist ein kreativer Prozess. Wie in den meisten kreativen Prozessen ist der Schlüssel zu einer guten Frage, noch mehr Fragen zu stellen. Es ist schwierig solche Fragen am Anfang der Analyse zu stellen, weil wir noch nicht wissen, welche Schlussfolgerungen im Datensatz enthalten sind. Von der anderen Seite hebt jede neue Frage einen anderen Aspekt hervor und erhöht die Chance, eine Entdeckung zu machen. Wir können schnell zu dem interessantesten Teil der Stichprobe übergehen und durch konsequente Fragen die Situation klären.
Es gibt keine Regeln, welche Fragen wir stellen müssen, um die Untersuchung durchzuführen. Aber zwei Typen von Fragen werden immer hilfreich sein:
-
Welcher Typ haben die Änderungen in meinen Variablen?
- Welchen Typ haben die Kovariationen zwischen den Variablen?
Definieren wir den Hauptbegriff.
Variationen stellen die Variabilität der Werte einer Variablen von einer Dimension in die andere dar. Es gibt eine Vielzahl an Variationen im alltäglichen Leben. Wenn man eine kontinuierliche Variable sieben Mal hintereinander misst, erhält man sieben verschieden Ergebnisse. Das gilt auch wenn Sie konstante Größen messen (z.B. Lichtgeschwindigkeit). Jede der Dimensionen wird einen Fehler enthalten, der sich immer ändert. Die Variablen eines Typs können sich auch ändern, wenn man verschiedene konkrete Gegenstände (z.B. die Augenfarbe verschiedener Menschen) oder ein Gegenstand zu verschiedenen Zeitpunkten misst (z.B. das Energieniveau eines Elektrons zu unterschiedlichen Zeitpunkten). Jede Variable hat einen eigenen Charakter der Variationen, die eine interessante Information aufdecken können. Die beste Weise, diese Information zu verstehen, ist die Werteverteilung der Variablen zu visualisieren. Das ist gerade der Fall, wenn ein Bild mehr als tausend Worte sagt.
2.1. Gesamtstatistik
Die Gesamtstatistik unserer Zeitreihe kann man mithilfe der Funktion table.Stats()::PerformenceAnalitics verfolgen.
> table.Stats(env$dataSet %>% tk_xts()) Using column `Data` for date_var. ftlm stlm rbci pcci Observations 7955.0000 7908.0000 7934.0000 7960.0000 NAs 42.0000 89.0000 63.0000 37.0000 Minimum -0.7597 -1.0213 -0.9523 -0.5517 Quartile 1 -0.0556 -0.1602 -0.0636 -0.0245 Median -0.0001 0.0062 -0.0016 -0.0001 Arithmetic Mean 0.0007 0.0025 0.0007 0.0001 Geometric Mean -0.0062 NaN -0.0084 -0.0011 Quartile 3 0.0562 0.1539 0.0675 0.0241 Maximum 2.7505 3.0407 2.3872 1.8859 SE Mean 0.0014 0.0033 0.0015 0.0006 LCL Mean (0.95) -0.0020 -0.0040 -0.0022 -0.0010 UCL Mean (0.95) 0.0034 0.0090 0.0035 0.0012 Variance 0.0152 0.0858 0.0172 0.0026 Stdev 0.1231 0.2929 0.1311 0.0506 Skewness 4.2129 1.7842 2.3037 6.4718 Kurtosis 84.6116 16.7471 45.0133 247.4208 v.fatl v.satl v.rftl v.rstl Observations 7959.0000 7933.0000 7954.0000 7907.0000 NAs 38.0000 64.0000 43.0000 90.0000 Minimum -0.3967 -0.0871 -0.1882 -0.4719 Quartile 1 -0.0225 -0.0111 -0.0142 -0.0759 Median -0.0006 0.0003 0.0000 0.0024 Arithmetic Mean 0.0002 0.0002 0.0002 0.0011 Geometric Mean -0.0009 0.0000 -0.0003 -0.0078 Quartile 3 0.0220 0.0110 0.0138 0.0751 Maximum 1.4832 0.3579 0.6513 1.3093 SE Mean 0.0005 0.0002 0.0003 0.0015 LCL Mean (0.95) -0.0009 -0.0003 -0.0005 -0.0020 UCL Mean (0.95) 0.0012 0.0007 0.0009 0.0041 Variance 0.0023 0.0005 0.0009 0.0188 Stdev 0.0483 0.0219 0.0308 0.1372 Skewness 5.2643 2.6705 3.9472 1.5682 Kurtosis 145.8441 36.9378 74.4182 13.5724 v.ftlm v.stlm v.rbci v.pcci Observations 7954.0000 7907.0000 7933.0000 7959.0000 NAs 43.0000 90.0000 64.0000 38.0000 Minimum -0.9500 -0.2055 -0.6361 -1.4732 Quartile 1 -0.0280 -0.0136 -0.0209 -0.0277 Median -0.0002 -0.0001 -0.0004 -0.0002 Arithmetic Mean 0.0000 0.0001 0.0000 0.0000 Geometric Mean -0.0018 -0.0003 -0.0009 NaN Quartile 3 0.0273 0.0143 0.0207 0.0278 Maximum 1.4536 0.3852 1.1254 1.9978 SE Mean 0.0006 0.0003 0.0005 0.0006 LCL Mean (0.95) -0.0012 -0.0005 -0.0009 -0.0013 UCL Mean (0.95) 0.0013 0.0007 0.0009 0.0013 Variance 0.0032 0.0007 0.0018 0.0034 Stdev 0.0561 0.0264 0.0427 0.0579 Skewness 1.2051 0.8513 2.0643 3.0207 Kurtosis 86.2425 23.0651 86.3768 233.1964
Was wir anhand dieser Tabelle sehen wir:
- Alle Prädiktoren haben eine (relativ) kleine Anzahl undefinierter Variablen NA.
- Alle Prädiktoren haben eine stark ausgeprägte Rechtsschiefe (skewness).
- Alle Prädiktoren haben eine hohe Kurtosis (kurtosis).
2.2. Visualisierung der Gesamtstatistik
“Der größte Wert eines Bildes besteht darin, dass es uns darauf aufmerksam macht, was wir nie erwartet haben zu sehen”. — John Tukey
Schauen wir uns die Variation und die Kovariation unserer Variablen im Datensatz dataSet an. Da die Anzahl der Variablen (14) es nicht erlaubt, diese in einem Chart zu platzieren, teilen wir sie in drei Gruppen auf.
require(GGally) evalq(ggpairs(dataSet, columns = 2:6, mapping = aes(color = Class), title = "DigFilter1"), env)
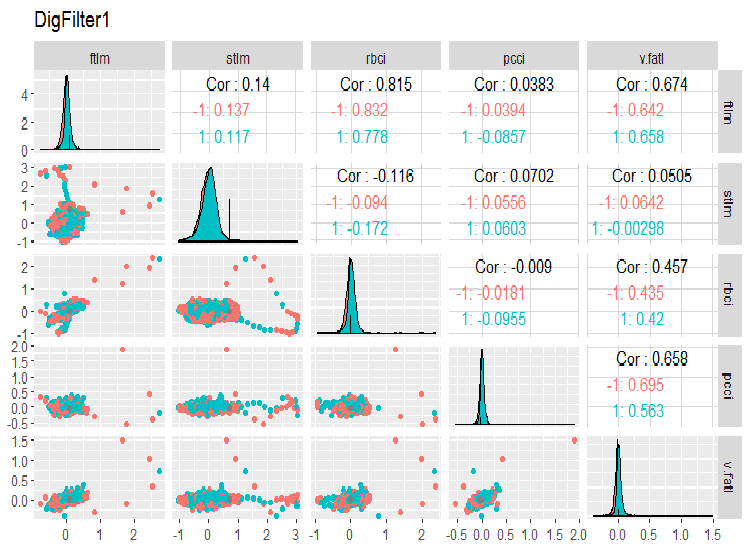
Abb. 6. Die erste Gruppe der Prädiktoren
evalq(ggpairs(dataSet, columns = 7:10, mapping = aes(color = Class), title = "DigFilter2"), env)
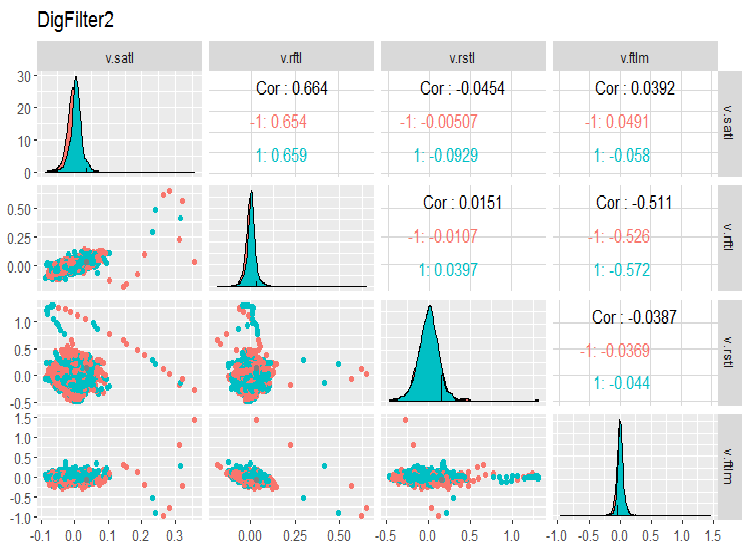
Abb. 7. Die zweite Gruppe der Prädiktoren
evalq(ggpairs(dataSet, columns = 11:14, mapping = aes(color = Class), title = "DigFilter3"), env)
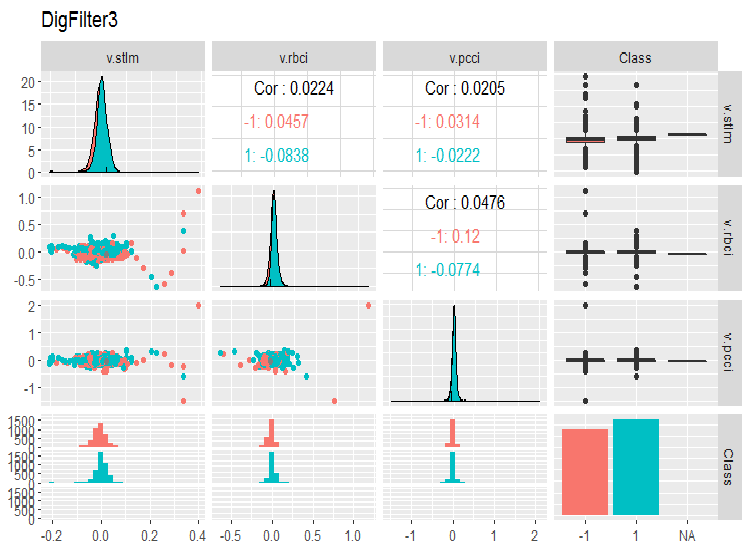
Abb. 8. Die dritte Gruppe der Prädiktoren
Was wir in den Charts sehen:
- alle Prädiktoren haben eine Verteilungsform, die nahe an der normalen ist, aber mit einer stark ausgeprägten Rechtsschiefe;
- alle Prädikatoren haben einen kleinen Interquartilsabstand (IQR);
- alle Prädiktoren haben erhebliche Ausreißer;
- die Anzahl der Beispiele auf den zwei Ebenen der Zielvariablen "Class" unterscheidet sich ein wenig von einander.
3. Datenaufbereitung
In der Regel besteht die Datenaufbereitung aus sieben Schritten:
- “imputation” — Entfernen oder Imputation fehlender/undefinierter Daten;
- “variance” — Entfernen der Variablen mit der Null- oder Nahe-Null-Varianz;
- “split” — Aufteilen des Datensatzes in train/valid/test;
- “scaling” — Skalieren des Bereichs der Variablen;
- “outliers” — Entfernen oder Imputation von Ausreißern;
- “sampling” — Korrigieren des Ungleichgewichts der Klassen;
- “denoise” — Entfernen oder Umdefinieren vom Rauschen;
- “selection” — Selektion irrelevanter Prädiktoren.
3.1. Bereinigen von Daten
Die erste Phase der Aufbereitung von Ausgangsdaten stellt das Entfernen oder die Imputation undefinierter Werte und Lücken in den Daten dar. Obwohl viele Modelle die Verwendung undefinierter Daten (NA) und fehlender Daten in Datensätzen zulassen, ist es besser, diese vor den Manipulationen zu entfernen. Diese Operation wird für den vollen Datensatz unabhängig vom verwendeten Modell durchgeführt.
Die Gesamtstatistik für unsere Rohdaten weist darauf hin, dass NA im Datensatz vorhanden sind. Das sind künstliche A, die sich bei der Berechnung digitaler Filter gebildet haben. Ihre Anzahl ist relativ klein, deswegen kann man sie entfernen. Wir haben bereits den Datensatz dataSet erhalten, der für die weitere Verarbeitung bereit ist. Bereinigen wir die Daten.
Im Allgemeinen versteht man unter einer "Bereinigung" folgendes:
- Entfernen von Prädiktoren mit einer Null- oder Nahe-Null-Varianz (method = c(“zv”, “nzv”));
- Entfernen stark korrelierter Variablen. Der Grenzwert der Korrelation wird von Nutzer gesetzt (method = “corr”), standardmäßig ist er gleich 0.9. Diese Phase ist nicht immer nötig, das hängt von den weiteren Methoden der Umwandlung ab;
- Entfernen von Prädiktoren, die nur einen einmaligen Wert in einer beliebigen Klasse haben (method = “conditionalX”).
Alle diese Operationen sind in der Funktion preProcess()::caret durch die oben angeführten Methoden implementiert und werden für den vollen Datensatz vor der Aufteilung in Einlern- und Testdatensätze durchgeführt.
require(caret)
evalq({preProClean <- preProcess(x = dataSet,method = c("zv", "nzv", "conditionalX", "corr"))
dataSetClean <- predict(preProClean, dataSet %>% na.omit)},
env)
Schauen wir, ob es entfernte Prädikatoren gibt, und was nach dem Bereinigen übrig geblieben ist:
> env$preProClean$method$remove #[1] "v.rbci" > dim(env$dataSetClean) [1] 7906 13 > colnames(env$dataSetClean) [1] "Data" "ftlm" "stlm" "rbci" "pcci" [6] "v.fatl" "v.satl" "v.rftl" "v.rstl" "v.ftlm" [11] "v.stlm" "v.pcci" "Class"
3.2. Erkennung und Verarbeitung von Ausreißern (outliers)
Probleme mit der Datenqualität, solche wie Schiefe oder Ausreißer, hängen oft voneinander ab. Dies macht eine vorläufige Verarbeitung aufwändig und erschwert die Aufgabe, Zusammenhänge und Tendenzen in der Stichprobe festzustellen.
Was ist ein Ausreißer?
Definieren wir den Begriff: unter einem Ausreißer verstehen wir eine Beobachtung, die zu groß oder zu klein im Vergleich zu den meisten anderen Beobachtungen ist. Eine gründliche Klassifikation von Ausreißern sowie Methoden deren Erkennung und Verarbeitung ist in [2] angeführt.
Typen der Ausreißer
Ausreißer verzerren die Verteilung von Variablen und die anhand solcher Daten trainierten Modelle. Es gibt eine Vielzahl von Methoden für die Erkennung und Verarbeitung von Ausreißern. Sie hängen davon ab, ob wir den Ausreißer global oder lokal identifizieren. Lokale Ausreißer stellen Ausreißer einer Variablen dar. Globale Ausreißer sind Ausreißer in einem mehrdimensionalen Raum, der durch eine Matrix oder einen Datenrahmen definiert wird.
Was verursacht Ausreißer?
Alle Ausreißer kann man nach ihrem Ursprung aufteilen:
Künstliche
- Eingabefehler — Fehler, die während des Sammelns, Schreibens oder der Verarbeitung von Daten auftreten;
- experimentelle Fehler;
- Stichprobenfehler.
Natürliche — Ausreißer, die durch die Natur der Variablen bedingt sind.
Welche Auswirkungen haben Ausreißer?
Die Ausreißer können die Ergebnisse der Datenanalyse oder einer statistischen Modellierung erheblich beeinträchtigen: sie erhöhen die Fehlervarianz und reduzieren die Leistung der statistischen Tests; wenn die Ausreißer nicht zufällig verteilt wurden, können sie auch die Normalität reduzieren; darüber hinaus können sie die grundlegenden Annahmen der Regressionsanalyse, Varianzanalyse und anderer statistischer Annahmen des Modells beeinflussen.
Wie kann man lokale Ausreißer erkennen?
Am häufigsten werden die Ausreißer durch das Visualisieren von Daten ermittelt. Eine einfache und breit verwendete Methode ist boxplot. Schauen wir uns zum Beispiel den Prädiktor ftlm an:
evalq(ggplot(dataSetClean, aes(x = factor(0),
y = ftlm,
color = 'red')) +
geom_boxplot() + xlab("") +
scale_x_discrete(breaks = NULL) +
coord_flip(),
env)
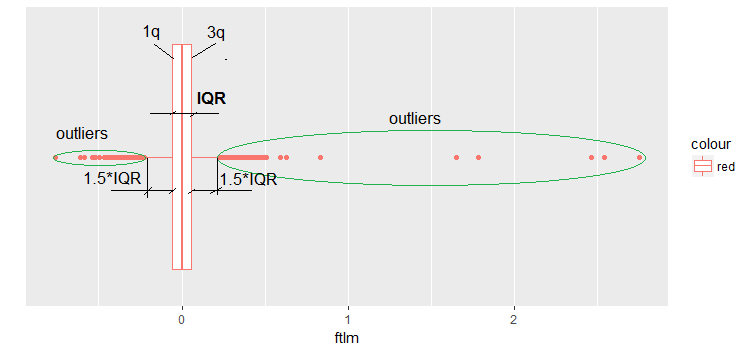
Abb.9. Boxplot ftlm
Erläuterungen zum Bild:
IQR — Interquartilsabstand, oder der Abstand zwischen dem ersten und dritten Quartil.
In diesem Zusammenhang gibt es mehrere Definitionen von Ausreißern:
- Jeder Wert, der kleiner als -1.5*IQR und größer +1.5*IQR ist, ist ein Ausreißer. Manchmal wird der Koeffizient auf 2 oder 3 gesetzt. Alle Werte zwischen 1.5*IQR und 3*IQR werden als "milde" Ausreißer bezeichnet, alle Werte, die oberhalb von 3*IQR liegen, sind extreme Ausreißer.
- Jeder Wert außerhalb des Bereichs vom 5. und 95. Perzentil kann als Ausreißer bezeichnet werden.
- Punkte mit einem Abstand von drei Standardabweichungen und mehr sind auch Ausreißer.
Weiterhin werden wir die erste Definition des Ausreißers verwenden (über IQR).
Wie werden Ausreißer verarbeitet?
Die meisten Methoden für die Verarbeitung von Ausreißern sind ähnlich den Methoden für die Verarbeitung undefinierter Werte NA: Entfernen, Umwandeln, Aufteilen, Imputation und andere statistische Methoden.
- Entfernen von Ausreißern: wir entfernen die Werte von Ausreißern, wenn sie infolge eines Eingabefehlers oder eines Verarbeitungsfehlers auftreten oder wenn es zu wenige Ausreißer gibt. Darüber hinaus können wir die Verteilung an beiden Enden schneiden, um Ausreißer zu entfernen. Zum Beispiel, jeweils 1% von oben und von unten zu entfernen.
- Transformation und Binning (Gruppieren von Werten in Intervalle):
- eine Transformation der Variablen kann Ausreißer ausschließen (dies wird im nächsten Abschnitt des Artikels betrachtet);
- natürlicher Logarithmus reduziert die Änderungen, die die Extremwerte verursachen (ebenso im nächsten Abschnitt betrachtet);
- Diskretisierung ist eine weitere Art, eine Variable umzuwandeln (s. den nächsten Abschnitt);
- wir können auch die Zuweisung von Gewichten für verschiedene Beobachtungen verwenden (dieses Thema wird nicht betrachtet).
Imputation: die gleichen Methoden, die wir für die Imputation undefinierter Werte verwenden, können auf Ausreißer angewandt werden. Man kann Mittelwert, Medianwert oder Modalwert verwenden. Vor der Imputation eines Wertes, müssen wir feststellen, ob wir mit einem natürlichen oder künstlichen Ausreißer zu tun haben. Wenn es um einen künstlichen Ausreißer geht, kann er imputiert werden.
Wenn es in einer Stichprobe eine erhebliche Anzahl von Ausreißern gibt, müssen wir diese separat in einem statistischen Modell betrachten. Hier werden wir nur von allgemeinen Methoden sprechen: Entfernen und Imputieren.
Entfernen von Ausreißern
Wir entfernen die Werte von Ausreißern, wenn sie infolge eines Eingabefehlers oder eines Verarbeitungsfehlers aufgetreten sind oder wenn es zu wenige Ausreißer gibt (nur beim Bestimmen statistischer Messwerte der Variablen).
Die Daten einer Variablen (z.B. ftlm) können ohne Ausreißer wie folgt extrahiert werden:
evalq({dataSetClean$ftlm -> x
out.ftlm <- x[!x %in% boxplot.stats(x)$out]},
env)
Oder so:
evalq({dataSetClean$ftlm -> x
out.ftlm1 <- x[x > quantile(x, .25) - 1.5*IQR(x) &
x < quantile(x, .75) + 1.5*IQR(x)]},
env)
Sind sie gleich?
> evalq(all.equal(out.ftlm, out.ftlm1), env)
[1] TRUE
Wie viele Ausreißer sind im Datensatz?
> nrow(env$dataSetClean) - length(env$out.ftlm) [1] 402
Schauen wir, wie ftlm ohne Ausreißer aussieht:
boxplot(env$out.ftlm, main = "ftlm without outliers", boxwex = 0.5)
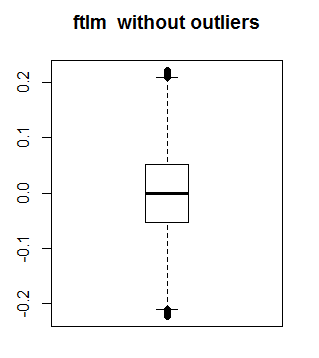
Abb. 10. ftlm ohne Ausreißer
Die oben beschriebene Methode kann nicht für Matrizes und Dataframes verwendet werden, denn jede Variable in einem Dataframe kann verschiedene Anzahl von Ausreißern haben. Für solche Stichproben eignet sich die Methode der Ersetzung lokaler Ausreißer durch NA mit der weiteren Verwendung von Standardmethoden für die Verarbeitung von NA. Schreiben wir eine Funktion, die lokale Ausreißer durch NA ersetzt:
#-------remove_outliers------------------------------- remove_outliers <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) y <- x y[x < (qnt[1] - H)] <- NA y[x > (qnt[2] + H)] <- NA y }
In unserem Datensatz dataSetClean ersetzen wir Ausreißer durch NA in allen Variablen außer c(Data, Class) und schauen, wie sich die Verteilung des erhaltenen Satzes x.out ändert:
evalq({
dataSetClean %>% select(-c(Data,Class)) %>% as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
remove_outliers(x[ ,i])
} -> x.out
colnames(x.out) <- colnames(x)
},
env)
par(mfrow = c(1, 1))
chart.Boxplot(env$x,
main = "x.out with outliers",
xlab = "")
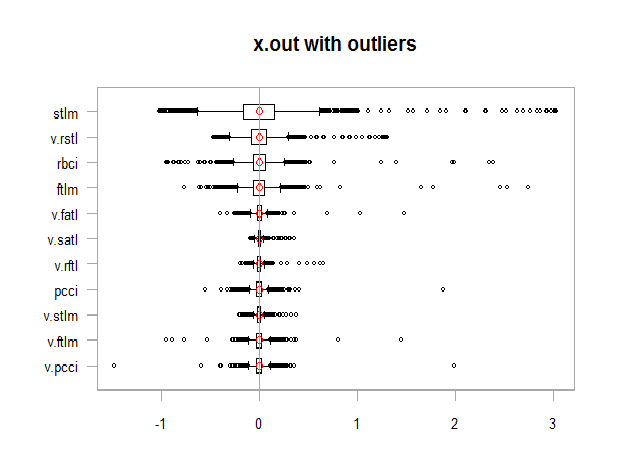
Abb. 11. Daten mit Ausreißern
chart.Boxplot(env$x.out, main = "x.out without outliers", xlab = "")
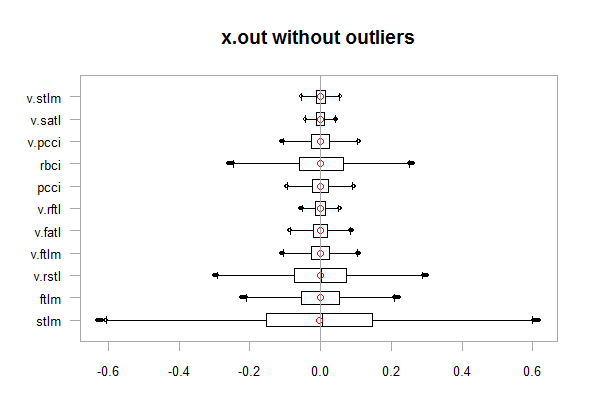
Abb.12. Daten ohne Ausreißer
Imputation von NA, die die Ausreißer ersetzten
Unter Imputation versteht man die Ersetzung fehlender, falscher oder ungültiger Werte durch andere Werte. Die Input-Daten für das Trainieren des Modells dürfen nur gültige Werte beinhalten. Mögliche Varianten:
- wir ersetzen NA durch mean, mediana, mod (dabei ändern sich die statistischen Charakteristiken des Datensatzes nicht)
- wir ersetzen die Ausreißer, die größer als 1.5*IQR sind, durch 0.95 Perzentil, und die Ausreißer, die kleiner als - 1.5*IQR sind, durch 0.05 Perzentil.
Schreiben wir eine Funktion, die die letzte Variante umsetzt, und schauen wir uns die Verteilung nach der Umwandlung an:
#-------capping_outliers-------------------------------
capping_outliers <- function(x, na.rm = TRUE, ...) {
qnt <- quantile(x, probs = c(.25, .75),
na.rm = na.rm, ...)
caps <- quantile(x, probs = c(.05, .95),
na.rm = na.rm, ...)
H <- 1.5 * IQR(x, na.rm = na.rm)
y <- x
y[x < (qnt[1] - H)] <- caps[1]
y[x > (qnt[2] + H)] <- caps[2]
y
}
evalq({dataSetClean %>% select(-c(Data,Class)) %>%
as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
capping_outliers(x[ ,i])
} -> x.cap
colnames(x.cap) <- colnames(x)
},
env)
chart.Boxplot(env$x.cap,
main = "x.cap with capping outliers",
xlab = "")
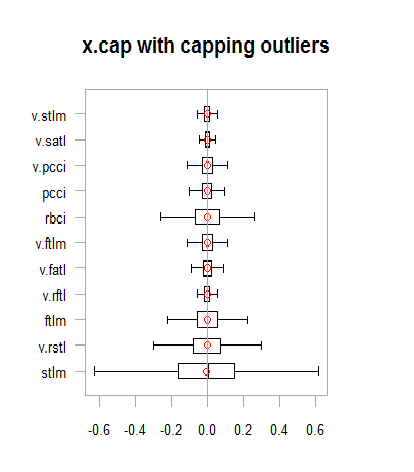
Abb.13. Datensatz mit imputierten Ausreißern
Schauen wir auf die Variation und die Kovariation unserer Variablen im Datensatz dataSetCap (das ist der gleiche Datensatz dataSet, aber bereinigt und mit imputierten lokalen Ausreißern). Da die Anzahl der Variablen (13) es nicht erlaubt, diese in einem Chart zu platzieren, teilen wir diese in drei Gruppen auf.
evalq(x.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetCap, env) require(GGally) evalq(ggpairs(dataSetCap, columns = 2:7, mapping = aes(color = Class), title = "PredCap1"), env)
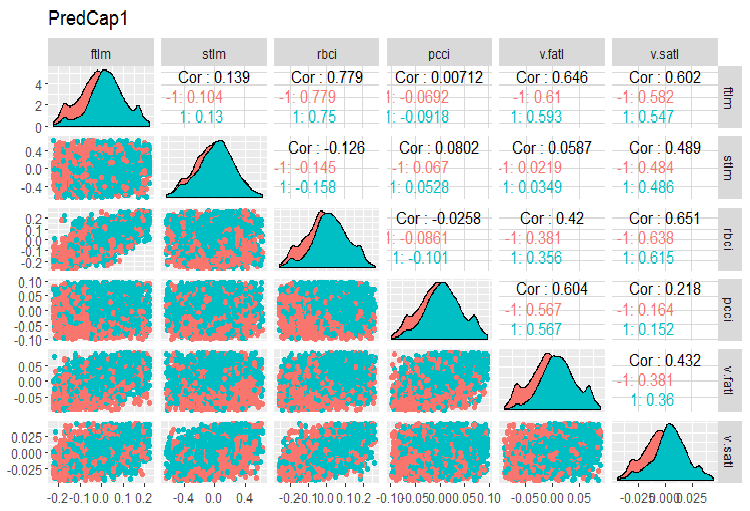
Abb.14. Variation und Kovariation des ersten Teils des Datensatzes mit imputierten Ausreißern.
Der zweite Teil des Datensatzes:
evalq(ggpairs(dataSetCap, columns = 8:13, mapping = aes(color = Class), title = "PredCap2"), env)
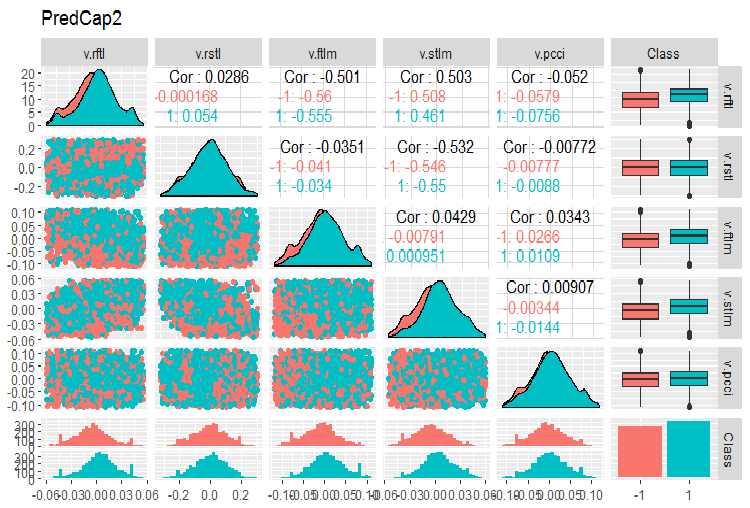
Abb.15. Variation und Kovariation des zweiten Teils des Datensatzes mit imputierten Ausreißern
Wie kann man globale Ausreißer erkennen?
Zwei- und mehrdimensionale Ausreißer werden gewöhnlich mithilfe des Einfluss- oder Distanz-Index. Um globale Ausreißer festzustellen, werden verschiedene Abstände verwendet. Wir können dafür mehrere Pakete, z.B. DMwR, mvoutliers, Rlof, verwenden. Globale Ausreißer werden mithilfe von LOF (local outlier factor) bewertet. Berechnen und vergleichen wir LOF für den Datensatz mit Ausreißern x und für den Datensatz mit imputierten Ausreißern x.cap.
##------DMwR2------------------- require(DMwR2) evalq(lof.x <- lofactor(x,10), env) evalq(lof.x.cap <- lofactor(x.cap,10), env) par(mfrow = c(1, 3)) boxplot(env$lof.x, main = "lof.x", boxwex = 0.5) boxplot(env$lof.x.cap, main = "lof.x.cap", boxwex = 0.5) hist(env$lof.x.cap, breaks = 20) par(mfrow = c(1, 1))
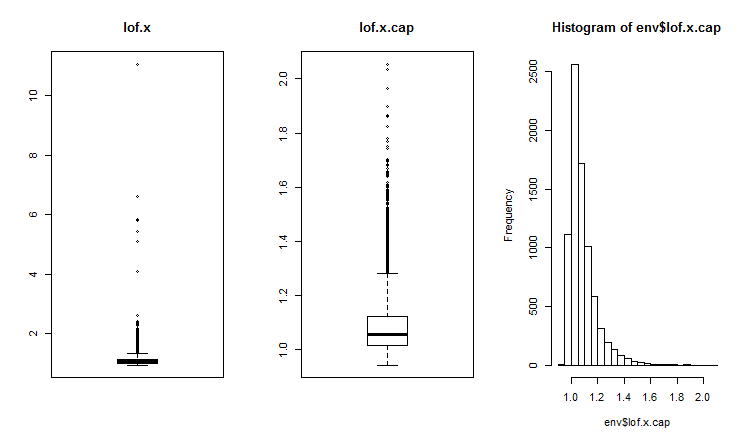
Abb.16. Globaler Ausreißerfaktor für einen Datensatz mit Ausreißern und einen Datensatz mit imputierten Ausreißern
Im Paket Rlof ist die Funktion lof() impelentiert. Sie findet den lokalen Faktor outlier [3] der Daten unter Verwendung von k Nachbarn. Lokaler Ausreißerfaktor (LOF) ist ein Wahrscheinlichkeitswert der Zugehörigkeit zu Ausreißern und wird für jede Beobachtung separat berechnet. Basierend auf diesem Wert trifft der Nutzer die Entscheidung, ob eine Beobachtung als Ausreißer betrachtet wird oder nicht.
Der LOF berücksichtigt die lokale Dichte, um festzustellen, ob eine Beobachtung ein Ausreißer ist. Das ist eine effizientere Implementierung des LOF unter Verwendung einer anderen Datenstruktur und Funktion zur Berechnung des Abstands im Vergleich zur Funktion lofactor(), die im Paket “dprep” verfügbar ist. Er unterstützt mehrere k Werte, die parallel berechnet werden, sowie verschiedene Abstandswerte, außer dem Euklidischen Abstand. Die Berechnungen werden parallel auf mehreren Kernen des Prozessors durchgeführt. Berechnen wir lofactor für dieselben Datensätze (x und x.cap) für 5, 6, 7, 8, 9 und 10 Nachbarn unter Verwendung der Minkowski Methode für die Berechnung des Abstands. Zeichnen wir die Histogramme dieser lofactor.
require(Rlof) evalq(Rlof.x <- lof(x, c(5:10), cores = 2, method = 'minkowski'), env) evalq(Rlof.x.cap <- lof(x.cap, c(5:10), cores = 2, method = 'minkowski'), env) par(mfrow = c(2, 3)) hist(env$Rlof.x.cap[ ,6], breaks = 20) hist(env$Rlof.x.cap[ ,5], breaks = 20) hist(env$Rlof.x.cap[ ,4], breaks = 20) hist(env$Rlof.x.cap[ ,3], breaks = 20) hist(env$Rlof.x.cap[ ,2], breaks = 20) hist(env$Rlof.x.cap[ ,1], breaks = 20) par(mfrow = c(1, 1))
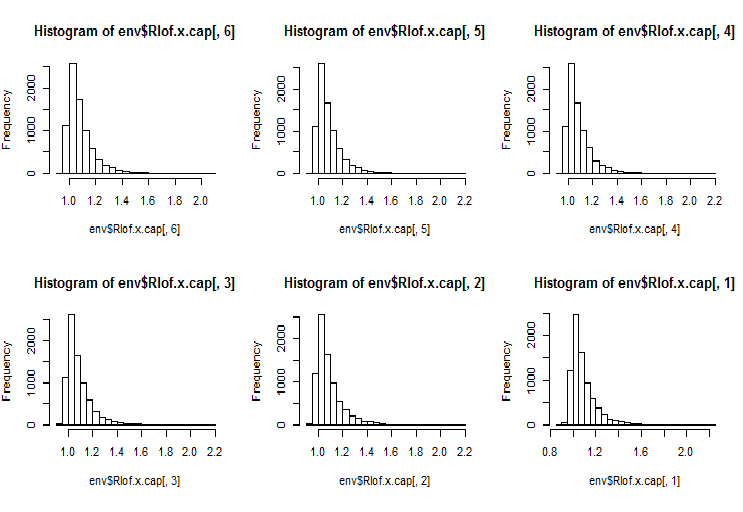
Abb.17. Globaler Ausreißerfaktor für k Nachbarn
Fast alle Punkte liegen im Bereich lofactor =1.6. Außerhalb des Bereichs:
> sum(env$Rlof.x.cap[ ,6] >= 1.6) [1] 32
Die unbedeutende Anzahl der Ausreißer ist akzeptabel für diese Datensatzgröße.
ANMERKUNG. Um die Bereichsgrenzen zu definieren, beim Überschreiten deren die Werte der Variablen als Ausreißer bezeichnet werden, muss man einen Trainigsdatensatz verwenden. Die Werte der Variablen des Test-/Validierungsdatensatzes werden mit den Parametern verarbeitet, die auf dem Trainigsdatensatz erhalten wurden. Welche Parameter sind das? Die in den vorherigen Berechnungen verwendeten Grenzen — upper = 1.5*IQR, lower = -1.5*IQR und cap =c(0.05, 0.95) percentil. Wenn andere Methoden für die Berechnung der Bereichsgrenzen und der Imputation von Ausreißern festgelegt wurden, muss man diese für den Trainigsdatensatz definieren, speichern und später bei der Verarbeitung der Datensätze valid/test verwenden.
Schreiben wir eine Funktion, die Zwischenberechnungen durchführt:
#-----prep.outlier-------------- prep.outlier <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) caps <- quantile(x, probs = c(.05, .95), na.rm = na.rm, ...) list(lower = qnt[1] - H, upper = qnt[2] + H, med = median(x), cap1 = caps[1], cap2 = caps[2]) }
Berechnen wir die Parameter, die für die Erkennung und Imputation von Ausreißern notwendig sind. Legen wir die vorläufige Länge des Trainingsdatensatzes als 4000 Balken am Anfang fest und die weiteren 2000 Balken werden wir als Testdatensatz verwenden.
evalq(
{train <- x[1:4000, ]
foreach(i = 1:ncol(train), .combine = "cbind") %do% {
prep.outlier(train[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
#pre.outl %<>% t()
},
env)
Schauen wir uns das Ergebnis an:
> env$pre.outl ftlm stlm rbci pcci lower.25% -0.2224942912 -0.59629203 -0.253231002 -9.902232e-02 upper.75% 0.2214486206 0.59242529 0.253529797 9.826936e-02 med -0.0001534451 0.00282525 -0.001184966 8.417127e-05 cap1.5% -0.1700418145 -0.40370452 -0.181326658 -6.892085e-02 cap2.95% 0.1676526431 0.39842675 0.183671973 6.853935e-02 v.fatl v.satl v.rftl v.rstl lower.25% -0.0900973332 -4.259328e-02 -0.0558921804 -0.2858430788 upper.75% 0.0888110249 4.178418e-02 0.0555115004 0.2889057397 med -0.0008581219 -2.130064e-05 -0.0001707447 -0.0001721546 cap1.5% -0.0658731640 -2.929586e-02 -0.0427927888 -0.1951978435 cap2.95% 0.0662353821 3.089833e-02 0.0411091859 0.1820803387 v.ftlm v.stlm v.pcci lower.25% -0.1115823754 -5.366875e-02 -0.1115905239 upper.75% 0.1108670403 5.367466e-02 0.1119495436 med -0.0003560178 -6.370034e-05 -0.0003173464 cap1.5% -0.0765431363 -3.686945e-02 -0.0765950814 cap2.95% 0.0789209957 3.614423e-02 0.0770439553
Wie wir sehen, werden für jede Variable im Datensatz das erste und das dritte Quartil und der Medianwert sowie das 5. und 95. Perzentil definiert. Das ist alles, was man für die Erkennung und Verarbeitung von Ausreißern benötigt.
Wir brauchen eine Funktion, die die Ausreißer jeden Datensatzes nach vordefinierten Parametern verarbeiten wird. Mögliche Varianten der Verarbeitung: Ersetzen von Ausreißern durch NA,Ersetzen von Ausreißern durch den Medianwert, Ersetzen von Ausreißern durch 5./95. Perzentil.
#---------treatOutlier--------------------------------- treatOutlier <- function(x, impute = TRUE, fill = FALSE, lower, upper, med, cap1, cap2){ if (impute) { x[x < lower] <- cap1 x[x > upper] <- cap2 return(x) } if (!fill) { x[x < lower | x > upper] <- NA return(x) } else { x[x < lower | x > upper] <- med return(x) } }
Da wir die notwendigen Parameter bereits im Trainigsdatensatz definiert haben, verarbeiten wir die Ausreißer im Trainingsdatensatz, indem wir diese durch das 5./95. Perzentil ersetzen. Danach verarbeiten wir auf die gleiche Weise Ausreißer im Testdatensatz und vergleichen die Verteilungen in den erhaltenen Datensätzen, indem wir drei Charts zeichnen.
#------------
evalq(
{
foreach(i = 1:ncol(train), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = train[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> train.out
colnames(train.out) <- colnames(train)
},
env
)
#-------------
evalq(
{test <- x[4001:6000, ]
foreach(i = 1:ncol(test), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = test[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> test.out
colnames(test.out) <- colnames(test)
},
env
)
#---------------
evalq(boxplot(train, main = "train with outliers"), env)
evalq(boxplot(train.out, main = "train.out without outliers"), env)
evalq(boxplot(test.out, main = "test.out without outliers"), env)
#------------------------
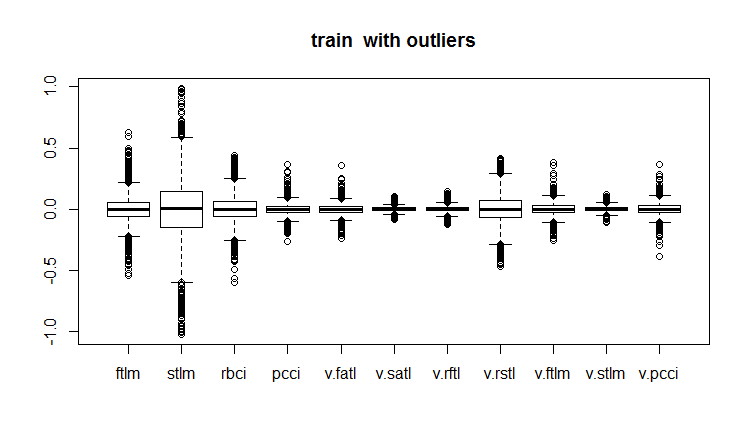
Abb.18. Trainingsdatensatz mit Ausreißern
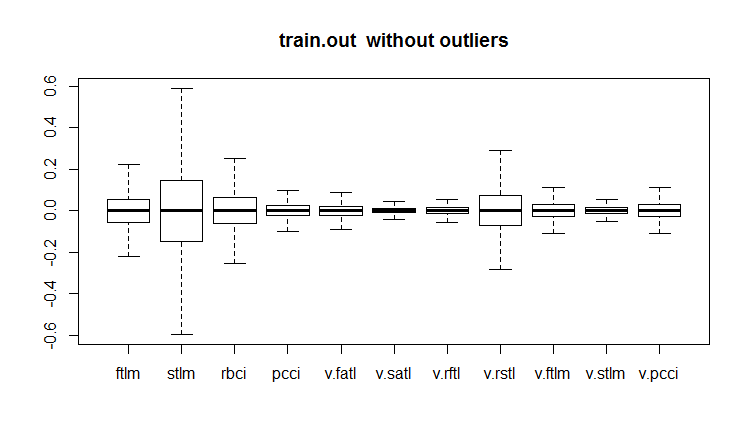
Abb.19. Trainingsdatensatz mit imputierten Ausreißern
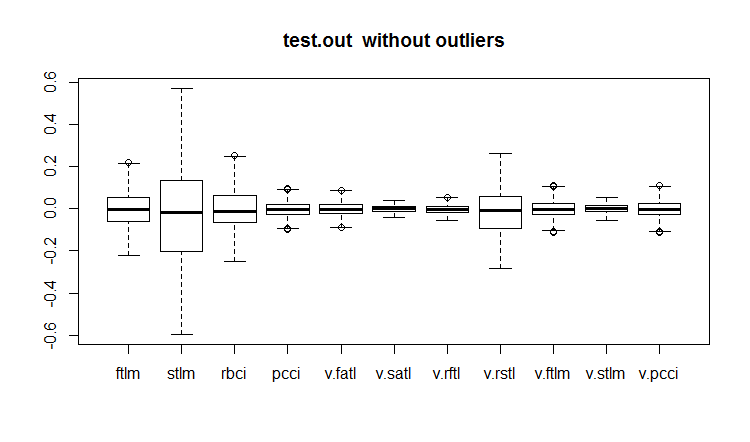
Abb.20. Testdatensatz mit imputierten Ausreißern
Nicht alle Modelle sind empfindlich gegenüber Ausreißern. Unempfindlich sind zum Beispiel die Modelle der "Entscheidungsbäume"(DT) und der "Random Forest" (RF).
Beim Erkennen und Verarbeiten von Ausreißern können auch weitere Pakete hilfreich sein, dazu gehören “univOutl”, “mvoutlier”, “outlier”, funModeling::prep.outlier().
3.3. Beseitigen der Schiefe (skewness)
Die Schiefe gibt die Form der Verteilung an. Die allgemeine Methode deren Überprüfung besteht darin, den Koeffizienten der Schiefe einer Variablen zu berechnen. In der Regel zeugt eine negative Schiefe davon, dass der Mittelwert kleiner als der Medianwert ist, und die Verteilung linksschief ist. Eine positive Schiefe weist darauf hin, dass der Mittelwert größer als der Medianwert ist, und die Verteilung rechtsschief ist.
Wenn die Schiefe der Prädiktoren gleich 0 ist, geht es um eine symmetrische Verteilung.
Wenn die Schiefe des Prädiktors kleiner als -1 oder größer als +1 ist, sind die Daten stark verzerrt.
Wenn die Schiefe des Prädiktors zwischen -1 und -1/2 oder zwischen +1 und +1/2 liegt, sind die Daten mäßig verzerrt.
Wenn die Schiefe des Prädiktors gleich -1/2 und +1/2 ist, sind die Daten ungefähr symmetrisch.
Die Rechtsschiefe wird durch Logarithmieren, die Linkschiefe — durch Exponieren beseitigt.
Wir haben bereits davon gesprochen, dass Schiefe, Ausreißer und andere Transformationen miteinander verbunden sind. Schauen wir, wie sich der Wert der Schiefe nach dem Entfernen und der Imputation von Ausreißern änderte.
evalq({
sk <- skewness(x)
sk.out <- skewness(x.out)
sk.cap <- skewness(x.cap)
},
env)
> env$sk
ftlm stlm rbci pcci v.fatl
Skewness 4.219857 1.785286 2.304655 6.491546 5.274871
v.satl v.rftl v.rstl v.ftlm v.stlm
Skewness 2.677162 3.954098 1.568675 1.207227 0.8516043
v.pcci
Skewness 3.031012
> env$sk.out
ftlm stlm rbci pcci
Skewness -0.04272076 -0.07893945 -0.02460354 0.01485785
v.fatl v.satl v.rftl v.rstl
Skewness 0.00780424 -0.02640635 -0.04663711 -0.04290957
v.ftlm v.stlm v.pcci
Skewness -0.0009597876 0.01997082 0.0007462494
> env$sk.cap
ftlm stlm rbci pcci
Skewness -0.03329392 -0.07911245 -0.02847851 0.01915228
v.fatl v.satl v.rftl v.rstl
Skewness 0.01412182 -0.02617518 -0.03412228 -0.04596505
v.ftlm v.stlm v.pcci
Skewness 0.008181183 0.009661169 0.002252508
Der Datensatz mit entfernten Ausreißern x.out sowie der mit imputierten Ausreißern x.cap sind ideal symmetrisch und brauchen nicht korrigiert zu werden.
Betrachten wir auch den Koeffizienten der Kurtosis. Die Kurtosis ist eine Maßzahl der Steilheit einer Wahrscheinlichkeitsfunktion. Bei einer normalen Verteilung ist der Koeffizient gleich Null. Er ist positiv, wenn die Spitze der Verteilung um den Erwartungswert steil ist und negativ bei einer flachen Wölbung.
require(PerformanceAnalytics)
evalq({
k <- kurtosis(x)
k.out <- kurtosis(x.out)
k.cap <- kurtosis(x.cap)
},
env)
> env$k
ftlm stlm rbci pcci
Excess Kurtosis 84.61177 16.77141 45.01858 247.9795
v.fatl v.satl v.rftl v.rstl
Excess Kurtosis 145.9547 36.99944 74.4307 13.57613
v.ftlm v.stlm v.pcci
Excess Kurtosis 86.36448 23.06635 233.5408
> env$k.out
ftlm stlm rbci
Excess Kurtosis -0.003083449 -0.1668102 -0.1197043
pcci v.fatl v.satl
Excess Kurtosis -0.05113439 -0.02738558 -0.04341552
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.01219999 -0.1316499 -0.0287925
v.stlm v.pcci
Excess Kurtosis -0.1530424 -0.09950709
> env$k.cap
ftlm stlm rbci
Excess Kurtosis -0.2314336 -0.3075185 -0.2982044
pcci v.fatl v.satl
Excess Kurtosis -0.2452504 -0.2389486 -0.2331203
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.2438431 -0.2673441 -0.2180059
v.stlm v.pcci
Excess Kurtosis -0.2763058 -0.2698028
Im Ausgangsdatensatz x sind die Spitzen der Verteilung der Variablen sehr steil (Kurtosis viel größer als 0). Im Datensatz x.out mit entfernten Ausreißern sind die Hochs nahe an einer "normalen" Steilheit, im Datensatz mit imputierten Ausreißern sind die Wölbungen flacher. Beide Datensätze erfordern keine Korrekturen.
Anhang
1. Die Zip-Datei DARCH12_1.zip beinhaltet Skripts zum ersten Teil des Artikels (dataRaw.R, PrepareData.R, FUNCTION.R) sowie das Bild der Sitzung Rstudio mit Quelldaten von Cotir.RData. Laden Sie diese in Rstudio und sie können alle Skripts laufen lassen und mit ihnen experimentieren. Sie können das von Git /Part_I herunterlaaden.
2. Die Zip-Datei ACTF.zip beinhaltet den Artikel "New Adaptive Method of Following the Tendency and Market Cycles" von V. Kravchuk
3. Die Zip-Datei R_intro.zip beinhaltet Fachliteratur zur R.
Links
[1] A Systematic Approach on Data Pre-processing In Data Mining. COMPUSOFT, An international journal of advanced computer technology, 2 (11), November-2013 (Volume-II, Issue-XI)
[2] Outlier Detection Techniques.Hans-Peter Kriegel, Peer Kröger, Arthur Zimek. Ludwig-Maximilians-Universität München.Munich, Germany
[3] Breuning, M., Kriegel, H., Ng, R.T, and Sander. J. (2000). LOF: Identifying density-based local outliers. In Proceedings of the ACM SIGMOD International Conference on Management of Data.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/3486
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Erstellen und Testen benutzerdefinierter Symbole im MetaTrader 5
Erstellen und Testen benutzerdefinierter Symbole im MetaTrader 5
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Hallo, wie nach Ihrem Artikel (1. Mal berühren R), rechts in der 2. Baustein des Codes wurde ich mit dem folgenden Fehler konfrontiert:
Fehler in evalq({ : Objekt 'env' nicht gefunden
Bedeutet env hier etwas, das in der PC-Software benannt wurde? Oder ist es wirklich ein Objekt, das automatisch erstellt wurde?
Toller Artikel, werde einen Weg finden, ihn zu übertreffen, wäre toll, wenn Sie helfen könnten :)
(Ich benutze RStudio und habe MRO 3.5.3 installiert (weil 3.4.0 veraltet war))
Hallo, nach Ihrem Artikel (berühren R zum ersten Mal), rechts in den zweiten Block von Code, stieß ich auf den folgenden Fehler:
Fehler in evalq ({: Objekt 'env' nicht gefunden
bedeutet env hier etwas, das in der PC-Software genannt wird? Oder ist es wirklich ein automatisch generiertes Objekt?
Toller Artikel, ich werde einen Weg finden, um es zu schlagen, es wäre toll, wenn Sie helfen könnten :)
(Ich verwende RStudio und installiere MRO 3.5.3 (da 3.4.0 veraltet ist))
Das env-Objekt wurde erstellt, um Daten von verschiedenen Tools zu trennen. Einfach am Anfang des Skripts schreiben
Viel Glück!
Lieber MR. Vladimir Perervenko, vielen Dank für Ihre schnelle Antwort, nach der Einnahme eines R-Kurses hoffe ich, zumindest genug zu machen, um das Studium Ihrer großartigen Arbeit zu verdienen, vielen Dank für den Austausch Herr Vladimir.
Mit besten Grüßen
Ferox
Hallo Herr Perervenko, ich hoffe, es geht Ihnen gut. Ich habe eine neue Frage, als Sie das erste Mal über ZigZag geschrieben haben:
in der 9. Zeile, was ist die Bedeutung des Dig-Objekts?
Ich konnte es weder im Projekt noch in den erforderlichen Paketen finden ...
Mit freundlichen Grüßen MR. Perervenko
Ferox
Es tut mir leid, meine dumme Frage, Herr Vladimir Perervenko.
Ich habe es bereits gelöst, es gibt keine Ausreden.
Mit freundlichen Grüßen