Neuroredes profundas (Parte I). Preparación de datos
2 460
0
Las DNN son ahora ampliamente utilizadas y se desarrollan activamente en muchas áreas diferentes. Los ejemplos más llamativos de su uso diario son el reconocimiento de diferentes patrones y del habla, así como la traducción automática de un idioma a otro. También se aplican al trading, por eso podemos considerar que su estudio en profundidad dentro del marco del rápido desarrollo del trading algorítmico puede ser muy útil y tener muchas perspectivas.
En los últimos años, los investigadores han propuesto y han confirmado de forma experimental multitud de nuevas ideas, métodos y enfoques para el uso de DNN. En esta serie de artículos se analizarán las principales corrientes de desarrollo del tema y su presente estado, así como diferentes ideas y métodos comprobados con experimentos prácticos. También le prestaremos especial atención a los índices de calida de las DNN. En nuestro trabajo utilizaremos solo redes neuronales multicapa totalmente conectadas.
Las cuatro cuestiones principales que concentrarán la atención de la serie de artículos son:
- La preparación, valoración y ampliación de los datos de entrada con la ayuda de varias transformaciones.
- Las nuevas posibilidades del paquete darch (v.0.12). Flexibilidad y posibilidades ampliadas.
- El uso de la ampliación de los resultados de predicción (optimización de los hiperparámetros de las DNN y los conjuntos de neuroredes).
- Las posibilidades gráficas para controlar el funcionamiento del experto tanto en el aprendizaje, como durante el funcionamiento.
Este artículo está dedicado a la preparación de los datos recibidos en el terminal comercial, para el uso de la neurored.
Contenido
- Introducción. El lenguaje R
- 1 Creación de un conjunto de datos inicial (no procesados)
- 2. Análisis exploratorio de datos
- 3. Preparación de datos
- 3.1. Limpieza de datos
- 3.2. Deteccción y procesamiento de valores atípicos (outliers)
- 3.3. Eliminando la asimetría
- Anexos
- Enlaces
Introducción
El desarrollo, el entrenamiento y la puesta a prueba de una red neuronal profunda consta de varias etapas esenciales, organizadas en un orden estricto. Al igual que sucede con cualquier modelo de aprendizaje de máquinas, el proceso de creación de una DNN se puede dividir en cuatro partes:
- preparación de los datos de entrada y salida para los experimentos;
- creación, entrenamiento, puesta a prueba y optimización de los parámetros del modelo.
La primera etapa ocupa la mayor parte del tiempo en la implementación del proyecto: cerca del 70%. Además, el funcionamiento del modelo depende en un 80% de sus resultados. Como bien sabemos, "lo que entra sucio - sale sucio". Por eso, analizaremos con mucho detalle la composición de los trabajos en esta etapa.
Para repetir los experimentos, será necesario instalar MRO 3.4.0 y Rstudio. Tanto en la red como en los archivos anexos al artículo hay información más que suficiente acerca de cómo instalar este software, así que no nos detendremos en ello con detalle.
El lenguaje R
Vamos a refrescar un poco alguna información importante sobre el lenguaje R. Se trata de un lenguaje de programación, así como un entorno para cálculo estadístico y construcción de gráficos, que fue desarrollado en 1996 por los científicos neozelandeses Ross lhaka y Robert Gentleman en la universidad de Auckland. R es un proyecto GNU, es decir, un software libre. Su filosofía de uso se ciñe a los siguientes principios (libertades):
- libertad de iniciar el programa con cualquier cometido (libertad 0);
- libertad para estudiar cómo funciona el programa y adaptarlo a las propias necesidades (libertad 1);
- libertad para distribuir copias para ayudar al prójimo (libertad 2);
- libertad para mejorar el programa y hacer de su mejora algo accesible a todos, para beneficio de la comunidad.
Hoy en día, el lenguaje R sigue su mejora y desarrollo, básicamente con los esfuerzos del "R Development Core Team" y del R Consortium, creado este año. La lista de los miembros del consorcio (IBM, Microsoft, Rstudio, Google, Mango, Oracle y otros) revela el gran apoyo recibido, el enorme interés por el uso del lenguaje y las maravillosas perspectivas del lenguaje en el futuro.
Ventajas del lenguaje R:
- A día de hoy, el lenguaje R, de facto, es el estándar en el cálculo estadístico.
- Continúa su desarrollo y es apoyado por la comunidad científica internacional en las universidades de todo el mundo.
- Dispone de un amplio surtido de paquetes para todos los campos avanzados de análisis de datos (Data mining). En este caso, desde la aparición de una nueva idea en las publicaciones científicas hasta su implementación en el paquete R transcurren no más de dos semanas.
- Y en último lugar, pero no menos importante, su uso es absolutamente gratuito.
1 Creación de un conjunto de datos inicial (no procesados)
"Todos los movimientos de precio anteriores, presentes y futuros están incluidos en el propio precio"
Existen multitud de métodos (paquetes), destinados a la preparación preliminar, la valoración y la elección de los predictores. Podemos ver una panorámica los métodos en [1]. Su diversidad viene explicada por la no menor diversidad de los datos del mundo real. Nuestro entendimiento del tipo de datos que estamos usando, definirá qué métodos de investigación y procesamiento elegiremos.
Los datos financieros, en cuya investigación nos ocupamos, son series tempoorales regulares jerarquizadas, "infinitas" y fácilmente extraíbles. La línea base representa las cotizaciones de OHLCV del instrumento en un marco temporal concreto.
De esta línea base proceden el resto de las series temporales:
- no paramétricas. Por ejemplo x^2, sqrt(abs(x)), x^3, -x^2, etcétera.
- funcionales no paramétricas. Por ejemplo, sin(2*n*x), ln(abs(x)), log(Pr(t)/Pr(t-1)) y etcétera
- paramétricas. Aquí se incluye un enorme número de todos los tipos de indicadores posibles, que básicamente se usan como predictores. Pueden ser tanto osciladores, como diferentes clases de filtros.
Como variable objetivo se usan o bien indicadores que generen señales (factores), o bien una serie de condiciones lógicas cuya ejecución da la señal.
1.1. Cotizaciones
Las cotizaciones de OHLC, Volume y time las recibimos del terminal en forma de vectores (o, h, l, cl, v, d). Escribiremos una función que unificará los vectores recibidos del temrinal en dataFrame. Además, trasladaremos la hora de comienzo al formato POSIXct.
#---pr.OHLCV-------------------
pr.OHLCV <- function(d, o, h, l, cl, v){
# (d, o, h, l, cl, v)- vector
require('magrittr')
require('dplyr')
require('anytime')
price <- cbind(Data = rev(d),
Open = rev(o), High = rev(h),
Low = rev(l), Close = rev(cl),
Vol = rev(v)) %>% as.tibble()
price$Data %<>% anytime(., tz = "CET")
return(price)
}
Puesto que hemos cargado los vectores de las cotizaciones en el entorno env, calculamos dataFrame pr y limpiamos el entorno env de variables innecesarias:
evalq({pr <- pr.OHLCV(Data, Open, High, Low, Close, Volume)
rm(list = c("Data", "Open", "High", "Low", "Close", "Volume"))
},
env)
Vamos a ver qué aspecto tiene este dataFrame al comienzo:
> head(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-01-10 11:00:00 122.758 122.893 122.746 122.859 2 2017-01-10 11:15:00 122.860 122.924 122.818 122.848 3 2017-01-10 11:30:00 122.850 122.856 122.705 122.720 4 2017-01-10 11:45:00 122.721 122.737 122.654 122.693 5 2017-01-10 12:00:00 122.692 122.850 122.692 122.818 6 2017-01-10 12:15:00 122.820 122.937 122.785 122.920 # ... with 1 more variables: Vol <dbl>
y al final:
> tail(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-05-05 20:30:00 123.795 123.895 123.780 123.888 2 2017-05-05 20:45:00 123.889 123.893 123.813 123.831 3 2017-05-05 21:00:00 123.833 123.934 123.825 123.916 4 2017-05-05 21:15:00 123.914 123.938 123.851 123.858 5 2017-05-05 21:30:00 123.859 123.864 123.781 123.781 6 2017-05-05 21:45:00 123.779 123.864 123.781 123.781 # ... with 1 more variables: Vol <dbl>
Bien, tenemos 8000 barras con una fecha inicial 10.01.2017 y final 05.05.2017. Añadimos al frame de datos pr precio medio — Medium Price, Precio Típico y Precio ponderado
evalq(pr %<>% mutate(., Med = (High + Low)/2, Typ = (High + Low + Close)/3, Wg = (High + Low + 2 * Close)/4, #CO = Close - Open, #HO = High - Open, #LO = Low - Open, dH = c(NA, diff(High)), dL = c(NA, diff(Low)) ), env)
1.2. Predictores
A diferencia de nuestros experimentos anteriores, hemos simplificado el conjunto de predictores. Los filtros digitales FATL, SATL, RFTL, RSTL ejercerán este papel. Se describen con detalle en el artículo de В. Kravchuk "New Adaptive Method of Following the Tendency and Market Cycles", que usted podrá encontrar en los archivos anexos a este artículo (ver capítulo "New Tools of Technical Analysis and their Interpretation). Aquí solo los enumeraremos brevemente.
- FATL (Fast Adaptive Trend Line) — línea de tendencia adaptativa «rápida»;
- SATL (Slow Adaptive Trend Line) — línea de tendencia adaptativa «lenta»;
- RFTL (Reference Fast Trend Line) — línea de tendencia de apoyo «rápida»;
- RSTL (Reference Slow Trend Line) — línea de tendencia de apoyo «lenta».
El ritmo de cambio de FATL y SATL se sigue según los indicadores FTLM (Fast Trend Line Momentum) y STLM (Slow Trend Line Momentum).
Entre los instrumentos técnicos que necesitaremos, hay dos osciladores más RBCI y PCCI. El índice RBCI (Range Bound Channel Index), está limitado por la franja del índice de canal que se calcula con la ayuda del filtro de banda (el filtro elimina la tendencia de baja frecuencia y el ruido de alta frecuencia). El índice PCCI (Perfect Commodity Channel Index) es un índice de canal de mercancías perfecto.
La función que calcula los filtros digitales FATL, SATL, RFTL, RSTL, tiene el aspecto siguiente:
#-----DigFiltr------------------------- DigFiltr <- function(X, type = 1){ # X - vector require(rowr) fatl <- c( +0.4360409450, +0.3658689069, +0.2460452079, +0.1104506886, -0.0054034585, -0.0760367731, -0.0933058722, -0.0670110374, -0.0190795053, +0.0259609206, +0.0502044896, +0.0477818607, +0.0249252327, -0.0047706151, -0.0272432537, -0.0338917071, -0.0244141482, -0.0055774838, +0.0128149838, +0.0226522218, +0.0208778257, +0.0100299086, -0.0036771622, -0.0136744850, -0.0160483392, -0.0108597376, -0.0016060704, +0.0069480557, +0.0110573605, +0.0095711419, +0.0040444064, -0.0023824623, -0.0067093714, -0.0072003400, -0.0047717710, 0.0005541115, 0.0007860160, 0.0130129076, 0.0040364019 ) rftl <- c(-0.0025097319, +0.0513007762 , +0.1142800493 , +0.1699342860 , +0.2025269304 , +0.2025269304, +0.1699342860 , +0.1142800493 , +0.0513007762 , -0.0025097319 , -0.0353166244, -0.0433375629 , -0.0311244617 , -0.0088618137 , +0.0120580088 , +0.0233183633, +0.0221931304 , +0.0115769653 , -0.0022157966 , -0.0126536111 , -0.0157416029, -0.0113395830 , -0.0025905610 , +0.0059521459 , +0.0105212252 , +0.0096970755, +0.0046585685 , -0.0017079230 , -0.0063513565 , -0.0074539350 , -0.0050439973, -0.0007459678 , +0.0032271474 , +0.0051357867 , +0.0044454862 , +0.0018784961, -0.0011065767 , -0.0031162862 , -0.0033443253 , -0.0022163335 , +0.0002573669, +0.0003650790 , +0.0060440751 , +0.0018747783) satl <- c(+0.0982862174, +0.0975682269 , +0.0961401078 , +0.0940230544, +0.0912437090 , +0.0878391006, +0.0838544303 , +0.0793406350 ,+0.0743569346 ,+0.0689666682 , +0.0632381578 ,+0.0572428925 , +0.0510534242,+0.0447468229, +0.0383959950, +0.0320735368, +0.0258537721 ,+0.0198005183 , +0.0139807863,+0.0084512448, +0.0032639979, -0.0015350359, -0.0059060082 ,-0.0098190256 , -0.0132507215, -0.0161875265, -0.0186164872, -0.0205446727, -0.0219739146 ,-0.0229204861 , -0.0234080863,-0.0234566315, -0.0231017777, -0.0223796900, -0.0213300463 ,-0.0199924534 , -0.0184126992,-0.0166377699, -0.0147139428, -0.0126796776, -0.0105938331 ,-0.0084736770 , -0.0063841850,-0.0043466731, -0.0023956944, -0.0005535180, +0.0011421469 ,+0.0026845693 , +0.0040471369,+0.0052380201, +0.0062194591, +0.0070340085, +0.0076266453 ,+0.0080376628 , +0.0083037666,+0.0083694798, +0.0082901022, +0.0080741359, +0.0077543820 ,+0.0073260526 , +0.0068163569,+0.0062325477, +0.0056078229, +0.0049516078, +0.0161380976 ) rstl <- c(-0.0074151919,-0.0060698985,-0.0044979052,-0.0027054278,-0.0007031702,+0.0014951741, +0.0038713513,+0.0064043271,+0.0090702334,+0.0118431116,+0.0146922652,+0.0175884606, +0.0204976517,+0.0233865835,+0.0262218588,+0.0289681736,+0.0315922931,+0.0340614696, +0.0363444061,+0.0384120882,+0.0402373884,+0.0417969735,+0.0430701377,+0.0440399188, +0.0446941124,+0.0450230100,+0.0450230100,+0.0446941124,+0.0440399188,+0.0430701377, +0.0417969735,+0.0402373884,+0.0384120882,+0.0363444061,+0.0340614696,+0.0315922931, +0.0289681736,+0.0262218588,+0.0233865835,+0.0204976517,+0.0175884606,+0.0146922652, +0.0118431116,+0.0090702334,+0.0064043271,+0.0038713513,+0.0014951741,-0.0007031702, -0.0027054278,-0.0044979052,-0.0060698985,-0.0074151919,-0.0085278517,-0.0094111161, -0.0100658241,-0.0104994302,-0.0107227904,-0.0107450280,-0.0105824763,-0.0102517019, -0.0097708805,-0.0091581551,-0.0084345004,-0.0076214397,-0.0067401718,-0.0058083144, -0.0048528295,-0.0038816271,-0.0029244713,-0.0019911267,-0.0010974211,-0.0002535559, +0.0005231953,+0.0012297491,+0.0018539149,+0.0023994354,+0.0028490136,+0.0032221429, +0.0034936183,+0.0036818974,+0.0038037944,+0.0038338964,+0.0037975350,+0.0036986051, +0.0035521320,+0.0033559226,+0.0031224409,+0.0028550092,+0.0025688349,+0.0022682355, +0.0073925495) if (type == 1) {k = fatl} if (type == 2) {k = rftl} if (type == 3) {k = satl} if (type == 4) {k = rstl} n <- length(k) m <- length(X) k <- rev(k) f <- rowr::rollApply(data = X, fun = function(x) {sum(x * k)}, window = n, minimum = n, align = "right") while (length(f) < m) { f <- c(NA,f)} return(f) }
Los calculamos y los añadimos al frame de datos pr
evalq(pr %<>% mutate(., fatl = DigFiltr(Close, 1), rftl = DigFiltr(Close, 2), satl = DigFiltr(Close, 3), rstl = DigFiltr(Close, 4) ), env)
Añadimos los osciladores FTLM, STLM, RBCI, PCCI, sus primeras diferencias y las primeras diferencias de los filtros digitales al frame de datos pr:
evalq(pr %<>% mutate(., ftlm = fatl - rftl, rbci = fatl - satl, stlm = satl - rstl, pcci = Close - fatl, v.fatl = c(NA, diff(fatl)), v.rftl = c(NA, diff(rftl)), v.satl = c(NA, diff(satl)), v.rstl = c(NA, diff(rstl)*10) ), env) evalq(pr %<>% mutate(., v.ftlm = c(NA, diff(ftlm)), v.stlm = c(NA, diff(stlm)), v.rbci = c(NA, diff(rbci)), v.pcci = c(NA, diff(pcci)) ), env)
1.3. Variable objetivo
Como indicador que genera la variable objetivo, usaremos ZigZag().
La función para calcularlo recibe en la entrada una serie temporal y dos parámetros: se trata de la longitud mínima de la curva (int o bien double) y el tipo de precio para el cálculo (Close, Med, Typ, Wd, con (High, Low) ).
#------ZZ----------------------------------- par <- c(25, 5) ZZ <- function(x, par) { # x - vector require(TTR) require(magrittr) ch = par[1] mode = par[2] if (ch > 1) ch <- ch/(10 ^ (Dig - 1)) switch(mode, xx <- x$Close, xx <- x$Med, xx <- x$Typ, xx <- x$Wd, xx <- x %>% select(High,Low)) zz <- ZigZag(xx, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]} return(zz) }
Calculamos el ZigZag, la primera diferencia, el signo de la primera diferencia y los añadimos al frame de datos pr:
evalq(pr %<>% cbind(., zigz = ZZ(., par = par)), env) evalq(pr %<>% cbind(., dz = diff(pr$zigz) %>% c(NA, .)), env) evalq(pr %<>% cbind(., sig = sign(pr$dz)), env)
1.4.Conjunto inicial de datos
Vamos a resumir brevemente qué hemos obtenido tras finalizar los anteriores cálculos y cómo lo hemos hecho.
Hemos obtenido del terminal los vectores OHLCV y una marca temporal del inicio de la barra del marco temporal М15 de EURJPY. A apartir de estos datos, se ha formado el frame de datos pr, al que se han añadido las variables FATL, SATL, RFTL, RSTL, FTLM, STLM, RBCI, PCCI y las primeras diferencias de las mismas. Asimismo, al frame de datos se ha añadido un ZigZag con un apalancamiento mínimo de 25 p (4 dígitos), su primera diferencia y el signo de primera diferencia (-1,1), que se usará como señal.
Hemos cargado todos estos datos no en el entorno global, sino en un nuevo entorno hijo env, en el que precisamente vamos a realizar todos los cálculos. El objetivo de esta división es usar conjuntos de datos de diferentes símbolos o marcos temporales sin conflicto de nombres al realizar los cálculos.
La estructura del frame de datos total pr se muestra más abajo. A partir de él se pueden elegir las variables necesarias para los cálculos posteriores.
str(env$pr) 'data.frame': 8000 obs. of 30 variables: $ Data : POSIXct, format: "2017-01-10 11:00:00" ... $ Open : num 123 123 123 123 123 ... $ High : num 123 123 123 123 123 ... $ Low : num 123 123 123 123 123 ... $ Close : num 123 123 123 123 123 ... $ Vol : num 3830 3360 3220 3241 3071 ... $ Med : num 123 123 123 123 123 ... $ Typ : num 123 123 123 123 123 ... $ Wg : num 123 123 123 123 123 ... $ dH : num NA 0.031 -0.068 -0.119 0.113 ... $ dL : num NA 0.072 -0.113 -0.051 0.038 ... $ fatl : num NA NA NA NA NA NA NA NA NA NA ... $ rftl : num NA NA NA NA NA NA NA NA NA NA ... $ satl : num NA NA NA NA NA NA NA NA NA NA ... $ rstl : num NA NA NA NA NA NA NA NA NA NA ... $ ftlm : num NA NA NA NA NA NA NA NA NA NA ... $ rbci : num NA NA NA NA NA NA NA NA NA NA ... $ stlm : num NA NA NA NA NA NA NA NA NA NA ... $ pcci : num NA NA NA NA NA NA NA NA NA NA ... $ v.fatl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rftl: num NA NA NA NA NA NA NA NA NA NA ... $ v.satl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rstl: num NA NA NA NA NA NA NA NA NA NA ... $ v.ftlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.stlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.rbci: num NA NA NA NA NA NA NA NA NA NA ... $ v.pcci: num NA NA NA NA NA NA NA NA NA NA ... $ zigz : num 123 123 123 123 123 ... $ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ... $ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
Elegimos en el frame de datos dataSet todos los predictores anteriormente calculados. Transformamos la variable objetivo sig en un factor y desplazamos una barra hacia el «futuro».
evalq(dataSet <- pr %>% tbl_df() %>%
dplyr::select(Data, ftlm, stlm, rbci, pcci,
v.fatl, v.satl, v.rftl, v.rstl,
v.ftlm, v.stlm, v.rbci, v.pcci, sig) %>%
dplyr::filter(., sig != 0) %>%
mutate(., Class = factor(sig, ordered = F) %>%
dplyr::lead()) %>%
dplyr::select(-sig),
env)
Análisis visual de datos
Vamos a construir el gráfico OHLC usando el paquete ggplot2. Tomamos los datos de los 2 últimos días y dibujamos el gráfico de cotizaciones en barras.
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + labs(title = "EURJPY Candlestick Chart", y = "Close Price", x = "") + theme_tq(), env)
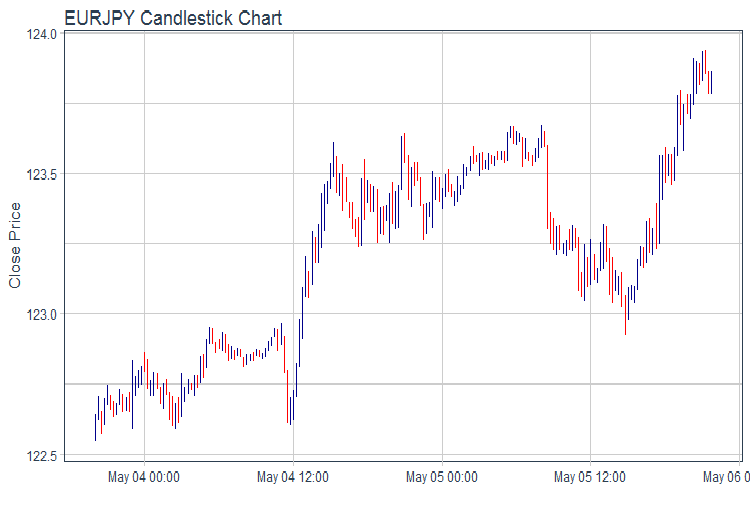
fig.1. Gráfico de cotizaciones
Construimos el gráfico FATL, SATL, RFTL, RSTL y ZZ:
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + geom_line(aes(Data, fatl), color = "steelblue", size = 1) + geom_line(aes(Data, rftl), color = "red", size = 1) + geom_line(aes(Data, satl), color = "gold", size = 1) + geom_line(aes(Data, rstl), color = "green", size = 1) + geom_line(aes(Data, zigz), color = "black", size = 1) + labs(title = "EURJPY Candlestick Chart", subtitle = "Combining Chart Geoms", y = "Close Price", x = "") + theme_tq(), env)
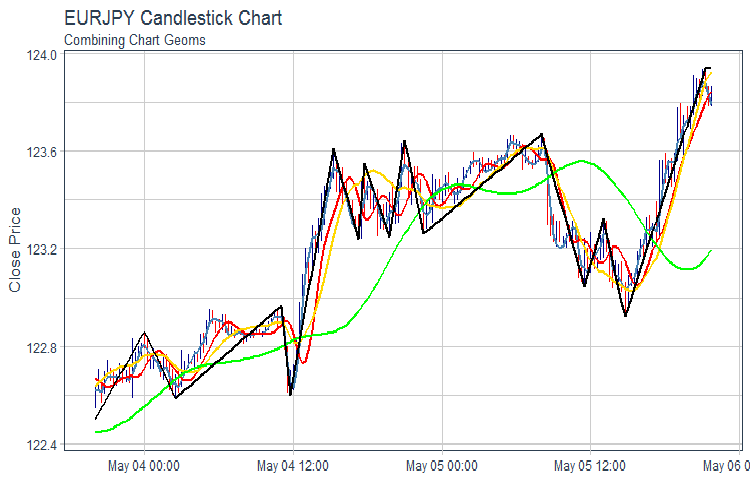
Fig.2. FATL, SATL, RFTL, RSTL y ZZ
Dividimos los osciladores en 3 grupos para una representación más cómoda.
require(dygraphs) evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, ftlm, stlm, rbci, pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator base") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "blue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
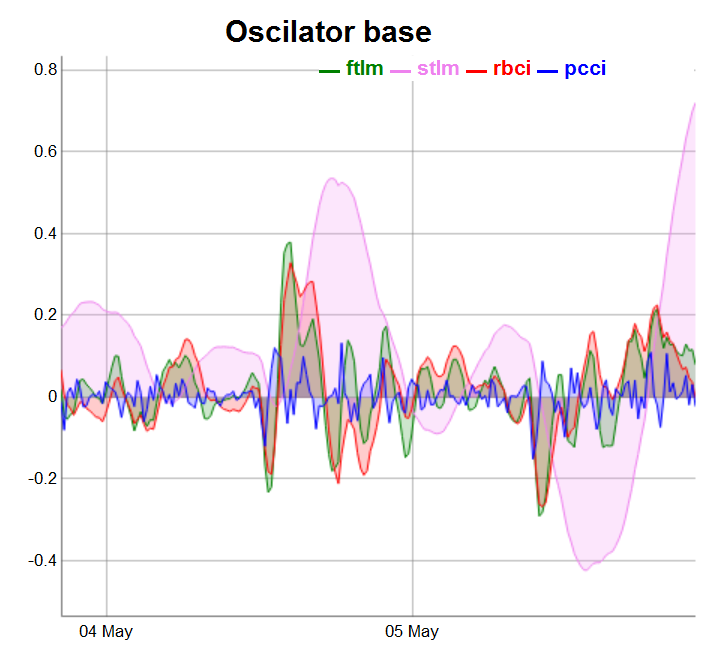
Fig.3. Osciladores básicos
evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, v.fatl, v.satl, v.rftl, v.rstl) %>% tk_xts() %>% dygraph(., main = "Oscilator 2") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
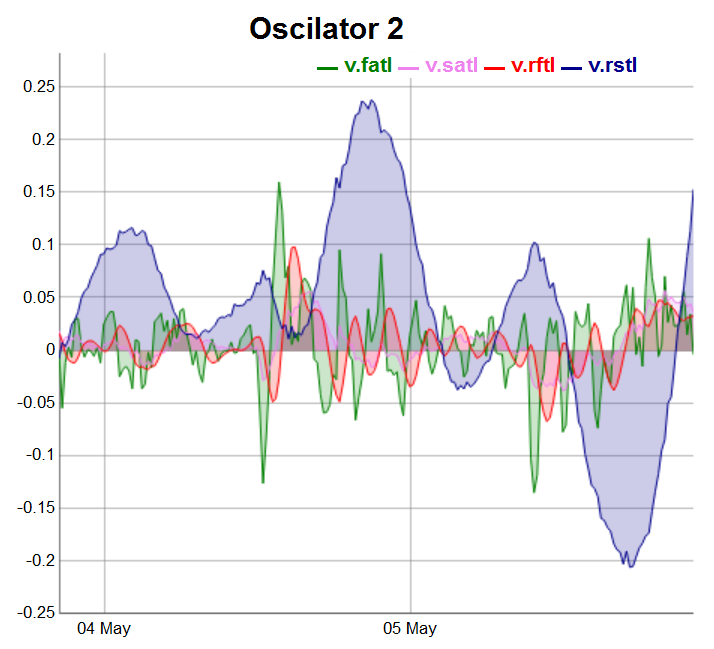
Fig.4. Osciladores del 2 grupo
Los osciladores del tercer grupo se dibujarán en las últimas 100 barras:
evalq(dataSet %>% tail(., 100) %>% tk_tbl %>% select(Data, v.ftlm, v.stlm, v.rbci, v.pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator 3") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
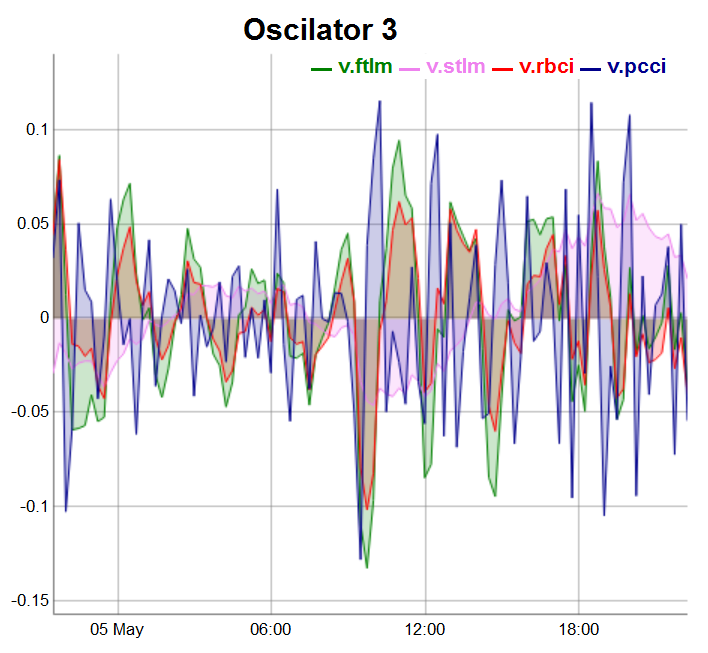
Fig.5. Osciladores del 3 grupo
2.Análisis exploratorio de datos (Exploratory data analysis, EDA)
“No existen las tareas estadísticas triviales, solo los procedimientos estadísticos dudosos.” — Sir David Cox
“Es mucho mejor encontrar una respuesta aproximada a un problema exacto, que obtener una respuesta exacta a un problema aproximado.” — John Tuckey
Estamos utilizando EDA para desarrollar la comprensión de nuestros datos. El método más sencillo de hacer esto es usar preguntas como herramienta de investigación. Cuando hacemos una pregunta, nos concentramos en una parte determinada de los datos. Esto ayuda a decidir qué gráficos, modelos o transformaciones es mejor usar.
El EDA es principalmente un proceso creativo. Y como en la mayoría de los procesos creativos, la clave para realizar las preguntas adecuadas es hacer aún más preguntas. Resulta complicado hacer preguntas relevantes al inicio del análisis, por eso no sabemos qué conclusiones sacaremos del conjunto de datos. Por otra parte, cada nueva pregunta que hacemos descubre un nuevo aspecto de los datos y aumenta la oportunidad de realizar descubrimientos. Podemos pasar rápidamente a una parte más interesante de la muestra y, mediante una serie de preguntas consecutivas, explorar y aclarar la situación.
No existen normas sobre qué preguntas debemos hacer para realizar la investigación. Sin embargo, hay dos tipos de preguntas que siempre nos resultarán útiles:
-
¿Qué tipo de cambio ha tenido lugar en mis variables?
- ¿Qué tipo de covariaciones han sucedido entre las variables?
Vamos a aclarar el concepto general.
Variaciones — tendencias del cambio de los valores de una variable de una medición a otra. Podrá ver con facilidad estos cambios en la vida real: si mide siete veces una variable continua, obtendrá siete resultados diferentes. Esto será cierto incluso si usted mide magnitudes constantes (por ejemplo, la velocidad de la luz). Cada una de las mediciones contendrá pequeños errores que cambiarán continuamente. Las variables de una categoría también pueden cambiar si medimos diferentes objetos concretos (por ejemplo, el color de los ojos de diferentes personas), o realizamos la medición en un momento diferente (por ejemplo, los niveles de energía de un electrón en momentos distintos). Cada variable tiene su propio carácter de variación, que puede descubrir información interesante. El mejor modo de entender la imagen general es visualizar la distribución de los valores de la variable. Es claramente una situación en la que una imagen es mejor que mil palabras.
2.1.Estadística total
La estadística total de nuestra serie temporal se puede calcular cómodamente con la ayuda de la función table.Stats()::PerformenceAnalitics.
> table.Stats(env$dataSet %>% tk_xts()) Using column `Data` for date_var. ftlm stlm rbci pcci Observations 7955.0000 7908.0000 7934.0000 7960.0000 NAs 42.0000 89.0000 63.0000 37.0000 Minimum -0.7597 -1.0213 -0.9523 -0.5517 Quartile 1 -0.0556 -0.1602 -0.0636 -0.0245 Median -0.0001 0.0062 -0.0016 -0.0001 Arithmetic Mean 0.0007 0.0025 0.0007 0.0001 Geometric Mean -0.0062 NaN -0.0084 -0.0011 Quartile 3 0.0562 0.1539 0.0675 0.0241 Maximum 2.7505 3.0407 2.3872 1.8859 SE Mean 0.0014 0.0033 0.0015 0.0006 LCL Mean (0.95) -0.0020 -0.0040 -0.0022 -0.0010 UCL Mean (0.95) 0.0034 0.0090 0.0035 0.0012 Variance 0.0152 0.0858 0.0172 0.0026 Stdev 0.1231 0.2929 0.1311 0.0506 Skewness 4.2129 1.7842 2.3037 6.4718 Kurtosis 84.6116 16.7471 45.0133 247.4208 v.fatl v.satl v.rftl v.rstl Observations 7959.0000 7933.0000 7954.0000 7907.0000 NAs 38.0000 64.0000 43.0000 90.0000 Minimum -0.3967 -0.0871 -0.1882 -0.4719 Quartile 1 -0.0225 -0.0111 -0.0142 -0.0759 Median -0.0006 0.0003 0.0000 0.0024 Arithmetic Mean 0.0002 0.0002 0.0002 0.0011 Geometric Mean -0.0009 0.0000 -0.0003 -0.0078 Quartile 3 0.0220 0.0110 0.0138 0.0751 Maximum 1.4832 0.3579 0.6513 1.3093 SE Mean 0.0005 0.0002 0.0003 0.0015 LCL Mean (0.95) -0.0009 -0.0003 -0.0005 -0.0020 UCL Mean (0.95) 0.0012 0.0007 0.0009 0.0041 Variance 0.0023 0.0005 0.0009 0.0188 Stdev 0.0483 0.0219 0.0308 0.1372 Skewness 5.2643 2.6705 3.9472 1.5682 Kurtosis 145.8441 36.9378 74.4182 13.5724 v.ftlm v.stlm v.rbci v.pcci Observations 7954.0000 7907.0000 7933.0000 7959.0000 NAs 43.0000 90.0000 64.0000 38.0000 Minimum -0.9500 -0.2055 -0.6361 -1.4732 Quartile 1 -0.0280 -0.0136 -0.0209 -0.0277 Median -0.0002 -0.0001 -0.0004 -0.0002 Arithmetic Mean 0.0000 0.0001 0.0000 0.0000 Geometric Mean -0.0018 -0.0003 -0.0009 NaN Quartile 3 0.0273 0.0143 0.0207 0.0278 Maximum 1.4536 0.3852 1.1254 1.9978 SE Mean 0.0006 0.0003 0.0005 0.0006 LCL Mean (0.95) -0.0012 -0.0005 -0.0009 -0.0013 UCL Mean (0.95) 0.0013 0.0007 0.0009 0.0013 Variance 0.0032 0.0007 0.0018 0.0034 Stdev 0.0561 0.0264 0.0427 0.0579 Skewness 1.2051 0.8513 2.0643 3.0207 Kurtosis 86.2425 23.0651 86.3768 233.1964
Qué podemos ver en este recuadro:
- Todos los predictores tienen una cantidad (relativamente) pequeña de variables NA indefinidas.
- Todos los predictores presentan una acusada asimetría derecha (skewness).
- Todos los predictores tienen una alta curtosis.
2.2.Visualización de la estadística total
“El mayor valor de una pintura reside en que nos hace notar lo que nunca esperábamos ver”. — John Tuckey
Vamos a analizar la variación y la covariación de nuestras variables en el conjunto dataSet. Puesto que le número de variables (14) no permite ubicarlas en un solo gráfico, vamos a dividirlas en tres grupos.
require(GGally) evalq(ggpairs(dataSet, columns = 2:6, mapping = aes(color = Class), title = "DigFilter1"), env)
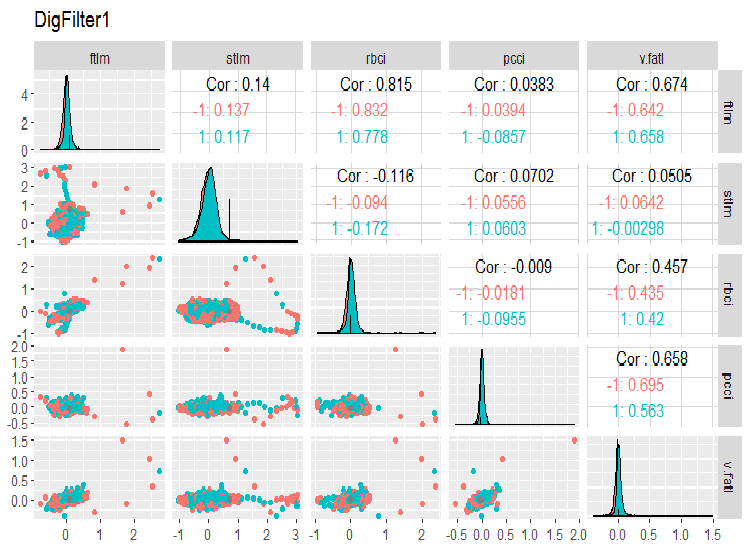
Fig. 6. Primer grupo de predictores
evalq(ggpairs(dataSet, columns = 7:10, mapping = aes(color = Class), title = "DigFilter2"), env)
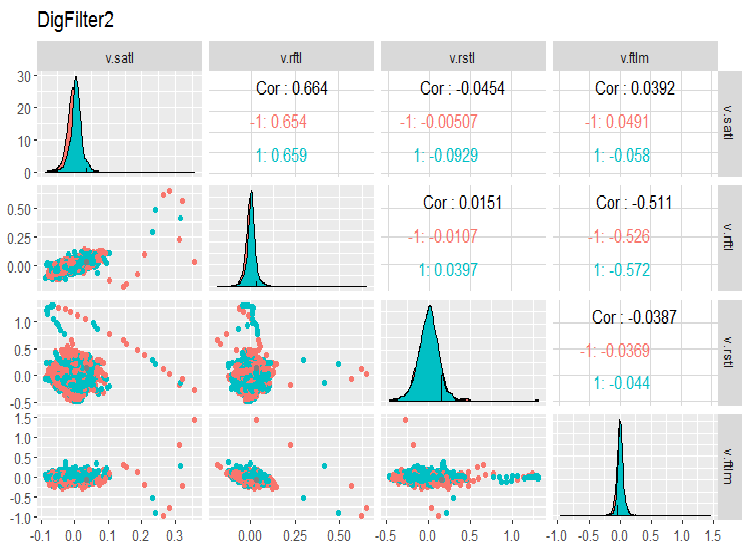
Fig. 7. Segundo grupo de predictores
evalq(ggpairs(dataSet, columns = 11:14, mapping = aes(color = Class), title = "DigFilter3"), env)
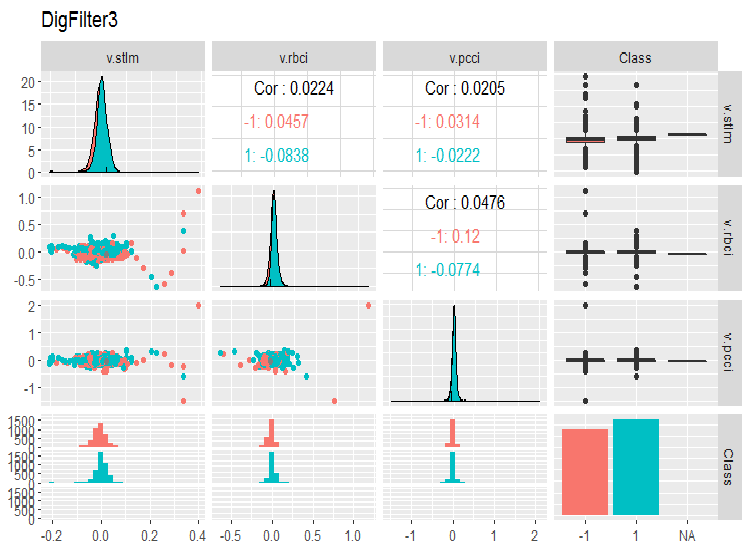
Fig. 8. Tercer grupo de predictores
Qué vemos en los gráficos:
- todos los predictores tienen una forma de distribución cercana a la normal, pero con una fuerte asimetría a la derecha;
- todos los predictores tienen un rango intercuartil estrecho (IQR);
- todos los predictores tienen valores atípicos significativos;
- el número de ejemplos en los dos niveles de la clase objetivo «Class” tiene un diferencia pequeña.
3.Preparación de los datos
La etapa de preparación de datos incluye tradicionalmente siete etapas:
- “imputation” — eliminación o imputación de datos perdidos/indefinidos;
- “variance” — eliminación de las variables con una varianza de cero o cercana a cero;
- “split” — división del conjunto de datos en los subconjuntos train/valid/test;
- “scaling” — escalado del rango de las variables;
- “outliers” — eliminación o imputación de valores atípicos (outliers);
- “sampling” — corrección del desequilibrio de las clases;
- “denoise” — elimiación o redifinición del ruido;
- “selection” — selección de los predictores irrelevantes.
3.1. Limpieza de datos
La primera etapa de preparación de los datos brutos es la eliminación o imputación de valores indefinidos de los valores y las pérdidas en los datos. A pesar de que muchos modelos permiten el uso de datos indifinidos (NA) y también lagunas en los conjuntos, es mejor eliminarlos hasta terminar las manipulaciones generales. Esta operación se realiza en el conjunto completo de datos e independientemente del modelo utilizado.
Más arriba hemos analizado la estadística total de los datos brutos, a partir de la cual se puede ver que hay NA presentes en el conjunto. Se trata de A artificiales que se han formado al calcular los filtros digitales. Son relativamente pocas, por eso es posible eliminarlas. Anteriormente hemos obtenido el conjunto de datos dataSet, preparado para su procesamiento posterior. Vamos a limpiarlo.
En general, entendemos por limpieza las siguientes operaciones:
- eliminación de predictores con una varianza de cero o próxima a cero (method = c(“zv”, “nzv”));
- eliminación de variables altamente correlacionadas. El umbral del coeficiente de correlación es establecido por el usuario (method = “corr”), por defecto, es igual a 0.9. Este estadio no es siempre necesario, dependiendo de los siguientes métodos de transformación;
- eliminación de los predictores que solo tengan un valor único en cualquier clase (method = “conditionalX”).
Todas estas operaciones son implementadas en la función preProcess()::caret por los métodos enumerados más arriba, y se ejecuta con el conjunto de datos al completo hasta la división en los conjuntos de entrenamiento y de prueba.
require(caret)
evalq({preProClean <- preProcess(x = dataSet,method = c("zv", "nzv", "conditionalX", "corr"))
dataSetClean <- predict(preProClean, dataSet %>% na.omit)},
env)
Vamos a ver si hay predictores eliminados, y qué ha quedado tras la limpieza:
> env$preProClean$method$remove #[1] "v.rbci" > dim(env$dataSetClean) [1] 7906 13 > colnames(env$dataSetClean) [1] "Data" "ftlm" "stlm" "rbci" "pcci" [6] "v.fatl" "v.satl" "v.rftl" "v.rstl" "v.ftlm" [11] "v.stlm" "v.pcci" "Class"
3.2. Deteccción y procesamiento de valores atípicos (outliers)
Los problemas con la calidad de los datos, tales como la asimetría y los valores atípicos (outliers) con frecuencia son interdependientes y están interrelacionados. Esto no solo hace el procesamiento preliminar bastante laborioso, sino que también dificulta la tarea de encontrar interconexiones y tendencias en nuestra muestra.
¿Qué son los valores atípicos (outliers)?
Vamos a dar una definición: entendemos por valor atípico una observación que es demasiado grande o demasiado pequeña en comparación con la mayoría de observaciones disponibles. La clasificación profunda de los valores atípicos, sus métodos de definición y su procesamiento se muestran en [2].
Tipos de valores atípicos
Los valores atípicos conllevan desviaciones significativas en la distribución de variables y en el aprendizaje basado en un modelo con datos semejantes. Existe un gran número de métodos de identificación y procesamiento de valores atípicos, que dependen de cómo los definamos: de forma local o global. Los valores atípicos locales son los valores atípicos de una variable. Los valores atípicos globales son los valores atípicos en un espacio multidimensional, definido por una matriz o un frame de datos.
¿Qué provoca los valores atípicos?
Los valores atípicos se pueden clasificar según su procedencia:
Artificiales
- error de introducción de datos — errores surgidos durante la recopilación, el guardado o el procesamiento de datos;
- errores del experimento;
- errores de la muestra.
Errores naturales, provocados por la propia naturaleza de la variable.
¿Qué influencia representan los valores atípicos?
Los valores atípicos pueden estropear los resultados del análisis de datos y el modelado estadístico: esto aumenta la dispersión de los errores y reduce la capacidad estadística de las pruebas; si los valores atípicos no están distribuidos de forma casual, pueden reducir la normalidad; los valores atípicos también pueden influir en las suposiones principales de los análisis de regresión y dispersión y otras asunciones del modelo.
¿Cómo determinar los "valores atípicos" locales?
Con mayor frecuencia, los valores atípicos se detectan con ayuda de la visualización. Un ejemplo muy sencillo y ampliamente utilizado es el diagrama de caja o boxplot. Por ejemplo, vamos a mirar el predictor ftlm:
evalq(ggplot(dataSetClean, aes(x = factor(0),
y = ftlm,
color = 'red')) +
geom_boxplot() + xlab("") +
scale_x_discrete(breaks = NULL) +
coord_flip(),
env)
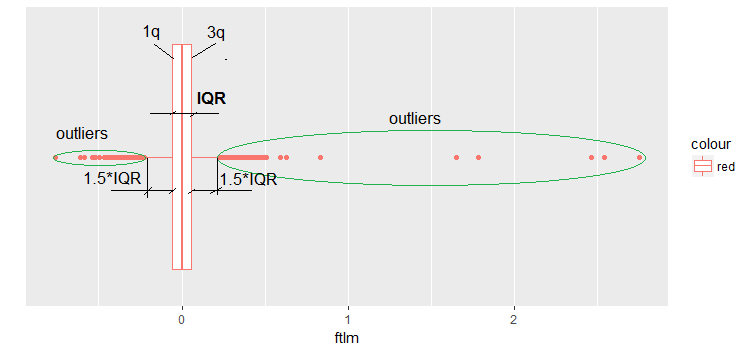
Fig.9. Boxplot ftlm
Algunas aclaraciones a la imagen:
IQR — rango intercuartílico o distancia entre el primer y el tercer cuartil.
Existen varias formas de definir los valores atípicos:
- Cualquier valor menor a -1.5*IQR y superior a +1.5*IQR es un valor atípico. Cuando se toma un coeficiente igual a 2 o 3. Todos los valores entre 1.5*IQR y 3*IQR son llamados valores atípicos medios, y todos los que está fuera de los límites 3*IQR, valores atípicos extremos.
- Cualquier valor fuera del rango de los percentiles 5 y 95 se puede considerar valor atípico.
- Los puntos ubicados a una distancia de tres o más MSD son también valores atípicos.
En lo sucesivo, vamos a utilizar la primera definición de los valores atípicos (a través IQR).
¿Cómo procesar los valores atípicos?
La mayoría de los métodos de procesamiento de valores atípicos se parecen a los métodos de procesamiento de los valores NA indefinidos: eliminación de las observaciones, transformación de las mismas, segmentación y otros métodos.
- Eliminación de los valores atípicos: eliminamos los valores si aparecen como resultado de un error en la introducción de los datos, un error en el procesamiento de los datos o si se observan muy pocos valores atípicos. Asimismo, podemos recortar la distribución en ambos extremos, para eliminar los valores atípicos. Por ejemplo, eliminar un 1% por encima y por debajo.
- Transformación y vinculación por segmentos (binning):
- la transformación de variables puede excluir los valores atípicos (veremos esto en el siguiente apartado);
- el logartimo natural del valor reduce los valores provocados por los valores extremos (también lo veremos en el siguiente apartado);
- la discretización también es una forma de transformar una variable (ver también el siguiente apartado);
- también podemos usar el proceso de atribución de pesos para diferentes observaciones (no vamos a analizar este tema).
Imputación: Los mismos métodos que hemos aplicado para la imputación de los valores indifinidos, los podremos aplicar a los valores atípicos. Podemos usar la media, la mediana o el modo. Antes de imputar los valores, deberemos analizar si estamos ante un valor atípico o uno artificial. Si es artificial, podemos pasar a la imputación.
Si en la muestra hay un número significativo de valores atípicos, deberemos analizarlos aparte del modelo estadístico. Aquí solo analizamos los métodos generales usados para luchar con los valores atípicos: la eliminación y la imputación.
Eliminación de valores atípicos
Eliminamos los valores de los valores atípicos si han aparecido a causa de un error en la introducción o el procesamiento de datos, o si el número de valores atípicos es muy bajo (solo al definir la métrica de las variables estadísticas).
Es posible extraer los datos de una variable (ftlm, por ejemplo) sin valores atípicos de esta forma:
evalq({dataSetClean$ftlm -> x
out.ftlm <- x[!x %in% boxplot.stats(x)$out]},
env)
O así:
evalq({dataSetClean$ftlm -> x
out.ftlm1 <- x[x > quantile(x, .25) - 1.5*IQR(x) &
x < quantile(x, .75) + 1.5*IQR(x)]},
env)
¿Son iguales?
> evalq(all.equal(out.ftlm, out.ftlm1), env)
[1] TRUE
¿Cuántos datos han entrado en los valores atípicos?
> nrow(env$dataSetClean) - length(env$out.ftlm) [1] 402
Veamos el aspecto que tiene ftlm sin valores atípicos:
boxplot(env$out.ftlm, main = "ftlm without outliers", boxwex = 0.5)
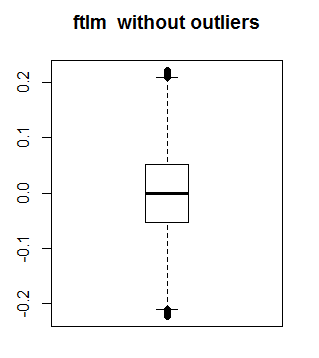
Fig. 10. ftlm sin valores atípicos
Es posible aplicar el método enunciado más arriba a matrices y frames de datos, puesto que cada variable en el frame de datos puede tener un número distinto de valores atípicos. Para estos valores atípicos es aplicable el método de sustitución de valores atípicos locales por NA, seguido de la aplicación de los métodos estándar de procesamiento de NA. Vamos a escribir una función que sustituya los valores atípicos por NA:
#-------remove_outliers------------------------------- remove_outliers <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) y <- x y[x < (qnt[1] - H)] <- NA y[x > (qnt[2] + H)] <- NA y }
Sustituimos los valores atípicos por NA en nuestro conjunto de datos dataSetClean en todas las variables excepto c(Data, Class), y vemos cómo cambia la distribución del conjunto obtenido x.out:
evalq({
dataSetClean %>% select(-c(Data,Class)) %>% as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
remove_outliers(x[ ,i])
} -> x.out
colnames(x.out) <- colnames(x)
},
env)
par(mfrow = c(1, 1))
chart.Boxplot(env$x,
main = "x.out with outliers",
xlab = "")
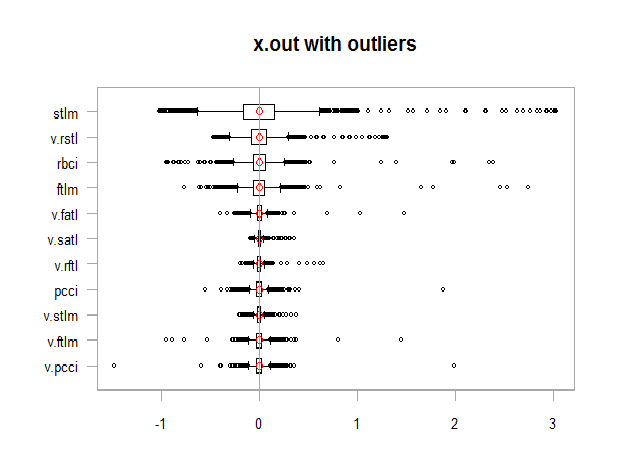
Fig. 11. Datos con valores atípicos
chart.Boxplot(env$x.out, main = "x.out without outliers", xlab = "")
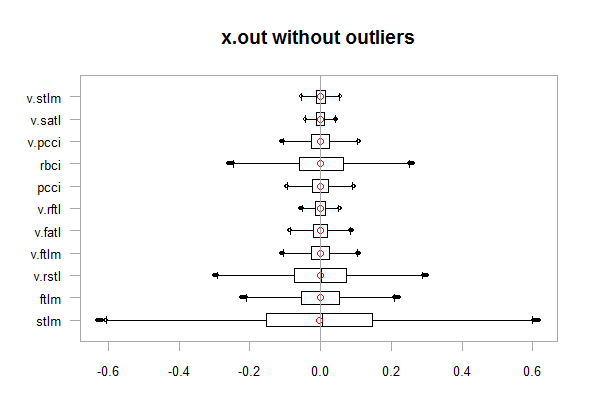
Fig.12. Datos sin valores atípicos
Imputando el NA que aparece en lugar de los valores atípicos
Entendemos por imputación el proceso de sustitución de los valores ausentes, incorrectos o inválidos por otros valores. Al suministrar los datos para el entrenamiento, deberemos sustituir NA por valores válidos. Variantes:
- sustituimos NA por mean, mediana, mod (en este caso, las características estadísticas no cambian)
- sustituimos los valores atípicos superiores a 1.5*IQR, por un percentil 0.95, y los valores atípicos menores a 1.5*IQR por un percentil 0.05.
Vamos a escribir una función que ejecute la última variante de acción. Después ejecutaremos la transformación y echaremos un vistazo a la distribución tras la transformación:
#-------capping_outliers-------------------------------
capping_outliers <- function(x, na.rm = TRUE, ...) {
qnt <- quantile(x, probs = c(.25, .75),
na.rm = na.rm, ...)
caps <- quantile(x, probs = c(.05, .95),
na.rm = na.rm, ...)
H <- 1.5 * IQR(x, na.rm = na.rm)
y <- x
y[x < (qnt[1] - H)] <- caps[1]
y[x > (qnt[2] + H)] <- caps[2]
y
}
evalq({dataSetClean %>% select(-c(Data,Class)) %>%
as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
capping_outliers(x[ ,i])
} -> x.cap
colnames(x.cap) <- colnames(x)
},
env)
chart.Boxplot(env$x.cap,
main = "x.cap with capping outliers",
xlab = "")
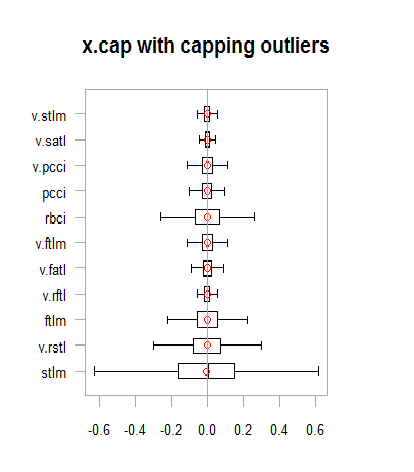
Fig.13. Conjunto de datos con valores atípicos imputados
Vamos a ver la variación y la covariación de nuestras variables en el conjunto dataSetCap (se trata del mismo conjunto dataSet, pero limpiado y con valores atípicos locales imputados). Puesto que el número de variables (13) no permite ubicarlas en un solo gráfico, vamos a dividirlas en tres grupos.
evalq(x.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetCap, env) require(GGally) evalq(ggpairs(dataSetCap, columns = 2:7, mapping = aes(color = Class), title = "PredCap1"), env)
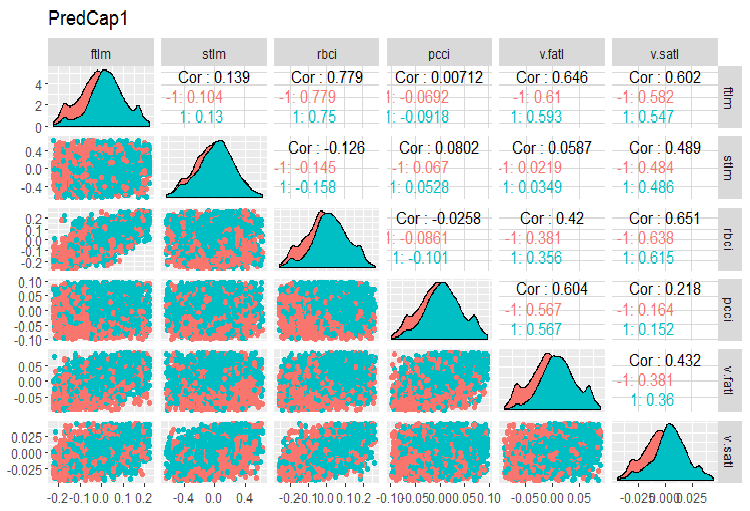
Fig.14. Variación y covariación de la primera parte del conjunto de datos con valores atípicos imputados.
Y la segunda parte del conjunto:
evalq(ggpairs(dataSetCap, columns = 8:13, mapping = aes(color = Class), title = "PredCap2"), env)
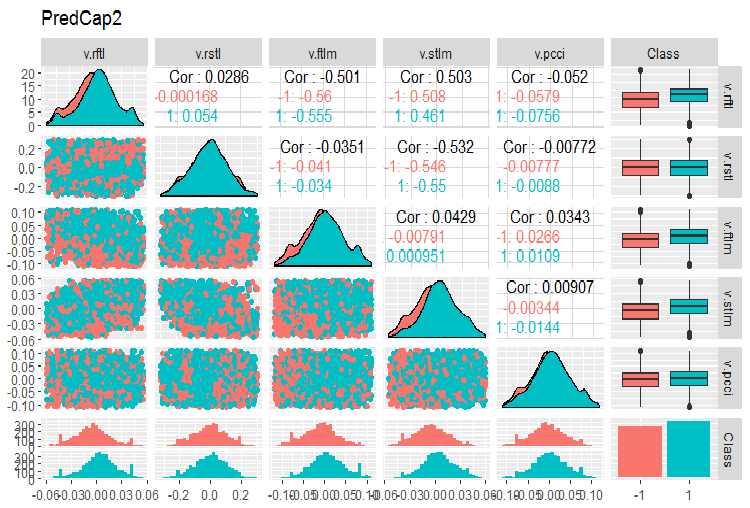
Fig.15. Variación y covariación de la segunda parte del conjunto de datos con valores atípicos imputados.
¿Cómo determinar los valores atípicos globales?
Los valores atípicos bidimensionales y multidimensionales se miden con la ayuda de un índice de influencia o proximidad. Para detectar los valores atípicos globales se usan diferentes distancias. Podemos utilizar varios paquetes (DMwR, mvoutliers,Rlof), que contienen funciones para determinar los valores atípicos globales, evaluados con la ayuda de LOF (local outlier factor), el factor de los valores atípicos locales. Calculamos y comparamos el LOF para un conjunto con los valores atípicos x y para un conjunto con los valores atípicos imputados x.cap.
##------DMwR2------------------- require(DMwR2) evalq(lof.x <- lofactor(x,10), env) evalq(lof.x.cap <- lofactor(x.cap,10), env) par(mfrow = c(1, 3)) boxplot(env$lof.x, main = "lof.x", boxwex = 0.5) boxplot(env$lof.x.cap, main = "lof.x.cap", boxwex = 0.5) hist(env$lof.x.cap, breaks = 20) par(mfrow = c(1, 1))
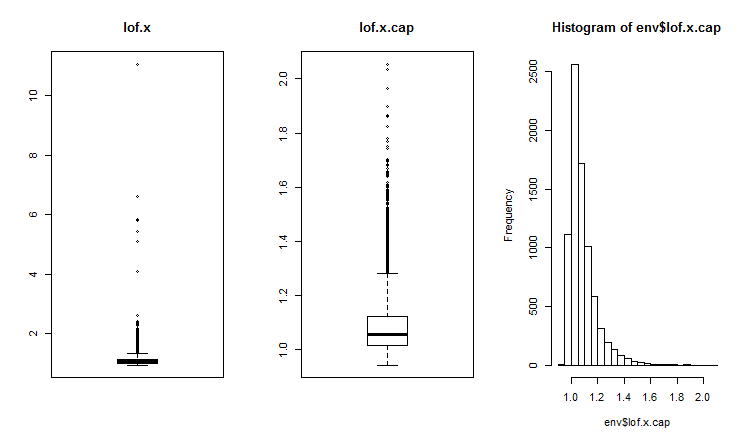
Fig.16. Factor global de los valores atípicos para un conjunto de datos con valores atípicos y un conjunto con valores atípicos imputados
En el paquete Rlof se implementa la función lof(). Encuentra el factor local outlier [3] de los datos de matriz usando los k vecinos más cercanos. El factor local de valor atípico (LOF) — mide la probabilidad de pertenencia a los valores atípicos. Se calcula para cada observación. Basándose en esta medida, el usuario decide si la observación se analizará como muestra o no.
El LOF tiene en cuenta el entorno de la observación para definir su aspecto. Esta es una implementación rápida del LOF que usa otra estructura de datos y funciones de cálculo de la distancia en comparación con la función lofactor(), disponible en el paquete “dprep”. Asimismo, soporta varios valores k que se calcularán de forma simultánea, así como varias medidas de distancia, además de la distancia euclidiana estándar. El cálculo se realiza simultáneamente en varios procesadores del ordenador. Calculamos lofactor para los dos mismos conjuntos (x y x.cap) para 5, 6, 7, 8, 9 y 10 vecinos usando el cálculo de la distancia “minkowski”. Construimos el histograma de estos lofactor.
require(Rlof) evalq(Rlof.x <- lof(x, c(5:10), cores = 2, method = 'minkowski'), env) evalq(Rlof.x.cap <- lof(x.cap, c(5:10), cores = 2, method = 'minkowski'), env) par(mfrow = c(2, 3)) hist(env$Rlof.x.cap[ ,6], breaks = 20) hist(env$Rlof.x.cap[ ,5], breaks = 20) hist(env$Rlof.x.cap[ ,4], breaks = 20) hist(env$Rlof.x.cap[ ,3], breaks = 20) hist(env$Rlof.x.cap[ ,2], breaks = 20) hist(env$Rlof.x.cap[ ,1], breaks = 20) par(mfrow = c(1, 1))
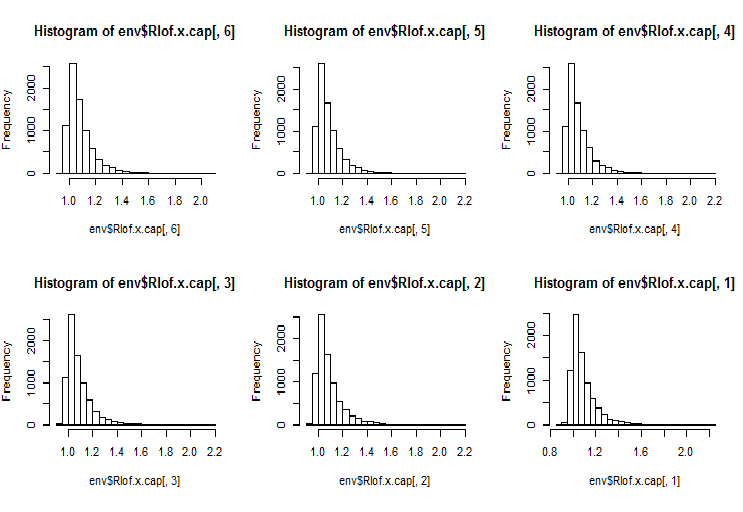
Fig.17. Factor global de valores atípicos para los diferentes valores de k vecinos
Prácticamente todas las observaciones se encuentran en los límites de lofactor =1.6. Fuera de este límite:
> sum(env$Rlof.x.cap[ ,6] >= 1.6) [1] 32
Se trata de un número insignificante de valores atípicos moderados para un tamaño de conjunto semejante.
NOTA. Al definir los límites, superando los cuales los valores de las variables se tratarán como valor atípico, se usará un conjunto de datos de entrenamiento Los valores de las variables de los conjuntos de prueba/validación se procesan con la ayuda de los parámetros obtenidos con el conjunto de entrenamiento. ¿De qué parámetros se trata? Los que hemos utilizado en cálculos anteriores son los límites upper = 1.5*IQR, lower = -1.5*IQR y cap =c(0.05, 0.95) percentil. Si se han aplicado otros métodos de cálculo de los límites y las imputaciones de los valores atípicos, se los definirá con el conjunto de entrenamiento, guardándolos y usándolos al procesar los conjuntos valid/test posteriormente.
Vamos a escribir la función que realizará el cálculo preliminar:
#-----prep.outlier-------------- prep.outlier <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) caps <- quantile(x, probs = c(.05, .95), na.rm = na.rm, ...) list(lower = qnt[1] - H, upper = qnt[2] + H, med = median(x), cap1 = caps[1], cap2 = caps[2]) }
Vamos a analizar los parámetros necesarios para definir e imputar los conjuntos. Adoptaremos preliminarmente la longitud train de un conjunto de 4000 barras al inicio y las siguientes 2000 barras las usaremos como test.
evalq(
{train <- x[1:4000, ]
foreach(i = 1:ncol(train), .combine = "cbind") %do% {
prep.outlier(train[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
#pre.outl %<>% t()
},
env)
Veamos el resultado:
> env$pre.outl ftlm stlm rbci pcci lower.25% -0.2224942912 -0.59629203 -0.253231002 -9.902232e-02 upper.75% 0.2214486206 0.59242529 0.253529797 9.826936e-02 med -0.0001534451 0.00282525 -0.001184966 8.417127e-05 cap1.5% -0.1700418145 -0.40370452 -0.181326658 -6.892085e-02 cap2.95% 0.1676526431 0.39842675 0.183671973 6.853935e-02 v.fatl v.satl v.rftl v.rstl lower.25% -0.0900973332 -4.259328e-02 -0.0558921804 -0.2858430788 upper.75% 0.0888110249 4.178418e-02 0.0555115004 0.2889057397 med -0.0008581219 -2.130064e-05 -0.0001707447 -0.0001721546 cap1.5% -0.0658731640 -2.929586e-02 -0.0427927888 -0.1951978435 cap2.95% 0.0662353821 3.089833e-02 0.0411091859 0.1820803387 v.ftlm v.stlm v.pcci lower.25% -0.1115823754 -5.366875e-02 -0.1115905239 upper.75% 0.1108670403 5.367466e-02 0.1119495436 med -0.0003560178 -6.370034e-05 -0.0003173464 cap1.5% -0.0765431363 -3.686945e-02 -0.0765950814 cap2.95% 0.0789209957 3.614423e-02 0.0770439553
Como podemos ver, para cada variable en el conjunto se han definido el primer cuartil, el tercero y la mediana, y también el percentil 5 y 95; esto es todo lo necesario para definir y procesar los valores atípicos.
Necesitamos una función que procese los valores atípicos de cualquier conjunto de datos según parámetros definidos con anterioridad. Posibles variantes de procesado: sustitución de los valores atípicos por NA,sustitución de los valores atípicos por una mediana, sustitución de los valores atípicos por percentil el 5/95.
#---------treatOutlier--------------------------------- treatOutlier <- function(x, impute = TRUE, fill = FALSE, lower, upper, med, cap1, cap2){ if (impute) { x[x < lower] <- cap1 x[x > upper] <- cap2 return(x) } if (!fill) { x[x < lower | x > upper] <- NA return(x) } else { x[x < lower | x > upper] <- med return(x) } }
Puesto que ya hemos definido los parámetros necesarios con el conjunto de entrenamiento, procesaremos los valores atípicos con el conjunto de entrenamiento, sustituyéndolos por el percentil 5/95. Después procesaremos de la misma forma los valores atípicos con el conjunto de prueba, y a continuación compararemos las distribuciones en los conjuntos obtenidos construyendo tres gráficos.
#------------
evalq(
{
foreach(i = 1:ncol(train), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = train[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> train.out
colnames(train.out) <- colnames(train)
},
env
)
#-------------
evalq(
{test <- x[4001:6000, ]
foreach(i = 1:ncol(test), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = test[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> test.out
colnames(test.out) <- colnames(test)
},
env
)
#---------------
evalq(boxplot(train, main = "train with outliers"), env)
evalq(boxplot(train.out, main = "train.out without outliers"), env)
evalq(boxplot(test.out, main = "test.out without outliers"), env)
#------------------------
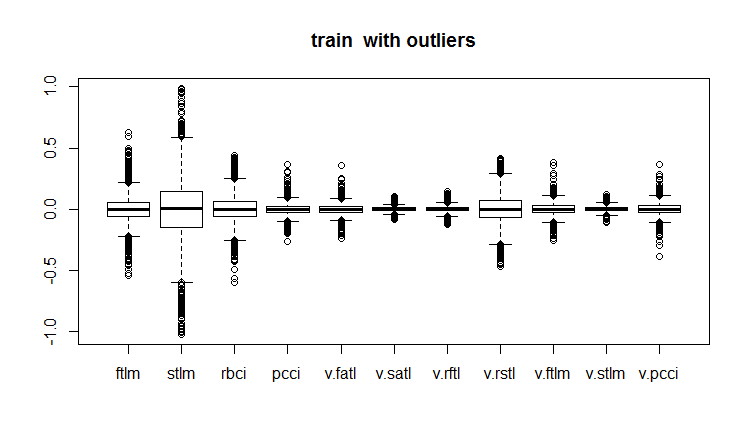
Fig.18. Conjunto de datos de entrenamiento con valores atípicos
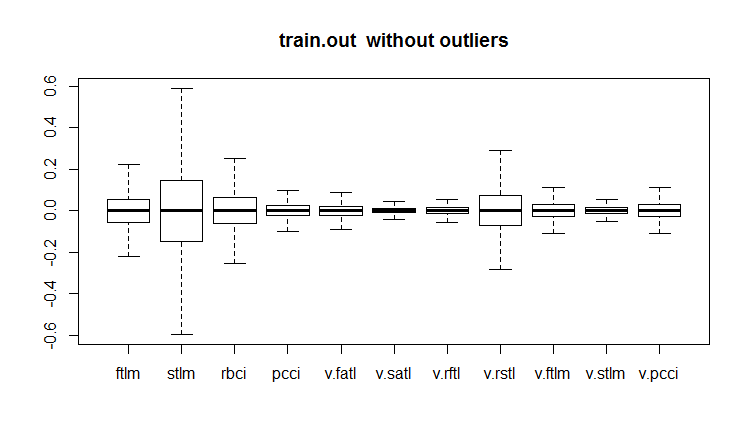
Fig.19. Conjunto de datos de entrenamiento con valores atípicos imputados
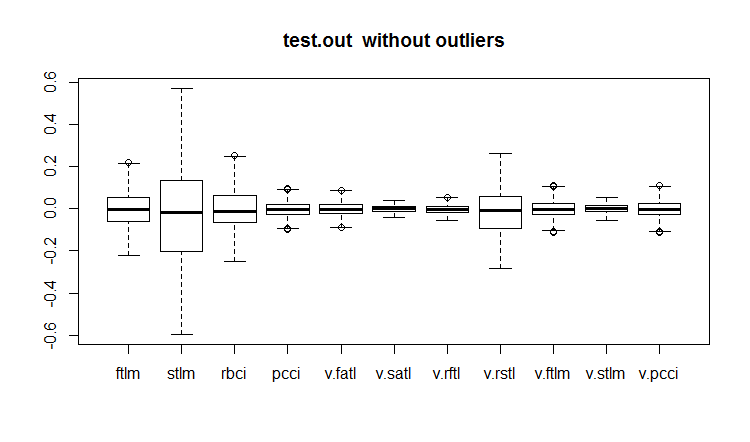
Fig.20. Conjunto de datos de prueba con valores atípicos imputados
No todos los modelos se muestran sensibles a los valores atípicos. Por ejemplo, los modelos como los árboles de decisión (DT) y los bosques aleatorios (RF) no son sensibles a ellos.
Al definir y procesar los valores atípicos, también pueden ser útiles otros paquetes: “univOutl”, “mvoutlier”, “outlier”, funModeling::prep.outlier().
3.3. Eliminando la asimetría (skewness)
La asimetría es una indicación de la forma de distribución. El método general para comprobarla es calcular el coficiente de asimetría de una variable. Normalmente, una asimetría negativa indica que la media es menor que la mediana, y la distribución tiene una asimetría a la izquierda. Una asimetría positiva indica que la media es mayor que la mediana, y la distribución de los datos tiene una asimetría a la derecha.
Si la asimetría del predictor es igual a 0, entonces los datos son totalmente simétricos.
Si la asimetría del predictor es menor a -1 o superior a +1, entonces los datos están fuertemente distorsinados.
Si la asimetría del predictor se encuentra entre -1 y -1/2 o entre +1 y +1/2, los datos están moderadamente distorsinados.
Si la asimetría del predictor es igual a -1/2 y +1/2, entonces los datos son aproximadamente simétricos.
La asimetría a la derecha se corrige usando logaritmos, a la izquierda, se corrige con una función exponencial.
Ya hemos hablado de que la asimetría, los valores atípicos y otras transformaciones están relacionados. Vamos a ver cómo ha cambiado el índice de asimetría después de eliminar e imputar los valores atípicos.
evalq({
sk <- skewness(x)
sk.out <- skewness(x.out)
sk.cap <- skewness(x.cap)
},
env)
> env$sk
ftlm stlm rbci pcci v.fatl
Skewness 4.219857 1.785286 2.304655 6.491546 5.274871
v.satl v.rftl v.rstl v.ftlm v.stlm
Skewness 2.677162 3.954098 1.568675 1.207227 0.8516043
v.pcci
Skewness 3.031012
> env$sk.out
ftlm stlm rbci pcci
Skewness -0.04272076 -0.07893945 -0.02460354 0.01485785
v.fatl v.satl v.rftl v.rstl
Skewness 0.00780424 -0.02640635 -0.04663711 -0.04290957
v.ftlm v.stlm v.pcci
Skewness -0.0009597876 0.01997082 0.0007462494
> env$sk.cap
ftlm stlm rbci pcci
Skewness -0.03329392 -0.07911245 -0.02847851 0.01915228
v.fatl v.satl v.rftl v.rstl
Skewness 0.01412182 -0.02617518 -0.03412228 -0.04596505
v.ftlm v.stlm v.pcci
Skewness 0.008181183 0.009661169 0.002252508
Como podemos ver, tanto el conjunto con valores atípicos eliminados x.out, como el conjunto con valores atípicos imputados x.cap tienen una simetría ideal y no necesitan ninguna corrección.
Vamos a comprobar también la curtosis (kurtosis). La curtosis (coeficiente de pico) — mide la agudeza del pico de distribución de una magnitud aleatoria. En una distribución normal es igual a 0. Es positivo si el pico de distribución cerca de la esperanza matemática es agudo, y negativo, si el pico es muy suave.
require(PerformanceAnalytics)
evalq({
k <- kurtosis(x)
k.out <- kurtosis(x.out)
k.cap <- kurtosis(x.cap)
},
env)
> env$k
ftlm stlm rbci pcci
Excess Kurtosis 84.61177 16.77141 45.01858 247.9795
v.fatl v.satl v.rftl v.rstl
Excess Kurtosis 145.9547 36.99944 74.4307 13.57613
v.ftlm v.stlm v.pcci
Excess Kurtosis 86.36448 23.06635 233.5408
> env$k.out
ftlm stlm rbci
Excess Kurtosis -0.003083449 -0.1668102 -0.1197043
pcci v.fatl v.satl
Excess Kurtosis -0.05113439 -0.02738558 -0.04341552
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.01219999 -0.1316499 -0.0287925
v.stlm v.pcci
Excess Kurtosis -0.1530424 -0.09950709
> env$k.cap
ftlm stlm rbci
Excess Kurtosis -0.2314336 -0.3075185 -0.2982044
pcci v.fatl v.satl
Excess Kurtosis -0.2452504 -0.2389486 -0.2331203
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.2438431 -0.2673441 -0.2180059
v.stlm v.pcci
Excess Kurtosis -0.2763058 -0.2698028
En el conjunto de datos original x los picos de distribución de las variables son extremadamente agudos (la curtosis es mucho mayor a 0). En el conjunto x.out con valores atípicos eliminados, los picos están próximos a la agudeza de pico normal; en el conjunto con valores atípicos imputados, las cimas son más suaves. Ninguno de los conjuntos necesita correcciones.
Anexos
1 En el directorio DARCH12_1.zip se encuentran los scripts para la primera parte del artículo (dataRaw.R, PrepareData.R, FUNCTION.R), así como las imágenes de la sesión de Rstudio con los datos originales de Cotir.RData. Cargue los datos en Rstudio, así usted podrá reproducir todos los scripts, y también experimentar con ellos. Asimismo, podrá descargar todo ello desde Git /Part_I.
2. En el directorio ACTF.zip encontrará el artículo de V.Kravchuk "New Adaptive Method of Following the Tendency and Market Cycles"
3. El directorio R_intro.zip contiene materiales de referencia sobre el lenguaje R.
Enlaces
[1] A Systematic Approach on Data Pre-processing In Data Mining. COMPUSOFT, An international journal of advanced computer technology, 2 (11), November-2013 (Volume-II, Issue-XI)
[2] Outlier Detection Techniques.Hans-Peter Kriegel, Peer Kröger, Arthur Zimek. Ludwig-Maximilians-Universität München.Munich, Germany
[3] Breuning, M., Kriegel, H., Ng, R.T, and Sander. J. (2000). LOF: Identifying density-based local outliers. In Proceedings of the ACM SIGMOD International Conference on Management of Data.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/3486
Neuroredes profundas (Parte II). Desarrollo y selección de predictores
TradeObjects: Automatización del trading a base de objetos gráficos en MetaTrader
Examinamos en la práctica el método adaptativo del seguimiento del mercado
Creación y simulación de símbolos personalizados en MetaTrader 5
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso