
Redes Neurais Profundas (Parte V). Otimização Bayesiana de hiperparâmetros de uma DNN
Conteúdo
- Introdução
- 1. Determinando os hiperparâmetros ótimos da DNN (darch)
- Gerando os conjuntos de dados de origem
- Removendo os preditores estatisticamente insignificantes
- Determinando os hiperparâmetros da DNN a serem otimizados e seus intervalos de valores
- Definindo as funções de pré-treinamento e o ajuste fino para a DNN
- Definindo a função de adequação para a otimização
- Calculando os parâmetros ótimos da DNN
- 2. Treinando e testando a DNN com os parâmetros ótimos
- 3. Analisando os resultados do teste da DNN com os parâmetros ótimos
- 4. Testando fora da amostra os modelos com parâmetros ótimos
- Conclusão
- Aplicação
Introdução
O artigo anterior considerou um modelo básico e um modelo da DNN com os parâmetros padrão. A qualidade de classificação desse modelo revelou-se insatisfatória. O que pode ser feito para melhorar a qualidade da classificação?
- Otimizar os hiperparâmetros da DNN
- Melhorar a regularização da DNN
- Aumentar o número de amostras de treinamento
- Alterar a estrutura da rede neural
Todas as oportunidades listadas para melhorar a DNN existente serão consideradas neste e nos próximos artigos. Vamos começar com a otimização dos hiperparâmetros da rede.
1. Determinando os hiperparâmetros ótimos da DNN
No caso geral, os hiperparâmetros da rede neural podem ser divididos em dois grupos: global e local (nodal). Os hiperparâmetros globais incluem o número de camadas ocultas, o número de neurônios em cada camada, o nível de aprendizado, o momento, a inicialização dos pesos dos neurônios. Hiperparâmetros locais — tipo de camada, função de ativação, dropout/dropconnect e outros parâmetros de regularização.
A estrutura da otimização dos hiperparâmetros é exibida na figura:
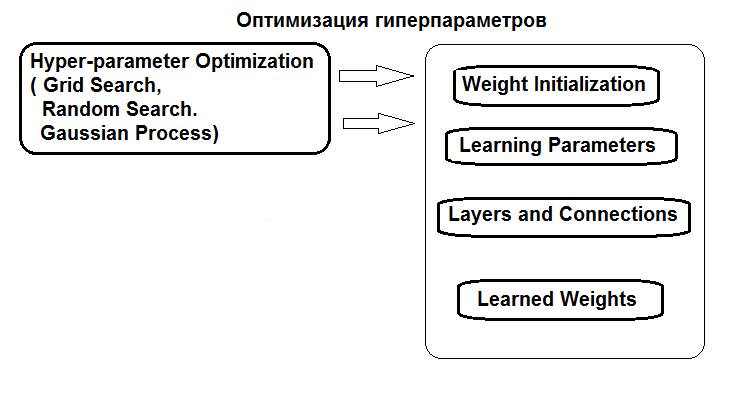
Fig.1. Estrutura dos hiperparâmetros da rede neural e seus métodos de otimização
Os hiperparâmetros podem ser otimizados de três maneiras:
- Grid search: para cada hiperparâmetro, é definido um vetor com vários valores fixos. Em seguida, usando a função caret::train() ou um script personalizado, o modelo é treinado em todas as combinações de valores do hiperparâmetro. Depois disso, o modelo com os melhores valores de qualidade de classificação é selecionado. Seus parâmetros serão considerados ótimos. A desvantagem deste método é que definindo uma grade de valores é mais provável que ele perca o ótimo.
- Otimização genética: busca estocástica dos melhores parâmetros utilizando algoritmos genéticos. Os diversos algoritmos de otimização genética foram discutidos em detalhes anteriormente. Portanto, eles não serão repetidos.
- E, finalmente, a otimização Bayesiana. Ele será usado neste artigo.
A abordagem Bayesiana inclui os processos Gaussianos e MCMC. O pacote rBayesianOptimization (versão 1.1.0) será usado. A teoria dos métodos aplicados é amplamente disponível na literatura e é fornecida neste artigo, por exemplo.
Para realizar uma otimização Bayesiana, é necessário:
- determinar a função de aptidão;
- determinar a lista e os limites das alterações nos hiperparâmetros.
A função de aptidão (FF) deve retornar um score de qualidade (critério de otimização, escalar) que deve ser maximizado durante a otimização, e os valores previstos da função objetivo. FF retornará o valor de mean(F1) — o valor médio de F1 para as duas classes. O modelo da DNN será treinado com pré-treinamento.
Gerando os conjuntos de dados de origem
Para os experimentos, a nova versão do MRO 3.4.2 será usada. Ele possui vários novos pacotes que não foram usados antes.
Execute o RStudio, vá para GitHub/Part_ para baixar o arquivo Cotir.RData com aspas, obtido a partir do terminal, e busque o arquivo FunPrepareData.R com as funções de preparação de dados do GitHub/Part_IV.
Anteriormente, foi determinado que um conjunto de dados com outliers imputados e dados normalizados possibilita obter melhores resultados no treinamento com pré-treinamento. Você também pode testar as outras opções de pré-processamento consideradas anteriormente.
Ao dividir em subconjuntos pretrain/train/val/test, nós usamos a primeira oportunidade para melhorar a qualidade da classificação — aumentar o número de amostras para treinamento. O número de amostras no subconjunto pretrain será aumentado para 4000.
#----Prepare------------- library(anytime) library(rowr) library(darch) library(rBayesianOptimization) library(foreach) library(magrittr) #source(file = "FunPrepareData.R") #source(file = "FUN_Optim.R") #---prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt, 4000, 1000, 500, 100, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) preproc <- PreNorm(DTcap, meth = meth) DTcap.n <- NormData(DTcap, preproc = preproc) }, env)
Ao mudar o parâmetro start na função SplitData(), é possível obter os conjuntos deslocados para a direita pela quantidade de start. Isso permite verificar a qualidade em diferentes partes da faixa de preço no futuro e determinar como ela se altera no histórico.
Removendo os preditores estatisticamente insignificantes
Remova duas variáveis estatisticamente insignificantes c(v.rstl, v.pcci). Eles foram determinados no o artigo anterior desta série.
##---Data DT-------------- require(foreach) evalq({ foreach(i = 1:4) %do% { DTcap.n[[i]] %>% dplyr::select(-c(v.rstl, v.pcci)) } -> DT list(pretrain = DT[[1]], train = DT[[2]], val = DT[[3]], test = DT[[4]]) -> DT }, env)
Crie os conjuntos de dados (pretrain/train/test/test1) para pré-treinamento, ajuste fino e teste, reunidos na lista X.
#-----Data X------------------
evalq({
list(
pretrain = list(
x = DT$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$pretrain$Class %>% as.data.frame()
),
train = list(
x = DT$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$train$Class %>% as.data.frame()
),
test = list(
x = DT$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$val$Class %>% as.data.frame()
),
test1 = list(
x = DT$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DT$test$Class %>% as.vector()
)
) -> X
}, env)
Os conjuntos para os experimentos estão prontos.
É necessário uma função para calcular as métricas dos resultados do teste. O valor da média (F1) será usado como critério de otimização (maximização). Carregue esta função no ambiente env.
evalq( #input actual & predicted vectors or actual vs predicted confusion matrix # https://github.com/saidbleik/Evaluation/blob/master/eval.R Evaluate <- function(actual=NULL, predicted=NULL, cm=NULL){ if (is.null(cm)) { actual = actual[!is.na(actual)] predicted = predicted[!is.na(predicted)] f = factor(union(unique(actual), unique(predicted))) actual = factor(actual, levels = levels(f)) predicted = factor(predicted, levels = levels(f)) cm = as.matrix(table(Actual = actual, Predicted = predicted)) } n = sum(cm) # number of instances nc = nrow(cm) # number of classes diag = diag(cm) # number of correctly classified instances per class rowsums = apply(cm, 1, sum) # number of instances per class colsums = apply(cm, 2, sum) # number of predictions per class p = rowsums / n # distribution of instances over the classes q = colsums / n # distribution of instances over the predicted classes #accuracy accuracy = sum(diag) / n #per class recall = diag / rowsums precision = diag / colsums f1 = 2 * precision * recall / (precision + recall) #macro macroPrecision = mean(precision) macroRecall = mean(recall) macroF1 = mean(f1) #1-vs-all matrix oneVsAll = lapply(1:nc, function(i){ v = c(cm[i,i], rowsums[i] - cm[i,i], colsums[i] - cm[i,i], n - rowsums[i] - colsums[i] + cm[i,i]); return(matrix(v, nrow = 2, byrow = T))}) s = matrix(0, nrow = 2, ncol = 2) for (i in 1:nc) {s = s + oneVsAll[[i]]} #avg accuracy avgAccuracy = sum(diag(s))/sum(s) #micro microPrf = (diag(s) / apply(s,1, sum))[1]; #majority class mcIndex = which(rowsums == max(rowsums))[1] # majority-class index mcAccuracy = as.numeric(p[mcIndex]) mcRecall = 0*p; mcRecall[mcIndex] = 1 mcPrecision = 0*p; mcPrecision[mcIndex] = p[mcIndex] mcF1 = 0*p; mcF1[mcIndex] = 2 * mcPrecision[mcIndex] / (mcPrecision[mcIndex] + 1) #random accuracy expAccuracy = sum(p*q) #kappa kappa = (accuracy - expAccuracy) / (1 - expAccuracy) #random guess rgAccuracy = 1 / nc rgPrecision = p rgRecall = 0*p + 1 / nc rgF1 = 2 * p / (nc * p + 1) #rnd weighted rwgAccurcy = sum(p^2) rwgPrecision = p rwgRecall = p rwgF1 = p classNames = names(diag) if (is.null(classNames)) classNames = paste("C",(1:nc),sep = "") return(list( ConfusionMatrix = cm, Metrics = data.frame( Class = classNames, Accuracy = accuracy, Precision = precision, Recall = recall, F1 = f1, MacroAvgPrecision = macroPrecision, MacroAvgRecall = macroRecall, MacroAvgF1 = macroF1, AvgAccuracy = avgAccuracy, MicroAvgPrecision = microPrf, MicroAvgRecall = microPrf, MicroAvgF1 = microPrf, MajorityClassAccuracy = mcAccuracy, MajorityClassPrecision = mcPrecision, MajorityClassRecall = mcRecall, MajorityClassF1 = mcF1, Kappa = kappa, RandomGuessAccuracy = rgAccuracy, RandomGuessPrecision = rgPrecision, RandomGuessRecall = rgRecall, RandomGuessF1 = rgF1, RandomWeightedGuessAccurcy = rwgAccurcy, RandomWeightedGuessPrecision = rwgPrecision, RandomWeightedGuessRecall = rwgRecall, RandomWeightedGuessWeightedF1 = rwgF1))) }, env) #-------------------------
A função retorna uma ampla gama de métricas, das quais apenas a F1 é necessária no momento.
Será utilizada uma rede neural com duas camadas ocultas, como na parte anterior do artigo. A DNN será treinada em duas etapas, com pré-treinamento. As opções possíveis são:
- Pré-treinamento:
- treinar somente a SRBM;
- treinar a SRBM + a camada superior da rede neural.
- Afinação:
- usa o método de treino backpropagation;
- usa o método de treino rpropagation.
Cada uma das quatro opções de treinamento possui um conjunto diferente de hiperparâmetros para otimização.
Definindo os hiperparâmetros para otimização
Vamos definir a lista de hiperparâmetros com os valores a serem otimizados, bem como a sua faixa de valores:
- n1, n2 — o número de neurônios em cada camada oculta. Os valores variam de 1 a 25. Antes de alimentar o modelo, o parâmetro é multiplicado por 2, pois requer um múltiplo de 2 (poolSize). Isso é necessário para a função de ativação maxout.
- fact1, fact2 — índices da função de ativação para cada camada oculta, selecionados da lista de funções de ativação definidas pelo vetor Fact <- c("tanhUnit", "maxoutUnit", "softplusUnit", "sigmoidUnit"). Você também pode adicionar outras funções.
- dr1, dr2 — o valor de dropout em cada camada, varia de 0 a 0.5.
- Lr.rbm — o nível de treinamento StackedRBM, varia de 0.01 a 1.0 no estágio de pré-treinamento.
- Lr.top — o nível de treinamento da camada superior da rede neural no estágio de pré-treinamento, variando de 0.01 a 1.0. Este parâmetro não é necessário para o pré-treinamento sem treinar a camada superior da rede neural.
- Lr.fine — o nível de treinamento da rede neural na fase de ajuste fino ao usar a backpropagation varia de 0.01 a 1.0. Este parâmetro não é necessário ao usar a rpropagation.
Uma descrição detalhada de todos os parâmetros é fornecida no artigo e na descrição do pacote. Todos os parâmetros da função darch() possuem valores padrão. Eles podem ser divididos em vários grupos.
- Parâmetros globais. Usado tanto para pré-treinamento e para ajuste fino.
- Parâmetros de pré-processamento de dados. São usados os recursos de caret::preProcess().
- Parâmetros para a SRBM. Usado apenas para pré-treinamento.
- Parâmetros da NN. Usado tanto para pré-treinamento como para ajuste fino, mas pode ter valores diferentes para cada estágio.
Os valores do parâmetro padrão podem ser alterados especificando uma lista de seus novos valores ou gravando-os explicitamente na função darch(). Aqui está uma breve descrição dos hiperparâmetros a serem otimizados.
Primeiro, defina os parâmetros globais da DNN, comum para as etapas pretrain/train.
Ln <- c(0, 2*n1, 2*n2, 0) — vetor indicando que uma rede neural de 4 camadas com duas camadas ocultas deve ser criada. O número de neurônios nas camadas de entrada e saída é determinado a partir dos dados de entrada, eles não podem ser especificados explicitamente. O número de neurônios nas camadas ocultas é de 2*n1 e 2*n2, respectivamente.
Em seguida, defina os níveis de treinamento para a RBM (Lr.rbm), para a camada superior da DNN durante o pré-treinamento (Lr.top) e para todas as camadas durante o ajuste fino (Lr.fine).
fact1/fact2 — índices da função de ativação para cada camada oculta de uma lista definida pelo vetor Fact. A função softmax é usada na camada de saída.
dr1/dr2 — Nível de dropout em cada camada oculta.
darch.trainLayers — indica as camadas a serem treinadas usando o pré-treinamento e as camadas a serem treinadas durante o ajuste fino.
Vamos escrever os hiperparâmetros e suas faixas de valores para cada uma das quatro opções de treinamento/otimização. Além disso, os parâmetros Bs.rbm = 100 (rbm.batchSize) e Bs.nn = 50 (darch.batchSize) são feitos externos por conveniência para encontrar as melhores opções de treinamento. Quando eles diminuem, a qualidade da classificação melhora, mas o tempo de otimização aumenta consideravelmente.
#-2---------------------- evalq({ #--InitParams--------------------- Fact <- c("tanhUnit","maxoutUnit","softplusUnit", "sigmoidUnit") wUpd <- c("weightDecayWeightUpdate", "maxoutWeightUpdate", "weightDecayWeightUpdate", "weightDecayWeightUpdate") #---SRBM + RP---------------- bonds1 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0)#, ) #---SRBM + BP---------------- bonds2 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.fine = c(0.01, 1.0) ) #---SRBM + upperLayer + BP---- bonds3 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.top = c(0.01, 1.0), Lr.fine = c(0.01, 1.0) ) #---SRBM + upperLayer + RP----- bonds4 <- list( #n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top n1 = c(1L, 25L), n2 = c(1L, 25L), fact1 = c(1L, 4L), fact2 = c(1L, 4L), dr1 = c(0, 0.5), dr2 = c(0, 0.5), Lr.rbm = c(0.01, 1.0), Lr.top = c(0.01, 1.0) ) Bs.rbm <- 100L Bs.nn <- 50L },envir = env)
Definindo a função de pré-treinamento e ajuste fino
A DNN será treinada usando todas as quatro opções. Todas as funções necessárias para isso estão disponíveis no script FUN_Optim.R, que deve ser baixado antes de iniciar os cálculos com Git/PartV.
As funções de pré-treinamento e ajuste fino para cada opção:
- pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm ) — pré-treinamento apenas para a SRBM
- pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) — pré-treinamento SRBM + camada superior (backpropagation)
- fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) — ajuste fino da DNN usando rpropagation
- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) — ajuste fino da DNN usando backpropagation
Para não confundir o artigo com a listagem de funções semelhantes, será considerado apenas a opção de pré-treinamento (SRBM + topLayer) + RP(ajuste fino da rpropagation). Em muitos experimentos, essa opção apresentou o melhor resultado na maioria dos casos. As funções para outras opções são semelhantes.
# SRBM + upper Layer (backpropagation) pretrainSRBM_topLayer <- function(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) # SRBM + upper Layer (backpropagation) { darch( x = X$pretrain$x, y = X$pretrain$y, xValid = X$train$x, yValid = X$train$y, #=====constant====================================== layers = Ln, paramsList = list(), darch = NULL, shuffleTrainData = T, seed = 54321, logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE. #--optimization parameters---------------------------------- darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"), darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2], "weightDecayWeightUpdate"), rbm.learnRate = Lr.rbm, bp.learnRate = Lr.top, darch.dropout = c(0, dr1, dr2), #=== params RBM ============== rbm.numEpochs = 30L, rbm.allData = T, rbm.batchSize = Bs.rbm, rbm.consecutive = F, rbm.errorFunction = mseError, #rmseError rbm.finalMomentum = 0.9, rbm.initialMomentum = 0.5, rbm.momentumRampLength = 1, rbm.lastLayer = -1, rbm.learnRateScale = 1, rbm.numCD = 1L, rbm.unitFunction = tanhUnitRbm, rbm.updateFunction = rbmUpdate, rbm.weightDecay = 2e-04, #=== parameters NN ======================== darch.numEpochs = 30L, darch.batchSize = Bs.nn, darch.trainLayers = c(FALSE, FALSE,TRUE ), darch.fineTuneFunction = "backpropagation", #rpropagation bp.learnRateScale = 1, #0.99 #--weight----------------- generateWeightsFunction = generateWeightsGlorotUniform, # generateWeightsUniform (default), # generateWeightsGlorotUniform, # generateWeightsHeUniform. # generateWeightsNormal, # generateWeightsGlorotNormal, # generateWeightsHeNormal, darch.weightDecay = 2e-04, normalizeWeights = T, normalizeWeightsBound = 15, #--parameters regularization----------- darch.dither = F, darch.dropout.dropConnect = F, darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2L, darch.maxout.unitFunction = "exponentialLinearUnit", darch.elu.alpha = 2, darch.returnBestModel = T #darch.returnBestModel.validationErrorFactor = 0, ) }
Nesta função, os valores do conjunto X$train são usados como o conjunto de validação.
Função para ajuste fino usando a rpropagation. Além dos parâmetros, uma estrutura pré-roteada da Dnn é passada para essa função.
fineTuneRP <- function(Ln, fact1, fact2, dr1, dr2, Dnn) # rpropagation { darch( x = X$train$x, y = X$train$y, #xValid = X$test$x, yValid = X$test$y, xValid = X$test$x %>% head(250), yValid = X$test$y %>% head(250), #=====constant====================================== layers = Ln, paramsList = list(), darch = Dnn, shuffleTrainData = T, seed = 54321, logLevel = "WARN", #FATAL, ERROR, WARN, DEBUG, and TRACE. rbm.numEpochs = 0L, #--optimization parameters---------------------------------- darch.unitFunction = c(Fact[fact1], Fact[fact2], "softmaxUnit"), darch.weightUpdateFunction = c(wUpd[fact1], wUpd[fact2], "weightDecayWeightUpdate"), darch.dropout = c(0, dr1, dr2), #=== parameters NN ======================== darch.numEpochs = 50L, darch.batchSize = Bs.nn, darch.trainLayers = c(TRUE,TRUE, TRUE), darch.fineTuneFunction = "rpropagation", #"rpropagation" "backpropagation" #=== params RPROP ====== rprop.decFact = 0.5, rprop.incFact = 1.2, rprop.initDelta = 1/80, rprop.maxDelta = 50, rprop.method = "iRprop+", rprop.minDelta = 1e-06, #--weight----------------- darch.weightDecay = 2e-04, normalizeWeights = T, normalizeWeightsBound = 15, #--parameters regularization----------- darch.dither = F, darch.dropout.dropConnect = F, darch.dropout.oneMaskPerEpoch = T, darch.maxout.poolSize = 2L, darch.maxout.unitFunction = "exponentialLinearUnit", darch.elu.alpha = 2, darch.returnBestModel = T #darch.returnBestModel.validationErrorFactor = 0, ) }
Aqui, os primeiros 250 valores do conjunto X$test são usados como o conjunto de validação. Todas as funções para todas as opções de treinamento devem ser carregadas no ambiente env.
Definindo a função de aptidão
Use essas duas funções para escrever uma função de adequação necessária para a otimização dos hiperparâmetros. Ela retorna o valor do critério de otimização Score = mean(F1), que deve ser otimizado, e os valores previstos da função objetivo Ypred.
#---SRBM + upperLayer + RP---- fitnes4.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) { Ln <- c(0, 2*n1, 2*n2, 0) #-- pretrainSRBM_topLayer(Ln, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top) -> Dnn fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn predict(Dnn, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(250) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics$F1 %>% mean() return(list(Score = Score, Pred = Ypred) }
Determinando os parâmetros ideais para a DNN
A função de otimização BayesianOptimization() é iniciada utilizando 10 pontos iniciais no espaço de hiperparâmetros obtidos aleatoriamente. Apesar do fato de que o cálculo é paralelizado em todos os núcleos do processador (Intel MKL), ele ainda leva um tempo considerável e depende do número de iterações e do tamanho de 'batchsize'. Para economizar tempo, comece com 10 iterações. No futuro, se os resultados forem insatisfatórios, a otimização poderá ser continuada usando os valores ideais da execução da otimização anterior como os valores iniciais.
Variante de treinamento SRBM + RP
#---SRBM + RP---------------- evalq( OPT_Res1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 7 n1 = 22.0000 n2 = 2.0000 fact1 = 3.0000 fact2 = 2.0000 dr1 = 0.4114 dr2 = 0.4818 Lr.rbm = 0.7889 Value = 0.7531
Vamos ver as variantes obtidas dos parâmetros ótimos e F1. A função BayesianOptimization() retorna vários valores: os melhores valores do parâmetro — Best_Par, o melhor valor do critério de otimização para esses parâmetros ótimos — Best_Value, histórico de otimização — History, e as previsões obtidas depois de todas as iterações — Pred. Vamos ver o histórico da otimização, classificando-a preliminarmente em ordem decrescente por 'Value'.
evalq({
OPT_Res1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init1
best.init1
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Value
1 22 2 3 2 0.41136623 0.48175897 0.78886312 0.7531204
2 23 8 4 2 0.16814464 0.16221565 0.08381839 0.7485614
3 19 17 3 3 0.17274258 0.46809117 0.72698789 0.7485614
4 25 25 4 2 0.30039573 0.26894463 0.11226139 0.7473266
5 11 24 3 2 0.31564303 0.11091751 0.40387209 0.7462520
6 1 6 3 4 0.36876218 0.17403265 0.90387675 0.7450260
7 25 25 3 1 0.06872059 0.42459582 0.40072731 0.7447972
8 1 25 4 1 0.24871843 0.18593687 0.31920691 0.7445628
9 18 1 4 3 0.49846810 0.38517469 0.51115471 0.7423566
10 13 25 4 1 0.37052548 0.07603925 0.87100360 0.7402597
Este é um bom resultado. Vamos fazer mais uma otimização, mas usando os valores da execução anterior best_init1 para inicializar 10 pontos no espaço de hiperparâmetros.
evalq( OPT_Res1.1 <- BayesianOptimization(fitnes1.DNN, bounds = bonds1, init_grid_dt = best.init1, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env) Best Parameters Found: Round = 1 n1 = 4.0000 n2 = 1.0000 fact1 = 1.0000 fact2 = 4.0000 dr1 = 0.1870 dr2 = 0.0000 Lr.rbm = 0.9728 Value = 0.7608
Vamos ver os 10 melhores resultados desta execução.
evalq({
OPT_Res1.1 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init1
best.init1
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Value
1 4 1 1 4 0.18701522 2.220446e-16 0.9728164 0.7607811
2 3 24 1 4 0.12698982 1.024231e-01 0.5540933 0.7549180
3 5 5 1 3 0.07366640 2.630144e-01 0.2156837 0.7542661
4 1 18 1 4 0.41907554 4.641130e-02 0.6092082 0.7509800
5 1 23 1 4 0.25279461 1.365197e-01 0.2957633 0.7504026
6 4 25 4 1 0.09500347 3.083338e-01 0.2522729 0.7488496
7 17 3 3 3 0.36117416 3.162195e-01 0.4214501 0.7458489
8 13 4 3 3 0.22496776 1.481455e-01 0.4448280 0.7437376
9 21 24 1 3 0.36154287 1.335931e-01 0.6749752 0.7435897
10 5 11 3 3 0.29627244 3.425604e-01 0.1251956 0.7423566
Não só o melhor resultado melhorou, mas também a composição de qualidade dos 10 melhores, as estatísticas 'Value' aumentaram. A otimização pode ser repetida várias vezes, selecionando diferentes pontos iniciais (por exemplo, tente otimizar para os 10 piores valores, etc.).
Para esta variante de treinamento, conheça os seguintes melhores parâmetros:
> env$OPT_Res1.1$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm 4.0000 1.0000 1.0000 4.0000 0.1870 0.0000 0.9728
Vamos interpretá-los. Os seguintes parâmetros ótimos foram obtidos:
- o número de neurônios da primeira camada oculta - 2*n1 = 8
- o número de neurônios da segunda camada oculta - 2*n2 = 2
- função de ativação da primeira camada oculta Fact[fact1] ="tanhdUnit"
- função de ativação da segunda camada oculta Fact[fact2] = "sigmoidUnit"
- nível de dropout da primeira camada oculta dr1 = 0.187
- nível de dropout da segunda camada oculta dr2 = 0.0
- nível de treinamento de SRBM no pré-treinamento Lr.rbm = 0.9729
Além de obter um resultado geralmente bom, uma estrutura interessante da DNN (10-8-2-2) foi formada.
Variante de treinamento SRBM + BP
#---SRBM + BP---------------- evalq( OPT_Res2 <- BayesianOptimization(fitnes2.DNN, bounds = bonds2, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)
Vamos ver os 10 melhores resultados:
> evalq({
+ OPT_Res2 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
+ dplyr::select(-Round) -> best.init2
+ best.init2
+ }, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.fine Value
1 23 24 2 1 0.45133494 0.14589979 0.89897498 0.2325569 0.7612619
2 3 24 4 3 0.07673542 0.42267387 0.59938522 0.4376796 0.7551184
3 15 13 4 1 0.32812018 0.45708556 0.09472489 0.8220925 0.7516732
4 7 18 3 1 0.15980725 0.12045896 0.82638047 0.2752569 0.7473167
5 7 23 3 3 0.37716019 0.23287775 0.61652190 0.9749432 0.7440724
6 21 23 3 1 0.22184400 0.08634275 0.08049532 0.3349808 0.7440647
7 23 8 3 4 0.26182910 0.11339229 0.31787446 0.9639373 0.7429621
8 5 2 1 1 0.25633998 0.27587931 0.17733507 0.4987357 0.7429471
9 1 24 1 2 0.12937722 0.22952235 0.19549144 0.6538553 0.7426660
10 18 8 4 1 0.44986721 0.28928018 0.12523905 0.2441150 0.7384895
O resultado é bom, a otimização adicional não é necessária.
Os melhores hiperparâmetros para esta variante:
> env$OPT_Res2$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.fine 23.0000 24.0000 2.0000 1.0000 0.4513 0.1459 0.8990 0.2326
Variante de treinamento da SRBM + upperLayer + BP
#---SRBM + upperLayer + BP---- evalq( OPT_Res3 <- BayesianOptimization(fitnes3.DNN, bounds = bonds3, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)Best Parameters Found: Round = 20 n1 = 24.0000 n2 = 5.0000 fact1 = 1.0000 fact2 = 2.0000 dr1 = 0.4060 dr2 = 0.2790 Lr.rbm = 0.9586 Lr.top = 0.8047 Lr.fine = 0.8687 Value = 0.7697
Vamos ver os 10 melhores resultados:
evalq({
OPT_Res3 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init3
best.init3
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Lr.fine Value
1 24 5 1 2 0.40597650 0.27897269 0.9585567 0.8046758 0.86871454 0.7696970
2 24 13 1 1 0.02456308 0.08652276 0.9807432 0.8033236 0.87293155 0.7603146
3 7 8 3 3 0.24115850 0.42538540 0.5970306 0.2897183 0.64518524 0.7543239
4 9 15 3 3 0.14951302 0.04013773 0.3734516 0.2499858 0.14993060 0.7521897
5 4 20 3 3 0.45660260 0.12858958 0.8280872 0.1998107 0.08997839 0.7505357
6 21 6 3 1 0.38742051 0.12644262 0.5145560 0.3599426 0.24159111 0.7403176
7 22 3 1 1 0.13356602 0.12940396 0.1188595 0.8979277 0.84890568 0.7369316
8 7 18 3 4 0.44786101 0.33788727 0.4302948 0.2660965 0.75709349 0.7357294
9 25 13 2 1 0.02456308 0.08652276 0.9908265 0.8065841 0.87293155 0.7353894
10 24 17 1 1 0.23273972 0.01572794 0.9193522 0.6654211 0.26861297 0.7346243
O resultado é bom, a otimização adicional não é necessária.
Os melhores hiperparâmetros para esta variante de treinamento:
> env$OPT_Res3$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Lr.fine 24.0000 5.0000 1.0000 2.0000 0.4060 0.2790 0.9586 0.8047 0.8687
Variante de treinamento da SRBM + upperLayer + RP
#---SRBM + upperLayer + RP---- evalq( OPT_Res4 <- BayesianOptimization(fitnes4.DNN, bounds = bonds4, init_grid_dt = NULL, init_points = 10, n_iter = 10, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE) , envir = env)Best Parameters Found: Round = 15 n1 = 23.0000 n2 = 7.0000 fact1 = 3.0000 fact2 = 1.0000 dr1 = 0.3482 dr2 = 0.4726 Lr.rbm = 0.0213 Lr.top = 0.5748 Value = 0.7625
As 10 melhores variantes dos hiperparâmetros:
evalq({
OPT_Res4 %$% History %>% dplyr::arrange(desc(Value)) %>% head(10) %>%
dplyr::select(-Round) -> best.init4
best.init4
}, env)
n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top Value
1 23 7 3 1 0.34823851 0.4726219 0.02129964 0.57482890 0.7625131
2 24 13 3 1 0.38677878 0.1006743 0.72237324 0.42955366 0.7560023
3 1 1 4 3 0.17036760 0.1465872 0.40598393 0.06420964 0.7554773
4 23 7 3 1 0.34471936 0.4726219 0.02129964 0.57405944 0.7536946
5 19 16 3 3 0.25563914 0.1349885 0.83913339 0.77474220 0.7516732
6 8 12 3 1 0.23000115 0.2758919 0.54359416 0.46533472 0.7475112
7 10 8 3 1 0.23661048 0.4030048 0.15234740 0.27667214 0.7458489
8 6 19 1 2 0.18992796 0.4779443 0.98278107 0.84591090 0.7391758
9 11 10 1 2 0.47157135 0.2730922 0.86300945 0.80325083 0.7369316
10 18 21 2 1 0.05182149 0.3503253 0.55296502 0.86458533 0.7359324
O resultado é bom, a otimização adicional não é necessária.
Obtenha os melhores hiperparâmetros para esta variante de treinamento:
> env$OPT_Res4$Best_Par %>% round(4) n1 n2 fact1 fact2 dr1 dr2 Lr.rbm Lr.top 23.0000 7.0000 3.0000 1.0000 0.3482 0.4726 0.0213 0.5748
Treinando e testando a DNN com os parâmetros ótimos
Vamos considerar as métricas obtidas testando as variantes.
Variante da SRBM + RP
Para testar a DNN com os parâmetros ótimos, vamos criar uma função especial. Ela será mostrada aqui, apenas para esta variante de treino. Ela é semelhante para outras variantes.
#---SRBM + RP---------------- test1.DNN <- function(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm) { Ln <- c(0, 2*n1, 2*n2, 0) #-- pretrainSRBM(Ln, fact1, fact2, dr1, dr2, Lr.rbm) -> Dnn fineTuneRP(Ln, fact1, fact2, dr1, dr2, Dnn) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(250) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(250) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Score <- Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) return(list(Score = Score, Pred = Ypred, Dnn = Dnn, Dnn.opt = Dnn.opt)) }
Os parâmetros da função test1.DNN() são os hiperparâmetros ótimos obtidos anteriormente. Em seguida, execute um pré-treinamento usando a função pretrainSRBM(), obtenha uma DNN pré-treinada, que é posteriormente alimentada para a função de ajuste fineTuneRP(), resultando em um treinamento Dnn.opt. Usando esta Dnn.opt e os últimos 250 valores do conjunto X$test$, obtenha os valores previstos da função objetivo Ypred. Usando o Ypred previsto e os valores reais da função objetivo yTest, calcule um número de métricas com a função Evaluate(). Várias opções para a seleção de métricas estão disponíveis aqui. Como resultado, a função gera uma lista dos seguintes objetos: Score — métricas de teste, Pred — valores previstos da função de objetivo, Dnn — DNN pré-treinada, Dnn.opt — DNN totalmente treinada.
Teste e visualização do resultado com os hiperparâmetros obtidos após a otimização adicional:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res1.1$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Ln <- c(0, 2*n1, 2*n2, 0)
#---train/test--------
Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
}, env)
env$Res1$Score
Accuracy Precision Recall F1
-1 0.74 0.718 0.724 0.721
1 0.74 0.759 0.754 0.757
O resultado é pior do que após a primeira otimização, o overfitting é evidente. Testando com os valores iniciais dos hiperparâmetros:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res1$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Ln <- c(0, 2*n1, 2*n2, 0)
#---train/test--------
Res1 <- test1.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm)
}, env)
env$Res1$Score
Accuracy Precision Recall F1
-1 0.756 0.757 0.698 0.726
1 0.756 0.755 0.806 0.780
O resultado é bom. Vamos traçar um gráfico do histórico de treinamento:
plot(env$Res1$Dnn.opt, type = "class")
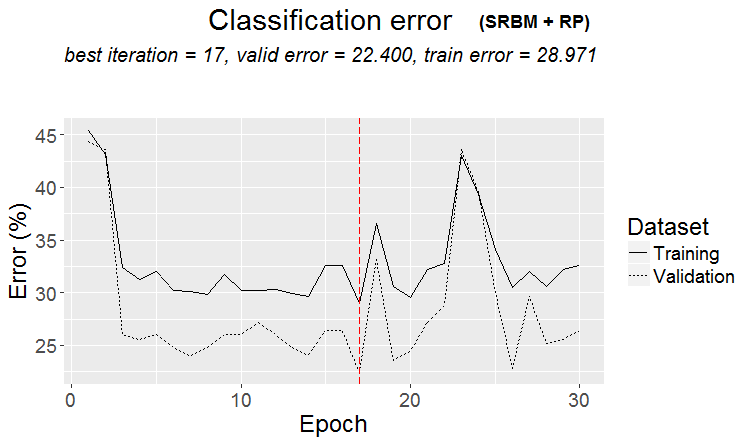
Fig.2. Histórico de treinamento da DNN pela variante SRBM + RP
Como pode ser visto na figura, o erro no conjunto de validação é menor que o erro no conjunto de treinamento. Isso significa que o modelo não sofreu overfitting e tem uma boa capacidade de generalização. A linha vertical vermelha indica os resultados do modelo que é considerado o melhor e que retornou como resultado após o treinamento.
Para as outras três variantes de treinamento, serão fornecidos apenas os resultados de cálculos e gráficos do histórico, sem mais detalhes. Tudo é calculado de forma semelhante.
Variante SRBM + BP
Testando:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res2$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]; Lr.fine = best.par[8]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res2 <- test2.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.fine)
}, env)
env$Res2$Score
Accuracy Precision Recall F1
-1 0.768 0.815 0.647 0.721
1 0.768 0.741 0.873 0.801
Pode-se dizer que o resultado é excelente. Vamos ver o histórico de treinamento:
plot(env$Res2$Dnn.opt, type = "class")
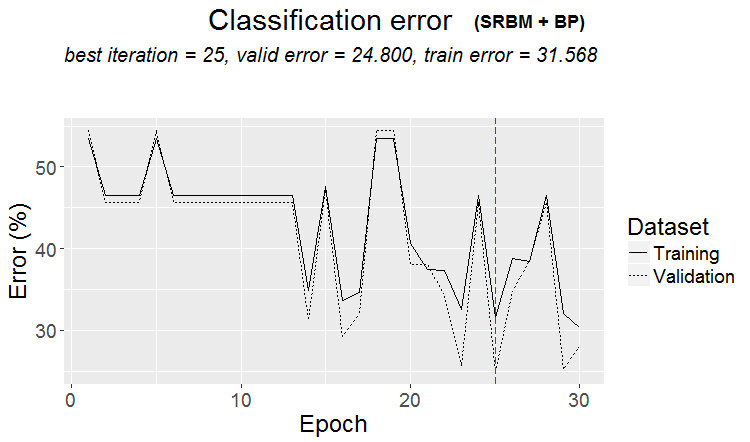
Fig.3. Histórico de treinamento da DNN pela variante SRBM + ВP
Variante SRBM + upperLayer + BP
Testando:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res3$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Lr.top = best.par[8]
Lr.fine = best.par[9]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res3 <- test3.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top, Lr.fine)
}, env)
env$Res3$Score
Accuracy Precision Recall F1
-1 0.772 0.771 0.724 0.747
1 0.772 0.773 0.813 0.793
Excelente resultado. Observe que usar o valor médio de F1 como critério de otimização produz a mesma qualidade para as duas classes, apesar do desequilíbrio entre elas.
Gráficos do histórico de treinamento:
plot(env$Res3$Dnn.opt, type = "class")
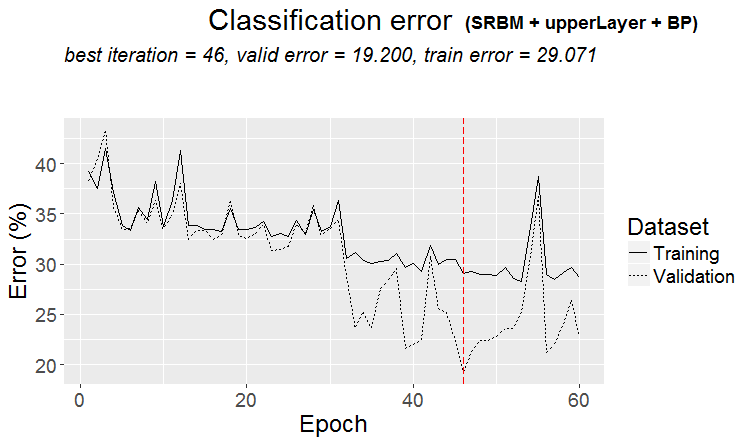
Fig. 4. Histórico de treinamento da DNN pela variante SRBM + upperLayer + BP
Variante SRBM + upperLayer + RP
Testando:
evalq({
#--BestParams--------------------------
best.par <- OPT_Res4$Best_Par %>% unname
# n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top
n1 = best.par[1]; n2 = best.par[2]
fact1 = best.par[3]; fact2 = best.par[4]
dr1 = best.par[5]; dr2 = best.par[6]
Lr.rbm = best.par[7]
Lr.top = best.par[8]
Ln <- c(0, 2*n1, 2*n2, 0)
#----train/test-------
Res4 <- test4.DNN(n1, n2, fact1, fact2, dr1, dr2, Lr.rbm, Lr.top)
}, env)
env$Res4$Score
Accuracy Precision Recall F1
-1 0.768 0.802 0.664 0.726
1 0.768 0.747 0.858 0.799
Um resultado muito bom. Vamos ver o gráfico do histórico de treinamento:
plot(env$Res4$Dnn.opt, type = "class")
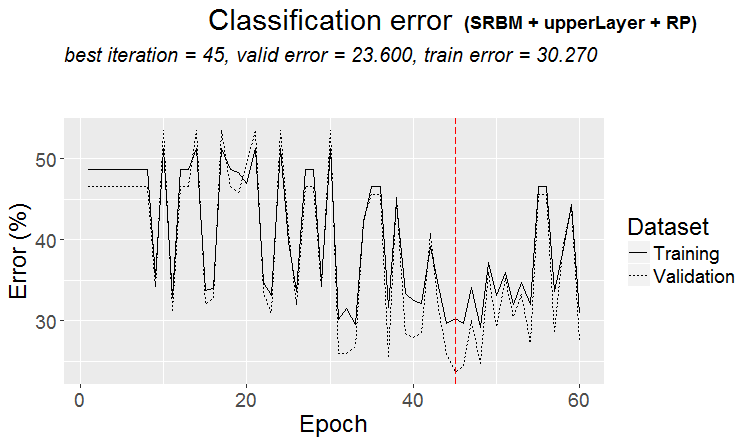
Fig. 5. Histórico de treinamento da DNN pela variante SRBM + upperLayer + RP
Analisando os resultados do teste da DNN com os parâmetros ótimos
Os resultados do treinamento e teste dos modelos da DNN treinados por diferentes variantes com valores otimizados de hiperparâmetros produzem bons resultados com uma precisão de 75 (+/-5)%. O erro de classificação de 25% é estável, não depende do método de treinamento e sugere que a estrutura de dados não corresponde à estrutura da função objetivo em um quarto dos casos. O mesmo resultado foi observado quando se estudou a presença das amostras de ruído no conjunto de dados de origem. Lá, o número deles também era de 25% e não dependia dos métodos de transformação dos preditores. Isto é normal. Pergunta: como melhorar a previsão sem sobrecarregar o modelo? Existem várias opções:
- usando um conjunto de redes neurais composto pelos melhores modelos treinados por 4 variantes;
- utilizando ensembles de redes neurais compostos pelos 10 melhores modelos, obtidos durante a otimização por cada variante de treinamento;
- renomear as amostras de ruído no conjunto de treinamento para uma classe adicional "0" e usar essa função objetiva (com três classes с("-1", "0", "1") para treinar o modelo da DNN;
- renomear as amostras classificadas de forma errada com a classe adicional "0" e usar essa função objetiva (com três classes с("-1", "0", "1")) para treinar o modelo da DNN.
A criação, o treinamento e o uso de ensembles serão considerados em detalhes no próximo artigo desta série.
O experimento com a remarcação dos exemplos de ruído merece um estudo separado e excede o escopo deste artigo. A ideia é simples. Usando a função ORBoostFilter::NoiseFiltersR considerada na parte anterior, determinar as amostras de ruído nos conjuntos de treinamento e validação simultaneamente. Na função objetivo, os valores das classes ("-1"/"1") correspondentes a essas amostras são substituídos pela classe "0". Ou seja, a função objetivo terá três classes. Desta forma, nós tentamos ensinar o modelo a não classificar as amostras de ruído, que geralmente causam o erro de classificação. Ao mesmo tempo, nós vamos nos basear na suposição de que o lucro perdido não é uma perda.
Testando fora da amostra os modelos com parâmetros ótimos
Vamos verificar por quanto tempo os parâmetros ótimos da DNN produzirão resultados com qualidade aceitável para os testes dos valores das cotações "futuras". O teste será realizado no ambiente restante após as otimizações anteriores e testado da seguinte maneira.
Use uma janela móvel de 1350 barras, train = 1000, test = 350 (para validação — as primeiras 250 amostras, para teste — as últimas 100 amostras) com passo 100 para percorrer os dados após as primeiras (4000 + 100) barras usadas para pré-treinamento. Faça 10 passos "fora da amostra". Em cada etapa, dois modelos serão treinados e testados:
- primeiro — usando a DNN pré-treinada, ou seja, executar um ajuste fino em um novo intervalo em cada etapa;
- segundo — treinando adicionalmente a DNN.opt, obtida após a otimização no estágio de ajuste fino, em um novo intervalo.
#---prepare----
evalq({
step <- 1:10
dt <- PrepareData(Data, Open, High, Low, Close, Volume)
DTforv <- foreach(i = step, .packages = "dplyr" ) %do% {
SplitData(dt, 4000, 1000, 350, 10, start = i*100) %>%
CappingData(., impute = T, fill = T, dither = F, pre.outl = pre.outl)%>%
NormData(., preproc = preproc) -> DTn
foreach(i = 1:4) %do% {
DTn[[i]] %>% dplyr::select(-c(v.rstl, v.pcci))
} -> DTn
list(pretrain = DTn[[1]],
train = DTn[[2]],
val = DTn[[3]],
test = DTn[[4]]) -> DTn
list(
pretrain = list(
x = DTn$pretrain %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$pretrain$Class %>% as.data.frame()
),
train = list(
x = DTn$train %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$train$Class %>% as.data.frame()
),
test = list(
x = DTn$val %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$val$Class %>% as.data.frame()
),
test1 = list(
x = DTn$test %>% dplyr::select(-c(Data, Class)) %>% as.data.frame(),
y = DTn$test$Class %>% as.vector()
)
)
}
}, env)
Realize a primeira parte do teste fora da amostra usando a DNN pré-treinada e os hiperparâmetros ótimos, obtidos a partir da variante de treinamento SRBM + upperLayer + BP.
#----#---SRBM + upperLayer + BP---- evalq({ #--BestParams-------------------------- best.par <- OPT_Res3$Best_Par %>% unname # n1, n2, fact1, fact2, dr1, dr2, Lr.rbm , Lr.top, Lr.fine n1 = best.par[1]; n2 = best.par[2] fact1 = best.par[3]; fact2 = best.par[4] dr1 = best.par[5]; dr2 = best.par[6] Lr.rbm = best.par[7] Lr.top = best.par[8] Lr.fine = best.par[9] Ln <- c(0, 2*n1, 2*n2, 0) foreach(i = step, .packages = "darch" ) %do% { DTforv[[i]] -> X if(i==1) Res3$Dnn -> Dnn #----train/test------- fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred yTest <- X$test$y[ ,1] %>% tail(100) #numIncorrect <- sum(Ypred != yTest) #Score <- 1 - round(numIncorrect/nrow(xTest), 2) Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>% round(3) } -> Score3_dnn }, env)
A segunda etapa do teste fora da amostra é usando a Dnn.opt obtida durante a otimização:
evalq({
foreach(i = step, .packages = "darch" ) %do% {
DTforv[[i]] -> X
if(i==1) {Res3$Dnn.opt -> Dnn}
#----train/test-------
fineTuneBP(Ln, fact1, fact2, dr1, dr2, Dnn, Lr.fine) -> Dnn.opt
predict(Dnn.opt, newdata = X$test$x %>% tail(100) , type = "class") -> Ypred
yTest <- X$test$y[ ,1] %>% tail(100)
#numIncorrect <- sum(Ypred != yTest)
#Score <- 1 - round(numIncorrect/nrow(xTest), 2)
Evaluate(actual = yTest, predicted = Ypred)$Metrics[ ,2:5] %>%
round(3)
} -> Score3_dnnOpt
}, env)
Compare os resultados do teste, colocando-os em uma tabela:
env$Score3_dnn env$Score3_dnnOpt
| iter | Score3_dnn | Score3_dnnOpt |
|---|---|---|
| Accuracy Precision Recall F1 | Accuracy Precision Recall F1 | |
| 1 | -1 0.76 0.737 0.667 0.7 1 0.76 0.774 0.828 0.8 |
-1 0.77 0.732 0.714 0.723 1 0.77 0.797 0.810 0.803 |
| 2 | -1 0.79 0.88 0.746 0.807 1 0.79 0.70 0.854 0.769 |
-1 0.78 0.836 0.78 0.807 1 0.78 0.711 0.78 0.744 |
| 3 | -1 0.69 0.807 0.697 0.748 1 0.69 0.535 0.676 0.597 |
-1 0.67 0.824 0.636 0.718 1 0.67 0.510 0.735 0.602 |
| 4 | -1 0.71 0.738 0.633 0.681 1 0.71 0.690 0.784 0.734 |
-1 0.68 0.681 0.653 0.667 1 0.68 0.679 0.706 0.692 |
| 5 | -1 0.56 0.595 0.481 0.532 1 0.56 0.534 0.646 0.585 |
-1 0.55 0.578 0.500 0.536 1 0.55 0.527 0.604 0.563 |
| 6 | -1 0.61 0.515 0.829 0.636 1 0.61 0.794 0.458 0.581 |
-1 0.66 0.564 0.756 0.646 1 0.66 0.778 0.593 0.673 |
| 7 | -1 0.67 0.55 0.595 0.571 1 0.67 0.75 0.714 0.732 |
-1 0.73 0.679 0.514 0.585 1 0.73 0.750 0.857 0.800 |
| 8 | -1 0.65 0.889 0.623 0.733 1 0.65 0.370 0.739 0.493 |
-1 0.68 0.869 0.688 0.768 1 0.68 0.385 0.652 0.484 |
| 9 | -1 0.55 0.818 0.562 0.667 1 0.55 0.222 0.500 0.308 |
-1 0.54 0.815 0.55 0.657 1 0.54 0.217 0.50 0.303 |
| 10 | -1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
-1 0.71 0.786 0.797 0.791 1 0.71 0.533 0.516 0.525 |
A tabela mostra que as duas primeiras etapas produzem bons resultados. A qualidade é na verdade a mesma nos dois primeiros passos de ambas as variantes e depois cai. Portanto, pode-se supor que, após a otimização e o teste, a DNN manterá a qualidade de classificação no nível do conjunto de teste em pelo menos 200-250 barras a seguir.
Existem muitas outras combinações para o treinamento adicional de modelos em testes fora da amostra mencionados no artigo e numerosos hiperparâmetros ajustáveis.
Conclusão
- O pacote darch v.0.12 fornece acesso a uma lista enorme de hiperparâmetros da DNN, oferecendo grandes oportunidades para ajustes profundos e finos.
- O uso da abordagem Bayesiana para otimizar os hiperparâmetros da DNN oferece uma ampla escolha de modelos com boa qualidade, que podem ser usados para a criação dos conjuntos.
- A otimização dos hiperparâmetros da DNN usando o método Bayesiano dá uma melhoria de 7 a 10% na qualidade da classificação.
- Para obter o melhor resultado, é necessário realizar múltiplas otimizações (10 - 20), seguidas da seleção do melhor resultado.
- O processo de otimização pode ser continuado passo a passo, alimentando os parâmetros obtidos nas execuções preliminares como os valores iniciais.
- O uso de hiperparâmetros obtidos durante a otimização na DNN garante que a qualidade de classificação de um teste direto seja mantida no nível de teste na seção com o tamanho igual ao conjunto de teste.
Para melhoramentos adicionais, faz sentido suplementar a lista de parâmetros otimizados com a função de treinamento rpropagation em 4 variantes, normalização de pesos de neurônios nas camadas ocultas normalizeWeights(TRUE, FALSE) e o limite superior desta normalização normalizeWeightsBound. Você pode experimentar outros parâmetros que, na sua opinião, podem influenciar a qualidade da classificação do modelo. Uma das principais vantagens do pacote darch é que ele fornece acesso a todos os parâmetros da rede neural. É possível determinar experimentalmente como cada parâmetro afeta a qualidade da classificação.
Apesar dos consideráveis custos de tempo, o uso da otimização Bayesiana é aconselhável.
O uso de um ensemble de redes neurais parece ser outra possibilidade para melhorar a qualidade da classificação. Esta opção de reforço em diferentes variantes será discutida na próxima parte do artigo.
Aplicação
O repositório GitHub/PartV contém:
1. FUN_Optim.R — funções necessárias para executar todos os cálculos descritos neste artigo.
2. RUN_Optim.R — cálculos realizados neste artigo.
3. SessionInfo. txt — pacotes usados em cálculos.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/4225
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Como criar um painel gráfico de qualquer nível de complexidade
Como criar um painel gráfico de qualquer nível de complexidade
 Trabalhemos com os resultados da otimização através da interface gráfica do usuário
Trabalhemos com os resultados da otimização através da interface gráfica do usuário
 Gráfico de saldo multissímbolo no MetaTrader 5
Gráfico de saldo multissímbolo no MetaTrader 5
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Outro retardado aqui
https://github.com/yanyachen/rBayesianOptimization/blob/master/R/Utility_Max.R
Também configurei maxit = 1 em vez de 100.
Por ... não pode ser passado, você pode simplesmente carregar sua função Utility_Max no R e usar a versão corrigida.
Eu a verifiquei na otimização do conjunto de redes neurais do artigo da Parte VI. Nem o maxit nem o controle têm um efeito visível no tempo de computação. A maior influência é o número de neurônios na camada oculta. Deixei assim
OPT_Res <- BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100, control = c(100, 50, 8)) elapsed = 14.42 Round = 1 numFeature = 9.0000 r = 7.0000 nh = 36.0000 fact = 9.0000 Value = 0.7530 elapsed = 42.94 Round = 2 numFeature = 4.0000 r = 8.0000 nh = 46.0000 fact = 6.0000 Value = 0.7450 elapsed = 9.50 Round = 3 numFeature = 11.0000 r = 5.0000 nh = 19.0000 fact = 5.0000 Value = 0.7580 elapsed = 14.17 Round = 4 numFeature = 10.0000 r = 4.0000 nh = 35.0000 fact = 4.0000 Value = 0.7480 elapsed = 12.36 Round = 5 numFeature = 8.0000 r = 4.0000 nh = 23.0000 fact = 6.0000 Value = 0.7450 elapsed = 25.61 Round = 6 numFeature = 12.0000 r = 8.0000 nh = 44.0000 fact = 7.0000 Value = 0.7490 elapsed = 8.03 Round = 7 numFeature = 12.0000 r = 9.0000 nh = 9.0000 fact = 2.0000 Value = 0.7470 elapsed = 14.24 Round = 8 numFeature = 8.0000 r = 4.0000 nh = 45.0000 fact = 2.0000 Value = 0.7620 elapsed = 9.05 Round = 9 numFeature = 7.0000 r = 8.0000 nh = 20.0000 fact = 10.0000 Value = 0.7390 elapsed = 17.53 Round = 10 numFeature = 12.0000 r = 9.0000 nh = 20.0000 fact = 6.0000 Value = 0.7410 elapsed = 4.77 Round = 11 numFeature = 9.0000 r = 2.0000 nh = 7.0000 fact = 2.0000 Value = 0.7570 elapsed = 8.87 Round = 12 numFeature = 6.0000 r = 1.0000 nh = 40.0000 fact = 8.0000 Value = 0.7730 elapsed = 14.16 Round = 13 numFeature = 8.0000 r = 6.0000 nh = 41.0000 fact = 10.0000 Value = 0.7390 elapsed = 21.61 Round = 14 numFeature = 9.0000 r = 6.0000 nh = 47.0000 fact = 7.0000 Value = 0.7620 elapsed = 5.14 Round = 15 numFeature = 13.0000 r = 3.0000 nh = 3.0000 fact = 5.0000 Value = 0.7260 elapsed = 5.66 Round = 16 numFeature = 6.0000 r = 9.0000 nh = 1.0000 fact = 9.0000 Value = 0.7090 elapsed = 7.26 Round = 17 numFeature = 9.0000 r = 2.0000 nh = 25.0000 fact = 1.0000 Value = 0.7550 elapsed = 32.09 Round = 18 numFeature = 11.0000 r = 7.0000 nh = 38.0000 fact = 6.0000 Value = 0.7600 elapsed = 17.18 Round = 19 numFeature = 5.0000 r = 3.0000 nh = 46.0000 fact = 6.0000 Value = 0.7500 elapsed = 11.08 Round = 20 numFeature = 6.0000 r = 4.0000 nh = 20.0000 fact = 6.0000 Value = 0.7590 elapsed = 4.47 Round = 21 numFeature = 6.0000 r = 2.0000 nh = 4.0000 fact = 2.0000 Value = 0.7390 elapsed = 5.27 Round = 22 numFeature = 6.0000 r = 2.0000 nh = 21.0000 fact = 10.0000 Value = 0.7520 elapsed = 7.96 Round = 23 numFeature = 7.0000 r = 1.0000 nh = 41.0000 fact = 7.0000 Value = 0.7730 elapsed = 12.31 Round = 24 numFeature = 7.0000 r = 3.0000 nh = 41.0000 fact = 3.0000 Value = 0.7730 elapsed = 7.64 Round = 25 numFeature = 8.0000 r = 4.0000 nh = 16.0000 fact = 7.0000 Value = 0.7420 elapsed = 6.24 Round = 26 numFeature = 13.0000 r = 5.0000 nh = 6.0000 fact = 1.0000 Value = 0.7600 elapsed = 8.41 Round = 27 numFeature = 11.0000 r = 8.0000 nh = 8.0000 fact = 7.0000 Value = 0.7420 elapsed = 8.48 Round = 28 numFeature = 6.0000 r = 7.0000 nh = 15.0000 fact = 2.0000 Value = 0.7580 elapsed = 10.11 Round = 29 numFeature = 12.0000 r = 6.0000 nh = 17.0000 fact = 4.0000 Value = 0.7310 elapsed = 6.03 Round = 30 numFeature = 8.0000 r = 3.0000 nh = 12.0000 fact = 1.0000 Value = 0.7540 elapsed = 8.58 Round = 31 numFeature = 13.0000 r = 5.0000 nh = 18.0000 fact = 2.0000 Value = 0.7300 elapsed = 6.78 Round = 32 numFeature = 13.0000 r = 2.0000 nh = 15.0000 fact = 8.0000 Value = 0.7320 elapsed = 9.54 Round = 33 numFeature = 10.0000 r = 3.0000 nh = 37.0000 fact = 9.0000 Value = 0.7420 elapsed = 8.19 Round = 34 numFeature = 6.0000 r = 1.0000 nh = 42.0000 fact = 3.0000 Value = 0.7630 elapsed = 12.34 Round = 35 numFeature = 7.0000 r = 2.0000 nh = 43.0000 fact = 8.0000 Value = 0.7570 elapsed = 20.47 Round = 36 numFeature = 7.0000 r = 8.0000 nh = 39.0000 fact = 2.0000 Value = 0.7670 elapsed = 11.51 Round = 37 numFeature = 5.0000 r = 9.0000 nh = 18.0000 fact = 3.0000 Value = 0.7540 elapsed = 32.71 Round = 38 numFeature = 7.0000 r = 7.0000 nh = 40.0000 fact = 6.0000 Value = 0.7540 elapsed = 28.33 Round = 39 numFeature = 7.0000 r = 9.0000 nh = 38.0000 fact = 5.0000 Value = 0.7550 elapsed = 22.87 Round = 40 numFeature = 12.0000 r = 6.0000 nh = 48.0000 fact = 3.0000 Value = 0.7580 Best Parameters Found: Round = 12 numFeature = 6.0000 r = 1.0000 nh = 40.0000 fact = 8.0000 Value = 0.7730 maxit = 100, control = c(100, 50, 8))Melhor 10
Valor - F1 médio. Não é um desempenho ruim.
Para acelerar os cálculos, precisamos reescrever algumas funções do pacote. A primeira coisa é substituir todos os ncol(), nrow(), que são muitos, por dim()[1], dim()[2]. Elas são executadas dezenas de vezes mais rápido. E provavelmente, como há apenas operações de matriz, usar GPU (pacote gpuR). Não poderei fazer isso sozinho, posso sugerir ao desenvolvedor?
Boa sorte
Verifiquei a otimização do conjunto de redes neurais do documento PartVI. Nem o maxit nem o controle têm um tempo de execução visível. A maior influência é o número de neurônios na camada oculta. Deixei assim
Melhor 10
Valor - F1 médio. Não é um desempenho ruim.
Para acelerar os cálculos, precisamos reescrever algumas funções do pacote. A primeira coisa é substituir todas as funções ncol(), nrow() por dim()[1], dim()[2]. Elas são executadas dezenas de vezes mais rápido. E provavelmente, como há apenas operações de matriz, usar GPU (pacote gpuR). Não poderei fazer isso sozinho, posso sugerir isso ao desenvolvedor?
Boa sorte
Otimize apenas alguns parâmetros. Eu otimizei 20 partes e, quando os pontos conhecidos se tornaram 20-40 partes, o cálculo apenas do GPfit levou dezenas de minutos; nessas condições, você verá a aceleração.
E o número de neurônios afeta apenas o tempo de cálculo do próprio NS.
Basta otimizar alguns parâmetros. Eu otimizei 20 peças e, quando os pontos conhecidos se tornaram 20-40 peças, o cálculo apenas do GPfit levou dezenas de minutos.
E o número de neurônios afeta apenas o tempo de cálculo do próprio NS.
Acho que sim.
Novo artigo Redes Neurais Profundas (Parte V). Otimização bayesiana de hiperparâmetros de DNN foi publicado:
Autor: Vladimir Perervenko