Глубокие нейросети (Часть I). Подготовка данных
11 221
25
Эта статья продолжает и развивает тему "Глубокие нейросети" (DNN), начатую мною в предыдущих статьях (1, 2, 3).
DNN получили широкое применение и интенсивное развитие в различных практических областях. Самые яркие примеры их повседневного использования — распознавание образов и речи, автоматический перевод с одного языка на другой. Применяются они и в трейдинге, поэтому их углубленное изучение на фоне очень быстрого развития алготрейдинга видится мне полезным и перспективным.
В последние годы исследователи предложили и экспериментально подтвердили множество новых идей, методов и подходов к использованию DNN. В этой серии статей будет рассмотрено состояние и основные направления развития темы, проверены на практических экспериментах различные идеи и методы, внимание будет уделено и качественным показателям DNN. В нашей работе будем использовать только многослойные полносвязные нейросети.
Четыре основных вопроса, на которых будет сфокусирована серия статей:
- Подготовка, оценка и усиление входных данных путем различных трансформаций.
- Новые возможности пакета darch (v.0.12). Гибкость и расширенные возможности.
- Применение усиление результатов предсказания (оптимизация гиперпараметров DNN и ансамбли нейросетей).
- Графические возможности для контроля работы эксперта как в процессе обучения, так и в процессе работы.
Настоящая статья посвящена подготовке данных, полученных в торговом терминале, к использованию в нейросети.
Содержание
- Введение. Язык R
- 1. Создание начального (сырого) набора данных
- 2. Разведочный анализ данных
- 3. Подготовка данных
- Приложение
- Ссылки
Введение
Разработка, обучение и тестирование глубокой нейронной сети состоят из основных этапов, идущих в строгой последовательности. Как и в случае любой модели машинного обучения, работу по созданию DNN можно разделить на две неравные части:
- подготовка входных и выходных данных для экспериментов;
- создание, обучение, тестирование и оптимизация параметров модели.
Первый этап занимает большую часть времени реализации проекта: около 70%. При этом от его результатов на 80% зависит результат работы модели. Как известно, "мусор на входе — мусор на выходе". Поэтому состав работ на этом этапе мы рассмотрим очень подробно.
Для повторения экспериментов вам необходимо будет установить MRO 3.4.0 и Rstudio. О том, как установить этот софт, есть достаточно информации и в Сети, и в приложенных к статье файлах, не будем на этом подробно останавливаться.
Язык R
Вспомним немного важной информации о языке R. Это язык программирования, а также среда для статистических вычислений и построения графиков, разработанная в 1996 году новозеландскими учеными Россом Ихака и Робертом Джентельменом при университете Окленда. R — это GNU-проект, то есть свободное программное обеспечение. Его философия использования которого к следующим принципам (свободам):
- свобода запускать программы в любых целях (свобода 0);
- свобода изучать, как работает программа, и адаптировать ее под свои нужды (свобода 1);
- свобода распространять копии, чтобы помочь своему ближнему (свобода 2);
- свобода улучшать программу и делать ваши улучшения общедоступными к выгоде всего сообщества.
Сегодня R улучшается и развивается в основном усилиями "R Development Core Team"и созданного в прошлом году R Consortium. Перечень членов консорциума (IBM, Microsoft, Rstudio, Google, Mango, Oracle и др) говорит об очень серьезной поддержке, большом интересе в использовании и прекрасных перспективах языка в будущем .
Преимущества языка R:
- На сегодняшний день язык R де-факто является стандартом в статистических вычислениях.
- Развивается и поддерживается мировым научным сообществом университетов мира.
- Широчайший набор пакетов по всем передовым направлениям интеллектуального анализа данных (Data mining). При этом от появления новой идеи в научных публикациях до их реализации в пакете R проходит не более 2 недель.
- Последнее по порядку, но едва ли не первое по значению — его использование бесплатно.
1. Создание начального (сырого) набора данных
"Всё предыдущее, текущее и будущее движение цены заключено в самой цене"
Существует множество методов (пакетов), предназначенных для предподготовки, оценки и выбора предикторов. Обзор этих методов приведен в [1]. Их разнообразие объясняется не меньшим разнообразием данных реального мира. От понимания того, какой тип данных мы используем, и будет зависеть, какие методы исследования и обработки мы выберем.
Финансовые данные, исследованием которых мы занимаемся — это иерархические, регулярные таймсерии, которые "бесконечны" и легко извлекаемы. Базовый ряд — это котировки OHLCV по инструменту на конкретном таймфрейме.
Из этого базового ряда происходят все остальные таймсерии:
- непараметрические — например x^2, sqrt(abs(x)), x^3, -x^2 и т.п.
- функциональные непараметрические — sin(2*n*x), ln(abs(x)), log(Pr(t)/Pr(t-1)) и т. д.
- параметрические — огромное количество всевозможных индикаторов, которые в основном и применяются в качестве предикторов. Это могут быть как осцилляторы, так и различного рода фильтры.
В качестве целевой переменной используются либо индикаторы, генерирующие сигналы (факторы), либо ряд логических условий, выполнение которых дает сигнал.
1.1. Котировки
Котировки OHLC, Volume и time мы получаем из терминала в виде векторов (o, h, l, cl, v, d). Напишем функцию, которая объединит векторы, полученные из терминала в dataFrame. При этом переведем время начала бара в формат POSIXct.
#---pr.OHLCV-------------------
pr.OHLCV <- function(d, o, h, l, cl, v){
# (d, o, h, l, cl, v)- vector
require('magrittr')
require('dplyr')
require('anytime')
price <- cbind(Data = rev(d),
Open = rev(o), High = rev(h),
Low = rev(l), Close = rev(cl),
Vol = rev(v)) %>% as.tibble()
price$Data %<>% anytime(., tz = "CET")
return(price)
} Поскольку мы загрузили векторы котировок в окружение env, вычислим dataFrame pr и подчистим окружение env от ненужных переменных:
evalq({pr <- pr.OHLCV(Data, Open, High, Low, Close, Volume)
rm(list = c("Data", "Open", "High", "Low", "Close", "Volume"))
},
env) Посмотрим, как выглядит этот dataFrame в начале: > head(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-01-10 11:00:00 122.758 122.893 122.746 122.859 2 2017-01-10 11:15:00 122.860 122.924 122.818 122.848 3 2017-01-10 11:30:00 122.850 122.856 122.705 122.720 4 2017-01-10 11:45:00 122.721 122.737 122.654 122.693 5 2017-01-10 12:00:00 122.692 122.850 122.692 122.818 6 2017-01-10 12:15:00 122.820 122.937 122.785 122.920 # ... with 1 more variables: Vol <dbl>
и в конце:
> tail(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-05-05 20:30:00 123.795 123.895 123.780 123.888 2 2017-05-05 20:45:00 123.889 123.893 123.813 123.831 3 2017-05-05 21:00:00 123.833 123.934 123.825 123.916 4 2017-05-05 21:15:00 123.914 123.938 123.851 123.858 5 2017-05-05 21:30:00 123.859 123.864 123.781 123.781 6 2017-05-05 21:45:00 123.779 123.864 123.781 123.781 # ... with 1 more variables: Vol <dbl>
Итак, у нас есть 8000 баров с начальной датой 10.01.2017 и конечной 05.05.2017. Добавим в датафрейм pr производные цены — Medium Price, Typical Price и Weighted Close
evalq(pr %<>% mutate(., Med = (High + Low)/2, Typ = (High + Low + Close)/3, Wg = (High + Low + 2 * Close)/4, #CO = Close - Open, #HO = High - Open, #LO = Low - Open, dH = c(NA, diff(High)), dL = c(NA, diff(Low)) ), env)
1.2. Предикторы
В отличие от предыдущих наших экспериментов, мы упростили набор предикторов. В их роли будут выступать цифровые фильтры FATL, SATL, RFTL, RSTL. Они подробно описаны в статье В. Кравчука "Новый адаптивный метод следования за тенденциями и рыночными циклами", которую вы можете найти в приложенных к данной статье файлах (см. главу "Новые инструменты технического анализа и их интерпретация). Здесь лишь кратко перечислим их.
- FATL (Fast Adaptive Trend Line) — «быстрая» адаптивная линия тренда;
- SATL (Slow Adaptive Trend Line) — «медленная» адаптивная линия тренда;
- RFTL (Reference Fast Trend Line) — опорная «быстрая» линия тренда;
- RSTL (Reference Slow Trend Line) — опорная «медленная» линия тренда.
Темп изменения FATL и SATL отслеживаются по индикаторам FTLM (Fast Trend Line Momentum) и STLM (Slow Trend Line Momentum).
Среди технических инструментов, которые нам понадобятся, есть еще два осциллятора — индексы RBCI и PCCI. Индекс RBCI (Range Bound Channel Index) — ограниченный по полосе индекс канала, который вычисляется с помощью полосового фильтра (фильтр удаляет низкочастотный тренд и высокочастотный шум). Индекс PCCI (Perfect Commodity Channel Index) — совершенный индекс товарного канала.
Функция, вычисляющая цифровые фильтры FATL, SATL, RFTL, RSTL, выглядит так:
#-----DigFiltr------------------------- DigFiltr <- function(X, type = 1){ # X - vector require(rowr) fatl <- c( +0.4360409450, +0.3658689069, +0.2460452079, +0.1104506886, -0.0054034585, -0.0760367731, -0.0933058722, -0.0670110374, -0.0190795053, +0.0259609206, +0.0502044896, +0.0477818607, +0.0249252327, -0.0047706151, -0.0272432537, -0.0338917071, -0.0244141482, -0.0055774838, +0.0128149838, +0.0226522218, +0.0208778257, +0.0100299086, -0.0036771622, -0.0136744850, -0.0160483392, -0.0108597376, -0.0016060704, +0.0069480557, +0.0110573605, +0.0095711419, +0.0040444064, -0.0023824623, -0.0067093714, -0.0072003400, -0.0047717710, 0.0005541115, 0.0007860160, 0.0130129076, 0.0040364019 ) rftl <- c(-0.0025097319, +0.0513007762 , +0.1142800493 , +0.1699342860 , +0.2025269304 , +0.2025269304, +0.1699342860 , +0.1142800493 , +0.0513007762 , -0.0025097319 , -0.0353166244, -0.0433375629 , -0.0311244617 , -0.0088618137 , +0.0120580088 , +0.0233183633, +0.0221931304 , +0.0115769653 , -0.0022157966 , -0.0126536111 , -0.0157416029, -0.0113395830 , -0.0025905610 , +0.0059521459 , +0.0105212252 , +0.0096970755, +0.0046585685 , -0.0017079230 , -0.0063513565 , -0.0074539350 , -0.0050439973, -0.0007459678 , +0.0032271474 , +0.0051357867 , +0.0044454862 , +0.0018784961, -0.0011065767 , -0.0031162862 , -0.0033443253 , -0.0022163335 , +0.0002573669, +0.0003650790 , +0.0060440751 , +0.0018747783) satl <- c(+0.0982862174, +0.0975682269 , +0.0961401078 , +0.0940230544, +0.0912437090 , +0.0878391006, +0.0838544303 , +0.0793406350 ,+0.0743569346 ,+0.0689666682 , +0.0632381578 ,+0.0572428925 , +0.0510534242,+0.0447468229, +0.0383959950, +0.0320735368, +0.0258537721 ,+0.0198005183 , +0.0139807863,+0.0084512448, +0.0032639979, -0.0015350359, -0.0059060082 ,-0.0098190256 , -0.0132507215, -0.0161875265, -0.0186164872, -0.0205446727, -0.0219739146 ,-0.0229204861 , -0.0234080863,-0.0234566315, -0.0231017777, -0.0223796900, -0.0213300463 ,-0.0199924534 , -0.0184126992,-0.0166377699, -0.0147139428, -0.0126796776, -0.0105938331 ,-0.0084736770 , -0.0063841850,-0.0043466731, -0.0023956944, -0.0005535180, +0.0011421469 ,+0.0026845693 , +0.0040471369,+0.0052380201, +0.0062194591, +0.0070340085, +0.0076266453 ,+0.0080376628 , +0.0083037666,+0.0083694798, +0.0082901022, +0.0080741359, +0.0077543820 ,+0.0073260526 , +0.0068163569,+0.0062325477, +0.0056078229, +0.0049516078, +0.0161380976 ) rstl <- c(-0.0074151919,-0.0060698985,-0.0044979052,-0.0027054278,-0.0007031702,+0.0014951741, +0.0038713513,+0.0064043271,+0.0090702334,+0.0118431116,+0.0146922652,+0.0175884606, +0.0204976517,+0.0233865835,+0.0262218588,+0.0289681736,+0.0315922931,+0.0340614696, +0.0363444061,+0.0384120882,+0.0402373884,+0.0417969735,+0.0430701377,+0.0440399188, +0.0446941124,+0.0450230100,+0.0450230100,+0.0446941124,+0.0440399188,+0.0430701377, +0.0417969735,+0.0402373884,+0.0384120882,+0.0363444061,+0.0340614696,+0.0315922931, +0.0289681736,+0.0262218588,+0.0233865835,+0.0204976517,+0.0175884606,+0.0146922652, +0.0118431116,+0.0090702334,+0.0064043271,+0.0038713513,+0.0014951741,-0.0007031702, -0.0027054278,-0.0044979052,-0.0060698985,-0.0074151919,-0.0085278517,-0.0094111161, -0.0100658241,-0.0104994302,-0.0107227904,-0.0107450280,-0.0105824763,-0.0102517019, -0.0097708805,-0.0091581551,-0.0084345004,-0.0076214397,-0.0067401718,-0.0058083144, -0.0048528295,-0.0038816271,-0.0029244713,-0.0019911267,-0.0010974211,-0.0002535559, +0.0005231953,+0.0012297491,+0.0018539149,+0.0023994354,+0.0028490136,+0.0032221429, +0.0034936183,+0.0036818974,+0.0038037944,+0.0038338964,+0.0037975350,+0.0036986051, +0.0035521320,+0.0033559226,+0.0031224409,+0.0028550092,+0.0025688349,+0.0022682355, +0.0073925495) if (type == 1) {k = fatl} if (type == 2) {k = rftl} if (type == 3) {k = satl} if (type == 4) {k = rstl} n <- length(k) m <- length(X) k <- rev(k) f <- rowr::rollApply(data = X, fun = function(x) {sum(x * k)}, window = n, minimum = n, align = "right") while (length(f) < m) { f <- c(NA,f)} return(f) }
Вычислим и добавим их в датафрейм pr
evalq(pr %<>% mutate(., fatl = DigFiltr(Close, 1), rftl = DigFiltr(Close, 2), satl = DigFiltr(Close, 3), rstl = DigFiltr(Close, 4) ), env)
Добавим осцилляторы FTLM, STLM, RBCI, PCCI, их первые разности и первые разности цифровых фильтров в датафрейм pr:
evalq(pr %<>% mutate(., ftlm = fatl - rftl, rbci = fatl - satl, stlm = satl - rstl, pcci = Close - fatl, v.fatl = c(NA, diff(fatl)), v.rftl = c(NA, diff(rftl)), v.satl = c(NA, diff(satl)), v.rstl = c(NA, diff(rstl)*10) ), env) evalq(pr %<>% mutate(., v.ftlm = c(NA, diff(ftlm)), v.stlm = c(NA, diff(stlm)), v.rbci = c(NA, diff(rbci)), v.pcci = c(NA, diff(pcci)) ), env)
1.3. Целевая
В качестве индикатора, генерирующего целевую переменную, будем использовать ZigZag().
Функция для его вычисления получает на вход таймсерию и два параметра: это минимальная длина колена (int либо double) и тип цены для вычисления (Close, Med, Typ, Wd, c (High, Low) ).
#------ZZ----------------------------------- par <- c(25, 5) ZZ <- function(x, par) { # x - vector require(TTR) require(magrittr) ch = par[1] mode = par[2] if (ch > 1) ch <- ch/(10 ^ (Dig - 1)) switch(mode, xx <- x$Close, xx <- x$Med, xx <- x$Typ, xx <- x$Wd, xx <- x %>% select(High,Low)) zz <- ZigZag(xx, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]} return(zz) }
Вычислим ZigZag, первую разность, знак первой разности и добавим их вдатафрейм pr:
evalq(pr %<>% cbind(., zigz = ZZ(., par = par)), env) evalq(pr %<>% cbind(., dz = diff(pr$zigz) %>% c(NA, .)), env) evalq(pr %<>% cbind(., sig = sign(pr$dz)), env)
1.4.Начальный набор данных
Коротко резюмируем, что и как мы получили в результате предыдущих вычислений.
Мы получили из терминала векторы OHLCV и временную метку начала бара таймфрейма М15 по EURJPY. Из этих данных был сформирован датафрейм pr, в который добавлены переменные FATL, SATL, RFTL, RSTL, FTLM, STLM, RBCI, PCCI и первые разности от них. Также в датафрейм добавлен ZigZag с минимальным плечом в 25 п (4 знака), его первая разность и знак первой разности (-1,1), который будет использоваться как сигнал.
Все эти данные мы загрузили не в глобальное окружение, а в новое, дочернее окружение env, в котором и будем проводить все последующие расчеты. Цель такого разделения состоит в том, чтобы использовать наборы данных с разных символов или таймфреймов без конфликта имен при вычислении.
Структура суммарного датафрейма pr приведена ниже. Из него удобно выбирать переменные, необходимые для последующих вычислений.
str(env$pr) 'data.frame': 8000 obs. of 30 variables: $ Data : POSIXct, format: "2017-01-10 11:00:00" ... $ Open : num 123 123 123 123 123 ... $ High : num 123 123 123 123 123 ... $ Low : num 123 123 123 123 123 ... $ Close : num 123 123 123 123 123 ... $ Vol : num 3830 3360 3220 3241 3071 ... $ Med : num 123 123 123 123 123 ... $ Typ : num 123 123 123 123 123 ... $ Wg : num 123 123 123 123 123 ... $ dH : num NA 0.031 -0.068 -0.119 0.113 ... $ dL : num NA 0.072 -0.113 -0.051 0.038 ... $ fatl : num NA NA NA NA NA NA NA NA NA NA ... $ rftl : num NA NA NA NA NA NA NA NA NA NA ... $ satl : num NA NA NA NA NA NA NA NA NA NA ... $ rstl : num NA NA NA NA NA NA NA NA NA NA ... $ ftlm : num NA NA NA NA NA NA NA NA NA NA ... $ rbci : num NA NA NA NA NA NA NA NA NA NA ... $ stlm : num NA NA NA NA NA NA NA NA NA NA ... $ pcci : num NA NA NA NA NA NA NA NA NA NA ... $ v.fatl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rftl: num NA NA NA NA NA NA NA NA NA NA ... $ v.satl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rstl: num NA NA NA NA NA NA NA NA NA NA ... $ v.ftlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.stlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.rbci: num NA NA NA NA NA NA NA NA NA NA ... $ v.pcci: num NA NA NA NA NA NA NA NA NA NA ... $ zigz : num 123 123 123 123 123 ... $ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ... $ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
Выберем в датафрейм dataSet все ранее расcчитанные предикторы. Целевую переменную sig преобразуем в фактор и сдвинем на один бар в «будущее».
evalq(dataSet <- pr %>% tbl_df() %>%
dplyr::select(Data, ftlm, stlm, rbci, pcci,
v.fatl, v.satl, v.rftl, v.rstl,
v.ftlm, v.stlm, v.rbci, v.pcci, sig) %>%
dplyr::filter(., sig != 0) %>%
mutate(., Class = factor(sig, ordered = F) %>%
dplyr::lead()) %>%
dplyr::select(-sig),
env) Визуальный анализ данных
Построим график OHLC c использованием пакета ggplot2. Возьмем данные за последние 2 дня и отрисуем график котировок в барах.
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + labs(title = "EURJPY Candlestick Chart", y = "Close Price", x = "") + theme_tq(), env)
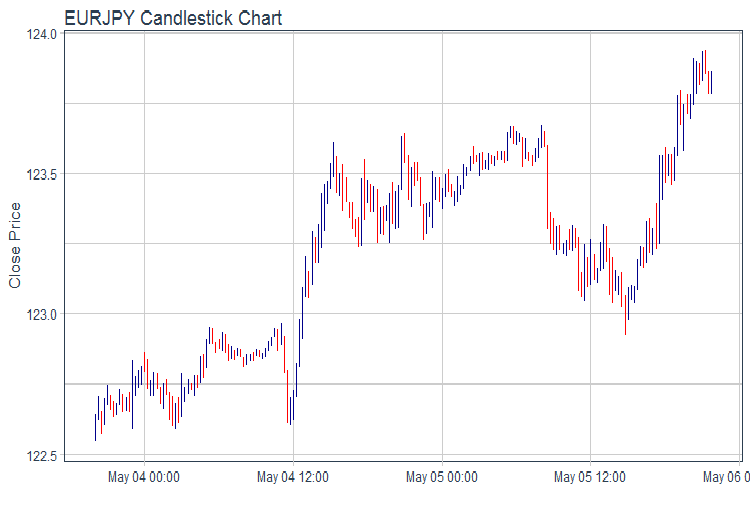
рис.1. График котировок
Построим график FATL, SATL, RFTL, RSTL и ZZ:
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + geom_line(aes(Data, fatl), color = "steelblue", size = 1) + geom_line(aes(Data, rftl), color = "red", size = 1) + geom_line(aes(Data, satl), color = "gold", size = 1) + geom_line(aes(Data, rstl), color = "green", size = 1) + geom_line(aes(Data, zigz), color = "black", size = 1) + labs(title = "EURJPY Candlestick Chart", subtitle = "Combining Chart Geoms", y = "Close Price", x = "") + theme_tq(), env)
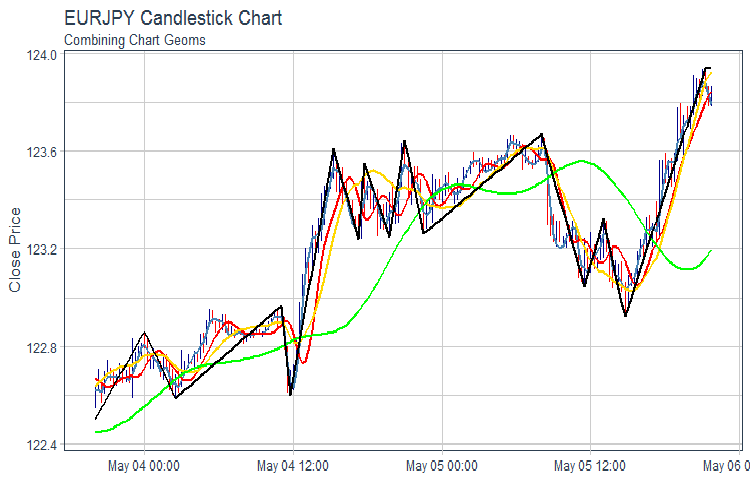
Рис.2. FATL, SATL, RFTL, RSTL и ZZ
Осцилляторы разобьем на 3 группы для более удобного отображения.
require(dygraphs) evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, ftlm, stlm, rbci, pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator base") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "blue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
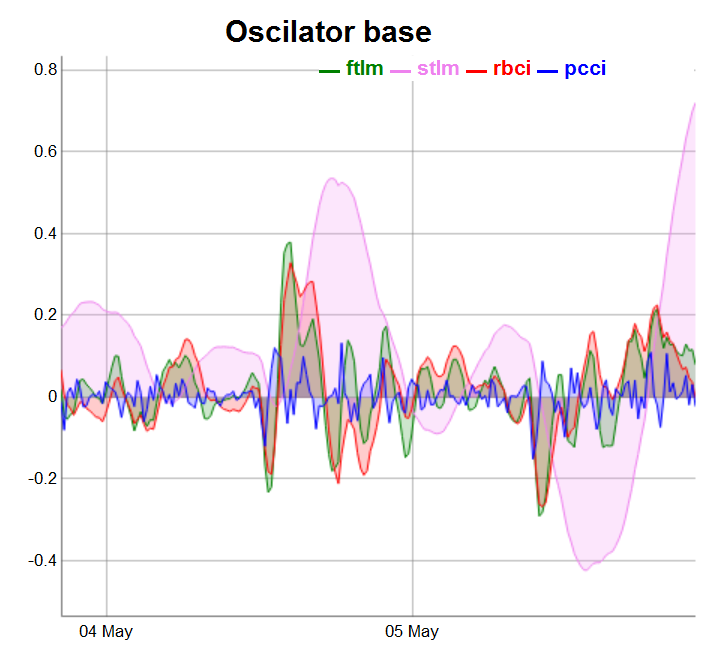
Рис.3. Осцилляторы базовые
evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, v.fatl, v.satl, v.rftl, v.rstl) %>% tk_xts() %>% dygraph(., main = "Oscilator 2") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
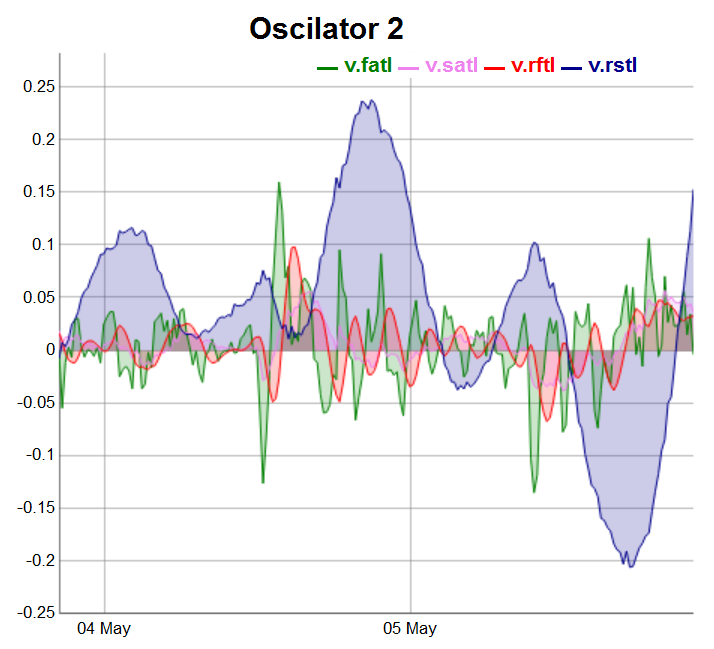
Рис.4. Осцилляторы 2 группы
Осцилляторы третьей группы будут отрисованы на последних 100 барах:
evalq(dataSet %>% tail(., 100) %>% tk_tbl %>% select(Data, v.ftlm, v.stlm, v.rbci, v.pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator 3") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
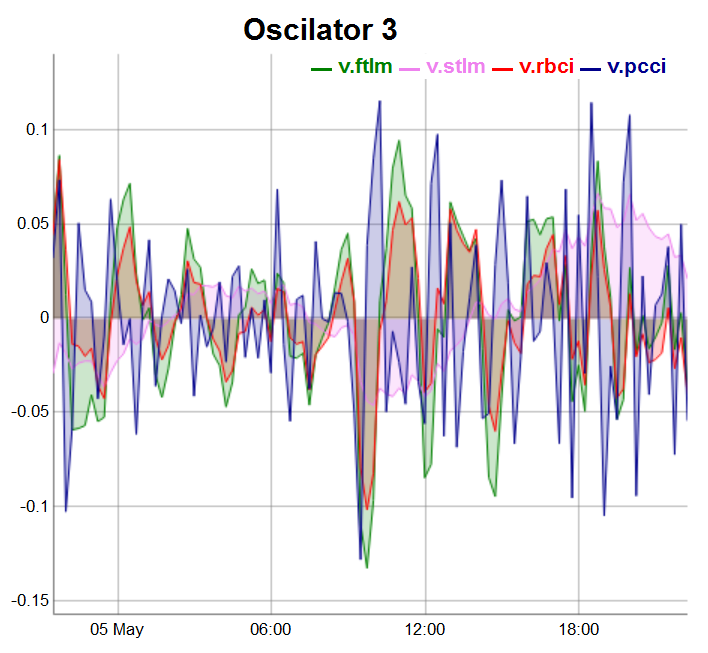
Рис.5. Осцилляторы 3 группы
2.Разведочный анализ данных (Exploratory data analysis, EDA)
“Не бывает обычных статистических вопросов — только сомнительные статистические процедуры.” — Сэр Дэвид Кокс
“Гораздо лучше приблизительный ответ на правильный вопрос, который часто расплывчат, чем точный ответ на неправильный вопрос, который всегда может быть точным.” — Джон Тьюки
Наша цель в EDA — развить понимание наших данных. Самый простой способ сделать это — использовать вопросы в качестве инструмента исследования. Когда мы задаем вопрос, то фокусируемся на определенной части данных. Это помогает нам решить, какие графы, модели или преобразования лучше всего применить.
EDA — это принципиально творческий процесс. И, как в большинстве творческих процессов, ключ к постановке качественных вопросов — это создание еще большего количества вопросов. Трудно задать раскрывающие вопросы в начале анализа, потому что мы не знаем, какие выводы содержатся в наборе данных. С другой стороны, каждый новый вопрос, который мы задаем, открывает новый аспект данных и увеличивает шанс сделать открытие. Мы можем быстро перейти в наиболее интересную часть выборки и путем последовательных вопросов все глубже прояснять ситуацию.
Нет правил о том, какие вопросы мы должны задать, чтобы выполнить исследования. Однако два типа вопросов всегда будут нам полезны:
- Какой тип изменений происходит в моих переменных?
- Какой тип ковариаций происходит между переменными?
Определимся с основным понятием.
Вариации — это тенденции изменения значений переменной от одного измерения к другому. Вы можете легко увидеть изменения в реальной жизни: если семь раз измерить любую непрерывную переменную, то вы получите семь разных результатов. Это верно, даже если вы измеряете постоянные величины (например, скорость света). Каждое из измерений будет содержать небольшие доли ошибок, которые постоянно меняются. Переменные из одной категории тоже могут меняться, если измерять разные конкретные предметы (например, цвет глаз у разных людей), или в разное время (например, уровни энергии электрона в разные моменты). У каждой переменной свой собственный характер вариаций, которые могут выявить интересную информацию. Лучший способ к пониманию картины — визуализировать распределение значений переменной. Это как раз тот случай, когда один рисунок лучше тысячи слов.
2.1.Суммарная статистика
Общую статистику нашей таймсерии удобно отслеживать с помощью функции table.Stats()::PerformenceAnalitics.
> table.Stats(env$dataSet %>% tk_xts()) Using column `Data` for date_var. ftlm stlm rbci pcci Observations 7955.0000 7908.0000 7934.0000 7960.0000 NAs 42.0000 89.0000 63.0000 37.0000 Minimum -0.7597 -1.0213 -0.9523 -0.5517 Quartile 1 -0.0556 -0.1602 -0.0636 -0.0245 Median -0.0001 0.0062 -0.0016 -0.0001 Arithmetic Mean 0.0007 0.0025 0.0007 0.0001 Geometric Mean -0.0062 NaN -0.0084 -0.0011 Quartile 3 0.0562 0.1539 0.0675 0.0241 Maximum 2.7505 3.0407 2.3872 1.8859 SE Mean 0.0014 0.0033 0.0015 0.0006 LCL Mean (0.95) -0.0020 -0.0040 -0.0022 -0.0010 UCL Mean (0.95) 0.0034 0.0090 0.0035 0.0012 Variance 0.0152 0.0858 0.0172 0.0026 Stdev 0.1231 0.2929 0.1311 0.0506 Skewness 4.2129 1.7842 2.3037 6.4718 Kurtosis 84.6116 16.7471 45.0133 247.4208 v.fatl v.satl v.rftl v.rstl Observations 7959.0000 7933.0000 7954.0000 7907.0000 NAs 38.0000 64.0000 43.0000 90.0000 Minimum -0.3967 -0.0871 -0.1882 -0.4719 Quartile 1 -0.0225 -0.0111 -0.0142 -0.0759 Median -0.0006 0.0003 0.0000 0.0024 Arithmetic Mean 0.0002 0.0002 0.0002 0.0011 Geometric Mean -0.0009 0.0000 -0.0003 -0.0078 Quartile 3 0.0220 0.0110 0.0138 0.0751 Maximum 1.4832 0.3579 0.6513 1.3093 SE Mean 0.0005 0.0002 0.0003 0.0015 LCL Mean (0.95) -0.0009 -0.0003 -0.0005 -0.0020 UCL Mean (0.95) 0.0012 0.0007 0.0009 0.0041 Variance 0.0023 0.0005 0.0009 0.0188 Stdev 0.0483 0.0219 0.0308 0.1372 Skewness 5.2643 2.6705 3.9472 1.5682 Kurtosis 145.8441 36.9378 74.4182 13.5724 v.ftlm v.stlm v.rbci v.pcci Observations 7954.0000 7907.0000 7933.0000 7959.0000 NAs 43.0000 90.0000 64.0000 38.0000 Minimum -0.9500 -0.2055 -0.6361 -1.4732 Quartile 1 -0.0280 -0.0136 -0.0209 -0.0277 Median -0.0002 -0.0001 -0.0004 -0.0002 Arithmetic Mean 0.0000 0.0001 0.0000 0.0000 Geometric Mean -0.0018 -0.0003 -0.0009 NaN Quartile 3 0.0273 0.0143 0.0207 0.0278 Maximum 1.4536 0.3852 1.1254 1.9978 SE Mean 0.0006 0.0003 0.0005 0.0006 LCL Mean (0.95) -0.0012 -0.0005 -0.0009 -0.0013 UCL Mean (0.95) 0.0013 0.0007 0.0009 0.0013 Variance 0.0032 0.0007 0.0018 0.0034 Stdev 0.0561 0.0264 0.0427 0.0579 Skewness 1.2051 0.8513 2.0643 3.0207 Kurtosis 86.2425 23.0651 86.3768 233.1964
Что мы видим из этой таблицы:
- Все предикторы имеют небольшое (относительно) количество неопределенных переменных NA.
- Все предикторы имеют большую правую асимметрию (skewness).
- Все предикторы имеют большую островерхость (kurtosis).
2.2.Визуализация суммарной статистики
“Самая большая ценность картины в том, что она заставляет нас заметить то, что мы никогда не ожидали увидеть”. — Джон Тьюки
Посмотрим вариацию и ковариацию наших переменных в наборе dataSet. Поскольку количество переменных (14) не позволяет разместить их на одном графике, разобьем их на три группы.
require(GGally) evalq(ggpairs(dataSet, columns = 2:6, mapping = aes(color = Class), title = "DigFilter1"), env)
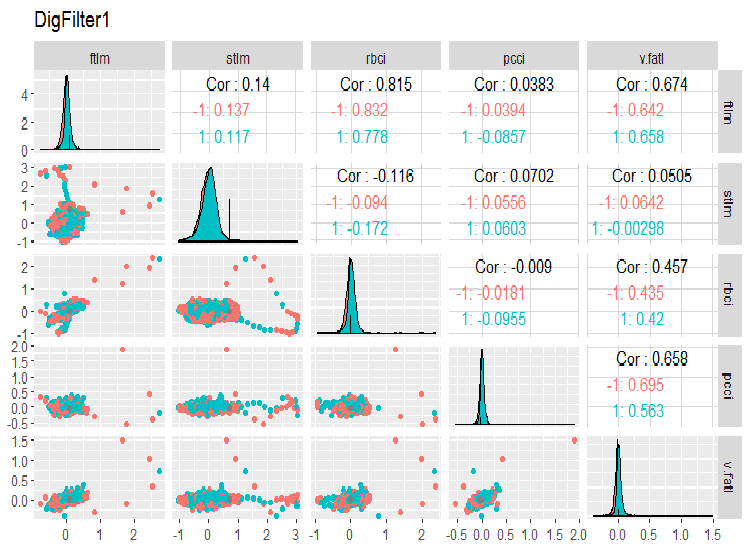
Рис. 6. Первая группа предикторов
evalq(ggpairs(dataSet, columns = 7:10, mapping = aes(color = Class), title = "DigFilter2"), env)
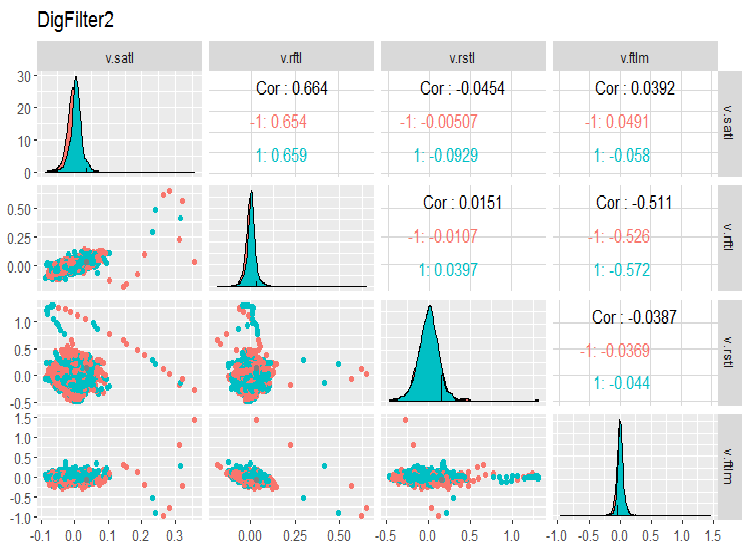
Рис. 7. Вторая группа предикторов
evalq(ggpairs(dataSet, columns = 11:14, mapping = aes(color = Class), title = "DigFilter3"), env)
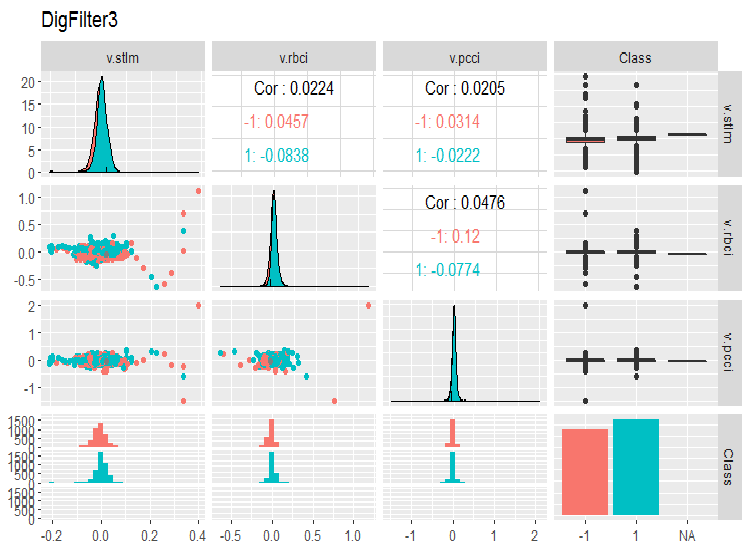
Рис. 8. Третья группа предикторов
Что мы видим на графиках:
- все предикторы имеют форму распределения, близкую к нормальной, но с сильной правой асимметрией;
- все предикторы имеют очень узкий внутриквартильный диапазон (IQR);
- все предикторы имеют значительные выбросы;
- количество примеров в двух уровнях целевой «Class” имеет небольшую разницу.
3.Подготовка данных
Стандартно в этап подготовки данных включают семь этапов:
- “imputation” — удаление или импутация пропущенных/неопределенных данных;
- “variance” — удаление переменных с нулевой или околонулевой дисперсией;
- “split” — разделение набора данных на поднаборы train/valid/test;
- “scaling” — масштабирование диапазона переменных;
- “outliers” — удаление или импутация выбросов;
- “sampling” — исправления дисбаланса классов;
- “denoise” — удаление или переопределение шумовых примеров;
- “selection” — выбор иррелевантных предикторов.
3.1. Очистка данных
Первый этап подготовки сырых данных — удаление или импутация неопределенных значений и пропусков в данных. Несмотря на то, что многие модели допускают использование неопределенных данных (NA) и пропусков в наборах, лучше удалить их до выполнения основных манипуляций. Эта операция проводится на полном наборе данных и независимо от используемой модели.
Выше мы смотрели суммарную статистику наших сырых данных, из которой видно, что NA присутствуют в наборе. Это искусственные A, которые образовались при вычислении цифровых фильтров. Их относительно немного, поэтому их можно удалить. Ранее мы получили набор данных dataSet, готовый для дальнейшей обработки. Очистим его.
В общем случае под очисткой понимают следующие операции:
- удаление предикторов с нулевой или околонулевой дисперсией (method = c(“zv”, “nzv”));
- удаление высококоррелированных переменных. Порог коэффициента корреляции устанавливается пользователем (method = “corr”), по умолчанию он равен 0.9. Эта стадия нужна не всегда, в зависимости от последующих методов преобразования;
- удаление предикторов, имеющих только одно уникальное значение в любом классе (method = “conditionalX”).
Все эти операции реализованы в функции preProcess()::caret методами, указанными выше, и выполняются на полном наборе данных до разделения на обучающий и тестовый наборы.
require(caret)
evalq({preProClean <- preProcess(x = dataSet,method = c("zv", "nzv", "conditionalX", "corr"))
dataSetClean <- predict(preProClean, dataSet %>% na.omit)},
env)Посмотрим, есть ли удаленные предикторы, и что осталось после очистки:
> env$preProClean$method$remove #[1] "v.rbci" > dim(env$dataSetClean) [1] 7906 13 > colnames(env$dataSetClean) [1] "Data" "ftlm" "stlm" "rbci" "pcci" [6] "v.fatl" "v.satl" "v.rftl" "v.rstl" "v.ftlm" [11] "v.stlm" "v.pcci" "Class"
3.2. Выявление и обработка выбросов (outliers)
Проблемы с качеством данных, такие как асимметрия и выбросы, часто взаимозависимы и взаимосвязаны. Это не только делает предварительную обработку трудоемкой, но и затрудняет задачу нахождения взаимосвязей и тенденций в нашей выборке.
Что такое выбросы?
Дадим рабочее определение: под выбросом мы будем понимать наблюдение, которое слишком велико или слишком мало по сравнению с большинством других имеющихся наблюдений. Глубокая классификация выбросов, методов их определения и обработки приведена в [2].
Типы выбросов
Выбросы вносят значительные искажения в распределение переменных и в обученную на таких данных модель. Существует большое количество методов идентификации и обработки выбросов, которые зависят от того, как мы определяем выброс — локально или глобально. Локальные выбросы — это выбросы одной переменной. Глобальные выбросы — это выбросы в многомерном пространстве, определяемом матрицей или датафреймом данных.
Чем вызваны выбросы?
Выбросы можно разделить по происхождению:
Искусственные
- ошибки ввода данных — ошибки, возникшие во время сбора, записи или обработки данных;
- ошибки эксперимента;
- ошибки выборки.
Естественные — выбросы, обусловленные природой переменной.
Каково влияние выбросов?
Выбросы могут серьезно испортить результаты анализа данных и статистического моделирования: это увеличивает дисперсию ошибок и снижает мощность статистических тестов; если выбросы не распределены случайным образом, они могут уменьшить нормальность; они также могут влиять на основные предположения регрессионного, дисперсионного анализа и других статистических допущений модели.
Как определить локальные "выбросы"?
Чаще всего выбросы выявляются с помощью визуализации. Простой и широко используемый способ — boxplot. Например, посмотрим предиктор ftlm:
evalq(ggplot(dataSetClean, aes(x = factor(0),
y = ftlm,
color = 'red')) +
geom_boxplot() + xlab("") +
scale_x_discrete(breaks = NULL) +
coord_flip(),
env)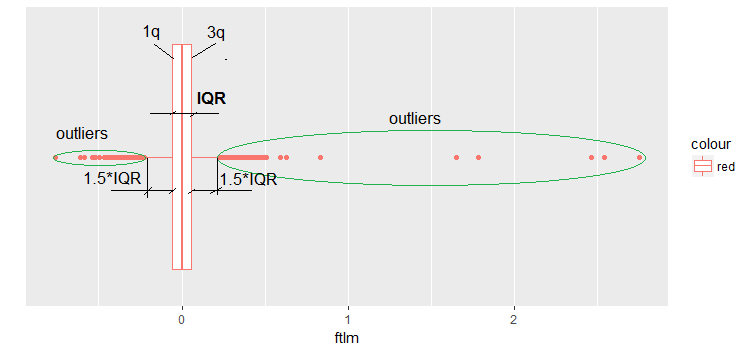
Рис.9. Боксплот ftlm
Некоторые пояснения к рисунку:
IQR — внутриквартильный диапазон, или расстояние между первым и третьим квартилем.
Существует несколько определений выбросов в этом свете:
- Любое значение, которое меньше -1.5*IQR и больше +1.5*IQR — выброс. Иногда коэффициент принимают равным 2 или 3. Все значения между 1.5*IQR и 3*IQR условно называют средними выбросами, а все, что за пределами 3*IQR — экстремальные выбросы.
- Любое значение вне диапазона 5-го и 95-го прецентилей можно рассматривать как выброс.
- Точки расположения данных на расстоянии трех и более СКО — тоже выбросы.
В дальнейшем будем использовать первое определение выбросов (через IQR).
Как обработать выбросы?
Большинство из способов обработки выбросов похожи на методы обработки неопределенных значений NA : удаление наблюдений, их трансформирование, сегментация, импутация и другие статистические методы.
- Удаление выбросов: мы удаляем значения выбросов, если они появляются в результате ошибки ввода данных, ошибки обработки данных, или же если наблюдений выбросов очень мало. Мы также можем использовать обрезку распределения с обоих концов, чтобы удалить выбросы. Например, отбросить по 1% сверху и снизу.
- Преобразования и связывание по сегментам (binning):
- преобразование переменных может исключить выбросы (это будет рассмотрено в следующем разделе);
- натуральный логарифм значения уменьшает изменения, вызванные экстремальными значениями (также будет рассмотрено в следующем разделе);
- дискретизация — это тоже форма преобразования переменной (также см. следующий раздел);
- мы также можем использовать процесс присвоения весов для разных наблюдений (эта тема рассматриваться не будет).
Импутация: Те же методы, которые мы применяем для импутации неопределенных значений, мы можем применить к выбросам. Можно использовать среднее, медиану, моду. Прежде чем импутировать значения, мы должны проанализировать, с естественным выбросом мы имеем дело или с искусственным. Если он искусственный, мы можем пойти на импутацию.
Если в выборке есть значительное количество выбросов, мы должны рассматривать их отдельно в статистической модели. Здесь мы обсудим лишь общие методы, используемые для борьбы с выбросами: удаление и импутацию.
Удаление выбросов
Мы удаляем значения выбросов, если они произошли из-за ошибки ввода или обработки данных, или если количествовыбросов очень мало (только при определении статистических метрик переменных).
Извлечь данные одной переменной (ftlm, например) без выбросов можно так:
evalq({dataSetClean$ftlm -> x
out.ftlm <- x[!x %in% boxplot.stats(x)$out]},
env) Или так:
evalq({dataSetClean$ftlm -> x
out.ftlm1 <- x[x > quantile(x, .25) - 1.5*IQR(x) &
x < quantile(x, .75) + 1.5*IQR(x)]},
env)
Одинаковы ли они?
> evalq(all.equal(out.ftlm, out.ftlm1), env)
[1] TRUE Сколько данных попало в выбросы?
> nrow(env$dataSetClean) - length(env$out.ftlm) [1] 402
Посмотрим, как выглядит ftlm без выбросов:
boxplot(env$out.ftlm, main = "ftlm without outliers", boxwex = 0.5)
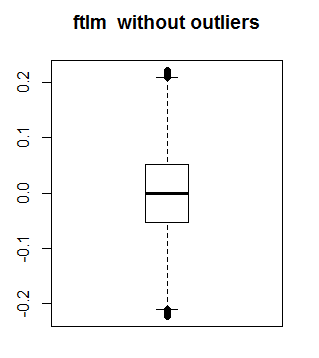
Рис. 10. ftlm без выбросов
Вышеописанный способ неприменим для матриц и датафреймов, поскольку каждая переменная в датафрейме может иметь различное количество выбросов. Для таких выборок данных приемлем метод замены локальных выбросов на NA с последующим применением стандартных методов обработки NA. Напишем функцию, заменяющую локальные выбросы на NA:
#-------remove_outliers------------------------------- remove_outliers <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) y <- x y[x < (qnt[1] - H)] <- NA y[x > (qnt[2] + H)] <- NA y }
Заменим в нашем наборе данных dataSetClean во всех переменных, кроме c(Data, Class), выбросы на NA и посмотрим, как изменится распределение полученного набора x.out:
evalq({
dataSetClean %>% select(-c(Data,Class)) %>% as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
remove_outliers(x[ ,i])
} -> x.out
colnames(x.out) <- colnames(x)
},
env)
par(mfrow = c(1, 1))
chart.Boxplot(env$x,
main = "x.out with outliers",
xlab = "")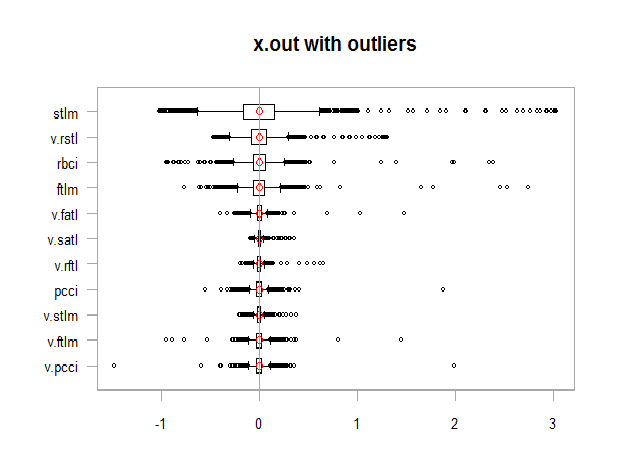 
Рис. 11. Данные с выбросами
chart.Boxplot(env$x.out, main = "x.out without outliers", xlab = "")
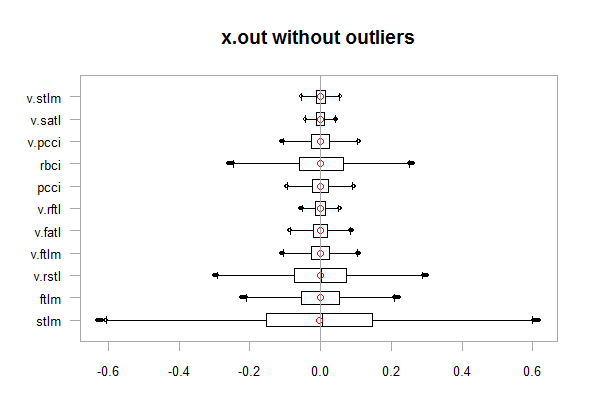
Рис.12. Данные без выбросов
Импутация NA, появившихся вместо выбросов
Под импутацией понимается процесс замены пропущенных, некорректных или несостоятельных значений другими значениями. При подаче данных для обучения модели мы должны заменить NA действительными значениями. Варианты:
- замещаем NA на mean, mediana, mod (при этом статистические характеристики набора не изменяются)
- замещаем выбросы, которые больше 1.5*IQR, на 0.95 персентиль, а выбросы, которые меньше - 1.5*IQR — на 0.05 персентиль.
Напишем функцию, выполняющую последний вариант действия, выполним преобразование и посмотрим на распределение после преобразования:
#-------capping_outliers-------------------------------
capping_outliers <- function(x, na.rm = TRUE, ...) {
qnt <- quantile(x, probs = c(.25, .75),
na.rm = na.rm, ...)
caps <- quantile(x, probs = c(.05, .95),
na.rm = na.rm, ...)
H <- 1.5 * IQR(x, na.rm = na.rm)
y <- x
y[x < (qnt[1] - H)] <- caps[1]
y[x > (qnt[2] + H)] <- caps[2]
y
}
evalq({dataSetClean %>% select(-c(Data,Class)) %>%
as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
capping_outliers(x[ ,i])
} -> x.cap
colnames(x.cap) <- colnames(x)
},
env)
chart.Boxplot(env$x.cap,
main = "x.cap with capping outliers",
xlab = "")
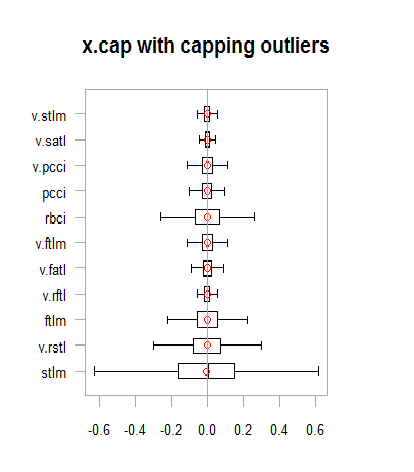
Рис.13. Набор данных с импутированными выбросами
Посмотрим вариацию и ковариацию наших переменных в наборе dataSetCap (это тот же набор dataSet, но очищенный и с импутированными локальными выбросами). Поскольку количество переменных (13) не позволяет разместить их на одном графике, разобьем их на две группы.
evalq(x.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetCap, env) require(GGally) evalq(ggpairs(dataSetCap, columns = 2:7, mapping = aes(color = Class), title = "PredCap1"), env)
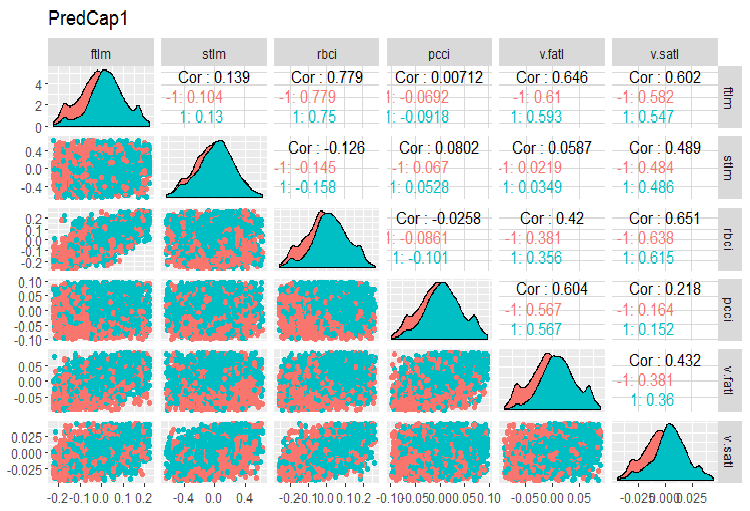
Рис.14. Вариация и ковариация первой части набора данных с импутированными выбросами.
И вторая часть набора:
evalq(ggpairs(dataSetCap, columns = 8:13, mapping = aes(color = Class), title = "PredCap2"), env)
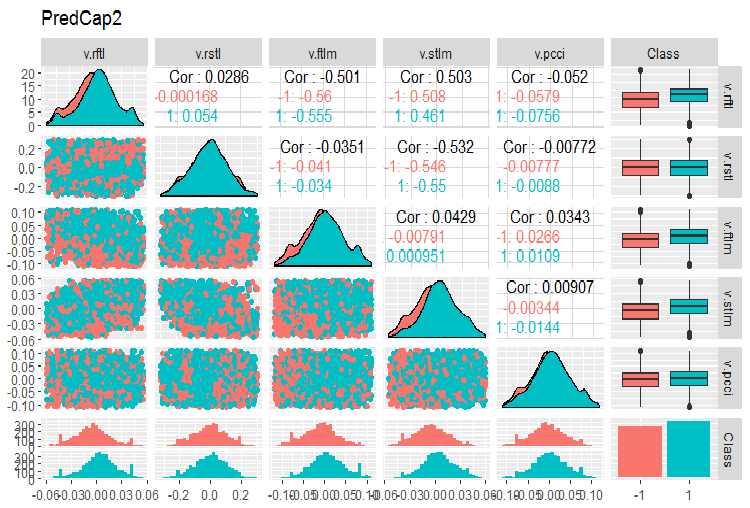
Рис.15. Вариация и ковариация второй части набора данных с импутированными выбросами
Как определить глобальные выбросы?
Двумерные и многомерные выбросы обычно измеряются с помощью индекса влияния или дистанции. Для обнаружения глобальных выбросов используют различные дистанции. Можем использовать несколько пакетов (DMwR, mvoutliers,Rlof), которые содержат функции для определения глобальных выбросов, оцениваемые с помощью LOF (local outlier factor) — фактора локальных выбросов. Вычислим и сравним LOF для набора с выбросами x и для набора с импутированными выбросами x.cap.
##------DMwR2------------------- require(DMwR2) evalq(lof.x <- lofactor(x,10), env) evalq(lof.x.cap <- lofactor(x.cap,10), env) par(mfrow = c(1, 3)) boxplot(env$lof.x, main = "lof.x", boxwex = 0.5) boxplot(env$lof.x.cap, main = "lof.x.cap", boxwex = 0.5) hist(env$lof.x.cap, breaks = 20) par(mfrow = c(1, 1))
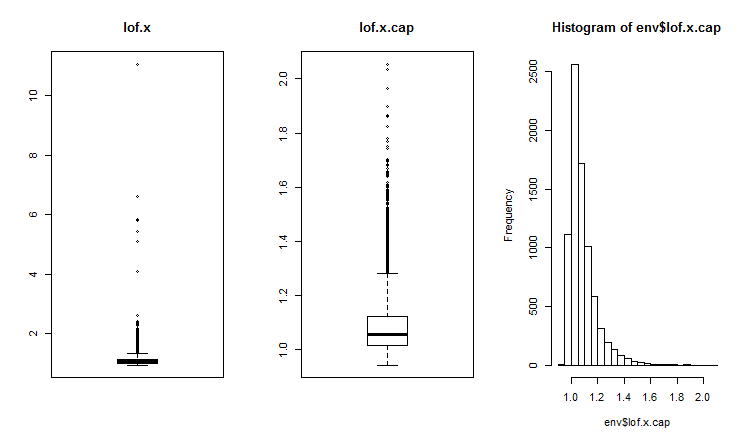
Рис.16. Глобальный фактор выбросов для набора данных с выбросами и набора с импутированными выбросами
В пакете Rlof реализована функция lof(). Она находит локальный фактор outlier [3] матричных данных с использованием k соседей. Локальный коэффициент выброса (LOF) — мера вероятности принадлежности к выбросам, которая рассчитывается для каждого наблюдения. На основе этой меры пользователь решает, будет ли наблюдение рассматриваться как выброс или нет.
LOF учитывает плотность окрестности вокруг наблюдения, чтобы определить ее внешность. Это более быстрая реализация LOF с использованием другой структуры данных и функции вычисления расстояния по сравнению с функцией lofactor(), доступной в пакете “dprep”. Он также поддерживает несколько значений k, которые будут вычисляться параллельно, а также различные меры расстояния, кроме стандартного евклидова расстояния. Вычисления выполняются параллельно на нескольких ядрах процессора. Вычислим lofactor для тех же двух наборов (x и x.cap) для 5, 6, 7, 8, 9 и 10 соседей с использованием метода вычисления расстояния “minkowski”. Построим гистограммы этих lofactor.
require(Rlof) evalq(Rlof.x <- lof(x, c(5:10), cores = 2, method = 'minkowski'), env) evalq(Rlof.x.cap <- lof(x.cap, c(5:10), cores = 2, method = 'minkowski'), env) par(mfrow = c(2, 3)) hist(env$Rlof.x.cap[ ,6], breaks = 20) hist(env$Rlof.x.cap[ ,5], breaks = 20) hist(env$Rlof.x.cap[ ,4], breaks = 20) hist(env$Rlof.x.cap[ ,3], breaks = 20) hist(env$Rlof.x.cap[ ,2], breaks = 20) hist(env$Rlof.x.cap[ ,1], breaks = 20) par(mfrow = c(1, 1))
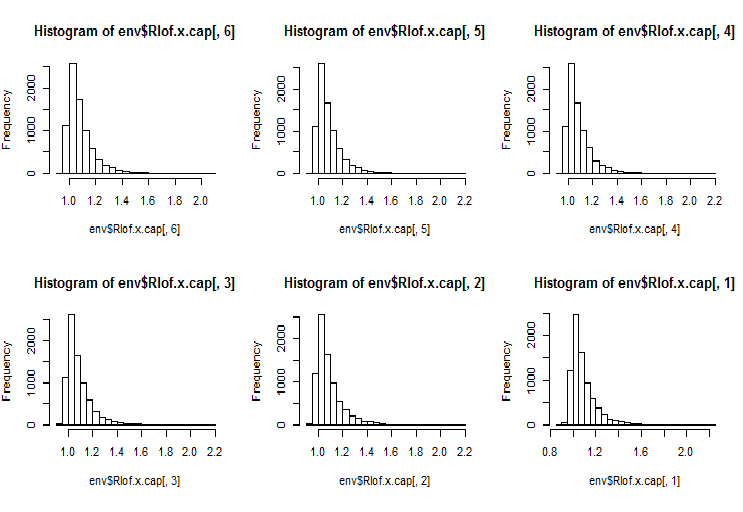
Рис.17. Глобальный фактор выбросов для различных значений к-соседей
Практически все наблюдения находятся в пределах lofactor =1.6. Вне этого предела:
> sum(env$Rlof.x.cap[ ,6] >= 1.6) [1] 32
Это незначительное количество умеренных выбросов приемлемо для такого размера набора.
ЗАМЕЧАНИЕ. При определении границ, выход значений переменных за которые может трактоваться как выброс, нужно применять тренировочный набор данных. Значения переменных тестового/валидационного наборов обрабатываются с помощью параметров, полученных на тренировочном наборе. Какие это параметры? Использованные нами в предыдущих вычислениях — границы upper = 1.5*IQR, lower = -1.5*IQR и cap =c(0.05, 0.95) percentil. Если были приняты другие методы вычисления границ и импутации выбросов, их нужно определить на тренировочном наборе, сохранить и использовать при обработке наборов valid/test в дальнейшем.
Напишем функцию, которая будет проводить предварительные вычисления:
#-----prep.outlier-------------- prep.outlier <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) caps <- quantile(x, probs = c(.05, .95), na.rm = na.rm, ...) list(lower = qnt[1] - H, upper = qnt[2] + H, med = median(x), cap1 = caps[1], cap2 = caps[2]) }
Вычислим параметры, необходимые для определения и импутации выбросов. Примем предварительно длину train набора в 4000 баров в начале, и следующие 2000 баров использовать как test.
evalq(
{train <- x[1:4000, ]
foreach(i = 1:ncol(train), .combine = "cbind") %do% {
prep.outlier(train[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
#pre.outl %<>% t()
},
env)Посмотрим на результат:
> env$pre.outl ftlm stlm rbci pcci lower.25% -0.2224942912 -0.59629203 -0.253231002 -9.902232e-02 upper.75% 0.2214486206 0.59242529 0.253529797 9.826936e-02 med -0.0001534451 0.00282525 -0.001184966 8.417127e-05 cap1.5% -0.1700418145 -0.40370452 -0.181326658 -6.892085e-02 cap2.95% 0.1676526431 0.39842675 0.183671973 6.853935e-02 v.fatl v.satl v.rftl v.rstl lower.25% -0.0900973332 -4.259328e-02 -0.0558921804 -0.2858430788 upper.75% 0.0888110249 4.178418e-02 0.0555115004 0.2889057397 med -0.0008581219 -2.130064e-05 -0.0001707447 -0.0001721546 cap1.5% -0.0658731640 -2.929586e-02 -0.0427927888 -0.1951978435 cap2.95% 0.0662353821 3.089833e-02 0.0411091859 0.1820803387 v.ftlm v.stlm v.pcci lower.25% -0.1115823754 -5.366875e-02 -0.1115905239 upper.75% 0.1108670403 5.367466e-02 0.1119495436 med -0.0003560178 -6.370034e-05 -0.0003173464 cap1.5% -0.0765431363 -3.686945e-02 -0.0765950814 cap2.95% 0.0789209957 3.614423e-02 0.0770439553
Как видим, для каждой переменной в наборе определены первый, третий квартиль и медиана, а также 5 и 95 персентиль — это все, что необходимо для определения и обработки выбросов.
Нам нужна функция, которая будет обрабатывать выбросы любого набора данных по предварительно определенным параметрам. Возможные варианты обработки: замещение выброса на NA,замещение выброса на медиану, замещение выбросов на 5/95 персентиль.
#---------treatOutlier--------------------------------- treatOutlier <- function(x, impute = TRUE, fill = FALSE, lower, upper, med, cap1, cap2){ if (impute) { x[x < lower] <- cap1 x[x > upper] <- cap2 return(x) } if (!fill) { x[x < lower | x > upper] <- NA return(x) } else { x[x < lower | x > upper] <- med return(x) } }
Поскольку мы уже определили необходимые параметры на тренировочном наборе, обработаем выбросы на тренировочном наборе, заменив их на 5/95 персентиля, затем так же обработаем выбросы на тестовом наборе данных, после чего сравним распределения в полученных наборах, построив три графика.
#------------
evalq(
{
foreach(i = 1:ncol(train), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = train[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> train.out
colnames(train.out) <- colnames(train)
},
env
)
#-------------
evalq(
{test <- x[4001:6000, ]
foreach(i = 1:ncol(test), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = test[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> test.out
colnames(test.out) <- colnames(test)
},
env
)
#---------------
evalq(boxplot(train, main = "train with outliers"), env)
evalq(boxplot(train.out, main = "train.out without outliers"), env)
evalq(boxplot(test.out, main = "test.out without outliers"), env)
#------------------------
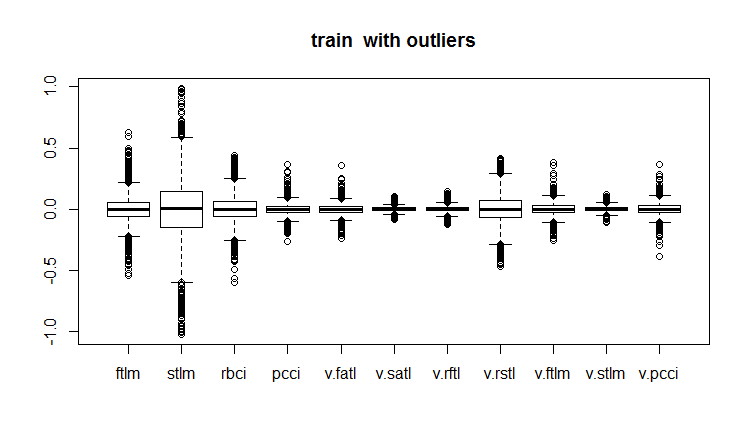
Рис.18. Тренировочный набор данных с выбросами
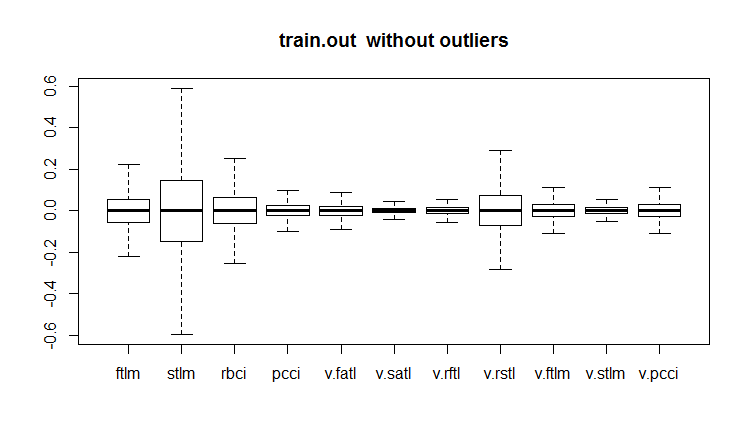
Рис.19. Тренировочный набор данных с импутированными выбросами
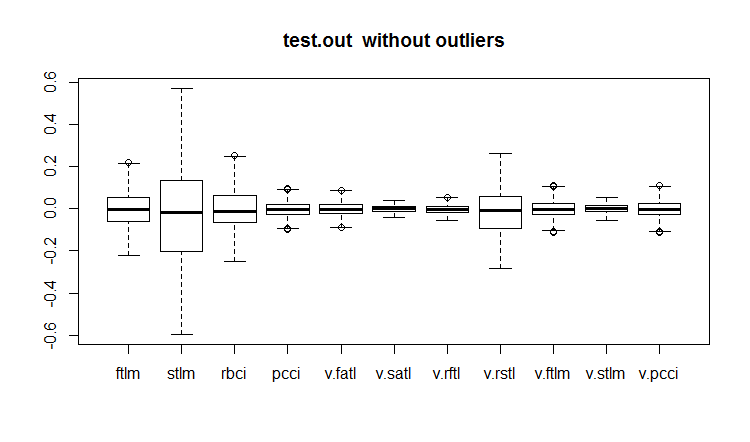
Рис.20. Тестовый набор данных с импутированными выбросами
Не все модели чувствительны к выбросам. Например, модели решающих деревьев (DT) и случайных лесов (RF) нечувствительны к ним.
При определении и обработке выбросов могут быть полезны и несколько других пакетов: “univOutl”, “mvoutlier”, “outlier”, funModeling::prep.outlier().
3.3. Устранение асимметрии (skewness)
Асимметрия — это показатель формы. Общий способ для ее проверки заключается в вычислении коэффициента асимметрии переменной. Как правило, отрицательная асимметрия свидетельствует о том, что средняя меньше, чем медиана, а распределение имеет левую асимметрию. Положительная асимметрия указывает на то, что средняя больше, чем медиана, а распределение данных имеет правую асимметрию.
Если асимметричность предиктора равно 0, то данные совершенно симметричны.
Если асимметрия предиктора меньше -1 или больше +1, данные сильно искажены.
Если асимметрия предиктора между -1 и -1/2 или между +1 и +1/2, то данные умеренно скошены.
Если асимметрия предиктора равно -1/2 и +1/2, то данные приблизительно симметричны.
Правая асимметрия исправляется логарифмированием, а левая — экспонированием.
Мы уже говорили, что асимметрия, выбросы и любые другие трансформации данных связаны. Посмотрим, как изменился показатель асимметрии после удаления и импутации выбросов.
evalq({
sk <- skewness(x)
sk.out <- skewness(x.out)
sk.cap <- skewness(x.cap)
},
env)
> env$sk
ftlm stlm rbci pcci v.fatl
Skewness 4.219857 1.785286 2.304655 6.491546 5.274871
v.satl v.rftl v.rstl v.ftlm v.stlm
Skewness 2.677162 3.954098 1.568675 1.207227 0.8516043
v.pcci
Skewness 3.031012
> env$sk.out
ftlm stlm rbci pcci
Skewness -0.04272076 -0.07893945 -0.02460354 0.01485785
v.fatl v.satl v.rftl v.rstl
Skewness 0.00780424 -0.02640635 -0.04663711 -0.04290957
v.ftlm v.stlm v.pcci
Skewness -0.0009597876 0.01997082 0.0007462494
> env$sk.cap
ftlm stlm rbci pcci
Skewness -0.03329392 -0.07911245 -0.02847851 0.01915228
v.fatl v.satl v.rftl v.rstl
Skewness 0.01412182 -0.02617518 -0.03412228 -0.04596505
v.ftlm v.stlm v.pcci
Skewness 0.008181183 0.009661169 0.002252508Как видим, и набор с удаленными выбросами x.out, и с импутированными выбросами x.cap идеально симметричны и не требуют никакого исправления.
Давайте посмотрим и на коэффициент эксцесса (kurtosis). Коэффицие́нт эксце́сса (коэффициент островершинности) — мера остроты пика распределения случайной величины. У нормального распределения равен 0. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик очень гладкий.
require(PerformanceAnalytics)
evalq({
k <- kurtosis(x)
k.out <- kurtosis(x.out)
k.cap <- kurtosis(x.cap)
},
env)
> env$k
ftlm stlm rbci pcci
Excess Kurtosis 84.61177 16.77141 45.01858 247.9795
v.fatl v.satl v.rftl v.rstl
Excess Kurtosis 145.9547 36.99944 74.4307 13.57613
v.ftlm v.stlm v.pcci
Excess Kurtosis 86.36448 23.06635 233.5408
> env$k.out
ftlm stlm rbci
Excess Kurtosis -0.003083449 -0.1668102 -0.1197043
pcci v.fatl v.satl
Excess Kurtosis -0.05113439 -0.02738558 -0.04341552
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.01219999 -0.1316499 -0.0287925
v.stlm v.pcci
Excess Kurtosis -0.1530424 -0.09950709
> env$k.cap
ftlm stlm rbci
Excess Kurtosis -0.2314336 -0.3075185 -0.2982044
pcci v.fatl v.satl
Excess Kurtosis -0.2452504 -0.2389486 -0.2331203
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.2438431 -0.2673441 -0.2180059
v.stlm v.pcci
Excess Kurtosis -0.2763058 -0.2698028В исходном наборе данных x пики распределения переменных чрезвычайно остры (эксцесс намного больше 0). В наборе x.out с удаленными выбросами пики близки к нормальной островерхости, в наборе с импутированными выбросами вершины более гладкие, и оба набора не требуют никаких корректировок.
Приложение
1. В архиве DARCH12_1.zip находятся скрипты к первой части статьи (dataRaw.R, PrepareData.R, FUNCTION.R), а также картинка сессии Rstudio с исходными данными Cotir.RData. Загрузив их в Rstudio, вы сможете воспроизвести все скрипты, а также экспериментировать с ними. Вы можете также скачать все это c Git /Part_I.
2. В архиве ACTF.zip статья В. Кравчука "Новый адаптивный метод следования за тенденциями и рыночными циклами"
3. В архиве R_intro.zip собрана литература по языку R.
Ссылки
[1] A Systematic Approach on Data Pre-processing In Data Mining. COMPUSOFT, An international journal of advanced computer technology, 2 (11), November-2013 (Volume-II, Issue-XI)
[2] Outlier Detection Techniques.Hans-Peter Kriegel, Peer Kröger, Arthur Zimek. Ludwig-Maximilians-Universität München.Munich, Germany
[3] Breuning, M., Kriegel, H., Ng, R.T, and Sander. J. (2000). LOF: Identifying density-based local outliers. In Proceedings of the ACM SIGMOD International Conference on Management of Data.
TradeObjects: Автоматизация торговли на основе графических объектов в MetaTrader
Графические интерфейсы XI: Поля ввода и комбо-боксы в ячейках таблицы (build 15)
Глубокие нейросети (Часть II). Разработка и выбор предикторов
Тестирование паттернов, возникающих при торговле корзинами валютных пар. Часть I
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Поэтому не люблю этот ggplot2. Вот работающий вариант который я не включил в статью.
#--------quantmod---------------------------- require(quantmod) require(timetk) evalq( pr %>% tk_xts(.) %>% chartSeries(x = OHLC(.), #c("auto", "candlesticks", #"matchsticks", "bars","line") type = "bars", subset = 'last 3 days',#weeks, months show.grid = T, name = "EURJPY M15", tyme.scale = T, log.scale = FALSE, line.type = "l", bar.type = "ohlc", theme = chartTheme('white', up.col = 4, dn.col = 2, grid.col = 3, main.col = 1, sub.col = 4), major.ticks = "day", minor.ticks = TRUE , plot = TRUE, color.vol = F, multi.col = F ), env)Так выглядит
Удачи
Поэтому не люблю этот ggplot2. Вот работающий вариант который я не включил в статью.
Так выглядит
Удачи
Спасибо!
В RStudio Ваш вариант нормально график строит, а из терминала МТ4 ни в какую. Второй день вожусь и не выходит через окружение env команда chartSeries.
Если возможно, поделитесь советником под MT4 выгружающим котировки и строящим график. Спасибо.
Смог только по старинке, как делал раньше. Ну очень не удобно все команды прописывать в терминале, а не в R.
Rv(R,"Data",tm);
Rv(R,"Time",tm);
Rv(R,"Open",o);
Rv(R,"High",hi);
Rv(R,"Low",lo);
Rv(R,"Close",clo);
Rv(R,"Volume",vol);
PREDICTION_COMMAND=
"library(magrittr)"+CR
+"library(dplyr)"+CR
+"library(xts)"+CR
+"library(quantmod)"+CR
+"price <- cbind(Time = rev(Time), Open = rev(Open), High = rev(High), Low = rev(Low), Close = rev(Close))"+CR
+"price_t <- price"+CR
+"dts = price_t[,1]"+CR
+"mydates = structure(price_t[,1],class=c('POSIXt','POSIXct'))"+CR
+"price_time <- xts(x=price_t[,c(2:5)], order.by=mydates, tzone='GMT')"+CR
;
RExecuteAsync(R,PREDICTION_COMMAND);
Rx(R,"chartSeries(price_time, type = 'bars', subset = 'last 3 days',show.grid = T,name = 'EURUSD M15',tyme.scale = T,log.scale = FALSE,line.type = 'l',bar.type = 'ohlc',theme = chartTheme('white',up.col = 4, dn.col = 2,grid.col = 3,main.col = 1,sub.col = 4), major.ticks = 'day', minor.ticks = TRUE ,plot = TRUE,color.vol = F,multi.col = F)");
Спасибо!
В RStudio Ваш вариант нормально график строит, а из терминала МТ4 ни в какую. Второй день вожусь и не выходит через окружение env команда chartSeries.
Если возможно, поделитесь советником под MT4 выгружающим котировки и строящим график. Спасибо.
Смог только по старинке, как делал раньше. Ну очень не удобно все команды прописывать в терминале, а не в R.
Rv(R,"Data",tm);
Rv(R,"Time",tm);
Rv(R,"Open",o);
Rv(R,"High",hi);
Rv(R,"Low",lo);
Rv(R,"Close",clo);
Rv(R,"Volume",vol);
PREDICTION_COMMAND=
"library(magrittr)"+CR
+"library(dplyr)"+CR
+"library(xts)"+CR
+"library(quantmod)"+CR
+"price <- cbind(Time = rev(Time), Open = rev(Open), High = rev(High), Low = rev(Low), Close = rev(Close))"+CR
+"price_t <- price"+CR
+"dts = price_t[,1]"+CR
+"mydates = structure(price_t[,1],class=c('POSIXt','POSIXct'))"+CR
+"price_time <- xts(x=price_t[,c(2:5)], order.by=mydates, tzone='GMT')"+CR
;
RExecuteAsync(R,PREDICTION_COMMAND);
Rx(R,"chartSeries(price_time, type = 'bars', subset = 'last 3 days',show.grid = T,name = 'EURUSD M15',tyme.scale = T,log.scale = FALSE,line.type = 'l',bar.type = 'ohlc',theme = chartTheme('white',up.col = 4, dn.col = 2,grid.col = 3,main.col = 1,sub.col = 4), major.ticks = 'day', minor.ticks = TRUE ,plot = TRUE,color.vol = F,multi.col = F)");
Добрый день.
Я не строю графики таким образом из МТ. Это громоздко и не удобно. Интерактивные и любые другие графики нужно строить из R через shiny.
В V части статьи я приложу советник с выводом простого графика. Правда я не пойму зачем Вам график котировок?
Я предполагал выводить график результатов тестирования, результатов торговли в реальном времени и с разбивкой по времени, символу и т.д. Может не все сделаю в этом эксперте.
Для работы с время/дата посмотрите более удобный пакет timekt. На Ваш выбор.
Удачи
Здравствуйте Владимир,
1) почему
умножается на 10, а остальные нет?
При нормализации эффект умножения - исчезнет.
2) Цифровые фильтры у вас считаются по ценам Close. На начало бара цена Close неизвестна (и равна Open). А считая по Close - получается подглядывание в будущее, которое немного повышает точность.
Может нужно считать фильтры по Close предыдущего бара или хотя бы по Open текущего бара?
Для эксперимента попробовал посчитать фильтры по Open - результаты стали похуже на несколько процентов.
По эксперименту из 6-й статьи
> #---5-----best----------------------
[1] 0.677 0.674 0.673 0.672 0.669 0.669 0.668
вместо полученных вами по Close [1] 0.720 0.718 0.718 0.715 0.713 0.713 0.712
3) Почему фильтры FATL, SATL, RFTL, RSTL исключены из дальнейших расчетов? Расчет ведется только на осцилляторах. Я попробовал их оставить, clusterSim посчитал их важными и не отсеял, в результате обучения получилась ошибка около 50%, т.е. они хоть и важны,но значительно ухудшают результат.Видимо имеет смысл использовать для нейросетей только осцилляторы в качестве входов?
Здравствуйте Владимир,
1) почему
умножается на 10, а остальные нет?
При нормализации эффект умножения - исчезнет.
2) Цифровые фильтры у вас считаются по ценам Close. На начало бара цена Close неизвестна (и равна Open). А считая по Close - получается подглядывание в будущее, которое немного повышает точность.
Может нужно считать фильтры по Close предыдущего бара или хотя бы по Open текущего бара?
Для эксперимента попробовал посчитать фильтры по Open - результаты стали похуже на несколько процентов.
По эксперименту из 6-й статьи
> #---5-----best----------------------
[1] 0.677 0.674 0.673 0.672 0.669 0.669 0.668
вместо полученных вами по Close [1] 0.720 0.718 0.718 0.715 0.713 0.713 0.712
3) Почему фильтры FATL, SATL, RFTL, RSTL исключены из дальнейших расчетов? Расчет ведется только на осцилляторах. Я попробовал их оставить, clusterSim посчитал их важными и не отсеял, в результате обучения получилась ошибка около 50%, т.е. они хоть и важны,но значительно ухудшают результат.Видимо имеет смысл использовать для нейросетей только осцилляторы в качестве входов?
Добрый день.
1. Этот предиктор имел очень малые значения и при нормализации мог выпасть. Я его просто подогнал в диапазон остальных предикторов. При применении метода SpatialSign предикторы не должны отличаться на порядки.
2. Все значения котировок берутся со сформировавшихся баров начиная с 1. Вообще зигзаг лучше считать по High/Low. В последних статьях я предусмотрел варианты расчета ZZ.
3. Эти 4 являются непрерывными линиями и неприменимы как входы. Применяется первая разность по ним
v.fatl = c(NA, diff(fatl)), v.rftl = c(NA, diff(rftl)), v.satl = c(NA, diff(satl)), v.rstl = c(NA, diff(rstl)*10))Цифровые фильтры имеют одно важное преимущество перед другими индикаторами - они непараметрические(условно говоря конечно). Но мне они очень нравятся.
Удачи