Rede neural profunda com Máquina de Boltzmann Restrita Empilhada. Auto-aprendizagem, auto-controle

Este artigo é uma continuação dos artigos anteriores sobre redes neurais profundas e seleção de preditores. Aqui, consideraremos as características de uma rede neural iniciada com a Stacked RBM (Máquina de Boltzmann Restrita Empilhada), bem como sua implementação no pacote "darch". Também será revelada a possibilidade de utilização de modelos ocultos de Markov para melhorar o desempenho quanto predição da rede neural. Finalmente, vamos implementar programaticamente uma cópia funcional do Expert Advisor.

Conteúdo

• 1. Diagrama de bloco do DBN
• 2. Preparação e seleção de dados
• 2.1. Variáveis de entrada
• 2.2. Variáveis de saída
• 2.3. Quadro de dados inicial
• 2.3.1. Exclusão de variáveis altamente correlacionadas
• 2.4. Seleção das variáveis mais importantes
• 3. Parte experimental.
• 3.1. Construção de modelos
• 3.1.1. Breve descrição do pacote "darch"
• 3.1.2. Construção do modelo DBN. Parâmetros.
• 3.2. Geração das amostras de treino e de teste.
• 3.2.1. Balanceamento de classes e pré-processamento.
• 3.2.2. Codificação da variável-alvo
• 3.3. Modelo de treinamento
• 3.3.1. Pré-treinamento
• 3.3.2. Treinamento fino
• 3.4. Teste do modelo. Métricas.
• 3.4.1. Descodificação da predição.
• 3.4.2. Melhoria do resultado de previsão
• Calibragem
• Suavização usando o modelo de cadeia de Markov
• Ajustamento dos sinais previstos na curva de equilíbrio teórico
• 3.4.3. Métricas
• 4. Diagrama de bloco do Expert Advisor
• 4.1. Descrição do trabalho do Expert Advisor
• 4.2. Auto-controle. Auto-aprendizagem
• Instalação e execução
• Formas e meios para melhorar os indicadores de qualidade.
• Conclusão

Introdução

Na preparação dos dados para fins de experimentação, vamos usar as variáveis​do artigo anterior sobre avaliação e seleção de preditores. Vamos formar um conjunto inicial, limpá-lo e selecionar as variáveis​importantes.

Vamos considerar maneiras de dividir a escolha inicial em conjuntos de treinamento, teste e validação.

Usando o pacote "darch" vamos construir o modelo de rede DBN e treiná-lo sobre nossos conjuntos de dados. Após testar o modelo, vamos obter métricas que nos permitirão avaliar a qualidade do modelo. Vamos considerar as diversas oportunidades que o pacote oferece para configurar as definições da rede neural.

Além disso, vamos ver como os modelos ocultos de Markov podem nos ajudar a melhorar as previsões da redes neurais.

Vamos desenvolver um Expert Advisor, onde o modelo será treinado periodicamente em tempo real sem interrupção da negociação, com base nos resultados da monitorização contínua. O modelo DBN do pacote "Darch" será utilizado no Expert Advisor. Nós também vamos incorporar o Expert Advisor construído usando o SAE DBN do artigo anterior.

Além disso, vamos indicar formas e métodos de melhoria dos indicadores qualitativos do modelo.

1. Diagrama de bloco da rede neural profunda inicializada pela Stacked RBM (DN_SRBM)

Lembro-lhe que DN_SRBM consiste do número n da RBM que é igual ao número de camadas ocultas de rede neural e, basicamente, da rede neural em si. A formação é realizada em duas fases.

A primeira etapa envolve o PRÉ-TREINAMENTO. Nela, cada RBM é sistematicamente treinados sem um supervisor no conjunto de entrada (sem alvo). Após este peso de camadas ocultas, as RBM são transferidas para as camadas ocultas relevantes da rede neural.

A segunda etapa envolve o ajuste fino, onde a rede neural é treinada com um supervisor. Informações detalhadas sobre ele foram fornecidas no artigo anterior, por isso não vamos repeti-las aqui. Vou simplesmente mencionar que, ao contrário do pacote "deepnet" que usamos no artigo anterior, o pacote "darch" nos ajuda a implementar oportunidades mais amplas na construção e ajuste do modelo. Falamos mais sobre isso ao criar o modelo. A Fig. 1 mostra o esquema estrutural e o processo de formação de DN_SRBM

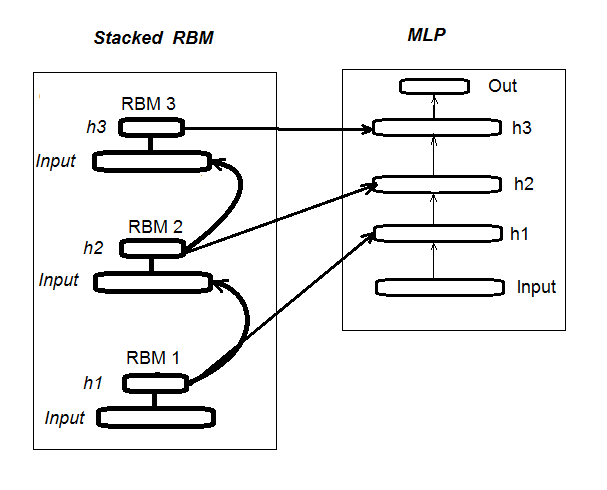
Fig. 1. Diagrama de bloco do DN SRBM

2. Preparação e seleção de dados

2.1. Variáveis de entrada (sintomas, preditores)

No artigo anterior, já foram considerados a avaliação e seleção de indicadores, por isso não há necessidade de fornecer informações adicionais quanto isso agora. Apenas vou mencionar que usamos 11 indicadores (todos são osciladores: ADX, aroon, ATR, CCI, chaikinVolatility, CMO, MACD, RSI, stoch, SMI, volatility). Uma série de variáveis foram selecionadas a partir de alguns indicadores. Desta forma, temos formado o conjunto de entrada de 17 variáveis. Vamos tomar cotações das últimas 6000 barras no par EURUSD, M30 a partir de 14/02/16 e calculamos os valores de indicador usando a função In().

#---2---------------------------------------------
In <- function(p = 16){
  require(TTR)
  require(dplyr)
  require(magrittr)
  adx <- ADX(price, n = p) %>% as.data.frame %>% 
    mutate(.,oscDX = DIp - DIn) %>% 
    transmute(.,DX, ADX, oscDX) %>% 
    as.matrix()
  ar <- aroon(price[ ,c('High', 'Low')], n = p) %>% 
    extract(,3)
  atr <- ATR(price, n = p, maType = "EMA") %>%
    extract(,1:2)
  cci <- CCI(price[ ,2:4], n = p)
  chv <- chaikinVolatility(price[ ,2:4], n = p)
  cmo <- CMO(price[ ,'Med'], n = p)
  macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% 
    as.data.frame() %>% 
    mutate(., vsig = signal %>% 
             diff %>% c(NA,.) %>% multiply_by(10)) %>% 
    transmute(., sign = signal, vsig) %>% 
    as.matrix()
  rsi <- RSI(price[ ,'Med'], n = p)
  stoh <- stoch(price[ ,2:4], nFastK = p, 
                nFastD =3, nSlowD = 3, 
                maType = "EMA") %>%
                                as.data.frame() %>% 
                                mutate(., oscK = fastK - fastD) %>%
                                transmute(.,slowD, oscK) %>% 
                                as.matrix()
  smi <- SMI(price[ ,2:4],n = p, nFast = 2, 
             nSlow = 25, nSig = 9)
  kst <- KST(price[ ,4])%>% as.data.frame() %>% 
                                mutate(., oscKST = kst - signal) %>%
                                select(.,oscKST) %>% as.matrix()
  In <- cbind(adx, ar, atr, cci, chv, cmo, macd, 
              rsi, stoh, smi, kst)
  return(In)
}

Na saída obtemos a matriz de dados de entrada.

2.2 Dados de saída (variável-alvo)

Tomamos como variável-alvo os sinais obtidos com ZZ. Função que calcula o ziguezague e o sinal é:

#----3------------------------------------------------
ZZ <- function(pr = price, ch = ch , mode="m") {
  require(TTR)
  require(magrittr)
  if (ch > 1) ch <- ch/(10 ^ (Dig - 1))
  if (mode == "m") {pr <- pr[ ,'Med']}
  if (mode == "hl") {pr <- pr[ ,c("High", "Low")]}
  if (mode == "cl") {pr <- pr[ ,c("Close")]}
  zz <- ZigZag(pr, change = ch, percent = F, 
               retrace = F, lastExtreme = T)
  n <- 1:length(zz)
  dz <- zz %>% diff %>% c(., NA)
  sig <- sign(dz)
  for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]}
  return(cbind(zz, sig))
}

Parâmetros da função:

pr = price – matriz de cotações OHLCMed;

ch – comprimento mínimo da curva do ziguezague em pontos (4 dígitos) ou em termos reais (por exemplo, ch = 0.0035);

mode – preço aplicado ( "m" - média, "hl" - High e Low. "cl" - Close), por padrão tomamos o médio.

A função retorna uma matriz com duas variáveis, nomeadamente, o ziguezague e o sinal obtido na base da inclinação do ziguezague no intervalo [-1;1]. Deslocamos o sinal para uma barra à esquerda (no futuro). Este sinal específico será utilizado para treinar a rede neural.

Calculamos os sinais para ZZ com um comprimento de curvatura de pelo menos 37 pontos (4 dígitos).

> out <- ZZ(ch = 37, mode = "m")
Loading required package: TTR
Loading required package: magrittr
> table(out[ ,2])

  -1    1 
2828 3162

Como podemos ver, as classes estão um pouco desequilibradas. Ao formar conjuntos para treinar o modelo, vamos tomar as medidas necessárias para nivelar-los.

2.3. Quadro de dados inicial

Vamos escrever a função que irá criar a quadro inicial de dados e, em seguida, limpá-la a partir de dados incertos (NA) e converter a variável-alvo para o fator com duas classes «-1» e «+1». Esta função combina as funções anteriormente descritas In() e ZZ(). Vamos cortar instantaneamente as últimas 500 barras que serão utilizadas para avaliar a qualidade da previsão do modelo.

#-----4---------------------------------
form.data <- function(n = 16, z = 37, len = 500){
  require(magrittr)
  x <- In(p = n)
  out <- ZZ(ch = z, mode = "m")
  data <- cbind(x, y = out[ ,2]) %>% 
    as.data.frame %>% head(., (nrow(x)-len))%>%
        na.omit
  data$y <- as.factor(data$y)
  return(data)
}

2.3.1. Exclusão de variáveis altamente correlacionadas

Nós vamos excluir - do nosso conjunto inicial - variáveis com um coeficiente de correlação superior a 0,9. Vamos escrever a função que irá formar o quadro de dados inicial, remover variáveis​altamente correlacionadas e retornar dados limpos.

Podemos verificar com antecedência quais são as variáveis que têm uma correlação acima de 0,9.

> data <- form.data(n = 16, z = 37) # preparamos a quadro de dados
> descCor <- cor(data[ ,-ncol(data)])# removemos a variável-alvo
> summary(descCor[upper.tri(descCor)])
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
-0.1887  0.0532  0.2077  0.3040  0.5716  0.9588 
> highCor <- caret::findCorrelation(descCor, cutoff = 0.9)
> highCor
[1] 12  9 15
> colnames(data[ ,highCor])
[1] "rsi" "cmo" "SMI"

Assim, as variáveis​acima listadas são sujeitas à remoção. Vamos excluí-los da quadro de dados.

> data.f <- data[ ,-highCor]
> colnames(data.f)
 [1] "DX"     "ADX"    "oscDX"  "ar"     "tr"    
 [6] "atr"    "cci"    "chv"    "sign"   "vsig"  
[11] "slowD"  "oscK"   "signal" "vol"    "Class" 

Vamos escrever isso de forma compacta numa função:

#---5-----------------------------------------------
cleaning <- function(n = 16, z = 37, cut = 0.9){
  data <- form.data(n, z)
  descCor <- cor(data[ ,-ncol(data)])
  highCor <- caret::findCorrelation(descCor, cutoff = cut)
  data.f <- data[ ,-highCor]
  return(data.f)
}
> data.f <- cleaning()

Nem todos os autores de pacotes e pesquisadores concordam que os dados altamente correlacionados devem ser retirados a partir dos conjuntos. No entanto, aqui devem ser comparados os resultados obtidos utilizando ambas as opções. No nosso caso, nós escolhemos a opção com exclusão.

2.4. Seleção das variáveis mais importantes

As variáveis​importantes serão selecionadas com base em três indicadores: importância global, importância local (em conjunto) e importância parcial por classes. Vamos aproveitar as possibilidades do pacote "randomUniformForest", conforme detalhado no artigo anterior. Todas as ações anteriores e seguintes serão reunidas numa função para compacidade. Uma vez executado, obteremos três conjuntos, como resultado:

• com as melhores variáveis​na contribuição e interação;
• com as melhores variáveis para a classe «-1»;
• com as melhores variáveis para a classe «+1».

#-----6------------------------------------------------
prepareBest <- function(n, z, cut, method){
  require(randomUniformForest) 
  require(magrittr)
  data.f <<- cleaning(n = n, z = z, cut = cut)
  idx <- rminer::holdout(y = data.f$Class)
  prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)], method = method)
  x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)])
  x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)])
  y.train <- data.f[idx$tr, ncol(data.f)]
  y.test <- data.f[idx$ts, ncol(data.f)]
#---------
  ruf <- randomUniformForest( X = x.train, Y = y.train,
                              xtest = x.test, ytest = y.test,
                              mtry = 1, ntree = 300,
                              threads = 2, nodesize = 1
                       )
  imp.ruf <- importance(ruf, Xtest = x.test)
  best <- imp.ruf$localVariableImportance$classVariableImportance %>% 
                  head(., 10) %>% rownames()
#-----partImport
  best.sell <- partialImportance(X = x.test, 
                                imp.ruf, 
                                whichClass = "-1",
                                nLocalFeatures = 7) %>% 
                                row.names() %>% 
                                as.numeric() %>% 
                                colnames(x.test)[.]
  best.buy <- partialImportance(X = x.test,
                                   imp.ruf,
                                   whichClass = "1",
                                nLocalFeatures = 7) %>% 
                                row.names() %>% 
                                as.numeric() %>% 
                                colnames(x.test)[.]
  dt <- list(best = best, buy = best.buy, sell = best.sell)
  return(dt)
}

Vamos esclarecer a ordem dos cálculos de funções. Parâmetros formais:

n – parâmetro de dados de entrada;

z – parâmetro de dados de saída;

cut – limite de correlação das variáveis;

method – método de pré-processamento de dados de entrada.

Ordem de cálculos:

• criamos o conjunto inicial de dados data.f , que tem removidas as variáveis altamente correlacionadas, e guardamo-lo para uso posterior.
• identificamos os índices dos conjuntos de treinamento e teste de idx;
• determinamos os parâmetros de pré-processamento de prep;
• dividimos o conjunto inicial em amostras de treinamento e testes, dados de entrada normalizados;
• treinamos e testamos o modelo ruf nos conjuntos obtidos;
• calculamos a importância das variáveis imp.ruf ;
• selecionamos as 10 variáveis​mais importantes em termos de contribuição e interação best ;
• selecionamos as 7 variáveis mais importantes para cada classe «-1» e «+1» best.buy, best.sell ;
• Criamos uma lista com os três conjuntos de preditores best, best.buy, best.sell.
  

Vamos calcular estes conjuntos e avaliar os valores de importância global, local e parcial das variáveis​selecionadas.

> dt <- prepareBest(16, 37, 0.9, c("center", "scale","spatialSign"))
Loading required package: randomUniformForest
Labels -1 1 have been converted to 1 2 for ease of computation and will be used internally 
       as a replacement.

1 - Global Variable Importance (14 most important based on information gain) :
Note: most predictive features are ordered by 'score' and plotted. Most discriminant ones
should also be taken into account by looking 'class' and 'class.frequency'.

   variables score class class.frequency percent
1        cci  4406    -1            0.51  100.00
2     signal  4344    -1            0.51   98.59
3        ADX  4337    -1            0.51   98.43
4       sign  4327    -1            0.51   98.21
5      slowD  4326    -1            0.51   98.18
6        chv  4296    -1            0.52   97.51
7       oscK  4294    -1            0.52   97.46
8        vol  4282    -1            0.51   97.19
9         ar  4271    -1            0.52   96.95
10       atr  4237    -1            0.51   96.16
11     oscDX  4200    -1            0.52   95.34
12        DX  4174    -1            0.51   94.73
13      vsig  4170    -1            0.52   94.65
14        tr  4075    -1            0.50   92.49
   percent.importance
1                   7
2                   7
3                   7
4                   7
5                   7
6                   7
7                   7
8                   7
9                   7
10                  7
11                  7
12                  7
13                  7
14                  7


2 - Local Variable importance
Variables interactions (10 most important variables at first (columns) and second (rows) order) :
For each variable (at each order), its interaction with others is computed.

                cci  slowD    atr     tr     DX
atr          0.1804 0.1546 0.1523 0.1147 0.1127
cci          0.1779 0.1521 0.1498 0.1122 0.1102
slowD        0.1633 0.1375 0.1352 0.0976 0.0956
DX           0.1578 0.1319 0.1297 0.0921 0.0901
vsig         0.1467 0.1209 0.1186 0.0810 0.0790
oscDX        0.1452 0.1194 0.1171 0.0795 0.0775
tr           0.1427 0.1168 0.1146 0.0770 0.0750
oscK         0.1381 0.1123 0.1101 0.0725 0.0705
sign         0.1361 0.1103 0.1081 0.0704 0.0685
signal       0.1326 0.1068 0.1045 0.0669 0.0650
avg1rstOrder 0.1452 0.1194 0.1171 0.0795 0.0775
               vsig  oscDX   oscK signal     ar
atr          0.1111 0.1040 0.1015 0.0951 0.0897
cci          0.1085 0.1015 0.0990 0.0925 0.0872
slowD        0.0940 0.0869 0.0844 0.0780 0.0726
DX           0.0884 0.0814 0.0789 0.0724 0.0671
vsig         0.0774 0.0703 0.0678 0.0614 0.0560
oscDX        0.0759 0.0688 0.0663 0.0599 0.0545
tr           0.0733 0.0663 0.0638 0.0573 0.0520
oscK         0.0688 0.0618 0.0593 0.0528 0.0475
sign         0.0668 0.0598 0.0573 0.0508 0.0455
signal       0.0633 0.0563 0.0537 0.0473 0.0419
avg1rstOrder 0.0759 0.0688 0.0663 0.0599 0.0545
                chv    vol   sign    ADX avg2ndOrder
atr          0.0850 0.0850 0.0847 0.0802      0.1108
cci          0.0824 0.0824 0.0822 0.0777      0.1083
slowD        0.0679 0.0679 0.0676 0.0631      0.0937
DX           0.0623 0.0623 0.0620 0.0576      0.0881
vsig         0.0513 0.0513 0.0510 0.0465      0.0771
oscDX        0.0497 0.0497 0.0495 0.0450      0.0756
tr           0.0472 0.0472 0.0470 0.0425      0.0731
oscK         0.0427 0.0427 0.0424 0.0379      0.0685
sign         0.0407 0.0407 0.0404 0.0359      0.0665
signal       0.0372 0.0372 0.0369 0.0324      0.0630
avg1rstOrder 0.0497 0.0497 0.0495 0.0450      0.0000


Variable Importance based on interactions (10 most important) :
   cci    atr  slowD     DX     tr   vsig  oscDX 
0.1384 0.1284 0.1182 0.0796 0.0735 0.0727 0.0677 
  oscK signal   sign 
0.0599 0.0509 0.0464 

Variable importance over labels (10 most important variables conditionally to each label) :
       Class -1 Class 1
cci        0.17    0.23
slowD      0.20    0.09
atr        0.14    0.15
tr         0.04    0.12
oscK       0.08    0.03
vsig       0.06    0.08
oscDX      0.04    0.08
DX         0.07    0.08
signal     0.05    0.04
ar         0.04    0.02

Resultados

1. Em termos de importância global todas as 14 variáveis de entrada são iguais.
2. As melhores 10 são definidos pela contribuição global (importância global) e interação (importância local).
3. As sete melhores variáveis em importância parcial para cada classe são mostradas nos gráficos abaixo.

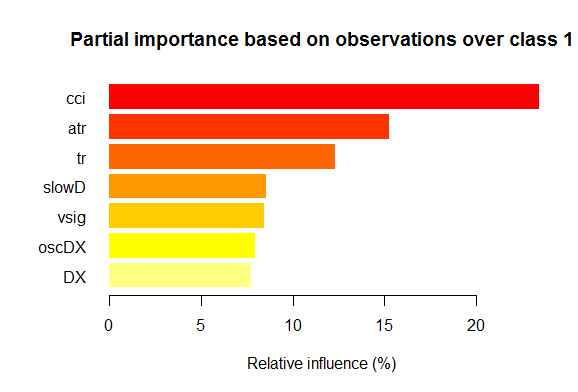
Fig. 2. Importância parcial das variáveis para a classe "1"

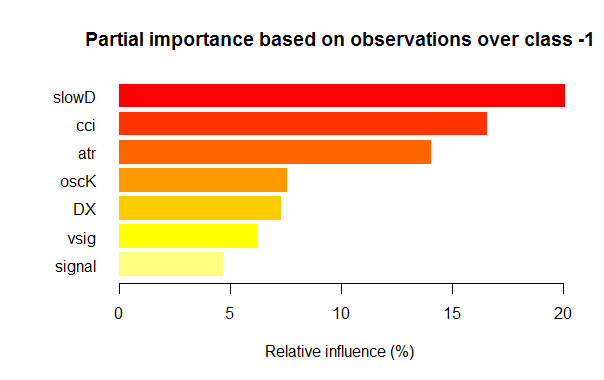
Fig. 3. Importância parcial das variáveis para a classe "-1"

Como podemos ver, para diferentes classes, as variáveis​mais importantes são diferentes tanto em estrutura quanto classificação. Assim, se para a classe "-1" a variável mais importante é slowD, então, para a classe "+1" ela está apenas no 4º lugar.

Então, nós temos as conjuntos de dados prontos. Agora podemos prosseguir com os experimentos.

3. Parte experimental.

Os experimentos serão realizados na linguagem R, nomeadamente, na Revolution R Open, version 3.2.2, distribuição da empresa Revolution Analytics. http://www.revolutionanalytics.com/revolution-r-open

Essa distribuição do tem uma série de caraterísticas sobre a linguagem R regular 3.2.2:

• cálculos rápidos e mais qualitativos através da aplicação do processamento multi-threaded com Intel® Math Kernel Library ;
  
• recursos avançados com Reproducible R Toolkit. Uma pequeno esclarecimento: a linguagem R está se desenvolvendo ativamente, melhorando constantemente os pacotes existentes e adicionando novos. O outro lado desse processo envolve a perda de reprodutibilidade. Ou seja, seus produtos, que foram escritos alguns meses atrás e estavam a funcionar bem, de repente param de funcionar após a próxima atualização de pacotes. Muito tempo é desperdiçado para identificar e liquidar erros causados pela mudança em qualquer um dos pacotes. Por exemplo, o Expert Advisor ligado ao primeiro artigo sobre redes neurais profundas estava funcionando bem no momento de sua criação. No entanto, poucos meses após a publicação, um grupo de usuários queixaram-se sobre a sua não-operabilidade. A análise mostrou que a atualização do pacote "svSocket" levou a um mau funcionamento do Expert Advisor, e eu era incapaz de encontrar a razão por trás disso. O Expert Advisor finalizado será anexado a este artigo. Este problema tornou-se uma questão premente, no entanto foi facilmente resolvido na Revolution Analytics. Agora, quando uma nova distribuição é liberada, a condição de todos os pacotes no depósito CRAN é fixado na data de lançamento, copiando-os em seu espelho. As alterações no depositário CRAN, após esta data, não podem afetar os pacotes "congelados" no espelho Revolution. Além disso, a partir de outubro de 2014, a empresa faz capturas de tela diárias do depositário CRAN, assim fixa o estado atual e versões de pacotes. Com ajuda de seu próprio pacote "checkpoint", agora podemos baixar os pacotes necessários que são relevantes na data que precisamos. Em outras palavras, operamos uma espécie de máquina do tempo.

E outra notícia. Revolutioneses atrás, quando a Microsoft comprou a Revolution Analytics prometeu apoiar seus desenvolvimentos e manteve a Revolution R Open (RRO) disponível gratuitamente. Isto foi seguido por inúmeras mensagens sobre novidades na RRO e Revolution R Enterpise (para não mencionar a integração da R com a SQL Server, PowerBI, Azure e Cortana Analitics). Agora nós temos a informação de que a próxima atualização RRO será chamada Microsoft R Open enquanto a Revolution R Enterprise será Microsoft R Server. Ah e só nos últimos dias, a Microsoft R anunciou que R vai para o Visual Studio. R Tools for Visual Studio (RTVS) segue o modelo Ferramentas Python para Visual Studio. Isto será uma adição livre para Visual Studio que irá proporcionar uma IDE completa para R com a possibilidade de editar e depurar os scripts de forma interativa.

No momento em que o artigo foi concluído, Microsoft R Open (R 3.2.3), já foi lançado, portanto, ainda mais no artigo vamos nos referir a pacotes para esta versão.

3.1. Construção de modelos

3.1.1. Breve descrição do pacote "darch"

O pacote "darch" ver. 0.10.0 oferece uma ampla gama de funções que não apenas permitem criar e treinar o modelo, mas também, literalmente, construir tijolo por tijolo e ajustá-lo de acordo com suas preferências. Conforme indicado anteriormente, a rede profunda consiste do número n da RBM (n = layers -1) e redes neurais MLP com um certo número de camadas. A pré-formação por camadas da RBM é executada em dados não formatados sem um supervisor. O treinamento fino da rede neural é realizado com um supervisor em dados formatados A divisão destas etapas de formação nos dá uma oportunidade de usar dados variados em volume (mas não em estrutura!) ou obter vários modelos finamente treinados com base num único pré-treinamento. Além disso, se os dados de pré-formação e aperfeiçoamento são os mesmos, é possível treinar de uma só vez, em vez de dividir em duas etapas. Ou você pode pular pré-treino e usar apenas a rede neural multicamadas, ou, por outro lado, utilizar apenas a RBM sem a rede neural. Ao mesmo tempo, temos acesso a todos os parâmetros internos. O pacote é destinado a usuários avançados. Além disso, vamos analisar os processos separados: pré-treinamento e aperfeiçoamento.

3.1.2. Construção do modelo DBN. Parâmetros.

Vamos descrever o processo de construção, formação e teste do modelo DBN.

1. Criamos o objeto de arquitetura profunda 'Darch' usando o construtor com os parâmetros necessários

newDArch(layers, batchSize, ff=FALSE, logLevel=INFO, genWeightFunc=generateWeights),

Onde:

• layers : matriz que indica o número de camadas e neurónios em cada camada. Por exemplo: layers = c(5,10,10,2) – uma camada de entrada com 5 neurônios (visíveis), duas camadas ocultas com 10 neurônios cada, e uma camada de saída com 2 saídas.
• BatchSize : tamanho da mini-escolha durante o treino.
• ff : indica se o formato FF deve ser utilizado em pesos, desvios e saídas. O formato FF é aplicado para guardar grandes volumes de dados usando compressão.
• LogLevel : nível de registro e de saída ao executar esta função.
• GenWeightFunction: função para gerar a matriz de pesos da RBM. Há uma oportunidade para usar a função de ativação do usuário.

O objeto darch contém (layers - 1)as RBM combinadas na rede acumulada que será utilizada para pré-treinamento da rede neural. Os dois atributos fineTuneFunction e executeFunction contêm funções para ajuste fino (por padrão backpropagation) e para execução (por padrão runDarch). O treinamento da rede neural é realizada com duas funções de formação: preTrainDArch() e fineTuneDArch(). A primeira função treina a rede da RBM sem um supervisor usando um método de divergência contrastante. A segunda função usa a função indicada no atributo fineTuneFunction para um ajuste fino da rede neural. Após o desempenho da rede neural, as saídas de cada camada podem ser encontradas no atributo executeOutputs ou a camada de saída apenas no atributo executeOutput.

2. Função de pré-treinamento do objeto darch

preTrainDArch(darch, dataSet, numEpoch = 1, numCD = 1, ..., trainOutputLayer = F),

Onde:

• darch: instância da classe 'Darch';
• dataSet : conjunto de dados para treinamento;
• numEpoch : número de épocas de treinamento;
• numCD : número de iterações de amostragem. Normalmente, um é suficiente;
• ... : Parâmetros adicionais que podem ser transferidos para a função trainRBM;
• trainOutputLayer : valor lógico que indica se a camada saída da RBM deve ser treinada.

A função executa a função de treinamento trainRBM() para cada RBM, copiando após a formação de pesos e deslocação (biases) para as camadas de rede neural relevantes do objeto darch.

3. Função de ajuste fino do objeto darch

fineTuneDArch(darch, dataSet, dataSetValid = NULL, numEpochs = 1, bootstrap = T, 
              isBin = FALSE, isClass = TRUE, stopErr = -Inf, stopClassErr = 101, 
              stopValidErr = -Inf, stopValidClassErr = 101, ...),

Onde:

• darch: instância da classe 'Darch';
• dataSet : conjunto de dados para treino (podem ser usados para validação) e teste;
• dataSetValid : conjunto de dados para validação;
• numxEpoch : número de épocas de treinamento;
• bootstrap : valor booleano, é necessário para aplicar inicialização ao criar validação de dados;
• isBin : indica se os dados de saída devem ser interpretados como valores lógicos. Por padrão — FALSE. Se for TRUE, cada valor superior a 0.5 será interpretado como 1, e inferior, como 0.
• isClass : indica se a rede está treinada para a classificação. Se for TRUE, serão determinadas estatísticas para classificação. Por padrão TRUE.
• stopErr : critério para parar o formação da rede neural devido a erro durante o treinamento. Por padrão -Inf;
• stopClassErr : critério para parar a formação da rede neural devido ao erro de classificação durante o treinamento. Por padrão 101;
• stopValidErr : critério para parar a rede neural devido a um erro na validação de dados. Por padrão -Inf;
• stopValidClassErr : critério para parar a rede neural devido ao erro de classificação durante a validação. Por padrão 101;
• ... : parâmetros adicionais que podem ser passados​para a função de treinamento.

A função treina a rede neural especificada usando a função armazenada no atributo fineTuneFunction do objeto darch. Os dados de saída (trainData, validData, testData) e as classes que lhe pertencem (targetData, validTargets, testTargets) podem ser transferidas camo dataSet ou matriz ff. Os dados e classes para validação e teste não são obrigatórios. Se eles são fornecidos, em seguida, a rede neural será executada com esses conjuntos de dados e as estatísticas serão calculadas. Os atributos isBin indica se os dados de saída devem ser interpretados como binários. Se isBin = TRUE, cada valor de saída superior a 0,5 é interpretado como 1, caso contrário, como 0 Além disso, podemos definir um critério de parada para o treinamento baseado em erro (stopErr, stopValidErr) ou classificação correta (stopClassErr, stopValidClassErr) nos conjuntos de formação ou validação.

Todos os parâmetros de função têm valores padrão. No entanto, estão disponíveis outros valores. Assim, por exemplo:

A função de ativação neuronal está disponível sigmoidUnitDerivative, linearUnitDerivative, softmaxUnitDerivative, tanSigmoidUnitDerivative. Por padrão —  sigmoidUnitDerivative.

As funções de ajuste fino da rede neural são por padrão a retro-propagação (backpropagation), a rpropagation -que também está disponível em quatro variações ("Rprop+", "Rprop-", "iRprop+", "iRprop-") - e minimizeClassifier (esta função é treinada pelo classificador de rede Darch usando o método do gradiente conjugado não-linear). Para os dois últimos algoritmos e para aqueles que têm um profundo conhecimento do assunto, é fornecida uma implementação separada de ajuste fino da rede neural com a possibilidade de configurar muitos dos seus vários parâmetros. Por exemplo:

rpropagation(darch, trainData, targetData, method="iRprop+",
             decFact=0.5, incFact=1.2, weightDecay=0, initDelta=0.0125,
             minDelta=0.000001, maxDelta=50, ...),

Onde:

• darch – objeto darch para treinamento;
• trainData – conjunto de dados de entrada para treinamento;
• targetData – saída esperada para o conjunto treinado;
• method – método para treinamento. Por padrão "iRprop+". Pode haver "Rprop+", "Rprop-", "iRprop-";
• decFact – fator decrescente para treinamento. Por padrão 0.5;
• incFact - fator crescente para treinamento. Por padrão 1.2;
• weightDecay – redução de peço durante o treinamento. Por padrão 0;
• initDelta – valor de inicialização durante a atualização. Por padrão 0.0125;
• minDelta – limite inferior para o tamanho do passo. Por padrão 0.000001;
• maxDelta – limite superior para o tamanho do passo. Por padrão 50.

A função retorna o objeto darch com a rede neural treinada.

3.2. Geração das amostras de treino e de teste.

Nós já formamos o conjunto inicial de dados. Agora, precisamos dividi-lo em treinamento, validação e teste. A relação, por padrão, é 2/3. Vários pacotes têm muitas funções que são usadas​para dividir conjuntos. Eu uso a função rminer::holdout() que calcula índices para dividir o conjunto inicial em o treinamento e teste.

holdout(y, ratio = 2/3, internalsplit = FALSE, mode = "stratified", iter = 1,
        seed = NULL, window=10, increment=1),

Onde:

• y – variável-alvo desejada, vector ou factor numérico, neste caso, é aplicada a separação estratificada (ou seja, as proporções entre as classes são as mesmas para todas as partes);
• ratio – rácio de separação (o tamanho do conjunto de formação é estabelecido em percentagem; ou o tamanho do conjunto de teste é estabelecido no número total de instâncias) ;
• internalsplit – se for TRUE, então os dados de treinamento são mais uma vez separados em conjuntos de treinamento e validação. A mesma proporção é aplicada para a separação interna;
• mode – modo de amostragem. Opções possíveis:
• stratified – divisão aleatória estratificada (se for o fator y; caso contrário, a divisão aleatória padrão);
• random – divisão aleatória padrão;
• order – modo estático, quando são usadas as primeiras instâncias para treinamento, enquanto as restantes, para teste (comumente utilizados para TimeSeries);
• rolling – janela móvel, mais vulgarmente conhecido como uma janela deslizante (amplamente aplicada na previsão dos mercados de ações e financeiros), é semelhante a order, exceto que window se refere ao tamanho da janela, iter, à iteração de rolamento e increment, ao número de amostras no qual a janela desliza para a frente a cada iteração. Em cada iteração, o tamanho do conjunto de treinamento é fixado com window, enquanto o conjunto de teste é equivalente a ratio, excepto para a última iteração (onde pode ser menos).
• incremental – modo incremental de re-treinamento, também conhecido como uma janela de aumento, é semelhante a ordem, exceto que window é o tamanho da janela inicial, iter, as iterações incrementais e increment, o número de exemplos adicionados a cada iteração Em cada iteração, o tamanho do conjunto de treinamento cresce (+ increment), enquanto o tamanho do conjunto de teste é equivalente ao ratio, excepto para a última iteração, onde ele pode ser menor.
• iter – número de iterações do modo incremental de re-treinamento (é usado apenas quando o modo = "rolling" ou "incremental", iter é definido num ciclo).
• seed – se for NULL, então é usado random seed, caso contrário, seed é fixado (durante outros cálculos retornará sempre o mesmo resultado);
• window – tamanho da janela de treinamento (se mode = "rolling") ou tamanho inicial da janela de treinamento (se mode = "incremental");
• increment – número de exemplos adicionados à janela de treinamento em cada iteração (se mode="incremental" ou mode="rolling").

3.2.1. Balanceamento de classes e pré-processamento.

Vamos escrever uma função que irá alinhar (se necessário) o número de classes na escolha para o número maior, dividir a escolha em conjuntos de treinamento e testes, realizar pré-processamento (normalização, se necessário) e retornar e retornar a lista com os conjuntos relevantes train, test. Para atingir o balanceamento, nós vamos usar a função caret::upSample(), ela adiciona amostras colhidas aleatoriamente com substituição, tornando a distribuição de classe igual. Devo dizer que nem todos os pesquisadores acham necessário o balançamento de classes. Mas, como já conhecido, a prática é o critério da verdade, e os resultados das minhas múltiplas experiências mostram que os conjuntos balançados sempre mostram melhores resultados durante o treinamento. Embora, ele não nos impede de experimentar por conta própria.

Para o pré-processamento vamos usar a função caret::preProcess(). Armazenamos os parâmetros de pré-processamento na variável prepr. Como já foram examinados e aplicados por nós em artigos anteriores, não irei me deter na sua descrição.

#---7----------------------------------------------------
prepareTrain <- function(x , y, 
                         rati, mod = "stratified", 
                         balance = F, 
                         norm, meth)
{
  require(magrittr)
  require(dplyr)
  t <- rminer::holdout(y = y, ratio = rati,
                       mode = mod)
  train <- cbind(x[t$tr, ], y = y[t$tr])
  if(balance){
    train <- caret::upSample(x = train[ ,best], 
                             y = train$y, 
                             list = F)%>% tbl_df
    train <- cbind(train[ ,best], select(train, y = Class))
  }
  test <- cbind(x[t$ts, ], y = y[t$ts])
  if (norm) {
    prepr <<- caret::preProcess(train[ ,best], method = meth)
    train = predict(prepr, train[ ,best])%>% cbind(., y = train$y)
    test =  predict(prepr, test[ ,best] %>% cbind(., y = test$y))
  }
  DT <- list(train = train,
             test = test)
  return(DT)
}

Um comentário sobre o pré-processamento: as variáveis​de entrada serão normalizadas para o intervalo (-1, 1).

3.2.2. Codificação da variável-alvo

Ao resolver tarefas de classificação, a variável-alvo é um fator com vários níveis (classes). No modelo, ela é definida como um vector (coluna), que consiste nos estados subsequentes alvo. Por exemplo, y = c("1", "1", "2", "3", "1"). A fim de treinar a rede neural, a variável-alvo deve ser codificada (transformada) para dentro da matriz, com um número de colunas igual ao número de classes. Em cada linha desta matriz, apenas uma coluna pode conter uma unidade. Essa transformação, juntamente com o uso da função de ativação softmax(), na camada de saída, permite a obtenção de probabilidades de estados da variável-alvo prevista em todas as classes. A função classvec2classmat() será utilizada para a codificação. Devo dizer que este não é o único ou o melhor método para codificar a variável-alvo, mas vamos usá-lo porque é simples.A transformação inversa (descodificação) dos valores previstos da variável-alvo é alcançada através de métodos diferentes que nós discutiremos em breve.

3.3. Modelo de treinamento

3.3.1. Pré-treinamento

Como mencionado acima, em primeiro lugar, criamos o objeto de arquitetura profunda chamado DArch, ele inclui o número necessário da RBM com os parâmetros de treinamento preliminar por padrão, bem como a rede neural iniciada com pesos aleatórios e a função de ativação do neurônio definido por padrão. Na fase de criação do objeto, se necessário, os parâmetros pré-treinamento podem ser alterados. Posteriormente, a rede da RBM vai ser pré-treinada sem um supervisor, enviando o conjunto de formação (sem variável-alvo) para a saída. Após concluída, obtemos DАrch onde os pesos e deslocações obtidos durante o pré-treinamento da RBM são transferidos para a rede neural. Devemos definir antecipadamente a distribuição dos neurônios escondidos em camadas numa forma de vetor (por exemplo):

L<- c( 14, 50, 50, 2)

O número de neurônios na camada de entrada é igual ao número de variáveis de entrada. Duas camadas ocultas conterão 50 neurônios cada, a camada de saída terá dois. Deixe-me explicar o último pedaço. Se a variável-alvo (factor) tem dois níveis (classes), então, na verdade, uma saída é suficiente. Mas a conversão de vetor para a matriz com duas colunas, cada uma delas correspondendo a uma classe, nos permite aplicar a função softmax(), que funciona bem nas tarefas de classificação, na camada de saída. Além disso, as saídas na forma de probabilidades de classe nos dará oportunidades adicionais na análise subsequente de resultados. Este assunto será abordado em breve.

O número de épocas, durante o treinamento, é definido experimentalmente, normalmente, ele está dentro do intervalo de 10-50.

O número de iteração de amostragem vai ficar por padrão, mas este parâmetro pode ser aumentado se você deseja experimentar. Ele será definido numa função separada:

#----8--------------------------------------------------------------
pretrainDBN <- function(L, Bs, dS, nE, nCD, InM = 0.5, FinM = 0.9)
{
  require(darch)
# criamos o objeto DArch
  dbn <- newDArch(layers = L, batchSize = Bs, logLevel = 5)
# definimos o momento inicial 
  setInitialMomentum(dbn) <- InM 
# definimos o momento final   
  setFinalMomentum(dbn) <- FinM
# definimos o tempo de alternância de momentos, desde o inicial até ao final   
  setMomentumSwitch(dbn) <- round(0.8 * nE)
  dbn <- preTrainDArch(dbn, dataSet = dS, 
                  numEpoch = nE,
                  numCD = nCD, 
                  trainOutputLayer = T)
  return(dbn)
}

3.3.2. Treinamento fino

Como já foi discutido anteriormente, o pacote oferece backpropagation(), rpropagation(), minimizeClassifier(), minimizeAutoencoder(). Os dois últimos não serão considerados, uma vez que eles não são suficientemente documentados no pacote, e não existem exemplos de como aplicá-los. Estas funções em minhas experiências não apresentaram bons resultados.

Eu também gostaria de acrescentar algo sobre as atualizações dos pacotes. Quando comecei a escrever este artigo, a versão atual era 0,9, e no momento em que foi concluído, foi lançada uma nova versão 0.10 com várias alterações. Todos os cálculos tiveram que ser refeitos. Com base nos resultados de testes curtos, posso dizer que a velocidade de operação tem aumentado consideravelmente, ao contrário da qualidade dos resultados (o que é mais uma falha do usuário do que do pacote).

Consideremos as duas primeiras funções. A primeira (backpropagation) é definida por padrão no objeto Darch e usa os parâmetros de treinamento da rede neural fornecidos aqui. A segunda (rpropagation) também tem parâmetros por padrão e quatro métodos de treinamento (descritos acima) "iRprop+" por padrão. Você certamente pode alterar tanto os parâmetros quanto o método de treinamento. Aplicar estas funções é fácil: altere, na função FineTuneDarch(), a função de ajuste

setFineTuneFunction(dbn) <- rpropagation  

Além da função de ajuste fino, devemos definir (se necessário) a função de ativação de neurônios em cada camada. Lembramos que, por padrão, todas as camadas são definidas sigmoidUnit. No pacote estão disponíveis sigmoidUnitDerivative, linearUnitDerivative, tanSigmoidUnitDerivative, softmaxUnitDerivative.O ajuste fino será definido com uma função separada, com a capacidade de escolher a função de afinar. Vamos recolher possíveis funções de ativação numa lista separada:

actFun <- list(sig = sigmoidUnitDerivative,
               tnh = tanSigmoidUnitDerivative,
               lin = linearUnitDerivative,
               soft = softmaxUnitDerivative)

Vamos escrever uma função de ajuste fino que vai treinar e gerar duas redes neurais: uma é a treinada usando a função backpropagation, enquanto a segunda, com ajuda da função rpropagation:

#-----9-----------------------------------------
fineMod <- function(variant=1, dbnin, dS, 
                    hd = 0.5, id = 0.2,
                    act = c(2,1), nE = 10)
{
  setDropoutOneMaskPerEpoch(dbnin) <- FALSE
  setDropoutHiddenLayers(dbnin) <- hd
  setDropoutInputLayer(dbnin) <- id
  layers <<- getLayers(dbnin)
  stopifnot(length(layers)==length(act))
  if(variant < 0 || variant >2) {variant = 1}
  for(i in 1:length(layers)){
    fun <- actFun %>% extract2(act[i])
    layers[[i]][[2]] <- fun
  }
  setLayers(dbnin) <- layers
  if(variant == 1 || variant == 2){ # backpropagation
    if(variant == 2){# rpropagation
      #setDropoutHiddenLayers(dbnin) <- 0.0
      setFineTuneFunction(dbnin) <- rpropagation
    }
    mod = fineTuneDArch(darch = dbnin, 
                        dataSet = dS, 
                        numEpochs = nE,
                        bootstrap = T)
    return(mod)
  }
}

Alguns esclarecimentos sobre os parâmetros formais da função.

• variant - seleção da função de ajuste fino(1- backpropagation, 2- rpropagation).
• dbnin - modelo de obtenção no resultado do pré-treinamento.
• dS - conjunto de dados para ajuste fino(dataSet).
• hd - coeficiente de amostragem (hiddenDropout) nas camadas ocultas da rede neural.
• id - coeficiente de amostragem(inputDropout) na camada de saída da rede neural.
• act - vetor com indicação da função de ativação dos neurônios em cada camada da rede neural. O comprimento de vector é uma unidade mais curto do que o número de camadas.
• nE - número de épocas de treinamento.

dataSet — nova variável que apareceu nesta versão. Eu realmente não entendo a razão por trás de seu aparecimento. Normalmente, a língua tem duas formas de transferência de variáveis para um modelo, isto é, usando quer o par (x, y) quer a fórmula (y~., data). A introdução desta variável não melhora a qualidade, mas confunde os usuários em vez. Embora o autor pode ter outras razões, que eu não conheço.

3.4. Teste do modelo. Métricas.

O teste do modelo de formação é realizado em conjuntos de teste. Deve-se considerar que vamos calcular duas métricas: Accuracy - formal - e K - qualitativa -. A informação relevante será fornecida abaixo. Para este fim, vamos precisar de dois conjuntos diferentes de dados, e eu vou explicar-lhe o porquê. Para calcular Accuracy, precisamos dos valores da variável-alvo, e o ZigZag, como nos lembramos de antes, mais frequentemente não é definido nas últimas barras. Portanto, o conjunto de teste para determinar Accuracy será definido com a função prepareTrain(), enquanto para definir indicadores de qualidade, vamos usar a seguinte função.

#---10-------------------------------------------
prepareTest <- function(n, z, norm, len = 501)
{
  x <- In(p = n ) %>% na.omit %>% extract( ,best) %>% 
    tail(., len)
  CO <- price[ ,"CO"] %>% tail(., len)
  if (norm) {
    x <- predict(prepr,x)
  }
  dt <- cbind(x = x, CO = CO) %>% as.data.frame()
  return(dt)
}

Os modelos serão testados nas últimas 500 barras do histórico.

Para o teste atual, serão usadas as funções testAcc() e testBal().

#---11-----
testAcc <- function(obj, typ = "bin"){
  x.ts <- DT$test[ ,best] %>% as.matrix()
  y.ts <- DT$test$y %>% as.integer() %>% subtract(1)
  out <- predict(obj, newdata = x.ts, type = typ) 
  if (soft){out <- max.col(out)-1} else {out %<>% as.vector()}               
  acc <- length(y.ts[y.ts == out])/length(y.ts) %>% 
    round(., digits = 4)
  return(list(Acc = acc, y.ts = y.ts, y = out))
}
#---12-----
testBal <- function(obj, typ = "bin") {
  require(fTrading)
  x <- DT.test[ ,best]
  CO <- DT.test$CO
  out <- predict(obj, newdata = x, type = typ) 
  if(soft){out <- max.col(out)-1} else {out %<>% as.vector()} 
  sig <- ifelse(out == 0, -1, 1)
  sig1 <- Hmisc::Lag(sig) %>% na.omit
  bal <- cumsum(sig1 * tail(CO, length(sig1)))
  K <- tail(bal, 1)/length(bal) * 10 ^ Dig
  Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
  dd <- maxDrawDown(bal)
  return(list(sig = sig, bal = bal, K = K, 
              Kmax = Kmax, dd = dd))
}

A primeira função retorna Acc e os valores das variáveis-alvo (reais ou previstos) para uma possível análise mais aprofundada. A segunda função retorna os sinais preditos sig do Expert Advisor, o equilíbrio obtido com base nestes sinais bal, o coeficiente de qualidade K, o valor máximo deste coeficiente na área testada Kmax e abaixamento máximo dd na mesma área.

No cálculo do equilíbrio, é importante lembrar que o último sinal previsto refere-se à barra futuro que não tem sido ainda formada, por conseguinte, deve ser suprimido nos cálculos. Fizemos isto deslocando o vetor sig uma barra à direita.

3.4.1. Descodificação da predição.

O resultado obtido pode ser descodificado (convertido a partir da matriz de vector) utilizando o método "WTA". A classe é igual ao número da coluna com um valor máximo da probabilidade, além disso é possível definir o limite do valor da probabilidade, abaixo do qual a classe não é determinada.

out <- classmat2classvec(out, threshold = 0.5) 
ou
out <- max.col(out)-1

Se o limite é definido como 0.5 ea maior probabilidade nas colunas é abaixo deste limite, obteremos uma classe adicional "não_definida." Isto deve ser levado em consideração ao calcular métricas como Accuracy.

3.4.2. Melhoria do resultado de previsão

Sera que é possível melhorar o resultado da previsão após a sua recepção? Existem três vias possíveis que podem ser aplicadas.

• Calibragem

A calibração é um cálculo dos intervalos que dão possibilidade a compatibilidade mais precisa com dados reais. No pacote CORElearn existe para este fim uma função especial:

CORElearn::calibrate(correctClass, predictedProb, class1 = 1,  
                     method = c("isoReg", "binIsoReg", "binning", "mdlMerge"),  
                     weight=NULL, noBins=10, assumeProbabilities=FALSE)

Onde:

• correctClass – vector com os rótulos corretos de classes para problemas de classificação;
• predictedProb – vetor com a classe predita 1 (probabilidade) do mesmo comprimento da correctClass;
• method — um dos ("isoReg", "binIsoReg", "binning", "mdlMerge"). Para mais informações, por favor leia a descrição do pacote;
• weight — vector (se indicado) deve ser do mesmo comprimento que correctClass, e fornecer pesos para cada observação, caso contrário, os pesos de todas as observações é igual a 1 por padrão;
• noBins — valor do parâmetro depende do method e determina o número desejado ou inicial de canais;
• assumeProbabilities — um valor booleano, se for TRUE, o valor em predictedProb é esperado no intervalo [0, 1], quer dizer, como uma avaliação de possibilidade, caso contrário, o algoritmo pode ser usado como uma regressão simples isotônica.

Este método é aplicado para uma variável-alvo com dois níveis estabelecidos por um vector.

• Suavização de resultados de previsão usando o modelo de cadeia de Markov

Este é um assunto vasto e complexo que merece um artigo separado, por isso eu não vou ir fundo na teoria, vou fornecer as informações mais básicas.

O processo de Markov  – é um processo aleatório com o seguinte recurso: para qualquer ponto no tempo t0 a probabilidade de qualquer estado do sistema no futuro depende apenas de seu estado no presente e não depende de quando e como o sistema atinge este estado.

Classificação dos processos aleatórios de Markov:

• com estados discretos e tempo discreto (cadeia de Markov);
• com estados contínuos e tempo discreto (consistência de Markov);
• com estados discretos e tempo contínuo (cadeia de Markov contínua);
• com estado contínuo e tempo contínuo.

Apenas processos de Markov com estados discretos S1, S2, ..., Sn. são considerados aqui adiante.

A cadeia de Markov é um processo aleatória de Markov com estados discretos e tempo discreto.
Os momentos t1, t2, ..., quando o sistema S pode alterar seu estado, são examinados como passos subsequentes do processo. Não é o momento t, mas o passo número 1,2,...,k,... é utilizado como um argumento de que o processo depende.

O processo aleatório é caracterizado por uma sequência de estados S(0), S(1), S(2), ..., S(k), ..., onde S(0) é o estado inicial (antes da primeira etapa); S(1) é o estado depois da primeira etapa; S(k)  é o estado depois do passo número k.

As probabilidades dos estados da cadeia de Markov  são Pi(k) probabilidades, que após o passo número k (e antes de (k + 1)) o sistema S estará em estado Si,(i = 1 , 2 , ..., n).

A distribuição inicial das probabilidades da cadeia de Markov consiste na distribuição de estados no início do processo.
A probabilidade de transição no passo número k a partir do estado Si para o estado Sj é a probabilidade condicional de que o sistema S , após o passo número k, apareça no estado Sj, com a condição de que ele (após o passo número k) ela se encontre no estado Si.

A cadeia uniforme de Markov é uma cadeia de Markov onde as probabilidades de transição não dependem do número do passo (de tempo), mas entre quais estados é realizada a transição.

As probabilidades de transição de uma cadeia uniforme de Markov Рij formam uma matriz quadrada de tamanho n x n. Tem as seguintes características:

1. Cada linha descreve o estado selecionado do sistema, e seus elementos são as probabilidades de todas as transições possíveis num passo a partir do estado selecionado (a partir do número i).
2. Os elementos de colunas são as probabilidades de todas as transições possíveis num passo para o conjunto do estado (j).
3. O total de probabilidades de cada linha é igual à unidade.
4. A diagonal principal indica as probabilidades Pij que o sistema não irá sair do estado Si, e permanecerá nele.

O processo de Markov pode ser observado e escondido. O modelo oculto de Markov (Hidden Markov Model(HMM)) consiste num par de processos estocásticos discretos {St} e {Xt}. O processo observado {Xt} está ligado a um processo não-observável (oculto) de Markov de estados {St} com ajuda das chamadas distribuições condicionais.

Estritamente falando, o processo observável de Markov de estados (classes) de nossa série de tempo de destino não é uniforme. Claramente, a probabilidade de transição de um estado para outro depende do tempo gasto no estado atual. Isso significa que durante os primeiros passos, após alterar o estado, a probabilidade de que ele vai mudar é baixa e cresce com o aumento de tempo gasto neste estado. Estes modelos são chamados de semi-Markov (HSMM). Não vamos ir profundo em sua revisão.

Mas a ideia é a seguinte: com base na ordem discreta de sinais ideais (alvo) obtidos a partir do ziguezague, vamos encontrar os parâmetros de HMM. Em seguida, tendo os sinais previstos pela rede neural, iremos suavizar-los usando HMM.

O que isso nos dá? Normalmente, na predição da rede neural, existem as chamadas "emissões", áreas de alteração de estado que são 1-2 bares longos. Sabemos que a variável-alvo não tem tais pequenos comprimentos. Ao aplicar o modelo obtido na variável-alvo para o fim previsto, podemos levá-lo a transições mais prováveis.

Usaremos o pacote "mhsmm" concebido para calcular modelos ocultos de Markov e modelos semi-Markov. Nós vamos usar a função smooth.discrete(), que simplesmente suaviza a série temporal de valores discretos.

obj <- smooth.discrete(y)

A sequência suavizada no final por padrão é a ordem mais provável de estados, ela é obtida utilizando o algoritmo Viterbi (também conhecido como decodificação global) Viterbi. Há também uma opção para utilizar outro método smoothed, onde serão identificados os estados individuais mais prováveis​(o chamado descodificação local).

Um método padrão é aplicado para suavizar a nova série temporal

sm.y <- predict(obj, x = new.y)

• Ajustamento dos sinais previstos na curva de equilíbrio teórico

O conceito é o seguinte. Tendo a linha de ajuste, podemos calcular o seu desvio em relação à média. Usando esses desvios vamos calcular sinais de correção. Em momentos quando o desvio for negativo, qeles executam ou desligam os sinais previstos ou torná-los o oposto. A ideia é geralmente boa, mas há uma desvantagem. A barra de zero tem um sinal previsto, mas não tem um valor de equilíbrio e, por conseguinte, um sinal de correção. Há duas maneiras de resolver esse problema: por meio da classificação, isto é, para prever o sinal de correção com base em sinais de correção e desvios existentes; por meio de regressão, ou seja, usando os desvios existentes nas barras formadas para preverdesvios no novo bar e para identificar o sinal de correção com base nele. Há uma solução mais fácil, você pode tomar o sinal de correção para uma nova barra na base da que já está formada.

Uma vez que os métodos acima mencionados já são conhecidos por nós e foram testados, vamos tentar implementar as oportunidades das cadeias de Markov.O pacote "markovchain", que apareceu recentemente, tem uma gama de funções que permitem determinar os parâmetros do modelo oculto de Markov e fazer uma previsão de condições futuras em várias barras futuras através do processo discreto observado. A idéia foi tomada a partir deste artigo.

3.4.3. Métricas

Para avaliar a qualidade da previsão do modelo, é aplicada toda a gama de métricas (Accuracy, AUC, ROC...). No artigo anterior eu mencionei que os indicadores formais não podem definir a qualidade no nosso caso. O objetivo do Expert Advisor é obter o máximo de lucro com um abaixamento aceitável. Para este efeito, o indicador de qualidade K foi introduzido, ele mostra o lucro médio em pontos em uma barra no segmento de histórico fixo com comprimento N. É calculado através da divisão do Return acumulado (sig, N) pelo comprimento do segmento N Accuracy será calculado apenas indicativamente.

Finalmente, vamos realizar os cálculos e obter resultados de teste:

• Os dados de saída. Nós já temos a matriz price[], obtida como resultado da execução da função price.OHLC(). Ela contém cotações, preço médio e o corpo das barras. Todos os dados de saída podem ser obtidos, baixando o "ícone" que aparece no anexo a Rstudio.

# Definimos as constantes  
n = 34; z = 37; cut = 0.9; soft = TRUE. 
# Definimos o método de processamento  
method = c("center", "scale","spatialSign")
# formamos o conjunto de saída de dados 
data.f <- form.data(n = n, z = z)
# definimos o conjunto de preditores importantes 
best <- prepareBest(n = n, z = z, cut = cut, norm = T, method) 
# Os cálculos levam cerca de 3 min num processador de 2 núcleos. Você pode pular esta etapa se quiser, 
# e usar todo o conjunto de indicadores no futuro. Portanto, comente a linha anterior e
# não comente as dois linhas inferiores.
# data.f <- form.data(n = n, z = z)
# best <- colnames(data.f) %>% head(., ncol(data.f) - 1)
# Preparamos o conjunto para treinamento da rede neural
DT <- prepareTrain(x = data.f[ , best],
                   y = data.f$y,
                   balance = TRUE,
                   rati = 501, mod = "stratified",
                   norm = TRUE, meth = method) 

# Carregamos as bibliotecas necessárias
require(darch)
require(foreach)
# Definimos as funções disponíveis de ativação
actFun <- list(sig = sigmoidUnitDerivative,
               tnh = tanSigmoidUnitDerivative,
               lin = linearUnitDerivative,
               soft = softmaxUnitDerivative)
# Convertemos a variável-alvo
if (soft) { y <- DT$train$y %>% classvec2classmat()} # para a matriz
if (!soft) {y = DT$train$y %>% as.integer() %>% subtract(1)} # para o vetor com valores [0, 1]
# criamos dataSet para treinamento
dataSet <- createDataSet(
  data = DT$train[ ,best] %>% as.matrix(), 
  targets = y ,
  scale = F
)
# Definimos as constantes para a rede neural
# Quantidade de neurônios na camada de entrada (número de preditores)
nIn <- ncol(dataSet@data)
# Número de neurônios na camada de saída
nOut <- ncol(dataSet@targets)
# Vetor com número de neurônios em cada camada da rede neural
# Se você quiser usar outra estrutura da rede neural, será necessário reescrever esse vetor
Layers = c(nIn, 2 * nIn , nOut)
# Outros dados relacionados ao treinamento
Bath = 50
nEp = 100
ncd = 1
# Pré-treinamento da rede neural
preMod <- pretrainDBN(Layers, Bath, dataSet, nEp, ncd)
# Parâmetros adicionais para o ajuste fino
Hid = 0.5; Ind = 0.2; nEp = 10
# Treinamos dois modelos, um com backpropagation, outro com rpropagation
# Fazemos isso somente para comparar os resultados
model <- foreach(i = 1:2, .packages = "darch") %do% {
  dbn <- preMod
  if (!soft) {act = c(2, 1)}
  if (soft) {act = c(2, 4)}
  fineMod(variant = i, dbnin = dbn, 
          hd = Hid, id = Ind,
          dS = dataSet, act = act, nE = nEp)
}
# Testamos para obter Accuracy
resAcc <- foreach(i = 1:2, .packages = "darch") %do% {
  testAcc(model[[i]]) 
}
# Preparamos o conjunto de dados para o teste quanto ao coeficiente de qualidade
DT.test <- prepareTest(n = n, z = z, T)
# Testamos 
resBal <- foreach(i = 1:2, .packages = "darch") %do% {
  testBal(model[[i]]) 
}

Conferimos os resultados:

> resAcc[[1]]$Acc
[1] 0.5728543
> resAcc[[2]]$Acc
[1] 0.5728543

É igualmente ruim para ambos os modelos.

Mas aqui é o coeficiente de qualidade:

> resBal[[1]]$K
[1] 5.8
> resBal[[1]]$Kmax
[1] 20.33673
> resBal[[2]]$Kmax
[1] 20.33673
> resBal[[2]]$K
[1] 5.8

Ele mostra o mesmo bom desempenho e ao mesmo tempo bons indicadores. No entanto, um grande abaixamento é de alguma forma alarmante:

> resBal[[1]]$dd$maxdrawdown
[1] 0.02767

Vamos tentar corrigir o abaixamento com um sinal de correção obtido a partir do cálculo abaixo:

bal <- resBal[[1]]$bal
# sinal nas últimas 500 barras
sig <- resBal[[1]]$sig[1:500]
# média a partir da linha de ajuste
ma <- pracma::movavg(bal,16, "t")
# momento a partir da média 
roc <- TTR::momentum(ma, 3)%>% na.omit
# desviação da linha de ajuste a partir da média
dbal <- (bal - ma) %>% tail(., length(roc))
# vamos somar dois vetores
dbr <- (roc + dbal) %>% as.matrix()
# calculamos o sinal de ajuste
sig.cor <- ifelse(dbr > 0, 1, -1) # sign(dbr) dará o mesmo resultado
# sinal resultante
S <- sig.cor * tail(sig, length(sig.cor))
# equilíbrio no sinal resultante
Bal <- cumsum(S * (price[ ,"CO"]%>% tail(.,length(S))))
# coeficiente de qualidade do sinal corregido
Kk <- tail(Bal, 1)/length(Bal) * 10 ^ Dig
> Kk
[1] 28.30382

O resultado de qualidade exibido do sinal corrigido é muito bom. Vamos ver como as linhas dbal, roc e dbr utilizadas para calcular o sinal de correção são apresentadas no gráfico de linha.

matplot(cbind(dbr, dbal, roc), t="l", col=c(1,2,4), lwd=c(2,1,1))
abline(h=0, col=2)
grid()

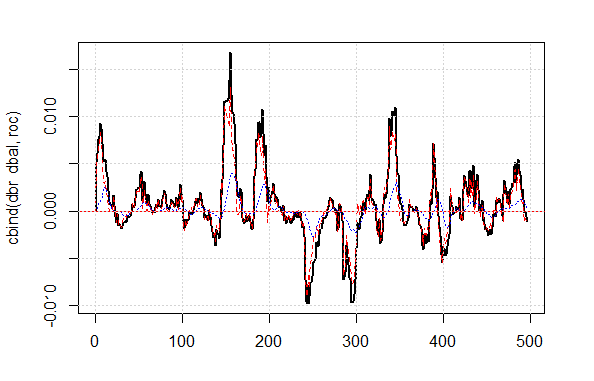
Fig. 4 Desvio da linha ajuste a partir da média

A linha de ajuste antes e após a correção dos sinais é mostrada na fig. 5.

plot(c(NA,NA,NA,Bal), t="l")
lines(bal, col= 2)
lines(ma, col= 4)

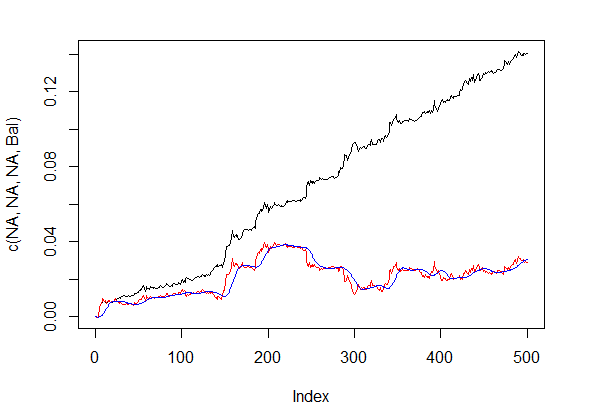
Fig. 5 A linha de ajuste antes e após a correção dos sinais

Assim, temos o valor do sinal previsto pela rede neural na barra de zero, mas não temos um valor de correção. Queremos usar o modelo oculto de Markov para prever este sinal. Com base nos estados observadas do sinal de correção, vamos identificar os parâmetros do modelo usando os valores de alguns dos últimos estados, prevemos o estado numa barra para a frente. Primeiro, vamos escrever a função correct(), que irá calcular o sinal de correção com base no que foi previsto, o sinal resultante e seus indicadores de qualidade. Em outras palavras, vamos anotar de maneira compacta os cálculos realizados anteriormente.

Gostaria de esclarecer: o "sinal" no artigo é uma sequência de números inteiros -1 e 1. O "estado" é uma sequência de números inteiros 1 e 2 correspondentes a estes sinais. Para conversões mútuas, vamos utilizar as funções:

#---13----------------------------------
        sig2stat <- function(x) {x %>% as.factor %>% as.numeric}
        stat2sig <- function(x) ifelse(x==1, -1, 1)
        #----14--correct-----------------------------------
        correct <- function(sig){
          sig <- Hmisc::Lag(sig) %>% na.omit
          bal <- cumsum(sig * (price[ ,6] %>% tail(.,length(sig))))
          ma <- pracma::movavg(bal, 16, "t")
          roc <- TTR::momentum(ma, 3)%>% na.omit
          dbal <- (bal - ma) %>% tail(., length(roc))
          dbr <- (roc + dbal) %>% as.matrix()
          sig.cor <- sign(dbr)
          S <- sig.cor * tail(sig, length(sig.cor))
          bal <- cumsum(S * (price[ ,6]%>% tail(.,length(S))))
          K <- tail(bal, 1)/length(bal) * 10 ^ Dig
          Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
          dd <- fTrading::maxDrawDown(bal)
          corr <<- list(sig.c = sig.cor, sig.res = S, bal = bal, Kmax = Kmax, K = K, dd = dd)
          return(corr)
         }

A fim de obter o vector de sinal com a previsão de uma barra para a frente, usaremos o pacote de "markovchain" e a função pred.sig().

#---15---markovchain----------------------------------
pred.sig <- function(sig, prev.bar = 10, nahead = 1){
          require(markovchain)
        # Transformamos os sinais de correção observados em estados 
          stat <- sig2stat(sig)
        # Calculamos os parâmetros do modelo
        # Se não existe um modelo no ambiente       
          if(!exists('MCbsp')){
             MCbsp <<- markovchainFit(data = stat, 
                                method = "bootstrap",
                                nboot = 10L,
                                name="Bootstrap MС")
         }
        # Definimos as constantes necessárias
          newData <- tail(stat, prev.bar)
          pr <- predict(object = MCbsp$estimate, 
                                newdata = newData,
                                n.ahead = nahead)
        # anexar o sinal predito ao sinal de entrada
          sig.pr <- c(sig, stat2sig(pr))
          return(sig.pr = sig.pr)
}

Agora, vamos anotar o cálculo do sinal resultante para execução do o Expert Advisor de forma compacta:

sig <- resBal[[1]]$sig
sig.cor <- correct(sig)
sig.c <- sig.cor$sig.c
pr.sig.cor <- pred.sig(sig.c)
sig.pr <- pr.sig.cor$sig.pr
# Vetor resultante para o Expert Advisor 
S <- sig.pr * tail(sig, length(sig.pr))

• Suavização do sinal previsto.

Vamos escrever uma função que irá suavizar o sinal discreto usando o modelo da cadeia oculta de Markov. Para isto, vamos utilizar o pacote "mhsmm".

#---16---smooth------------------------------------
smoooth <- function(sig){
# suavizamos o sinal previsto
# definimos os parâmetros do modelo oculto de Markov
# Se não existe um modelo no ambiente 
    require(mhsmm)
    if(!exists('obj.sm')){
         obj.sm <<- sig2stat(sig)%>% smooth.discrete()
    }
# suavizamos o sinal obtido pelo modelo
    sig.s <- predict(obj.sm, x = sig2stat(sig))%>% 
             extract2(1)%>% stat2sig()
# calculamos o ajuste do sinal suavizado
     sig.s1 <- Hmisc::Lag(sig.s) %>% na.omit
     bal <- cumsum(sig.s1 * (price[ ,6]%>% tail(.,length(sig.s1))))
     K <- tail(bal, 1)/length(bal) * 10 ^ Dig
     Kmax <- max(bal)/which.max(bal) * 10 ^ Dig
     dd <- fTrading::maxDrawDown(bal)
     return(list(sig = sig.s, bal = bal, Kmax = Kmax, K = K, dd = dd))
}

Calculamos e nivelamos o ajuste dos sinais previstos e suavizados.

sig <- resBal[[1]]$sig
sig.sm <- smoooth(sig)
plot(sig.sm$bal, t="l")
lines(resBal[[1]]$bal, col=2)

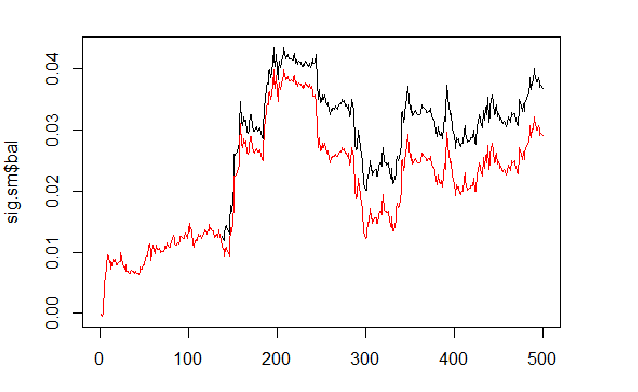
Fig. 6 Ajuste nos sinais previstos e suavizados

Como podemos ver, a qualidade melhorou ligeiramente, mas o abaixamento ainda permanece. Nós não vamos usar este método no nosso Expert Advisor.

sig.sm$dd
$maxdrawdown
[1] 0.02335
$from
[1] 208
$to
[1] 300

4. Diagrama de bloco do algoritmo do Expert Advisor

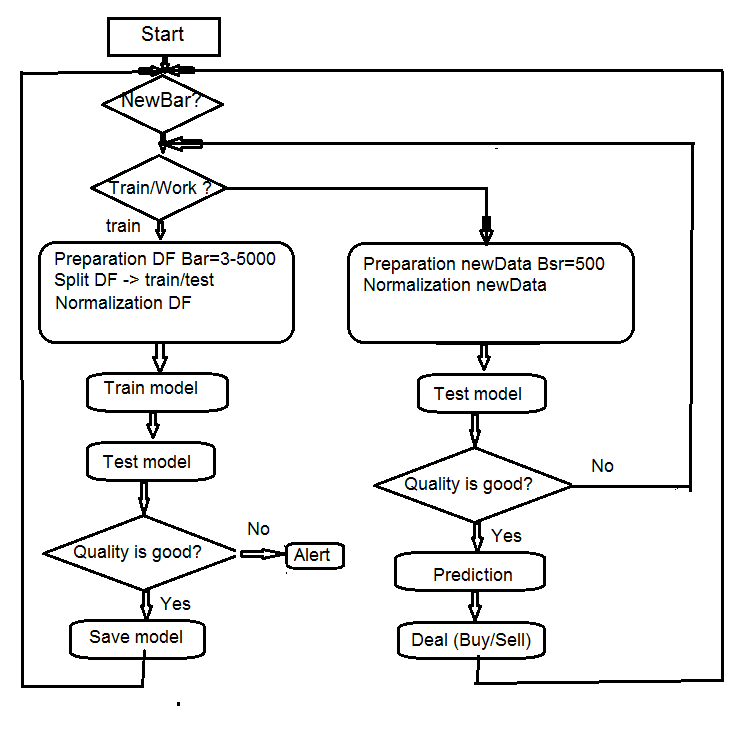
Fig. 7 Diagrama de blocos do algoritmo do Expert Advisor

4.1. Descrição do trabalho do Expert Advisor

Como o trabalho do Expert Advisor ocorre em duas correntes (mql e Rterm), vamos descrever o processo de sua interação. Vamos discutir as operações realizadas em cada corrente separadamente.

4.1.1 MQL

Após colocar o Expert Advisor no gráfico:

Na função init()

• verificamos as configurações do terminal (disponibilidade DLL, permissão para operar);
• definimos o temporizador;
• executamos Rterm;
• calculamos e transferimos as constantes necessárias para o trabalho com o ambiente de processo R;
• verificamos se funciona Rterm, se não - alert;
• saímos de init().
  

Na função deinit()

• paramos o temporizador;
• excluímos os objetos gráficos;
• Paramos Rterm.

Na função onTimer()

• verificamos se funciona Rterm;
• Se Rterm não estiver ocupado e a nova barra (LastTime != Time[0]):
• definimos a profundidade do histórico, dependendo se esta é a primeira execução do Expert Advisor;
• formamos quatro vetores de cotações (Open, High, Low, Close) e transferimos para Rterm;
• executamos o script e saímos sem receberem os resultados do seu desempenho;
• definimos o sinalizador get_sig = true;
• definimos LastTime= Time[0].
  
• Caso contrário, se funcionar Rterm, não está ocupado e o sinalizador é get_sig = true:
• definimos o comprimento do vetor sig, que temos de obter a partir de Rterm;
• ajustar o tamanho do vetor de recepção para o tamanho da fonte. Ao não acompanhar, o processo R vai cair;
• obtemos uma sequência de sinais (vetor);
• baseado no último sinal podemos definir qual é a operação é necessário executar (BUY, SELL, Nothing);
• se obter o sinal real, não ERR, redefinimos o sinalizador get_sig=false.
  
• O resto é padrão:
• CheckForClose()
• CheckForOpen()

Nosso especialista nesta parte é um "Executor", que efetua encomendas obtidas a partir da sua parte que pode "pensar", ele envia ordens, controla o estado de posições abertas e possíveis erros ao abri-las, e realiza muitas outras funções de um Expert Advisor padrão.

4.1.2 Rterm

O script operacional consiste de duas partes. Uma parte é executada na primeira entrada, a outra parte após as seguintes.

• se first:
• carregamos (se necessário) as bibliotecas necessárias do depositário na Internet e instalamos no ambiente Rterm;
• definimos as funções necessárias;
• criamos a matriz de cotações;
• preparamos o conjunto de dados para treinamento e testar o modelo;
• criamos o modelo e treinamos o modelo;
• testamos o modelo;
• calculamos os sinais para execução;
• verificamos a qualidade da previsão. Se ela for maior ou igual ao mínimo definido, então continuamos. Caso contrário, enviamos alerta.
• se !first:
• preparamos o conjunto de dados para teste e previsão;
• testamos o modelo nos dados novos;
• calculamos os sinais para execução;
• verificamos a qualidade da previsão. Se ela for maior ou igual ao mínimo, continuamos. Caso contrário, definimos first = TRUE, ou seja, precisamos treinar o modelo.

4.2. Auto-controle e auto-aprendizagem

Realizamos o controle de qualidade de sinais com o modelo usando o coeficiente K. Existem duas maneiras de identificar os limites da qualidade aceitável. Primeiro — definir a queda máxima do coeficiente em relação ao seu valor máximo. Ou seja, se K < Kmax * 0.8, então devemos re-treinar o Expert Advisor ou pará-lo de realizar sinais. Segundo — definimos o valor mínimo K, que, depois de ter sido atingido, exige que as mesmas ações. Nós vamos usar o segundo método no Expert Advisor.

5. Instalação e execução

Há dois Expert Advisors anexados a este artigo: e_DNSAE.mq4 e e_DNRBM.mq4. Ambos usam os mesmos conjuntos de dados e quase o mesmo conjunto de funções. A diferença reside no modelo de rede profunda usado. O primeiro usa DN, SAE iniciado e o pacote "deepnet". A descrição do pacote pode ser encontrada no artigo anterior em redes neurais profundas. O segundo utiliza DN, a RBM iniciada e o pacote "darch".

Por padrão:

• *.mq4 na pasta ~/MQL4/Expert
• *.mqh na pasta ~/MQL4/Include
• *.dll na pasta ~/MQL4/Libraries
• *.r na pasta C:/RData

Verificamos o caminho para linguagem R e os scripts (como no mq4: #define e *.r: source() ).

Quando o Expert Advisor é iniciado pela primeira vez, ele irá baixar as bibliotecas necessárias a partir do repositório e colocá-las no ambiente Rterm. Você também pode instalá-los com antecedência de acordo com a lista em anexo.

Normalmente, o processo R "cai" especificamente devido à ausência de bibliotecas necessárias, caminhos indicados erradamente para os scripts, e devido aos erros de sintaxe no script.

Separadamente foi anexada a captura de tela de sessão com os dados iniciais, e você pode abri-la com rstudio para verificar que todas as funções estão trabalhando, bem como realizar experimentos.

6. Formas e meios para melhorar os indicadores de qualidade.

Existem algumas maneiras de melhorar os indicadores qualitativos.

• avaliação e seleção dos preditores — aplicar algoritmo genético de otimização (GA).
• determinar os parâmetros ideais de preditores e variável-alvo — GA.
• determinar os parâmetros óptimos de uma rede neural — GA.

A implementação dessas ações irá melhorar significativamente os indicadores qualitativos.

Conclusão

As experiências com o pacote "darch" mostraram os seguintes resultados.

• Глубокая нейросеть, инициируемая RBM, обучается хуже чем, с SAE. Para nós não é novidade.
• A rede é treinada rapidamente.
• O pacote tem um grande potencial na melhoria da qualidade de predição, fornecendo acesso a quase todos os parâmetros internos do modelo.
• O pacote permite usar apenas uma rede neural ou uma RBM com um grande conjunto de parâmetros em relação aos outros, os padrões.
• O pacote está em constante evolução, e o desenvolvedor promete introduzir recursos adicionais na próxima versão.
• A integração da linguagem R com os terminais MT4/MT5, como foi prometido pelos desenvolvedores, vai dar aos traders uma oportunidade de usar os mais novos algoritmos sem qualquer DLL adicional.

Anexo

1. A sessão R do processo Sess_DNRBM_GBPUSD_30
2. O arquivo com o Expert Advisor " e_DNRBM "
3. O arquivo com o Expert Advisor " e_DNSAE"