
Avaliação e seleção de variáveis para os modelos de aprendizado da máquina
Introdução
Este artigo foca sobre as especificidades de escolha, o pré-condicionamento e avaliação das variáveis de entrada para uso em modelos de aprendizagem da máquina, vários métodos de normalização e as suas características serão descritas aqui. Também serão revelados momentos importantes do processo que influenciam muito o resultado final dos modelos de treinamento a serem revelados. Olharemos com mais atenção e avaliaremos métodos novos e pouco conhecidos para determinar a informatividade e visualização dos dados de entrada.
Com o pacote "RandomUniformForests" calcularemos e analisaremos a importância do conceito de uma variável em diferentes níveis e em várias combinações, a correspondência dos preditores e um alvo, bem como a interação entre os preditores, e ainda, a seleção de um conjunto ideal de preditores, tendo em conta todos os aspectos de importância.
Com o pacote "RoughSets", olharemos a um mesmo problema de escolher preditores a partir de um ângulo diferente e com base em outro conceito. Mostraremos que não é somente um conjunto de preditores ideal, onde um conjunto de exemplos de treinamentos também serão otimizados.
Todos os cálculos e experiências serão executados na linguagem R, para ser específico - na Revolution R Open 3.2.1 .
1. Variáveis de entrada (sinais, preditores)
Todas as variáveis, de entrada (independentes, preditores) e de saída (alvo), podem ser dos seguintes tipos:
Binárias - existem dois valores: {0,1}, {-1,1}, {"sim", "não"}, {"masculino", "feminino"}.
Nominais (fatores) com um número finito de níveis. Por exemplo, o fator "dia da semana" tem sete níveis, e cada um deles pode ser nomeado (segunda, terça etc). Fatores podem ser ordenados e desordenados. Por exemplo, o fator "hora do dia" tem 24 níveis e é ordenado. O fator "distrito de uma cidade" com 32 níveis é desordenado, uma vez que todos os níveis são de igual importância. Devem ser especificados explicitamente, ao declarar um fator ordenado.
Quantitativas (numérico) contínuas. A gama de variáveis contínuas a partir do Inf (infinito) para + inf.
As cotações de dados "cruas" (OHLC) não são utilizadas como variáveis de entradas numéricas. O logaritmo da diferença ou o logaritmo da razão da cotação são aplicados. No entanto, vários indicadores combinados em conjuntos são mais frequentemente utilizados. Tipicamente, um conjunto de dados de entrada é formado como uma matriz, se todas as variáveis são uniformes, ou mais comumente, como um quadro de dados, onde cada coluna é uma variável e uma linha é um estado de variáveis num determinado ponto. Uma variável alvo é colocada na última (ou na primeiro) coluna.
1.1. Cleanup
O "cleanup" implica o seguinte:
a) A remoção ou a transformação da falta (incerteza) de dados "NA.
Muitos modelos não permitem lacunas nos dados de entrada. Por isso, ou excluimos as linhas com dados perdidos ou preenchemos as lacunas com dados interpolados. Para tais propósitos as respectivas funções são fornecidas em vários pacotes. A remoção dados NA incertos é incorporada normalmente por padrão, mas é melhor fazê-lo por si mesmo através na.omit(dt) antes do treinamento em andamento.
b) Remoção das variáveis "opcionais zero" (numérico e nominal).
Alguns casos (especialmente durante a transformação ou conversão de variáveis) de preditores aparecem com um simples valor único ou vários desses valores que ocorrem numa freqüência muito baixa. Muitos modelos levam a uma operação colapsada ou instável. Os preditores com variação quase zero devem ser identificados e eliminados antes da simulação. A fim de identificar e remover esses preditores, o pacote da função especial "caret" caret::nearZeroVar() pode ser usado. A necessidade a partir deste ponto está em debate.
c) Identificação e eliminação dos preditores correlacionados (numérico).
Enquanto alguns modelos lidam excepcionalmente bem com os preditores correlacionados (por exemplo PLS, LARS e similares, utilizando a regularização L1), outros modelos podem obter vantagens em reduzir o nível de correlação entre os preditores. Para identificar e remover preditores fortemente correlacionados (coeficiente de correlação do limite é definido, por exemplo > 0,9), usamos a função caret::findCorrelation() a partir do mesmo pacote "caret". Este é um pacote muito poderoso que eu recomendo fortemente para análise.
d) Identificação e remoção de dependências lineares (fatores).
A função caret::findLinearCombos() utiliza o QR-expansion de transferências de matrizes para definir as combinações lineares entre elas (se existirem). Por exemplo, vamos analisar a seguinte matriz:
ltfrDesign <- matrix(0, nrow = 6, ncol = 6) ltfrDesign[, 1] <- c(1, 1, 1, 1, 1, 1) ltfrDesign[, 2] <- c(1, 1, 1, 0, 0, 0) ltfrDesign[, 3] <- c(0, 0, 0, 1, 1, 1) ltfrDesign[, 4] <- c(1, 0, 0, 1, 0, 0) ltfrDesign[, 5] <- c(0, 1, 0, 0, 1, 0) ltfrDesign[, 6] <- c(0, 0, 1, 0, 0, 1)
Por favor, note que as colunas 2 e 3 são adicionadas a primeira. Do mesmo modo, as colunas 4, 5 e 6 são formadas na primeira coluna. A função caret::findLinearCombos() retornará a lista, que enumerará essas dependências juntamente com o vetor de posições das colunas, que podem ser deletadas para remover as dependências lineares.
comboInfo <- findLinearCombos(ltfrDesign) comboInfo $linearCombos $linearCombos[[1]] [1] 3 1 2 $linearCombos[[2]] [1] 6 1 4 5 $remove [1] 3 6 ltfrDesign[, -comboInfo$remove] [,1] [,2] [,3] [,4] [1,] 1 1 1 0 [2,] 1 1 0 1 [3,] 1 1 0 0 [4,] 1 0 1 0 [5,] 1 0 0 1 [6,] 1 0 0 0
Estes tipos de dependências podem ocorrer quando se utiliza um grande número de preditores binários, ou quando os preditores de fator são convertidos em "modelos".
1.2. Transformação, pré-processamento de dados
Muitos modelos exigem dados de entrada numéricos para estarem num determinado intervalo (normalização, padronização), ou para serem convertidos de uma determinada maneira (fatores). Por exemplo, as redes neurais e máquinas de vetores de suporte (SVM) aceitam dados de entrada nas coordenadas [-1, 1] ou [0, 1]. Muitos pacotes na linguagem R oferecem recursos especiais para tal transformação ou executaren a conversão em si mesmos. Por favor, lembre-se que a definição de parâmetros de pré-processamento é realizada apenas no um conjunto de treinamento de dados de entrada. Configuração de Teste e validação, novos dados e modelos de predição de entrada são convertidos com os parâmetros obtidos no conjunto de treinamento.
Normalização (escala)
Uma fórmula geral de converter uma variável na variação {+ h, -l). Dependendo do intervalo desejado h = +1; l = (-1 ou 0). Alguns recursos recomendam a redução do intervalo para {-0.9; 0,9} ou {0,1; 0,9}, a fim de evitar o uso de seções de saturação das funções de ativação (tanh/sig). Isso se refere às redes neurais, SVM e outros modelos com funções nomeadas de ativação .
Xn = (x - min(x)) / (max(x) - min(x)) * (h - l) + l;
A transformação inversa (denormalização) é executada com base na fórmula:
x = (x - l) / (h - l) * (max(x) - min(x)) + min(x);
Normalização
Sabendo-se que uma distribuição variável é próxima da normal, é possível normalizar com a seguinte fórmula
x = (x - mean(x)) / sd(x)
Alguns pacotes têm funções especiais previstas para pré-processamento. Assim, a função preProcess(), do pacote "caret", oferece os seguintes métodos de pré-processamento: "BoxCox", "YeoJohnson", "expoTrans", "center", "scale", "range", "knnImpute", "bagImpute", "medianImpute", "pca", "ica" e "spatialSign".
"BoxCox", "YeoJohnson", "expoTrans"
A conversão Yeо-Johnson é um pouco semelhante ao modelo Box-Cox, no entanto aceita preditores com valores zero ou negativos (enquanto os valores de preditor para a transformação Box-Cox devem ser estritamente positivos). A transformação exponencial de Manly (1976) também pode ser usada para dados positivos e negativos.
A transformação "range" dimensiona os dados nas coordenadas [0, 1]. Isto é importante! Se novas amostras têm valores maiores ou menores que os utilizados no conjunto de treinamento, então os valores serão fora desta faixa e o resultado da previsão será incorreto.
"center" — a média é deduzida, "scale" é dividida pelo desvio-padrão (escala). Normalmente, eles são usados em conjunto, que é chamado de "normalização".
"knnImpute", "bagImpute", "medianImpute" — cálculo dos dados em falta ou indefinidos usando diferentes algoritmos.
"spatialSign" — transformação, projeta os dados de predição do círculo único nas dimensões р, onde р é um número de preditores. Essencialmente, os dados do vetor são divididos pela sua norma. Os dados anteriores da transformação devem ser centrados e escalados.
"pca" — em alguns casos, a análise de componente principal tem de ser utilizada para a transformação dos dados a um subespaço menor, onde as novas variáveis não se correlacionam uma com a outra. Usando este método, a centragem e dimensionamento são automaticamente realizadas, e os nomes das colunas são alterados para PC1, PC2, etc.
"isa" — Da mesma forma, a análise de componentes independentes pode ser usada para encontrar novas variáveis que são combinações lineares do conjunto original, onde os componentes são independentes (ao contrário dos não relacionados no PCA). Novas variáveis serão marcadas como IC1, IC2, etc.
O excelente pacote "clusterSim", designado para encontrar os procedimentos ideais de agrupamento de dados, tem a função dataNormalization() que normaliza os dados em 18 maneiras nas colunas e linhas. Vou simplesmente listar todas elas:
n1 — padronização ((x – mean) / sd);
n2 — padronização posicional ((x – median) / mad);
n3 — unitização ((x – mean) / range);
n3а — unitização posicional ((x – median) / range);
n4 — unitização com o mínimo de zeros ((x – min) / range);
n5 — normalização na coordenada <-1, 1> ((x – mean) / max(abs(x – mean)));
n5a — normalização posicional na coordenada <-1,1> ((x – median) / max(abs(x-median)));
n6 — transformação do quociente (x/sd);
n6a — transformação do quociente posicional (x/mad);
n7 — transformação do quociente (x/range);
n8 — transformação do quociente (x/max);
n9 — transformação do quociente (x/mean);
n9a — transformação do quociente posicional (x/median);
n10 — transformação do quociente (x/sum);
n11 — transformação do quociente (x/sqrt(SSQ));
n12 — normalização ((x-mean)/sqrt(sum((x-mean)^2)));
n12a — normalização posicional ((x-median)/sqrt(sum((x-median)^2)));
n13 — normalização com zero sendo o ponto central ((x-midrange)/(range/2)).
"Variáveis Dummy" - muitos modelos exigem a transformação dos preditores para "dummies". A função dummyVar() do pacote "caret" pode ser usada para esta finalidade. A função usa uma fórmula e um conjunto de dados, exibindo o objeto que pode ser usado para criar variáveis dummy.
2. Os dados de saída (variável-alvo)
Já que estamos resolvendo o problema da classificação, a variável alvo é um fator com um número de níveis (classes). A maioria dos modelos mostram melhores resultados quando treinam num alvo com duas classes. Com muitas classes especiais, medidas adicionais são tomadas para tratar de tais questões. A variável-alvo é codificada no processo de preparação dos dados de treinamento e descodificada depois da predição.
As classes são codificadas de várias maneiras. O pacote RSNNS da "Simulação de Redes Neurais na Universidade de Stuttgart" fornece duas funções - decodeClassLabels() , que codifica as classes de vetor nas matriz que contêm as colunas correspondentes às classes e encodeClassLabels(), que faz a transformação inversa após a predição do modelo. Por exemplo:
> data(iris) > labels <- decodeClassLabels(iris[,5]) > class <- encodeClassLabels(labels) > head(labels) setosa versicolor virginica [1,] 1 0 0 [2,] 1 0 0 [3,] 1 0 0 [4,] 1 0 0 [5,] 1 0 0 [6,] 1 0 0 > head(class) [1] 1 1 1 1 1 1
O número de saídas do modelo é, portanto, igual ao número de classes alvo. Este não é o único método de codificação (1-1) que se aplica ao alvo. Se o alvo tem duas classes, você pode gerenciar com uma saída. A codificação de uma variável alvo na matriz definitivamente tem um inúmeras vantagens.
3. Avaliação e seleção de preditores
Experiências têm demonstrado, que o aumento dos dados de entrada (preditor) nem sempre leva à melhoria de um modelo, muito pelo contrário. O resultado é realmente afetado entre 3 a 5 preditores. Em muitos pacotes de agregação, tais como "rminer", "caret", "SuperLearner" e "MLR" existem funções "built-in" para o cálculo da importância das variáveis e sua seleção. A maioria das abordagens para reduzir o número de preditores pode ser separada em duas categorias (usando a terminologia de John, Kohavi e Pfleger, 1994):
- Filtragem. Os métodos de filtragem avaliam externamente a relevância dos preditores dos modelos de predição, e por fim, o modelo utiliza apenas os preditores que atendem a determinados critérios. Por exemplo, tarefas de classificação para cada preditor podem ser avaliadam individualmente, a fim de verificar se existe uma relação plausível entre o predictor e as classes observadas. Somente preditores com importantes dependências de prognósticos devem ser incluídos no modelo de classificação.
Wrapper. Os métodos "wrapper" avaliam diferentes modelos, utilizando procedimentos que adicionam e/ou removem preditores para encontrar a melhor combinação que otimiza a eficiência do modelo. Em essência, os métodos "wrapper" são algoritmos de busca que consideram preditores como entradas e usa os modelos de eficiência como saídas que precisam ser otimizadas. Há muitas maneiras de iteração dos preditores: recursivo de remoção/aditivos, algoritmos genéticos, anelamento simulado e muitos outros.
Neste artigo não vamos considerar técnicas "wrapper", em vez disso iremos analisar novos métodos e abordagens da filtragem, o que a meu ver, elimina todos os inconvenientes acima indicados.
3.1. Filtragem
Com o uso de vários métodos externos e critérios, a importância (capacidade informacional) dos preditores é estabelecida. A contribuição de cada variável na melhoria da qualidade da predição do modelo está implícito aqui na sua importância.
Normalmente são três opções disponíveis:
Utilizando um número específico de preditores mais importantes.
Utilizando a percentagem do número total de preditores mais importantes
- Utilizando os preditores, cuja importância ultrapassa o limiar.
Todos os casos permitem a otimização da quantidade, percentagem ou limiar.
Vamos formar o conjunto de dados de entrada e saída para considerar métodos específicos e realização de experiências.
Dados de entrada
Vamos incluir 11 indicadores (osciladores), sem preferências anteriores no conjunto de entrada. Usaremos diversas variáveis a partir de alguns indicadores. Então vamos escrever uma função que forma o conjunto de entrada de 17 variáveis.
As cotações das últimas 4000 barras no TF = M30 / EURUSD serão usadas.
In <- function(p = 16){ require(TTR) require(dplyr) require(magrittr) adx <- ADX(price, n = p) %>% as.data.frame %>% mutate(.,oscDX = DIp -DIn) %>% transmute(.,DX, ADX, oscDX) %>% as.matrix() ar <- aroon(price[ ,c('High', 'Low')], n = p)%>% extract(,3) atr <- ATR(price, n = p, maType = "EMA") %>% extract(,1:2) cci <- CCI(price[ ,2:4], n = p) chv <- chaikinVolatility(price[ ,2:4], n = p) cmo <- CMO(price[ ,'Med'], n = p) macd <- MACD(price[ ,'Med'], 12, 26, 9) %>% as.data.frame() %>% mutate(., vsig = signal %>% diff %>% c(NA,.) %>% multiply_by(10)) %>% transmute(., sign = signal, vsig) %>% as.matrix() rsi <- RSI(price[ ,'Med'], n = p) stoh <- stoch(price[ ,2:4], nFastK = p, nFastD =3, nSlowD = 3, maType = "EMA")%>% as.data.frame() %>% mutate(., oscK = fastK - fastD)%>% transmute(.,slowD, oscK)%>% as.matrix() smi <- SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9) vol <- volatility(price[ ,1:4], n = p, calc = "yang.zhang", N = 144) In <- cbind(adx, ar, atr, cci, chv, cmo, macd, rsi, stoh, smi, vol) return(In) }
Estes indicadores são muito bem conhecidos e amplamente aplicados, de modo que não vamos discuti-los novamente. Vou simplesmente comentar o aceitável no cálculo do método "pipe" (%>%) a partir do pacote "magrittr" com base no exemplo do indicador MACD. A ordem escrita será a seguinte:
O indicador é calculado para retornar duas variáveis (macd, signal) .
A matriz obtida é convertida à estrutura de dados.
Uma nova variável vsig é adicionada na estrutura de dados (na ordem escrita):
- A variável signal é utilizada;
- A primeira diferença é calculada;
- Os vetores NA são adicionados no início, pois o cálculo da primeira diferença é o vetor de uma unidade mais curta do que o original;
- É multiplicado por 10.
Apenas as variáveis vsig são necessárias (colunas), os sinais são escolhidos a partir da estrutura de dados.
A estrutura de dados é convertida na matriz.
Este método de cálculo é muito conveniente, no caso em que os resultados intermédios não são necessários. Além disso, as fórmulas são mais fáceis de ler e compreender.
Vamos obter a matriz de dados de entrada e olhar para o conteúdo.
x <- In(p = 16) > summary(x) DX ADX oscDX Min. : 0.02685 Min. : 5.291 Min. :-93.889 1st Qu.: 8.11788 1st Qu.:14.268 1st Qu.: -9.486 Median :16.63550 Median :18.586 Median : 5.889 Mean :20.70162 Mean :20.716 Mean : 4.227 3rd Qu.:29.90428 3rd Qu.:24.885 3rd Qu.: 19.693 Max. :79.80812 Max. :59.488 Max. : 64.764 NA's :16 NA's :31 NA's :16 ar tr atr Min. :-100.0000 Min. :0.0000000 Min. :0.000224 1st Qu.: -50.0000 1st Qu.:0.0002500 1st Qu.:0.000553 Median : -6.2500 Median :0.0005600 Median :0.000724 Mean : -0.8064 Mean :0.0008031 Mean :0.000800 3rd Qu.: 50.0000 3rd Qu.:0.0010400 3rd Qu.:0.000970 Max. : 100.0000 Max. :0.0150300 Max. :0.003104 NA's :16 NA's :1 NA's :16 cci chv cmo Min. :-515.375 Min. :-0.67428 Min. :-88.5697 1st Qu.: -84.417 1st Qu.:-0.33704 1st Qu.:-29.9447 Median : -5.674 Median : 0.03057 Median : -2.4055 Mean : -1.831 Mean : 0.11572 Mean : -0.6737 3rd Qu.: 83.517 3rd Qu.: 0.44393 3rd Qu.: 28.0323 Max. : 387.814 Max. : 3.25326 Max. : 94.0649 NA's :15 NA's :31 NA's :16 sign vsig rsi Min. :-0.38844 Min. :-0.43815 Min. :12.59 1st Qu.:-0.07124 1st Qu.:-0.05054 1st Qu.:39.89 Median :-0.00770 Median : 0.00009 Median :49.40 Mean :-0.00383 Mean :-0.00013 Mean :49.56 3rd Qu.: 0.05075 3rd Qu.: 0.05203 3rd Qu.:58.87 Max. : 0.38630 Max. : 0.34871 Max. :89.42 NA's :33 NA's :34 NA's :16 slowD oscK SMI Min. :0.0499 Min. :-0.415723 Min. :-74.122 1st Qu.:0.2523 1st Qu.:-0.043000 1st Qu.:-33.002 Median :0.4720 Median : 0.000294 Median : -5.238 Mean :0.4859 Mean :-0.000017 Mean : -4.089 3rd Qu.:0.7124 3rd Qu.: 0.045448 3rd Qu.: 22.156 Max. :0.9448 Max. : 0.448486 Max. : 75.079 NA's :19 NA's :17 NA's :25 signal vol Min. :-71.539 Min. :0.003516 1st Qu.:-31.749 1st Qu.:0.008204 Median : -5.319 Median :0.011274 Mean : -4.071 Mean :0.012337 3rd Qu.: 19.128 3rd Qu.:0.015312 Max. : 71.695 Max. :0.048948 NA's :33 NA's :16
Saída de Dados (alvo)
Como uma variável alvo usaremos sinais recebidos do indicador ZZ. Abaixo está a fórmula para calcular o zigzag e sinal:
ZZ <- function(pr = price, ch = ch , mode="m") { require(TTR) if(ch > 1) ch <- ch/(10 ^ (Dig - 1)) if(mode == "m"){pr <- pr[ ,'Med']} if(mode == "hl") {pr <- pr[ ,c("High", "Low")]} if(mode == "cl") {pr <- pr[ ,c("Close")]} zz <- ZigZag(pr, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1]} dz <- zz %>% diff %>% c(0,.) sig <- sign(dz) return(cbind(zz, sig)) }
Os parâmetros da função:
- pr = preço — matriz das cotações OHLCMed;
- ch — comprimento mínimo de uma virada zigzag em pontos (4 sinais);
- mode — preço aplicado (m — média, hl — "High" e "Low", cl — "Close"). A média é usado como padrão.
A função retorna a matriz com duas variáveis - o zigzag e o sinal obtido com base na inclinação do zigzag no intervalo [-1; 1].
Calculamos sinais de dois ZZ com um comprimento da perna diferente:
out1 <- ZZ(ch = 25) out2 <- ZZ(ch = 50)
No gráfico os indicadores vão olhar de acordo com:
> matplot(tail(cbind(out1[ ,1], out2[ ,1]), 500), t="l")
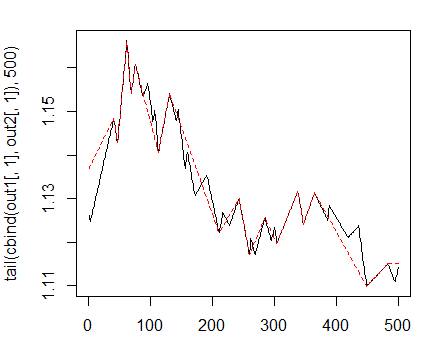
Fig. 1. Zigzags, com comprimento mínimo de viradas com 25/75 pontos
A seguir, vamos usar o primeiro ZZ com uma perna mais curta. Vamos combinar variáveis de entrada e alvo na estrutura de dados em geral, remover dados indefinidos com uma condição = "0" e retirar a classe "0" a partir do alvo.
> data <- cbind(as.data.frame(x) , Class = factor(out1[ ,2])) %>% + na.omit > data <- data[data$Class != 0, ] > data$Class <- rminer::delevels(data$Class, c("0", "1"), "1")
Olhe para a distribuição de classes no alvo:
> table(data$Class) -1 1 1980 1985
Pelo que podemos ver, as classes são bem equilibrados. Uma vez que temos um conjunto de dados de entrada e saída preparados, podemos começar a avaliar a importância dos preditores.
Primeiro vamos verificar como correlacionar os dados de entrada:
> descCor <- cor(data[ ,-ncol(data)]) > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.20170 0.03803 0.26310 0.31750 0.57240 0.95730
Quais variáveis de entrada têm correlação acima de 90%?
> highCor <- caret::findCorrelation(descCor, cutoff = .90) > highCor [1] 12 15
A resposta é — rsi e SMI. Vamos formar um conjunto de dados sem estes dois e verificar a correlação dos restantes.
> data.f <- data[ ,-highCor] > descCor <- cor(data.f[ ,-ncol(data.f)]) > summary(descCor[upper.tri(descCor)]) Min. 1st Qu. Median Mean 3rd Qu. Max. -0.20170 0.03219 0.21610 0.27060 0.47820 0.89880
Para avaliar a variável de importância (VI), usaremos o novo pacote "Random Uniform Forests", ele tem uma grande variedade de instrumentos para a sua profunda análise e visualização. De acordo com a intenção dos desenvolvedores do pacote, o principal objetivo para determinar a importância das variáveis é avaliar o que, quando, onde e como afeta o problema a ser resolvido.
O pacote oferece várias medidas importantes de uma variável em profundidade. Vamos considerá-las antes de entrar numa avaliação mais profunda.
A Variável Global de Importância define as variáveis que reduzem o erro de predição ao máximo, mas não nos que diz como a variável de importância afeta as respostas.
Por exemplo, gostaríamos de saber quais variáveis têm uma influência mais forte sobre a classe separada, ou qual é a interação entre as variáveis.
A variável de importância é medida por todas as unidades e árvores e que permite que todas as variáveis tenham um valor, assim como os pontos de corte são acidentais. Portanto, cada variável tem chances iguais de serem selecionadas, mas ela estará recebendo a importância devida somente se for a única que reduz, principalmente, a entropia em cada nó.
Variável Local de Importância
Definição: Um preditor é localmente importante na primeira ordem, se a mesma observação e todas as árvores são as que têm a maior frequência de ocorrência dentro do nó do terminal.
Importância Parcial
Definição: O preditor é parcialmente importante, se a mesma observação, classe ou todas as ordens são as que têm a maior frequência de ocorrência dentro do nó do terminal.
Interações
Queremos saber, como os preditores influenciam os problemas e quando considerá-los. Por exemplo, algumas variáveis têm um impacto relativamente baixo sobre um problema, mas um forte impacto sobre as variáveis mais relevantes, ou uma variável, obtendo um monte de interação umas com as outras, o que torna esta variável influente. Vamos definir o que é a interação.
Definição: Um preditor interage com outro, se ambos têm a mesma observação e para todas as árvores, respectivamente terão a primeira e a segunda maior frequência de ocorrência sobre o nó do terminal.
Dependências parciais
Estas são as ferramentas que permitem determinar como uma variável (ou um par de variáveis) afeta o valor da resposta, sabendo os valores de todas as outras variáveis. Para ser mais específico, uma dependência parcial é a área onde o efeito máximo de influência da variável é exercido com base no valor da resposta. O conceito de uma dependência parcial chegou de Friedman (2002), que a utilizou no Gradient Boosting Machines (GBM), no entanto no pacote Random Uniform Forests foi implementado de forma diferente.
De acordo com as idéias do pacote Random Uniform Forests, podemos determinar a importância de uma variável com base no seguinte esquema: Importância = contribuição + interação, onde a contribuição é a influência de uma variável (em relação a influenciar todos) sobre os erros de predição, e a interação é um impacto sobre outras variáveis.
Vamos prosseguir com os experimentos
Vamos dividir nossos conjunto de dados, data.f[], no treinamento e testar os conjuntos com uma relação de 2/3, normalizar na faixa de -1;1 e testar o modelo. Para a separação, vamos utilizar a função rminer::holdout() que irá dividir o conjunto em dois. Para a normalização usamos a função caret::preProcess() e o método = c("spatialSign"). Ao treinar o modelo, o pacote irá automaticamente paralelizar os cálculos entre os núcleos do processador disponíveis, menos o que usa "pacote doParallel". Pode indicar um número específico de núcleos a serem usados no cálculo com a opção de "segmentos".> idx <- rminer::holdout(y = data.f$Class)
> prep <- caret::preProcess(x = data.f[idx$tr, -ncol(data.f)],
+ method = c("spatialSign"))
> x.train <- predict(prep, data.f[idx$tr, -ncol(data.f)])
> x.test <- predict(prep, data.f[idx$ts, -ncol(data.f)])
> y.train <- data.f[idx$tr, ncol(data.f)]
> y.test <- data.f[idx$ts, ncol(data.f)]
> ruf <- randomUniformForest( X = x.train,
+ Y = y.train,
+ xtest = x.test,
+ ytest = y.test,
+ mtry = 1, ntree = 300,
+ threads = 2,
+ nodesize = 2
+ )
Etiquetas -1 1 foram convertidas a 1 2 para facilitar a computação e serão usadas internamente como um substituto.
> print(ruf)
Chamada:
randomUniformForest.default(X = x.train, Y = y.train, xtest = x.test,
ytest = y.test, ntree = 300, mtry = 1, nodesize = 2, threads = 2)
Tipo de "Random Uniform Forest": Classificação
paramsObject
ntree 300
mtry 1
nodesize 2
maxnodes Inf
replace TRUE
bagging FALSE
depth Inf
depthcontrol FALSE
OOB TRUE
importance TRUE
subsamplerate 1
classwt FALSE
classcutoff FALSE
oversampling FALSE
outputperturbationsampling FALSE
targetclass -1
rebalancedsampling FALSE
randomcombination FALSE
randomfeature FALSE
categorical variables FALSE
featureselectionrule entropy
avaliação Out-of-bag (OOB)
Estimativa da taxa de erro OOB : 20.2%
Vínculo de taxa de erro OOB (com desvio de 1%): 21.26%
Matriz de confusão OOB:
Referência
Prediction -1 1 class.error
-1 1066 280 0.2080
1 254 1043 0.1958
Estimativa OOB de AUC: 0.798
Estimativa OOB de AUPR: 0.7191
Estimativa OOB de F1-score: 0.7962
Estimativa da média geométrica OOB (Ajustada): 0.7979
Limites de Breiman
Predição de erro esperado (nas classes aproximadamente equilibradas): 18,42%
Limite superior: 27.76%
Correlação média entre as árvores: 0.0472
Força (margem): 0.4516
Desvio padrão da força: 0.2379
Configuração de teste
Taxa de erro: 19.97%
Confusão da matriz:
Referência
Prediction -1 1 class.error
-1 541 145 0.2114
1 119 517 0.1871
Área Sob a Curva ROC: 0.8003
Área Sob a Curva de Precisão-Recuperação: 0.7994
Pontos F1: 0.7966
Média geométrica: 0.8001
Vamos decifrar isto delicadamente:
- Erro de treinamento (erro interno) deu 1% do desvio = 21.26%.
- Limites de Breiman - propriedades teóricas propostas por Breiman (2001). Desde que o pacote "Random Uniform Forests" herde as propriedades do pacote "Random Forests", são aplicáveis aqui. A classificação obtem duas opções de erro de predição, correlação média entre as árvores, força e desvio padrão de força.
- Expectativa do erro de predição = 18.42%. O erro do limite superior = 27.76%.
- Testando erro = 19.97% (erro externo). Se a avaliação externa é inferior ou igual a avaliação interna e menos do que o limite superior dos limites de Breiman, então um retreinamento provavelmente não vai ocorrer.
Vamos ver o gráfico de um erro de treinamento:
> plot(ruf)
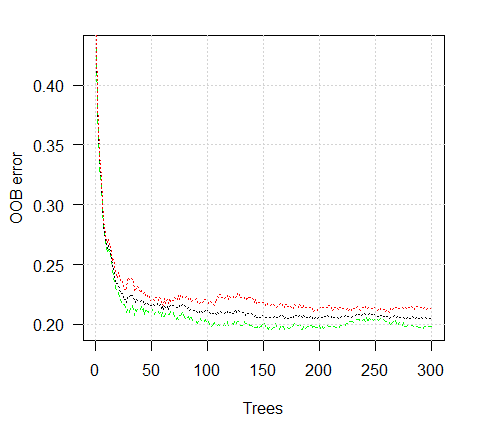
Fig. 2. Formação de erro, dependendo do número de árvores (trees)
> summary(ruf) Variável Global de Importância: Nota: a maioria dos recursos preditivos são ordenados pelo 'escore' e plotados. A maioria daqueles mais discriminantes também devem ser utilizados dentro da conta pela "class" e 'class.frequency'. Escore percentual das variáveis class e class.frequency 1 cci 2568 1 0.50 100.00 2 signal 2438 1 0.51 94.92 3 slowD 2437 1 0.51 94.90 4 oscK 2410 1 0.50 93.85 5 ADX 2400 -1 0.51 93.44 6 vol 2395 1 0.51 93.24 7 atr 2392 -1 0.51 93.15 8 sign 2388 1 0.50 92.97 9 vsig 2383 1 0.50 92.81 10 ar 2363 -1 0.51 92.01 11 chv 2327 -1 0.50 90.62 12 cmo 2318 -1 0.51 90.28 13 DX 2314 1 0.50 90.10 14 oscDX 2302 -1 0.51 89.64 15 tr 2217 1 0.52 86.31 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 6 14 6 15 6 Sumário do tamanho médio da árvore (número de nós): Min. 1st Qu. Median Mean 3rd Qu. Max. 3 1044 1313 1213 1524 1861 Sumário dos nós médios da Folha (número de nós do terminal) Min. 1st Qu. Median Mean 3rd Qu. Max. 2 522 657 607 762 931 Sumário do tamanho dos nós da Folha (número de observações por nós da folha): Min. 1st Qu. Median Mean 3rd Qu. Max. 1.000 1.000 2.000 4.355 3.000 2632.000 Profundidade média da árvore : 10 Profundidade teórica da árvore (equilibrada) : 11
Nós vemos que todas as nossas variáveis de entrada são significativas e importantes. É indicado que as classes das variáveis apareçam com mais frequência.
E mais algumas estatísticas:
> pr.ruf <- predict(ruf, x.test, type = "response"); > ms.ruf <- model.stats(pr.ruf, y.test) Configuração de teste Margem de erro: 19.97% Confusão da matriz: Referência Prediction -1 1 class.error -1 540 144 0.2105 1 120 518 0.1881 Área Sob a Curva ROC: 0.8003 Área Sob a Curva de Precisão-Recuperação: 0.7991 Escore-F1: 0.7969 Média geométrica: 0.8001
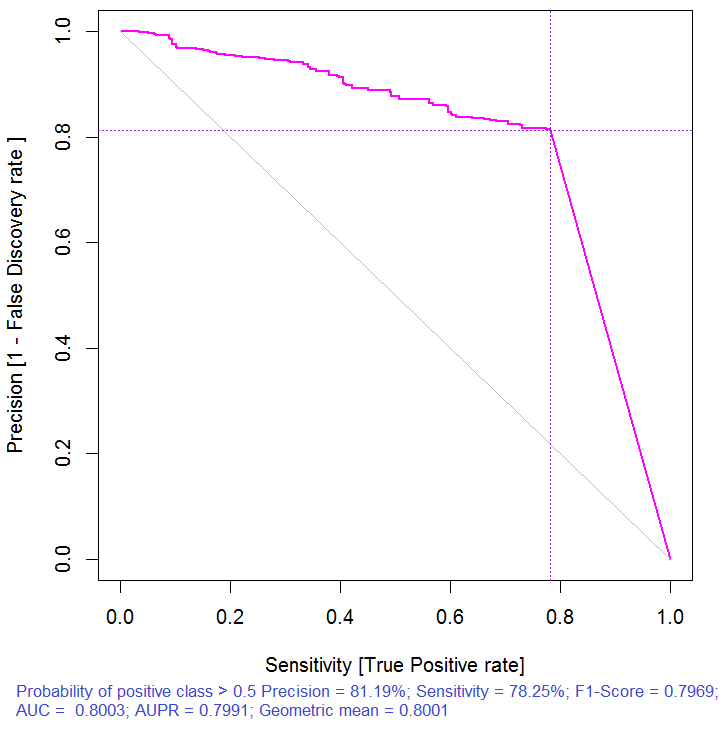
Fig. 3. Curva de Precisão-Recuperação
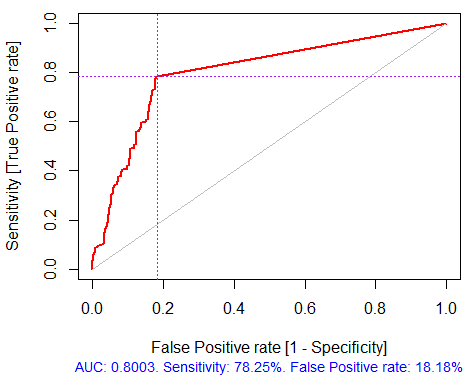
Fig. 4. Curva ROC ou curva de erro
Normalmente pararíamos aqui, como é oferecido por muitos pacotes de filtragem, mas então teríamos de selecionar vários preditores com os melhores indicadores de importância global. Esta escolha não fornece bons resultados, uma vez que não tem em conta a influência mútua dos preditores.
> imp.ruf <- importance(ruf, Xtest = x.test, maxInteractions = 3) 1 - Importância da Variável Global (15 mais importantes com base no ganho de informações) : Nota: a maioria dos recursos preditivos são ordenados pelo 'escore' e plotados. A maioria daqueles mais discriminantes também devem ser utilizados dentro da conta pela "class" e 'class.frequency'. Escore percentual das variáveis class e class.frequency 1 cci 2568 1 0.50 100.00 2 signal 2438 1 0.51 94.92 3 slowD 2437 1 0.51 94.90 4 oscK 2410 1 0.50 93.85 5 ADX 2400 -1 0.51 93.44 6 vol 2395 1 0.51 93.24 7 atr 2392 -1 0.51 93.15 8 sign 2388 1 0.50 92.97 9 vsig 2383 1 0.50 92.81 10 ar 2363 -1 0.51 92.01 11 chv 2327 -1 0.50 90.62 12 cmo 2318 -1 0.51 90.28 13 DX 2314 1 0.50 90.10 14 oscDX 2302 -1 0.51 89.64 15 tr 2217 1 0.52 86.31 percent.importance 1 7 2 7 3 7 4 7 5 7 6 7 7 7 8 7 9 7 10 7 11 7 12 7 13 6 14 6 15 6 2 - Variável Local de Importância Interações de variáveis (10 variáveis mais importantes na primeira (colunas) e segunda (linhas) ordem): Para cada variável (em cada ordem), a sua interação com os outros é computadorizada. cci cmo slowD oscK signal atr chv cmo 0.1933 0.1893 0.1345 0.1261 0.1146 0.1088 0.1062 cci 0.1770 0.1730 0.1182 0.1098 0.0983 0.0925 0.0899 slowD 0.1615 0.1575 0.1027 0.0943 0.0828 0.0770 0.0744 signal 0.1570 0.1530 0.0981 0.0897 0.0782 0.0725 0.0698 atr 0.1490 0.1450 0.0902 0.0818 0.0703 0.0646 0.0619 ADX 0.1468 0.1428 0.0879 0.0795 0.0680 0.0623 0.0596 ar 0.1452 0.1413 0.0864 0.0780 0.0665 0.0608 0.0581 oscK 0.1441 0.1401 0.0853 0.0769 0.0654 0.0596 0.0570 DX 0.1407 0.1367 0.0819 0.0735 0.0620 0.0562 0.0536 oscDX 0.1396 0.1356 0.0807 0.0723 0.0608 0.0551 0.0524 avg1rstOrder 0.1483 0.1443 0.0895 0.0811 0.0696 0.0638 0.0612 ADX tr ar vsig DX oscDX sign cmo 0.1026 0.1022 0.1013 0.1000 0.0977 0.0973 0.0964 cci 0.0864 0.0859 0.0850 0.0837 0.0815 0.0810 0.0802 slowD 0.0708 0.0704 0.0695 0.0682 0.0660 0.0655 0.0647 signal 0.0663 0.0659 0.0650 0.0637 0.0614 0.0610 0.0601 atr 0.0584 0.0579 0.0570 0.0557 0.0535 0.0531 0.0522 ADX 0.0561 0.0557 0.0548 0.0534 0.0512 0.0508 0.0499 ar 0.0546 0.0541 0.0533 0.0519 0.0497 0.0493 0.0484 oscK 0.0534 0.0530 0.0521 0.0508 0.0486 0.0481 0.0473 DX 0.0500 0.0496 0.0487 0.0474 0.0452 0.0447 0.0439 oscDX 0.0489 0.0485 0.0476 0.0463 0.0440 0.0436 0.0427 avg1rstOrder 0.0577 0.0572 0.0563 0.0550 0.0528 0.0524 0.0515 vol avg2ndOrder cmo 0.0889 0.1173 cci 0.0726 0.1010 slowD 0.0571 0.0855 signal 0.0526 0.0810 atr 0.0447 0.0730 ADX 0.0424 0.0707 ar 0.0409 0.0692 oscK 0.0397 0.0681 DX 0.0363 0.0647 oscDX 0.0352 0.0636 avg1rstOrder 0.0439 0.0000 Variável de Importância baseada em interações (10 mais importante): cmo cci slowD signal oscK atr ADX ar 0.1447 0.1419 0.0877 0.0716 0.0674 0.0621 0.0563 0.0533 chv DX 0.0520 0.0485 Variável de importância ao longo das etiquetas (10 variáveis mais importantes condicionalmente para cada etiqueta) : Class -1 Class 1 cci 0.16 0.23 cmo 0.20 0.18 slowD 0.09 0.10 oscK 0.09 0.07 signal 0.05 0.07 tr 0.02 0.07 ADX 0.06 0.03 chv 0.06 0.04 atr 0.05 0.06 ar 0.05 0.03
Pelo que vemos, a importância das variáveis, com base na interação com os outros, destaca o top 10 que não coincide com a ordem da importância global. E finalmente, a importância das variáveis por classes tendo em conta a suas contribuições e envolvimentos. Por favor, note que a variável tr, com base na importância global, estava no último lugar e, em teoria, deveria ter sido abandonada, mas na verdade subiu para o sexto lugar devido à interação forte.
Assim, as variáveis top 10:
> best <- Cs(cci, cmo, slowD, oscK, signal, tr, ADX. chv, atr, ar)Vamos verificar, como a qualidade do modelo melhorou com o conjunto da maioria dos importantes preditores.
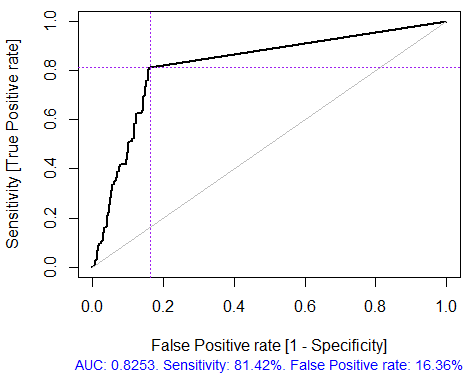
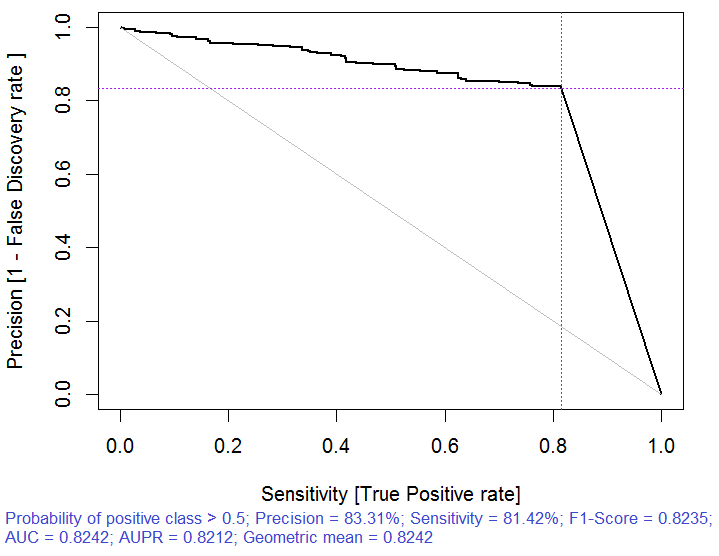
> x.tr <- x.train[ ,best] > x.tst <- x.test[ ,best] > ruf.opt <- randomUniformForest(X = x.tr, + Y = y.train, + xtest = x.tst, + ytest = y.test, + ntree = 300, + mtry = "random", + nodesize = 1, + threads = 2) Etiquetas -1 1 foram convertidas para 1 2, para facilitar a computação e serão usadas internamente como um substituto. > ruf.opt Chamada: randomUniformForest.default(X = x.tr, Y = y.train, xtest = x.tst, ytest = y.test, ntree = 300, mtry = "random", nodesize = 1, threads = 2) Tipo de "Random Uniform Forest": Classificação paramsObject ntree 300 mtry random nodesize 1 maxnodes Inf replace TRUE bagging FALSE depth Inf depthcontrol FALSE OOB TRUE importance TRUE subsamplerate 1 classwt FALSE classcutoff FALSE oversampling FALSE outputperturbationsampling FALSE targetclass -1 rebalancedsampling FALSE randomcombination FALSE randomfeature FALSE categorical variables FALSE featureselectionrule entropy avaliação Out-of-bag (OOB) Estimativa da taxa de erro OOB : 18.69% Vínculo de taxa de erro OOB (com desvio de 1%): 19.67% Matriz de confusão OOB: Referência Prediction -1 1 class.error -1 1079 253 0.1899 1 241 1070 0.1838 Estimativa OOB de AUC: 0.8131 Estimativa OOB de AUPR: 0.7381 Estimativa OOB de F1-score: 0.8125 Estimativa da média geométrica OOB (Ajustado): 0.8131 Limites de Breiman Predição de erro esperado (nas classes aproximadamente equilibradas): 14.98% Limite superior: 28.18% correlação média entre árvores: 0.0666 Força (margem): 0.5548 Desvio padrão da força: 0.2945 > pr.ruf.opt <- predict(ruf.opt, x.tst, type = "response") > ms.ruf.opt <- model.stats(pr.ruf.opt, y.test) Configuração de teste Taxa de erro: 17.55% Confusão da matriz: Referência Prediction -1 1 class.error -1 552 124 0.1834 1 108 538 0.1672 Área Sob a Curva ROC: 0.8245 Área Sob a Curva de Precisão-Recuperação: 0.8212 Pontos F1: 0.8226 Média geométrica: 0.8244
Fig. 5. Curva ROC ou curva de erro
Fig. 6. Curva de Precisão-Recuperação
A qualidade melhorou claramente. O erro de predição no teste configura 17.55%, é menor do que o nível superior 28.18%, portanto o retreinamento é altamente improvável. O modelo tem vários outros hiperparâmetros, cuja o ajuste permite reforçar ainda mais a qualidade do modelo, no entanto, este não é o objetivo deste artigo.
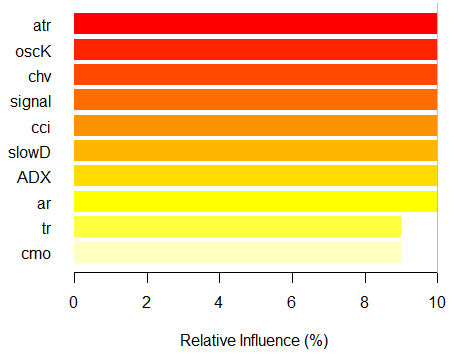
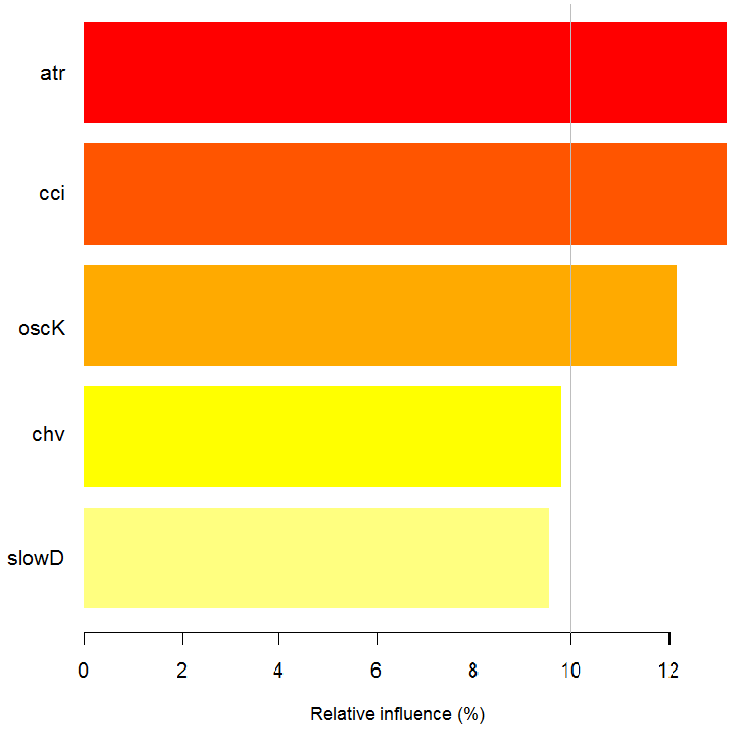
> imp.ruf.opt <- importance(ruf.opt, Xtest = x.tst) Variáveis relevantes foram extraídas. 1 - Variável Global de Importância (10 mais importantes com base no ganho de informações) : Nota: a maioria dos recursos preditivos são ordenados pelo 'escore' e plotados. A maioria daqueles mais discriminantes também devem ser utilizados dentro da conta pela "class" e 'class.frequency'. Escore percentual das variáveis class e class.frequency 1 atr 3556 -1 0.50 100.00 2 oscK 3487 -1 0.51 98.07 3 chv 3465 1 0.51 97.45 4 signal 3432 1 0.51 96.51 5 cci 3424 1 0.50 96.30 6 slowD 3415 1 0.51 96.04 7 ADX 3397 -1 0.50 95.52 8 ar 3369 -1 0.50 94.76 9 tr 3221 1 0.53 90.59 10 cmo 3177 -1 0.50 89.36 percent.importance 1 10 2 10 3 10 4 10 5 10 6 10 7 10 8 10 9 9 10 9 2 - Variável Local de Importância Interações de variáveis (10 variáveis mais importantes na primeira (colunas) e segunda (linhas) ordem): Para cada variável (em cada ordem), a sua interação com os outros é computadorizada. atr cci oscK slowD ADX tr chv cci 0.1748 0.1625 0.1620 0.1439 0.1411 0.1373 0.1349 atr 0.1650 0.1526 0.1522 0.1341 0.1312 0.1274 0.1251 oscK 0.1586 0.1462 0.1457 0.1277 0.1248 0.1210 0.1186 chv 0.1499 0.1375 0.1370 0.1190 0.1161 0.1123 0.1099 ar 0.1450 0.1326 0.1321 0.1140 0.1112 0.1074 0.1050 signal 0.1423 0.1300 0.1295 0.1114 0.1085 0.1047 0.1024 ADX 0.1397 0.1273 0.1268 0.1088 0.1059 0.1021 0.0997 slowD 0.1385 0.1262 0.1257 0.1076 0.1048 0.1010 0.0986 cmo 0.1276 0.1152 0.1147 0.0967 0.0938 0.0900 0.0876 tr 0.1242 0.1118 0.1113 0.0932 0.0904 0.0866 0.0842 avg1rstOrder 0.1466 0.1342 0.1337 0.1156 0.1128 0.1090 0.1066 signal ar cmo avg2ndOrder cci 0.1282 0.1182 0.1087 0.1412 atr 0.1184 0.1084 0.0989 0.1313 oscK 0.1120 0.1020 0.0925 0.1249 chv 0.1033 0.0933 0.0838 0.1162 ar 0.0984 0.0884 0.0789 0.1113 signal 0.0957 0.0857 0.0762 0.1086 ADX 0.0931 0.0831 0.0736 0.1060 slowD 0.0919 0.0819 0.0724 0.1049 cmo 0.0810 0.0710 0.0615 0.0939 tr 0.0776 0.0676 0.0581 0.0905 avg1rstOrder 0.0999 0.0900 0.0804 0.0000 Variável de Importância baseada nas interações (10 mais importantes) : atr cci oscK chv slowD ADX signal ar 0.1341 0.1335 0.1218 0.0978 0.0955 0.0952 0.0898 0.0849 tr cmo 0.0802 0.0672 Variável de importância sobre as etiquetas (10 mais importantes variáveis condicionalmente a cada rótulo): Class -1 Class 1 atr 0.17 0.14 oscK 0.16 0.11 tr 0.03 0.16 cci 0.14 0.13 slowD 0.12 0.09 ADX 0.10 0.10 chv 0.08 0.10 signal 0.09 0.07 cmo 0.07 0.03 ar 0.06 0.06
Fig. 7. A importância das variáveis com base no ganho de informações
Como podemos ver, as variáveis de importância globais quase estabilizaram, mas as variáveis de importância por classes estão classificadas de forma diferente. A variável tr assume o terceiro lugar.
Dependência parcial sobre o preditor
A dependência parcial das variáveis mais importantes serão consideradas.
> plot(imp.ruf.opt, Xtest = x.tst)
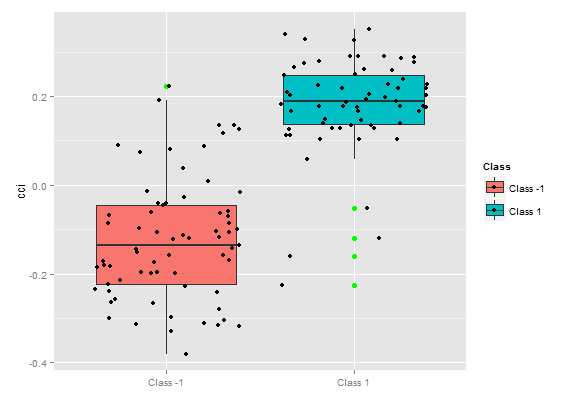
Fig. 8. Dependência parcial da variável cci
> pd.signal <- partialDependenceOverResponses(x.tst, + imp.ruf.opt, + whichFeature = "signal", + whichOrder = "all" + )
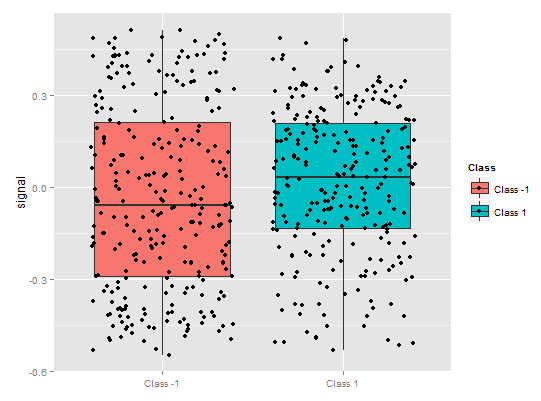
Fig. 9. Dependência parcial da variável sinal
Há uma imagem completamente diferente de uma dependência parcial de um preditor de sinal na figura acima. É observada a cobertura de dados quase completa para ambas as classes.
> pd.tr <- partialDependenceOverResponses(x.tst,
imp.ruf.opt,
whichFeature = "tr",
whichOrder = "all"
)
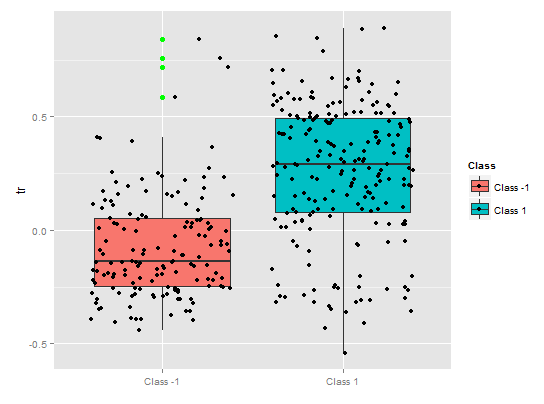
Uma dependência parcial do preditor tr mostra a separação razoável por classes, ainda há uma considerável cobertura aqui.
Fig. 10. Dependência parcial da variável tr
> pd.chv <- partialDependenceOverResponses(x.tst,
imp.ruf.opt,
whichFeature = "chv",
whichOrder = "all")
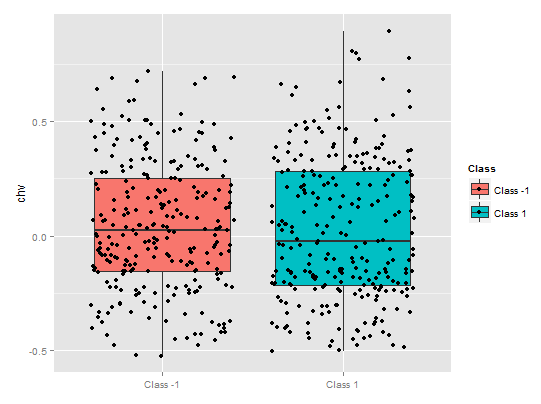
A dependência parcial do preditor chv é absolutamente deplorável. É observada a cobertura de dados quase completa por classes .
Fig. 11. Dependência parcial da variável chv
Desta forma, podemos determinar visualmente como os dados do preditor estão ligados às classes e como eles são separáveis.
A importância da variável ao longo das classes
"A importância da variável" sobre as classes fornece uma perspectiva local: a classe é fixa, o que significa que primeiro é a decisão de fixar a classe, considerando as variáveis que são importantes e agem como constantes, e finalmente, as variáveis importantes para cada classe são consideradas. Assim, cada variável tem importância, como se não houvesse outras classes.
Aqui nós não estamos interessados em variáveis que levaram à escolha de uma classe, mas variáveis que serão importantes para a classe, quando esta última for selecionada. A ordem das variáveis fornece a sua classificação livre em relação as suas avaliações em cada classe, sem consideração da importância da classe.
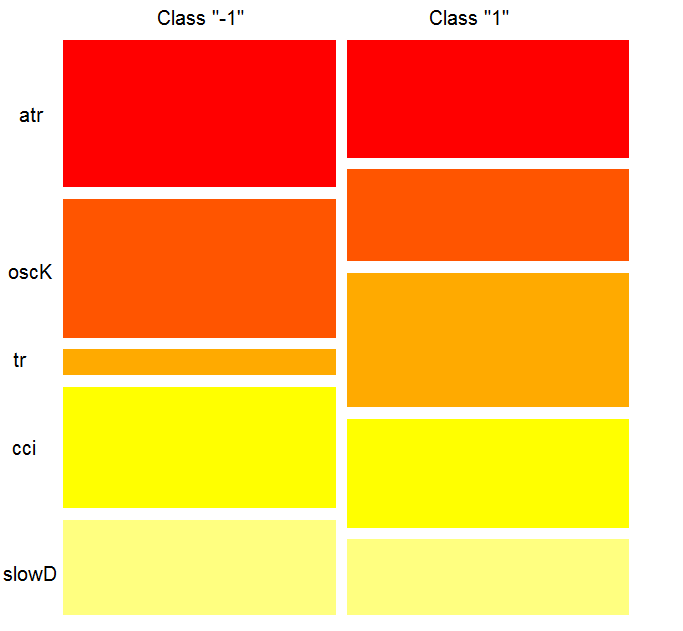
O que o gráfico mostrou? O preditor tr é consideravelmente mais importante para a classe "1" do que para a classe "-1". E vice-versa, o preditor oscK para a classe "-1" é mais importante do que para a classe "1". Preditores têm diferentes importâncias em diferentes classes.
Fig. 12. A importância da variável ao longo das classes
A importância de variáveis baseadas em interações
O gráfico abaixo mostra, como cada variável é apresentado na interação conjunta com qualquer outra variável. Uma observação importante: a primeira variável não é necessariamente a mais importante, em vez disso, mas é a que tem o maior impacto mútuo com as outras.Variáveis das interações sobre as observações
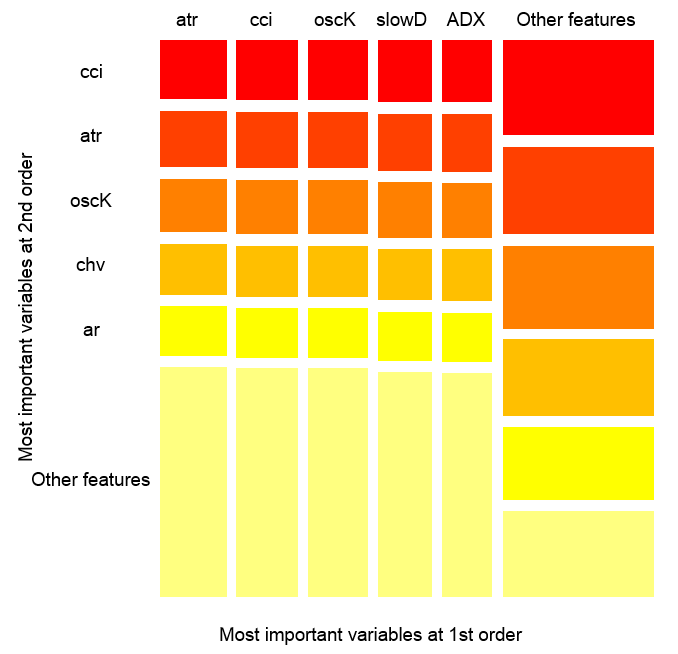
Fig. 14. A importância das variáveis sobre as observações
A figura acima mostra a interação da primeira e segunda ordem para todos os preditores de acordo com a definição, ocorrendo durante a interação e sua área é igual a unidade. A primeira ordem indica que variáveis (ordenados por influência descendente) são as mais importantes, caso a decisão seja feita tendo em conta apenas uma variável. A segunda ordem indica que, se a variável desconhecida já está selecionada na primeira ordem, então a segunda variável mais importante pertence a uma da segunda ordem.
Para esclarecimento, a interação fornece uma tabela de recursos ordenados. A primeira ordem fornece oportunidades ordenadas das variáveis mais importantes. A segunda ordem fornece oportunidades ordenadas das segundas variáveis mais importantes. A intersecção de um par de variáveis apresenta sua influência mútua relativa de todas as possíveis influências mútuas. Por favor, note que estas medidas dependem tanto do modelo como dos dados. Portanto, a confiança nas medições depende diretamente da confiança nas predições. Podemos também acrescentar, que uma meta variável chamada de "outros sinais" ocorre, o que significa a permissão ao algoritmo para mostrar o modo de exibição padrão da visualização das variáveis agrupadas menos relevantes.
Importância parcial
Você pode olhar para a importância parcial com base em observações do x.tst sobre a classe "-1".
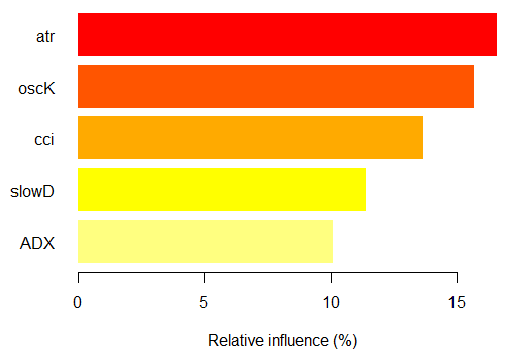
> par.imp.ruf <- partialImportance(X = x.tst, + imp.ruf.opt, + whichClass = "-1") Influência relativa: 67.41% Baseada sobre x.tst e classe «-1»
Fig. 15. Importância parcial das variáveis baseadas em observações sobre a classe "-1"
Como podemos ver, os preditores mais importantes da classe "-1" são cinco preditores mostrados na figura acima.
Agora, o mesmo para a classe "+1"
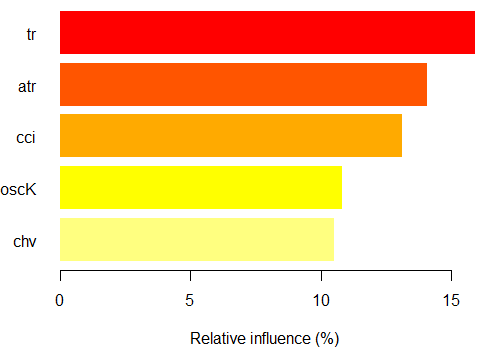
> par.imp.ruf <- partialImportance(X = x.tst, + imp.ruf.opt, + whichClass = "1") Influência relativa: 64.45%
Fig. 16. Importância parcial de variáveis baseadas nas observações sobre a classe "+1"
Vemos que os preditores são diferentes tanto em estrutura como nas posições.
Vamos ver a dependência parcial entre os preditores cci e atr, que são os mais importantes na primeira e segunda ordem de interação do preditor.
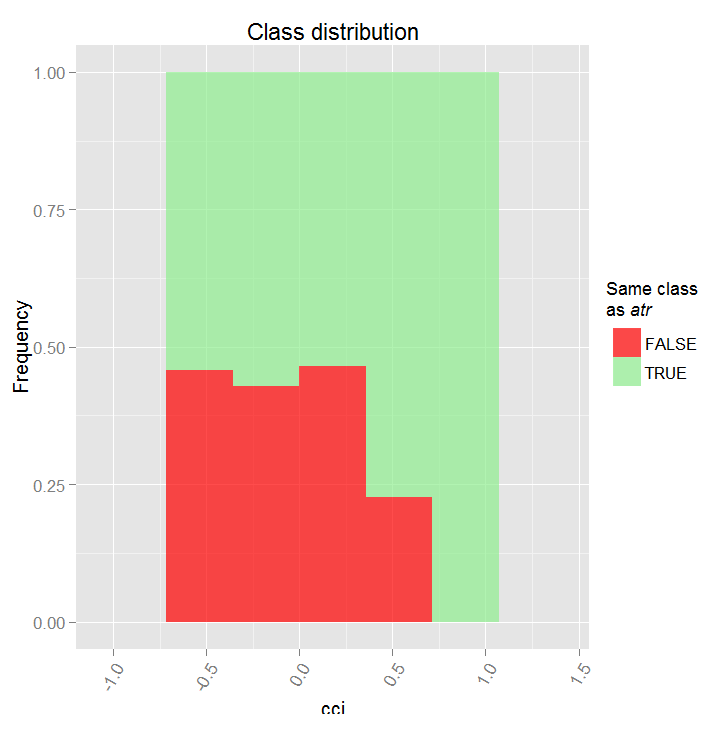
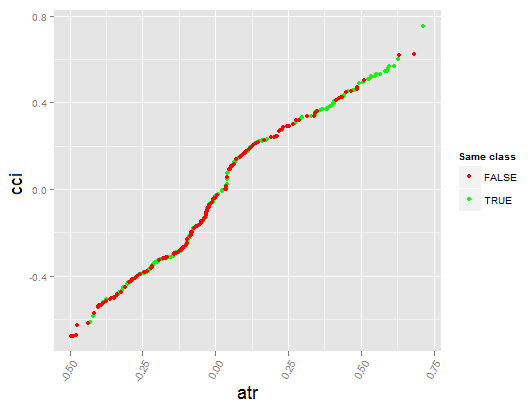
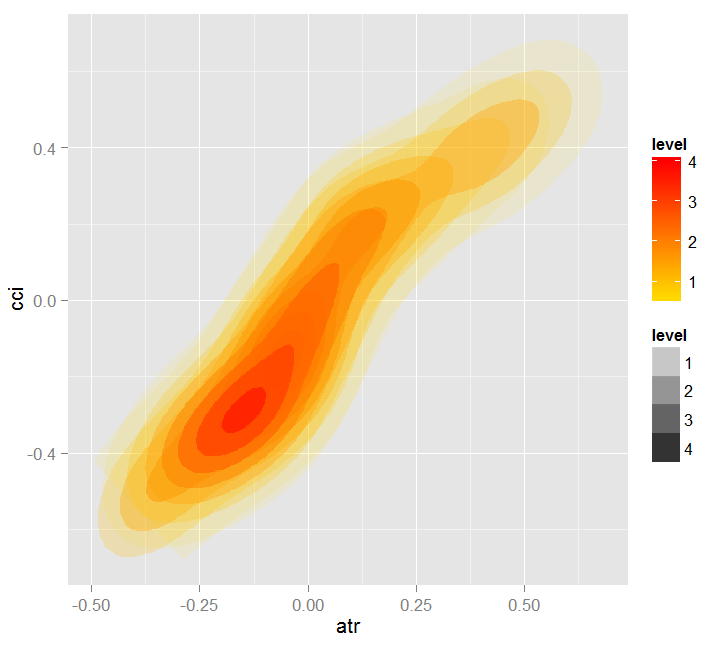
> par.dep.1 <- partialDependenceBetweenPredictors(Xtest = x.tst, + imp.ruf.opt, + features = Cs(atr, cci), + whichOrder = "all", + perspective = T) Nível das interações entre a atr e a cci na primeira ordem: 0.1748 (99.97% da(s) característica(s) com nível máximo) Nível das interações entre a atr e a cci na primeira ordem: 0.1526 (87.28% da(s) característica(s) com nível máximo) Distribuição de classe: para uma variável do par, apresenta a probabilidade estimada de que a variável tem a mesma classe do que a outra. Se a mesma classe tende a ser VERDADEIRA, então a variável tem, possivelmente, uma influência sobre a outra (para categoria ou valores considerados) ao prever uma etiqueta Dependência: para o par de variáveis, exibe a forma da sua dependência e o acordo estimado em predizer a mesma classe, para os valores que definem a dependência. No caso de variáveis categóricas, a tabulação cruzada é usada. Heatmap: para o par de variáveis, exibe a área onde a dependência é a mais efetiva. Quanto mais escura for a cor, mais forte é a dependência. A partir do par de variáveis, aquele que domina , é possivelmente a mais discriminante (olhando para 'Variável Global de Importância') e/ou a que tem o maior nível de interações (olhando para uma Variável de Importância baseada em interações (10 mais importante):
Fig. 17. Dependência parcial entre preditores cci e atr
Fig. 18. Dependência entre preditores atr e cci
Dependência entre preditores atr e cci Heatmap de dependência entre preditores atr and cci
Variável Global de Importância foi determinada para descrever quais variáveis globais têm a maior influência sobre a redução dos erros de predição.
Variável Local de Importância descreve o que faz uma variável influente, utilizando a sua interação com as outras.
Isto leva para a importância parcial que mostra quando uma variável é mais importante. O último passo na análise da importância da variável é uma dependência parcial que define quando e/ou como cada uma das variáveis está associada com uma resposta.
Para resumir: uma variável de importância no pacote "Random Uniform Forests" vai desde o mais alto ao mais baixo nível com detalhamento. Em primeiro lugar, nós encontramos quais variáveis são importantes e aprendemos as nuances de peso em cada classe. Então descobrimos o que as torna influente, considerando sua interação e escolha de uma variável, considerando primeiro todas as classes como uma. O próximo passo - aprendemos onde elas obtêm a sua influência considerando, dentro de cada classe, quando ela é fixa. Finalmente, obtemos quando e como a variável pode ser/é importante olhando para a "dependência parcial". Todas as medidas, com exceção da "variável global de importância", operam em qualquer formação ou conjunto de teste.
A avaliação de vários níveis apresentados dos preditores permite selecionar os mais importantes e criar conjuntos ideais, reduzindo significativamente a dimensão dos dados e melhorando a qualidade das predições.
Você pode avaliar e escolher não só preditores, mas também os itens de observação mais informativos.
Vamos olhar para outro pacote interessante — "RoughSet".
Breve descrição: Existem duas seções principais abordados neste pacote: o "Rough Set Theory" (RST) e o "Fuzzy Rough Set Theory" (FRST). RST foi proposto por Z. Pawlak (1982, 1991), fornece instrumentos matemáticos sofisticados para modelar e analisar sistemas de informação que incluem heterogeneidade e imprecisões. Usando as relações de indistinguibilidade entre RST de objetos que não requerem parâmetros adicionais para extrair informações.
A primeira teoria, a extensão RST, foi proposto por D. Dubois e H. Prade (1990), que combina os conceitos de incerteza e indistinguibilidade que são expressos em conjuntos difusos propostos por L.A. Zadeh (1965) e RST. Este conceito permite analisar atributos contínuos (variáveis) sem discretização de dados preliminares. Com base nos conceitos acima descritos, muitos métodos têm sido propostos e utilizados em diversas áreas. A fim de resolver os problemas dos métodos, usamos a relação de indistinguibilidade e o conceito de aproximação inferior e superior.
Por favor, permita-me uma pequena digressão.
Um método de representação do conhecimento normalmente desempenha um papel importante no sistema de informação. Os métodos mais conhecidos de apresentar o conhecimento nos sistemas de formação de conceitos indutivos são: regras de produção, árvores de decisão, o cálculo de predicados e redes semânticas.
Para extrair e generalizar o conhecimento armazenado nas matrizes informativas reais, os seguintes problemas principais aparecem:
- Estes dados são muito diferentes (quantitativo, qualitativo, estrutural).
- Bases de dados reais são normalmente grandes, portanto algoritmos de complexidade exponencial para obter conhecimento da base de dados podem parecer inaceitáveis.
- A informação contida nos arrays de dados reais pode ser incompleta, excessiva, distorcida, controversa e alguns valores de uma série de atributos podem ser completamente ausentes. Portanto, você deve usar apenas os atributos existentes na construção das regras de classificação.
Atualmente para extrair conhecimento a partir da base de dados (Data Mining), a teoria dos conjuntos irregulares está sendo cada vez mais utilizada como referencial teórico e como um conjunto de métodos práticos.
Conjuntos aproximados têm limites indefinidos, ou seja, eles não podem ser descritos com precisão por um conjunto de recursos disponíveis.
A teoria dos conjuntos aproximados foi proposto por Zdzislaw Pawlak em 1982 e tornou-se um novo instrumento matemático para operação com informações incompletas. O conceito mais importante desta teoria é uma assim chamada aproximação superior e inferior dos conjuntos aproximados, que permite avaliar a possibilidade ou a necessidade dos elementos pertencentes a um conjunto com limites "fuzzy".
A aproximação inferior é constituída de elementos que definitivamente pertencem a X, uma aproximação superior contém elementos que possivelmente pertencem a X. A região limite do conjunto X é a diferença entre a maior e a menor aproximação, isto é, a região de fronteira tem elementos do conjunto X que pertencem a uma aproximação mais elevada do que uma outra aproximação inferior.
Um conceito simples, mas poderoso de conjuntos aproximados que tornou-se uma base para vários estudos teóricos - lógica, álgebra, topologia e estudos aplicados - inteligência artificial, raciocínio aproximado, análise de dados intelectual, teoria de decisão, processamento de imagens e reconhecimento de padrões.
O conceito de "configuração aproximada" lida com "a imperfeição de dados" referente a "granularidade" da informação. Este conceito é inerente topologicamente e complementa outras abordagens bem conhecidas que são usadas para operações com informações incompletas, como: conjuntos fuzzy, raciocínio Bayesian, redes neurais, algoritmos evolutivos, métodos estatísticos de análise de dados, etc.
Vamos prosseguir. Todos os métodos fornecidos neste pacote podem ser agrupados de acordo:
conceitos básicos de RST e FRST. Nesta parte podemos observar quatro tarefas diferentes: relação de indiscernibilidade, aproximação inferior e superior, região positiva e matriz de discernibilidade.
Discretização. É usado para converter os dados físicos para nominal. Da persepctiva RST, esta tarefa tenta manter a discernibilidade entre objetos.
Seleção de características. Este é um processo para encontrar subconjuntos de variáveis que estão tentando obter a mesma qualidade que o conjunto completo de preditores. Em outras palavras, o objetivo é selecionar as características essenciais e eliminar as suas dependências. É útil e necessário quando somos confrontados com um conjunto de dados contendo vários recursos. Em termos de RST e FRST, a escolha dos preditores refere-se à pesquisa de super redutores e redutores.
Seleção da instância. Este processo visa eliminar cópias ruidosas, desnecessárias ou conflitantes do conjunto de dados do treino, enquanto salva as coerentes. Assim, uma boa precisão da classificação é obtida pela remoção dos exemplares que não fornecem uma contribuição positiva.
Indução de regras. Como já mencionado, a tarefa indutiva de regras é usada para gerar regras, proporcionando o conhecimento da tabela de solução. Normalmente, este processo é chamado de fase de treinamento na aprendizagem da máquina.
Predição/classificação. Esta tarefa é utilizada para prever valores de uma variável a partir do novo conjunto de dados (conjunto de teste).
Vamos explorar apenas duas categorias desta lista - a escolha de preditores e a seleção de amostras.
Vamos formar o conjunto de dados de entrada e saída. Usaremos os mesmos dados que obtidos antes, mas vamos transformá-los na classe "DecisionTable", onde o pacote opera.> library(RoughSets) Carregando pacote exigido: Rcpp > require(magrittr) > data.tr <- SF.asDecisionTable(data.f[idx$tr, ], + decision.attr = 16, + indx.nominal = 16) > data.tst <- SF.asDecisionTable(data.f[idx$ts, ], + decision.attr = 16, + indx.nominal = 16 + ) > true.class <- data.tst[ ,ncol(data.tst)]Como já mencionado anteriormente, RST usa dados nominais. Uma vez que temos dados numéricos contínuos, vamos convertê-los em dados nominais, utilizando uma função de discretização especializada disponível a partir do pacote.
> cut.values <- D.global.discernibility.heuristic.RST(data.tr) > data.tr.d <- SF.applyDecTable(data.tr, cut.values)
Vamos ver o que obtemos como resultado:
> summary(data.tr.d) DX ADX (12.5,20.7]: 588 (17.6,19.4]: 300 (20.7, Inf]:1106 (19.4,25.4]: 601 [-Inf,12.5]: 948 (25.4,31.9]: 294 (31.9, Inf]: 343 [-Inf,17.6]:1104 oscDX ar (1.81, Inf]:1502 (-40.6,40.6]:999 [-Inf,1.81]:1140 (40.6,71.9] :453 (71.9, Inf] :377 [-Inf,-40.6]:813 tr atr (0.000205,0.000365]:395 (0.00072,0.00123]:1077 (0.000365,0.0005] :292 (0.00123, Inf] : 277 (0.0005,0.00102] :733 [-Inf,0.00072] :1288 (0.00102,0.00196] :489 (0.00196, Inf] :203 [-Inf,0.000205] :530 cci chv (-6.61, Inf]:1356 (-0.398,0.185]:1080 [-Inf,-6.61]:1286 (0.185,0.588] : 544 (0.588, Inf] : 511 [-Inf,-0.398] : 507 cmo sign (5.81,54.1]: 930 [-Inf, Inf]:2642 (54.1, Inf]: 232 [-Inf,5.81]:1480 vsig slowD (0.0252, Inf]:1005 [-Inf, Inf]:2642 [-Inf,0.0252]:1637 oscK signal (-0.0403,0.000545]:633 (-11.4, Inf]:1499 (0.000545,0.033] :493 [-Inf,-11.4]:1143 (0.033, Inf] :824 [-Inf,-0.0403] :692 vol Class (0.0055,0.00779]:394 -1:1319 (0.00779,0.0112]:756 1 :1323 (0.0112,0.0154] :671 (0.0154, Inf] :670 [-Inf,0.0055] :151
Vemos que os preditores são discretizados de formas diferentes. Variáveis como: slowD, sign não estiveram separadas. Variáveis de sinal, vsig, cci, oscDX são simplesmente divididas em duas áreas. As outras variáveis são divididas entre 3 e 6 classes.
Vamos selecionar as variáveis importantes:
> reduct1 <- FS.quickreduct.RST(data.tr.d, control = list()) > best1 <- reduct1$reduct > best1 DX ADX oscDX ar tr atr cci 1 2 3 4 5 6 7 chv cmo vsig oscK signal vol 8 9 11 13 14 15
Os dados que não foram divididos (slowD, sign) são removidos a partir do conjunto. Vamos realizar o conjunto de teste de discretização e transformá-lo de acordo com a redução efetuada.
> data.tst.d <- SF.applyDecTable(data.tst, cut.values) > new.data.tr <- SF.applyDecTable(data.tr.d, reduct1) > new.data.tst <- SF.applyDecTable(data.tst.d, reduct1)
Agora, usando uma excelente oportunidade do pacote, chamada de "regras de indução", vamos extrair um conjunto de regras que se ligam aos preditores e um alvo. Uma das seguintes opções serão utilizadas:
> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9, timesCovered = 3)
Vamos verificar o conjunto de testes e como essas regras funcionam na predição:
> pred.vals <- predict(rules, new.data.tst) > table(pred.vals) pred.vals -1 1 655 667
Métricas:
> caret::confusionMatrix(true.class, pred.vals[ ,1]) Matriz de Confusão e Estatística Referência Predição -1 1 -1 497 163 1 158 504 Precisão : 0.7572 95% CI : (0.7331, 0.7801) Sem Taxa de Informação : 0.5045 P-Value [Acc > NIR] : <2e-16 Kappa : 0.5144 Teste de Mcnemar P-Value : 0.8233 Sensibilidade : 0.7588 Especificidade : 0.7556 Valor Predição Pos : 0.7530 Valor Predição Neg : 0.7613 Predomínio : 0.4955 Taxa de Detecção : 0.3759 Detecção de Prevalência : 0.4992 Precisão Balanceada : 0.7572 Classe 'Positive' : -1
E agora - uma escolha de exemplos significantes:
> ##-----Seleção de Instância----------- > res.1 <- IS.FRIS.FRST(decision.table = data.tr, control = list(threshold.tau = 0.5, alpha = 1, type.aggregation = c("t.tnorm", "lukasiewicz"), t.implicator = "lukasiewicz")) > new.data.tr <- SF.applyDecTable(data.tr, res.1) > nrow(new.data.tr) [1] 2353Aproximadamente 300 exemplos foram avaliados como menores e descartados. Vamos extrair um conjunto de regras a partir deste conjunto e comparar a qualidade de predição com um conjunto anterior.
> rules <- RI.AQRules.RST(new.data.tr, confidence = 0.9,
timesCovered = 3)
> pred.vals <- predict(rules, new.data.tst)
> table(pred.vals)
pred.vals
-1 1
638 684
> caret::confusionMatrix(true.class, pred.vals[ ,1])
Matriz de Confusão e Estatística
Referência
Predição -1 1
-1 506 154
1 132 530
Precisão : 0.7837
95% CI : (0.7605, 0.8056)
Sem Taxa de Informação : 0.5174
P-Value [Acc > NIR] : <2e-16
Kappa : 0.5673
Teste de Mcnemar P-Value : 0.2143
Sensibilidade : 0.7931
Especificidade : 0.7749
Valor Predição Pos : 0.7667
Valor Predição Neg : 0.8006
Predomínio : 0.4826
Taxa de Detecção : 0.3828
Detecção de Prevalência : 0.4992
Precisão Balanceada : 0.7840
Classe 'Positive' : -1
A qualidade é maior do que no caso anterior. Observa-se que, como no pacote RandomUniformForests, é impossível obter resultados reprodutíveis em experiências repetidas, então cada novo lançamento dá um resultado ligeiramente diferente.
Como as regras olham? Vamos ver:> head(rules) [[1]] [[1]]$idx [1] 6 4 11 [[1]]$values [1] "(85.1, Inf]" "(0.00137, Inf]" "(0.0374, Inf]" [[1]]$consequent [1] "1" [[1]]$support [1] 1335 1349 1363 1368 1372 1390 1407 1424 1449 1454 [11] 1461 1472 1533 1546 1588 1590 1600 1625 1630 1661 [21] 1667 1704 1720 1742 1771 1777 1816 1835 1851 1877 [31] 1883 1903 1907 1912 1913 1920 1933 1946 1955 1981 [41] 1982 1998 2002 2039 2040 2099 2107 2126 2128 2191 [51] 2195 2254 2272 2298 2301 2326 2355 2356 2369 2396 [61] 2472 2489 2497 2531 2564 2583 2602 2643 [[1]]$laplace 1 0.9857143
Esta é uma lista contendo os seguintes dados:
- $idx — preditores de índice que participam nesta regra. No exemplo acima, estes são 6 ("atr"), 4 ("ar") e 11 ("vsig").
- $values — uma série de indicadores de valor, onde esta regra opera.
- $consequent — solução: class = "1". Para fazê-lo soar compreensível: se "atr" nesta faixa "(85.1, Inf]" E "ar" está na faixa "(0.00137, Inf]" E "vsig" na faixa "(0.0374, Inf]", ENTÃO Class = "1".
- $support — índices de exemplos que suportam esta solução.
- $laplace — uma avaliação do nível de confiança para esta regra.
Um cálculo de regras leva um tempo considerável.
Conclusão
Nós consideramos as novas oportunidades com base na avaliação preditiva, sua visualização e escolhemos a mais valiosa. Examinamos, também, diferentes níveis de importâncias, dependências de predição e seus impactos sobre as respostas. Os resultados dos experimentos serão aplicadas no próximo artigo, onde nós vamos considerar redes profundas com RBM.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/2029
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 MQL5 para iniciantes: Proteção antivandalismo de objetos gráficos
MQL5 para iniciantes: Proteção antivandalismo de objetos gráficos
 Agora a plataforma MetaTrader 5 possui um sistema de cobertura de registro de posições
Agora a plataforma MetaTrader 5 possui um sistema de cobertura de registro de posições
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
em tempo real, você usa 'sem as últimas 300 barras'!
Você parece tão estúpido que pode usar isso em tempo real?
Todos os seus artigos estão errados, porque a definição do seu objetivo está errada. Todos não podem funcionar em tempo real, pois, se você seguir seu argumento, o sinal acontecerá depois de 300 barras.
Todos não podem trabalhar em tempo real, pois, seguindo seu ponto de vista, o único problema acontecerá depois de 300 barras.
em tempo real, você usa 'sem as últimas 300 barras'!
Você parece tão estúpido que pode usar isso em tempo real?
Todos os seus artigos estão errados, porque a definição do seu objetivo está errada. Todos não podem funcionar em tempo real, pois, se você seguir seu argumento, o sinal acontecerá depois de 300 barras.
Tudo não pode funcionar em tempo real, já que, de acordo com seu ponto de vista, seu sinal acontecerá depois de 300 barras.
Você realmente não entende a visão do autor, é muito ingênuo em sua própria imaginação, e a estupidez do que diz é apenas mapeada em você mesmo.
Para Vladimir Perervenko: obrigado novamente por esses artigos maravilhosos, você fez e faz uma pesquisa muito boa! essa coisa estúpida do "freewalk", nem todos os chineses gostam dele.
Respondi a você na próxima ramificação.
Oi Vladimir,
Não encontrei sua resposta para essa pergunta. Também não tenho certeza de qual é o valor de Dig. Você poderia especificar, por favor?
Prezados,
Alguém pode me dizer o que significa a variável --Dig-- definida na função ZZ . É uma constante? Se sim, qual deve ser o valor dessa constante?
Dig - o número de dígitos após o ponto decimal entre aspas. Talvez 5 ou 3.
Desculpe-me pelo atraso na resposta. Não vi a pergunta. A discussão está espalhada por vários ramos. Não tenho tempo para acompanhá-la.
Desculpe-me.
O artigo é volumoso, obrigado pelo trabalho.
No entanto, ele é questionável:
1. usar a estratificação com um alvo selecionado que é rotulado em cada barra. A mistura de duas amostras não representativas geralmente melhora o resultado, o que o distorce.
2- A seleção de recursos com base em modelos construídos, especialmente considerando a primeira divisão de randoms e o método guloso, é mais um método de redução de recursos para o método de construção de modelos. O método guloso nem sempre é correto e estável. Nesse caso, talvez você precise usar subamostras diferentes, pelo menos.
Não entendi o segundo método até o final - é o mesmo com um primeiro preditor aleatório e, em seguida, tentamos criar uma folha ou criamos uma árvore e deixamos a melhor folha, que é usada para avaliação?