Redes Neurais de Terceira Geração: Redes Profundas

MetaTrader 5 — Indicadores | 27 julho 2015, 11:50

8 081

Vladimir Perervenko

Conteúdo

Redes Neurais de Segunda Geração

Aprendizagem Profunda

2.1. Contexto
2.2. Autoencoders. Autoencoder e Máquinas de Boltzmann Restritas. Diferenças e peculiaridades
- 2.2.1. Autoencoder
- 2.2.2. Máquina de Boltzmann Restrita, RBM
2.3. Redes Auto-Associativas empilhadas. Autoencoder Empilhado SAE, Máquina de Boltzmann Restrita Empilhada (Stacked RBM)
2.4. Treinamento das Redes Profundas (DN). Etapas. Peculiaridades

Experimentos Práticos

A implementação (Indicador e o Expert Advisor)

Introdução

Este artigo vai considerar as principais idéias deste assunto, tais como a Aprendizagem Profunda e a Rede Profunda sem cálculos complexos em termos leigos.

Experimentos com os dados reais confirmam (ou não) as vantagens teóricas das redes neurais profundas sobre as mais superficiais por definição métrica e comparação (não tenho certeza sobre a definição de métricas e comparação). A tarefa em mãos é a classificação. Nós vamos criar um indicador e um Expert Advisor baseado em um modelo de rede neural profunda e trabalhar em conjunto de acordo com o esquema cliente/servidor e, em seguida, testá-los.

Presume-se que o leitor tenha uma idéia razoável dos conceitos básicos usados em redes neurais.

1. Redes Neurais de Segunda Geração

As redes neurais são concebidos para lidar com uma ampla gama de problemas relacionados com o processamento de imagem.

Abaixo está uma lista de problemas tipicamente resolvidas pelas redes neurais:

Aproximação de funções por um conjunto de pontos (regressão);
Classificação de dados pelo conjunto especificado de classes;
Agrupamento de dados com a identificação de classes de protótipo previamente desconhecidos;
Compressão de informação;
Restaurar dados perdidos;
Memória associativa;
Otimização, controle ótimo etc.

Da lista acima, somente a "Classificação" que será discutida neste artigo.

1.1. A Arquitetura de Conexões

A forma do processamento de informação é muito afetado pela ausência ou presença de loops de feedback na rede. Se não houver loops de feedback entre os neurônios (ou seja, a rede tem uma estrutura de camadas sequenciais, onde cada neurônio recebe as informações somente a partir do nível anterior), o processamento de informação na rede é unidirecional. O sinal de entrada é processado por uma sequência de camadas e a resposta é recebida através do número de ciclos igual ao número de camadas.

A presença de loops de feedback podem deixar a dinâmica de uma rede neural (chamado neste caso de recorrente) imprevisível. Na verdade, uma rede pode entrar em um "loop eterno" e nunca produzir uma resposta. Ao mesmo tempo, de acordo com Turing, não há nenhum algoritmo para uma rede recorrente arbitrária identificar se os seus elementos estão entrando em equilíbrio (o problema da parada).

De um modo geral, o fato dos neurônios em redes recorrentes participarem no processamento de informação, muitas vezes, permite que tais redes processem a informação a um nível mais profundo de maneiras diferentes. Neste caso, devem ser tomadas medidas especiais para que a rede não entre em loop para sempre. Por exemplo, usar conexões simétricas, como numa rede de Hopfield ou limitar forçadamente o número de iterações.

Tipo de Treinamento Tipo de conexão	Supervisionado	Não supervisionado
Sem loops de feedback	Perceptrons de múltiplas camadas (função de aproximação, classificação)	Rede competitiva, mapas auto-organizável (compressão de dados, separação de recurso)
Com loops de feedback	Perceptron recorrente (previsão de séries temporais, treinamento on-line)	Rede de Hopfield (memória associativa, agrupamento de dados, otimização)

Tabela 1. Classificação da rede neural pelo tipo da conexão e do treinamento

1.2. Principais tipos de Redes Neurais

Tendo começado com o perceptron, as redes neurais tiveram um longo caminho para sua evolução. Hoje em dia um grande número de redes neurais se diferem pela estrutura de formação e dos métodos utilizados.

Os mais famosos são:

1.2.1. Redes MLP (Perceptron de Múltiplas Camadas) de Alimentação Direta com Múltiplas Camadas Totalmente Conectadas

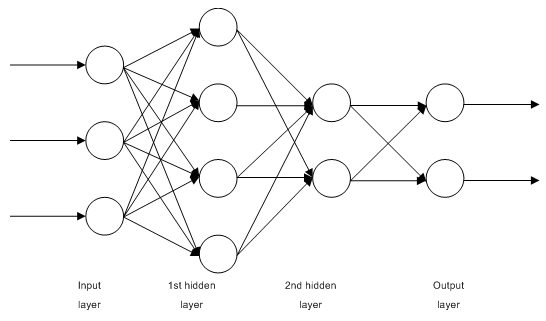
Fig. 1. Estrutura de uma rede neural de múltiplas camada

1.2.2. Rede de Jordan são redes parcialmente recorrentes e semelhantes às redes de Elman.

Ela pode ser tratada como uma rede de alimentação de entrada com neurônios de contexto adicionais na camada de entrada.

Esses neurônios de contexto são alimentados por si mesmos (feedback direto) e dos neurônios de entrada. Os neurônios de contexto preservam o estado atual da rede. Em uma rede de Jordan o número de contexto e de neurônios de entrada devem ser o mesmo.

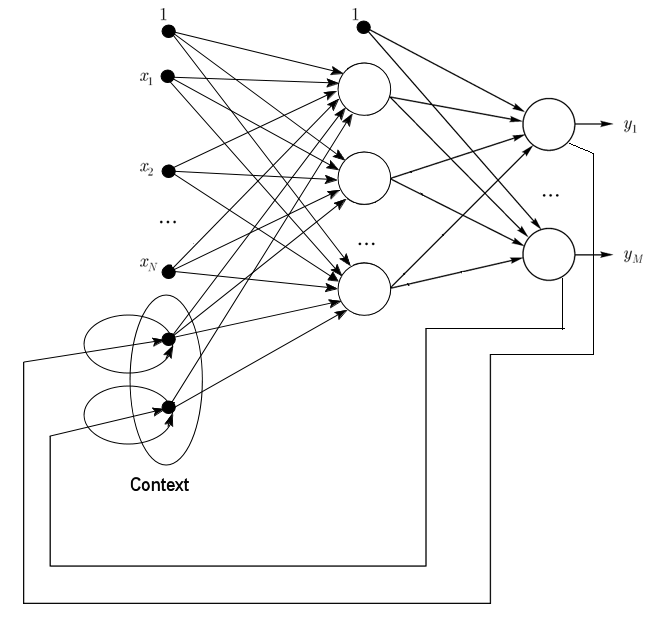
Fig. 2. Estrutura de uma rede de Jordan

1.2.3. Rede de Elman são redes parcialmente recorrentes e semelhante às redes de Jordan. A diferença entre as redes de Elman e de Jordan é que, em uma rede de Elman os neurônios de contexto são alimentados por neurônios de saída, e não por aqueles na camada escondida. Além disso, não há nenhum feedback direto nos neurônios de contexto.

Em uma rede de Elman o número de contexto e de neurônios escondidos devem ser o mesmo. A principal vantagem das redes de Elman é que o número de neurônios de contexto é definido não pelo número de saídas como na rede de Jordan, mas pelo número de neurônios escondidos, que faz com que a rede seja mais flexível. Os neurônios escondidos podem ser facilmente adicionados ou retirados, ao contrário do número de saídas.

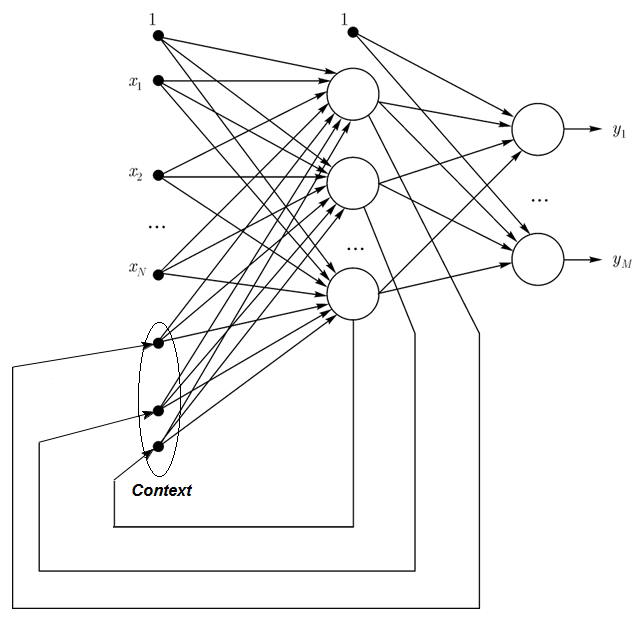
Fig. 3. Estrutura de uma rede de Elman

1.2.4. Rede de Função de Base Radial (RBF) - É uma rede neural de alimentação direta que contém uma camada intermediária (escondida) de neurônios radialmente simétricos. Tal neurônio converte a distância a partir de um vetor de entrada especificado ao seu centro correspondente por alguma lei não-linear geralmente considerada como sendo Gaussiana.

As redes RBF têm muitas vantagens sobre as redes de múltiplas camadas de alimentação direta. Primeiro de tudo, eles emulam (não tenho certeza sobre a palavra) uma função arbitrária não linear com apenas uma camada intermediária, o que poupa o desenvolvedor da necessidade de decidir sobre o número de camadas. Em seguida, os parâmetros na combinação linear na camada de saída podem ser otimizados com a ajuda de métodos amplamente conhecidos de otimização linear. E por último, trabalhar rápido e não ter dificuldades com os mínimos locais que interferem muito na retro-propagação. Essa é a razão por que a rede RBF aprende muito mais rápido do que quando se utiliza a retro-propagação

Desvantagens da RBF: essas redes têm características extrapolação fracas e acabam por ser complicadas quando o vetor de entrada é grande.

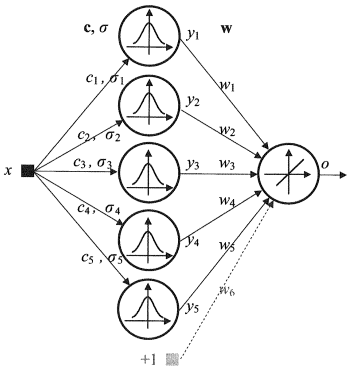
Fig. 4. Estrutura de uma RBF

1.2.5. Aprendizagem Dinâmica por Quantização Vetorial, Redes DLVQ são muito semelhantes aos mapas auto-organizáveis (SOM). Ao contrário de SOM, as redes DLVQ são capazes de um aprendizado supervisionado e de carecerem de uma relação de vizinhança entre os protótipos. O vector de quantização tem um uso mais amplo do que o de agrupamento.

1.2.6. Rede de Hopfield é uma rede totalmente conectada com uma matriz de conexão simétrica. Durante a operação, a dinâmica de tais redes convergem para um dos estados de equilíbrio. Estes estados de equilíbrio são mínimos locais do recurso conhecido como energia da rede. Tal rede pode ser usada como um sistema de memória associativa de conteúdo endereçável, como um filtro e para tratar alguns desafios de otimização.

Ao contrário de muitas redes neurais que trabalham até elas receberem uma resposta em um certo número de contatos, as redes de Hopfield trabalham até atingir o estado de equilíbrio que é quando o próximo estado de uma rede é exatamente o mesmo que a anterior. Neste caso, o estado inicial é um padrão de entrada e no estado de equilíbrio, o estado de saída é recebido. O treinamento de uma rede de Hopfield requer um padrão de treinamento a ser apresentado nas camadas de entrada e saída, simultaneamente.

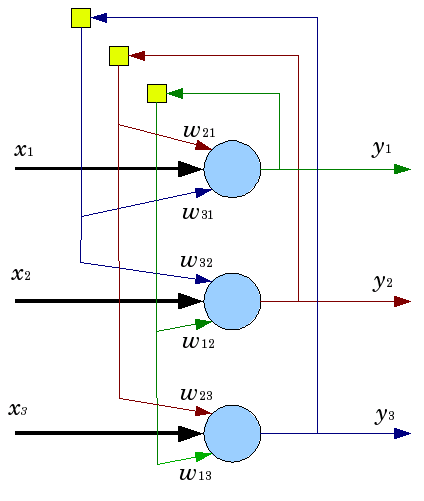
Fig. 5. Estrutura da rede de Hopfield com três neurônios

Apesar das características atraentes, uma rede de Hopfield clássica está longe de ser a ideal. Ela possui memória limitada, cerca de 15% do número de neurônios na rede N, enquanto que os sistemas de memória endereçada podem armazenar até 2N de imagens diferentes, utilizando N bits.

Além disso, as redes de Hopfield não são capazes de reconhecer se a imagem esta deslocada ou girada em relação à sua posição armazenada inicial. Estas e outras desvantagens definem a percepção de uma rede de Hopfield como um modelo teórico conveniente para estudo em vez de um instrumento prático para uso diário.

Muitos outros (rede recorrente de Hemming, rede de Grossberg, redes da teoria da ressonância adaptativa (ART-1, ART-2) etc) não foram mencionados neste artigo já que elas estão fora do âmbito de nosso interesse.

1.3. Métodos de Treinamento

A capacidade de aprender coisas novas é a principal característica de um cérebro humano. No caso de redes neurais artificiais, a aprendizagem é um processo de configuração de arquitetura de rede (a estrutura de conexões entre os neurônios) e dos pesos das ligações sinápticas (que afetam o coeficiente dos sinais) para obter uma solução eficaz para a tarefa em si. Normalmente a formação de uma rede neural é efetuada numa amostra de dados. O processo de formação segue um determinado algoritmo e com o passar do tempo, a reação de rede para os sinais de entrada devem melhorar.

Há três paradigmas principais de aprendizagem: supervisionada, não supervisionada e combinada. No primeiro caso, os acertos para cada exemplo de entrada são conhecidos e os pesos tentam minimizar o erro. A aprendizagem não supervisionada permite categorizar as amostras através da explicação da estrutura interna e da natureza dos dados. Na formação combinada ambas as abordagens acima são utilizadas.

1.3.1. Principais Regras da Aprendizagem da Rede Neural

Há quatro regras principais de aprendizagem baseadas na arquitetura de rede conectada com elas: correção de erros, a lei de Boltzmann, a regra de Hebb e o aprendizado competitivo.

1.3.1.1. Correção de Erros

Cada exemplo de entrada tem um valor de saída desejado especificado (valor objetivo), o qual pode incompatibilizar um valor real (previsão). A regra de aprendizagem da correção de erro se faz usando a diferença entre os valores objetivo e de previsão para ajuste direto dos pesos a fim de diminuir o erro. O treinamento é realizado somente no caso de um resultado erróneo. Esta regra de aprendizagem tem inúmeras modificações.

1.3.1.2. Regra de Boltzmann

A regra de Boltzmann é uma regra estocástica de aprendizagem por analogia com os princípios termodinâmicos. Isso resulta em coeficientes de peso dos neurônios ajustados de acordo com a distribuição probabilística desejada. Aprender a regra de Boltzmann pode ser considerado como um caso isolado de correção de um erro onde este signifique uma discrepância na correlação dos estados de dois modos.

1.3.1.3. Regra de Hebb

A regra de Hebb é o algoritmo de aprendizagem mais famoso das redes neurais. A ideia deste método é que se os neurônios de ambos os lados de uma sinapse ativarem simultaneamente e regularmente, então, a força dessa ligação sináptica aumenta. Uma particularidade importante aqui é que a mudança do peso sináptico depende apenas da atividade dos neurônios ligados a esta sinapse. Existem muitas variações a esta regra, que diferem em peculiaridades a modificação do peso da sinapse.

1.3.1.4. Aprendizagem Competitiva

Ao contrário da regra de aprendizagem de Hebb, onde um número de neurônios de saída pode ativar simultaneamente, aqui os neurônios de saída competem uns contra os outros. Um neurônio de saída com o valor máximo da soma dos pesos é o "vencedor" e "o vencedor leva tudo". As saídas de outros neurônios de saída são definidas para inativo. No aprendizado, apenas os pesos do "vencedor" será modificado, visando o aumento da proximidade com a instância de entrada atual.

Há uma série de algoritmos que abordam os diferentes problemas de aprendizagem. A retro-propagação, um dos algoritmos modernos mais eficientes, é um deles. O princípio por trás disso é que a mudança de peso sináptico acontece em consideração ao gradiente local da função de erro.

A diferença entre as respostas corretas e reais de uma rede neural avaliada na camada de saída é propagada de volta - para o fluxo de sinais (Fig.5). Desta forma, cada neurônio pode definir a contribuição do seu peso para o erro cumulativo da rede. A regra de aprendizagem mais simples é o método de descida mais íngreme, que é a mudança de peso sináptico proporcionalmente à sua contribuição para o erro cumulativo.

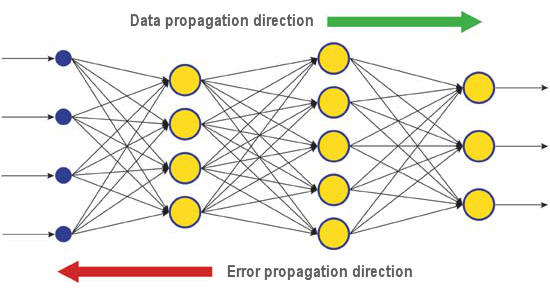
Fig. 6. O padrão de dados e difusão do erro em uma rede quando a aprendizagem é feita através da retro-propagação

Certamente, este tipo de aprendizagem em rede neural não garante o melhor resultado de aprendizagem já que há sempre uma possibilidade de que o algoritmo entre em um mínimo local. Existem técnicas especiais que permitem obter a solução encontrada a partir de um ponto extremo local. Se depois de algumas aplicações desta técnica, a rede neural tem a mesma decisão, então pode-se concluir que a solução encontrada é mais provável de ser a ideal.

1.4. Desvantagens

A principal dificuldade do uso de redes neurais é a chamada "maldição da dimensionalidade". Quando as dimensões de entrada e o número de camadas são aumentados, a complexidade da rede e o tempo de aprendizagem estão crescendo exponencialmente e o resultado recebido nem sempre é o ideal.
Outra dificuldade do uso de redes neurais é que as tradicionais são incapazes de explicar como elas estão resolvendo as tarefas. Em alguns campos de aplicação como medicamento esta explicação é mais importante do que o próprio resultado. A representação do resultado interno é muitas vezes tão complexa que é impossível analisar, exceto os casos mais simples que normalmente não são de nenhum interesse.

2. Aprendizagem Profunda

Hoje a teoria e a prática do aprendizado de máquina está passando por uma "revolução profunda", causada pela implementação bem sucedida dos métodos de aprendizagem profundos, representando as redes neurais de terceira geração. Ao contrário das redes clássicas de segunda geração utilizadas nos anos 80-90 do século passado, os novos paradigmas de aprendizagem resolveram uma série de problemas que limitavam a expansão e a implementação bem sucedida das redes neurais tradicionais.

Redes treinadas com algoritmos de aprendizagem profundos não se destacam apenas pelos melhores métodos alternativos em precisão, mas em alguns casos revelaram rudimentos sobre a compreensão dos sentidos da informação de entrada. O reconhecimento de imagem e análise de informações de texto são os exemplos mais brilhantes.

Hoje, os métodos industriais mais avançados da visão computacional e de reconhecimento de voz são baseados em redes profundas. Gigantes da indústria de TI como Apple, Google, Facebook estão empregando pesquisadores em desenvolvimento de redes neurais profundas.

2.1. Contexto

Uma equipe de estudantes de pós-graduação da Universidade de Toronto liderada pelo professor Geoffrey E. Hinton ganhou o primeiro prêmio em um concurso patrocinado pela Merck. Usando um conjunto limitado de dados, que descreve a estrutura química de 15 moléculas, o grupo de G. Hinton conseguiu criar e aplicar um sistema especial que define quais dessas moléculas tinha mais chande de ser um medicamento eficaz.

A peculiaridade desse trabalho foi que os desenvolvedores usaram uma rede neural artificial baseada na aprendizagem profunda. Como resultado, esse sistema conseguiu realizar cálculos e pesquisas com base em um conjunto muito limitado de dados de origem, considerando que o treinamento de uma rede neural normalmente requer uma quantidade significativa de informações colocadas no sistema.

O resultado da equipe de Hinton foi particularmente impressionante porque a equipe decidiu entrar no concurso no último minuto. Acrescentando isto, o sistema de aprendizagem profunda foi desenvolvido sem o conhecimento específico sobre como as moléculas se ligam aos seus objetivos. A implementação bem sucedida de uma aprendizagem mais profunda foi mais uma conquista no desenvolvimento da inteligência artificial no ano de 2012.

Então, no verão de 2012, Jeff Dean e Andrew Y. Ng da Google apresentou um novo sistema de reconhecimento de imagem com taxa de precisão de 15,8%, onde para treinar um sistema de cluster de 16.000 nós eles usaram a rede IMAGEnet contendo uma biblioteca de 14 milhões de fotos de 20.000 objetos diferentes. No ano passado, um programa criado por cientistas suíços superou um ser humano no reconhecimento de imagens de sinais de trânsito. O programa vencedor identificou com precisão 99.46% das imagens em um conjunto de 50.000; a pontuação máxima em um grupo de 32 participantes humanos foi de 99.22% e a média para os seres humanos era de 98.84%. Em outubro de 2012, Richard F. Rashid, um coordenador de programas científicos da Microsoft apresentou em uma conferência em Tianjin, China uma tecnologia de tradução simultânea do Inglês para Mandarim acompanhado por uma simulação de sua própria voz.

Todas estas tecnologias que demonstram um avanço no domínio da inteligência artificial são baseados no método de aprendizagem profunda, até certo ponto. A principal contribuição para a teoria da aprendizagem profunda está sendo feita pelo professor Hinton, o tataraneto de George Boole, um cientista Inglês, fundador dos computadores contemporâneos subjacentes a álgebra de Boole.

Os métodos comuns da teoria de aprendizagem profunda da aprendizagem de máquina com algoritmos especiais para a análise de informações de entrada a vários níveis de apresentação. A peculiaridade da nova abordagem é que o aprendizado profundo estuda o assunto até que ele encontre suficientes níveis de cunho informativo para dar conta de todos os fatores que podem influenciar os parâmetros do objeto em questão.

Desta forma, uma rede neural com base em tal abordagem requer menos informações de entrada para a aprendizagem e uma rede treinada é capaz de analisar as informações com um maior nível de precisão do que as redes neurais habituais. O professor Hinton e seus colegas afirmam que sua tecnologia é especialmente boa para a busca de peculiaridades em matrizes de informações multi-dimensionais bem estruturadas.

As tecnologias de inteligência artificial (IA), em particular o aprendizado profundo, são amplamente utilizados em diferentes sistemas, incluindo o assistente pessoal inteligente Apple Siri com base nas tecnologias da Nuance Communications e no reconhecimento de endereços no Google Street View. No entanto, os cientistas estão estimando o sucesso nesta esfera com muito cuidado ja que a história da criação de uma inteligência artificial está cheio de promessas otimistas e decepções.

Na década de 1960, os cientistas acreditavam que seria necessário apenas 10 anos para criar uma inteligência artificial inteiramente caracterizada. Então, na década de 1980, houve uma onda de jovens empresas oferecendo uma "inteligência artificial pronta", seguido pela "era do gelo" nesta esfera, que durou até recentemente. Hoje amplas capacidades computacionais disponíveis em serviços de nuvem fornecer um novo nível de implementação da poderosa rede neural, usando uma nova base teórica e algorítmica.

Deve-se notar que as redes neurais, mesmo as de terceira geração, como as redes neurais convolucionais, auto-associadores, máquinas de Boltzmann, nada têm em comum com os neurônios biológicos, exceto o nome.

O novo paradigma de aprendizagem implementa a idéia de aprendizagem em duas etapas. Na primeira fase, a informação sobre a estrutura interna dos dados de entrada é extraída a partir de uma grande variedade de dados não formatados com auto associadora através de um treinamento camada-por-camada não supervisionado. Em seguida, usando esta informação em uma rede neural multi-camada, ele passa por treinamento supervisionado pelos métodos conhecidos que utilizam dados formatados. Ao mesmo tempo, a quantidade de dados não formatados deve ser tão grande quanto possível. Dados formatados pode ser muito menor em tamanho. No nosso caso, não é de importância imediata.

2.2. Autoencoders. Autoencoder e Máquinas de Boltzmann Restritas. Diferenças e peculiaridades

2.2.1. Autoencoder

O primeiro auto-associador (АА) foi um Neocognitron Fukushima.

A sua estrutura é apresentada na Fig.7.

Fig. 7. O Neocognitron Fukushima

A finalidade de um auto-associador (АА) é para receber na saída a imagem mais precisa da entrada quanto possível.

Existem dois tipos de АА - geradoras e sintetizadoras. Uma máquina de Boltzmann restrita pertence ao primeiro tipo e um autoencoder representa o segundo tipo.

Um autoencoder é uma rede neural com uma camada aberta. Usando o algoritmo de aprendizado não supervisionado e a retro-propagação, ele define um valor objetivo igual ao vetor de entrada, ou seja, y = x.

Um exemplo de um autoencoder é apresentado na Fig.8.

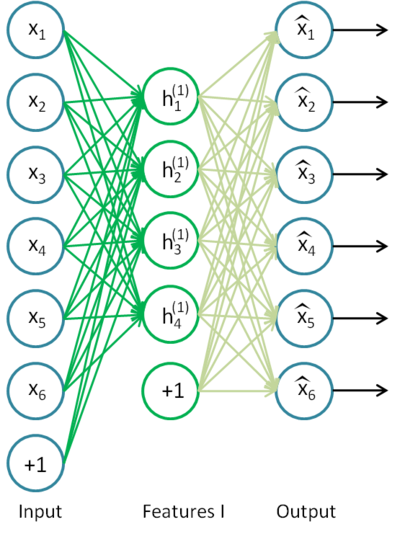
Fig. 8. A estrutura de um autoencoder

O autoencoder está tentando construir a função h(x) = x. Em outras palavras, ele tenta encontrar uma aproximação de uma função, assegurando que um feedback da rede neural é aproximadamente igual aos valores dos parâmetros de entrada. Para a solução do problema ser não-trivial, o número de neurônios na camada aberta deve ser menor do que a dimensão dos dados de entrada (como na imagem).

Ele permite a compressão de dados, quando o sinal de entrada é passado para a saída da rede. Por exemplo, se o vetor de entrada é um conjunto de níveis de brilho de uma imagem de 10х10 pixels de tamanho (100 características), o número de neurônios da camada oculta é de 50, a rede é forçada a aprender a comprimir a imagem. O requisito h(x) = x significa que, com base nos níveis de ativação dos cinquenta neurônios da camada oculta, a camada de saída é para restaurar 100 pixels da imagem inicial. Essa compressão é possível se existirem interconexões ocultas, correlação característica ou qualquer estrutura. Desta forma, uma operação autoencoder lembra o método de Análise de Componentes Principais (PCA) no sentido de que os dados de entrada ficam reduzida.

Surpreendentemente, as experiências conduzidas pelo Bengio et Al. (2007), mostraram que quando o treinamento com um descente gradiente estocástico, as redes autoencoder não-linear com o número de neurônios escondidos maiores do que o número de entradas (também chamado "superabundante") tinha apresentação útil, tendo em conta o erro de conformidade da rede que tomou essa apresentação a partir da entrada.

Mais tarde, quando a idéia de dispersão apareceu, um autoencoder escasso era amplamente utilizado.

O autoencoder esparso é um autoencoder que tem um número de neurônios escondidos significativamente maior do que a dimensão de entrada, mas que têm uma ativação escassa. A ativação esparsa ocorre quando número de neurônios inativos na camada oculta é significativamente maior do que o número de ativos. Se nós descrevermos a espacialidade informalmente, então, um neurônio pode ser considerado ativa se o valor da sua função é próximo de 1. Se uma função sigmóide está em uso, então, o valor do neurônio inativo deve ser perto de 0 (para a função da tangente hiperbólica o valor deve ser perto de -1).

Existe uma variação de um autoencoder chamado de denoising autoencoder (Vincent et al., 2008). Este é o mesmo autoencoder mas o seu treinamento tem algumas peculiaridades. Ao treinar esta rede, os dados "corrompidos" são de entrada (alguns valores são substituídos por 0). Ao mesmo tempo, há dados "corretos" para comparar com os dados de saída. Desta forma, um autoencoder pode restaurar os dados danificados.

2.2.2. Máquina de Boltzmann Restrita, RBM.

Nós não vamos centrar sobre a história de uma máquina de Boltzmann restrita (RBM). Tudo o que precisamos saber é que ele começou com as redes neurais recorrentes com um feedback que eram muito difícil de se treinar. Devido a esta dificuldade de aprendizagem, mais modelos recurrentes restritos apareceram, assim, algoritmos de aprendizagem de modo mais simples puderam ser aplicados. Uma rede neural de Hopfield era um desses tais modelos. John Hopfield foi a pessoa que introduziu o conceito da energia de rede, sendo comparada a dinâmica das redes neurais com a termodinâmica.

O próximo passo no caminho para uma RBM foram as máquinas regulares de Boltzmann. Elas diferem de uma rede de Hopfield por ter natureza estocástica e seus neurônios são divididos em dois grupos que descrevem estados visíveis e ocultos (semelhante a um modelo oculto de Markov). Uma máquina de Boltzmann restrita é diferente de uma regular na ausência de conexões entre os neurônios de uma camada.

Figo. 9 representa uma estrutura RBM.

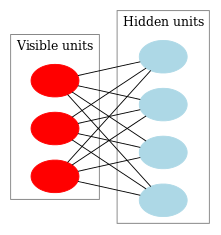
Fig. 9. Uma estrutura RBM

A peculiaridade deste modelo é que nos atuais estados de neurônios de um grupo, os estados de neurônios de um outro grupo vão ser independentes um do outro. Agora nós podemos passar para alguma teoria em que essa propriedade tem o papel fundamental.

Interpretação e objetivo

Uma RBM é interpretada semelhante a um modelo oculto de Markov. Temos um número de estados que podemos observar (neurônios visíveis) e um número de estados ocultos que não podemos ver diretamente (neurônios ocultos). Nós podemos chegar a uma conclusão baseada na probabilidade sobre os estados ocultos que confiam nos estados que podemos observar. Depois que tal modelo foi treinado, nós temos uma oportunidade para tirar conclusões sobre os estados visíveis sabendo que as ocultas estão seguindo o teorema de Bayes. Isso permite gerar dados a partir da distribuição da probabilidade usada para treinar o modelo.

Dessa forma, podemos formular o objetivo de treinamento de um modelo: os parâmetros do modelo devem ser ajustadas de maneira que o vetor restaurado a partir do estado inicial seja mais próximo que o original. Um vetor restaurado é um vetor recebido por uma inferência probabilística de estados ocultos, os quais, por sua vez, foram recebidos por uma inferência probabilística de estados visíveis, ou seja, a partir do vetor original.

Algoritmo de aprendizagem Divergência Comparativa CD-k

Este algoritmo foi inventado pelo professor Hinton em 2002 e é extremamente simples. A idéia principal é que os valores de expectativa matemática são substituídos por valores definidos. A noção do processo de amostragem de Gibbs.

O CD-k se parece com:

O estado dos neurônios visíveis é definido como sendo igual ao padrão de entrada;
As probabilidades dos estados das camadas ocultas são desenhadas;
Cada neurônio da camada escondida é atribuído o estado "1" com probabilidade igual ao seu estado atual;
Probabilidades dos estados de camadas visíveis são desenhados com base na camada oculta;
Se a iteração atual é menor do que k, então, retorna para a etapa 2;
As probabilidades dos estados das camadas ocultas são desenhadas;

Nas palestras de Hinton, ela se parece com:

Fig.10. Algoritmo de aprendizagem de CD-k

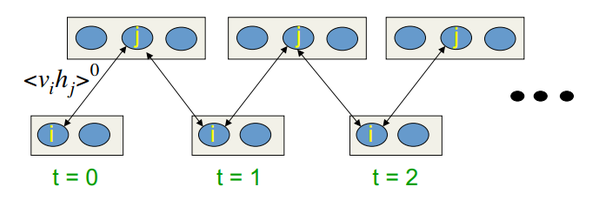
Fig. 10. Algoritmo de aprendizagem de CD-k

Em outras palavras, quanto maior o tempo que nós fazemos amostragem, mais preciso será o gradiente. O professor afirma que o resultado recebido para CD-1, ou seja, apenas uma iteração de amostragem, já está bom.

2.3. Redes Auto-Associativas empilhadas. Autoencoder Empilhado SAE, Máquina de Boltzmann Restrita Empilhada (Stacked RBM)

Para a extração de abstrações de alto nível a partir do conjunto de dados de entrada, auto-associadores são combinados em uma rede.

Fig. 11 representa uma estrutura do stackеd autoencoder e uma rede neural, que em conjunto representam uma rede neural profunda com pesos inicializados por um autoencoder empilhado

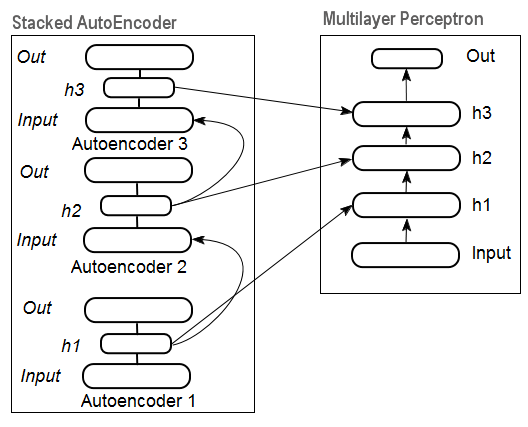
Fig. 11. Estrutura de uma DN SAE

Na Fig.12 existe um padrão de um RBM empilhado (SRBM) e uma rede neural, que em conjunto representam uma rede neural profunda com pesos inicializados por SRBM.

Estas ilustrações das estruturas de rede profundas enfatizam o fato de que a informação é extraída de baixo para cima.

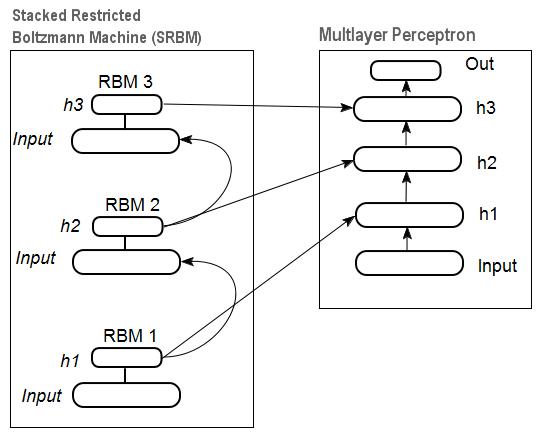
Fig. 12. Estrutura de uma DN SRBM

2.4. Treinamento das Redes Profundas (DN). Etapas. Peculiaridades

O treinando de redes profundas compreende de duas fases. Na primeira etapa, uma rede auto-associador (SAE ou SRBM, dependendo do tipo DN) recebe treinamento supervisionado em uma matriz de dados não formatado. Depois disso, os neurônios da camada oculta da MLP ordinária são inicializados pelos pesos das camadas ocultas recebidas após o treinamento. Fig. 11 e fig. 12 representam um padrão de processos de aprendizagem e de transferência. Após a formação do primeiro АЕ/RBM, os pesos dos neurônios da camada oculta torna-se entradas da segunda etc. Desta forma, a generalização da informação sobre a estrutura (linha, contorno, patter etc) é extraído dos dados.

A segunda etapa é o tempo para o ajuste fino do MLP (estágio supervisionado) no conjunto de dados formatado usando os métodos bem conhecidos. A prática provou que tais conjuntos de inicialização definem os pesos das camadas dos neurônios escondidos da MLP para o mínimo global e o seguinte ajuste fino toma um tempo muito curto.

Além disso, para as redes profundas com o número de camadas superiores a três, D. Hinton sugeriu que um ajuste fino deve ser realizado em duas etapas. Na primeira fase, apenas duas camadas superiores devem ser treinadas e na segunda o resto da rede.

Deve ser mencionado que uma SRBM tem resultados menos estáveis de treinamento sem a supervisão de um SAE.

Nota. Muitas vezes estes termos são confusos. Um SRBM é identificado com uma rede DBN de crença profunda. Apesar do fato de um RBM ser derivado de DBN, estas estruturas são totalmente diferentes. A DBN é uma rede neural de multi-camadas, com os pesos do neurônio de camadas ocultas inicializados aleatoriamente por padrões binários.

3. Experimentos Práticos

As redes profundas serão executadas em R.

3.1. A linguagem R

História. R é uma linguagem de programação e um ambiente para cálculos estatísticos e gráficos, desenvolvido em 1996 por Ross Ihaka e Robert Gentleman, dois cientistas da Nova Zelândia, na Universidade Aokland.

R é um projeto GNU, que é um software livre e sua filosofia vai segue os seguintes princípios:

liberdade para lançar programas para qualquer fim (liberdade 0);
liberdade de aprender como um programa funciona e adaptá-lo para as necessidades próprias (liberdade 1);
liberdade de distribuir cópias para ajudar os outros (liberdade 2);
liberdade para melhorar o programa e deixar a sociedade se beneficiar dessas melhorias.

Na perspectiva histórica, R é uma alternativa para a implementação de S. Este último foi desenvolvido por John Chambers e seus colegas na empresa Bell Labs em 1976. Hoje, R ainda está sendo melhorado pela R Development Core Team, incluindo John Chambers.

Para repetir experimentos, você vai precisar instalar R e Rstudio. Informações sobre onde fazer o download e como pode ser encontrado na internet. Se houver alguma dúvida, podemos discuti-las nos comentários do artigo.

Vantagens de R:

Hoje R é o padrão para cálculos estatísticos.
Ele está sendo desenvolvido e suportado pela comunidade científica global de universidades.
O conjunto amplo de pacotes para todos os campos avançados de mineração de dados. O tempo entre a publicação da ideia e a sua implementação no pacote de R é geralmente não maior que 2 semanas.
E por último mas não menos importante, ele é absolutamente livre. Um famoso desenvolvedor de um sistema operacional livre, disse uma vez: "Os programas são como o sexo - é melhor quando é livre".

3.2. Formas de Implementação e Temas Abordados

Existem duas formas possíveis de implementação.

O primeiro envolve o uso de programas únicos por John Hinton para Matlab. Para isso, o "R.matlab" é exigido. Este pacote tem os métodos writeMat() e readMat() para ler e gravar os arquivos MAT. Ele permite a comunicação (implementação de código, envio e recebimento de objetos etc) do Matlab v6 ou superior, iniciado localmente ou no link do host remoto cliente-servidor. Detalhes podem ser encontrados na descrição do pacote. Este é o caminho para aqueles que estão confortáveis com a utilização do Matlab. Eu não tentei usar este método, mas existe a possibilidade de vincular o Matlab e a MQL desta forma.

A segunda forma de execução é usar os pacotes R sobre este tema. Nós vamos explorá-lo.

Há três pacotes que eu conheço que estão conectados com o tema deste artigo:

"deepnet" é um pacote simples que implementa os modelos DN SAE e DN SRBM. O comprimento do conjunto de dados de entrada na aprendizagem supervisionada e na não supervisionada é o mesmo. Não dá uma oportunidade para realizar o ajuste fino do sistema em duas etapas. Usado para a exploração e experimentação de modelos no início.
"darh" é um pacote avançado e abrangente para a modelagem DN SRBM. Há um modelo para DN SAE mas eu não consegui iniciá-lo. Este pacote é para usuários experientes, permite criar e ajustar um modelo de qualquer nível de complexidade. Ele baseia-se nos programas únicos por Hinton na linguagem m para Matlab.
"H2O" é um pacote extensivo para a formação de redes profundas (não só eles) em grandes conjuntos de dados (>1 1 Гб) escrito em arquivos CSV.

Nas experiências abaixo, vamos usar o pacote "deepnet".

3.3. Preparando os Dados de Entrada e de Destino para o Experimento

A mineração de dados hoje tem uma certa ordem de trabalho:

Seleção de dados de entrada (estudo, análise, preparação preliminar, avaliação). Quebrando os dados para o treinamento, validação e teste de conjuntos (amostras);
Treinamento de um modelo sobre o conjunto de dados de treinamento e seleção de um modelo(s) sobre aquele de validação.;
Avaliação da qualidade do modelo(s) na amostra de teste e definir os parâmetros ótimos do modelo ou o melhor modelo do conjunto através de determinadas medidas;
Deixar o modelo(s) iniciar o trabalho.

A primeira fase é a mais demorada e ela é muito importante para o resultado final. Para ser justo, esta fase não é formalizada e em geral ela é quase uma forma de arte. Depende muito da experiência do investigador. Porém! A obtenção de avaliações quantitativas dos dados de entrada estabelecidos para selecionar os mais importantes é muito importante. A seleção automática das melhores variáveis para um determinado modelo é ainda melhor neste caso. R fornece uma ampla funcionalidade para enfrentar os desafios em todas as fases.

A fonte de dados não só é muito importante, mas também tem uma série de aspectos a considerar. Ela merece um artigo separado. Como o objetivo deste artigo é para contar sobre uma coisa complexa em palavras muito simples, vamos discutir pontos importantes, mas não vou entrar em muitos detalhes.

3.3.1. Dados Iniciais

Para a nossa classificação, precisamos de um conjunto de (entrada) variáveis independentes e uma variável objetivo. Uma vez que a principal vantagem acentuada das redes profundas é a sua capacidade de aprender rapidamente em grandes amostras de entrada, vamos criar um conjunto de dados de entrada que compreende 17 preditores (11 indicadores). O ZigZag tem um papel da variável objetivo. Baixe no ambiente R os vetores de Abertura, Máxima, Mínima, Fechamento das cotações das 4000 barras profundas. A maneira de fazer isso é discutido abaixo na descrição de escrever um indicador. Nesta fase, não é importante. Todos os outros cálculos serão realizados em R.

Construir uma matriz de 4 vetores, preço médio e o tamanho do corpo da barra. Transformando isto em uma função:

pr.OHLC <- function (o, h, l, c) 
{
  #Vetores de cotações em uma matriz sendo anteriormente expandida
  #Indexação das séries temporais dos vetores em R começa com 1. 
  #Direção de indexação é do velho para o novo.   
  price <- cbind(Open = rev(o), High = rev(h), Low = rev(l), Close = rev(c))
  Med <- (price[, 2] + price[, 3])/2
  CO <- price[, 4] - price[, 1]
  #Adiciona Med e CO para a matriz
  price <- cbind(price, Med, CO)
}

Veja o resultado (estado em 08.10.14 12:00)

> head(price)
        Open    High     Low   Close      Med     CO
[1,] 1.33848 1.33851 1.33824 1.33844 1.338375 -4e-05
[2,] 1.33843 1.33868 1.33842 1.33851 1.338550  8e-05
[3,] 1.33849 1.33862 1.33846 1.33859 1.338540  1e-04
[4,] 1.33858 1.33861 1.33856 1.33859 1.338585  1e-05
[5,] 1.33862 1.33868 1.33855 1.33855 1.338615 -7e-05
[6,] 1.33853 1.33856 1.33846 1.33855 1.338510  2e-05

3.3.2. Dados de entrada (Preditores)

Lista dos indicadores. Os indicadores foram selecionados aleatoriamente, sem preferências para ganhar a diferença máxima dos tamanhos de entrada.

O cálculo de todos os indicadores é realizada utilizando o pacote "TTR" que contém vários indicadores.

3.3.2.1. Índice de Movimento Direcional de Welles Wilder - ADX(HLC, n) - 4 saídas (Dip, Din,DX, ADX)

Calcula e vê o que se parece nas primeiras 200 barras:

> library(TTR)
> adx<-ADX(price, n = 16)
> plot.ts(head(adx, 200))

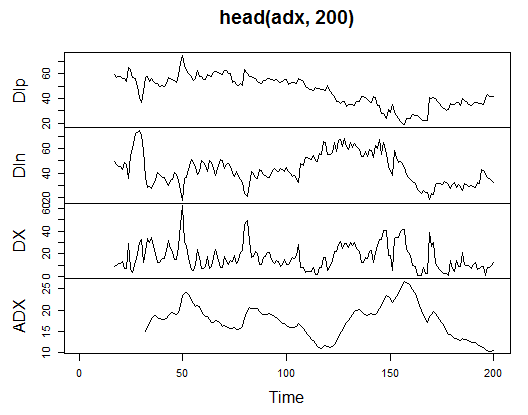
Fig. 13. Indicador Índice de Movimento Direcional de Welles Wilder - ADX(HLC, n)

> summary(adx)
      DIp             DIn                DX                 ADX    
 Min.   :15.90   Min.   :  5.468   Min.   : 0.00831      Min.   : 5.482   
 1st Qu.:41.21   1st Qu.: 33.599   1st Qu.: 8.05849      1st Qu.:14.046 
 Median :47.36   Median : 43.216   Median :16.95423      Median :18.099
 Mean   :47.14   Mean   : 46.170   Mean   :19.73032      Mean   :19.609 
 3rd Qu.:53.31   3rd Qu.: 55.315   3rd Qu.:27.97471      3rd Qu.:23.961     
 Max.   :80.12   Max.   :199.251   Max.   :81.08751      Max.   :52.413
 NA's   :16      NA's   :16        NA's   :16            NA's   :31

No início da matriz existem 31 valores indefinidos (NA). Em seguida, execute os mesmos cálculos para todos os indicadores, sem explicações detalhadas.

3.3.2.2. aroon(HL, n) - 1 out (oscilador)

Calcula e vê as primeiras 200 barras de apenas uma variável do "oscilador"

> ar<-aroon(price[ , c('High', 'Low')], n = 16)[ ,'oscillator']
> plot(head(ar, 200), t = "l")
> abline(h = 0)

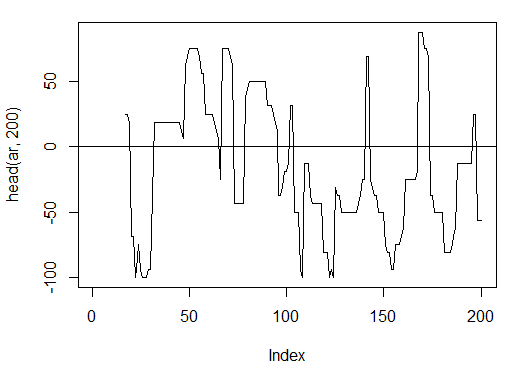
Fig. 14. Indicador aroon(HL, n)

> summary(ar)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
-100.00  -56.25  -18.75   -7.67   43.75  100.00      16

3.3.2.3. Índice de Canal de Commodities - CCI(HLC, n) - 1 saída

> cci<-CCI(price[ ,2:4], n = 16)
> plot.ts(head(cci, 200))
> abline(h = 0)

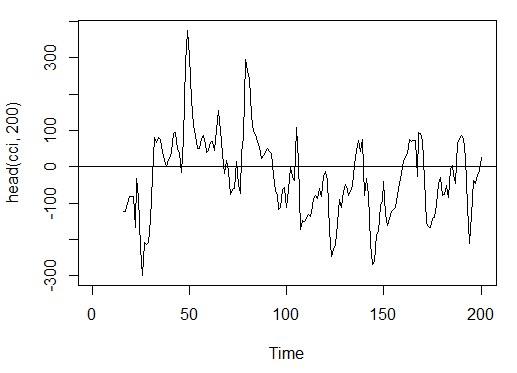
Fig. 15. Indicador Índice de Canal de Commodities - CCI(HLC, n)

> summary(cci)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
-469.10  -90.95  -18.74  -14.03   66.91  388.20      15

3.3.2.4. Volatilidade de Chaikin - chaikinVolatility (HLC, n) - 1 saída

> chv<-chaikinVolatility(price[ , 2:4], n = 16)
> summary(chv)
    Min.  1st Qu.   Median     Mean  3rd Qu.     Max.     NA's 
-0.67570 -0.29940  0.02085  0.12890  0.41580  5.15700       31 
> plot(head(chv, 200), t = "l")
> abline(h = 0)

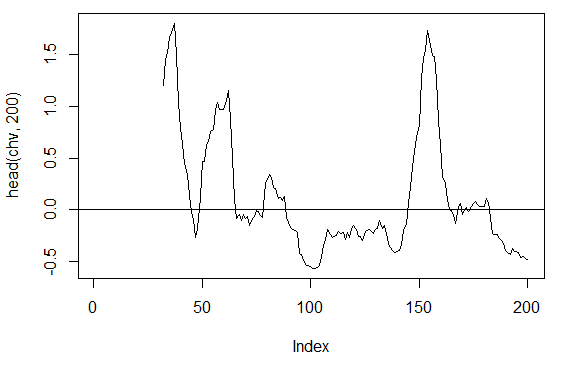
Fig. 16. Indicador chaikinVolatility (HLC, n)

3.3.2.5. Oscilador Momento de Chande - CMO(Med, n) - 1 saída

> cmo<-CMO(price[ ,'Med'], n = 16)
> plot(head(cmo, 200), t = "l")
> abline(h = 0)

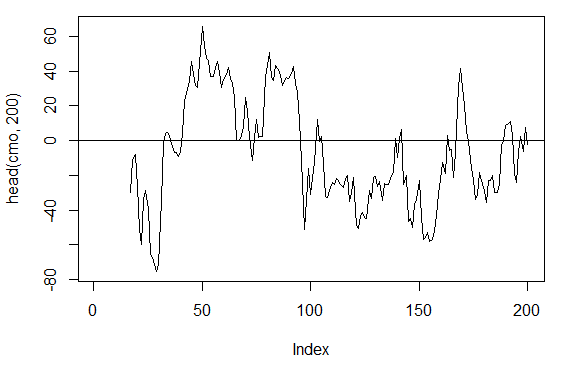
Fig. 17. Indicador Oscilador Momento de Chande - CMO(Med, n)

> summary(cmo)
   Min.    1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
-97.670 -32.650  -5.400  -6.075  19.530  93.080      16

3.3.2.6. Oscilador MACD - MACD(Med, nFast, nSlow, nSig) 1 saída é usada (macd)

> macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd']
> plot(head(macd, 200), t = "l")
> abline(h = 0)

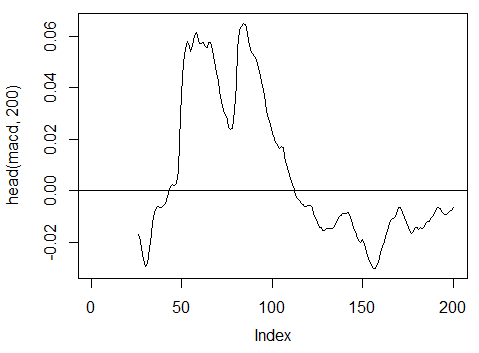
Fig. 18. Indicador Oscilador MACD

> summary(macd)
     Min.   1st Qu.    Median      Mean   3rd Qu.      Max.      NA's
-0.346900 -0.025150 -0.005716 -0.011370  0.013790  0.088880      25

3.3.2.7. OsMA(Med,nFast, nSlow, nSig) – 1 saída

> osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal']
> plot(head(osma, 200), t = "l")
> abline(h = 0)

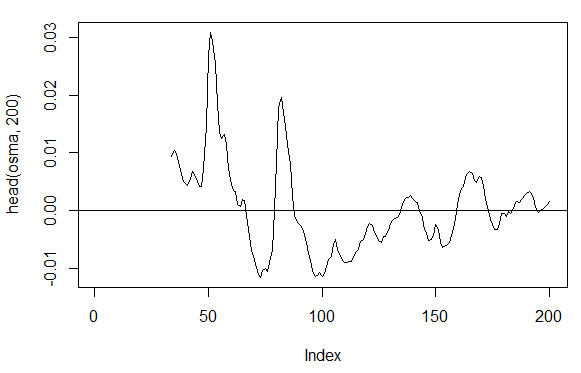
Fig. 19. Indicador OsMA(Med,nFast, nSlow, nSig)

> summary(osma)
    Min.  1st Qu.   Median     Mean  3rd Qu.     Max.     NA's 
-0.10560 -0.00526  0.00034  0.00007  0.00646  0.05922       33

3.3.2.8. Índice de Força Relativa - RSI(Med, n) - 1 saída

> rsi<-RSI(price[ ,'Med'], n = 16)
> plot(head(rsi, 200), t = "l")
> abline(h = 50)

Fig. 20. Indicador Índice de Força Relativa - RSI(Med, n)

> summary(rsi)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
   5.32   37.33   47.15   46.53   55.71   84.82      16

3.3.2.9. Oscilador Estocástico - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3) - 3 saídas

> stoh<-stoch(price[ ,2:4], 14, 3, 3)
> plot.ts(head(stoh, 200))

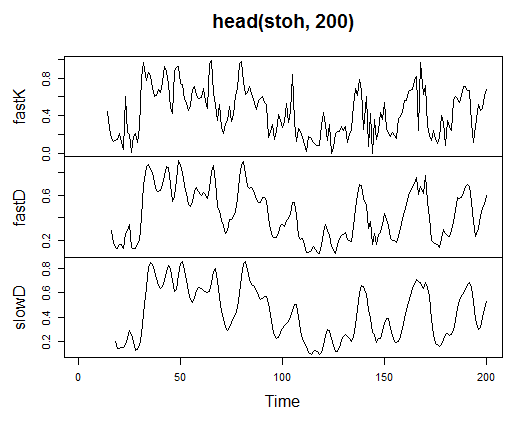
Fig. 21. Indicador Oscilador Estocástico - stoch(HLC, nFastK=14, nFastD=3, nSlowD=3)

> summary(stoh)
     fastK            fastD             slowD        
 Min.   :0.0000   Min.   :0.01782   Min.   :0.02388  
 1st Qu.:0.2250   1st Qu.:0.23948   1st Qu.:0.24873  
 Median :0.4450   Median :0.44205   Median :0.44113  
 Mean   :0.4622   Mean   :0.46212   Mean   :0.46207  
 3rd Qu.:0.6842   3rd Qu.:0.67088   3rd Qu.:0.66709  
 Max.   :1.0000   Max.   :0.99074   Max.   :0.97626  
 NA's   :13       NA's   :15        NA's   :17

3.3.2.10. Índice Momento Estocástico - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9) - 2 saídas

> smi<-SMI(price[ ,2:4],n = 13, nFast = 2, nSlow = 25, nSig = 9)
> plot.ts(head(smi, 200))

Fig. 22. Indicador Índice de Momento Estocástico - SMI(HLC, n = 13, nFast = 2, nSlow = 25, nSig = 9)

> summary(smi)
      SMI              signal       
 Min.   :-82.185   Min.   :-78.470  
 1st Qu.:-33.392   1st Qu.:-31.307  
 Median : -9.320   Median : -8.839  
 Mean   : -8.942   Mean   : -8.985  
 3rd Qu.: 15.664   3rd Qu.: 14.069  
 Max.   : 71.878   Max.   : 63.865  
 NA's   :25        NA's   :33

3.3.2.11. Volatility (Yang e Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)- 1 saída

> vol<-volatility(price[ ,1:4],n = 16,calc = "yang.zhang", N =96)
> plot.ts(head(vol, 200))

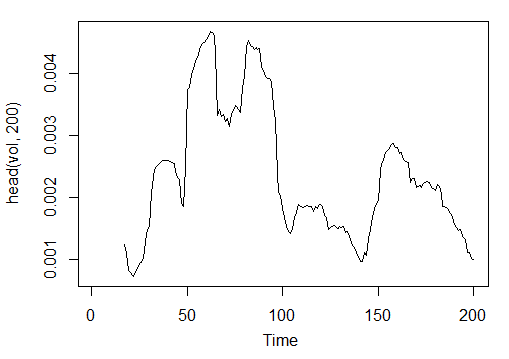
Fig. 23. Indicador Volatility (Yang e Zhang) - volatility(OHLC, n, calc="yang.zhang", N=96)

> summary(vol)
    Min.  1st Qu.   Median     Mean  3rd Qu.     Max.      NA's
0.000599 0.001858 0.002638 0.003127 0.004015 0.012840      16

Portanto, nós temos 17 variáveis de 11 indicadores para o EURUSD no período М15 para a amostra OHLC de 4000 barras de profundidade.

Use-os para formar uma matriz e escrever os parâmetros acima em uma função com um parâmetro formal р, que será necessário para a otimização.

Calcula-se a matriz dos parâmetros de entrada utilizando a fórmula:

In<-function(p = 16){
  adx<-ADX(price, n = p);
  ar<-aroon(price[ ,c('High', 'Low')], n=p)[ ,'oscillator'];
  cci<-CCI(price[ ,2:4], n = p);
  chv<-chaikinVolatility(price[ ,2:4], n = p);
  cmo<-CMO(price[ ,'Med'], n = p);
  macd<-MACD(price[ ,'Med'], 12, 26, 9)[ ,'macd'];
  osma<-macd - MACD(price[ ,'Med'],12, 26, 9)[ ,'signal'];
  rsi<-RSI(price[ ,'Med'], n = p);
  stoh<-stoch(price[ ,2:4],14, 3, 3);
  smi<-SMI(price[ ,2:4],n = p, nFast = 2, nSlow = 25, nSig = 9);
  vol<-volatility(price[ ,1:4],n = p,calc="yang.zhang", N=96);
  In<-cbind(adx, ar, cci, chv, cmo, macd, osma, rsi, stoh, smi, vol);
  return(In)
}

> X<-In()
> tail(X)
             DIp      DIn       DX      ADX   ar      cci       chv
[3995,] 46.49620 36.32411 12.28212 18.17544 25.0 168.0407 0.1835102
[3996,] 52.99009 31.61164 25.26952 18.61882 37.5 227.7030 0.3189822
[3997,] 58.11948 28.16241 34.72000 19.62515 37.5 145.2337 0.3448520
[3998,] 56.00323 30.48687 29.50206 20.24245 37.5 118.5831 0.3068059
[3999,] 55.96197 28.78737 32.06467 20.98134 37.5 116.5376 0.3517668
[4000,] 54.97777 26.85440 34.36713 21.81795 62.5 160.0767 0.6169701
             cmo         macd       osma      rsi     fastK
[3995,] 29.71342 -0.020870825 0.01666593 52.91932 0.8832685
[3996,] 41.89526 -0.009654368 0.02230591 61.49793 0.8833819
[3997,] 30.98237 -0.002051532 0.02392699 58.94513 0.7259475
[3998,] 33.84813  0.003454534 0.02354645 58.00549 0.7930029
[3999,] 38.84892  0.009590136 0.02374564 60.63806 0.8367347
[4000,] 54.71698  0.019303110 0.02676689 66.64815 0.9354120
            fastD     slowD        SMI    signal         vol
[3995,] 0.7773581 0.7735064 -35.095406 -47.27712 0.003643196
[3996,] 0.7691688 0.7761507 -26.482951 -43.11828 0.003858942
[3997,] 0.8308660 0.7924643 -19.699762 -38.43458 0.003920541
[3998,] 0.8007775 0.8002707 -13.141932 -33.37605 0.003916109
[3999,] 0.7852284 0.8056239  -6.569699 -28.01478 0.003999789
[4000,] 0.8550499 0.8136852   2.197810 -21.97226 0.004293766

Dados de entrada brutos são preparados.

3.3.3. Dados de Saída (Objetivo)

Agora nós vamos formar a saída (dados de destino). Como dissemos antes, nós vamos usar o ZigZag.

Nós vamos usar o ZigZag com uma largura do canal de 37 pontos grandes. O ZigZag será calculado pelo preço médio. O indicador pode ser calculado pelos preços HL, no entanto, o preço médio é preferível pois o indicador é mais estável no neste caso. Tendo extraído o sinal (0 - Compra, 1 -Venda), nós convertemos em uma matriz de entrada, que assume o modelo de rede.

Escreva uma função:

Out<-function(ch=0.0037){
  # ZigZag tem valores em cada barra e não só nos pontos 
  zz<-ZigZag(price[ ,'Med'], change = ch, percent = F, retrace = F, lastExtreme = T);
  n<-1:length(zz);
  #Nas últimas barras substitua os valores indefinidos para os últimos conhecidos
  for(i in n) { if(is.na(zz[i])) zz[i] = zz[i-1];}
  #Define a velocidade das mudanças de ZigZag e move uma barra para a frente
  dz<-c(diff(zz), NA);
  #Se a velociade >0 - signal = 0(Compra), if <0, signal = 1 (Venda) se não NA
  sig<-ifelse(dz>0, 0, if else(dz<0, 1, NA));
  return(sig);
}

Calcula os sinais.

> Y<-Out()
> table(Y)
Y
   0    1 
1567 2423

A relação de classe está desequilibrada. O número de exemplos de uma classe é maior do que o outro. Todos os modelos de classificação são hostil para com tais conjuntos.

Ao separar os dados em amostras de treinamento e teste, vamos corrigir esta situação.

3.3.4. Liberação dos Dados

Limpar os nossos conjuntos de dados a partir de dados indefinidos. Limpando neste caso implica uma rodada mais ampla de tarefas. Ele inclui compensação "praticamente zero variáveis" e altamente correlacionados, bem como algumas outras tarefas que não vamos discutir aqui.

Escreva uma função e elimine os dados

Clearing<-function(x, y){
  dt<-cbind(x,y);
  n<-ncol(dt)
  dt<-na.omit(dt)
  return(dt);  
}
> dt<-Clearing(X,Y); nrow(dt)
[1] 3957

A matriz tornou-se mais 43 barras mais curtas.

3.3.5. Formação das amostras de Teste e Treino

Existem várias maneiras de quebrar os dados de origem para as amostras de treinamento e teste. Nós vamos empregar a divisão aleatória periódica dos dados de origem para treiná-los e testá-los na proporção de 8/10. É importante que as amostras sejam estratificadas, o que significa que a razão entre as instâncias de classe nas amostras de teste e de treinamento devem corresponder à razão de classe no conjunto de dados de origem. Além disso, seria benéfico retificar as desigualdades de classe no conjunto de dados de origem. Há duas maneiras de fazê-lo - ou o nivelar pelo maior ou pela menor classe. À medida que nós exigimos mais exemplos, nós vamos para o nível da maior classe "1". Neste caso nós vamos usar o pacote "caret".

Vamos formar um novo conjunto equilibrado em que o número de casos de ambas as classes são o mesmo e são iguais ao maior.

3.3.6. Classe de Balanceamento

Abaixo esta a função que os nivelam o número de classes pelo lado maior (se a divergência é superior a 15%) e retorna uma matriz equilibrada

Balancing<-function(DT){
  #Calculata uma tabela com um número de classes
  cl<-table(DT[ ,ncol(DT)]);
  #Se a divergência é inferior a 15%, retorna a matriz inicial
  if(max(cl)/min(cl)<= 1.15) return(DT)
  #Caso contrário nivela pelo lado maior
  DT<-if(max(cl)/min(cl)> 1.15){ 
         upSample(x = DT[ ,-ncol(DT)],y = as.factor(DT[ , ncol(DT)]), yname = "Y")
        }
  #Converte у (fator) em um número
  DT$Y<-as.numeric(DT$Y)
  #Recodifica у de 1,2 em 0,1
  DT$Y<-ifelse(DT$Y == 1, 0, 1)
  #Converte o quadro de dados em uma matriz
  DT<-as.matrix(DT)
  return(DT);
}

Explicação. Na primeira linha ele calcula o número de ocorrências de cada classe (vetor, com a dimensão igual ao número de classes).

Localiza a razão entre o maior vetor para o menor e se ela for menor que o limite de um conjunto, sai. Se a proporção é maior, então ele calcular a função, depois de ter posto em х e Y separadamente. Y deve ser previamente convertido em um fator.

Este é o requisito para os parâmetros formais da função upsample(). Uma vez que não precisamos da variável objetivo como um fator, nós convertemos de volta para a forma numérica com os valores 0 e 1. Por favor, note que quando converter uma variável numérica (0,1) em um fator, recebemos variáveis de texto "0" e "1". Na conversão revertida para as variáveis numéricas, temos 1 e 2 (!). Nós substituímos com 0 e 1. O nosso conjunto de dados é convertido a partir do "quadro de dados" para a classe "matriz". Calculando-o:

dt.b<-Balancing(dt)
x<-dt.b[ ,-ncol(dt.b)]
y<-dt.b[ , ncol(dt.b)]

Desta forma, nós temos a fonte do conjunto de dados dt (entrada e saída) e o conjunto equilibrado dt.b.

Divida-o em amostras de treinamento e de teste

Obter os índices das amostras de treinamento e de teste do pacote "Rminer" usando a função holdout().

> library('rminer')
> t<-holdout(y, ratio = 8/10, mode = "random")

O objeto t é uma lista contendo os índices do treinamento (t$tr) e o teste (t$ts) do conjunto de dados. Os conjuntos recebidos são estratificados.

3.3.7. Pré-Processamento

Nossa fonte de dados de entrada contém variáveis com diferentes faixas de valores. Essencialmente, as redes são profundas redes regulares com uma forma peculiar de inicializar os pesos.

As redes neurais podem receber as variáveis de entrada no intervalo (-1, 1) ou (0, 1). Normalizar as variáveis de entrada para a faixa de [-1, 1].

Para isso o utilizar a função preprocess() do pacote "caret". Por favor, note que os parâmetros de pré-processamento devem ser calculados sobre o conjunto de dados de treinamento e serem guardados para mais pré-processamento dos dados de teste estabelecidos e os dados de entrada recentes

> spSign<-preProcess(x[t$tr, ], method = "spatialSign")
> x.tr<-predict(spSign, x[t$tr, ])
> x.ts<-predict(spSign, x[t$ts, ])

Agora temos tudo para a construção, formação e teste de uma rede neural profunda.

3.4. Modelos de Construção, Treinamento e Testes

Nós vamos construir e treinar o modelo DN SAE. A fórmula do modelo e descrição das variáveis:

sae.dnn.train(x, y, hidden = c(10), activationfun = "sigm", learningrate = 0.8, momentum = 0.5, learningrate_scale = 1, output = "sigm", sae_output = "linear",
  numepochs = 3, batchsize = 100, hidden_dropout = 0, visible_dropout = 0)

onde:

х é uma matriz de dados de entrada;
y é um vetor ou matriz de variáveis objetivo;
hidden é um vetor com um número de neurônios em cada camada escondida. Por padrão с(10);
activationfun é uma função de ativação de neurônios escondidos. Pode ser "sigm", "linear", "tanh". Por padrão "sigm";
learningrate é um nível de treinamento para a descida do gradiente. Por padrão = 0.8;
momentum é o impulso para o gradiente descendente. Por padrão = 0.5;
learningrate_scale o nível de treinamento pode ser multiplicado por este valor depois de cada iteração. Por padrão =1.0;
numepochs é um número de iterações de formação. Por padrão =3;
batchsize é o tamanho de uma pequena quantidade de dados a serem treinados. Por padrão =100;
output é a função de ativação para neurônios de saída pode ser "SIGM", "linear", "softmax". Por padrão "sigm";
sae_output é a função de ativação dos neurônios de saída de SAE, pode ser "SIGM", "linear", "softmax". Por padrão "linear";
hidden_dropout é uma parte removível para as camadas ocultas. Por padrão =0;
visible_dropout é uma parte removível da camada visível (entrada). Por padrão =0.

Vamos criar um modelo com as seguintes dimensões (17, 100, 100, 100, 1), treiná-lo, note o tempo de aprendizagem e observe a previsão.

> system.time(SAE<-sae.dnn.train(x= x.tr, y= y[t$tr], hidden=c(100,100,100), activationfun = "tanh", learningrate = 0.6, momentum = 0.5, learningrate_scale = 1.0, output = "sigm", sae_output = "linear", numepochs = 10, batchsize = 100, hidden_dropout = 0, visible_dropout = 0))
begin to train sae ......
training layer 1 autoencoder ...
training layer 2 autoencoder ...
training layer 3 autoencoder ...
sae has been trained.
begin to train deep nn ......
deep nn has been trained.
   user  system elapsed 
  12.92    0.00   13.09

Como podemos ver, isso acontece em duas etapas. Primeiramente o autoencoder é treinado camada por camada e, em seguida, a rede neural.

O pequeno número de vezes de treinamento e o imenso número de neurônios ocultos nas três camadas foram criados de propósito. Todo o processo levou 13 segundos!

Vamos avaliar as previsões sobre o conjunto de teste dos preditores.

> pr.sae<-nn.predict(SAE, x.ts);
> summary(pr.sae)
       V1        
 Min.   :0.2649  
 1st Qu.:0.2649  
 Median :0.5881  
 Mean   :0.5116  
 3rd Qu.:0.7410  
 Max.   :0.7410

Converte para os níveis 0,1 e calcula as medidas

> pr<-ifelse(pr.sae>mean(pr.sae), 1, 0)
> confusionMatrix(y[t$ts], pr)
Confusion Matrix and Statistics

          Reference
Prediction   0   1
         0 316 128
         1 134 378
                                         
               Accuracy : 0.7259         
                 95% CI : (0.6965, 0.754)
    No Information Rate : 0.5293         
    P-Value [Acc > NIR] : <2e-16         
                                         
                  Kappa : 0.4496         
 Mcnemar's Test P-Value : 0.7574         
                                         
            Sensitivity : 0.7022         
            Specificity : 0.7470         
         Pos Pred Value : 0.7117         
         Neg Pred Value : 0.7383         
             Prevalence : 0.4707         
         Detection Rate : 0.3305         
   Detection Prevalence : 0.4644         
      Balanced Accuracy : 0.7246         
                                         
       'Positive' Class : 0

Este não é um excelente coeficiente. Nós estamos mais interessados no lucro que vamos ter usando esses sinais do que o seu coeficiente. Verifica as últimas 500 barra (cerca de uma semana). Vamos receber sinais sobre os últimas 500 barras sequenciais de nossa rede treinada.

Normalizar as últimas 500 barras dos dados de entrada, receber previsões a partir da rede neural treinada e convertê-los em sinais -1 = (Venda) e 1 = (Buy)

> new.x<-predict(spSign,tail(dt[ ,-ncol(dt)], 500))
> pr.sae1<-nn.predict(SAE, new.x)
> pr.sig<-ifelse(pr.sae1>mean(pr.sae1), -1, 1)
> table(pr.sig)
pr.sig
 -1   1 
235 265 
> new.y<-ifelse(tail(dt[  , ncol(dt)], 500) == 0, 1, -1)
> table(new.y)
new.y
 -1   1 
201 299 
> cm1<-confusionMatrix(new.y, pr.sig)
> cm1
Confusion Matrix and Statistics

          Reference
Prediction  -1   1
        -1 160  41
        1   75 224
                                          
               Accuracy : 0.768           
                 95% CI : (0.7285, 0.8043)
    No Information Rate : 0.53            
    P-Value [Acc > NIR] : < 2.2e-16       
                                          
                  Kappa : 0.5305          
 Mcnemar's Test P-Value : 0.002184        
                                          
            Sensitivity : 0.6809          
            Specificity : 0.8453          
         Pos Pred Value : 0.7960          
         Neg Pred Value : 0.7492          
             Prevalence : 0.4700          
         Detection Rate : 0.3200          
   Detection Prevalence : 0.4020          
      Balanced Accuracy : 0.7631          
                                          
       'Positive' Class : -1

O coeficiente de Precisão não é ruim, mas estamos mais interessados no lucro, não no coeficiente.

Teste o lucro para as últimas 500 barras usando os nossos sinais previstos e obtenha a curva de equilíbrio:

> bal<-cumsum(tail(price[ , 'CO'], 500) * pr.sig)
> plot(bal, t = "l")
> abline(h = 0)

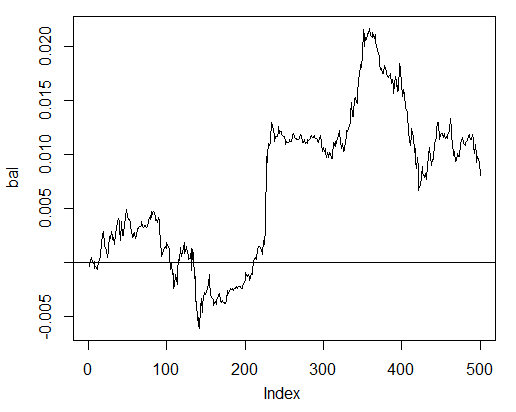
Fig. 24. Balanço sobre as últimas 500 barras pelos sinais de rede neural

O saldo foi calculado sem levar em consideração o spread, desvio e outras realidades do mercado ao vivo.

Agora compare com o equilíbrio que seria obtido a partir dos sinais ideais de ZZ. A linha vermelha é o equilíbrio pelos sinais da rede neural:

> bal.zz<-cumsum(tail(price[ , 'CO'], 500) * new.y)
> plot(bal.zz,  t = "l")
> lines(bal,  col = 2)

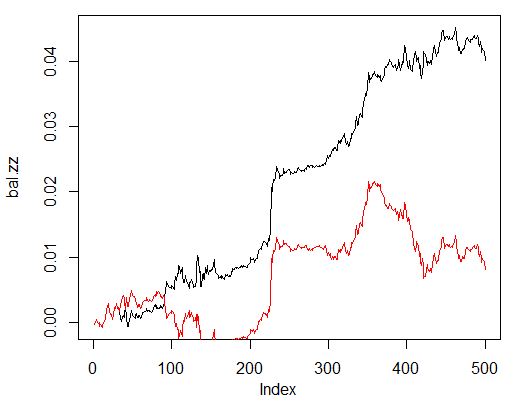
Fig. 25. Balanço sobre as últimas 500 barras pelos sinais da rede neural e os sinais ZigZag

Há potencial para melhorias.

Faça duas funções para facilitar as duas funções auxiliares Estimation() e Testing(). O primeiro irá gerar os coeficientes de Precisão/Erro (Accuracy/Err) e o segundo o saldo Bal/BalZZ.

Ele permite obter um resultado imediato alterando alguns parâmetros de rede e ver quais os parâmetros que influenciam a qualidade da rede.

Tendo escrito uma função de fitness, os parâmetros de rede ideal podem ser encontrados usando o algoritmo evolutivo (genético), sem quaisquer interrupções para o processo de negociação. Nós não vamos dedicar tempo a ele neste artigo, consideraremos ele em detalhes alguma outra hora.

Segue abaixo a função Estimation()calculando os coeficientes Erro/Precisão:

Estimation<-function(X, Y, r = 8/10, m = "random", norm = "spatialSign",
                     h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, 
                     out = "sigm", sae = "linear", Ep = 10, Bs = 50, 
                     CM=F){
  #Indices de treinamento e teste do conjunto de dados
  t<-holdout(Y, ratio = r, mode = m)
  #Parâmetros de pré-processamento
  prepr<-preProcess(X[t$tr,  ], method = norm)
  #Divide em dados de treinamento e teste dos conjuntos com pré-processamento 
  x.tr<-predict(prepr, X[t$tr,  ])
  x.ts<-predict(prepr, X[t$ts,  ])
  y.tr<- Y[t$tr]; y.ts<- Y[t$ts]
  #Treina o modelo
  SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, 
                     activationfun = act,
                     learningrate = LR, momentum = Mom, 
                      output = out, sae_output = sae, 
                     numepochs = Ep, batchsize = Bs)
  #Obtem uma previsão sobre o conjunto de dados de teste
  pr.sae<-nn.predict(SAE, x.ts)
  #Recodifica em sinais 1,0
  pr<-ifelse(pr.sae>mean(pr.sae), 1, 0)
  #Calcula o coeficiente de precisão ou o erro de classificação
  if(CM) err<-unname(confusionMatrix(y.ts, pr)$overall[1])
  if(!CM) err<-nn.test(SAE, x.ts, y.ts, mean(pr.sae))
  return(err)
}

Parâmetros formais:

X - matriz de entrada dos preditores;
Y - vetor da variável objetivo;
r - taxa de treino/teste;
m - modo de formação da amostra (aleatória ou consequente);
norm - modo dos parâmetros de entrada normalizados ([ -1, 1]= "spatialSign";[0, 1]="range");
h - vetor com um número de neurônios nas camadas escondidas;
act - função de ativação dos neurônios ocultos;
LR - nível de treinamento;
Мом - impulso;
out - função de ativação da camada de saída;
sae - função de ativação do autoencoder;
Ep - número de epochs de treinamento;
Bs - tamanho da pequena amostra;
CM - Variável booleana, se TRUE imprime a Precisão. Se não o Erro.

Como exemplo, vamos calcular o erro de classificação no conjunto de dados desequilibrado dt pela rede com três camadas ocultas contendo 30 neurônios cada um;

> Err<-Estimation(X = dt[ ,-ncol(dt)], Y = dt[ ,ncol(dt)], h=c(30, 30, 30), LR= 0.7)
begin to train sae ......
training layer 1 autoencoder ...
training layer 2 autoencoder ...
training layer 3 autoencoder ...
sae has been trained.
begin to train deep nn ......
deep nn has been trained.
> Err
[1] 0.1376263

A função Testing() calcula o saldo pelos sinais de previsão ou por aqueles ideais (ZigZag):

Testing<-function(dt1, dt2, r=8/10, m = "random", norm = "spatialSign",
                     h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, 
                     out = "sigm", sae = "linear", Ep = 10, Bs=50, 
                     pr = T, bar = 500){
  X<-dt1[  ,-ncol(dt1)]
  Y<-dt1[  ,ncol(dt1)]
  t<-holdout(Y,  ratio = r,  mode = m)
  prepr<-preProcess(X[t$tr,  ], method = norm)
  x.tr<-predict(prepr, X[t$tr,  ])
  y.tr<- Y[t$tr]; 
  SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, 
                     activationfun = act,
                     learningrate = LR, momentum = Mom, 
                     output = out, sae_output = sae, 
                     numepochs = Ep, batchsize = Bs)
  X<-dt2[ ,-ncol(dt2)]
  Y<-dt2[ ,ncol(dt2)]
  x.ts<-predict(prepr, tail(X, bar))
  y.ts<-tail(Y, bar)
  pr.sae<-nn.predict(SAE, x.ts)
  sig<-ifelse(pr.sae>mean(pr.sae), -1, 1)
  sig.zz<-ifelse(y.ts == 0, 1,-1 )
  bal<-cumsum(tail(price[  ,'CO'], bar) * sig)
  bal.zz<-cumsum(tail(price[  ,'CO'], bar) * sig.zz)
  if(pr) return(bal)
  if(!pr) return(bal.zz)
}

Parâmetros formais:

dt1 - matriz da grandeza de entrada e do destino utilizado para a formação da rede;
dt2 - matriz das variáveis de entrada e de destino utilizados para testar a rede;
pr - variável booleana, se TRUE imprime o saldo pelos sinais de previsão, caso contrário, por ZigZag;
bar - o número das últimas barras a serem usadas para calcular o saldo.

Calcula o equilíbrio das últimas 500 barras de nosso conjunto de dados dt ao treinar o conjunto de dados equilibrado dt.b pela rede neural com os mesmos parâmetros como acima:

> Bal<-Testing(dt.b, dt, h=c(30, 30, 30), LR= 0.7)
begin to train sae ......
training layer 1 autoencoder ...
training layer 2 autoencoder ...
training layer 3 autoencoder ...
sae has been trained.
begin to train deep nn ......
deep nn has been trained.
> plot(Bal, t = "l")
> abline(h = 0)

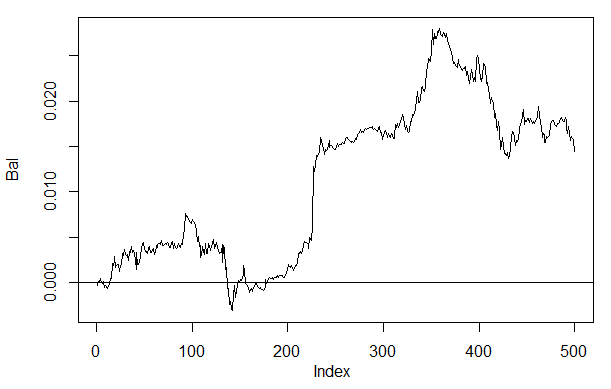
Fig. 26. Saldo sobre as últimas 500 barras pelos sinais da rede neural h(30,30,30)

Se compararmos o resultado com o saldo obtido anteriormente, em seguida, podemos ver uma melhora significativa. Embora este não seja o ponto mais interessante aqui.

Se dermos uma olhada na plotagem dos preços nas últimas 500 barras, então podemos ver quais partes dele foram mais bem aceitos pela nossa rede (150-350 barras).

> plot(tail(price[  ,'Close'], 500), t = "l")
> abline(v = c(150,350), col=2)

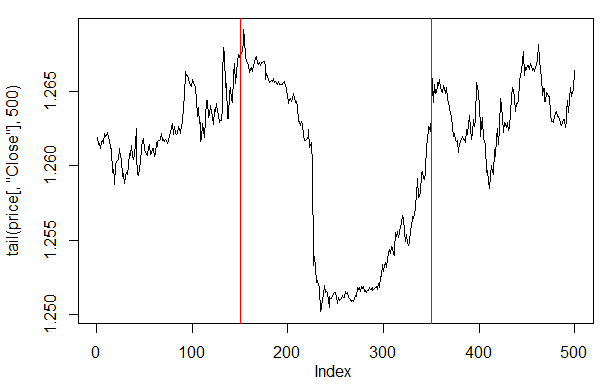
Fig. 27. Plotagem do preço de Fechamento nas últimas 500 barras

Nota: Ao descodificar as saídas de previsão, foi utilizada uma versão simplificada maior/menor do que a média, embora outras versões possam também ser utilizadas.

Se os valores são maiores do que 0.6 ou menos do que 0.4, o segmento instável de 0.4-0.6 é cortado. Fronteiras entre as classes mais precisas podem ser obtidas na calibração. Isso vai ser discutido mais tarde.

Nossa função Testing() será alterada um pouco se um parâmetro adicional dec for introduzido. Isto irá permitir-nos selecionar uma forma de decodificar ("mean" ou "60/40") e verificar os valores previstos e qual o impacto que vai ter no saldo.

Testing.1<-function(dt1, dt2, r = 8/10, m = "random", norm = "spatialSign",
                     h = c(10), act = "tanh", LR = 0.8, Mom = 0.5, 
                     out = "sigm", sae = "linear", Ep = 10, Bs = 50, 
                     pr = T, bar = 500, dec=1){
  X<-dt1[ ,-ncol(dt1)]
  Y<-dt1[ ,ncol(dt1)]
  t<-holdout(Y, ratio = r, mode = m)
  prepr<-preProcess(X[t$tr, ], method = norm)
  x.tr<-predict(prepr, X[t$tr, ])
  y.tr<- Y[t$tr]; 
  SAE<-sae.dnn.train(x = x.tr , y = y.tr , hidden = h, 
                     activationfun = act,
                     learningrate = LR, momentum = Mom, 
                     output = out, sae_output = sae, 
                     numepochs = Ep, batchsize = Bs)
  X<-dt2[ ,-ncol(dt2)]
  Y<-dt2[ ,ncol(dt2)]
  x.ts<-predict(prepr, tail(X, bar))
  y.ts<-tail(Y, bar)
  pr.sae<-nn.predict(SAE, x.ts)
  #Variante +/- mean
  if(dec == 1) sig<-ifelse(pr.sae>mean(pr.sae), -1, 1)
  #Variante 60/40
  if(dec == 2) sig<-ifelse(pr.sae>0.6, -1, ifelse(pr.sae<0.4, 1, 0))
  sig.zz<-ifelse(y.ts == 0, 1,-1 )
  bal<-cumsum(tail(price[  ,'CO'], bar) * sig)
  bal.zz<-cumsum(tail(price[  ,'CO'], bar) * sig.zz)
  if(pr) return(bal)
  if(!pr) return(bal.zz)
}

Calcula e avalia o saldo com o primeiro e o segundo meio de descodificação.

A fim de repetir os resultados, ajustar o gerador de números pseudo-aleatórios na mesma posição.

> set.seed<-1245
> Bal1<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 1)
begin to train sae ......
training layer 1 autoencoder ...
training layer 2 autoencoder ...
training layer 3 autoencoder ...
sae has been trained.
begin to train deep nn ......
deep nn has been trained.
> set.seed<-1245
> Bal2<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2)
begin to train sae ......
training layer 1 autoencoder ...
training layer 2 autoencoder ...
training layer 3 autoencoder ...
sae has been trained.
begin to train deep nn ......
deep nn has been trained.
> plot(Bal2, t = "l")
> lines(Bal1, col = 2)

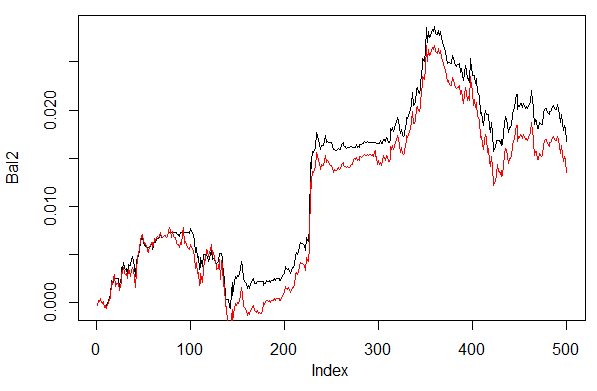
Fig. 28. Saldo das últimas 500 barras pelos sinais de rede neural com diferentes formas de previsões de decodificação

Claramente, o saldo pelo segundo caminho 60/40 parece melhor. Há espaço para melhoria neste aspecto também.

Aqui é a última coisa a verificar. Em teoria, um conjunto de várias redes neurais dá um resultado melhor e mais estável. Vamos testar um conjunto constituído por várias redes, que são treinadas nas mesmas amostras, embora elas possam ser treinadas em amostras independentes. O resultado da previsão do conjunto é uma média simples das previsões de todas as redes. Existem outras formas mais complexas de média.

Nós vamos melhorar a nossa função Testing() pela adição de mais um parâmetro - ans = 1 especificando o número de redes em conjunto.

3.4.1. Cálculos Paralelos

Já que os cálculos de vários modelos independentes podem ser facilmente de forma paralela, vamos aproveitar a oportunidade proporcionada pela linguagem R e criar um cluster que consiste em vários núcleos do processador ou de computadores de uma rede local, independentemente dos sistemas operacionais que estes computadores utilizam.

Para isso, precisamos dos pacotes "foreach" e "doParallel". Abaixo está uma função muito simples que irá lançar um cluster para todos os núcleos do nosso processador.

library(doParallel)
library(foreach)
puskCluster<-function(){
  cores<-detectCores()
  cl<-makePSOCKcluster(cores)
  registerDoParallel(cl)
  clusterSetRNGStream(cl)
 return(cl)
}

Vários pontos são esclarecidos abaixo. Nas primeiras duas linhas que carregam as bibliotecas necessárias. Eles precisam ser previamente instalado no seu computador. Em seguida, nós definimos quantos núcleos há no processador, criamos um cluster, registramos um pacote para computações paralelas, instalamos um gerador de números pseudo-aleatórios independente em cada fluxo de cálculos e retornamos o identificador do cluster. A qualidade do gerador de números pseudo-aleatórios para os cálculos de cada modelo é extremamente importante embora este seja um tópico separado.

Depois que o cluster for lançado e todos os cálculos necessários forem feitos, devemos nos lembrar de pará-lo:

cl<-puskCluster()
stopCluster(cl)

As computações paralelas vão ser realizadas pela fórmula seguinte a partir do pacote "foreach":

SAE<-foreach(times(ans), .packages = "deepnet") %dopar%  
                sae.dnn.train(x = x.tr , y = y.tr , hidden = h, 
                        activationfun = act,
                        learningrate = LR, momentum = Mom, 
                        output = out, sae_output = sae, 
                        numepochs = Ep, batchsize = Bs)

Onde times(ans) é uma série de redes que queremos obter e .packages aponta para o pacote para tomar a função calculada.

O resultado tem uma forma de uma lista e contém o número de redes treinadas que precisamos.

Então, nós exigimos a previsão de cada rede e calculamos a média.

pr.sae<-(foreach(i = 1:ans, .combine = "+") %do%  nn.predict(SAE[[i]], x.ts))/ans

Aqui i é um vetor dos índices rede treinada,.combine="+" especifica de que forma as previsões retornadas em todas as redes neurais são supostamente devolvidas. Neste caso, nós exigimos o retorno da soma e efetuamos estes cálculos em sequência, não de uma forma paralela (operador %do%). A soma obtida será divida pelo número de redes neurais e este será o o fim do resultado. Isto é agradável e simples.

Calcula o saldo obtido a partir dos conjuntos que consistem de 3 e 4 redes neurais com os mesmos parâmetros que aqueles acima e utilizando o caminho de decodificação 60/40. Compara com os resultados em uma rede neural. Para avaliar a eficácia das computações paralelas, aumenta o número de epochs a 300 e o tempo do processo de obtenção da previsão.

1. Uma rede neural:

> system.time(Bal21<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.000057
####loss on step 20000 is : 0.000043
training layer 2 autoencoder ...
####loss on step 10000 is : 0.000081
####loss on step 20000 is : 0.000086
training layer 3 autoencoder ...
####loss on step 10000 is : 0.000072
####loss on step 20000 is : 0.000066
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.069451
####loss on step 20000 is : 0.079629
deep nn has been trained.
   user  system elapsed 
 115.78    0.00  116.96 
> plot(Bal21, t = "l")
> abline(h = 0)

2. Exemplo de três redes neurais:

> system.time(Bal41<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=3))
   user  system elapsed 
   0.22    0.06  233.64 
> lines(Bal41, col=4)

3. Exemplo de 4 redes neurais:

> system.time(Bal44<-Testing.2(dt.b, dt, h = c(30, 30, 30), LR = 0.7, Ep=300, dec = 2, ans=4))
   user  system elapsed 
   0.13    0.03  247.86 
> lines(Bal44, col=2)

O tempo de execução na computação paralela é ótima se o número de fluxos múltiplos é o número de núcleos. Eu usei dois núcleos.

Dizendo que, não há vantagens significativas no saldo. Na tabela abaixo, a linha azul indica três redes, a Vermelha - 4 redes e a preta 1 rede.

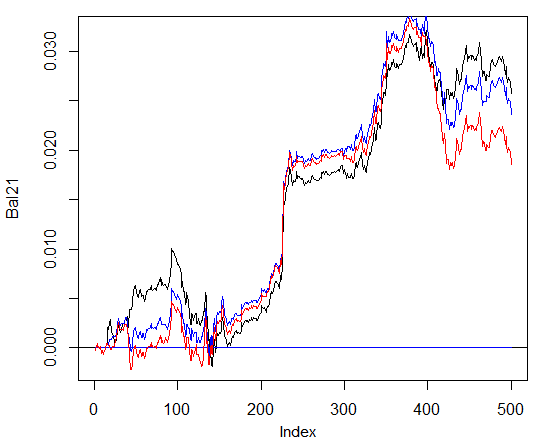
Fig. 29. Saldo sobre as últimas 500 barras pelos sinais dos conjuntos que consistem em 3 e 4 de redes neurais e uma rede

Em geral, o resultado depende de muitos parâmetros, a partir de dados de entrada e de saída, o caminho da sua normalização, o número de camadas escondidas e o número de neurônios nessas camadas, o nível de formação, o número de epochs de treinamento e muitos outros.

Últimos três exemplos. Calcula o saldo das últimas 1000 barras com três redes neurais com números diferentes de neurônios ocultos em três camadas ocultas.

> system.time(Bal0<-Testing.1(dt.b, dt, h = c(30, 30, 30), LR = 0.7, dec = 2, Ep=300, bar=1000))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.000054
####loss on step 20000 is : 0.000044
training layer 2 autoencoder ...
####loss on step 10000 is : 0.000078
####loss on step 20000 is : 0.000079
training layer 3 autoencoder ...
####loss on step 10000 is : 0.000090
####loss on step 20000 is : 0.000072
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.072633
####loss on step 20000 is : 0.057917
deep nn has been trained.
   user  system elapsed 
 116.09    0.02  116.26 
> max(Bal0)
[1] 0.04725
> plot(Bal0, t="l")
> tail(Bal0,1)
[1] 0.03514

O lucro máximo é de 472 pontos, no última barra 351 pontos. No gráfico ela é desenhada em preto.

> system.time(Bal0<-Testing.1(dt.b, dt, h = c(13, 8, 5), LR = 0.7, dec = 2, Ep=300, bar=1000))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.005217
####loss on step 20000 is : 0.004846
training layer 2 autoencoder ...
####loss on step 10000 is : 0.051324
####loss on step 20000 is : 0.046230
training layer 3 autoencoder ...
####loss on step 10000 is : 0.023292
####loss on step 20000 is : 0.026113
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.057788
####loss on step 20000 is : 0.056932
deep nn has been trained.
   user  system elapsed 
  64.04    0.01   64.24 
Warning message:
In sae$encoder[[i - 1]]$W[[1]] %*% t(train_x) + sae$encoder[[i -  :
  longer object length is not a multiple of shorter object length
> lines(Bal0, col="blue")

Isto é claramente uma variação ineficaz.

A terceira variação:

> system.time(Bal0<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=1000))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.000018
####loss on step 20000 is : 0.000013
training layer 2 autoencoder ...
####loss on step 10000 is : 0.000062
####loss on step 20000 is : 0.000048
training layer 3 autoencoder ...
####loss on step 10000 is : 0.000053
####loss on step 20000 is : 0.000055
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.096490
####loss on step 20000 is : 0.084860
deep nn has been trained.
   user  system elapsed 
 186.18    0.00  186.39 
> lines(Bal0, col="red")
> max(Bal0)
[1] 0.0543

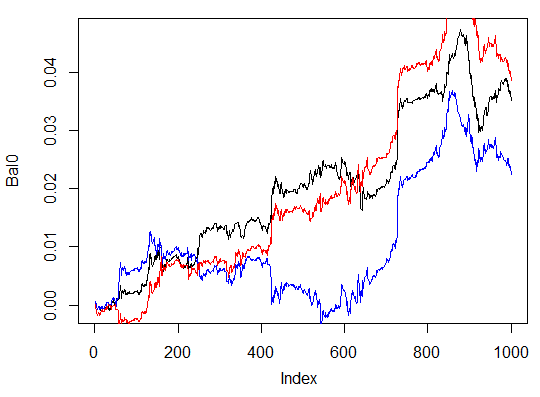
Fig. 30. Saldo das últimas 1000 barras pelos sinais de três redes neurais com diferentes números de neurônios escondidos

Os resultados mostram que a terceira variante é o melhor dos três com o lucro máximo de 543 pontos. Nós só mudamos o número de neurônios ocultos e isso levou a uma melhoria significativa. A busca de parâmetros ideais deve ser realizada através de algoritmos evolucionários. Isso é com o leitor a explorar.

Deve-se ter em mente que o algoritmo do autor não foi totalmente implementado neste pacote.

4. A implementação (Indicador e o Expert Advisor)

Agora vamos escrever um programa para o indicador e um Expert Advisor usando uma rede profunda para receber os sinais de negociação.

Existem duas formas para tal implementação:

A primeira. O treinamento da rede neural é realizado no Rstudio manualmente. Depois de obter os resultados aceitáveis, salve a rede no catálogo apropriado. Em seguida, inicie o EA e o indicador no gráfico. O EA vai carregar a rede treinada. O indicador prepara um vetor de novos dados de entrada em cada nova barra e passa para o EA. O EA apresenta os dados da rede, recebe um sinal e, em seguida, atua sobre ele. O EA está continuando com suas atividades habituais, tais como a abertura e fechamento de ordens, trailing etc... O objetivo do indicador é preparar e passar os novos dados de entrada para o EA a cada novo barra e, mais importante, apresentar sinais de previsão pela rede em um gráfico. A prática mostra que o controle visual é a forma mais eficiente de avaliar uma rede neural.
A segunda maneira. Inicie o EA e o indicador no gráfico. No primeiro lançamento, o indicador passa para o EA um grande conjunto preparado de dados de entrada e saída. A EA inicia o treinamento, faz os testes e seleciona a melhor rede neural. Depois disso o trabalho continua como na primeira forma.

Nós vamos escrever o link do indicador-EA seguindo o primeiro algoritmo. Um EA com o mínimo de rebaixamento.

Porque é tão difícil? Esta maneira de implementação permite conectar inúmeros indicadores colocados em diferentes símbolos/períodos em um EA e consequentemente trabalhar com eles. Para isso, o EA tem que passar por alguma modernização. Nós vamos falar sobre isso mais tarde.

Abaixo está a estrutura de interação entre o indicador e o EA:

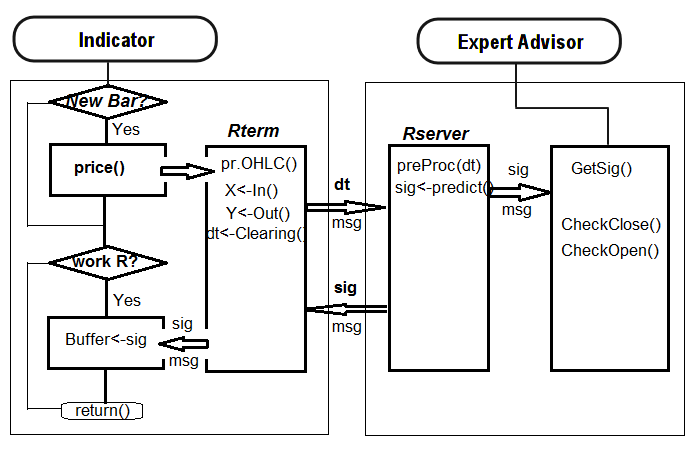
Fig. 31. Estrutura de interação entre o indicador e o EA

4.1. Treinando e Salvando o Modelo

Usando o indicador no gráfico de nosso interesse, obtemos os dados de origem necessários. Para isso, coloque o indicador no gráfico, depois de definir uma variável send=false, ou seja, a representação visual não é para ser enviada para o servidor. No primeiro lançamento deste símbolo ou período, o indicador cria os seguintes diretórios /Symbol/TF/Test_Data/ no arquivo de dados do terminal (/MQL4/Files).

Tal organização de diretórios oferece a oportunidade de não colocar resultados de experiências juntos no treinamento preliminar dos modelos e não substituir os dados antigos com os novos. Os resultados intermediários serão armazenadas no arquivo do diretório /Symbol/TF/Test_Data/ e o modelo do EA para usar no trabalho será localizado em /Symbol/TF/ (ele terá de ser colocado lá manualmente). O mesmo resultado será no primeiro lançamento do EA em um novo símbolo ou período.

Assim, para o EURUSD, М30, existem 4000 barras em 14/10/2014. Exigimos o quadro de dados dt[].

Classes do Saldo:

> dt.b<-Balancing(dt)
> table(dt.b[ ,ncol(dt.b)])
   0    1 
2288 2288

Agora, com a função Testing.1() previamente escrita, é possível treinar a rede neural profunda com 500 e 300 epochs e avaliar o saldo obtido nas últimas 500 barras pelos sinais previstos pela rede neural.

> system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=500, bar=500))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.000017
####loss on step 20000 is : 0.000015
####loss on step 30000 is : 0.000015
training layer 2 autoencoder ...
####loss on step 10000 is : 0.000044
####loss on step 20000 is : 0.000041
####loss on step 30000 is : 0.000039
training layer 3 autoencoder ...
####loss on step 10000 is : 0.000042
####loss on step 20000 is : 0.000042
####loss on step 30000 is : 0.000036
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.089417
####loss on step 20000 is : 0.043276
####loss on step 30000 is : 0.069399
deep nn has been trained.
   user  system elapsed 
 267.59    0.08  269.37 
> plot(bal, t="l")

Salve a rede neural com um nome diferente e treine outro

> SAE1<-SAE
> system.time(bal<-Testing.1(dt.b, dt, h = c(50, 50, 50), LR = 0.7, dec = 2, Ep=300, bar=500))
begin to train sae ......
training layer 1 autoencoder ...
####loss on step 10000 is : 0.000020
####loss on step 20000 is : 0.000016
training layer 2 autoencoder ...
####loss on step 10000 is : 0.000050
####loss on step 20000 is : 0.000050
training layer 3 autoencoder ...
####loss on step 10000 is : 0.000051
####loss on step 20000 is : 0.000043
sae has been trained.
begin to train deep nn ......
####loss on step 10000 is : 0.083888
####loss on step 20000 is : 0.083941
deep nn has been trained.
   user  system elapsed 
 155.32    0.02  156.25 
> lines(bal, col=2)

Dê uma olhada nos gráficos do saldo (o último resultado destacado em vermelho).

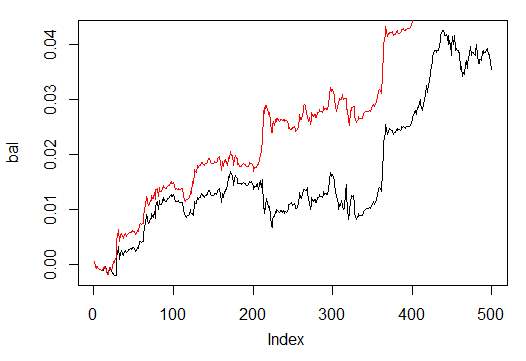
Fig. 32. Saldo sobre as últimas 500 barras pelos sinais de redes neurais treinadas em 500 e 300 epochs

Como podemos ver, a rede neural treinada em 300 epochs, mostrou um resultado melhor do que a rede treinada em 500 epochs.

O tempo de treinamento do último é adequado para um retreinamento rápido durante uma sessão de negociação neste período.

Para mais trabalho em um gráfico real, precisamos de dois objetos: o modelo "SAE" treinado e os parâmetros de normalização "Prepr" para os dados de entrada. Salve-os no diretório relevante, em meu caso, isso é "D:/Alpari Limited MT4/MQL4/Files/EURUSD/M30/Test_2014-10-14". Isso é definido e funciona como um grupo de trabalho, se você abriu no rstudio a área de trabalho "i_SAE_EURUSD_30.Rdata" salvo pelo indicador.

save(SAE, prepr, file="SAE.model")

No arquivo "SAE.model", nós salvamos o próprio modelo e os parâmetros de normalização. Usando o modelo sem eles não faz sentido. Você pode experimentar e salvar os modelos que você gosta todos os dias. Eles serão salvos nas pastas "/File/Symbol/TF/Test_Data". Para o EA usar o modelo, coloque manualmente o arquivo "SAE.model" para a pasta "File/Symbol/TF/". Esta pasta pode conter apenas um modelo e o EA utilizará ele para o trabalho.

Tendo carregao o arquivo "SAE.model", o EA carrega estes objetos para a área de trabalho para uso. Neste ponto, a parte manual do trabalho foi finalizada, você pode colocar o indicador-EA no gráfico e testá-lo em tempo real.

Para avaliar a eficácia do trabalho do EA, são necessários critérios quantitativos. O coeficiente de precisão não é bastante adequado para este propósito.

A média da razão da previsão do saldo recebido pelo ZigZag e a relação de equilíbrio na última barra para o número de barras. No nosso caso, este é o saldo pelo ZigZag:

sig.zz<-ifelse(tail(dt[  , ncol(dt)], 500) == 0, 1, -1)
bal.zz<-cumsum(tail(price[  , 'CO'], 500) * sig.zz)
Kzz<-mean(bal.zz / bal)
> Kzz
[1] 0.9173312

Esta é um score muito alto, mas é relativo.

Se formos ver o que se parece ao longo do tempo, podemos ver que para as primeiros 50-100 barras, esse é um índice instável, embora mais tarde torna-se quase que constante. As estatísticas estão abaixo:

> plot(bal/bal.zz, t="l")
> summary(bal/bal.zz)
    Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
-15.2500   0.7341   0.7844   0.9173   0.8833  55.0000

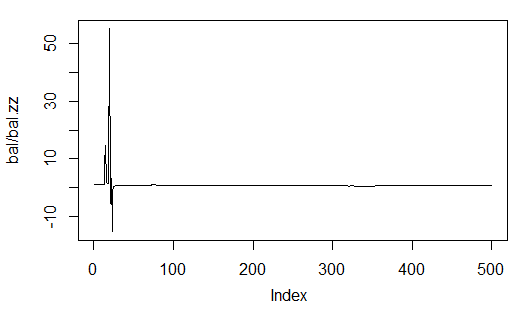
Fig. 33. Razão do saldo da estimativa para o saldo obtido pelo ZigZag

A segunda é mais precisa, pois mostra quantos pontos de lucro são para uma barra em um trecho de N barras.

Por exemplo, o saldo pela previsão da rede neural na faixa de 500 barras:

> Kb<-tail(bal,1)/length(bal)*10^Dig
> Kb
[1] 11.508

pelos sinais ZigZag:

> Kbz<-tail(bal.zz,1)/length(bal)*10^Dig
> Kbz
[1] 13.784

Quando o limite inferior de eficácia em um dos parâmetros é definido, nós sabemos o momento em que podemos treinar a rede neural ou otimizar seus parâmetros.

O EA vai exibir os seguintes parâmetros no gráfico: OP - operação executada, Acc - Precisão, K - é o Kb definido anteriormente, Kmax - o mesmo parâmetro como Kb mas definido sobre o saldo máximo e ele fornece uma idéia de quanto esse parâmetro difere na última barra da máxima.

4.2. Instalação e Lançamento da Ordem

No arquivo anexado SAE.zip você pode encontrar:

O indicador i_SAE.mq4, coloque-o na pasta ~/MQL4/Indicators/
O EA e_SAE.mq4, coloque-o na pasta ~/MQL4/Experts/
A biblioteca mt4Rb7.dll, coloque-o na pasta ~/MQL4/Libraries/
O arquivo de cabeçalho mt4Rb7.mqh, coloque-o na pasta ~/MQL4/Include/. O arquivo da biblioteca e cabeçalho foram desenvolvidos e gentilmente cedido por Bernd Kreuss. O nome incluí o índice da última mudança (b7). Quando há um grande número de versões com os mesmos nomes, existem confusões que levam muito tempo para corrigir.
Scripts em R: i_SAE.r (script indicador principal), i_SAE_fun.r (funções do script indicador), e_SAE.r (EA script), e_SAE_init.r (EA script de inicialização), SAE_SetDir.r (script de validação e criação dos diretórios necessários). Como os scripts não dependem nem do símbolo, nem de um período, eles podem ser localizados em um diretório separado. No meu caso, isso é em "C:Rdata/SAE/". O diretório "C:Rdata/" contém scripts diferentes não associadas a qualquer determinado projeto. Se você colocar os scripts em uma pasta diferente da minha, então, faça as correções apropriadas no indicador e no EA corrigindo o caminho para os scripts.
SAE.model é um arquivo com o modelo "SAE" e os parâmetros de normalização "Prepr". O modelo foi treinado no EURUSD (M30), última data de 14/10/14. O processo de treinamento foi descrito acima.

Também não se esqueça do caminho para o diretório onde a língua R foi armazenado em seu computador.

É preferível seguir a seguinte ordem para começar a trabalhar. Coloque o EA no gráfico. Se você decidir colocar uma EA em um outro símbolo, a porta, diferente dos servidores lançados anteriormente, deve ser especificado. Por exemplo, a porta 8886 (por padrão porta 8888).

Nota. Esta é uma maneira absolutamente ineficiente. Cada servidor tem um tamanho de 120-130 Mb. Isto é o que as coisas são hoje.

Após a inicialização normal do EA, o alerta "No calculation results! Symbol" aparecerá. Em seguida, instale o indicador com o parâmetro externo send = true e porta do servidor especificada que o indicador irá se conectar(ver acima). Se tudo funcionar corretamente, os dados reais "operation", Precisão, K e Kmax aparecerá na sequência de saída e a negociação irá começar.

O controle eficiente do processo pode ser melhor facilitado a partir do Gerenciador de Tarefas do Windows. Se Rterm não aparecer na lista após o EA ou indicador ser lançado, então, o processo foi interrompido por R. A principal razão de tais rupturas é um erro de sintaxe nos scripts, incompatibilidade do comprimento do vetor MQL de recebimento e o vetor extraído de Rterm.

Os scripts podem ser depurados em rstudio através do lançamento do script linha por linha, do início ao fim.

Infelizmente eu não consegui lançar o EA no testador, portanto, ele tem de ser testado em uma conta demo.

4.3. Formas e Métodos de Melhorar as Características Qualitativas

Alterar o conjunto dos indicadores utilizados na entrada.
Mudar a maneira da normalização dos dados de entrada.
Otimizar os parâmetros do "supervisor" e os indicadores na entrada.
Alterar a codificação da variável de entrada para a matriz com duas colunas. Calibrar o sinal de previsão.
Otimizar os parâmetros de rede (número de neurônios nas camadas ocultas, número de camadas, o nível de aprendizagem, número de epochs).

Conclusão

Nós criamos, treinamos e testamos os modelos de rede profundas com a inicialização dos pesos de neurônios nas camadas escondidas de SAE. As redes treinam muito rapidamente e permite um treinamento sem interromper o processo de negociação.

Os resultados apresentados por redes neurais são médios em termos de métricas. O resultado ideal não era o objetivo inicial.

Usando esse modelo e uma avaliação permanente do coeficiente de eficácia, o modelo pode ser treinado novamente e otimizado sem interromper o processo de negociação.

Anexo:

SAE.zip - indicador, EA e arquivos anexos.
R_intro.zip - literatura sobre R e Rstudio em Russo.
DeepLearning.zip - literatura de Aprendizagem Profunda.

Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/1103

Arquivos anexados |

Baixar como ZIP

DeepLearning.zip (6542.81 KB)

R-intro.zip (15278.8 KB)

sae.zip (394.31 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Outros artigos do autor

Ir para discussão

Desenhando Medidores com Mostrador usando a classe CCanvas

Podemos encontrar medidores com mostrador em carros e aviões, na produção industrial e na vida cotidiana. Eles são utilizados em todos os domínios que requerem uma resposta rápida a um comportamento de valor controlado. Este artigo descreve a biblioteca de medidores com mostrador para o MetaTrader 5.

Florestas Aleatórias na Previsão das Tendências

Este artigo considera o uso do pacote Rattle na busca automática de padrões para prever as posições compradas ou vendidas dos pares de moedas no Forex. Este artigo pode ser útil tanto para novatos quanto para profissionais experientes.

Otimização. Algumas idéias simples

O processo de otimização pode exigir recursos significativos de seu computador ou mesmo dos agentes de teste da MQL5 Cloud Network. Este artigo compreende algumas idéias simples que eu uso para a facilitação do trabalho e a melhoria do Strategy Tester do MetaTrader 5. Eu tive essas idéias a partir da documentação, fórum e artigos.

Programando os Modos do EA Usando a Abordagem Orientada a Objetos

Este artigo explica a idéia da programação multi-modo de um robô de negociação em MQL5. Cada modalidade é implementada com a abordagem orientada a objetos. São fornecidos as instâncias de ambos os modos de hierarquias de classe e das classes para testes. A programação multi-modo de robôs de negociação presumi-se levar em conta todas as peculiaridades de cada modo operacional de um EA escrito em MQL5. Funções e enumerações são criadas para identificar o modo.