
ディープニューラルネットワーク(その1)データの準備
DNNは広く使用されており、多くの分野で積極的に開発されています。ニューラルネットワークの日常的な使用の最も一般的な例は、音声認識と画像認識、及び言語間の自動翻訳です。DNNは取引にも使用されます。アルゴリズム取引の急速な発展は、DNNの徹底的な研究の有用性をうかがわせます。
最近、開発者はDNNの使用に関する多くの新しいアイデア、方法、及びアプローチを考えつき、実験的に証明しています。この一連の記事では、DNNの発展の状態と主な方向性について検討します。実践的な実験を使用したさまざまなアイデアや方法のテストとDNNの質的特性には、多くのスペースが設けられています。作業には、完全接続の多層ネットワークだけを使用します。
記事には4つの重点分野があります。
- 様々な変換による入力データの準備、評価、拡大
- darchパッケージ(v.0.12)の新機能、柔軟性と拡張機能
- 予測結果の拡大(DNNとニューラルネットワークのアンサンブルのハイパーパラメータの最適化)の使用
- エキスパートアドバイザーの作業を学習と作業の両方において制御するグラフィカル機能
本稿では、取引端末で受け取ったデータのニューラルネットワークで使用するための準備を考察します。
内容
はじめに
ディープニューラルネットワークの開発、訓練、テストは、厳密なシーケンスを持つ段階で行われます。機械学習の任意のモデルと同様、DNNを作成する過程は、2つの不等な部分に分割できます。
- 実験用入出力データの準備
- DNNパラメータの作成、訓練、検証、及び最適化
第1段階はプロジェクト時間の約70%を占めます。DNNの作業結果は、この段階の成功に大きく依存します。結局のところはGIGO(garbage in garbage out)です。このため、この段階での一連の行動は詳細に説明されます。
実験を繰り返すには、MRO 3.4.0とRstudioをインストールする必要があります。このソフトウェアのインストール手順は、インターネット上で簡単に見つけることができます。この情報は本稿の添付ファイルにも含まれているので、詳細は考察されません。
R言語
Rについていくつか重要なことを思い出してみましょう。これは、統計的な計算とグラフィックスのためのプログラミング言語と環境で、1996年に、ニュージーランドの科学者ロスイハカ氏とオークランド大学のロバートジェントルマン氏によって開発されました。RはオープンソースソフトウェアであるGNUプロジェクトで、オープンソースソフトウェアを使用するアプローチは、以下の原則(自由)に従います。
- 任意の目的のためにプログラムを立ち上げる自由(自由0)
- プログラムの仕組みを研究してプログラマーのニーズに適応させる自由(自由1)
- 隣人を助けるためにコピーを配布する自由(自由2)
- プログラムを改善して変更されたバージョンを配布し、コミュニティ全体に利益をもたらす自由
現在Rは「R開発コアチーム」と昨年設立された Rコンソーシアムによって主に改善され、開発されています。コンソーシアムのメンバー(IBM、Microsoft、Rstudio、Google、Mango、Oracleなど)のリストは、言語の優れた支持、重要な関心及び見通しを示しています。
下記はRのメリットです。
- 現在の統計計算の標準
- 世界の科学界による支持と開発
- データマイニングにおけるすべての高度な方向に関するパッケージの幅広いセット。新しいアイデアは科学者による発表後2週間以内にはRで実装されるということには言及するべきである」。
- そして最後に重要なこととして、それは絶対に無償であるということ
1. 初期(生)データの作成
「過去、現在、将来のすべての価格変動は価格自体に含まれている」
事前準備、評価、予測子の選択のために設計された方法(パッケージ)は数多くあります。[1]にはこれらの方法のレビューが見られ、その多様性は、実世界のデータの多様性によって説明されます。探索及び処理の方法は使用中のデータ型によって定義されます。
ここでは経済的データを検討します。これらは無限で簡単に抽出できる階層的な通常の時間系列です。基本行は、特定の時間枠での製品のOHLCV相場です。
他のすべての時系列はこの基本行から来ます。
- ノンパラメトリック:例えば、x^2、sqrt(abs(x))、x^3、-x^2など
- 機能的ノンパラメトリック:例えば、sin(2*n*x)、ln(abs(x))、log(Pr(t)/Pr(t-1)) など
- パラメトリック:これには様々な指標が属し、主に予測変数として使用されます。それらはオシレータと異なる種類のフィルタの両方になります。
シグナルを生成する指標(因子)またはシグナルを生成する一連の条件文は目標変数として使用できます。
1.1. 相場
(o, h, l, cl, v, d) ベクトルとして端末から取得するOHLC相場、数量と時間。dataFrameで端末から受け取ったベクトルを結合する関数を書く必要があります。そのために、バーの開始時刻の形式をPOSIXct形式に変更します。
#---pr.OHLCV-------------------
pr.OHLCV <- function(d, o, h, l, cl, v){
# (d, o, h, l, cl, v)- ベクトル
require('magrittr')
require('dplyr')
require('anytime')
price <- cbind(Data = rev(d),
Open = rev(o), High = rev(h),
Low = rev(l), Close = rev(cl),
Vol = rev(v)) %>% as.tibble()
price$Data %<>% anytime(., tz = "CET")
return(price)
}
相場ベクトルは環境envに読み込まれているので、dataFrame prを計算し、未使用変数から環境envをクリアします。
evalq({pr <- pr.OHLCV(Data, Open, High, Low, Close, Volume)
rm(list = c("Data", "Open", "High", "Low", "Close", "Volume"))
},
env)
このdataFrameの始まりがどのようであるかを見てみたいと思います。
> head(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-01-10 11:00:00 122.758 122.893 122.746 122.859 2 2017-01-10 11:15:00 122.860 122.924 122.818 122.848 3 2017-01-10 11:30:00 122.850 122.856 122.705 122.720 4 2017-01-10 11:45:00 122.721 122.737 122.654 122.693 5 2017-01-10 12:00:00 122.692 122.850 122.692 122.818 6 2017-01-10 12:15:00 122.820 122.937 122.785 122.920 # ... 追加変数をあと一つ:Vol <dbl>
そして下記は最後です。
> tail(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-05-05 20:30:00 123.795 123.895 123.780 123.888 2 2017-05-05 20:45:00 123.889 123.893 123.813 123.831 3 2017-05-05 21:00:00 123.833 123.934 123.825 123.916 4 2017-05-05 21:15:00 123.914 123.938 123.851 123.858 5 2017-05-05 21:30:00 123.859 123.864 123.781 123.781 6 2017-05-05 21:45:00 123.779 123.864 123.781 123.781 # ... 追加変数をあと一つ:Vol <dbl>
つまり、開始日が10.01.2017、終了日が05.05.2017の8000のバーがあることになります。価格の派生物である平均価格、標準価格及び加重終値をdataframe prに加えましょう。
evalq(pr %<>% mutate(., Med = (High + Low)/2, Typ = (High + Low + Close)/3, Wg = (High + Low + 2 * Close)/4, #CO = 終値 - 始値、 #HO = 終値 - 始値、 #LO = 低値 - 始値、 dH = c(NA, diff(High)), dL = c(NA, diff(Low)) ), env)
1.2. 予測子
ここでは一連の単純化された予測変数を使って作業します。その役割を果たすのはFATL、SATL、RFTL、RSTLデジタルフィルタです。それらは、V. Kravchukによる論文"New Adaptive Method of Following the Tendency and Market Cycles"(動向及び市場サイクルに従う新しい適応的方法)に記載されています。この記事は、本稿に添付されたファイルにあります("New Tools of Technical Analysis and their Interpretation"(新しい分析ツールとその解釈)章を参照) 。ここではそれらを一覧するだけにします。
- FATL(高速適応トレンドライン)
- SATL(低速適応トレンドライン)
- RFTL(参照高速トレンドライン)
- RSTL(参照低速トレンドライン)
FATSとSALTの変化率は、 FILM(高速トレンドラインモメンタム)と STLM(低速トレンドラインモメンタム)指標を使用して監視できます。
RBCIとPCCIの2つのオシレータが必要です。RBCI (Range Bound Channel Index)インデックスは、チャネルフィルタを使用して計算される帯域幅限定チャネルインデックスです。このフィルタは、低周波トレンドと低周波ノイズを除去します。PCCI (Perfect Commodity Channel Index)インデックスは、完璧なコモディティチャネルインデックスです。
FATL、SATL、RFTL、RSTLデジタルフィルタを計算する関数は次のようになります。
#-----DigFiltr------------------------- DigFiltr <- function(X, type = 1){ # X - ベクトル require(rowr) fatl <- c( +0.4360409450, +0.3658689069, +0.2460452079, +0.1104506886, -0.0054034585, -0.0760367731, -0.0933058722, -0.0670110374, -0.0190795053, +0.0259609206, +0.0502044896, +0.0477818607, +0.0249252327, -0.0047706151, -0.0272432537, -0.0338917071, -0.0244141482, -0.0055774838, +0.0128149838, +0.0226522218, +0.0208778257, +0.0100299086, -0.0036771622, -0.0136744850, -0.0160483392, -0.0108597376, -0.0016060704, +0.0069480557, +0.0110573605, +0.0095711419, +0.0040444064, -0.0023824623, -0.0067093714, -0.0072003400, -0.0047717710, 0.0005541115, 0.0007860160, 0.0130129076, 0.0040364019 ) rftl <- c(-0.0025097319, +0.0513007762 , +0.1142800493 , +0.1699342860 , +0.2025269304 , +0.2025269304, +0.1699342860 , +0.1142800493 , +0.0513007762 , -0.0025097319 , -0.0353166244, -0.0433375629 , -0.0311244617 , -0.0088618137 , +0.0120580088 , +0.0233183633, +0.0221931304 , +0.0115769653 , -0.0022157966 , -0.0126536111 , -0.0157416029, -0.0113395830 , -0.0025905610 , +0.0059521459 , +0.0105212252 , +0.0096970755, +0.0046585685 , -0.0017079230 , -0.0063513565 , -0.0074539350 , -0.0050439973, -0.0007459678 , +0.0032271474 , +0.0051357867 , +0.0044454862 , +0.0018784961, -0.0011065767 , -0.0031162862 , -0.0033443253 , -0.0022163335 , +0.0002573669, +0.0003650790 , +0.0060440751 , +0.0018747783) satl <- c(+0.0982862174, +0.0975682269 , +0.0961401078 , +0.0940230544, +0.0912437090 , +0.0878391006, +0.0838544303 , +0.0793406350 ,+0.0743569346 ,+0.0689666682 , +0.0632381578 ,+0.0572428925 , +0.0510534242,+0.0447468229, +0.0383959950, +0.0320735368, +0.0258537721 ,+0.0198005183 , +0.0139807863,+0.0084512448, +0.0032639979, -0.0015350359, -0.0059060082 ,-0.0098190256 , -0.0132507215, -0.0161875265, -0.0186164872, -0.0205446727, -0.0219739146 ,-0.0229204861 , -0.0234080863,-0.0234566315, -0.0231017777, -0.0223796900, -0.0213300463 ,-0.0199924534 , -0.0184126992,-0.0166377699, -0.0147139428, -0.0126796776, -0.0105938331 ,-0.0084736770 , -0.0063841850,-0.0043466731, -0.0023956944, -0.0005535180, +0.0011421469 ,+0.0026845693 , +0.0040471369,+0.0052380201, +0.0062194591, +0.0070340085, +0.0076266453 ,+0.0080376628 , +0.0083037666,+0.0083694798, +0.0082901022, +0.0080741359, +0.0077543820 ,+0.0073260526 , +0.0068163569,+0.0062325477, +0.0056078229, +0.0049516078, +0.0161380976 ) rstl <- c(-0.0074151919,-0.0060698985,-0.0044979052,-0.0027054278,-0.0007031702,+0.0014951741, +0.0038713513,+0.0064043271,+0.0090702334,+0.0118431116,+0.0146922652,+0.0175884606, +0.0204976517,+0.0233865835,+0.0262218588,+0.0289681736,+0.0315922931,+0.0340614696, +0.0363444061,+0.0384120882,+0.0402373884,+0.0417969735,+0.0430701377,+0.0440399188, +0.0446941124,+0.0450230100,+0.0450230100,+0.0446941124,+0.0440399188,+0.0430701377, +0.0417969735,+0.0402373884,+0.0384120882,+0.0363444061,+0.0340614696,+0.0315922931, +0.0289681736,+0.0262218588,+0.0233865835,+0.0204976517,+0.0175884606,+0.0146922652, +0.0118431116,+0.0090702334,+0.0064043271,+0.0038713513,+0.0014951741,-0.0007031702, -0.0027054278,-0.0044979052,-0.0060698985,-0.0074151919,-0.0085278517,-0.0094111161, -0.0100658241,-0.0104994302,-0.0107227904,-0.0107450280,-0.0105824763,-0.0102517019, -0.0097708805,-0.0091581551,-0.0084345004,-0.0076214397,-0.0067401718,-0.0058083144, -0.0048528295,-0.0038816271,-0.0029244713,-0.0019911267,-0.0010974211,-0.0002535559, +0.0005231953,+0.0012297491,+0.0018539149,+0.0023994354,+0.0028490136,+0.0032221429, +0.0034936183,+0.0036818974,+0.0038037944,+0.0038338964,+0.0037975350,+0.0036986051, +0.0035521320,+0.0033559226,+0.0031224409,+0.0028550092,+0.0025688349,+0.0022682355, +0.0073925495) if (type == 1) {k = fatl} if (type == 2) {k = rftl} if (type == 3) {k = satl} if (type == 4) {k = rstl} n <- length(k) m <- length(X) k <- rev(k) f <- rowr::rollApply(data = X, fun = function(x) {sum(x * k)}, window = n, minimum = n, align = "right") while (length(f) < m) { f <- c(NA,f)} return(f) }
計算後は、それらをデータフレームprに追加します。
evalq(pr %<>% mutate(., fatl = DigFiltr(Close, 1), rftl = DigFiltr(Close, 2), satl = DigFiltr(Close, 3), rstl = DigFiltr(Close, 4) ), env)
FTLM、STLM、RBCI、PCCIオシレータとデジタルフィルタの最初の違いと最初の違いをデータフレーム prに追加します。
evalq(pr %<>% mutate(., ftlm = fatl - rftl, rbci = fatl - satl, stlm = satl - rstl, pcci = Close - fatl, v.fatl = c(NA, diff(fatl)), v.rftl = c(NA, diff(rftl)), v.satl = c(NA, diff(satl)), v.rstl = c(NA, diff(rstl)*10) ), env) evalq(pr %<>% mutate(., v.ftlm = c(NA, diff(ftlm)), v.stlm = c(NA, diff(stlm)), v.rbci = c(NA, diff(rbci)), v.pcci = c(NA, diff(pcci)) ), env)
1.3. 目標変数
ZigZag()は目標変数を生成する指標として使用されます。
計算のための関数は時系列と屈曲の最小長(intまたはdouble)と計算のための価格の種類(Close、Med、Typ、Wd、(High, Low)を伴う )の2つのパラメータを受け取ります。
#------ZZ----------------------------------- par <- c(25, 5) ZZ <- function(x, par) { # x - ベクトル require(TTR) require(magrittr) ch = par[1] mode = par[2] if (ch > 1) ch <- ch/(10 ^ (Dig - 1)) switch(mode, xx <- x$Close, xx <- x$Med, xx <- x$Typ, xx <- x$Wd, xx <- x %>% select(High,Low)) zz <- ZigZag(xx, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]} return(zz) }
ジグザグ、最初の差、最初の差の符号を計算し、それらをデータフレームprに加えます。
evalq(pr %<>% cbind(., zigz = ZZ(., par = par)), env) evalq(pr %<>% cbind(., dz = diff(pr$zigz) %>% c(NA, .)), env) evalq(pr %<>% cbind(., sig = sign(pr$dz)), env)
1.4. 初期データセット
計算の結果としてどのようなデータが得られるかをまとめましょう。
端末から、EURJPYのM15時間枠にOHLCVベクトルとバーの始まりの一時的なマークを受け取りました。これらのデータはprデータフレームを形成しました。変数 FAT、SALT、RFTL、RSTL、FILM、STLM、RBCI、PCCIとその最初の違いがこのデータフレームに追加されました。ジグザグは25ポイント(小数点以下4桁)を最小限に活用し、その最初の差と、シグナルとして使用される最初の差(-1,1)の符号もデータフレームに追加されました。
これらのデータはすべてグローバル環境ではなく、すべての計算が実行される新しい子環境envに読み込まれました。この隔離によって、計算中に名前の競合が発生することなく、異なる銘柄や時間枠のデータセットを使用できます。
以下にデータフレームpr全体の構造を示します。以下の計算に必要な変数は、これから簡単に抽出できます。
str(env$pr) 'data.frame': 8000 obs. of 30 variables: $ Data : POSIXct, format: "2017-01-10 11:00:00" ... $ Open : num 123 123 123 123 123 ... $ High : num 123 123 123 123 123 ... $ Low : num 123 123 123 123 123 ... $ Close : num 123 123 123 123 123 ... $ Vol : num 3830 3360 3220 3241 3071 ... $ Med : num 123 123 123 123 123 ... $ Typ : num 123 123 123 123 123 ... $ Wg : num 123 123 123 123 123 ... $ dH : num NA 0.031 -0.068 -0.119 0.113 ... $ dL : num NA 0.072 -0.113 -0.051 0.038 ... $ fatl : num NA NA NA NA NA NA NA NA NA NA ... $ rftl : num NA NA NA NA NA NA NA NA NA NA ... $ satl : num NA NA NA NA NA NA NA NA NA NA ... $ rstl : num NA NA NA NA NA NA NA NA NA NA ... $ ftlm : num NA NA NA NA NA NA NA NA NA NA ... $ rbci : num NA NA NA NA NA NA NA NA NA NA ... $ stlm : num NA NA NA NA NA NA NA NA NA NA ... $ pcci : num NA NA NA NA NA NA NA NA NA NA ... $ v.fatl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rftl: num NA NA NA NA NA NA NA NA NA NA ... $ v.satl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rstl: num NA NA NA NA NA NA NA NA NA NA ... $ v.ftlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.stlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.rbci: num NA NA NA NA NA NA NA NA NA NA ... $ v.pcci: num NA NA NA NA NA NA NA NA NA NA ... $ zigz : num 123 123 123 123 123 ... $ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ... $ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
dataSetデータフレームから以前に計算されたすべての予測子を選択します。目標変数sigを係数に変換し、1バー分前方(将来)に移動します。
evalq(dataSet <- pr %>% tbl_df() %>%
dplyr::select(Data, ftlm, stlm, rbci, pcci,
v.fatl, v.satl, v.rftl, v.rstl,
v.ftlm, v.stlm, v.rbci, v.pcci, sig) %>%
dplyr::filter(., sig != 0) %>%
mutate(., Class = factor(sig, ordered = F) %>%
dplyr::lead()) %>%
dplyr::select(-sig),
env)
データ分析の可視化
OHLCチャートの描画にはggplot2パッケージを使用します。最後の2日間のデータをとって、棒グラフで図表を描きます。
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + labs(title = "EURJPY Candlestick Chart", y = "Close Price", x = "") + theme_tq(), env)
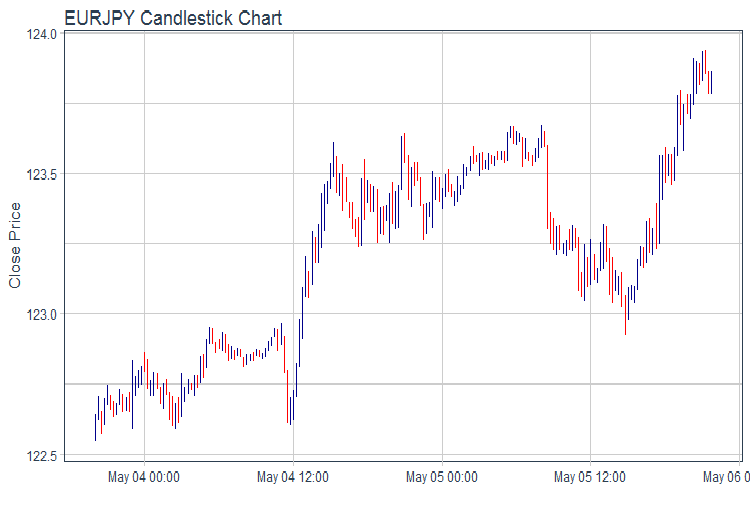
図1 相場のチャート
FATL, SATL, RFTL, RSTLとZZのチャートを描画します。
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + geom_line(aes(Data, fatl), color = "steelblue", size = 1) + geom_line(aes(Data, rftl), color = "red", size = 1) + geom_line(aes(Data, satl), color = "gold", size = 1) + geom_line(aes(Data, rstl), color = "green", size = 1) + geom_line(aes(Data, zigz), color = "black", size = 1) + labs(title = "EURJPY Candlestick Chart", subtitle = "Combining Chart Geoms", y = "Close Price", x = "") + theme_tq(), env)
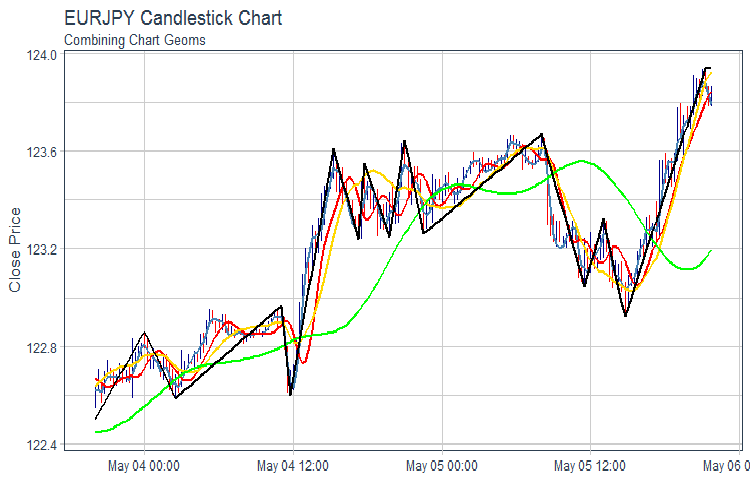
図2 FATL、SATL、RFTL、RSTL 及びZZ
より便利な表現のためにオシレーターを3つのグループに分けます。
require(dygraphs) evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, ftlm, stlm, rbci, pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator base") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "blue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
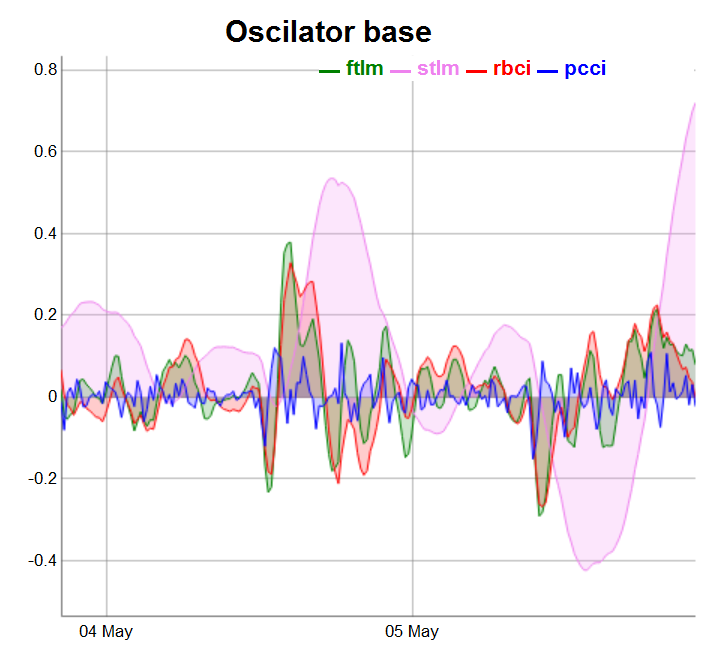
図3 基本オシレータ
evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, v.fatl, v.satl, v.rftl, v.rstl) %>% tk_xts() %>% dygraph(., main = "Oscilator 2") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
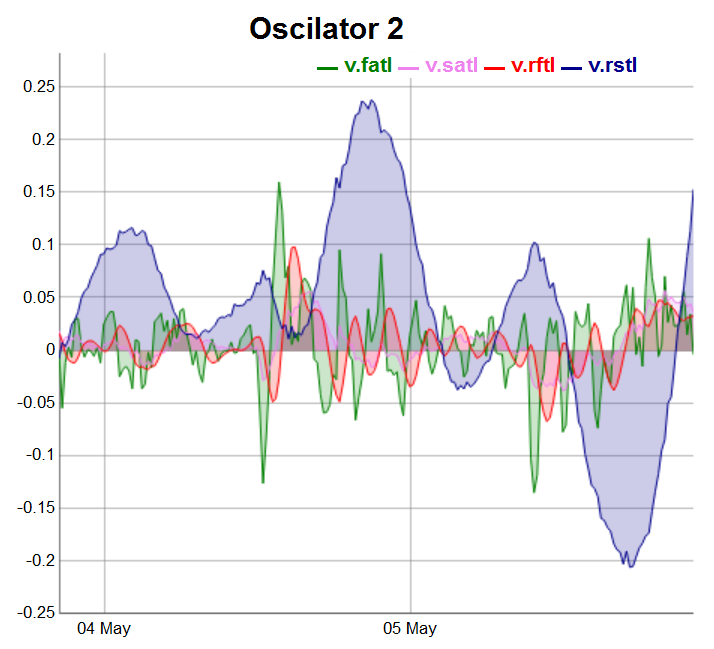
図4 第2群のオシレータ
第3群のオシレータは、最後の100バーに描画されます。
evalq(dataSet %>% tail(., 100) %>% tk_tbl %>% select(Data, v.ftlm, v.stlm, v.rbci, v.pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator 3") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
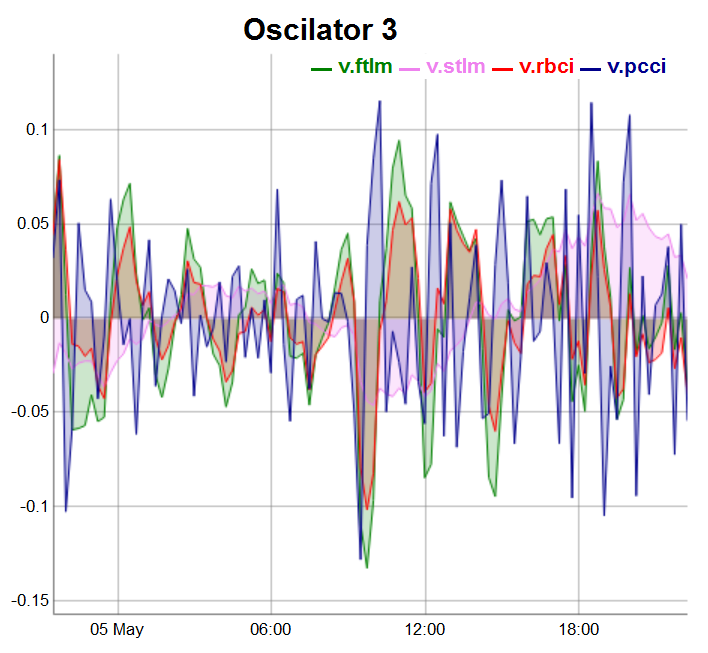
図5 第3群のオシレータ
2. 探索的データ解析(EDA)
「統計的な質問にささいなものはない、疑わしい統計的な手順はある」 - David Cox卿
「正しい問題に対するおおよその答えは、おおよその問題に対する正確な答えよりもかなり価値がある」 - John Tukey
ここでは、EDAを使用して、使用中のデータの理解を深めていきます。これを行う最も簡単な方法は、リサーチツールとしての質問を使用することです。質問をするときは、データの特定の部分に焦点を当てます。これは、使用するチャート、モデル、及び変換を決定するのに役立ちます。
EDAは本質的に創造的なプロセスです。最も創造的なプロセスと同様に、良い質問をするための鍵は、より多くの質問を作成することです。分析の初めに基本的な質問をするのは難しいですが、これはデータセットに含まれる結論がわからないためです。一方、我々が聞くすべての新しい質問は、データの新しい側面を強調し、発見の機会を増やします。データセットの中で最も興味深い部分にすばやく移動し、順次質問することで状況を明確にすることができます。
データを調査するためにどのような質問をするべきかについての規則はありません。そうは言いましたが、役に立つ質問には2つの種類があります。
-
変数がどのような変化しているか
- 変数間にはどのような共分散が起こっているか
原理の概念を定義しましょう。
変動とは、変数の値が異なる測定で変化する傾向のことです。日常生活にはさまざまな変動があります。どんな変数でも7回連続測定すると、7つの異なる値が得られます。これは、たとえ光の速度などの定数についても当てはまります。各測定には、毎回異なる誤差が含まれています。同じ型の変数も変化することがあります。例は、異なる人の目の色や異なる時の電子エネルギーレベルです。各変数には、興味深い情報を明らかにする変動の独自の特徴があります。この情報を理解する最良の方法は、変数値の分布を視覚化することです。一見は百聞にしかずとはこのことです。
2.1. 全体統計
時系列の全体統計はtable.Stats()::PerformenceAnalitics関数を使用して追跡すると便利です。
> table.Stats(env$dataSet %>% tk_xts()) Using column `Data` for date_var. ftlm stlm rbci pcci Observations 7955.0000 7908.0000 7934.0000 7960.0000 NAs 42.0000 89.0000 63.0000 37.0000 Minimum -0.7597 -1.0213 -0.9523 -0.5517 Quartile 1 -0.0556 -0.1602 -0.0636 -0.0245 Median -0.0001 0.0062 -0.0016 -0.0001 Arithmetic Mean 0.0007 0.0025 0.0007 0.0001 Geometric Mean -0.0062 NaN -0.0084 -0.0011 Quartile 3 0.0562 0.1539 0.0675 0.0241 Maximum 2.7505 3.0407 2.3872 1.8859 SE Mean 0.0014 0.0033 0.0015 0.0006 LCL Mean (0.95) -0.0020 -0.0040 -0.0022 -0.0010 UCL Mean (0.95) 0.0034 0.0090 0.0035 0.0012 Variance 0.0152 0.0858 0.0172 0.0026 Stdev 0.1231 0.2929 0.1311 0.0506 Skewness 4.2129 1.7842 2.3037 6.4718 Kurtosis 84.6116 16.7471 45.0133 247.4208 v.fatl v.satl v.rftl v.rstl Observations 7959.0000 7933.0000 7954.0000 7907.0000 NAs 38.0000 64.0000 43.0000 90.0000 Minimum -0.3967 -0.0871 -0.1882 -0.4719 Quartile 1 -0.0225 -0.0111 -0.0142 -0.0759 Median -0.0006 0.0003 0.0000 0.0024 Arithmetic Mean 0.0002 0.0002 0.0002 0.0011 Geometric Mean -0.0009 0.0000 -0.0003 -0.0078 Quartile 3 0.0220 0.0110 0.0138 0.0751 Maximum 1.4832 0.3579 0.6513 1.3093 SE Mean 0.0005 0.0002 0.0003 0.0015 LCL Mean (0.95) -0.0009 -0.0003 -0.0005 -0.0020 UCL Mean (0.95) 0.0012 0.0007 0.0009 0.0041 Variance 0.0023 0.0005 0.0009 0.0188 Stdev 0.0483 0.0219 0.0308 0.1372 Skewness 5.2643 2.6705 3.9472 1.5682 Kurtosis 145.8441 36.9378 74.4182 13.5724 v.ftlm v.stlm v.rbci v.pcci Observations 7954.0000 7907.0000 7933.0000 7959.0000 NAs 43.0000 90.0000 64.0000 38.0000 Minimum -0.9500 -0.2055 -0.6361 -1.4732 Quartile 1 -0.0280 -0.0136 -0.0209 -0.0277 Median -0.0002 -0.0001 -0.0004 -0.0002 Arithmetic Mean 0.0000 0.0001 0.0000 0.0000 Geometric Mean -0.0018 -0.0003 -0.0009 NaN Quartile 3 0.0273 0.0143 0.0207 0.0278 Maximum 1.4536 0.3852 1.1254 1.9978 SE Mean 0.0006 0.0003 0.0005 0.0006 LCL Mean (0.95) -0.0012 -0.0005 -0.0009 -0.0013 UCL Mean (0.95) 0.0013 0.0007 0.0009 0.0013 Variance 0.0032 0.0007 0.0018 0.0034 Stdev 0.0561 0.0264 0.0427 0.0579 Skewness 1.2051 0.8513 2.0643 3.0207 Kurtosis 86.2425 23.0651 86.3768 233.1964
この表が教えてくれるものは次のとおりです。
- 全ての予測変数には、未定義の変数NAが比較的少数しかない
- 全ての予測変数には、顕著な右歪みがある
- 全ての予測子は高い尖度を有する
2.2. 全体統計の可視化
「図の最大の価値は、私たちが見たこともないものに気づかせるときである」— John Tukey
dataSet変数の変化と共分散を見てみましょう。変数(14)の数は1つのチャートで表現することができないため、3つのグループに分割する必要があります。
require(GGally) evalq(ggpairs(dataSet, columns = 2:6, mapping = aes(color = Class), title = "DigFilter1"), env)
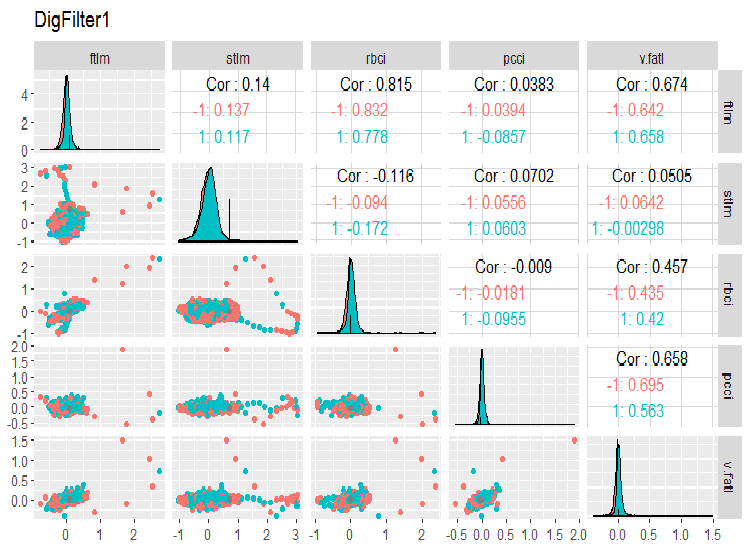
図6 予測子の第1グループ
evalq(ggpairs(dataSet, columns = 7:10, mapping = aes(color = Class), title = "DigFilter2"), env)
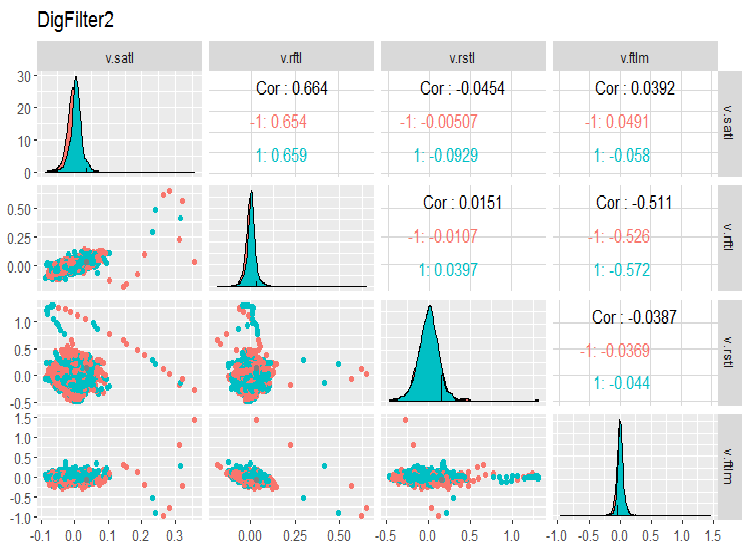
図7 予測子の第2グループ
evalq(ggpairs(dataSet, columns = 11:14, mapping = aes(color = Class), title = "DigFilter3"), env)
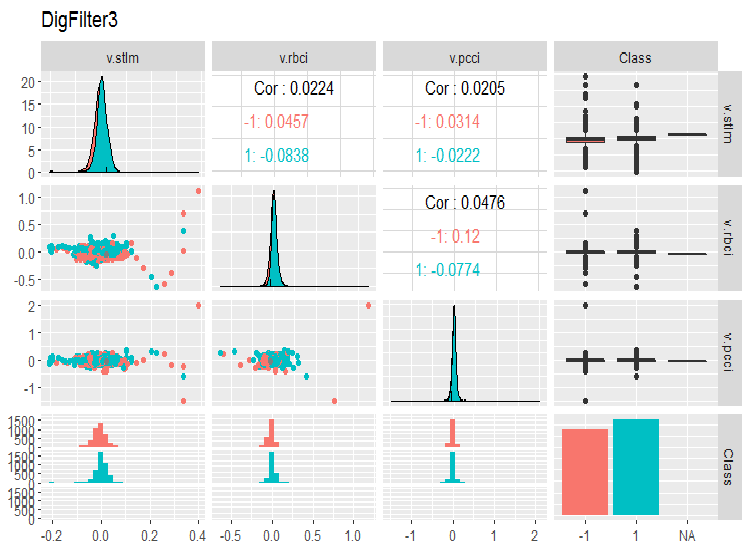
図8 予測子の第3グループ
チャート上には以下がみられるべきです。
- すべての予測子は正常な分布に近い形状をしており右の歪みははっきりとしている
- すべての予測変数には非常に狭い四分位範囲(IQR)がある
- すべての予測変数には顕著な外れ値がある
- 目標変数"Class”の2つのレベルの例の数はわずかな差がある
3. データの準備
通常、データの準備には7つの段階があります。
- 「補完」 - 欠落した/定義されていないデータの削除または転用
- 「分散」 - 分散がゼロまたはゼロに近い変数の削除
- 「分割」 - データセットの訓練/有効/検証サブセットへの分割
- 「スケーリング」 - 変数の範囲のスケーリング
- 「外れ値」- 外れ値の除去または転用
- 「サンプリング」 - クラスの不均衡の修正
- 「ノイズ除去」 - ノイズの除去または再定義
- 「選択」 - 無関係な予測子の選択
3.1. データクリーニング
未処理のデータを準備する最初の段階は、データ内の未定義の値と隙間を削除することです。多くのモデルでは、未定義データ(NA)とデータセットのギャップを使用できますが、メインアクションを開始する前に削除することをお勧めします。この操作は、モデルに関係なく全データセットに対して実行されます。
ここでの生データの全体統計は、データセットにNAが含まれていることを示しました。これらは人工的なAで、デジタルフィルタを計算するときに表示されます。その数はあまり多くないので、削除することができます。後で処理する準備ができているdataSetはすでに存在するので、クリーニングしましょう。
一般的な場合、クリーニングとは次の操作を意味します。
- ゼロまたはゼロに近い分散予測子を削除 (method = c(“zv”, “nzv”))
- 相関の高い変数の削除。相関係数の閾値を設定するのはユーザーの責任で(method = "corr")、デフォルト値は0.9である。この段階は必ずしも必要ではなく、続く変換方法に依存する。
- 任意のクラス (method = “conditionalX“)で一意の値を1つしか持たない予測変数の削除
これらの操作はすべて、上記の方法でpreProcess()::caret 関数で実装されています。これらの操作は、訓練セットとテストセットに分けられる前に完全なデータセットに実行されます。
require(caret)
evalq({preProClean <- preProcess(x = dataSet,method = c("zv", "nzv", "conditionalX", "corr"))
dataSetClean <- predict(preProClean, dataSet %>% na.omit)},
env)
削除された予測子が存在するかどうか、及びクリーニングの後で何があるかを確認してみましょう。
> env$preProClean$method$remove #[1] "v.rbci" > dim(env$dataSetClean) [1] 7906 13 > colnames(env$dataSetClean) [1] "Data" "ftlm" "stlm" "rbci" "pcci" [6] "v.fatl" "v.satl" "v.rftl" "v.rstl" "v.ftlm" [11] "v.stlm" "v.pcci" "Class"
3.2. 外れ値の特定と処理
歪度や外れ値などのデータ品質の問題は、しばしば相互関係を持ち、相互依存しています。これは、データの事前処理を時間を費やすだけでなく、データセット内の相関及び傾向を見つけることを困難にします。
外れ値とは何か
外れ値が他の観測値から離れすぎる観測値であることに同意しましょう。外れ値の詳細な分類、その識別方法及び処理の方法は、[2]に記載されています。
外れ値の種類
外れ値は、変数の分布やそのようなデータを使用してモデルの訓練に大きな歪みをもたらします。外れ値を特定して処理するには多くの方法があります。方法の選択は主に外れ値を局所的に特定するか全域的に特定するかに依存します。局所的な外れ値は、1つの変数の外れ値です。全域的な外れ値は、行列またはデータフレームのいずれかによって定義された多次元空間内の外れ値です。
外れ値の原因とは何か
外れ値は原因によって分けることができます。
人工的
- データ入力誤差(データの収集、記録、及び処理中に発生した誤差)
- 実験誤差
- サンプリング誤差
変数の性質によって引き起こされる自然誤差
外れ値はどんな影響を持つか
外れ値は、データ分析と統計モデリングの結果を破壊する可能性があります。これにより、誤差分散が増加し、テストの統計力が低下します。外れ値の分布がランダムでない場合、正常性が低下する可能性があります。外れ値は、回帰分析と分散分析の主な仮定に加えて、モデルの他の統計的仮定に影響を与える可能性があります。
局地的外れ値はどのように認識できるか
通常、外れ値はデータを視覚化することによって明らかにすることができます。最も簡単で広く使用されている方法の1つがボックスプロットです。ftlm予測子を例に挙げてみましょう。
evalq(ggplot(dataSetClean, aes(x = factor(0),
y = ftlm,
color = 'red')) +
geom_boxplot() + xlab("") +
scale_x_discrete(breaks = NULL) +
coord_flip(),
env)
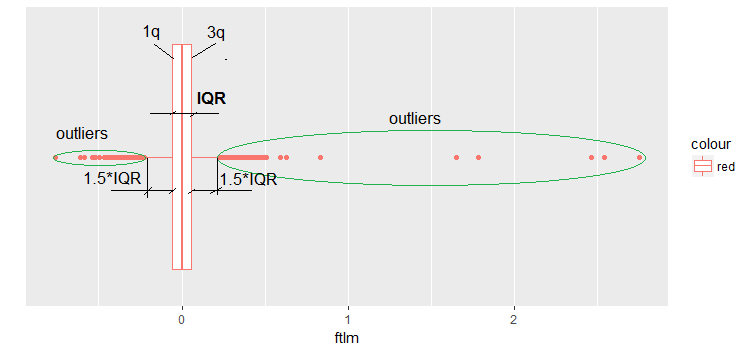
図9 ftlmボックスプロット
ダイアグラムへのコメントのいくつかは次の通りです。
IQRは、四分位範囲または第1四分位点と第3四分位点との間の距離です。
これによって、いくつかの方法で外れ値を定義することができます。
- -1.5 * IQRより小さく、+ 1.5 * IQRより大きい値は外れ値である。場合によっては、係数は2または3に設定される。1.5 * IQRと3 * IQRの間のすべての値は平均外れ値と呼ばれ、3 * IQR以上の値は極限外れ値と呼ばれる。
- 5パーセンタイルと95パーセンタイルの外にあるように見える値は、外れ値とみなすことができる。
- 3つ以上のMSDをプロットした点も外れ値である。
今後は、IQRを使った最初の定義を使用します。
外れ値はどのように処理できるか
外れ値を処理するほとんどの方法は、NA除去観測、観測の変換、セグメント化、代理処理などの処理方法に似ています。
- 外れ値の除去:データ入力エラーの結果として外れ値が表示される場合、または外れ値の数が非常に少ない場合は、外れ値の値を削除します。外れ値を除去するために分布の末尾を調整することもできます。例えば、上下から1%を捨てることができます。
- 変換とビニング:
- 変数の変換は外れ値を除外することができます(これについては、本稿の次の部分での次の部分で説明します)。
- 自然対数は、極端な値に対応する変化を減少させます(これについては、本稿の次の部分で詳しく説明します)。
- 離散化も変数を変換する方法です(次の部分を参照)。
- 観測に重み付けを使用することもできます(本稿ではこれについては説明しません)。
インピュテーション(データの補完):外れ値は、定義されていない値を補完するために使用するのと同じメソッドを使用して補完することができます。そのためには、平均、中央値、及び最頻値が使用できます。値を補完する前に、外れ値が自然であるか人工的であるかを確認する必要があります。外れ値が人工的なものであれば、補完することができます。
サンプルに相当数の外れ値が含まれている場合は、統計モデルで個別に分析する必要があります。ここでは外れ値に取り組むために使用される一般的な方法について議論されます。それらは除去と補完です。
外れ値の除去
外れ値は、データの入力か処理によって発生した場合や外れ値の数が非常に少ない場合(統計変数メトリックを特定する場合のみ)は削除する必要があります。
1つの変数(例えば、ftlm)のデータは、外れ値なしで次のように抽出できます。
evalq({dataSetClean$ftlm -> x
out.ftlm <- x[!x %in% boxplot.stats(x)$out]},
env)
または
evalq({dataSetClean$ftlm -> x
out.ftlm1 <- x[x > quantile(x, .25) - 1.5*IQR(x) &
x < quantile(x, .75) + 1.5*IQR(x)]},
env)
これらは同一なのでしょうか。
> evalq(all.equal(out.ftlm, out.ftlm1), env)
[1] TRUE
データセットにいくつの外れ値があるのでしょうか?
> nrow(env$dataSetClean) - length(env$out.ftlm) [1] 402
ftlmは外れ値なしでは次のようになります。
boxplot(env$out.ftlm, main = "ftlm without outliers", boxwex = 0.5)
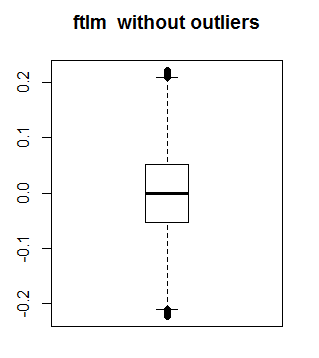
図10 外れ値なしのftlm
データフレーム内のすべての変数は異なる数の外れ値を持つ可能性があるため、上記の方法は行列とデータフレームには適していません。このようなサンプルには、NAに局所的外れ値を置き換えた後、NAを処理する標準的な方法が適しています。以下にはNAに局地的外れ値を代入する関数を示します。
#-------remove_outliers------------------------------- remove_outliers <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) y <- x y[x < (qnt[1] - H)] <- NA y[x > (qnt[2] + H)] <- NA y }
c(Data, Class)以外のすべての変数でdataSetClean及びNAの外れ値以外を変更してみましょう。これで、新しいx.out:セット の分布がどのように変化するかを見てみましょう。
evalq({
dataSetClean %>% select(-c(Data,Class)) %>% as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
remove_outliers(x[ ,i])
} -> x.out
colnames(x.out) <- colnames(x)
},
env)
par(mfrow = c(1, 1))
chart.Boxplot(env$x,
main = "x.out with outliers",
xlab = "")
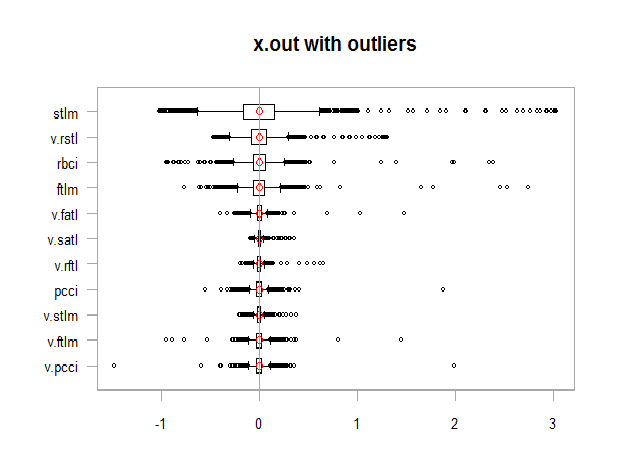
図11 外れ値を含むデータ
chart.Boxplot(env$x.out, main = "x.out without outliers", xlab = "")
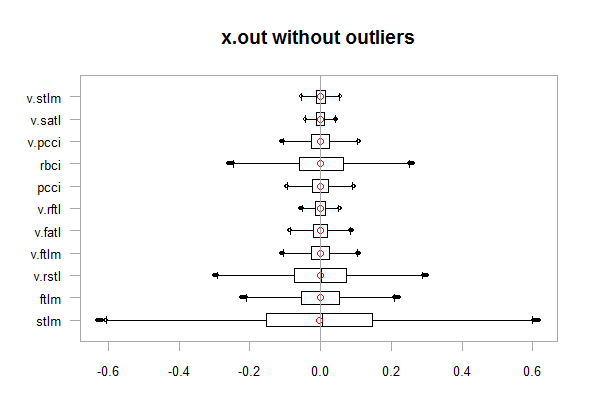
図12 外れ値なしのデータ
現れるNAの外れ値への補完
補完とは、欠損、不正確または無効な値を他の値に置き換えることです。モデルを訓練するための入力データには有効な値のみを含める必要があります。次のいずれかができます。
- 平均、中央値、最頻値を代用する(セットの統計的特性は変化しない)
- 1.5*IQRより大きい外れ値を0.95パーセンタイルで置き換え、- 1.5*IQRより小さい外れ値を0.05パーセンタイルで代用する
2番目のアクションを実行する関数を記述し、変換が終わったら、その分布を見てみましょう。
#-------capping_outliers-------------------------------
capping_outliers <- function(x, na.rm = TRUE, ...) {
qnt <- quantile(x, probs = c(.25, .75),
na.rm = na.rm, ...)
caps <- quantile(x, probs = c(.05, .95),
na.rm = na.rm, ...)
H <- 1.5 * IQR(x, na.rm = na.rm)
y <- x
y[x < (qnt[1] - H)] <- caps[1]
y[x > (qnt[2] + H)] <- caps[2]
y
}
evalq({dataSetClean %>% select(-c(Data,Class)) %>%
as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
capping_outliers(x[ ,i])
} -> x.cap
colnames(x.cap) <- colnames(x)
},
env)
chart.Boxplot(env$x.cap,
main = "x.cap with capping outliers",
xlab = "")
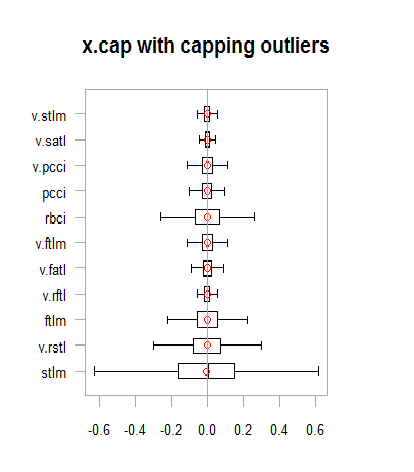
図13 補完された外れ値を持つデータセット
dataSetCap の変動と共分散を考えてみましょう。これはデータセットと同じですが、クリーニングされており、補完された局地的外れ値を含みます。変数の数 (13) が多く同じチャートに入れることができないので、2つのグループに分けます。
evalq(x.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetCap, env) require(GGally) evalq(ggpairs(dataSetCap, columns = 2:7, mapping = aes(color = Class), title = "PredCap1"), env)
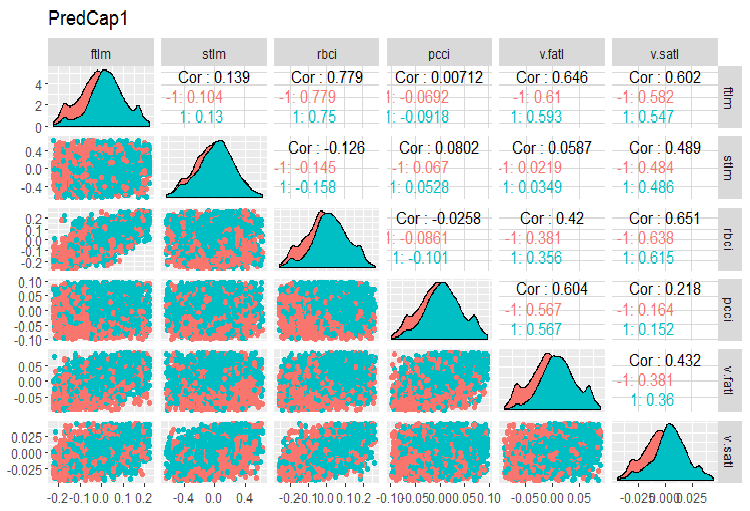
図14 補完された外れ値を持つデータセットの最初の部分の変動と共分散
そして下記がセットの第2部です。
evalq(ggpairs(dataSetCap, columns = 8:13, mapping = aes(color = Class), title = "PredCap2"), env)
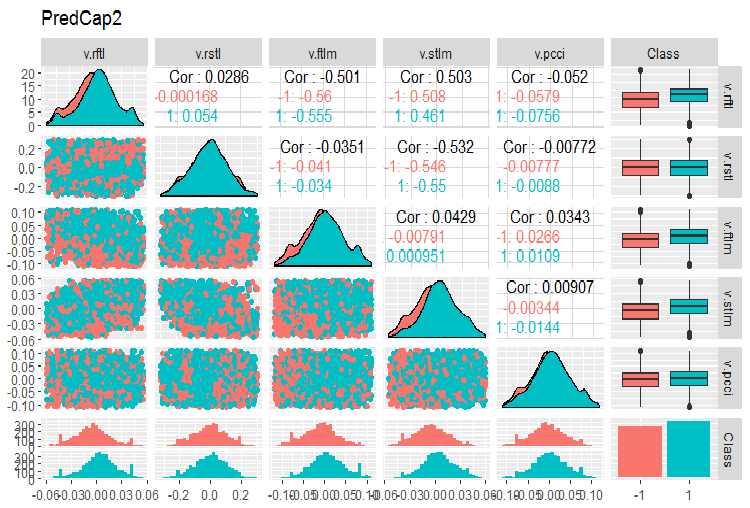
図15 補完された外れ値を持つデータセットの2番目の部分の変動と共分散
全域的外れ値はどのように特定できるか
通常、2次元または多次元の外れ値は、影響度インデックスまたは近接度インデックスを使用して識別されます。全域的外れ値を識別するにはさまざまな距離が使用され、これにはDMwR、mvoutliers、Rlofのようなパッケージを使用することができます。全域的外れ値はLOF(局所的外れ値)とともに評価されます。外れ値xを持つセットと補完された外れ値x.capを持つセットのLOFが計算され比較されます。
##------DMwR2------------------- require(DMwR2) evalq(lof.x <- lofactor(x,10), env) evalq(lof.x.cap <- lofactor(x.cap,10), env) par(mfrow = c(1, 3)) boxplot(env$lof.x, main = "lof.x", boxwex = 0.5) boxplot(env$lof.x.cap, main = "lof.x.cap", boxwex = 0.5) hist(env$lof.x.cap, breaks = 20) par(mfrow = c(1, 1))
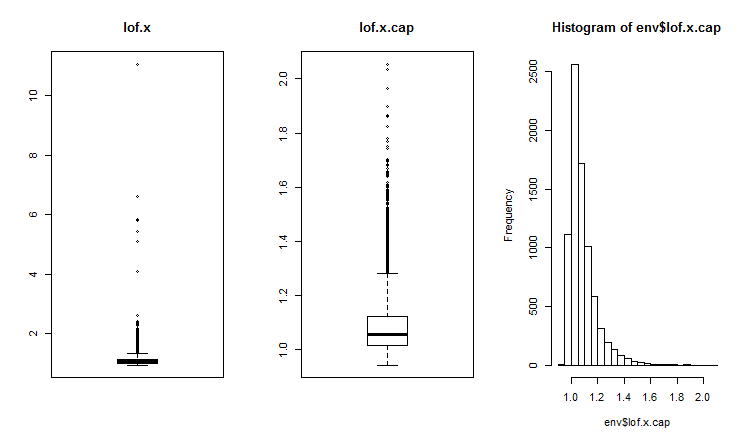
図16 外れ値を持つデータセットと補完された外れ値を持つデータセットの全域的外れ値因子
lof()関数は Rlofパッケージで実装されていて、k最近傍を使用して行列データの局所的外れ値因子を見出します[3]。局所的外れ値因子(LOF)とは、観測値ごとに計算された外れ値に属する確率です。この確率に基づいて、観測値が外れ値であるかどうかを決定します。
LOFは、観測値が外れ値であるかどうかを識別するために局所密度を考慮に入れます。これは、 "dprep"パッケージで利用可能なlofactor()関数とは別の構造のデータと距離計算の関数を使用したLOFのより効率的な実装で、同時に計算されるkのいくつかの値、及び標準のユークリッド距離に加えて距離のさまざまな尺度をサポートする予定です。計算は、複数のプロセッサコアで同時に実行されます。“minkowski” を使って距離を計算し、同じ2つのセット(x及びx.cap)のlofactorを5、6、7、8、9、10の隣人で計算しましょう。これらのlofactorsのヒストグラムを描きましょう。
require(Rlof) evalq(Rlof.x <- lof(x, c(5:10), cores = 2, method = 'minkowski'), env) evalq(Rlof.x.cap <- lof(x.cap, c(5:10), cores = 2, method = 'minkowski'), env) par(mfrow = c(2, 3)) hist(env$Rlof.x.cap[ ,6], breaks = 20) hist(env$Rlof.x.cap[ ,5], breaks = 20) hist(env$Rlof.x.cap[ ,4], breaks = 20) hist(env$Rlof.x.cap[ ,3], breaks = 20) hist(env$Rlof.x.cap[ ,2], breaks = 20) hist(env$Rlof.x.cap[ ,1], breaks = 20) par(mfrow = c(1, 1))
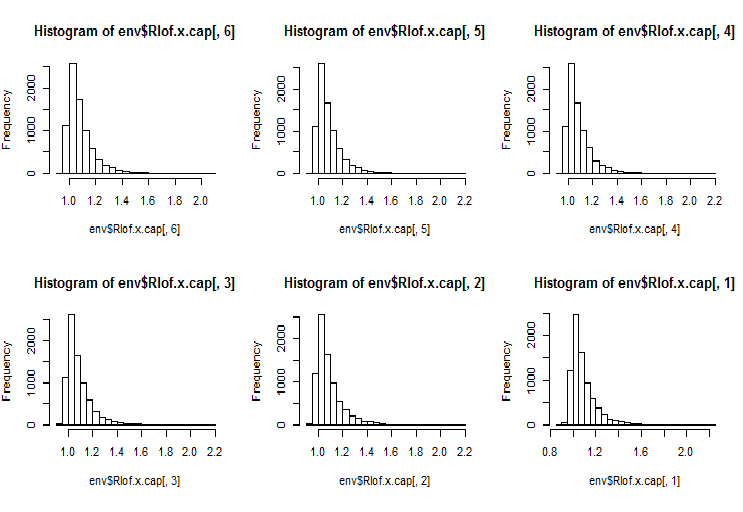
図17 k隣人での全域的外れ値因子
ほぼすべての観測値はlofactor =1.6の範囲内にあります。以下はこの範囲外の観測値です。
> sum(env$Rlof.x.cap[ ,6] >= 1.6) [1] 32
この中程度の外れ値の数は、このサイズのセットに対してはごく少ないものです。
注意事項観測値が外れ値として扱われる範囲の境界を識別するには、訓練データセットを使用する必要があります。テスト/検証データセットの変数の値は、訓練セットによって得られたパラメータを使用して処理されます。これらのパラメータは何かというと、上限= 1.5*IQR、下限= -1.5*IQR、キャップ=c(0.05, 0.95) パーセンタイルです。これらは以前の計算で使用されました。範囲の限界の計算と外れ値の補完に他の方法が使用された場合は、それらを訓練データセット用に定義し、検証データセットとテストデータセットを処理するために保存及び格納する必要があります。
予備計算を実行する関数を記述しましょう。
#-----prep.outlier-------------- prep.outlier <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) caps <- quantile(x, probs = c(.05, .95), na.rm = na.rm, ...) list(lower = qnt[1] - H, upper = qnt[2] + H, med = median(x), cap1 = caps[1], cap2 = caps[2]) }
外れ値を特定し、補完させるために必要なパラメータを計算します。訓練セットの予備の長さを最初に4000バーとし、次の2000バーをテストデータセットとして使用します。
evalq(
{train <- x[1:4000, ]
foreach(i = 1:ncol(train), .combine = "cbind") %do% {
prep.outlier(train[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
#pre.outl %<>% t()
},
env)
結果をみてみましょう。
> env$pre.outl ftlm stlm rbci pcci lower.25% -0.2224942912 -0.59629203 -0.253231002 -9.902232e-02 upper.75% 0.2214486206 0.59242529 0.253529797 9.826936e-02 med -0.0001534451 0.00282525 -0.001184966 8.417127e-05 cap1.5% -0.1700418145 -0.40370452 -0.181326658 -6.892085e-02 cap2.95% 0.1676526431 0.39842675 0.183671973 6.853935e-02 v.fatl v.satl v.rftl v.rstl lower.25% -0.0900973332 -4.259328e-02 -0.0558921804 -0.2858430788 upper.75% 0.0888110249 4.178418e-02 0.0555115004 0.2889057397 med -0.0008581219 -2.130064e-05 -0.0001707447 -0.0001721546 cap1.5% -0.0658731640 -2.929586e-02 -0.0427927888 -0.1951978435 cap2.95% 0.0662353821 3.089833e-02 0.0411091859 0.1820803387 v.ftlm v.stlm v.pcci lower.25% -0.1115823754 -5.366875e-02 -0.1115905239 upper.75% 0.1108670403 5.367466e-02 0.1119495436 med -0.0003560178 -6.370034e-05 -0.0003173464 cap1.5% -0.0765431363 -3.686945e-02 -0.0765950814 cap2.95% 0.0789209957 3.614423e-02 0.0770439553
ここでわかるように、セットのすべての変数に対して第1四分位、第3四分位、中央値、5パーセンタイル及び95パーセンタイルが定義されています。外れ値の特定と処理に必要なのはこれですべてです。
以前に設定されたパラメータを使用して任意のデータセットの外れ値を処理する関数が必要です。可能な処理方法は、 NAに外れ値を代入し、中央値に外れ値を代入し、5/95パーセンタイルに外れ値を代入することです。
#---------treatOutlier--------------------------------- treatOutlier <- function(x, impute = TRUE, fill = FALSE, lower, upper, med, cap1, cap2){ if (impute) { x[x < lower] <- cap1 x[x > upper] <- cap2 return(x) } if (!fill) { x[x < lower | x > upper] <- NA return(x) } else { x[x < lower | x > upper] <- med return(x) } }
訓練セットに必要なパラメータを定義したので、5/95パーセンタイルの代わりに訓練セットの外れ値を処理してみましょう。その後、テストデータセットの外れ値を処理します。3つのチャートをプロットした得られたセットの分布を比較します。
#------------
evalq(
{
foreach(i = 1:ncol(train), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = train[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> train.out
colnames(train.out) <- colnames(train)
},
env
)
#-------------
evalq(
{test <- x[4001:6000, ]
foreach(i = 1:ncol(test), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = test[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> test.out
colnames(test.out) <- colnames(test)
},
env
)
#---------------
evalq(boxplot(train, main = "train with outliers"), env)
evalq(boxplot(train.out, main = "train.out without outliers"), env)
evalq(boxplot(test.out, main = "test.out without outliers"), env)
#------------------------
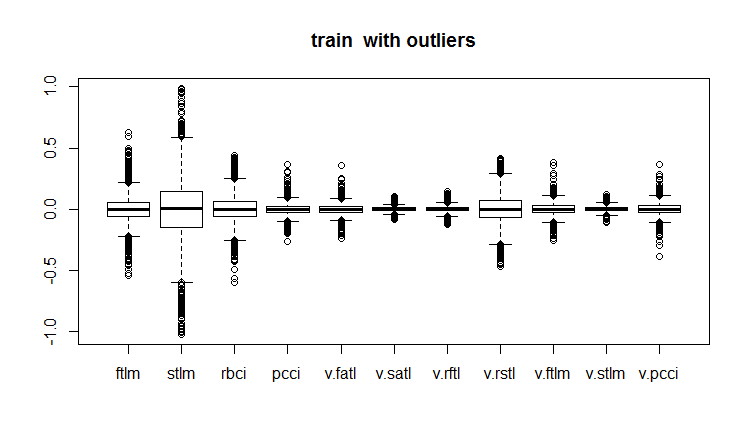
図18 外れ値を含む訓練データセット
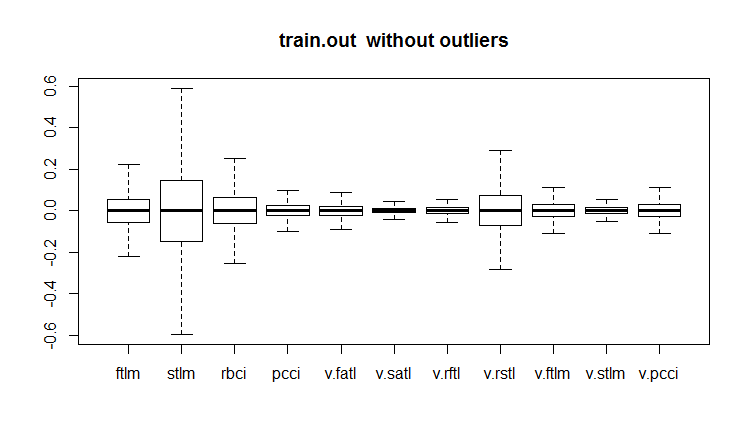
図19 補完された外れ値を持つ訓練データセット
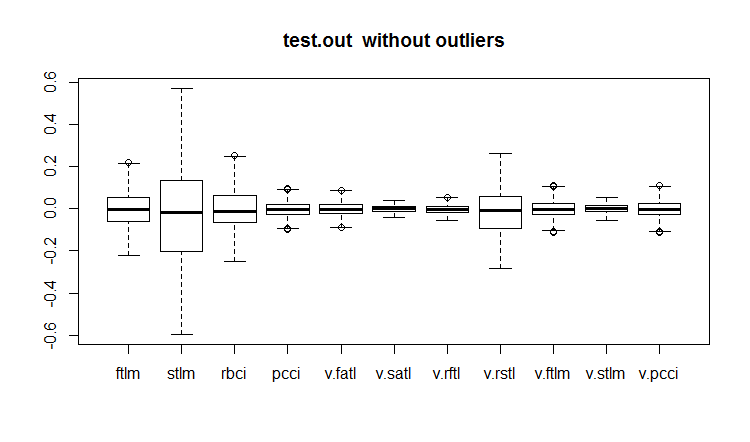
図20 補完された外れ値を持つデータセット
すべてのモデルが外れ値に敏感であるわけではなく、例えば、ツリー (DT) とランダムフォレスト(RF)を特定するモデルは、それらに影響されません。
外れ値を定義して処理するときには、他の "univOutl"、 "mvoutlier"、 “outlier”、funModeling::prep.outlier()のようなパッケージが有用かもしれません。
3.3. 歪度の排除
歪度は、分布の形式を示すもので、その評価には、一般的に変数の歪度係数が計算されます。通常、負の歪度は、平均が中央値より小さくて分布が左に歪んでいることを示し、正の歪度は、平均が中央値より大きくて分布が右に歪んでいることを示します。
予測子歪度が0の場合、データは完全に対称です。
予測子歪度が-1より小さいかまたは+1より大きい場合、データは著しく歪みます。
予測子歪度が-1と-1/2または+1と+1/2の間にある場合、データは適度に歪みます。
予測子歪度が-1/2と+1/2に等しい場合、データはほぼ対称です。
右の歪度は指数関数を使って左の歪度は対数を使って補正できます。
これで、歪度、外れ値及び他の変換が互いに関係していることが確認されました。歪度の指数が外れ値が削除されて補完された後にどのように変化したかを見てみましょう。
evalq({
sk <- skewness(x)
sk.out <- skewness(x.out)
sk.cap <- skewness(x.cap)
},
env)
> env$sk
ftlm stlm rbci pcci v.fatl
Skewness 4.219857 1.785286 2.304655 6.491546 5.274871
v.satl v.rftl v.rstl v.ftlm v.stlm
Skewness 2.677162 3.954098 1.568675 1.207227 0.8516043
v.pcci
Skewness 3.031012
> env$sk.out
ftlm stlm rbci pcci
Skewness -0.04272076 -0.07893945 -0.02460354 0.01485785
v.fatl v.satl v.rftl v.rstl
Skewness 0.00780424 -0.02640635 -0.04663711 -0.04290957
v.ftlm v.stlm v.pcci
Skewness -0.0009597876 0.01997082 0.0007462494
> env$sk.cap
ftlm stlm rbci pcci
Skewness -0.03329392 -0.07911245 -0.02847851 0.01915228
v.fatl v.satl v.rftl v.rstl
Skewness 0.01412182 -0.02617518 -0.03412228 -0.04596505
v.ftlm v.stlm v.pcci
Skewness 0.008181183 0.009661169 0.002252508
お分かりのように、外れ値x.outと補完された外れ値x.cap を持つセットは完全に対称であり、修正を必要としません。
尖度も評価しましょう。尖度または尖り係数は、ランダム変数分布の尖りの尺度です。正規分布の尖度は0です。尖度は、数学的期待値の周りの分布の尖りが鋭い場合は正で、尖りが滑らかな場合は負です。
require(PerformanceAnalytics)
evalq({
k <- kurtosis(x)
k.out <- kurtosis(x.out)
k.cap <- kurtosis(x.cap)
},
env)
> env$k
ftlm stlm rbci pcci
Excess Kurtosis 84.61177 16.77141 45.01858 247.9795
v.fatl v.satl v.rftl v.rstl
Excess Kurtosis 145.9547 36.99944 74.4307 13.57613
v.ftlm v.stlm v.pcci
Excess Kurtosis 86.36448 23.06635 233.5408
> env$k.out
ftlm stlm rbci
Excess Kurtosis -0.003083449 -0.1668102 -0.1197043
pcci v.fatl v.satl
Excess Kurtosis -0.05113439 -0.02738558 -0.04341552
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.01219999 -0.1316499 -0.0287925
v.stlm v.pcci
Excess Kurtosis -0.1530424 -0.09950709
> env$k.cap
ftlm stlm rbci
Excess Kurtosis -0.2314336 -0.3075185 -0.2982044
pcci v.fatl v.satl
Excess Kurtosis -0.2452504 -0.2389486 -0.2331203
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.2438431 -0.2673441 -0.2180059
v.stlm v.pcci
Excess Kurtosis -0.2763058 -0.2698028
初期データセット x における分布の尖りは非常に鋭い(尖度は0よりもはるかに大きい)ものです。外れ値x.outが削除されたセットでは、 尖度はほぼ正常です。外れ値が補完されたセットの尖りはより滑らかです。両方のデータセットは修正を必要としません。
適用
1. DARCH12_1.zipアーカイブには、記事の最初の部分(dataRaw.R、PrepareData.R、FUNCTION.R)のスクリプトと、初期データCotir.RDataを持つRstudioセッションを表す図が含まれています。Rstudioにデータをロードすると、すべてのスクリプトを表示してそれらを操作できます。Git /Part_Iからのダウンロードも可能です。
2. ACTF.zipアーカイブには V. Kravchukの "New Adaptive Method of Following the Tendency and Market Cycles"(動向及び市場サイクルに従う新しい適応的方法)が含まれています。
3. R_intro.zipアーカイブにはRに関する参考資料が含まれています。
リンク
[1] A Systematic Approach on Data Pre-processing In Data Mining. COMPUSOFT, An international journal of advanced computer technology, 2 (11), November-2013 (Volume-II, Issue-XI)
[2] Outlier Detection Techniques.Hans-Peter Kriegel, Peer Kröger, Arthur Zimek. Ludwig-Maximilians-Universität München.Munich, Germany
[3] Breuning, M., Kriegel, H., Ng, R.T, and Sander. J. (2000). LOF: Identifying density-based local outliers. In Proceedings of the ACM SIGMOD International Conference on Management of Data.
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/3486
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 ユニバーサルEA: シンボルプロパティへのアクセス (その 8)
ユニバーサルEA: シンボルプロパティへのアクセス (その 8)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
こんにちは、あなたの記事(Rを触るのは初めて)に従って、コードの2番目のブリックで、私は以下のエラーに直面しました:
evalq({ : オブジェクト 'env' が見つかりません。
ここでいうenvとは、PCソフトで命名された何かのことでしょうか?それとも自動的に作成されたオブジェクトなのでしょうか?
素晴らしい記事です。これを超える方法を見つけるつもりです。)
(RStudioを使用し、MRO 3.5.3をインストールしました(3.4.0が古かったため))
こんにちは、あなたの記事に従って(初めてRに触れました)、コードの2番目のブロックで、次のエラーに遭遇しました:
evalq のエラー ({: オブジェクト 'env' が見つかりません。
ここでenvとは、PCソフトウェアで命名された何かを意味するのでしょうか?それとも本当に自動生成されたオブジェクトなのでしょうか?
素晴らしい記事です、私はそれを打ち負かす方法を見つけるでしょう、あなたが助けてくれるなら、それは素晴らしいことです :)
(RStudioを使用し、MRO 3.5.3(3.4.0は非推奨)をインストール)
envオブジェクトは様々なツールからのデータを分離するために作成しました。スクリプトの最初に
頑張ってください。
親愛なるMr.ウラジミール・ペレヴェンコさん、迅速な回答をありがとうございました。Rコースを受講した後、少なくともあなたの素晴らしい仕事を学ぶに値するだけの成果を上げたいと思います。
ありがとうございました。
フェロックス
ペレヴェンコさん、お元気ですか?新しい質問があります:
9行目のDigオブジェクトの意味は何ですか?
プロジェクトでも、必要なパッケージでも見つけられませんでした.
よろしくお願いします。ペレヴェンコ
フェロックス
ウラジーミル・ペレヴェンコさん、私の愚かな質問で申し訳ありません。
もう解決しました。
よろしくお願いします。