
Redes Neurais Profundas (Parte II). Desenvolvimento e seleção de preditores
Conteúdo
- Introdução
- 1. Criação das características
- 2. Escolhendo preditores
- Conclusão
- Aplicação
Introdução
No artigo anterior nós consideramos diferentes aspectos da obtenção e preparação de dados de entrada e da variável objetivo. Para obter os scripts do primeiro artigo, você precisa implementar todos os scripts da primeira parte ou baixar os resultados do cálculo da primeira parte do aplicativo RStudio.
1. Criação das características
A criação de características é uma ciência (e arte) de obter informações adicionais a partir dos dados em mãos. Nosso objetivo não é adicionar novos dados, mas fazer uso do que nós já temos. Novas capacidades nos permitem obter novos recursos de uma amostra de dados. Esses recursos permitem rotulagem, caracterização e divisão mais precisa do conjunto de dados de treinamento. Isso proporciona uma precisão adicional.
Este processo pode ser dividido em duas etapas:
- Transformação. Dependendo do cenário, este pode ser um dos quatro tipos de transformação: normalização de dados, remoção das variáveis assimétricas, remoção dos valores atípicos e discretização.
- Criação das características. A extração de uma nova variável das já existentes é chamado de criação de uma nova característica. Isso pode revelar relacionamentos ocultos no conjunto de dados.
1.1. Transformação das características
1.1.1. Transformação
O que é a transformação de uma variável?
Na modelagem de dados, uma transformação é uma substituição de uma variável por uma função dessa variável. Por exemplo, esta poderia ser a mudança da variável x pela raiz quadrada ou cúbica ou logarítmica de x. Em outras palavras, a transformação é um processo que altera a distribuição de uma variável e a relação dessa variável com outras.
Lembre-se quando a transformação de uma variável é útil.
- Quando queremos mudar a escala de uma variável ou padronizar seus valores para uma melhor compreensão. Essa transformação é necessária se diferentes dados tiverem diferentes escalas. Isso não resulta na mudança da forma de distribuição.
- Quando as relações complexas não lineares e curvilíneas entre as variáveis devem ser transformadas em uma relação linear. Isso é mais vívido e proporciona uma melhor capacidade de previsão. Nesse caso, um gráfico de dispersão pode ser usado para encontrar uma relação entre duas variáveis contínuas. Normalmente, uma transformação logarítmica é usada em tal situação.
- Quando uma distribuição assimétrica precisa ser alterada para uma simétrica para uma interpretação e análise mais simples. Alguns métodos de modelagem requerem uma distribuição normal de variáveis. Portanto, quando lidamos com uma distribuição não uniforme, nós podemos usar as transformações que reduzem a afinidade. Para uma distribuição enviesada à direta, nós tomamos uma raiz quadrada, cúbica ou logarítmica de uma variável, enquanto que a distribuição enviesada à esquerda é suavizada elevando-se ao quadrado/cubo ou usando a função exponencial.
- Quando uma variável contínua precisa ser transformada em uma discreta. O método de tal transformação é a discretização.
Quais são os métodos gerais de transformação?
Existem vários métodos utilizados para a transformação de variáveis. Nós já mencionamos alguns deles: raiz quadrada/cúbica, logaritmos, funções trigonométricas e segmentação. Examine alguns métodos em detalhes e identifique suas vantagens e desvantagens.
- Calculando o logaritmo. Este é um método de transformação geral usado para alterar a forma da distribuição de uma variável. Isso geralmente é usado para reduzir o viés à direita. Esta função não é aplicável a valores zero e negativos.
- Raiz quadrada/cúbica. Esta função tem um impacto significativo na distribuição da variável, embora não tão poderosa quanto o cálculo do logaritmo. A vantagem da raiz cúbica é que ela pode ser usada para valores zero e negativos. A raiz quadrada pode ser calculada apenas para valores positivos maiores ou iguais a zero.
- Discretização/binning. Isso é usado para a categorização de valores. A discretização é adequada para dados originais, percentil e frequências. A escolha do método de categorização é baseada na natureza dos dados. Nós podemos realizar uma segmentação conjunta de variáveis interdependentes.
Qualquer transformação de dados leva à mudança da distribuição. Para ilustrar isso, nós usaremos exemplos de dois métodos de transformação.
Dois problemas do nosso conjunto de dados iniciais são os outliers e a assimetria à direita. Nós já consideramos as maneiras de remover os outliers. Agora, nós vamos tentar remover/reduzir a assimetria primeiro e depois remover os valores atípicos.
Método 1.
Para livrar-se da forte assimetria à direta do conjunto de dados x, nós vamos levar o logaritmo para a base 2 e, em seguida, remover os outliers. Como os valores das variáveis no conjunto de dados inicial são muito menores que 1 e existem valores negativos entre eles, nós calculamos o logaritmo das variáveis adicionando 1 a cada um deles para aumentar a precisão. Vamos ver o que acontecerá com a curva.
evalq({x.ln <- apply(x, 2, function(x) log2(x + 1))
sk.ln <- skewness(x.ln)},
env)
> env$sk.ln
ftlm stlm rbci pcci v.fatl
Skewness -0.2715663 -2.660613 -4.484301 0.4267873 1.253008
v.satl v.rftl v.rstl v.ftlm v.stlm
Skewness 1.83489 2.065224 -0.0343451 -15.62414 0.01529019
v.pcci
Skewness 0.1811206
Três variáveis — stlm, rbci e v.ftlm possuem uma assimetria à esquerda. As variáveis v.fatl, v.satl e v.rftl ainda estão enviesadas à direita. A assimetria de outras variáveis foi igualada. Vamos remover e imputar os outliers a partir deste conjunto de dados e, em seguida, olhar para a assimetria e distribuição das variáveis:
evalq({
foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
remove_outliers(x.ln[ ,i])
} -> x.ln.out
colnames(x.ln.out) <- colnames(x.ln)
},
env)
evalq({
foreach(i = 1:ncol(x.ln), .combine = "cbind") %do% {
capping_outliers(x.ln[ ,i])
} -> x.ln.cap
colnames(x.ln.cap) <- colnames(x.ln)
},
env)
evalq({
sk.ln.out <- skewness(x.ln.out)
sk.ln.cap <- skewness(x.ln.cap)
},
env)
> env$sk.ln.out
ftlm stlm rbci pcci
Skewness -0.119055 -0.3549119 -0.1099921 -0.01476384
v.fatl v.satl v.rftl v.rstl
Skewness -0.02896319 -0.03634833 -0.06259749 -0.2120127
v.ftlm v.stlm v.pcci
Skewness -0.05819699 -0.01661317 -0.05420077
> env$sk.ln.cap
ftlm stlm rbci pcci
Skewness -0.1814781 -0.4582045 -0.1658855 -0.02849945
v.fatl v.satl v.rftl v.rstl
Skewness -0.04336238 -0.04400781 -0.0692754 -0.2269408
v.ftlm v.stlm v.pcci
Skewness -0.06184128 -0.02856397 -0.06258243
Os dados em ambos os conjuntos de dados (x.out e x.cap) são quase simétricos. A distribuição é exibida nos diagramas abaixo.
par(mfrow = c(2,2)) boxplot(env$x.ln, main = "x.ln with outliers", xlab = "") boxplot(env$x.ln.out, main = "x.ln.out without outliers", xlab = "") boxplot(env$x.ln.cap, main = "x.ln.cap with imputed outliers", xlab = "") par(mfrow = c(1,1))
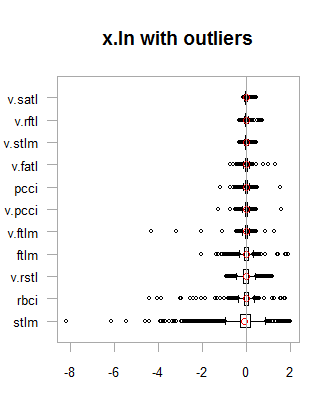

Fig.1. Dados com transformação logarítmica com e sem outliers
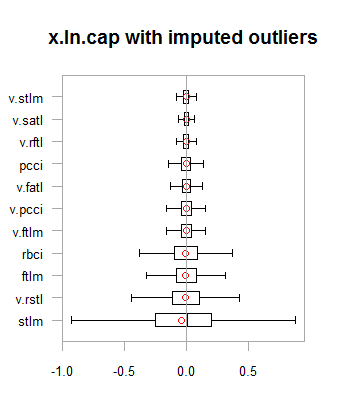
Fig.2. Dados com transformação logarítmica com outliers imputados
Os resultados são bem semelhantes à transformação anterior com uma exceção. A faixa de variação das variáveis se tornou mais ampla.
Vamos transformar o dataframe x.ln.cap e ver a variação e covariação do conjunto:
evalq(x.ln.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetLnCap, env)
Desenhar os gráficos:
require(GGally) evalq(ggpairs(dataSetLnCap, columns = 2:7, mapping = aes(color = Class), title = "PredLnCap1"), env) evalq(ggpairs(dataSetLnCap, columns = 8:13, mapping = aes(color = Class), title = "PredLnCap2"), env)
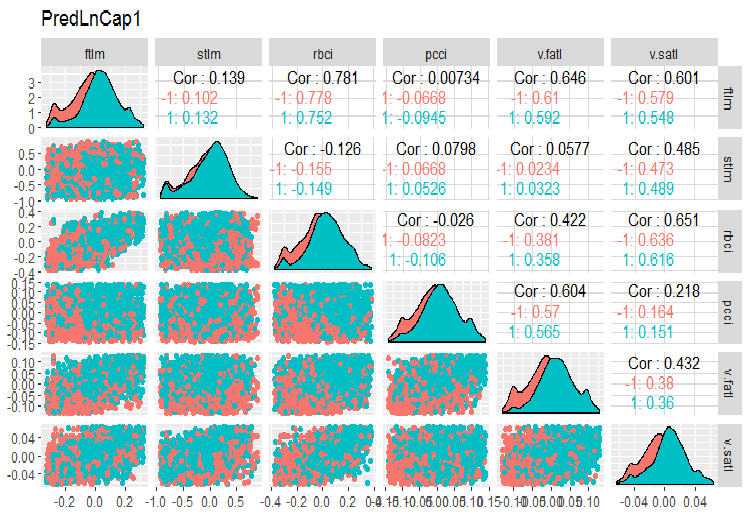
Fig.3. Parâmetros de dados com transformação logarítmica, parte 1
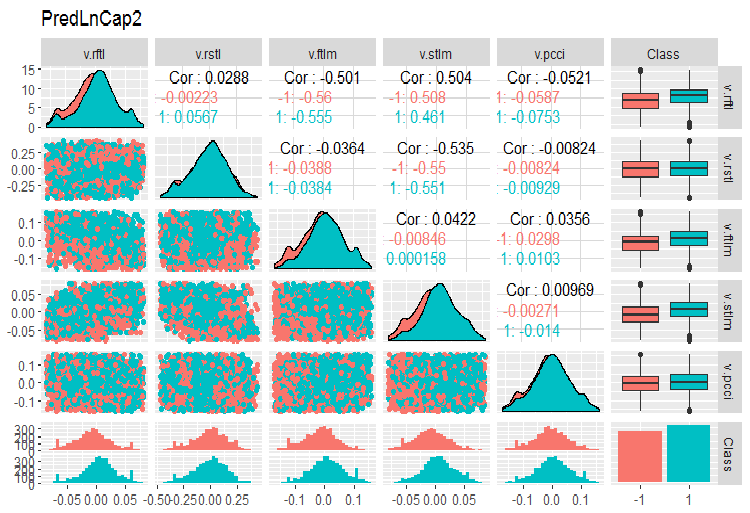
Fig. 4. Parâmetros de dados com transformação logarítmica, parte 2
Método 2.
Transforme os dados usando a função sin(2*pi*x), remova e impute os outliers e, em seguida, avalie a afinidade, a distribuição dos outliers e a covariação das variáveis transformadas nos gráficos.
evalq({x.sin <- apply(x, 2, function(x) sin(2*pi*x))
sk.sin <- skewness(x.sin)
},
env)
#----------
evalq({
foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
remove_outliers(x.sin[ ,i])
} -> x.sin.out
colnames(x.sin.out) <- colnames(x.sin)
},
env)
#-----------------
evalq({
foreach(i = 1:ncol(x.sin), .combine = "cbind") %do% {
capping_outliers(x.sin[ ,i])
} -> x.sin.cap
colnames(x.sin.cap) <- colnames(x.sin)
},
env)
#-----------
evalq({
sk.sin.out <- skewness(x.sin.out)
sk.sin.cap <- skewness(x.sin.cap)
},
env)
Qual a assimetria desses conjuntos de dados transformados?
env$sk.sin ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.0009679463 v.fatl v.satl v.rftl v.rstl Skewness 0.03280465 0.5217757 0.05611136 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.04923953 -0.2123434 0.01738377 > env$sk.sin.out ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.03532892 v.fatl v.satl v.rftl v.rstl Skewness 0.00360966 -0.02380975 -0.05336561 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.0009366441 0.01835948 0.0008843329 > env$sk.sin.cap ftlm stlm rbci pcci Skewness -0.02536085 -0.04234074 -0.00587189 0.03283132 v.fatl v.satl v.rftl v.rstl Skewness 0.007588308 -0.02424707 -0.04106469 -0.02825112 v.ftlm v.stlm v.pcci Skewness 0.007003051 0.009237835 0.002101687
Como você pode ver, essa transformação tornou todos os conjuntos de dados simétricos. Vamos ver como são esses conjuntos:
par(mfrow = c(2, 2)) boxplot(env$x.sin, main = "x.sin with outlier") abline(h = 0, col = 2) boxplot(env$x.sin.out, main = "x.sin.out without outlier") abline(h = 0, col = 2) boxplot(env$x.sin.cap, main = "x.sin.cap with capping outlier") abline(h = 0, col = 2) par(mfrow = c(1, 1))
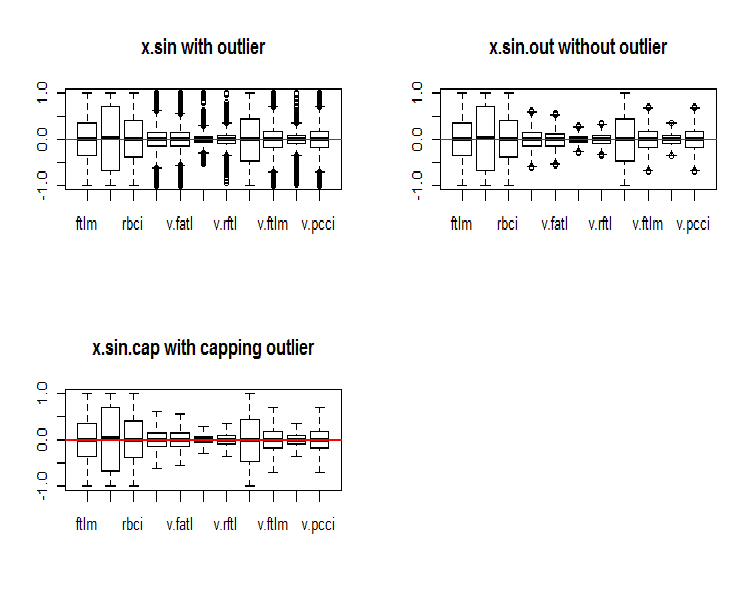
Fig.5. Conjunto de dados transformado pela função sin()
À primeira vista, esses conjuntos de dados parecem melhores que os anteriores (os iniciais e os transformados).
Agora, nós queremos ver a distribuição de NA em variáveis após o outliers terem sido removidos.
require(VIM)
evalq(a <- aggr(x.sin.out), env)
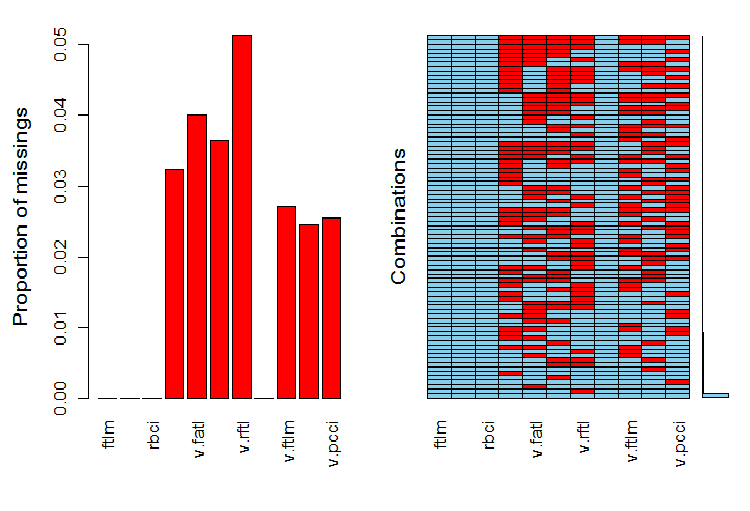
Fig.6. Distribuição de NA no conjunto de dados
A parte esquerda do gráfico mostra o número relativo de dados indefinidos em cada variável. O lado direito mostra as combinações de exemplos com um número diferente de NA (aumentando de baixo para cima). Nós podemos ver os valores:
> print(env$a) Ausência em variáveis: Contagem da Variável pcci 256 v.fatl 317 v.satl 289 v.rftl 406 v.ftlm 215 v.stlm 194 v.pcci 201
Qual é a distribuição de NA nas variáveis?
par(mfrow = c(3, 4)) evalq( foreach(i = 1:ncol(x.sin.out)) %do% { barMiss(x.sin.out, pos = i, only.miss = TRUE, main = "x.sin.out without outlier") }, env ) par(mfrow = c(1, 1))
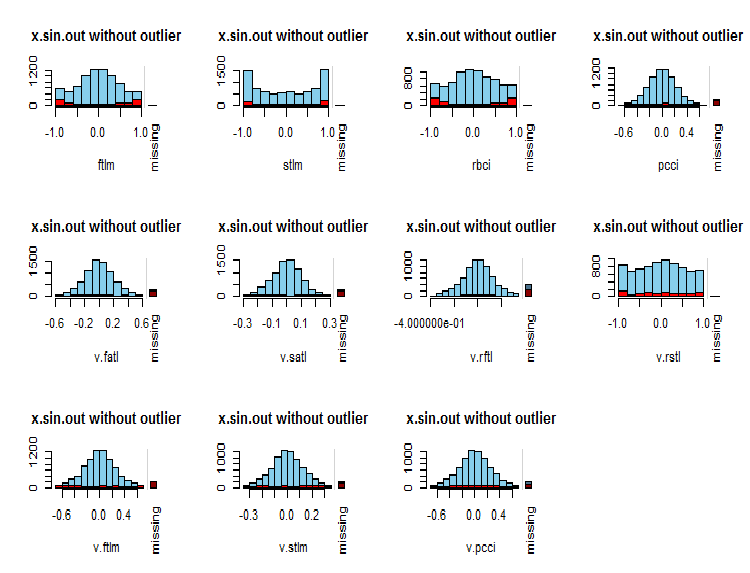
Fig.7. Distribuição de NA em variáveis
Os valores observados da variável são mostrados em azul e o número de NA de outras variáveis em diferentes faixas de valores da variável atual é exibido em vermelho. A barra à direita representa a contribuição da variável atual para o número total de NA de todas as variáveis.
Finalmente, vamos dar uma olhada na variação e covariação do conjunto de dados transformados com valores atípicos imputados.
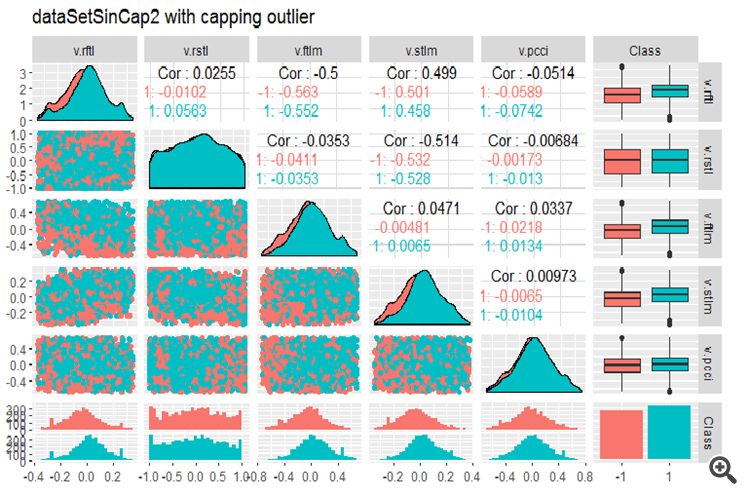
#--------------- evalq(x.sin.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetSinCap, env) require(GGally) evalq(ggpairs(dataSetSinCap, columns = 2:7, mapping = aes(color = Class), title = "dataSetSinCap1 with capping outlier "), env) evalq(ggpairs(dataSetSinCap, columns = 8:13, mapping = aes(color = Class), title = "dataSetSinCap2 with capping outlier"), env) #---------------------------
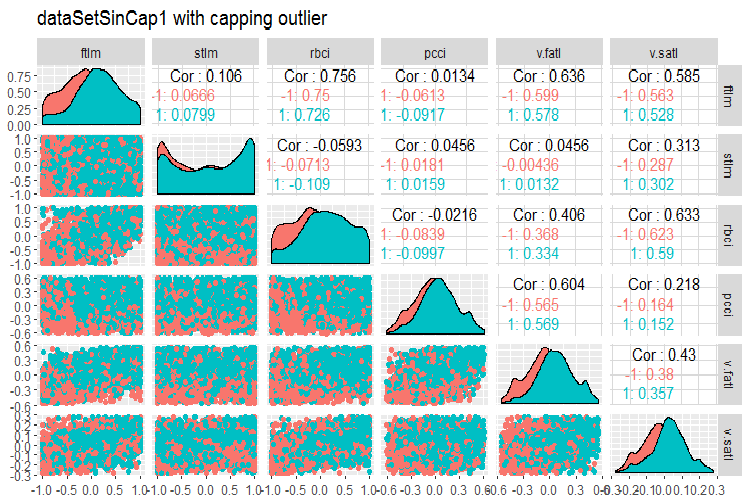
Fig.8. Parâmetros de sin()-dados transformados, parte 1
Fig.9. Parâmetros de sin()-dados transformados, parte 2
1.1.2. Normalização
Estamos preparando dados para uma rede neural, portanto as variáveis devem ser trazidas dentro do intervalo de { -1..+1 }. Para isso, a função preProcess()::caret com o method = “spatialSign” será usado. Alternativamente, os dados podem ser centrados ou dimensionados antes da normalização. Este é um processo muito simples e não vamos considerá-la neste artigo.
Há uma coisa para se ter em mente, no entanto. Os parâmetros de normalização obtidos a partir do conjunto de dados de treinamento devem ser usados para os conjuntos de teste e validação.
Para uma maior utilização do conjunto de dados obtidos nos cálculos anteriores (dataSet sem remover os valores altamente correlacionados), vamos dividir em treinar/testar/avaliar e trazê-los dentro da faixa (-1, +1) sem padronização.
Realizando a normalização com a padronização, tenha em mente que, quando os parâmetros de normalização (média/mediana, sd/mad) são definidos, os parâmetros de outliers imputadores também devem ser definidos. Avançando, eles serão usados para treinar/avaliar/testar. No início deste artigo, nós escrevemos duas funções: prep.outlier() e treatOutlier(). Eles são projetados para esse fim.
Sequência das operações:
- Define os parâmetros para os outliers no treinamento
- Remove os outliers no treinamento
- Define os parâmetros de padronização no treinamento
- Imputa os outliers em train/val/test
- Normalizar o train/val/test
Nós não vamos considerar essa variante aqui. Você pode estudá-la por conta própria.
Divide os dados em train/val/test
evalq(
{
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
list(clean = data.frame(dataSet) %>% na.omit(),
train = clean[train, ],
val = clean[val, ],
test = clean[test, ]) -> DT
}, env)
Define os parâmetros para a normalização do conjunto train e define e normaliza os outliers em train/val/test:
require(foreach)
evalq(
{
preProcess(DT$train, method = "spatialSign") -> preproc
list(train = predict(preproc, DT$train),
val = predict(preproc, DT$val),
test = predict(preproc, DT$test)
) -> DTn
},
env)
Vamos dar uma olhada nas estatísticas totais do conjunto de treinamento:
> table.Stats(env$DTn$train %>% tk_xts()) Using column `Data` for date_var. ftlm stlm rbci pcci Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5909 -0.7624 -0.6114 -0.8086 Quartile 1 -0.2054 -0.2157 -0.2203 -0.2110 Median 0.0145 0.0246 0.0147 0.0068 Arithmetic Mean 0.0070 0.0190 0.0085 0.0028 Geometric Mean -0.0316 -0.0396 -0.0332 -0.0438 Quartile 3 0.2139 0.2462 0.2341 0.2277 Maximum 0.6314 0.8047 0.7573 0.7539 SE Mean 0.0060 0.0073 0.0063 0.0065 LCL Mean (0.95) -0.0047 0.0047 -0.0037 -0.0100 UCL Mean (0.95) 0.0188 0.0333 0.0208 0.0155 Variance 0.0719 0.1058 0.0784 0.0848 Stdev 0.2682 0.3252 0.2800 0.2912 Skewness -0.0762 -0.0221 -0.0169 -0.0272 Kurtosis -0.8759 -0.6688 -0.8782 -0.7090 v.fatl v.satl v.rftl v.rstl Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5160 -0.5943 -0.6037 -0.7591 Quartile 1 -0.2134 -0.2195 -0.1988 -0.2321 Median 0.0015 0.0301 0.0230 0.0277 Arithmetic Mean 0.0032 0.0151 0.0118 0.0177 Geometric Mean -0.0323 -0.0267 -0.0289 -0.0429 Quartile 3 0.2210 0.2467 0.2233 0.2657 Maximum 0.5093 0.5893 0.6714 0.7346 SE Mean 0.0058 0.0063 0.0062 0.0074 LCL Mean (0.95) -0.0082 0.0028 -0.0003 0.0033 UCL Mean (0.95) 0.0146 0.0274 0.0238 0.0321 Variance 0.0675 0.0783 0.0757 0.1083 Stdev 0.2599 0.2798 0.2751 0.3291 Skewness -0.0119 -0.0956 -0.0648 -0.0562 Kurtosis -1.0788 -1.0359 -0.7957 -0.7275 v.ftlm v.stlm v.rbci v.pcci Observations 2000.0000 2000.0000 2000.0000 2000.0000 NAs 0.0000 0.0000 0.0000 0.0000 Minimum -0.5627 -0.6279 -0.5925 -0.7860 Quartile 1 -0.2215 -0.2363 -0.2245 -0.2256 Median -0.0018 0.0092 -0.0015 -0.0054 Arithmetic Mean -0.0037 0.0036 -0.0037 0.0013 Geometric Mean -0.0426 -0.0411 -0.0433 -0.0537 Quartile 3 0.2165 0.2372 0.2180 0.2276 Maximum 0.5577 0.6322 0.5740 0.9051 SE Mean 0.0061 0.0065 0.0061 0.0070 LCL Mean (0.95) -0.0155 -0.0091 -0.0157 -0.0124 UCL Mean (0.95) 0.0082 0.0163 0.0082 0.0150 Variance 0.0732 0.0836 0.0742 0.0975 Stdev 0.2706 0.2892 0.2724 0.3123 Skewness 0.0106 -0.0004 -0.0014 0.0232 Kurtosis -1.0040 -1.0083 -1.0043 -0.4159
Esta tabela nos mostra que as variáveis são simétricas e possuem parâmetros muito próximos.
Agora, vamos dar uma olhada na distribuição de variáveis nos conjuntos de train/val/test:
boxplot(env$DTn$train %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Train") abline(v = 0, col = 2) boxplot(env$DTn$test %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Test") abline(v = 0, col = 2) boxplot(env$DTn$val %>% dplyr::select(-c(Data, Class)), horizontal = T, main = "Val") abline(v = 0, col = 2)
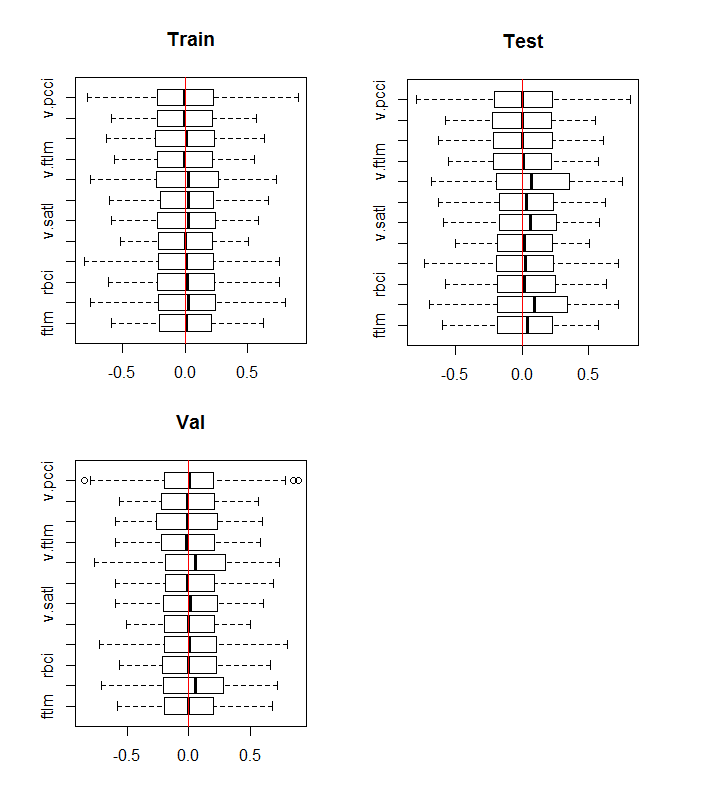
Fig.10. Distribuição de variáveis nos conjuntos de train/val/test após a normalização
A distribuição é quase a mesma em todos os conjuntos. Nós também temos que considerar a correlação e covariação das variáveis no conjunto de treinamento:
require(GGally) evalq(ggpairs(DTn$train, columns = 2:7, mapping = aes(color = Class), title = "DTn$train1 "), env) evalq(ggpairs(DTn$train, columns = 8:14, mapping = aes(color = Class), title = "DTn$train2"), env)
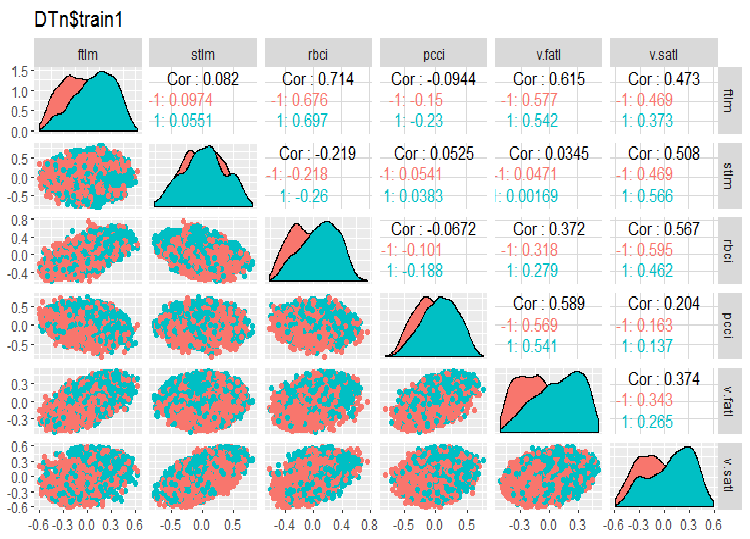
Fig.11. Variação e covariação do conjunto 1 de treinamento
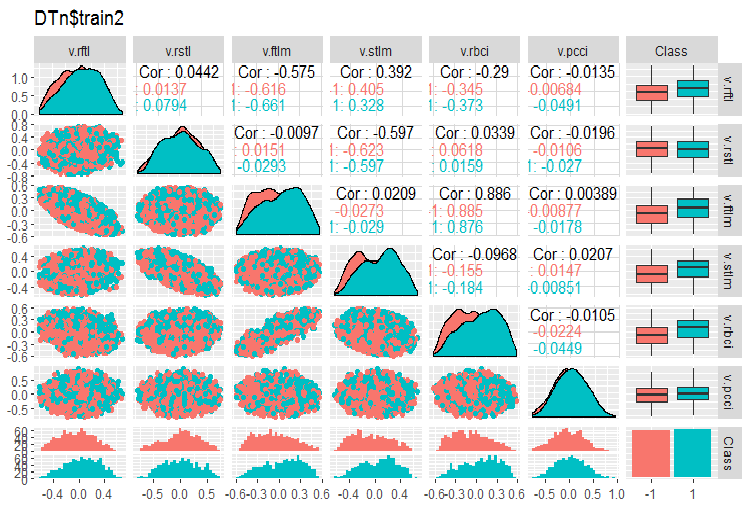
Fig.12. Variação e covariação do conjunto 2 de treinamento
Não há dados altamente correlacionados, a distribuição é embalada e não tem valores esporádicos. Os dados podem ser bem divididos. Em face disso, existem apenas duas variáveis problemáticas - stlm e v.rstl. Nós verificamos essa declaração mais tarde quando avaliarmos a relevância dos preditores. Agora, nós podemos observar a correlação desses preditores e a variável objetivo:
> funModeling::correlation_table(env$DTn$train %>% tbl_df %>% + select(-Data), str_target = 'Class') Variable Class 1 Class 1.00 2 v.fatl 0.38 3 ftlm 0.34 4 rbci 0.28 5 v.rbci 0.28 6 v.satl 0.27 7 pcci 0.24 8 v.ftlm 0.22 9 v.stlm 0.22 10 v.rftl 0.18 11 v.pcci 0.08 12 stlm 0.03 13 v.rstl -0.01As variáveis nomeadas estão na parte inferior da tabela com coeficientes de correlação bem pequenos. A relevância da variável v.pcci. também deve ser verificada. Vamos verificar a variável v.fatl nos conjuntos train/val/test:
require(ggvis) evalq( DTn$train %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$train$v.fatl"), env) evalq( DTn$val %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$val$v.fatl"), env) evalq( DTn$test %>% ggvis(~v.fatl, fill = ~Class) %>% group_by(Class) %>% layer_densities() %>% add_legend("fill", title = "DTn$test$v.fatl"), env)
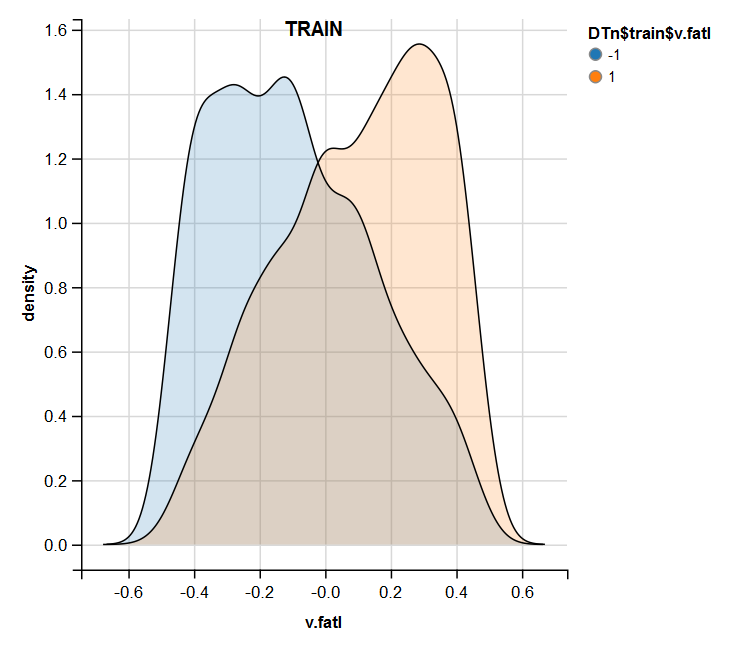
Fig.13. Distribuição da variável v.fatl no conjunto de treinamentos após a normalização
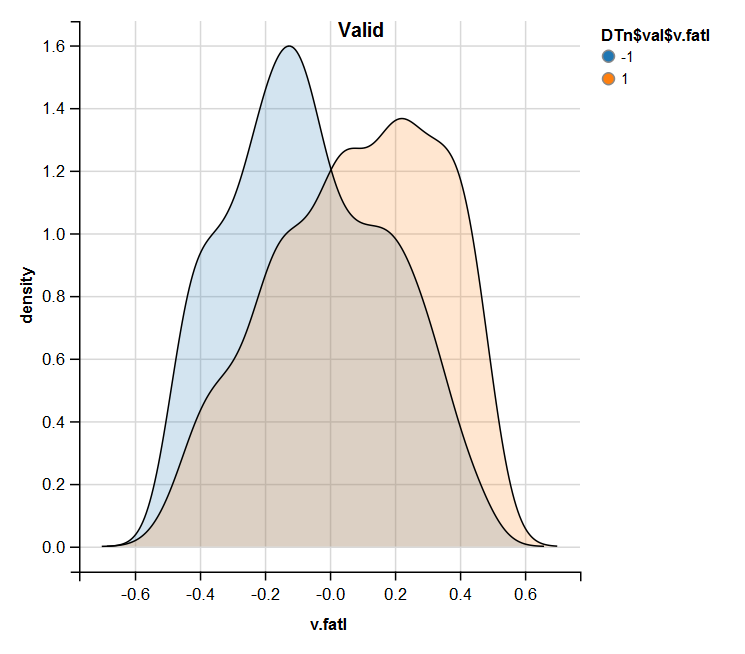
Fig.14. Distribuição da variável v.fatl no conjunto válido após a normalização
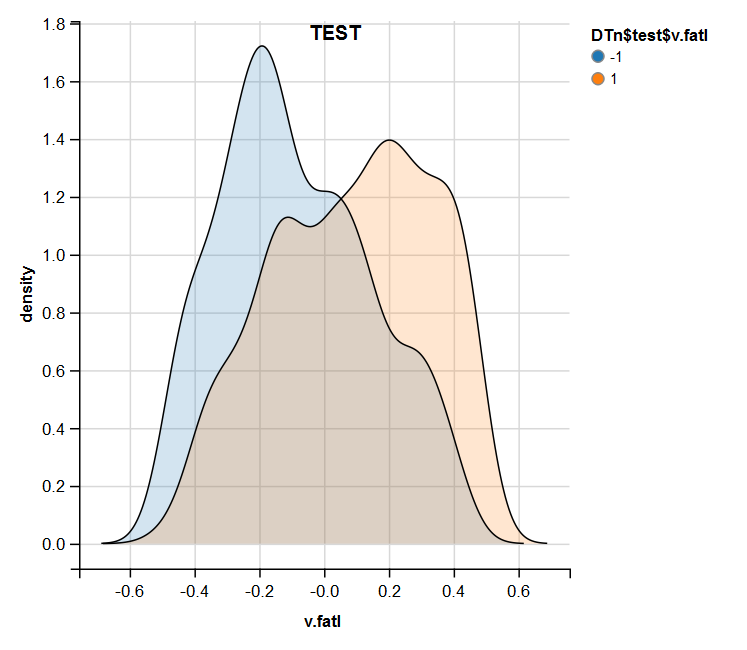
Fig.15. Distribuição da variável v.fatl no conjunto de teste após a normalização
A análise realizada mostra que a normalização geralmente produz uma boa distribuição de preditores sem valores atípicos e dados altamente correlacionados. De fato, isso depende do caráter dos dados brutos.
1.1.3. Discretização
A discretização refere-se ao processo de transformação de uma variável contínua em uma discreta dividindo seus valores em áreas. Os limites dessas áreas podem ser definidos usando vários métodos.
Os métodos de separação podem ser divididos em dois grupos: métodos quantitativos, que não envolvem a relação com a variável objetivo e os métodos que levam em conta o intervalo da variável objetivo.
O primeiro grupo de métodos é quase totalmente abrangido pela função cut2()::Hmisc. A amostra pode ser dividida em um número predefinido de áreas com limites especificados, em quartis, em áreas com um número mínimo de exemplos em cada um e em áreas equifrequentes.
O segundo grupo de métodos é mais interessante porque divide a variável em áreas conectadas aos níveis da variável objetivo. Vamos considerar vários pacotes realizando esses métodos.
Discretização. Este pacote é um conjunto de algoritmos de discretização com o treinador. Isso também pode ser agrupado em termos "de cima para baixo" e "de baixo para cima", que implementam os algoritmos de discretização. Vamos considerar alguns deles no exemplo de nosso dataSet.
Em primeiro lugar, vamos limpar o conjunto (sem remover as variáveis altamente correlacionadas) e depois dividi-la em conjuntos de treinamento/avaliação/teste na razão de 2000/1000/1000.
require(discretization)
require(caret)
require(pipeR)
evalq(
{
dataSet %>%
preProcess(.,
method = c("zv", "nzv", "conditionalX")) %>%
predict(., dataSet) %>%
na.omit -> dataSetClean
train = 1:2000
val = 2001:3000
test = 3001:4000
DT <- list()
list(train = dataSetClean[train, ],
val = dataSetClean[val, ],
test = dataSetClean[test, ]) -> DT
},
env)
Nós vamos usar a função mdlp()::discretization que descreve a discretização usando o comprimento mínimo da descrição. Esta função discretiza atributos contínuos da matriz pelo critério de entropia com o comprimento mínimo da descrição como o critério de parada.
evalq(
pipeline({
DT$train
select(-Data)
as.data.frame()
mdlp()}) -> mdlp.train, envir = env)
A função retorna uma lista com dois espaços. Eles são: cutp - um quadro de dados com pontos de corte para cada variável e Disc.data - um quadro de dados com variáveis rotuladas.
> env$mdlp.train%>%str() List of 2 $ cutp :List of 12 ..$ : num [1:2] -0.0534 0.0278 ..$ : chr "All" ..$ : num -0.0166 ..$ : num [1:2] -0.0205 0.0493 ..$ : num [1:3] -0.0519 -0.0055 0.019 ..$ : num 0.000865 ..$ : num -0.00909 ..$ : chr "All" ..$ : num 0.0176 ..$ : num [1:2] -0.011 0.0257 ..$ : num [1:3] -0.03612 0.00385 0.03988 ..$ : chr "All" $ Disc.data:'data.frame': 2000 obs. of 13 variables: ..$ ftlm : int [1:2000] 3 3 3 3 3 2 1 1 1 1 ... ..$ stlm : int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ rbci : int [1:2000] 2 2 2 2 2 2 1 1 1 1 ... ..$ pcci : int [1:2000] 2 2 1 2 2 1 1 2 3 2 ... ..$ v.fatl: int [1:2000] 4 4 3 4 3 1 1 2 3 2 ... ..$ v.satl: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ... ..$ v.rftl: int [1:2000] 1 2 2 2 2 2 2 2 1 1 ... ..$ v.rstl: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ v.ftlm: int [1:2000] 2 2 1 1 1 1 1 1 2 1 ... ..$ v.stlm: int [1:2000] 1 1 1 2 2 1 1 1 1 1 ... ..$ v.rbci: int [1:2000] 4 4 3 3 2 1 1 2 3 2 ... ..$ v.pcci: int [1:2000] 1 1 1 1 1 1 1 1 1 1 ... ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ...
O que o primeiro espaço nos diz?
Nós temos três variáveis não marcadas com os valores não conectados com a variável objetivo. Estes são 2,8 e 12 (stlm, v.rstl, v.pcci). Eles podem ser removidos sem a perda de qualidade do conjunto de dados. Observe que essas variáveis foram definidas como irrelevantes na parte anterior do artigo.
Quatro variáveis são divididas em duas classes, três variáveis são divididas em três classes e duas variáveis são divididas em quatro classes.
Segmente os conjuntos val/test, usando pontos de corte obtidos a partir do conjunto train. Para isso, remova as variáveis não marcadas do conjunto train e salve-o no dataframe train.d. Então, use a função findInterval() para rotular o conjunto test/val usando os pontos de corte obtidos anteriormente.
evalq(
{
mdlp.train$cutp %>%
lapply(., function(x) is.numeric(x)) %>%
unlist -> idx # bool
#----train-----------------
mdlp.train$Disc.data[ ,idx] -> train.d
#---test------------
DT$test %>%
select(-c(Data, Class)) %>%
as.data.frame() -> test.d
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {findInterval(test.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$test$Class) -> test.d
colnames(test.d) <- colnames(train.d)
#-----val-----------------
DT$val %>%
select(-c(Data, Class)) %>%
as.data.frame() -> val.d
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {findInterval(val.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$val$Class) -> val.d
colnames(val.d) <- colnames(train.d)
},env
)
Como são esses conjuntos?
> env$train.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 3 2 2 4 1 1 2 1 4 1 2 3 2 2 4 1 2 2 1 4 1 3 3 2 1 3 1 2 1 1 3 1 4 3 2 2 4 2 2 1 2 3 1 5 3 2 2 3 2 2 1 2 2 1 6 2 2 1 1 1 2 1 1 1 -1 > env$test.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 1 1 1 2 1 1 1 1 2 -1 2 1 1 3 3 1 1 2 2 3 -1 3 1 1 2 2 1 1 1 2 2 -1 4 2 1 2 3 1 1 2 2 3 1 5 2 2 2 3 1 1 1 2 3 1 6 2 2 2 4 1 1 2 2 3 1 > env$val.d %>% head() ftlm rbci pcci v.fatl v.satl v.rftl v.ftlm v.stlm v.rbci Class 1 2 2 2 2 2 2 1 2 2 1 2 2 2 2 2 2 2 1 2 2 1 3 2 2 2 3 2 2 1 2 2 1 4 2 2 2 4 2 2 2 2 3 1 5 2 2 2 3 2 2 1 2 2 1 6 2 2 2 3 2 2 2 2 2 1 > env$train.d$v.fatl %>% table() . 1 2 3 4 211 693 519 577 > env$test.d$v.fatl %>% table() . 1 2 3 4 49 376 313 262 > env$val.d$v.fatl %>% table() . 1 2 3 4 68 379 295 258
O uso adicional dos conjuntos com dados discretos depende do modelo em uso. Se esta é uma rede neural, os preditores terão de ser transformados em variáveis dummy. Quão bem essas classes são divididas por essas variáveis? Quão bem elas se correlacionam com a variável objetivo? Vamos tornar essas relações visuais com a cross-plot()::funModeling. Cross_plot mostra como a variável de entrada se correlaciona com a variável objetivo que recebe o coeficiente de verossimilhança para cada intervalo de cada entrada.
Vamos considerar três variáveis v.fatl, ftlm e v.satl divididos em 4, 3 e 2 faixas, respectivamente. Desenhar os gráficos:
evalq(
cross_plot(data = train.d,
str_input = c("v.fatl", "ftlm", "v.satl"),
str_target = "Class",
auto_binning = F,
plot_type = "both"), #'quantity' 'percentual'
env
)
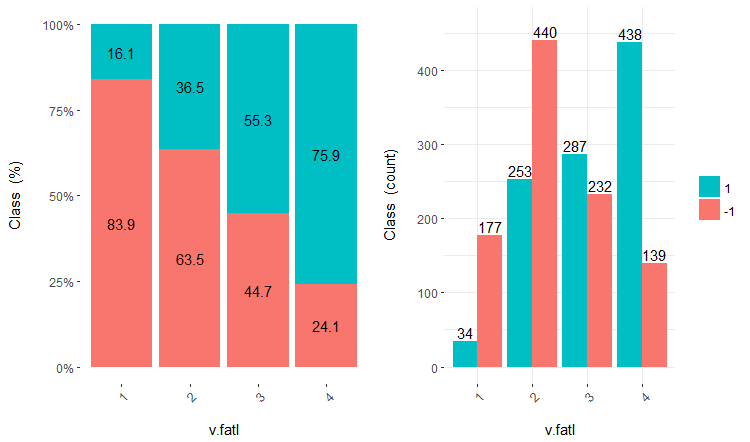
Fig.16. Cross-plot da variável v.fatl/Class
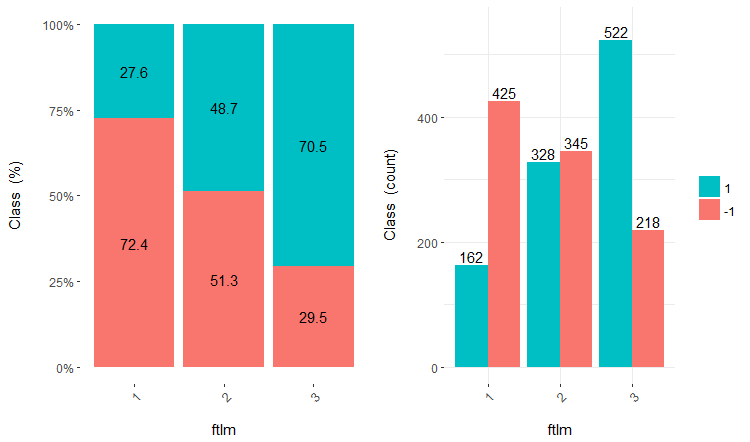
Fig.17. Cross-plot da variável ftlm/Class
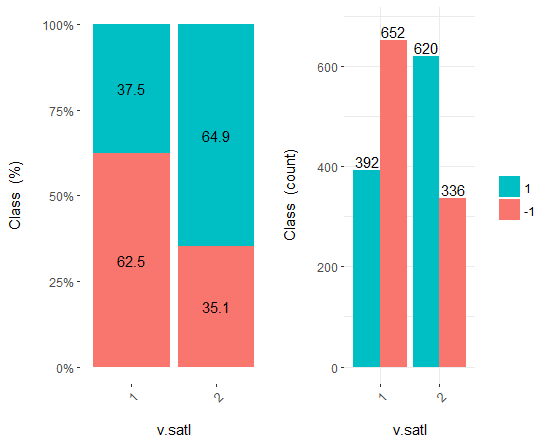
Fig.18. Cross-plot da variável v.satl/Class
Você pode ver que os preditores estão bem correlacionados com os níveis da variável objetivo, têm limiares pronunciadas que dividem os níveis da variável Class.
Os preditores podem simplesmente ser divididos em áreas iguais (de forma não ótima) para ver em que caso eles se correlacionarão com a variável objetivo. Vamos dividir três variáveis anteriores e duas ruins (stlm, v.rstl) do conjunto train em 10 áreas equifrequentes e olhar o seu cross-plot com a variável objetivo:
evalq(
cross_plot(
DT$train %>% select(-Data) %>%
select(c(v.satl, ftlm, v.fatl, stlm, v.rstl, Class)) %>%
as.data.frame(),
str_input = Cs(v.satl, ftlm, v.fatl, stlm, v.rstl),
str_target = "Class",
auto_binning = T,
plot_type = "both"), #'quantity' 'percentual'
env
)
Desenha cinco gráficos dessas variáveis:
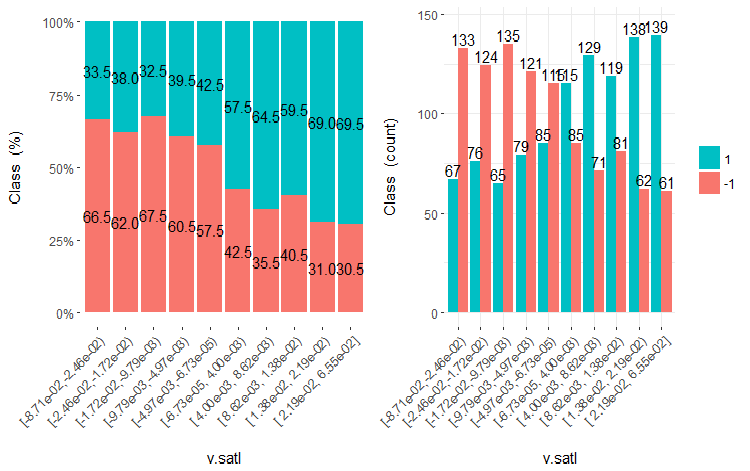
Fig.19. Cross-plot da variável v.satl (10 áreas) vs Class
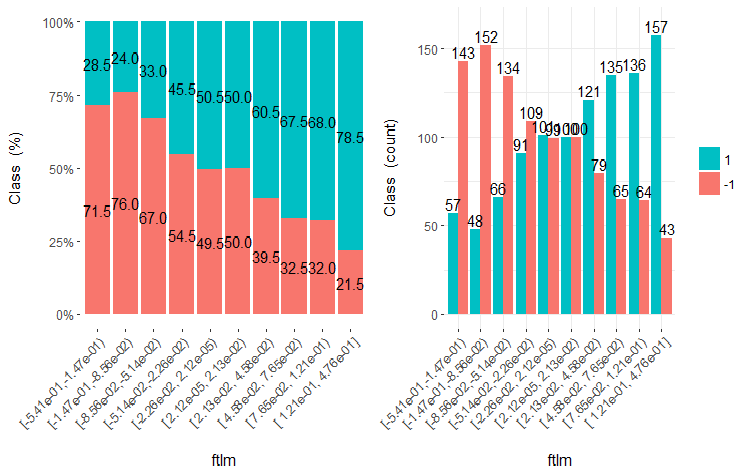
Fig.20. Cross-plot da variável ftlml (10 áreas) vs Class
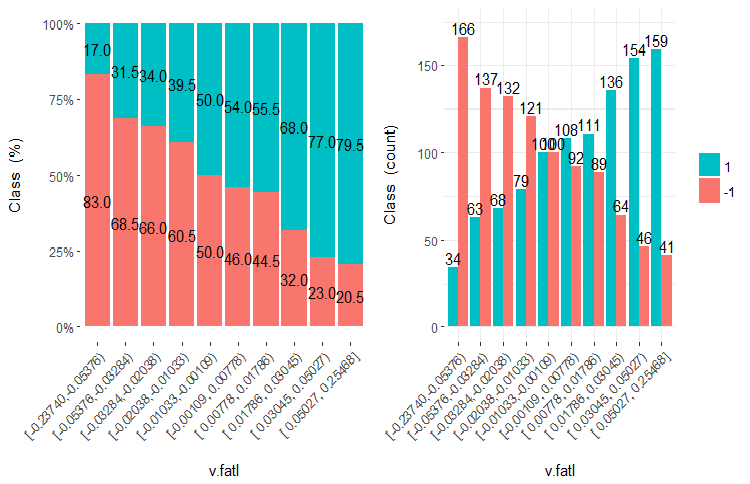
Fig.21. Cross-plot da variável v.fatl (10 áreas) vs Class
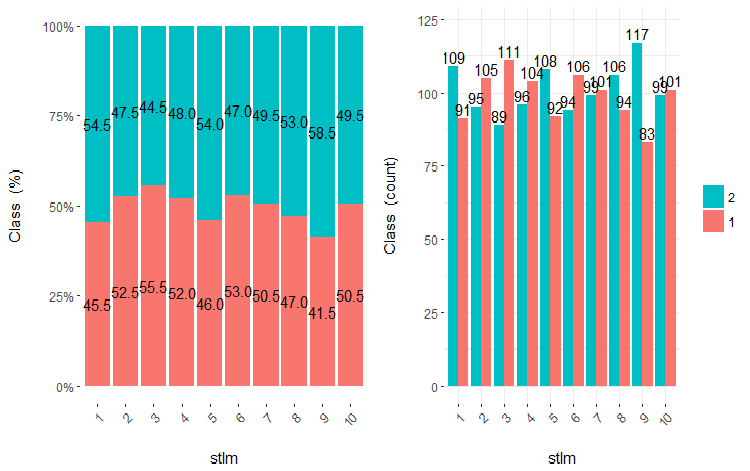
Fig.22. Cross-plot da variável stlm (10 áreas) vs Class
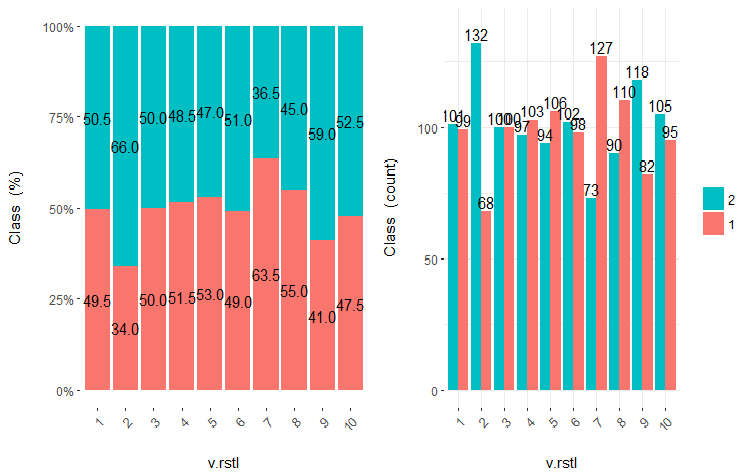
Fig.23. Cross-plot da variável v.rstl (10 áreas) vs Class
É claro que a partir dos diagramas que mesmo quando as variáveis foram divididas em 10 áreas discretas equifrequentes, as variáveis v.fatl, ftlm e v.satl têm um limiar bem pronunciado de níveis de divisão das variáveis. Fica claro do por que as duas outras variáveis (stlm, v.rstl) são irrelevantes. Esta é uma maneira eficiente de identificar a importância dos preditores. Nós voltaremos a isso mais adiante neste artigo.
Agora, vejamos como a variável de entrada se correlaciona com a variável objetivo, comparando-os usando o método Bayesiano taxa de conversão posterior. É útil comparar valores categóricos que não tenham uma ordem interna. Para isso, nós usaremos a função bayes_plot::funModeling. Vamos obter as variáveis v.fatl, ftlm e v.satl dos conjuntos train.d, val.d e test.d.
#------BayesTrain------------------- evalq( { bayesian_plot(train.d, input = "v.fatl", target = "Class", title = "Bayesian comparison train$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(train.d, input = "ftlm", target = "Class", title = "Bayesian comparison train$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(train.d, input = "v.satl", target = "Class", title = "Bayesian comparison train$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #------------BayesTest------------------------ evalq( { bayesian_plot(test.d, input = "v.fatl", target = "Class", title = "Bayesian comparison test$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(test.d, input = "ftlm", target = "Class", title = "Bayesian comparison test$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(test.d, input = "v.satl", target = "Class", title = "Bayesian comparison test$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #-------------BayesVal--------------------------------- evalq( { bayesian_plot(val.d, input = "v.fatl", target = "Class", title = "Bayesian comparison val$v.fatl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(val.d, input = "ftlm", target = "Class", title = "Bayesian comparison val$ftlm/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) evalq( { bayesian_plot(val.d, input = "v.satl", target = "Class", title = "Bayesian comparison val$v.satl/Class", plot_all = F, extra_above = 5, extra_under = 5) },env ) #------------------------------------------
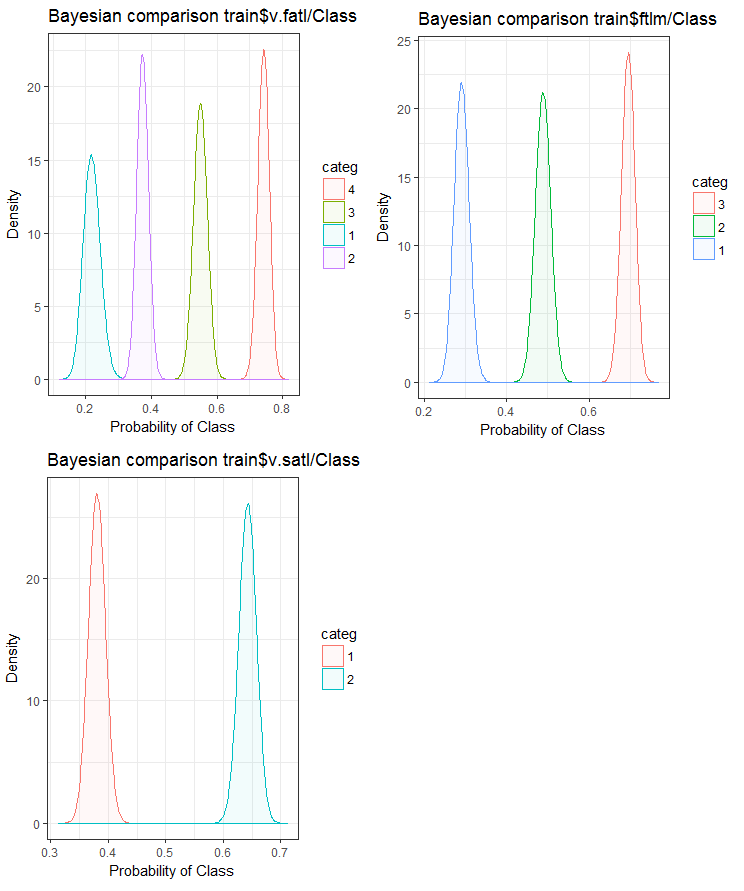
Fig.24. Comparação bayesiana das variáveis com a variável objetivo no conjunto train
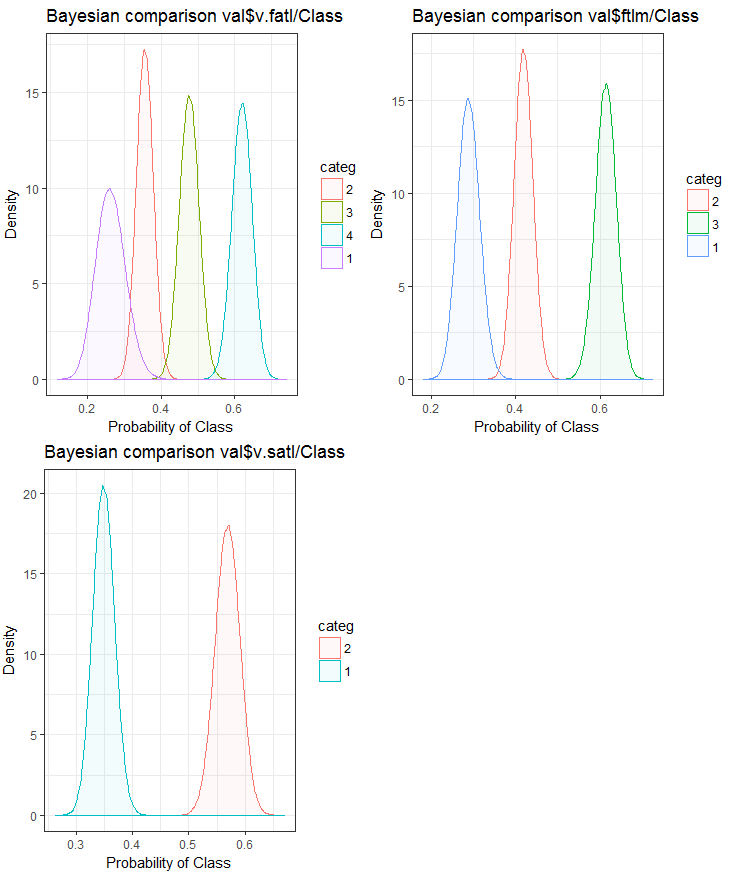
Fig.25. Comparação bayesiana das variáveis com a variável objetivo no conjunto val
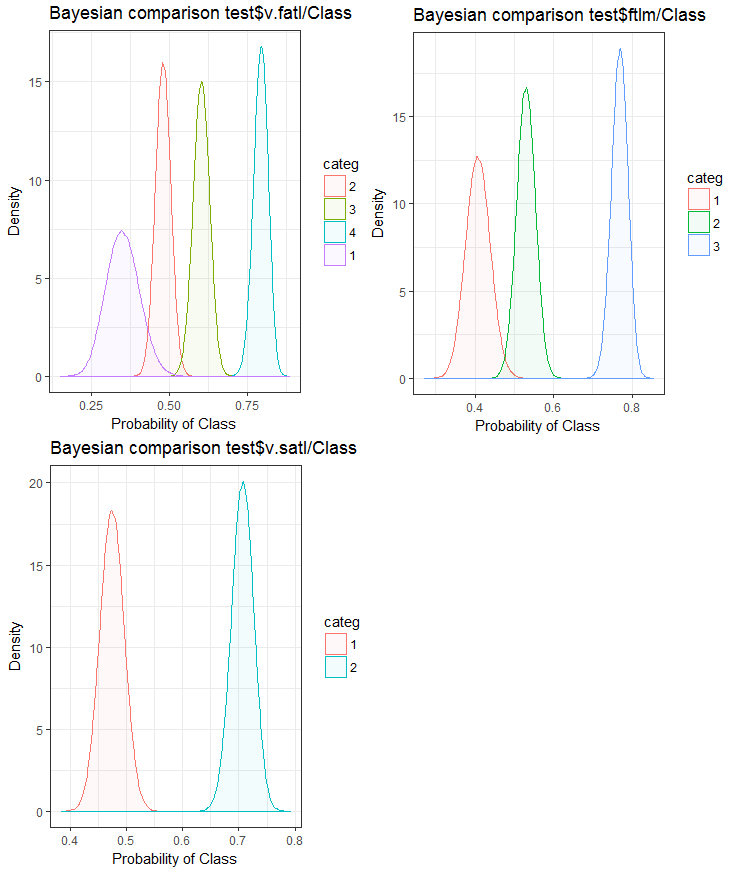
Fig.26. Comparação bayesiana das variáveis com a variável objetivo no conjunto test
Nós podemos ver que a correlação dos preditores com a variável objetivo é derivar mais na variável com 4 níveis e mais. Essa derivação é menor nas variáveis com dois grupos. Avançando, será útil verificar se a precisão do modelo será afetada usando somente preditores de dois intervalos.
A mesma tarefa de dividir uma variável em áreas próximas aos níveis da variável objetivo pode ser resolvida de outra maneira - usando o pacote smbinning. Você pode verificar você mesmo. O artigo anterior considera outro método interessante de discretização. Ele pode ser implementado usando o pacote "RoughSets".
A discretização é um método eficiente de transformação de preditores. Infelizmente, nem todos os modelos podem funcionar com preditores de fatores.
1.2. Criação de novas características
A criação de uma variável é um processo de criação de novas variáveis com base naquelas existentes. Vejamos o conjunto de dados onde a data (dd-mm-yy) é uma variável de entrada. Nós podemos criar novas variáveis que estarão melhor conectadas com o variável objetivo - dia, meses, ano, dia da semana. Este passo é usado para revelar relacionamentos ocultos na variável.
A criação de variáveis derivadas refere-se ao processo de criação de uma nova variável usando um conjunto de funções e vários métodos a partir de uma variável existente. O tipo da variável a criar depende da curiosidade do analista de negócios, o conjunto de hipóteses e seus conhecimentos teóricos. A escolha dos métodos é extensa. Tomando o logaritmo, a segmentação, a elevação para a enésima potência são apenas alguns exemplos dos métodos de transformação.
A criação das variáveis dummy é outro método popular de trabalhar com variáveis. Normalmente, as variáveis dummy são usadas na transformação de variáveis categóricas em números. A variável categórica pode ter valores de 0 e 1. Nós podemos criar variáveis dummy para mais de duas classes de variáveis categóricas com variáveis N e N-1.
Neste artigo, nós discutimos situações que encontramos diariamente como analistas. Listadas abaixo, existem várias maneiras de extrair ao máximo a informação de um conjunto de dados.
- Use os valores de dados e tempo como variáveis. Novas variáveis podem ser criadas levando em consideração as diferenças de data e hora.
- Crie novas razões e proporções. Em vez de armazenar entradas e saídas passadas no conjunto de dados, suas taxas podem ser incluídas. Isso pode ter um significado maior.
- Use as transformações padrões. Analisando as flutuações e as áreas da variável juntamente com o resultado, nós podemos ver se a correlação melhorará após as transformações básicas. As transformações mais utilizadas são as variações log, exp, quadrática e trigonométricas.
- Verifique as variáveis para a sazonalidade e crie um modelo para o período requerido (semana, mês, sessão, etc.).
É intuitivo que o comportamento do mercado na segunda-feira seja diferente do de quarta-feira e quinta-feira. Isso significa que o dia da semana é uma característica importante. A hora do dia é igualmente importante para o mercado. Isso define se esta é a sessão asiática, européia ou americana. Como podemos definir esses recursos?
Vamos usar o pacote timekit para isso. tk_augment_timeseries_signature() é a função central do pacote. Isso adiciona os rótulos de tempo do conjunto de dados inicial pr, toda a linha de dados de tempo que podem ser úteis como recursos e parâmetros adicionais do grupo. Quais são os dados?
| Index | o valor do índice que foi resolvido |
| Index.num | o valor numérico do índice em segundos. Base “1970-01-01 00:00:00” |
| diff | diferença em segundos com o valor numérico anterior do índice |
| Year | ano, componente do index |
| half | metade do componente do index |
| quarter | trimestre, componente do index |
| month | mês, componente do index com base 1 |
| month.xts | mês, componente do index com a base 0, o mesmo que implementado em xts |
| month.lbl | mês como o fator ordenado. Começa em janeiro e termina em dezembro |
| day | dia, componente do index |
| hour | hora, componente do index |
| minute | minuto, componente do index |
| second | segundo, componente do index |
| hour12 | componente da hora na escala de 12 horas |
| am.pm | manhã (am) = 1, tarde (pm) = 2 |
| wday | dia da semana com base 1 domingo = 1, sábado = 7 |
| wday.xts | dia da semana com base 0, o mesmo que implementado em xts. Sunday = 0, Saturday = 6 |
| wday.lbl | rótulo do dia da semana como um fator ordenado. Começa no domingo e termina no sábado |
| mday | dia do mês |
| qday | dia do trimestre |
| yday | dia do ano. |
| mweek | semana do mês |
| week | número da semana em um ano (começa com domingo) |
| week.iso | número da semana em um ano de acordo com o ISO (Inicia na segunda-feira) |
| week2 | módulo para a frequência quinzenal |
| week3 | módulo para a frequência de três semanas |
| week4 | módulo para a frequência quad-semanal |
Vamos tomar o conjunto de dados inicial pr, fortalecê-lo com a função tk_augment_timeseries_signature(), adicionar ao conjunto de dados inicial as variávies mday, wday.lbl, hour,, remover variáveis indefinidas (NA) e agrupar dados pelo dias da semana.
evalq(
{
tk_augment_timeseries_signature(pr) %>%
select(c(mday, wday.lbl, hour)) %>%
cbind(pr, .) -> pr.augm
pr.compl <- pr.augm[complete.cases(pr.augm), ]
pr.nest <- pr.compl %>% group_by(wday.lbl) %>% nest()
},
env)
> str(env$pr.augm)
'data.frame': 8000 obs. of 33 variables:
$ Data : POSIXct, format: "2017-01-10 11:00:00" ...
$ Open : num 123 123 123 123 123 ...
$ High : num 123 123 123 123 123 ...
$ Low : num 123 123 123 123 123 ...
$ Close : num 123 123 123 123 123 ...
$ Vol : num 3830 3360 3220 3241 3071 ...
..................................................
$ zigz : num 123 123 123 123 123 ...
$ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ...
$ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
$ mday : int 10 10 10 10 10 10 10 10 10 10 ...
$ wday.lbl: Ord.factor w/ 7 levels "Sunday"<"Monday"<..: 3 3 3 3 3 3 3 3 3 3 ...
$ hour : int 11 11 11 11 12 12 12 12 13 13 ...
O mesmo resultado pode ser alcançado se usarmos a biblioteca lubridate, tendo excluído os dados para domingo.
require(lubridate)
evalq({pr %>% mutate(.,
wday = wday(Data), #label = TRUE, abbr = TRUE),
day = day(Data),
hour = hour(Data)) %>%
filter(wday != "Sat") -> pr1
pr1.nest <- pr1 %>% na.omit %>%
group_by(wday) %>% nest()},
env
)
#-------
str(env$pr1)
'data.frame': 7924 obs. of 33 variables:
$ Data : POSIXct, format: "2017-01-10 11:00:00" ...
$ Open : num 123 123 123 123 123 ...
$ High : num 123 123 123 123 123 ...
$ Low : num 123 123 123 123 123 ...
$ Close : num 123 123 123 123 123 ...
$ Vol : num 3830 3360 3220 3241 3071 ...
..........................................
$ zigz : num 123 123 123 123 123 ...
$ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ...
$ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
$ wday : int 3 3 3 3 3 3 3 3 3 3 ...
$ day : int 10 10 10 10 10 10 10 10 10 10 ...
$ hour : int 11 11 11 11 12 12 12 12 13 13 ...
Os dados agrupados pelos dias da semana são os seguintes (domingo = 1, segunda-feira = 2 e assim por diante):
> env$pr1.nest # A tibble: 5 × 2 wday data <int> <list> 1 4 <tibble [1,593 Ч 32]> 2 5 <tibble [1,632 Ч 32]> 3 6 <tibble [1,624 Ч 32]> 4 2 <tibble [1,448 Ч 32]> 5 3 <tibble [1,536 Ч 32]>
Além disso, as variáveis dL, dH do conjunto de dados pr podem ser usadas nas últimas três barras.
2. Escolhendo preditores
Existem muitas maneiras e critérios de avaliar a importância dos preditores. Alguns deles foram consideradas nos artigos anteriores. Uma vez que neste artigo a ênfase está na visualização, vamos comparar um método visual e analítico de avaliar a importância dos preditores.
2.1. Avaliação visual
Vamos usar o smbinning pacote. Anteriormente, nós usamos o pacote FunModeling para avaliar os preditores. Nós chegamos à conclusão de que a visualização de um relacionamento é uma maneira simples e confiável de identificar a relevância dos preditores. Vamos testar como o pacote smbinning irá lidar com os dados normalizados e transformados. Nós vamos descobrir como a transformação dos preditores afetam sua importância.
Reúna em um conjunto de dados log-transformados, seno-transformados, tanh-transformados e normalizados e avalie a dependência da variável de objetivo e preditores nestes conjuntos.
A sequência de processamento do conjunto primário (exibido no diagrama abaixo) é o seguinte: limpe os dados brutos no dataSet (sem remover os dados altamente correlacionados), divida o dataSet nos conjuntos train/val/test e obtém o conjunto DT. Em seguida, executa as ações para cada tipo de transformação de acordo com o diagrama de blocos abaixo. Vamos reunir tudo em um script:
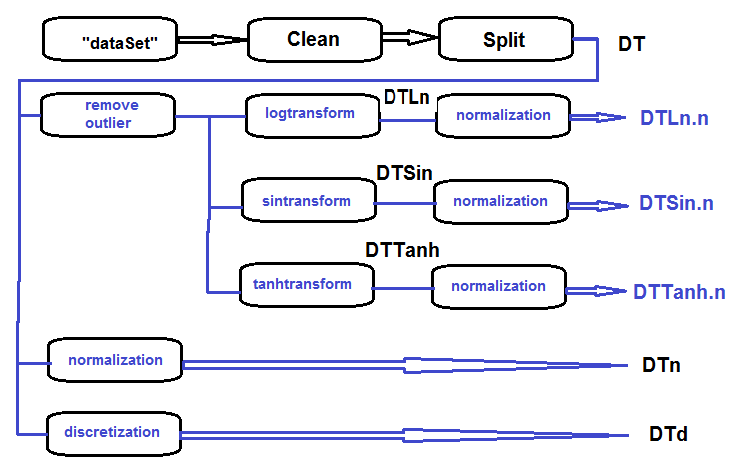
Fig.27. Diagrama de blocos do processamento preliminar
Limpa o conjunto, divide-o em conjuntos train/val/test e remove os dados desnecessários:
#----Clean--------------------- require(caret) require(pipeR) evalq( { train = 1:2000 val = 2001:3000 test = 3001:4000 DT <- list() dataSet %>% preProcess(., method = c("zv", "nzv", "conditionalX")) %>% predict(., dataSet) %>% na.omit -> dataSetClean list(train = dataSetClean[train, ], val = dataSetClean[val, ], test = dataSetClean[test, ]) -> DT rm(dataSetClean, train, val, test) }, env)
Processa todos os valores atípicos em todos os conjuntos:
#------outlier-------------
evalq({
# define the new list for the result
DTcap <- list()
# go through the three sets
foreach(i = 1:3) %do% {
DT[[i]] %>%
# remove columns with (Data, Class)
select(-c(Data, Class)) %>%
# transform into data.frame and store in the temporary variable x
as.data.frame() -> x
if (i == 1) {
# define parameters of outliers in the first input
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
prep.outlier(x[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
}
# substitute outliers for 5/95 % and store the result in x.cap
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = x[ ,i], impute = T, fill = T,
lower = lower, upper = upper,
med = med, cap1 = cap1, cap2 = cap2)
} %>% as.data.frame() -> x.cap
colnames(x.cap) <- colnames(x)
return(x.cap)
} -> Dtcap
#remove unnecessary variables
rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env)
Transforma as variáveis em todos os conjuntos Dtcap sem outliers com a função log(x+1). Obtém a lista DTLn com três conjuntos de variáveis log-transformadas.
#------logtrans------------
evalq({
DTLn <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) log2(x + 1)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTLn
},
env)
Transforma as variáveis em todos os conjuntos Dtcap sem os outliers com a função sin(2*pi*x). Obtém a lista DTSin com três conjuntos de variáveis seno-transformadas.
#------sintrans--------------
evalq({
DTSin <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) sin(2*pi*x)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTSin
},
env)
Transforma as variáveis em todos os conjuntos Dtcap sem outliers com a função tanh(x). Obtém a lista DTTanh com três conjuntos de variáveis tanh-transformada.
#------tanhTrans----------
evalq({
DTTanh <- list()
foreach(i = 1:3) %do% {
DTcap[[i]] %>%
apply(., 2, function(x) tanh(x)) %>%
as.data.frame() %>%
cbind(., Class = DT[[i]]$Class)
} -> DTTanh
},
env)
Normaliza os conjuntos DT, DTLn, DTSin, DTTanh.
#------normalize----------- evalq( { # define parameters of normalization preProcess(DT$train, method = "spatialSign") -> preproc list(train = predict(preproc, DT$train), val = predict(preproc, DT$val), test = predict(preproc, DT$test) ) -> DTn }, env) #--ln--- evalq( { preProcess(DTLn[[1]], method = "spatialSign") -> preprocLn list(train = predict(preprocLn, DTLn[[1]]), val = predict(preprocLn, DTLn[[2]]), test = predict(preprocLn, DTLn[[3]]) ) -> DTLn.n }, env) #---sin--- evalq( { preProcess(DTSin[[1]], method = "spatialSign") -> preprocSin list(train = predict(preprocSin, DTSin[[1]]), val = predict(preprocSin, DTSin[[2]]), test = predict(preprocSin, DTSin[[3]]) ) -> DTSin.n }, env) #-----tanh----------------- evalq( { preProcess(DTTanh[[1]], method = "spatialSign") -> preprocTanh list(train = predict(preprocTanh, DTTanh[[1]]), val = predict(preprocTanh, DTTanh[[2]]), test = predict(preprocTanh, DTTanh[[3]]) ) -> DTTanh.n }, env)
Usa a função mdlp::discretization para discretizar o conjunto DT
##------discretize----------
#--------preCut---------------------
# define the cutpoints
require(pipeR)
require(discretization)
evalq(
#require(pipeR)
# takes some time !
pipeline({
DT$train
select(-Data)
as.data.frame()
mdlp()
}) -> mdlp.train,
env)
#-------cut_opt----------
evalq(
{
DTd <- list()
mdlp.train$cutp %>%
# define the columns that have to be discretized
lapply(., function(x) is.numeric(x)) %>%
unlist -> idx # bool
#----train-----------------
mdlp.train$Disc.data[ ,idx] -> DTd$train
#---test------------
DT$test %>%
select(-c(Data, Class)) %>%
as.data.frame() -> test.d
# rearrange data according to calculated ranges
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(test.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$test$Class) -> DTd$test
colnames(DTd$test) <- colnames(DTd$train)
#-----val-----------------
DT$val %>%
select(-c(Data, Class)) %>%
as.data.frame() -> val.d
# rearrange data according to calculated ranges
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(val.d[ ,i],
vec = mdlp.train$cutp[[i]],
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$val$Class) -> DTd$val
colnames(DTd$val) <- colnames(DTd$train)
# tidy up
rm(test.d, val.d)
},
env
)
Vamos lembrar quais variáveis o conjunto de dados original DT$train contém:
require(funModeling)
plot_num(env$DT$train %>% select(-Data), bins = 20)
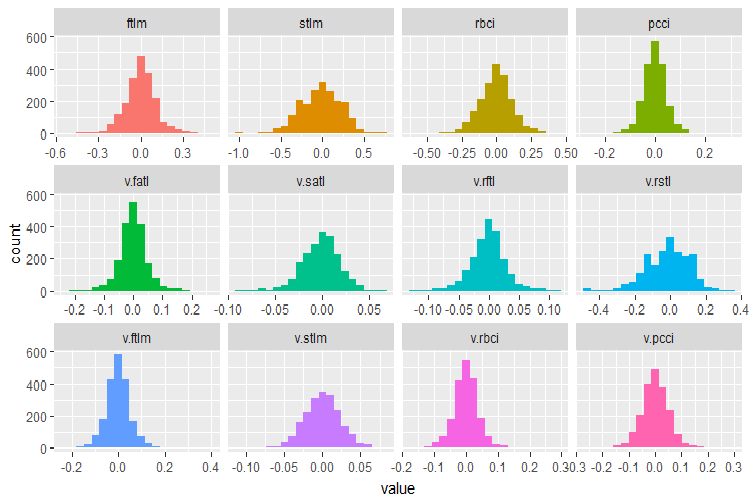
Fig.28. Distribuição de variáveis no conjunto de dados do DT$train
Use as capacidades do pacote smbinning para identificar os preditores relevantes nos subconjuntos train de todos os conjuntos de dados normalizados obtidos anteriormente (Dtn, DTLn.n, DTSin.n e DTTanh.n). A variável objetivo neste pacote deve ser numérica e ter valores (0, 1). Vamos escrever uma função para conversões necessárias.
#-------------------------------- require(smbinning) targ.int <- function(x){ x %>% tbl_df() %>% mutate(Cl = (as.numeric(Class) - 1) %>% as.integer()) %>% select(-Class) %>% as.data.frame() }
Além disso, esse pacote não aceita variáveis que tenham um ponto no nome. A função abaixo irá renomear todas as variáveis com um ponto em variáveis com um sublinhado.
renamepr <- function(X){
X %<>% rename(v_fatl = v.fatl,
v_satl = v.satl,
v_rftl = v.rftl,
v_rstl = v.rstl,
v_ftlm = v.ftlm,
v_stlm = v.stlm,
v_rbci = v.rbci,
v_pcci = v.pcci)
return(X)
}
Calcula e trata os gráficos com preditores relevantes.
par(mfrow = c(2,2)) #--Ln-------------- evalq({ df <- renamepr(DTLn.n[[1]]) %>% targ.int sumivt.ln.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.ln.n, cex = 0.7) rm(df) }, env) #---Sin----------------- evalq({ df <- renamepr(DTSin.n[[1]]) %>% targ.int sumivt.sin.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.sin.n, cex = 0.7) rm(df) }, env) #---norm------------- evalq({ df <- renamepr(DTn[[1]]) %>% targ.int sumivt.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.n, cex = 0.7) rm(df) }, env) #-----Tanh---------------- evalq({ df <- renamepr(DTTanh.n[[1]]) %>% targ.int sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl') smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.7) rm(df) }, env) par(mfrow = c(1,1))
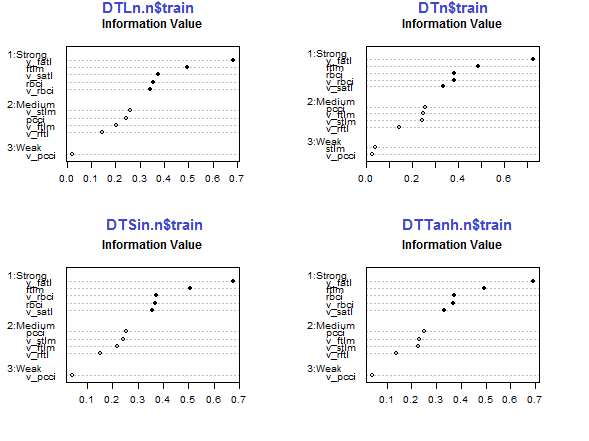
Fig.29. Importância dos preditores no subconjunto train de conjuntos normalizados
Os cinco preditores v_fatl, ftlm, v_satl, rbci, v_rbci são fortes em todos os conjuntos, embora sua ordem seja diferente. Os quatro preditores pcci, v_ftlm, v_stlm, v_rftl tem força média. Preditores v_pcci e stlm são fracos. A distribuição das variáveis pode ser vista para cada conjunto na ordem de sua importância:
env$sumivt.ln.n Char IV Process 5 v_fatl 0.6823 Numeric binning OK 1 ftlm 0.4926 Numeric binning OK 6 v_satl 0.3737 Numeric binning OK 3 rbci 0.3551 Numeric binning OK 11 v_rbci 0.3424 Numeric binning OK 10 v_stlm 0.2591 Numeric binning OK 4 pcci 0.2440 Numeric binning OK 9 v_ftlm 0.2023 Numeric binning OK 7 v_rftl 0.1442 Numeric binning OK 12 v_pcci 0.0222 Numeric binning OK 2 stlm NA No significant splits 8 v_rstl NA No significant splits
As últimas três variáveis podem ser descartadas. Dessa forma, apenas as cinco mais fortes e quatro médios serão deixados. Vamos definir os nomes das melhores variáveis (IV > 0.1).
evalq(sumivt.sin.n$Char[sumivt.sin.n$IV > 0.1] %>% na.omit %>% as.character() -> best.sin.n, env) > env$best.sin.n [1] "v_fatl" "ftlm" "rbci" "v_rbci" "v_satl" "pcci" [7] "v_ftlm" "v_stlm" "v_rftl"
Vejamos as variáveis v_fatl и ftlm em maior detalhe.
evalq({
df <- renamepr(DTTanh.n[[1]]) %>% targ.int
x = 'v_fatl'
y = 'Cl'
res <- smbinning(df = df,
y = y,
x = x)
#res$ivtable # Tabulation and Information Value
#res$iv # Information value
#res$bands # Bins or bands
#res$ctree # Decision tree from partykit
par(mfrow = c(2,2))
sub = paste0(x, " vs ", y) #rbci vs Cl"
boxplot(df[[x]]~df[[y]],
horizontal = TRUE,
frame = FALSE, col = "lightblue",
main = "Distribution")
mtext(sub,3) #ftlm
smbinning.plot(res, option = "dist",
sub = sub) #"pcci vs Cl")
smbinning.plot(res, option = "goodrate", #"badrate"
sub = sub) #"pcci vs Cl")
smbinning.plot(res, option = "WoE",
sub = sub) #"pcci vs Cl")
par(mfrow = c(1, 1))
}, env)
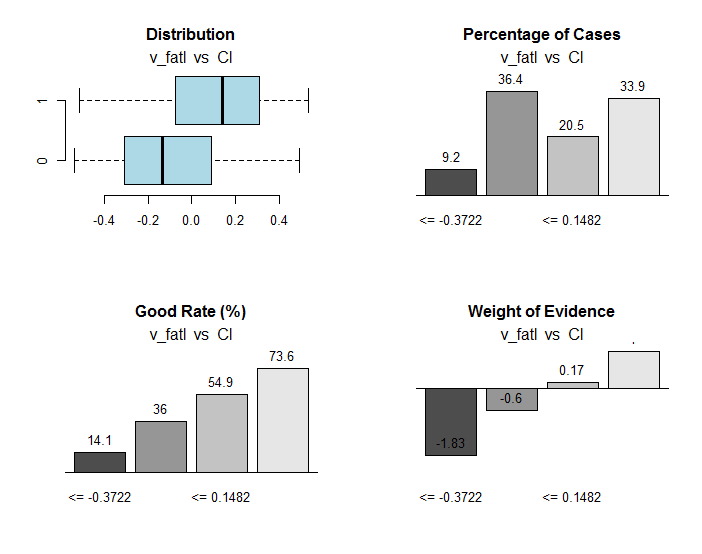
Fig.30. Conexão dos intervalos da variável v_fatl com a variável objetivo Cl
Juntamente com informações úteis, o objeto res contém os pontos de divisão da variável em intervalos otimamente conectados com a variável objetivo. No nosso caso particular, existem quatro intervalos.
> env$res$cuts [1] -0.3722 -0.0433 0.1482
Vamos fazer o mesmo cálculo para a variável ftlme desenhar os gráficos:
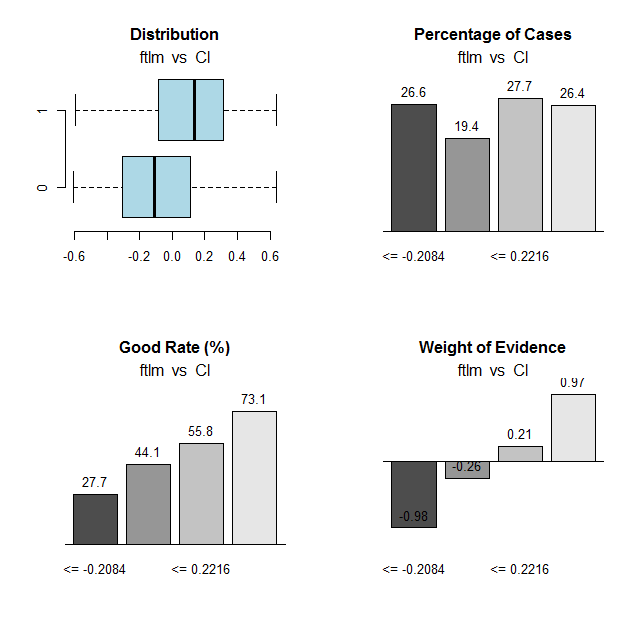
Fig.31. Conexão das faixas da variável ftlm com a variável objetivo Cl
Pontos de corte do intervalo:
> env$res$cuts [1] -0.2084 -0.0150 0.2216
Os pontos de corte nos permitirão discretizar as variáveis em nossos conjuntos e ver o quanto deles os diferentes itens diferem:
- variáveis importantes anteriormente definidas usando a função mdlp::discretização das variáveis definidas usando a função smbinning::smbinning;
- dividindo as variáveis em intervalos.
Nós já temos um conjunto de dados discretizado com a função mdlp::discretization DTd. Vamos fazer o mesmo, mas desta vez vamos usar a função smbinning::smbinning para apenas o subconjunto train.
Defina os pontos de corte:
evalq({
res <- list()
DT$train %>% renamepr() %>% targ.int() -> df
x <- colnames(df)
y <- "Cl"
foreach(i = 1:(ncol(df) - 1)) %do% {
smbinning(df, y = y, x = x[i])
} -> res
res %>% lapply(., function(x) x[1] %>% is.list) %>%
unlist -> idx
}, env)
Discretize the DT$train: subset
evalq({
DT1.d <- list()
DT$train %>% renamepr() %>%
targ.int() %>% select(-Cl) -> train
foreach(i = 1:length(idx), .combine = 'cbind') %do% {
if (idx[i]) {
findInterval(train[ ,i],
vec = res[[i]]$cuts,
rightmost.closed = FALSE,
all.inside = F,
left.open = F)
}
} %>% as.data.frame() %>% add(1) %>%
cbind(., DT$train$Class) -> DT1.d$train
colnames(DT1.d$train) <- colnames(train)[idx] %>%
c(., 'Class')
},
env)
Identifica as melhores variáveis com a importância maior que 0.1 em ordem crescente:
evalq({
DT$train %>% renamepr() %>% targ.int() -> df
sumivt.dt1.d = smbinning.sumiv(df = df, y = 'Cl')
sumivt.dt1.d$Char[sumivt.dt1.d$IV > 0.1] %>%
na.omit %>% as.character() -> best.dt1.d
rm(df)
},
env)
Desenha um gráfico de variáveis de divisão no conjunto DTd$train:
require(funModeling) plot_num(env$DTd$train)
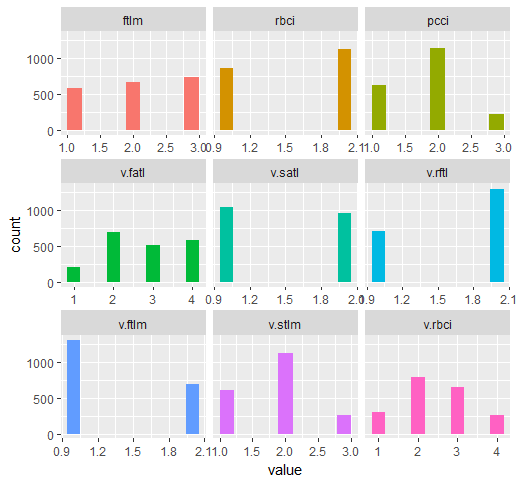
Fig.32. Variáveis do conjunto train DT$ discretizados com a função mdlp
O gráfico do conjunto DT1.d com todas as variáveis e com os melhores é exibido abaixo.
plot_num(env$DT1.d$train)
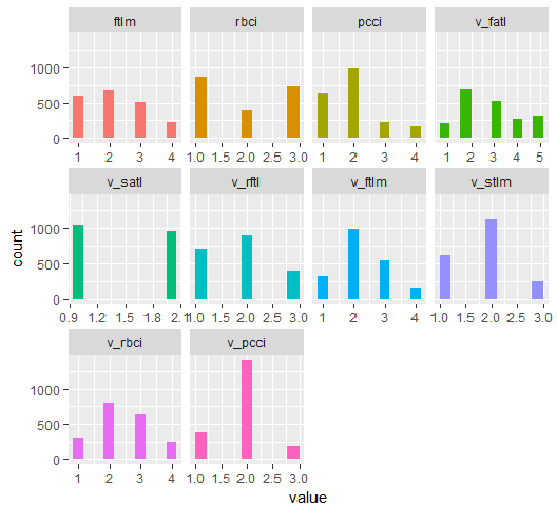
Fig.33. Variáveis do conjunto d$train DT1 discretizado com a função smbinning
plot_num(env$DT1.d$train[ ,env$best.dt1.d])
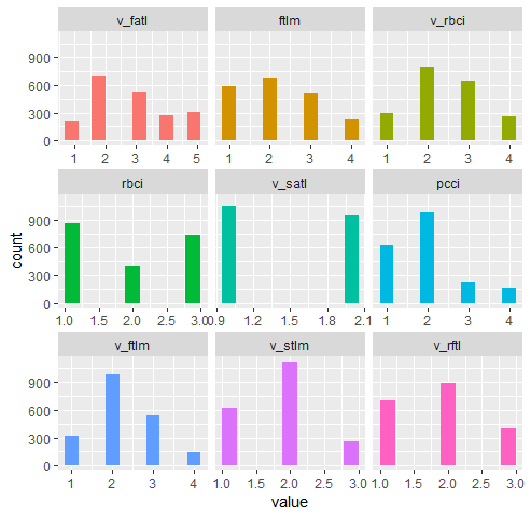
Fig.34. Variáveis do conjunto DT1.d$train discretizado com a função smbinning (os melhores estão dispostos em ordem crescente de importância da informação)
O que nós podemos ver nos gráficos? As variáveis definidas como importantes são as mesmas em ambos os casos, mas a divisão em intervalos difere. Deve ser testado qual variante fornece uma melhor previsão no modelo.
2.2. Avaliação analítica
Existem muitos métodos analíticos para identificar a importância dos preditores de acordo com vários critérios. Consideramos alguns deles anteriormente. Agora, eu gostaria de testar uma abordagem incomum para a escolha dos preditores.
Nós vamos usar o pacote varbvs. Na função implementada varbvs estão: algoritmos rápidos para a instalação de modelos bayesianos de escolha de variáveis e cálculo de coeficientes Bayesianos, onde o resultado (ou variável objetivo) é modelado com regressão linear ou regressão logística. Esses algoritmos baseiam-se nas aproximações variacionais descritas em "Scalable variational inference for Bayesian variable selection in regression, and its accuracy in genetic association studies" (P. Carbonetto e M. Stephens, Bayesian Analysis 7, 2012, páginas 73-108). Este software foi utilizado para trabalhar com grandes conjuntos de dados com mais de um milhão de variáveis e com milhares de amostras.
A função varbvs() recebe uma matriz e a variável objetivo recebe um vetor numérico (0, 1) como dados de entrada. Usando esse método, vamos testar quais preditores serão definidos como importantes em nosso conjunto com dados normalizados DTTanh.n$train .
require(varbvs)
evalq({
train <- DTTanh.n$train %>% targ.int() %>% as.matrix()
fit <- varbvs(X = train[ ,-ncol(train)] ,
Z = NULL,
y = train[ ,ncol(train)] %>% as.vector(),
"binomial",
logodds = seq(-2,-0.5,0.1),
optimize.eta = T,
initialize.params = T,
verbose = T, nr = 100
)
print(summary(fit))
}, env)
Welcome to -- * *
VARBVS version 2.0.3 -- | | |
large-scale Bayesian -- || | | | || | | |
variable selection -- | || | | | | || || |||| || | ||
****************************************************************************
Copyright (C) 2012-2017 Peter Carbonetto.
See http://www.gnu.org/licenses/gpl.html for the full license.
Fitting variational approximation for Bayesian variable selection model.
family: binomial num. hyperparameter settings: 16
samples: 2000 convergence tolerance 1.0e-04
variables: 12 iid variable selection prior: yes
covariates: 0 fit prior var. of coefs (sa): yes
intercept: yes fit approx. factors (eta): yes
Finding best initialization for 16 combinations of hyperparameters.
-iteration- variational max. incl variance params
outer inner lower bound change vars sigma sa
0016 00018 -1.204193e+03 6.1e-05 0003.3 NA 3.3e+00
Computing marginal likelihood for 16 combinations of hyperparameters.
-iteration- variational max. incl variance params
outer inner lower bound change vars sigma sa
0016 00002 -1.204193e+03 3.2e-05 0003.3 NA 3.3e+00
Summary of fitted Bayesian variable selection model:
family: binomial num. hyperparameter settings: 16
samples: 2000 iid variable selection prior: yes
variables: 12 fit prior var. of coefs (sa): yes
covariates: 1 fit approx. factors (eta): yes
maximum log-likelihood lower bound: -1204.1931
Hyperparameters:
estimate Pr>0.95 candidate values
sa 3.49 [3.25,3.6] NA--NA
logodds -0.75 [-1.30,-0.50] (-2.00)--(-0.50)
Selected variables by probability cutoff:
>0.10 >0.25 >0.50 >0.75 >0.90 >0.95
3 3 3 3 3 3
Top 5 variables by inclusion probability:
index variable prob PVE coef* Pr(coef.>0.95)
1 1 ftlm 1.0000 NA 2.442 [+2.104,+2.900]
2 4 pcci 1.0000 NA 2.088 [+1.763,+2.391]
3 3 rbci 0.9558 NA 0.709 [+0.369,+1.051]
4 10 v.stlm 0.0356 NA 0.197 [-0.137,+0.529]
5 6 v.satl 0.0325 NA 0.185 [-0.136,+0.501]
*See help(varbvs) about interpreting coefficients in logistic regression.
Como você pode ver, os cinco melhores preditores foram identificados (ftlm, pcci, rbci, v.stlm, v.satl). Eles estão no top dez, que identificamos anteriormente, mas em uma ordem diferente e com outros pesos de importância. Uma vez que já temos um modelo, vamos verificar o resultado que obteremos nos conjuntos de validação e teste.
Conjunto de validação:
#-----------------
evalq({
val <- DTTanh.n$val %>% targ.int() %>%
as.matrix()
y = val[ ,ncol(val)] %>% as.vector()
pr <- predict(fit, X = val[ ,-ncol(val)] ,
Z = NULL)
}, env)
cm.val <- confusionMatrix(table(env$y, env$pr))
> cm.val
Confusion Matrix and Statistics
0 1
0 347 204
1 137 312
Accuracy : 0.659
95% CI : (0.6287, 0.6884)
No Information Rate : 0.516
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.3202
Mcnemar's Test P-Value : 0.0003514
Sensitivity : 0.7169
Specificity : 0.6047
Pos Pred Value : 0.6298
Neg Pred Value : 0.6949
Prevalence : 0.4840
Detection Rate : 0.3470
Detection Prevalence : 0.5510
Balanced Accuracy : 0.6608
'Positive' Class : 0
O resultado não parece impressionante. Test set:
evalq({
test <- DTTanh.n$test %>% targ.int() %>%
as.matrix()
y = test[ ,ncol(test)] %>% as.vector()
pr <- predict(fit, X = test[ ,-ncol(test)] ,
Z = NULL)
}, env)
cm.test <- confusionMatrix(table(env$y, env$pr))
> cm.test
Confusion Matrix and Statistics
0 1
0 270 140
1 186 404
Accuracy : 0.674
95% CI : (0.644, 0.703)
No Information Rate : 0.544
P-Value [Acc > NIR] : < 2e-16
Kappa : 0.3375
Mcnemar's Test P-Value : 0.01269
Sensitivity : 0.5921
Specificity : 0.7426
Pos Pred Value : 0.6585
Neg Pred Value : 0.6847
Prevalence : 0.4560
Detection Rate : 0.2700
Detection Prevalence : 0.4100
Balanced Accuracy : 0.6674
'Positive' Class : 0
O resultado é quase o mesmo. Isso significa que o modelo não foi re-treinado e generaliza bem os dados.
Então, de acordo com varbvs, os melhores são ftlm, pcci, rbci, v.stlm, v.satl.
2.3. Rede neural
À medida que estamos estudando redes neurais, vamos testar quais preditores a rede neural selecionará como os mais importantes.
Nós vamos usar o pacote FCNN4R que fornece a interface para os principais programas da biblioteca FCNN em C++. O FCNN baseia-se em uma representação completamente nova da rede neural que implica eficiência, modularidade e capacidade de expansão. O FCNN4R permite a aprendizagem padrão (backpropagation, Rprop, recozimento simulado, gradiente estocástico) e algoritmos de poda (magnitude mínima, Optimal Brain Surgeon), embora vejo esse pacote como um mecanismo de cálculo eficiente, acima de tudo.
Os usuários podem facilmente implementar seu algoritmo usando métodos de gradiente rápido, juntamente com a funcionalidade de restaurar a rede (removendo pesos e neurônios excessivos, reorganizando os dados de entrada e redes de união).
As redes podem ser exportadas para as funções C para poderem ser integradas em qualquer solução de programa.
Crie uma rede totalmente conectada com duas camadas ocultas. O número de neurônios em cada camada: entrada = 12 (número de preditores), saída = 1. Inicie os neurônios por peso aleatório na faixa de +/- 0,17. Defina funções de ativação em cada camada da rede neural (exceto a entrada) = c ("tanh", "tanh", "sigmoid"). Prepare os conjuntos train/val/teste.
O script abaixo executa essa sequência de ações.
require(FCNN4R)
evalq({
mlp_net(layers = c(12, 8, 5, 1), name = "n.tanh") %>%
mlp_rnd_weights(a = 0.17) %>%
mlp_set_activation(layer = c(2, 3, 4),
activation = c("tanh", "tanh", "sigmoid"), #"threshold", "sym_threshold",
#"linear", "sigmoid", "sym_sigmoid",
#"tanh", "sigmoid_approx",
#"sym_sigmoid_approx"),
slope = 0) -> Ntanh #show()
#-------
train <- DTTanh.n$train %>% targ.int() %>% as.matrix()
test <- DTTanh.n$test %>% targ.int() %>% as.matrix()
val <- DTTanh.n$val %>% targ.int() %>% as.matrix()
}, env)
Nós vamos usar o método de treinamento rprop. Defina as constantes: tol — o erro quando o treinamento deve ser interrompido se esse nível for atingido, max_ep — o número de épocas após as quais o treinamento deve ser interrompido, l2reg — coeficiente de regularização. Treine a rede com esses parâmetros e avalie visualmente a rede e o erro de treinamento que temos.
evalq({
tol <- 1e-1
max_ep = 1000
l2reg = 0.0001
net_rp <- mlp_teach_rprop(Ntanh,
input = train[ ,-ncol(train)],
output = train[ ,ncol(train)] %>% as.matrix(),
tol_level = tol,
max_epochs = max_ep,
l2reg = l2reg,
u = 1.2, d = 0.5,
gmax = 50, gmin = 1e-06,
report_freq = 100)
}, env)
plot(env$net_rp$mse, t = "l",
main = paste0("max_epochs =", env$max_ep, " l2reg = ", env$l2reg))
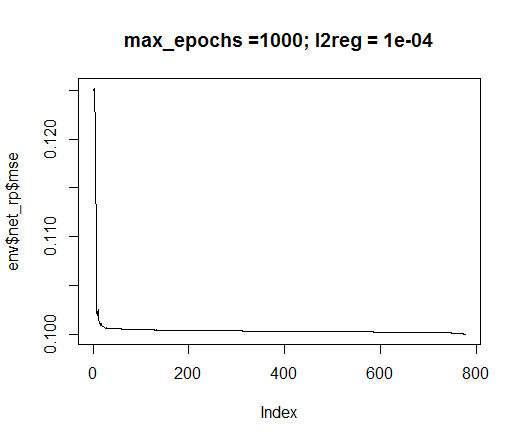
Fig.35. Erro no treinamento de redes neurais
evalq(mlp_plot(net_rp$net, FALSE), envir = env)
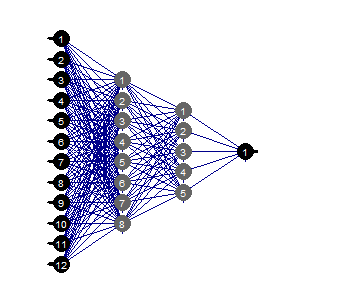
Fig.36. Estrutura da rede neural
Poda
A poda do valor mínimo é um algoritmo simples de usar. Aqui, os pesos com o menor valor absoluto são desligados em cada etapa. Este algoritmo requer o relé de rede quase em cada etapa e dá resultados sub-ótimos.
evalq({
tol <- 1e-1
max_ep = 1000
l2reg = 0.0001
mlp_prune_mag(net_rp$net,
input = train[ ,-ncol(train)],
output = train[ ,ncol(train)] %>% as.matrix(),
tol_level = tol,
max_reteach_epochs = max_ep,
report = FALSE,
plots = TRUE) -> net_rp_prune
}, env)
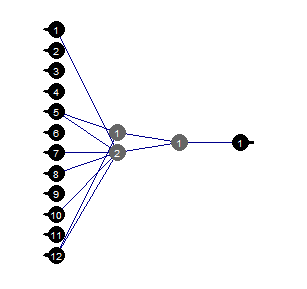
Fig.37. Rede neural de podas
Podemos ver isso com uma certa estrutura da rede neural, configuração inicial, funções de ativação e erro de aprendizado, a rede neural com a estrutura (12, 2, 1, 1) é suficiente. Quais os preditores foram escolhidos pela rede neural?
evalq( best <- train %>% tbl_df %>% select(c(1,5,7,8,10,12)) %>% colnames(), env) env$best [1] "ftlm" "v.fatl" "v.rftl" "v.rstl" "v.stlm" [6] "v.pcci"
As variáveis v.rstl e v.pcci não estão presentes entre as melhores nove variáveis definidas anteriormente.
Eu gostaria de salientar aqui que mostramos que uma rede neural pode selecionar de forma independente e automática importantes preditores. Essa escolha depende não apenas dos preditores, mas sim da estrutura e dos parâmetros da rede.
Tenha um ótimo experimento!
Conclusão
Na parte a seguir, falaremos sobre formas de excluir exemplos de ruído do conjunto, como diminuir o tamanho das entradas e o efeito que isso terá junto com formas de dividir dados originais em train/val/test.
Aplicação
1. Você pode baixar os scripts FeatureTransformation.R, FeatureSelect.R, FeatureSelect_analitic.R FeatureSelect_NN.R e os diagramas que mostram o trabalho dos scripts da Part_1 deste artigo RData do Git/Parte II.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/3507
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Redes Neurais Profundas (Parte I). Preparando os Dados
Redes Neurais Profundas (Parte I). Preparando os Dados
 Criação e teste de símbolos personalizados na MetaTrader 5
Criação e teste de símbolos personalizados na MetaTrader 5
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
O pacote R funModeling não tem a função "?
Por quê?
Espero sinceramente sua resposta!
Senhor, tentei executar seu código R, MAS o pacote R "funModeling" não tem a função "bayesian_plot()", por quê? Será que a versão do pacote não está correta?
Por quê?
Espero sinceramente sua resposta!
Esse recurso foi removido nas versões recentes do pacote por motivos desconhecidos. Infelizmente
В последних релизах пакета эту функцию убрали. Причина мне неизвестна.
Obrigado por sua resposta oportuna