Redes Neurais Profundas (Parte III). Seleção da amostra e redução de dimensionalidade

Conteúdo

• Introdução
• 1. Seleção da amostra
  
• 2. Redução da dimensionalidade
  
• 2.1. Análise de Componentes Principais (PCA)
• 2.2. Análise de Componentes Independentes (ICA)
• 2.3. Análise Probabilística de Componentes Principais (PPCA)
• 2.4. Autoencoder (PCA não-linear)
  
• 2.5. PCA não-linear inverso (NLPCA)
• 3. Dividindo o conjunto de dados nos conjuntos train/valid/test
• Conclusão
• Aplicação

Introdução

Este é o terceiro (e último) artigo que descreve a preparação de dados - o estágio mais importante do trabalho com redes neurais. Nós consideraremos dois métodos muito importantes de preparação de dados. Eles estão removendo o ruído e reduzindo a dimensionalidade de entrada. As descrições dos métodos serão acompanhadas de exemplos e gráficos detalhados.

1. Seleção da amostra

As amostras de ruído referem-se a rotulagem incorreta das amostras de treino. Esta é uma peculiaridade muito indesejável dos dados. Para superar isso, usaremos o pacote NoiseFilterR onde os filtros de ruído clássicos e contemporâneos são implementados em R.

Ultimamente, a mineração de dados teve que lidar com problemas cada vez mais complexos relacionados a natureza dos dados. Não é o volume dos dados, mas sua imperfeição e formas diferentes apresentam aos exploradores uma multiplicidade de vários cenários. Consequentemente, o processamento preliminar de dados tornou-se uma parte importante do processo KDD (descoberta de conhecimento em bases de dados). Ao mesmo tempo, o desenvolvimento do software para o processamento preliminar de dados fornece ferramentas suficientes para o trabalho.

É necessário o processamento preliminar de dados para os próximos algoritmos para poder extrair a informação máxima de um conjunto de dados. Este é um dos estágios que mais consomem energia e tempo em todo o processo de KDD. O processamento preliminar de dados pode ser dividido em subtarefas. Por exemplo, estes podem ser a seleção de preditores ou a remoção de dados ausentes e de ruído. A seleção de preditores visa extrair os atributos mais importantes para o treinamento, o que permite simplificar os modelos e reduzir o tempo de cálculo. O processamento dos dados ausentes é necessário para armazenar o máximo de dados possível. Os dados de ruído são dados incorretos ou aqueles que se destacam da distribuição de dados.

Todos esses problemas podem ser resolvidos com os softwares disponíveis, que são muito utilizados. Por exemplo, a ferramenta KEEL (RKEEL) contém um amplo conjunto de algoritmos de processamento de dados preliminares que abrangem todas as manipulações mencionadas acima. Existem outras soluções populares, como a WEKA (RWEKA) ou RapidMiner para a seleção de preditores. Há também uma série de programas complexos e únicos para mineração de dados, como R, KNIME ou Python.

Quanto ao software estatístico R, The Comprehensive R Archive Network (CRAN) contém muitos pacotes para a resolução de problemas de processamento de dados preliminares.

Os conjuntos de dados reais sempre contêm imperfeições e ruídos. Este ruído tem um impacto negativo no treinamento de classificadores, o que, por sua vez, reduz a precisão da predição, complica os modelos e aumenta o tempo de cálculo.

A literatura designada em classificação distingue dois tipos diferentes de ruído: o ruído do atributo e o ruído de rotulagem (ou ruído de classe). O primeiro ocorre devido as imperfeições dos atributos do conjunto de dados de treinamento e o segundo ocorre devido aos erros nos métodos de classificação. O pacote NoiseFiltersR centra-se principalmente no ruído de classe - o mais prejudicial, pois a qualidade da rotulagem é muito importante para os classificadores de treinamento.

Duas abordagens principais para resolver o problema do ruído de classe são descritas aqui. Você pode estudá-los em detalhes no trabalho recente de Benoit Frenay e Michel Verleysen.

• Por outro lado, esta é uma abordagem no nível de algoritmo, quando um problema é resolvido criando um algoritmo de classificação robusto, ele não é muito afetado pela presença de ruído. Cada algoritmo neste caso será uma solução específica, não universal.
  
• Por outro lado, uma abordagem no nível de dados (filtros) é uma tentativa de desenvolver uma estratégia de limpeza de dados que será realizada antes do treinamento do classificador. O pacote NoiseFiltersR utiliza a segunda abordagem. Isso ocorre porque ele permite o processamento preliminar de dados apenas uma vez e após isso, os classificadores podem ser alterados quantas vezes for necessário.

Os seguintes classificadores são resistentes ao ruído: С4.5, J48 e Jrip (WEKA).

Vamos conduzir um experimento. Vamos tratar os seguintes conjuntos de dados: DT (dados brutos antes do processamento preliminar), DTn (apenas o conjunto de dados brutos normalizados), DTTanh.n (sem outliers, transformados em tangente hiperbólica e normalizado) e o conjunto de treinamento com a função ORBoostFilter() que é um filtro para remover o ruído. Vamos ver como a distribuição se altera após tal processamento.

evalq({
  #-----DT---------------------
  out11 <- ORBoostFilter(Class~., data = DT$train, N = 10, useDecisionStump = TRUE)
  DT$train_clean1 <- out11$cleanData
  #----------DTTanh.n------------------------
  out1 <- ORBoostFilter(Class~., data = DTTanh.n$train, N = 10, useDecisionStump = TRUE)
  DTTanh.n$train_clean1 <- out1$cleanData
  #-----------DTn--------------------------------
  out12 <- ORBoostFilter(Class~., data = DTn$train, N = 10, useDecisionStump = TRUE)
  DTn$train_clean1 <- out12$cleanData
},
env)
#---Ris1-----------------
require(funModeling)
evalq({
  par(mfrow = c(1,3))
  par(las = 1)
  boxplot(DT$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
          main = "DT$train_clean1")
  boxplot(DTn$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
          main = "DTn$train_clean1")
  boxplot(DTTanh.n$train_clean1 %>% select(-c(Data,Class)), horizontal = TRUE,
          main = "DTTanh.n$train_clean1")
  par(mfrow = c(1,1))
}, env)

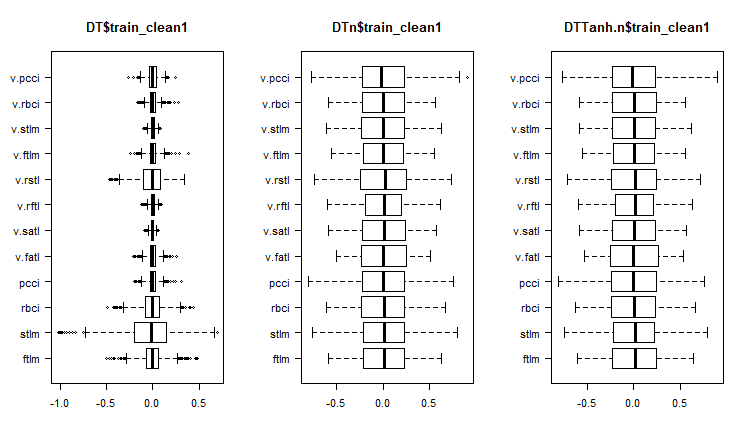
Fig. 1. Distribuição de preditores nos conjuntos após a remoção de amostras de ruído

Vamos ver quais são a variação e covariância nestes conjuntos:

#----Ris2------------------
require(GGally)
evalq(ggpairs(DT$train_clean1 %>% select(-Data), 
              columns = c(1:6, 13), 
              mapping = aes(color = Class),
              title = "DT$train_clean1/1"), 
      env)

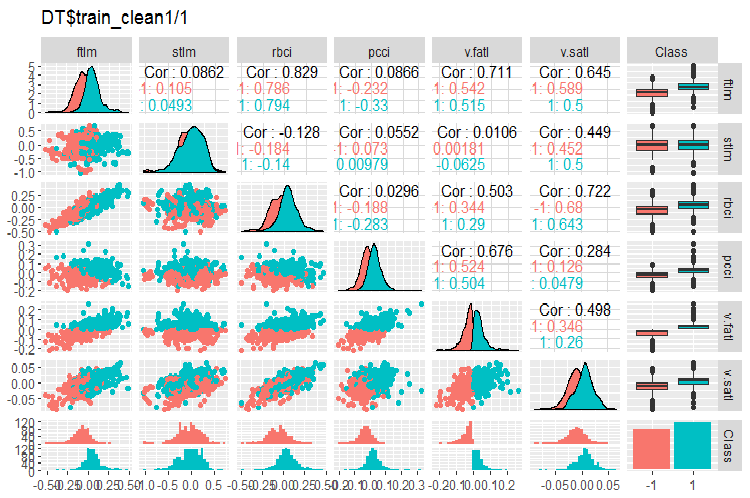
Fig. 2. Variação e covariância no conjunto DT$train_clean1/1 após a remoção de amostras de ruído

#-----Ris3---
evalq(ggpairs(DT$train_clean1 %>% select(-Data), 
              columns = 7:13, 
              mapping = aes(color = Class),
              title = "DT$train_clean1/2"), 
      env)

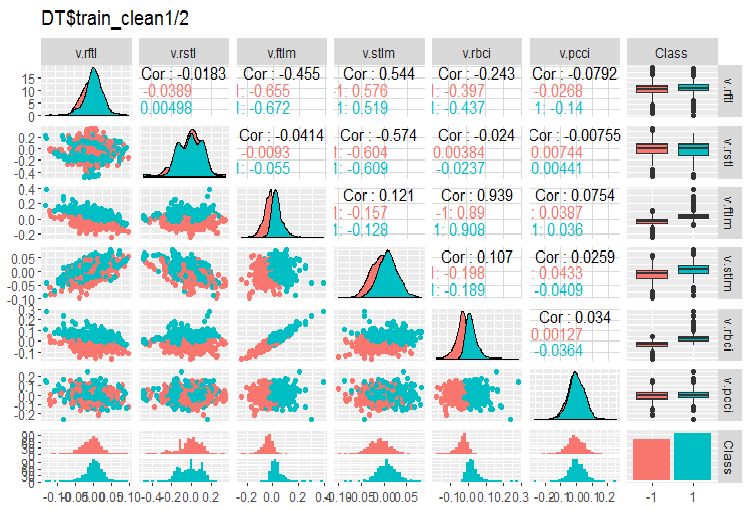
Fig. 3. Variação e covariância no conjunto DT$train_clean1/2 após a remoção de amostras de ruído

Quantas amostras foram removidas do conjunto DT$train?

> env$out11$remIdx %>% length()
[1] 658

Foi próximo de 30%. Há duas maneiras de tratarmos isso. O primeiro é remover amostras de ruído do conjunto train e passar para o modelo de treinamento. O segundo é reorganizá-los com um novo rótulo de classe e treinar o modelo em todo o conjunto train, mas com um nível adicional da variável objetivo. Com este número de amostras de ruído, o segundo cenário parece mais favorável. Nós devemos testar isso.

O que podemos ver nos gráficos de distribuição de variáveis ​​sem ruído?

1. A divisão muito distinta da distribuição de preditores pela variável objetivo. É altamente provável que isso aumentará significativamente a precisão do modelo que estamos treinando.
2. Quase todos os valores atípicos foram removidos.

Nós vamos limpar os conjuntos de dados DTn$train DTTanh.n$train utilizando o filtro. Você ficará surpreso ao ver que existem tantas variáveis ​​de ruído quanto há no primeiro caso.

c(env$out1$remIdx %>% length(), env$out12$remIdx %>% length())
[1] 652 653

Isso significa que nenhuma transformação torna úteis as amostras de ruído? Isso vale a pena testar.

Vamos dar uma olhada na variação e covariância do conjunto DTTanh.n$train depois de remover as variáveis ​​de ruído.

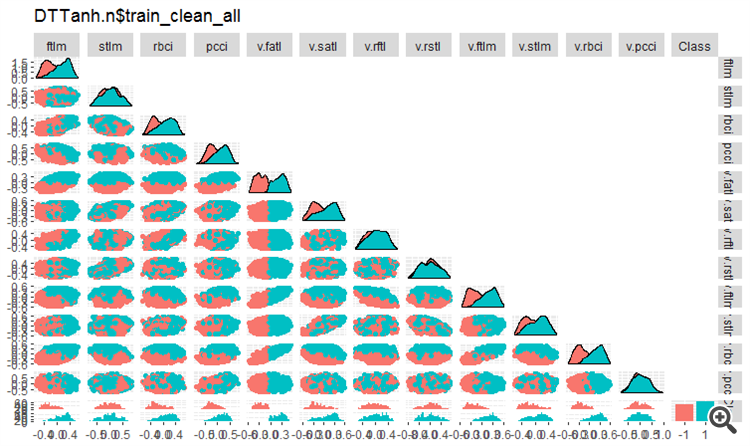
#----Ris4-----------------------
evalq(ggpairs(DTTanh.n$train_clean1, columns = 1:13, 
              mapping = aes(color = Class),
              upper = "blank",
              title = "DTTanh.n$train_clean_all"), 
      env)

Fig. 4. Variação e covariância no conjunto DTTanh.n$train_clean após a remoção de amostras de ruído.

A covariância de todas as variáveis ​​com a variável v.fatl. é muito interessante. Nós podemos identificar visualmente os preditores irrelevantes para a variável objetivo. Eles são a stlm, v.rftl, v.rstl, v.pcci. Nós vamos testar essa suposição usando outros métodos em outro conjunto.

O mesmo gráfico para o DTn$train_clean1:

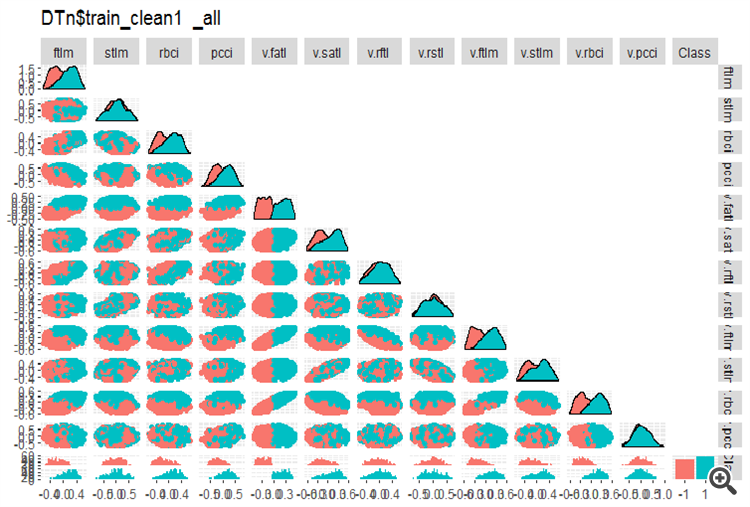
#-------ris5----------
require(GGally)
evalq(ggpairs(DTn$train_clean1 %>% select(-Data), 
              columns = 1:13, 
              mapping = aes(color = Class),
              upper = "blank",
              title = "DTn$train_clean1_all"), 
      env)

Fig. 5. Variação e covariância no conjunto DTn$train_clean após a remoção das amostras de ruído.

Aqui nós podemos ver que a variação dos preditores stlm, v.rftl, v.rstl, v.pcci não são divididos pelos níveis da variável objetivo. Cabe ao desenvolvedor decidir o que fazer com as variáveis ​​de ruído após a realização de experimentos de treinamento com um modelo.

Agora, vamos ver como a importância dos preditores se alterou nesses conjuntos de dados depois que as amostras de ruído foram removidas.

#--------Ris6---------------------------
require(smbinning)
par(mfrow = c(1,3))
evalq({
  df <- renamepr(DT$train_clean1) %>% targ.int
  sumivt.dt = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.dt, cex = 0.8)
  rm(df)
}, 
env)
evalq({
  df <- renamepr(DTTanh.n$train_clean1) %>% targ.int
  sumivt.tanh.n = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.tanh.n, cex = 0.8)
  rm(df)
}, 
env)
evalq({
  df <- renamepr(DTn$train_clean1) %>% targ.int
  sumivt.dtn = smbinning.sumiv(df = df, y = 'Cl')
  smbinning.sumiv.plot(sumivt.dtn, cex = 0.8)
  rm(df)
}, 
env)
par(mfrow = c(1, 1))

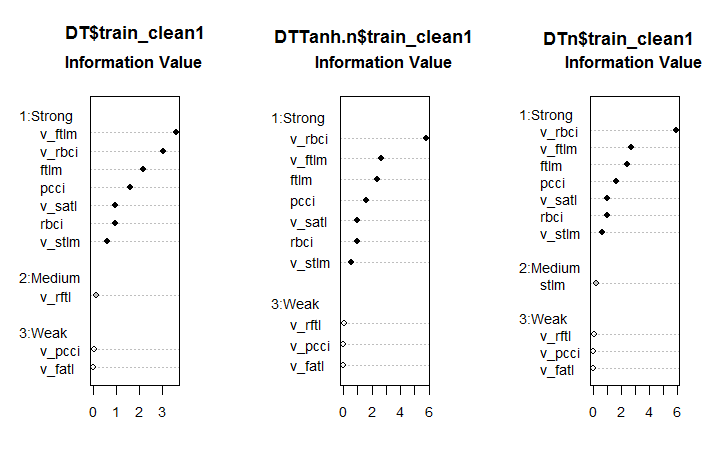
Fig. 6. Importância dos preditores em três conjuntos

Este é um resultado inesperado. A variável v.fatl acabou por ser a mais fraca da mais fraca!

Os sete preditores mais fortes são os mesmos em todos os conjuntos. Um preditor de potência média apareceu no primeiro e no terceiro conjunto. Este cálculo identificou os preditores stlm, v.rftl, v.rstl, v.pcci como irrelevantes, o que é consistente com o cálculo anterior. Todos esses cálculos devem ser verificados pelos experimentos com um modelo real.

O pacote NoiseFilterR possui mais de uma dúzia de outros filtros para identificar amostras de ruído. Tenha um ótimo experimento!

2. Redução da dimensionalidade

A redução da dimensão refere-se à transformação dos dados iniciais com uma dimensionalidade maior em uma nova representação de uma dimensionalidade menor que mantém a informação principal. Idealmente, a dimensionalidade da representação transformada é igual à dimensionalidade interna dos dados. A dimensionalidade interna dos dados é o número mínimo de variáveis ​​necessárias para expressar todas as características possíveis dos dados. Estes são os algoritmos tradicionalmente utilizados para reduzir a dimensionalidade: Análise de Componentes Principais (PCA), Análise de Componentes Independentes (ICA) e a Decomposição de Valor Singular (SVD), etc.

A redução da dimensão permite suavizar a chamada maldição da dimensionalidade e outras características indesejáveis ​​dos espaços de alta dimensionalidade. Na fase de descrição de dados, tem-se os seguintes propósitos.

• Reduz os custos computacionais durante o processamento de dados
• Diminui a necessidade de retreinamento. Quanto menor os recursos, menos objetos são necessários para uma restauração robusta do relacionamento oculto nos dados e melhor a qualidade da restauração desses relacionamentos.
• Dados comprimidos para um armazenamento de informações mais eficaz. Em tais casos, juntamente com a transformação X → T, deve haver uma oportunidade para realizar a transformação inversa T → X
• Visualização dos dados. Projetar uma amostra em um espaço bidimensional ou tridimensional permite representação desta amostra graficamente
• Extração de novos recursos. Novos recursos obtidos durante a transformação X → T podem ter um impacto significativo durante a implementação das soluções para reconhecimento (como a análise de componentes principais, por exemplo)

Observe que todos os métodos de reduções de dimensionalidade descritas brevemente abaixo pertencem à classe de treinamento não supervisionado. Isso significa que somente a descrição dos objetos X (preditores) está desempenhando um papel de informação inicial.

2.1. PCA, Análise de Componentes Principais

(Análise de componentes principais, PCA) é o método mais simples para reduzir a dimensionalidade dos dados. As principais ideias desse método datam do século XIX. O princípio deste método é encontrar um hiperplano de dimensão definida no espaço inicial e projetar o conjunto de dados para este hiperplano. O hiperplano com o menor erro de dados projetados (soma de desvios quadrados) é selecionado.

A dimensionalidade do espaço reduzido d pode ser predefinido pelo usuário. Este valor é fácil de selecionar se tivermos um problema de visualização de dados (d = 2 ou d = 3) ou um problema de colocar um conjunto de dados em uma memória definida. Em outros casos, a escolha de d não é óbvia por pressupostos anteriores.

Existe um método heurístico simples para selecionar o valor de d pelo método dos principais componentes. Uma das peculiaridades do método dos componentes principais é que todos os espaços reduzidos para d = 1, 2,. . . estão inseridos um no outro. Desta maneira, uma vez que todos os autovetores e autovalores da matriz de covariância são calculados, nós podemos obter um espaço reduzido para qualquer valor de d. Então, para selecionar o valor de d, os autovalores podem ser mostrados no gráfico na ordem decrescente e o limiar de corte pode ser definido de maneira que os valores insignificantes diferentes de zero estejam do lado direito. Outra maneira de selecionar o valor d é selecionar o limiar para que uma certa porcentagem da área total sob a curva permaneça à direita (por exemplo, 5% ou 1%).

Em termos simples, a PCA pode ser tratada como uma supressão preliminar de preditores de ruído se seu número for significativo (>50).

2.2. ICA, Análise de Componentes Independentes

Ao contrário da PCA, a análise de componentes independentes é uma coisa recente, ganhando popularidade rapidamente em várias áreas de exploração de dados.

Diferente da análise de componentes principais, as transformações ICA requerem um modelo. O modelo mais comum é o pressuposto de que as variáveis ​​P são medidas a partir da transformação linear p de variáveis ​​independentes. O objetivo do ICA é restaurar as variáveis ​​independentes iniciais. A maioria dos algoritmos ICA, primeiramente, habilita o clareamento de dados e, em seguida, rotaciona os dados de forma que os componentes resultantes sejam tão independentes quanto possível. Quando os componentes são construídos sequencialmente, isso implica uma busca de uma grande projeção não Gaussiana que não está conectada com as projeções destacadas anteriormente.

O método de componentes independentes é amplamente utilizado durante o processamento do sinal. Esta técnica transforma linearmente os dados iniciais em novos componentes. Os novos componentes serão tão independentes estatisticamente quanto possível. Componentes independentes não são necessariamente ortogonais, mas sua independência estatística é uma condição mais rigorosa do que a ausência de correlação estatística em PCA.

Os métodos PCA e ICA são implementados no pacote caret pela função preProcess(). Nesta função, pode-se definir o número de componentes principais ou porcentagem cumulativa de dispersão coberta pela PCA. A Análise de Componentes Independentes possui duas etapas. Em primeiro lugar, os parâmetros necessários são calculados no conjunto de dados train. Então, os conjuntos de dados e todos os novos dados que chegam mais tarde são transformados usando a função predict().

Tabela 1. Características comparativas de PCA e ICA

Método	Vantagens	Desvantagens	Peculiaridades	Resultado obtido na maioria dos casos	Modo de calcular novos componentes principais
PCA	Simplicidade de cálculos	Linearidade das transformações Alta sensibilidade à outliers Não aceita NA	Não singularidade da solução (incerteza rotacional). Todo novo cálculo baseado em um teste de treinamento produzirá diferentes componentes principais.	Т — matriz de pontuação (scores) com dimensões [I x A] P — matriz de carregamento (loadings) com dimensões [J x A]. Matriz de transição do espaço Х[, J] para o PCA[, A] E — matriz de restos com dimensões [I x J]	Tnew = Xnew * P
ICA	Simplicidade de cálculos	Padronização compulsória de dados Linearidade das transformações Alta sensibilidade à outliers não aceita NA Aplicável ao número de componentes 2 — 5	Com uma grande diferença na dimensionalidade do conjunto de dados de entrada e componentes independentes, usado consecutivamente PCA -> ICA.	W — matriz de divisão K — matriz de pré-clareamento	Snew =scale( Xnew )* W * K

Vamos realizar um experimento. Carregue os resultados dos cálculos do script da primeira parte do artigo Part_1.Rda em Rstudio. Abaixo está o conteúdo de env:

> ls(env)
 [1] "cap1"         "cap2"         "Close"        "Data"         "dataSet"     
 [6] "dataSetCap"   "dataSetClean" "dataSetOut"   "High"         "i"           
[11] "k"            "k.cap"        "k.out"        "lof.x"        "lof.x.cap"   
[16] "Low"          "lower"        "med"          "Open"         "out.ftlm"    
[21] "out.ftlm1"    "pr"           "pre.outl"     "preProClean"  "Rlof.x"      
[26] "Rlof.x.cap"   "sk"           "sk.cap"       "sk.out"       "test"        
[31] "test.out"     "train"        "train.out"    "upper"        "Volume"      
[36] "x"            "x.cap"        "x.out" 

Pegue o conjunto de dados x.cap com outliers imputados e calcule os seus componentes principais e independentes usando a função preProcess::caret. Especifique explicitamente o número de componentes para PCA e ICA. Não vamos especificar o caminho da normalização para ICA.

require(caret)
evalq({
  prePCA <- preProcess(x.cap, 
                       pcaComp = 5,
                       method = Hmisc::Cs(center, scale, pca))
  preICA <- preProcess(x.cap,
                       n.comp = 3, 
                       method = "ica")
}, env)

Vejamos os parâmetros de transformação:

> str(env$prePCA)
List of 20
 $ dim              : int [1:2] 7906 11
 $ bc               : NULL
 $ yj               : NULL
 $ et               : NULL
 $ invHyperbolicSine: NULL
 $ mean             : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ std              : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ ranges           : NULL
 $ rotation         : num [1:11, 1:5] -0.428 -0.091 -0.437 -0.107 -0.32 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  .. ..$ : chr [1:5] "PC1" "PC2" "PC3" "PC4" ...
 $ method           :List of 4
  ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ pca   : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ ignore: chr(0) 
 $ thresh           : num 0.95
 $ pcaComp          : num 5
 $ numComp          : num 5
 $ ica              : NULL
 $ wildcards        :List of 2
  ..$ PCA: chr(0) 
  ..$ ICA: chr(0) 
 $ k                : num 5
 $ knnSummary       :function (x, ...)  
 $ bagImp           : NULL
 $ median           : NULL
 $ data             : NULL
 - attr(*, "class")= chr "preProcess"

Estamos interessados ​​em três espaços. Eles são prePCA$mean, prePCA$std (parâmetros de normalização) e prePCA$rotation (matriz de rotação e carregamentos).

> str(env$preICA)
List of 20
 $ dim              : int [1:2] 7906 11
 $ bc               : NULL
 $ yj               : NULL
 $ et               : NULL
 $ invHyperbolicSine: NULL
 $ mean             : Named num [1:11] -0.001042 -0.003567 -0.000155 -0.000104 -0.000267 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ std              : Named num [1:11] 0.091 0.237 0.1023 0.0377 0.0356 ...
  ..- attr(*, "names")= chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
 $ ranges           : NULL
 $ rotation         : NULL
 $ method           :List of 4
  ..$ ica   : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ center: chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ scale : chr [1:11] "ftlm" "stlm" "rbci" "pcci" ...
  ..$ ignore: chr(0) 
 $ thresh           : num 0.95
 $ pcaComp          : NULL
 $ numComp          : NULL
 $ ica              :List of 3
  ..$ row.norm: logi FALSE
  ..$ K       : num [1:11, 1:3] -0.214 -0.0455 -0.2185 -0.0534 -0.1604 ...
  ..$ W       : num [1:3, 1:3] -0.587 0.77 -0.25 -0.734 -0.636 ...
 $ wildcards        :List of 2
  ..$ PCA: chr(0) 
  ..$ ICA: chr(0) 
 $ k                : num 5
 $ knnSummary       :function (x, ...)  
 $ bagImp           : NULL
 $ median           : NULL
 $ data             : NULL
 - attr(*, "class")= chr "preProcess"

Aqui nós temos temos o mesmo $mean e $std e duas matrizes $K e $W. O pacote caret para o cálculo da ICA usa o pacote fastICA com o seguinte algoritmo:

• depois que a matriz inicial estiver centrada (a normalização das linhas é possível), nós obtemos a matriz Х
• então a matriz Х é projetada nas direções dos principais componentes e nós obtemos PCA = X * K como resultado
• Depois disso, o PCA é multiplicado pela matriz não misturada e nós obtemos os componentes independentes ICA = X * K * W

Vamos calcular o PCA e ICA de duas maneiras usando a função predict::caret e os parâmetros obtidos pela função preProcess.

require(magrittr)
evalq({
  pca <- predict(prePCA, x.cap)
  ica <- predict(preICA, x.cap)
  pca1 <- ((x.cap %>% scale(prePCA$mean, prePCA$std)) %*% 
                   prePCA$rotation) 
  ica1 <- ((x.cap %>% scale(preICA$mean, preICA$std)) %*% 
                   preICA$ica$K) %*% preICA$ica$W
  colnames(ica1) <- colnames(ica1, do.NULL = FALSE, prefix = 'ICA')
    
},env)
evalq(all_equal(pca, pca1), env)
# [1] TRUE
evalq(all_equal(ica, ica1), env)
# [1] TRUE

O resultado é idêntico, o que era esperado.

Usando o pacote pcaPP é uma maneira mais confiável para o cálculo de PCA. Este método identifica os principais componentes com mais precisão.

O pacote fastICA contém muitos recursos e parâmetros adicionais para um cálculo mais flexível e completo de componentes independentes. Eu recomendaria usar o fastICA e não uma função em caret.

2.3 Análise Probabilística de Componentes Principais (PPCA)

PCA tem um modelo probabilístico - PPCA. Restaurar este método em termos probabilísticos dá uma série de vantagens.

• Uma oportunidade para usar o algoritmo ЕМ para pesquisar uma solução. O algoritmo ЕМ é um procedimento de cálculo mais eficaz na situação em que d «D
• Corrigir o processamento de valores em falta. Eles são simplesmente adicionados à lista de variáveis ​​ocultas dos modelos probabilísticos. Em seguida, o algoritmo ЕМ é aplicado a este modelo.
• Uma possibilidade de transição para o modelo de distribuição de mistura que amplia a aplicabilidade do método
• Uma possibilidade de usar a abordagem bayesiana para resolver problemas de seleção de um modelo. Em particular, pode ser construído um esquema teoricamente justificado de selecionar a dimensionalidade do espaço reduzido d (veja [24, 25])
• Possibilidade de gerar novos objetos a partir do modelo probabilístico
• Por uma questão de classificação - possibilidade de modelar distribuições de classes de objeto separadas para uso posterior nos esquemas de classificação
• O valor da função de verossimilhança é um critério universal que permite comparar diferentes modelos probabilísticos uns com os outros. Especificamente, os outliers em um conjunto de dados podem ser facilmente identificados usando o valor de verossimilhança.

Semelhante ao modelo clássico de PCA, o modelo probabilístico PCA é invariante em relação à escolha da base no hiperplano.

Ao contrário do modelo clássico de PCA, onde apenas o hiperplano explicando o melhor conjunto de dados é restaurado, o modelo probabilístico restaura todo o modelo de variabilidade de dados. Ou seja, descreve a dispersão de dados em todas as direções. Portanto, a solução inclui não apenas os vetores de base de direção do hiperplano definidos pelos vetores próprios da matriz de covariância, mas também os comprimentos desses vetores de base.

Para usar o РРСА e outros métodos não-lineares de obtenção de componentes principais, o pacote pcaMethods pode ser usado.

O pacote pcaMethods é um conjunto de várias realizações de PCA e de ferramentas para validação cruzada e visualização de resultados. Os métodos permitem principalmente aplicar a PCA a conjuntos de dados incompletos e, portanto, eles podem ser usados ​​para a avaliação de valores ausentes (NA). O pacote pode ser encontrado no repositório Bioconductor e pode ser instalado conforme descrito abaixo.

source("https://bioconductor.org/biocLite.R")
biocLite("pcaMethods")
library(pcaMethods)

Todos os métodos do pacote retornam a classe geral pcaRes que contém o resultado. Isso proporciona ao usuário boa flexibilidade. A função wrapper pca() permite o acesso a todos os tipos exigidos de РСА através do seu argumento de nomeação. Abaixo está uma lista de algoritmos com uma breve descrição:

• A svdPCA é uma função wrapper para a função padrão prcomp.
• svdImpute que é a implementação do algoritmo para imputar NA. Isso é tolerante a um grande número de NA (>10%).
  
• PCA probabilístico (ppca). PPCA é tolerante ao número de NA entre 10% e 15%.
• PCA Bayesiano (bpca). Semelhante ao PCA probabilístico, isso usa a abordagem EM com o modelo Bayesiano para calcular a probabilidade de restauração do valor. Este algoritmo é tolerante ao número relativamente grande de dados ausentes (> 10%). As pontuações e carregamentos, obtidos por este método, são diferentes dos obtidos usando um PCA ordinário. Isso está relacionado com o fato de o BPCA ter sido desenvolvido especialmente para a avaliação de valores ausentes e é baseado na estrutura Bayesiana de variação (VBF) com identificação automática de relevância (ARD). Este algoritmo não força a ortogonalidade entre os carregamentos. Na verdade, os autores do BPCA descobriram que, incluindo o critério de ortogonalidade, as previsões pioraram.
• PCA não-linear inversa (NLPCA) é mais adequado para dados experimentais onde a relação entre preditores e a variável objetivo não é linear. A NLPCA é baseada no treinamento da parte de descodificação da rede neural associativa (autoencoder). Os carregamentos podem ser vistos na camada oculta da rede. Os valores ausentes nos dados de treinamento são ignorados no cálculo do erro durante o back propagation. Desta forma, o NLPCA pode ser usado para o processamento de valores ausentes da mesma forma que para um padrão РСА. A única diferença é que as cargas P agora são representadas por uma rede neural. Estudaremos esta forma de redução de dimensionalidade com mais detalhes na seção "Autoencoder".
• Nipals PCA é uma avaliação não-linear por mínimos quadrados parciais iterativos. Este é um algoritmo no núcleo da regressão PLS, que pode executar PCA com valores ausentes, deixando-os fora dos respectivos produtos internos. É tolerante um pequeno número (geralmente, não maior que 5%) de dados ausentes.
• A imputação dos mínimos quadrados locais (LLS) é o algoritmo/função llsImpute() para a avaliação de valores ausentes com base na combinação linear de vizinhos mais próximos da variável incompleta. A distância entre variáveis ​​é definida como o valor absoluto dos coeficientes de correlação de Pearson, Spearman ou Kendall. A combinação linear ideal pode ser encontrada resolvendo um problema local de mínimos quadrados.

Na implementação atual, são apresentadas duas formas de avaliar os valores ausentes. Estes métodos diferem ligeiramente. O primeiro caminho é a limitação da busca do vizinho no subconjunto de variáveis ​​completas. Este método é preferível quando o número de variáveis ​​indefinidas é razoavelmente baixo. O segundo método considera todas as variáveis ​​como candidatos. Os valores que faltam aqui são primeiramente substituídos pela média das colunas. Em seguida, este método itera usando a avaliação atual como a entrada para a regressão LLS até que as alterações entre a avaliação nova e antiga caiam abaixo de um determinado limite (0,001)

Infelizmente, o tópico deste artigo e seu volume não me permitem escrever sobre todos os algoritmos sugeridos deste brilhante pacote. Nós apenas analisaremos a NLPCA em comparação com o autoencoder mais tarde.

2.4. Autoencoder

As redes auto-associativas têm sido amplamente utilizadas desde que as redes neurais profundas apareceram. Em um dos meus artigos anteriores nós consideramos em detalhes a estrutura e as características dos autoencoders de treinamento (АЕ), autoencoders empilhados, máquina de Boltzmann restrita (RBM) e outros.

O Autoencoder é uma rede neural com uma ou várias camadas ocultas e o número de neurônios na camada de entrada igual ao número de neurônios na camada de saída. O objetivo principal de АЕ é representar os dados de entrada com a maior precisão possível. Os mesmos métodos de treinamento, regularização e ativação de neurônios utilizados para redes neurais padrão são usados ​​para AE. Um modelo de AE ​​pode ser construído usando qualquer pacote para a construção de redes neurais, que permite extrair uma matriz de pesos de camadas ocultas. Nós vamos usar o pacote autoencoder. O exemplo abaixo ajudará a recordar as possíveis estruturas do AE:

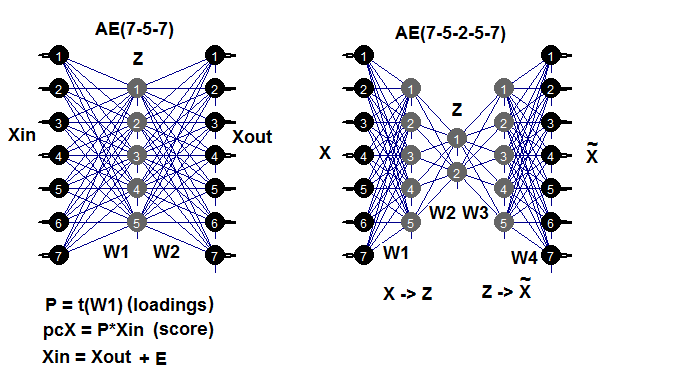
Fig. 7. Diagrama estrutural dos autoencoders (de três e cinco camadas)

A matriz de peso W1 entre a primeira (entrada) e a camada oculta é o carregamento obtido como resultado do treinamento. Depois de projetar (multiplicação) da matriz de entrada Xin no carregamento Р, nós obteremos uma matriz reduzida (componentes principais, essencialmente). Nós podemos obter o mesmo resultado usando a função predict(). Esta função permite obter a saída da camada oculta (se hidden.output = TRUE) ou a camada de saída do autoencoder (se hidden.output = FALSE).

Após o treinamento do AE, nós podemos extrair a matriz de peso W1 e o erro de recuperação do modelo. Se nós também inserimos o conjunto de dados de teste, nós podemos também obter o erro de teste do modelo. O erro de treinamento depende muito dos parâmetros do AE ​​e ainda mais da razão n.hidden/n.in. Quanto maior esta relação, maior o erro de recuperação. Se pretendemos alcançar uma redução significativa da dimensionalidade, dois AE podem ser conectados, consequentemente. Por exemplo, se houver 12 entradas, nós podemos treinar um modelo 12-7-12, executar a predict() da camada oculta e inseri-la em um autoencoder 7-3-7. A redução será 12 -> 3. Tenha um ótimo experimento!

Deve-se mencionar que, embora o pacote reivindique uma capacidade para criar e treinar um AE de várias camadas, eu não consegui fazê-lo.

Vamos conduzir um experimento. Você já tem a Part_1.RData com os resultados de cálculo da primeira parte do artigo. Abaixo está uma sequência de cálculo:

• crie os conjuntos de dados train/val/test do conjunto dataSet e obtenha a lista DT;
• impute os outliers e obtenha a lista DTcap;
• normalize nossos conjuntos sucessivamente usando os métodos com ("center", "scale", "spatialSign"). Você pode usar outros métodos de transformação e normalização, que nós consideramos antes;
• treine o modelo de autoencoder com três neurônios na camada oculta. Você pode explorar outras variantes. À medida que o número de neurônios ocultos aumenta, o erro de recuperação diminui;
• usando o modelo treinado e a predict(), obtenha o resultado da camada oculta. Esta é essencialmente uma matriz reduzida (РСА). Adicione uma variável objetivo a ela;
• desenhe os gráficos de variação e covariância das amostras reduzidas train/val/test/.
  

require(FCNN4R)
require(deepnet)
require(darch)
require(tidyverse)
require(magrittr)
#----Clean---------------------
require(caret)
require(pipeR)
evalq(
  {
    train = 1:2000
    val = 2001:3000
    test = 3001:4000
    DT <- list()
    dataSet %>%
      preProcess(., method = c("zv", "nzv", "conditionalX")) %>%
      predict(., dataSet) %>%
      na.omit -> dataSetClean
    list(train = dataSetClean[train, ], 
         val = dataSetClean[val, ], 
         test = dataSetClean[test, ]) -> DT
    rm(dataSetClean, train, val, test)
  }, 
  env)
#------outlier-------------
require(foreach)
evalq({
  DTcap <- list()
  foreach(i = 1:3) %do% {
    DT[[i]] %>% 
      select(-c(Data, Class)) %>%
      as.data.frame() -> x
    if (i == 1) {
      foreach(i = 1:ncol(x), .combine = "cbind") %do% {
        prep.outlier(x[ ,i]) %>% unlist()
      } -> pre.outl
      colnames(pre.outl) <- colnames(x)
    } 
    foreach(i = 1:ncol(x), .combine = "cbind") %do% {
      stopifnot(exists("pre.outl", envir = env))
      lower = pre.outl['lower.25%', i] 
      upper = pre.outl['upper.75%', i]
      med = pre.outl['med', i]
      cap1 = pre.outl['cap1.5%', i] 
      cap2 = pre.outl['cap2.95%', i] 
      treatOutlier(x = x[ ,i], impute = T, fill = T, 
                   lower = lower, upper = upper, 
                   med = med, cap1 = cap1, cap2 = cap2) 
    } %>% as.data.frame() -> x.cap
    colnames(x.cap) <- colnames(x)
    return(x.cap)
  } -> DTcap
  foreach(i = 1:3) %do% {
    cbind(DTcap[[i]], Class = DT[[i]]$Class)
  } -> DTcap
  DTcap$train <- DTcap[[1]]
  DTcap$val <- DTcap[[2]]
  DTcap$test <- DTcap[[3]]
  rm(lower, upper, med, cap1, cap2, x.cap, x)
}, env)
#------normalize-----------
evalq(
  {
    method <- c("center", "scale", "spatialSign") #, "expoTrans") #"YeoJohnson", 
                                                 # "spatialSign"
    preProcess(DTcap$train, method = method) -> preproc 
    list(train = predict(preproc, DTcap$train), 
         val = predict(preproc, DTcap$val),
         test = predict(preproc, DTcap$test)
    ) -> DTcap.n
    #foreach(i = 1:3) %do% {
    #  cbind(DTcap.n[[i]], Class = DT[[i]]$Class)
    #} -> DTcap.n
  }, 
  env) 
#----train-------
require(autoencoder)
evalq({
  train <-  DTcap.n$train %>% select(-Class) %>% as.matrix()
  val <-  DTcap.n$val %>% select(-Class) %>% as.matrix()
  test <-  DTcap.n$test %>% select(-Class) %>% as.matrix()
  ## Set up the autoencoder architecture:
  nl = 3                    ## number of layers (default is 3: input, hidden, output)
  unit.type = "tanh"        ## specify the network unit type, i.e., the unit's 
   ## activation function ("logistic" or "tanh")
  N.input = ncol(train)   ## number of units (neurons) in the input layer (one unit per pixel)
  N.hidden = 3              ## number of units in the hidden layer
  lambda = 0.0002           ## weight decay parameter     
  beta = 0                  ## weight of sparsity penalty term 
  rho = 0.01                ## desired sparsity parameter
  epsilon <- 0.001          ## a small parameter for initialization of weights 
   ## as small gaussian random numbers sampled from N(0,epsilon^2)
  max.iterations = 3000     ## number of iterations in optimizer
   ## Train the autoencoder on training.matrix using BFGS 
 ##optimization method 
  AE_13 <- autoencode(X.train = train, X.test = val,
                      nl = nl, N.hidden = N.hidden, 
                      unit.type = unit.type,
                      lambda = lambda,
                      beta = beta,
                      rho = rho,
                      epsilon = epsilon,
                      optim.method = "BFGS", #"BFGS", "L-BFGS-B", "CG"
                      max.iterations = max.iterations,
                      rescale.flag = FALSE, 
                      rescaling.offset = 0.001)}, env)
## Report mean squared error for training and test sets:
#cat("autoencode(): mean squared error for training set: ",
#    round(env$AE_13$mean.error.training.set,3),"\n")
## Extract weights W and biases b from autoencoder.object:
#evalq(P <- AE_13$W, env)
#-----predict-----------
evalq({
  #Train <- predict(AE_13, X.input = train, hidden.output = FALSE) 
  pcTrain <- predict(AE_13, X.input = train, hidden.output = TRUE)$X.output %>%
    tbl_df %>% cbind(., Class = DTcap.n$train$Class)
  #Val <- predict(AE_13, X.input = val, hidden.output = FALSE) 
  pcVal <- predict(AE_13, X.input = val, hidden.output = TRUE)$X.output %>%
    tbl_df %>% cbind(., Class = DTcap.n$val$Class)
  #Test <- predict(AE_13, X.input = test, hidden.output = FALSE) 
  pcTest <- predict(AE_13, X.input = test, hidden.output = TRUE)$X.output %>%
    tbl_df %>% cbind(., Class = DTcap.n$test$Class)
}, env)
#-----graph---------------
require(GGally)
evalq({
  ggpairs(pcTrain,columns = 1:ncol(pcTrain), 
          mapping = aes(color = Class),
          title = "pcTrain")}, 
  env)
evalq({
  ggpairs(pcVal,columns = 1:ncol(pcVal), 
          mapping = aes(color = Class),
          title = "pcVal")}, 
  env)
evalq({
  ggpairs(pcTest,columns = 1:ncol(pcTest), 
          mapping = aes(color = Class),
          title = "pcTest")}, 
  env)

Vamos dar uma olhada nos gráficos 

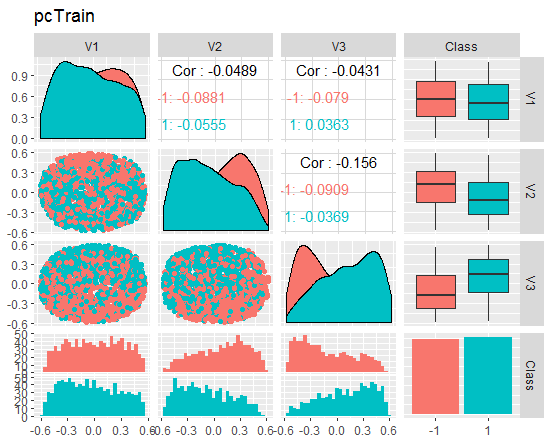
Fig. 8. Variação e covariância do conjunto train reduzido

 

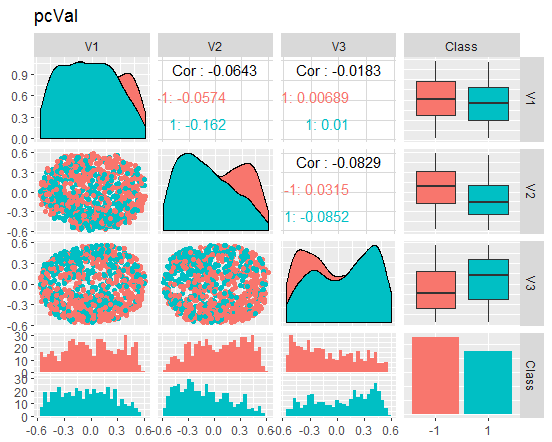
Fig. 9. Variação e covariância do conjunto val reduzido

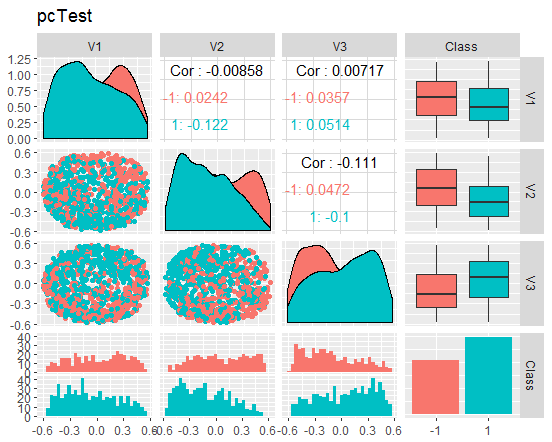
Fig. 10. Variação e covariância do conjunto test reduzido

O que esses gráficos nos dizem? Nós podemos ver que os principais componentes (V1, V2, V3) estão bem divididos pelos níveis da variável objetivo. As distribuições nos conjuntos de train/val/test estão enviesadas. Nós devemos remover o ruído das amostras e ver se isso melhora a imagem. Você pode fazer isso por conta própria.

Pequena digressão: NLPCA

Para poder dividir os dados pelos principais componentes, é importante distinguir os aplicativos para a redução de dimensionalidade pura e aplicações onde se concentra principalmente na identificação e reconhecimento de componentes únicos e significativos, que geralmente é chamado de extração de recursos.

As aplicações para a redução da dimensionalidade pura com o ênfase na supressão de ruído e na compressão de dados requerem apenas um subespaço com alta capacidade descritiva. As formas separadas dos componentes tornam este subespaço não limitado e, portanto, não precisa ser exclusivo. O único requisito é que o subespaço forneça informações máximas sobre o erro quadrático médio (MSE). Como os componentes separados que abrangem este subespaço são processados ​​pelo algoritmo sem qualquer ordem definida ou pesagem diferenciada, isso é chamado tipo de treinamento simétrico. Este tipo de treinamento inclui um PCA não-linear, realizado por uma rede neural auto-associativa padrão (autoencoder), que é, portanto, chamado de s-NLPCA. Na parte anterior do artigo nós consideramos esta variante.

O PCA hierárquico não-linear (h-NLPCA) fornece não apenas um subespaço não-linear ótimo coberto por componentes, mas também limita os componentes não-lineares por uma ordem hierárquica igual, semelhante aos componentes lineares no PCA padrão. A hierarquia neste contexto é explicada por duas propriedades importantes: escalabilidade e estabilidade. A escalabilidade significa que os primeiros n componentes explicam a dispersão máxima que pode ser coberta por sub-espaços n-dimensionais. A estabilidade significa que o i-ésimo componente da solução n-componente é idêntico ao i-ésimo componente da solução m-component.

A ordem hierárquica produz componentes não correlacionados. A não-linearidade também significa que a h-NLPCA é capaz de remover correlações complexas não-lineares entre os componentes. Isso ajuda a filtrar os componentes úteis e significativos. Além disso, escalando um componente não-linear não correlacionado para uma dispersão unitária, nós obtemos o clareamento não-linear complexo (transformação esférica). Este é um processamento preliminar útil para tais aplicações, como regressão, classificação ou divisão cega de fontes. Como o clareamento não-linear elimina relacionamentos não-lineares em dados, os métodos mais utilizados podem ser lineares. Isto é especialmente importante para o ICA, que pode ser ampliado para uma abordagem não-linear com o uso deste clareamento não-linear.

Como nós podemos alcançar uma ordem hierárquica? Uma simples classificação de componentes processados ​​simetricamente por dispersão não produz a ordem hierárquica necessária - nem linear, nem não-linear. Uma hierarquia pode ser alcançada por dois métodos interconectados: por meio da dispersão restante no espaço do componente ou da limitação do erro quadrático de reconstrução no espaço original. Semelhante ao PCA linear, o i-ésimo componente terá que levar em consideração a maior i-ésima dispersão.

Em um caso não-linear, essa limitação pode ser ineficaz ou não unitária sem limitações adicionais. Pelo contrário, o erro de recuperação pode ser controlado muito melhor, pois é um valor absoluto invariante para qualquer escala em uma transformação. Portanto, a limitação hierárquica de um erro é um método mais efetivo. Em um caso linear simples, nós podemos alcançar o arranjo hierárquico dos componentes pela abordagem sequencial, onde os componentes são extraídos um a um da dispersão remanescente, definidos pelo erro quadrático das dispersões anteriores. Em um caso não-linear, isso não funciona nem sequencialmente nem simultaneamente ao treinar várias redes em paralelo. A dispersão restante não pode ser interpretada pelo erro quadrático independente da transformação não-linear. A solução é usar apenas uma rede neural com uma hierarquia de sub-redes. Isso nos permite formular a hierarquia imediatamente na função de erro.

2.5. PCA inverso não-linear

Nesta parte do artigo, um PCA não-linear irá resolver um problema inverso. Considerando que o problema original é prever a saída da entrada definida, o problema inverso é a avaliação da entrada que melhor combina com um resultado definido. Como não conhecemos o modelo, nem o processo de geração de dados, nós somos apresentados com um problema chamado de reversão cega.

Um PCA linear simples pode ser considerado igualmente bom tanto nos problemas originais como reversos, dependendo se os componentes necessários são previstos como saídas ou avaliados como dados de entrada por um algoritmo correspondente. A rede auto-associativa (АЕ) está modelando simultaneamente os modelos direto e reverso.

O modelo direto é definido pela primeira parte do АЕ pela função de extração Fextr: X → Z. O modelo inverso é definido pela segunda parte do AE, pela função geradora Fgen: Z → X. O primeiro modelo é mais adequado para um PCA linear e não funciona também no caso de um PCA não-linear. Isso acontece porque esse modelo pode ser muito complexo e difícil de resolver devido ao problema "de um para muitos". Dois conjuntos idênticos X podem corresponder com valores diferentes de componentes Z.

A RNA não-linear inversa requer apenas a segunda parte da rede auto-associativa (Fig.11), que é ilustrada pela rede 3-7-12. Esta parte da geração é o reflexo reverso de Fgen, que gera ou reconstrói padrões de tamanho grande de Х a partir de suas imagens Z de menor dimensionalidade. Estes valores dos componentes Z são agora entradas desconhecidas que podem ser avaliadas propagando erros parciais σ de volta para a camada de entrada Z.

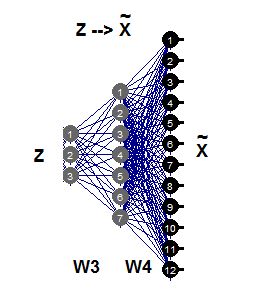
Fig. 11. РСА inverso não-linear

Vamos comparar os resultados obtidos com o AE e usar a função nlpca::pcaMethods. Esta função foi mencionada anteriormente neste artigo. Faça o cálculo dos mesmos dados com o mesmo requisito de redução inicial 12 -> 3 e compare os resultados.

Para isso, pegue o conjunto DTcap.n$train, remova a classe da variável objetivo e converta-a em uma matriz. Centre o conjunto. Defina a estrutura da rede neural como (3,8,12), o resto dos parâmetros pode ser encontrado no script abaixo. Depois de obter o resultado, individualize os principais componentes (pontuação), adicione a variável objetivo e trace um gráfico.

Deve-se mencionar que este algoritmo é muito lento e cada novo lançamento produz um novo resultado diferente do anterior.

require(pcaMethods)
evalq({
  DTcap.n$train %>% tbl_df %>%
    select(-Class) %>% as.matrix() %>%
    prep(scale = "none", center = TRUE) -> train
  resNLPCA <- pca(train, 
                  method = "nlpca", weightDecay = 0.01,
                  unitsPerLayer = c(3, 8, 12),
                  center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
                  nPcs = 3, completeObs = FALSE, 
                  subset = NULL, cv = "none", # "none""q2"), ...) 
                  maxSteps = 1100)
  rm(train)},
  env)
#--------
evalq(
   pcTrain <- resNLPCA@scores %>% tbl_df %>% 
           cbind(., Class = DTcap.n$train$Class)
, env)
#------graph-------
require(GGally)
evalq({
  ggpairs(pcTrain,columns = 1:ncol(pcTrain), 
          mapping = aes(color = Class),
          title = "pcTrain -> NLPCA(3-8-12) wd = 0.01")}, 
  env)
#----------

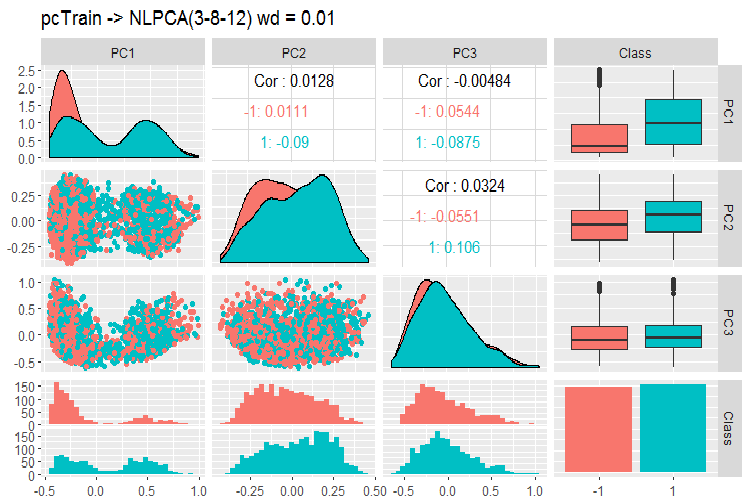
Fig. 12. Variação e covariância dos principais componentes usando NLPCA

O que podemos ver neste gráfico? Os principais componentes são bem divididos pelos níveis da variável objetivo e têm uma correlação muito baixa. O terceiro componente parece desnecessário. Vamos dar uma olhada nas informações gerais sobre o modelo.

> print(env$resNLPCA)
nlpca calculated PCA
Importance of component(s):
                 PC1    PC2     PC3
R2            0.3769 0.2718 0.09731
Cumulative R2 0.3769 0.6487 0.74599
12      Variables
2000    Samples
0       NAs ( 0 %)
3       Calculated component(s)
Data was mean centered before running PCA 
Data was NOT scaled before running PCA 
Scores structure:
[1] 2000    3
Loadings structure:
Inverse hierarchical neural network architecture
3 8 12 
Functions in layers
linr tanh linr 
hierarchic layer: 1 
hierarchic coefficients: 1 1 1 0.01 
scaling factor: 0.3260982 

Há um problema aqui. O resultado não retorna as matrizes de peso W3 e W4. Em outras palavras, não temos um P de carregamento e não podemos obter os principais componentes S (pontuação) nos conjuntos de teste e validação. Este problema persiste em outros dois métodos decentes de redução da dimensionalidade - tSNE, ICS. Nós podemos resolver esses problemas de forma razoavelmente fácil, mas é melhor não seguir uma rota com um resultado desconhecido.

O pacote contém mais dois métodos - o РСА probabilístico e o Bayesiano. Eles são rápidos e retorna a carga, o que permite obter componentes principais nos conjuntos de validação e teste. Eu vou exibir um exemplo apenas para o PPCA.

#=======PPCA===================
evalq({
  DTcap.n$train %>% tbl_df %>%
    select(-Class) %>% as.matrix() -> train
  DTcap.n$val %>% tbl_df %>%
    select(-Class) %>% as.matrix() -> val
  DTcap.n$test %>% tbl_df %>%
    select(-Class) %>% as.matrix() -> test
  resPPCA <- pca(train, method = "ppca",
                  center = TRUE, scale = "none",# c("none", "pareto", "vector", "uv")
                  nPcs = 3, completeObs = FALSE, 
                  subset = NULL, cv = "none", # "none""q2"), ...) 
                  maxIterations = 3000)
  },
  env)
#-----------
>print(env$resPPCA)
ppca calculated PCA
Importance of component(s):
 PC1 PC2 PC3
R2 0.2873 0.2499 0.1881
Cumulative R2 0.2873 0.5372 0.7253
12 	Variables
2000 	Samples
0 	NAs ( 0 %)
3 	Calculated component(s)
Data was mean centered before running PCA 
Data was NOT scaled before running PCA 
Scores structure:
[1] 2000 3
Loadings structure:
[1] 12 3

Desenhe um gráfico para carregamentos e pontuações para os componentes 1 e 2:

slplot(env$resPPCA, pcs = c(1,2), 
       lcex = 0.9, sub = "Probabilistic PCA")

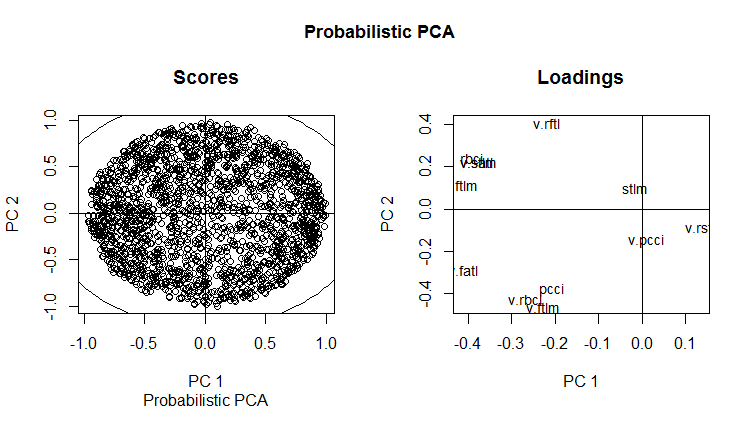
Fig. 13. РСА probabilística de РС1 e РС2 (carregamentos e pontuações)

Os gráficos de variação e covariância dos componentes principais dos conjuntos PPCA train/val/test são mostrados abaixo. Você pode encontrar os scripts no GitHub.

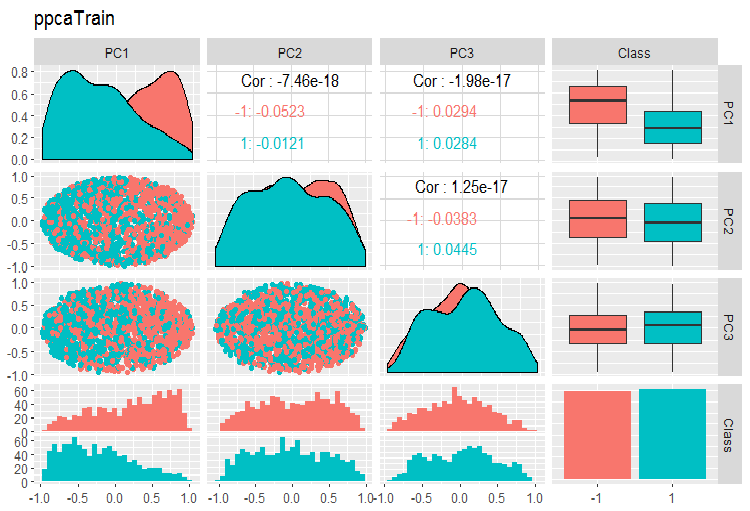
Fig. 14. Variação e covariância dos principais componentes do conjunto de train obtidos com PPCA

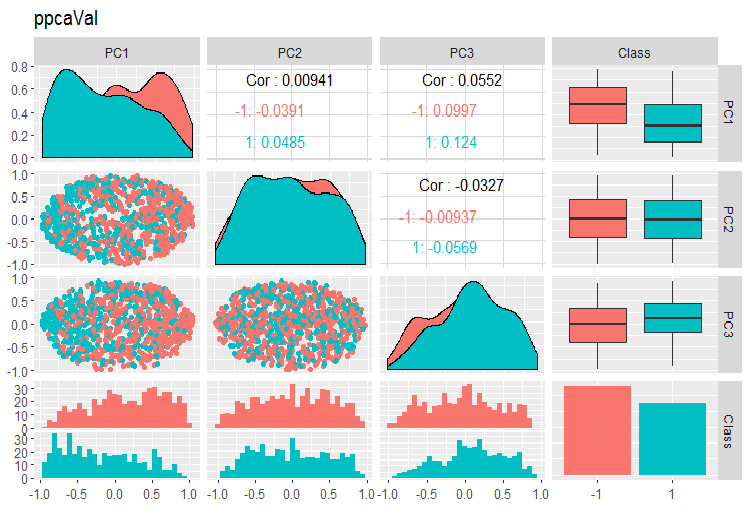
Fig. 15. Variação e covariância de componentes principais do conjunto val obtidos com PPCA

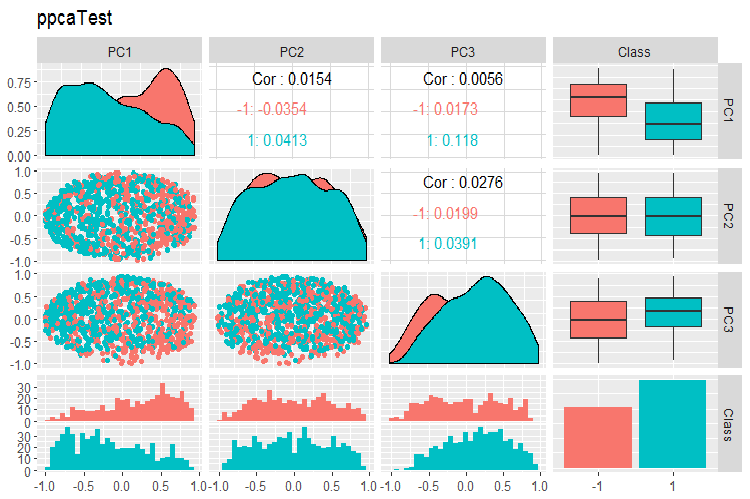
Fig. 16. Variação e covariância de componentes principais do conjunto de testes obtidos com PPCA

A divisão dos componentes principais obtidos com PPCA pelos níveis da variável objetivo não é de melhor qualidade que a mesma redução usando o autoencoder considerado anteriormente. As vantagens de PPCA e BPCA são velocidade e simplicidade. A qualidade deve ser avaliada usando um determinado modelo de classificação.

3.Dividindo o conjunto de dados nos conjuntos train/val/test

Nesta parte, tudo permanece o mesmo que foi descrito nos artigos anteriores. Durante o treinamento: train/valid/test, janela deslizante, janela de crescimento, as vezes bootstrap. Durante a escolha do modelo: validação cruzada. A questão de identificar um tamanho suficiente desses conjuntos ainda é uma questão em aberto.

Gostaria de mencionar uma declaração interessante da Win Wector LLC sobre o uso dos conjuntos de treinamento durante as transformações de pré-processamento. Eles dizem que, se os componentes principais foram identificados no conjunto de treinamento, o modelo deve ser treinado em componentes principais obtidos no conjunto de dados de validação. Isso significa que um conjunto usado não pode ser usado para treinar um modelo. Isso pode ser testado quando a rede é treinada.

Conclusão

Nós consideramos quase todas as etapas de preparação de dados para o treinamento das redes neurais profundas. Como você pode ver, este é um estágio complexo e demorado, que exige um bom conhecimento teórico. Sem entendimento e habilidades para a preparação dos dados para os seguintes estágios, todas as outras ações não fazem sentido.

É impossível alcançar um bom resultado sem controle visual de todos os cálculos na fase de preparação de dados. O impaciente e preguiçoso irá desfrutar dos pacotes "preprocomb" e "metaheur", o que ajudará a encontrar as fases de preparação preliminar automaticamente mais adequadas.

Aplicação

Os scripts usados ​​neste artigo podem ser encontrados no GitHub/Part_III.