
Redes Neurais Profundas (Parte VIII). Melhorando a qualidade de classificação dos bagging de ensembles
Conteúdo
- Introdução
- Preparação dos Dados Iniciais
- Processamento de amostras com ruído no subconjunto pretrain
- Treinamento de ensembles de classificadores de redes neurais utilizando dados iniciais sem ruído e o cálculo de previsões contínuas das redes neurais nos subconjuntos de teste
- Determinação dos limites para as previsões contínuas obtidas, convertendo-as em rótulos de classe e calculando métricas para as redes neurais
- Testando os ensembles
- Otimização dos hiperparâmetros dos conjuntos de classificadores de redes neurais
- Otimização dos hiperparâmetros de pós-processamento
- Combinação dos melhores ensembles em um super ensemble, bem como as suas saídas
- Análise dos resultados experimentais
- Conclusão
- Anexos
Introdução
Nos dois artigos anteriores (1, 2), nós criamos um ensemble de classificadores de redes neurais ELM. Naquela época, nós discutimos como a qualidade da classificação poderia ser melhorada. Entre as muitas soluções possíveis, duas foram escolhidas: reduzir o impacto das amostras com ruído e selecionar o limiar ideal, pelo qual as previsões contínuas das redes neurais do conjunto são convertidas em rótulos de classe. Neste artigo, eu proponho testar experimentalmente como a qualidade de classificação é afetada por:
- métodos de eliminação de ruídos,
- tipos de limiares,
- otimização de hiperparâmetros das redes neurais e pós-processamento do conjunto.
Em seguida, comparar a qualidade da classificação obtida pela média e por uma votação por maioria simples do super ensemble composto pelos melhores ensembles após os resultados da otimização. Todos os cálculos são realizados no ambiente R 3.4.4.
1. Preparação dos Dados Iniciais
Para preparar os dados iniciais, nós usaremos os scripts descritos anteriormente.
No primeiro bloco (Library), carregamos as funções e bibliotecas necessárias.
No segundo bloco (prepare), usando as cotações com registros de data e hora obtidos do terminal, calculamos os valores dos indicadores (neste caso, são filtros digitais) e as variáveis adicionais baseadas em OHLC. É combinado este conjunto de dados no dataframe dt. Em seguida, é definido os parâmetros dos outliers nesses dados e atribuído a eles. Em seguida, é definido os parâmetros de normalização e os dados são normalizados. Nós obtemos o conjunto resultante dos dados de entrada DTcap.n.
No terceiro bloco (Data X1), é gerado dois conjuntos:
- data1 — contendo todos os 13 indicadores com o atributo de horário Data e a variável objetivo Class;
- X1 — o mesmo conjunto de preditores, mas sem o atributo de horário. O objetivo é convertido em um valor numérico (0, 1).
No quarto bloco (Data X2), também é gerado dois conjuntos:
- data2 — contendo 7 preditores e um atributo de horário (Data, CO, HO, LO, HL, dC, dH, dL);
- Х2 — os mesmos preditores, mas sem o atributo de horário.
#--1--Library------------- patch <- "C:/Users/Vladimir/Documents/Market/Statya_DARCH2/PartVIII/PartVIII/" source(file = paste0(patch,"importar.R")) source(file = paste0(patch,"Library.R")) source(file = paste0(patch,"FunPrepareData_VII.R")) source(file = paste0(patch,"FUN_Stacking_VIII.R")) import_fun(NoiseFiltersR, GE, noise) #--2-prepare---- evalq({ dt <- PrepareData(Data, Open, High, Low, Close, Volume) DT <- SplitData(dt$features, 4000, 1000, 500, 250, start = 1) pre.outl <- PreOutlier(DT$pretrain) DTcap <- CappingData(DT, impute = T, fill = T, dither = F, pre.outl = pre.outl) meth <- qc(expoTrans, range)# "spatialSign" "expoTrans" "range" "spatialSign", preproc <- PreNorm(DTcap$pretrain, meth = meth, rang = c(-0.95, 0.95)) DTcap.n <- NormData(DTcap, preproc = preproc) }, env) #--3-Data X1------------- evalq({ subset <- qc(pretrain, train, test, test1) foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, ftlm, stlm, rbci, pcci, fars, v.fatl, v.satl, v.rftl, v.rstl,v.ftlm, v.stlm, v.rbci, v.pcci, Class)} -> data1 names(data1) <- subset X1 <- vector(mode = "list", 4) foreach(i = 1:length(X1)) %do% { data1[[i]] %>% dp$select(-c(Data, Class)) %>% as.data.frame() -> x data1[[i]]$Class %>% as.numeric() %>% subtract(1) -> y list(x = x, y = y)} -> X1 names(X1) <- subset }, env) #--4-Data-X2------------- evalq({ foreach(i = 1:length(DTcap.n)) %do% { DTcap.n[[i]] ->.; dp$select(., Data, CO, HO, LO, HL, dC, dH, dL)} -> data2 names(data2) <- subset X2 <- vector(mode = "list", 4) foreach(i = 1:length(X2)) %do% { data2[[i]] %>% dp$select(-Data) %>% as.data.frame() -> x DT[[i]]$dz -> y list(x = x, y = y)} -> X2 names(X2) <- subset rm(dt, DT, pre.outl, DTcap, meth, preproc) }, env)
No quinto bloco (bestF), é classificado os preditores do conjunto Х1 em ordem crescente de importância (orderX1). São selecionados aqueles com o coeficiente acima de 0.5 (featureX1). São impressos os coeficientes e nomes dos preditores selecionados.
#--5--bestF----------------------------------- #require(clusterSim) evalq({ orderF(x = X1$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4, distance = NULL, # "d1" - Manhattan, "d2" - Euclidean, #"d3" - Chebychev (max), "d4" - squared Euclidean, #"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis method = "kmeans" ,#"kmeans" (default) , "single", #"ward.D", "ward.D2", "complete", "average", "mcquitty", #"median", "centroid", "pam" Index = "cRAND") -> rx1 rx1$stopri[ ,1] -> orderX1 featureX1 <- dp$filter(rx1$stopri %>% as.data.frame(), rx1$stopri[ ,2] > 0.5) %>% dp$select(V1) %>% unlist() %>% unname() }, env) print(env$rx1$stopri) [,1] [,2] [1,] 6 1.0423206 [2,] 12 1.0229287 [3,] 7 0.9614459 [4,] 10 0.9526798 [5,] 5 0.8884596 [6,] 1 0.8055126 [7,] 3 0.7959655 [8,] 11 0.7594309 [9,] 8 0.6960105 [10,] 2 0.6626440 [11,] 4 0.4905196 [12,] 9 0.3554887 [13,] 13 0.2269289 colnames(env$X1$pretrain$x)[env$featureX1] [1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl" [10] "stlm"
Os mesmos cálculos são realizados para o segundo conjunto de dados Х2. Nós obtemos orderX2 e featureX2.
evalq({
orderF(x = X2$pretrain$x %>% as.matrix(), type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx2
rx2$stopri[ ,1] -> orderX2
featureX2 <- dp$filter(rx2$stopri %>% as.data.frame(), rx2$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx2$stopri)
[,1] [,2]
[1,] 1 1.6650259
[2,] 5 1.6636689
[3,] 3 0.7751799
[4,] 2 0.7751351
[5,] 6 0.5692846
[6,] 7 0.5496889
[7,] 4 0.4970882
colnames(env$X2$pretrain$x)[env$featureX2]
[1] "CO" "dC" "LO" "HO" "dH" "dL"
Isso conclui a preparação dos dados iniciais para os experimentos. Nós preparamos dois conjuntos de dados X1/data1, X2/data2 e os preditores orderX1, orderX2 classificados por importância. Todos os scripts acima estão localizados no arquivo Prepare_VIII.R.
2. Processamento de amostras com ruído no subconjunto pretrain
Muitos autores de artigos, inclusive eu, dedicaram suas publicações à filtragem dos preditores com ruído. Eu proponho aqui explorar outro recurso, igualmente importante, mas menos usado — a identificação e o processamento de amostras com ruído nos conjuntos de dados. Então, por que alguns exemplos de conjuntos de dados são considerados com ruído e quais métodos podem ser usados para processá-los? Eu vou tentar explicar.
Assim, nós nos deparamos com a tarefa de classificação, enquanto temos um conjunto de treinamento de preditores e um objetivo. Considera-se que o objetivo corresponde bem à estrutura interna do conjunto de treinamento. Mas, na realidade, a estrutura de dados do conjunto de preditores é muito mais complicada do que a estrutura proposta do objetivo. Acontece que o conjunto contém exemplos que correspondem bem ao objetivo, enquanto há alguns que não correspondem a ele, distorcendo muito o modelo na aprendizagem. Como resultado, isso leva a uma diminuição na qualidade de classificação do modelo. As abordagens para identificar e processar as amostras com ruído já foram consideradas em detalhe. Aqui, nós verificamos como a qualidade de classificação é afetada por três métodos de processamento:
- correção dos exemplos erroneamente rotulados;
- remoção deles do conjunto;
- alocação para uma classe separada.
As amostras com ruído serão identificadas e processadas usando a função NoiseFiltersR::GE(). Ele procura as amostras com ruído e modifica seus rótulos (corrigindo a rotulagem incorreta). Exemplos que não podem ser rotulados novamente são removidos. As amostras identificadas com ruído também podem ser removidas manualmente do conjunto ou movidas para uma classe separada, atribuindo um novo rótulo à elas. Todos os cálculos acima são realizados no subconjunto 'pretrain', já que ele será usado para treinar o ensemble. Veja o resultado da função:
#---------------------------
import_fun(NoiseFiltersR, GE, noise)
#-----------------------
evalq({
out <- noise(x = data1[[1]] %>% dp$select(-Data))
summary(out, explicit = TRUE)
}, env)
Filter GE applied to dataset
Call:
GE(x = data1[[1]] %>% dp$select(-Data))
Parameters:
k: 5
kk: 3
Results:
Number of removed instances: 0 (0 %)
Number of repaired instances: 819 (20.46988 %)
Explicit indexes for removed instances:
.......
Estrutura de saída da função out:
> str(env$out) List of 7 $ cleanData :'data.frame': 4001 obs. of 14 variables: ..$ ftlm : num [1:4001] 0.293 0.492 0.47 0.518 0.395 ... ..$ stlm : num [1:4001] 0.204 0.185 0.161 0.153 0.142 ... ..$ rbci : num [1:4001] -0.0434 0.1156 0.1501 0.25 0.248 ... ..$ pcci : num [1:4001] -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... ..$ fars : num [1:4001] 0.208 0.255 0.246 0.279 0.267 ... ..$ v.fatl: num [1:4001] 0.4963 0.4635 0.0842 0.3707 0.0542 ... ..$ v.satl: num [1:4001] -0.0146 0.0248 -0.0353 0.1797 0.1205 ... ..$ v.rftl: num [1:4001] -0.2695 -0.0809 0.1752 0.3637 0.5305 ... ..$ v.rstl: num [1:4001] 0.398 0.362 0.386 0.374 0.357 ... ..$ v.ftlm: num [1:4001] 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... ..$ v.stlm: num [1:4001] -0.275 -0.226 -0.285 -0.11 -0.148 ... ..$ v.rbci: num [1:4001] 0.5374 0.4811 0.0978 0.2992 -0.0141 ... ..$ v.pcci: num [1:4001] -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... ..$ Class : Factor w/ 2 levels "-1","1": 2 2 2 2 2 1 1 1 1 1 ... $ remIdx : int(0) $ repIdx : int [1:819] 16 27 30 31 32 34 36 38 46 58 ... $ repLab : Factor w/ 2 levels "-1","1": 2 2 2 1 1 2 2 2 1 1 ... $ parameters:List of 2 ..$ k : num 5 ..$ kk: num 3 $ call : language GE(x = data1[[1]] %>% dp$select(-Data)) $ extraInf : NULL - attr(*, "class")= chr "filter"
Onde:
- out$cleanData — o conjunto de dados após a correção da rotulagem das amostras com ruído,
- out$remIdx — índices das amostras removidas (nenhum no exemplo out),
- out$repIdx — índices das amostras com objetivo rotulados novamente,
- out$repLab — novos rótulos destas amostras com ruído. Assim, nós podemos removê-los do conjunto ou atribuir um novo rótulo a eles usando out$repIdx.
Uma vez determinados os índices das amostras com ruído, são preparados quatro conjuntos de dados para treinar os ensembles combinados na estrutura denoiseX1pretrain.
- denoiseX1pretrain$origin — o conjunto original de pré-treinamento;
- denoiseX1pretrain$repaired — conjunto de dados com a rotulagem das amostras com ruído corrigidas;
- denoiseX1pretrain$removed — conjunto de dados com as amostras com ruído removidas;
- denoiseX1pretrain$relabeled — conjunto de dados com as amostras com ruído atribuídas a um novo rótulo (ou seja, o objetivo agora tem três classes).
#--2-Data Xrepair-------------
#library(NoiseFiltersR)
evalq({
out <- noise(x = data1$pretrain %>% dp$select(-Data))
Yrelab <- X1$pretrain$y
Yrelab[out$repIdx] <- 2L
X1rem <- data1$pretrain[-out$repIdx, ] %>% dp$select(-Data)
denoiseX1pretrain <- list(origin = list(x = X1$pretrain$x, y = X1$pretrain$y),
repaired = list(x = X1$pretrain$x, y = out$cleanData$Class %>%
as.numeric() %>% subtract(1)),
removed = list(x = X1rem %>% dp$select(-Class),
y = X1rem$Class %>% as.numeric() %>% subtract(1)),
relabeled = list(x = X1$pretrain$x, y = Yrelab))
rm(out, Yrelab, X1rem)
}, env)
Os subconjuntos denoiseX1pretrain$origin|repaired|relabeled possuem os preditores х idênticos, mas o objetivo y é diferente em cada conjunto. Vamos dar uma olhada em sua estrutura:
#------------------------- env$denoiseX1pretrain$repaired$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$relabeled$x %>% str() 'data.frame': 4001 obs. of 13 variables: $ ftlm : num 0.293 0.492 0.47 0.518 0.395 ... $ stlm : num 0.204 0.185 0.161 0.153 0.142 ... $ rbci : num -0.0434 0.1156 0.1501 0.25 0.248 ... $ pcci : num -0.0196 -0.0964 -0.4455 0.2685 -0.0349 ... $ fars : num 0.208 0.255 0.246 0.279 0.267 ... $ v.fatl: num 0.4963 0.4635 0.0842 0.3707 0.0542 ... $ v.satl: num -0.0146 0.0248 -0.0353 0.1797 0.1205 ... $ v.rftl: num -0.2695 -0.0809 0.1752 0.3637 0.5305 ... $ v.rstl: num 0.398 0.362 0.386 0.374 0.357 ... $ v.ftlm: num 0.5244 0.4039 -0.0296 0.1088 -0.2299 ... $ v.stlm: num -0.275 -0.226 -0.285 -0.11 -0.148 ... $ v.rbci: num 0.5374 0.4811 0.0978 0.2992 -0.0141 ... $ v.pcci: num -0.8779 -0.0706 -0.3125 0.6311 -0.2712 ... env$denoiseX1pretrain$repaired$y %>% table() . 0 1 1888 2113 env$denoiseX1pretrain$removed$y %>% table() . 0 1 1509 1673 env$denoiseX1pretrain$relabeled$y %>% table() . 0 1 2 1509 1673 819
Já que o número de amostras no conjunto denoiseX1pretrain$removed foi alterado, vamos verificar como o significado dos preditores foi alterado:
evalq({
orderF(x = denoiseX1pretrain$removed$x %>% as.matrix(),
type = "metric", s = 1, 4,
distance = NULL, # "d1" - Manhattan, "d2" - Euclidean,
#"d3" - Chebychev (max), "d4" - squared Euclidean,
#"d5" - GDM1, "d6" - Canberra, "d7" - Bray-Curtis
method = "kmeans" ,#"kmeans" (default) , "single",
#"ward.D", "ward.D2", "complete", "average", "mcquitty",
#"median", "centroid", "pam"
Index = "cRAND") -> rx1rem
rx1rem$stopri[ ,1] -> orderX1rem
featureX1rem <- dp$filter(rx1rem$stopri %>% as.data.frame(),
rx1rem$stopri[ ,2] > 0.5) %>%
dp$select(V1) %>% unlist() %>% unname()
}, env)
print(env$rx1rem$stopri)
[,1] [,2]
[1,] 6 1.0790642
[2,] 12 1.0320772
[3,] 7 0.9629750
[4,] 10 0.9515987
[5,] 5 0.8426669
[6,] 1 0.8138830
[7,] 3 0.7934568
[8,] 11 0.7682185
[9,] 8 0.6720211
[10,] 2 0.6355753
[11,] 4 0.5159589
[12,] 9 0.3670544
[13,] 13 0.2170575
colnames(env$X1$pretrain$x)[env$featureX1rem]
[1] "v.fatl" "v.rbci" "v.satl" "v.ftlm" "fars" "ftlm" "rbci" "v.stlm" "v.rftl"
[10] "stlm" "pcci"
A ordem e a composição dos melhores preditores foram alteradas. Isso precisará ser considerado ao treinar os ensembles.
Então, nós temos 4 subconjuntos prontos: denoiseX1pretrain$origin, repaired, removed, relabeled. Eles serão usados para treinar os ensembles ELM. Os Scripts para eliminação de ruídos dos dados estão localizados no arquivo Denoise.R. A estrutura dos dados iniciais Х1 e denoiseX1pretrain tem a seguinte aparência:

Fig. 1. A estrutura dos dados iniciais.
3 Treinamento de ensembles de classificadores de redes neurais utilizando dados iniciais sem ruído e o cálculo de previsões contínuas das redes neurais nos subconjuntos de teste
Vamos escrever uma função para treinar o ensemble e receber as previsões que servirão posteriormente como dados de entrada para o combinador treinável no stacking de ensemble.
Tais cálculos já foram realizados no artigo anterior, portanto, seus detalhes não serão discutidos. Em resumo:
- no bloco 1 (Input), é definido as constantes;
- no bloco 2 (createEns), é definido a função CreateEns(), que criaria um ensemble de classificadores de redes neurais individuais com parâmetros constantes e inicialização reproduzível;
- no bloco 3 (GetInputData), a função GetInputData() calcula as predições de três subconjuntos Х1$ train/test/test1 usando o ensemble Ens.
#--1--Input------------- evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear n <- 500 r = 7L SEED <- 12345 #--2-createENS---------------------- createEns <- function(r = 7L, nh = 5L, fact = 7L, X, Y){ Xtrain <- X[ , featureX1] k <- 1 rng <- RNGseq(n, SEED) #---creste Ensemble--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, ], y = Y[idx], nhid = nh, actfun = Fact[fact]) } return(Ens) } #--3-GetInputData -FUN----------- GetInputData <- function(Ens, X, Y){ #---predict-InputPretrain-------------- Xtrain <- X[ ,featureX1] k <- 1 rng <- RNGseq(n, SEED) #---create Ensemble--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Y, ratio = r/10, mode = "random")$tr k <- k + 1 predict(Ens[[i]], newdata = Xtrain[-idx, ]) } %>% unname() -> InputPretrain #---predict-InputTrain-- Xtest <- X1$train$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest) } -> InputTrain #[ ,n] #---predict--InputTest---- Xtest1 <- X1$test$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest1) } -> InputTest #[ ,n] #---predict--InputTest1---- Xtest2 <- X1$test1$x[ , featureX1] foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest2) } -> InputTest1 #[ ,n] #---res------------------------- return(list(InputPretrain = InputPretrain, InputTrain = InputTrain, InputTest = InputTest, InputTest1 = InputTest1)) } }, env)
Nós já temos o conjunto denoiseX1pretrain com quatro grupos de dados para os ensembles de treinamento: original (origin), com a rotulagem corrigida (repaired), com as amostras com ruído removidas (removed) e rotuladas novamente (relabeled). Após o treinamento do ensemble em cada um desses grupos de dados, nós obtemos quatro ensembles. Usando estes ensembles com a função GetInputData(), nós obtemos quatro grupos de predições em três subconjuntos: train, test e test1. Abaixo estão os scripts separados para cada ensemble na forma expandida (somente para depuração e facilidade de compreensão).
#---4--createEns--origin-------------- evalq({ Ens.origin <- vector(mode = "list", n) res.origin <- vector("list", 4) x <- denoiseX1pretrain$origin$x %>% as.matrix() y <- denoiseX1pretrain$origin$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.origin GetInputData(Ens = Ens.origin, X = x, Y = y) -> res.origin }, env) #---4--createEns--repaired-------------- evalq({ Ens.repaired <- vector(mode = "list", n) res.repaired <- vector("list", 4) x <- denoiseX1pretrain$repaired$x %>% as.matrix() y <- denoiseX1pretrain$repaired$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.repaired GetInputData(Ens = Ens.repaired, X = x, Y = y) -> res.repaired }, env) #---4--createEns--removed-------------- evalq({ Ens.removed <- vector(mode = "list", n) res.removed <- vector("list", 4) x <- denoiseX1pretrain$removed$x %>% as.matrix() y <- denoiseX1pretrain$removed$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.removed GetInputData(Ens = Ens.removed, X = x, Y = y) -> res.removed }, env) #---4--createEns--relabeled-------------- evalq({ Ens.relab <- vector(mode = "list", n) res.relab <- vector("list", 4) x <- denoiseX1pretrain$relabeled$x %>% as.matrix() y <- denoiseX1pretrain$relabeled$y createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> Ens.relab GetInputData(Ens = Ens.relab, X = x, Y = y) -> res.relab }, env)
A estrutura dos resultados das predições do ensemble é exibido abaixo:
> env$res.origin %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.747 0.774 0.733 0.642 0.28 ... $ InputTrain : num [1:1001, 1:500] 0.742 0.727 0.731 0.66 0.642 ... $ InputTest : num [1:501, 1:500] 0.466 0.446 0.493 0.594 0.501 ... $ InputTest1 : num [1:251, 1:500] 0.093 0.101 0.391 0.547 0.416 ... > env$res.repaired %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 0.815 0.869 0.856 0.719 0.296 ... $ InputTrain : num [1:1001, 1:500] 0.871 0.932 0.889 0.75 0.737 ... $ InputTest : num [1:501, 1:500] 0.551 0.488 0.516 0.629 0.455 ... $ InputTest1 : num [1:251, 1:500] -0.00444 0.00877 0.35583 0.54344 0.40121 ... > env$res.removed %>% str() List of 4 $ InputPretrain: num [1:955, 1:500] 0.68 0.424 0.846 0.153 0.242 ... $ InputTrain : num [1:1001, 1:500] 0.864 0.981 0.784 0.624 0.713 ... $ InputTest : num [1:501, 1:500] 0.755 0.514 0.439 0.515 0.156 ... $ InputTest1 : num [1:251, 1:500] 0.105 0.108 0.511 0.622 0.339 ... > env$res.relab %>% str() List of 4 $ InputPretrain: num [1:1201, 1:500] 1.11 1.148 1.12 1.07 0.551 ... $ InputTrain : num [1:1001, 1:500] 1.043 0.954 1.088 1.117 1.094 ... $ InputTest : num [1:501, 1:500] 0.76 0.744 0.809 0.933 0.891 ... $ InputTest1 : num [1:251, 1:500] 0.176 0.19 0.615 0.851 0.66 ...
Vamos ver como é a distribuição dessas saídas/entradas. Veja as 10 primeiras saídas dos conjuntos InputTrain[ ,1:10]:
#------Ris InputTrain------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTrain[ ,1:10], horizontal = T, main = "res.origin$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTrain[ ,1:10], horizontal = T, main = "res.repaired$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTrain[ ,1:10], horizontal = T, main = "res.removed$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTrain[ ,1:10], horizontal = T, main = "res.relab$InputTrain[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
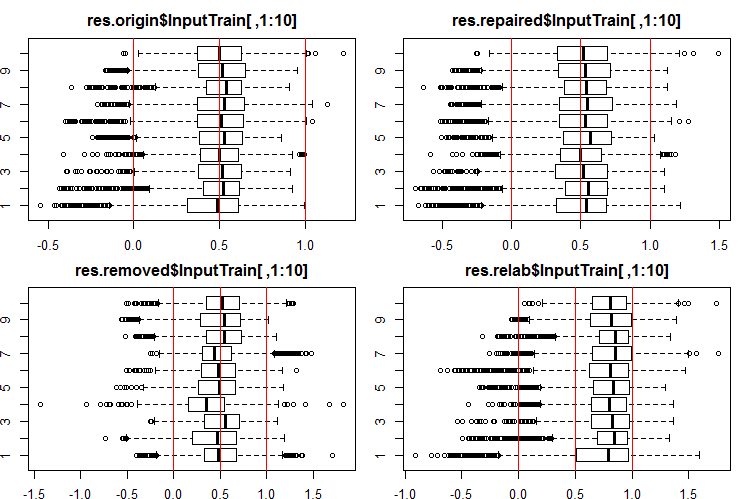
Fig. 2. Distribuição das predições das saídas de InputTrain usando quatro ensembles diferentes.
Veja as 10 primeiras saídas dos conjuntos InputTest[ ,1:10]:
#------Ris InputTest------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2), las = 1) boxplot(env$res.origin$InputTest[ ,1:10], horizontal = T, main = "res.origin$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest[ ,1:10], horizontal = T, main = "res.repaired$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest[ ,1:10], horizontal = T, main = "res.removed$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest[ ,1:10], horizontal = T, main = "res.relab$InputTest[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
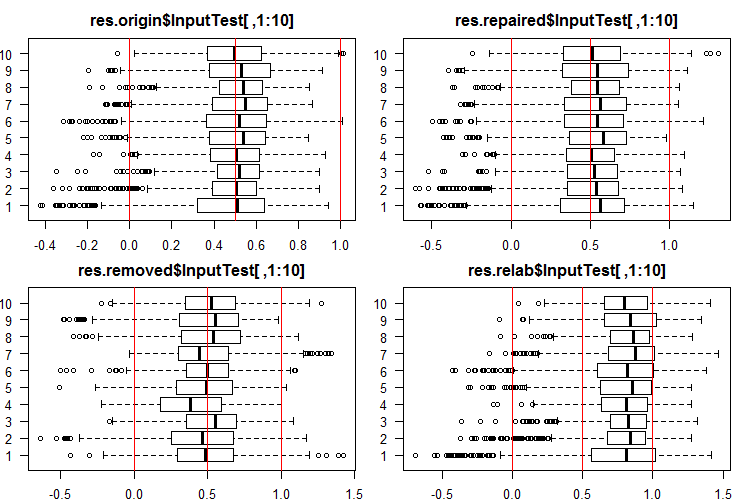
Fig. 3. Distribuição das predições das saídas de InputTest usando quatro ensembles diferentes.
Veja as 10 primeiras saídas dos conjuntos InputTest1[ ,1:10]:
#------Ris InputTest1------ par(mfrow = c(2, 2), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$res.origin$InputTest1[ ,1:10], horizontal = T, main = "res.origin$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.repaired$InputTest1[ ,1:10], horizontal = T, main = "res.repaired$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.removed$InputTest1[ ,1:10], horizontal = T, main = "res.removed$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) boxplot(env$res.relab$InputTest1[ ,1:10], horizontal = T, main = "res.relab$InputTest1[ ,1:10]") abline(v = c(0, 0.5, 1.0), col = 2) par(mfrow = c(1, 1))
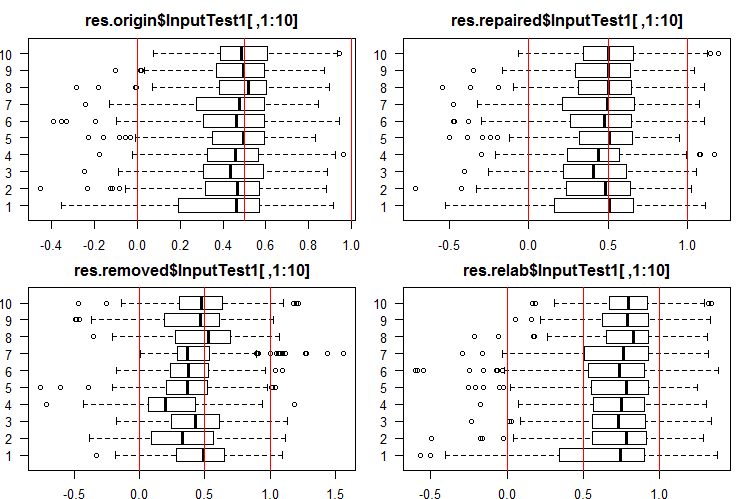
Fig. 4. Distribuição das predições das saídas de InputTest1 usando quatro ensembles diferentes.
A distribuição de todas as predições difere grandemente das previsões obtidas a partir dos dados normalizados pelo método SpatialSign nas experiências anteriores. Você pode experimentar diferentes métodos de normalização por conta própria.
Após o cálculo da previsão dos subconjuntos X1$train/test/test1 usando cada ensemble, nós obtemos quatro grupos de dados — res.origin, res.repaired, res.removed e res.relab, com suas distribuições exibidas nas Figuras 2-4.
Vamos determinar a qualidade de classificação de cada conjunto, convertendo as previsões contínuas em rótulos de classe.
4 Determinação dos limites para as previsões contínuas obtidas, convertendo-as em rótulos de classe e calculando métricas para as redes neurais
Para converter os dados contínuos em rótulos de classe, são usados um ou vários limiares de divisão nessas classes. As previsões contínuas dos conjuntos InputTrain, obtidas a partir da quinta rede neural de todos os ensembles, são as seguintes:
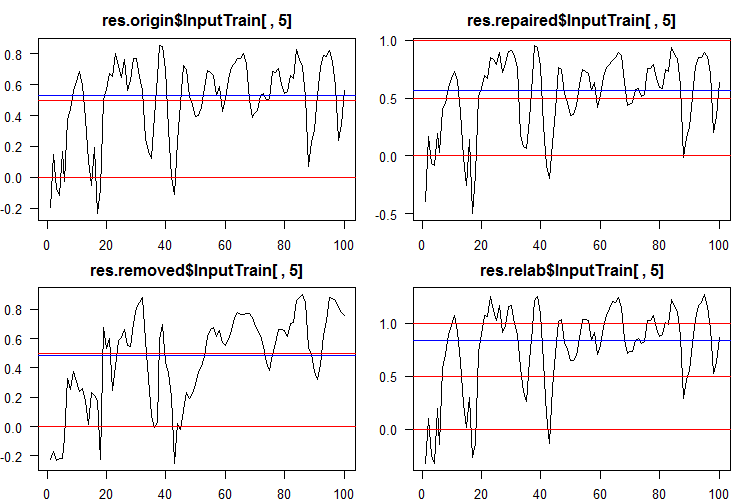
Fig. 5. Previsões contínuas da quinta rede neural de vários ensembles.
Como você pode ver, os gráficos da previsão contínua dos modelos origin, repaired, relabeled são semelhantes em forma, mas possuem um intervalo diferente. A linha do modelo de predição removed é consideravelmente diferente em sua forma.
Para simplificar os cálculos subsequentes, são coletados todos os modelos e suas previsões em uma estrutura predX1. Para fazer isso, escrevemos uma função compacta que repete todos os cálculos em um ciclo. Aqui encontramos o script e uma foto da estrutura de predX1:
library("doFuture")
#---predX1------------------
evalq({
group <- qc(origin, repaired, removed, relabeled)
predX1 <- vector("list", 4)
foreach(i = 1:4, .packages = "elmNN") %do% {
x <- denoiseX1pretrain[[i]]$x %>% as.matrix()
y <- denoiseX1pretrain[[i]]$y
SEED = 12345
createEns(r = 7L, nh = 5L, fact = 7L, X = x, Y = y) -> ens
GetInputData(Ens = ens, X = x, Y = y) -> pred
return(list(ensemble = ens, pred = pred))
} -> predX1
names(predX1) <- group
}, env)
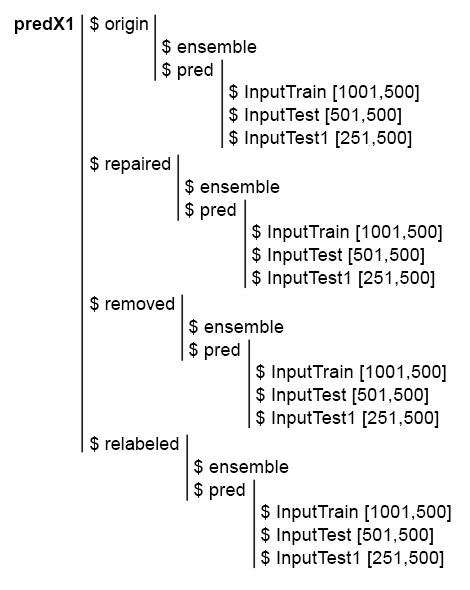
Fig. 6. Estrutura do conjunto predX1
Lembre-se de que para obter as métricas da qualidade de previsão do ensemble, duas operações precisam ser executadas: poda e média (ou votação por maioria simples). Para a poda, é necessário converter todas as saídas de toda rede neural do ensemble de forma contínua em rótulos de classe. Em seguida, são definidos as métricas de cada rede neural e selecionado um certo número delas com as melhores pontuações. Então, calcula-se a média das previsões contínuas dessas melhores redes neurais e obtém uma previsão média contínua do ensemble. Mais uma vez, é definido o limiar, convertido a previsão média em rótulos de classe e calculado as pontuações finais da qualidade de classificação do ensemble.
Assim, é necessário converter a previsão contínua em rótulos de classe duas vezes. Os limiares de conversão nesses dois estágios podem ser iguais ou diferentes. Quais variantes de limiares podem ser usadas?
- O limiar padrão. Nesse caso, é igual a 0.5.
- Limiar igual à mediana. Eu acho que é a mais confiável. Mas a mediana pode ser determinada apenas no conjunto de validação, enquanto que ela pode ser aplicada somente ao testar os subconjuntos subsequentes. Por exemplo, nós definimos os limiares no subconjunto InputTrain, que mais tarde será usado nos subconjuntos InputTest e InputTest1.
- Limiar otimizado para vários critérios. Por exemplo, ele pode ser o erro de classificação mínimo, a precisão máxima "1" ou "0" etc. Os limiares ideais são sempre determinados no subconjunto InputTrain e usado nos subconjuntos InputTest e InputTest1.
- Ao calcular a média das saídas das melhores redes neurais, a calibração pode ser usada. Alguns autores escrevem que somente as saídas bem calibradas podem ser suavizadas. A confirmação desta declaração está além do escopo deste artigo.
O limiar ideal será determinado utilizando a função InformationValue::optimalCutoff(). Ela é descrita em detalhes no pacote.
Para determinar os limiares para os pontos 1 e 2, não são necessários cálculos adicionais. Para calcular os limiares ideais para o ponto 3, vamos escrever a função GetThreshold().
#--function------------------------- evalq({ import_fun("InformationValue", optimalCutoff, CutOff) import_fun("InformationValue", youdensIndex, th_youdens) GetThreshold <- function(X, Y, type){ switch(type, half = 0.5, med = median(X), mce = CutOff(Y, X, "misclasserror"), both = CutOff(Y, X,"Both"), ones = CutOff(Y, X, "Ones"), zeros = CutOff(Y, X, "Zeros") ) } }, env)
Somente os quatro primeiros tipos de limiares descritos nesta função (half, med, mce, both) serão calculados. Os dois primeiros são os limiares da metade e da mediana. O limiar mce fornece o erro mínimo de classificação, o limiar both — o valor máximo do coeficiente youdensIndex = (sensitivity + specificity —1). A ordem de cálculo será a seguinte:
1. No conjunto predX1, calcula-se os quatro tipos de limiares para cada uma das 500 redes neurais do ensemble no subconjunto InputTrain, separadamente em cada grupo de dados (origin, repaired, removed e relabeled).
2. Em seguida, usando esses limiares, as previsões contínuas de todos os conjuntos de redes neurais são convertidos em todos os subconjuntos (train|test|test1) em classes e determinado os valores médios F1. Nós obtemos quatro grupos de métricas contendo três subconjuntos cada. Abaixo está um script passo-a-passo para o grupo origin.
4 tipos de limites são definidos no subconjunto predX1$origin$pred$InputTrain:
#--threshold--train--origin--------
evalq({
Ytest = X1$train$y
Ytest1 = X1$test$y
Ytest2 = X1$test1$y
testX1 <- vector("list", 4)
names(testX1) <- group
type <- qc(half, med, mce, both)
registerDoFuture()
cl <- makeCluster(4)
plan(cluster, workers = cl)
foreach(i = 1:4, .combine = "cbind") %dopar% {# type
foreach(j = 1:500, .combine = "c") %do% {
GetThreshold(predX1$origin$pred$InputTrain[ ,j], Ytest, type[i])
}
} -> testX1$origin$Threshold
stopCluster(cl)
dimnames(testX1$origin$Threshold) <- list(NULL,type)
}, env)
Nós usamos dois loops aninhados em cada cálculo. No loop externo, é selecionado o tipo de limite, criado um cluster e paralelizado o cálculo para 4 núcleos. No loop interno, iterar-se sobre as predições InputTrain de cada uma das 500 redes neurais que compõem o ensemble. 4 tipos de limiares são definidos para cada um. A estrutura dos dados obtidos será a seguinte:
> env$testX1$origin$Threshold %>% str() num [1:500, 1:4] 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "half" "med" "mce" "both" > env$testX1$origin$Threshold %>% head() half med mce both [1,] 0.5 0.5033552 0.3725180 0.5125180 [2,] 0.5 0.4918041 0.5118821 0.5118821 [3,] 0.5 0.5005034 0.5394191 0.5394191 [4,] 0.5 0.5138439 0.4764055 0.5164055 [5,] 0.5 0.5241393 0.5165478 0.5165478 [6,] 0.5 0.4673319 0.4508287 0.4608287
Usando os limiares obtidos, encobrimos as previsões contínuas do grupo origin dos subconjuntos train, test e test1 em rótulos de classe e calculamos as métricas (mean(F1)).
#--train--------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTrain[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTrainScore
dimnames(testX1$origin$InputTrainScore)[[2]] <- type
}, env)
#--test-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {# type
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTestScore
dimnames(testX1$origin$InputTestScore)[[2]] <- type
}, env)
#--test1-----------------------------
evalq({
foreach(i = 1:4, .combine = "cbind") %do% {
foreach(j = 1:500, .combine = "c") %do% {
ifelse(predX1$origin$pred$InputTest1[ ,j] > testX1$origin$Threshold[j, i], 1, 0) ->.;
Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean()
}
} -> testX1$origin$InputTest1Score
dimnames(testX1$origin$InputTest1Score)[[2]] <- type
}, env)
Veja a distribuição de métricas no grupo origin e três de seus subconjuntos. O script abaixo é para o grupo origin:
k <- 1L #origin # k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
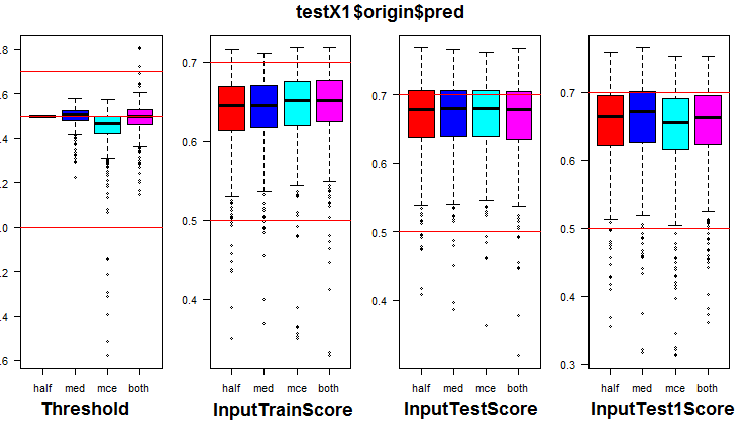
Fig. 7. Distribuição dos limiares e métricas no grupo origin
A visualização mostrou que usar "med" como limiar para o grupo de dados origin não dá uma melhoria visível na qualidade em comparação com o limiar "half".
Calculamos todos os 4 tipos de limiares em todos os grupos (esteja preparado pois levará bastante tempo e memória).
library("doFuture") #--threshold--train--------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y registerDoFuture() cl <- makeCluster(4) plan(cluster, workers = cl) while (k <= 4) { # group foreach(i = 1:4, .combine = "cbind") %dopar% {# type foreach(j = 1:500, .combine = "c") %do% { GetThreshold(predX1[[k]]$pred$InputTrain[ ,j], Ytest, type[i]) } } -> testX1[[k]]$Threshold dimnames(testX1[[k]]$Threshold) <- list(NULL,type) k <- k + 1 } stopCluster(cl) }, env)
Usando os limiares obtidos, calculamos as métricas em todos os grupos e subconjuntos:
#--train-------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTrain[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTrainScore dimnames(testX1[[k]]$InputTrainScore)[[2]] <- type k <- k + 1 } }, env) #--test----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest1, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTestScore dimnames(testX1[[k]]$InputTestScore)[[2]] <- type k <- k + 1 } }, env) #--test1----------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling while (k <= 4) { foreach(i = 1:4, .combine = "cbind") %do% { foreach(j = 1:500, .combine = "c") %do% { ifelse(predX1[[k]]$pred$InputTest1[ ,j] > testX1[[k]]$Threshold[j, i], 1, 0) ->.; Evaluate(actual = Ytest2, predicted = .)$Metrics$F1 %>% mean() } } -> testX1[[k]]$InputTest1Score dimnames(testX1[[k]]$InputTest1Score)[[2]] <- type k <- k + 1 } }, env)
Para cada grupo de dados, nós adicionamos métricas de cada uma das 500 redes neurais do ensemble com quatro limiares diferentes em três subconjuntos.
Vamos ver como as métricas são distribuídas em cada grupo e subconjunto. O script é fornecido para o subconjunto repaired. Ele é semelhante a outros grupos, apenas o número do grupo que é diferente. Para maior clareza, os gráficos de todos os grupos serão apresentados.
# k <- 1L #origin k <- 2L #repaired # k <- 3L #removed # k <- 4L #relabeling par(mfrow = c(1,4), mai = c(0.3, 0.3, 0.4, 0.2)) boxplot(env$testX1[[k]]$Threshold, horizontal = F, main = paste0(env$group[k],"$$Threshold"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTrainScore, horizontal = F, main = paste0(env$group[k],"$$InputTrainScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTestScore, horizontal = F, main = paste0(env$group[k],"$$InputTestScore"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) boxplot(env$testX1[[k]]$InputTest1Score, horizontal = F, main = paste0(env$group[k],"$$InputTest1Score"), col = c(2,4,5,6)) abline(h = c(0, 0.5, 0.7), col = 2) par(mfrow = c(1, 1))
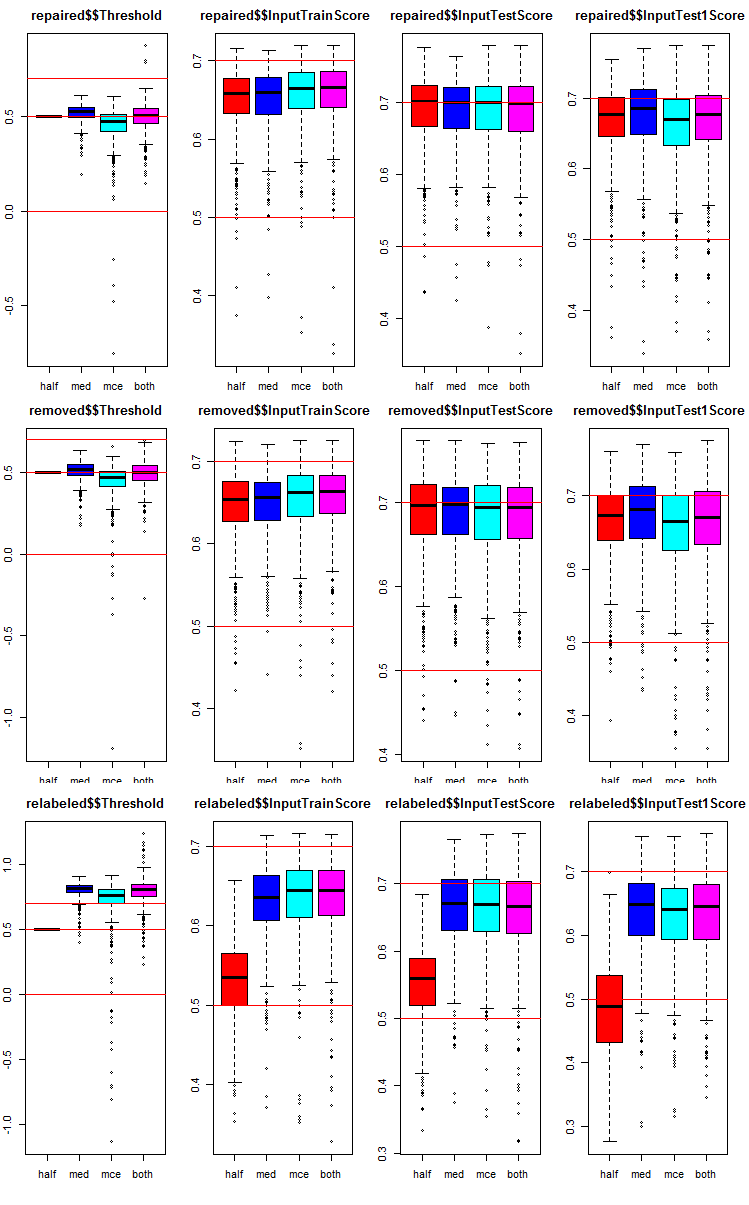
Fig. 8. Gráficos de distribuição das métricas de predição da rede neural do ensemble em três grupos de dados com três subconjuntos e quatro limiares diferentes.
Comum em todos os grupos:
- as métricas do subconjunto de teste (InputTestScore) são melhores que as métricas do conjunto de validação (InputTrainScore);
- as métricas do segundo subconjunto de teste (InputTest1Score) são visivelmente piores que as métricas do primeiro subconjunto de teste;
- O limite do tipo "half" não mostra resultados piores que os outros em todos os subconjuntos, exceto em relabeled.
5. Testando os ensembles
5.1. Determinação de 7 redes neurais com as melhores métricas em cada ensemble e em cada grupo de dados no subconjunto InputTrain
Execução da poda. Em cada grupo de dados do subconjunto testX1, é necessário selecionar 7 valores de InputTrainScore com os maiores valores da média F1. Seus índices serão os índices das melhores redes neurais do ensemble. O script é fornecido abaixo, e ele também pode ser encontrado no arquivo Test.R.
#--bestNN---------------------------------------- evalq({ nb <- 3L k <- 1L while (k <= 4) { foreach(j = 1:4, .combine = "cbind") %do% { testX1[[k]]$InputTrainScore[ ,j] %>% order(decreasing = TRUE) %>% head(2*nb + 1) } -> testX1[[k]]$bestNN dimnames(testX1[[k]]$bestNN) <- list(NULL, type) k <- k + 1 } }, env)
Nós obtivemos os índices das redes neurais com as melhores pontuações em quatro grupos de dados (origin, repaired, removed, relabeled). Vamos dar uma olhada mais de perto e comparar o quanto essas melhores redes neurais diferem dependendo do grupo de dados e do tipo de limiar.
> env$testX1$origin$bestNN half med mce both [1,] 415 75 415 415 [2,] 191 190 220 220 [3,] 469 220 191 191 [4,] 220 469 469 469 [5,] 265 287 57 444 [6,] 393 227 393 57 [7,] 75 322 444 393 > env$testX1$repaired$bestNN half med mce both [1,] 393 393 154 154 [2,] 415 92 205 205 [3,] 205 154 220 220 [4,] 462 190 393 393 [5,] 435 392 287 287 [6,] 392 220 90 90 [7,] 265 287 415 415 > env$testX1$removed$bestNN half med mce both [1,] 283 130 283 283 [2,] 207 110 300 300 [3,] 308 308 110 110 [4,] 159 134 192 130 [5,] 382 207 207 192 [6,] 192 283 130 308 [7,] 130 114 134 207 env$testX1$relabeled$bestNN half med mce both [1,] 234 205 205 205 [2,] 69 287 469 469 [3,] 137 191 287 287 [4,] 269 57 191 191 [5,] 344 469 415 415 [6,] 164 75 444 444 [7,] 184 220 57 57
Você pode ver que os índices de redes neurais com os tipos de limiar "mce" e "both" coincidem com muita frequência.
5.2. Média de predições contínuas dessas 7 melhores redes neurais.
Depois de escolher as 7 melhores redes neurais, é calculado a média delas em cada grupo de dados, nos subconjuntos InputTrain, InputTest, InputTest1 e por cada tipo de limiar. Script para processar o subconjunto InputTrain em 4 grupos:
#--Averaging--train------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTrain[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TrainYpred dimnames(testX1[[k]]$TrainYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
Vamos dar uma olhada na estrutura e nas pontuações estatísticas das predições contínuas médias obtidas no grupo de dados repaired:
> env$testX1$repaired$TrainYpred %>% str() num [1:1001, 1:4] 0.849 0.978 0.918 0.785 0.814 ... - attr(*, "dimnames")=List of 2 ..$ : NULL ..$ : chr [1:4] "Y.aver_half" "Y.aver_med" "Y.aver_mce" "Y.aver_both" > env$testX1$repaired$TrainYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.2202 Min. :-0.4021 Min. :-0.4106 Min. :-0.4106 1st Qu.: 0.3348 1st Qu.: 0.3530 1st Qu.: 0.3512 1st Qu.: 0.3512 Median : 0.5323 Median : 0.5462 Median : 0.5462 Median : 0.5462 Mean : 0.5172 Mean : 0.5010 Mean : 0.5012 Mean : 0.5012 3rd Qu.: 0.7227 3rd Qu.: 0.7153 3rd Qu.: 0.7111 3rd Qu.: 0.7111 Max. : 1.1874 Max. : 1.0813 Max. : 1.1039 Max. : 1.1039
As estatísticas dos dois últimos tipos de limiar são idênticas aqui também. Aqui estão os scripts para os dois subconjuntos restantes InputTest, InputTest1:
#--Averaging--test------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$TestYpred dimnames(testX1[[k]]$TestYpred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env) #--Averaging--test1------------------------ evalq({ k <- 1L while (k <= 4) {# group foreach(j = 1:4, .combine = "cbind") %do% {# type bestNN <- testX1[[k]]$bestNN[ ,j] predX1[[k]]$pred$InputTest1[ ,bestNN] %>% apply(1, function(x) sum(x)) %>% divide_by((2*nb + 1)) } -> testX1[[k]]$Test1Ypred dimnames(testX1[[k]]$Test1Ypred) <- list(NULL, paste0("Y.aver_", type)) k <- k + 1 } }, env)
Vamos dar uma olhada nas estatísticas do subconjunto InputTest do grupo de dados repaired:
> env$testX1$repaired$TestYpred %>% summary() Y.aver_half Y.aver_med Y.aver_mce Y.aver_both Min. :-0.1524 Min. :-0.5055 Min. :-0.5044 Min. :-0.5044 1st Qu.: 0.2888 1st Qu.: 0.3276 1st Qu.: 0.3122 1st Qu.: 0.3122 Median : 0.5177 Median : 0.5231 Median : 0.5134 Median : 0.5134 Mean : 0.5114 Mean : 0.4976 Mean : 0.4946 Mean : 0.4946 3rd Qu.: 0.7466 3rd Qu.: 0.7116 3rd Qu.: 0.7149 3rd Qu.: 0.7149 Max. : 1.1978 Max. : 1.0428 Max. : 1.0722 Max. : 1.0722
As estatísticas dos dois últimos tipos de limiar são idênticas aqui também.
5.3. Definindo os limiares para as predições contínuas médias
Agora nós temos as predições médias de cada ensemble. Eles precisam ser convertidos em rótulos de classe e as métricas finais de qualidade para todos os grupos de dados e tipos de limiar. Para fazer isso, semelhante aos cálculos anteriores, determinamos os melhores limiares usando apenas os subconjuntos de InputTrain. O script fornecido abaixo calcula os limiares em cada grupo e em cada subconjunto:
#-th_aver------------------------------ evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) Ytest = X1$train$y Ytest1 = X1$test$y Ytest2 = X1$test1$y while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold GetThreshold(testX1[[k]]$TrainYpred[ ,j], Ytest, type[i]) } } -> testX1[[k]]$th_aver dimnames(testX1[[k]]$th_aver) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env)
5.4. Convertemos as predições contínuas médias dos ensembles em rótulos de classe e calculamos as métricas dos ensembles nos subconjuntos InputTrain, InputTest e InputTest1 de todos os grupos de dados.
Com os limiares th_aver calculados acima, definimos as métricas:
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TrainScore dimnames(testX1[[k]]$TrainScore) <- list(type, colnames(testX1[[k]]$TrainYpred)) k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest1, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$TestScore dimnames(testX1[[k]]$TestScore) <- list(type, colnames(testX1[[k]]$TestYpred)) k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin #k <- 2L #repaired #k <- 3L #removed #k <- 4L #relabeling type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type subset foreach(i = 1:4, .combine = "c") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, 0) -> clAver Evaluate(actual = Ytest2, predicted = clAver)$Metrics$F1 %>% mean() %>% round(3) } } -> testX1[[k]]$Test1Score dimnames(testX1[[k]]$Test1Score) <- list(type, colnames(testX1[[k]]$Test1Ypred)) k <- k + 1 } }, env)
Vamos criar uma tabela de resumo e analisar as métricas obtidas. Vamos começar com o grupo origin (suas amostras com ruído não foram processadas de forma alguma). Nós estamos procurando as pontuações TestScore e Test1Score. As pontuações do subconjunto TestTrain são indicativas, elas são necessárias para a comparação com as pontuações dos testes:
> env$testX1$origin$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.711 0.708 0.712 0.712 med 0.711 0.713 0.707 0.707 mce 0.712 0.704 0.717 0.717 both 0.711 0.706 0.717 0.717 > env$testX1$origin$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.750 0.738 0.745 0.745 med 0.748 0.742 0.746 0.746 mce 0.742 0.720 0.747 0.747 both 0.748 0.730 0.747 0.747 > env$testX1$origin$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.735 0.732 0.716 0.716 med 0.733 0.753 0.745 0.745 mce 0.735 0.717 0.716 0.716 both 0.733 0.750 0.716 0.716
O que a tabela proposta mostra?
O melhor resultado de 0.750 em TestScore foi mostrado pela variante com o limiar "half" em ambas as transformações (tanto na poda como na média). No entanto, a qualidade cai para 0.735 no subconjunto Test1Score.
Um resultado mais estável de ~0.745 em ambos os subconjuntos é mostrado pelas variantes de limiar (med, mce, both) ao realizar a poda e por med quando esta é suavizada.
Veja o próximo grupo de dados — repaired (com a rotulagem corrigida das amostras com ruído):
> env$testX1$repaired$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.711 0.717 0.717 med 0.709 0.709 0.713 0.713 mce 0.728 0.714 0.709 0.709 both 0.728 0.711 0.717 0.717 > env$testX1$repaired$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.759 0.761 0.756 0.756 med 0.754 0.748 0.747 0.747 mce 0.758 0.755 0.743 0.743 both 0.758 0.732 0.754 0.754 > env$testX1$repaired$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.744 0.724 0.724 med 0.738 0.748 0.744 0.744 mce 0.697 0.720 0.677 0.677 both 0.697 0.743 0.731 0.731
O melhor resultado exibido na tabela é 0.759 na combinação half/half. Um resultado mais estável de ~0.750 em ambos os subconjuntos é mostrado pelas variantes de limiar (half, med, mce, both) ao realizar a poda e por med quando esta é suavizada.
Veja o próximo grupo de dados — removed (com as amostras com ruído removidas do conjunto):
> env$testX1$removed$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.713 0.720 0.724 0.718 med 0.715 0.717 0.715 0.717 mce 0.721 0.722 0.725 0.723 both 0.721 0.720 0.725 0.723 > env$testX1$removed$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.761 0.769 0.761 0.751 med 0.752 0.749 0.760 0.752 mce 0.749 0.755 0.753 0.737 both 0.749 0.736 0.753 0.760 > env$testX1$removed$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.712 0.732 0.716 0.720 med 0.729 0.748 0.740 0.736 mce 0.685 0.724 0.721 0.685 both 0.685 0.755 0.721 0.733
Analisamos a tabela. O melhor resultado foi de 0.769 em TestScore e mostrado pela variante com os limiares med/half. No entanto, a qualidade cai para 0.732 no subconjunto Test1Score. Para o subconjunto TestScore, a melhor combinação de limiares quando a poda (half, med, mce, both) e a half quando suavizada produz as melhores pontuações de todos os grupos.
Veja o último grupo de dados — relabeled (com as amostras com ruído isoladas em uma classe separada):
> env$testX1$relabeled$TrainScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.672 0.559 0.529 0.529 med 0.715 0.715 0.711 0.711 mce 0.712 0.715 0.717 0.717 both 0.710 0.718 0.720 0.720 > env$testX1$relabeled$TestScore Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.719 0.572 0.555 0.555 med 0.736 0.748 0.746 0.746 mce 0.739 0.747 0.745 0.745 both 0.710 0.756 0.754 0.754 > env$testX1$relabeled$Test1Score Y.aver_half Y.aver_med Y.aver_mce Y.aver_both half 0.664 0.498 0.466 0.466 med 0.721 0.748 0.740 0.740 mce 0.739 0.732 0.716 0.716 both 0.734 0.737 0.735 0.735
Os melhores resultados para este grupo são produzidos pela seguinte combinação de limiares: (med, mce, both) ao realizar a poda e both ou med quando suavizados.
Tenha em mente que você pode obter valores diferentes dos meus.
A figura abaixo mostra a estrutura de dados do testX1 após todos os cálculos acima:

Fig. 9. A estrutura de dados do testX1.
6. Otimização dos hiperparâmetros dos conjuntos de classificadores de redes neurais
Todos os cálculos anteriores foram realizados em ensembles com os mesmos hiperparâmetros das redes neurais, definidos com base em experiência pessoal. Como você deve saber, os hiperparâmetros das redes neurais, como outros modelos, precisam ser otimizados para um conjunto de dados específico para a obtenção dos melhores resultados. Para treinamento, nós usamos os dados sem ruídos separados em 4 grupos (origin, repaired, removed e relabeled). Portanto, é necessário obter os hiperparâmetros ótimos das redes neurais do conjunto precisamente para esses conjuntos. Todas as questões relacionadas à otimização Bayesiana foram amplamente discutidas no artigo anterior, então os detalhes deles não serão considerados aqui.
4 hiperparâmetros das redes neurais serão otimizados:
- o número de preditores — numFeature = c(3L, 13L) na faixa de 3 a 13;
- a porcentagem de amostras utilizadas no treinamento — r = c(1L, 10L) na faixa de 10% a 100%;
- o número de neurônios na camada oculta — nh = c(1L, 51L) na faixa de 1 a 51;
- o tipo de função de ativação — fact = c(1L, 10L) índice na lista de funções de ativação Fact.
Definimos as constantes:
##===OPTIM=============================== evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear bonds <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L) ) }, env)
Nós escreva uma função de avaliação que retornará o indicador de qualidade Score = mean(F1) e a predição do ensemble nos rótulos de classe. A poda (seleção das melhores redes neurais do ensemble) e a média da predição contínua serão realizadas usando o mesmo limiar = 0.5. Esta opção foi comprovada como sendo muito boa antes — pelo menos para a primeira aproximação. Aqui está o script:
#---Fitnes -FUN----------- evalq({ n <- 500 numEns <- 3 # SEED <- c(12345, 1235809) fitnes <- function(numFeature, r, nh, fact){ bestF <- orderX %>% head(numFeature) k <- 1 rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > 0.5, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred ifelse(ensPred > 0.5, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
A variável SEED comentada tem dois valores. Isso é necessário para verificar o impacto desse parâmetro no resultado experimentalmente. Eu realizei a otimização com os mesmos dados e parâmetros iniciais, mas com dois valores diferentes de SEED. O melhor resultado foi mostrado pelo SEED = 1235809. Este valor será usado nos scripts abaixo. Mas os hiperparâmetros obtidos e as pontuações de qualidade da classificação serão fornecidas para ambos os valores de SEED. Você pode experimentar outros valores.
Vamos verificar se a função de avaliação funciona, quanto tempo leva um passo de seus cálculos e ver o resultado:
evalq({
Ytrain <- X1$pretrain$y
Ytest <- X1$train$y
Ytest1 <- X1$test$y
Xtrain <- X1$pretrain$x
Xtest <- X1$train$x
Xtest1 <- X1$test$x
orderX <- orderX1
SEED <- 1235809
system.time(
res <- fitnes(numFeature = 10, r = 7, nh = 5, fact = 2)
)
}, env)
user system elapsed
5.89 0.00 5.99
env$res$Score
[1] 0.741
Abaixo está o script para otimizar os hiperparâmetros das redes neurais sucessivamente para cada grupo de dados sem ruído. Usamos 20 pontos da inicialização aleatória inicial e 20 iterações subsequentes.
#---Optim Ensemble----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes, bounds = bonds, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100, control = c(100, 50, 8)) } -> OPT_Res1 group <- qc(origin, repaired, removed, relabeled) names(OPT_Res1) <- group }, env)
Depois de iniciar a execução do script, seja paciente por cerca de meia hora (depende do seu hardware). Classificamos os valores Score obtidos em ordem decrescente e escolhemos os três melhores. Essas pontuações são atribuídas às variáveis best.res (para SEED = 12345) e best.res1 (para SEED = 1235809).
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res
names(best.res) <- group
}, env)
evalq({
foreach(i = 1:4) %do% {
OPT_Res1[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3)
} -> best.res1
names(best.res1) <- group
}, env)
Veja as melhores pontuações:
env$best.res # $origin # Round numFeature r nh fact Value # 1 39 10 7 20 2 0.769 # 2 12 6 4 38 2 0.766 # 3 38 4 3 15 2 0.766 # # $repaired # Round numFeature r nh fact Value # 1 5 10 5 20 7 0.767 # 2 7 5 2 36 9 0.766 # 3 28 5 10 6 8 0.766 # # $removed # Round numFeature r nh fact Value # 1 1 11 6 44 9 0.764 # 2 8 8 6 26 7 0.764 # 3 19 12 1 40 5 0.763 # # $relabeled # Round numFeature r nh fact Value # 1 24 9 10 1 10 0.746 # 2 7 9 9 2 8 0.745 # 3 32 4 1 1 10 0.738
O mesmo para as pontuações best.res1:
> env$best.res1 $origin Round numFeature r nh fact Value 1 19 8 3 41 2 0.777 2 32 8 1 33 2 0.777 3 23 6 1 35 1 0.770 $repaired Round numFeature r nh fact Value 1 26 9 4 17 3 0.772 2 33 11 9 30 9 0.771 3 38 5 4 17 2 0.770 $removed Round numFeature r nh fact Value 1 30 5 4 17 2 0.770 2 8 8 2 13 6 0.769 3 32 5 3 22 7 0.766 $relabeled Round numFeature r nh fact Value 1 34 12 5 8 9 0.777 2 33 9 5 4 9 0.763 3 36 12 7 4 9 0.760
Como você pode ver, esses resultados parecem melhores. Para comparação, você pode imprimir não os três primeiros resultados, mas dez: as diferenças serão ainda mais perceptíveis.
Cada execução da otimização gerará valores e resultados de hiperparâmetros diferentes. Os hiperparâmetros podem ser otimizados usando diferentes configurações iniciais de RNG, bem como com uma inicialização inicial específica.
Vamos coletar os melhores hiperparâmetros das redes neurais dos conjuntos para os 4 grupos de dados. Eles serão necessários mais tarde para criar os conjuntos com hiperparâmetros ótimos.
#---best.param-------------------
evalq({
foreach(i = 1:4, .combine = "rbind") %do% {
OPT_Res1[[i]]$Best_Par %>% unname()
} -> best.par1
dimnames(best.par1) <- list(group, qc(numFeature, r, nh, fact))
}, env)
Os hiperparâmetros:
> env$best.par1 numFeature r nh fact origin 8 3 41 2 repaired 9 4 17 3 removed 5 4 17 2 relabeled 12 5 8 9
Todos os scripts deste script estão disponíveis no arquivo Optim_VIII.R.
7. Otimização dos hiperparâmetros de pós-processamento (limiares para a poda e média)
A otimização dos hiperparâmetros das redes neurais fornece um pequeno aumento na qualidade da classificação. Como foi comprovado anteriormente, a combinação dos tipos de limiares quando acontece a poda e a média tem um impacto mais forte na qualidade de classificação.
Nós já otimizamos os hiperparâmetros com uma combinação constante de limiares half/half. Talvez essa combinação não seja ótima. Vamos repetir a otimização com dois parâmetros otimizados adicionais th1 = c(1L, 2L)) — tipo de limiar ao podar o ensemble (selecionando as melhores redes neurais) — e th2 = c(1L, 4L) — tipo de limiar ao converter a predição média do ensemble em rótulos de classe. Definimos as constantes e os intervalos de valores dos hiperparâmetros a serem otimizados.
##===OPTIM=============================== evalq({ #type of activation function. Fact <- c("sig", #: sigmoid "sin", #: sine "radbas", #: radial basis "hardlim", #: hard-limit "hardlims", #: symmetric hard-limit "satlins", #: satlins "tansig", #: tan-sigmoid "tribas", #: triangular basis "poslin", #: positive linear "purelin") #: linear bonds_m <- list( numFeature = c(3L, 13L), r = c(1L, 10L), nh = c(1L, 51L), fact = c(1L, 10L), th1 = c(1L, 2L), th2 = c(1L, 4L) ) }, env)
Para a função de avaliação. Ela ligeiramente modificada: foi adicionado dois parâmetros formais th1, th2. No corpo da função e no bloco 'best', calculamos o limiar dependendo de th1. No bloco 'test-average', nós determinamos o limiar usando a função GetThreshold(), dependendo do tipo do limiar de th2.
#---Fitnes -FUN----------- evalq({ n <- 500L numEns <- 3L # SEED <- c(12345, 1235809) fitnes_m <- function(numFeature, r, nh, fact, th1, th2){ bestF <- orderX %>% head(numFeature) k <- 1L rng <- RNGseq(n, SEED) #---train--- Ens <- foreach(i = 1:n, .packages = "elmNN") %do% { rngtools::setRNG(rng[[k]]) idx <- rminer::holdout(Ytrain, ratio = r/10, mode = "random")$tr k <- k + 1 elmtrain(x = Xtrain[idx, bestF], y = Ytrain[idx], nhid = nh, actfun = Fact[fact]) } #---predict--- foreach(i = 1:n, .packages = "elmNN", .combine = "cbind") %do% { predict(Ens[[i]], newdata = Xtest[ , bestF]) } -> y.pr #[ ,n] #---best--- ifelse(th1 == 1L, 0.5, median(y.pr)) -> th foreach(i = 1:n, .combine = "c") %do% { ifelse(y.pr[ ,i] > th, 1, 0) -> Ypred Evaluate(actual = Ytest, predicted = Ypred)$Metrics$F1 %>% mean() } -> Score Score %>% order(decreasing = TRUE) %>% head((numEns*2 + 1)) -> bestNN #---test-aver-------- foreach(i = 1:n, .packages = "elmNN", .combine = "+") %:% when(i %in% bestNN) %do% { predict(Ens[[i]], newdata = Xtest1[ , bestF])} %>% divide_by(length(bestNN)) -> ensPred th <- GetThreshold(ensPred, Yts$Ytest1, type[th2]) ifelse(ensPred > th, 1, 0) -> ensPred Evaluate(actual = Ytest1, predicted = ensPred)$Metrics$F1 %>% mean() %>% round(3) -> Score return(list(Score = Score, Pred = ensPred)) } }, env)
Verificamos quanto tempo demora uma iteração dessa função e se ela funciona:
#---res fitnes------- evalq({ Ytrain <- X1$pretrain$y Ytest <- X1$train$y Ytest1 <- X1$test$y Xtrain <- X1$pretrain$x Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 th1 <- 1 th2 <- 4 system.time( res_m <- fitnes_m(numFeature = 10, r = 7, nh = 5, fact = 2, th1, th2) ) }, env) user system elapsed 6.13 0.04 6.32 > env$res_m$Score [1] 0.748
O tempo de execução da função não teve uma mudança significativa. Após isso, executamos a otimização e aguardamos o resultado:
#---Optim Ensemble----- library(rBayesianOptimization) evalq({ Ytest <- X1$train$y Ytest1 <- X1$test$y Xtest <- X1$train$x Xtest1 <- X1$test$x orderX <- orderX1 SEED <- 1235809 OPT_Res1 <- vector("list", 4) foreach(i = 1:4) %do% { Xtrain <- denoiseX1pretrain[[i]]$x Ytrain <- denoiseX1pretrain[[i]]$y BayesianOptimization(fitnes_m, bounds = bonds_m, init_grid_dt = NULL, init_points = 20, n_iter = 20, acq = "ucb", kappa = 2.576, eps = 0.0, verbose = TRUE, maxit = 100) #, control = c(100, 50, 8)) } -> OPT_Res_m group <- qc(origin, repaired, removed, relabeled) names(OPT_Res_m) <- group }, env)
Selecionamos os 10 melhores hiperparâmetros obtidos para cada grupo de dados:
#---OptPar------
evalq({
foreach(i = 1:4) %do% {
OPT_Res_m[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(10)
} -> best.res_m
names(best.res_m) <- group
}, env)
$origin
Round numFeature r nh fact th1 th2 Value
1 19 8 3 41 2 2 4 0.778
2 25 6 8 51 8 2 4 0.778
3 39 9 1 22 1 2 4 0.777
4 32 8 1 21 2 2 4 0.772
5 10 6 5 32 3 1 3 0.769
6 22 7 2 30 9 1 4 0.769
7 28 6 10 25 5 1 4 0.769
8 30 7 9 33 2 2 4 0.768
9 40 9 2 48 10 2 4 0.768
10 23 9 1 2 10 2 4 0.767
$repaired
Round numFeature r nh fact th1 th2 Value
1 39 7 8 39 8 1 4 0.782
2 2 5 8 50 3 2 3 0.775
3 3 12 6 7 8 1 1 0.769
4 24 5 10 45 5 2 3 0.769
5 10 7 8 40 2 1 4 0.768
6 13 5 8 40 2 2 4 0.768
7 9 6 9 13 2 2 3 0.766
8 19 5 7 46 6 2 1 0.765
9 40 9 8 50 6 1 4 0.764
10 20 9 3 28 9 1 3 0.763
$removed
Round numFeature r nh fact th1 th2 Value
1 40 7 2 39 8 1 3 0.786
2 13 5 3 48 3 2 3 0.776
3 8 5 6 18 1 1 1 0.772
4 5 5 10 24 3 1 3 0.771
5 29 13 7 1 1 1 4 0.771
6 9 7 3 25 7 1 4 0.770
7 17 9 2 17 1 1 4 0.770
8 19 7 7 25 2 1 3 0.768
9 4 10 6 19 7 1 3 0.765
10 2 4 4 47 7 2 3 0.764
$relabeled
Round numFeature r nh fact th1 th2 Value
1 7 8 1 13 1 2 4 0.778
2 26 8 1 19 6 2 4 0.768
3 3 6 3 45 4 2 2 0.766
4 20 6 2 40 10 2 2 0.766
5 13 4 3 18 2 2 3 0.762
6 10 10 6 4 8 1 3 0.761
7 31 11 10 16 1 2 4 0.760
8 15 13 7 7 1 2 3 0.759
9 5 7 3 20 2 1 4 0.758
10 9 9 3 22 8 2 3 0.758
Há uma ligeira melhoria na qualidade. Os melhores hiperparâmetros para cada grupo de dados são muito diferentes dos hiperparâmetros obtidos durante a otimização anterior, sem considerar a combinação diferente de limiares. As melhores pontuações de qualidade são demonstradas pelos grupos de dados que foram rotulados novamente repaired) e as amostras com eliminação de rúido (removed).
#---best.param------------------- evalq({ foreach(i = 1:4, .combine = "rbind") %do% { OPT_Res_m[[i]]$Best_Par %>% unname() } -> best.par_m dimnames(best.par_m) <- list(group, qc(numFeature, r, nh, fact, th1, th2)) }, env) # > env$best.par_m------------------------ # numFeature r nh fact th1 th2 # origin 8 3 41 2 2 4 # repaired 7 8 39 8 1 4 # removed 7 2 39 8 1 3 # relabeled 8 1 13 1 2 4
Os scripts usados nesta seção estão disponíveis no arquivo Optim_mVIII.R.
8. Combinação dos melhores ensembles em um super ensemble, bem como as suas saídas
Combinamos os melhores conjuntos de ensembles várias vezes em um super ensemble, e suas saídas em forma de cascata por votação por maioria simples.
Primeiro, combinamos os resultados dos melhores ensembles obtidos durante a otimização. Após a otimização, a função retorna não apenas os melhores hiperparâmetros, mas também o histórico de predições nos rótulos de classe em todas as iterações. Foi gerado um super ensemble dos 5 melhores ensembles de cada grupo de dados e usado a votação por maioria simples para verificar se as pontuações de qualidade de classificação melhoraram essa variante.
Os cálculos são realizados na seguinte sequência:
- iterar sequencialmente 4 grupos de dados em um loop;
- determinar os índices das 5 melhores previsões em cada grupo de dados;
- combinar as previsões com esses índices em um dataframe;
- alterar o rótulo de classe de "0" para "-1" em todas as predições;
- soma destas previsões linha por linha;
- converção desses valores somados em rótulos de classe (-1, 0, 1) de acordo com a condição: se o valor for maior que 3, então class = 1; se menor que -3, então class = -1; caso contrário, class = 0
Aqui está o script que realiza esses cálculos:
#--Index-best-------------------
evalq({
prVot <- vector("list", 4)
foreach(i = 1:4) %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(.) ifelse(. == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x)) ->.;
ifelse(. > 3, 1, ifelse(. < -3, -1, 0))
} -> prVot
names(prVot) <- group
}, env)
Nós temos uma terceira classe adicional "0". Se "-1", é "Sell", "1" é "Buy", e "0" é "not sure". Como o Expert Advisor reage a este sinal fica por conta do usuário. Ele pode ficar de fora do mercado, ou pode estar no mercado e não fazer nada, esperando por um novo sinal para a ação. Os modelos de comportamento devem ser construídos e verificados ao testar o expert.
Para obter as métricas, é necessário:
- iterar sequencialmente sobre cada grupo de dados em um loop;
- alterar no valor real do objetivo Ytest1, o rótulo de classe "0" pelo rótulo "-1";
- combinar o objetivo prVot atual e previsto obtido acima em um dataframe;
- remover as linhas com o valor de prVot = 0 do dataframe;
- calcular as métricas.
Calcule e veja o resultado.
evalq({
foreach(i = 1:4) %do% { #group
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = prVot[[i]]) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred)
} -> Score
names(Score) <- group
}, env)
env$Score
$origin
$origin$metrics
Accuracy Precision Recall F1
-1 0.806 0.809 0.762 0.785
1 0.806 0.804 0.845 0.824
$origin$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 157 49
1 37 201
Accuracy : 0.8063
95% CI : (0.7664, 0.842)
No Information Rate : 0.5631
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6091
Mcnemar's Test P-Value : 0.2356
Sensitivity : 0.8093
Specificity : 0.8040
Pos Pred Value : 0.7621
Neg Pred Value : 0.8445
Prevalence : 0.4369
Detection Rate : 0.3536
Detection Prevalence : 0.4640
Balanced Accuracy : 0.8066
'Positive' Class : -1
$repaired
$repaired$metrics
Accuracy Precision Recall F1
-1 0.82 0.826 0.770 0.797
1 0.82 0.816 0.863 0.839
$repaired$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 147 44
1 31 195
Accuracy : 0.8201
95% CI : (0.7798, 0.8558)
No Information Rate : 0.5731
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6358
Mcnemar's Test P-Value : 0.1659
Sensitivity : 0.8258
Specificity : 0.8159
Pos Pred Value : 0.7696
Neg Pred Value : 0.8628
Prevalence : 0.4269
Detection Rate : 0.3525
Detection Prevalence : 0.4580
Balanced Accuracy : 0.8209
'Positive' Class : -1
$removed
$removed$metrics
Accuracy Precision Recall F1
-1 0.819 0.843 0.740 0.788
1 0.819 0.802 0.885 0.841
$removed$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 145 51
1 27 207
Accuracy : 0.8186
95% CI : (0.7789, 0.8539)
No Information Rate : 0.6
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.6307
Mcnemar's Test P-Value : 0.009208
Sensitivity : 0.8430
Specificity : 0.8023
Pos Pred Value : 0.7398
Neg Pred Value : 0.8846
Prevalence : 0.4000
Detection Rate : 0.3372
Detection Prevalence : 0.4558
Balanced Accuracy : 0.8227
'Positive' Class : -1
$relabeled
$relabeled$metrics
Accuracy Precision Recall F1
-1 0.815 0.809 0.801 0.805
1 0.815 0.820 0.828 0.824
$relabeled$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 157 39
1 37 178
Accuracy : 0.8151
95% CI : (0.7741, 0.8515)
No Information Rate : 0.528
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6292
Mcnemar's Test P-Value : 0.9087
Sensitivity : 0.8093
Specificity : 0.8203
Pos Pred Value : 0.8010
Neg Pred Value : 0.8279
Prevalence : 0.4720
Detection Rate : 0.3820
Detection Prevalence : 0.4769
Balanced Accuracy : 0.8148
'Positive' Class : -1
#---------------------------------------
A qualidade melhorou significativamente em todos os grupos. As melhores pontuações de 'Balanced Accuracy' foram obtidas nos grupos removed (0.8227) e repaired (0.8209).
Vamos combinar as predições do grupo usando a votação por maioria simples também. Executamos a combinação em cascata:
- iterar todos os grupos de dados em um loop;
- determinar os índices dos passos com os melhores resultados;
- selecionar as predições desses melhores passos;
- em cada coluna, substituir o rótulo de classe "0" pelo rótulo "-1";
- somar as predições no grupo linha por linha.
Veja o resultado obtido:
#--Index-best-------------------
evalq({
foreach(i = 1:4, .combine = "+") %do% { #group
best.res_m[[i]]$Round %>% head(5) -> ind
OPT_Res_m[[i]]$Pred %>% dp$select(ind) ->.;
apply(., 2, function(x) ifelse(x == 0, -1, 1)) ->.;
apply(., 1, function(x) sum(x))
} -> prVotSum
}, env)
> env$prVotSum %>% table()
.
-20 -18 -16 -14 -12 -10 -8 -6 -4 -2 0 2 4 6 8 10 12 14 16 18 20
166 12 4 6 7 6 5 3 6 1 4 4 5 6 5 10 7 3 8 24 209
Deixamos apenas os maiores valores de votação e calculamos as métricas:
evalq({
pred <- {prVotSum ->.;
ifelse(. > 18, 1, ifelse(. < -18, -1, 0))}
Ytest1 ->.;
ifelse(. == 0, -1, 1) ->.;
cbind(actual = ., pred = pred) %>% as.data.frame() ->.;
dp$filter(., pred != 0) -> tabl
Eval(tabl$actual, tabl$pred) -> ScoreSum
}, env)
env$ScoreSum
> env$ScoreSum
$metrics
Accuracy Precision Recall F1
-1 0.835 0.849 0.792 0.820
1 0.835 0.823 0.873 0.847
$confMatr
Confusion Matrix and Statistics
predicted
actual -1 1
-1 141 37
1 25 172
Accuracy : 0.8347
95% CI : (0.7931, 0.8708)
No Information Rate : 0.5573
P-Value [Acc > NIR] : <2e-16
Kappa : 0.6674
Mcnemar's Test P-Value : 0.1624
Sensitivity : 0.8494
Specificity : 0.8230
Pos Pred Value : 0.7921
Neg Pred Value : 0.8731
Prevalence : 0.4427
Detection Rate : 0.3760
Detection Prevalence : 0.4747
Balanced Accuracy : 0.8362
'Positive' Class : -1
Isso produziu uma pontuação muito boa de Balanced Accuracy = 0.8362.
Os scripts descritos nesta seção estão disponíveis no arquivo Voting.R.
Mas não devemos esquecer de uma nuance. Ao otimizar os hiperparâmetros, nós usamos o conjunto de teste InputTest. Isso significa que nós podemos começar a trabalhar com o próximo conjunto de teste InputTest1. A combinação dos conjuntos em cascata é mais provável de produzir o mesmo efeito positivo sem a otimização dos hiperparâmetros. Verifique nos resultados da média obtidos anteriormente.
Combinamos as saídas médias dos conjuntos obtidos na seção 5.2.
Reproduzimos os cálculos descritos na seção 5.4, com uma alteração. Ao converter a predição média contínua em rótulos de classe, esses rótulos serão [-1, 0, 1]. A sequência de cálculo em cada subconjunto train/test/test1:
- iterar sequencialmente 4 grupos de dados em um loop;
- por 4 tipos de limiares de poda;
- por 4 tipos de limiares de média;
- converter a previsão média contínua do ensemble em rótulos de classe [-1, 1];
- somá-los por 4 tipos de limiares de média;
- renomear o somatório com novos rótulos [-1, 0, 1];
- adicionar o resultado obtido à estrutura de VotAver.
#---train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) VotAver <- vector("list", 4) names(VotAver) <- group while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TrainYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Train.clVoting dimnames(VotAver[[k]]$Train.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test------------------------------ evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$TestYpred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test.clVoting dimnames(VotAver[[k]]$Test.clVoting) <- list(NULL, type) k <- k + 1 } }, env) #---test1------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(j = 1:4, .combine = "cbind") %do% {# type aver foreach(i = 1:4, .combine = "+") %do% {# type threshold ifelse(testX1[[k]]$Test1Ypred[ ,j] > testX1[[k]]$th_aver[i,j], 1, -1) } ->.; ifelse(. > 2, 1, ifelse(. < -2, -1, 0)) } -> VotAver[[k]]$Test1.clVoting dimnames(VotAver[[k]]$Test1.clVoting) <- list(NULL, type) k <- k + 1 } }, env)
Uma vez que as previsões médias renomeadas em subconjuntos e grupos forem determinadas, calculamos as suas métricas. Sequência de cálculos:
- iterar sobre os grupos em um loop;
- iterar mais de 4 tipos de limiares de média;
- alterar o rótulo da classe na predição atual de "0" para "-1";
- combinar a predição atual e renomeada para o dataframe;
- remover as linhas com a predição igual a 0 do dataframe;
- calcular as métricas e adicioná-las à estrutura de VotAver.
#---Metrics--train------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TrainScoreVot names(VotAver[[k]]$TrainScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest1 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$TestScoreVot names(VotAver[[k]]$TestScoreVot) <- type k <- k + 1 } }, env) #---Metrics--test1------------------------------------- evalq({ k <- 1L #origin type <- qc(half, med, mce, both) while (k <= 4) { # group foreach(i = 1:4) %do% {# type threshold Ytest2 ->.; ifelse(. == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVoting[ ,i]) %>% as.data.frame() ->.; dp$filter(., pred != 0) -> tbl Evaluate(actual = tbl$actual, predicted = tbl$pred)$Metrics$F1 %>% mean() %>% round(3) #Eval(tbl$actual,tbl$pred) } -> VotAver[[k]]$Test1ScoreVot names(VotAver[[k]]$Test1ScoreVot) <- type k <- k + 1 } }, env)
Colete os dados em um formato legível e visualize-os:
#----TrainScoreVot-------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TrainScoreVot %>% unlist() %>% unname()
} -> TrainScoreVot
dimnames(TrainScoreVot) <- list(group, type)
}, env)
> env$TrainScoreVot
half med mce both
origin 0.738 0.750 0.742 0.752
repaired 0.741 0.743 0.741 0.741
removed 0.748 0.755 0.755 0.755
relabeled 0.717 0.741 0.740 0.758
#-----TestScoreVot----------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$TestScoreVot %>% unlist() %>% unname()
} -> TestScoreVot
dimnames(TestScoreVot) <- list(group, type)
}, env)
> env$TestScoreVot
half med mce both
origin 0.774 0.789 0.797 0.804
repaired 0.777 0.788 0.778 0.778
removed 0.801 0.808 0.809 0.809
relabeled 0.773 0.789 0.802 0.816
#----Test1ScoreVot--------------------------
evalq({
foreach(k = 1:4, .combine = "rbind") %do% { # group
VotAver[[k]]$Test1ScoreVot %>% unlist() %>% unname()
} -> Test1ScoreVot
dimnames(Test1ScoreVot) <- list(group, type)
}, env)
> env$Test1ScoreVot
half med mce both
origin 0.737 0.757 0.757 0.755
repaired 0.756 0.743 0.754 0.754
removed 0.759 0.757 0.745 0.745
relabeled 0.734 0.705 0.697 0.713
Os melhores resultados foram exibidos no subconjunto de teste no grupo de dados 'removed', com o processamento de amostras com ruído.
Mais uma vez, nós combinamos os resultados em cada subconjunto de cada grupo de dados por tipos de média.
#==Variant-2========================================== #--TrainScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Train.clVoting ->.; apply(., 1, function(x) sum(x)) ->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Train.clVotingSum ifelse(Ytest == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Train.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TrainScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--TestScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test.clVotingSum ifelse(Ytest1 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$TestScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env) #--Test1ScoreVotSum------------------------------- evalq({ k <- 1L while(k <= 4){ # group VotAver[[k]]$Test1.clVoting ->.; apply(., 1, function(x) sum(x))->.; ifelse(. > 3, 1, ifelse(. < -3, -1, 0)) -> VotAver[[k]]$Test1.clVotingSum ifelse(Ytest2 == 0, -1, 1) ->.; cbind(actual = ., pred = VotAver[[k]]$Test1.clVotingSum) ->.; as.data.frame(.) ->.; dp$filter(., pred != 0) ->.; Evaluate(actual = .$actual, predicted = .$pred)$Metrics$F1 ->.; mean(.) %>% round(3) -> VotAver[[k]]$Test1ScoreVotSum #Eval(tbl$actual,tbl$pred) k <- k + 1 } }, env)
Coletamos os resultados de uma forma legível.
evalq({
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TrainScoreVotSum %>% unlist() %>% unname()
} -> TrainScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$TestScoreVotSum %>% unlist() %>% unname()
} -> TestScoreVotSum
foreach(k = 1:4, .combine = "c") %do% { # group
VotAver[[k]]$Test1ScoreVotSum %>% unlist() %>% unname()
} -> Test1ScoreVotSum
ScoreVotSum <- cbind(TrainScoreVotSum, TestScoreVotSum, Test1ScoreVotSum)
dimnames(ScoreVotSum ) <- list(group, qc(TrainScoreVotSum, TestScoreVotSum,
Test1ScoreVotSum))
}, env)
> env$ScoreVotSum
TrainScoreVotSum TestScoreVotSum Test1ScoreVotSum
origin 0.763 0.807 0.762
repaired 0.752 0.802 0.748
removed 0.761 0.810 0.765
relabeled 0.766 0.825 (!!) 0.711
Considere os resultados do conjunto de testes. Surpreendentemente, o método relabeled teve o melhor resultado. Os resultados em todos os grupos são melhores que os obtidos na seção 5.4. O método de combinar as saídas do ensemble em cascata por votação por maioria simples dá uma melhoria na qualidade de classificação (Accuracy) de 5% para 7%.
Os scripts desta seção estão localizados no arquivo Voting_aver.R. A estrutura dos dados obtidos é exibida na figura abaixo:

Fig. 10. A estrutura de dados de VotAver.
A figura abaixo fornece um esquema simplificado de todos os cálculos: ela mostra as etapas, os scripts utilizados e as estruturas de dados.
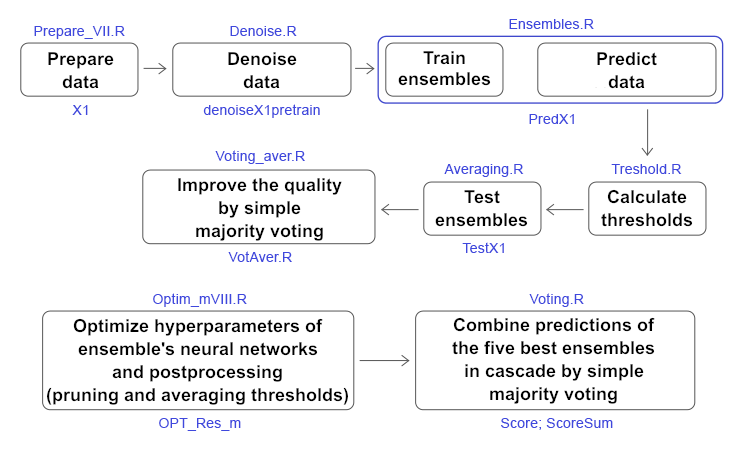
Fig. 11. Estrutura e sequência dos cálculos principais no artigo.
8. Análise dos resultados experimentais
Nós processamos as amostras com ruído dos conjuntos de dados iniciais nos subconjuntos pretrain (!) de três maneiras:
- realocado os dados "erroneamente" rotulados sem alterar o número de classes (repaired);
- removido as amostras com "ruído" do subconjunto (removed);
- isolado as amostras com "ruído" em uma classe separada (relabeled).
Quatro grupos de dados (origin, repaired, removed, relabeled) foram obtidos na estrutura denoiseX1pretrain. Use-os para treinar o ensemble composto por 500 classificadores de redes neurais ELM. Obtenha quatro conjuntos. Calcule as predições contínuas de três subconjuntos Х1$train/test/test1 usando esses 4 ensembles e colete-os na estrutura predX1.
Em seguida, calcule 4 tipos de limiares para previsões contínuas de cada uma das 500 redes neurais de cada conjunto no subconjunto InputTrain (!). Usando esses limiares, converta as previsões contínuas em rótulos de classe (0, 1). Calcular as métricas (mean(F1)) para cada rede neural dos ensembles e coletá-las na estrutura testX1$$(InputTrainScore|InputTestScore|InputTest1Score). A visualização da distribuição das métricas em 4 grupos de dados e 3 subconjuntos mostra:
- primeiro, as métricas no primeiro subconjunto de testes são maiores que no InputTrainS em todos os grupos;
- segundo, as métricas são visualmente mais altas nos grupos repaired e removed do que nos outros dois.
Agora selecione as 7 melhores redes neurais com os maiores valores de mean(F1) em cada ensemble e calcule a média de suas predições contínuas. Adicione seus valores à estrutura testX1$$(TrainYpred|TestYpred|Test1Ypred). Calcule os limiares th_aver no subconjunto TrainYpred, determine as métricas de todas as previsões contínuas médias e adicione-as à estrutura testX1$$(TrainScore|TestScore|Test1Score). Agora eles podem ser analisados.
Com uma combinação diferente dos limiares de poda e de média em diferentes grupos de dados, nós obtemos as métricas na faixa de 0.75 a 0.77. O melhor resultado foi obtido no grupo removed com as amostras com "ruído" removidas.
A otimização dos hiperparâmetros das redes neurais fornece um aumento estável nas métricas de 0.77+ em todos os grupos.
A otimização dos hiperparâmetros e os limiares de pós-processamento (poda e média) das redes neurais fornece um resultado estávelmente alto de cerca de 0.78+ em todos os grupos com amostras processadas de "ruído".
Crie um super ensemble de vários conjuntos com os hiperparâmetros ótimos, faça as predições desses ensembles e combine-os por votação por maioria simples em cada grupo de dados. Como resultado, obtenha as métricas nos grupos repaired and removed na faixa de 0.82+. Combinando estas predições dos super ensembles por votação por maioria simples, é obtido o valor final da métrica de 0.836. Assim, combinando as predições em cascata por votação por maioria simples dá uma melhoria na qualidade de 6-7%.
Verifique esta declaração sobre as predições médias do ensemble recebido anteriormente. Depois de repetir os cálculos e as conversões nos grupos, obtenha métricas de 0.8+ ou mais no grupo removed do subconjunto de Test. Continuando a combinação em cascata, obtenha métricas com valores de 0,8+ no subconjunto Test em todos os grupos de dados.
Pode-se concluir que a combinação das predições de conjunto em cascata pela votação simples melhora a qualidade da classificação.
Conclusão
Neste artigo, três métodos para melhorar a qualidade do bagging de ensembles foram considerados, assim como a otimização de hiperparâmetros das redes neurais do ensemble e do pós-processamento. Com base nos resultados dos experimentos, as seguintes conclusões podem ser tiradas:
- processar as amostras com ruído usando os métodos repaired e removed melhoram significativamente a qualidade de classificação dos ensembles;
- selecionar o tipo de limiar para a poda e a média, bem como sua combinação afeta significativamente a qualidade da classificação;
- combinar vários conjuntos em um super ensemble com suas predições combinadas em cascata pela votação por maioria simples, fornece o maior aumento na qualidade de classificação;
- otimizar os hiperparâmetros das redes neurais dos conjuntos e o pós-processamento melhora ligeiramente as pontuações de qualidade de classificação. É aconselhável realizar a primeira otimização em novos dados e repeti-los periodicamente quando a qualidade diminui. A periodicidade é determinada experimentalmente.
Anexos
GitHub/PartVIII contêm os seguintes arquivos::
- Importar.R — funções de importação de pacotes.
- Library.R — bibliotecas necessárias.
- FunPrepareData_VII.R — funções para a preparação dos dados iniciais.
- FunStacking_VIII.R — funções para criar e testar o ensemble.
- Prepare_VIII.R — funções e scripts para preparar os dados iniciais para os combinadores treináveis.
- Denoise.R — scripts para processar amostras com ruído.
- Ensemles.R — scripts para criar os ensembles.
- Threshold.R — scripts para determinar os limiares.
- Test.R — scripts para testar os ensembles.
- Averaging.R — scripts para calcular a média das saídas contínuas dos ensembles.
- Voting_aver.R — Combinação das saídas médias em cascata por votação por maioria simples.
- Optim_VIII.R — scripts para a otimização dos hiperparâmetros das redes neurais.
- Optim_mVIII.R — scripts para a otimização dos hiperparâmetros das redes neurais e pós-processamento.
- Voting.R — combinando as saídas do super ensemble em cascata por votação por maioria simples.
- SessionInfo_VII.txt — lista de pacotes usados nos scripts do artigo.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/4722
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Escrita de indicadores de bolsa com controle de volume usando o indicador delta como exemplo
Escrita de indicadores de bolsa com controle de volume usando o indicador delta como exemplo
 Integração de um EA em MQL e bancos de dados (SQL Server, .NET e C#)
Integração de um EA em MQL e bancos de dados (SQL Server, .NET e C#)
 Gráfico PairPlot baseado em CGraphic para analisar correlações entre arrays de dados (séries temporais)
Gráfico PairPlot baseado em CGraphic para analisar correlações entre arrays de dados (séries temporais)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Depois de escolher os 7 melhores conjuntos e classificá-los [=1,0,1], gostaria de extrair os dados para treiná-los em um modelo do Keras, mas não consigo encontrar os quadros de dados específicos.
A Figura 11 mostra o esquema estrutural dos cálculos. Acima de cada estágio está o nome do script. Abaixo de cada estágio está o nome da estrutura de dados resultante. Quais dados você deseja usar?
Se você quiser usar as previsões contínuas médias dos sete melhores conjuntos, elas estarão na estrutura
k = c(origem/reparado/removido/rotulado)
j = c( half, mean, med, both)
Se você precisar das previsões dos sete melhores na forma binária, elas estarão na estrutura
Olá novamente,
Estou recebendo os seguintes erros, que não consigo resolver - alguma dica?
Erro 1: "in { : task 1 failed - "object 'History' not found" , quando executo o seguinte segmento de código:
#---OptPar------ evalq({ foreach(i = 1:4) %do% { OPT_Res[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3) } -> best.res names(best.res) <- group }, env) evalq({ foreach(i = 1:4) %do% { OPT_Res1[[i]] %$% History %>% dp$arrange(desc(Value)) %>% head(3) } -> best.res1 names(best.res1) <- group }, env)Não tenho certeza de onde o objeto History é criado e não consegui encontrá-lo no repositório do github nos vários arquivos .R deste artigo
Erro 2: "Yts" não encontrado, quando executo o seguinte segmento de código:
Também não tenho certeza de quando/como o "Yts" está sendo criado
Acho que ambos podem ser resolvidos por um trecho de código que pode estar faltando no repositório do github?
Agradeceria qualquer ajuda que você pudesse fornecer, muito obrigado desde já