深度神经网络 (第 I 部)。准备数据
9 150
1
DNN 在许多领域得到广泛的应用和发展。日常使用神经网络的最常见例子是语言和图像识别, 以及从一种语言到另一种语言的自动翻译。DNN 也能用于交易。鉴于算法交易的快速发展, 对 DNN 的深入研究似乎是有用的。
最近, 开发人员已经提出了许多新的使用 DNN 的思路, 方法和途径, 并通过实验一一证明它们。本系列文章将研究 DNN 发展的状况和主要方向。有极大的空间可致力于使用实际实验和 DNN 的定性特征来测试各种思路和方法。在我们的工作中将仅使用多层完全连接的网络。
文章将有四个着重关注领域:
- 准备, 评估和经过各种变换放大的入场数据。
- darch 软件包的新功能 (v.0.12)。灵活性和扩展功能。
- 运用预测结果放大 (DNN 和神经网络合奏的超参数优化)。
- 在学习和工作期间控制智能交易系统操作的图形能力。
本文将研究准备用于神经网络的接收自交易终端中的数据。
内容
概述
深度神经网络的开发、训练和测试应按严格顺序分阶段完成。与任何机器学习模型类似, 创建 DNN 的过程可以分为两个不相等的部分:
- 准备进行实验用的输入和输出数据;
- DNN 的创建、训练、测试和参数优化。
第一阶段占用大部分时间 - 约 70%。DNN 的操作在很大程度上取决于这个阶段的成功。毕竟, 塞进的是垃圾 - 出来的还是垃圾。这就是为什么我们将详细描述这一阶段的行动顺序。
为了重复实验, 您需要安装 MRO 3.4.0 和 Rstudio。有关此软件的安装说明可以在互联网上轻松找到。本文附带的文件也包含这些信息, 所以我们不再赘言。
R 语言
我们来回忆一下关于 R 的一些重要事情。它是统计计算和图形专用的编程语言和环境。它于 1996 年由新西兰科学家 Ross Ihaka 和 Robert Gentleman 在奥克兰大学开发。R 是一个 GNU 项目, 此为开源软件。使用开源软件的方法取决于以下原则 (自由度):
- 为任何目的启动开发的自由 (自由度 0);
- 研究程序如何运作并令其适合程序员需求的自由 (自由度 1);
- 分发副本的自由, 以便您可以帮助您的邻居 (自由度 2);
- 改善程序, 分发修订版本的自由, 令整个社区受益。
如今 R 主要由 "R 开发核心团队" 和去年成立的 R 联盟 进行改进和开发。联盟成员名单 (IBM, Microsoft, Rstudio, Google, Mango, Oracle 等) 表明其受到良好的支持, 显著的兴趣和良好的语言前景。
R 的优势:
- 如今, R 是统计计算的标准。
- 它得到全球科学界的支持和发展。
- 整套软件包涵盖数据挖掘的所有高级方向。必须要说到的是, 自科学家们发表新观念, 之后在 R 中实现这一想法的间隔时间不超过两周。
- 而且, 最后但非同小可的是, 它是绝对免费的。
1. 创建初始 (原始) 数据
"所有以前的, 当前的和未来的价格走势蕴含在价格本身"
有许多方法 (软件包) 设计用于初步准备、评估和预测选择。这些方法的评论可以在 [1] 中找到。它们的变体可由现实世界数据的多样性来解释。使用中的数据类型将定义探索和处理的方法。
我们正在探索 财务数据。这些具有层次结构, 规则的时间序列永无终止, 且可以很容易地提取。基准行是指定时间帧的金融工具的 OHLCV 报价。
所有其它时间序列来自这个基本行:
- 非参数化。例如, x^2, sqrt(abs(x)), x^3, -x^2 等等。
- 功能参数化。例如, sin(2*n*x), ln(abs(x)), log(Pr(t)/Pr(t-1)) 等等。
- 参数化。这里属于一定数量的不同指标, 主要用来预测。它们可以是振荡器和不同种类的过滤器。
无论指标生成的信号 (因子), 或条件语句序列产生的信号都可作为目标变量使用。
1.1. 报价
OHLC 报价, 交易量和时间我们可以从终端的 (o, h, l, cl, v, d) 向量 获得。我们需要编写一个函数以便在数据帧中加入接收自终端的向量。为此, 我们将柱线的开始时间格式改为 POSIXct 格式。
#---pr.OHLCV-------------------
pr.OHLCV <- function(d, o, h, l, cl, v){
# (d, o, h, l, cl, v)- vector
require('magrittr')
require('dplyr')
require('anytime')
price <- cbind(Data = rev(d),
Open = rev(o), High = rev(h),
Low = rev(l), Close = rev(cl),
Vol = rev(v)) %>% as.tibble()
price$Data %<>% anytime(., tz = "CET")
return(price)
}
由于报价向量已被加载到环境 env 中, 我们来计算数据帧 pr 并清除环境变量:
evalq({pr <- pr.OHLCV(Data, Open, High, Low, Close, Volume)
rm(list = c("Data", "Open", "High", "Low", "Close", "Volume"))
},
env)
我们想看看这个数据帧开头的样子:
> head(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-01-10 11:00:00 122.758 122.893 122.746 122.859 2 2017-01-10 11:15:00 122.860 122.924 122.818 122.848 3 2017-01-10 11:30:00 122.850 122.856 122.705 122.720 4 2017-01-10 11:45:00 122.721 122.737 122.654 122.693 5 2017-01-10 12:00:00 122.692 122.850 122.692 122.818 6 2017-01-10 12:15:00 122.820 122.937 122.785 122.920 # ... with 1 more variables: Vol <dbl>
以及结尾:
> tail(env$pr) # A tibble: 6 x 6 Data Open High Low Close <dttm> <dbl> <dbl> <dbl> <dbl> 1 2017-05-05 20:30:00 123.795 123.895 123.780 123.888 2 2017-05-05 20:45:00 123.889 123.893 123.813 123.831 3 2017-05-05 21:00:00 123.833 123.934 123.825 123.916 4 2017-05-05 21:15:00 123.914 123.938 123.851 123.858 5 2017-05-05 21:30:00 123.859 123.864 123.781 123.781 6 2017-05-05 21:45:00 123.779 123.864 123.781 123.781 # ... with 1 more variables: Vol <dbl>
所以, 有 8000 根柱线开始日期为 10.01.2017 结束日期为 05.05.2017。 我们将价格的衍生物加入到 数据帧 pr — 中间价格, 典型价格 和 加权收盘价
evalq(pr %<>% mutate(., Med = (High + Low)/2, Typ = (High + Low + Close)/3, Wg = (High + Low + 2 * Close)/4, #CO = Close - Open, #HO = High - Open, #LO = Low - Open, dH = c(NA, diff(High)), dL = c(NA, diff(Low)) ), env)
1.2. 预测
我们将使用一组简化的预测器。数字滤波器 FATL, SATL, RFTL, RSTL 将扮演这个角色。它们在 V. Kravchuk 的 "跟随趋势和市场周期的新自适应方法" 一文中有详细描述, 其可在本文附件中找到 (参见 "技术分析新工具及其解释" 章节)。在这里我将列举它们。
- FATL (快速自适应趋势线);
- SATL (慢速自适应趋势线);
- RFTL (引用快速趋势线);
- RSTL (引用慢速趋势线).
FATS 和 SALT 的变化率可使用 FILM (快速趋势线动量) 和 STLM (慢速趋势线动量) 指标进行监控。
我们需要的技术工具当中有两个振荡器 - 指数 RBCI 和 PCCI。RBCI (范围界限通道指数) 指数是通道带宽限定指数, 其值根据通道滤波器的均值计算得出。滤波器可以去除低频趋势和低频噪声。PCCI (完美商品通道指数) 指数是完美的商品通道指数。
计算数字滤波器 FATL, SATL, RFTL, RSTL 的函数如下:
#-----DigFiltr------------------------- DigFiltr <- function(X, type = 1){ # X - vector require(rowr) fatl <- c( +0.4360409450, +0.3658689069, +0.2460452079, +0.1104506886, -0.0054034585, -0.0760367731, -0.0933058722, -0.0670110374, -0.0190795053, +0.0259609206, +0.0502044896, +0.0477818607, +0.0249252327, -0.0047706151, -0.0272432537, -0.0338917071, -0.0244141482, -0.0055774838, +0.0128149838, +0.0226522218, +0.0208778257, +0.0100299086, -0.0036771622, -0.0136744850, -0.0160483392, -0.0108597376, -0.0016060704, +0.0069480557, +0.0110573605, +0.0095711419, +0.0040444064, -0.0023824623, -0.0067093714, -0.0072003400, -0.0047717710, 0.0005541115, 0.0007860160, 0.0130129076, 0.0040364019 ) rftl <- c(-0.0025097319, +0.0513007762 , +0.1142800493 , +0.1699342860 , +0.2025269304 , +0.2025269304, +0.1699342860 , +0.1142800493 , +0.0513007762 , -0.0025097319 , -0.0353166244, -0.0433375629 , -0.0311244617 , -0.0088618137 , +0.0120580088 , +0.0233183633, +0.0221931304 , +0.0115769653 , -0.0022157966 , -0.0126536111 , -0.0157416029, -0.0113395830 , -0.0025905610 , +0.0059521459 , +0.0105212252 , +0.0096970755, +0.0046585685 , -0.0017079230 , -0.0063513565 , -0.0074539350 , -0.0050439973, -0.0007459678 , +0.0032271474 , +0.0051357867 , +0.0044454862 , +0.0018784961, -0.0011065767 , -0.0031162862 , -0.0033443253 , -0.0022163335 , +0.0002573669, +0.0003650790 , +0.0060440751 , +0.0018747783) satl <- c(+0.0982862174, +0.0975682269 , +0.0961401078 , +0.0940230544, +0.0912437090 , +0.0878391006, +0.0838544303 , +0.0793406350 ,+0.0743569346 ,+0.0689666682 , +0.0632381578 ,+0.0572428925 , +0.0510534242,+0.0447468229, +0.0383959950, +0.0320735368, +0.0258537721 ,+0.0198005183 , +0.0139807863,+0.0084512448, +0.0032639979, -0.0015350359, -0.0059060082 ,-0.0098190256 , -0.0132507215, -0.0161875265, -0.0186164872, -0.0205446727, -0.0219739146 ,-0.0229204861 , -0.0234080863,-0.0234566315, -0.0231017777, -0.0223796900, -0.0213300463 ,-0.0199924534 , -0.0184126992,-0.0166377699, -0.0147139428, -0.0126796776, -0.0105938331 ,-0.0084736770 , -0.0063841850,-0.0043466731, -0.0023956944, -0.0005535180, +0.0011421469 ,+0.0026845693 , +0.0040471369,+0.0052380201, +0.0062194591, +0.0070340085, +0.0076266453 ,+0.0080376628 , +0.0083037666,+0.0083694798, +0.0082901022, +0.0080741359, +0.0077543820 ,+0.0073260526 , +0.0068163569,+0.0062325477, +0.0056078229, +0.0049516078, +0.0161380976 ) rstl <- c(-0.0074151919,-0.0060698985,-0.0044979052,-0.0027054278,-0.0007031702,+0.0014951741, +0.0038713513,+0.0064043271,+0.0090702334,+0.0118431116,+0.0146922652,+0.0175884606, +0.0204976517,+0.0233865835,+0.0262218588,+0.0289681736,+0.0315922931,+0.0340614696, +0.0363444061,+0.0384120882,+0.0402373884,+0.0417969735,+0.0430701377,+0.0440399188, +0.0446941124,+0.0450230100,+0.0450230100,+0.0446941124,+0.0440399188,+0.0430701377, +0.0417969735,+0.0402373884,+0.0384120882,+0.0363444061,+0.0340614696,+0.0315922931, +0.0289681736,+0.0262218588,+0.0233865835,+0.0204976517,+0.0175884606,+0.0146922652, +0.0118431116,+0.0090702334,+0.0064043271,+0.0038713513,+0.0014951741,-0.0007031702, -0.0027054278,-0.0044979052,-0.0060698985,-0.0074151919,-0.0085278517,-0.0094111161, -0.0100658241,-0.0104994302,-0.0107227904,-0.0107450280,-0.0105824763,-0.0102517019, -0.0097708805,-0.0091581551,-0.0084345004,-0.0076214397,-0.0067401718,-0.0058083144, -0.0048528295,-0.0038816271,-0.0029244713,-0.0019911267,-0.0010974211,-0.0002535559, +0.0005231953,+0.0012297491,+0.0018539149,+0.0023994354,+0.0028490136,+0.0032221429, +0.0034936183,+0.0036818974,+0.0038037944,+0.0038338964,+0.0037975350,+0.0036986051, +0.0035521320,+0.0033559226,+0.0031224409,+0.0028550092,+0.0025688349,+0.0022682355, +0.0073925495) if (type == 1) {k = fatl} if (type == 2) {k = rftl} if (type == 3) {k = satl} if (type == 4) {k = rstl} n <- length(k) m <- length(X) k <- rev(k) f <- rowr::rollApply(data = X, fun = function(x) {sum(x * k)}, window = n, minimum = n, align = "right") while (length(f) < m) { f <- c(NA,f)} return(f) }
计算完毕后, 将它们添加到数据帧 pr
evalq(pr %<>% mutate(., fatl = DigFiltr(Close, 1), rftl = DigFiltr(Close, 2), satl = DigFiltr(Close, 3), rstl = DigFiltr(Close, 4) ), env)
添加振荡器 FTLM, STLM, RBCI, PCCI, 它们的第一个差值以及数字滤波器的第一个差值至数据帧 pr。
evalq(pr %<>% mutate(., ftlm = fatl - rftl, rbci = fatl - satl, stlm = satl - rstl, pcci = Close - fatl, v.fatl = c(NA, diff(fatl)), v.rftl = c(NA, diff(rftl)), v.satl = c(NA, diff(satl)), v.rstl = c(NA, diff(rstl)*10) ), env) evalq(pr %<>% mutate(., v.ftlm = c(NA, diff(ftlm)), v.stlm = c(NA, diff(stlm)), v.rbci = c(NA, diff(rbci)), v.pcci = c(NA, diff(pcci)) ), env)
1.3. 目标变量
ZigZag() 将用作生成目标变量的指标。
函数的计算需要接收时间序列和两个参数: 最小弯曲长度 (int 或 double) 和计算的价格类型 (收盘价, 中间价, 典型价, 加权(最高价, 最低价))。
#------ZZ----------------------------------- par <- c(25, 5) ZZ <- function(x, par) { # x - vector require(TTR) require(magrittr) ch = par[1] mode = par[2] if (ch > 1) ch <- ch/(10 ^ (Dig - 1)) switch(mode, xx <- x$Close, xx <- x$Med, xx <- x$Typ, xx <- x$Wd, xx <- x %>% select(High,Low)) zz <- ZigZag(xx, change = ch, percent = F, retrace = F, lastExtreme = T) n <- 1:length(zz) for (i in n) { if (is.na(zz[i])) zz[i] = zz[i - 1]} return(zz) }
计算 ZigZag, 第一个差值, 第一个差值的符号, 并将它们添加到数据框 pr:
evalq(pr %<>% cbind(., zigz = ZZ(., par = par)), env) evalq(pr %<>% cbind(., dz = diff(pr$zigz) %>% c(NA, .)), env) evalq(pr %<>% cbind(., sig = sign(pr$dz)), env)
1.4.初始数据集合
我们来总结一下我们应得的计算结果是什么数据。
我们收到来自终端的 OHLCV 向量, 并在 EURJPY 的 M15 时间帧柱线开始处的临时标记。这些数据已在 pr 数据帧里形成。变量 FATL, SATL, RFTL, RSTL, FTLM, STLM, RBCI, PCCI 和它们的第一个差值已被添加到此数据帧内。ZigZag 带有 25 点(4 位小数) 的最小杠杆, 其第一个差值和第一个差值 (-1,1) 的符号将被用作信号, 也被添加到数据帧中。
所有这些数据都不会加载到全局环境中, 而是加载到新的子环境 env 中, 所有计算将在其内执行。这样划分将允许在计算期间使用来自不同符号或时间帧的数据集合而没有名称冲突。
总数据帧 pr 的结构如下所示。可以轻松地从中提取以下计算所需的变量。
str(env$pr) 'data.frame': 8000 obs. of 30 variables: $ Data : POSIXct, format: "2017-01-10 11:00:00" ... $ Open : num 123 123 123 123 123 ... $ High : num 123 123 123 123 123 ... $ Low : num 123 123 123 123 123 ... $ Close : num 123 123 123 123 123 ... $ Vol : num 3830 3360 3220 3241 3071 ... $ Med : num 123 123 123 123 123 ... $ Typ : num 123 123 123 123 123 ... $ Wg : num 123 123 123 123 123 ... $ dH : num NA 0.031 -0.068 -0.119 0.113 ... $ dL : num NA 0.072 -0.113 -0.051 0.038 ... $ fatl : num NA NA NA NA NA NA NA NA NA NA ... $ rftl : num NA NA NA NA NA NA NA NA NA NA ... $ satl : num NA NA NA NA NA NA NA NA NA NA ... $ rstl : num NA NA NA NA NA NA NA NA NA NA ... $ ftlm : num NA NA NA NA NA NA NA NA NA NA ... $ rbci : num NA NA NA NA NA NA NA NA NA NA ... $ stlm : num NA NA NA NA NA NA NA NA NA NA ... $ pcci : num NA NA NA NA NA NA NA NA NA NA ... $ v.fatl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rftl: num NA NA NA NA NA NA NA NA NA NA ... $ v.satl: num NA NA NA NA NA NA NA NA NA NA ... $ v.rstl: num NA NA NA NA NA NA NA NA NA NA ... $ v.ftlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.stlm: num NA NA NA NA NA NA NA NA NA NA ... $ v.rbci: num NA NA NA NA NA NA NA NA NA NA ... $ v.pcci: num NA NA NA NA NA NA NA NA NA NA ... $ zigz : num 123 123 123 123 123 ... $ dz : num NA -0.0162 -0.0162 -0.0162 -0.0162 ... $ sig : num NA -1 -1 -1 -1 -1 -1 -1 -1 -1 ...
从 dataSet 数据帧中选择先前计算的所有预测器。将目标变量 sig 转换为一个因子, 并向前移动一根柱线 (将来方向)。
evalq(dataSet <- pr %>% tbl_df() %>%
dplyr::select(Data, ftlm, stlm, rbci, pcci,
v.fatl, v.satl, v.rftl, v.rstl,
v.ftlm, v.stlm, v.rbci, v.pcci, sig) %>%
dplyr::filter(., sig != 0) %>%
mutate(., Class = factor(sig, ordered = F) %>%
dplyr::lead()) %>%
dplyr::select(-sig),
env)
可视化数据分析
使用 ggplot2 软件包绘制 OHLC 图表。取最后两天的数据, 并用柱线绘制报价图表。
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + labs(title = "EURJPY Candlestick Chart", y = "Close Price", x = "") + theme_tq(), env)
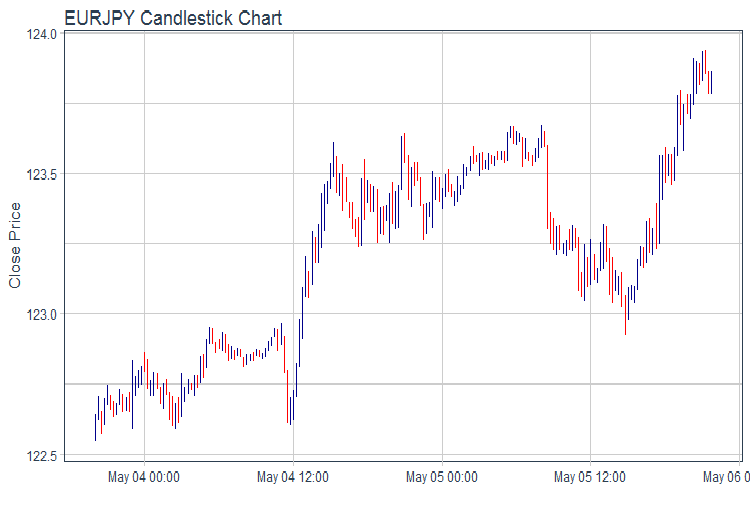
图例.1. 报价图表
绘制 FATL, SATL, RFTL, RSTL 和 ZZ:图表
evalq(pr %>% tail(., 200) %>% ggplot(aes(x = Data, y = Close)) + geom_candlestick(aes(open = Open, high = High, low = Low, close = Close)) + geom_line(aes(Data, fatl), color = "steelblue", size = 1) + geom_line(aes(Data, rftl), color = "red", size = 1) + geom_line(aes(Data, satl), color = "gold", size = 1) + geom_line(aes(Data, rstl), color = "green", size = 1) + geom_line(aes(Data, zigz), color = "black", size = 1) + labs(title = "EURJPY Candlestick Chart", subtitle = "Combining Chart Geoms", y = "Close Price", x = "") + theme_tq(), env)
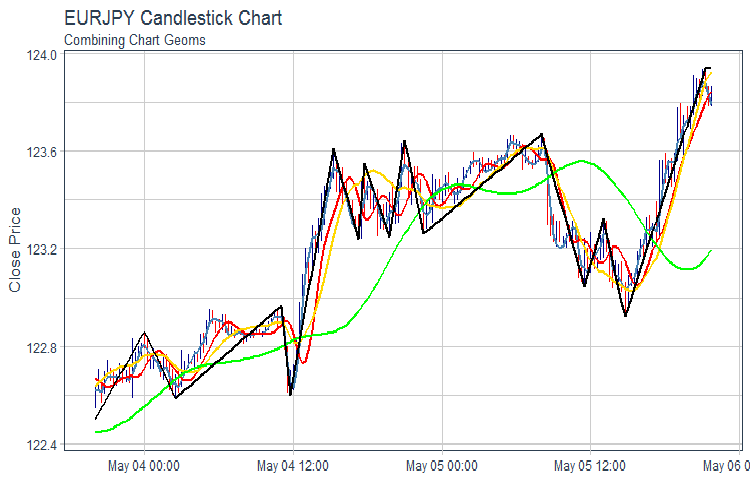
图例.2. FATL, SATL, RFTL, RSTL 和 ZZ
将振荡器划分为三组, 以便更方便的呈现。
require(dygraphs) evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, ftlm, stlm, rbci, pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator base") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "blue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
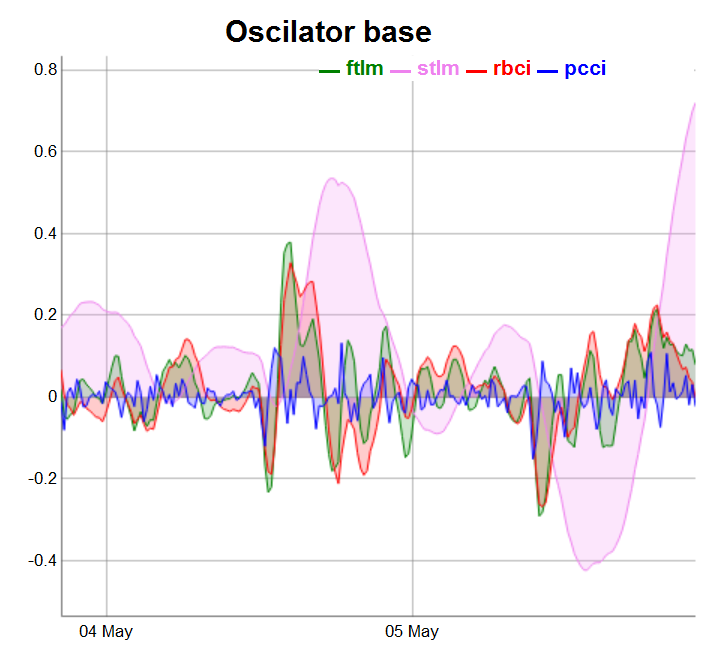
图例.3. 基准振荡器
evalq(dataSet %>% tail(., 200) %>% tk_tbl %>% select(Data, v.fatl, v.satl, v.rftl, v.rstl) %>% tk_xts() %>% dygraph(., main = "Oscilator 2") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
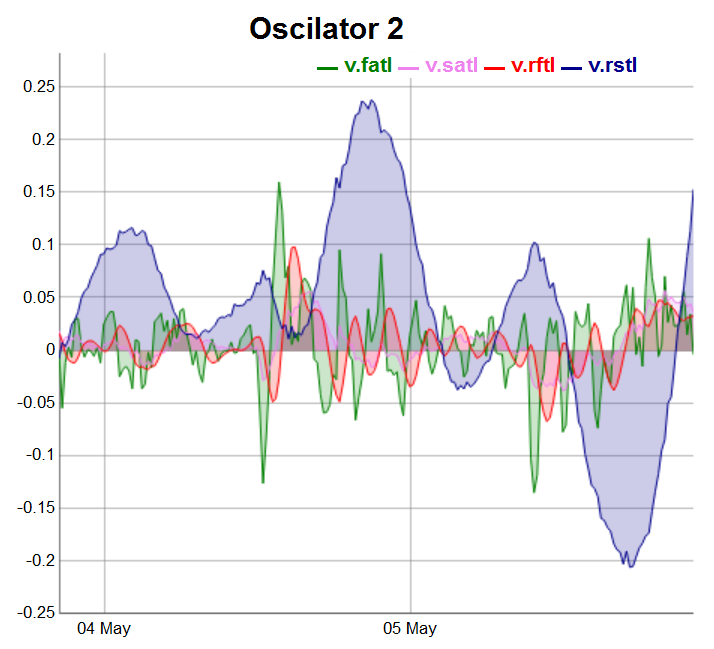
图例.4. 第二组振荡器
第三组振荡器将在最后 100 根柱线绘制:
evalq(dataSet %>% tail(., 100) %>% tk_tbl %>% select(Data, v.ftlm, v.stlm, v.rbci, v.pcci) %>% tk_xts() %>% dygraph(., main = "Oscilator 3") %>% dyOptions(., fillGraph = TRUE, fillAlpha = 0.2, drawGapEdgePoints = TRUE, colors = c("green", "violet", "red", "darkblue"), digitsAfterDecimal = Dig) %>% dyLegend(show = "always", hideOnMouseOut = TRUE), env)
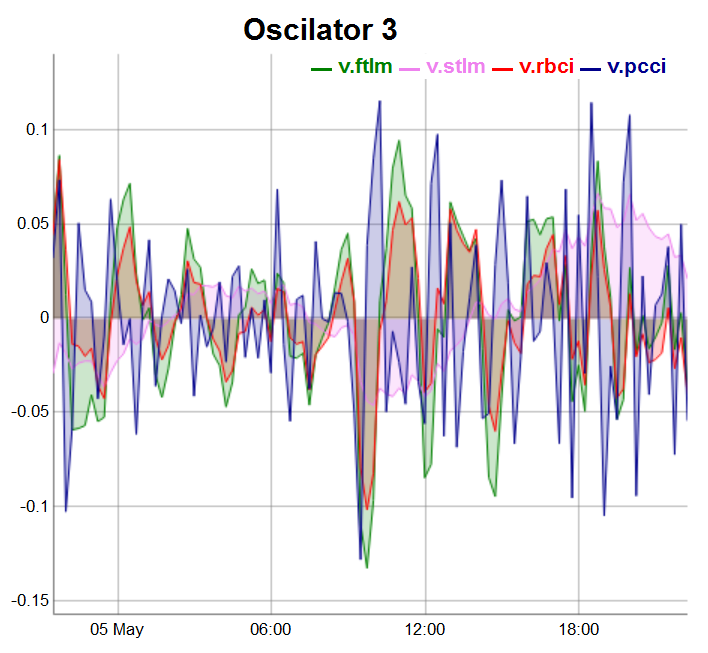
图例.5. 第三组振荡器
2.探索性数据分析, EDA
"没有无谓的统计问题, 只有可疑的统计过程。" — David Cox 爵士
"正确问题的近似答案比一个含糊问题的确切答案更具有价值。" — John Tukey
我们正在使用 EDA 开发所用数据的理解。最简单的方式是使用问题作为研究工具。当我们提出一个问题时, 我们将关注点放在数据的某一部分上。这将有助于决定要使用的图表, 模型和变换。
EDA 本质上是一个创造性的过程。与大多数创意过程类似, 提出一个好问题的关键在于创造更多的问题。在分析开始时, 很难提出基本问题, 因为我们不知道数据集合包含哪些结论。另一方面, 我们提出的每个新问题都突出了数据的一个新视角, 增加了我们发现的机会。我们可以快速移动到数据集合中最有趣的部分, 并通过随后的问题来澄清状况。
没有规定我们在研究数据时应该问哪些问题。话虽如此, 有两种类型的问题是很有用的:
-
我的变量正在经历什么类型的变化？
- 变量之间正在发生什么类型的协变？
我们来定义原则概念。
变化 是在不同测量时变量值变化的趋势。日常生活中有很多变化的例子。如果您测量任何连续变量七次, 您将获得七个不同的值。即使对于常数也是如此, 例如光速。每次测量均会包含略有不同的小误差。相同类型的变量也可以变化。举例, 不同人的眼睛颜色, 或不同时间的电子能量水平。每个变量都有自己的变化特征, 可以示意有趣的信息。了解此信息的最佳方式是可视化变量值的分布。这就是一张示意图解胜过千言万语的案例。
2.1.总体统计
时间序列的总体统计信息使用 table.Stats()::PerformanceAnalytics 函数进行跟踪很方便。
> table.Stats(env$dataSet %>% tk_xts()) Using column `Data` for date_var. ftlm stlm rbci pcci Observations 7955.0000 7908.0000 7934.0000 7960.0000 NAs 42.0000 89.0000 63.0000 37.0000 Minimum -0.7597 -1.0213 -0.9523 -0.5517 Quartile 1 -0.0556 -0.1602 -0.0636 -0.0245 Median -0.0001 0.0062 -0.0016 -0.0001 Arithmetic Mean 0.0007 0.0025 0.0007 0.0001 Geometric Mean -0.0062 NaN -0.0084 -0.0011 Quartile 3 0.0562 0.1539 0.0675 0.0241 Maximum 2.7505 3.0407 2.3872 1.8859 SE Mean 0.0014 0.0033 0.0015 0.0006 LCL Mean (0.95) -0.0020 -0.0040 -0.0022 -0.0010 UCL Mean (0.95) 0.0034 0.0090 0.0035 0.0012 Variance 0.0152 0.0858 0.0172 0.0026 Stdev 0.1231 0.2929 0.1311 0.0506 Skewness 4.2129 1.7842 2.3037 6.4718 Kurtosis 84.6116 16.7471 45.0133 247.4208 v.fatl v.satl v.rftl v.rstl Observations 7959.0000 7933.0000 7954.0000 7907.0000 NAs 38.0000 64.0000 43.0000 90.0000 Minimum -0.3967 -0.0871 -0.1882 -0.4719 Quartile 1 -0.0225 -0.0111 -0.0142 -0.0759 Median -0.0006 0.0003 0.0000 0.0024 Arithmetic Mean 0.0002 0.0002 0.0002 0.0011 Geometric Mean -0.0009 0.0000 -0.0003 -0.0078 Quartile 3 0.0220 0.0110 0.0138 0.0751 Maximum 1.4832 0.3579 0.6513 1.3093 SE Mean 0.0005 0.0002 0.0003 0.0015 LCL Mean (0.95) -0.0009 -0.0003 -0.0005 -0.0020 UCL Mean (0.95) 0.0012 0.0007 0.0009 0.0041 Variance 0.0023 0.0005 0.0009 0.0188 Stdev 0.0483 0.0219 0.0308 0.1372 Skewness 5.2643 2.6705 3.9472 1.5682 Kurtosis 145.8441 36.9378 74.4182 13.5724 v.ftlm v.stlm v.rbci v.pcci Observations 7954.0000 7907.0000 7933.0000 7959.0000 NAs 43.0000 90.0000 64.0000 38.0000 Minimum -0.9500 -0.2055 -0.6361 -1.4732 Quartile 1 -0.0280 -0.0136 -0.0209 -0.0277 Median -0.0002 -0.0001 -0.0004 -0.0002 Arithmetic Mean 0.0000 0.0001 0.0000 0.0000 Geometric Mean -0.0018 -0.0003 -0.0009 NaN Quartile 3 0.0273 0.0143 0.0207 0.0278 Maximum 1.4536 0.3852 1.1254 1.9978 SE Mean 0.0006 0.0003 0.0005 0.0006 LCL Mean (0.95) -0.0012 -0.0005 -0.0009 -0.0013 UCL Mean (0.95) 0.0013 0.0007 0.0009 0.0013 Variance 0.0032 0.0007 0.0018 0.0034 Stdev 0.0561 0.0264 0.0427 0.0579 Skewness 1.2051 0.8513 2.0643 3.0207 Kurtosis 86.2425 23.0651 86.3768 233.1964
此处这张表格告诉我们:
- 所有预测器都有相对较小数量的未定义变量 NA。
- 所有预测器都具有明显的正态偏差。
- 所有预测器均具有较高峰度。
2.2.可视化总体统计
"一张图片的最大价值在于它迫使我们注意到我们从未期待看到的"。— John Tukey
我们来看看 dataSet 中变量之间的变化和协变。由于变量的数量 (14) 不允许我们在一张图表上表示它们, 因此不得不将它们分成三组。
require(GGally) evalq(ggpairs(dataSet, columns = 2:6, mapping = aes(color = Class), title = "DigFilter1"), env)
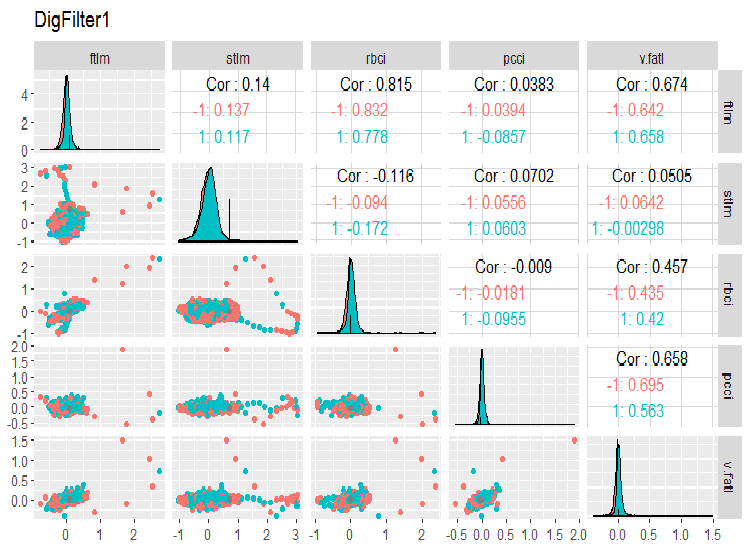
图例. 6. 第一组预测器
evalq(ggpairs(dataSet, columns = 7:10, mapping = aes(color = Class), title = "DigFilter2"), env)
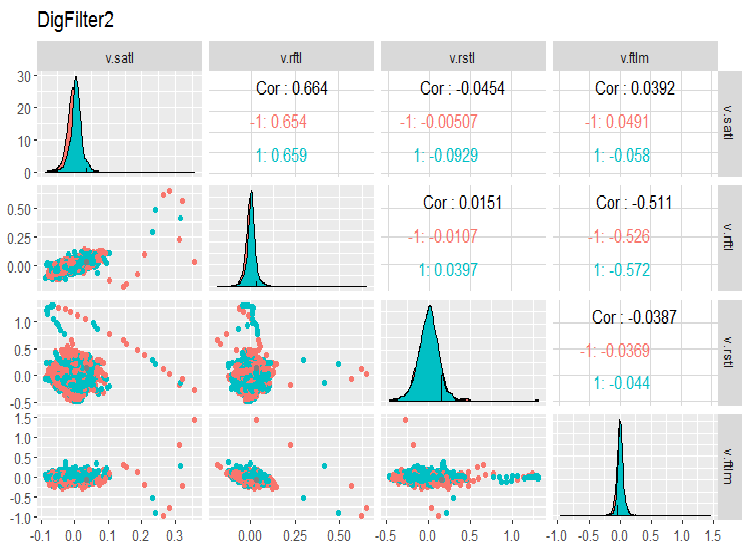
图例. 7. 第二组预测器
evalq(ggpairs(dataSet, columns = 11:14, mapping = aes(color = Class), title = "DigFilter3"), env)
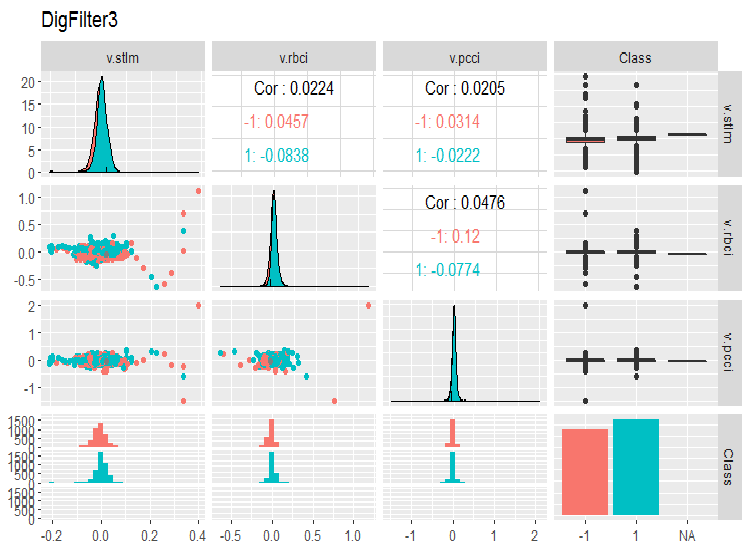
图例. 8. 第三组预测器
这是我们应该在图表上看到的:
- 所有预测器都具有接近正态分布的形状, 尽管有一个非常显著的正态偏差;
- 所有预测器的四分位数范围都很窄 (IQR);
- 所有预测器都有显赫的异常值;
- 目标变量 "Class" 两个级别的示例数量有一个小的差异。
3.准备数据
正常的话, 准备数据有七个阶段:
- “imputation 插补” — 删除或插补缺失/未定义的数据;
- “variance 方差” — 去除零或接近零色散的变量;
- “split 切分” — 将数据集合划分为训练/有效/测试子集;
- “scaling 缩放” — 缩放变量的范围;
- “outliers 异常值” — 去除或插补异常值;
- “sampling 抽样” — 调整分类不平衡;
- “denoise 降噪” — 消除或重新定义噪音;
- “selection 选择” — 选择不相关的预测器。
3.1. 数据清理
准备原始数据的第一阶段是删除或插补数据中未定义的数值和缺口。虽然许多模型允许使用未定义的数据 (NA) 和数据集合中的缺口, 但在开始主要操作之前, 最好清除它们。无论模型如何, 都对完整数据集合进行此操作。
我们的原始数据的总体统计数据表明数据集合包含 NA。这些是在计算数字滤波器时出现的人造 A。它们不会太多, 所以可以删除它们。我们已经获得了 dataSet, 准备好进一步处理。我们来清理一下。
在通常情况下, 清理意味着以下操作:
- 去除零或接近零色散的预测器 (method = c(“zv”, “nzv”));
- 去除高度相关的变量。由用户设定相关系数的阈值 (method = “corr”)。其省缺值为 0.9。这个阶段并非一定需要。这取决于以下变换方法;
- 去除任何类中只有一个唯一值的预测器 (method = “conditionalX”)。
所有这些操作都在上述方法 preProcess()::caret 函数里实现。切分 训练和测试集合之前, 针对 完整的 数据集合进行这些操作。
require(caret)
evalq({preProClean <- preProcess(x = dataSet,method = c("zv", "nzv", "conditionalX", "corr"))
dataSetClean <- predict(preProClean, dataSet %>% na.omit)},
env)
让我们看看是否有任何预测器被删除, 以及清理后我们有什么:
> env$preProClean$method$remove #[1] "v.rbci" > dim(env$dataSetClean) [1] 7906 13 > colnames(env$dataSetClean) [1] "Data" "ftlm" "stlm" "rbci" "pcci" [6] "v.fatl" "v.satl" "v.rftl" "v.rstl" "v.ftlm" [11] "v.stlm" "v.pcci" "Class"
3.2. 识别和处理异常值
数据品质问题, 诸如偏度和异常值之类常常相互关联且相互依赖。这不仅使得数据的初步处理消耗时间, 而且令发现数据集合中的相关性和趋势变得困难。
什么是异常值？
我们同意 异常值 是一个与其它观测距离甚远的观察结果。[2] 中描述了异常值的详细分类, 及其识别和处理方法。
异常值的类型
异常值会导致变量分布和使用此类数据对模型进行培训的结果产生严重扭曲。有许多识别和处理异常值的方法。方法的选择主要取决于我们是否在局部或全局识别异常值。局部异常值只是一个变量的异常值。全局异常值是由矩阵或数据帧定义的多维空间中的异常值。
什么原因导致异常值？
异常值可以按原点划分:
人为
- 数据输入错误。这属于收集、记录和处理数据时发生的错误;
- 实验误差;
- 抽样误差。
自然 误差由变量的性质导致。
异常值有什么影响？
异常值可能会破坏数据分析和统计建模的结果。这增加了误差分散, 降低了测试的统计学功效。如果异常值不是随机分布, 则可以降低正态性。异常值也可以影响回归和色散分析的主要假设, 以及模型的其它统计假设。
我们如何识别局部异常值？
通常可以通过可视化数据来揭示异常值。最简单和最广泛使用的方法之一是 boxplot。我们以 ftlm 预测器为例:
evalq(ggplot(dataSetClean, aes(x = factor(0),
y = ftlm,
color = 'red')) +
geom_boxplot() + xlab("") +
scale_x_discrete(breaks = NULL) +
coord_flip(),
env)
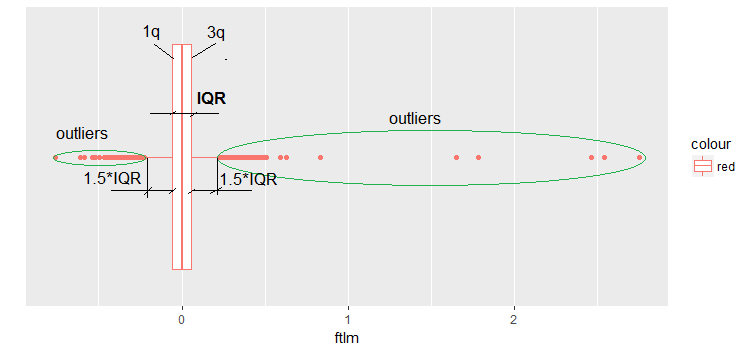
图例.9. Boxplot ftlm
示意图的一些评论:
IQR 是四分位范围, 或第一和第三个四分位数之间的距离。
这样, 我们可以通过几种方式定义异常值:
- 任何小于 -1.5*IQR 且大于 +1.5*IQR 的数值都是异常值。有时, 系数设置为 2 或 3。1.5*IQR 和 3*IQR 之间的所有值称为异常均值, 高于3*IQR 的值称为极端异常值。
- 任何超出第 5 和第 95 百分位的数值都可以被视为异常值,
- 三个或更多 MSD 的点也是异常值。
从现在起, 我们将使用第一种异常值定义 - 通过 IQR。
如何处理异常值？
处理异常值的大多数方法类似于处理 NA 的方法 - 去除观测、变换观测、分段、插补等。
- 去除 异常值。如果异常值作为数据输入错误的结果出现, 或异常值数量非常小的情况下, 我们将剔除异常值。我们也可以裁剪分布的末端以便消除异常值。例如, 我们可以从顶部和底部舍弃 1%。
- 变换 及合并:
- 变量的变换可以排除异常值 (这将在文章的下一部分进行研究);
- 自然对数降低由极值引起的变化 (这也将在文章的下一部分进行详细讨论);
- 离散化也是变换变量的一种方式 (见下一部分);
- 我们也可以使用权重分配来观测 (我们不会在本文中讨论这个)。
插补。我们可以运用插补未定义值的相同方法来插补异常值。因此, 可以使用平均值, 中间值和模数。在插补数值之前, 有必要确定异常值是自然的还是人为的。如果异常值是人为的, 可以插补。
如果样本含有大量异常值, 则应在统计模型中分别进行分析。我们将讨论用于解决异常值的一般方法。它们是 去除 和 插补。
去除异常值
必须删除异常值, 如果它们是由数据输入引起的, 处理数据或异常值的数量非常小 (仅在识别统计变量指标时)。
可以如下提取一个变量 (例如, ftlm) 的数据, 且不会有异常值:
evalq({dataSetClean$ftlm -> x
out.ftlm <- x[!x %in% boxplot.stats(x)$out]},
env)
或:
evalq({dataSetClean$ftlm -> x
out.ftlm1 <- x[x > quantile(x, .25) - 1.5*IQR(x) &
x < quantile(x, .75) + 1.5*IQR(x)]},
env)
它们是否相同？
> evalq(all.equal(out.ftlm, out.ftlm1), env)
[1] TRUE
数据集合中有多少异常值？
> nrow(env$dataSetClean) - length(env$out.ftlm) [1] 402
不含异常值的 ftlm 看起来是这样:
boxplot(env$out.ftlm, main = "ftlm without outliers", boxwex = 0.5)
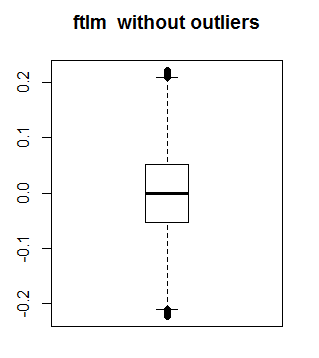
图例. 10. 不含异常值的 ftlm
上述方法不适合于矩阵和数据帧, 因为数据帧中的每个变量可以具有不同数量的异常值。将局部异常值以 NA 替换的方法, 然后采用标准的、适用于这种样本的 NA 处理方法。将局部异常值替换为 NA 的函数如下所示:
#-------remove_outliers------------------------------- remove_outliers <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) y <- x y[x < (qnt[1] - H)] <- NA y[x > (qnt[2] + H)] <- NA y }
我们在所有变量里修改 dataSetClean, 除了 c(Data, Class), 和 NA 的异常值之外。完成后, 让我们看看新集合 x.out: 的分布情况如何变化。
evalq({
dataSetClean %>% select(-c(Data,Class)) %>% as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
remove_outliers(x[ ,i])
} -> x.out
colnames(x.out) <- colnames(x)
},
env)
par(mfrow = c(1, 1))
chart.Boxplot(env$x,
main = "x.out with outliers",
xlab = "")
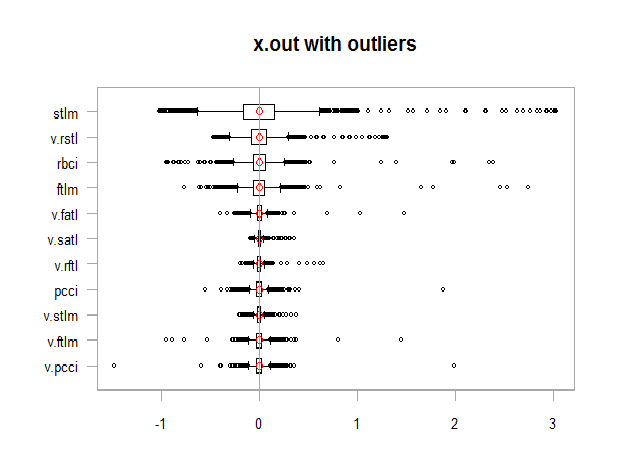
图例. 11. 含有异常值的数据
chart.Boxplot(env$x.out, main = "x.out without outliers", xlab = "")
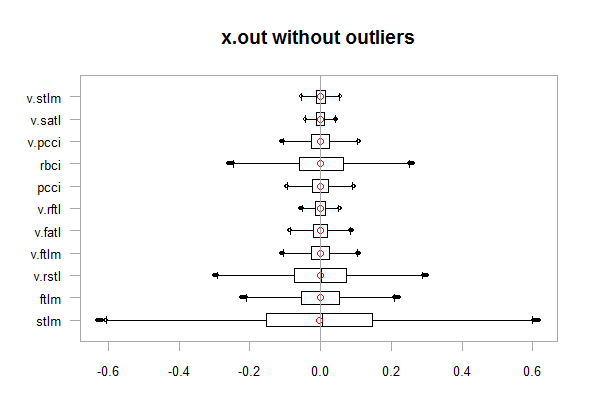
图例.12. 不含异常值的数据
插补 NA替换出现的异常值
插补是使用其它值替换缺失, 不正确或无效的数值。训练模型的输入数据只能包含有效值。您也可以:
- 用 NA 代替平均值, 中间数, 模数 (该集合的统计特征不会改变)
- 将大于 1.5*IQR 的异常值替换为 0.95 百分数, 并将异常值小于 -1.5*IQR 替换为 0.05 百分数。
我们来编写一个函数执行最后一个版本的动作。变换完成后, 我们来看看分布:
#-------capping_outliers-------------------------------
capping_outliers <- function(x, na.rm = TRUE, ...) {
qnt <- quantile(x, probs = c(.25, .75),
na.rm = na.rm, ...)
caps <- quantile(x, probs = c(.05, .95),
na.rm = na.rm, ...)
H <- 1.5 * IQR(x, na.rm = na.rm)
y <- x
y[x < (qnt[1] - H)] <- caps[1]
y[x > (qnt[2] + H)] <- caps[2]
y
}
evalq({dataSetClean %>% select(-c(Data,Class)) %>%
as.data.frame() -> x
foreach(i = 1:ncol(x), .combine = "cbind") %do% {
capping_outliers(x[ ,i])
} -> x.cap
colnames(x.cap) <- colnames(x)
},
env)
chart.Boxplot(env$x.cap,
main = "x.cap with capping outliers",
xlab = "")
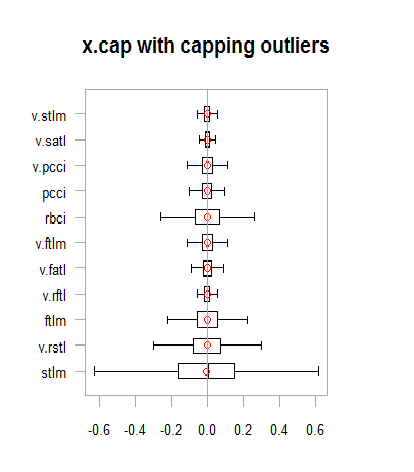
图例.13. 含有插补异常值的数据集合
我们来研究 数据集合 Cap 中的变化和协变。这与 dataSet 相同, 但经过清理并包含插补的局部异常值。变量的数量 (13) 使它们不可能放在同一个图表上, 所以不得不把它们分成两组。
evalq(x.cap %>% tbl_df() %>% cbind(Data = dataSetClean$Data, ., Class = dataSetClean$Class) -> dataSetCap, env) require(GGally) evalq(ggpairs(dataSetCap, columns = 2:7, mapping = aes(color = Class), title = "PredCap1"), env)
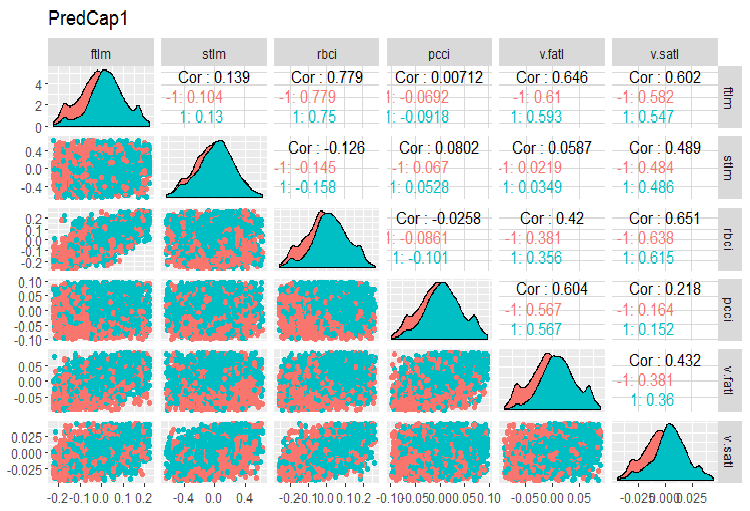
图例.14. 含有插补异常值的数据集合的第一部分的变化和共变。
以及集合的第二部分:
evalq(ggpairs(dataSetCap, columns = 8:13, mapping = aes(color = Class), title = "PredCap2"), env)
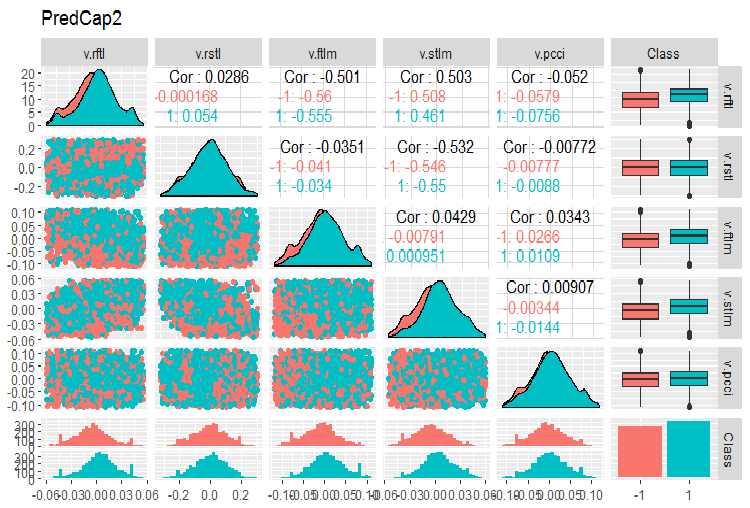
图例.15. 含有插补异常值的数据集合的第二部分的变化和共变。
如何识别全局异常值？
二维或多维异常值通常使用冲突或邻近指数来识别。用各种距离识别全局异常值。可以使用像 DMwR, mvoutliers, Rlof 这样的软件包来完成。全局异常值用 LOF (局部异常值因子) 进行评估。计算并比较含有异常值的集合 x以及含有插补异常值 x.cap 的 LOF。
##------DMwR2------------------- require(DMwR2) evalq(lof.x <- lofactor(x,10), env) evalq(lof.x.cap <- lofactor(x.cap,10), env) par(mfrow = c(1, 3)) boxplot(env$lof.x, main = "lof.x", boxwex = 0.5) boxplot(env$lof.x.cap, main = "lof.x.cap", boxwex = 0.5) hist(env$lof.x.cap, breaks = 20) par(mfrow = c(1, 1))
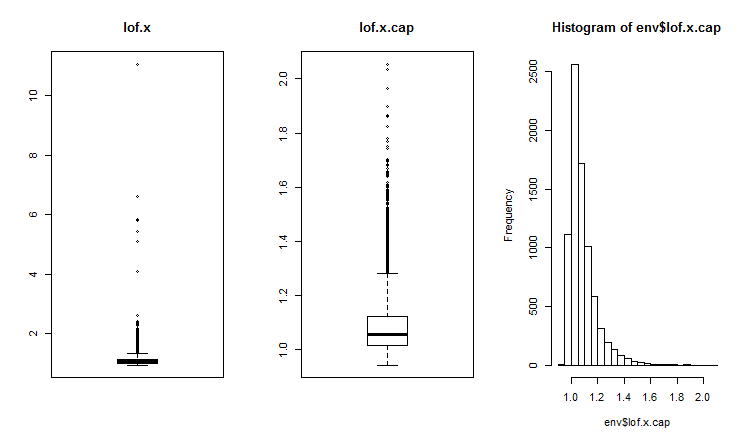
图例.16. 含有异常值的数据集合的全局异常因子和带有插补异常值的数据集合
lof() 函数已在 Rlof 软件包里实现。它使用最近的邻居 k 查找矩阵数据的局部异常因子 [3]。局部异常因子 (LOF) 属于为每个观测值计算出的异常值的概率。基于这个概率, 用户决定观测值是否为异常值。
LOF 会考虑到局部密度, 以便识别观测值是否为异常值。这是使用另一种数据结构和距离计算函数来更有效地实现 LOF, 并与 "dprep" 软件包中提供的 lofactor() 函数进行比较。它支持同时计算数个 k 值, 以及含标准欧几里德在内的各种距离测量。计算在处理器的几个核心上同时完成。我们使用计算距离的 "minkowski" 方法计算两个相同集合 (x 和 x.cap) 比邻 5, 6, 7, 8, 9 和 10 的 lofactor。我们来绘制这些 lofactors 的直方图。
require(Rlof) evalq(Rlof.x <- lof(x, c(5:10), cores = 2, method = 'minkowski'), env) evalq(Rlof.x.cap <- lof(x.cap, c(5:10), cores = 2, method = 'minkowski'), env) par(mfrow = c(2, 3)) hist(env$Rlof.x.cap[ ,6], breaks = 20) hist(env$Rlof.x.cap[ ,5], breaks = 20) hist(env$Rlof.x.cap[ ,4], breaks = 20) hist(env$Rlof.x.cap[ ,3], breaks = 20) hist(env$Rlof.x.cap[ ,2], breaks = 20) hist(env$Rlof.x.cap[ ,1], breaks = 20) par(mfrow = c(1, 1))
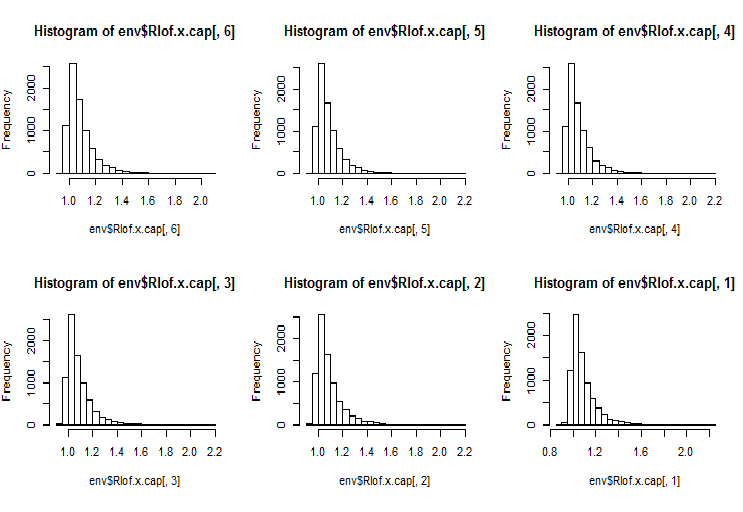
图例.17. k 个比邻的全局异常因子
几乎所有观测值都在范围 lofactor =1.6 之内。超出这个范围:
> sum(env$Rlof.x.cap[ ,6] >= 1.6) [1] 32
对于集合的尺寸来讲, 这个中等偏差值的数量不大。
注意, 为了识别范围限制, 应该使用训练数据集合, 超过的观测值将被视为异常值。测试/验证数据集合的变量数值会使用来自训练集合获得的参数进行处理。这些是什么参数？这些是限制 upper = 1.5*IQR, lower = -1.5*IQR 以及 cap =c(0.05, 0.95) 百分数。我们在以前的计算中用过它们。如果使用计算异常值范围限制和插补的其它方法, 则必须为训练数据集合定义它们, 保存和存储正在处理的验证和测试数据集合。
我们来编写执行初步计算的函数:
#-----prep.outlier-------------- prep.outlier <- function(x, na.rm = TRUE, ...) { qnt <- quantile(x, probs = c(.25, .75), na.rm = na.rm, ...) H <- 1.5 * IQR(x, na.rm = na.rm) caps <- quantile(x, probs = c(.05, .95), na.rm = na.rm, ...) list(lower = qnt[1] - H, upper = qnt[2] + H, med = median(x), cap1 = caps[1], cap2 = caps[2]) }
计算识别和插补异常值所需的参数。训练集合的初始长度为首先的 4000 根柱线, 并使用随后的 2000 根柱线作为测试数据集合。
evalq(
{train <- x[1:4000, ]
foreach(i = 1:ncol(train), .combine = "cbind") %do% {
prep.outlier(train[ ,i]) %>% unlist()
} -> pre.outl
colnames(pre.outl) <- colnames(x)
#pre.outl %<>% t()
},
env)
我们来看看结果:
> env$pre.outl ftlm stlm rbci pcci lower.25% -0.2224942912 -0.59629203 -0.253231002 -9.902232e-02 upper.75% 0.2214486206 0.59242529 0.253529797 9.826936e-02 med -0.0001534451 0.00282525 -0.001184966 8.417127e-05 cap1.5% -0.1700418145 -0.40370452 -0.181326658 -6.892085e-02 cap2.95% 0.1676526431 0.39842675 0.183671973 6.853935e-02 v.fatl v.satl v.rftl v.rstl lower.25% -0.0900973332 -4.259328e-02 -0.0558921804 -0.2858430788 upper.75% 0.0888110249 4.178418e-02 0.0555115004 0.2889057397 med -0.0008581219 -2.130064e-05 -0.0001707447 -0.0001721546 cap1.5% -0.0658731640 -2.929586e-02 -0.0427927888 -0.1951978435 cap2.95% 0.0662353821 3.089833e-02 0.0411091859 0.1820803387 v.ftlm v.stlm v.pcci lower.25% -0.1115823754 -5.366875e-02 -0.1115905239 upper.75% 0.1108670403 5.367466e-02 0.1119495436 med -0.0003560178 -6.370034e-05 -0.0003173464 cap1.5% -0.0765431363 -3.686945e-02 -0.0765950814 cap2.95% 0.0789209957 3.614423e-02 0.0770439553
正如我们所见, 第一和第三个四分位数和中位数以及第 5 和第 95 百分位数是为集合中的每个变量定义的。这就是识别和处理异常值所需的一切。
我们需要一个函数使用先前设置的参数处理任何数据集合的异常值。可能的处理方式: 将异常值替换为 NA, 以中位数和第 5/95 百分位数代替异常值。
#---------treatOutlier--------------------------------- treatOutlier <- function(x, impute = TRUE, fill = FALSE, lower, upper, med, cap1, cap2){ if (impute) { x[x < lower] <- cap1 x[x > upper] <- cap2 return(x) } if (!fill) { x[x < lower | x > upper] <- NA return(x) } else { x[x < lower | x > upper] <- med return(x) } }
由于我们已定义了训练集合所需的参数, 我们用第 5/95 百分位数替换训练集合的异常值。然后处理测试数据集合的异常值。比较所获集合的分布, 绘制了三张图表。
#------------
evalq(
{
foreach(i = 1:ncol(train), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = train[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> train.out
colnames(train.out) <- colnames(train)
},
env
)
#-------------
evalq(
{test <- x[4001:6000, ]
foreach(i = 1:ncol(test), .combine = 'cbind') %do% {
stopifnot(exists("pre.outl", envir = env))
lower = pre.outl['lower.25%', i]
upper = pre.outl['upper.75%', i]
med = pre.outl['med', i]
cap1 = pre.outl['cap1.5%', i]
cap2 = pre.outl['cap2.95%', i]
treatOutlier(x = test[ ,i], impute = T, fill = T, lower = lower,
upper = upper, med = med, cap1 = cap1, cap2 = cap2)
} -> test.out
colnames(test.out) <- colnames(test)
},
env
)
#---------------
evalq(boxplot(train, main = "train with outliers"), env)
evalq(boxplot(train.out, main = "train.out without outliers"), env)
evalq(boxplot(test.out, main = "test.out without outliers"), env)
#------------------------
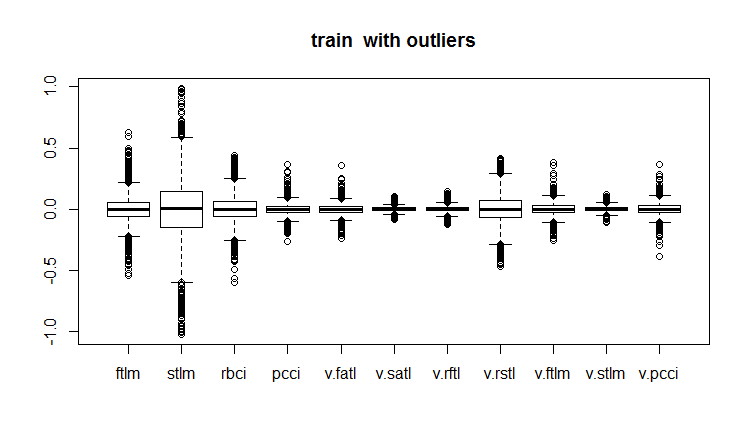
图例.18. 含异常值的训练数据集合
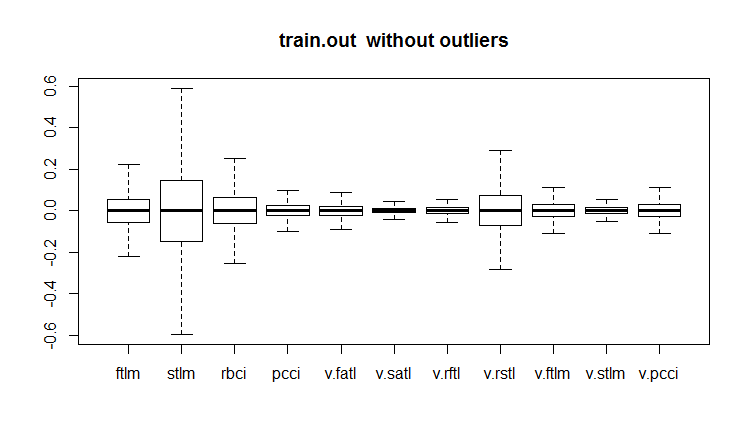
图例.19. 含插补异常值的训练数据集合
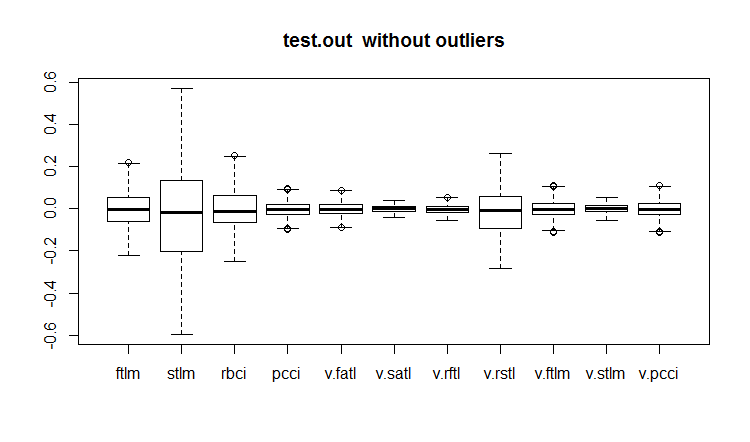
图例.20. 含插补异常值的测试数据集合
并非所有模型都对异常值敏感。举例, 诸如确定树 (DT) 和随机森林 (RF) 模型均对它们不敏感。
当定义和处理异常值时, 其它一些软件包也许是有用的。它们是: “univOutl”, “mvoutlier”, “outlier”, funModeling::prep.outlier()。
3.3. 消除偏态
偏态以分布形式表示。计算变量的偏度系数是评估它的一般方式。通常, 负偏态表示平均值小于中值, 分布保持偏离。正偏态表示平均值大于中值, 分布具有正确的偏度。
如果预测器偏度为 0, 则数据绝对对称。
如果预测器偏度小于 -1 或大于 +1, 则数据明显失真。
如果预测器偏度在 -1 和 -1/2 之间或 +1 和 +1/2 之间, 则数据中度失真。
如果预测器偏度等于 -1/2 和 +1/2, 则数据接近对称。
可以取对数来校正偏度, 并通过使用指数函数来保持偏离。
我们已经确定了偏度, 异常值和其它变化的关系。我们来看看去除和插补异常值之后, 偏度指数如何变化。
evalq({
sk <- skewness(x)
sk.out <- skewness(x.out)
sk.cap <- skewness(x.cap)
},
env)
> env$sk
ftlm stlm rbci pcci v.fatl
Skewness 4.219857 1.785286 2.304655 6.491546 5.274871
v.satl v.rftl v.rstl v.ftlm v.stlm
Skewness 2.677162 3.954098 1.568675 1.207227 0.8516043
v.pcci
Skewness 3.031012
> env$sk.out
ftlm stlm rbci pcci
Skewness -0.04272076 -0.07893945 -0.02460354 0.01485785
v.fatl v.satl v.rftl v.rstl
Skewness 0.00780424 -0.02640635 -0.04663711 -0.04290957
v.ftlm v.stlm v.pcci
Skewness -0.0009597876 0.01997082 0.0007462494
> env$sk.cap
ftlm stlm rbci pcci
Skewness -0.03329392 -0.07911245 -0.02847851 0.01915228
v.fatl v.satl v.rftl v.rstl
Skewness 0.01412182 -0.02617518 -0.03412228 -0.04596505
v.ftlm v.stlm v.pcci
Skewness 0.008181183 0.009661169 0.002252508
r如您所见, 已删除的异常值 x.out 和含插补异常值的 x.cap 集合是绝对对称的, 不需要任何校正。
我们也可以评估峰度。峰度 (Kurtosis) 或峰值系数是随机变量分布的峰值度量。正态分布的峰度为 0。如果分布峰值围绕数学期望呈尖锐状, 则峰度为正, 若峰值是平滑的, 则峰度为负。
require(PerformanceAnalytics)
evalq({
k <- kurtosis(x)
k.out <- kurtosis(x.out)
k.cap <- kurtosis(x.cap)
},
env)
> env$k
ftlm stlm rbci pcci
Excess Kurtosis 84.61177 16.77141 45.01858 247.9795
v.fatl v.satl v.rftl v.rstl
Excess Kurtosis 145.9547 36.99944 74.4307 13.57613
v.ftlm v.stlm v.pcci
Excess Kurtosis 86.36448 23.06635 233.5408
> env$k.out
ftlm stlm rbci
Excess Kurtosis -0.003083449 -0.1668102 -0.1197043
pcci v.fatl v.satl
Excess Kurtosis -0.05113439 -0.02738558 -0.04341552
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.01219999 -0.1316499 -0.0287925
v.stlm v.pcci
Excess Kurtosis -0.1530424 -0.09950709
> env$k.cap
ftlm stlm rbci
Excess Kurtosis -0.2314336 -0.3075185 -0.2982044
pcci v.fatl v.satl
Excess Kurtosis -0.2452504 -0.2389486 -0.2331203
v.rftl v.rstl v.ftlm
Excess Kurtosis -0.2438431 -0.2673441 -0.2180059
v.stlm v.pcci
Excess Kurtosis -0.2763058 -0.2698028
在初始数据集 x 中的分布峰值非常尖锐 (峰度远大于 0), 在含有去除的异常值 x.out 的集合中, 峰值非常接近正常的峰值。含有插补异常值的集合具有更平滑的峰值。两个数据集合都不需要任何校正。
应用
1. DARCH12_1.zip 存档包含文章第一部分的脚本 (dataRaw.R, PrepareData.R, FUNCTION.R) 以及表现 Rstudio 会话的示意图, 其初始数据为 Cotir.RData。将数据加载到 Rstudio 中, 您将会看到所有的脚本并可用之操作。您也可以从 Git/Part_I 下载它们。
2. ACTF.zip 存档包含 V. Kravchuk 的 "跟随趋势和市场周期的新自适应方法" 一文
3. R_intro.zip 存档包含 R 的参考资料。
链接
[1] 数据挖掘中数据预处理的系统方法。COMPUSOFT, 一本国际性高级计算机技术杂志, 2 (11), 2013 年 11 月刊 (卷-II, 发行-XI)
[2] 异常值检测技术。Hans-Peter Kriegel, Peer Kröger, Arthur Zimek. 德国慕尼黑大学 Ludwig-Maximilians
[3] Breuning, M., Kriegel, H., Ng, R.T, 和 Sander. J. (2000). LOF: 识别基于密度的局部异常值。ACM SIGMOD 国际数据管理会议的论文集。
本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/3486
如何进行交易信号的定量分析, 并从中选择最佳交易信号
Finally translated into Chinese, and worthy of careful study of good articles!