Функции активации нейронов при обучении: ключ к быстрой сходимости?

MetaTrader 5 — Примеры | 21 января 2025, 09:14

423

Andrey Dik

Введение

В предыдущей статье мы рассмотрели свойства простой нейронной сети MLP в качестве аппроксиматора (обучение с подкреплением) в составе торгового советника. При этом не уделялось особого внимания свойствам функций активации, а использовалась популярная сигмоида гиперболического тангенса. Также в одной из статей мы обсуждали возможности известного и широко применяемого алгоритма ADAM, но модифицированного мной в независимый популяционный метод глобальной оптимизации ADAMm.

В этой статье мы углубимся в возможности нейронной сети как интерполятора данных (обучение с учителем), акцентируя внимание на свойствах функций активации нейронов. Мы будем использовать встроенный в нейронную сеть алгоритм оптимизации ADAM (так, как это обычно и делается в применении нейронных сетей) и проведем исследования влияния функции активации и её производной на скорость сходимости алгоритма оптимизации.

Представьте себе реку со множеством притоков. В обычном состоянии вода течёт свободно, создавая сложный узор течений и водоворотов. Но что произойдет, если мы начнем строить систему шлюзов и плотин? Мы сможем контролировать поток воды, направлять его в нужное русло и регулировать силу течения. Функция активации в нейронных сетях выполняет аналогичную роль: она решает, какой сигнал пропустить дальше, а какой задержать или ослабить. Без неё нейронная сеть была бы просто набором линейных преобразований.

Функция активации добавляет динамику в работу нейронной сети, позволяя улавливать тонкие нюансы в данных. Например, в задаче распознавания лиц функция активации помогает сети замечать мельчайшие детали, такие как изгиб бровей или форма подбородка. Правильный выбор функции активации влияет на то, как нейронная сеть справляется с различными задачами. Некоторые функции лучше подходят для начальных этапов обучения, обеспечивая чёткие и понятные сигналы. Другие функции позволяют сети улавливать более тонкие закономерности на продвинутых этапах, а третьи — отсекают всё лишнее, оставляя только самое важное.

Если не знать свойства функций активации, то можно столкнуться с проблемами. Нейронная сеть может начать "спотыкаться" на простых задачах или "не замечать" важные детали. Основная задача функций активации — внесение нелинейности в нейронную сеть и нормализация выходных значений.

Цель этой статьи — выявить проблемы, связанные с использованием различных функций активации, и их влияние на точность прохождения нейронной сети через точки примеров (интерполяция) при минимизации ошибки. Мы также выясним, действительно ли функции активации влияют на скорость сходимости, или это свойство используемого алгоритма оптимизации. В качестве эталонного алгоритма мы применим модифицированный популяционный ADAMm, который использует элементы стохастичности, и проведем тесты со встроенным в MLP ADAM (классическое использование). Последний интуитивно должен иметь преимущество, так как имеет прямой доступ к градиенту поверхности фитнес-функции благодаря производной функции активации. В то время как популяционный стохастический ADAMm не имеет доступа к производной и совершенно не представляет себе поверхность задачи оптимизации. Давайте проследим, что из этого получится, и сделаем выводы.

Статья имеет исследовательский характер и повествование идет в порядке проведения эксперимента.

Реализация нейронной сети MLP со встроенным ADAM

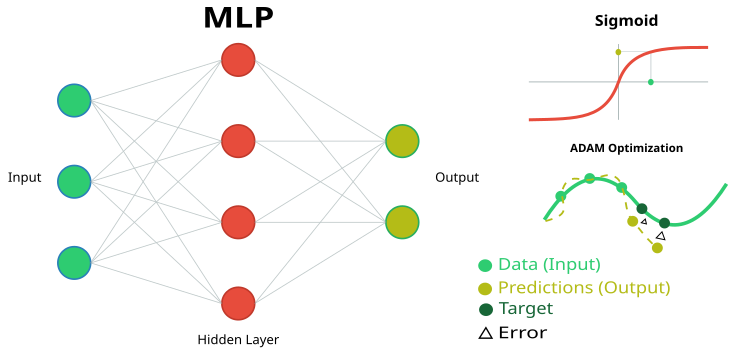
Рисунок 1. Схематичное изображение нейронной сети MLP и ее обучение

Для проведения текущего исследования нам потребуется простой и прозрачный код нейронной сети MLP, без использования специализированных и встроенных в язык MQL5 матричных вычислений. Это позволит нам четко понять, что именно происходит в логике нейронной сети, а также разобраться в том, от чего зависят те или иные результаты.

Реализуем многослойный персептрон (MLP) со встроенным алгоритмом оптимизации ADAM (Adaptive Moment Estimation). Класс и структура представляют собой часть реализации нейронной сети, в которой определены основные компоненты: нейроны, слои нейронов и веса.

1. Класс"C_Neuro" представляет собой нейрон, который является основной единицей в нейронной сети.

C_Neuron() — конструктор, инициализирует значения свойств "m" и "v" нулями. Эти значения используются для алгоритма оптимизации.
out — выходное значение нейрона после применения функции активации.
delta — дельта ошибки, используемая для вычисления градиента в процессе обучения.
bias — значение смещения, добавляется к входам нейрона.
m и v — используются для хранения первых и вторых моментов для смещения, используются методом оптимизации ADAM.

2. Структура "S_NeuronLayer" представляет слой нейронов. "C_Neuron n []" — массив нейронов в слое нейронной сети.

Для хранения весов между нейронами мы используем объектно-ориентированный подход вместо простых двумерных массивов. В основе лежит класс "C_Weight", который хранит не только сам вес соединения, но и параметры для оптимизации - первый и второй моменты, используемые в алгоритме ADAM. Структура данных организована иерархически: "S_WeightsLayer" содержит массив структур "S_WeightsLayerR", которые в свою очередь содержат массивы объектов "C_Weight". Это позволяет легко адресовать любой вес в сети через понятную цепочку индексов.

Например, чтобы обратиться к весу соединения между первым нейроном нулевого слоя и вторым нейроном следующего слоя, мы используем запись: wL [0].nOnL [1].nOnR [2].w. Здесь первый индекс указывает на пару соседних слоев, второй — на нейрон в левом слое, третий — на нейрон в правом слое.

//——————————————————————————————————————————————————————————————————————————————
// Класс нейрона
class C_Neuron
{
  public:
  C_Neuron ()
  {
    m = 0.0;
    v = 0.0;
  }
  double out;   // Выход нейрона после функции активации
  double delta; // Дельта ошибки
  double bias;  // Смещение
  double m;     // Первый момент смещения
  double v;     // Второй момент смещения
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Структура слоя нейронов
struct S_NeuronLayer
{
    C_Neuron n []; // нейроны в слое
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Класс веса
class C_Weight
{
  public:
  C_Weight ()
  {
    w = 0.0;
    m = 0.0;
    v = 0.0;
  }

  double w; // Вес
  double m; // Первый момент
  double v; // Второй момент
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Структура весов для нейронов справа
struct S_WeightsLayerR
{
    C_Weight nOnR [];
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
//Структура весов для нейронов слева
struct S_WeightsLayer
{
    S_WeightsLayerR nOnL [];
};
//——————————————————————————————————————————————————————————————————————————————

Класс "C_MLPa" многослойного персептрона (MLP) реализует основные функции нейронной сети, включая прямой проход и обучение методом обратного распространения ошибки с использованием алгоритма оптимизации ADAM. Давайте разберем, что он умеет делать:

Структура сети:

Сеть состоит из последовательных слоев: входной -> скрытые слои -> выходной слой.
Каждый нейрон в слое соединен со всеми нейронами следующего слоя (полносвязная сеть).

Основные возможности:

Init — метод создание сети с заданной конфигурацией.
ImportWeights и ExportWeights — загрузка и сохранение весов сети.
ForwProp — прямой проход: получение ответа сети на входные данные.
BackProp — обучение сети на основе обратного распространения ошибок.

Параметры обучения (алгоритм ADAM):

alpha (0.001) — насколько быстро сеть учится.
beta1 (0.9) и beta2 (0.999) — параметры, помогающие сети учиться стабильно.
epsilon (1e-8) — маленькое число для защиты от деления на ноль.

Внутренние компоненты:

BackProp — хранит информацию о размере каждого слоя (layersSize).
Содержит все нейроны (nL) и веса между ними (wL).
Ведет подсчет количества весов (wC) и слоев (nLC).
actFunc — использует выбранную функцию активации.

По сути, этот класс — это "мозг" нейронной сети, который умеет принимать входные данные, обрабатывать их через систему нейронов и весов, выдавать результат и учиться на своих ошибках, постепенно улучшая точность своих предсказаний.

//+----------------------------------------------------------------------------+
//| Класс многослойного персептрона (MLP)                                      |
//| Реализует прямой проход по полносвязной нейронной сети и обучение методом  |
//| обратного распространения ошибки алгоритмом оптимизации ADAM               |
//| Архитектура: Lin -> L1 -> L2 -> ... Ln -> Lout                             |
//+----------------------------------------------------------------------------+
class C_MLPa
{
  public: //--------------------------------------------------------------------
  ~C_MLPa ()
  {
    delete actFunc;
  }
  C_MLPa ()
  {
    alpha   = 0.001;   // Скорость обучения
    beta1   = 0.9;     // Коэффициент затухания для первого момента
    beta2   = 0.999;   // Коэффициент затухания для второго момента
    epsilon = 1e-8;    // Малая константа для численной стабильности
  }

  // Инициализация сети с заданной конфигурацией, Возвращает общее количество весов в сети или 0 в случае ошибки
  int    Init          (int &layerConfig [], int actFuncType, int seed);
  bool   ImportWeights (double &weights []);  // Импорт весов
  bool   ExportWeights (double &weights []);  // Экспорт весов

  // Прямой проход по сети
  void   ForwProp (double &inLayer  [],  // входные значения
                   double &outLayer []); // значения выходного слоя

  // Обратное распространение ошибки с оптимизацией алгоритмом ADAM
  void   BackProp (double &errors []);

  // Получить общее количество весов в сети
  int    GetWcount () { return wC; }

  // Параметры оптимизации ADAM
  double alpha;          // Скорость обучения
  double beta1;          // Коэффициент затухания для первого момента
  double beta2;          // Коэффициент затухания для второго момента
  double epsilon;        // Малая константа для численной стабильности

  int layersSize    [];  // Размер каждого слоя (количество нейронов)
  S_NeuronLayer  nL [];  // Слои нейронов,                    пример обращения: nLayers [].n [].a
  S_WeightsLayer wL [];  // Слои весов между слоями нейронов, пример обращения: wLayers [].nOnLeft [].nOnRight [].w

  private: //-------------------------------------------------------------------
  int            wC;       // Общее количество весов в сети (включая смещения)
  int            nLC;      // Общее количество слоев нейронов (включая входной и выходной)
  int            wLC;      // Общее количество слоев весов (между слоями нейронов)
  int            t;        // Счетчик итераций
  C_Base_ActFunc *actFunc; // Функции активации и их производные
};
//——————————————————————————————————————————————————————————————————————————————

Метод "Init" инициализирует структуру многослойного персептрона, устанавливая количество нейронов в каждом слое, выбирая функцию активации и генерируя начальные веса для нейронов. Он проверяет корректность конфигурации сети и возвращает общее количество необходимых весов или 0 в случае ошибки.

Параметры:

layerConfig [] — массив, содержащий количество нейронов в каждом слое сети.
actFuncType — тип функции активации, которая использоваться в нейронной сети (например, сигмоидная и т.д.).
seed — зерно, инициализирующее число для генератора случайных чисел, что позволяет получать воспроизводимые результаты при инициализации весов.

Логика работы:

Метод определяет количество слоев на основе переданного массива"layerConfig".
Проверяет, что количество слоев не меньше 2, и что каждый слой содержит положительное количество нейронов. В случае ошибки — выводит сообщение и завершает выполнение.
Копирует размеры слоев в массив "layersSize" и инициализирует массивы для хранения нейронов и весов.
Вычисляет общее количество весов, необходимых для соединения нейронов между слоями.
Инициализирует веса с использованием метода Xavier, что, теоретически, помогает избежать проблем с затуханием или взрывом градиентов.
В зависимости от переданного типа функции активации создает соответствующий объект функции активации.
Инициализирует счетчик итераций нулем, используется в алгоритме ADAM.

//+----------------------------------------------------------------------------+
//| Инициализация сети                                                         |
//| layerConfig - массив с количеством нейронов в каждом слое                  |
//| Возвращает общее количество необходимых весов или 0 при ошибке             |
//+----------------------------------------------------------------------------+
int C_MLPa::Init (int &layerConfig [], int actFuncType, int seed)
{
  nLC = ArraySize (layerConfig);

  if (nLC < 2)
  {
    Print ("Ошибка конфигурации сети! Меньше 2 слоев!");
    return 0;
  }

  // Проверка конфигурации
  for (int i = 0; i < nLC; i++)
  {
    if (layerConfig [i] <= 0)
    {
      Print ("Ошибка конфигурации сети! Слой №" + string (i + 1) + " содержит 0 нейронов!");
      return 0;
    }
  }

  wLC = nLC - 1;
  ArrayCopy (layersSize, layerConfig, 0, 0, WHOLE_ARRAY);

  // Инициализация слоев нейронов
  ArrayResize (nL, nLC);
  for (int i = 0; i < nLC; i++)
  {
    ArrayResize (nL [i].n, layersSize [i]);
  }

  // Инициализация слоев весов
  ArrayResize (wL, wLC);
  for (int w = 0; w < wLC; w++)
  {
    ArrayResize (wL [w].nOnL, layersSize [w]);
    for (int n = 0; n < layersSize [w]; n++)
    {
      ArrayResize (wL [w].nOnL [n].nOnR, layersSize [w + 1]);
    }
  }

  // Подсчет общего количества весов
  wC = 0;
  for (int i = 0; i < nLC - 1; i++) wC += layersSize [i] * layersSize [i + 1] + layersSize [i + 1];

  // Инициализация весов
  double weights [];  ArrayResize (weights, wC);

  srand (seed);
  
  //Xavier: U(-√(6/(n₁+n₂)), √(6/(n₁+n₂)))
  double n = sqrt (6.0 / (layersSize [0] + layersSize [nLC - 1]));
  for (int i = 0; i < wC; i++)
  {
    weights [i] = (2.0 * n) * (rand () / 32767.0) - n;
  }

  ImportWeights (weights);

  switch (actFuncType)
  {
    case eActACON:      actFunc = new C_ActACON      (); break;
    case eActAlgSigm:   actFunc = new C_ActAlgSigm   (); break;
    case eActBentIdent: actFunc = new C_ActBentIdent (); break;
    case eActRatSigm:   actFunc = new C_ActRatSigm   (); break;
    case eActSiLU:      actFunc = new C_ActSiLU      (); break;
    case eActSoftPlus:  actFunc = new C_ActSoftPlus  (); break;
    default:            actFunc = new C_ActTanh      (); break;
  }

  t = 0;
  return wC;
}
//——————————————————————————————————————————————————————————————————————————————

Давайте далее разберем два метода:"ImportWeights" и "ExportWeights". Эти методы предназначены для импорта и экспорта весов и смещений многослойного персептрона. "ImportWeights" — отвечает за импорт весов и смещений из массива"weights" в структуру нейронной сети.

Сначала метод проверяет, совпадает ли размер переданного массива "weights" с количеством весов, хранящимся в переменной "wC". Если размеры не совпадают, метод возвращает "false", указывая на ошибку.

Переменная "wCNT" используется для отслеживания текущего индекса в массиве "weights".
Циклы по слоям и нейронам:

Внешний цикл проходит по каждому слою, начиная со второго (индекс 1), поскольку первый слой — это входной слой и для него нет ни весов ни смещений.
Внутренний цикл проходит по каждому нейрону в текущем слое.
Для каждого нейрона устанавливается значение смещения "bias" из массива "weights", и счетчик "wCNT" увеличивается.
Вложенный цикл проходит по всем нейронам предыдущего слоя, устанавливая веса, которые соединяют нейроны текущего слоя с нейронами предыдущего слоя.

"ExportWeights" — метод отвечает за экспорт весов и смещений из структуры нейронной сети в массив "weights". Логика метода аналогична логике метода "ImportWeights". Оба эти метода позволяют сохранять веса и смещения во внешней программе по отношению к классу сети, использовать обученную сеть в дальнейшем, а так же позволяют использовать внешние алгоритмы оптимизации, такие как популяционные.

//+----------------------------------------------------------------------------+
//| Импорт весов и смещений сети                                               |
//+----------------------------------------------------------------------------+
bool C_MLPa::ImportWeights (double &weights [])
{
  if (ArraySize (weights) != wC) return false;

  int wCNT = 0;

  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      nL [ln].n [n].bias = weights [wCNT++];

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        wL [ln - 1].nOnL [w].nOnR [n].w = weights [wCNT++];
      }
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

//+----------------------------------------------------------------------------+
//| Экспорт весов и смещений сети                                              |
//+----------------------------------------------------------------------------+
bool C_MLPa::ExportWeights (double &weights [])
{
  ArrayResize (weights, wC);

  int wCNT = 0;

  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      weights [wCNT++] = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        weights [wCNT++] = wL [ln - 1].nOnL [w].nOnR [n].w;
      }
    }
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Метод"ForwProp" (прямой проход) выполняет последовательное вычисление значений всех слоев многослойного персептрона от входного слоя к выходному. Он принимает входные значения, обрабатывает их через скрытые слои и генерирует выходные значения. Параметры:

inLayer [] — массив входных значений для нейронной сети (на рисунке 1 зеленым цветом).
outLayer [] — массив, в который будут записаны значения выходного слоя после обработки (на рисунке 1 желтым цветом).

Метод инициализирует значения активации для нейронов входного слоя, копируя входные значения из массива "inLayer" в соответствующие нейроны.

Обработка скрытых и выходного слоев:

Внешний цикл проходит по всем слоям, начиная со второго (индекс 1), поскольку первый слой — это входной слой.
Внутренний цикл проходит по каждому нейрону текущего слоя.
Для каждого нейрона вычисляется сумма взвешенных входов:

Начинается с добавления смещения (bias) нейрона.
Вложенный цикл проходит по всем нейронам предыдущего слоя, добавляя к "val" произведение выходного значения нейрона предыдущего слоя и соответствующего веса.

После вычисления суммы, к значению "val" применяется функция активации, и результат сохраняется в выход значении нейрона текущего слоя.

После обработки всех слоев, метод копирует выходные значения из последнего слоя (выходного слоя) в массив "outLayer".

//+----------------------------------------------------------------------------+
//| Прямой проход по сети                                                      |
//| Последовательно вычисляет значения всех слоев от входа к выходу            |
//+----------------------------------------------------------------------------+
void C_MLPa::ForwProp (double &inLayer  [],  // входные значения
                       double &outLayer [])  // значения выходного слоя
{
  double val;

  // Установка значений активации входного слоя
  for (int n = 0; n < layersSize [0]; n++)
  {
    nL [0].n [n].out = inLayer [n];
  }

  // Обработка скрытых и выходного слоев
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      val = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w;
      }

      nL [ln].n [n].out = actFunc.Activ (val); // Применение функции активации
    }
  }

  // Установка значений выходного слоя
  for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out;
}
//——————————————————————————————————————————————————————————————————————————————

Метод"BackProp" реализует обратное распространение ошибки в многослойном персептроне. Он обновляет значения весов и смещений всех слоев от выходного к входному, используя алгоритм оптимизации ADAM. Логика работы:

Переменная "t" увеличивается на единицу, чтобы отслеживать количество итераций и используется в формуле логики ADAM.

Вычисление дельт для всех слоев:

Внешний цикл проходит по слоям в обратном порядке, начиная с выходного слоя и заканчивая входным.
Внутренний цикл проходит по нейронам текущего слоя.
Если текущий слой — выходной, дельта (delta) вычисляется как произведение ошибки (errors [nCurr]) и производной функции активации для выходного нейрона.
Для скрытых слоев дельта вычисляется как сумма произведений дельт следующего слоя на соответствующие веса.
После этого дельта корректируется с учетом производной функции активации, и результат сохраняется в nL [ln].n [nCurr].delta.

Обновление смещений с использованием ADAM:

Внешний цикл проходит по всем слоям, начиная со второго.
Для каждого нейрона текущего слоя обновляются моменты смещения "m" и "v" с использованием параметров "beta1" и "beta2".
Затем происходит коррекция моментов смещения "m_hat" и "v_hat".
Наконец, смещение обновляется с использованием скорректированных моментов.

Обновление весов с использованием ADAM:

Внешний цикл проходит по всем весовым слоям.
Внутренние циклы проходят по нейронам текущего слоя и следующего слоя.
Для каждого веса вычисляется градиент, который затем используется для обновления моментов "m" и "v".
После коррекции моментов весов "m_hat" и "v_hat", веса обновляются с использованием скорректированных моментов.

//+----------------------------------------------------------------------------+
//| Обратный проход по сети                                                    |
//| Обновляет значения весов и смещений всех слоев от выхода к входу           |
//+----------------------------------------------------------------------------+
void C_MLPa::BackProp (double &errors [])
{
  t++;  // Увеличение счетчика итераций

  double delta;     // дельта текущего нейрона
  double deltaNext; // дельта нейрона в следующем слое, связанного с текущим нейроном
  double out;       // значение нейрона после применения функции активации
  double deriv;     // производная
  double w;         // вес для связи текущего нейрона с нейроном следующего слоя

  // 1. Вычисление дельт для всех слоев ----------------------------------------
  for (int ln = nLC - 1; ln > 0; ln--)                  // проход по слоям в обратном порядке от выходного к входному
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)        // проход по нейронам текущего слоя
    {
      if (ln == nLC - 1)
      {
        delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out);
      }
      else
      {
        delta = 0.0;

        // Суммируем произведения дельт следующего слоя на соответствующие веса
        for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // проход по нейронам следующего слоя в обычном порядке
        {
          deltaNext = nL [ln + 1].n [nNext].delta;
          w         = wL [ln].nOnL [nCurr].nOnR [nNext].w;
          delta    += deltaNext * w;
        }
      }

      // Дельта с учетом производной сигмоиды
      out   = nL [ln].n [nCurr].out;
      deriv = actFunc.Deriv (out);
      nL [ln].n [nCurr].delta = delta * deriv;
    }
  }

  // 2. Обновление смещений с использованием ADAM ------------------------------
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)
    {
      delta = nL [ln].n [nCurr].delta;

      // Обновление моментов смещения
      nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta;
      nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta;

      // Коррекция моментов смещения
      double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t));
      double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t));

      // Обновление смещения
      nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon);
    }
  }

  // 3. Обновление весов с использованием ADAM ---------------------------------
  for (int lw = 0; lw < wLC; lw++)
  {
    for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++)
    {
      for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++)
      {
        deltaNext = nL [lw + 1].n [nNext].delta;
        out       = nL [lw].n [nCurr].out;
        double gradient = deltaNext * out;

        // Обновление моментов для весов
        wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient;
        wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient;

        // Коррекция моментов весов
        double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t));
        double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t));

        // Обновление веса
        wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon);
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Код стенда для отрисовки функций активаций

Стенд предназначен для тестирования на корректность работы различных функций активации, используемых в нейронных сетях, а так же для отображения в виде графика. Полученные изображения используются далее в статье для визуальной оценки их внешнего вида. Код достаточно простой и описывать его нет особого смысла.

#include <Graphics\Graphic.mqh>
#include <Math\AOs\NeuroNets\MLPa.mqh>

#define SIZE_X 750
#define SIZE_Y 200

//--- input parameters
input E_Act ACT = eActTanh;
input int   CNT = 10000;

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  ObjectDelete (ChartID (), "Test");
  double activ [];
  double deriv [];

  //----------------------------------------------------------------------------
  C_Base_ActFunc *act;
  switch (ACT)
  {
    default:            act = new C_ActTanh      (); break;
    case eActAlgSigm:   act = new C_ActAlgSigm   (); break;
    case eActRatSigm:   act = new C_ActRatSigm   (); break;
    
    case eActSoftPlus:  act = new C_ActSoftPlus  (); break;
    case eActBentIdent: act = new C_ActBentIdent (); break;
    case eActSiLU:      act = new C_ActSiLU      (); break;
    
    case eActACON:      act = new C_ActACON      (); break;
    case eActSnake:     act = new C_ActSnake     (); break;
    case eActSERF:      act = new C_ActSERF      (); break;
  }
  
  //----------------------------------------------------------------------------
  ActFuncTest (act, activ, deriv, CNT, -10, 10);
  
  //----------------------------------------------------------------------------
  CGraphic gr_test;
  gr_test.Create (0, "Test", 0, 0, 20, SIZE_X, SIZE_Y + 20);
  gr_test.YAxis ().Name (act.GetFuncName () + ": Value");
  gr_test.YAxis ().NameSize (13);
  gr_test.HistorySymbolSize (10);
  gr_test.CurveAdd (activ, ColorToARGB (clrRed,  255), CURVE_LINES, "activ");
  gr_test.CurveAdd (deriv, ColorToARGB (clrBlue, 255), CURVE_LINES, "deriv");
  gr_test.CurvePlotAll ();
  gr_test.Redraw (true);
  gr_test.Update ();
  
  //----------------------------------------------------------------------------
  delete act;
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
void ActFuncTest (C_Base_ActFunc &act, double &arrayAct [], double &arrayDer [], int testCount, double min, double max)
{
  Print (act.GetFuncName (), " [", min, "; ", max, "]");
  Print (act.Activ (min), " ", act.Activ (0), " ", act.Activ (max));
  Print (act.Deriv (min), " ", act.Deriv (0), " ", act.Deriv (max));

  ArrayResize (arrayAct, testCount);
  ArrayResize (arrayDer, testCount);
  double x    = 0.0;
  double step = (max - min) / testCount;
  
  for (int i = 0; i < testCount; i++)
  {
    x = min + step * i;

    arrayAct [i] = act.Activ (x);
    arrayDer [i] = act.Deriv (x);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Код классов функций активаций

Существует множество различных функций активации нейронов, применяемых в разнообразных задачах нейронных сетей. Я постарался выбрать такие функции, которые включают как широко известный гиперболический тангенс, так и менее известные, как функция активации Змея (Snake), при этом исключил из рассмотрения очень похожие по внешнему виду и свойствам функции. Условно их можно разделить на три группы:

Сигмоидные функции,
Нелинейные переключатели,
Периодического вида функции.

Реализуем базовый класс "C_Base_ActFunc" для функций активации нейронов. Он содержит две виртуальные функции: "Activ" для вычисления активации и "Deriv" для вычисления производной. Метод "GetFuncName()" возвращает имя функции активации, хранящееся в защищенной ячейке "funcName". Класс предназначен для наследования, чтобы создавать конкретные реализации функций активации. Создав объект функции активации мы сможем ускорить вычисления за счет отсутствия необходимости многочисленного использования "if" и "switch".

//——————————————————————————————————————————————————————————————————————————————
// Базовый класс функции активации нейрона
class C_Base_ActFunc
{
  public:
  virtual double Activ (double inp) = 0; // Виртуальная функция активации
  virtual double Deriv (double inp) = 0; // Виртуальная функция производной
  string         GetFuncName () {return funcName;}
  protected:
  string funcName;
};
//——————————————————————————————————————————————————————————————————————————————

Класс "C_ActTanh" реализует функцию активации гиперболического тангенса и её производную и наследуется от базового класса "C_Base_ActFunc". В конструкторе класса устанавливается имя функции активации в переменной "funcName" как "ActTanh". Метод активации:

Activ (double x) вычисляет значение функции активации гиперболического тангенса по формуле: f(x) = 2 / (1 + exp ( − 2 ⋅ (x)) − 1. Эта формула преобразует входное значение "x" в диапазон от -1 до 1.

Метод производной:

Deriv(double x) вычисляет производную функции активации. Производная гиперболического тангенса выражается как: f′(x) = 1 − (f (x)) ^ 2, где f(x) — это значение функции активации, вычисленное для текущего "x". Производная показывает, насколько быстро функция меняется в зависимости от входного значения.

//——————————————————————————————————————————————————————————————————————————————
// Гиперболический тангенс
class C_ActTanh : public C_Base_ActFunc
{
  public:
  C_ActTanh () {funcName = "ActTanh";}

  double Activ (double x)
  {
    return 2.0 / (1.0 + exp (-2 * (x))) - 1.0;
  }

  double Deriv (double x)
  {
    //1 - (f(x))^2
    double fx = Activ (x);
    return 1.0 - fx * fx;
  }
};
//——————————————————————————————————————————————————————————————————————————————

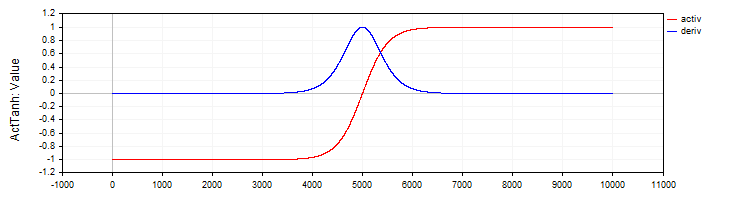
Рисунок 2. Гиперболический тангенс и его производная

Класс "C_ActAlgSigm" аналогично классу "C_ActTanh" реализует алгебраическую сигмоиду как функцию активации с методами для вычисления активации и её производной.

//——————————————————————————————————————————————————————————————————————————————
// Алгебраическая сигмоида
class C_ActAlgSigm : public C_Base_ActFunc
{
  public:
  C_ActAlgSigm () {funcName = "ActAlgSigm";}

  double Activ (double x)
  {
    return x / sqrt (1.0 + x * x);
  }

  double Deriv (double x)
  {
    // (1 / sqrt (1 + x * x))^3
    double d = 1.0 / sqrt (1.0 + x * x);
    return d * d * d;
  }
};
//——————————————————————————————————————————————————————————————————————————————

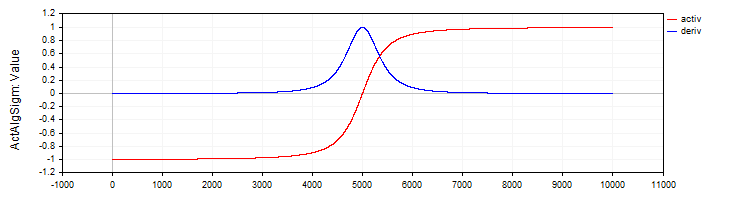
Рисунок 3. Алгебраическая сигмоида и ее производная

Класс "C_ActRatSigm" реализует рациональную сигмоиду с методами активации и производной.

//——————————————————————————————————————————————————————————————————————————————
// Рациональная сигмоида
class C_ActRatSigm : public C_Base_ActFunc
{
  public:
  C_ActRatSigm () {funcName = "ActRatSigm";}

  double Activ (double x)
  {
    return x / (1.0 + fabs (x));
  }

  double Deriv (double x)
  {
    //1 / (1 + abs (x))^2
    double d = 1.0 + fabs (x);
    return 1.0 / (d * d);
  }
};
//——————————————————————————————————————————————————————————————————————————————

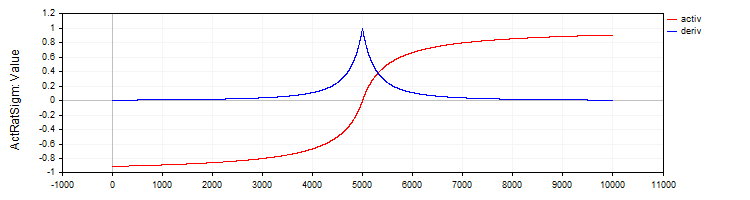
Рисунок 4. Рациональная сигмоида и ее производная

Класс "C_ActSoftPlus" реализует функцию активации "Softplus" и её производную.

//——————————————————————————————————————————————————————————————————————————————
// Softplus
class C_ActSoftPlus : public C_Base_ActFunc
{
  public:
  C_ActSoftPlus () {funcName = "ActSoftPlus";}

  double Activ (double x)
  {
    return log (1.0 + exp (x));
  }

  double Deriv (double x)
  {
    return 1.0 / (1.0 + exp (-x));
  }
};
//——————————————————————————————————————————————————————————————————————————————

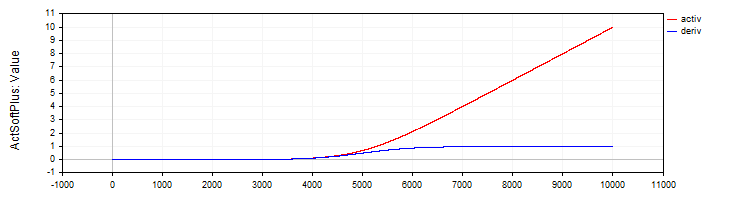
Рисунок 5. Функция "SoftPlus" и ее производная

Класс "C_ActBentIdent" реализует функцию активации "Bent Identity" и её производную.

//——————————————————————————————————————————————————————————————————————————————
// Bent Identity
class C_ActBentIdent : public C_Base_ActFunc
{
  public:
  C_ActBentIdent () {funcName = "ActBentIdent";}

  double Activ (double x)
  {
    return (sqrt (x * x + 1.0) - 1.0) / 2.0 + x;
  }

  double Deriv (double x)
  {
    return x / (2.0 * sqrt (x * x + 1.0)) + 1.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

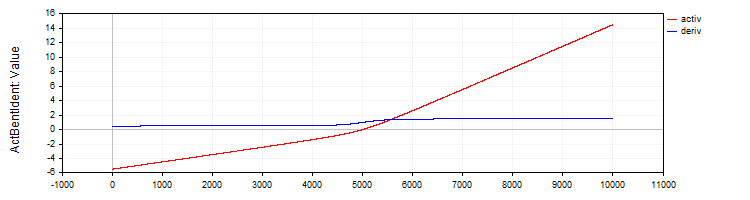
Рисунок 6. Функция "Bent Identity" и ее производная

Класс "C_ActSiLU" предоставляет реализацию функции активации "SiLU" и её производной.

//——————————————————————————————————————————————————————————————————————————————
// SiLU (Swish)
class C_ActSiLU : public C_Base_ActFunc
{
  public:
  C_ActSiLU () {funcName = "ActSiLU";}

  double Activ (double x)
  {
    return x / (1.0 + exp (-x));
  }

  double Deriv (double x)
  {
    if (x == 0.0) return 0.5;

    // f(x) + (f(x)*(1 - f(x)))/ x
    double fx = Activ (x);
    return fx + (fx * (1.0 - fx)) / x;
  }
};
//——————————————————————————————————————————————————————————————————————————————

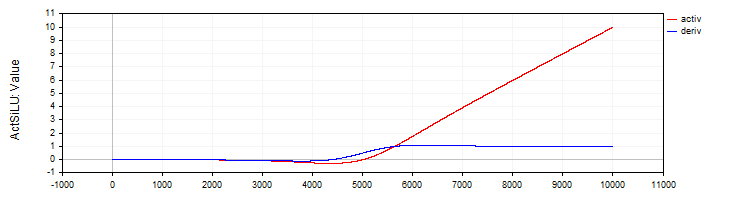
Рисунок 7. Функция "SiLU" и ее производная

Класс "C_ActACON" реализует функцию активации "ACON" и её производную.

//——————————————————————————————————————————————————————————————————————————————
// ACON
class C_ActACON : public C_Base_ActFunc
{
  public:
  C_ActACON () {funcName = "ActACON";}

  double Activ (double x)
  {
    return (x * cos (x) + sin (x)) / (1.0 + fabs (x));
  }

  double Deriv (double x)
  {
    if (x == 0.0) return 2.0;

    //[2 * cos(x) - x * sin(x)] / [|x| + 1] - x * (sin(x) + x * cos(x)) / [|x| * ((|x| + 1)²)]
    double sinX   = sin  (x);
    double cosX   = cos  (x);
    double fabsX  = fabs (x);
    double fabsXp = fabsX + 1.0;

    // Разделяем формулу на две части
    double part1 = (2.0 * cosX - x * sinX) / fabsXp;
    double part2 = -x * (sinX + x * cosX) / (fabsX * fabsXp * fabsXp);
    return part1 + part2;
  }
};
//——————————————————————————————————————————————————————————————————————————————

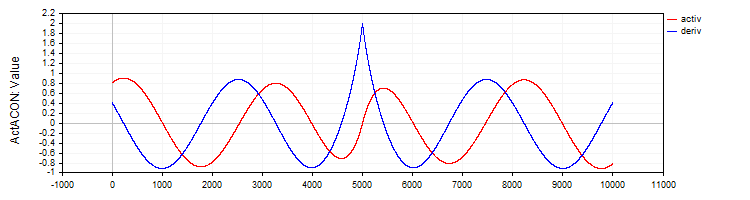
Рисунок 8. Функция "ACON" и ее производная

Класс "C_ActSERF" реализует функцию активации "SERF" и её производную.

//——————————————————————————————————————————————————————————————————————————————
// SERF (Функция сигмоидально-взвешенного экспоненциального выпрямления)
class C_ActSERF : public C_Base_ActFunc
{
  public:
  C_ActSERF ()
  {
    alpha    = 0.5;
    funcName = "ActSERF";
  }

  double Activ (double x)
  {
    double sigmoid = 1.0 / (1.0 + exp (-alpha * x));

    if (x >= 0) return sigmoid * x;
    else return sigmoid * (exp (x) - 1.0);
  }

  double Deriv (double x)
  {
    double sigmoid = 1.0 / (1.0 + exp (-alpha * x));
    double sigmoidDeriv = alpha * sigmoid * (1.0 - sigmoid);
    double e = exp (x);
    if (x >= 0) return sigmoid + x * sigmoidDeriv;
    else return sigmoid * e + (e - 1.0) * sigmoidDeriv;
  }

  private:
  double alpha;
};
//——————————————————————————————————————————————————————————————————————————————

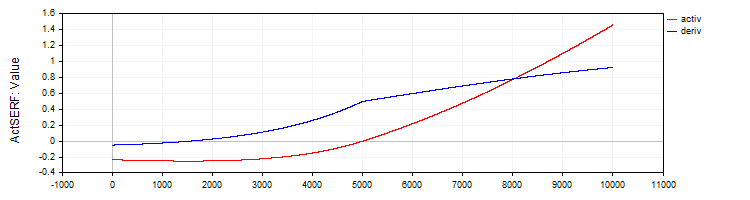
Рисунок 9. Функция "SERF" и ее производная

Класс "C_ActSNAKE" реализует функцию активации "SNAKE" и её производную.

//——————————————————————————————————————————————————————————————————————————————
// Snake (Периодическая активационная функция)
class C_ActSnake : public C_Base_ActFunc
{
  public:
  C_ActSnake ()
  {
    frequency = 1;
    funcName  = "ActSnake";
  }

  double Activ (double x)
  {
    double sinx = sin (frequency * x);
    return x + sinx * sinx;
  }

  double Deriv (double x)
  {
    double fx = frequency * x;
    return 1.0 + 2.0 * sin (fx) * cos (fx) * frequency;
  }

  private:
  double frequency;
};
//——————————————————————————————————————————————————————————————————————————————

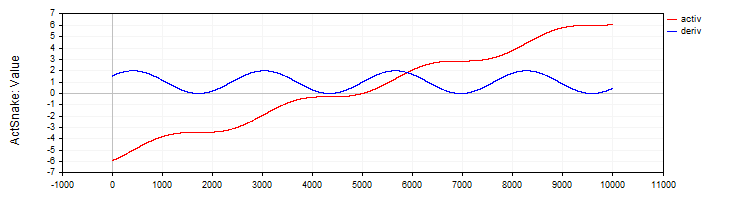
Рисунок 10. Функция "SNAKE" и ее производная

Испытание функций активации

Теперь пришло время рассмотреть, как происходит обучение сети MLP с различными функциями активации. Сложность функции активации для алгоритма оптимизации можно наглядно продемонстрировать на конфигурации MLP 1-1-1, используя всего один пример в обучении (одно значение на вход и одно целевое значение).

На первый взгляд это может показаться неочевидным: почему такая простая задача вызывает интерес? Здесь кроется важный методологический момент: использование единственной точки данных позволяет нам изолировать и исследовать именно сложность самой функции активации и её влияние на процесс оптимизации. Когда мы работаем с большим набором данных, на процесс обучения влияют множество факторов: распределение данных, взаимозависимости между примерами и проявление их влияния при прохождении через функцию активации. Используя только одну точку, мы убираем все эти внешние факторы и можем сосредоточиться на том, насколько сложно алгоритму оптимизации работать именно с конкретной функцией активации.

Дело в том, что нейронная сеть, проходящая через единственную точку интерполируемой функции, может иметь бесчисленное множество вариантов весов. Это может показаться невероятным, но следует из уравнения "in * w + b = out", где in - вход сети, w - вес, b - смещение, out - выход сети для конфигурации 1-1.

Проблем с такой конфигурацией не возникает, однако, они появляются при добавлении еще одного слоя, то есть при конфигурации 1-1-1. В этом случае, даже простейшая задача становится нетривиальной для алгоритма оптимизации, так как пространство поиска решения существенно усложняется: теперь нужно найти правильную комбинацию весов через промежуточный слой с его функцией активации. Именно эта сложность и позволяет нам оценить, насколько эффективно различные алгоритмы оптимизации справляются с настройкой весов при работе с разными функциями активации.

Ниже представлены таблицы с результатами работы алгоритмов ADAM в классической реализации и популяционного ADAMm. Для обоих алгоритмов было выполнено 10'000 итераций, при этом, для популяционного алгоритма учитывалось наличие популяции, а общее количество расчетов нейронной сети оставалось одинаковым. В распечатках указано зерно генератора псевдослучайных чисел (для воспроизведения проблемных вариантов запусков обучения), итерация, на которой был получен наилучший результат, и результат на текущей эпохе, кратной 1000.

Инициализация весов проводилась случайными числами по методу Хавьера для ADAM и случайными числами в диапазоне [-10; 10] для ADAMm. Выполнялись несколько тестов с различными зернами, и выбирались наихудшие результаты. Процесс подбора весов завершался либо по достижению максимального количества итераций, либо при снижении ошибки ниже 0.000001.

Таблица результатов для сигмоидных функций активации:

Tanh	AlgSigm	RatSigm
MLP config: 1\|1\|1, Weights: 4, Activation func: eActTanh, Seed: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Best result iteration: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001	MLP config: 1\|1\|1, Weights: 4, Activation func: eActAlgSigm, Seed: 4 -----Integrated ADAM----- 0: 0.1878131682539310, 0: 0.18781316825393096 0: 0.1878131682539310, 1000: 0.22880505258129305 0: 0.1878131682539310, 2000: 0.2395439537933131 0: 0.1878131682539310, 3000: 0.24376284285887292 0: 0.1878131682539310, 4000: 0.24584964230029535 0: 0.1878131682539310, 5000: 0.2470364071634453 0: 0.1878131682539310, 6000: 0.24777681648987268 0: 0.1878131682539310, 7000: 0.2482702131676117 0: 0.1878131682539310, 8000: 0.24861563983949608 0: 0.1878131682539310, 9000: 0.2488669473265396 Best result iteration: 0, Err: 0.187813 -----Population-based ADAMm----- 0: 0.2481251241755712 1000: 0.0000009070157679 Best result iteration: 1000, Err: 0.000001	MLP config: 1\|1\|1, Weights: 4, Activation func: eActRatSigm, Seed: 4 -----Integrated ADAM----- 0: 0.0354471509280691, 0: 0.03544715092806905 0: 0.0354471509280691, 1000: 0.10064226929576263 0: 0.0354471509280691, 2000: 0.13866170841306655 0: 0.0354471509280691, 3000: 0.16067944018111643 0: 0.0354471509280691, 4000: 0.17502946224977484 0: 0.0354471509280691, 5000: 0.18520767592761297 0: 0.0354471509280691, 6000: 0.19285431843628092 0: 0.0354471509280691, 7000: 0.1988366186290051 0: 0.0354471509280691, 8000: 0.20365853142896836 0: 0.0354471509280691, 9000: 0.20763502064394074 Best result iteration: 0, Err: 0.035447 -----Population-based ADAMm----- 0: 0.1928944265733889 Best result iteration: 688, Err: 0.000000

Таблица результатов для функций активации типа SiLU:

SoftPlus	BentIdent	SiLU
MLP config: 1\|1\|1, Weights: 4, Activation func: eActSoftPlus, Seed: 2 -----Integrated ADAM----- 0: 0.5380138004155748, 0: 0.5380138004155747 0: 0.5380138004155748, 1000: 131.77685264891647 0: 0.5380138004155748, 2000: 1996.1250363225556 0: 0.5380138004155748, 3000: 8050.259717531171 0: 0.5380138004155748, 4000: 20321.169969814575 0: 0.5380138004155748, 5000: 40601.21872791767 0: 0.5380138004155748, 6000: 70655.44591598355 0: 0.5380138004155748, 7000: 112311.81150857621 0: 0.5380138004155748, 8000: 167489.98562842538 0: 0.5380138004155748, 9000: 238207.27978678182 Best result iteration: 0, Err: 0.538014 -----Population-based ADAMm----- 0: 18.4801637203493884 778: 0.0000022070092175 Best result iteration: 1176, Err: 0.000001	MLP config: 1\|1\|1, Weights: 4, Activation func: eActBentIdent, Seed: 4 -----Integrated ADAM----- 0: 15.1221330593320857, 0: 15.122133059332086 0: 15.1221330593320857, 1000: 185.646717568436 0: 15.1221330593320857, 2000: 1003.1026112225994 0: 15.1221330593320857, 3000: 2955.8393027057205 0: 15.1221330593320857, 4000: 6429.902382962495 0: 15.1221330593320857, 5000: 11774.781156010686 0: 15.1221330593320857, 6000: 19342.379583340015 0: 15.1221330593320857, 7000: 29501.355075464813 0: 15.1221330593320857, 8000: 42640.534930000824 0: 15.1221330593320857, 9000: 59168.850722337185 Best result iteration: 0, Err: 15.122133 -----Population-based ADAMm----- 0: 7818.0964949082390376 Best result iteration: 15, Err: 0.000001	MLP config: 1\|1\|1, Weights: 4, Activation func: eActSiLU, Seed: 2 -----Integrated ADAM----- 0: 0.0021199944516222, 0: 0.0021199944516222444 0: 0.0021199944516222, 1000: 4.924850697388685 0: 0.0021199944516222, 2000: 14.827133542234415 0: 0.0021199944516222, 3000: 28.814259008218087 0: 0.0021199944516222, 4000: 45.93517121925276 0: 0.0021199944516222, 5000: 65.82077308420028 0: 0.0021199944516222, 6000: 88.26782602934948 0: 0.0021199944516222, 7000: 113.15535264604428 0: 0.0021199944516222, 8000: 140.41067538093935 0: 0.0021199944516222, 9000: 169.9878269747845 Best result iteration: 0, Err: 0.002120 -----Population-based ADAMm----- 0: 17.2288020548757288 1000: 0.0000030959186317 Best result iteration: 1150, Err: 0.000001

Таблица результатов для периодических функций активации:

ACON	SERF	Snake
MLP config: 1\|1\|1, Weights: 4, Activation func: eActACON, Seed: 3 -----Integrated ADAM----- 0: 0.8183728267492676, 0: 0.8183728267492675 160: 0.5853150801288914, 1000: 1.2003151947973498 2000: 0.0177702331540612, 2000: 0.017770233154061187 3000: 0.0055801976952827, 3000: 0.005580197695282676 4000: 0.0023096724537356, 4000: 0.002309672453735598 5000: 0.0010238849157595, 5000: 0.0010238849157594616 6000: 0.0004581612824611, 6000: 0.0004581612824611273 7000: 0.0002019092359805, 7000: 0.00020190923598049711 8000: 0.0000867118074097, 8000: 0.00008671180740972474 9000: 0.0000361764073840, 9000: 0.00003617640738397845 Best result iteration: 9999, Err: 0.000015 -----Population-based ADAMm----- 0: 1.3784017183806672 Best result iteration: 481, Err: 0.000000	MLP config: 1\|1\|1, Weights: 4, Activation func: eActSERF, Seed: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Best result iteration: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001	MLP config: 1\|1\|1, Weights: 4, Activation func: eActSnake, Seed: 4 -----Integrated ADAM----- 0: 0.2415125490594974, 0: 0.24151254905949734 0: 0.2415125490594974, 1000: 0.24987227299268625 0: 0.2415125490594974, 2000: 0.24999778562849811 0: 0.2415125490594974, 3000: 0.24999995996010888 0: 0.2415125490594974, 4000: 0.2499999992693791 0: 0.2415125490594974, 5000: 0.24999999998663514 0: 0.2415125490594974, 6000: 0.2499999999997553 0: 0.2415125490594974, 7000: 0.24999999999999556 0: 0.2415125490594974, 8000: 0.25 0: 0.2415125490594974, 9000: 0.25 Best result iteration: 0, Err: 0.241513 -----Population-based ADAMm----- 0: 0.2499999999999871 Best result iteration: 883, Err: 0.000001

Теперь можно сделать предварительные выводы о сложности функций активации для классического градиентного ADAM и популяционного ADAMm. Хотя обычный ADAM имеет непосредственную информацию о градиенте функции активации, то есть буквально знает направление наискорейшего спуска, он не справился с такой простой, на первый взгляд, задачей. По результатам самой простой функцией для ADAM оказался ACON, на ней он смог последовательно минимизировать ошибку. А вот функции типа SiLU оказались для него проблемой: на них ошибка не только не уменьшалась, но и стремительно росла. Очевидно, что так как для ADAM не были введены граничные условия весов и смещений, он, выбрав неправильное направление, увеличивал значения весов. Веса свободно разлетались в стороны, ничем не ограниченные и буквально сдуваемые направленным ветром производной функции активации.

Проблема только усугубится, если использовать большее количество нейронов в слоях, ведь каждый нейрон принимает на вход сумму произведений выходов нейронов предыдущего слоя на соответствующий вес. Таким образом, сумма может стать настолько большой, что станет невозможно корректно вычислить экспоненциальную функцию.

Как видим, для популяционного ADAMm не представляет проблемы ни одна из функций активации. Он стабильно сходится на всех из них, и лишь на некоторых количество итераций слегка превысило 1000.

Доработка классов функций активации, MLP и ADAM

Чтобы исправить ситуацию с разлетающимися весами в нейронной сети, внесем изменения в классы функций активации. Это позволит отслеживать границы соответствующих функций и предотвратить накопление большой суммы при ее подаче на нейрон, а так же ограничит значения самих весов и смещений.

Добавим в базовый класс методы "GetBoundUp" и "GetBoundLo", которые предоставляют доступ к границам соответствующих функций активации, позволяя другим классам или функциям получать информацию о допустимых значениях.

Ниже приведен код базового класса и класса гиперболического тангенса, в которые внесены изменения (остальной код остался без изменений). Остальные классы других функций активации выполнены аналогично, с соответствующими им собственными границами.

//——————————————————————————————————————————————————————————————————————————————
// Базовый класс функции активации нейрона
class C_Base_ActFunc
{
  public:
  double         GetBoundUp  () { return boundUp;}
  double         GetBoundLo  () { return boundLo;}
  protected:
  double boundUp;  // верхняя граница входного диапазона
  double boundLo;  // нижняя граница входного диапазона
};
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Гиперболический тангенс
class C_ActTanh : public C_Base_ActFunc
{
  public:
  C_ActTanh ()
  {
    boundUp  =  6.0;
    boundLo  = -6.0;
  }
};
//——————————————————————————————————————————————————————————————————————————————

Теперь добавим в код метода прямого прохода MLP проверку значений суммы перед подачей ее на функцию активации нейрона, чтобы убедиться, что она не выходят за пределы заданных границ. Нет смысла наращивать сумму больше заданных границ, кроме того, это позволит сделать раннюю остановку при вычислении суммы для конфигурации сетей с большим количеством нейронов в слоях, что может существенно ускорить вычисления.

Проверка верхней границы: в данном фрагменте кода проверяется, превышает ли текущее значение суммы установленную верхнюю границу. Если значение больше этой границы, оно устанавливается равным этой границе, и выполнение цикла прерывается. Аналогично выполняется проверка нижней границы.

//+----------------------------------------------------------------------------+
//| Прямой проход по сети                                                      |
//| Последовательно вычисляет значения всех слоев от входа к выходу            |
//+----------------------------------------------------------------------------+
void C_MLPa::ForwProp (double &inLayer  [],  // входные значения
                       double &outLayer [])  // значения выходного слоя
{
  double val;

  // Установка значений активации входного слоя
  for (int n = 0; n < layersSize [0]; n++)
  {
    nL [0].n [n].out = inLayer [n];
  }

  // Обработка скрытых и выходного слоев
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int n = 0; n < layersSize [ln]; n++)
    {
      val = nL [ln].n [n].bias;

      for (int w = 0; w < layersSize [ln - 1]; w++)
      {
        val += nL [ln - 1].n [w].out * wL [ln - 1].nOnL [w].nOnR [n].w;

        if (val >  actFunc.GetBoundUp ())
        {
          val =  actFunc.GetBoundUp ();
          break;
        }
        if (val < actFunc.GetBoundLo ())
        {
          val = actFunc.GetBoundLo ();
          break;
        }
      }

      nL [ln].n [n].out = actFunc.Activ (val); // Применение функции активации
    }
  }

  // Установка значений выходного слоя
  for (int n = 0; n < layersSize [nLC - 1]; n++) outLayer [n] = nL [nLC - 1].n [n].out;
}
//——————————————————————————————————————————————————————————————————————————————

Теперь добавим код проверок границ в метод обратного распространения ошибки. В этих добавках реализована логика отражения значений смещений и весов от заданных границ к обратной границе. Это необходимо для обеспечения того, чтобы значения не выходили за пределы допустимых диапазонов, предотвращая неконтролируемое увеличение или уменьшение весов и смещений.

Простое отсечение значений по границе привело бы к застою в обучении, так как вес просто упирался бы в границу, и изменение весов стало бы невозможным. Именно для предотвращения таких ситуаций реализовано отражение, а не отсечение значений. Таким образом обеспечивается "оживление" или своеобразная "встряска" при подстройке весов и смещений.

//+----------------------------------------------------------------------------+
//| Обратный проход по сети                                                    |
//| Обновляет значения весов и смещений всех слоев от выхода к входу           |
//+----------------------------------------------------------------------------+
void C_MLPa::BackProp (double &errors [])
{
  t++;  // Увеличение счетчика итераций

  double delta;     // дельта текущего нейрона
  double deltaNext; // дельта нейрона в следующем слое, связанного с текущим нейроном
  double out;       // значение нейрона после применения функции активации
  double deriv;     // производная
  double w;         // вес для связи текущего нейрона с нейроном следующего слоя
  double bias;      // смещение

  // 1. Вычисление дельт для всех слоев ----------------------------------------
  for (int ln = nLC - 1; ln > 0; ln--)                  // проход по слоям в обратном порядке от выходного к входному
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)        // проход по нейронам текущего слоя
    {
      if (ln == nLC - 1)
      {
        delta = errors [nCurr] * actFunc.Deriv (nL [ln].n [nCurr].out);
      }
      else
      {
        delta = 0.0;

        // Суммируем произведения дельт следующего слоя на соответствующие веса
        for (int nNext = 0; nNext < layersSize [ln + 1]; nNext++) // проход по нейронам следующего слоя в обычном порядке
        {
          deltaNext = nL [ln + 1].n [nNext].delta;
          w         = wL [ln].nOnL [nCurr].nOnR [nNext].w;
          delta    += deltaNext * w;
        }
      }

      // Дельта с учетом производной сигмоиды
      out   = nL [ln].n [nCurr].out;
      deriv = actFunc.Deriv (out);
      nL [ln].n [nCurr].delta = delta * deriv;
    }
  }

  // 2. Обновление смещений с использованием ADAM ------------------------------
  for (int ln = 1; ln < nLC; ln++)
  {
    for (int nCurr = 0; nCurr < layersSize [ln]; nCurr++)
    {
      delta = nL [ln].n [nCurr].delta;

      // Обновление моментов смещения
      nL [ln].n [nCurr].m = beta1 * nL [ln].n [nCurr].m + (1.0 - beta1) * delta;
      nL [ln].n [nCurr].v = beta2 * nL [ln].n [nCurr].v + (1.0 - beta2) * delta * delta;

      // Коррекция моментов смещения
      double m_hat = nL [ln].n [nCurr].m / (1.0 - pow (beta1, t));
      double v_hat = nL [ln].n [nCurr].v / (1.0 - pow (beta2, t));

      // Обновление смещения
      nL [ln].n [nCurr].bias += alpha * m_hat / (sqrt (v_hat) + epsilon);
      bias = nL [ln].n [nCurr].bias;

      if (bias < actFunc.GetBoundLo ())
      {
        nL [ln].n [nCurr].bias = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - bias);  // отражаем от нижней границы
      }
      else
        if (bias > actFunc.GetBoundUp ())
        {
          nL [ln].n [nCurr].bias = actFunc.GetBoundLo () + (bias - actFunc.GetBoundUp ());  // отражаем от верхней границы
        }
    }
  }

  // 3. Обновление весов с использованием ADAM ---------------------------------
  for (int lw = 0; lw < wLC; lw++)
  {
    for (int nCurr = 0; nCurr < layersSize [lw]; nCurr++)
    {
      for (int nNext = 0; nNext < layersSize [lw + 1]; nNext++)
      {
        deltaNext = nL [lw + 1].n [nNext].delta;
        out       = nL [lw].n [nCurr].out;
        double gradient = deltaNext * out;

        // Обновление моментов для весов
        wL [lw].nOnL [nCurr].nOnR [nNext].m = beta1 * wL [lw].nOnL [nCurr].nOnR [nNext].m + (1.0 - beta1) * gradient;
        wL [lw].nOnL [nCurr].nOnR [nNext].v = beta2 * wL [lw].nOnL [nCurr].nOnR [nNext].v + (1.0 - beta2) * gradient * gradient;

        // Коррекция моментов весов
        double m_hat = wL [lw].nOnL [nCurr].nOnR [nNext].m / (1.0 - pow (beta1, t));
        double v_hat = wL [lw].nOnL [nCurr].nOnR [nNext].v / (1.0 - pow (beta2, t));

        // Обновление веса
        wL [lw].nOnL [nCurr].nOnR [nNext].w += alpha * m_hat / (sqrt (v_hat) + epsilon);
        w = wL [lw].nOnL [nCurr].nOnR [nNext].w;

        if (w < actFunc.GetBoundLo ())
        {
          wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundUp () - (actFunc.GetBoundLo () - w);  // отражаем от нижней границы
        }
        else
          if (w > actFunc.GetBoundUp ())
          {
            wL [lw].nOnL [nCurr].nOnR [nNext].w = actFunc.GetBoundLo () + (w - actFunc.GetBoundUp ());  // отражаем от верхней границы
          }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Теперь повторим те же самые тесты, как и выше, и посмотрим на полученные результаты. Теперь взрыва весов не наблюдается, и не происходит лавинообразного роста ошибки на протяжении обучения.

Таблица результатов для сигмоидных функций активации:

Tanh	AlgSigm	RatSigm
MLP config: 1\|1\|1, Weights: 4, Activation func: eActTanh, Seed: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001	MLP config: 1\|1\|1, Weights: 4, Activation func: eActAlgSigm, Seed: 2 -----Integrated ADAM----- 0: 0.0095411465043040, 0: 0.009541146504303972 0: 0.0095411465043040, 1000: 0.20977102640908893 0: 0.0095411465043040, 2000: 0.23464558094398064 0: 0.0095411465043040, 3000: 0.23657904914082925 0: 0.0095411465043040, 4000: 0.17812555648593617 0: 0.0095411465043040, 5000: 2.1749975763135927 0: 0.0095411465043040, 6000: 2.2093668968051166 0: 0.0095411465043040, 7000: 2.1657244506071813 0: 0.0095411465043040, 8000: 1.9330415523200173 0: 0.0095411465043040, 9000: 0.10441382194622865 Best result iteration: 0, Err: 0.009541 -----Population-based ADAMm----- 0: 0.2201830630768654 Best result iteration: 750, Err: 0.000001	MLP config: 1\|1\|1, Weights: 4, Activation func: eActRatSigm, Seed: 1 -----Integrated ADAM----- 0: 1.2866075458561122, 0: 1.2866075458561121 1000: 0.2796061866784148, 1000: 0.2796061866784148 2000: 0.0450819127087337, 2000: 0.04508191270873367 3000: 0.0200306843648248, 3000: 0.020030684364824806 4000: 0.0098744349153286, 4000: 0.009874434915328582 5000: 0.0049448920462547, 5000: 0.00494489204625467 6000: 0.0024344513388710, 6000: 0.00243445133887102 7000: 0.0011602603038120, 7000: 0.0011602603038120354 8000: 0.0005316894732581, 8000: 0.0005316894732581081 9000: 0.0002339388712666, 9000: 0.00023393887126662818 Best result iteration: 9999, Err: 0.000099 -----Population-based ADAMm----- 0: 1.8418367346938778 Best result iteration: 645, Err: 0.000000

Таблица результатов для функций активации типа SiLU:

SoftPlus	BentIdent	SiLU
MLP config: 1\|1\|1, Weights: 4, Activation func: eActSoftPlus, Seed: 2 -----Integrated ADAM----- 0: 0.5380138004155748, 0: 0.5380138004155747 0: 0.5380138004155748, 1000: 12.377378915308087 0: 0.5380138004155748, 2000: 12.377378915308087 3000: 0.1996421769021168, 3000: 0.19964217690211675 4000: 0.1985425345613517, 4000: 0.19854253456135168 5000: 0.1966512639256550, 5000: 0.19665126392565502 6000: 0.1933509943676914, 6000: 0.1933509943676914 7000: 0.1874142582090466, 7000: 0.18741425820904659 8000: 0.1762132792048514, 8000: 0.17621327920485136 9000: 0.1538331138702293, 9000: 0.15383311387022927 Best result iteration: 9999, Err: 0.109364 -----Population-based ADAMm----- 0: 12.3773789153080873 Best result iteration: 677, Err: 0.000001	MLP config: 1\|1\|1, Weights: 4, Activation func: eActBentIdent, Seed: 4 -----Integrated ADAM----- 0: 15.1221330593320857, 0: 15.122133059332086 0: 15.1221330593320857, 1000: 25.619316876852988 1922: 8.6344718719116980, 2000: 8.634471871911698 1922: 8.6344718719116980, 3000: 8.634471871911698 1922: 8.6344718719116980, 4000: 8.634471871911698 1922: 8.6344718719116980, 5000: 8.634471871911698 1922: 8.6344718719116980, 6000: 8.634471871911698 6652: 4.3033564303197833, 7000: 8.634471871911698 6652: 4.3033564303197833, 8000: 8.634471871911698 6652: 4.3033564303197833, 9000: 7.11489380279475 Best result iteration: 9999, Err: 3.589207 -----Population-based ADAMm----- 0: 25.6193168768529880 Best result iteration: 15, Err: 0.000001	MLP config: 1\|1\|1, Weights: 4, Activation func: eActSiLU, Seed: 4 -----Integrated ADAM----- 0: 0.6585816582701970, 0: 0.658581658270197 0: 0.6585816582701970, 1000: 5.142928362480306 1393: 0.3271208998291733, 2000: 0.32712089982917325 1393: 0.3271208998291733, 3000: 0.32712089982917325 1393: 0.3271208998291733, 4000: 0.4029355474095988 5000: 0.0114993205601383, 5000: 0.011499320560138332 6000: 0.0003946998191595, 6000: 0.00039469981915948605 7000: 0.0000686308316624, 7000: 0.00006863083166239227 8000: 0.0000176901182322, 8000: 0.000017690118232197302 9000: 0.0000053723044223, 9000: 0.000005372304422295116 Best result iteration: 9999, Err: 0.000002 -----Population-based ADAMm----- 0: 19.9499415647445524 1000: 0.0000057228950379 Best result iteration: 1051, Err: 0.000000

Таблица результатов для периодических функций активации:

ACON	SERF	Snake
MLP config: 1\|1\|1, Weights: 4, Activation func: eActACON, Seed: 3 -----Integrated ADAM----- 0: 0.8183728267492676, 0: 0.8183728267492675 160: 0.5853150801288914, 1000: 1.2003151947973498 2000: 0.0177702331540612, 2000: 0.017770233154061187 3000: 0.0055801976952827, 3000: 0.005580197695282676 4000: 0.0023096724537356, 4000: 0.002309672453735598 5000: 0.0010238849157595, 5000: 0.0010238849157594616 6000: 0.0004581612824611, 6000: 0.0004581612824611273 7000: 0.0002019092359805, 7000: 0.00020190923598049711 8000: 0.0000867118074097, 8000: 0.00008671180740972474 9000: 0.0000361764073840, 9000: 0.00003617640738397845 Best result iteration: 9999, Err: 0.000015 -----Population-based ADAMm----- 0: 1.3784017183806672 Best result iteration: 300, Err: 0.000000	MLP config: 1\|1\|1, Weights: 4, Activation func: eActSERF, Seed: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001	MLP config: 1\|1\|1, Weights: 4, Activation func: eActSnake, Seed: 2 -----Integrated ADAM----- 0: 0.0169277701441132, 0: 0.016927770144113192 0: 0.0169277701441132, 1000: 0.24726166610109795 0: 0.0169277701441132, 2000: 0.24996248252671016 0: 0.0169277701441132, 3000: 0.2499877118017991 0: 0.0169277701441132, 4000: 0.2260068617570163 0: 0.0169277701441132, 5000: 2.2499589217599363 0: 0.0169277701441132, 6000: 2.2499631351033904 0: 0.0169277701441132, 7000: 2.248459789732414 0: 0.0169277701441132, 8000: 2.146138260175548 0: 0.0169277701441132, 9000: 0.15279792149898394 Best result iteration: 0, Err: 0.016928 -----Population-based ADAMm----- 0: 0.2491964938729135 1000: 0.0000010386817829 Best result iteration: 1050, Err: 0.000001

Выводы

Итак, давайте подведем итоги нашего исследования. Напомню суть эксперимента: мы взяли два алгоритма оптимизации, построенных на одной логике, но работающих принципиально по-разному. Первый (классический ADAM) — это встроенный оптимизатор, который работает изнутри нейронной сети, имея прямой доступ к функциям активации и всей внутренней структуре — словно штурман с детальной картой местности. Второй (популяционный ADAMm) — внешний оптимизатор, работает с нейронной сетью как с "черным ящиком", не имея никакой информации о её внутреннем устройстве и специфике задачи — как путешественник, который находит дорогу, ориентируясь только по звездам и общему направлению.

В качестве объекта исследования мы использовали одну и ту же нейронную сеть для обоих алгоритмов. Это критически важно, поскольку позволяет нам локализовать источник возможных проблем: если возникают трудности в работе с определенными функциями активации, мы можем быть уверены, что это не проблема самой нейронной сети, а особенность взаимодействия алгоритма оптимизации с этими функциями.

Такая экспериментальная установка позволяет нам четко увидеть, как различные функции активации проявляют себя в контексте разных подходов к оптимизации. Важно отметить, что мы намеренно не рассматриваем вопрос обобщающей способности сети или её работу с новыми данными. Наша цель — исследовать именно взаимовлияние функций активации и алгоритмов оптимизации, их совместимость и эффективность их взаимодействия.

Этот подход позволяет нам получить чистую картину того, как разные стратегии оптимизации справляются с различными функциями активации, без влияния посторонних факторов. И результаты эксперимента наглядно показывают, что иногда "слепой" внешний оптимизатор может оказаться эффективнее, чем алгоритм, обладающий полной информацией о структуре сети.

На всех функциях активации внешний ADAMm показал быструю и стабильную сходимость, из чего можно сделать вывод, что для него не играет особой роли свойства функции активации, с другой стороны классический встроенный ADAM столкнулся с серьезными проблемами.

Теперь рассмотрим поведение встроенного ADAM на каждой из функций активаций и суммируем в следующие выводы:

1. Проблемные функции (застревание или медленная сходимость):

TanH (гиперболический тангенс)
AlgSigm (алгебраическая сигмоида)
SERF (сигмоидально-взвешенное экспоненциальное выпрямление)
Snake (периодическая функция)

2. Успешные случаи (сходимость):

RatSigm (рациональная сигмоида), лучшая из сигмоидных
SoftPlus
BentIdent (изогнутая идентичность)
SiLU (Swish), лучшая из второй группы
ACON (адаптивная функция), лучшая из периодических

3. Закономерности:

Классические сигмоидальные функции (TanH, AlgSigm) показывают проблемы с застреванием. Более современные адаптивные функции (ACON, SiLU) демонстрируют лучшую сходимость. Из периодических функций ACON показывает сходимость, а Snake застревает.

Таким образом, в представленном исследовании разработан комплексный подход к оптимизации нейронных сетей, объединяющий контроль весов, границы функций активации и процесс обучения в единую взаимосвязанную систему. Ключевым нововведением стало внедрение методов GetBoundUp и GetBoundLo, позволяющих каждой функции активации определять собственные границы, которые затем используются для контроля весов сети. Этот механизм дополнен системой раннего прерывания суммирования при достижении границ, что не только предотвращает избыточные вычисления, особенно в крупных сетях, но и обеспечивает контроль значений до применения функции активации.

Особенно важным элементом стал механизм отражения весов, который, в отличие от традиционного отсечения или нормализации, предотвращает застой в обучении через своеобразную "встряску" весов при достижении границ. Это решение позволяет сохранить возможность изменения весов даже в критических ситуациях, обеспечивая непрерывность процесса обучения. Системная интеграция всех этих компонентов создает эффективный механизм предотвращения разлета весов без потери гибкости обучения, что особенно важно при работе с различными функциями активации. Такой комплексный подход не только решает проблему контроля весов, но и открывает новые перспективы в понимании взаимодействия различных компонентов нейронной сети в процессе обучения.

Проведенное исследование не говорит об бесполезности ADAM в обучении нейронных сетей, а лишь заостряет внимание на его реакции на те или иные функции активации. Возможно, для больших нейронных сетей ему вообще нет альтернативы (или его современные аналоги методов градиентного спуска), это может стать следующей темой для рассмотрения эффективности ADAM (как представителя современных алгоритмов оптимизации методом обратного распространения ошибки) в в контексте крупномасштабных нейронных сетей, а также изучение влияния выбора функций активации на обобщающую способность сети и стабильность её работы на новых данных.

Программы, используемые в статье

#	Имя	Тип	Описание
1	#C_AO.mqh	Включаемый файл	Родительский класс популяционных алгоритмов оптимизации
2	#C_AO_enum.mqh	Включаемый файл	Перечисление популяционных алгоритмов оптимизации
3	MLPa.mqh	Скрипт	Нейронная сеть MLP с ADAM
4	Tests and Drawing act func.mq5	Скрипт	Скрипт визуального построения функций активации
5	Test act func in training.mq5	Скрипт	Скрипт обучения MLP с ADAM и ADAMm

Прикрепленные файлы |

Загрузить ZIP

MLP_ADAM.ZIP (139.81 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (9)

CODE X | 28 июн. 2025 в 23:41

Думаю, возникло недопонимание между тем, что я хотел сказать, и тем, что я на самом деле изложил в виде текста.

В этот раз я постараюсь быть немного яснее. 🙂 Когда мы хотим КЛАССИФИЦИРОВАТЬ вещи, такие как изображения, предметы, фигуры, звуки, короче говоря, где будут царить вероятности. Нам нужно ограничить значения в нейронной сети так, чтобы они попадали в заданный диапазон. Обычно этот диапазон составляет от -1 до 1. Но он может быть и от 0 до 1, в зависимости от того, как быстро, с какой скоростью и каким образом обрабатывается входная информация, с которой мы хотим познакомить сеть, и как она лучше всего направляет свое обучение, чтобы создать классификацию вещей. В ЭТОМ СЛУЧАЕ НАМ ПОНАДОБЯТСЯ функции активации. Именно для того, чтобы удерживать значения в этом диапазоне. В итоге мы получим средства для генерации значений с точки зрения вероятности того, что входные данные являются теми или иными. Это факт, и я его не отрицаю. Настолько, что нам часто приходится нормализовать или стандартизировать входные данные.

Однако нейронные сети используются не только для классификации, они также могут и используются для сохранения знаний. В этом случае от функций активации во многих случаях следует отказаться. Деталь: Бывают случаи, когда нам нужно что-то ограничить. Но это очень специфические случаи. Все дело в том, что эти функции мешают сети выполнять свое предназначение. А оно заключается именно в сохранении знаний. И на самом деле я частично согласен с замечанием Станислава Короткого о том, что сеть в таких случаях можно свернуть до чего-то эквивалентного одному слою, если не использовать функции активации. Но когда это произойдет, это будет один из нескольких случаев, поскольку есть случаи, когда одного полинома с несколькими переменными недостаточно, чтобы представить или, лучше сказать, сохранить знания. В этом случае нам придется использовать дополнительные слои, чтобы результат действительно можно было воспроизвести. Или же можно сгенерировать новые. Немного запутанно объяснять это вот так, без должной демонстрации. Но это работает.

Большая проблема в том, что из-за моды на все сейчас, в последние 10 лет или около того, если мне не изменяет память, это было связано с искусственным интеллектом и нейронными сетями. Хотя бизнес по-настоящему расцвел только в последние пять лет. Многие люди совершенно не знают, что это такое на самом деле. И как они на самом деле работают. Это происходит потому, что все, кого я вижу, всегда используют готовые фреймворки. А это совершенно не помогает понять, как работают нейронные сети. Это просто уравнение с несколькими переменными. В академических кругах их изучают уже несколько десятилетий. И даже когда они вышли за пределы академических кругов, их никогда не анонсировали с такой помпой. На начальном этапе и в течение длительного времени ФУНКЦИИ АКТИВАЦИИ НЕ ИСПОЛЬЗОВАЛИСЬ. Но цель сетей, которые в то время даже не назывались нейросетями, была другой. Однако из-за того, что три человека хотели извлечь из них выгоду, они были разрекламированы, что, на мой взгляд, несколько неправильно. Правильнее всего, по крайней мере с моей точки зрения, было бы правильно объяснить их суть. Именно так, чтобы не создавать путаницы в умах многих людей. Но это не страшно, они втроем делают кучу денег, а люди теряются больше, чем собака, упавшая с грузовика для вывоза мусора. В любом случае, я не хочу отговаривать вас от написания новых статей, Андрей Дик, но я хочу, чтобы вы продолжали учиться и старались еще глубже погрузиться в эту тему. Я видел, что вы пытались использовать чистый MQL5 для создания системы. Что, кстати, очень хорошо. Это привлекло мое внимание, и я понял, что ваша статья очень хорошо написана и спланирована. Я просто хотел обратить ваше внимание на этот момент и заставить вас подумать об этом немного больше. На самом деле, эта тема очень интересна, и о ней мало кто знает. Но вы взялись и изучили ее.

Debates em alto nível, são sempre interessantes, pois nos faz crescer e pensar fora da caixa. Brigas não nos leva a nada, e só nos faz perder tempo. 👍

Andrey Dik | 29 июн. 2025 в 07:42

CODE X #:
...

Ваш пост похож на выражение "Реактивный турбо-двигатель на самом деле это паровой двигатель, таким он был задуман изначально."

Rorschach | 29 июн. 2025 в 17:05

В качестве ф-ии активации можно использовать что угодно, хоть косинус, результат получается на уровне популярных. Рекомендуется использовать relu (со сдвигом bias 0.1 (не рекомендуется использовать вместе с инициализацией случайным блужданием)), т.к. он простой (быстро считается) и лучше идет обучение: Эти блоки легко оптимизировать, потому что они очень похожи на линейные. Разница только в том, что блок линейной ректификации в половине своей области определения выводит 0. Поэтому производная блока линейной ректификации остается большой всюду, где блок активен. Градиенты не только велики, но еще и согласованы. Вторая производная операции ректификации всюду равна нулю, а первая производная равна 1 всюду, где блок активен. Это означает, что направление градиента гораздо полезнее для обучения, чем в случае, когда функция активации подвержена эффектам второго порядка... При инициализации параметров аффинного преобразования рекомендуется присваивать всем элементам b небольшое положительное значение, например 0.1. Тогда блок линейной ректификации в начальный момент с большой вероятностью окажется активен для большинства обучающих примеров, и производная будет отлична от нуля.

В отличие от кусочно-линейных, сигмоидальные блоки близки к асимптоте в большей части своей области определения – приближаются к высокому значению, когда z стремится к бесконечности, и к низкому, когда z стремится к минус бесконечности. Высокой чувствительностью они обладают только в окрестности нуля. Из-за насыщения сигмоидальных блоков градиентное обучение сильно затруднено. Поэтому использование их в качестве скрытых блоков в сетях прямого распространения ныне не рекомендуется... Если использовать сигмоидальную функцию активации необходимо, то лучше взять не логистическую сигмоиду, а гиперболический тангенс. Он ближе к тождественной функции в том смысле, что tanh(0) = 0, тогда как σ(0) = 1/2. Поскольку tanh походит на тождественную функцию в окрестности нуля, обучение глубокой нейронной сети напоминает обучение линейной модели при условии что сигналы активации сети удается удерживать на низком уровне. При этом обучение сети с функцией активации tanh упрощается.

Для lstm нужно использовать сигмоид или арктангенс (рекомендуется устанавливать смещение 1 для вентиля забывания): Сигмоидальные функции активации все же применяются, но не в сетях прямого распространения. К рекуррентным сетям, многим вероятностным моделям и некоторым автокодировщикам предъявляются дополнительные требования, исключающие использование кусочно-линейных функций активации и делающие сигмоидальные блоки более подходящими, несмотря на проблемы насыщения.

Линейная активация и уменьшение параметров: Если каждый слой сети состоит только из линейных преобразований, то сеть в целом будет линейной. Однако некоторые слои могут быть и чисто линейными – это вполне нормально. Рассмотрим слой нейронной сети, имеющий n входов и p выходов. Его можно заменить двумя слоями, в одном из которых используется матрица весов U, а в другом – матрица весов V. Если в первом слое нет функции активации, то мы, по сути дела, разложили на множители матрицу весов исходного слоя, основанного на W. Если U порождает q выходов, то U и V вместе содержат только (n + p)q параметров, тогда как W – np параметров. Для малых q экономия параметров может быть существенной. Платой за это является ограничение – линейное преобразование должно иметь низкий ранг, но таких низкоранговых связей часто достаточно. Таким образом, линейные скрытые блоки предлагают эффективный способ уменьшить число параметров сети.

Релу больше подходит для глубоких сетей: Несмотря на популярность ректификации в ранних моделях, в 1980-е годы ее почти всюду заменили сигмоиды, поскольку они лучше работают в очень малых нейронных сетях.

Но в целом оно лучше: для небольших наборов данных использование ректифицирующих нелинейностей даже важнее, чем обучение весов скрытых слоев. Случайных весов достаточно для распространения полезной информации по сети с линейной ректификацией, что позволяет классифицирующему выходному слою обучаться отображению различных векторов признаков на идентификаторы классов. Если доступно больше данных, то процесс обучения начинает извлекать так много полезных знаний, что превосходит по качеству случайным образом выбранные параметры... обучение гораздо легче проходит в ректифицированных линейных сетях, чем в глубоких сетях, для которых функции активации характеризуются кривизной или двусторонним насыщением...

Maxim Dmitrievsky | 31 июл. 2025 в 16:48

CODE X #:

Думаю, возникло недопонимание между тем, что я хотел сказать, и тем, что я на самом деле изложил в виде текста.

Да, нелинейность - это косвенный эффект, который дают ф-ии активации. Изначально они предназначались для перевода из одной области определения целевой в другую, например для задач классификации. "Нелинейность" же может достигаться разными способами, например за счет увеличения количества признаков или их преобразования, либо за счет ядер, которые преобразуют признаки.

Простейший пример - логистическая регрессия, которая остается линейной, несмотря на ф-ю активации в конце.

Но в многослойных сетях нелинейность получается за счет количества слоев с ф-ями активации, просто как следствие преобразований по типу ядер.

Maxim Dmitrievsky | 31 июл. 2025 в 17:05

Историческая справка:

Вы правы в том, что концепции, лежащие в основе логистической регрессии и ранних нейронных сетей, появились раньше, чем современные глубокие нейронные сети.

Давайте посмотрим на хронологию:

Логистическая функция была разработана в 19 веке. Её использование в качестве статистической модели для классификации (логистическая регрессия) стало популярным в середине 20 века (примерно 1940-50-е годы).
Первая математическая модель нейрона (модель Мак-Каллока и Питтса) с функцией активации появилась в 1943 году. Она использовала простую пороговую функцию.
Перцептрон, однослойная нейронная сеть, был разработан Фрэнком Розенблаттом в 1958 году. Он использовал пороговую функцию активации и мог решать только линейно разделимые задачи.
Прорыв в области глубокого обучения и многослойных сетей произошел только с появлением алгоритма обратного распространения ошибки (backpropagation), который был популяризирован в 1986 годуработами Румельхарта, Хинтона и Уильямса.

Именно этот алгоритм сделал практичным обучение многослойных нейронных сетей и показал, что для его работы нужны не просто пороговые, а дифференцируемые нелинейные функции активации (такие как сигмоида, а позже и ReLU).

Вывод:

Исторически получается, что:

Сначала были модели (логистическая регрессия, перцептрон), которые были по сути однослойными.
В этих моделях функция активации действительно выполняла роль преобразования в нужную область (из линейной суммы в бинарный класс или вероятность), так как вся модель оставалась линейной.
Позже, с появлением многослойных сетей, возникла новая, принципиально более важная роль функции активации — вносить нелинейность в скрытые слои, чтобы сеть могла учиться.

Введение в MQL5 (Часть 8): Руководство для начинающих по созданию советников (II)

В этой статье рассматриваются частые вопросы, которые начинающие программисты задают на форуме MQL5. Также демонстрируются практические решения. Мы научимся совершать основные действия: покупку и продажу, получение цен свечей, а также управление торговыми аспектами, включая торговые лимиты, периоды и пороговые значения прибыли/убытка. В статье представлены пошаговые инструкции, которые помогут вам лучше понять и реализовать обсуждаемые концепции на MQL5.

Пользовательский индикатор: Отображение сделок входа, выхода и разворота позиции на неттинговых счетах

В данной статье мы рассмотрим нестандартный способ создания индикатора в MQL5. Вместо того, чтобы фокусироваться на тренде или графическом паттерне, нашей целью будет управление собственными позициями, включая частичные входы и выходы. Мы будем активно использовать динамические матрицы и некоторые торговые функции, связанные с историей сделок и открытыми позициями, чтобы указать на графике, где осуществились данные сделки.

Нейросимвольные системы в алготрейдинге: Объединение символьных правил и нейронных сетей

Статья рассказывает об опыте разработки гибридной торговой системы, объединяющей классический технический анализ с нейронными сетями. Автор подробно разбирает архитектуру системы — от базового анализа паттернов и структуры нейросети до механизмов принятия торговых решений, делясь реальным кодом и практическими наблюдениями.

От начального до среднего уровня: Переменные (II)

Сегодня мы рассмотрим, как работать со статическими переменными. Этот вопрос часто ставит в тупик многих программистов, как начинающих, так и имеющих некоторый опыт, и это связано с тем, что существует несколько советов и рекомендаций, которые необходимо соблюдать при использовании данного механизма. Представленные здесь материалы предназначены исключительно для дидактических целей. Ни в коем случае нельзя рассматривать это как приложение, чьей целью будет что-то иное помимо изучения и освоения представленных концепций.