Discussão do artigo "Funções de ativação de neurônios durante o aprendizado: chave para uma convergência rápida?"
Este trecho no artigo me chamou atenção. Mesmo o artigo estando muito bem escrito e dando detalhes de como ele foi elaborado e pensado. Neste trecho existe uma sutileza sobre seu entendimento do assunto. Talvez você esteja com viés por conta de que todos insistem em dizer certas coisas sobre redes neurais. Mas como seu artigo ficou bem escrito e você explicou os detalhes envolvidos. Decidi antecipar algo que irei mostrar no futuro. O artigo para isto já foi escrito, mas quero primeiro terminar de explicar como construir o Replay / Simulador, onde está faltando poucos artigos para finalizar a publicação. Entenda o seguinte: As funções de ativação NÃO são utilizadas para gerar não linearidade nas equações. Mas sim servem como um tipo de filtro com o objetivo de reduzir a quantidade de camadas ou perceptrons dentro da própria rede que estará sendo construída. Agilizando assim o processo de convergência dos dados em uma direção específica. Durante este processo podemos objetivar a classificação ou retenção de conhecimento. Sendo que no final obteremos um ou outro resultado, mas nunca ambos.
Neste meu artigo, https://www.mql5.com/pt/articles/13745, demonstro isto de maneira relativamente simples. Apesar de ali, eu esteja apenas iniciando a explicação de como entender a rede neural. Mas como seu artigo ficou bem escrito, e você se dedicou bastante, vou lhe dar uma dica. Pegue alguns dados aparentemente aleatórios e remova as funções de ativação dos perceptrons. Depois disto, comece a tentar fazer a convergência. Você vai notar que ela não irá ficar muito boa. MAS se você começar a acrescentar camadas e/ou mais perceptrons, a convergência irá começar a melhorar com o tempo. Isto irá lhe ajudar a entender melhor o motivo pelo qual funções de ativação são necessárias. 😁👍

- www.mql5.com
Essa passagem do artigo chamou minha atenção. Embora o artigo esteja muito bem escrito e detalhe como ele foi projetado e pensado, há uma sutileza em seu argumento. Há uma sutileza em sua compreensão do assunto nessa passagem. Talvez você seja tendencioso porque todos insistem em dizer certas coisas sobre as redes neurais. Mas seu artigo está bem escrito e você explicou os detalhes. Decidi antecipar o que mostrarei no futuro. O artigo para isso já está escrito, mas antes quero terminar de explicar como construir um Replay / Simulador, onde faltam apenas alguns artigos para concluir a publicação. Entenda o seguinte: As funções de ativação NÃO são usadas para criar não linearidade nas equações. Em vez disso, elas servem como um tipo de filtro cujo objetivo é reduzir o número de camadas ou perceptrons na rede que está sendo construída. Isso acelera o processo de convergência dos dados em uma determinada direção. Durante esse processo, podemos ter como objetivo a classificação ou a retenção de conhecimento. O resultado final será um ou outro, mas nunca ambos.
A tradução automática provavelmente não é muito precisa, mas o destaque está incorreto. É a não linearidade que aumenta o poder computacional da rede e não apenas acelera o processo de convergência (o que você mesmo disse em outra frase), mas fundamentalmente permite resolver problemas que não podem ser resolvidos sem a introdução da não linearidade (não importa quantas camadas você adicione). Além disso, sem a não linearidade, qualquer rede neural (síncrona) pode ser "colapsada" em uma rede equivalente de camada única.
É a não linearidade que aumenta o poder computacional da rede e não só acelera o processo de convergência (o que você mesmo disse em outra frase), mas também permite resolver problemas que não podem ser resolvidos sem a introdução da não linearidade (não importa quantas camadas sejam adicionadas). Além disso, sem a não linearidade, qualquer rede neural (síncrona) pode ser "colapsada" em uma rede equivalente de camada única.
+100500
Muito bem dito. Enquanto eu estava escrevendo minha resposta, vi que ela já havia sido respondida.
Vou dizer mais: sim, qualquer função não linear pode ser descrita por funções lineares por partes em um número que tende ao infinito com erro de descrição que tende a zero. Mas por que, se as funções de ativação não lineares são usadas apenas para simplificar a descrição do objeto no problema?
Acho que ficou um mal entendido entre o que eu pretendia dizer e o que realmente coloquei em forma de texto.
Vou tentar ser um pouco mais claro desta vez.🙂 Quando estamos querendo CLASSIFICAR coisas, como imagens, objetos, figura, sons, enfim, onde as probabilidades irão reinar. Precisamos limitar os valores dentro da rede neural, de forma que eles fiquem dentro de um dado range. Este range normalmente gira entre -1 e 1. Mas também podem girar entre 0 e 1 dependendo do qual rápido, da taxa de acerto, e do tipo de tratamento dado as informações de entrada, que queremos que a rede venha a ter contato, e como isto direcionar da melhor forma o próprio aprendizado a fim de criar a classificação das coisas. NESTE CASO, PRECISAMOS SIM de funções de ativação. Justamente para manter os valores dentro do referido range. No final teremos meios de gerar valores em termos de probabilidade da entrada ser uma coisa ou outra. Isto é fato e não nego tal coisa. Tanto que muitas das vezes precisamos normalizar ou padronizar os dados de entrada.
Porém, redes neurais não são usadas apenas para classificação de coisas, elas também podem e são usadas para retenção de conhecimento. Neste caso as funções de ativação devem ser descartadas em muitos dos casos. Detalhe: Existem casos em que precisaremos limitar as coisas. Mas são casos muito específicos. Isto por que estas funções atrapalham a rede em cumprir seu objetivo. Que é justamente reter conhecimento. E de fato concordo, em parte, com o comentário do Stanislav Korotky em dizer que a rede, nestes casos, pode ser colapsada em algo equivalente a uma única camada, caso não venhamos a usar funções de ativação. Mas isto quando acontece, seria um entre diversos casos, já que existem casos que apenas e somente um único polinômio com diversas variáveis não é suficiente para representar, ou melhor dizendo, reter o conhecimento. Neste caso precisaríamos usar camadas extras para que o resultado possa realmente ser replicado. Ou novos possam ser gerados. Isto é meio confuso de explicar assim, sem uma demonstração adequada. Mas funciona.
O grande problema é que devido a moda de tudo agora, nos 10 últimos anos para cá, se não me falha a memória, estar ligado a inteligência artificial e redes neurais. Apesar do negócio ter tomado folego apenas os últimos 5 anos. Muita gente desconhece completamente o que elas realmente são. Ou como elas de fato funcionam. Isto porque todo mundo que vejo está sempre usando framework já prontos. E isto não ajuda em nada entender como redes neurais trabalha. Pois elas não passam de uma equação multi variável. Elas já são estudas a décadas no meio acadêmico. E mesmo quando saia do meio acadêmico, elas nunca eram anunciadas com tanto alvoroço e barulho. Durante a fase inicial e por um bom tempo NÃO ERAM USADAS FUNÇÕES DE ATIVAÇÃO. Mas o objetivo das redes, que na época nem se chamava de redes neurais, era outro. Porém, por conta de 3 pessoas querendo lucrar com isto, elas vieram a publico de uma maneira um tanto quanto errada, ao meu ver. O correto, pelo menos no meu entender, seria que elas fossem devidamente explicadas. Justamente para não gerar tanta confusão na mente de tanta gente. Mas tudo bem, os 3 estão ganhando rios de dinheiro enquanto o povo fica mais perdido que cachorro que caiu do caminhão de mudança. Quem sou eu então para ir contra ? De qualquer maneira, não quero te desmotivar a fazer novos artigos, Andrey Dik quero sim que você continue estudando e tente se aprofundar ainda mais neste assunto. Pois vi que você tentou usar MQL5 puro para criar o sistema. O que é muito bom por sinal. E isto chamou a minha atenção, me fazendo ver que seu artigo foi muito bem escrito e planejado. Apenas queria chamar atenção para aquele ponto específico e assim fazer você pensar um pouco mais a respeito do assunto. Pois de fato este assunto é muito interessante e tem muita coisa que poucos sabem. Mas você foi atrás e procurou estudar a respeito.
Debates em alto nível, são sempre interessantes, pois nos faz crescer e pensar fora da caixa. Brigas não nos leva a nada, e só nos faz perder tempo. 👍

- 2025.01.21
- MetaQuotes
- www.mql5.com
Qualquer coisa pode ser usada como função de ativação, até mesmo o cosseno, o resultado está no nível dos mais populares. Recomenda-se usar relu (com polarização de 0,1(não é recomendável usá-lojunto com a inicialização de passeio aleatório)) porque é simples (contagem rápida) e melhor aprendizado: Esses blocos são fáceis de otimizar porque são muito semelhantes aos blocos lineares.A única diferençaé que um bloco de retificação linear produz 0 na metade do seu domínio dedefinição. Portanto, a derivada de um bloco de retificação linear permanece grande em todos os lugares em que o bloco está ativo. Além de os gradientes serem grandes, eles também são consistentes. A segunda derivada da operação de retificação é zero em todos os lugares, e a primeiraderivada é 1 em todos os lugares em que o bloco está ativo. Isso significa que a direção do gradiente é muito mais útil para o aprendizado do que quando a função de ativação está sujeita a efeitos de segunda ordem... Ao inicializar os parâmetros de transformação afim, recomenda-seatribuir um pequeno valor positivo atodos os elementos de b, por exemplo, 0,1. Assim, é muito provável que o bloco de retificação linear esteja ativo no momento inicial para a maioria dos exemplos de treinamento, e a derivada será diferente de zero.
Diferentemente dosblocos lineares por partes,os blocos sigmoidaisestão próximos da assíntota na maior parte de seu domínio de definição - aproximando-se de um valor alto quando z tende ao infinito e de um valor baixo quando z tende a menos infinito.Eles têm alta sensibilidadesomente nas proximidades de zero. Devido à saturação dos blocos sigmoidais, o aprendizado de gradiente é muito prejudicado. Portanto, usá-los como blocos ocultos em redes de propagação direta não é recomendado atualmente... Se for necessário usar a função de ativação sigmoidal, é melhor usar a tangente hiperbólica em vez da sigmoidal logística . Ela está mais próxima da função de identidade no sentido de que tanh(0) = 0, enquanto σ(0) = 1/2. Como tanh se assemelha a uma função de identidade na vizinhança de zero, o treinamento de umarede neural profundase assemelha ao treinamento de um modelo linear, desde que os sinais de ativação da rede possam ser mantidos baixos.Nesse caso, o treinamento de uma rede com a função de ativação tanh é simplificado.
Para o lstm, precisamos usar sigmoide ou arctangente(recomenda-se definir o deslocamentocomo 1 para a ventilação de esquecimento): As funções de ativação sigmoidal ainda são usadas, mas não em redes feedforward . As redes recorrentes, muitos modelos probabilísticos e alguns autoencoders têm requisitos adicionais que impedem o uso de funções de ativação linear por partes e tornam os blocossigmoidais mais apropriados, apesar dos problemas de saturação.
Ativação linear e redução de parâmetros: se cada camada da rede consistir apenas em transformações lineares, a rede como um todo será linear. Entretanto, algumas camadas também podem ser puramente lineares , o que não é problema. Considere uma camada de uma rede neural que tenha n entradas e p saídas. Ela pode ser substituída por duas camadas, uma com uma matriz de peso U e a outra com uma matriz de peso V. Se a primeira camada não tiver função de ativação, basicamente decompusemos a matriz de peso da camada original com base em Wem multiplicadores . Se U gerar q saídas, então U e V juntas contêm apenas (n + p)q parâmetros, enquanto W contém np parâmetros. Para q pequeno, a economia de parâmetros pode sersubstancial. A recompensa é uma limitação - a transformação linear deve ter uma classificação baixa, mas esses links de classificação baixa geralmente são suficientes. Assim, os blocos ocultos lineares oferecem uma maneira eficiente de reduzir o número deparâmetros da rede.
Relu é melhor para redes profundas: Apesar da popularidade da retificação nos primeiros modelos, ela foi quase universalmente substituída pela sigmoide na década de 1980 porque funciona melhor para redes neurais muito pequenas.
Mas ela é melhor em geral: para conjuntos de dados pequenos ,usar não linearidades retificadoras é ainda mais importante do que aprender os pesos da camada oculta.Os pesos aleatórios são suficientes para propagarinformações úteispela rede com retificação linear, permitindo que acamadadesaídade classificaçãoseja treinada para mapear diferentes vetores de recursosparaidentificadoresde classe. Se houver mais dados disponíveis, o processo de aprendizagem começa a extrair tanto conhecimento útil que supera osparâmetros selecionados aleatoriamente... o aprendizado é muito mais fácil em redes lineares retificadas do que em redes profundas para as quais asfunções de ativação são caracterizadas por curvatura ou saturação bidirecional...
Acho que houve um mal-entendido entre o que eu queria dizer e o que eu realmente expus em forma de texto.
Tentarei ser um pouco mais claro desta vez. 🙂 Quando queremos CATEGORIZAR coisas como imagens, objetos, formas, sons, enfim, onde as probabilidades reinam. Precisamos restringir os valores na rede neural para que fiquem dentro de um determinado intervalo. Normalmente, esse intervalo está entre -1 e 1, mas também pode estar entre 0 e 1, dependendo da rapidez, da taxa e da maneira como as informações de entrada que queremos que a rede aprenda são processadas e como ela direciona melhor seu aprendizado para criar uma classificação das coisas. NESSE CASO, PRECISAREMOS DE funções de ativação. Elas servem para manter os valores dentro desse intervalo. Acabaremos com um meio de gerar valores em termos da probabilidade de que as entradas sejam uma ou outra. Isso é um fato, e eu não o nego. Tanto é assim que muitas vezes precisamos normalizar ou padronizar os dados de entrada.
No entanto, as redes neurais não são usadas somente para classificação, elas podem ser e são usadas também para retenção de conhecimento. Nesse caso, as funções de ativação devem ser descartadas em muitos casos. Detalhe: há casos em que precisamos restringir algo. Mas esses são casos muito específicos. A questão é que essas funções impedem que a rede cumpra seu objetivo. E esse objetivo é preservar o conhecimento. E, de fato, concordo parcialmente com o comentário de Stanislav Korotsky de que a rede, nesses casos, pode ser reduzida a algo equivalente a uma única camada se você não usar funções de ativação. Mas quando isso acontecer, será um dos vários casos, porque há casos em que um único polinômio com várias variáveis não é suficiente para representar ou, melhor dizendo, armazenar conhecimento. Nesse caso, teremos de usar camadas adicionais para que o resultado possa de fato ser reproduzido. Como alternativa, novas camadas podem ser geradas. É um pouco confuso explicar dessa forma, sem uma demonstração adequada. Mas funciona.
O grande problema é que, devido à moda de tudo agora, nos últimos 10 anos, se não me falha a memória, tudo gira em torno de inteligência artificial e redes neurais. Embora o negócio só tenha realmente florescido nos últimos cinco anos. Muitas pessoas desconhecem completamente o que essas coisas realmente são. E como elas realmente funcionam. Isso ocorre porque todos que vejo estão sempre usando estruturas prontas para uso. E isso não ajuda em nada a entender como as redes neurais funcionam. É apenas uma equação com algumas variáveis. Elas têm sido estudadas no meio acadêmico há décadas. E mesmo quando saíram do meio acadêmico, nunca foram anunciadas com tanta pompa. Inicialmente, e por um longo tempo. AS FUNÇÕES DE ATIVAÇÃO NÃO ERAM USADAS. Mas o objetivo das redes, que nem sequer eram chamadas de redes neurais na época, era diferente. No entanto, como três pessoas queriam capitalizá-las, elas foram exaltadas, o que considero um tanto errado. A coisa certa a fazer, pelo menos do meu ponto de vista, teria sido explicar adequadamente sua essência. Exatamente para não criar confusão na mente de muitas pessoas. Mas tudo bem, os três ganham muito dinheiro e as pessoas estão mais perdidas do que um cachorro caindo de um caminhão de lixo. De qualquer forma, não quero desencorajá-lo a escrever mais artigos, Andrew Dick, mas quero que você continue aprendendo e tente se aprofundar ainda mais nesse tópico. Vi que você tentou usar MQL5 pura para criar um sistema. O que é muito bom, por sinal. Isso chamou minha atenção e percebi que seu artigo está muito bem escrito e planejado. Eu só queria chamar sua atenção para esse ponto e fazê-lo pensar um pouco mais sobre ele. Esse tópico é de fato muito interessante e poucas pessoas sabem sobre ele. Mas você o abordou e pesquisou.
Sim, a não linearidade é um efeito indireto que os phs de ativação têm. Eles foram originalmente planejados para traduzir de um domínio de definição de alvo para outro, por exemplo, para tarefas de classificação. A "não linearidade" pode ser obtida de diferentes maneiras, por exemplo, aumentando o número de recursos ou transformando-os, ou por núcleos que transformam os recursos.
O exemplo mais simples é a regressão logística, que permanece linear apesar da função de ativação no final.
Mas nas redes multicamadas, a não linearidade é obtida devido ao número de camadas com funções de ativação, simplesmente como consequência de transformações do tipo kernel.Contexto histórico:
Você está correto ao afirmar que os conceitos subjacentes à regressão logística e às primeiras redes neurais vieram antes das redes neurais profundas modernas.
Vamos dar uma olhada na cronologia:
-
Afunção logística foi desenvolvida no século XIX. Seu uso como modelo estatístico para classificação (regressão logística) tornou-se popular em meados do século XX (aproximadamente entre as décadas de 1940 e 1950).
-
O primeiro modelo matemático de um neurônio (o modelo de McCulloch e Pitts) com uma função de ativação surgiu em 1943. Ele usava uma função de limiar simples.
-
O perceptron, uma rede neural de camada única, foi desenvolvido por Frank Rosenblatt em 1958. Ele usava uma função de ativação de limiar e só podia resolver problemas linearmente separáveis.
-
Oavanço na aprendizagem profunda enas redes multicamadas ocorreu somente com o advento do algoritmo de retropropagação, popularizado em 1986 por Rumelhart, Hinton e Williams.
Foi esse algoritmo que tornou prático o treinamento de redes neurais multicamadas e mostrou que ele exige não apenas limiar, mas funções de ativação não lineares diferenciáveis (como sigmoide e, posteriormente, ReLU).
Conclusão:
Historicamente, verifica-se que:
-
Primeiro, havia modelos (regressão logística, perceptron) que eram essencialmente modelos de uma camada.
-
Nesses modelos, a função de ativação realmente agia como uma transformação para o domínio desejado (de uma soma linear para uma classe binária ou probabilidade), já que o modelo inteiro permanecia linear.
-
Mais tarde, com o advento das redes multicamadas, surgiu um novo papel, fundamentalmente mais importante, da função de ativação: introduzir a não linearidade nas camadas ocultas para que a rede pudesse aprender.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Funções de ativação de neurônios durante o aprendizado: chave para uma convergência rápida? foi publicado:
Imagine um rio com muitos afluentes. Em condições normais, a água flui livremente, formando um padrão complexo de correntes e redemoinhos. Mas o que acontece se começarmos a construir um sistema de eclusas e represas? Conseguiremos controlar o fluxo da água, direcioná-lo para o caminho desejado e regular a força da corrente. A função de ativação em redes neurais cumpre papel semelhante: ela decide qual sinal deve ser transmitido adiante, qual deve ser retido ou enfraquecido. Sem ela, uma rede neural seria apenas um conjunto de transformações lineares.
A função de ativação traz dinâmica ao funcionamento da rede neural, permitindo capturar sutilezas nos dados. Por exemplo, em tarefas de reconhecimento facial, a função de ativação ajuda a rede a perceber detalhes mínimos, como a curvatura das sobrancelhas ou o formato do queixo. A escolha adequada da função de ativação afeta diretamente como a rede neural lida com diferentes tarefas. Algumas funções são mais eficazes nas fases iniciais do aprendizado, fornecendo sinais claros e compreensíveis. Outras permitem que a rede capte padrões mais sutis em estágios avançados. E há aquelas que eliminam tudo o que é desnecessário, preservando apenas o essencial.
Se não conhecermos as propriedades das funções de ativação, podemos nos deparar com problemas. A rede neural pode começar a "tropeçar" em tarefas simples ou "ignorar" detalhes importantes. A principal tarefa das funções de ativação é introduzir não linearidade na rede neural e normalizar os valores de saída.
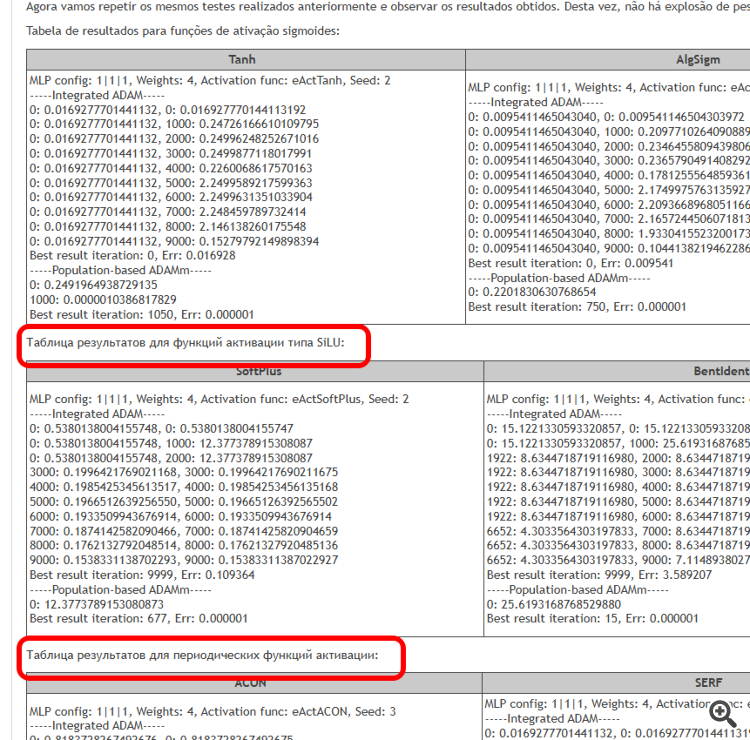
O objetivo deste artigo é identificar os problemas associados ao uso de diferentes funções de ativação e seu impacto na precisão com que a rede neural atravessa os pontos dos exemplos (interpolação) durante a minimização do erro. Também vamos investigar se as funções de ativação realmente influenciam a velocidade de convergência ou se isso é uma característica do algoritmo de otimização utilizado. Como referência, aplicaremos o ADAMm populacional modificado, que utiliza elementos de estocasticidade, e realizaremos testes com o ADAM incorporado no MLP (uso clássico). Este último, intuitivamente, deveria ter vantagem, pois tem acesso direto ao gradiente da superfície da função de fitness graças à derivada da função de ativação. Já o ADAMm populacional estocástico não tem acesso à derivada e não tem nenhuma noção da superfície do problema de otimização. Vamos observar o que resulta disso e tirar conclusões.
Autor: Andrey Dik