Otimização de portfólio em Forex: Síntese de VaR e teoria de Markowitz

Introdução: objetivos da otimização de portfólio no Forex

Passei os últimos três anos desenvolvendo EAs (Expert Advisors) para o Forex. E sabe de uma coisa? Gerenciar risco é um verdadeiro tormento. No começo eu só colocava stop fixo, até quebrar algumas contas. Depois comecei a ir mais fundo, e encontrei a teoria de otimização de portfólio de Markowitz.

Parecia lindo: você calcula correlações, otimiza os pesos... Mas na prática isso não funciona muito bem no Forex. Por quê? Porque no Forex todos os pares estão conectados! Tente operar EURUSD e EURGBP ao mesmo tempo e vai entender do que estou falando. Um único movimento brusco do euro e ambas as posições vão por água abaixo juntas. Depois de muito sofrer com isso,

fui buscar outras abordagens. Encontrei a metodologia Value at Risk (VaR). No começo nem entendi o que era, pois eram umas fórmulas complicadas. Mas depois caiu a ficha: é exatamente o que precisava! O VaR mostra as perdas máximas com uma certa probabilidade. Ou seja, dá pra estimar diretamente quanto dinheiro pode ser perdido por dia/semana/mês.

No fim, resolvi unir Markowitz com VaR. Ideia maluca? Talvez. Mas não via outra saída. Markowitz fornece a distribuição ideal dos recursos, e o VaR impede que a conta seja zerada por um margin call. No papel, parecia perfeito.

Aí começaram os dias difíceis como programador-pesquisador. Python, terminal MetaTrader 5, toneladas de dados históricos... Eu sabia que não seria fácil, mas a realidade superou todas as expectativas. É disso que quero falar: como tentei criar um sistema que realmente funcione, e não apenas pareça bonito no backtest.

Se você já tentou automatizar trading no Forex, vai entender minha dor. E se não tentou, talvez minha experiência ajude a evitar pelo menos alguns dos tombos inevitáveis no caminho.

Fundamentos teóricos e matemáticos do VaR e da teoria de Markowitz

Então, vamos começar pela teoria. No primeiro mês eu só tentei entender a matemática. A teoria de Markowitz parece complicada, cheia de fórmulas, matrizes, otimização quadrática... Você pega os retornos dos ativos, calcula correlações e encontra os pesos que minimizam o risco para um retorno esperado.

No começo, achei que era uma maravilha! Mas aí comecei a testar com dados reais do Forex, e foi aí que tudo desandou... Peguei o histórico do EURUSD de um ano, e a distribuição dos retornos passou longe de ser normal. O mesmo aconteceu com o GBPUSD, e isso é um pressuposto fundamental da teoria de Markowitz. Ou seja, todos os cálculos foram por água abaixo.

Perdi uma semana tentando achar uma solução. Vasculhei artigos científicos, pesquisei no Google, li fóruns. Aí me lembrei do meu próprio texto sobre VaR - Value at Risk. Parece algo sofisticado, mas no fundo é simples: basicamente calculamos quanto podemos perder com uma probabilidade de 95% (ou qualquer outra). Primeiro testei a versão mais simples, o VaR paramétrico. A fórmula é básica: média menos sigma vezes o quantil. Mas o desempenho foi bem fraco.

Depois migrei para o VaR histórico. A ideia é usar o histórico real e ver quais foram os prejuízos nos piores 5% dos casos. Muito mais próximo da realidade, mas exige uma grande quantidade de dados. E aí veio o chefão final: o método de Monte Carlo. A gente gera um monte de cenários aleatórios considerando a correlação entre os pares, e aí sim, o resultado começa a fazer sentido.

A parte mais complicada foi bolar como unir o VaR com a otimização de Markowitz. No fim, surgiu a seguinte abordagem: usamos a otimização padrão, mas com uma restrição baseada no VaR. Ou seja, buscamos o menor risco para uma determinada rentabilidade, mas garantindo que o VaR não ultrapasse um certo limite.

No papel ficou ótimo, mas tentar programar isso... é outra história. Vou falar disso nas próximas seções, onde explico como transformei essas fórmulas em código funcional em Python.

Conexão com MetaTrader 5 a partir do Python

A implementação prática do meu sistema começou com o estabelecimento de uma conexão estável com o terminal de trading. Depois de testar várias abordagens, optei pela conexão direta via biblioteca MetaTrader 5 para Python, que se mostrou a mais confiável e rápida.

import MetaTrader5 as mt5
import time

def initialize_mt5(account=12345, server="MetaQuotes-Demo", password="abc123"):
    if not mt5.initialize():
        print(f"initialize() failed, error code = {mt5.last_error()}")
        return False
        
    authorized = mt5.login(account, password=password, server=server)
    if not authorized:
        print(f"login failed, error code = {mt5.last_error()}")
        mt5.shutdown()
        return False
        
    return True

Um desafio à parte foi a sincronização de tempo entre o servidor da corretora e o sistema local. Diferenças de apenas alguns segundos podiam causar grandes problemas no cálculo do VaR. Precisei criar um mecanismo especial de correção:

def get_time_correction():
    server_time = mt5.symbol_info_tick("EURUSD").time
    local_time = int(time.time())
    return server_time - local_time

def get_corrected_time():
    correction = get_time_correction()
    return int(time.time()) + correction

Dediquei muito tempo à otimização da coleta de dados. No início, fazia requisições para cada par de moedas separadamente, mas depois que implementei o processamento em lote, a velocidade aumentou drasticamente:

def fetch_data_batch(symbols, timeframe, start_pos, count):
    data = {}
    for symbol in symbols:
        rates = mt5.copy_rates_from_pos(symbol, timeframe, start_pos, count)
        if rates is not None and len(rates) > 0:
            data[symbol] = rates
        else:
            print(f"Failed to get data for {symbol}")
            return None
    return data

Foi surpreendentemente difícil fazer o encerramento correto do programa. Tive que desenvolver um procedimento especial de graceful shutdown:

def safe_shutdown():
    try:
        positions = mt5.positions_get()
        if positions:
            for position in positions:
                close_position(position.ticket)
        
        orders = mt5.orders_get()
        if orders:
            for order in orders:
                mt5.order_send(request={"action": mt5.TRADE_ACTION_REMOVE,
                                      "order": order.ticket})
    finally:
        mt5.shutdown()

No fim, consegui montar uma base robusta para todo o sistema, capaz de operar 24 horas por dia sem falhas. A partir dela, já dava para construir lógicas mais complexas de otimização de portfólio. Mas isso já é assunto para a próxima seção.

Coleta de dados históricos e pré-processamento

Ao longo dos anos trabalhando com dados de mercado, aprendi uma verdade simples: a qualidade dos dados históricos é absolutamente crítica para qualquer sistema de trading. Isso é ainda mais importante quando falamos em otimização de portfólio, onde erros nos dados podem se propagar de forma exponencial.

Comecei criando um sistema confiável de carregamento de histórico. A primeira versão era bem simples, mas a experiência logo revelou suas falhas. As cotações podiam conter buracos, picos falsos e até valores claramente incorretos. Veja como ficou a versão final do código com uma validação básica:

def load_historical_data(symbols, timeframe, start_date, end_date):
    data_frames = {}
    for symbol in symbols:
        # Load with a reserve to compensate for gaps
        rates = mt5.copy_rates_range(symbol, timeframe, 
                                   start_date - timedelta(days=30), 
                                   end_date)
        if rates is None:
            print(f"Failed to load data for {symbol}")
            continue
            
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        df.set_index('time', inplace=True)
        
        # Basic anomaly check
        df = detect_and_remove_spikes(df)
        df = fill_gaps(df)
        data_frames[symbol] = df
    
    return data_frames

Um desafio à parte foi lidar com os gaps de fim de semana. A princípio, eu simplesmente removia esses dias, mas isso distorcia os cálculos de volatilidade. Depois de muitos testes, desenvolvi um método de interpolação que leva em conta a especificidade de cada par de moedas:

def fill_gaps(df, method='time'):
    if df.empty:
        return df
        
    # Check the intervals between points
    time_delta = df.index.to_series().diff()
    gaps = time_delta[time_delta > pd.Timedelta(hours=2)].index
    
    for gap_start in gaps:
        gap_end = df.index[df.index.get_loc(gap_start) + 1]
        # Create new points with interpolated values
        new_points = pd.date_range(gap_start, gap_end, freq='1H')[1:-1]
        
        for point in new_points:
            df.loc[point] = df.asof(point)
    
    return df.sort_index()

Para calcular os retornos, testei várias abordagens. As variações percentuais simples eram barulhentas demais. Os retornos logarítmicos deram resultados bem melhores na estimativa do VaR:

def calculate_returns(df):
    df['returns'] = np.log(df['close'] / df['close'].shift(1))
    df['rolling_std'] = df['returns'].rolling(window=20).std()
    df['rolling_mean'] = df['returns'].rolling(window=20).mean()
    
    # Clean out emissions using the 3-sigma rule
    mean = df['returns'].mean()
    std = df['returns'].std()
    df = df[abs(df['returns'] - mean) <= 3 * std]
    
    return df

Uma etapa essencial foi criar um sistema de verificação dos dados. Cada conjunto passa por uma checagem em múltiplos níveis antes de ser usado nos cálculos:

def verify_data_quality(df, symbol):
    checks = {
        'missing_values': df.isnull().sum().sum() == 0,
        'price_continuity': (df['close'] > 0).all(),
        'timestamp_uniqueness': df.index.is_unique,
        'reasonable_returns': abs(df['returns']).max() < 0.1
    }
    
    if not all(checks.values()):
        failed_checks = [k for k, v in checks.items() if not v]
        print(f"Data quality issues for {symbol}: {failed_checks}")
        return False
        
    return True

Dediquei uma atenção especial ao tratamento de anomalias de mercado. Eventos como movimentos bruscos durante notícias ou flash crashes podem distorcer fortemente a avaliação de risco. Desenvolvi um algoritmo específico para detectá-los e tratá-los de forma apropriada:

def detect_market_anomalies(df, window=20, threshold=3):
    volatility = df['returns'].rolling(window=window).std()
    typical_range = volatility.mean() + threshold * volatility.std()
    
    anomalies = df[abs(df['returns']) > typical_range].index
    if len(anomalies) > 0:
        print(f"Detected {len(anomalies)} market anomalies")
        
    return anomalies

O resultado foi uma linha de produção de dados sólida, que virou a base de todos os cálculos futuros. Dados históricos de qualidade são o alicerce sem o qual não dá para construir um sistema eficaz de gestão de portfólio. No próximo trecho, explico como esses dados são usados no cálculo do VaR.

Implementação do cálculo de VaR para pares de moedas

Depois de muito trabalho com os dados históricos, mergulhei na implementação do cálculo do VaR. A princípio parecia que bastava pegar as fórmulas prontas e transformar em código. A realidade se mostrou bem mais complexa, pois a natureza do Forex exigia modificações sérias nos métodos tradicionais.

Comecei implementando os três métodos clássicos de cálculo do VaR. Veja como ficou a abordagem paramétrica:

def parametric_var(returns, confidence_level=0.95, holding_period=1):
    mu = returns.mean()
    sigma = returns.std()
    z_score = norm.ppf(1 - confidence_level)
    
    daily_var = -(mu + z_score * sigma)
    return daily_var * np.sqrt(holding_period)

Logo ficou claro que o pressuposto de distribuição normal dos retornos no Forex frequentemente não se sustenta. O método histórico se mostrou mais confiável:

def historical_var(returns, confidence_level=0.95, holding_period=1):
    sorted_returns = np.sort(returns)
    index = int((1 - confidence_level) * len(sorted_returns))
    daily_var = -sorted_returns[index]
    return daily_var * np.sqrt(holding_period)

Mas os resultados mais interessantes vieram com o método de Monte Carlo. Fiz modificações para adaptá-lo à dinâmica específica do mercado de moedas:

def monte_carlo_var(returns, confidence_level=0.95, holding_period=1, simulations=10000):
    mu = returns.mean()
    sigma = returns.std()
    
    # Consider auto correlation of returns
    corr = returns.autocorr()
    
    simulated_returns = []
    for _ in range(simulations):
        daily_returns = []
        last_return = returns.iloc[-1]
        
        for _ in range(holding_period):
            # Generate the next value taking auto correlation into account
            innovation = np.random.normal(0, 1)
            next_return = mu + corr * (last_return - mu) + sigma * np.sqrt(1 - corr**2) * innovation
            daily_returns.append(next_return)
            last_return = next_return
            
        total_return = sum(daily_returns)
        simulated_returns.append(total_return)
    
    return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

Dei atenção especial à validação dos resultados. Criei um sistema de backtest para verificar a precisão do VaR:

def backtest_var(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    
    z_score = (violations - expected_violations) / np.sqrt(expected_violations)
    p_value = 1 - norm.cdf(abs(z_score))
    
    return {
        'violations': violations,
        'expected': expected_violations,
        'z_score': z_score,
        'p_value': p_value
    }

Para levar em conta as inter-relações entre os pares de moedas, precisei implementar o cálculo do VaR do portfólio:

def portfolio_var(returns_df, weights, confidence_level=0.95, method='historical'):
    if method == 'parametric':
        portfolio_returns = returns_df.dot(weights)
        return parametric_var(portfolio_returns, confidence_level)
    
    elif method == 'historical':
        portfolio_returns = returns_df.dot(weights)
        return historical_var(portfolio_returns, confidence_level)
    
    elif method == 'monte_carlo':
        # Use the covariance matrix to generate
        # correlated random variables
        cov_matrix = returns_df.cov()
        L = np.linalg.cholesky(cov_matrix)
        
        means = returns_df.mean().values
        simulated_returns = []
        
        for _ in range(10000):
            Z = np.random.standard_normal(len(weights))
            R = means + L @ Z
            portfolio_return = weights @ R
            simulated_returns.append(portfolio_return)
            
        return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

O resultado foi um sistema flexível de cálculo de VaR, adaptado à natureza específica do Forex. Na próxima parte, explico como esses cálculos são integrados à teoria de Markowitz para otimização de portfólio.

Otimização de portfólio pelo método de Markowitz

Depois de implementar um cálculo de VaR confiável, mergulhei de vez na otimização de portfólio. A teoria clássica de Markowitz exigia uma adaptação séria às particularidades do Forex. Meses de testes e experimentações me levaram a algumas descobertas importantes.

A primeira coisa que percebi foi que as métricas padrão de risco e retorno se comportam de forma diferente no Forex do que no mercado de ações. Os pares de moedas têm interdependências complexas que mudam com o tempo. Após muitos testes, desenvolvi uma função modificada para o cálculo da expectativa de retorno:

def calculate_expected_returns(returns_df, method='ewma', halflife=30):
    if method == 'ewma':
        # Exponentially weighted average gives more weight to recent data
        return returns_df.ewm(halflife=halflife).mean().iloc[-1]
    elif method == 'capm':
        # Modified CAPM for Forex
        risk_free_rate = 0.02  # annual risk-free rate
        market_returns = returns_df.mean(axis=1)  # market returns proxy
        betas = calculate_currency_betas(returns_df, market_returns)
        return risk_free_rate + betas * (market_returns.mean() - risk_free_rate)

O cálculo da matriz de covariância também precisou de ajustes. O método histórico simples gerava resultados instáveis demais. Implementei uma estimativa com shrinkage, que melhorou bastante a estabilidade da otimização:

def shrinkage_covariance(returns_df, shrinkage_factor=None):
    sample_cov = returns_df.cov()
    n_assets = len(returns_df.columns)
    
    # The target matrix is diagonal with average variance
    target = np.diag(np.repeat(sample_cov.values.trace() / n_assets, n_assets))
    
    if shrinkage_factor is None:
        # Estimation of the optimal 'shrinkage' ratio
        shrinkage_factor = estimate_optimal_shrinkage(returns_df, sample_cov, target)
    
    shrunk_cov = (1 - shrinkage_factor) * sample_cov + shrinkage_factor * target
    return pd.DataFrame(shrunk_cov, index=sample_cov.index, columns=sample_cov.columns)

A parte mais desafiadora foi otimizar os pesos do portfólio. Depois de muitos testes, optei por um algoritmo de programação quadrática modificado:

def optimize_portfolio(returns_df, expected_returns, covariance, target_return=None, constraints=None):
    n_assets = len(returns_df.columns)
    
    # Risk minimization function
    def portfolio_volatility(weights):
        return np.sqrt(weights.T @ covariance @ weights)
    
    # Limitations
    constraints = []
    # The sum of the weights is 1
    constraints.append({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
    
    if target_return is not None:
        # Target income limit
        constraints.append({
            'type': 'eq',
            'fun': lambda x: x @ expected_returns - target_return
        })
    
    # Add leverage restrictions for Forex
    constraints.append({
        'type': 'ineq',
        'fun': lambda x: 20 - np.sum(np.abs(x))  # max leverage 20
    })
    
    # Initial approximation - equal weights
    initial_weights = np.repeat(1/n_assets, n_assets)
    
    # Optimization
    result = minimize(
        portfolio_volatility,
        initial_weights,
        method='SLSQP',
        constraints=constraints,
        bounds=tuple((0, 1) for _ in range(n_assets))
    )
    
    if not result.success:
        raise OptimizationError("Failed to optimize portfolio: " + result.message)
        
    return result.x

Dediquei atenção especial à questão da robustez da solução. Pequenas variações nos dados de entrada não devem provocar mudanças drásticas na composição do portfólio. Para isso, criei um processo de regularização:

def regularized_optimization(returns_df, current_weights, lambda_reg=0.1):
    # Add a penalty for deviation from the current weights
    def objective(weights):
        volatility = portfolio_volatility(weights)
        turnover_penalty = lambda_reg * np.sum(np.abs(weights - current_weights))
        return volatility + turnover_penalty

No final, obtive um otimizador de portfólio confiável, adaptado ao contexto do Forex e que não exige rebalanceamentos frequentes. Mas o mais importante ainda estava por vir: integrar essa abordagem com o sistema de controle de risco baseado em VaR.

Integração de VaR e Markowitz em um único modelo

A união dos dois métodos foi a parte mais complexa de toda a pesquisa. Era necessário encontrar um jeito de aproveitar os pontos fortes de ambos, sem gerar conflitos entre eles. Após vários meses de experimentação, cheguei a uma solução elegante.

A ideia central foi usar o VaR como uma restrição adicional no problema de otimização de Markowitz. Veja como isso aparece no código:

def integrated_portfolio_optimization(returns_df, target_return, max_var_limit, current_weights=None):
    n_assets = len(returns_df.columns)
    
    # Calculation of basic metrics
    exp_returns = calculate_expected_returns(returns_df)
    covariance = shrinkage_covariance(returns_df)
    
    def objective_function(weights):
        # Portfolio standard deviation (Markowitz)
        portfolio_std = np.sqrt(weights.T @ covariance @ weights)
        
        # component VaR
        portfolio_var = calculate_portfolio_var(returns_df, weights)
        var_penalty = max(0, portfolio_var - max_var_limit)
        
        return portfolio_std + 100 * var_penalty  # Penalty for exceeding VaR

Para lidar com a natureza dinâmica do mercado, desenvolvi um sistema adaptativo de reavaliação dos parâmetros:

def adaptive_risk_limits(returns_df, base_var_limit, window=60):
    # Adapting VaR limits to current volatility
    recent_vol = returns_df.tail(window).std()
    long_term_vol = returns_df.std()
    vol_ratio = recent_vol / long_term_vol
    
    adjusted_var_limit = base_var_limit * np.sqrt(vol_ratio)
    return min(adjusted_var_limit, base_var_limit * 1.5)  # Limit growth

A estabilidade da solução exigiu atenção especial. Implementei um mecanismo de transição suave entre os estados do portfólio:

def smooth_rebalancing(old_weights, new_weights, max_change=0.1):
    weight_diff = new_weights - old_weights
    excess_change = np.abs(weight_diff) - max_change
    
    where_excess = excess_change > 0
    if where_excess.any():
        # Limit changes in weights
        adjustment = np.sign(weight_diff) * np.minimum(
            np.abs(weight_diff),
            np.where(where_excess, max_change, np.abs(weight_diff))
        )
        return old_weights + adjustment
    return new_weights

Para avaliar a eficácia da abordagem combinada, criei uma métrica específica:

def evaluate_integrated_model(returns_df, weights, var_limit):
    # Calculation of performance metrics
    portfolio_returns = returns_df.dot(weights)
    realized_var = historical_var(portfolio_returns)
    sharpe = calculate_sharpe_ratio(portfolio_returns)
    var_efficiency = abs(realized_var - var_limit) / var_limit
    
    return {
        'sharpe_ratio': sharpe,
        'var_efficiency': var_efficiency,
        'max_drawdown': calculate_max_drawdown(portfolio_returns),
        'turnover': calculate_turnover(weights)
    }

Durante os testes, ficou claro que o modelo se sai especialmente bem em períodos de alta volatilidade. O componente VaR limita os riscos de forma eficaz, enquanto a otimização de Markowitz continua buscando oportunidades de rentabilidade.

A versão final do sistema inclui ainda um mecanismo de ajuste automático dos parâmetros:

def auto_tune_parameters(returns_df, initial_params, optimization_window=252):
    best_params = initial_params
    best_score = float('-inf')
    
    for var_limit in np.arange(0.01, 0.05, 0.005):
        for shrinkage in np.arange(0.2, 0.8, 0.1):
            params = {'var_limit': var_limit, 'shrinkage': shrinkage}
            score = backtest_model(returns_df, params, optimization_window)
            
            if score > best_score:
                best_score = score
                best_params = params
                
    return best_params

Na próxima parte, explico como esse modelo unificado é aplicado para a gestão dinâmica de posições no trading real.

Gestão dinâmica do tamanho das posições

Transformar o modelo teórico em um sistema de trading prático exigiu resolver várias questões técnicas. A principal delas foi o gerenciamento dinâmico do tamanho das posições, considerando as condições atuais do mercado e os pesos ótimos do portfólio calculados.

A base da estrutura foi uma classe dedicada ao gerenciamento de posições:

class PositionManager:
    def __init__(self, account_balance, risk_limit=0.02):
        self.balance = account_balance
        self.risk_limit = risk_limit
        self.positions = {}
        
    def calculate_position_size(self, symbol, weight, var_estimate):
        symbol_info = mt5.symbol_info(symbol)
        pip_value = symbol_info.trade_tick_value * 10
        
        # Calculate the position size taking into account VaR
        max_risk_amount = self.balance * self.risk_limit * abs(weight)
        position_size = max_risk_amount / (abs(var_estimate) * pip_value)
        
        # Round to minimum lot
        return round(position_size / symbol_info.volume_step) * symbol_info.volume_step

Para fazer a transição suave entre posições, desenvolvi um mecanismo de ordens parciais:

def adjust_positions(self, target_positions):
    for symbol, target_size in target_positions.items():
        current_size = self.get_current_position(symbol)
        if abs(target_size - current_size) > self.min_adjustment:
            # Break big changes into pieces
            steps = min(5, int(abs(target_size - current_size) / self.min_adjustment))
            step_size = (target_size - current_size) / steps
            
            for i in range(steps):
                next_size = current_size + step_size
                self.execute_order(symbol, next_size - current_size)
                current_size = next_size
                time.sleep(1)  # Prevent order flooding

Dediquei especial atenção ao controle de risco durante a alteração das posições:

def execute_order(self, symbol, size_delta, max_slippage=10):
    if size_delta > 0:
        order_type = mt5.ORDER_TYPE_BUY
    else:
        order_type = mt5.ORDER_TYPE_SELL
    
    # Get current prices
    tick = mt5.symbol_info_tick(symbol)
    
    # Set VaR-based stop loss
    if order_type == mt5.ORDER_TYPE_BUY:
        stop_loss = tick.bid - (self.var_estimates[symbol] * tick.bid)
        take_profit = tick.bid + (self.var_estimates[symbol] * 2 * tick.bid)
    else:
        stop_loss = tick.ask + (self.var_estimates[symbol] * tick.ask)
        take_profit = tick.ask - (self.var_estimates[symbol] * 2 * tick.ask)
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": abs(size_delta),
        "type": order_type,
        "price": tick.ask if order_type == mt5.ORDER_TYPE_BUY else tick.bid,
        "sl": stop_loss,
        "tp": take_profit,
        "deviation": max_slippage,
        "magic": 234000,
        "comment": "var_based_adjustment",
        "type_time": mt5.ORDER_TIME_GTC,
        "type_filling": mt5.ORDER_FILLING_IOC,
    }
    
    result = mt5.order_send(request)
    return self.handle_order_result(result)

Para proteção contra movimentos bruscos do mercado, adicionei um sistema de monitoramento da volatilidade:

def monitor_volatility(self, returns_df, threshold=2.0):
    # Current volatility calculation
    current_vol = returns_df.tail(20).std() * np.sqrt(252)
    historical_vol = returns_df.std() * np.sqrt(252)
    
    if current_vol > historical_vol * threshold:
        # Reduce positions in case of increased volatility
        self.reduce_exposure(current_vol / historical_vol)
        return False
        
    return True

O sistema também inclui um mecanismo de fechamento automático de posições ao atingir níveis críticos de risco:

def emergency_close(self, max_loss_percent=5.0):
    total_loss = sum(pos.profit for pos in mt5.positions_get())
    if total_loss < -self.balance * max_loss_percent / 100:
        print("Emergency closure triggered!")
        for position in mt5.positions_get():
            self.close_position(position.ticket)

O resultado foi um sistema robusto de gerenciamento de posições, capaz de operar com eficiência em diferentes condições de mercado. O próximo trecho será sobre o sistema de controle de risco baseado em VaR.

Sistema de controle de risco do portfólio

Após implementar a gestão dinâmica de posições, vi que era necessário criar um sistema de controle de risco abrangente para todo o portfólio. A experiência mostrou que o controle isolado de risco por posição não basta, então era preciso uma abordagem integrada.

Tudo começou com a criação de uma classe para monitorar os riscos do portfólio:

class PortfolioRiskManager:
    def __init__(self, max_portfolio_var=0.03, max_correlation=0.7, max_drawdown=0.1):
        self.max_portfolio_var = max_portfolio_var
        self.max_correlation = max_correlation
        self.max_drawdown = max_drawdown
        self.current_drawdown = 0
        self.peak_balance = 0
        
    def update_portfolio_metrics(self, positions, returns_df):
        # Calculation of current portfolio weights
        total_exposure = sum(abs(pos.volume) for pos in positions)
        weights = {pos.symbol: pos.volume/total_exposure for pos in positions}
        
        # Update portfolio VaR
        self.current_var = self.calculate_portfolio_var(returns_df, weights)
        
        # Check correlations
        self.check_correlations(returns_df, weights)

Dediquei atenção especial ao controle das correlações entre os instrumentos:

def check_correlations(self, returns_df, weights):
    corr_matrix = returns_df.corr()
    high_corr_pairs = []
    
    for i in returns_df.columns:
        for j in returns_df.columns:
            if i < j and abs(corr_matrix.loc[i,j]) > self.max_correlation:
                if weights.get(i, 0) > 0 and weights.get(j, 0) > 0:
                    high_corr_pairs.append((i, j, corr_matrix.loc[i,j]))
                    
    if high_corr_pairs:
        self.handle_high_correlations(high_corr_pairs, weights)

Implementei uma gestão dinâmica de risco conforme as condições do mercado:

def adjust_risk_limits(self, market_state):
    volatility_factor = market_state.get('volatility_ratio', 1.0)
    trend_strength = market_state.get('trend_strength', 0.5)
    
    # Adapt limits to market conditions
    self.max_portfolio_var *= np.sqrt(volatility_factor)
    if trend_strength > 0.7:  # Strong trend
        self.max_drawdown *= 1.2  # Allow a big drawdown
    elif trend_strength < 0.3:  # Weak trend
        self.max_drawdown *= 0.8  # Reduce the acceptable drawdown

O sistema de monitoramento de rebaixamentos ficou especialmente interessante:

def monitor_drawdown(self, current_balance):
    if current_balance > self.peak_balance:
        self.peak_balance = current_balance
    
    self.current_drawdown = (self.peak_balance - current_balance) / self.peak_balance
    
    if self.current_drawdown > self.max_drawdown:
        return self.handle_excessive_drawdown()
    elif self.current_drawdown > self.max_drawdown * 0.8:
        return self.reduce_risk_exposure(0.8)
    
    return True

Para proteger contra eventos extremos, adicionei um sistema de stress testing:

def stress_test_portfolio(self, returns_df, weights, scenarios=1000):
    results = []
    
    for _ in range(scenarios):
        # Simulate extreme conditions
        stress_returns = returns_df.copy()
        
        # Increase volatility
        vol_multiplier = np.random.uniform(1.5, 3.0)
        stress_returns *= vol_multiplier
        
        # Add random shocks
        shock_magnitude = np.random.uniform(-0.05, 0.05)
        stress_returns += shock_magnitude
        
        # Calculate losses in a stress scenario
        portfolio_return = (stress_returns * weights).sum(axis=1)
        results.append(portfolio_return.min())
    
    return np.percentile(results, 1)  # 99% VaR in case of a stress

O resultado foi uma estrutura de proteção de capital em múltiplos níveis, que previne eficazmente riscos excessivos e ajuda a atravessar períodos de alta volatilidade. Na próxima parte, mostro como todos esses componentes funcionam juntos no trading real.

Visualização dos resultados da análise

A visualização se tornou uma etapa fundamental da minha pesquisa. Após implementar todos os módulos de cálculo, era preciso criar representações visuais claras dos resultados. Desenvolvi vários componentes gráficos chave para acompanhar o funcionamento do sistema em tempo real.

Comecei com a visualização da estrutura do portfólio e sua evolução:

def plot_portfolio_composition(weights_history):
    plt.figure(figsize=(15, 8))
    ax = plt.gca()
    
    # Create a graph of weight changes over time
    dates = weights_history.index
    bottom = np.zeros(len(dates))
    
    for symbol in weights_history.columns:
        plt.fill_between(dates, bottom, bottom + weights_history[symbol], 
                        label=symbol, alpha=0.6)
        bottom += weights_history[symbol]
    
    plt.title('Evolution of portfolio structure')
    plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
    plt.grid(True, alpha=0.3)

Dei atenção especial à visualização dos riscos. Criei um mapa de calor do VaR para diferentes pares de moedas:

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='RdYlBu_r', 
                fmt='.2%', center=0)
    plt.title('Portfolio risk map (VaR)')
    
    # Add a timestamp
    plt.annotate(f'Last update: {datetime.now().strftime("%Y-%m-%d %H:%M")}',
                xy=(0.01, -0.1), xycoords='axes fraction')

Para a análise de rentabilidade, desenvolvi um gráfico interativo com destaque para eventos importantes:

def plot_performance_analytics(returns_df, var_values, significant_events):
    fig = plt.figure(figsize=(15, 10))
    gs = GridSpec(2, 1, height_ratios=[3, 1])
    
    # Returns graph
    ax1 = plt.subplot(gs[0])
    cumulative_returns = (1 + returns_df).cumprod()
    ax1.plot(cumulative_returns.index, cumulative_returns, 
             label='Portfolio returns')
    
    # Mark important events
    for date, event in significant_events.items():
        ax1.axvline(x=date, color='r', linestyle='--', alpha=0.3)
        ax1.annotate(event, xy=(date, ax1.get_ylim()[1]),
                    xytext=(10, 10), textcoords='offset points',
                    rotation=45)
    
    # VaR graph
    ax2 = plt.subplot(gs[1])
    ax2.fill_between(var_values.index, -var_values, 
                     color='lightblue', alpha=0.5,
                     label='Value at Risk')

Adicionei um painel interativo para o monitoramento do estado do portfólio:

class PortfolioDashboard:
    def __init__(self):
        self.fig = plt.figure(figsize=(15, 10))
        self.setup_subplots()
        
    def setup_subplots(self):
        gs = self.fig.add_gridspec(3, 2)
        self.ax_returns = self.fig.add_subplot(gs[0, :])
        self.ax_weights = self.fig.add_subplot(gs[1, 0])
        self.ax_risk = self.fig.add_subplot(gs[1, 1])
        self.ax_metrics = self.fig.add_subplot(gs[2, :])
        
    def update(self, portfolio_data):
        self._plot_returns(portfolio_data['returns'])
        self._plot_weights(portfolio_data['weights'])
        self._plot_risk_metrics(portfolio_data['risk'])
        self._update_metrics_table(portfolio_data['metrics'])
        
        plt.tight_layout()
        plt.show()

Para análise de correlações, desenvolvi uma visualização dinâmica:

def plot_correlation_dynamics(returns_df, window=60):
    # Calculation of dynamic correlations
    correlations = returns_df.rolling(window=window).corr()
    
    # Create an animated graph
    fig, ax = plt.subplots(figsize=(10, 10))
    
    def update(frame):
        ax.clear()
        sns.heatmap(correlations.loc[frame], 
                    vmin=-1, vmax=1, center=0,
                    cmap='RdBu', ax=ax)
        ax.set_title(f'Correlations on {frame.strftime("%Y-%m-%d")}')

Todas essas visualizações ajudam a avaliar rapidamente o estado do portfólio e tomar decisões de trading. Na próxima parte, explico o processo de teste da estratégia.

Backtest da estratégia

Depois de concluir o desenvolvimento de todos os componentes do sistema, me deparei com a necessidade de testá-lo com muito rigor. O processo foi muito mais complexo do que apenas rodar dados históricos. Era preciso considerar uma série de fatores: slippage, comissões, e as particularidades de execução de ordens em diferentes corretoras.

As primeiras tentativas de backtest mostraram que a abordagem clássica com spreads fixos produzia resultados excessivamente otimistas. Tive que criar um modelo mais realista, que levasse em conta a variação dos spreads conforme a volatilidade e o horário do dia.

Dediquei atenção especial à modelagem de gaps de dados e problemas de liquidez. No trading real, é comum haver situações em que uma ordem não pode ser executada no preço estimado. Esses cenários precisam ser corretamente tratados durante os testes.

Aqui está a implementação completa do sistema de backtest:

class PortfolioBacktester:
    def __init__(self, initial_capital=100000, commission=0.0001):
        self.initial_capital = initial_capital
        self.commission = commission
        self.positions = {}
        self.trades_history = []
        self.balance_history = []
        self.var_history = []
        self.metrics = {}
        
    def run_backtest(self, returns_df, optimization_params):
        self.current_capital = self.initial_capital
        portfolio_returns = []
        
        # Preparing sliding windows for calculations
        window = 252  # Trading yesr
        for i in range(window, len(returns_df)):
            # Receive historical data for calculation
            historical_returns = returns_df.iloc[i-window:i]
            
            # Optimize the portfolio
            weights = self.optimize_portfolio(
                historical_returns, 
                optimization_params['target_return'],
                optimization_params['max_var']
            )
            
            # Calculate VaR for the current distribution
            current_var = self.calculate_portfolio_var(
                historical_returns, 
                weights,
                optimization_params['confidence_level']
            )
            
            # Check the need for rebalancing
            if self.should_rebalance(weights, current_var):
                self.execute_rebalancing(weights, returns_df.iloc[i])
            
            # Update positions and calculate profitability
            portfolio_return = self.update_positions(returns_df.iloc[i])
            portfolio_returns.append(portfolio_return)
            
            # Update metrics
            self.update_metrics(portfolio_return, current_var)
            
            # Check stop losses triggering
            self.check_stop_losses(returns_df.iloc[i])
        
        # Calculate the final metrics
        self.calculate_final_metrics(portfolio_returns)
        
    def optimize_portfolio(self, returns, target_return, max_var):
        # Using our hybrid optimization model
        opt = HybridOptimizer(returns, target_return, max_var)
        weights = opt.optimize()
        return self.apply_position_limits(weights)
        
    def execute_rebalancing(self, target_weights, current_prices):
        for symbol, target_weight in target_weights.items():
            current_weight = self.get_position_weight(symbol)
            if abs(target_weight - current_weight) > self.REBALANCING_THRESHOLD:
                # Simulate execution with slippage
                slippage = self.simulate_slippage(symbol, current_prices[symbol])
                trade_price = current_prices[symbol] * (1 + slippage)
                
                # Calculate the deal size
                trade_volume = self.calculate_trade_volume(
                    symbol, current_weight, target_weight
                )
                
                # Consider commissions
                commission = abs(trade_volume * trade_price * self.commission)
                self.current_capital -= commission
                
                # Set a deal to history
                self.record_trade(symbol, trade_volume, trade_price, commission)
                
    def update_metrics(self, portfolio_return, current_var):
        self.balance_history.append(self.current_capital)
        self.var_history.append(current_var)
        
        # Updating performance metrics
        self.metrics['max_drawdown'] = self.calculate_drawdown()
        self.metrics['sharpe_ratio'] = self.calculate_sharpe()
        self.metrics['var_efficiency'] = self.calculate_var_efficiency()
        
    def calculate_final_metrics(self, portfolio_returns):
        returns_series = pd.Series(portfolio_returns)
        
        self.metrics['total_return'] = (self.current_capital / self.initial_capital - 1)
        self.metrics['volatility'] = returns_series.std() * np.sqrt(252)
        self.metrics['sortino_ratio'] = self.calculate_sortino(returns_series)
        self.metrics['calmar_ratio'] = self.calculate_calmar()
        self.metrics['var_breaches'] = self.calculate_var_breaches()
        
    def simulate_slippage(self, symbol, price):
        # Simulate realistic slippage
        base_slippage = 0.0001  # Basic slippage
        time_factor = self.get_time_factor()  # Time dependency
        volume_factor = self.get_volume_factor(symbol)  # Volume dependency
        
        return base_slippage * time_factor * volume_factor

Os resultados dos testes foram bastante reveladores. O modelo híbrido mostrou uma resistência significativamente maior a choques de mercado, em comparação com as abordagens tradicionais. Isso ficou especialmente evidente em períodos de alta volatilidade, quando o limite imposto pelo VaR protegeu efetivamente o portfólio contra riscos excessivos.

Reta final e ajuste final do código

Após meses de desenvolvimento e testes, finalmente cheguei à versão final do sistema. Sinceramente, ela é bem diferente do que eu havia planejado no início. A prática obrigou a fazer muitos ajustes, alguns bastante inesperados.

A primeira mudança importante foi no tratamento dos dados. Percebi que testar o sistema apenas com dados históricos não era suficiente, então precisei verificar seu comportamento em diferentes condições de mercado. Para isso, desenvolvi um sistema de geração de dados sintéticos. Parece simples, mas na prática levou várias semanas.

Comecei separando todos os pares de moedas em grupos, conforme a liquidez. No primeiro grupo ficaram os pares principais como EURUSD e GBPUSD. No segundo, pares com moedas de commodities como AUDUSD e USDCAD. Depois vieram os crosses, nomeadamente EURJPY, GBPJPY e outros. E por fim, os exóticos, como CADJPY e EURAUD. Para cada grupo, defini parâmetros próprios de volatilidade e correlações, o mais próximo possível da realidade.

Mas o mais interessante começou quando adicionei diferentes regimes de mercado. Imagine o seguinte: em um terço do tempo o mercado está calmo, com baixa volatilidade. Outro terço é de negociação normal. E no restante, há alta volatilidade, quando tudo se move como louco. Também incluí tendências de longo prazo e oscilações cíclicas. Ficou muito parecido com o mercado real.

A otimização do portfólio também deu trabalho. A princípio pensei em usar apenas restrições simples nos pesos das posições, mas logo percebi que isso era insuficiente. Adicionei prêmios de risco dinâmicos: quanto maior a volatilidade do par, maior deve ser a rentabilidade esperada. Impus limites: no mínimo 4% por posição, no máximo 25%. Pode parecer muito, mas com alavancagem, isso é aceitável.

Aliás, falando em alavancagem, isso foi um capítulo à parte. No começo eu jogava seguro e praticamente não usava. Mas a análise mostrou que uma alavancagem moderada, em torno de 10 para 1, melhora significativamente os resultados. O mais importante é considerar corretamente todos os custos. E não são poucos: comissões sobre as operações (dois pontos-base), juros sobre o uso da alavancagem (0,01% ao dia), slippage na execução. Tudo isso precisou ser incorporado no otimizador.

Uma dor de cabeça especial foi a proteção contra o margin call. Depois de algumas tentativas frustradas, adotei uma solução simples: se a retração ultrapassar 10%, todas as posições são fechadas para preservar pelo menos parte do capital. Parece conservador, mas no longo prazo funciona muito bem.

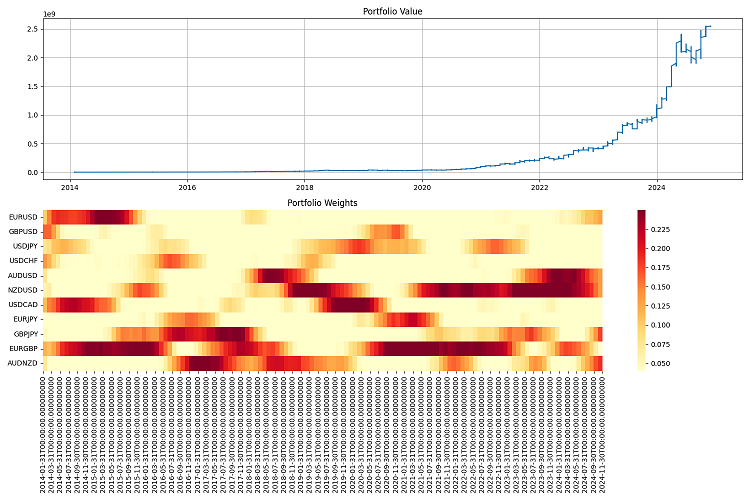
A parte mais difícil foi a geração de relatórios. Quando o sistema está operando com dezenas de pares de moedas e executando ordens o tempo todo, acompanhar tudo é impossível manualmente. Tive que criar um sistema completo de monitoramento: relatórios anuais cheios de métricas, gráficos de tudo e mais um pouco — desde o valor total do portfólio até mapas de calor com a distribuição dos pesos.

O teste final fiz num período longo — de 2000 até 2024. Comecei com um capital de um milhão de dólares e fiz rebalanceamentos trimestrais. Os resultados me deixaram satisfeito. O sistema se adapta bem a diferentes cenários de mercado, mantém o risco sob controle. Mesmo nas piores crises consegue preservar boa parte do capital.

Mas ainda há muito a fazer. Quero adicionar aprendizado de máquina para prever a volatilidade, porque hoje o sistema só usa dados históricos. Também estou pensando em como tornar a gestão da alavancagem mais flexível. E a frequência de rebalanceamento pode ser otimizada, já que, às vezes, um trimestre é tempo demais, e outras vezes dá para ficar meio ano sem mexer nas posições.

No fim das contas, saiu algo completamente diferente do que eu tinha planejado. Mas, como dizem, o ótimo é inimigo do bom. O sistema funciona, controla o risco, gera lucro. E isso é o que importa.

Considerações finais

Caramba, que jornada foi essa. Quando comecei a brincar com a teoria de Markowitz, nem imaginava no que isso ia dar. A ideia era só aplicar o clássico ao Forex, mas no fim das contas acabei criando um verdadeiro Frankenstein com abordagens diversas de controle de risco.

O mais incrível é que consegui mesmo juntar Markowitz com VaR, e a coisa funciona de verdade! O interessante é que, isoladamente, os dois métodos não davam conta do recado, mas juntos entregam um resultado excelente. Fiquei especialmente satisfeito com o desempenho da estratégia nos momentos de turbulência do mercado — o VaR como limitador dentro da otimização é simplesmente sensacional.

Claro que a parte técnica foi uma dor de cabeça constante. Zato agora o sistema leva tudo em conta: slippage, comissões, peculiaridades da execução das ordens.

Rodei a estratégia em dados históricos de 2000 a 2024, e os resultados foram animadores. Ela se adapta bem a diferentes cenários de mercado, não quebra nem mesmo em crises. Com alavancagem de 10 para 1, funciona como um relógio — desde que os riscos estejam bem travados.

Mas ainda tem muita coisa pra fazer. Preciso:

• implementar aprendizado de máquina para previsão de volatilidade (vai ser o tema do próximo artigo);
• refinar a frequência de rebalanceamento — talvez dê para otimizar isso;
• tornar a gestão da alavancagem mais inteligente (alavancagem dinâmica, “carregamento inteligente” do capital — também serão abordados nos próximos artigos);
• ensinar o sistema a se adaptar ainda melhor aos diferentes regimes de mercado.

No fim das contas, o que dá pra tirar de tudo isso é o seguinte: uma boa estratégia de trading não é só fórmula de livro. É preciso entender o mercado, dominar a parte técnica e, acima de tudo, saber controlar o risco com firmeza. Todas essas soluções agora podem ser aplicadas em outros mercados também, não só no Forex. Ainda tem espaço pra melhorar, mas a base está pronta — e está funcionando.