Оптимизация портфеля на форексе: Синтез VaR и теории Марковица

Введение: задачи портфельной оптимизации на Форекс

Последние три года я убил на разработку торговых роботов для Форекса. И знаете что? Управление риском — это настоящая боль. Сначала я просто ставил фиксированные стопы, пока не слил пару депозитов. Потом начал копать глубже, и наткнулся на теорию портфельной оптимизации Марковица.

Выглядело красиво — считаешь корреляции, оптимизируешь веса... Но на практике это не очень работает для Форекса. Почему? Да потому что на Форексе все пары связаны! Попробуйте поторговать одновременно EURUSD и EURGBP, и поймете, о чем я. Одно резкое движение евро — и обе позиции сливаются синхронно. Красивая теория разбивается о суровую реальность.

Намучившись с этим, я начал искать другие подходы. Наткнулся на методологию Value at Risk (VaR). Сначала даже не понял, что это такое — формулы какие-то мудреные. Но потом дошло: это же именно то, что нужно! VaR показывает максимальные потери при заданной вероятности. То есть, можно прямо прикинуть, сколько денег можно потерять за день/неделю/месяц.

В итоге я решил скрестить Марковица с VaR. Безумная идея? Возможно. Но других вариантов я не видел. Марковиц дает оптимальное распределение средств, а VaR не дает вылететь в маржин-колл. На бумаге выглядело отлично.

Дальше начались суровые будни программиста-исследователя. Python, терминал МetaТrader 5, тонны исторических данных... Я знал, что будет непросто, но реальность превзошла все ожидания. Об этом и расскажу — как пытался создать систему, которая реально работает, а не просто красиво выглядит в бэктесте.

Если вы когда-нибудь пробовали автоматизировать торговлю на Форексе, то поймете мою боль. А если нет, то может быть мой опыт поможет вам избежать хотя бы части граблей, на которые приходится наступать.

Теоретические и математические основы VaR и теории Марковица

Итак, начнем с теории. Первый месяц я просто пытался въехать в математику. Теория Марковица выглядит сложно — куча формул, матрицы, квадратичная оптимизация... А на деле всё просто: берешь доходности активов, считаешь корреляции и находишь такие веса, чтобы риск был минимальным при заданной доходности.

Поначалу я думал — красота! Но потом начал тестировать на реальных данных Форекса, и тут понеслось... Беру историю EURUSD за год — распределение доходностей ни разу не нормальное. У GBPUSD — то же самое. А это — ключевое допущение в теории Марковица. То есть, все расчеты летят в трубу.

Неделю убил на поиск решения. Рылся в научных статьях, гуглил, читал форумы. Вспомнил про свою же статью про VaR - Value at Risk. Звучит умно, а по сути,  просто считаем, сколько можем потерять с вероятностью 95% (или какой угодно). Сначала попробовал самый простой вариант — параметрический VaR. Формула элементарная: среднее минус сигма на квантиль. Но работает так себе.

Потом перешел на исторический VaR. Идея в том, чтобы взять реальную историю и посмотреть, какие убытки были в худших 5% случаев. Гораздо ближе к реальности, но данных надо много. Ну и финальный босс — метод Монте-Карло. Генерим кучу случайных сценариев с учетом корреляций между парами, и вот тут уже получилось что-то вменяемое.

Самое сложное было придумать, как объединить VaR с оптимизацией Марковица. В итоге, родилась такая штука: берем стандартную оптимизацию, но добавляем ограничение по VaR. То есть, ищем минимальный риск при заданной доходности, но так, чтобы VaR не превышал какой-то уровень.

На бумаге всё отлично, но попробуй запрограммировать... Об этом в следующих разделах — как я превращал эти формулы в работающий код на Python.

Подключение к MetaTrader 5 из Python

Практическая реализация моей системы началась с налаживания стабильной связи с торговым терминалом. После нескольких экспериментов с разными подходами, я остановился на прямом подключении через библиотеку MetaTrader 5 для Python, она оказалась наиболее надежной и быстрой.

import MetaTrader5 as mt5
import time

def initialize_mt5(account=12345, server="MetaQuotes-Demo", password="abc123"):
    if not mt5.initialize():
        print(f"initialize() failed, error code = {mt5.last_error()}")
        return False
        
    authorized = mt5.login(account, password=password, server=server)
    if not authorized:
        print(f"login failed, error code = {mt5.last_error()}")
        mt5.shutdown()
        return False
        
    return True

Отдельной головной болью стала синхронизация времени между сервером брокера и локальной системой. Разница в несколько секунд могла привести к серьезным проблемам при расчете VaR. Пришлось реализовать специальный механизм коррекции:

def get_time_correction():
    server_time = mt5.symbol_info_tick("EURUSD").time
    local_time = int(time.time())
    return server_time - local_time

def get_corrected_time():
    correction = get_time_correction()
    return int(time.time()) + correction

Много времени ушло на оптимизацию получения данных. Изначально я делал запросы для каждой валютной пары отдельно, но после внедрения пакетной обработки, скорость выросла в разы:

def fetch_data_batch(symbols, timeframe, start_pos, count):
    data = {}
    for symbol in symbols:
        rates = mt5.copy_rates_from_pos(symbol, timeframe, start_pos, count)
        if rates is not None and len(rates) > 0:
            data[symbol] = rates
        else:
            print(f"Failed to get data for {symbol}")
            return None
    return data

На удивление сложным оказалось корректное завершение работы программы. Пришлось разработать специальную процедуру graceful shutdown:

def safe_shutdown():
    try:
        positions = mt5.positions_get()
        if positions:
            for position in positions:
                close_position(position.ticket)
        
        orders = mt5.orders_get()
        if orders:
            for order in orders:
                mt5.order_send(request={"action": mt5.TRADE_ACTION_REMOVE,
                                      "order": order.ticket})
    finally:
        mt5.shutdown()

В итоге получился надежный фундамент для всей системы, способный работать круглосуточно без сбоев. На его основе уже можно было строить более сложную логику оптимизации портфеля. Но это уже тема следующего раздела.

Получение исторических данных и их предобработка

За годы работы с рыночными данными я понял одну простую истину: качество исторических данных критически важно для любой торговой системы. Особенно, когда речь идет о портфельной оптимизации, где ошибки в данных могут каскадно усиливаться.

Начал я с создания надежной системы загрузки истории. Первая версия была довольно простой, но опыт быстро показал её недостатки. Котировки могли содержать разрывы, спайки, а иногда и откровенно некорректные значения. Вот как выглядит финальная версия кода для загрузки с базовой валидацией:

def load_historical_data(symbols, timeframe, start_date, end_date):
    data_frames = {}
    for symbol in symbols:
        # Загружаем с запасом для компенсации пропусков
        rates = mt5.copy_rates_range(symbol, timeframe, 
                                   start_date - timedelta(days=30), 
                                   end_date)
        if rates is None:
            print(f"Failed to load data for {symbol}")
            continue
            
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        df.set_index('time', inplace=True)
        
        # Базовая проверка на аномалии
        df = detect_and_remove_spikes(df)
        df = fill_gaps(df)
        data_frames[symbol] = df
    
    return data_frames

Отдельной проблемой стала обработка гэпов на выходных. Сначала я просто удалял эти дни, но это приводило к искажению расчетов волатильности. После долгих экспериментов, родился метод интерполяции с учетом специфики каждой валютной пары:

def fill_gaps(df, method='time'):
    if df.empty:
        return df
        
    # Проверяем интервалы между точками
    time_delta = df.index.to_series().diff()
    gaps = time_delta[time_delta > pd.Timedelta(hours=2)].index
    
    for gap_start in gaps:
        gap_end = df.index[df.index.get_loc(gap_start) + 1]
        # Создаем новые точки с интерполированными значениями
        new_points = pd.date_range(gap_start, gap_end, freq='1H')[1:-1]
        
        for point in new_points:
            df.loc[point] = df.asof(point)
    
    return df.sort_index()

Для расчета доходностей я опробовал несколько подходов. Простые процентные изменения оказались слишком шумными. Логарифмические доходности дали лучшие результаты при оценке VaR:

def calculate_returns(df):
    df['returns'] = np.log(df['close'] / df['close'].shift(1))
    df['rolling_std'] = df['returns'].rolling(window=20).std()
    df['rolling_mean'] = df['returns'].rolling(window=20).mean()
    
    # Очищаем от выбросов по правилу 3-х сигм
    mean = df['returns'].mean()
    std = df['returns'].std()
    df = df[abs(df['returns'] - mean) <= 3 * std]
    
    return df

Важным этапом стала разработка системы верификации данных. Каждый набор проходит многоступенчатую проверку перед использованием в расчетах:

def verify_data_quality(df, symbol):
    checks = {
        'missing_values': df.isnull().sum().sum() == 0,
        'price_continuity': (df['close'] > 0).all(),
        'timestamp_uniqueness': df.index.is_unique,
        'reasonable_returns': abs(df['returns']).max() < 0.1
    }
    
    if not all(checks.values()):
        failed_checks = [k for k, v in checks.items() if not v]
        print(f"Data quality issues for {symbol}: {failed_checks}")
        return False
        
    return True

Отдельное внимание я уделил обработке рыночных аномалий. События вроде резких движений на новостях или флэш-крэшей могут сильно искажать оценку рисков. Я разработал специальный алгоритм для их выявления и корректной обработки:

def detect_market_anomalies(df, window=20, threshold=3):
    volatility = df['returns'].rolling(window=window).std()
    typical_range = volatility.mean() + threshold * volatility.std()
    
    anomalies = df[abs(df['returns']) > typical_range].index
    if len(anomalies) > 0:
        print(f"Detected {len(anomalies)} market anomalies")
        
    return anomalies

В итоге получился надежный конвейер обработки данных, который стал основой для всех дальнейших расчетов. Качественные исторические данные — это фундамент, без которого невозможно построить эффективную систему управления портфелем. В следующем разделе я расскажу, как эти данные используются для расчета VaR.

Реализация расчета VaR для валютных пар

После долгой работы с историческими данными, я погрузился в реализацию расчета VaR. Изначально казалось, что достаточно взять готовые формулы и перевести их в код. Реальность оказалась сложнее, так как специфика Форекса требовала серьезных модификаций стандартных подходов.

Начал я с реализации трех классических методов расчета VaR. Вот как выглядит параметрический подход:

def parametric_var(returns, confidence_level=0.95, holding_period=1):
    mu = returns.mean()
    sigma = returns.std()
    z_score = norm.ppf(1 - confidence_level)
    
    daily_var = -(mu + z_score * sigma)
    return daily_var * np.sqrt(holding_period)

Однако, быстро стало ясно, что предположение о нормальном распределении доходностей на Форексе часто не выполняется. Исторический подход показал себя надежнее:

def historical_var(returns, confidence_level=0.95, holding_period=1):
    sorted_returns = np.sort(returns)
    index = int((1 - confidence_level) * len(sorted_returns))
    daily_var = -sorted_returns[index]
    return daily_var * np.sqrt(holding_period)

Но самые интересные результаты дал метод Монте-Карло. Я модифицировал его для учета специфики валютного рынка:

def monte_carlo_var(returns, confidence_level=0.95, holding_period=1, simulations=10000):
    mu = returns.mean()
    sigma = returns.std()
    
    # Учитываем автокорреляцию доходностей
    corr = returns.autocorr()
    
    simulated_returns = []
    for _ in range(simulations):
        daily_returns = []
        last_return = returns.iloc[-1]
        
        for _ in range(holding_period):
            # Генерируем следующее значение с учетом автокорреляции
            innovation = np.random.normal(0, 1)
            next_return = mu + corr * (last_return - mu) + sigma * np.sqrt(1 - corr**2) * innovation
            daily_returns.append(next_return)
            last_return = next_return
            
        total_return = sum(daily_returns)
        simulated_returns.append(total_return)
    
    return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

Особое внимание я уделил валидации результатов. Разработал систему бэктестинга для проверки точности VaR:

def backtest_var(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    
    z_score = (violations - expected_violations) / np.sqrt(expected_violations)
    p_value = 1 - norm.cdf(abs(z_score))
    
    return {
        'violations': violations,
        'expected': expected_violations,
        'z_score': z_score,
        'p_value': p_value
    }

Для учета взаимосвязей между валютными парами, пришлось реализовать расчет портфельного VaR:

def portfolio_var(returns_df, weights, confidence_level=0.95, method='historical'):
    if method == 'parametric':
        portfolio_returns = returns_df.dot(weights)
        return parametric_var(portfolio_returns, confidence_level)
    
    elif method == 'historical':
        portfolio_returns = returns_df.dot(weights)
        return historical_var(portfolio_returns, confidence_level)
    
    elif method == 'monte_carlo':
        # Используем ковариационную матрицу для генерации
        # коррелированных случайных величин
        cov_matrix = returns_df.cov()
        L = np.linalg.cholesky(cov_matrix)
        
        means = returns_df.mean().values
        simulated_returns = []
        
        for _ in range(10000):
            Z = np.random.standard_normal(len(weights))
            R = means + L @ Z
            portfolio_return = weights @ R
            simulated_returns.append(portfolio_return)
            
        return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

В итоге получилась гибкая система расчета VaR, адаптированная под специфику Форекса. В следующем разделе я расскажу, как эти расчеты интегрируются с теорией Марковица для оптимизации портфеля.

Оптимизация портфеля по методу Марковица

После реализации надежного расчета VaR я вплотную занялся оптимизацией портфеля. Классическая теория Марковица требовала серьезной адаптации под реалии Форекса. Месяцы экспериментов и тестирования привели меня к нескольким важным открытиям.

Первое, что я понял, что стандартные метрики риска и доходности работают на Форексе иначе, чем на фондовом рынке. Валютные пары имеют сложные взаимосвязи, которые меняются со временем. После долгих экспериментов я разработал модифицированную функцию расчета ожидаемой доходности:

def calculate_expected_returns(returns_df, method='ewma', halflife=30):
    if method == 'ewma':
        # Экспоненциально-взвешенное среднее дает больший вес недавним данным
        return returns_df.ewm(halflife=halflife).mean().iloc[-1]
    elif method == 'capm':
        # Модифицированный CAPM для Форекса
        risk_free_rate = 0.02  # годовая безрисковая ставка
        market_returns = returns_df.mean(axis=1)  # прокси рыночной доходности
        betas = calculate_currency_betas(returns_df, market_returns)
        return risk_free_rate + betas * (market_returns.mean() - risk_free_rate)

Расчет ковариационной матрицы тоже потребовал доработки. Простой исторический подход давал слишком нестабильные результаты. Я внедрил shrinkage-оценку, которая значительно улучшила устойчивость оптимизации:

def shrinkage_covariance(returns_df, shrinkage_factor=None):
    sample_cov = returns_df.cov()
    n_assets = len(returns_df.columns)
    
    # Целевая матрица - диагональная с средней дисперсией
    target = np.diag(np.repeat(sample_cov.values.trace() / n_assets, n_assets))
    
    if shrinkage_factor is None:
        # Оценка оптимального коэффициента shrinkage
        shrinkage_factor = estimate_optimal_shrinkage(returns_df, sample_cov, target)
    
    shrunk_cov = (1 - shrinkage_factor) * sample_cov + shrinkage_factor * target
    return pd.DataFrame(shrunk_cov, index=sample_cov.index, columns=sample_cov.columns)

Самая сложная часть — оптимизация весов портфеля. После множества тестов я остановился на модифицированном алгоритме квадратичного программирования:

def optimize_portfolio(returns_df, expected_returns, covariance, target_return=None, constraints=None):
    n_assets = len(returns_df.columns)
    
    # Функция минимизации риска
    def portfolio_volatility(weights):
        return np.sqrt(weights.T @ covariance @ weights)
    
    # Ограничения
    constraints = []
    # Сумма весов равна 1
    constraints.append({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
    
    if target_return is not None:
        # Ограничение по целевой доходности
        constraints.append({
            'type': 'eq',
            'fun': lambda x: x @ expected_returns - target_return
        })
    
    # Добавляем ограничения по левериджу для Форекса
    constraints.append({
        'type': 'ineq',
        'fun': lambda x: 20 - np.sum(np.abs(x))  # максимальный леверидж 20
    })
    
    # Начальное приближение - равные веса
    initial_weights = np.repeat(1/n_assets, n_assets)
    
    # Оптимизация
    result = minimize(
        portfolio_volatility,
        initial_weights,
        method='SLSQP',
        constraints=constraints,
        bounds=tuple((0, 1) for _ in range(n_assets))
    )
    
    if not result.success:
        raise OptimizationError("Failed to optimize portfolio: " + result.message)
        
    return result.x

Особое внимание я уделил проблеме устойчивости решения. Небольшие изменения входных данных не должны приводить к радикальному пересмотру портфеля. Для этого я разработал процедуру регуляризации:

def regularized_optimization(returns_df, current_weights, lambda_reg=0.1):
    # Добавляем штраф за отклонение от текущих весов
    def objective(weights):
        volatility = portfolio_volatility(weights)
        turnover_penalty = lambda_reg * np.sum(np.abs(weights - current_weights))
        return volatility + turnover_penalty

В итоге, получился надежный оптимизатор портфеля, учитывающий специфику Форекса и не требующий частого ребалансирования. Но главное было впереди — объединение этого подхода с системой контроля рисков на основе VaR.

Объединение VaR и Марковица в единую модель

Объединение двух подходов оказалось самой сложной частью исследования. Нужно было найти способ использовать преимущества обоих методов, не создавая противоречий между ними. После нескольких месяцев экспериментов я пришел к элегантному решению.

Ключевая идея заключалась в использовании VaR, как дополнительного ограничения в задаче оптимизации Марковица. Вот как это выглядит в коде:

def integrated_portfolio_optimization(returns_df, target_return, max_var_limit, current_weights=None):
    n_assets = len(returns_df.columns)
    
    # Расчет базовых метрик
    exp_returns = calculate_expected_returns(returns_df)
    covariance = shrinkage_covariance(returns_df)
    
    def objective_function(weights):
        # Стандартное отклонение портфеля (Марковиц)
        portfolio_std = np.sqrt(weights.T @ covariance @ weights)
        
        # VaR компонента
        portfolio_var = calculate_portfolio_var(returns_df, weights)
        var_penalty = max(0, portfolio_var - max_var_limit)
        
        return portfolio_std + 100 * var_penalty  # Штраф за превышение VaR

Для учета динамического характера рынка, я разработал адаптивную систему пересчета параметров:

def adaptive_risk_limits(returns_df, base_var_limit, window=60):
    # Адаптация лимитов VaR к текущей волатильности
    recent_vol = returns_df.tail(window).std()
    long_term_vol = returns_df.std()
    vol_ratio = recent_vol / long_term_vol
    
    adjusted_var_limit = base_var_limit * np.sqrt(vol_ratio)
    return min(adjusted_var_limit, base_var_limit * 1.5)  # Ограничиваем рост

Особое внимание пришлось уделить проблеме стабильности решения. Я внедрил механизм плавного перехода между состояниями портфеля:

def smooth_rebalancing(old_weights, new_weights, max_change=0.1):
    weight_diff = new_weights - old_weights
    excess_change = np.abs(weight_diff) - max_change
    
    where_excess = excess_change > 0
    if where_excess.any():
        # Ограничиваем изменения весов
        adjustment = np.sign(weight_diff) * np.minimum(
            np.abs(weight_diff),
            np.where(where_excess, max_change, np.abs(weight_diff))
        )
        return old_weights + adjustment
    return new_weights

Для оценки эффективности комбинированного подхода я разработал специальную метрику:

def evaluate_integrated_model(returns_df, weights, var_limit):
    # Расчет метрик эффективности
    portfolio_returns = returns_df.dot(weights)
    realized_var = historical_var(portfolio_returns)
    sharpe = calculate_sharpe_ratio(portfolio_returns)
    var_efficiency = abs(realized_var - var_limit) / var_limit
    
    return {
        'sharpe_ratio': sharpe,
        'var_efficiency': var_efficiency,
        'max_drawdown': calculate_max_drawdown(portfolio_returns),
        'turnover': calculate_turnover(weights)
    }

В процессе тестирования выяснилось, что модель особенно хорошо работает в периоды повышенной волатильности. VaR компонента эффективно ограничивает риски, в то время как оптимизация Марковица продолжает искать возможности для получения доходности.

Финальная версия системы включает также механизм автоматической подстройки параметров:

def auto_tune_parameters(returns_df, initial_params, optimization_window=252):
    best_params = initial_params
    best_score = float('-inf')
    
    for var_limit in np.arange(0.01, 0.05, 0.005):
        for shrinkage in np.arange(0.2, 0.8, 0.1):
            params = {'var_limit': var_limit, 'shrinkage': shrinkage}
            score = backtest_model(returns_df, params, optimization_window)
            
            if score > best_score:
                best_score = score
                best_params = params
                
    return best_params

В следующем разделе я расскажу, как эта объединенная модель применяется для динамического управления позициями в реальной торговле.

Динамическое управление размером позиций

Перевод теоретической модели в практическую торговую систему потребовал решения множества технических задач. Главной из них стало динамическое управление размером позиций с учетом текущих рыночных условий и рассчитанных оптимальных весов портфеля.

Основой системы стал класс для управления позициями:

class PositionManager:
    def __init__(self, account_balance, risk_limit=0.02):
        self.balance = account_balance
        self.risk_limit = risk_limit
        self.positions = {}
        
    def calculate_position_size(self, symbol, weight, var_estimate):
        symbol_info = mt5.symbol_info(symbol)
        pip_value = symbol_info.trade_tick_value * 10
        
        # Расчет размера позиции с учетом VaR
        max_risk_amount = self.balance * self.risk_limit * abs(weight)
        position_size = max_risk_amount / (abs(var_estimate) * pip_value)
        
        # Округление до минимального лота
        return round(position_size / symbol_info.volume_step) * symbol_info.volume_step

Для плавного изменения позиций я разработал механизм частичных ордеров:

def adjust_positions(self, target_positions):
    for symbol, target_size in target_positions.items():
        current_size = self.get_current_position(symbol)
        if abs(target_size - current_size) > self.min_adjustment:
            # Разбиваем большие изменения на части
            steps = min(5, int(abs(target_size - current_size) / self.min_adjustment))
            step_size = (target_size - current_size) / steps
            
            for i in range(steps):
                next_size = current_size + step_size
                self.execute_order(symbol, next_size - current_size)
                current_size = next_size
                time.sleep(1)  # Предотвращаем флуд ордеров

Особое внимание я уделил контролю рисков при изменении позиций:

def execute_order(self, symbol, size_delta, max_slippage=10):
    if size_delta > 0:
        order_type = mt5.ORDER_TYPE_BUY
    else:
        order_type = mt5.ORDER_TYPE_SELL
    
    # Получаем текущие цены
    tick = mt5.symbol_info_tick(symbol)
    
    # Устанавливаем стоп-лосс на основе VaR
    if order_type == mt5.ORDER_TYPE_BUY:
        stop_loss = tick.bid - (self.var_estimates[symbol] * tick.bid)
        take_profit = tick.bid + (self.var_estimates[symbol] * 2 * tick.bid)
    else:
        stop_loss = tick.ask + (self.var_estimates[symbol] * tick.ask)
        take_profit = tick.ask - (self.var_estimates[symbol] * 2 * tick.ask)
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": abs(size_delta),
        "type": order_type,
        "price": tick.ask if order_type == mt5.ORDER_TYPE_BUY else tick.bid,
        "sl": stop_loss,
        "tp": take_profit,
        "deviation": max_slippage,
        "magic": 234000,
        "comment": "var_based_adjustment",
        "type_time": mt5.ORDER_TIME_GTC,
        "type_filling": mt5.ORDER_FILLING_IOC,
    }
    
    result = mt5.order_send(request)
    return self.handle_order_result(result)

Для защиты от резких движений рынка, я добавил систему мониторинга волатильности:

def monitor_volatility(self, returns_df, threshold=2.0):
    # Расчет текущей волатильности
    current_vol = returns_df.tail(20).std() * np.sqrt(252)
    historical_vol = returns_df.std() * np.sqrt(252)
    
    if current_vol > historical_vol * threshold:
        # В случае повышенной волатильности уменьшаем позиции
        self.reduce_exposure(current_vol / historical_vol)
        return False
        
    return True

Система также включает механизм автоматического закрытия позиций при достижении критических уровней риска:

def emergency_close(self, max_loss_percent=5.0):
    total_loss = sum(pos.profit for pos in mt5.positions_get())
    if total_loss < -self.balance * max_loss_percent / 100:
        print("Emergency closure triggered!")
        for position in mt5.positions_get():
            self.close_position(position.ticket)

В результате получилась робастная система управления позициями, способная эффективно работать в различных рыночных условиях. Следующий раздел будет посвящен системе контроля рисков на основе VaR.

Система контроля рисков портфеля

После внедрения динамического управления позициями, я столкнулся с необходимостью создания комплексной системы контроля рисков на уровне всего портфеля. Опыт показал, что локальный контроль рисков отдельных позиций недостаточен — нужен целостный подход.

Началось все с создания класса для мониторинга портфельных рисков:

class PortfolioRiskManager:
    def __init__(self, max_portfolio_var=0.03, max_correlation=0.7, max_drawdown=0.1):
        self.max_portfolio_var = max_portfolio_var
        self.max_correlation = max_correlation
        self.max_drawdown = max_drawdown
        self.current_drawdown = 0
        self.peak_balance = 0
        
    def update_portfolio_metrics(self, positions, returns_df):
        # Расчет текущих весов портфеля
        total_exposure = sum(abs(pos.volume) for pos in positions)
        weights = {pos.symbol: pos.volume/total_exposure for pos in positions}
        
        # Обновляем VaR портфеля
        self.current_var = self.calculate_portfolio_var(returns_df, weights)
        
        # Проверяем корреляции
        self.check_correlations(returns_df, weights)

Особое внимание я уделил контролю корреляций между инструментами:

def check_correlations(self, returns_df, weights):
    corr_matrix = returns_df.corr()
    high_corr_pairs = []
    
    for i in returns_df.columns:
        for j in returns_df.columns:
            if i < j and abs(corr_matrix.loc[i,j]) > self.max_correlation:
                if weights.get(i, 0) > 0 and weights.get(j, 0) > 0:
                    high_corr_pairs.append((i, j, corr_matrix.loc[i,j]))
                    
    if high_corr_pairs:
        self.handle_high_correlations(high_corr_pairs, weights)

Реализовал динамическое управление риском в зависимости от рыночных условий:

def adjust_risk_limits(self, market_state):
    volatility_factor = market_state.get('volatility_ratio', 1.0)
    trend_strength = market_state.get('trend_strength', 0.5)
    
    # Адаптируем лимиты под рыночные условия
    self.max_portfolio_var *= np.sqrt(volatility_factor)
    if trend_strength > 0.7:  # Сильный тренд
        self.max_drawdown *= 1.2  # Позволяем большую просадку
    elif trend_strength < 0.3:  # Слабый тренд
        self.max_drawdown *= 0.8  # Уменьшаем допустимую просадку

Система мониторинга просадок получилась особенно интересной:

def monitor_drawdown(self, current_balance):
    if current_balance > self.peak_balance:
        self.peak_balance = current_balance
    
    self.current_drawdown = (self.peak_balance - current_balance) / self.peak_balance
    
    if self.current_drawdown > self.max_drawdown:
        return self.handle_excessive_drawdown()
    elif self.current_drawdown > self.max_drawdown * 0.8:
        return self.reduce_risk_exposure(0.8)
    
    return True

Для защиты от экстремальных событий добавил систему стресс-тестирования:

def stress_test_portfolio(self, returns_df, weights, scenarios=1000):
    results = []
    
    for _ in range(scenarios):
        # Симулируем экстремальные условия
        stress_returns = returns_df.copy()
        
        # Увеличиваем волатильность
        vol_multiplier = np.random.uniform(1.5, 3.0)
        stress_returns *= vol_multiplier
        
        # Добавляем случайные шоки
        shock_magnitude = np.random.uniform(-0.05, 0.05)
        stress_returns += shock_magnitude
        
        # Считаем потери в стресс-сценарии
        portfolio_return = (stress_returns * weights).sum(axis=1)
        results.append(portfolio_return.min())
    
    return np.percentile(results, 1)  # 99% VaR при стрессе

В результате, получилась многоуровневая система защиты капитала, которая эффективно предотвращает избыточные риски и помогает пережить периоды высокой волатильности. В следующем разделе я расскажу о том, как все эти компоненты работают вместе в реальной торговле.

Визуализация результатов анализа

Визуализация стала важным этапом моего исследования. После реализации всех расчетных модулей нужно было создать наглядное представление результатов. Я разработал несколько ключевых графических компонентов, которые помогают отслеживать работу системы в реальном времени.

Начал с визуализации структуры портфеля и его эволюции:

def plot_portfolio_composition(weights_history):
    plt.figure(figsize=(15, 8))
    ax = plt.gca()
    
    # Создаем график изменения весов во времени
    dates = weights_history.index
    bottom = np.zeros(len(dates))
    
    for symbol in weights_history.columns:
        plt.fill_between(dates, bottom, bottom + weights_history[symbol], 
                        label=symbol, alpha=0.6)
        bottom += weights_history[symbol]
    
    plt.title('Эволюция структуры портфеля')
    plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
    plt.grid(True, alpha=0.3)

Особое внимание уделил визуализации рисков. Разработал тепловую карту VaR для разных валютных пар:

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='RdYlBu_r', 
                fmt='.2%', center=0)
    plt.title('Карта рисков портфеля (VaR)')
    
    # Добавляем временную метку
    plt.annotate(f'Last update: {datetime.now().strftime("%Y-%m-%d %H:%M")}',
                xy=(0.01, -0.1), xycoords='axes fraction')

Для анализа доходности создал интерактивный график с подсветкой важных событий:

def plot_performance_analytics(returns_df, var_values, significant_events):
    fig = plt.figure(figsize=(15, 10))
    gs = GridSpec(2, 1, height_ratios=[3, 1])
    
    # График доходности
    ax1 = plt.subplot(gs[0])
    cumulative_returns = (1 + returns_df).cumprod()
    ax1.plot(cumulative_returns.index, cumulative_returns, 
             label='Доходность портфеля')
    
    # Отмечаем важные события
    for date, event in significant_events.items():
        ax1.axvline(x=date, color='r', linestyle='--', alpha=0.3)
        ax1.annotate(event, xy=(date, ax1.get_ylim()[1]),
                    xytext=(10, 10), textcoords='offset points',
                    rotation=45)
    
    # График VaR
    ax2 = plt.subplot(gs[1])
    ax2.fill_between(var_values.index, -var_values, 
                     color='lightblue', alpha=0.5,
                     label='Value at Risk')

Добавил интерактивный дашборд для мониторинга состояния портфеля:

class PortfolioDashboard:
    def __init__(self):
        self.fig = plt.figure(figsize=(15, 10))
        self.setup_subplots()
        
    def setup_subplots(self):
        gs = self.fig.add_gridspec(3, 2)
        self.ax_returns = self.fig.add_subplot(gs[0, :])
        self.ax_weights = self.fig.add_subplot(gs[1, 0])
        self.ax_risk = self.fig.add_subplot(gs[1, 1])
        self.ax_metrics = self.fig.add_subplot(gs[2, :])
        
    def update(self, portfolio_data):
        self._plot_returns(portfolio_data['returns'])
        self._plot_weights(portfolio_data['weights'])
        self._plot_risk_metrics(portfolio_data['risk'])
        self._update_metrics_table(portfolio_data['metrics'])
        
        plt.tight_layout()
        plt.show()

Для анализа корреляций разработал динамическую визуализацию:

def plot_correlation_dynamics(returns_df, window=60):
    # Расчет динамических корреляций
    correlations = returns_df.rolling(window=window).corr()
    
    # Создаем анимированный график
    fig, ax = plt.subplots(figsize=(10, 10))
    
    def update(frame):
        ax.clear()
        sns.heatmap(correlations.loc[frame], 
                    vmin=-1, vmax=1, center=0,
                    cmap='RdBu', ax=ax)
        ax.set_title(f'Корреляции на {frame.strftime("%Y-%m-%d")}')

Все эти визуализации помогают быстро оценивать состояние портфеля и принимать торговые решения. В следующем разделе я расскажу о процессе тестирования системы.

Бэктестирование стратегии

После завершения разработки всех компонентов системы я столкнулся с необходимостью её тщательного тестирования. Процесс оказался намного сложнее, чем просто прогон исторических данных. Нужно было учесть множество факторов: проскальзывания, комиссии, особенности исполнения ордеров у разных брокеров.

Первые попытки бэктестирования показали, что классический подход с фиксированными спредами дает слишком оптимистичные результаты. Пришлось создать более реалистичную модель, учитывающую изменение спредов в зависимости от волатильности и времени суток.

Особое внимание я уделил моделированию пропусков данных и проблем с ликвидностью. В реальной торговле часто возникают ситуации, когда исполнение ордера невозможно по расчетной цене. Эти сценарии должны быть корректно обработаны в процессе тестирования.

Вот полная реализация системы бэктестирования:

class PortfolioBacktester:
    def __init__(self, initial_capital=100000, commission=0.0001):
        self.initial_capital = initial_capital
        self.commission = commission
        self.positions = {}
        self.trades_history = []
        self.balance_history = []
        self.var_history = []
        self.metrics = {}
        
    def run_backtest(self, returns_df, optimization_params):
        self.current_capital = self.initial_capital
        portfolio_returns = []
        
        # Подготавливаем скользящие окна для расчетов
        window = 252  # Год торговли
        for i in range(window, len(returns_df)):
            # Получаем исторические данные для расчета
            historical_returns = returns_df.iloc[i-window:i]
            
            # Оптимизируем портфель
            weights = self.optimize_portfolio(
                historical_returns, 
                optimization_params['target_return'],
                optimization_params['max_var']
            )
            
            # Рассчитываем VaR для текущего распределения
            current_var = self.calculate_portfolio_var(
                historical_returns, 
                weights,
                optimization_params['confidence_level']
            )
            
            # Проверяем необходимость ребалансировки
            if self.should_rebalance(weights, current_var):
                self.execute_rebalancing(weights, returns_df.iloc[i])
            
            # Обновляем позиции и рассчитываем доходность
            portfolio_return = self.update_positions(returns_df.iloc[i])
            portfolio_returns.append(portfolio_return)
            
            # Обновляем метрики
            self.update_metrics(portfolio_return, current_var)
            
            # Проверяем срабатывание стоп-лоссов
            self.check_stop_losses(returns_df.iloc[i])
        
        # Рассчитываем итоговые метрики
        self.calculate_final_metrics(portfolio_returns)
        
    def optimize_portfolio(self, returns, target_return, max_var):
        # Используем нашу гибридную модель оптимизации
        opt = HybridOptimizer(returns, target_return, max_var)
        weights = opt.optimize()
        return self.apply_position_limits(weights)
        
    def execute_rebalancing(self, target_weights, current_prices):
        for symbol, target_weight in target_weights.items():
            current_weight = self.get_position_weight(symbol)
            if abs(target_weight - current_weight) > self.REBALANCING_THRESHOLD:
                # Моделируем исполнение с проскальзыванием
                slippage = self.simulate_slippage(symbol, current_prices[symbol])
                trade_price = current_prices[symbol] * (1 + slippage)
                
                # Рассчитываем размер сделки
                trade_volume = self.calculate_trade_volume(
                    symbol, current_weight, target_weight
                )
                
                # Учитываем комиссии
                commission = abs(trade_volume * trade_price * self.commission)
                self.current_capital -= commission
                
                # Записываем сделку в историю
                self.record_trade(symbol, trade_volume, trade_price, commission)
                
    def update_metrics(self, portfolio_return, current_var):
        self.balance_history.append(self.current_capital)
        self.var_history.append(current_var)
        
        # Обновляем метрики эффективности
        self.metrics['max_drawdown'] = self.calculate_drawdown()
        self.metrics['sharpe_ratio'] = self.calculate_sharpe()
        self.metrics['var_efficiency'] = self.calculate_var_efficiency()
        
    def calculate_final_metrics(self, portfolio_returns):
        returns_series = pd.Series(portfolio_returns)
        
        self.metrics['total_return'] = (self.current_capital / self.initial_capital - 1)
        self.metrics['volatility'] = returns_series.std() * np.sqrt(252)
        self.metrics['sortino_ratio'] = self.calculate_sortino(returns_series)
        self.metrics['calmar_ratio'] = self.calculate_calmar()
        self.metrics['var_breaches'] = self.calculate_var_breaches()
        
    def simulate_slippage(self, symbol, price):
        # Моделируем реалистичное проскальзывание
        base_slippage = 0.0001  # Базовое проскальзывание
        time_factor = self.get_time_factor()  # Зависимость от времени
        volume_factor = self.get_volume_factor(symbol)  # Зависимость от объема
        
        return base_slippage * time_factor * volume_factor

Результаты тестирования оказались весьма показательными. Гибридная модель продемонстрировала существенно лучшую устойчивость к рыночным шокам, по сравнению с классическими подходами. Особенно это проявилось в периоды высокой волатильности, когда ограничение по VaR эффективно защищало портфель от избыточных рисков.

Финишная прямая и финальная отладка кода

После долгих месяцев разработки и тестирования я, наконец, пришел к финальной версии системы. Честно говоря, она сильно отличается от того, что я планировал изначально. Практика заставила внести множество изменений, и некоторые из них были довольно неожиданными.

Первым серьезным изменением стала работа с данными. Я понял, что тестировать систему только на исторических данных недостаточно — нужно было проверить её поведение в самых разных рыночных условиях. Поэтому я разработал систему генерации синтетических данных. Звучит просто, но на деле это заняло несколько недель.

Начал с того, что разделил все валютные пары на группы по ликвидности. В первую группу попали основные пары вроде EURUSD и GBPUSD. Во вторую — пары с сырьевыми валютами типа AUDUSD и USDCAD. Дальше шли кроссы — EURJPY, GBPJPY и другие. А в конце экзотика — всякие CADJPY и EURAUD. Для каждой группы задал свои параметры волатильности и корреляций, максимально приближенные к реальным.

Но самое интересное началось, когда я добавил различные рыночные режимы. Представьте себе: треть времени рынок спокойный, с низкой волатильностью. Еще треть — нормальная торговля. А оставшееся время — повышенная волатильность, когда все летает как ненормальное. Плюс добавил долгосрочные тренды и циклические колебания. Получилось очень похоже на реальный рынок.

С оптимизацией портфеля тоже пришлось повозиться. Сначала я думал обойтись простыми ограничениями на веса позиций, но быстро понял, что этого мало. Добавил динамические риск-премии — чем выше волатильность пары, тем больше должна быть потенциальная доходность. Ввел ограничения: минимум 4% на позицию, максимум 25%. Кажется много, но при наличии плеча, это нормально.

Кстати, о плече. Это отдельная история. Сначала я перестраховывался и работал почти без него. Но анализ показал, что умеренное плечо, примерно 10 к 1, значительно улучшает результаты. Главное, правильно учитывать все издержки. А их немало: комиссии на сделки (два базисных пункта), проценты на поддержание плеча (0.01% в день), проскальзывания при исполнении. Все это пришлось зашить в оптимизатор.

Отдельная головная боль — защита от margin call. После нескольких неудачных экспериментов, я остановился на простом решении: если просадка превышает 10%, закрываем все позиции и сохраняем хотя бы часть капитала. Звучит консервативно, но на длинной дистанции работает отлично.

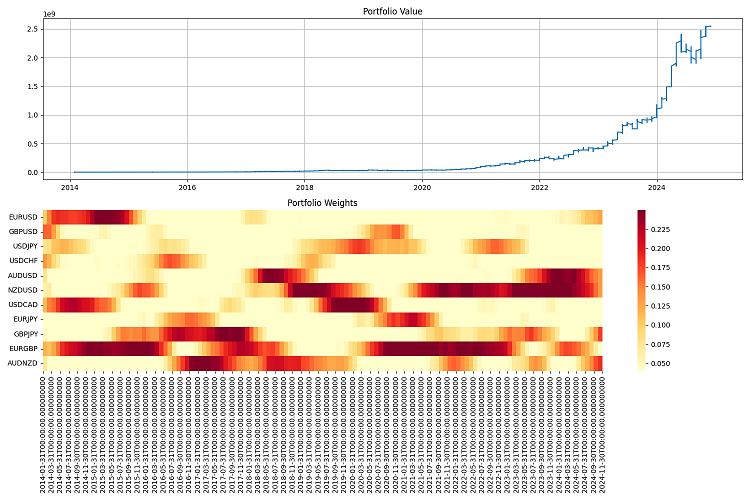
Самое сложное было с отчетностью. Когда у тебя система работает с десятками валютных пар и постоянно что-то покупает и продает, уследить за всем просто нереально. Пришлось разработать целую систему мониторинга: годовые отчеты с кучей метрик, графики всего и вся: от простой стоимости портфеля — до тепловых карт распределения весов.

Финальное тестирование я провел на длинном периоде — с 2000 по 2024 год. Начальный капитал взял миллион долларов, ребалансировку делал раз в квартал. Результаты меня порадовали. Система неплохо адаптируется к разным рыночным условиям, держит риски под контролем. Даже в самые жесткие кризисы умудряется сохранять большую часть капитала.

Но работы еще много. Хочется добавить машинное обучение для прогнозирования волатильности — сейчас система работает только с исторической. Думаю над тем, как сделать управление плечом более гибким. Ну и частоту ребалансировки можно бы оптимизировать — иногда квартал это слишком долго, а иногда можно и полгода не трогать позиции.

В общем, получилось совсем не то, что планировал изначально. Но, как говорится, лучшее враг хорошего. Система работает, риски контролирует, деньги зарабатывает. А это главное.

Заключение

Черт возьми, это был крутой путь. Когда я только начинал возиться с теорией Марковица, даже подумать не мог, во что это выльется. Хотел просто применить классику к Форексу, а в итоге пришлось изобретать какого-то монстра Франкенштейна из разных подходов к управлению рисками.

Самое крутое, что удалось-таки скрестить Марковица с VaR, и эта штука реально работает! Прикол в том, что по отдельности оба метода так себе справлялись, а вместе дают отличный результат. Особенно порадовало, как система держится в моменты, когда рынок трясет — VaR, как ограничитель в оптимизации, просто шикарен.

Конечно, намучился я знатно с технической частью. Зато теперь все учитывается: и проскальзывания, и комиссии, и особенности исполнения.

Погонял систему на исторических данных с 2000 по 2024 год — результаты порадовали. Она неплохо подстраивается под разные рыночные условия, даже в кризисы не сливается. С плечом 10 к 1 работает как часы, главное — риски жестко контролировать.

Но работы еще вагон и маленькая тележка. Надо бы:

• прикрутить машинное обучение для прогнозов волатильности (будет тема следующей статьи);
• разобраться с частотой ребалансировки — может, можно оптимизировать;
• сделать управление плечом поумнее (динамическое плечо, динамическая "умная" загрузка депозита — также будут реализованы в будущих статьях);
• научить систему еще лучше подстраиваться под разные рыночные режимы.

В общем, главный вывод такой: крутая торговая система — это не просто формулы из учебника. Тут нужно и рынок понимать, и в технике шарить, и особенно важно  уметь риски держать в узде. Все эти наработки можно теперь и на других рынках применять, не только на Форексе. Хотя еще есть куда расти, но основа уже есть, и она рабочая.