Optimización de portafolios en Fórex: Síntesis de VaR y la teoría de Markowitz

Introducción: Problemas de optimización de portafolios en Fórex

He pasado los últimos tres años desarrollando robots comerciales en Fórex. ¿Y sabe qué? Gestionar el riesgo es un auténtico suplicio. Al principio solo puse stops fijos hasta que vacié un par de depósitos. Entonces empecé a profundizar y me encontré con la teoría de optimización de portafolios de Markowitz.

Tenía una pinta preciosa: calculas las correlaciones, optimizas los pesos... Pero en la práctica, no funciona muy bien para el mercado de divisas. ¿Y por qué? Porque en Fórex, ¡todos los pares están conectados! Pruebe a negociar con EURUSD y EURGBP al mismo tiempo y verá a lo que me refiero. Un movimiento brusco del euro, y ambas posiciones se fusionarán de forma sincronizada. La hermosa teoría se hace añicos ante la cruda realidad.

Harto de esto, empecé a buscar otros enfoques. Entonces me familiaricé con la metodología Value at Risk (VaR). Al principio ni siquiera me daba cuenta de lo que era, las fórmulas me resultaron muy complicadas. Pero entonces me di cuenta: ¡eso es exactamente lo que necesitaba! El VaR muestra la pérdida máxima para una probabilidad dada, es decir, puede calcular directamente cuánto dinero se puede perder en un día/semana/mes.

Al final, decidí cruzar Markowitz con el VaR. ¿Una idea loca? Tal vez. Pero no vi otras opciones. Markowitz proporciona la asignación óptima de los fondos, mientras que el VaR evita que se produzca un ajuste de márgenes. Sobre el papel tenía muy buena pinta.

Entonces comenzó la dura rutina de un programador-investigador. Python, el terminal MetaTrader 5, toneladas de datos históricos... Sabía que no sería fácil, pero la realidad superó las expectativas. De eso es de lo que hablaré: de cómo traté de crear un sistema que realmente funcionara, no uno que solo se viera bien en el backtest.

Si alguna vez ha tratado de automatizar el trading de divisas, usted entenderá mi dolor. Y si no, quizá mi experiencia le ayude a evitar al menos parte del dolor de la segunda piedra con la que, tarde o temprano, tropezará.

Fundamentos teóricos y matemáticos del VaR y de la teoría de Markowitz

Empecemos por la teoría. Durante el primer mes solo intenté sumergirme en las matemáticas. La teoría de Markowitz parece complicada: muchas fórmulas, matrices, optimización cuadrática... Pero en realidad, es sencilla: se toman los rendimientos de los activos, se calculan las correlaciones y se encuentran las ponderaciones que minimizan el riesgo para un rendimiento determinado.

Al principio pensé: qué maravilla! Pero entonces empecé a realizar pruebas con datos reales de divisas, y la cosa se torció.... Tomé la historia de EURUSD durante un año: la distribución de los rendimientos nunca es normal. Con GBPUSD pasó lo mismo. Y este es un supuesto clave en la teoría de Markowitz. Es decir, todos los cálculos se marchan por el desagüe.

Tardé una semana en encontrar una solución. Profundicé en artículos científicos, busqué en Google, leí foros. Incluso recordé mi propio artículo sobre el VaR (Value at Risk). Suena inteligente, pero en esencia, no supone más que calcular cuánto podemos perder con una probabilidad del 95% (o la que sea). Primero probé la opción más sencilla: el VaR paramétrico, cuya fórmula es elemental: media menos sigma por cuantil. Pero funciona regular.

Luego pasé al VaR histórico, cuya idea consiste en tomar la historia real y ver cuáles han sido las pérdidas en el peor 5% de los casos. Es mucho más cercano a la realidad, pero se necesitan demasiados datos. Bueno, y luego está el jefe final: el método de Montecarlo. Generamos un montón de escenarios aleatorios considerando las correlaciones entre pares, y aquí obtuvimos algo más o menos cuerdo.

Lo más difícil fue averiguar cómo combinar el VaR con la optimización de Markowitz. Al final, me surgió la siguiente idea: podemos tomar la optimización estándar, pero añadiendo una restricción de VaR. Es decir, buscamos el mínimo riesgo con una rentabilidad dada, pero de manera que el VaR no supere cierto nivel.

Está bien sobre el papel, pero intenta ahora programarlo.... Hablaremos sobre esto en las siguientes secciones: cómo convertí estas fórmulas en código Python funcional.

Conexión a MetaTrader 5 desde Python

La aplicación práctica de mi sistema comenzó con el establecimiento de una conexión estable con el terminal comercial. Después de varios experimentos con diferentes enfoques, me decidí por la conexión directa a través de la biblioteca MetaTrader 5 para Python; resultó ser el modo más fiable y más rápido.

import MetaTrader5 as mt5
import time

def initialize_mt5(account=12345, server="MetaQuotes-Demo", password="abc123"):
    if not mt5.initialize():
        print(f"initialize() failed, error code = {mt5.last_error()}")
        return False
        
    authorized = mt5.login(account, password=password, server=server)
    if not authorized:
        print(f"login failed, error code = {mt5.last_error()}")
        mt5.shutdown()
        return False
        
    return True

Otro quebradero de cabeza era la sincronización horaria entre el servidor del bróker y el sistema local. Una diferencia de unos segundos podría haber causado graves problemas en el cálculo del VaR. Así que tuve que aplicar un mecanismo especial de corrección:

def get_time_correction():
    server_time = mt5.symbol_info_tick("EURUSD").time
    local_time = int(time.time())
    return server_time - local_time

def get_corrected_time():
    correction = get_time_correction()
    return int(time.time()) + correction

Dediqué mucho tiempo a optimizar la adquisición de los datos. Al principio, realizaba consultas para cada par de divisas por separado, pero tras implementar el procesamiento por lotes, la velocidad se multiplicó varias veces:

def fetch_data_batch(symbols, timeframe, start_pos, count):
    data = {}
    for symbol in symbols:
        rates = mt5.copy_rates_from_pos(symbol, timeframe, start_pos, count)
        if rates is not None and len(rates) > 0:
            data[symbol] = rates
        else:
            print(f"Failed to get data for {symbol}")
            return None
    return data

Fue sorprendentemente difícil terminar el programa correctamente. Me vi obligado a desarrollar un procedimiento especial graceful shutdown:

def safe_shutdown():
    try:
        positions = mt5.positions_get()
        if positions:
            for position in positions:
                close_position(position.ticket)
        
        orders = mt5.orders_get()
        if orders:
            for order in orders:
                mt5.order_send(request={"action": mt5.TRADE_ACTION_REMOVE,
                                      "order": order.ticket})
    finally:
        mt5.shutdown()

El resultado es una base fiable para todo el sistema, capaz de funcionar las 24 horas del día sin fallos. Sobre esta base ya era posible construir una lógica de optimización de portafolios más compleja. Pero ese será un tema de la próxima sección.

La obtención de los datos históricos y su procesamiento previo

A lo largo de los años que llevo trabajando con datos de mercado, he aprendido una verdad muy simple: la calidad de los datos históricos resulta fundamental para cualquier sistema comercial, sobre todo cuando se trata de la optimización de portafolios, donde los errores en los datos pueden producirse en cascada.

Empecé por crear un sistema sólido para cargar la historia. La primera versión era bastante simple, pero la experiencia demostró rápidamente sus deficiencias. Las cotizaciones pueden contener discontinuidades, picos y, en ocasiones, valores totalmente incorrectos. Este es el aspecto de la versión final del código para descargar con validación básica:

def load_historical_data(symbols, timeframe, start_date, end_date):
    data_frames = {}
    for symbol in symbols:
        # Load with a reserve to compensate for gaps
        rates = mt5.copy_rates_range(symbol, timeframe, 
                                   start_date - timedelta(days=30), 
                                   end_date)
        if rates is None:
            print(f"Failed to load data for {symbol}")
            continue
            
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        df.set_index('time', inplace=True)
        
        # Basic anomaly check
        df = detect_and_remove_spikes(df)
        df = fill_gaps(df)
        data_frames[symbol] = df
    
    return data_frames

Otro problema fue la gestión de las discontinuidades durante el fin de semana. Al principio simplemente borraba esos días, pero eso distorsionaba los cálculos de volatilidad. Tras mucha experimentación, nació el método de interpolación, que considera las particularidades de cada par de divisas:

def fill_gaps(df, method='time'):
    if df.empty:
        return df
        
    # Check the intervals between points
    time_delta = df.index.to_series().diff()
    gaps = time_delta[time_delta > pd.Timedelta(hours=2)].index
    
    for gap_start in gaps:
        gap_end = df.index[df.index.get_loc(gap_start) + 1]
        # Create new points with interpolated values
        new_points = pd.date_range(gap_start, gap_end, freq='1H')[1:-1]
        
        for point in new_points:
            df.loc[point] = df.asof(point)
    
    return df.sort_index()

Para calcular los rendimientos, probé enfoques diversos. Los cambios porcentuales simples resultaron demasiado ruidosos. Los rendimientos logarítmicos ofrecieron los mejores resultados para la estimación del VaR:

def calculate_returns(df):
    df['returns'] = np.log(df['close'] / df['close'].shift(1))
    df['rolling_std'] = df['returns'].rolling(window=20).std()
    df['rolling_mean'] = df['returns'].rolling(window=20).mean()
    
    # Clean out emissions using the 3-sigma rule
    mean = df['returns'].mean()
    std = df['returns'].std()
    df = df[abs(df['returns'] - mean) <= 3 * std]
    
    return df

Un paso importante fue el desarrollo de un sistema de verificación de datos. Cada conjunto se somete a un proceso de verificación de varias etapas antes de ser usado en los cálculos:

def verify_data_quality(df, symbol):
    checks = {
        'missing_values': df.isnull().sum().sum() == 0,
        'price_continuity': (df['close'] > 0).all(),
        'timestamp_uniqueness': df.index.is_unique,
        'reasonable_returns': abs(df['returns']).max() < 0.1
    }
    
    if not all(checks.values()):
        failed_checks = [k for k, v in checks.items() if not v]
        print(f"Data quality issues for {symbol}: {failed_checks}")
        return False
        
    return True

Presté especial atención al procesamiento de las anomalías del mercado. Acontecimientos como los movimientos bruscos en las noticias o las caídas repentinas pueden distorsionar seriamente la evaluación del riesgo. Desarrollé un algoritmo especial para identificarlas y procesarlas correctamente:

def detect_market_anomalies(df, window=20, threshold=3):
    volatility = df['returns'].rolling(window=window).std()
    typical_range = volatility.mean() + threshold * volatility.std()
    
    anomalies = df[abs(df['returns']) > typical_range].index
    if len(anomalies) > 0:
        print(f"Detected {len(anomalies)} market anomalies")
        
    return anomalies

El resultado fue un sólido sistema de procesamiento de datos que se convirtió en la base de todos los cálculos posteriores. Los datos históricos de calidad suponen la base sin la cual resulta imposible construir un sistema eficaz de gestión de portafolios. En la siguiente sección, analizaré cómo se usan estos datos para calcular el VaR.

Aplicación del cálculo del VaR para los pares de divisas

Después de trabajar con datos históricos durante mucho tiempo, abordé la aplicación del cálculo del VaR. Al principio, parecía que todo lo que había que hacer era tomar fórmulas ya listas y convertirlas en código. La realidad resultó ser más complicada, pues las especificidades de Fórex exigían serias modificaciones de los planteamientos estándar.

Empecé aplicando los tres métodos clásicos de cálculo del VaR. Este es el aspecto del enfoque paramétrico:

def parametric_var(returns, confidence_level=0.95, holding_period=1):
    mu = returns.mean()
    sigma = returns.std()
    z_score = norm.ppf(1 - confidence_level)
    
    daily_var = -(mu + z_score * sigma)
    return daily_var * np.sqrt(holding_period)

Sin embargo, pronto quedó claro que la hipótesis de una distribución normal de los rendimientos en el mercado de divisas con frecuencia no se cumple. El enfoque histórico ha demostrado ser más fiable:

def historical_var(returns, confidence_level=0.95, holding_period=1):
    sorted_returns = np.sort(returns)
    index = int((1 - confidence_level) * len(sorted_returns))
    daily_var = -sorted_returns[index]
    return daily_var * np.sqrt(holding_period)

No obstante, los resultados más interesantes proceden del método de Montecarlo. Lo he modificado para considerar las particularidades del mercado de divisas:

def monte_carlo_var(returns, confidence_level=0.95, holding_period=1, simulations=10000):
    mu = returns.mean()
    sigma = returns.std()
    
    # Consider auto correlation of returns
    corr = returns.autocorr()
    
    simulated_returns = []
    for _ in range(simulations):
        daily_returns = []
        last_return = returns.iloc[-1]
        
        for _ in range(holding_period):
            # Generate the next value taking auto correlation into account
            innovation = np.random.normal(0, 1)
            next_return = mu + corr * (last_return - mu) + sigma * np.sqrt(1 - corr**2) * innovation
            daily_returns.append(next_return)
            last_return = next_return
            
        total_return = sum(daily_returns)
        simulated_returns.append(total_return)
    
    return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

Presté especial atención a la validación de los resultados. Desarrollé de un sistema de backtesting para verificar la precisión del VaR:

def backtest_var(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    
    z_score = (violations - expected_violations) / np.sqrt(expected_violations)
    p_value = 1 - norm.cdf(abs(z_score))
    
    return {
        'violations': violations,
        'expected': expected_violations,
        'z_score': z_score,
        'p_value': p_value
    }

Para considerar las interrelaciones entre pares de divisas, tuve que aplicar un cálculo del VaR de portafolio:

def portfolio_var(returns_df, weights, confidence_level=0.95, method='historical'):
    if method == 'parametric':
        portfolio_returns = returns_df.dot(weights)
        return parametric_var(portfolio_returns, confidence_level)
    
    elif method == 'historical':
        portfolio_returns = returns_df.dot(weights)
        return historical_var(portfolio_returns, confidence_level)
    
    elif method == 'monte_carlo':
        # Use the covariance matrix to generate
        # correlated random variables
        cov_matrix = returns_df.cov()
        L = np.linalg.cholesky(cov_matrix)
        
        means = returns_df.mean().values
        simulated_returns = []
        
        for _ in range(10000):
            Z = np.random.standard_normal(len(weights))
            R = means + L @ Z
            portfolio_return = weights @ R
            simulated_returns.append(portfolio_return)
            
        return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

El resultado es un sistema de cálculo del VaR flexible y adaptado a las peculiaridades del mercado de divisas. En la siguiente sección, analizaré cómo se integran estos cálculos con la teoría de Markowitz para la optimización de portafolios.

Optimización de portafolios con el método de Markowitz

Tras aplicar un sólido cálculo del VaR, me puse manos a la obra para optimizar el portafolio. La teoría clásica de Markowitz requería una seria adaptación a las realidades de Fórex. Meses de experimentación y pruebas me llevaron a varios descubrimientos importantes.

Lo primero que noté es que las métricas estándar de riesgo y rentabilidad funcionan de forma distinta en el mercado de divisas y en el mercado bursátil. Los pares de divisas tienen relaciones complejas que cambian con el tiempo. Tras muchos experimentos, desarrollé una función modificada para calcular los rendimientos esperados:

def calculate_expected_returns(returns_df, method='ewma', halflife=30):
    if method == 'ewma':
        # Exponentially weighted average gives more weight to recent data
        return returns_df.ewm(halflife=halflife).mean().iloc[-1]
    elif method == 'capm':
        # Modified CAPM for Forex
        risk_free_rate = 0.02  # annual risk-free rate
        market_returns = returns_df.mean(axis=1)  # market returns proxy
        betas = calculate_currency_betas(returns_df, market_returns)
        return risk_free_rate + betas * (market_returns.mean() - risk_free_rate)

También tuve que perfeccionar el cálculo de la matriz de covarianza. El enfoque histórico simple dio resultados demasiado inestables. Así que introduje la estimación por contracción, que mejoró mucho la solidez de la optimización:

def shrinkage_covariance(returns_df, shrinkage_factor=None):
    sample_cov = returns_df.cov()
    n_assets = len(returns_df.columns)
    
    # The target matrix is diagonal with average variance
    target = np.diag(np.repeat(sample_cov.values.trace() / n_assets, n_assets))
    
    if shrinkage_factor is None:
        # Estimation of the optimal 'shrinkage' ratio
        shrinkage_factor = estimate_optimal_shrinkage(returns_df, sample_cov, target)
    
    shrunk_cov = (1 - shrinkage_factor) * sample_cov + shrinkage_factor * target
    return pd.DataFrame(shrunk_cov, index=sample_cov.index, columns=sample_cov.columns)

Lo más difícil fue optimizar las ponderaciones del portafolio. Tras muchas pruebas, opté por un algoritmo de programación cuadrática modificado:

def optimize_portfolio(returns_df, expected_returns, covariance, target_return=None, constraints=None):
    n_assets = len(returns_df.columns)
    
    # Risk minimization function
    def portfolio_volatility(weights):
        return np.sqrt(weights.T @ covariance @ weights)
    
    # Limitations
    constraints = []
    # The sum of the weights is 1
    constraints.append({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
    
    if target_return is not None:
        # Target income limit
        constraints.append({
            'type': 'eq',
            'fun': lambda x: x @ expected_returns - target_return
        })
    
    # Add leverage restrictions for Forex
    constraints.append({
        'type': 'ineq',
        'fun': lambda x: 20 - np.sum(np.abs(x))  # max leverage 20
    })
    
    # Initial approximation - equal weights
    initial_weights = np.repeat(1/n_assets, n_assets)
    
    # Optimization
    result = minimize(
        portfolio_volatility,
        initial_weights,
        method='SLSQP',
        constraints=constraints,
        bounds=tuple((0, 1) for _ in range(n_assets))
    )
    
    if not result.success:
        raise OptimizationError("Failed to optimize portfolio: " + result.message)
        
    return result.x

Presté especial atención al problema de la estabilidad de la solución. Los pequeños cambios en los datos de entrada no deben provocar una revisión radical del portafolio. Para ello, desarrollé un procedimiento de regularización:

def regularized_optimization(returns_df, current_weights, lambda_reg=0.1):
    # Add a penalty for deviation from the current weights
    def objective(weights):
        volatility = portfolio_volatility(weights)
        turnover_penalty = lambda_reg * np.sum(np.abs(weights - current_weights))
        return volatility + turnover_penalty

El resultado fue un optimizador de portafolios fiable que considera las particularidades del mercado de divisas y no requiere reajustes frecuentes. Pero lo principal estaba por llegar: la combinación de este enfoque con un marco de control de riesgos basado en el VaR.

Combinación del VaR y Markowitz en un único modelo

La combinación de ambos enfoques resultó ser la parte más compleja del estudio. Tenía que encontrar la manera de aprovechar las ventajas de ambos métodos sin crear contradicciones entre ellos. Tras meses de experimentación, di con una solución elegante.

La idea clave era usar el VaR como una restricción adicional en un problema de optimización de Markowitz. Este sería su aspecto en forma de código:

def integrated_portfolio_optimization(returns_df, target_return, max_var_limit, current_weights=None):
    n_assets = len(returns_df.columns)
    
    # Calculation of basic metrics
    exp_returns = calculate_expected_returns(returns_df)
    covariance = shrinkage_covariance(returns_df)
    
    def objective_function(weights):
        # Portfolio standard deviation (Markowitz)
        portfolio_std = np.sqrt(weights.T @ covariance @ weights)
        
        # component VaR
        portfolio_var = calculate_portfolio_var(returns_df, weights)
        var_penalty = max(0, portfolio_var - max_var_limit)
        
        return portfolio_std + 100 * var_penalty  # Penalty for exceeding VaR

Para tener en consideración la naturaleza dinámica del mercado, desarrollé un sistema adaptativo de recálculo de parámetros:

def adaptive_risk_limits(returns_df, base_var_limit, window=60):
    # Adapting VaR limits to current volatility
    recent_vol = returns_df.tail(window).std()
    long_term_vol = returns_df.std()
    vol_ratio = recent_vol / long_term_vol
    
    adjusted_var_limit = base_var_limit * np.sqrt(vol_ratio)
    return min(adjusted_var_limit, base_var_limit * 1.5)  # Limit growth

Asimismo, tuve que prestar especial atención al problema de la estabilidad de la solución. Implementé un mecanismo para transiciones suaves entre los estados del portafolio:

def smooth_rebalancing(old_weights, new_weights, max_change=0.1):
    weight_diff = new_weights - old_weights
    excess_change = np.abs(weight_diff) - max_change
    
    where_excess = excess_change > 0
    if where_excess.any():
        # Limit changes in weights
        adjustment = np.sign(weight_diff) * np.minimum(
            np.abs(weight_diff),
            np.where(where_excess, max_change, np.abs(weight_diff))
        )
        return old_weights + adjustment
    return new_weights

Para evaluar la eficacia del enfoque combinado, desarrollé una métrica concreta:

def evaluate_integrated_model(returns_df, weights, var_limit):
    # Calculation of performance metrics
    portfolio_returns = returns_df.dot(weights)
    realized_var = historical_var(portfolio_returns)
    sharpe = calculate_sharpe_ratio(portfolio_returns)
    var_efficiency = abs(realized_var - var_limit) / var_limit
    
    return {
        'sharpe_ratio': sharpe,
        'var_efficiency': var_efficiency,
        'max_drawdown': calculate_max_drawdown(portfolio_returns),
        'turnover': calculate_turnover(weights)
    }

En el proceso de prueba, resultó que el modelo funciona especialmente bien durante los periodos de mayor volatilidad. El componente del VaR limita eficazmente el riesgo, mientras que la optimización de Markowitz sigue buscando oportunidades de rendimiento.

La versión final del sistema también incluye un mecanismo de configuración automática de los parámetros:

def auto_tune_parameters(returns_df, initial_params, optimization_window=252):
    best_params = initial_params
    best_score = float('-inf')
    
    for var_limit in np.arange(0.01, 0.05, 0.005):
        for shrinkage in np.arange(0.2, 0.8, 0.1):
            params = {'var_limit': var_limit, 'shrinkage': shrinkage}
            score = backtest_model(returns_df, params, optimization_window)
            
            if score > best_score:
                best_score = score
                best_params = params
                
    return best_params

En la siguiente sección, analizaré cómo se aplica este modelo combinado a la gestión dinámica de posiciones en la negociación real.

Control dinámico del tamaño de la posición

La conversión del modelo teórico en un sistema comercial práctico requirió la solución de numerosos problemas técnicos. El principal fue la gestión dinámica del tamaño de las posiciones considerando las condiciones actuales del mercado y calculando las ponderaciones óptimas del portafolio.

El núcleo del sistema era una clase para la gestión de posiciones:

class PositionManager:
    def __init__(self, account_balance, risk_limit=0.02):
        self.balance = account_balance
        self.risk_limit = risk_limit
        self.positions = {}
        
    def calculate_position_size(self, symbol, weight, var_estimate):
        symbol_info = mt5.symbol_info(symbol)
        pip_value = symbol_info.trade_tick_value * 10
        
        # Calculate the position size taking into account VaR
        max_risk_amount = self.balance * self.risk_limit * abs(weight)
        position_size = max_risk_amount / (abs(var_estimate) * pip_value)
        
        # Round to minimum lot
        return round(position_size / symbol_info.volume_step) * symbol_info.volume_step

Para suavizar los cambios de posición, desarrollé un mecanismo de órdenes parciales:

def adjust_positions(self, target_positions):
    for symbol, target_size in target_positions.items():
        current_size = self.get_current_position(symbol)
        if abs(target_size - current_size) > self.min_adjustment:
            # Break big changes into pieces
            steps = min(5, int(abs(target_size - current_size) / self.min_adjustment))
            step_size = (target_size - current_size) / steps
            
            for i in range(steps):
                next_size = current_size + step_size
                self.execute_order(symbol, next_size - current_size)
                current_size = next_size
                time.sleep(1)  # Prevent order flooding

Presté especial atención al control del riesgo al cambiar de posición:

def execute_order(self, symbol, size_delta, max_slippage=10):
    if size_delta > 0:
        order_type = mt5.ORDER_TYPE_BUY
    else:
        order_type = mt5.ORDER_TYPE_SELL
    
    # Get current prices
    tick = mt5.symbol_info_tick(symbol)
    
    # Set VaR-based stop loss
    if order_type == mt5.ORDER_TYPE_BUY:
        stop_loss = tick.bid - (self.var_estimates[symbol] * tick.bid)
        take_profit = tick.bid + (self.var_estimates[symbol] * 2 * tick.bid)
    else:
        stop_loss = tick.ask + (self.var_estimates[symbol] * tick.ask)
        take_profit = tick.ask - (self.var_estimates[symbol] * 2 * tick.ask)
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": abs(size_delta),
        "type": order_type,
        "price": tick.ask if order_type == mt5.ORDER_TYPE_BUY else tick.bid,
        "sl": stop_loss,
        "tp": take_profit,
        "deviation": max_slippage,
        "magic": 234000,
        "comment": "var_based_adjustment",
        "type_time": mt5.ORDER_TIME_GTC,
        "type_filling": mt5.ORDER_FILLING_IOC,
    }
    
    result = mt5.order_send(request)
    return self.handle_order_result(result)

Para protegerme contra movimientos bruscos del mercado, añadí un sistema de control de la volatilidad:

def monitor_volatility(self, returns_df, threshold=2.0):
    # Current volatility calculation
    current_vol = returns_df.tail(20).std() * np.sqrt(252)
    historical_vol = returns_df.std() * np.sqrt(252)
    
    if current_vol > historical_vol * threshold:
        # Reduce positions in case of increased volatility
        self.reduce_exposure(current_vol / historical_vol)
        return False
        
    return True

El sistema también incluye un mecanismo para cerrar automáticamente las posiciones al alcanzar niveles críticos de riesgo:

def emergency_close(self, max_loss_percent=5.0):
    total_loss = sum(pos.profit for pos in mt5.positions_get())
    if total_loss < -self.balance * max_loss_percent / 100:
        print("Emergency closure triggered!")
        for position in mt5.positions_get():
            self.close_position(position.ticket)

El resultado es un sólido sistema de gestión de posiciones que puede operar eficazmente en diversas condiciones de mercado. La siguiente sección se centrará en un sistema de control de riesgos basado en el VaR.

Sistema de control del riesgo del portafolio

Tras implantar la gestión dinámica de posiciones, se me planteó la necesidad de un sistema integral de control de riesgos a nivel del portafolio completo. La experiencia me ha demostrado que el control localizado de riesgos de elementos individuales resulta insuficiente: se necesita un enfoque holístico.

Comencé con la creación de una clase para controlar el riesgo del portafolio:

class PortfolioRiskManager:
    def __init__(self, max_portfolio_var=0.03, max_correlation=0.7, max_drawdown=0.1):
        self.max_portfolio_var = max_portfolio_var
        self.max_correlation = max_correlation
        self.max_drawdown = max_drawdown
        self.current_drawdown = 0
        self.peak_balance = 0
        
    def update_portfolio_metrics(self, positions, returns_df):
        # Calculation of current portfolio weights
        total_exposure = sum(abs(pos.volume) for pos in positions)
        weights = {pos.symbol: pos.volume/total_exposure for pos in positions}
        
        # Update portfolio VaR
        self.current_var = self.calculate_portfolio_var(returns_df, weights)
        
        # Check correlations
        self.check_correlations(returns_df, weights)

Presté atención sobre todo al control de las correlaciones entre instrumentos:

def check_correlations(self, returns_df, weights):
    corr_matrix = returns_df.corr()
    high_corr_pairs = []
    
    for i in returns_df.columns:
        for j in returns_df.columns:
            if i < j and abs(corr_matrix.loc[i,j]) > self.max_correlation:
                if weights.get(i, 0) > 0 and weights.get(j, 0) > 0:
                    high_corr_pairs.append((i, j, corr_matrix.loc[i,j]))
                    
    if high_corr_pairs:
        self.handle_high_correlations(high_corr_pairs, weights)

Luego implanté una gestión dinámica del riesgo en función de las condiciones del mercado:

def adjust_risk_limits(self, market_state):
    volatility_factor = market_state.get('volatility_ratio', 1.0)
    trend_strength = market_state.get('trend_strength', 0.5)
    
    # Adapt limits to market conditions
    self.max_portfolio_var *= np.sqrt(volatility_factor)
    if trend_strength > 0.7:  # Strong trend
        self.max_drawdown *= 1.2  # Allow a big drawdown
    elif trend_strength < 0.3:  # Weak trend
        self.max_drawdown *= 0.8  # Reduce the acceptable drawdown

El sistema de control de la reducción resultó especialmente interesante:

def monitor_drawdown(self, current_balance):
    if current_balance > self.peak_balance:
        self.peak_balance = current_balance
    
    self.current_drawdown = (self.peak_balance - current_balance) / self.peak_balance
    
    if self.current_drawdown > self.max_drawdown:
        return self.handle_excessive_drawdown()
    elif self.current_drawdown > self.max_drawdown * 0.8:
        return self.reduce_risk_exposure(0.8)
    
    return True

Después añadí un sistema de pruebas de resistencia para mayor protección contra sucesos extremos:

def stress_test_portfolio(self, returns_df, weights, scenarios=1000):
    results = []
    
    for _ in range(scenarios):
        # Simulate extreme conditions
        stress_returns = returns_df.copy()
        
        # Increase volatility
        vol_multiplier = np.random.uniform(1.5, 3.0)
        stress_returns *= vol_multiplier
        
        # Add random shocks
        shock_magnitude = np.random.uniform(-0.05, 0.05)
        stress_returns += shock_magnitude
        
        # Calculate losses in a stress scenario
        portfolio_return = (stress_returns * weights).sum(axis=1)
        results.append(portfolio_return.min())
    
    return np.percentile(results, 1)  # 99% VaR in case of a stress

El resultado fue un sistema de protección del capital de varios niveles que previene eficazmente los riesgos excesivos y ayuda a sobrevivir en periodos de gran volatilidad. En la siguiente sección, analizaré cómo funcionan conjuntamente todos estos componentes en el trading real.

Visualización de los resultados de los análisis

La visualización constituía una etapa importante de mi investigación. Tras implantar todos los módulos de cálculo, había que implementar la visualización de los resultados. Así que desarrollé algunos componentes gráficos clave para ayudar a supervisar el sistema en tiempo real.

Comencé visualizando la estructura del portafolio y su evolución:

def plot_portfolio_composition(weights_history):
    plt.figure(figsize=(15, 8))
    ax = plt.gca()
    
    # Create a graph of weight changes over time
    dates = weights_history.index
    bottom = np.zeros(len(dates))
    
    for symbol in weights_history.columns:
        plt.fill_between(dates, bottom, bottom + weights_history[symbol], 
                        label=symbol, alpha=0.6)
        bottom += weights_history[symbol]
    
    plt.title('Evolution of portfolio structure')
    plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
    plt.grid(True, alpha=0.3)

Prestamos especial atención a la visualización del riesgo. Luego desarrollé un mapa de calor del VaR para diferentes pares de divisas:

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='RdYlBu_r', 
                fmt='.2%', center=0)
    plt.title('Portfolio risk map (VaR)')
    
    # Add a timestamp
    plt.annotate(f'Last update: {datetime.now().strftime("%Y-%m-%d %H:%M")}',
                xy=(0.01, -0.1), xycoords='axes fraction')

Para analizar los rendimientos, creé un gráfico interactivo en el que se destacan los eventos importantes:

def plot_performance_analytics(returns_df, var_values, significant_events):
    fig = plt.figure(figsize=(15, 10))
    gs = GridSpec(2, 1, height_ratios=[3, 1])
    
    # Returns graph
    ax1 = plt.subplot(gs[0])
    cumulative_returns = (1 + returns_df).cumprod()
    ax1.plot(cumulative_returns.index, cumulative_returns, 
             label='Portfolio returns')
    
    # Mark important events
    for date, event in significant_events.items():
        ax1.axvline(x=date, color='r', linestyle='--', alpha=0.3)
        ax1.annotate(event, xy=(date, ax1.get_ylim()[1]),
                    xytext=(10, 10), textcoords='offset points',
                    rotation=45)
    
    # VaR graph
    ax2 = plt.subplot(gs[1])
    ax2.fill_between(var_values.index, -var_values, 
                     color='lightblue', alpha=0.5,
                     label='Value at Risk')

Después añadí un panel interactivo para supervisar el estado del portafolio:

class PortfolioDashboard:
    def __init__(self):
        self.fig = plt.figure(figsize=(15, 10))
        self.setup_subplots()
        
    def setup_subplots(self):
        gs = self.fig.add_gridspec(3, 2)
        self.ax_returns = self.fig.add_subplot(gs[0, :])
        self.ax_weights = self.fig.add_subplot(gs[1, 0])
        self.ax_risk = self.fig.add_subplot(gs[1, 1])
        self.ax_metrics = self.fig.add_subplot(gs[2, :])
        
    def update(self, portfolio_data):
        self._plot_returns(portfolio_data['returns'])
        self._plot_weights(portfolio_data['weights'])
        self._plot_risk_metrics(portfolio_data['risk'])
        self._update_metrics_table(portfolio_data['metrics'])
        
        plt.tight_layout()
        plt.show()

Y desarrollé una visualización dinámica para analizar las correlaciones:

def plot_correlation_dynamics(returns_df, window=60):
    # Calculation of dynamic correlations
    correlations = returns_df.rolling(window=window).corr()
    
    # Create an animated graph
    fig, ax = plt.subplots(figsize=(10, 10))
    
    def update(frame):
        ax.clear()
        sns.heatmap(correlations.loc[frame], 
                    vmin=-1, vmax=1, center=0,
                    cmap='RdBu', ax=ax)
        ax.set_title(f'Correlations on {frame.strftime("%Y-%m-%d")}')

Todas estas visualizaciones ayudan a evaluar rápidamente el estado del portafolio y tomar decisiones comerciales. En la próxima sección hablaré del proceso de prueba del sistema.

Backtesting de las estrategias

Tras finalizar el desarrollo de todos los componentes del sistema, tenía que probarlo a fondo. El proceso resultó ser mucho más complicado que el simple análisis de los datos históricos. Tuve que tener en cuenta muchos factores: deslizamientos, comisiones, peculiaridades de la ejecución de órdenes en distintos brókeres.

Los primeros intentos de backtesting mostraron que el enfoque clásico con spreads fijos da resultados demasiado optimistas. Hubo que crear un modelo más realista que tuviera en cuenta la variación de los spreads en función de la volatilidad y la hora del día.

Presté sobre todo atención a la modelización de las omisiones de datos y los problemas de liquidez. En la negociación real, con frecuencia se dan situaciones en las que resulta imposible ejecutar una orden al precio de liquidación. Estas situaciones deben tratarse correctamente durante la prueba.

Aquí está la implementación completa del sistema de backtesting:

class PortfolioBacktester:
    def __init__(self, initial_capital=100000, commission=0.0001):
        self.initial_capital = initial_capital
        self.commission = commission
        self.positions = {}
        self.trades_history = []
        self.balance_history = []
        self.var_history = []
        self.metrics = {}
        
    def run_backtest(self, returns_df, optimization_params):
        self.current_capital = self.initial_capital
        portfolio_returns = []
        
        # Preparing sliding windows for calculations
        window = 252  # Trading yesr
        for i in range(window, len(returns_df)):
            # Receive historical data for calculation
            historical_returns = returns_df.iloc[i-window:i]
            
            # Optimize the portfolio
            weights = self.optimize_portfolio(
                historical_returns, 
                optimization_params['target_return'],
                optimization_params['max_var']
            )
            
            # Calculate VaR for the current distribution
            current_var = self.calculate_portfolio_var(
                historical_returns, 
                weights,
                optimization_params['confidence_level']
            )
            
            # Check the need for rebalancing
            if self.should_rebalance(weights, current_var):
                self.execute_rebalancing(weights, returns_df.iloc[i])
            
            # Update positions and calculate profitability
            portfolio_return = self.update_positions(returns_df.iloc[i])
            portfolio_returns.append(portfolio_return)
            
            # Update metrics
            self.update_metrics(portfolio_return, current_var)
            
            # Check stop losses triggering
            self.check_stop_losses(returns_df.iloc[i])
        
        # Calculate the final metrics
        self.calculate_final_metrics(portfolio_returns)
        
    def optimize_portfolio(self, returns, target_return, max_var):
        # Using our hybrid optimization model
        opt = HybridOptimizer(returns, target_return, max_var)
        weights = opt.optimize()
        return self.apply_position_limits(weights)
        
    def execute_rebalancing(self, target_weights, current_prices):
        for symbol, target_weight in target_weights.items():
            current_weight = self.get_position_weight(symbol)
            if abs(target_weight - current_weight) > self.REBALANCING_THRESHOLD:
                # Simulate execution with slippage
                slippage = self.simulate_slippage(symbol, current_prices[symbol])
                trade_price = current_prices[symbol] * (1 + slippage)
                
                # Calculate the deal size
                trade_volume = self.calculate_trade_volume(
                    symbol, current_weight, target_weight
                )
                
                # Consider commissions
                commission = abs(trade_volume * trade_price * self.commission)
                self.current_capital -= commission
                
                # Set a deal to history
                self.record_trade(symbol, trade_volume, trade_price, commission)
                
    def update_metrics(self, portfolio_return, current_var):
        self.balance_history.append(self.current_capital)
        self.var_history.append(current_var)
        
        # Updating performance metrics
        self.metrics['max_drawdown'] = self.calculate_drawdown()
        self.metrics['sharpe_ratio'] = self.calculate_sharpe()
        self.metrics['var_efficiency'] = self.calculate_var_efficiency()
        
    def calculate_final_metrics(self, portfolio_returns):
        returns_series = pd.Series(portfolio_returns)
        
        self.metrics['total_return'] = (self.current_capital / self.initial_capital - 1)
        self.metrics['volatility'] = returns_series.std() * np.sqrt(252)
        self.metrics['sortino_ratio'] = self.calculate_sortino(returns_series)
        self.metrics['calmar_ratio'] = self.calculate_calmar()
        self.metrics['var_breaches'] = self.calculate_var_breaches()
        
    def simulate_slippage(self, symbol, price):
        # Simulate realistic slippage
        base_slippage = 0.0001  # Basic slippage
        time_factor = self.get_time_factor()  # Time dependency
        volume_factor = self.get_volume_factor(symbol)  # Volume dependency
        
        return base_slippage * time_factor * volume_factor

Los resultados de la prueba resultaron bastante reveladores. El modelo híbrido demostró una resistencia significativamente mayor a las perturbaciones del mercado que los enfoques clásicos. Esto resultó especialmente evidente durante los periodos de alta volatilidad, cuando la restricción del VaR protegió eficazmente el portafolio contra un riesgo excesivo.

Recta final y depuración definitiva del código

Tras muchos meses de desarrollo y pruebas, por fin llegué a la versión final del sistema. Si le soy sincero, resulta muy diferente de lo que había planeado en un principio. La práctica me obligó a hacer muchos cambios, y algunos de ellos son bastante inesperados.

El primer cambio importante fue el procesamiento de los datos. Me di cuenta de que no bastaba con probar el sistema solo con datos históricos, sino que debía comprobar su comportamiento en distintas condiciones de mercado. Por eso desarrollé un sistema para generar datos sintéticos. Suena simple, pero en realidad llevó unas cuantas semanas.

Empecé dividiendo todos los pares de divisas por grupos de liquidez. El primer grupo incluye pares importantes como EURUSD y GBPUSD. En el segundo, pares con divisas de materias primas como AUDUSD y USDCAD. A continuación llegaron los tipos cruzados: EURJPY, GBPJPY y otros. Y al final, los exóticos, todo tipo de CADJPY y EURAUD. Para cada grupo, establecí sus propios parámetros de volatilidad y correlaciones, lo más parecidos posible a los reales.

Pero lo más interesante empezó cuando añadí los diferentes modos de mercado. Imagínese esto: un tercio del tiempo el mercado está tranquilo, con baja volatilidad. Otro tercio supone el comercio normal. Y el resto del tiempo es de gran volatilidad, cuando todo vuela como un huracán. Además, añadí las tendencias a largo plazo y las fluctuaciones cíclicas. Resultó ser muy similar al mercado real.

La optimización del portafolio también supuso un reto. Al principio pensé en suprimir las restricciones simples sobre el peso de los artículos, pero enseguida me di cuenta de que no era suficiente. Así que añadí primas de riesgo dinámicas: cuanto mayor sea la volatilidad de un par, mayor debería ser la rentabilidad potencial. Límites introducidos: mínimo 4% por posición, máximo 25%. Parece mucho, pero si hay apalancamiento, está bien.

Hablando del apalancamiento, esa es una historia aparte. Al principio, me aseguré en exceso y trabajé casi sin él. Pero el análisis demostró que un apalancamiento moderado, de aproximadamente 10 a 1, mejora sustancialmente los resultados. La clave está en considerar adecuadamente todos los costes. Y son muchos: comisiones sobre las transacciones (dos puntos básicos), intereses por mantener el apalancamiento (0,01% al día), deslizamientos en la ejecución. Todo esto había que incluirlo en el optimizador.

Otro quebradero de cabeza era la protección contra el margin call. Tras varios experimentos infructuosos, me decidí por una solución sencilla: si la reducción supera el 10%, cerraremos todas las posiciones y conservaremos al menos una parte del capital. Suena conservador, pero funciona muy bien a largo plazo.

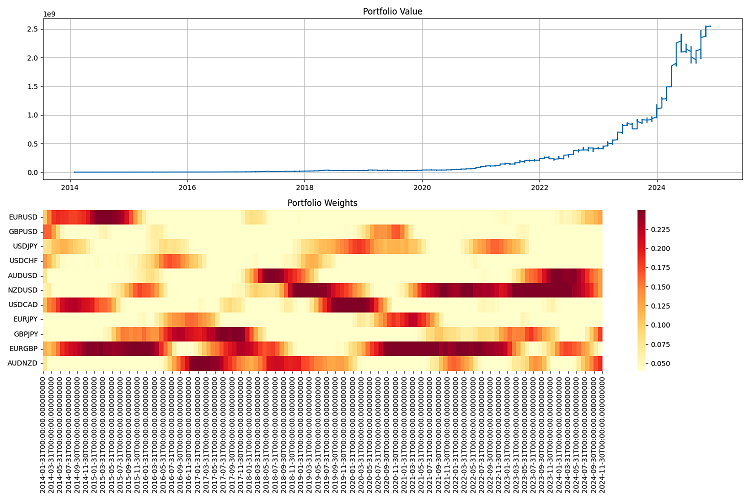
Lo más difícil fueron los informes. Cuando tenemos un sistema trabajando con docenas de pares de divisas y comprando y vendiendo algo constantemente, resulta inocente como poco hacer un seguimiento de todo. Por ello, tuve que desarrollar un sistema de seguimiento completo: informes anuales con un montón de métricas, gráficos de todo tipo, desde el simple valor del portafolio hasta mapas de calor de la distribución de pesos.

Hice las pruebas finales durante un periodo considerable, de 2000 a 2024. El capital inicial fue de un millón de dólares, el reequilibrio se hacía una vez al trimestre. Y quedé satisfecho con los resultados. El sistema se adapta bien a las distintas condiciones del mercado y mantiene bajo control los riesgos. Incluso en las crisis más duras, logra conservar la mayor parte de su capital.

Pero aún queda mucho trabajo por delante. Me gustaría añadir el aprendizaje automático para predecir la volatilidad; ahora mismo el sistema solo funciona con la volatilidad histórica. También pienso en cómo flexibilizar el control de los apalancamientos. Bueno, la frecuencia del reequilibrio podría optimizarse: a veces un trimestre supone demasiado tiempo, y a veces resulta posible no tocar posiciones durante medio año.

En definitiva, no salió en absoluto como había planeado en un principio. Pero, como suele decirse, no hay que pecar de perfeccionistas. El sistema funciona, los riesgos están bajo control controlan y se gana dinero. Eso es lo que importa.

Conclusión

Uf, la verdad es que ha sido un camino difícil. Cuando empecé a juguetear con la teoría de Markowitz, no tenía ni idea de lo que implicaba. Yo solo quería aplicar los clásicos al Fórex, pero al final tuve que inventarme un monstruo de Frankenstein partiendo de diferentes enfoques de la gestión del riesgo.

Lo mejor es que hemos logrado cruzar Markowitz con el VaR, ¡y esto sí que funciona! Resulta curioso que, por separado, ambos métodos funcionan más o menos bien, pero juntos ofrecen resultados aún mejores. Estoy especialmente satisfecho de cómo se comporta el sistema en momentos en los que el mercado se tambalea: el VaR como restricción en la optimización resulta impresionante.

Obviamente, he tenido muchos problemas con la parte técnica. Pero ahora todo se tiene en cuenta: los deslizamientos, las comisiones y las peculiaridades de la ejecución.

He usado el sistema con datos históricos de 2000 a 2024 y los resultados han sido satisfactorios. Se adapta bien a las distintas condiciones del mercado, e incluso en las crisis no se sufren pérdidas sustanciales. Con un apalancamiento de 10 a 1 funciona como un reloj, lo principal es que los riesgos quedan totalmente bajo control.

Pero aún queda mucho trabajo por hacer. Deberíamos:

• incluir el aprendizaje automático para las previsiones de volatilidad (será el tema del próximo artículo);
• averiguar la frecuencia de reequilibrio: tal vez pueda optimizarse;
• hacer más inteligente la gestión del apalancamiento (apalancamiento dinámico, carga dinámica "inteligente" de los depósitos; esto también se implementará en futuros artículos);
• enseñar al sistema a adaptarse aún mejor a los distintos modos de mercado.

En general, la conclusión principal es la siguiente: un sistema comercial genial no está formado solo por las fórmulas de un libro de texto. Aquí tenemos que entender el mercado, comprender las técnicas y, sobre todo, saber controlar los riesgos. Todos estos avances pueden aplicarse ahora en otros mercados, no solo en Fórex. Aunque todavía hay margen para crecer, la base está ya ahí y funciona.