外汇投资组合优化：风险价值理论与马科维茨理论的融合

引言：外汇市场的投资组合优化任务

过去三年，我一直在为外汇市场开发交易机器人。你知道吗？风险管理真是个令人头疼的问题。起初，我只是设置固定的止损，直到我爆了几个仓。然后我开始深入研究，并接触到了马科维茨的投资组合优化理论。

这理论看起来很棒——你计算相关性，优化权重……但在现实中，这对于外汇市场来说效果并不好。为什么呢？因为外汇市场中所有货币对都是相互关联的！试着同时交易EURUSD和EURGBP，你就会明白我的意思了。一次欧元的大幅波动，两个头寸就会同步亏损。美好的理论被残酷的现实击得粉碎。

受够了这一切，我开始寻找其他方法。最终，我接触到了风险价值（VaR）方法论。起初，我甚至不明白这是什么——一堆复杂的方程。但后来我恍然大悟——这正是我需要的东西！VaR显示了在给定概率下的最大损失。换句话说，我们可以直接估算出一天/一周/一个月内可能会损失多少钱。

最后，我决定将马科维茨理论与VaR结合起来。听起来很疯狂？也许是吧。但我没有看到其他选择。马科维茨理论提供最优的资金配置，而VaR则能防止我们爆仓。这在纸面上看起来非常完美。

接着，研究型程序员的艰苦日常开始了。Python、MetaTrader 5终端、海量的历史数据……我知道这不会容易，但现实的艰难程度超出了我的所有预期。这正是我将要讲述的——我如何尝试创建一个真正能工作的系统，而不仅仅是在回测中看起来很漂亮。

如果你曾尝试过自动化外汇交易，你就会理解我的痛苦。如果没有，那么我的经验或许能帮助你避开至少一些你不得不踩的坑。

VaR和马科维茨的理论与数学基础

那么，让我们从理论开始。第一个月，我只是在努力搞懂数学。马科维茨理论看起来很复杂——一堆方程、矩阵、二次优化……但实际上，一切都很简单：你获取资产回报率，计算相关性，然后找到在给定回报率下风险最小的权重。

起初我还挺高兴的！但接着我开始用真实的外汇数据进行测试，然后问题就来了……当使用EURUSD一年的历史数据时，其回报率的分布根本不是正态分布。GBPUSD也是如此。而这正是马科维茨理论的一个关键假设。换句话说，所有的计算都白费了。

我花了一周时间寻找解决方案。我翻遍了科学文章，用谷歌搜索，阅读论坛。我回想起我那篇关于风险价值（VaR）的文章。这名字听起来很高级，但实际上，我们只是计算在95%（或其他任何水平）的概率下，我们可能会损失多少。我首先尝试了最简单的方法——参数化VaR。方程很简单：均值减去标准差乘以分位数。效果平平。

然后我转向历史模拟法VaR。思路是取真实的历史数据，看看在最差的5%的情况下，损失是多少。这方法更接近现实，但需要大量的数据。最终的大Boss是蒙特卡洛方法。我们生成大量考虑了货币对之间相关性的随机情景，终于得到了一些有意义的结果。

最困难的部分是弄清楚如何将VaR与马科维茨优化结合起来。最终，我想出了这样一个办法：我们采用标准的优化，但增加一个VaR限制。我们在给定回报率下寻找最小风险，但同时要确保VaR不超过某个特定水平。

在纸面上一切都很完美，但我们需要把它编程实现……在接下来的章节中，我将展示我如何将这些方程转化为可运行的Python代码。

从Python连接到MetaTrader 5

我系统的实际实现始于与交易终端建立稳定的连接。在尝试了不同的方法后，我最终选择了通过Python的MetaTrader 5库进行直接连接，事实证明这是最可靠、最快速的方式。

import MetaTrader5 as mt5
import time

def initialize_mt5(account=12345, server="MetaQuotes-Demo", password="abc123"):
    if not mt5.initialize():
        print(f"initialize() failed, error code = {mt5.last_error()}")
        return False
        
    authorized = mt5.login(account, password=password, server=server)
    if not authorized:
        print(f"login failed, error code = {mt5.last_error()}")
        mt5.shutdown()
        return False
        
    return True

另一个让人头疼的问题，是经纪商服务器与本地系统之间的时间同步。在计算风险价值时，哪怕只有几秒钟的时间差，都可能导致严重的问题。因此，必须实现一个特殊的校正机制：

def get_time_correction():
    server_time = mt5.symbol_info_tick("EURUSD").time
    local_time = int(time.time())
    return server_time - local_time

def get_corrected_time():
    correction = get_time_correction()
    return int(time.time()) + correction

在数据获取的优化上，我们花费了大量时间。最初，我针对每一个货币对都单独发起请求，但在实现了批量处理后，速度提升了好几倍：

def fetch_data_batch(symbols, timeframe, start_pos, count):
    data = {}
    for symbol in symbols:
        rates = mt5.copy_rates_from_pos(symbol, timeframe, start_pos, count)
        if rates is not None and len(rates) > 0:
            data[symbol] = rates
        else:
            print(f"Failed to get data for {symbol}")
            return None
    return data

事实证明，要正确地终止程序，出人意料地困难。因此，必须开发一个特殊的“优雅关闭”程序：

def safe_shutdown():
    try:
        positions = mt5.positions_get()
        if positions:
            for position in positions:
                close_position(position.ticket)
        
        orders = mt5.orders_get()
        if orders:
            for order in orders:
                mt5.order_send(request={"action": mt5.TRADE_ACTION_REMOVE,
                                      "order": order.ticket})
    finally:
        mt5.shutdown()

最终，我们为整个系统打造了一个可靠的基础，使其能够全天候无故障地运行。在此基础上，已经可以构建更为复杂的投资组合优化逻辑了。不过，这已经是下一章节的主题了。

获取历史数据及其预处理

在处理市场数据的这些年里，我领悟了一个简单的真理：对于任何交易系统而言，历史数据的质量都至关重要。尤其是在进行投资组合优化时，数据错误的影响会像瀑布一样层层放大。

我首先着手创建一个可靠的历史数据加载系统。第一个版本相当简单，但实践很快就暴露了它的缺陷。行情数据中可能存在缺口、异常尖峰，有时甚至会出现完全错误的数值。以下就是最终版本的代码，它包含了基础的数据验证功能：

def load_historical_data(symbols, timeframe, start_date, end_date):
    data_frames = {}
    for symbol in symbols:
        # Load with a reserve to compensate for gaps
        rates = mt5.copy_rates_range(symbol, timeframe, 
                                   start_date - timedelta(days=30), 
                                   end_date)
        if rates is None:
            print(f"Failed to load data for {symbol}")
            continue
            
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        df.set_index('time', inplace=True)
        
        # Basic anomaly check
        df = detect_and_remove_spikes(df)
        df = fill_gaps(df)
        data_frames[symbol] = df
    
    return data_frames

另一个独立的问题是处理周末的数据缺口。起初，我简单地移除了这些日期，但这会扭曲波动率的计算结果。经过长时间的实验，最终诞生了一种插值方法，该方法会考虑到每种货币对的独特性：

def fill_gaps(df, method='time'):
    if df.empty:
        return df
        
    # Check the intervals between points
    time_delta = df.index.to_series().diff()
    gaps = time_delta[time_delta > pd.Timedelta(hours=2)].index
    
    for gap_start in gaps:
        gap_end = df.index[df.index.get_loc(gap_start) + 1]
        # Create new points with interpolated values
        new_points = pd.date_range(gap_start, gap_end, freq='1H')[1:-1]
        
        for point in new_points:
            df.loc[point] = df.asof(point)
    
    return df.sort_index()

我尝试了几种不同的方法来计算收益率。简单的百分比变动法被证明噪声过大。而在估算风险价值时，对数收益率的表现最为出色：

def calculate_returns(df):
    df['returns'] = np.log(df['close'] / df['close'].shift(1))
    df['rolling_std'] = df['returns'].rolling(window=20).std()
    df['rolling_mean'] = df['returns'].rolling(window=20).mean()
    
    # Clean out emissions using the 3-sigma rule
    mean = df['returns'].mean()
    std = df['returns'].std()
    df = df[abs(df['returns'] - mean) <= 3 * std]
    
    return df

数据验证系统的开发，被证明是一个重要的里程碑。在用于计算之前，每一组数据都必须经过多阶段的检查：

def verify_data_quality(df, symbol):
    checks = {
        'missing_values': df.isnull().sum().sum() == 0,
        'price_continuity': (df['close'] > 0).all(),
        'timestamp_uniqueness': df.index.is_unique,
        'reasonable_returns': abs(df['returns']).max() < 0.1
    }
    
    if not all(checks.values()):
        failed_checks = [k for k, v in checks.items() if not v]
        print(f"Data quality issues for {symbol}: {failed_checks}")
        return False
        
    return True

我特别关注了对市场异常情况的处理。各类事件，例如由新闻引发的剧烈波动或闪电崩盘，都可能会严重扭曲风险评估。为此，我开发了一套专门的算法，用以正确地识别和处理这些情况：

def detect_market_anomalies(df, window=20, threshold=3):
    volatility = df['returns'].rolling(window=window).std()
    typical_range = volatility.mean() + threshold * volatility.std()
    
    anomalies = df[abs(df['returns']) > typical_range].index
    if len(anomalies) > 0:
        print(f"Detected {len(anomalies)} market anomalies")
        
    return anomalies

最终，我们得到了一个可靠的数据处理方法，它成为了所有后续计算的基础。高质量的历史数据是基石，没有它，就不可能构建出一个高效的组合管理系统。在下一节中，我将探讨这些数据是如何被用于计算风险价值的。

货币对风险价值计算的实现

在长时间处理历史数据之后，我深入到了风险价值计算的实现工作中。起初，我以为只需将现成的方程式翻译成代码就足够了。但现实情况要复杂得多，因为外汇市场的特殊性要求对标准方法进行重大修改。

我首先实现了三种经典的VaR计算方法。参数化方法如下所示：

def parametric_var(returns, confidence_level=0.95, holding_period=1):
    mu = returns.mean()
    sigma = returns.std()
    z_score = norm.ppf(1 - confidence_level)
    
    daily_var = -(mu + z_score * sigma)
    return daily_var * np.sqrt(holding_period)

然而，我们很快就清楚地认识到，外汇市场收益率服从正态分布的假设往往并不成立。历史模拟法被证明更为可靠：

def historical_var(returns, confidence_level=0.95, holding_period=1):
    sorted_returns = np.sort(returns)
    index = int((1 - confidence_level) * len(sorted_returns))
    daily_var = -sorted_returns[index]
    return daily_var * np.sqrt(holding_period)

但最有趣的结果是由蒙特卡洛方法提供的。我对其进行了修改，以使其能够考虑到外汇市场的特殊性：

def monte_carlo_var(returns, confidence_level=0.95, holding_period=1, simulations=10000):
    mu = returns.mean()
    sigma = returns.std()
    
    # Consider auto correlation of returns
    corr = returns.autocorr()
    
    simulated_returns = []
    for _ in range(simulations):
        daily_returns = []
        last_return = returns.iloc[-1]
        
        for _ in range(holding_period):
            # Generate the next value taking auto correlation into account
            innovation = np.random.normal(0, 1)
            next_return = mu + corr * (last_return - mu) + sigma * np.sqrt(1 - corr**2) * innovation
            daily_returns.append(next_return)
            last_return = next_return
            
        total_return = sum(daily_returns)
        simulated_returns.append(total_return)
    
    return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

我特别关注了对结果的验证。为此，我还开发了一套回测系统，用以检验风险价值的准确性：

def backtest_var(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    
    z_score = (violations - expected_violations) / np.sqrt(expected_violations)
    p_value = 1 - norm.cdf(abs(z_score))
    
    return {
        'violations': violations,
        'expected': expected_violations,
        'z_score': z_score,
        'p_value': p_value
    }

为了将货币对之间的相关性纳入考量，就必须实现投资组合风险价值的计算：

def portfolio_var(returns_df, weights, confidence_level=0.95, method='historical'):
    if method == 'parametric':
        portfolio_returns = returns_df.dot(weights)
        return parametric_var(portfolio_returns, confidence_level)
    
    elif method == 'historical':
        portfolio_returns = returns_df.dot(weights)
        return historical_var(portfolio_returns, confidence_level)
    
    elif method == 'monte_carlo':
        # Use the covariance matrix to generate
        # correlated random variables
        cov_matrix = returns_df.cov()
        L = np.linalg.cholesky(cov_matrix)
        
        means = returns_df.mean().values
        simulated_returns = []
        
        for _ in range(10000):
            Z = np.random.standard_normal(len(weights))
            R = means + L @ Z
            portfolio_return = weights @ R
            simulated_returns.append(portfolio_return)
            
        return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

最终，我们得到了一个灵活的风险价值（VaR）计算系统，它专为外汇市场的特性而做了适配。在下一节中，我将探讨这些计算是如何与马科维茨理论相结合，以实现投资组合优化的。

使用马科维茨方法进行投资组合优化

在实现了可靠的风险价值计算之后，我开始将重心转向投资组合优化。马科维茨的经典理论需要进行重大的调整，才能适应外汇市场的现实情况。经过数月的实验与测试，我得出了几项重要的发现。

我首先意识到的是，标准的风险与回报指标在外汇市场的运作方式与在股票市场有所不同。货币对之间存在着随时间变化的复杂关系。经过大量实验，我开发了一个修正后的期望回报计算函数：

def calculate_expected_returns(returns_df, method='ewma', halflife=30):
    if method == 'ewma':
        # Exponentially weighted average gives more weight to recent data
        return returns_df.ewm(halflife=halflife).mean().iloc[-1]
    elif method == 'capm':
        # Modified CAPM for Forex
        risk_free_rate = 0.02  # annual risk-free rate
        market_returns = returns_df.mean(axis=1)  # market returns proxy
        betas = calculate_currency_betas(returns_df, market_returns)
        return risk_free_rate + betas * (market_returns.mean() - risk_free_rate)

协方差矩阵的计算也同样需要进行一些修正。简单的历史数据方法会产生过于不稳定的结果。我实现了收缩估计法，它显著提升了优化的稳健性：

def shrinkage_covariance(returns_df, shrinkage_factor=None):
    sample_cov = returns_df.cov()
    n_assets = len(returns_df.columns)
    
    # The target matrix is diagonal with average variance
    target = np.diag(np.repeat(sample_cov.values.trace() / n_assets, n_assets))
    
    if shrinkage_factor is None:
        # Estimation of the optimal 'shrinkage' ratio
        shrinkage_factor = estimate_optimal_shrinkage(returns_df, sample_cov, target)
    
    shrunk_cov = (1 - shrinkage_factor) * sample_cov + shrinkage_factor * target
    return pd.DataFrame(shrunk_cov, index=sample_cov.index, columns=sample_cov.columns)

最困难的部分是优化投资组合权重。经过多次测试，我最终选定了一种修正的二次规划算法：

def optimize_portfolio(returns_df, expected_returns, covariance, target_return=None, constraints=None):
    n_assets = len(returns_df.columns)
    
    # Risk minimization function
    def portfolio_volatility(weights):
        return np.sqrt(weights.T @ covariance @ weights)
    
    # Limitations
    constraints = []
    # The sum of the weights is 1
    constraints.append({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
    
    if target_return is not None:
        # Target income limit
        constraints.append({
            'type': 'eq',
            'fun': lambda x: x @ expected_returns - target_return
        })
    
    # Add leverage restrictions for Forex
    constraints.append({
        'type': 'ineq',
        'fun': lambda x: 20 - np.sum(np.abs(x))  # max leverage 20
    })
    
    # Initial approximation - equal weights
    initial_weights = np.repeat(1/n_assets, n_assets)
    
    # Optimization
    result = minimize(
        portfolio_volatility,
        initial_weights,
        method='SLSQP',
        constraints=constraints,
        bounds=tuple((0, 1) for _ in range(n_assets))
    )
    
    if not result.success:
        raise OptimizationError("Failed to optimize portfolio: " + result.message)
        
    return result.x

我特别关注了解的稳定性问题。输入数据的微小变化，不应导致投资组合发生根本性的改变。为此，我开发了一套正则化流程：

def regularized_optimization(returns_df, current_weights, lambda_reg=0.1):
    # Add a penalty for deviation from the current weights
    def objective(weights):
        volatility = portfolio_volatility(weights)
        turnover_penalty = lambda_reg * np.sum(np.abs(weights - current_weights))
        return volatility + turnover_penalty

最终，我们得到了一个可靠的投资组合优化器，它既考虑了外汇市场的特殊性，又不需要频繁的再平衡。但最核心的挑战还在后面——将这种方法与基于风险价值的控制系统结合起来。

将 VaR 与马科维茨模型整合为单一模型

事实证明，将这两种方法结合起来是整个项目中最具挑战性的部分。我必须找到一种方法，既能利用两种方法的优势，又不会在它们之间产生矛盾。经过数月的实验，我想出了一个优雅的解决方案。

核心思想是，将风险价值作为马科维茨优化问题中的一个附加约束条件。它在代码中的实现如下：

def integrated_portfolio_optimization(returns_df, target_return, max_var_limit, current_weights=None):
    n_assets = len(returns_df.columns)
    
    # Calculation of basic metrics
    exp_returns = calculate_expected_returns(returns_df)
    covariance = shrinkage_covariance(returns_df)
    
    def objective_function(weights):
        # Portfolio standard deviation (Markowitz)
        portfolio_std = np.sqrt(weights.T @ covariance @ weights)
        
        # component VaR
        portfolio_var = calculate_portfolio_var(returns_df, weights)
        var_penalty = max(0, portfolio_var - max_var_limit)
        
        return portfolio_std + 100 * var_penalty  # Penalty for exceeding VaR

为了考虑市场的动态特性，我开发了一个用于重新计算参数的自适应系统：

def adaptive_risk_limits(returns_df, base_var_limit, window=60):
    # Adapting VaR limits to current volatility
    recent_vol = returns_df.tail(window).std()
    long_term_vol = returns_df.std()
    vol_ratio = recent_vol / long_term_vol
    
    adjusted_var_limit = base_var_limit * np.sqrt(vol_ratio)
    return min(adjusted_var_limit, base_var_limit * 1.5)  # Limit growth

必须特别关注解的稳定性问题。我实现了一个在投资组合状态之间平滑过渡的机制：

def smooth_rebalancing(old_weights, new_weights, max_change=0.1):
    weight_diff = new_weights - old_weights
    excess_change = np.abs(weight_diff) - max_change
    
    where_excess = excess_change > 0
    if where_excess.any():
        # Limit changes in weights
        adjustment = np.sign(weight_diff) * np.minimum(
            np.abs(weight_diff),
            np.where(where_excess, max_change, np.abs(weight_diff))
        )
        return old_weights + adjustment
    return new_weights

我开发了一个专门的指标来评估这种整合方法的效率：

def evaluate_integrated_model(returns_df, weights, var_limit):
    # Calculation of performance metrics
    portfolio_returns = returns_df.dot(weights)
    realized_var = historical_var(portfolio_returns)
    sharpe = calculate_sharpe_ratio(portfolio_returns)
    var_efficiency = abs(realized_var - var_limit) / var_limit
    
    return {
        'sharpe_ratio': sharpe,
        'var_efficiency': var_efficiency,
        'max_drawdown': calculate_max_drawdown(portfolio_returns),
        'turnover': calculate_turnover(weights)
    }

在测试过程中，我们发现该模型在波动率加剧的时期表现得尤为出色。VaR 组件有效地限制了风险，而马科维茨优化则继续寻求盈利的机会。

该系统的最终版本还包括一个自动参数调整机制：

def auto_tune_parameters(returns_df, initial_params, optimization_window=252):
    best_params = initial_params
    best_score = float('-inf')
    
    for var_limit in np.arange(0.01, 0.05, 0.005):
        for shrinkage in np.arange(0.2, 0.8, 0.1):
            params = {'var_limit': var_limit, 'shrinkage': shrinkage}
            score = backtest_model(returns_df, params, optimization_window)
            
            if score > best_score:
                best_score = score
                best_params = params
                
    return best_params

在下一节中，我将讨论这个组合模型是如何在实际交易中应用于动态仓位管理的。

动态仓位规模管理

将理论模型转化为一个实用的交易系统，需要解决许多技术问题。其中最主要的问题，就是如何结合当前市场状况与计算出的最优投资组合权重，来对仓位规模进行动态管理。

该系统的基础是一个用于管理仓位的类：

class PositionManager:
    def __init__(self, account_balance, risk_limit=0.02):
        self.balance = account_balance
        self.risk_limit = risk_limit
        self.positions = {}
        
    def calculate_position_size(self, symbol, weight, var_estimate):
        symbol_info = mt5.symbol_info(symbol)
        pip_value = symbol_info.trade_tick_value * 10
        
        # Calculate the position size taking into account VaR
        max_risk_amount = self.balance * self.risk_limit * abs(weight)
        position_size = max_risk_amount / (abs(var_estimate) * pip_value)
        
        # Round to minimum lot
        return round(position_size / symbol_info.volume_step) * symbol_info.volume_step

为了平滑地调整仓位，我开发了一套部分订单管理机制：

def adjust_positions(self, target_positions):
    for symbol, target_size in target_positions.items():
        current_size = self.get_current_position(symbol)
        if abs(target_size - current_size) > self.min_adjustment:
            # Break big changes into pieces
            steps = min(5, int(abs(target_size - current_size) / self.min_adjustment))
            step_size = (target_size - current_size) / steps
            
            for i in range(steps):
                next_size = current_size + step_size
                self.execute_order(symbol, next_size - current_size)
                current_size = next_size
                time.sleep(1)  # Prevent order flooding

在调整仓位时，我特别关注了风险控制：

def execute_order(self, symbol, size_delta, max_slippage=10):
    if size_delta > 0:
        order_type = mt5.ORDER_TYPE_BUY
    else:
        order_type = mt5.ORDER_TYPE_SELL
    
    # Get current prices
    tick = mt5.symbol_info_tick(symbol)
    
    # Set VaR-based stop loss
    if order_type == mt5.ORDER_TYPE_BUY:
        stop_loss = tick.bid - (self.var_estimates[symbol] * tick.bid)
        take_profit = tick.bid + (self.var_estimates[symbol] * 2 * tick.bid)
    else:
        stop_loss = tick.ask + (self.var_estimates[symbol] * tick.ask)
        take_profit = tick.ask - (self.var_estimates[symbol] * 2 * tick.ask)
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": abs(size_delta),
        "type": order_type,
        "price": tick.ask if order_type == mt5.ORDER_TYPE_BUY else tick.bid,
        "sl": stop_loss,
        "tp": take_profit,
        "deviation": max_slippage,
        "magic": 234000,
        "comment": "var_based_adjustment",
        "type_time": mt5.ORDER_TIME_GTC,
        "type_filling": mt5.ORDER_FILLING_IOC,
    }
    
    result = mt5.order_send(request)
    return self.handle_order_result(result)

我增加了一套波动率监控系统，以防范市场的剧烈波动：

def monitor_volatility(self, returns_df, threshold=2.0):
    # Current volatility calculation
    current_vol = returns_df.tail(20).std() * np.sqrt(252)
    historical_vol = returns_df.std() * np.sqrt(252)
    
    if current_vol > historical_vol * threshold:
        # Reduce positions in case of increased volatility
        self.reduce_exposure(current_vol / historical_vol)
        return False
        
    return True

该系统还包含一套自动平仓机制，当触及关键风险水平时便会触发：

def emergency_close(self, max_loss_percent=5.0):
    total_loss = sum(pos.profit for pos in mt5.positions_get())
    if total_loss < -self.balance * max_loss_percent / 100:
        print("Emergency closure triggered!")
        for position in mt5.positions_get():
            self.close_position(position.ticket)

最终，我们得到了一个稳健的仓位管理系统，它能够在多种市场条件下有效运作。下一节将重点介绍基于 VaR 的风险控制系统。

投资组合风险控制系统

在实现了动态仓位管理之后，我面临着在投资组合层面创建一套全面风险控制系统的需求。经验表明，仅对单个仓位进行局部风险控制是远远不够的——我们需要一种整体性的方法。

我首先从创建一个用于监控投资组合风险的类开始：

class PortfolioRiskManager:
    def __init__(self, max_portfolio_var=0.03, max_correlation=0.7, max_drawdown=0.1):
        self.max_portfolio_var = max_portfolio_var
        self.max_correlation = max_correlation
        self.max_drawdown = max_drawdown
        self.current_drawdown = 0
        self.peak_balance = 0
        
    def update_portfolio_metrics(self, positions, returns_df):
        # Calculation of current portfolio weights
        total_exposure = sum(abs(pos.volume) for pos in positions)
        weights = {pos.symbol: pos.volume/total_exposure for pos in positions}
        
        # Update portfolio VaR
        self.current_var = self.calculate_portfolio_var(returns_df, weights)
        
        # Check correlations
        self.check_correlations(returns_df, weights)

我特别关注了不同金融工具之间的相关性：

def check_correlations(self, returns_df, weights):
    corr_matrix = returns_df.corr()
    high_corr_pairs = []
    
    for i in returns_df.columns:
        for j in returns_df.columns:
            if i < j and abs(corr_matrix.loc[i,j]) > self.max_correlation:
                if weights.get(i, 0) > 0 and weights.get(j, 0) > 0:
                    high_corr_pairs.append((i, j, corr_matrix.loc[i,j]))
                    
    if high_corr_pairs:
        self.handle_high_correlations(high_corr_pairs, weights)

我实现了基于市场条件的动态风险管理：

def adjust_risk_limits(self, market_state):
    volatility_factor = market_state.get('volatility_ratio', 1.0)
    trend_strength = market_state.get('trend_strength', 0.5)
    
    # Adapt limits to market conditions
    self.max_portfolio_var *= np.sqrt(volatility_factor)
    if trend_strength > 0.7:  # Strong trend
        self.max_drawdown *= 1.2  # Allow a big drawdown
    elif trend_strength < 0.3:  # Weak trend
        self.max_drawdown *= 0.8  # Reduce the acceptable drawdown

回撤监控系统的开发过程，结果被证明是特别有意思的：

def monitor_drawdown(self, current_balance):
    if current_balance > self.peak_balance:
        self.peak_balance = current_balance
    
    self.current_drawdown = (self.peak_balance - current_balance) / self.peak_balance
    
    if self.current_drawdown > self.max_drawdown:
        return self.handle_excessive_drawdown()
    elif self.current_drawdown > self.max_drawdown * 0.8:
        return self.reduce_risk_exposure(0.8)
    
    return True

我增加了一套压力测试系统，以防范极端事件的发生：

def stress_test_portfolio(self, returns_df, weights, scenarios=1000):
    results = []
    
    for _ in range(scenarios):
        # Simulate extreme conditions
        stress_returns = returns_df.copy()
        
        # Increase volatility
        vol_multiplier = np.random.uniform(1.5, 3.0)
        stress_returns *= vol_multiplier
        
        # Add random shocks
        shock_magnitude = np.random.uniform(-0.05, 0.05)
        stress_returns += shock_magnitude
        
        # Calculate losses in a stress scenario
        portfolio_return = (stress_returns * weights).sum(axis=1)
        results.append(portfolio_return.min())
    
    return np.percentile(results, 1)  # 99% VaR in case of a stress

最终，我构建了一个多层次的本金保护体系，它能有效防范过度风险，并帮助系统在高波动时期得以生存。在下一节中，我将探讨所有这些组件是如何在实盘交易中协同工作的。

分析结果的可视化

可视化成为了我研究工作中一个至关重要的环节。在实现了所有的计算模块之后，有必要将分析结果以图形化的方式呈现出来。为此，我开发了几个关键的图形组件，用以实时监控系统的运行表现。

我首先从投资组合的结构及其演变过程入手进行可视化：

def plot_portfolio_composition(weights_history):
    plt.figure(figsize=(15, 8))
    ax = plt.gca()
    
    # Create a graph of weight changes over time
    dates = weights_history.index
    bottom = np.zeros(len(dates))
    
    for symbol in weights_history.columns:
        plt.fill_between(dates, bottom, bottom + weights_history[symbol], 
                        label=symbol, alpha=0.6)
        bottom += weights_history[symbol]
    
    plt.title('Evolution of portfolio structure')
    plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
    plt.grid(True, alpha=0.3)

尤其关注可视化风险水平。我还为不同的货币对开发了一张 VaR 热力图：

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='RdYlBu_r', 
                fmt='.2%', center=0)
    plt.title('Portfolio risk map (VaR)')
    
    # Add a timestamp
    plt.annotate(f'Last update: {datetime.now().strftime("%Y-%m-%d %H:%M")}',
                xy=(0.01, -0.1), xycoords='axes fraction')

为了分析盈利情况，我创建了一张交互式图表，并在其中高亮标注了重要事件：

def plot_performance_analytics(returns_df, var_values, significant_events):
    fig = plt.figure(figsize=(15, 10))
    gs = GridSpec(2, 1, height_ratios=[3, 1])
    
    # Returns graph
    ax1 = plt.subplot(gs[0])
    cumulative_returns = (1 + returns_df).cumprod()
    ax1.plot(cumulative_returns.index, cumulative_returns, 
             label='Portfolio returns')
    
    # Mark important events
    for date, event in significant_events.items():
        ax1.axvline(x=date, color='r', linestyle='--', alpha=0.3)
        ax1.annotate(event, xy=(date, ax1.get_ylim()[1]),
                    xytext=(10, 10), textcoords='offset points',
                    rotation=45)
    
    # VaR graph
    ax2 = plt.subplot(gs[1])
    ax2.fill_between(var_values.index, -var_values, 
                     color='lightblue', alpha=0.5,
                     label='Value at Risk')

我增加了一个交互式仪表盘，用于监控投资组合状态：

class PortfolioDashboard:
    def __init__(self):
        self.fig = plt.figure(figsize=(15, 10))
        self.setup_subplots()
        
    def setup_subplots(self):
        gs = self.fig.add_gridspec(3, 2)
        self.ax_returns = self.fig.add_subplot(gs[0, :])
        self.ax_weights = self.fig.add_subplot(gs[1, 0])
        self.ax_risk = self.fig.add_subplot(gs[1, 1])
        self.ax_metrics = self.fig.add_subplot(gs[2, :])
        
    def update(self, portfolio_data):
        self._plot_returns(portfolio_data['returns'])
        self._plot_weights(portfolio_data['weights'])
        self._plot_risk_metrics(portfolio_data['risk'])
        self._update_metrics_table(portfolio_data['metrics'])
        
        plt.tight_layout()
        plt.show()

我开发了一个动态可视化工具，用以分析相关性：

def plot_correlation_dynamics(returns_df, window=60):
    # Calculation of dynamic correlations
    correlations = returns_df.rolling(window=window).corr()
    
    # Create an animated graph
    fig, ax = plt.subplots(figsize=(10, 10))
    
    def update(frame):
        ax.clear()
        sns.heatmap(correlations.loc[frame], 
                    vmin=-1, vmax=1, center=0,
                    cmap='RdBu', ax=ax)
        ax.set_title(f'Correlations on {frame.strftime("%Y-%m-%d")}')

所有这些可视化工具，都有助于快速评估投资组合的状态并做出交易决策。在下一节中，我将对系统进行测试。

策略回测

在完成系统所有组件的开发后，我面临着对其进行全面测试的需求。这个过程远比简单地运行历史数据要复杂得多。有必要考虑诸多因素：滑点、佣金，以及在不同经纪商处订单执行的具体情况。

初步的回测尝试表明，采用固定点差的经典方法会得出过于乐观的结果。因此，有必要创建一个更贴近现实的模型，该模型需能根据波动率和一天中的不同时段来考虑点差的变化。

我特别关注了对数据缺失和流动性问题的建模。在实盘交易中，订单无法按预期价格成交的情况时有发生。这些场景在测试中必须得到正确处理。

以下是回测系统的完整实现：

class PortfolioBacktester:
    def __init__(self, initial_capital=100000, commission=0.0001):
        self.initial_capital = initial_capital
        self.commission = commission
        self.positions = {}
        self.trades_history = []
        self.balance_history = []
        self.var_history = []
        self.metrics = {}
        
    def run_backtest(self, returns_df, optimization_params):
        self.current_capital = self.initial_capital
        portfolio_returns = []
        
        # Preparing sliding windows for calculations
        window = 252  # Trading yesr
        for i in range(window, len(returns_df)):
            # Receive historical data for calculation
            historical_returns = returns_df.iloc[i-window:i]
            
            # Optimize the portfolio
            weights = self.optimize_portfolio(
                historical_returns, 
                optimization_params['target_return'],
                optimization_params['max_var']
            )
            
            # Calculate VaR for the current distribution
            current_var = self.calculate_portfolio_var(
                historical_returns, 
                weights,
                optimization_params['confidence_level']
            )
            
            # Check the need for rebalancing
            if self.should_rebalance(weights, current_var):
                self.execute_rebalancing(weights, returns_df.iloc[i])
            
            # Update positions and calculate profitability
            portfolio_return = self.update_positions(returns_df.iloc[i])
            portfolio_returns.append(portfolio_return)
            
            # Update metrics
            self.update_metrics(portfolio_return, current_var)
            
            # Check stop losses triggering
            self.check_stop_losses(returns_df.iloc[i])
        
        # Calculate the final metrics
        self.calculate_final_metrics(portfolio_returns)
        
    def optimize_portfolio(self, returns, target_return, max_var):
        # Using our hybrid optimization model
        opt = HybridOptimizer(returns, target_return, max_var)
        weights = opt.optimize()
        return self.apply_position_limits(weights)
        
    def execute_rebalancing(self, target_weights, current_prices):
        for symbol, target_weight in target_weights.items():
            current_weight = self.get_position_weight(symbol)
            if abs(target_weight - current_weight) > self.REBALANCING_THRESHOLD:
                # Simulate execution with slippage
                slippage = self.simulate_slippage(symbol, current_prices[symbol])
                trade_price = current_prices[symbol] * (1 + slippage)
                
                # Calculate the deal size
                trade_volume = self.calculate_trade_volume(
                    symbol, current_weight, target_weight
                )
                
                # Consider commissions
                commission = abs(trade_volume * trade_price * self.commission)
                self.current_capital -= commission
                
                # Set a deal to history
                self.record_trade(symbol, trade_volume, trade_price, commission)
                
    def update_metrics(self, portfolio_return, current_var):
        self.balance_history.append(self.current_capital)
        self.var_history.append(current_var)
        
        # Updating performance metrics
        self.metrics['max_drawdown'] = self.calculate_drawdown()
        self.metrics['sharpe_ratio'] = self.calculate_sharpe()
        self.metrics['var_efficiency'] = self.calculate_var_efficiency()
        
    def calculate_final_metrics(self, portfolio_returns):
        returns_series = pd.Series(portfolio_returns)
        
        self.metrics['total_return'] = (self.current_capital / self.initial_capital - 1)
        self.metrics['volatility'] = returns_series.std() * np.sqrt(252)
        self.metrics['sortino_ratio'] = self.calculate_sortino(returns_series)
        self.metrics['calmar_ratio'] = self.calculate_calmar()
        self.metrics['var_breaches'] = self.calculate_var_breaches()
        
    def simulate_slippage(self, symbol, price):
        # Simulate realistic slippage
        base_slippage = 0.0001  # Basic slippage
        time_factor = self.get_time_factor()  # Time dependency
        volume_factor = self.get_volume_factor(symbol)  # Volume dependency
        
        return base_slippage * time_factor * volume_factor

测试结果相当有启发性。与经典方法相比，该混合模型展现出了显著更强的市场冲击抵御能力。这一点在高波动性时期尤为明显，此时，风险价值限额有效地保护了投资组合免受过度风险的侵害。

最终调试

经过数月的开发和测试，我终于完成了系统的最终版本。说实话，它与我最开始的设想大相径庭。实践迫使我做出了许多改变，其中一些相当出人意料。

第一个重大改变在于数据处理方式。我意识到，仅在历史数据上测试系统是远远不够的——有必要检查其在各种市场条件下的行为表现。因此，我开发了一套合成数据生成系统。这听起来简单，但实际上花了我好几周的时间。

我首先根据流动性将所有货币对进行分组。第一组是主要货币对，如EURUSD和GBPUSD。第二组是商品货币对，如AUDUSD和USDCAD。接下来是交叉盘——EURJPY、GBPJPY等。最后是奇异货币对，如CADJPY和EURAUD。我为每个组设定了各自的波动率和相关性参数，并尽可能使其贴近真实情况。

但最有趣的部分始于我加入了不同的市场模式。想象一下：三分之一的时间市场风平浪静，波动率很低。另外三分之一是正常交易。而剩下的时间则是波动加剧，一切都像疯了一样地波动。此外，我还加入了长期趋势和周期性波动。最终的结果与真实市场非常相似。

投资组合优化也颇费了一番功夫。起初，我以为通过对仓位权重设置简单限制就足够了，但我很快意识到这远远不够。于是，我加入了动态风险溢价——货币对的波动性越高，其潜在回报也应越高。我引入了限制：单笔仓位最低4%，最高25%。这听起来似乎很多，但如果你使用杠杆，这很正常。

说到杠杆。这又是另一回事了。起初，我为了安全起见，几乎没用杠杆。但分析表明，适度的杠杆，大约10倍，能显著改善结果。关键在于要正确计算所有成本。而成本项目相当多：交易佣金（2个基点）、杠杆维持利息（每日0.01%）、执行滑点。所有这些都必须被纳入优化器的考量之中。

另一个令人头疼的问题是防范追加保证金。经过几次不成功的实验后，我采用了一个简单的解决方案：如果回撤超过10%，就关闭所有仓位，至少保住一部分本金。这听起来很保守，但从长远来看效果非常好。

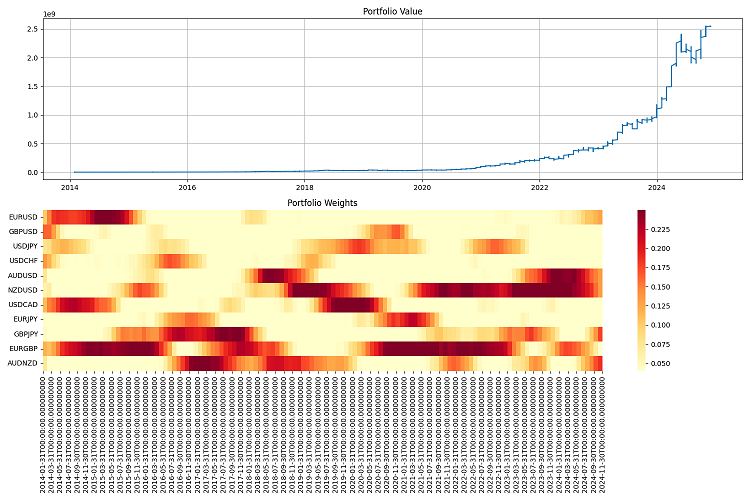
最困难的部分是报告生成。当你的系统同时处理几十个货币对，并且不停地买卖时，根本不可能手动追踪所有情况。我不得不开发一整套监控系统：包含大量指标的年度报告，以及各种你能想到的图表：从简单的投资组合净值到权重分布的热力图。

我进行了长达一个时期的最终测试——从2000年到2024年。我以一百万美元作为初始资本，并每季度进行一次再平衡。结果令我非常满意。该系统能很好地适应不同的市场条件，并将风险控制在可接受范围内。即使在最严重的危机中，它也能设法保住大部分资本。

但仍有大量工作要做。我希望加入机器学习来预测波动率。目前，系统仅基于历史数据进行运作。此外，我正在思考如何让杠杆管理更加灵活。再平衡的频率也可以进行优化。有时一个季度太长了，而有时你又可以半年都不动仓位。

总而言之，最终成品与我最初的计划完全不同。但正如人们常说的，完美是好的敌人。系统能够运行，能控制风险，并且能赚钱。这才是最重要的。

结论

这真是一段酷炫的旅程。当我最初开始摆弄马科维茨理论时，我完全无法想象它最终会演变成什么样子。我本只是想在外汇市场上应用一种常规方法，但最终却不得不从各种风险管理方法中拼凑出一个类似“科学怪人”的混合体。

最酷的是，我成功地将马科维茨理论与风险价值结合在了一起，而且这玩意儿真的管用！有趣的是，这两种方法单独使用时都表现平平，但组合在一起却能产生卓越的效果。最让我满意的是，当市场剧烈震荡时，系统的表现依然坚挺。作为优化过程中的一个限制器，风险价值的表现简直令人惊叹。

当然，我在技术实现上遇到了一大堆麻烦。但现在，一切都考虑周全了：滑点、佣金，以及执行特性。

我用2000年至2024年的历史数据对系统进行了回测。结果相当不错。它能很好地适应不同的市场状况，甚至在危机期间也未曾崩溃。在10倍杠杆下，它运行得像时钟一样精准。关键在于，要严格控制风险。

但依然有海量的工作等着我去做。我希望能够：

• 将机器学习加入波动率预测（这将是下一篇文章的主题）；
• 理清再平衡的频率问题——或许它还能被进一步优化；
• 让杠杆管理变得更智能（动态杠杆和动态“智能”保证金加载也将在未来的文章中实现）；
• 训练系统，使其能更好地适应不同的市场行情。

总而言之，核心结论是：一个出色的交易系统，并不仅仅是教科书上的几个公式。在这里，你需要理解市场，精通技术，而尤其重要的是，要懂得如何牢牢控制住风险。现在，所有这些开发成果都可以应用到其他市场，而不仅仅是外汇。尽管仍有成长空间，但基础已经打下，并且它行之有效。