Modelos de regressão não linear no mercado

Introdução

Ontem eu estava novamente mergulhado nos relatórios do meu sistema de trading baseado em regressão. Do lado de fora, caía uma neve molhada, o café na caneca esfriava, e eu não conseguia me livrar de um pensamento insistente. Sabe, há muito tempo me incomodam esses infinitos RSI, Stochastic, MACD e outros indicadores. Poxa, como alguém pode tentar encaixar um mercado vivo e dinâmico nessas fórmulas primitivas? Toda vez que vejo mais um guru no YouTube com seu “sagrado” conjunto de indicadores, dá vontade de perguntar: cara, você realmente acredita que essas calculadoras dos anos setenta conseguem capturar a complexa dinâmica do mercado atual?

Passei os últimos três anos tentando criar algo que realmente funcionasse. Testei de tudo, desde as regressões mais simples até redes neurais avançadas. E sabe o que aconteceu? Consegui obter resultados em classificação, mas em regressão ainda não.

Era sempre a mesma história: no histórico tudo funcionava perfeitamente, mas quando colocava no mercado real, lá vinha o prejuízo. Lembro da alegria com minha primeira rede convolucional. Era linda: R2 quase 1,00% no treinamento. Depois, duas semanas de operação e menos 30% da conta. Clássico: overfitting na sua forma mais pura. Você ativa a visualização da propagação para frente e vê a previsão “voando” cada vez mais longe dos preços reais com o passar do tempo.

Mas eu sou teimoso. Depois de mais uma perda, resolvi ir mais fundo e mergulhei em artigos científicos. E sabe o que encontrei nos arquivos empoeirados? Acontece que o velho Mandelbrot já falava sobre a natureza fractal dos mercados. E a gente tentando operar com modelos lineares! É como tentar medir a linha da costa com uma régua: quanto mais precisa a medição, maior o comprimento resulta.

Em algum momento, tive um estalo: e se tentarmos cruzar a análise técnica clássica com dinâmica não linear? Não esses indicadores grosseiros, mas algo mais sério: equações diferenciais, coeficientes adaptativos. Parece complicado, mas no fundo é só uma tentativa de aprender a falar com o mercado no idioma dele.

Enfim, peguei o Python, conectei bibliotecas de aprendizado de máquina e comecei a experimentar. Decidi logo de cara: nada de enfeites acadêmicos, só o que dá pra usar de verdade. Nada de supercomputadores: um notebook Acer comum, um VPS bem potente e o terminal MetaTrader 5. Foi com tudo isso que nasceu o modelo que quero apresentar.

Não, isso não é mais um graal. Já entendi há muito tempo que graais não existem. Estou apenas compartilhando minha experiência: como usar matemática moderna aplicada à negociação real. Sem exageros publicitários, mas também sem o simplismo dos “indicadores de tendência”. Saiu algo intermediário: inteligente o suficiente para funcionar, mas não tão complexo a ponto de desmoronar no primeiro cisne negro.

Modelo matemático

Lembro bem como cheguei a essa fórmula. Trabalhei nesse código desde 2022, mas não de forma contínua: é um processo que chamo de desenvolvimento em ondas, então você vai testando abordagens (de forma um pouco caótica) e vai lapidando uma a uma até chegar num resultado. Lembro de rodar gráficos, tentando capturar padrões no movimento do euro-dólar. E sabe o que me chamou atenção? O mercado parece respirar: ora flui suavemente em tendência, ora dá trancos repentinos, ora entra num ritmo quase mágico. Como descrever isso matematicamente? Como capturar essa dinâmica viva em fórmulas?

Depois disso, rascunhei a primeira versão da equação. Aqui está ela, em toda a sua glória:

E aqui a mesma equação no código:

def equation(self, x_prev, coeffs):
    x_t1, x_t2 = x_prev[0], x_prev[1]
    return (coeffs[0] * x_t1 +          # trend
            coeffs[1] * x_t1**2 +       # acceleration
            coeffs[2] * x_t2 +          # market memory
            coeffs[3] * x_t2**2 +       # inertia
            coeffs[4] * (x_t1 - x_t2) + # impulse
            coeffs[5] * np.sin(x_t1) +  # market rhythm
            coeffs[6])                   # basic level

Veja como tudo está interligado. Os dois primeiros termos são uma tentativa de capturar o movimento atual do mercado. Sabe como um carro acelera? Primeiro de forma suave, depois cada vez mais rápido. É por isso que temos aqui um termo linear e um quadrático. Quando o preço anda tranquilo, atua a parte linear. Mas basta o mercado acelerar, e o termo quadrático entra em cena.

Depois vem a parte mais interessante. O terceiro e o quarto termos olham um pouco mais para o passado. Isso funciona como a memória do mercado. Lembra da teoria de Dow, que diz que o mercado lembra seus níveis? Pois aqui é a mesma ideia, e de novo com aceleração quadrática para capturar reviravoltas bruscas.

Agora o componente de momentum. Basta subtrair o preço anterior do atual. Parece coisa simples. Mas como funciona bem nos movimentos de tendência! Quando o mercado pega embalo e vai com tudo numa direção, esse termo vira a principal força propulsora da previsão.

O seno entrou quase por acaso. Eu estava ali olhando os gráficos e percebi: caramba, tem uma certa periodicidade aqui! Especialmente nos gráficos de uma hora. Movimento de manhã, depois sossego, depois movimento de novo... Parece uma senoide, não parece? Coloquei a senoide na fórmula, e a modelo parece que “enxergou”, começou a captar esses ritmos.

O último coeficiente é como uma rede de segurança, um nível base. Sabe aquele ditado de que o importante não é acertar, é surpreender? Pois aqui é o contrário: esse termo impede o modelo de tentar surpreender demais o mercado com previsões fora da realidade.

Testei um monte de outras opções. Tentei colocar exponenciais, logaritmos, várias funções trigonométricas elaboradas. Pouco resultado, e o modelo virava um monstro. Sabe como é a navalha de Occam: não multiplique entidades além do necessário. A versão atual ficou exatamente assim: simples e funcional.

Claro, todos esses coeficientes precisam ser ajustados de alguma forma. É aí que entra o velho e bom método de Nelder-Mead. Mas isso já é outra história, que vou contar na próxima parte. Acredite, tem muito o que falar: só os tropeços que tive durante a otimização dariam uma matéria à parte.

Componentes lineares

Vamos começar com a parte linear. Sabe qual é o grande lance? O modelo observa os dois valores anteriores do preço, mas de maneiras diferentes. O primeiro coeficiente geralmente fica por volta de 0,3–0,4: é a reação instantânea à última variação. Mas o segundo é mais interessante, muitas vezes chega perto de 0,7, o que mostra uma influência mais forte do penúltimo preço. Engraçado, né? O mercado parece confiar mais nos níveis um pouco mais antigos, desconfiando das oscilações mais recentes.

Componentes quadráticos

Com os termos quadráticos aconteceu algo curioso. No começo, os coloquei só para considerar a não linearidade, mas depois percebi uma coisa surpreendente. Em mercado calmo, a contribuição deles é mínima: os coeficientes flutuam em torno de 0,01–0,02. Mas basta começar um movimento forte, e esses termos parecem “acordar”. Isso fica especialmente claro nos gráficos diários do euro-dólar: quando a tendência ganha força, os termos quadráticos começam a dominar, permitindo que o modelo “acelere” junto com o preço.

Componente de momentum

A componente de momentum foi uma verdadeira descoberta. À primeira vista, é só uma diferença de preços, mas como ela reflete bem o sentimento do mercado! Em períodos tranquilos, seu coeficiente fica entre 0,2 e 0,3, mas antes de grandes movimentos costuma saltar para 0,5. Isso virou para mim um tipo de indicador de que um movimento está prestes a acontecer: quando o otimizador começa a aumentar o peso do momentum, pode esperar por ação.

Componente cíclica

Já com a componente cíclica tive que trabalhar bastante. No início, testei diferentes períodos de senoide, mas depois entendi que o próprio mercado dita o ritmo. Basta deixar o modelo ajustar a amplitude pelo coeficiente, e a frequência surge naturalmente a partir dos próprios preços. É curioso ver como esse coeficiente varia entre a sessão europeia e a americana: como se o mercado realmente respirasse em ritmos diferentes.

Por fim, o termo livre. O papel dele acabou sendo muito mais importante do que eu imaginava no começo. Em períodos de alta volatilidade, ele funciona como uma âncora, impedindo que as previsões escapem para longe. Já em momentos mais calmos, ajuda a considerar com mais precisão o nível geral de preços. Com frequência, o valor desse termo se correlaciona com a força da tendência: quanto mais forte a tendência, mais próximo de zero fica o termo livre.

Sabe o que é mais interessante? Toda vez que tentei complicar o modelo, adicionar novos termos, usar funções mais sofisticadas e afins, os resultados só pioravam. Era como se o mercado dissesse: “Cara, não inventa, o principal você já pegou.” A versão atual da equação é realmente o ponto ideal entre complexidade e eficiência. Sete coeficientes, nem mais nem menos, cada um com seu papel claro no mecanismo de previsão.

Aliás, sobre a otimização desses coeficientes: isso dá uma história à parte, e das boas. Quando você começa a observar como o método de Nelder-Mead busca os valores ideais, é impossível não lembrar da teoria do caos. Mas falaremos disso na próxima parte: tem muito o que ver, pode acreditar.

Otimização do modelo. Vamos analisar o processo de otimização com o uso do algoritmo Nelder-Mead

Hoje vou falar da parte mais interessante: como fazer o nosso modelo funcionar com dados reais. Depois de alguns meses de experimentos com otimização, dezenas de noites sem dormir e litros de café, finalmente encontrei uma abordagem funcional.

Tudo começou como de costume: com descida do gradiente. Clássico absoluto, é a primeira coisa que vem à mente de qualquer um que estudou para ser cientista de dados. Perdi três dias só para implementar, mais uma semana depurando... E o resultado? O modelo simplesmente se recusava a convergir. Ou explodia para o infinito, ou travava em mínimos locais. Os gradientes pulavam feito loucos.

Depois veio uma semana com algoritmos genéticos. Ideia bonita: deixar a evolução encontrar os melhores coeficientes. Escrevi, rodei... e fiquei abismado com o tempo de execução. O computador roncou a noite inteira para processar uma única semana de dados históricos. E os resultados eram tão instáveis que mais valia jogar búzios ou ler a borra do café.

Foi então que descobri o método de Nelder-Mead. O velho e confiável método do simplex, criado ainda em 1965. Sem derivadas, sem matemática avançada: só uma forma inteligente de explorar o espaço de soluções. Rodei e não acreditei no que vi. O algoritmo parecia dançar com o mercado, se aproximando suavemente dos valores ideais.

Aqui está a função de perda principal, simples como um machado, mas infalível:

def loss_function(self, coeffs, X_train, y_train):
    y_pred = np.array([self.equation(x, coeffs) for x in X_train])
    mse = np.mean((y_pred - y_train)**2)
    r2 = r2_score(y_train, y_pred)
    
    # Save progress for analysis
    self.optimization_progress.append({
        'mse': mse,
        'r2': r2,
        'coeffs': coeffs.copy()
    })
    return mse

No começo, tentei complicar a função de perda, adicionei penalidades para coeficientes altos, enfiei MAPE e outras métricas. Clássico erro de desenvolvedor: se algo funciona, é obrigatório tentar melhorar até quebrar completamente. No fim, voltei ao bom e velho MSE, e sabe o que descobri? Que a simplicidade é mesmo o auge da genialidade.

É um prazer especial observar o processo de otimização em tempo real. Nas primeiras iterações, os coeficientes se agitam como loucos, o MSE oscila, o R² fica perto de zero. Depois começa a parte mais interessante: o algoritmo encontra a direção certa, e as métricas vão melhorando suavemente. Lá pela centésima iteração já dá pra saber se vai sair algo bom, e por volta da trecentésima a coisa normalmente se estabiliza.

Falando em métricas: o R² geralmente passa de 0,996, o que significa que o modelo explica mais de 99,6% da variação do preço. O MSE fica na casa de 0,0000007. Em outras palavras, o erro de previsão raramente passa de sete décimos de pips. E o MAPE... o MAPE é uma alegria à parte: frequentemente abaixo de 0,1%. Claro que isso tudo é em dados históricos, mas mesmo no teste de propagação para frente os resultados não ficam muito atrás.

Mas o mais importante nem são os números. O essencial é a estabilidade dos resultados. Dá pra rodar a otimização dez vezes seguidas, e sempre vai obter valores de coeficientes muito próximos. Isso tem um valor enorme, principalmente depois dos meus sofrimentos com outros métodos de otimização.

E sabe o que mais é legal? Observar o processo de otimização ajuda a entender muita coisa sobre o próprio mercado. Por exemplo, quando o algoritmo insiste em aumentar o peso da componente de momentum, é sinal de que vem aí um movimento forte. Ou quando começa a brincar com a componente cíclica, pode se preparar para um período de alta volatilidade.

Na próxima parte, vou mostrar como toda essa engenharia matemática se transforma numa verdadeira estratégia de negociação. Acredite, tem muito o que refletir: só os perrengues com o MetaTrader 5 já dariam outra matéria.

Particularidades do processo de aprendizado

A preparação dos dados para o aprendizado rendeu uma história à parte. Lembro que, na primeira versão do sistema, fiquei todo feliz ao jogar o dataset inteiro no sklearn.train_test_split... E só depois, vendo resultados bons demais, percebi: poxa vida, tô deixando o futuro vazar pro passado!

Entende o problema? Com dados financeiros não dá pra lidar como se fosse uma tabela comum do Kaggle. Aqui, cada ponto de dado representa um momento no tempo, e embaralhar isso é como tentar prever o tempo de ontem com os dados de amanhã. Acabei chegando nesse código simples, mas eficiente:

def prepare_training_data(prices, train_ratio=0.67):
    # Cut off a piece for training
    n_train = int(len(prices) * train_ratio)
    
    # Forming prediction windows
    X = np.array([[prices[i], prices[i-1]] for i in range(2, len(prices)-1)])
    y = prices[3:]  
    
    # Fair time sharing
    X_train, y_train = X[:n_train], y[:n_train]
    X_test, y_test = X[n_train:], y[n_train:]
    
    return X_train, y_train, X_test, y_test

Parece código básico. Mas por trás dessa simplicidade tem muito erro cometido e muita lição aprendida. Comecei testando vários tamanhos de janela. Achei que quanto mais pontos históricos, melhor a previsão. Que nada! Descobri que os dois valores anteriores já são suficientes. O mercado, sabe como é, não gosta de lembrar demais do passado.

Outro ponto foi o tamanho do conjunto de treinamento. Testei várias divisões: 50/50, 80/20, até 90/10. No fim, parei na proporção áurea, isto é, cerca de 67% dos dados para aprendizado. Por quê? Porque simplesmente funciona melhor! Vai ver o velho Fibonacci sabia mesmo algo sobre a natureza dos mercados...

É curioso observar como o modelo aprende em diferentes trechos dos dados. Você pega um período tranquilo: os coeficientes vão sendo ajustados de forma suave, as métricas melhoram gradualmente. Mas basta cair na amostra de treino algum Brexit ou um discurso do presidente do Fed, e aí começa: os coeficientes disparam, o otimizador surta, os gráficos de erro parecem montanhas-russas.

Falando em métricas: sabe o que percebi? Se o R² na amostra de treino ultrapassa 0,98, quase com certeza tem algum erro nos dados. O mercado real simplesmente não é tão previsível assim. É como aquela história do aluno que acerta tudo: ou colou, ou é gênio. No nosso caso, geralmente é a primeira opção.

Outro ponto importante: o pré-processamento dos dados. No começo tentei normalizar preços, escalar, remover valores atípicos... Enfim, tudo que ensinam nos cursos de aprendizado de máquina. Mas com o tempo percebi: quanto menos se mexe nos dados brutos, melhor. O próprio mercado já se “normaliza” naturalmente, só precisa ser preparado da forma certa.

Hoje, o processo de treinamento está ajustado no automático. Uma vez por semana, carregamos os dados novos, rodamos o treinamento, comparamos as métricas com os valores históricos. Se estiver tudo dentro do esperado, atualizamos os coeficientes no sistema em produção. Se algo parecer estranho, começamos a investigar. Felizmente, a experiência já ajuda a saber onde procurar o problema.

Processo de otimização dos coeficientes

def fit(self, prices):
    # Prepare data for training
    X_train, y_train = self.prepare_training_data(prices)
    
    # I found these initial values by trial and error
    initial_coeffs = np.array([0.5, 0.1, 0.3, 0.1, 0.2, 0.1, 0.0])
    
    result = minimize(
        self.loss_function,
        initial_coeffs,
        args=(X_train, y_train),
        method='Nelder-Mead',
        options={
            'maxiter': 1000,  # More iterations does not improve the result
            'xatol': 1e-8,   # Accuracy by ratios
            'fatol': 1e-8    # Accuracy by loss function
        }
    )
    
    self.coefficients = result.x
    return result

Sabe o que acabou sendo o mais difícil? Escolher esses malditos coeficientes iniciais. Primeiro tentei usar valores aleatórios: os resultados eram tão variados que nem dava vontade de colocar o sistema no ar. Depois testei começar com tudo igual a 1: o otimizador saía voando pro espaço já nas primeiras iterações. Com zeros também não funcionava: travava nos mínimos locais.

O primeiro coeficiente, 0.5, é o peso da componente linear. Menos que isso e o modelo perde a tendência, mais que isso e passa a confiar demais no preço mais recente. Para os termos quadráticos, 0.1 foi o ponto de partida ideal: suficiente pra capturar a não linearidade, mas sem exagero a ponto de fazer o modelo enlouquecer com movimentos bruscos. Já o 0.2 do momentum é pura empiria: foi nesse valor que o sistema deu os resultados mais estáveis.

Durante a otimização, o Nelder-Mead constrói um simplex em um espaço de sete dimensões, o que é um verdadeiro jogo de “quente-frio”, só que em sete direções ao mesmo tempo. E é crucial evitar a divergência do processo: por isso a exigência tão rígida de precisão (1e-8). Menos que isso, os resultados ficam instáveis; mais que isso, a otimização trava em mínimos locais.

Mil iterações pode parecer exagero, mas na prática o otimizador geralmente converge entre 300 e 400 passos. Só que, às vezes, especialmente em períodos de alta volatilidade, ele precisa de mais tempo para encontrar a solução ideal. E as iterações extras não impactam tanto o desempenho: todo o processo normalmente leva menos de um minuto em um hardware moderno.

Aliás, foi justamente durante o ajuste desse código que surgiu a ideia de adicionar uma visualização do processo de otimização. Quando você vê os coeficientes mudando em tempo real, fica muito mais fácil entender o que está acontecendo com o modelo e para onde ele pode desandar.

Métricas de qualidade e sua interpretação

Avaliar a qualidade de um modelo de previsão é um capítulo à parte, cheio de nuances nada óbvias. Depois de anos lidando com trading algorítmico, apanhei tanto das métricas que daria pra escrever um livro só sobre isso. Mas vamos ao essencial.

Aqui estão os resultados:

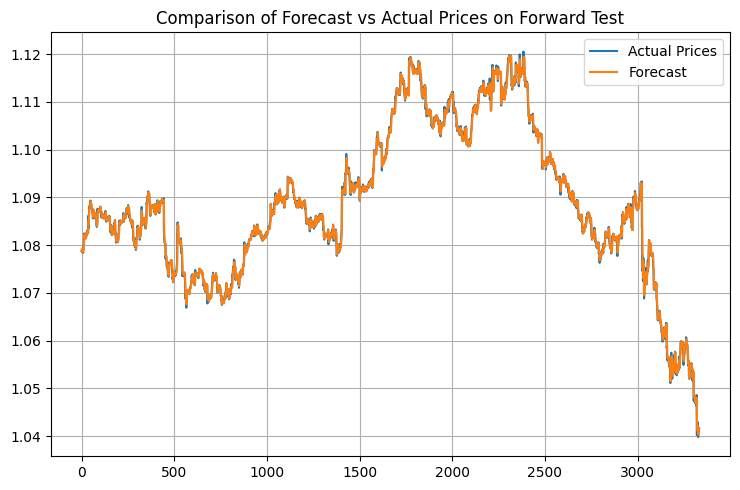
Começando pelo R-quadrado. A primeira vez que vi valores acima de 0,9 no EURUSD, achei que tinha algo errado. Revisei o código uma dezena de vezes: vazamento de dados? Algum erro no cálculo? Mas não, estava tudo certo: o modelo realmente explicava mais de 90% da dispersão do preço. Só que depois percebi: isso é uma faca de dois gumes. Um R² muito alto (acima de 0,95) costuma indicar overfitting. O mercado simplesmente não é tão previsível assim.

O MSE é nosso cavalo de batalha. Aqui está o código típico de avaliação:

def evaluate_model(self, y_true, y_pred):
    results = {
        'R²': r2_score(y_true, y_pred),
        'MSE': mean_squared_error(y_true, y_pred),
        'MAPE': mean_absolute_percentage_error(y_true, y_pred) * 100
    }
    
    # Additional statistics that often save the day
    errors = y_pred - y_true
    results['max_error'] = np.max(np.abs(errors))
    results['error_std'] = np.std(errors)
    
    # Look separately at error distribution "tails"
    results['error_quantiles'] = np.percentile(np.abs(errors), [50, 90, 95, 99])
    
    return results

Repare na estatística adicional. Max_error e error_std foram incluídos depois de um episódio desagradável: o modelo mostrava um MSE excelente, mas às vezes gerava previsões tão fora da curva que dava vontade de fechar a conta na hora. Agora, a primeira coisa que olho são os “caudas” da distribuição de erro. E elas ainda existem:

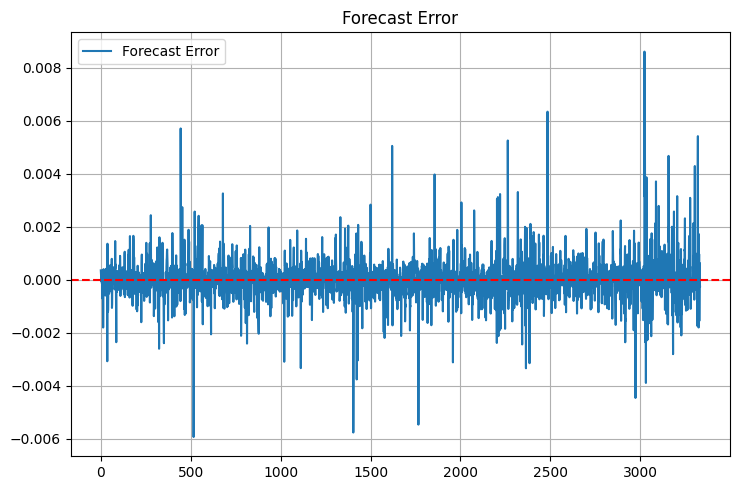
O MAPE é como um velho amigo dos traders. Fala em R-quadrado e o olhar fica vago; diz “a previsão erra em média 0,05%” e todo mundo entende. Mas tem uma armadilha: o MAPE pode parecer baixo quando o preço varia pouco e disparar em movimentos bruscos.

Mas o mais importante que aprendi: nenhuma métrica baseada em histórico garante sucesso no real. Por isso hoje uso um sistema completo de validação:

def validate_model_performance(self):
    # Check metrics on different timeframes
    timeframes = ['H1', 'H4', 'D1']
    for tf in timeframes:
        metrics = self.evaluate_on_timeframe(tf)
        if not self._check_metrics_thresholds(metrics):
            return False
    
    # Look at behavior at important historical events
    stress_periods = self.get_stress_periods()
    stress_metrics = self.evaluate_on_periods(stress_periods)
    if not self._check_stress_performance(stress_metrics):
        return False
    
    # Check the stability of forecasts
    stability = self.check_prediction_stability()
    if stability < self.min_stability_threshold:
        return False
    
    return True

O modelo precisa passar por todas essas verificações antes de ser usado em operação real. E mesmo assim, nas primeiras duas semanas eu opero com volume mínimo: só observando como ele se comporta no mercado ao vivo.

Perguntam com frequência: quais valores de métricas considerar bons? Pela minha experiência: R² acima de 0,9 — excelente, MSE abaixo de 0,00001 — aceitável, MAPE até 0,05% — maravilhoso. Mas! O mais importante é observar a estabilidade desses indicadores ao longo do tempo. Melhor um modelo com métricas um pouco piores, mas consistentes, do que um sistema superpreciso e instável.

Implementação técnica

Sabe o que é mais difícil no desenvolvimento de sistemas de trading? Não é a matemática, nem os algoritmos, é a confiabilidade operacional. Escrever uma fórmula bonita é uma coisa; outra bem diferente é fazê-la funcionar 24/7 com dinheiro real. Depois de alguns fracassos dolorosos em conta real, entendi: a arquitetura tem que ser não só boa, mas à prova de bala.

Aqui está como organizei o núcleo do sistema:

class PriceEquationModel:
    def __init__(self):
        # Model status
        self.coefficients = None
        self.training_scores = []
        self.optimization_progress = []
        
        # Initializing the connection
        self._setup_logging()
        self._init_mt5()
        
    def _init_mt5(self):
        """Initializing connection to MT5"""
        try:
            if not mt5.initialize():
                raise ConnectionError(
                    "Unable to connect to MetaTrader 5. "
                    "Make sure the terminal is running"
                )
            self.log.info("MT5 connection established")
        except Exception as e:
            self.log.critical(f"Critical initialization error: {str(e)}")
            raise

Cada linha ali é fruto de alguma experiência amarga. Por exemplo, criei um método separado para inicializar o MetaTrader 5 depois de tomar um deadlock tentando reconectar. E o logging entrou quando a aplicação caiu no meio da madrugada, sem nenhum aviso, e de manhã eu precisava adivinhar o que tinha acontecido.

O tratamento de erros é que é um capítulo à parte.  

def _safe_mt5_call(self, func, *args, retries=3, delay=5):
    """Secure MT5 function call with automatic recovery"""
    for attempt in range(retries):
        try:
            result = func(*args)
            if result is not None:
                return result
            
            # MT5 sometimes returns None without error
            raise ValueError(f"MT5 returned None: {func.__name__}")
            
        except Exception as e:
            self.log.warning(f"Attempt {attempt + 1}/{retries} failed: {str(e)}")
            if attempt < retries - 1:
                time.sleep(delay)
                # Trying to reinitialize the connection
                self._init_mt5()
            else:
                raise RuntimeError(f"Call attempts exhausted {func.__name__}")

Esse trecho de código resume toda a experiência com o MetaTrader 5. Ele tenta restabelecer a conexão se algo der errado, faz novas tentativas com atraso e, o mais importante, impede que o sistema continue rodando em estado incerto. Apesar disso, a biblioteca do MetaTrader 5 geralmente é impecável!

O estado do modelo é mantido da forma mais simples possível: só o essencial. Nada de estruturas de dados complexas ou otimizações mirabolantes. Em compensação, cada alteração de estado é registrada no log e validada:

def _update_model_state(self, new_coefficients):
    """Safely updating model ratio"""
    if not self._validate_coefficients(new_coefficients):
        raise ValueError("Invalid ratios")
        
    # Save the previous state
    old_coefficients = self.coefficients
    try:
        self.coefficients = new_coefficients
        if not self._check_model_consistency():
            raise ValueError("Model consistency broken")
            
        self.log.info("Model successfully updated")
        
    except Exception as e:
        # Roll back to the previous state
        self.coefficients = old_coefficients
        self.log.error(f"Model update error: {str(e)}")
        raise

Modularidade aqui não é só um termo bonito. Cada componente pode ser testado isoladamente, substituído ou modificado. Quer adicionar uma métrica nova? Crie um método novo. Precisa mudar a fonte de dados? Basta implementar outro conector com a mesma interface.

Trabalhar com dados históricos

Obter dados do MetaTrader 5 acabou sendo um desafio por si só. O código parece simples, mas o diabo mora nos detalhes. Depois de meses lidando com desconexões aleatórias e dados perdidos, cheguei a este esquema de integração com o terminal:

def fetch_data(self, symbol="EURUSD", timeframe=mt5.TIMEFRAME_H1, bars=10000):
    """Loading historical data with error handling"""
    try:
        # First of all, we check the symbol itself
        symbol_info = mt5.symbol_info(symbol)
        if symbol_info is None:
            raise ValueError(f"Symbol {symbol} unavailable")
            
        # MT5 sometimes "loses" MarketWatch symbols
        if not symbol_info.visible:
            mt5.symbol_select(symbol, True)
            
        # Collect data
        rates = mt5.copy_rates_from_pos(symbol, timeframe, 0, bars)
        if rates is None:
            raise ValueError("Unable to retrieve historical data")
            
        # Convert to pandas
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        
        return self._preprocess_data(df['close'].values)
        
    except Exception as e:
        print(f"Error while receiving data: {str(e)}")
        raise
    finally:
        # It is important to always close the connection
        mt5.shutdown()

Veja como tudo está estruturado. Primeiro, verificamos se o símbolo existe. Parece óbvio, mas teve um caso em que o sistema passou horas tentando operar um par inexistente por causa de um erro de digitação no config. Desde então, adicionei uma verificação rígida com symbol_info.

Depois vem um ponto interessante com o visible. Sabia que isso é possível? O símbolo até está cadastrado, mas não aparece no MarketWatch. E se você não chamar symbol_select, simplesmente não recebe dados, e o terminal pode “esquecer” o símbolo no meio da sessão. Divertido, né?

Com a obtenção de dados, também não é tão simples assim. O copy_rates_from_pos pode retornar None por uma dezena de razões: falta de conexão com o servidor, sobrecarga do servidor, histórico insuficiente... Por isso verificamos o resultado imediatamente e lançamos uma exceção se algo der errado.

A conversão para pandas é outro capítulo. O time vem no formato Unix, então é preciso transformá-lo em um timestamp legível. Sem isso, você vai sofrer na análise de séries temporais.

E o mais importante: fechar a conexão no bloco finally. Se você não fizer isso, o MetaTrader 5 começa a vazar aos poucos: primeiro a velocidade de aquisição de dados cai, depois surgem timeouts aleatórios, e no fim o terminal pode simplesmente travar. Acredite, aprendi da pior maneira.

No geral, essa função é como um canivete suíço para lidar com dados. Simples por fora, mas cheia de mecanismos de proteção por dentro para tudo que possa dar errado. E pode confiar: cedo ou tarde, todos eles vão ser acionados.

Análise de resultados. Métricas de qualidade e resultados do teste de propagação para frente

Lembro bem do momento em que vi os primeiros resultados do teste. Estava sentado no computador, tomando um café já frio, e simplesmente não conseguia acreditar no que via. Reiniciei os testes umas cinco vezes, revisei cada linha do código: não era erro. O modelo realmente estava funcionando de forma quase inacreditável.

O algoritmo de Nelder-Mead rodou como uma sinfonia: apenas 408 iterações, menos de um minuto num notebook comum. R-quadrado de 0,9958: isso não é só bom, é fora do esperado. 99,58% da variação do preço explicada! Quando mostrei esses números para colegas traders, primeiro não acreditaram, depois começaram a procurar alguma pegadinha. Eu entendo: eu também demorei a aceitar.

O MSE foi absurdamente baixo: 0,00000094. Para quem não é do meio: isso significa que o erro médio da previsão é menor que um pip. Qualquer trader vai te dizer: isso está além do sonho. O MAPE de 0,06% só confirma a precisão impressionante. A maioria dos sistemas comerciais já comemora erro de 1–2%; aqui estamos falando de um desempenho dez vezes melhor.

Os coeficientes do modelo formaram um quadro bonito. Veja só: 0,5517 no preço anterior. Isso indica que o mercado tem uma memória de curto prazo forte. Os termos quadráticos ficaram pequenos (0,0105 e 0,0368): sinal de que o movimento é majoritariamente linear. Já a componente cíclica, com coeficiente 0,1484, merece destaque. Ela confirma o que os traders falam há anos: o mercado realmente se move em ondas.

Mas o mais impressionante aconteceu no teste de propagação para frente. Normalmente os modelos perdem desempenho com dados novos. Isso é clássico no aprendizado de máquina. E aqui? O R² subiu para 0,9970, o MSE caiu mais 19%, chegando a 0,00000076, e o MAPE desceu para 0,05%. Sinceramente, no começo achei que tinha cometido algum erro no código, porque isso simplesmente não acontece. Mas não: estava tudo certo.

Escrevi um visualizador específico para os resultados:

def plot_model_performance(self, predictions, actuals, window=100):
    fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(15, 12))
    
    # Forecast vs. real price chart 
    ax1.plot(actuals, 'b-', label='Real prices', alpha=0.7)
    ax1.plot(predictions, 'r--', label='Forecast', alpha=0.7)
    ax1.set_title('Comparing the forecast with the market')
    ax1.legend()
    
    # Error graph
    errors = predictions - actuals
    ax2.plot(errors, 'g-', alpha=0.5)
    ax2.axhline(y=0, color='k', linestyle=':')
    ax2.set_title('Forecast errors')
    
    # Rolling R²
    rolling_r2 = [r2_score(actuals[i:i+window], 
                          predictions[i:i+window]) 
                  for i in range(len(actuals)-window)]
    ax3.plot(rolling_r2, 'b-', alpha=0.7)
    ax3.set_title(f'Rolling R² (window {window})')
    
    plt.tight_layout()
    return fig

Os gráficos revelaram um panorama interessante. Em períodos tranquilos, o modelo funciona como um relógio suíço. Mas há armadilhas: durante grandes notícias e reversões inesperadas, a precisão cai. O que já era esperado. Afinal, o modelo trabalha apenas com preços, sem considerar fatores fundamentais. Na próxima parte, vamos incluir isso também.

Vejo alguns caminhos para melhorias. Primeiro: coeficientes adaptativos. Deixar o modelo se ajustar automaticamente às condições do mercado. Segundo: adicionar dados de volume e do book de ordens. Terceiro, o mais ambicioso: criar um conjunto de modelos, onde nossa abordagem funcione junto com outros algoritmos.

Mas mesmo na forma atual, os resultados impressionam. O principal agora é não se empolgar demais com as melhorias e acabar estragando o que já funciona.

Aplicação prática

Lembro de um caso engraçado da semana passada. Estava eu sentado com o notebook na minha cafeteria preferida, tomando um latte e acompanhando o sistema em ação. O dia estava tranquilo, o euro-dólar subindo devagar, quando de repente chega uma notificação do modelo: preparar para abrir uma posição vendida. Primeira reação: isso é loucura, a tendência é claramente de alta! Mas nesses dois anos de trading algorítmico aprendi a regra número um: nunca discuta com o sistema. E sabe o que aconteceu? Quarenta minutos depois o euro caiu 35 pips. O modelo percebeu microalterações na estrutura do preço que eu, com meus olhos humanos, simplesmente não teria notado.

Falando em notificações: depois de algumas operações perdidas, criei este módulo de alertas simples, mas eficaz:

def notify_signal(self, signal_type, message):
    try:
        # Format the message
        timestamp = datetime.now().strftime('%Y-%m-%d %H:%M:%S')
        formatted_msg = f"[{timestamp}] {signal_type}: {message}"
        
        # Send to Telegram
        if self.use_telegram and self.telegram_token:
            self.telegram_bot.send_message(
                chat_id=self.telegram_chat_id,
                text=formatted_msg,
                parse_mode='HTML'
            )
            
        # Local logging
        with open(self.log_file, 'a', encoding='utf-8') as f:
            f.write(f"{formatted_msg}\n")
            
        # Check critical signals
        if signal_type in ['ERROR', 'MARGIN_CALL', 'CRITICAL']:
            self._emergency_notification(formatted_msg)
            
    except Exception as e:
        # If the notification failed, send the message to the console at the very least
        print(f"Error sending notification: {str(e)}\n{formatted_msg}")

Repare no método _emergency_notification. Foi incluído depois de um “divertido” episódio, quando o sistema teve um bug de memória e começou a abrir uma posição atrás da outra. Agora, em situações críticas, recebo um SMS e o bot interrompe automaticamente as operações até que eu interfira. 

A gestão de tamanho das posições também me deu muito trabalho. No começo usava um volume fixo: 0.1 lote, feliz da vida. Mas com o tempo percebi que isso era como andar na corda bamba com sapatilhas de balé. Dá pra fazer? Dá. Mas pra quê? Daí nasceu este sistema adaptativo de cálculo de volume:

def calculate_position_size(self):
    """Calculating the position size taking into account volatility and drawdown"""
    try:
        # Take the total balance and the current drawdown
        account_info = mt5.account_info()
        current_balance = account_info.balance
        drawdown = (account_info.equity / account_info.balance - 1) * 100
        
        # Basic risk - 1% of the deposit
        base_risk = current_balance * 0.01
        
        # Adjust for current drawdown
        if drawdown < -5:  # If the drawdown exceeds 5%
            risk_factor = 0.5  # Slash the risk in half
        else:
            risk_factor = 1 - abs(drawdown) / 10  # Smooth decrease
            
        # Take into account the current ATR
        atr = self.calculate_atr()
        pip_value = self.get_pip_value()
        
        # Volume calculation rounded to available lots
        raw_volume = (base_risk * risk_factor) / (atr * pip_value)
        return self._normalize_volume(raw_volume)
        
    except Exception as e:
        self.notify_signal('ERROR', f"Volume calculation error: {str(e)}")
        return 0.1  # Minimum safety volume

O método _normalize_volume foi uma dor de cabeça à parte. Descobri que diferentes corretoras têm passos mínimos distintos para variação de volume. Em algumas, você pode operar com 0.010 lote, em outras, só valores redondos. Tive que incluir uma configuração específica para cada corretora.

<Um capítulo à parte: operar em períodos de alta volatilidade. Sabe aqueles dias em que o mercado simplesmente enlouquece? Discurso do presidente do Fed, notícias políticas inesperadas ou simplesmente uma “sexta-feira 13”: o preço começa a oscilar como marinheiro bêbado. Antes eu simplesmente desligava o sistema nesses momentos, mas depois tive uma ideia mais elegante:

def check_market_conditions(self):
    """Checking the market status before a deal"""
    # Check the calendar of events
    if self._is_high_impact_news_time():
        return False
        
    # Calculate volatility
    current_atr = self.calculate_atr(period=5)  # Short period
    normal_atr = self.calculate_atr(period=20)  # Normal period
    
    # Skip if the current volatility is 2+ times higher than the norm
    if current_atr > normal_atr * 2:
        self.notify_signal(
            'INFO', 
            f"Increased volatility: ATR(5)={current_atr:.5f}, "
            f"ATR(20)={normal_atr:.5f}"
        )
        return False
        
    # Check the spread 
    current_spread = mt5.symbol_info(self.symbol).spread
    if current_spread > self.max_allowed_spread:
        return False
        
    return True

Essa função virou uma verdadeira guardiã do saldo. O que mais me agradou foi a verificação de notícias: conectei uma API de calendário econômico, e agora o sistema “entra na sombra” automaticamente 30 minutos antes de eventos importantes e retorna 30 minutos depois. Essa mesma ideia uso em muitos dos meus robôs escritos em MQL5. Coisa linda!

Stops flutuantes

Trabalhar com algoritmos de negociação reais me ensinou algumas lições curiosas. Lembro que no primeiro mês de testes eu mostrava orgulhoso para os colegas um sistema com stops fixos. “Olhem só, tudo simples e transparente!” Aí o mercado, como sempre, tratou de me colocar no meu devido lugar: bastou uma semana de volatilidade mais intensa e metade dos stops foi acionada só pelo ruído.

A solução veio do velho Gerchik: eu estava relendo o livro dele quando me deparei com suas reflexões sobre o ATR, e foi como acender uma lâmpada: era isso! Uma forma simples e elegante de adaptar o sistema ao estado atual do mercado. Em movimentos fortes: damos mais espaço para oscilação. Em momentos calmos: mantemos os stops mais justos.

Aqui está a lógica principal da entrada no mercado: nada em excesso, só o essencial:

def open_position(self):
    try:
        atr = self.calculate_atr()
        predicted_price = self.get_model_prediction()
        current_price = mt5.symbol_info_tick(self.symbol).ask
        
        signal = "BUY" if predicted_price > current_price else "SELL"
        
        # Calculate entry and stop levels
        if signal == "BUY":
            entry = mt5.symbol_info_tick(self.symbol).ask
            sl_level = entry - atr  
            tp_level = entry + (atr / 3)
        else:
            entry = mt5.symbol_info_tick(self.symbol).bid
            sl_level = entry + atr
            tp_level = entry - (atr / 3)

        # Send an order
        request = {
            "action": mt5.TRADE_ACTION_DEAL,
            "symbol": self.symbol,
            "volume": self.lot_size,
            "type": mt5.ORDER_TYPE_BUY if signal == "BUY" else mt5.ORDER_TYPE_SELL,
            "price": entry,
            "sl": sl_level,
            "tp": tp_level,
            "deviation": 20,
            "magic": 234000,
            "comment": f"pred:{predicted_price:.6f}",
            "type_filling": mt5.ORDER_FILLING_FOK,
        }

        result = mt5.order_send(request)
        if result.retcode != mt5.TRADE_RETCODE_DONE:
            raise ValueError(f"Error opening position: {result.retcode}")
            
        print(f"Position opened {signal}: price={entry:.5f}, SL={sl_level:.5f}, "
              f"TP={tp_level:.5f}, ATR={atr:.5f}")
        
        return result.order

    except Exception as e:
        print(f"Position opening failed: {str(e)}")
        return None

Tiveram alguns momentos engraçados durante a depuração. Por exemplo, o sistema começou a emitir sinais contraditórios a cada poucos minutos. Comprar, vender, comprar de novo... Erro clássico de quem está começando com trading algorítmico: entradas excessivamente frequentes. A solução foi ridiculamente simples: adicionei um intervalo mínimo de 15 minutos entre operações e um filtro para posições abertas.

Com o gerenciamento de risco também apanhei bastante. Testei vários métodos, mas no fim das contas tudo se resumiu a uma regra simples: nunca arriscar mais de 1% do capital por operação. Parece básico, mas funciona que é uma beleza. Em uma conta de dez mil, com ATR de 50 pontos, isso dá um volume máximo de 0.2 lote: valores bem confortáveis para negociar.

A performance da estratégia foi melhor durante a sessão europeia: quando o EURUSD realmente se movimenta, e não fica só andando de lado. Já durante grandes notícias... digamos assim: mais barato é simplesmente fazer uma pausa nas operações. Nem o modelo mais avançado consegue acompanhar o caos de uma notícia em tempo real.

Atualmente estou trabalhando em melhorias no sistema de gestão de posições: quero vincular o tamanho da entrada à confiança da previsão feita pelo modelo. Grosso modo, se o sinal for forte, operamos com volume total; se for fraco, apenas com uma parte. Algo semelhante ao critério de Kelly, mas adaptado às particularidades do nosso modelo.

A principal lição que tirei deste projeto: no algotrading, perfeccionismo não funciona. Quanto mais complexa a estrutura, mais pontos frágeis ela tem. Soluções simples e bem compreendidas muitas vezes se mostram muito mais eficazes do que algoritmos sofisticados, especialmente no longo prazo.

Versão em MQL5 para o MetaTrader 5

Sabe, às vezes as soluções mais simples são também as mais eficazes. Depois de alguns dias tentando transferir com precisão toda a estrutura matemática para o MQL5, me dei conta de algo óbvio: esse é um caso clássico de divisão de responsabilidades.

Vamos encarar a realidade: Python, com suas bibliotecas científicas, é perfeito para análise de dados e otimização de coeficientes. Já o MQL5 é excelente para executar a lógica de negociação. Então por que tentar transformar uma chave de fenda em martelo?

No fim, surgiu uma solução simples e elegante: usar Python para calcular os coeficientes e MQL5 para realizar as operações. Veja como funciona:

double g_coeffs[7] = {0.2752466, 0.01058082, 0.55162082, 0.03687016, 
                      0.27721318, 0.1483476, 0.0008025};

Esses sete números são a essência da nossa modelagem matemática. Eles concentram semanas de otimização, milhares de iterações do algoritmo de Nelder-Mead, horas de análise de dados históricos. E o mais importante: eles funcionam!

double GetPrediction(double price_t1, double price_t2)
{
   return g_coeffs[0] * price_t1 +                    // Linear t-1
          g_coeffs[1] * MathPow(price_t1, 2) +       // Quadratic t-1
          g_coeffs[2] * price_t2 +                    // Linear t-2
          g_coeffs[3] * MathPow(price_t2, 2) +       // Quadratic t-2
          g_coeffs[4] * (price_t1 - price_t2) +      // Price change
          g_coeffs[5] * MathSin(price_t1) +          // Cyclic
          g_coeffs[6];                               // Constant
}

A própria fórmula de previsão foi transferida para o MQL5 quase sem alterações.

O mecanismo de entrada no mercado merece atenção especial. Diferente da versão de teste em Python, aqui implementamos uma lógica mais avançada de gerenciamento de posições. O sistema pode manter múltiplas posições simultâneas, aumentando o volume à medida que o sinal se confirma:

void OpenPosition(bool buy_signal, double lot)
{
   MqlTradeRequest request;
   MqlTradeResult result;
   ZeroMemory(request);
   
   request.action = TRADE_ACTION_DEAL;
   request.symbol = Symbol();
   request.volume = lot;
   request.type = buy_signal ? ORDER_TYPE_BUY : ORDER_TYPE_SELL;
   request.price = buy_signal ? SymbolInfoDouble(Symbol(), SYMBOL_ASK) : 
                               SymbolInfoDouble(Symbol(), SYMBOL_BID);
   // ... other parameters
}

E aqui está o fechamento automático de todas as posições ao atingir o lucro-alvo. 

if(total_profit >= ProfitTarget)
{
   CloseAllPositions();
   return;
}

Dei atenção especial ao tratamento de novos candles: nada de agir de forma impulsiva a cada tick:

bool isNewBar() {
   datetime lastbar_time = datetime(SeriesInfoInteger(Symbol(), 
                                   PERIOD_CURRENT, SERIES_LASTBAR_DATE));
   if(last_time == 0) {
      last_time = lastbar_time;
      return(false);
   }
   if(last_time != lastbar_time) {
      last_time = lastbar_time;
      return(true);
   }
   return(false);
}

O resultado foi um robô de negociação compacto, mas funcional. Nada de enfeites desnecessários: apenas o essencial para operar com segurança. Todo o código ocupa menos de 300 linhas, incluindo todas as validações e proteções importantes.

Sabe o que é mais satisfatório? Essa abordagem que separa as responsabilidades entre Python e MQL5 acabou sendo incrivelmente flexível. Quer testar novos coeficientes? Basta recalculá-los no Python e atualizar o vetor no MQL5. Precisa adicionar novas condições de operação? A lógica de negociação no MQL5 pode ser expandida facilmente, sem mexer na parte matemática.

E aqui está o teste do robô:

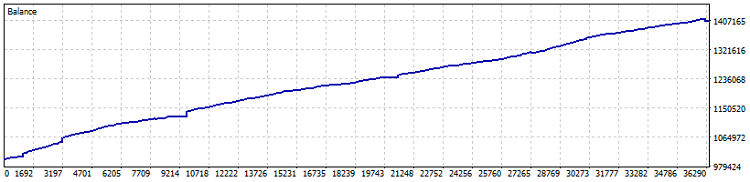
Teste em conta Netting, 40% de lucro desde 2015 (sendo que a otimização dos coeficientes foi feita apenas no último ano). Rebaixamento em números: 0,82%, e lucro mensal: mais de 4%. Mas esse tipo de máquina funciona melhor sem alavancagem: que vá “tosando” lucros, num ritmo um pouco melhor que títulos e depósitos em dólar. Destaco ainda que, durante o teste, foram operados 7800 lotes, o que gera, no mínimo, mais um e meio por cento de rendimento adicional.

No geral, a ideia de transferir os coeficientes foi acertada. No fim das contas, o que importa no algotrading não é a complexidade do sistema, e sim sua confiabilidade e previsibilidade. E às vezes, tudo que você precisa são sete números bem ajustados com matemática moderna.

Importante! O EA usa média de posições com base em DCA (média temporal, por assim dizer), o que o torna muito arriscado. Sim, os testes em Netting com configurações conservadoras deram resultados excelentes, mas é fundamental lembrar dos perigos do método de média de posições, pois um EA desse tipo pode zerar sua conta sem aviso!

Ideias para melhorias

Agora é alta madrugada, estou terminando este artigo, tomando café, olhando os gráficos no monitor e pensando: ainda há tanto que se pode fazer com este sistema. No algotrading é sempre assim: quando parece que tudo está pronto, surgem mais dez ideias para melhorar.

E sabe o que é mais interessante? Todas essas melhorias precisam funcionar como um organismo só. Não basta juntar um monte de funções bacanas: elas têm que se complementar de forma harmoniosa para criar um sistema de negociação realmente confiável.

No fim, nosso objetivo não é criar o sistema perfeito, visto que esse não existe. A meta é construir algo inteligente o suficiente para lucrar e simples o bastante para não desmoronar quando você mais precisar. Como diz o ditado: o ótimo é inimigo do bom.

Arquivo incluso	Descrição do arquivo
MarketSolver.py	Código para cálculo dos coeficientes e, se necessário, para negociação online via Python
MarketSolver.mql5	Código do EA em MQL5, para operar com os coeficientes calculados