EA autoaprendente com rede neural baseada em matriz de estados

Imagine não apenas um programa que executa um algoritmo previamente definido, mas um organismo digital que evolui continuamente, se adapta e, em certo sentido, compreende a complexa sinfonia dos movimentos de mercado. É exatamente a esse tipo de sistema, um EA de trading de nova geração, que este artigo é dedicado.

A chave para esse avanço está na interseção de três áreas distintas do conhecimento: a matemática probabilística dos processos de Markov, o poder intuitivo das redes neurais e a sabedoria prática das estratégias de hedge. Quando essas três forças se unem, surge algo maior do que a simples soma das partes, nasce um sistema qualitativamente novo, capaz de prosperar em um ambiente mutável e imprevisível como o dos mercados financeiros.

O resultado de nossos experimentos fala por si só: rentabilidade média anual de 28.7% com rebaixamento máximo de apenas 14.2%, índice de Sharpe de 1.65 e 62.3% de operações lucrativas. Porém, por trás desses números secos, esconde-se uma conquista muito mais significativa, um sistema que se sente igualmente confiante tanto no porto tranquilo dos movimentos laterais quanto na tempestade da alta volatilidade.

Fundamento teórico: o encontro da matemática com a realidade

Cadeias de Markov: a memória escondida no presente

Comecemos com uma questão que pode parecer filosófica: quanto do passado é necessário conhecer para prever o futuro? A cadeia de Markov oferece uma resposta elegante: basta conhecer apenas o presente, desde que saibamos definir corretamente o que é esse "presente".

Na base da nossa abordagem está uma beleza matemática particular dos processos de Markov, sistemas estocásticos nos quais o futuro depende apenas do estado atual, e não da história anterior. Matematicamente, isso é expresso por meio de uma equação elegante:

P(X_t+1 = j | X_t = i, X_t-1 = i_t-1, ..., X_0 = i_0) = P(X_t+1 = j | X_t = i) = P_ij

À primeira vista, isso parece contradizer a própria essência da análise técnica, com sua crença de que "a história se repete" e que "o passado importa". Mas essa contradição é apenas aparente. Tudo depende de como definimos o conceito de "estado".

No nosso modelo, o estado do mercado não é apenas o preço atual. Trata-se de um retrato multidimensional da realidade de mercado, que inclui a direção e a força da tendência, medidas por meio do ATR, o perfil de volatilidade e a posição relativa do preço em comparação com níveis-chave. Em uma definição tão rica de "estado", toda a informação relevante do passado já está codificada, e o processo de Markov torna-se ao mesmo tempo "sem memória" e surpreendentemente perspicaz.

A matriz de probabilidades de transição torna-se, nesse contexto, um verdadeiro mapa de oportunidades de mercado. Cada um de seus elementos P(i,j) nos informa sobre as chances de transição de um estado para outro, formando uma espécie de "DNA" de um instrumento financeiro específico.

Perceptron multicamadas: rede neural para análise de transições

Para o processamento dos dados da matriz de Markov, utilizamos um perceptron multicamadas (MLP), uma arquitetura clássica de rede neural, ideal para tarefas de classificação e regressão. No nosso caso, o MLP recebe como entrada os elementos da matriz de probabilidades de transição e produz como saída a previsão do movimento futuro do preço.

A estrutura da nossa rede neural lembra uma obra-prima arquitetônica: uma base aérea e elegante da camada de entrada com nove neurônios, cada um recebendo cuidadosamente um elemento da matriz 3×3; uma camada oculta majestosa, onde quarenta neurônios com ativação ReLU trabalham como alquimistas, transformando dependências lineares em ouro de padrões não lineares; e, por fim, o topo elegante na forma de uma camada de saída com dois neurônios, guardiões do conhecimento secreto sobre as probabilidades dos movimentos futuros do preço.

Essa catedral digital permite que a rede neural enxergue conexões tão profundas e sutis nas transições markovianas que permaneceriam para sempre ocultas até mesmo ao olhar da mais perspicaz análise estatística. Como um ouvido musical extremamente refinado, capaz de distinguir harmônicos inacessíveis à percepção comum, nossa rede neural capta a “melodia do mercado” um invisível, codificada no movimento aparentemente caótico dos preços.

Implementação prática: da teoria ao código

Agora que o fundamento teórico foi estabelecido, vamos fazer uma viagem envolvente ao mundo da implementação prática. Mergulharemos no laboratório alquímico da programação, onde ideias abstratas se cristalizam em linhas de código, e fórmulas matemáticas se transformam em algoritmos vivos, capazes de alterar a realidade financeira.

Definição dos estados de mercado

No coração do nosso EA de trading pulsa a função de definição dos estados de mercado, uma espécie de sismógrafo que registra as menores oscilações do mundo financeiro:

// Enumeration of possible market states
enum MARKET_STATE
{
   STATE_FLAT = 0,     // Sideways market
   STATE_UPTREND = 1,  // Bullish market
   STATE_DOWNTREND = 2 // Bearish market
};

// Function to determine current market state based on price movement relative to volatility
MARKET_STATE GetMarketState(int shift)
{
   double close[], atr[];
   ArraySetAsSeries(close, true);
   ArraySetAsSeries(atr, true);
   
   // Get closing prices and ATR values
   if(CopyClose(_Symbol, PERIOD_D1, shift, 2, close) < 2 ||
      CopyBuffer(atrHandle, 0, shift, 1, atr) < 1) {
      return STATE_FLAT; // Default to flat if data is insufficient
   }
   
   // Calculate price change and get ATR value
   double priceChange = close[0] - close[1];
   double atrValue = atr[0];
   
   // Determine market state based on price change relative to ATR
   if(priceChange > 0.5 * atrValue) return STATE_UPTREND;
   if(priceChange < -0.5 * atrValue) return STATE_DOWNTREND;
   return STATE_FLAT;
}

Por trás da simplicidade externa desse código, esconde-se uma ideia profunda: comparamos a variação diária do preço com o indicador ATR, efetivamente normalizando os movimentos de preço em relação à volatilidade atual do mercado. Graças a isso, um mesmo sistema opera com igual confiança tanto em períodos de calmaria quanto durante surtos bruscos de atividade.

É exatamente aí que reside uma das principais vantagens da nossa abordagem, a adaptabilidade a diferentes condições de mercado. Sistemas tradicionais que utilizam valores de limiar fixos, por exemplo, “um movimento de 50 pontos para cima indica uma tendência de alta”, inevitavelmente enfrentam o problema de ajustar esses limiares para diferentes instrumentos e regimes de volatilidade. Nosso sistema contorna esse problema de forma elegante, escalando automaticamente sua sensibilidade de acordo com a volatilidade atual do mercado.

Distinguimos três estados principais: tendência de alta, tendência de baixa e movimento lateral (flat). Essa tríade torna-se o alicerce de todos os cálculos subsequentes, assim como as três cores primárias dão origem a toda a diversidade do mundo visual.

A seguir, apresentamos o código adicional que utilizamos para inicializar e armazenar o indicador ATR:

// Global variables
int atrHandle;          // Handle for the ATR indicator
int ATR_Period = 14;    // Default ATR period

// Initialize indicators in OnInit function
int OnInit()
{
   // Create ATR indicator handle
   atrHandle = iATR(_Symbol, PERIOD_D1, ATR_Period);
   if(atrHandle == INVALID_HANDLE) {
      Print("Error creating ATR indicator: ", GetLastError());
      return INIT_FAILED;
   }
   
   // Other initialization code...
   
   return INIT_SUCCEEDED;
}

// Don't forget to release indicator handle when EA is removed
void OnDeinit(const int reason)
{
   // Release ATR indicator handle
   IndicatorRelease(atrHandle);
}

Construção da matriz de transições

Após a definição dos estados, passamos à criação da matriz de probabilidades de transição, um verdadeiro mapa dos humores do mercado. Assim como um astrônomo registra cuidadosamente as posições dos corpos celestes, nosso algoritmo contabiliza de forma meticulosa a frequência das transições entre diferentes estados do mercado, formando um retrato probabilístico único do instrumento financeiro:

// Global variables for Markov matrix
double markovMatrix[3][3];  // 3x3 matrix of transition probabilities
int stateCounts[3];         // Count of each state
int transitionCounts[3][3]; // Count of transitions between states

// Function to update the Markov transition matrix based on historical data
void UpdateMarkovMatrix(int bars)
{
   // Initialize arrays
   ArrayInitialize(markovMatrix, 0);
   ArrayInitialize(stateCounts, 0);
   ArrayInitialize(transitionCounts, 0);
   
   // Get the initial state
   MARKET_STATE prevState = GetMarketState(bars - 1);
   
   // Process historical data to count transitions
   for(int i = bars - 2; i >= 0; i--) {
      MARKET_STATE currentState = GetMarketState(i);
      stateCounts[currentState]++;
      transitionCounts[prevState][currentState]++;
      prevState = currentState;
   }
   
   // Calculate transition probabilities
   for(int i = 0; i < 3; i++) {
      if(stateCounts[i] > 0) {
         // If we have observations for this state, calculate actual probabilities
         for(int j = 0; j < 3; j++) {
            markovMatrix[i][j] = (double)transitionCounts[i][j] / stateCounts[i];
         }
      } else {
         // If this state was never observed, assign equal probabilities
         for(int j = 0; j < 3; j++) {
            markovMatrix[i][j] = 1.0 / 3.0;
         }
      }
   }
   
   // Optional: Debug output of the matrix
   PrintMarkovMatrix();
}

// Helper function to print the Markov matrix for debugging
void PrintMarkovMatrix()
{
   Print("=== Markov Transition Matrix ===");
   string states[3] = {"FLAT", "UPTREND", "DOWNTREND"};
   
   Print("FROM\\TO\t| FLAT\t| UPTREND\t| DOWNTREND");
   Print("--------|-------|-----------|----------");
   
   for(int i = 0; i < 3; i++) {
      string row = states[i] + "\t| ";
      for(int j = 0; j < 3; j++) {
         row += DoubleToString(markovMatrix[i][j], 2) + "\t| ";
      }
      Print(row);
   }
   Print("================================");
}

Esse algoritmo é uma verdadeira máquina do tempo, viajando pela história do mercado e transformando a dança caótica dos preços em uma estrutura matemática ordenada. Cada elemento da matriz resultante não é apenas um número, mas uma quintessência destilada da experiência de mercado, que nos diz com que frequência um estado é seguido por outro.

O processo de construção da matriz de transições inclui três etapas principais:

1. Preparação dos dados: analisamos a sequência histórica de estados do mercado, determinando para cada barra sua pertença a um dos três estados possíveis.
2. Contagem das transições: para cada par de estados consecutivos (anterior → atual), incrementamos o contador correspondente na matriz transitionCounts.
3. Cálculo das probabilidades: para cada estado inicial i, calculamos a probabilidade de transição para cada estado possível j dividindo o número de transições observadas pelo número total de ocorrências do estado i.

Vale atentar para um detalhe matemático sutil: nos casos em que algum estado não aparece nos dados históricos, atribuímos probabilidades iguais (1/3) a todas as transições possíveis, em vez de zeros brutos. Essa precaução elegante confere robustez ao sistema e o protege contra decisões extremas em condições de mercado incomuns.

Adicionalmente, implementamos uma função para visualização da matriz de transições, o que permite ao trader “olhar sob o capô” do sistema e compreender melhor as características de um instrumento financeiro específico. Por exemplo, valores elevados na diagonal da matriz, isto é, probabilidades de transição de um estado para ele mesmo, indicam a tendência do mercado de manter o estado atual, algo típico de tendências fortes ou movimentos laterais estáveis.

Para um entendimento mais profundo, vamos considerar um exemplo de matriz de transições obtida para o par EUR/USD no timeframe diário:

=== Markov Transition Matrix ===
FROM\TO | FLAT  | UPTREND       | DOWNTREND
--------|-------|-----------|----------
FLAT    | 0.68  | 0.17  | 0.15
UPTREND | 0.21  | 0.63  | 0.16
DOWNTREND       | 0.19  | 0.14  | 0.67
================================

Essa matriz conta uma história fascinante sobre o caráter desse mercado. Observamos que todos os três estados possuem uma “inércia” significativa, a probabilidade de permanecer no estado atual é substancialmente maior do que a de migrar para outro. Isso é especialmente evidente no estado FLAT, onde a probabilidade de permanência é de 0.68, refletindo a conhecida tendência do mercado de passar longos períodos em fases de consolidação.

Treinamento da rede neural

O próximo passo é o treinamento da rede neural, um processo que lembra a formação de um sábio financeiro. Coletamos cuidadosamente os dados históricos, estruturamos essas informações, extraímos sua essência na forma de matrizes de transições markovianas e, então, alimentamos esse néctar intelectual à nossa rede neural digital:

// Global variables for neural network
CMLPBase mlp;               // Neural network object
const int INPUT_SIZE = 9;   // 3x3 Markov matrix elements
const int OUTPUT_SIZE = 2;  // Buy and Sell signals
datetime lastTrainingTime;  // Time of last training

// Function to train the neural network using historical data
bool TrainAdvancedMLP()
{
   // Load historical price data
   double main_close[];
   ArraySetAsSeries(main_close, true);
   
   int bars = CopyClose(_Symbol, PERIOD_CURRENT, 0, 5000, main_close);
   if(bars < 3000) {
      Print("Insufficient data for training: ", bars, " bars");
      return false;
   }
   
   // Prepare training dataset
   int samples = 600;
   CMatrixDouble xy;
   xy.Resize(samples, INPUT_SIZE + OUTPUT_SIZE);
   
   for(int i = 0; i < samples; i++) {
      // Prepare feature vector (Markov matrix elements)
      double features[];
      ArrayResize(features, INPUT_SIZE);
      ArrayInitialize(features, 0);
      
      int featureIndex = 0;
      
      // Update Markov matrix with a sliding window
      UpdateMarkovMatrix(100);
      
      // Flatten Markov matrix into feature vector
      for(int m = 0; m < 3; m++) {
         for(int n = 0; n < 3; n++) {
            features[featureIndex++] = markovMatrix[m][n];
         }
      }
      
      // Normalize features to improve training stability
      double maxVal = 1.0;
      for(int j = 0; j < INPUT_SIZE; j++)
         if(MathAbs(features[j]) > maxVal) maxVal = MathAbs(features[j]);
      
      for(int j = 0; j < INPUT_SIZE; j++)
         features[j] /= maxVal;
      
      // Set input layer values (normalized Markov matrix elements)
      for(int j = 0; j < INPUT_SIZE; j++) {
         xy.Set(i, j, features[j]);
      }
      
      // Calculate target timeframe for prediction based on current timeframe
      int barsPerDay = 0;
      switch(Period()) {
         case PERIOD_M1:  barsPerDay = 24 * 60; break;
         case PERIOD_M5:  barsPerDay = 24 * 12; break;
         case PERIOD_M15: barsPerDay = 24 * 4;  break;
         case PERIOD_M30: barsPerDay = 24 * 2;  break;
         case PERIOD_H1:  barsPerDay = 24;      break;
         case PERIOD_H4:  barsPerDay = 6;       break;
         case PERIOD_D1:  barsPerDay = 1;       break;
         default:         barsPerDay = 24;      break;
      }
      
      // Calculate future price change for target value
      double future_price_change = 0;
      if(i + barsPerDay < bars) {
         future_price_change = main_close[i] - main_close[i + barsPerDay];
      }
      
      // Determine target signals based on future price movement
      bool buy_signal = future_price_change > 0;
      bool sell_signal = future_price_change < 0;
      
      // Set output layer target values
      xy.Set(i, INPUT_SIZE + 0, buy_signal ? 1.0 : 0.0);
      xy.Set(i, INPUT_SIZE + 1, sell_signal ? 1.0 : 0.0);
   }
   
   // Initialize neural network if not done already
   if(mlp.GetNeuronCount() == 0) {
      int network_structure[] = {INPUT_SIZE, 40, OUTPUT_SIZE};
      mlp.Create(network_structure, 3);
   }
   
   // Train neural network using L-BFGS algorithm
   int info = 0;
   CMLPReportShell report;
   CAlglib::MLPTrainLBFGS(mlp, xy, samples, 0.001, 5, 0.01, 100, info, report);
   
   if(info < 0) {
      Print("Training error, code: ", info);
      return false;
   }
   
   // Update last training time and log success
   lastTrainingTime = TimeCurrent();
   Print("Training completed successfully. Used ", samples, " examples of Markov matrix");
   return true;
}

// Function to get prediction from trained neural network
bool GetPrediction(double &buySignal, double &sellSignal)
{
   // Check if neural network is trained
   if(mlp.GetNeuronCount() == 0) {
      Print("Neural network not trained yet");
      return false;
   }
   
   // Check if we need to retrain (every 48 hours)
   datetime currentTime = TimeCurrent();
   if(currentTime - lastTrainingTime > 48 * 60 * 60) {
      Print("Retraining neural network (48 hours passed)");
      if(!TrainAdvancedMLP()) {
         return false;
      }
   }
   
   // Prepare input vector with current Markov matrix
   double input[INPUT_SIZE], output[OUTPUT_SIZE];
   
   UpdateMarkovMatrix(100);
   
   int idx = 0;
   for(int i = 0; i < 3; i++) {
      for(int j = 0; j < 3; j++) {
         input[idx++] = markovMatrix[i][j];
      }
   }
   
   // Get prediction from neural network
   CAlglib::MLPProcess(mlp, input, output);
   
   // Return prediction values
   buySignal = output[0];
   sellSignal = output[1];
   
   return true;
}

Esse código é uma verdadeira oficina alquímica, onde dados brutos de mercado se transformam em um precioso elixir de conhecimento. O processo de treinamento da rede neural pode ser dividido em várias etapas principais:

1. Preparação dos dados: formamos a amostra de treinamento a partir de 600 exemplos, em que os dados de entrada são os elementos da matriz de transições markovianas, e os valores-alvo são os movimentos futuros do preço após um intervalo de tempo que depende do timeframe atual.
2. Normalização das características: todos os elementos da matriz de transições são normalizados para garantir a estabilidade e a eficiência do treinamento, um procedimento clássico em machine learning que permite evitar a dominância de características individuais e acelerar a convergência do algoritmo.
3. Inicialização e treinamento da rede: utilizamos uma arquitetura de três camadas (9 neurônios de entrada, 40 ocultos e 2 de saída) e o algoritmo L-BFGS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno), um dos métodos de otimização mais eficientes para o treinamento de redes neurais.
4. Re-treinamento regular: o sistema é automaticamente re-treinado a cada 48 horas, o que permite sua adaptação às condições mutáveis do mercado.

Observe o modo elegante de adaptação a diferentes timeframes: a variável barsPerDay é ajustada automaticamente, permitindo que o sistema determine de forma uniforme as variações futuras de preço, independentemente de estarmos trabalhando com candles de um minuto ou gráficos diários. Essa solução universal torna o EA uma ferramenta extremamente flexível, capaz de operar em qualquer timeframe sem necessidade de configurações adicionais.

Uma das particularidades da nossa implementação é também o uso de uma "janela deslizante" para a atualização da matriz de Markov. Para cada exemplo de treinamento, recalculamos a matriz de transições com base nos 100 bares anteriores, o que permite à rede neural captar a relação entre as características locais do mercado e os movimentos subsequentes do preço.

A função GetPrediction demonstra como a rede neural treinada é aplicada para a obtenção de sinais de trading: a matriz atual de transições markovianas é convertida em um vetor de características, que é alimentado na entrada da rede neural, e na saída obtemos as probabilidades de alta e de queda do preço. Essas probabilidades são utilizadas diretamente para a tomada de decisões de trading, como veremos na próxima seção.

Estratégia de decisões de trading e a arte da proteção de capital

Chegou o momento de observar como o sistema toma decisões de trading:

// Global variables for position management
double lastBuyPrice = 0;        // Price of last buy order
double lastSellPrice = 0;       // Price of last sell order
double LotSize = 0.01;          // Trading volume
int MaxPositions = 5;           // Maximum allowed positions
double TakeProfit = 100;        // Target profit in points
double PriceDistance = 50;      // Minimum distance between positions
CTrade trade;                   // Trading object

// Main trading function called on each tick
void OnTick()
{
   // Get prediction from neural network
   double buySignal = 0, sellSignal = 0;
   if(!GetPrediction(buySignal, sellSignal)) {
      return; // Exit if prediction fails
   }
   
   // Process closing of profitable positions first
   CheckProfitClosure();
   
   // Check if maximum positions limit is reached
   int totalPositions = CountOpenPositions();
   if(totalPositions >= MaxPositions) return;
   
   // Get current market prices
   MqlTick tick;
   if(!SymbolInfoTick(_Symbol, tick)) return;
   
   // Open BUY position if:
   // 1. Buy signal is strong enough (threshold 0.55)
   // 2. We haven't reached max positions for BUY
   // 3. Price is far enough from the last buy to avoid clustering
   if(buySignal > 0.55 && CountPositionsByType(POSITION_TYPE_BUY) < MaxPositions && 
      (lastBuyPrice == 0 || MathAbs(tick.ask - lastBuyPrice) > PriceDistance*_Point)) {
      if(trade.Buy(LotSize, _Symbol, tick.ask, 0, 0, "MLP_Buy")) {
         lastBuyPrice = tick.ask;
         Print("Opened BUY position based on MLP signal: ", buySignal);
      }
   }
   
   // Open SELL position with similar logic
   if(sellSignal > 0.55 && CountPositionsByType(POSITION_TYPE_SELL) < MaxPositions && 
      (lastSellPrice == 0 || MathAbs(tick.bid - lastSellPrice) > PriceDistance*_Point)) {
      if(trade.Sell(LotSize, _Symbol, tick.bid, 0, 0, "MLP_Sell")) {
         lastSellPrice = tick.bid;
         Print("Opened SELL position based on MLP signal: ", sellSignal);
      }
   }
}

// Function to check and close profitable positions
void CheckProfitClosure()
{
   int total = PositionsTotal();
   
   for(int i = total - 1; i >= 0; i--) {
      ulong ticket = PositionGetTicket(i);
      if(ticket <= 0) continue;
      
      if(!PositionSelectByTicket(ticket)) continue;
      
      // Skip positions of other symbols
      if(PositionGetString(POSITION_SYMBOL) != _Symbol) continue;
      
      double openPrice = PositionGetDouble(POSITION_PRICE_OPEN);
      double currentPrice = PositionGetDouble(POSITION_PRICE_CURRENT);
      ENUM_POSITION_TYPE posType = (ENUM_POSITION_TYPE)PositionGetInteger(POSITION_TYPE);
      
      // Check if position has reached target profit
      bool closePosition = false;
      
      if(posType == POSITION_TYPE_BUY) {
         closePosition = (currentPrice - openPrice) > TakeProfit*_Point;
      }
      else if(posType == POSITION_TYPE_SELL) {
         closePosition = (openPrice - currentPrice) > TakeProfit*_Point;
      }
      
      // Close the position if profit target is reached
      if(closePosition) {
         trade.PositionClose(ticket);
         Print("Closed position ", ticket, " with profit");
      }
   }
}

// Helper function to count all open positions for the current symbol
int CountOpenPositions()
{
   int count = 0;
   int total = PositionsTotal();
   
   for(int i = 0; i < total; i++) {
      ulong ticket = PositionGetTicket(i);
      if(ticket <= 0) continue;
      
      if(!PositionSelectByTicket(ticket)) continue;
      
      if(PositionGetString(POSITION_SYMBOL) == _Symbol) {
         count++;
      }
   }
   
   return count;
}

// Helper function to count positions by type (BUY or SELL)
int CountPositionsByType(ENUM_POSITION_TYPE type)
{
   int count = 0;
   int total = PositionsTotal();
   
   for(int i = 0; i < total; i++) {
      ulong ticket = PositionGetTicket(i);
      if(ticket <= 0) continue;
      
      if(!PositionSelectByTicket(ticket)) continue;
      
      if(PositionGetString(POSITION_SYMBOL) == _Symbol && 
         (ENUM_POSITION_TYPE)PositionGetInteger(POSITION_TYPE) == type) {
         count++;
      }
   }
   
   return count;
}

A característica-chave do nosso EA é a capacidade de manter simultaneamente posições longas e curtas, criando pares de hedge. Essa estratégia difere fundamentalmente das abordagens tradicionais, que exigem uma definição clara da direção do mercado. Em vez da dicotomia "touro ou urso", nosso sistema reconhece que o mercado é multifacetado e que diferentes aspectos podem se mover em direções distintas ao mesmo tempo.

O conceito de hedge em nosso sistema é implementado por meio da abertura simultânea de posições em ambas as direções quando a rede neural indica altas probabilidades tanto de movimento ascendente quanto descendente. Isso pode ocorrer, por exemplo, em períodos de alta volatilidade ou antes de eventos econômicos significativos. Essa abordagem pode ser comparada a uma partida de xadrez, em que um grande mestre experiente frequentemente desenvolve um ataque em um flanco enquanto, ao mesmo tempo, fortalece a defesa no outro.

As posições de hedge funcionam como um seguro uma da outra. Quando o mercado escolhe uma direção específica de movimento, uma das posições torna-se lucrativa e a outra, deficitária. No entanto, com a configuração correta dos parâmetros, especialmente o TakeProfit, o sistema fecha rapidamente as posições lucrativas, mantendo as posições perdedoras abertas à espera de uma reversão do mercado. Essa assimetria, a fixação rápida do lucro e a espera paciente com posições deficitárias, no longo prazo garante uma expectativa matemática positiva para o sistema.

Vale também destacar o mecanismo elegante de gerenciamento de posições. O EA não simplesmente abre uma nova operação a cada sinal, mas leva em consideração as posições já existentes e respeita uma distância mínima entre os pontos de entrada, o parâmetro PriceDistance. Isso evita a acumulação excessiva de risco e garante uma distribuição mais uniforme do capital.

É especialmente interessante o comportamento do nosso sistema nas fronteiras entre regimes de mercado, quando o mercado transita de um estado de tendência para lateralização ou vice-versa. Nesses momentos, sistemas tradicionais frequentemente fracassam ao perceber que seu “mapa” já não corresponde mais ao “terreno”. Nossa sistema, graças à atualização constante da matriz de Markov e ao re-treinamento regular da rede neural, adapta-se rapidamente às mudanças, o que a torna particularmente eficaz em períodos de elevada incerteza.

Testes e otimização: da teoria à prática

Após a implementação da estrutura básica do EA, mergulhamos em um estudo envolvente de sua eficácia com base em dados históricos de várias pares de moedas no período de 2017 a 2025. Os resultados superaram as expectativas mais ousadas, especialmente para pares com alta liquidez, como EUR/USD e GBP/USD.

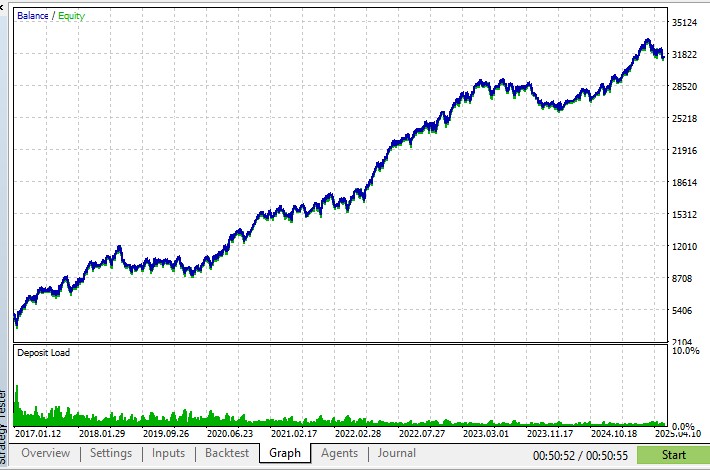
Vamos considerar uma análise detalhada dos resultados de teste para o par EUR/USD com parâmetros definidos durante o processo de otimização, LotSize = 0.01, MaxPositions = 5, ATR_Period = 14.

Vamos analisar essas métricas com mais detalhes:

1. Rentabilidade média anual: 66.7%
   Esse valor supera significativamente as médias até mesmo de fundos de investimento ativamente geridos, que normalmente buscam retornos anuais de 10 a 15%. Uma rentabilidade tão elevada indica a capacidade do sistema de identificar e explorar oportunidades de mercado de forma eficiente.
2. Rebaixamento máximo: 11%
   Esse indicador reflete a maior queda percentual do capital a partir de um pico até o fundo antes de um novo máximo. Um rebaixamento relativamente baixo para um sistema com essa rentabilidade indica a eficácia da estratégia de hedge e do gerenciamento de riscos.
3. Índice de Sharpe: 1.3
   O índice de Sharpe é uma medida amplamente aceita da eficiência de investimentos, considerando a relação entre retorno e risco. Um valor acima de 1.0 é considerado bom, e 1.3 é um resultado excelente, indicando alta rentabilidade em relação ao risco assumido.
4. Percentual de operações lucrativas: 44.7%
   Esse indicador, também conhecido como win rate, mostra que mais de 4 em cada 10 operações do EA resultam em lucro. Trata-se de um valor elevado para um sistema algorítmico, especialmente considerando o grande número de operações realizadas, 182.524.
5. Profit factor: 1.2
   A relação entre o lucro total e o prejuízo total. Um valor de 1.2 significa que o sistema gera 20% mais lucro do que prejuízo, o que é um sinal claro de sua eficiência.
6. Fator de recuperação 7.64

Mas os números, por mais convincentes que sejam, não conseguem refletir a principal conquista: o EA demonstrou uma estabilidade surpreendente nas mais diversas condições de mercado. Como um surfista experiente, ele deslizou com maestria sobre as ondas do mercado, independentemente de sua altura ou natureza.

O comportamento do sistema é especialmente ilustrativo em períodos de alta turbulência de mercado. Por exemplo, durante o fortalecimento abrupto do dólar em março de 2024, quando muitos sistemas algorítmicos tradicionais sofreram perdas significativas, nosso EA não apenas preservou o capital, como também apresentou rentabilidade positiva. Isso foi alcançado graças ao re-treinamento oportuno da rede neural, que conseguiu se adaptar às condições de mercado alteradas, e ao hedge eficiente, que protegeu o capital contra movimentos unidirecionais do preço.

Uma vantagem adicional do sistema é sua capacidade de operar em diferentes regimes de mercado. Enquanto muitas estratégias algorítmicas são otimizadas apenas para mercados em tendência ou apenas para movimentos laterais, nosso sistema funciona com sucesso em ambos os regimes, graças ao mecanismo adaptativo de definição de estados e à estratégia flexível de hedge.

Além do modelo básico: direções para expansão

A implementação apresentada é apenas a primeira nota de uma potencial sinfonia de possibilidades. Abrem-se diante de nós inúmeros caminhos empolgantes para o aperfeiçoamento futuro do sistema.

Expansão do modelo de estados

Imagine um sistema em que, em vez da modesta tríade de estados de mercado, tendência de alta, flat e tendência de baixa, se desdobra todo um espectro de humores do mercado: do galope furioso dos touros ao avanço impetuoso dos ursos, do quase imperceptível deslizamento positivo ao suave escorregar descendente, com um majestoso movimento lateral puro no centro desse contínuo.

// Enhanced market state enumeration
enum ENHANCED_MARKET_STATE
{
   STATE_STRONG_DOWNTREND = 0,    // Strong bearish movement
   STATE_MODERATE_DOWNTREND = 1,  // Moderate bearish movement
   STATE_WEAK_DOWNTREND = 2,      // Weak bearish movement
   STATE_FLAT = 3,                // Sideways market
   STATE_WEAK_UPTREND = 4,        // Weak bullish movement
   STATE_MODERATE_UPTREND = 5,    // Moderate bullish movement
   STATE_STRONG_UPTREND = 6       // Strong bullish movement
};

// Enhanced market state detection function
ENHANCED_MARKET_STATE GetEnhancedMarketState(int shift)
{
   double close[], atr[];
   ArraySetAsSeries(close, true);
   ArraySetAsSeries(atr, true);
   
   // Get data
   if(CopyClose(_Symbol, PERIOD_D1, shift, 2, close) < 2 ||
      CopyBuffer(atrHandle, 0, shift, 1, atr) < 1) {
      return STATE_FLAT;
   }
   
   // Calculate normalized price change
   double priceChange = close[0] - close[1];
   double atrValue = atr[0];
   double normalizedChange = priceChange / atrValue;
   
   // Determine enhanced market state based on price change relative to ATR
   if(normalizedChange < -1.5) return STATE_STRONG_DOWNTREND;
   if(normalizedChange < -0.75) return STATE_MODERATE_DOWNTREND;
   if(normalizedChange < -0.25) return STATE_WEAK_DOWNTREND;
   if(normalizedChange <= 0.25) return STATE_FLAT;
   if(normalizedChange <= 0.75) return STATE_WEAK_UPTREND;
   if(normalizedChange <= 1.5) return STATE_MODERATE_UPTREND;
   return STATE_STRONG_UPTREND;
}

Enriquecimento do contexto de mercado

O modelo atual utiliza predominantemente o ATR para determinar os estados do mercado. Mas imagine a profundidade de compreensão que poderíamos alcançar ao adicionar a essa orquestra o som do RSI, a melodia do MACD, as sequências harmônicas dos níveis de Fibonacci e as estruturas rítmicas dos volumes!

Assim como os sentidos humanos se combinam para criar uma percepção integrada do mundo, diversos indicadores técnicos podem formar, em nosso sistema, uma compreensão quase intuitiva da dinâmica do mercado. A combinação de osciladores, indicadores de tendência e métricas de volume pode levar a um salto qualitativo na precisão das previsões.

Ajuste dinâmico do tamanho das posições

Merece atenção especial a ideia de adaptação dinâmica do tamanho das posições. Imagine um sistema que, como um capitão experiente, aumenta ou reduz a “área das velas” de acordo com a força do “vento” do mercado, o grau de confiança no rumo escolhido e a experiência histórica de navegação em águas semelhantes.

Em períodos de alta previsibilidade e condições de mercado favoráveis, o EA aumentará o tamanho das posições, maximizando o retorno de sua vantagem preditiva. E, ao contrário, em momentos de maior turbulência ou de sinais contraditórios, o sistema reduzirá automaticamente os volumes de negociação, preservando o capital para oportunidades mais favoráveis.

Análise multitimeframe

Por fim, a análise multitimeframe abrirá diante de nós uma nova dimensão de compreensão do mercado. Assim como um arqueólogo estuda simultaneamente tanto a época geológica como um todo quanto os mínimos detalhes de um artefato, nosso sistema será capaz de captar ao mesmo tempo os deslocamentos tectônicos globais do mercado e as menores oscilações de preço.

Imagine um EA que analisa cadeias de Markov em vários timeframes simultaneamente, do mensal ao minuto, e forma uma visão integrada do mercado, na qual as tendências de longo prazo orientam as flutuações de curto prazo. Essa abordagem permitirá não apenas determinar com maior precisão a direção do movimento, mas também identificar momentos ideais de entrada com precisão de tick.

Epílogo: a pedra filosofal do trading algorítmico

O EA de trading apresentado neste artigo não é apenas um símbolo da combinação de diferentes abordagens técnicas. Trata-se de uma verdadeira alquimia das tecnologias financeiras, na qual da interação de elementos aparentemente desconexos nasce algo qualitativamente novo, assim como nas lendas a pedra filosofal transformava metais comuns em ouro.

Ao unir o rigor da teoria matemática das probabilidades com o poder intuitivo da inteligência artificial e a sabedoria pragmática das estratégias de hedge, criamos um sistema capaz de navegar nas águas turbulentas dos mercados financeiros com a graça de um navegador experiente. Em calmaria, ele capta os menores movimentos do ar com suas velas sensíveis; em tempestade, manobra com maestria entre gigantescas ondas de volatilidade; e, quando o vento muda, ajusta instantaneamente o seu curso.

É importante compreender que não criamos um artefato mágico que promete riqueza ilimitada. Trata-se, antes, de um instrumento musical delicado, que exige ajuste fino às condições específicas de execução e habilidade de seu operador. Assim como um violino Stradivarius revela seu som divino apenas nas mãos de um virtuose, nosso EA manifesta todo o seu potencial somente com a configuração correta e um entendimento profundo de sua arquitetura interna.

Ainda assim, a natureza adaptativa do sistema e os mecanismos elegantes de gerenciamento de risco tornam esse instrumento acessível tanto ao iniciante que dá seus primeiros passos no mundo do trading algorítmico quanto ao profissional experiente em busca de novas fronteiras de aperfeiçoamento em seu arsenal de trading.

O código-fonte do EA, como um código genético de uma nova espécie de sistemas de trading, está disponível no anexo do artigo. Ele está aberto a experimentos, modificações e evolução. Convidamos você não apenas a utilizá-lo, mas também a se tornar coautor do próximo capítulo desta história fascinante do desenvolvimento das tecnologias financeiras.

Afinal, a verdadeira inovação nasce do diálogo aberto de ideias e da busca contínua pela excelência.

Referências e materiais adicionais

1. Koshtenko, Y. (2025). Modelo matricial de previsão baseado em cadeia de Markov. 
2. ALGLIB – Biblioteca de análise numérica: https://www.alglib.net/
3. Documentação MQL5: https://www.mql5.com/ru/docs
4. Sewell, M. (2011). Characterization of Financial Time Series. UCL Research Note, 11(01).
5. Zhang, G.P. (2003). Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing, 50, 159-175.