Indicador do modelo CAPM no mercado Forex

Desenvolvimento histórico do modelo CAPM

O surgimento do modelo de precificação de ativos de capital foi resultado de mudanças revolucionárias na compreensão da relação entre risco e rentabilidade nos mercados financeiros. No início da década de 1960, a ciência financeira vivia um período de desenvolvimento intensivo, quando pesquisadores buscavam criar modelos matematicamente rigorosos para explicar a precificação de ativos.

As premissas para a criação do CAPM foram estabelecidas nos trabalhos de Harry Markowitz, que em 1952 apresentou a teoria moderna de portfólios. Markowitz demonstrou como os investidores podem otimizar a relação entre risco e rentabilidade por meio da diversificação do portfólio. Seu conceito de fronteira eficiente tornou-se a base para desenvolvimentos teóricos posteriores na área de finanças.

William Sharpe, ao trabalhar no desenvolvimento das ideias de Markowitz, deparou-se com o problema prático da complexidade computacional da otimização de portfólios. Naquela época, o poder computacional era limitado, e o cálculo da matriz de covariância para um grande número de ativos representava um sério problema técnico. Isso levou Sharpe a buscar um modelo simplificado que preservasse o rigor teórico, mas fosse mais prático na aplicação.

Em 1964, Sharpe publicou seu famoso artigo "Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk", no qual o modelo CAPM foi apresentado pela primeira vez. Independentemente de Sharpe, ideias semelhantes estavam sendo desenvolvidas por John Lintner e Jan Mossin, o que confirmava o caráter fundamental das regularidades descobertas. Por sua contribuição ao desenvolvimento da teoria financeira, Sharpe foi agraciado com o Prêmio Nobel de Economia em 1990.

O modelo rapidamente ganhou reconhecimento nos círculos acadêmicos e tornou-se a base para inúmeras aplicações práticas na gestão de investimentos. Já na década de 1970, o CAPM era amplamente utilizado por fundos de investimento e corporações para avaliar o custo de capital e tomar decisões de investimento.

Estrutura matemática do modelo clássico CAPM

O modelo clássico CAPM baseia-se em uma série de premissas-chave que determinam sua estrutura matemática e aplicabilidade prática. A fórmula central do modelo expressa a rentabilidade esperada de um ativo por meio de um sistema de parâmetros inter-relacionados:

E(Ri) = Rf + βi × (E(Rm) - Rf)

onde E(Ri) representa a rentabilidade esperada do ativo i, Rf denota a taxa de retorno livre de risco, βi é o coeficiente beta do ativo i, e E(Rm) é a rentabilidade esperada do portfólio de mercado.

O coeficiente beta desempenha um papel central no modelo e é definido como a razão entre a covariância da rentabilidade do ativo com a rentabilidade do mercado e a variância da rentabilidade do mercado:

βi = Cov(Ri, Rm) / Var(Rm)

Esse indicador mede a sensibilidade da rentabilidade de um ativo específico às mudanças na rentabilidade geral do mercado. Ativos com beta maior que um demonstram maior volatilidade em comparação com o mercado, enquanto ativos com beta menor que um são menos voláteis.

O modelo pressupõe a existência de uma relação linear entre o risco sistemático, medido por meio do beta, e a rentabilidade esperada. Essa relação é representada graficamente na forma da linha do mercado de títulos financeiros (Security Market Line), que mostra as relações de equilíbrio entre risco e rentabilidade para todos os ativos da economia.

As premissas fundamentais do CAPM incluem concorrência perfeita nos mercados, ausência de custos de transação, expectativas idênticas de todos os investidores em relação às rentabilidades futuras, possibilidade de crédito e endividamento ilimitados à taxa livre de risco, bem como distribuição normal das rentabilidades dos ativos.

O modelo também pressupõe que todos os investidores sejam maximizadores racionais de utilidade, que tomam decisões exclusivamente com base na rentabilidade esperada e no risco do portfólio. Além disso, assume-se que os investidores possuem o mesmo horizonte de investimento e a mesma informação sobre o mercado.

O risco não sistemático, no âmbito do CAPM, é completamente eliminado por meio da diversificação do portfólio, de modo que os investidores recebem compensação apenas pela assunção do risco sistemático. Isso significa que, em equilíbrio, todos os portfólios eficientes devem situar-se sobre uma única linha reta nas coordenadas "risco-rentabilidade".

Fundamentos teóricos da adaptação do CAPM para o mercado cambial

A fórmula clássica do CAPM expressa a rentabilidade esperada de um ativo por meio da taxa livre de risco e do prêmio pelo risco sistemático. No contexto dos pares de moedas, esse conceito adquire um significado especial, pois cada par de moedas representa o valor relativo de duas economias nacionais, com todos os riscos macroeconômicos a elas inerentes.

Em nossa implementação para a plataforma MetaTrader 5, modificamos a abordagem clássica, substituindo o coeficiente beta por um prêmio de risco dinâmico baseado na volatilidade histórica do par de moedas. Essa decisão decorre da especificidade do mercado cambial, no qual o risco sistemático se manifesta por meio da variabilidade das oscilações cambiais, e não por meio da correlação com um portfólio de mercado.

//--- input parameters
input int      InpPeriod = 20;              // Период для расчета
input double   InpRiskFreeRate = 0.05;      // Безрисковая ставка (годовая)
input double   InpRiskPremium = 0.02;       // Премия за риск валютной пары
input bool     InpShowInfo = true;          // Показывать информационную панель

//--- indicator buffers
double ExpectedReturnBuffer[];
double RiskPremiumBuffer[];

Uma característica-chave da implementação é o uso de uma abordagem robusta para o cálculo da variância das rentabilidades. Aplicamos uma estimativa não viesada da variância e tratamos corretamente os casos de insuficiência de dados, o que é criticamente importante para manter a estabilidade dos cálculos em condições de lacunas de mercado ou baixa liquidez.

A anualização da volatilidade é realizada utilizando o coeficiente padrão da raiz quadrada de 252, o que corresponde ao número de dias de negociação no ano. Essa abordagem permite trazer os indicadores de volatilidade para uma escala comparável às taxas livres de risco, que tradicionalmente são cotadas em base anual.

//--- аннуализируем показатели (252 торговых дня)
double annual_volatility = volatility * MathSqrt(252.0);
double annual_return = mean_return * 252.0;

//--- рассчитываем премию за риск на основе волатильности
double dynamic_risk_premium = InpRiskPremium * (annual_volatility / 0.15);

Interpretação econômica dos resultados do indicador

O aspecto mais interessante do indicador desenvolvido é o seu comportamento em diferentes condições de mercado. Observações empíricas mostram que a rentabilidade esperada e o prêmio de risco demonstram uma tendência pronunciada de crescimento justamente nos períodos de extremos de mercado. Esse fenômeno possui raízes econômicas profundas e reflete os princípios fundamentais de precificação nos mercados financeiros.

Durante a formação de picos locais, a volatilidade do par de moedas naturalmente aumenta, pois os participantes do mercado revisam suas expectativas em relação aos movimentos futuros da taxa de câmbio. O aumento da incerteza leva à elevação do prêmio de risco que os investidores exigem para manter esse ativo. Situação semelhante é observada durante a formação de fundos de mercado, quando sentimentos de pânico e a fixação em massa de prejuízos criam uma rentabilidade futura excedente.

void ShowInfoPanel(int current_bar)
{
    string info = "";
    info += "=== CAPM Forex Model ===\n";
    info += StringFormat("Risk Premium: %.2f%%\n", RiskPremiumBuffer[current_bar] * 100);
    info += StringFormat("Expected Return: %.2f%%\n", ExpectedReturnBuffer[current_bar] * 100);
    
    if(current_volatility > 0.20)
        info += "Status: HIGH RISK\n";
    else if(current_volatility > 0.10)
        info += "Status: MEDIUM RISK\n";
    else
        info += "Status: LOW RISK\n";
}

Esse comportamento do indicador está em conformidade com a teoria clássica dos mercados eficientes, segundo a qual um risco mais elevado deve ser compensado por uma rentabilidade esperada maior. No contexto do trading cambial, isso significa que períodos de maior volatilidade potencialmente oferecem oportunidades mais favoráveis de obtenção de lucro, mas exigem, de forma correspondente, uma abordagem mais cautelosa na gestão de riscos.

Implementação técnica e aspectos computacionais

A arquitetura do indicador é construída com base no uso de dois buffers de dados principais, cada um dos quais desempenha uma função analítica específica. ExpectedReturnBuffer contém os valores da rentabilidade esperada, calculados com base na fórmula CAPM modificada, enquanto RiskPremiumBuffer reflete a dinâmica do prêmio de risco em função das variações da volatilidade.

//--- plot Expected Return
#property indicator_label1  "Expected Return"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  2

//--- plot Risk Premium
#property indicator_label2  "Risk Premium"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_style2  STYLE_DASH
#property indicator_width2  1

A função CalculateCurrentVolatility representa uma implementação otimizada do algoritmo de cálculo da volatilidade atual, utilizando as funções integradas do MetaTrader 5 para trabalhar com dados históricos. A aplicação da função CopyClose garante acesso eficiente aos dados de preços, sem a necessidade de iterar por todo o array de cotações.

double CalculateCurrentVolatility(int current_bar)
{
    if(current_bar < InpPeriod) 
        return 0.0;
    
    double returns_sum = 0.0;
    double returns_sq_sum = 0.0;
    int valid_count = 0;
    
    // Получаем данные цен закрытия для расчета
    double prices[];
    int copied = CopyClose(Symbol(), PERIOD_CURRENT, current_bar - InpPeriod, InpPeriod + 1, prices);
    
    if(copied <= InpPeriod)
        return 0.0;
    
    // Рассчитываем доходности
    for(int j = 1; j < ArraySize(prices); j++)
    {
        if(prices[j-1] > 0)
        {
            double daily_return = (prices[j] - prices[j-1]) / prices[j-1];
            returns_sum += daily_return;
            returns_sq_sum += daily_return * daily_return;
            valid_count++;
        }
    }
    
    if(valid_count < 2) 
        return 0.0;
    
    double mean_return = returns_sum / valid_count;
    double variance = (returns_sq_sum / valid_count) - (mean_return * mean_return);
    double volatility = MathSqrt(MathMax(variance, 0.0));
    
    return volatility * MathSqrt(252.0); // аннуализированная волатильность
}

Importância prática do indicador em sistemas de negociação

O indicador CAPM desenvolvido demonstra elevada relevância prática, justamente devido à sua capacidade de avaliar quantitativamente as mudanças na relação entre risco e rentabilidade na dinâmica do mercado. Quando um par de moedas se aproxima de níveis críticos de suporte ou resistência, o indicador registra o aumento da volatilidade e, consequentemente, eleva a estimativa da rentabilidade esperada.

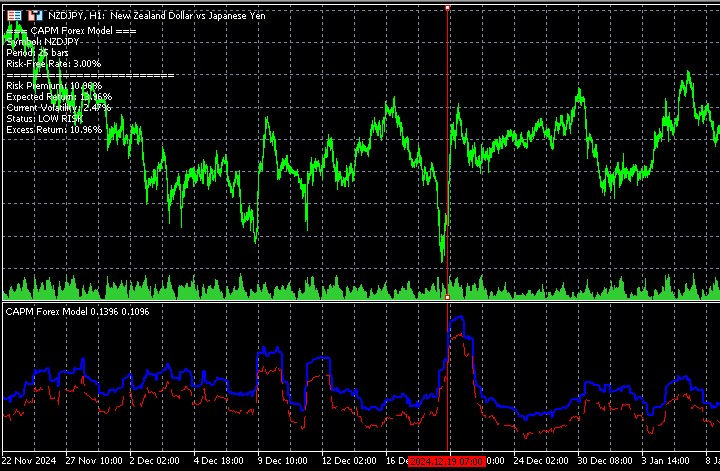
Essa característica torna o indicador especialmente útil para traders que aplicam estratégias contra a tendência. O crescimento dos indicadores de risco e rentabilidade nos extremos pode servir como um sinal para a busca de pontos de entrada contra a tendência atual, uma vez que a volatilidade elevada frequentemente antecede movimentos de reversão.

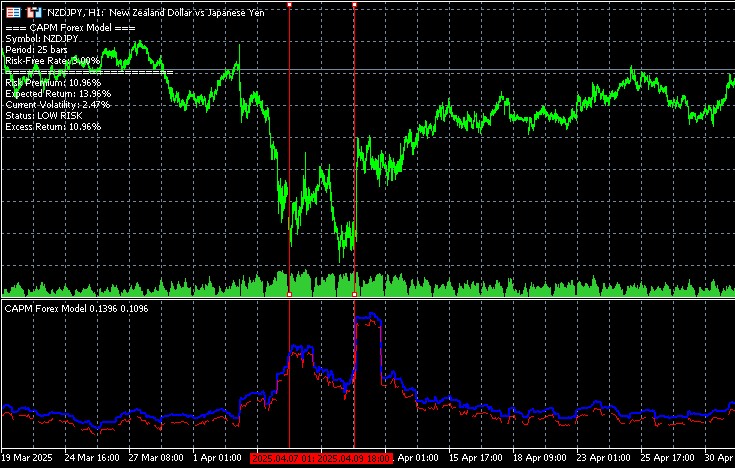
Para estratégias de seguimento de tendência, o indicador fornece informações sobre o quanto o movimento atual do preço corresponde a uma avaliação justa do risco. Se o movimento efetivo exceder significativamente a rentabilidade esperada calculada pelo indicador, isso pode indicar a formação de uma bolha especulativa ou uma reação excessiva do mercado às notícias.

Desvantagens do modelo e direções de desenvolvimento

Apesar da utilidade prática, o modelo CAPM adaptado para o mercado cambial possui uma série de limitações conceituais que devem ser consideradas na interpretação dos resultados. A principal premissa de distribuição normal das rentabilidades nem sempre corresponde às características reais dos mercados de câmbio, especialmente em períodos de choques macroeconômicos ou crises políticas.

O modelo também não leva em conta os efeitos de autocorrelação nas séries de rentabilidade, que podem ser significativos para dados de alta frequência. Além disso, o uso de uma taxa livre de risco fixa pode não refletir a dinâmica real das taxas de juros dos bancos centrais, especialmente em períodos de política monetária ativa.

Uma direção promissora para o desenvolvimento do indicador é a integração com dados macroeconômicos para o ajuste dinâmico da taxa livre de risco de acordo com as decisões atuais dos bancos centrais. Também é de interesse a implementação de algoritmos adaptativos para a configuração automática dos parâmetros do modelo, dependendo do regime de volatilidade de um determinado par de moedas.

A inclusão de elementos de aprendizado de máquina pode permitir que o indicador se adapte às condições mutáveis do mercado e aumente a precisão da previsão da rentabilidade esperada. Essa abordagem é especialmente relevante no contexto dos modernos sistemas de trading algorítmico, nos quais a velocidade de adaptação a novos regimes de mercado é um fator crítico de sucesso.

O indicador CAPM desenvolvido representa uma tentativa bem-sucedida de aplicar a teoria financeira clássica às especificidades do trading cambial. Sua capacidade de avaliar quantitativamente a dinâmica da relação entre risco e rentabilidade o torna uma ferramenta valiosa para a tomada de decisões de trading fundamentadas em um ambiente de mercado em constante mudança.

Conclusão

A pesquisa realizada mostrou que a adaptação do modelo CAPM ao mercado cambial pode ser implementada de forma eficaz na forma de um indicador para o MetaTrader 5. A ferramenta desenvolvida avalia dinamicamente a rentabilidade esperada dos pares de moedas com base na volatilidade e identifica com sucesso períodos de risco elevado e potencial.

O indicador demonstra que modelos clássicos, quando corretamente implementados do ponto de vista técnico, permanecem relevantes no trading moderno e são capazes de melhorar a qualidade das decisões de negociação.