Indicador de previsão ARIMA em MQL5

Meteorologistas não adivinham olhando borra de café quando elaboram a previsão do tempo. Eles analisam o que aconteceu no passado para entender o que acontecerá amanhã. De maneira muito semelhante funciona o modelo ARIMA, apenas que, em vez de nuvens e pressão atmosférica, ele estuda os preços nos mercados financeiros.

ARIMA é a sigla de "Modelo Autorregressivo Integrado de Média Móvel". O nome assusta, mas na prática trata-se de um sistema bastante lógico. Imagine que você está tentando prever quanto custará o par EUR/USD amanhã, com base em como ele se comportou nos últimos dias.

Três pilares do modelo ARIMA

Autorregressão (AR), memória do passado

A primeira parte do modelo é chamada de autorregressão. Essa palavra bonita significa uma coisa simples: o preço de hoje depende do preço de ontem, de anteontem e assim por diante. É como se o mercado se lembrasse do seu passado e construísse o futuro com base nele.

Se o EUR/USD subiu três dias seguidos, existe a probabilidade de que amanhã ele também suba. Não é garantido, mas a tendência pode continuar. A parte autorregressiva do modelo captura exatamente esses padrões, analisando o quanto os valores passados influenciam o valor atual.

A matemática por trás das palavras simples: imagine que você tenha a cotação do EUR/USD dos últimos cinco dias: 1.0800, 1.0825, 1.0850, 1.0875, 1.0900. A autorregressão diz: "Veja, a cada dia a cotação subiu cerca de 25 pontos (0.0025), portanto amanhã ela estará por volta de 1.0925". O modelo encontra coeficientes, números que mostram o quanto o preço de ontem influencia o de hoje, o de anteontem influencia o de hoje, e assim por diante.

A fórmula fica mais ou menos assim: preco_de_amanha = 0.7 × preco_de_hoje + 0.2 × preco_de_ontem + 0.1 × preco_de_anteontem. Esses coeficientes 0.7, 0.2 e 0.1 o modelo seleciona por conta própria, analisando o histórico. Quanto maior o coeficiente, mais forte é a influência daquele dia na previsão.

Integração (I), domando o caos

Imagine que você está olhando para o gráfico do EUR/USD e vê uma completa bagunça: 1.0800, 1.0850, 1.0820, 1.0880, 1.0860. O preço sobe e desce como um marinheiro bêbado, sem nenhuma lógica à primeira vista. Dados assim os matemáticos chamam de não estacionários, e os traders chamam de dor de cabeça.

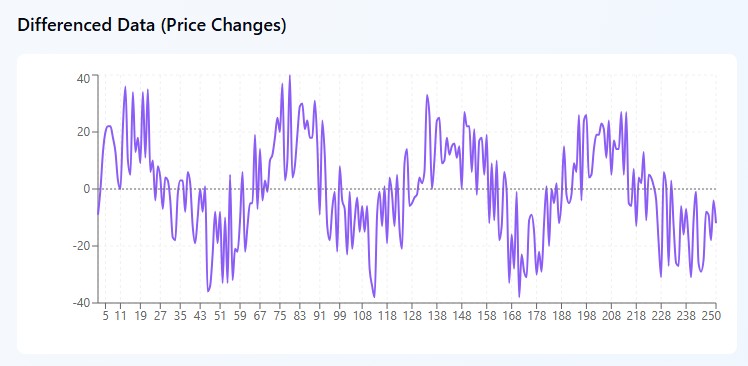
Mas aqui vem o truque: em vez de tentar encontrar sentido nos próprios preços, o ARIMA faz um movimento inteligente. Ele não olha para quanto custa o par de moedas, mas para o quanto ele mudou de um dia para o outro. Pegamos os mesmos números e calculamos as diferenças: +50 pontos, -30 pontos, +60 pontos, -20 pontos. E, de repente, o caos se transforma em padrão! O mercado oscila entre altas de 50 a 60 pontos e quedas de 20 a 30 pontos.

É como se você não acompanhasse onde o pêndulo está, mas apenas para que lado e com que força ele oscila. Matematicamente, é tudo simples: pegamos o preço de hoje, subtraímos o de ontem e obtemos a variação. Às vezes é preciso ir além e pegar a "variação das variações", ou seja, a diferenciação de segunda ordem. Parece assustador, mas o princípio continua o mesmo: buscamos padrões onde, à primeira vista, eles não existem.

Média móvel (MA), aprendendo com os erros

E agora a parte mais interessante: o modelo sabe aprender com os próprios erros. Parece ficção científica, mas a lógica é de ferro. Quando o ARIMA ontem previu o EUR/USD no nível de 1.0800, e ele de fato foi negociado a 1.0825, esse erro de 25 pontos não é apenas uma imprecisão chata. Isso é informação!

Imagine um amigo que sempre se atrasa exatamente 10 minutos. Quando ele diz "chego às seis", você já sabe, na prática será às 6:10. O modelo faz a mesma coisa com os próprios deslizes. Se por três dias seguidos ele prevê um preço abaixo do real em 10 pontos, então ele memoriza esses erros e, na próxima vez, mentalmente soma: "Normalmente eu subestimo em 10 pontos, então a previsão precisa de um ajuste".

A fórmula pode ficar mais ou menos assim: "Ajuste = 0.5 × erro de ontem + 0.3 × erro de anteontem". O modelo não apenas erra, ele erra com inteligência, extraindo benefício de cada deslize.

Como o ARIMA usa a psicologia do mercado

Inércia do movimento

Os mercados têm inércia. Se o EUR/USD sobe por vários dias seguidos, todo mundo quer comprá-lo, isso empurra o preço ainda mais para cima. O ARIMA captura exatamente essa inércia.

Na prática: a cotação sobe por cinco dias de 1.0800 para 1.0900 (+20 pontos por dia). O modelo atribui um peso grande aos dias mais recentes e prevê a continuação da tendência.

Retorno à média

Ao mesmo tempo, os mercados tendem a um nível "justo". Se o preço se desviou muito para um lado, mais cedo ou mais tarde ele tenta voltar.

Exemplo: o EUR/USD normalmente é negociado na faixa de 1.0800-1.0900. Se por causa de notícias ele disparou para 1.1000, o modelo, via o componente de média móvel, levará em conta que esses movimentos extremos normalmente se corrigem.

Padrões cíclicos

Muitos pares de moedas exibem comportamento cíclico, padrões semanais, mensais ou sazonais. O ARIMA consegue capturá-los com a configuração correta.

Desvantagens do modelo: quando o ARIMA não funciona

O ARIMA não é um Graal mágico. Ele funciona com a suposição de que o futuro é parecido com o passado. Quando essa suposição é quebrada, o modelo dá previsões imprecisas.

O modelo funciona mal quando:

• Saem notícias econômicas inesperadas
• Muda a política monetária dos bancos centrais
• Acontecem crises geopolíticas
• O mercado entra em um novo regime (por exemplo, passa de tendência para lateralização)

O ARIMA funciona melhor em:

• Condições de mercado estáveis
• Períodos sem mudanças fundamentais fortes
• Em instrumentos com padrões técnicos bem marcados

Implementação prática em MQL5

Criar um indicador ARIMA funcional é mais do que apenas fórmulas. É preciso uma arquitetura bem pensada, que dê conta do processamento de dados em tempo real.

No coração do indicador está um módulo que estima os coeficientes do modelo. Ele usa o método de máxima verossimilhança, parece complicado, mas é apenas uma forma de encontrar parâmetros com os quais o modelo explique melhor os dados observados.

A estrutura de dados do indicador inclui vários buffers interligados: o buffer principal de valores previstos ForecastBuffer, o buffer auxiliar de preços históricos PriceBuffer e o buffer de erros ErrorBuffer para armazenar os resíduos do modelo. Essa organização garante o uso ideal da memória e alta velocidade de cálculo.

A inicialização do sistema pressupõe a criação de arrays dinâmicos para armazenar os dados de preços brutos, a série diferenciada, os coeficientes de autorregressão e de média móvel, bem como o array de resíduos. Os valores iniciais dos coeficientes são definidos no nível de 0.1, o que garante a estabilidade do algoritmo de otimização na fase inicial.

int OnInit()
{
   // Настройка буферов индикатора для визуализации результатов
   SetIndexBuffer(0, ForecastBuffer, INDICATOR_DATA);
   SetIndexBuffer(1, PriceBuffer, INDICATOR_CALCULATIONS);
   SetIndexBuffer(2, ErrorBuffer, INDICATOR_CALCULATIONS);
   
   // Установка режима временных серий для корректной работы с историческими данными
   ArraySetAsSeries(ForecastBuffer, true);
   ArraySetAsSeries(PriceBuffer, true);
   ArraySetAsSeries(ErrorBuffer, true);
   
   // Конфигурация отображения прогноза с соответствующим сдвигом во времени
   PlotIndexSetString(0, PLOT_LABEL, "ARIMA Forecast");
   PlotIndexSetInteger(0, PLOT_SHIFT, forecast_bars);
   
   // Инициализация рабочих массивов с предварительно заданными размерами
   ArrayResize(prices, lookback);
   ArrayResize(differenced, lookback);
   ArrayResize(ar_coeffs, p);
   ArrayResize(ma_coeffs, q);
   ArrayResize(errors, lookback);
   
   // Установка начальных значений коэффициентов модели
   for(int i = 0; i < p; i++) ar_coeffs[i] = 0.1;
   for(int i = 0; i < q; i++) ma_coeffs[i] = 0.1;
   
   return(INIT_SUCCEEDED);
}

Parâmetros de entrada do modelo

A configuração do indicador é realizada por meio do sistema de parâmetros de entrada, cada um dos quais desempenha um papel crítico na definição do comportamento do modelo. O parâmetro lookback determina o volume de dados históricos usados para o treinamento do modelo, o parâmetro forecast_bars define o horizonte de previsão, e o trio de parâmetros p, d, q determina a especificação do modelo ARIMA.

//--- Входные параметры конфигурации модели
input int lookback = 200;        // Период ретроспективного анализа для ARIMA
input int forecast_bars = 20;    // Количество прогнозируемых временных интервалов
input int p = 3;                 // Порядок авторегрессионной компоненты
input int d = 1;                 // Степень дифференцирования временного ряда
input int q = 2;                 // Порядок компоненты скользящего среднего
input double learning_rate = 0.01; // Коэффициент скорости обучения
input int max_iterations = 100;   // Максимальное количество итераций оптимизации

Metodologia de avaliação dos parâmetros do modelo

O elemento central do algoritmo é a função de cálculo da função logarítmica de verossimilhança, que serve como critério de qualidade do ajuste do modelo aos dados observados. A implementação dessa função baseia-se na suposição de distribuição normal dos resíduos do modelo, o que permite utilizar uma expressão analítica para a densidade de probabilidade.

Função de verossimilhança e cálculo dos resíduos

O algoritmo de cálculo da função logarítmica de verossimilhança representa um processo iterativo no qual, para cada instante de tempo, os resíduos do modelo são calculados como a diferença entre o valor observado e a previsão do modelo. A componente autorregressiva é formada como uma combinação linear dos valores anteriores da série diferenciada, enquanto a componente de média móvel utiliza os valores anteriores dos erros do modelo.

double ComputeLogLikelihood(double &data[], double &ar[], double &ma[])
{
   double ll = 0.0;
   double residuals[];
   ArrayResize(residuals, lookback);
   ArrayInitialize(residuals, 0.0);
   
   // Итерационное вычисление остатков модели
   for(int i = p; i < lookback; i++)
   {
      double ar_part = 0.0;
      double ma_part = 0.0;
      
      // Формирование авторегрессионной компоненты
      for(int j = 0; j < p && i - j - 1 >= 0; j++)
         ar_part += ar[j] * data[i - j - 1];
      
      // Формирование компоненты скользящего среднего
      for(int j = 0; j < q && i - j - 1 >= 0; j++)
         ma_part += ma[j] * errors[i - j - 1];
      
      // Вычисление остатка и обновление массива ошибок
      residuals[i] = data[i] - (ar_part + ma_part);
      errors[i] = residuals[i];
      
      // Накопление логарифмической функции правдоподобия
      ll -= 0.5 * MathLog(2 * M_PI) + 0.5 * residuals[i] * residuals[i];
   }
   
   return ll;
}

Procedimento de otimização dos coeficientes

O procedimento de otimização dos coeficientes é implementado por meio do método de descida do gradiente com tamanho de passo adaptativo. O algoritmo atualiza iterativamente os valores dos coeficientes na direção oposta ao gradiente da função objetivo, garantindo a convergência para um ótimo local da função de verossimilhança.

void OptimizeCoefficients(double &data[])
{
   double temp_ar[], temp_ma[];
   ArrayCopy(temp_ar, ar_coeffs);
   ArrayCopy(temp_ma, ma_coeffs);
   
   double best_ll = -DBL_MAX;
   double grad_ar[], grad_ma[];
   ArrayResize(grad_ar, p);
   ArrayResize(grad_ma, q);
   
   // Итерационный процесс оптимизации
   for(int iter = 0; iter < max_iterations; iter++)
   {
      ArrayInitialize(grad_ar, 0.0);
      ArrayInitialize(grad_ma, 0.0);
      
      // Вычисление градиентов функции правдоподобия
      for(int i = p; i < lookback; i++)
      {
         double ar_part = 0.0, ma_part = 0.0;
         
         // Формирование компонент модели
         for(int j = 0; j < p && i - j - 1 >= 0; j++)
            ar_part += temp_ar[j] * data[i - j - 1];
         for(int j = 0; j < q && i - j - 1 >= 0; j++)
            ma_part += temp_ma[j] * errors[i - j - 1];
         
         double residual = data[i] - (ar_part + ma_part);
         
         // Накопление градиентов по AR коэффициентам
         for(int j = 0; j < p && i - j - 1 >= 0; j++)
            grad_ar[j] += -residual * data[i - j - 1];
            
         // Накопление градиентов по MA коэффициентам
         for(int j = 0; j < q && i - j - 1 >= 0; j++)
            grad_ma[j] += -residual * errors[i - j - 1];
      }
      
      // Обновление коэффициентов согласно правилу градиентного спуска
      for(int j = 0; j < p; j++)
         temp_ar[j] += learning_rate * grad_ar[j] / lookback;
      for(int j = 0; j < q; j++)
         temp_ma[j] += learning_rate * grad_ma[j] / lookback;
      
      // Оценка качества текущего приближения
      double current_ll = ComputeLogLikelihood(data, temp_ar, temp_ma);
      
      // Критерий остановки и обновление оптимального решения
      if(current_ll > best_ll)
      {
         best_ll = current_ll;
         ArrayCopy(ar_coeffs, temp_ar);
         ArrayCopy(ma_coeffs, temp_ma);
      }
      else
      {
         break; // Преждевременная остановка при отсутствии улучшения
      }
   }
}

É dada atenção especial ao cálculo das derivadas parciais da função de verossimilhança em relação a cada um dos parâmetros otimizados. Os gradientes para os coeficientes de autorregressão são calculados como a soma dos produtos dos resíduos pelos valores de defasagem correspondentes da série diferenciada, enquanto os gradientes para os coeficientes de média móvel são determinados por meio dos produtos dos resíduos pelos valores anteriores dos erros.

Algoritmo de previsão e reversão da diferenciação

A geração dos valores previstos é realizada de forma recursiva, começando a partir do último valor observado da série temporal. Em cada etapa da previsão, é calculada a componente autorregressiva como uma combinação linear dos valores anteriores da série diferenciada com os coeficientes correspondentes. A componente de média móvel é formada de maneira análoga, por meio de uma soma ponderada dos resíduos anteriores do modelo.

Procedimento principal de cálculos

A função central OnCalculate representa o núcleo do processo computacional, integrando todos os componentes do algoritmo em um fluxo único de processamento de dados. A função realiza o processamento sequencial dos dados de mercado recebidos, a aplicação do procedimento de diferenciação, a otimização dos parâmetros do modelo e a geração dos valores previstos.

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   ArraySetAsSeries(close, true);
   ArraySetAsSeries(time, true);
   
   // Проверка достаточности исторических данных
   if(rates_total < lookback + forecast_bars) return(0);
   
   // Формирование массива цен закрытия
   for(int i = 0; i < lookback; i++)
   {
      prices[i] = close[i];
      PriceBuffer[i] = close[i];
   }
   
   // Применение процедуры дифференцирования
   for(int i = 0; i < lookback - d; i++)
   {
      if(d == 1)
         differenced[i] = prices[i] - prices[i + 1];
      else if(d == 2)
         differenced[i] = (prices[i] - prices[i + 1]) - (prices[i + 1] - prices[i + 2]);
      else
         differenced[i] = prices[i];
   }
   
   // Оптимизация коэффициентов AR и MA
   ArrayInitialize(errors, 0.0);
   OptimizeCoefficients(differenced);
   
   // Генерация ARIMA прогноза
   double forecast[];
   ArrayResize(forecast, forecast_bars);
   double undiff[];
   ArrayResize(undiff, forecast_bars);
   
   // Инициализация прогнозного процесса
   forecast[0] = prices[0];
   undiff[0] = prices[0];
   
   // Итерационное формирование прогноза
   for(int i = 1; i < forecast_bars; i++)
   {
      double ar_part = 0.0;
      double ma_part = 0.0;
      
      // Вычисление авторегрессионной компоненты
      for(int j = 0; j < p && i - j - 1 >= 0; j++)
         ar_part += ar_coeffs[j] * (j < lookback ? differenced[j] : forecast[i - j - 1]);
      
      // Вычисление компоненты скользящего среднего
      for(int j = 0; j < q && i - j - 1 >= 0; j++)
         ma_part += ma_coeffs[j] * errors[j];
      
      // Формирование прогнозного значения
      forecast[i] = ar_part + ma_part;
      
      // Процедура обращения дифференцирования
      if(d == 1)
         undiff[i] = undiff[i - 1] + forecast[i];
      else if(d == 2)
         undiff[i] = undiff[i - 1] + (undiff[i - 1] - (i >= 2 ? undiff[i - 2] : prices[1])) + forecast[i];
      else
         undiff[i] = forecast[i];
      
      // Обновление массива ошибок для следующих итераций
      errors[i % lookback] = forecast[i] - (i < lookback ? differenced[i] : 0.0);
   }
   
   // Заполнение выходного буфера прогнозными значениями
   for(int i = 0; i < forecast_bars; i++)
   {
      ForecastBuffer[i] = undiff[i];
   }
   
   // Расширение исторических данных для непрерывности отображения
   for(int i = forecast_bars; i < lookback; i++)
   {
      ForecastBuffer[i] = prices[i - forecast_bars];
   }
   
   return(rates_total);
}

O procedimento de reversão da diferenciação representa uma etapa criticamente importante, garantindo a restauração correta da escala original dos valores previstos. No caso da diferenciação de primeira ordem, cada valor previsto é obtido pela soma do valor anterior não diferenciado com a previsão correspondente da primeira diferença. Ao utilizar a diferenciação de segunda ordem, aplica-se uma fórmula recursiva mais complexa, que leva em conta a curvatura da série temporal.

Aspectos computacionais e otimização de desempenho

A eficiência do algoritmo é amplamente determinada pela correta organização do processo computacional e pelo uso ideal dos recursos do processador. A função principal OnCalculate é estruturada de forma a minimizar a quantidade de cálculos redundantes quando novos dados de mercado chegam.

O procedimento de diferenciação é implementado levando em consideração diferentes ordens de transformação. Para a diferenciação de primeira ordem, calcula-se a diferença simples entre observações adjacentes, enquanto que, para a segunda ordem, é aplicada a fórmula da segunda diferença, permitindo eliminar não apenas a tendência, mas também as mudanças na velocidade da tendência.

Um aspecto crítico da implementação é o gerenciamento de memória e o trabalho correto com arrays de comprimento variável. O uso das funções ArrayResize e ArraySetAsSeries garante a adaptação da estrutura de dados aos parâmetros mutáveis do modelo e às particularidades da organização dos dados no MetaTrader 5.

Calibração dos parâmetros e adaptação às condições de mercado

A aplicação bem-sucedida do modelo ARIMA em condições reais de negociação exige uma calibração cuidadosa dos parâmetros, levando em conta as especificidades do instrumento financeiro específico e do horizonte temporal de análise. O parâmetro lookback define a profundidade da análise histórica e deve ser suficiente para garantir a significância estatística das estimativas, mas não tão grande a ponto de incluir informações obsoletas.

A escolha das ordens p, d e q do modelo representa um compromisso entre a precisão da descrição dos dados e a complexidade computacional. O aumento da ordem de autorregressão p permite considerar dependências temporais mais complexas, porém um excesso de complexidade do modelo pode levar ao sobreajuste e à redução da qualidade da previsão em novos dados.

O parâmetro de taxa de aprendizado learning_rate exige uma configuração especialmente cuidadosa, pois um valor muito alto pode levar a oscilações do algoritmo de otimização, enquanto um valor muito baixo desacelera a convergência para o ótimo.

Validação estatística e avaliação da qualidade da previsão

Uma avaliação objetiva da qualidade do funcionamento do indicador exige a aplicação de um conjunto de critérios estatísticos que permitam caracterizar quantitativamente a precisão da previsão. Entre as métricas mais informativas, destacam-se o erro absoluto médio, a raiz do erro quadrático médio e o coeficiente de determinação.

Métricas de qualidade da previsão

A implementação das funções de avaliação da qualidade da previsão possibilita a realização de uma análise quantitativa da eficácia do modelo e a comparação entre diferentes especificações do ARIMA. O erro absoluto médio fornece uma medida intuitiva do desvio das previsões em relação aos valores reais, expressa nas unidades de medida da série temporal original.

// Функция вычисления средней абсолютной ошибки
double CalculateMAE(double &actual[], double &predicted[], int size)
{
   double mae = 0.0;
   for(int i = 0; i < size; i++)
   {
      mae += MathAbs(actual[i] - predicted[i]);
   }
   return mae / size;
}

// Функция вычисления корня среднеквадратичной ошибки
double CalculateRMSE(double &actual[], double &predicted[], int size)
{
   double mse = 0.0;
   for(int i = 0; i < size; i++)
   {
      double error = actual[i] - predicted[i];
      mse += error * error;
   }
   return MathSqrt(mse / size);
}

// Функция расчета коэффициента детерминации
double CalculateR2(double &actual[], double &predicted[], int size)
{
   double actual_mean = 0.0;
   for(int i = 0; i < size; i++)
      actual_mean += actual[i];
   actual_mean /= size;
   
   double ss_tot = 0.0, ss_res = 0.0;
   for(int i = 0; i < size; i++)
   {
      ss_tot += (actual[i] - actual_mean) * (actual[i] - actual_mean);
      ss_res += (actual[i] - predicted[i]) * (actual[i] - predicted[i]);
   }
   
   return 1.0 - (ss_res / ss_tot);
}

Diagnóstico dos resíduos do modelo

A análise dos resíduos do modelo representa um aspecto criticamente importante da validação, permitindo identificar desvios sistemáticos em relação às premissas do modelo. O teste de Ljung-Box para autocorrelação dos resíduos fornece uma verificação da adequação da especificação do modelo, enquanto o teste de Jarque-Bera permite avaliar a normalidade da distribuição dos resíduos.

// Функция вычисления автокорреляционной функции остатков
double CalculateAutocorrelation(double &residuals[], int lag, int size)
{
   double mean = 0.0;
   for(int i = 0; i < size; i++)
      mean += residuals[i];
   mean /= size;
   
   double numerator = 0.0, denominator = 0.0;
   
   for(int i = lag; i < size; i++)
   {
      numerator += (residuals[i] - mean) * (residuals[i - lag] - mean);
   }
   
   for(int i = 0; i < size; i++)
   {
      denominator += (residuals[i] - mean) * (residuals[i] - mean);
   }
   
   return numerator / denominator;
}

// Статистика Льюнга-Бокса для проверки автокорреляции
double LjungBoxTest(double &residuals[], int max_lag, int size)
{
   double lb_stat = 0.0;
   
   for(int k = 1; k <= max_lag; k++)
   {
      double rho_k = CalculateAutocorrelation(residuals, k, size);
      lb_stat += (rho_k * rho_k) / (size - k);
   }
   
   return size * (size + 2) * lb_stat;
}

O procedimento de validação cruzada permite avaliar a robustez do modelo frente a mudanças na composição do conjunto de treinamento. A metodologia de janela deslizante fornece uma avaliação mais realista da qualidade da previsão em condições próximas à negociação real, quando o modelo é aplicado sequencialmente a novos dados sem reotimização dos parâmetros.

A análise dos resíduos do modelo fornece informações importantes sobre a conformidade das premissas do modelo com as características dos dados reais. Testes de autocorrelação dos resíduos permitem identificar dependências temporais não consideradas, enquanto testes de normalidade da distribuição dos resíduos verificam a correção do modelo estatístico utilizado.

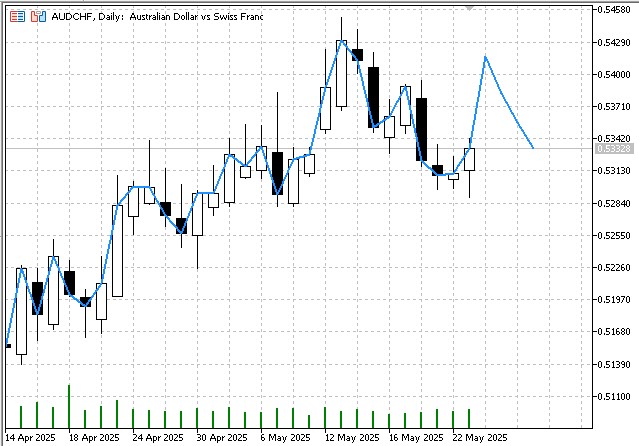
O resultado final do funcionamento do indicador será uma previsão para o horizonte especificado:

Perspectivas de desenvolvimento e modificação do algoritmo

Pesquisas modernas na área de análise de séries temporais financeiras abrem amplas possibilidades para o desenvolvimento do modelo ARIMA básico. A inclusão de componentes sazonais no âmbito do modelo SARIMA permite considerar padrões cíclicos característicos de muitos instrumentos financeiros. Métodos de regularização, como penalização L1 e L2, são capazes de aumentar a robustez do modelo a valores atípicos e evitar o sobreajuste.

Modificações adaptativas do algoritmo, que pressupõem a alteração dinâmica dos parâmetros do modelo em função das condições atuais de mercado, apresentam especial interesse para a negociação de alta frequência. A integração de métodos de aprendizado de máquina pode garantir a seleção automática da especificação ótima do modelo sem a participação de um analista.

Extensões multivariadas do modelo ARIMA abrem possibilidades para a modelagem simultânea de vários instrumentos financeiros inter-relacionados, o que é especialmente relevante para a gestão de portfólios e estratégias de arbitragem.

Considerações finais

A implementação apresentada do indicador ARIMA no ambiente MQL5 demonstra a possibilidade de adaptação bem-sucedida de métodos econométricos clássicos às tarefas do trading algorítmico. O seguimento rigoroso da metodologia estatística, em combinação com uma implementação de software eficiente, garante a criação de uma ferramenta confiável para a análise de séries temporais financeiras.

A aplicação prática do indicador exige um entendimento profundo tanto dos fundamentos matemáticos do modelo quanto das particularidades do mercado em que ele é utilizado. O modelo funciona claramente pior em sistemas com tendências instáveis.