Ciclos e trading

Introdução

A principal tarefa do trader é prever o movimento do preço. Essa previsão é feita com base em algum modelo. Um dos modelos mais simples e visuais é o modelo de movimento cíclico do preço.

A ideia principal de qualquer modelo cíclico é que diferentes fatores, sobrepostos entre si, criam ciclos no movimento do preço. Esses ciclos podem variar em duração e intensidade. Se conhecermos os parâmetros desses ciclos, operar no mercado se torna muito simples: abrir uma posição de buy quando o ciclo atinge o mínimo e de sell quando o ciclo atinge seu máximo.

Vamos ver como esse modelo pode ser usado na prática.

Ciclo simples

Para descrever ciclos, geralmente se usam as funções trigonométricas seno e cosseno. Mas também é possível definir um ciclo de outra forma, nomeadamente usando diferenças finitas.

Como exemplo, vamos considerar uma equação em que a segunda diferença é proporcional ao valor da série temporal:

Esta é a equação de um oscilador harmônico. À primeira vista, não parece nada de especial. Mas essa equação tem uma propriedade interessante. Se o valor do coeficiente R estiver entre 0 e 4, então a equação pode pertencer somente a uma senóide. Esse coeficiente depende do período do ciclo N. Ou seja, é possível ajustar seu valor para que a equação reaja apenas a ciclos com uma determinada frequência:

Agora vamos ver como essa equação pode ser aplicada na prática. Se a aplicarmos aos preços p[], precisaremos do valor do nível m, em torno do qual ocorre a oscilação do preço.

Para evitar o cálculo desse nível médio, vou usar um pequeno truque. Vamos lembrar o que acontece do ponto de vista matemático quando o ciclo atinge um ponto de máximo ou mínimo. Nesses momentos, a primeira derivada muda de sinal.

Em vez da derivada, vamos usar a primeira diferença da equação original. Este é o destino nada fácil do trader, isto é, buscar diferenças das diferenças. Mas essa abordagem simplifica bastante os cálculos. Só precisamos definir o valor do coeficiente R. A forma final da fórmula será a seguinte:

Daqui para frente, vou chamar essas fórmulas de fórmulas do algoritmo de negociação. Com base nessa fórmula, podemos criar uma estratégia de negociação. Primeiro, farei uma pequena modificação — em vez do preço atual, pode-se usar qualquer variante da média móvel clássica. A essência da estratégia é bem simples. Abertura e fechamento das posições ocorrem quando há uma mudança de sinal na equação:

• de negativo para positivo — abrir buy, fechar sell;
• de positivo para negativo — abrir sell, fechar buy.

A variação do saldo desse EA pode ser assim.

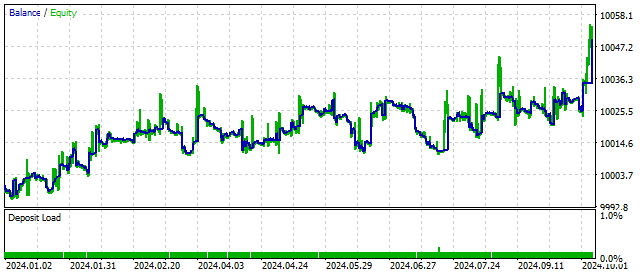
Essa estratégia de negociação tem potencial. Mas ainda precisa de aprimoramentos.

Ciclo com amortecimento

A estratégia que analisamos anteriormente possui uma falha séria. Essa falha está no fato de que a estratégia parte da suposição de que o ciclo iniciado irá durar bastante tempo. Na prática, o ciclo depende de muitos fatores externos e pode se desfazer logo após começar.

Para eliminar essa falha, podemos usar o modelo de oscilador harmônico com amortecimento das oscilações. A equação desse ciclo também é definida por diferenças finitas:

A velocidade com que as oscilações se dissipam depende do parâmetro S. Quanto maior esse valor, mais rápido ocorre o amortecimento. O valor crítico desse parâmetro pode ser encontrado pela fórmula:

A partir desse valor, o movimento do oscilador deixa de ser oscilatório.

Já sabemos o que fazer com essa equação. Precisamos encontrar sua primeira diferença, que será a responsável por gerar os sinais de negociação.

Com a adição desse novo parâmetro, a estratégia de negociação pode se tornar mais flexível e lucrativa. Por exemplo, é assim que o saldo se comporta com o valor crítico de S.

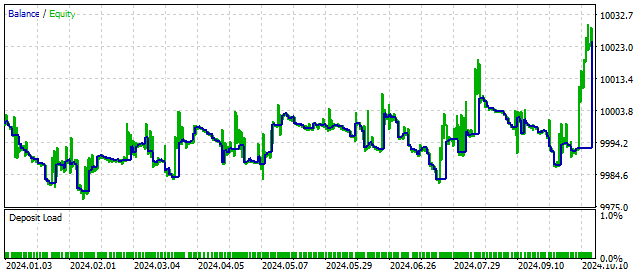
Em termos conceituais, o parâmetro S deve ser positivo. Mas isso não é uma exigência obrigatória. Se atribuirmos a esse parâmetro um valor negativo, a equação original passará a descrever oscilações com amplitude crescente. Assim, o EA pode reagir ao início de um ciclo e, potencialmente, aumentar a lucratividade. Os resultados do trading nesse caso podem ser os seguintes:

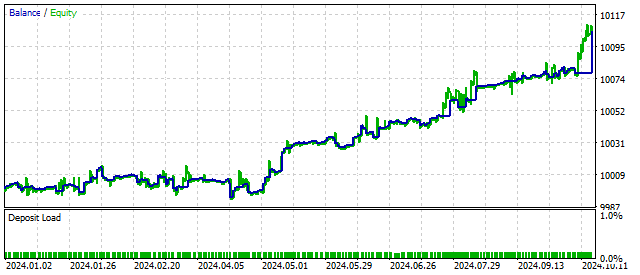
Como você pode ver, o aumento da complexidade do modelo cíclico pode melhorar os resultados do trading. Vamos tentar deixá-lo ainda mais complexo.

Ondas de Elliott

O princípio das ondas de Elliott é conhecido há muito tempo e amplamente utilizado no trading. Vamos tentar aplicar um modelo cíclico às ondas de Elliott.

As cinco primeiras ondas de Elliott podem ser modeladas como a soma de duas senoides com amplitudes e períodos diferentes:

Para isso, devem ser atendidas as seguintes condições:

Como resultado, podemos obter algo assim:

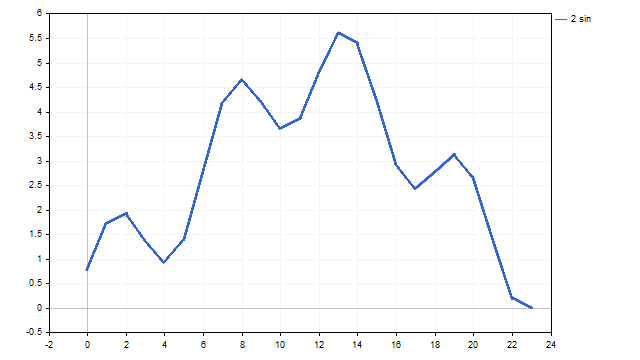
Não fica exatamente como nos livros, já que fica um pouco anguloso, mas bastante semelhante.

A soma de duas senoides pode ser modelada com diferenças finitas:

Onde, é o valor da diferença finita de ordem n, no ponto da série de preços com índice i. O que precisamos fazer com essa equação já sabemos, assim devemos calcular a diferença da soma das diferenças, e assim obter os sinais de negociação:

O uso da soma de duas senoides permite ajustar o funcionamento do EA para situações de mercado mais complexas. O uso desse algoritmo de negociação pode resultar tanto em um aumento nas entradas no mercado quanto em uma melhora na lucratividade dessas entradas.

Este pode ser o resultado obtido por um EA construído com base no princípio das ondas de Elliott:

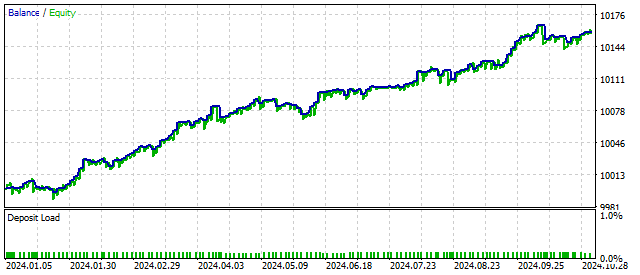
Como você pode ver, mesmo uma pequena complexificação do modelo cíclico pode trazer resultados positivos.

Oscilador harmônico generalizado

Já analisamos três modelos baseados no oscilador harmônico. Cada um desses modelos foi construído com suposições iniciais diferentes. Mas, no fim, todos resultaram em alguma soma de diferenças finitas.

Podemos construir um modelo mais geral. A ideia é simples: primeiro, calculamos a diferença de uma ordem pré-definida e somamos com diferenças de ordens mais baixas, até a primeira. Cada diferença de ordem inferior é multiplicada por um coeficiente de peso próprio.

Como exemplo, usei a diferença de 7ª ordem. A fórmula do algoritmo de negociação será:

Esse modelo pode incorporar várias combinações de ciclos e seus comportamentos. Já vimos antes que, quanto mais complexo o modelo, melhores podem ser os resultados no trading. Neste caso, a variação do saldo pode ser a seguinte:

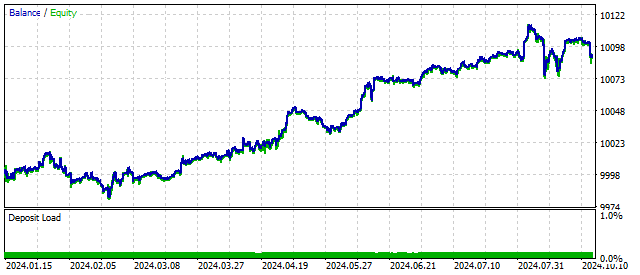
Aumentar a ordem da diferença superior torna o modelo mais flexível. O oscilador generalizado responderá apenas a certas combinações de preços. Em outras palavras, ele busca por determinados padrões. No entanto, é preciso lembrar que, quanto maior a ordem do oscilador, mais raros serão os padrões que ele identifica.

Outra característica desse algoritmo é que os coeficientes podem variar dentro de intervalos muito amplos. Mesmo estimar esses limites pode ser difícil. Por outro lado, ajustar os coeficientes permite configurar o algoritmo para que ele responda a padrões não cíclicos no comportamento do preço.

Osciladores não lineares

Modelos lineares são simples e intuitivos. No entanto, o comportamento dos preços no mercado pode ser não linear. Por exemplo, uma mudança brusca de preço é mais bem descrita com modelos não lineares. A principal vantagem dos modelos não lineares é que eles conseguem descrever comportamentos muito complexos de séries temporais. Quando você ouve os termos “caótico, estocástico”, isso se refere a modelos não lineares.

Um dos modelos mais simples é o oscilador de assinatura. Sua fórmula é bastante parecida com a do oscilador harmônico. E, como função não linear, é usada a função sinal. A fórmula do algoritmo de negociação fica assim:

Onde, sign – é a função sinal.

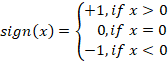
Graças a essa função, o oscilador pode operar em 5 modos diferentes. A mudança de modo depende do movimento do preço. A não linearidade do oscilador nos dá esperança de que o trading com ele seja mais flexível e estável. A variação do saldo ao usar esse algoritmo pode ser assim:

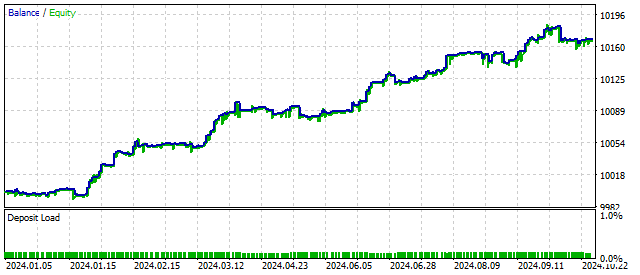
Agora, vamos analisar o oscilador com não linearidade quadrática. Sua fórmula é muito simples:

Para aplicar essa fórmula na prática, precisamos ajustá-la um pouco.

Primeiramente, vamos precisar de um nível médio em torno do qual o preço oscila. Lembrando que, em vez dos preços reais, podemos usar seu valor suavizado (SMA). Assim, o nível médio será igual à média das médias móveis.

Calcular a média das médias — à primeira vista pode parecer intimidador. Em 1910, Andrey Markov publicou o livro “Cálculo de Diferenças Finitas”. Nessa obra, ele demonstrou que a média de um grande número de SMA é equivalente à aplicação de uma LWMA a todos os valores da série temporal. Mais uma vez, as diferenças finitas simplificam os cálculos.

A fórmula do algoritmo de negociação do oscilador quadrático será a seguinte:

A não linearidade quadrática permite alternar os modos de operação do oscilador de maneira mais suave, mas com maior amplitude. E isso pode melhorar os resultados no trading.

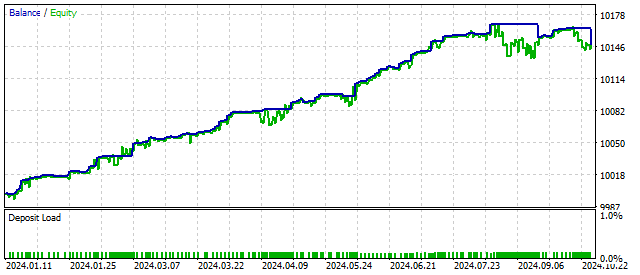
Outro exemplo de não linearidade quadrática é o oscilador de Van der Pol. Esse oscilador foi um dos primeiros exemplos de modelagem do caos determinístico. Graças às suas propriedades, a equação de Van der Pol encontrou aplicação não apenas na teoria das oscilações, mas também em outras áreas — física, biologia e mais.

O próprio oscilador de Van der Pol é uma modificação do oscilador com não linearidade quadrática, e a fórmula do seu algoritmo de negociação é assim:

À primeira vista, esse oscilador parece instável. Na prática, seus parâmetros podem variar em uma faixa bastante ampla, sem afetar os resultados da negociação.

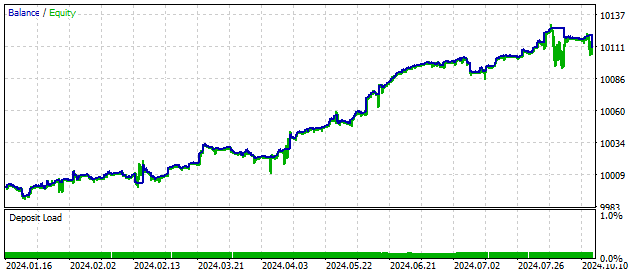
Em 1918, Georg Duffing estudou a equação do oscilador com não linearidade cúbica. Esse oscilador também pode modelar comportamentos caóticos do preço. Mas ele tem outra característica — dependendo das condições externas e de seus próprios parâmetros, esse oscilador pode existir em dois estados estáveis.

A equação do algoritmo de negociação do oscilador de Duffing é uma soma de um oscilador harmônico de 3ª ordem com um binômio cúbico:

O desempenho desse oscilador é comparável ao de outros modelos não lineares.

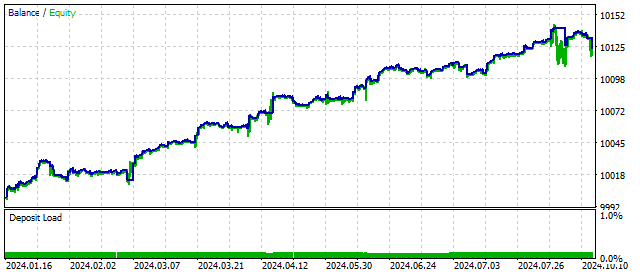
Na verdade, é possível criar um número enorme de modelos não lineares. Qualquer função não linear pode se tornar um gerador de caos. A não linearidade dos três osciladores anteriores foi baseada em certos princípios e conceitos da física. A econofísica é uma área útil, mas não é necessário segui-la o tempo todo e em todas as situações.

Por exemplo, vou adicionar ao algoritmo de negociação uma não linearidade baseada em uma função logarítmica:

Você pode me perguntar: de onde surgiram esses logaritmos, com base em que ideias eu os incluí? Minha resposta será bem simples — porque eu quis.

Mas, se eu tiver um tempo para pensar melhor, a resposta será um pouco diferente. Qual é a diferença entre dois preços consecutivos? Digamos, 100 pontos. E qual a diferença entre os logaritmos desses preços? Haverá algo além de zeros? Aqui está minha nova resposta: do lado esquerdo temos um oscilador comum, do lado direito — um filtro que pode influenciar a abertura de posições. E esse filtro só se manifestará durante movimentos fortes de preço. Vamos verificar seu funcionamento.

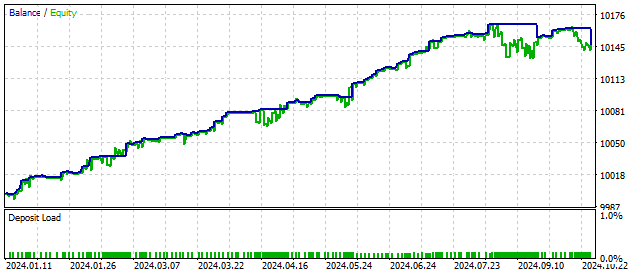
O resultado é parecido com o do oscilador com não linearidade quadrática. O filtro funciona. Mas é importante lembrar que todas as ideias, por mais geniais que sejam, precisam ser testadas no testador antes de serem aplicadas na prática.

Forças externas

Até agora, analisamos osciladores autônomos. Imagine um pêndulo. Ele balança uniformemente de um lado para o outro. Seus ciclos se repetem continuamente. Por que esse pêndulo balança, por que ele se move exatamente assim são perguntas às quais não podemos responder. Esse é um exemplo de oscilador autônomo.

Agora, empurre esse pêndulo. Primeiro para um lado, depois para o outro. Os ciclos do pêndulo começam a mudar, porque sua frequência e amplitude instantâneas se alteram. Sob a ação de forças externas, o pêndulo deixa de ser autônomo.

Vamos tentar aplicar esse mesmo conceito a um oscilador harmônico. Sua fórmula será modificada e ficará assim:

Onde F[n] — alguma força externa. Que força é essa, como ela atua, em que direção — nada sei sobre isso. Eu apenas suponho que ela exista. E agora surge a pergunta: até que ponto essa complexificação do modelo é justificável? Vamos testar.

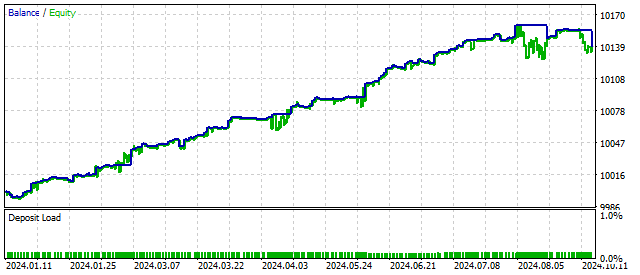
Este resultado foi obtido partindo da suposição de que essa força externa está relacionada aos valores dos preços da seguinte maneira:

Fiz essa suposição por um único motivo e é que a matéria inteira foi sobre diferenças finitas, então aqui também usei coeficientes da 2ª diferença. Mas você pode fazer suas próprias suposições. Por exemplo, a força externa pode estar relacionada à diferença entre os preços de fechamento e abertura, aos volumes de ticks, etc. Você também pode incluir um elemento de não linearidade:

No fim das contas, essa força desconhecida pode depender de vários componentes. Generalize tudo o que puder, enquanto for possível. Qualquer suposição sua pode impactar positivamente os resultados no trading.

Conclusão

Como você pôde ver, o uso de modelos cíclicos no trading é bastante justificável. A principal vantagem desses modelos é que eles oferecem centenas de combinações de parâmetros que entregam resultados estáveis ao longo do tempo. O trader precisa selecionar algumas dezenas de variantes que não sejam correlacionadas entre si.

Neste artigo, abordei apenas alguns dos osciladores mais populares. Ainda há muitas outras soluções que podem ser usadas para construir modelos cíclicos (e não apenas isso).

Os testes dos EAs foram realizados por mim sob as seguintes condições: EURUSD, H1, 01/01/2024 – 30/10/2024

Durante a redação do artigo, utilizei os seguintes programas:

Nome	Tipo	Descrição
Harmonic Oscillator	Expert Advisor	iPeriod – período da média móvel Type – tipo da média móvel R – coeficiente do oscilador, valor permitido: 1 ... 399
Damped Harmonic Oscillator	Expert Advisor	S – coeficiente de amortecimento, valor permitido: -1000 ... +1000
scr Elliott wave	script	A1, A2 – amplitudes das senoides N1, N2 – períodos das senoides Width – espessura da linha Pause – atraso na exibição do resultado Screenshot – se for true, cria e salva uma imagem na pasta Files
Elliott wave	Expert Advisor	R, S – coeficientes do oscilador, valor permitido: 0 ... 1000
Generalized Harmonic Oscillator	Expert Advisor	valor permitido dos coeficientes: -1000 ... +1000
Sign Oscillator	Expert Advisor
Quadratic Oscillator	Expert Advisor
Van der Pol Oscillator	Expert Advisor
Duffing Oscillator	Expert Advisor
Log Oscillator	Expert Advisor
Non-Autonomous Oscillator	Expert Advisor