Ciclos e Forex

Introdução

A ciclicidade é um dos principais fatores em nosso mundo. Os ciclos ajudam a organizar a vida das pessoas. Ao conhecer a ordem cíclica, podemos prever o futuro. Por exemplo, afirmo com confiança que o ano de 2025 começará em 1º de janeiro. Dentro de alguns meses, saberemos quão precisa foi minha previsão.

Os ciclos no Forex podem estar relacionados a diferentes fatores, como notícias econômicas, horários do dia, dias da semana, meses do ano e estações. O estudo desses ciclos pode ajudar o trader a prever o comportamento futuro dos preços e a tomar decisões de negociação mais fundamentadas.

Os ciclos podem ser encontrados até mesmo onde não deveriam existir. Até mesmo o interesse pelos ciclos e ondas no Forex tem um caráter cíclico:

• artigo "Implementação da análise automática das ondas de Elliott" — 2011
• artigo "Ondas de Wolfe" — 2017
• artigo "Sazonalidade no mercado Forex e suas possibilidades de uso" —  2023
• artigo "Filtro de sazonalidade e períodos temporais em modelos de deep learning com ONNX e Python no EA" — 2024.

Como se pode ver, os artigos foram publicados com uma periodicidade de seis anos. Somente o último artigo quebrou esse ciclo. Mas será que há alguma outra explicação para essa anomalia?

Vamos tentar encontrar respostas para duas perguntas. Existem ciclos no movimento dos preços? E, caso existam, como podemos utilizá-los no trading?

Busca por ciclos

No trading, os ciclos podem estar relacionados a tendências ou padrões recorrentes. Por exemplo, o preço pode oscilar dentro de um canal específico. E esse comportamento pode persistir por um longo período.

Para extrair a componente cíclica de uma série temporal, podem ser utilizados análise espectral, polinômios trigonométricos, periodogramas, função de autocorrelação e algoritmos de detecção de ciclos.

Além disso, um método simples para identificar ciclos é a média móvel simples (SMA). Esse método é o mais direto e intuitivo. Suponha que temos uma série temporal que representa um ciclo com período N. Se aplicarmos uma SMA com o mesmo período, obteremos um nível médio em torno do qual as oscilações ocorrem. O uso de SMA com outros períodos permite identificar processos oscilatórios diferentes do original. No entanto, apesar dessas diferenças, é possível recuperar os parâmetros do ciclo original por meio dessas médias móveis.

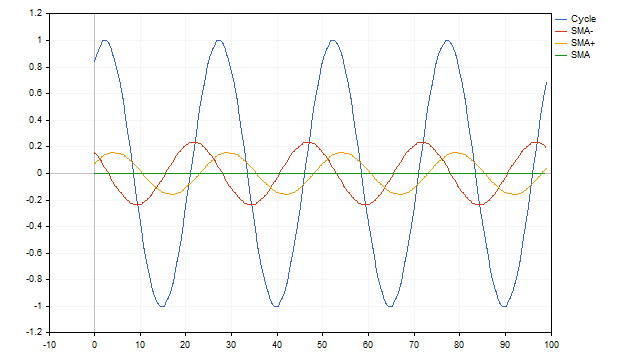
Algumas séries temporais podem representar a soma de ciclos com diferentes períodos. Nesse caso, as médias móveis também lidam muito bem com a situação. O algoritmo é bastante simples. Primeiro, subtraímos do conjunto de dados original os valores da média móvel com o maior período. Em seguida, subtraímos os valores da próxima média móvel dos resíduos obtidos e repetimos o processo até restarem apenas zeros. Precisamos de mais SMA.

Da mesma forma, as médias móveis simples conseguem lidar com um modelo de série temporal composto por ciclo + tendência. Aqui, a SMA atua como um detector simultâneo do ciclo e da tendência.

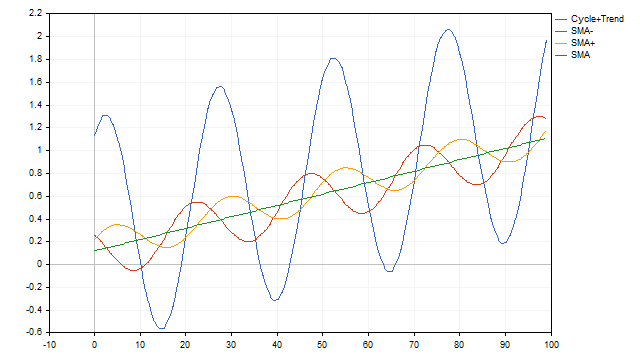
Até agora, aplicamos a média móvel simples a uma série temporal determinística, em que as equações do ciclo e da tendência eram rigidamente definidas e não mudavam ao longo do tempo. Agora, vamos adicionar aleatoriedade à série temporal original e observar como a SMA se comporta nessa situação. Tomaremos a amplitude do ciclo como referência, estabelecendo-a em 100%. Suponha que essa amplitude possa variar aleatoriamente dentro de um intervalo de 10% para mais ou para menos. A velocidade da tendência pode variar entre 0% e 1%. Além disso, adicionaremos um ruído branco de 10%. A SMA consegue lidar bem com essa configuração.

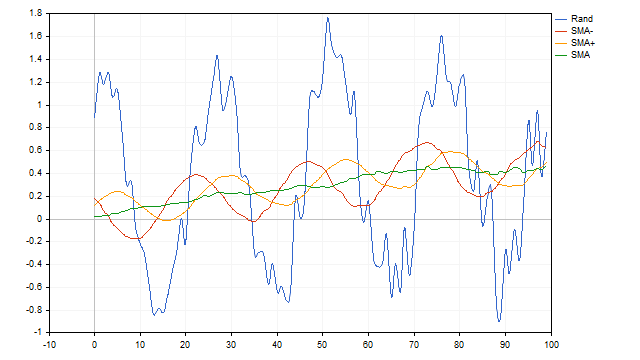
Parece que encontramos o indicador dos nossos sonhos. Infelizmente, as desvantagens da SMA podem superar as vantagens. A média móvel simples não consegue filtrar ciclos compostos apenas por meias-ondas positivas ou negativas. Além disso, esse indicador tem baixa capacidade de resolução. Em termos simples, ele não conseguirá distinguir um sinal útil se o ruído ultrapassar um limite determinado.

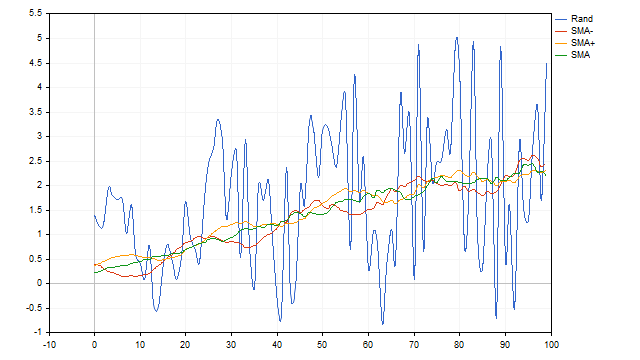
Outro pequeno problema é que, antes de aplicar a SMA, seria ideal saber previamente qual ciclo queremos destacar. Isso nos leva a duas questões fundamentais:

• existe um ciclo na série temporal que estamos analisando?
• se existe um ciclo, como podemos determinar seus parâmetros?

Para responder a essas perguntas, podemos utilizar a técnica de mapeamento de pontos.

Olhe para esse gráfico. Você consegue dizer o que ele representa?

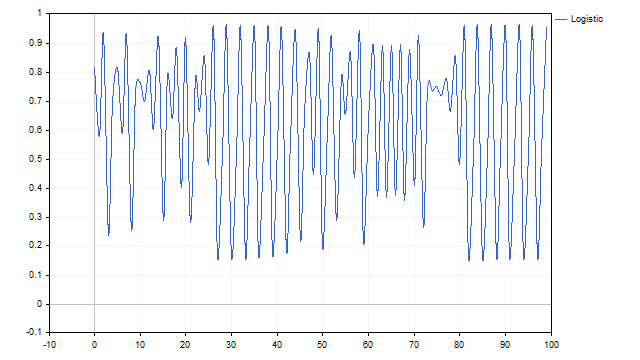
Talvez seja um gráfico da soma de vários ciclos. Ou pode ser parte do Grande Plano dos Daleks.

Temos uma série temporal unidimensional com valores Z[i]. A partir dela, construirei um gráfico bidimensional, no qual as coordenadas de cada ponto seguirão a seguinte regra de indexação (como em séries temporais):

X[i] = Z[i];

Y[i] = Z[i-1].

O objetivo dessa transformação é visualizar a relação entre dois valores consecutivos da série temporal original. Por exemplo, esse gráfico aparentemente aleatório gera a seguinte representação.

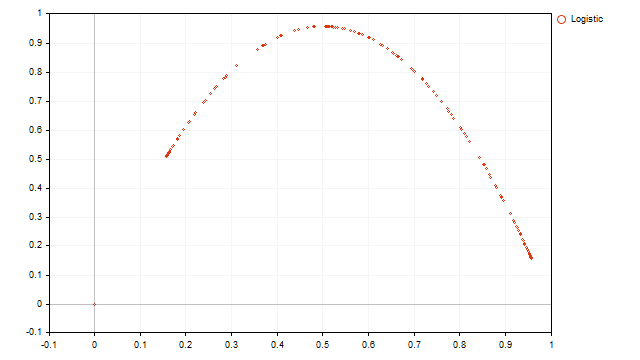
Observamos uma parábola comum. Conhecendo as propriedades da parábola, podemos formular a equação da série temporal original.

Para encontrar os coeficientes dessa equação, podemos usar o método dos mínimos quadrados. Como resultado, obteremos um mapeamento logístico, que foi exatamente o que gerou os valores da série temporal original.

Embora o método de mapeamento de pontos possa ser aplicado a qualquer série temporal, nem sempre ele fornece uma visão clara e bem definida do comportamento dos dados.

Por exemplo, vamos analisar um gerador de números pseudoaleatórios. Seu gráfico se parece com o seguinte:

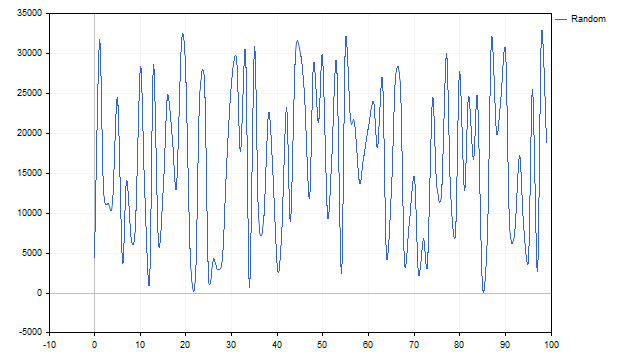
Podemos perceber claramente a soma de vários ciclos. Agora, vamos esclarecer tudo. Construímos o mapeamento de pontos a partir dos valores obtidos.

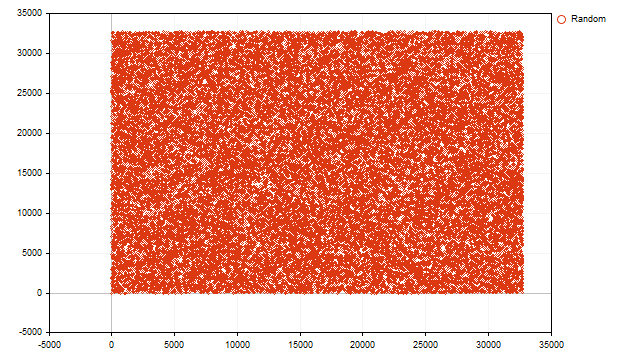
Os pontos preenchem todo o plano de maneira uniforme. A partir disso, podemos concluir que o valor atual do gerador de números pseudoaleatórios não depende do valor anterior e que todas as coincidências são puramente aleatórias.

Já a representação gráfica de um processo cíclico assume uma forma cíclica.

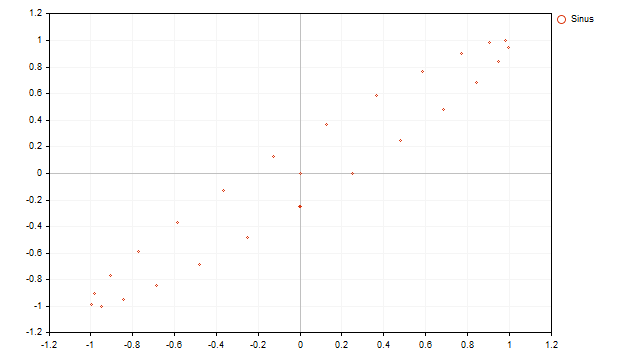
Agora, veremos como é o mapeamento de pontos dos preços reais:

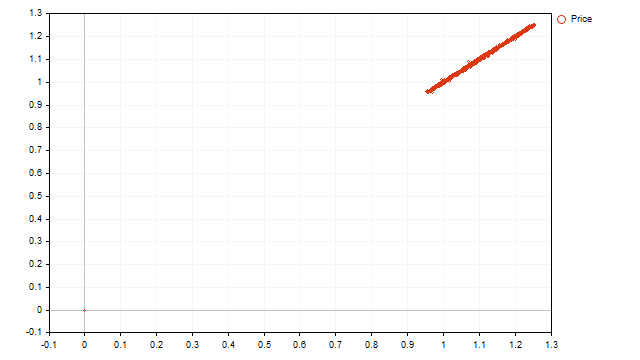
Vemos uma tendência linear crescente, mas não há ciclos aparentes. No entanto, ainda não é hora de desespero. A partir dessa imagem, podemos tirar as seguintes conclusões:

• a tendência é o principal fator que determina o movimento dos preços;
• a força da tendência é suficientemente grande para mascarar processos cíclicos.

A conclusão é óbvia — precisamos de mais métodos para identificar ciclos.

Ciclos e aleatoriedade

Em 1927, Evgeny Slutsky publicou o artigo "A soma de causas aleatórias como fonte de processos cíclicos". Nesse trabalho, ele demonstrou brilhantemente que processos cíclicos e ondulatórios podem surgir como resultado da interação (por exemplo, soma) de variáveis aleatórias.

Vamos testar essa teoria em séries temporais financeiras. Como variável aleatória inicial, tomaremos os preços de diferentes símbolos. Procederemos da seguinte maneira: para o par de moedas atual, utilizamos o preço da barra mais recente, enquanto para todos os outros símbolos, usamos o preço da barra anterior. Assim, a fórmula da variável aleatória será aproximadamente a seguinte:

Dessa forma, a variável aleatória resultante dependerá de um grande número de valores anteriores dos preços de diferentes símbolos. Para reforçar essa dependência, aplicamos uma média móvel a essas variáveis.

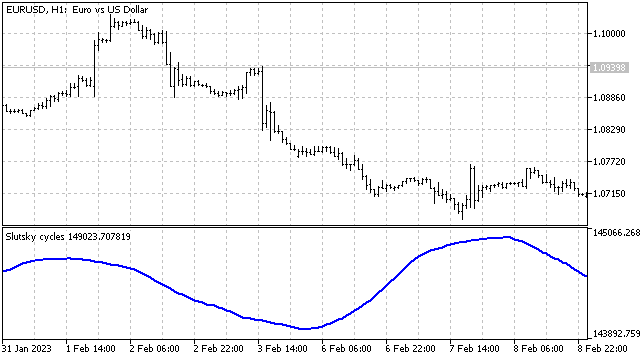
Os processos ondulatórios estão presentes. No entanto, gostaríamos de saber se esses processos são realmente cíclicos? Caso sejam, quais são seus parâmetros?

Para responder a essas perguntas, podemos usar as diferenças finitas. Lembre-se de que a primeira diferença é obtida subtraindo o valor atual da série temporal do valor anterior:

A segunda diferença finita é calculada subtraindo as primeiras diferenças.

Essa diferença nos interessa porque, sob certas condições, pode indicar a presença de um ciclo no processo. Suponha que estamos lidando com um ciclo qualquer. Seja a o valor inicial do ângulo e s o passo de sua variação. Assim, os três últimos pontos da série temporal podem ser definidos da seguinte forma:

Usando identidades trigonométricas, encontramos a segunda diferença desses valores:

Essa é a fórmula de um oscilador harmônico discreto. Vale destacar que aqui o termo "oscilador" se refere a um sistema oscilatório, e não a um indicador técnico.

Não é possível aplicar essa fórmula diretamente aos preços. No lado esquerdo da equação, podemos utilizar quaisquer valores reais como estão, mas no lado direito, precisaremos fazer algumas modificações.

Para destacar as oscilações, primeiro devemos encontrar o nível em torno do qual elas ocorrem. Chamaremos esse nível de MA. Assim, a fórmula assume a seguinte forma:

No lado esquerdo da equação, MA se cancela, restando apenas os termos no lado direito.

Esse nível pode ser calculado de diversas maneiras. Por exemplo, podemos eliminar a tendência da série temporal original ou calcular a média de todos os seus valores. No entanto, ambos os métodos apresentam uma desvantagem comum: eles dependem fortemente dos dados históricos e não respondem adequadamente às mudanças recentes do mercado. Para contornar esse problema, utilizarei um algoritmo de cálculo de indicadores adaptativos. Com isso, o nível MA se ajustará à situação atual do mercado. O resultado será um indicador que permite acompanhar o nível em torno do qual ocorrem oscilações da média móvel. No exemplo, usei a SMA, mas, na prática, qualquer método de suavização de preços pode ser aplicado.

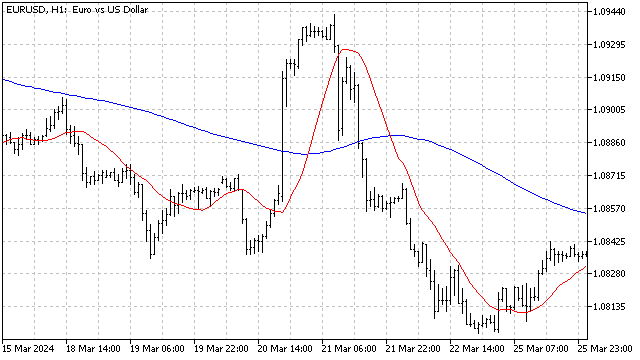
Infelizmente, o oscilador harmônico possui algumas limitações que devem ser consideradas. Ele funciona bem com sinais senoidais. No entanto, até mesmo uma combinação de senóides pode causar dificuldades, pois o oscilador pode não ser capaz de identificar o ciclo mais relevante.

Muitas dessas limitações podem ser superadas utilizando a segunda diferença. Visualmente, sua forma permanece a mesma. No entanto, podemos alterar a distância entre os termos dessa diferença. Por exemplo, suponha que estou analisando um gráfico no time frame H1 e acredito que o movimento dos preços pode apresentar um ciclo diário (com período igual a 24). Nesse caso, utilizarei a segunda diferença da seguinte forma:

Se houver um ou mais ciclos no movimento dos preços, a segunda diferença será igual a zero. A forma exata desses ciclos não é importante, e sim a sua repetição relativamente consistente. Além disso, a segunda diferença é eficaz para identificar tendências. A única exigência é que a duração dessa tendência seja pelo menos o dobro do período do ciclo.

Como podemos aplicar esse método na prática? Suponha que o movimento do preço contenha um ciclo estável com algumas variações aleatórias. Nesse caso, se calcularmos a soma das últimas diferenças (por exemplo, das 24 mais recentes), os erros aleatórios tenderão a se compensar. Isso significa que, se o ciclo e/ou a tendência forem estáveis, a soma das diferenças oscilará em torno de zero. No entanto, quando ocorrem perturbações no mercado — como o início de uma nova tendência, o surgimento de um novo ciclo ou o término de um ciclo antigo —, a soma das diferenças começará a se desviar significativamente. Além disso, esses desvios podem assumir um comportamento cíclico. Isso nos leva a uma conclusão interessante: as rupturas nos ciclos podem, por sua vez, ter uma natureza cíclica. Um verdadeiro mercado de Schrödinger.

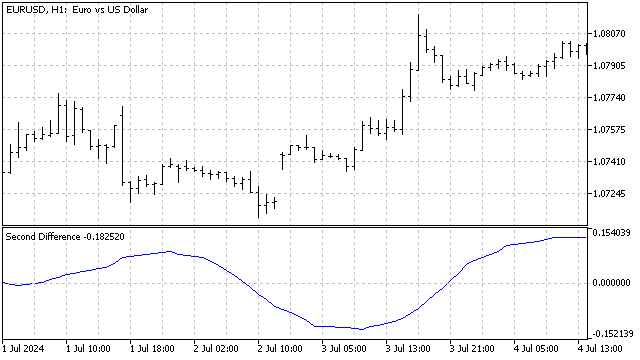
No geral, o uso de diferenças finitas é extremamente útil na análise de mercado. Elas podem ser utilizadas diretamente, combinadas entre si ou mescladas com outros indicadores. Dessa maneira, é possível desenvolver novas ferramentas interessantes para o estudo do movimento dos preços.

Outras diferenças

Na análise de séries temporais, não é obrigatório usar apenas as diferenças clássicas. Podemos construir diferenças personalizadas, adaptadas às nossas necessidades. Para isso, podemos utilizar os princípios empregados na construção de wavelets.. 

Vamos começar com um número que representará a onda inicial. A opção mais simples e óbvia é usar o número 1. Adicionamos um zero à direita e outro à esquerda, resultando na sequência "0, 1, 0". A partir do segundo número, subtraímos o valor à esquerda do valor à direita.

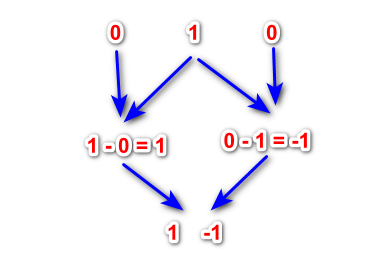
Isso gera um wavelet de primeiro nível. Em seguida, adicionamos zeros à esquerda e à direita dos coeficientes obtidos e repetimos a operação. Esse processo pode ser repetido até que se alcance o wavelet desejado. Essas diferenças possuem algumas propriedades dos wavelets clássicos e podem ser aplicadas na análise de séries temporais financeiras.

Como onda inicial, podemos escolher qualquer grupo de números, como 1, 2, 1 ou 1, 1, 1. No entanto, os coeficientes da onda inicial não devem ser simétricos em relação ao centro da onda. Não há problema se a onda inicial for representada por uma sequência como 3, 2, 1. Além disso, números negativos também podem ser utilizados.

Como todas essas diferenças resultam em coeficientes cuja soma é igual a zero, elas já constituem osciladores prontos para uso.

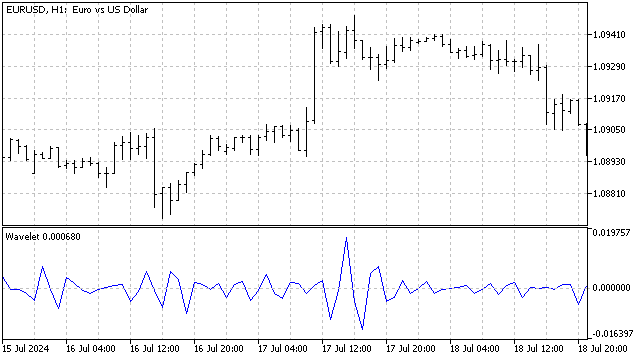
A principal desvantagem desse tipo de diferença é que não temos como prever com precisão qual será o resultado ao aplicar uma determinada onda inicial.

A principal vantagem dessas diferenças é que, com elas, podemos reconstruir o sinal original. Por exemplo, se conhecemos os valores da primeira e da segunda diferença, podemos reconstruir a série temporal passo a passo. Ao subtrairmos a primeira diferença do valor atual da série, obtemos o valor anterior. Com esses dois valores e a segunda diferença, é possível calcular o próximo valor da série, e assim por diante.

Essa propriedade permite identificar segmentos semelhantes no histórico. Se as diferenças em diferentes níveis forem aproximadamente iguais, significa que estamos diante de movimentos de preço semelhantes.

Conclusão

É importante lembrar que o mercado raramente segue ciclos previsíveis. Mesmo quando um ciclo é identificado, há sempre o risco de a estrutura do mercado mudar. As ondas existem, mas seu comportamento exige um estudo mais aprofundado. De qualquer forma, compreender a ciclicidade do mercado pode ser uma ferramenta útil para qualquer trader. Ao analisar ciclos, podemos descobrir novas abordagens e estratégias de análise técnica.

Os seguintes programas estão anexados ao artigo:

nome	tipo	características
Dot Mapping	script	diferentes tipos de mapeamento Logistic - logístico; Random - gerador de números pseudoaleatórios; Integrated - série integrada; Price - preços reais; Linear - tendência linear; Sinus - ciclo; SinusTrend - ciclo + tendência; Sinus3 - soma de três ciclos. Após a execução do script, as imagens são salvas na pasta Files
Slutsky cycles	indicador	Processa todos os símbolos disponíveis no Market Watch
Slutsky MA	indicador	iPeriod - período do indicador; Smoothing - parâmetro de suavização
Second Difference	indicador	Sampling - frequência de amostragem
scr Wavelet	script	exibe coeficientes de wavelet InpWave - lista de coeficientes da onda inicial. Os coeficientes são números inteiros separados por vírgula; Lvl - nível desejado do wavelet
Wavelet	indicador	usa wavelets na forma de um oscilador InpWave - lista de coeficientes da onda inicial. Os coeficientes são números inteiros separados por vírgula; Lvl - nível desejado do wavelet