Métodos de William Gann (Parte III): A astrologia funciona?

Introdução

No mercado financeiro, há uma busca constante por novos métodos de análise e previsão. Até mesmo as ideias mais improváveis são exploradas. Um dos enfoques mais incomuns e absolutamente únicos é o uso da astrologia no trading, popularizado pelo renomado trader William Gann.

Já abordamos as ferramentas de Gann em artigos anteriores. Aqui estão a primeira e segunda partes. Agora, vamos nos concentrar em investigar a influência da posição dos planetas e estrelas nos mercados globais.

Combinaremos tecnologia de ponta com conhecimentos antigos, utilizando a linguagem de programação Python e a plataforma MetaTrader 5 para explorar a relação entre fenômenos astronômicos e os movimentos do par euro-dólar. Também abordaremos a teoria da astrologia financeira e nos aventuraremos na parte prática do desenvolvimento de um sistema de previsão.

Analisaremos o processo de coleta e sincronização de dados astronômicos e financeiros, construiremos uma matriz de correlação e visualizaremos os resultados. 

Base teórica da astrologia nas finanças

Sabe, eu já me interesso por esse assunto há muito tempo e, hoje, quero compartilhar minhas reflexões sobre o impacto da astrologia nos mercados financeiros. É um campo verdadeiramente fascinante, embora bastante controverso.

A ideia central da astrologia financeira, pelo que entendo, é que os movimentos dos corpos celestes estão, de alguma forma, ligados aos ciclos do mercado. Essa teoria tem uma longa e rica história, ganhando especial notoriedade graças a William Gann, um dos traders mais influentes do século passado.

Refleti bastante sobre os princípios fundamentais dessa abordagem. Por exemplo, a ideia da ciclicidade, segundo a qual os movimentos das estrelas e planetas, assim como os mercados, possuem uma natureza cíclica. Ou os aspectos planetários, segundo os quais determinadas configurações planetárias exercem forte influência nos mercados. E quanto aos signos do zodíaco? izem que a passagem dos planetas por diferentes constelações zodiacais também afeta o mercado.

Vale a pena mencionar separadamente os ciclos lunares e a atividade solar. Já vi análises sugerindo que as fases da Lua estão relacionadas a oscilações de curto prazo no mercado, enquanto as erupções solares influenciam tendências de longo prazo. Hipóteses interessantes, não acha?

William Gann, aliás, foi um verdadeiro pioneiro nesse campo. Ele desenvolveu uma série de ferramentas, como seu famoso Quadrado de 9, baseadas em astronomia, geometria e sequências numéricas. Suas teorias ainda geram debates acalorados.

É claro que não podemos deixar de mencionar que a comunidade científica, em geral, é cética em relação à astrologia. Em muitos países, ela é oficialmente reconhecida como uma pseudociência. E, para ser sincero, ainda não existem evidências robustas da eficácia dos métodos astrológicos no campo das finanças. Muitas vezes, as correlações observadas são simplesmente resultado de vieses cognitivos.

Mas sabe de uma coisa? Apesar disso, há muitos traders que defendem fervorosamente as ideias da astrologia financeira. Isso nos faz pensar, não é mesmo?

É por isso que decidi conduzir minha própria pesquisa. Quero tentar avaliar objetivamente a influência da astrologia nos mercados financeiros, utilizando métodos estatísticos e big data. Quem sabe, talvez descubramos algo interessante? De qualquer forma, será uma jornada fascinante por um mundo onde as estrelas e os gráficos do mercado se encontram.

Visão geral das bibliotecas Python utilizadas

Vou precisar de um verdadeiro arsenal de bibliotecas Python. 

Para começar, escolhi o pacote Skyfield para obter dados astronômicos. Depois de avaliar diversas ferramentas, o Skyfield me impressionou pela precisão. Com ele, consigo coletar informações sobre a posição dos corpos celestes e as fases da Lua com altíssima precisão nos dígitos decimais, exatamente o que preciso para os meus conjuntos de dados.

Quanto aos dados do mercado, optei pela biblioteca oficial do MetaTrader 5 para Python. Ela permite carregar dados históricos de pares de moedas e até mesmo abrir operações, se necessário.

O Pandas será nosso fiel companheiro na manipulação dos dados. Já a utilizei muitas vezes antes e ela é simplesmente indispensável para trabalhar com séries temporais. Usá-la-ei para pré-processar e sincronizar todos os dados coletados.

Para análise estatística, optei pela biblioteca SciPy. Seu conjunto de funcionalidades é impressionante, especialmente as ferramentas para análise de correlação e regressão. Espero que elas me ajudem a identificar padrões interessantes.

Para visualizar os resultados, escolhi velhos amigos: Matplotlib e Seaborn. Adoro essas bibliotecas pela flexibilidade que oferecem na criação de gráficos. Tenho certeza de que elas nos ajudarão a apresentar todas as descobertas de maneira clara.

O kit já está montado. É como montar um computador potente com componentes de primeira linha. Agora temos tudo o que precisamos para conduzir uma investigação completa sobre o impacto dos fatores astrológicos nos mercados financeiros. Mal posso esperar para mergulhar nos dados e começar a testar minhas hipóteses!

Coleta de dados astronômicos

import pandas as pd
import numpy as np
from skyfield.api import load, wgs84, utc
from skyfield.data import mpc
from datetime import datetime, timedelta
import requests

# Loading planet ephemerides
planets = load('de421.bsp')
earth = planets['earth']
ts = load.timescale()

def get_planet_positions(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    planet_positions = {}
    planet_ids = {
        'mercury': 'MERCURY BARYCENTER',
        'venus': 'VENUS BARYCENTER',
        'mars': 'MARS BARYCENTER',
        'jupiter': 'JUPITER BARYCENTER',
        'saturn': 'SATURN BARYCENTER',
        'uranus': 'URANUS BARYCENTER',
        'neptune': 'NEPTUNE BARYCENTER'
    }
    for planet, planet_id in planet_ids.items():
        planet_obj = planets[planet_id]
        astrometric = earth.at(t).observe(planet_obj)
        ra, dec, _ = astrometric.radec()
        planet_positions[planet] = {'ra': ra.hours, 'dec': dec.degrees}
    return planet_positions

def get_moon_phase(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    eph = load('de421.bsp')
    moon, sun, earth = eph['moon'], eph['sun'], eph['earth']
    
    e = earth.at(t)
    _, m, _ = e.observe(moon).apparent().ecliptic_latlon()
    _, s, _ = e.observe(sun).apparent().ecliptic_latlon()
    
    phase = (m.degrees - s.degrees) % 360
    return phase

def get_solar_activity(date):
    # Get solar activity data from NOAA API
    url = f"https://services.swpc.noaa.gov/json/solar-cycle/observed-solar-cycle-indices.json"
    response = requests.get(url)
    data = response.json()
    
    # Convert date to 'YYYY-MM' format
    target_date = date.strftime("%Y-%m")
    
    # Find the closest date in the data
    closest_data = min(data, key=lambda x: abs(datetime.strptime(x['time-tag'], "%Y-%m") - datetime.strptime(target_date, "%Y-%m")))
    
    return {
        'sunspot_number': closest_data.get('ssn', None),
        'f10.7_flux': closest_data.get('f10.7', None)
    }

def calculate_aspects(positions):
    aspects = {}
    planets = list(positions.keys())
    for i in range(len(planets)):
        for j in range(i+1, len(planets)):
            planet1 = planets[i]
            planet2 = planets[j]
            ra1 = positions[planet1]['ra']
            ra2 = positions[planet2]['ra']
            angle = abs(ra1 - ra2) % 24
            angle = min(angle, 24 - angle) * 15  # Convert to degrees
            
            if abs(angle - 0) <= 10 or abs(angle - 180) <= 10:
                aspects[f"{planet1}_{planet2}"] = "conjunction" if abs(angle - 0) <= 10 else "opposition"
            elif abs(angle - 90) <= 10:
                aspects[f"{planet1}_{planet2}"] = "square"
            elif abs(angle - 120) <= 10:
                aspects[f"{planet1}_{planet2}"] = "trine"
    
    return aspects

start_date = datetime(2024, 4, 1, tzinfo=utc)
end_date = datetime(2024, 5, 31, tzinfo=utc)
current_date = start_date
astronomical_data = []

while current_date <= end_date:
    planet_positions = get_planet_positions(current_date)
    moon_phase = get_moon_phase(current_date)
    try:
        solar_activity = get_solar_activity(current_date)
    except Exception as e:
        print(f"Error getting solar activity for {current_date}: {e}")
        solar_activity = {'sunspot_number': None, 'f10.7_flux': None}
    aspects = calculate_aspects(planet_positions)
    
    data = {
        'date': current_date,
        'moon_phase': moon_phase,
        'sunspot_number': solar_activity.get('sunspot_number'),
        'f10.7_flux': solar_activity.get('f10.7_flux'),
        **planet_positions,
        **aspects
    }
    astronomical_data.append(data)
    
    current_date += timedelta(days=1)
    print(f"Processed: {current_date}")

# Convert data to DataFrame
df = pd.DataFrame(astronomical_data)

# Save data to CSV file
df.to_csv('astronomical_data_2018_2024.csv', index=False)
print("Data saved to astronomical_data_2018_2024.csv")

Este código em Python realiza a tarefa de coleta de dados astronômicos que utilizaremos posteriormente para a análise do mercado.

O código cobre o período de 1º de janeiro de 2018 a 31 de maio de 2024 e coleta uma série de informações, incluindo:

• Posições dos planetas – Vênus, Mercúrio, Marte, Júpiter, Saturno, Urano, Netuno
• Fases da Lua
• Atividade solar
• Aspectos planetários (quando os planetas se alinham de uma maneira específica em relação uns aos outros)

O script inclui a importação de bibliotecas, um loop principal e o salvamento dos dados em formato Excel. Ele utiliza a já mencionada biblioteca Skyfield para calcular as posições planetárias, Pandas para manipulação dos dados e a biblioteca Requests para obter informações sobre a atividade solar.

As principais funções incluem: get_planet_positions(), que obtém as posições dos planetas (ascensão reta e declinação); get_moon_phase(), que determina a fase atual da Lua; get_solar_activity(), que faz a requisição direta dos dados de atividade solar via API da NOAA; calculate_aspects(), que calcula os aspectos planetários – as relações entre as posições dos planetas.

Dentro do laço, percorremos cada dia do período analisado e coletamos todas essas informações. No final, salvamos tudo em um único arquivo Excel para uso futuro. 

Obtenção de dados financeiros via MetaTrader 5

Para obter os dados financeiros, utilizaremos a biblioteca MetaTrader 5 para Python. Ela permite carregar dados financeiros diretamente da corretora e obter séries temporais de preços para qualquer ativo. A seguir, apresentamos nosso código para carregar os dados históricos: 

import MetaTrader5 as mt5
import pandas as pd
from datetime import datetime

# Connect to MetaTrader5
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# Set query parameters
symbol = "EURUSD"
timeframe = mt5.TIMEFRAME_D1
start_date = datetime(2018, 1, 1)
end_date = datetime(2024, 12, 31)

# Request historical data
rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)

# Convert data to DataFrame
df = pd.DataFrame(rates)
df['time'] = pd.to_datetime(df['time'], unit='s')

# Save data to CSV file
df.to_csv(f'{symbol}_data.csv', index=False)

# Terminate the connection to MetaTrader5
mt5.shutdown()

O script se conecta ao terminal de negociação, recupera os dados do par euro-dólar no timeframe D1, cria um dataframe e os salva em um arquivo CSV. 

Sincronização de dados astronômicos e financeiros

Agora que temos os dados astronômicos e os dados do euro-dólar, precisamos sincronizá-los. Vamos combiná-los por data, de modo que nosso conjunto final contenha tanto informações financeiras quanto astronômicas.

import pandas as pd

# Load data
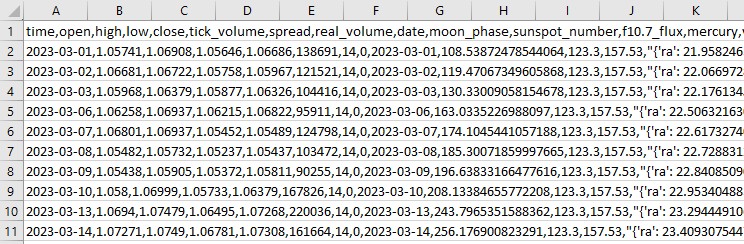
astro_data = pd.read_csv('astronomical_data_2018_2024.csv')
financial_data = pd.read_csv('EURUSD_data.csv')

# Convert date columns to datetime
astro_data['date'] = pd.to_datetime(astro_data['date'])
financial_data['time'] = pd.to_datetime(financial_data['time'])

# Merge data
merged_data = pd.merge(financial_data, astro_data, left_on='time', right_on='date', how='inner')

# Save merged data
merged_data.to_csv('merged_astro_financial_data.csv', index=False)

O script carrega todos os dados salvos, formata as colunas de data no formato datetime e mescla os datasets com base nas datas. Por fim, geramos um arquivo CSV contendo todas as informações necessárias para a análise futura.

Análise estatística das correlações

Agora vamos seguir em frente. Temos um conjunto de dados completo e chegou o momento de descobrir se há alguma correlação entre os dados astronômicos e os movimentos do mercado. Usaremos a função corr() da biblioteca Pandas para calcular as correlações e, em seguida, combinaremos os códigos anteriores em um único script.

Aqui está o código final:

import pandas as pd
import numpy as np
from skyfield.api import load, wgs84, utc
from skyfield.data import mpc
from datetime import datetime, timedelta
import requests
import MetaTrader5 as mt5
import seaborn as sns
import matplotlib.pyplot as plt

# Part 1: Collecting astronomical data

# Loading planetary ephemerides
planets = load('de421.bsp')
earth = planets['earth']
ts = load.timescale()

def get_planet_positions(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    planet_positions = {}
    planet_ids = {
        'mercury': 'MERCURY BARYCENTER',
        'venus': 'VENUS BARYCENTER',
        'mars': 'MARS BARYCENTER',
        'jupiter': 'JUPITER BARYCENTER',
        'saturn': 'SATURN BARYCENTER',
        'uranus': 'URANUS BARYCENTER',
        'neptune': 'NEPTUNE BARYCENTER'
    }
    for planet, planet_id in planet_ids.items():
        planet_obj = planets[planet_id]
        astrometric = earth.at(t).observe(planet_obj)
        ra, dec, _ = astrometric.radec()
        planet_positions[planet] = {'ra': ra.hours, 'dec': dec.degrees}
    return planet_positions

def get_moon_phase(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    eph = load('de421.bsp')
    moon, sun, earth = eph['moon'], eph['sun'], eph['earth']

    e = earth.at(t)
    _, m, _ = e.observe(moon).apparent().ecliptic_latlon()
    _, s, _ = e.observe(sun).apparent().ecliptic_latlon()

    phase = (m.degrees - s.degrees) % 360
    return phase

def get_solar_activity(date):
    url = f"https://services.swpc.noaa.gov/json/solar-cycle/observed-solar-cycle-indices.json"
    response = requests.get(url)
    data = response.json()

    target_date = date.strftime("%Y-%m")

    closest_data = min(data, key=lambda x: abs(datetime.strptime(x['time-tag'], "%Y-%m") - datetime.strptime(target_date, "%Y-%m")))

    return {
        'sunspot_number': closest_data.get('ssn', None),
        'f10.7_flux': closest_data.get('f10.7', None)
    }

def calculate_aspects(positions):
    aspects = {}
    planets = list(positions.keys())
    for i in range(len(planets)):
        for j in range(i+1, len(planets)):
            planet1 = planets[i]
            planet2 = planets[j]
            ra1 = positions[planet1]['ra']
            ra2 = positions[planet2]['ra']
            angle = abs(ra1 - ra2) % 24
            angle = min(angle, 24 - angle) * 15  # Convert to degrees

            if abs(angle - 0) <= 10 or abs(angle - 180) <= 10:
                aspects[f"{planet1}_{planet2}"] = "conjunction" if abs(angle - 0) <= 10 else "opposition"
            elif abs(angle - 90) <= 10:
                aspects[f"{planet1}_{planet2}"] = "square"
            elif abs(angle - 120) <= 10:
                aspects[f"{planet1}_{planet2}"] = "trine"

    return aspects

# Collecting astronomical data
start_date = datetime(2024, 3, 1, tzinfo=utc)
end_date = datetime(2024, 7, 30, tzinfo=utc)
current_date = start_date
astronomical_data = []

while current_date <= end_date:
    planet_positions = get_planet_positions(current_date)
    moon_phase = get_moon_phase(current_date)
    try:
        solar_activity = get_solar_activity(current_date)
    except Exception as e:
        print(f"Error getting solar activity for {current_date}: {e}")
        solar_activity = {'sunspot_number': None, 'f10.7_flux': None}
    aspects = calculate_aspects(planet_positions)

    data = {
        'date': current_date,
        'moon_phase': moon_phase,
        'sunspot_number': solar_activity.get('sunspot_number'),
        'f10.7_flux': solar_activity.get('f10.7_flux'),
        **planet_positions,
        **aspects
    }
    astronomical_data.append(data)

    current_date += timedelta(days=1)
    print(f"Processed: {current_date}")

# Convert data to DataFrame and save
astro_df = pd.DataFrame(astronomical_data)
astro_df.to_csv('astronomical_data_2018_2024.csv', index=False)
print("Astronomical data saved to astronomical_data_2018_2024.csv")

# Part 2: Retrieving financial data via MetaTrader5

# Initialize connection to MetaTrader5
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# Set request parameters
symbol = "EURUSD"
timeframe = mt5.TIMEFRAME_D1
start_date = datetime(2024, 3, 1)
end_date = datetime(2024, 7, 30)

# Request historical data
rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)

# Convert data to DataFrame
financial_df = pd.DataFrame(rates)
financial_df['time'] = pd.to_datetime(financial_df['time'], unit='s')

# Save financial data
financial_df.to_csv(f'{symbol}_data.csv', index=False)
print(f"Financial data saved to {symbol}_data.csv")

# Shutdown MetaTrader5 connection
mt5.shutdown()

# Part 3: Synchronizing astronomical and financial data

# Load data
astro_df = pd.read_csv('astronomical_data_2018_2024.csv')
financial_df = pd.read_csv('EURUSD_data.csv')

# Convert date columns to datetime
astro_df['date'] = pd.to_datetime(astro_df['date']).dt.tz_localize(None)
financial_df['time'] = pd.to_datetime(financial_df['time'])

# Merge data
merged_data = pd.merge(financial_df, astro_df, left_on='time', right_on='date', how='inner')

# Save merged data
merged_data.to_csv('merged_astro_financial_data.csv', index=False)
print("Merged data saved to merged_astro_financial_data.csv")

# Part 4: Statistical analysis of correlations

# Select numeric columns for correlation analysis
numeric_columns = merged_data.select_dtypes(include=[np.number]).columns

# Create lags for astronomical data
for col in numeric_columns:
    if col not in ['open', 'high', 'low', 'close', 'tick_volume', 'spread', 'real_volume']:
        for lag in range(1, 6):  # Create lags from 1 to 5
            merged_data[f'{col}_lag{lag}'] = merged_data[col].shift(lag)

# Update list of numeric columns
numeric_columns = merged_data.select_dtypes(include=[np.number]).columns

# Calculate correlation matrix
correlation_matrix = merged_data[numeric_columns].corr()

# Create heatmap of correlations
plt.figure(figsize=(20, 16))
sns.heatmap(correlation_matrix, annot=False, cmap='coolwarm', vmin=-1, vmax=1, center=0)
plt.title('Correlation Matrix of Astronomical Factors (with Lags) and EURUSD Prices')
plt.tight_layout()
plt.savefig('correlation_heatmap_with_lags.png')
plt.close()

# Output the most significant correlations with the closing price
significant_correlations = correlation_matrix['close'].sort_values(key=abs, ascending=False)
print("Most significant correlations with the closing price:")
print(significant_correlations)

# Create a separate correlation matrix for astronomical data with lags and the current price
astro_columns = [col for col in numeric_columns if col not in ['open', 'high', 'low', 'tick_volume', 'spread', 'real_volume']]
astro_columns.append('close')  # Add the current closing price
astro_correlation_matrix = merged_data[astro_columns].corr()

# Create heatmap of correlations for astronomical data with lags and the current price
import seaborn as sns
import matplotlib.pyplot as plt

# Increase the header and axis label font
plt.figure(figsize=(18, 14))
sns.heatmap(astro_correlation_matrix, annot=False, cmap='coolwarm', vmin=-1, vmax=1, center=0, cbar_kws={'label': 'Correlation'})
plt.title('Correlation matrix of astronomical factors (with lags) and current EURUSD price', fontsize=24)
plt.xlabel('X-axis Label', fontsize=30)
plt.ylabel('Y-axis Label', fontsize=30)
plt.xticks(fontsize=30)
plt.yticks(fontsize=30)
plt.tight_layout()
plt.savefig('astro_correlation_heatmap_with_lags.png')
plt.close()

print("Analysis completed. Results saved in CSV and PNG files.")

Este script gera um mapa de correlações entre todas as variáveis do conjunto de dados, além de exibir uma matriz de correlação em formato de heatmap e listar as correlações mais significativas com os preços de fechamento (close).

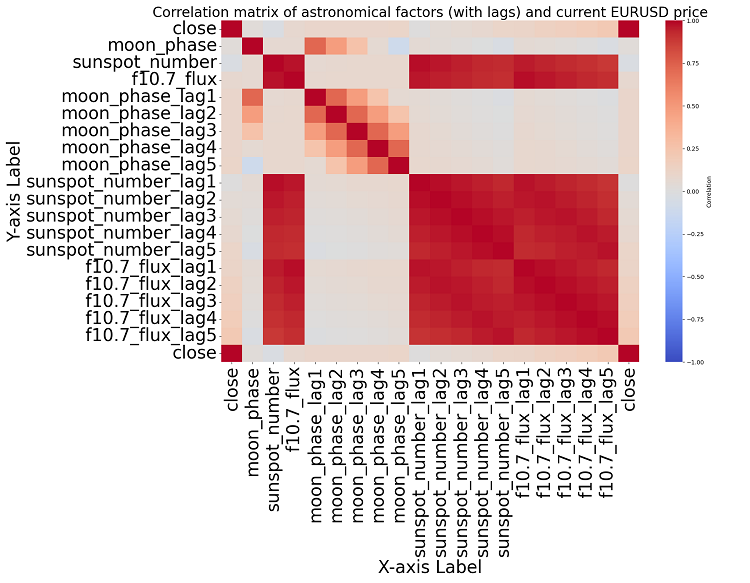
A presença ou ausência de correlação não implica necessariamente uma relação de causa e efeito. Mesmo que encontrássemos fortes correlações entre os dados astronômicos e os movimentos dos preços, isso não significaria que um fator determina o outro. Seriam necessários mais estudos, pois o mapa de correlações é apenas o nível mais básico de análise.

Aprofundando a questão, não identificamos nenhuma correlação significativa nos dados. Nenhum dos indicadores astronômicos passados apresenta uma relação clara com os dados do mercado.

Chamando o aprendizado de máquina para ajudar

Então, comecei a pensar no que fazer a seguir e decidi recorrer a um modelo de aprendizado de máquina. Escrevi dois scripts usando a biblioteca CatBoost para tentar prever os preços futuros a partir dos dados do conjunto como variáveis de entrada. Aqui está a primeira abordagem — um modelo de regressão: 

import pandas as pd
import numpy as np
from catboost import CatBoostRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import matplotlib.pyplot as plt
from sklearn.preprocessing import LabelEncoder

# Loading data
data = pd.read_csv('merged_astro_financial_data.csv')

# Converting date to datetime
data['date'] = pd.to_datetime(data['date'])

# Creating lags for financial data
for col in ['open', 'high', 'low', 'close']:
    for lag in range(1, 6):  # Creating lags from 1 to 5
        data[f'{col}_lag{lag}'] = data[col].shift(lag)

# Creating lags for astronomical data
astro_cols = ['mercury', 'venus', 'mars', 'jupiter', 'saturn', 'uranus', 'neptune']
for col in astro_cols:
    data[f'{col}_ra'] = data[col].apply(lambda x: eval(x)['ra'] if pd.notna(x) else np.nan)
    data[f'{col}_dec'] = data[col].apply(lambda x: eval(x)['dec'] if pd.notna(x) else np.nan)
    for lag in range(1, 6):  # Lags from 1 to 5
        data[f'{col}_ra_lag{lag}'] = data[f'{col}_ra'].shift(lag)
        data[f'{col}_dec_lag{lag}'] = data[f'{col}_dec'].shift(lag)
    data.drop(columns=[col, f'{col}_ra', f'{col}_dec'], inplace=True)

# Converting aspects to numerical features
aspect_cols = ['mercury_saturn', 'venus_mars', 'venus_jupiter', 'venus_uranus', 
               'mars_jupiter', 'mars_uranus', 'jupiter_uranus', 'mercury_neptune', 
               'venus_saturn', 'venus_neptune', 'mars_saturn', 'mercury_venus', 
               'mars_neptune', 'mercury_uranus', 'saturn_neptune', 'mercury_jupiter', 
               'mercury_mars', 'jupiter_saturn']

# Using LabelEncoder for encoding aspects
label_encoders = {}
for col in aspect_cols:
    label_encoders[col] = LabelEncoder()
    data[col] = label_encoders[col].fit_transform(data[col].astype(str))

# Filling missing values with mean values for numeric columns
numeric_cols = data.select_dtypes(include=[np.number]).columns
data[numeric_cols] = data[numeric_cols].fillna(data[numeric_cols].mean())

# Removing rows with missing values
data = data.dropna()

# Preparing features and target variable
features = [col for col in data.columns if col not in ['date', 'time', 'close']]
X = data[features]
y = data['close']

# Splitting data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

# Creating and training the CatBoost model
model = CatBoostRegressor(iterations=500, learning_rate=0.1, depth=9, random_state=1)
model.fit(X_train, y_train, eval_set=(X_test, y_test), early_stopping_rounds=200, verbose=100)

# Evaluating the model
y_pred = model.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
mae = mean_absolute_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print(f"Mean Squared Error: {mse}")
print(f"Mean Absolute Error: {mae}")
print(f"R-squared Score: {r2}")

# Visualizing feature importance
feature_importance = model.feature_importances_
feature_names = X.columns
sorted_idx = np.argsort(feature_importance)
pos = np.arange(sorted_idx.shape[0]) + 0.5
plt.figure(figsize=(12, 6))
plt.barh(pos, feature_importance[sorted_idx], align='center')
plt.yticks(pos, np.array(feature_names)[sorted_idx])
plt.xlabel('Feature Importance')
plt.title('Feature Importance')
plt.show()

# Predicting the next value
def predict_next():
    # Selecting the last row of data
    last_data = data.iloc[-1]
    input_features = last_data[features].values.reshape(1, -1)
    # Prediction
    prediction = model.predict(input_features)
    print(f"Prediction for the next closing price: {prediction[0]}")

# Example of using the function to predict the next value
predict_next()

O segundo modelo trata-se de uma classificação:

import pandas as pd
import numpy as np
from skyfield.api import load, utc
from datetime import datetime, timedelta
import requests
import MetaTrader5 as mt5
import seaborn as sns
import matplotlib.pyplot as plt
from catboost import CatBoostClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
from sklearn.preprocessing import LabelEncoder

# Part 1: Collecting astronomical data

planets = load('de421.bsp')
earth = planets['earth']
ts = load.timescale()

def get_planet_positions(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    planet_positions = {}
    planet_ids = {
        'mercury': 'MERCURY BARYCENTER',
        'venus': 'VENUS BARYCENTER',
        'mars': 'MARS BARYCENTER',
        'jupiter': 'JUPITER BARYCENTER',
        'saturn': 'SATURN BARYCENTER',
        'uranus': 'URANUS BARYCENTER',
        'neptune': 'NEPTUNE BARYCENTER'
    }
    for planet, planet_id in planet_ids.items():
        planet_obj = planets[planet_id]
        astrometric = earth.at(t).observe(planet_obj)
        ra, dec, _ = astrometric.radec()
        planet_positions[planet] = {'ra': ra.hours, 'dec': dec.degrees}
    return planet_positions

def get_moon_phase(date):
    t = ts.from_datetime(date.replace(tzinfo=utc))
    eph = load('de421.bsp')
    moon, sun, earth = eph['moon'], eph['sun'], eph['earth']
    
    e = earth.at(t)
    _, m, _ = e.observe(moon).apparent().ecliptic_latlon()
    _, s, _ = e.observe(sun).apparent().ecliptic_latlon()
    
    phase = (m.degrees - s.degrees) % 360
    return phase

def get_solar_activity(date):
    url = f"https://services.swpc.noaa.gov/json/solar-cycle/observed-solar-cycle-indices.json"
    response = requests.get(url)
    data = response.json()
    
    target_date = date.strftime("%Y-%m")
    
    closest_data = min(data, key=lambda x: abs(datetime.strptime(x['time-tag'], "%Y-%m") - datetime.strptime(target_date, "%Y-%m")))
    
    return {
        'sunspot_number': closest_data.get('ssn', None),
        'f10.7_flux': closest_data.get('f10.7', None)
    }

def calculate_aspects(positions):
    aspects = {}
    planets = list(positions.keys())
    for i in range(len(planets)):
        for j in range(i+1, len(planets)):
            planet1 = planets[i]
            planet2 = planets[j]
            ra1 = positions[planet1]['ra']
            ra2 = positions[planet2]['ra']
            angle = abs(ra1 - ra2) % 24
            angle = min(angle, 24 - angle) * 15  # Convert to degrees
            
            if abs(angle - 0) <= 10 or abs(angle - 180) <= 10:
                aspects[f"{planet1}_{planet2}"] = "conjunction" if abs(angle - 0) <= 10 else "opposition"
            elif abs(angle - 90) <= 10:
                aspects[f"{planet1}_{planet2}"] = "square"
            elif abs(angle - 120) <= 10:
                aspects[f"{planet1}_{planet2}"] = "trine"
    
    return aspects

# Part 2: Obtaining financial data through MetaTrader5

def get_financial_data(symbol, start_date, end_date):
    if not mt5.initialize():
        print("initialize() failed")
        mt5.shutdown()
        return None

    timeframe = mt5.TIMEFRAME_D1

    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    mt5.shutdown()

    financial_df = pd.DataFrame(rates)
    financial_df['time'] = pd.to_datetime(financial_df['time'], unit='s')
    return financial_df

# Part 3: Synchronizing astronomical and financial data

def sync_data(astro_df, financial_df):
    astro_df['date'] = pd.to_datetime(astro_df['date']).dt.tz_localize(None)
    financial_df['time'] = pd.to_datetime(financial_df['time'])
    merged_data = pd.merge(financial_df, astro_df, left_on='time', right_on='date', how='inner')
    return merged_data

# Part 4: Training the model and making predictions

def train_and_predict(merged_data):
    # Converting aspects to numerical features
    aspect_cols = [col for col in merged_data.columns if '_' in col and col not in ['date', 'time']]
    label_encoders = {}
    for col in aspect_cols:
        label_encoders[col] = LabelEncoder()
        merged_data[col] = label_encoders[col].fit_transform(merged_data[col].astype(str))
    
    # Creating lags for financial data
    for col in ['open', 'high', 'low', 'close']:
        for lag in range(1, 6):
            merged_data[f'{col}_lag{lag}'] = merged_data[col].shift(lag)
    
    # Creating lags for astronomical data
    astro_cols = ['mercury', 'venus', 'mars', 'jupiter', 'saturn', 'uranus', 'neptune']
    for col in astro_cols:
        merged_data[f'{col}_ra'] = merged_data[col].apply(lambda x: eval(x)['ra'] if pd.notna(x) else np.nan)
        merged_data[f'{col}_dec'] = merged_data[col].apply(lambda x: eval(x)['dec'] if pd.notna(x) else np.nan)
        for lag in range(1, 6):
            merged_data[f'{col}_ra_lag{lag}'] = merged_data[f'{col}_ra'].shift(lag)
            merged_data[f'{col}_dec_lag{lag}'] = merged_data[f'{col}_dec'].shift(lag)
        merged_data.drop(columns=[col, f'{col}_ra', f'{col}_dec'], inplace=True)

    # Filling missing values with mean values for numeric columns
    numeric_cols = merged_data.select_dtypes(include=[np.number]).columns
    merged_data[numeric_cols] = merged_data[numeric_cols].fillna(merged_data[numeric_cols].mean())

    merged_data = merged_data.dropna()

    # Creating binary target variable
    merged_data['price_change'] = (merged_data['close'].shift(-1) > merged_data['close']).astype(int)

    # Removing rows with missing values in the target variable
    merged_data = merged_data.dropna(subset=['price_change'])

    features = [col for col in merged_data.columns if col not in ['date', 'time', 'close', 'price_change']]
    X = merged_data[features]
    y = merged_data['price_change']

    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

    model = CatBoostClassifier(iterations=500, learning_rate=0.1, depth=9, random_state=1)
    model.fit(X_train, y_train, eval_set=(X_test, y_test), early_stopping_rounds=200, verbose=100)

    y_pred = model.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)
    clf_report = classification_report(y_test, y_pred)
    conf_matrix = confusion_matrix(y_test, y_pred)

    print(f"Accuracy: {accuracy}")
    print("Classification Report:")
    print(clf_report)
    print("Confusion Matrix:")
    print(conf_matrix)

    # Visualizing feature importance
    feature_importance = model.feature_importances_
    feature_names = X.columns
    sorted_idx = np.argsort(feature_importance)
    pos = np.arange(sorted_idx.shape[0]) + 0.5

    plt.figure(figsize=(12, 6))
    plt.barh(pos, feature_importance[sorted_idx], align='center')
    plt.yticks(pos, np.array(feature_names)[sorted_idx])
    plt.xlabel('Feature Importance')
    plt.title('Feature Importance')
    plt.show()

    # Predicting the next value
    def predict_next():
        last_data = merged_data.iloc[-1]
        input_features = last_data[features].values.reshape(1, -1)
        prediction = model.predict(input_features)
        print(f"Price change prediction (0: will decrease, 1: will increase): {prediction[0]}")

    predict_next()

# Main program
start_date = datetime(2023, 3, 1)
end_date = datetime(2024, 7, 30)

astro_data = []
current_date = start_date

while current_date <= end_date:
    planet_positions = get_planet_positions(current_date)
    moon_phase = get_moon_phase(current_date)
    try:
        solar_activity = get_solar_activity(current_date)
    except Exception as e:
        print(f"Error getting solar activity for {current_date}: {e}")
        solar_activity = {'sunspot_number': None, 'f10.7_flux': None}
    aspects = calculate_aspects(planet_positions)
    
    astro_data.append({
        'date': current_date,
        'mercury': str(planet_positions['mercury']),
        'venus': str(planet_positions['venus']),
        'mars': str(planet_positions['mars']),
        'jupiter': str(planet_positions['jupiter']),
        'saturn': str(planet_positions['saturn']),
        'uranus': str(planet_positions['uranus']),
        'neptune': str(planet_positions['neptune']),
        'moon_phase': moon_phase,
        **solar_activity,
        **aspects
    })
    
    current_date += timedelta(days=1)

astro_df = pd.DataFrame(astro_data)

symbol = "EURUSD"
financial_data = get_financial_data(symbol, start_date, end_date)

if financial_data is not None:
    merged_data = sync_data(astro_df, financial_data)
    train_and_predict(merged_data)

Infelizmente, nenhum dos dois modelos é preciso. A acurácia da classificação ficou um pouco acima de 50%, o que significa que poderíamos obter resultados semelhantes lançando uma moeda ao alto.

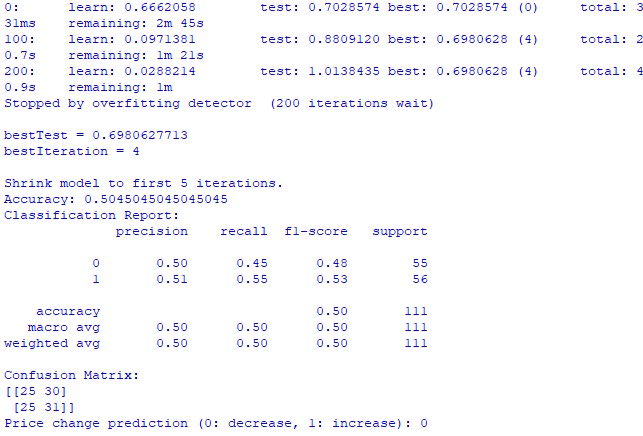
Talvez os resultados possam ser melhorados ou eu tenha dedicado pouca atenção ao modelo de regressão. Pode ser que seja possível prever os preços utilizando a posição dos planetas, a atividade lunar e solar. Se eu tiver vontade, farei um novo artigo sobre o tema.

Resultados da pesquisa

Agora, chegou a hora de analisar os resultados do estudo. Após realizar uma análise simples e desenvolver dois modelos de previsão, foi possível traçar um panorama sobre o possível impacto da astrologia no mercado. 

Análise de correlação. O mapa de interdependências gerado não revelou nenhuma correlação significativa entre a posição dos planetas e o preço de fechamento do par de moedas EUR/USD. Todas as correlações ficaram abaixo de 0,3, o que nos leva a concluir que a posição dos planetas provavelmente não tem relação alguma com os mercados financeiros.

Modelo de regressão CatBoost. Os resultados do modelo de regressão demonstraram uma capacidade bastante fraca de prever valores exatos dos preços futuros de fechamento com base nos dados astronômicos.

As métricas do modelo, como MSE, MAE e R², apresentaram resultados fracos e explicaram muito pouco da variação dos dados. Além disso, o modelo indicou que os fatores mais importantes para a previsão são os lags (preços passados), e não a posição dos planetas. Isso significa que o próprio preço é um preditor muito mais relevante do que qualquer posição planetária no sistema solar?

Modelo de classificação CatBoost. Esse modelo apresentou um desempenho extremamente fraco na previsão de crescimento ou queda dos preços. A precisão mal ultrapassou 50%, o que confirma mais uma vez que a astronomia não tem qualquer efeito prático no mercado real.

Considerações finais

Os resultados da pesquisa são bastante claros – os métodos da astrologia e as tentativas de prever os preços do mercado real com base em indicadores astronômicos são completamente inúteis. Talvez eu volte a esse tema no futuro, mas, por enquanto, os ensinamentos de William Gann parecem ser apenas uma forma de "criar mistério", mascarando soluções ineficazes sob uma camada de complexidade, com o objetivo final de vender livros e cursos de trading.

Será que uma versão aprimorada do modelo, incluindo os ângulos de Gann, os valores do Quadrado de 9 e os níveis da Grade de Gann, poderia apresentar um desempenho melhor? Ainda não sabemos. Confesso que estou um pouco decepcionado com os resultados do estudo.

Ainda assim, há indícios de que os ângulos de Gann possam ser utilizados para previsões mais precisas. O preço, de certa maneira, interage com os ângulos e reage a eles, como observado em estudos anteriores. Talvez seja possível incluir os ângulos como variáveis úteis no treinamento de modelos de aprendizado de máquina. De qualquer forma, pretendo criar um conjunto de dados baseado nisso e verificar os resultados que posso obter.