Zyklen und Forex

Einführung

Die Zyklizität ist einer der wichtigsten Faktoren in unserer Welt. Zyklen ermöglichen es den Menschen, ihr Leben zu gestalten. Wenn wir die zyklische Anordnung kennen würden, könnten wir die Zukunft vorhersagen. Ich kann zum Beispiel getrost sagen, dass das Jahr 2025 mit dem 1. Januar beginnt.

Die Zyklen im Forexhandel können mit verschiedenen Faktoren zusammenhängen: Wirtschaftsnachrichten, Tageszeit, Wochentage, Monate des Jahres und Jahreszeiten. Das Studium dieser Zyklen kann einem Händler dabei helfen, zukünftige Kursbewegungen vorherzusagen und fundiertere Handelsentscheidungen zu treffen.

Zyklen können ganz unerwartet auftreten. Sogar das Interesse an Zyklen und Wellen im Devisenhandel ist zyklischer Natur:

• Artikel „Die Implementierung der automatischen Analyse der Elliott-Wellen in MQL5“ — 2011
• Artikel „Wolfe-Wellen“ — 2017
• Artikel „Von der Saisonalität des Devisenmarktes profitieren“ — 2023
• Artikel „Saisonalitätsfilterung und Zeitspanne für Deep Learning ONNX Modelle mit Python für EA“ — 2024.

Wie Sie sehen können, wurden die Artikel alle 6 Jahre veröffentlicht. Erst der letzte Artikel hat diesen Kreislauf durchbrochen. Aber vielleicht gibt es eine andere Erklärung für diese Abweichung?

Lassen Sie uns versuchen, Antworten auf zwei Fragen zu finden. Gibt es Zyklen in der Preisentwicklung? Und wenn es sie gibt, wie können sie im Handel genutzt werden?

Auf der Suche nach Zyklen

Im Handel können Zyklen mit wiederkehrenden Markttrends oder -mustern in Verbindung gebracht werden. Zum Beispiel kann der Preis innerhalb eines bestimmten Kanals schwanken. Und ein solches Verhalten kann noch lange anhalten.

Wir können Spektralanalyse, Trigonometrische Polynome, Periodogramm, Autokorrelation und Zyklenerkennung verwenden, um die zyklische Komponente aus einer Zeitreihe zu extrahieren.

Wir können auch einen einfachen gleitenden Durchschnitt verwenden, um den Zyklus zu ermitteln. Diese Methode ist die einfachste und anschaulichste. Nehmen wir an, dass wir eine Zeitreihe haben, die ein Zyklus mit der Periode N ist. Wenn wir eine SMA mit der gleichen Periode auf diese Reihe anwenden, erhalten wir einen Durchschnittswert, um den herum die Schwingungen auftreten. Die Verwendung von SMA mit anderen Perioden ermöglicht es uns, Schwingungsprozesse zu erhalten, die sich vom Original unterscheiden. Aber trotz dieser Unterschiede ist es möglich, mit Hilfe solcher Durchschnittswerte die Parameter des ursprünglichen Zyklus wiederherzustellen.

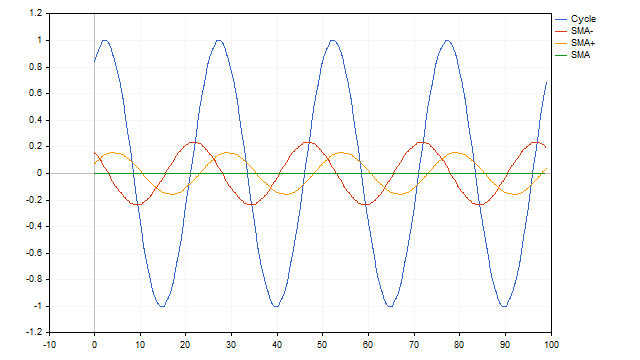
Einige Zeitreihen können aus einer Summe von Zyklen mit unterschiedlichen Zeiträumen bestehen. In diesem Fall sind die gleitenden Durchschnitte ebenfalls gut geeignet. Der Algorithmus ist recht einfach. Zunächst subtrahieren wir die Werte des Durchschnitts mit der größten Periode von der ursprünglichen Reihe. Wir subtrahieren die Werte des nächsten Durchschnitts von den sich ergebenden Resten und setzen diesen Vorgang fort, bis wir nur noch Nullen haben. Wir brauchen mehr SMA.

Mit gleitenden Durchschnitten lässt sich das Modell der Zyklus- und Trendzeitreihen ebenso leicht handhaben. In diesem Fall fungiert der SMA gleichzeitig als Zyklus- und Trenddetektor.

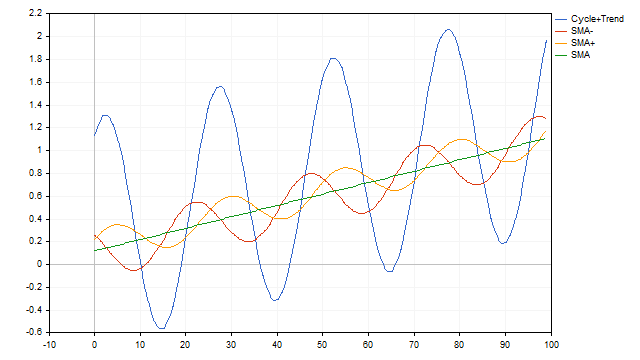
Bis zu diesem Punkt haben wir einen gleitenden Durchschnitt auf eine deterministische Zeitreihe angewandt - die Zyklus- und Trendgleichungen waren starr definiert und änderten sich im Laufe der Zeit nicht. Fügen wir der ursprünglichen Zeitreihe etwas Zufälligkeit hinzu und sehen wir uns an, wie SMA mit dieser Situation umgeht. Wir nehmen die Zyklusamplitude als 100 % an. Nehmen wir an, dass sich die Amplitude zufällig innerhalb von 10 % in beide Richtungen ändern kann. Die Trendgeschwindigkeit kann zwischen 0 und 1 % liegen. Und fügen wir 10 % weißes Rauschen hinzu. Auch diese Aufgabe wird von SMA erfolgreich gemeistert.

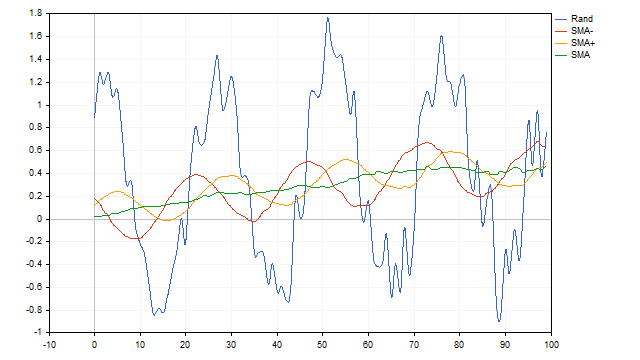
Es scheint, dass wir den perfekten Indikator gefunden haben. Leider überwiegen die Nachteile der SMA möglicherweise ihre Vorteile. Der gleitende Durchschnitt ist nicht in der Lage, Zyklen zu erkennen, die nur aus positiven oder negativen Halbwellen bestehen. Darüber hinaus hat dieser Indikator eine geringe Auflösung. Vereinfacht ausgedrückt, ist es nicht in der Lage, ein Nutzsignal zu isolieren, wenn das Rauschen eine bestimmte Grenze überschreitet.

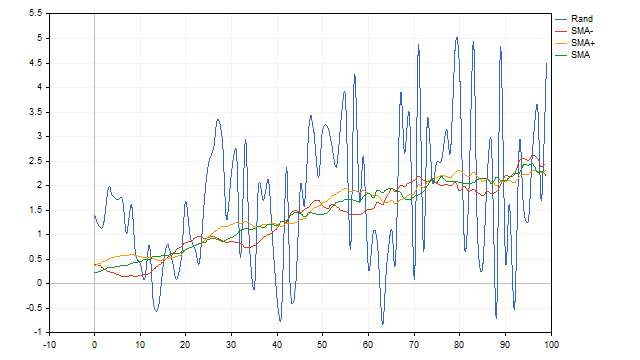
Ein weiterer kleiner Nachteil ist, dass es ratsam ist, vor der Verwendung von SMA im Voraus zu wissen, welchen Zyklus wir auswählen müssen. Hier stehen wir vor zwei Fragen:

• Gibt es einen Zyklus in den von uns untersuchten Zeitreihen?
• Wenn es einen Zyklus gibt, wie können wir dann seine Parameter kennen?

Um diese Fragen zu beantworten, können wir die Punktzuordnung verwenden.

Sehen Sie sich diese Grafik an. Können Sie sagen, was es zeigt?

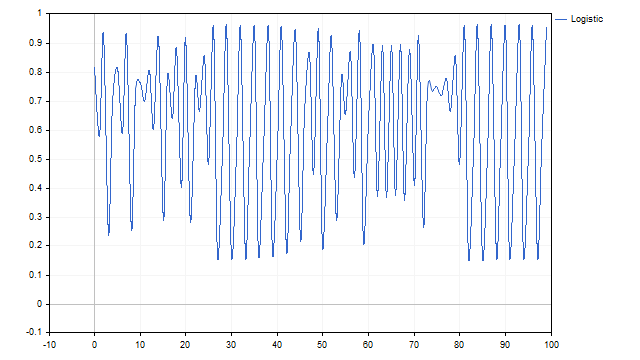
Es ist möglich, dass es sich um eine Grafik der Summe mehrerer Zyklen handelt. Oder vielleicht ist es Teil des Masterplans der Daleks.

Wir haben also eine eindimensionale Zeitreihe mit Z[i]-Werten. Auf dieser Grundlage werde ich einen zweidimensionalen Graphen konstruieren, und die Koordinaten jedes Punktes dieses Graphen werden nach der folgenden Regel festgelegt (Indexierung wie bei Zeitreihen):

X[i] = Z[i];

Y[i] = Z[i-1].

Der Sinn dieser Transformation ist, dass ich die Beziehung zwischen zwei benachbarten Werten der ursprünglichen Zeitreihe anzeigen möchte. Dieses obskure Diagramm zeigt zum Beispiel die folgende Anzeige.

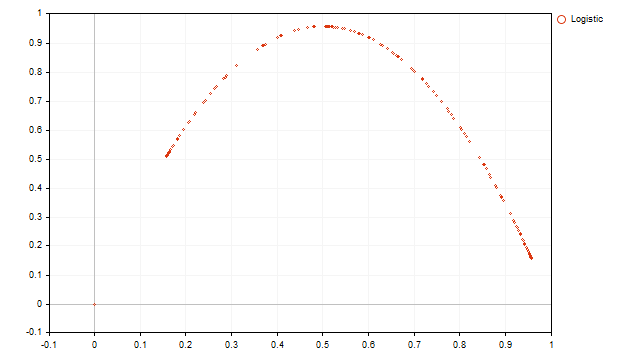
Wir können eine übliche Parabel erkennen. Da wir die Eigenschaften der Parabel kennen, können wir die Gleichung der ursprünglichen Zeitreihe formulieren:

Um die Gleichungsverhältnisse zu ermitteln, können wir die Methode der kleinsten Quadrate anwenden. Als Ergebnis erhalten wir eine logistische Gleichung, die zur Erzeugung der Werte der ursprünglichen Zeitreihe verwendet wurde.

Die Punktdiagramm-Methode kann auf jede beliebige Zeitreihe angewandt werden, aber sie liefert nicht immer eine klare und präzise Darstellung der Zeitreihe.

Betrachten wir zum Beispiel den Pseudo-Zufallszahlengenerator. Die Grafik sieht wie folgt aus:

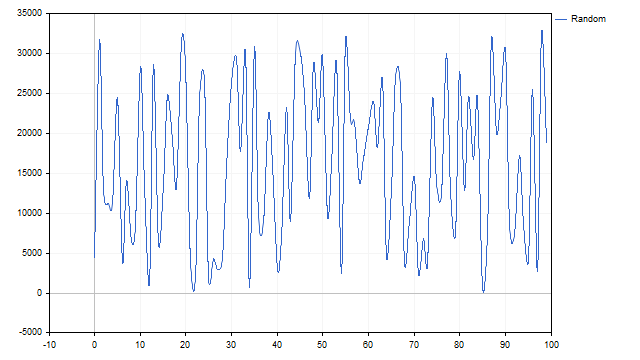
Die Addition mehrerer Zyklen ist deutlich sichtbar. Jetzt werden wir das alles herausfinden. Konstruieren wir eine Punktdarstellung der erhaltenen Werte.

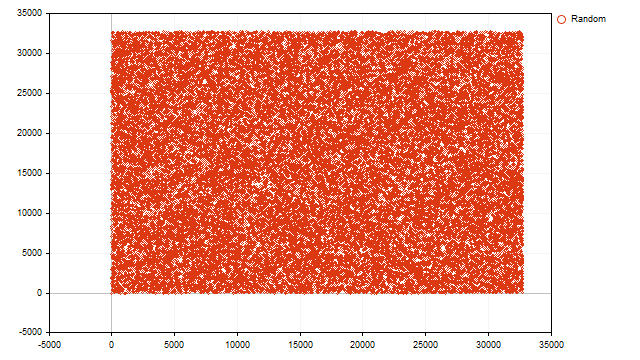
Alle Punkte füllen gleichmäßig die gesamte Ebene aus. Daraus können wir schließen, dass der aktuelle Wert des Pseudo-Zufallszahlengenerators nicht vom vorherigen Wert abhängt und alle Übereinstimmungen zufällig sind.

Die Anzeige eines zyklischen Prozesses sieht zyklisch aus:

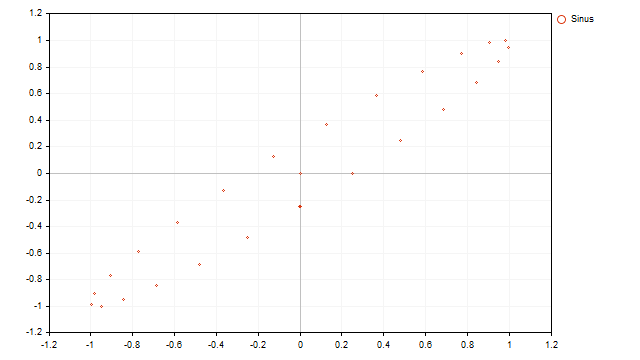
Schauen wir uns nun an, wie die gepunktete Anzeige der realen Preise aussieht:

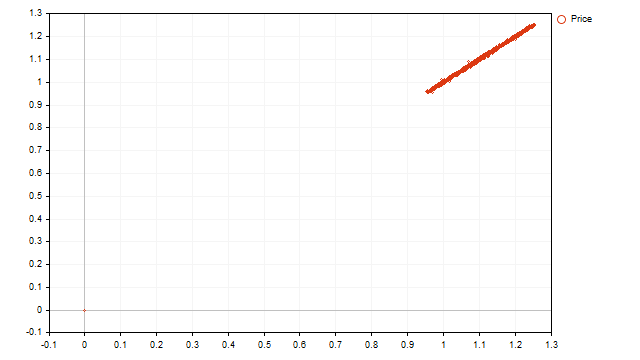
Wir sehen einen zunehmenden linearen Trend und keine Zyklen. Es ist jedoch noch zu früh, um in Verzweiflung zu verfallen. Aus der Betrachtung dieses Bildes lassen sich folgende Schlüsse ziehen:

• Der Trend ist der wichtigste Faktor, der die Preisbewegung bestimmt.
• Die Stärke des Trends ist groß genug und kann zyklische Prozesse überdecken.

Die Schlussfolgerung liegt auf der Hand: Wir brauchen mehr Möglichkeiten zur Identifizierung von Zyklen.

Zyklen und Zufälligkeit

1927 veröffentlichte Jewgeni Jewgenjewitsch Sluzki den Artikel „Addition von Zufallsursachen als Quelle zyklischer Prozesse“. In dieser Arbeit zeigte er auf brillante Weise, dass zyklische und wellenförmige Prozesse durch die Interaktion (z. B. Addition) von Zufallsvariablen entstehen können.

Testen wir, wie diese Theorie bei finanziellen Zeitreihen funktioniert. Wir nehmen die Preise der verschiedenen Symbole als anfängliche Zufallsvariable. In diesem Fall gehen wir wie folgt vor: Für das aktuelle Paar nehmen wir den Preis des aktuellen Balkens, für alle nachfolgenden Symbole nehmen wir den Preis des vorherigen Balkens. Die Gleichung für die Zufallsvariable lautet also ungefähr wie folgt:

Die sich ergebende Zufallsvariable hängt also von einer großen Anzahl früherer Kurswerte verschiedener Symbole ab. Verstärken wir diese Abhängigkeit, indem wir auf der Grundlage dieser Werte einen gleitenden Durchschnitt bilden.

Es gibt wellenartige Prozesse. Aber wir würden gerne wissen, ob sie zyklisch sind? Und wenn es einen Zyklus gibt, was sind seine Parameter?

Zur Beantwortung dieser Fragen können wir finite Differenzen nutzen. Die 1. Differenz ergibt sich durch Subtraktion des vorherigen Wertes der Zeitreihe vom aktuellen Wert:

Die zweite endliche Differenz ergibt sich durch Subtraktion der ersten Differenzen.

Dieser Unterschied ist interessant, weil er unter bestimmten Bedingungen auf den zyklischen Charakter des Prozesses hinweisen kann. Gehen wir davon aus, dass wir es mit einer Art Zyklus zu tun haben. a sei der Anfangswert des Winkels und s sein Änderungsschritt. Dann können die letzten drei Punkte der Zeitreihe wie folgt festgelegt werden:

Verwenden Sie die Formelsammlung Trigonometrie, um die 2. Differenz dieser Werte zu finden:

Dies ist die Gleichung für den diskreten harmonischen Oszillator. Bitte beachten Sie, dass mit Oszillator hier ein schwingendes System und nicht ein Indikator gemeint ist.

Es ist nicht einfach, diese Gleichung auf die Preise zu übertragen. Auf der linken Seite der Gleichung können wir alle realen Werte so verwenden, wie sie sind, aber auf der rechten Seite müssen wir einige Änderungen vornehmen.

Um die Fluktuationen zu isolieren, müssen wir zunächst das Niveau finden, um das sie auftreten. Bezeichnen wir sie als MA. Dann sieht die Gleichung wie folgt aus:

Auf der linken Seite werden sich die MV gegenseitig absorbieren, aber auf der rechten Seite werden sie bestehen bleiben.

Es gibt mehrere Möglichkeiten, diesen Wert zu berechnen. So kann man beispielsweise zunächst den Trend aus der ursprünglichen Zeitreihe entfernen oder den Durchschnitt aller Werte der Reihe ermitteln. Beide Methoden haben einen gemeinsamen Nachteil: Sie sind stark von historischen Daten abhängig und reagieren nur schwach auf aktuelle Marktveränderungen. Um diesen Nachteil zu beseitigen, werde ich den Algorithmus zur Berechnung adaptiver Indikatoren verwenden. In diesem Fall passt sich der gleitende Durchschnitt der aktuellen Marktsituation an. Als Ergebnis erhalten wir einen Indikator, der uns erlaubt, das Niveau zu verfolgen, um das der gleitende Durchschnitt schwankt. Für das Beispiel habe ich SMA verwendet, aber in der Praxis können Sie jede beliebige Preismittelung verwenden.

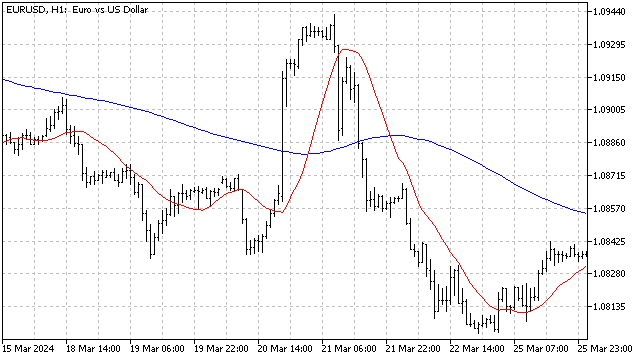
Leider hat der harmonische Oszillator eine Reihe von Nachteilen, die bei seiner Verwendung berücksichtigt werden müssen. Es funktioniert gut mit Sinussignalen. Aber auch eine Mischung von Sinusschwingungen kann Schwierigkeiten verursachen - der Oszillator ist einfach nicht in der Lage, den wichtigsten Zyklus auszuwählen.

Die meisten Unzulänglichkeiten können mit Hilfe der 2. Differenz lösen. Äußerlich ist sie gleich geblieben. Aber wir können den Abstand zwischen den Gliedern dieser Differenz ändern. Ich habe zum Beispiel ein Chart mit dem Zeitrahmen H1 geöffnet. Ich gehe davon aus, dass es einen täglichen Zyklus in der Kursbewegung geben kann (Zeitraum ist 24). Dann werde ich die zweite Differenz wie folgt verwenden:

Wenn es einen oder mehrere Zyklen in der Preisbewegung gibt, ist die 2. Differenz gleich Null. Das Aussehen dieser Zyklen ist nicht wichtig. Die Hauptsache ist, dass sie mehr oder weniger korrekt wiederholt werden. Auch die 2. Differenz kann leicht mit dem Trend mithalten. Die einzige Bedingung ist, dass die Länge dieses Trends nicht weniger als das Doppelte des Zeitraums beträgt.

Wie kann diese Methode in der Praxis angewendet werden? Nehmen wir an, dass es einen stabilen Zyklus in der Preisbewegung mit einigen zufälligen Abweichungen gibt. Wenn wir dann die Summe mehrerer (in meinem Fall 24) letzter Werte der Differenzen finden, dann gleichen sich zufällige Fehler aus. Das heißt, wenn der Zyklus und/oder der Trend stabil ist, schwankt die Summe der Differenzen um Null. Kommt es zu Störungen auf dem Markt (Beginn eines neuen Trends, Beginn eines neuen Zyklus oder Ende eines alten Zyklus), beginnt die Summe der Differenzen deutlich abzuweichen. Außerdem können diese Abweichungen zyklisch auftreten. Daraus können wir schließen, dass Zyklusstörungen zyklischer Natur sein können. Es ist wie ein Schrödinger-Markt.

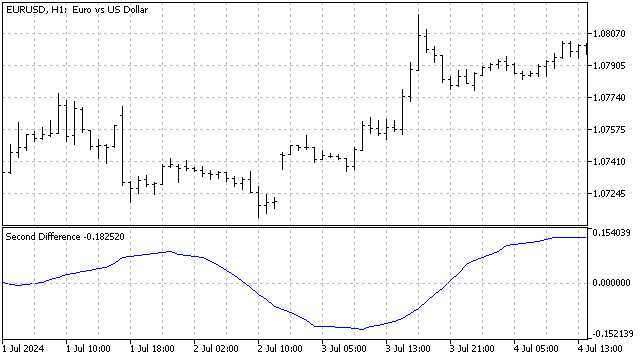
Im Allgemeinen kann die Verwendung von finiten Differenzen bei der Marktanalyse sehr nützlich sein. Sie können unverändert verwendet, miteinander kombiniert und mit anderen Indikatoren gepaart werden. Dadurch erhalten Sie neue interessante Instrumente zur Untersuchung von Kursbewegungen.

Andere Unterschiede

Es ist nicht notwendig, bei der Analyse von Zeitreihen klassische Differenzen zu verwenden. Wir können je nach unseren Aufgaben Unterschiede machen. Zu diesem Zweck können wir die bei der Konstruktion von Wavelet angewandten Prinzipien nutzen. 

Nehmen wir eine Zahl, die die erste Welle darstellt. Die einfachste und naheliegendste Möglichkeit ist, 1. Wir setzen 0 rechts und links von dieser Zahl. Wir erhalten eine Zeichenfolge wie diese: „0, 1, 0“. Nun gehen wir, ausgehend von der zweiten Zahl, von links nach rechts und subtrahieren die linke Zahl von der rechten.

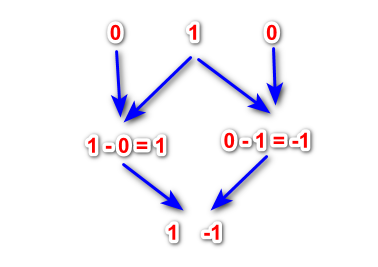
Auf diese Weise erhalten wir ein Wavelet der Stufe 1. Wir setzen links und rechts der sich ergebenden Verhältnisse Nullen ein und führen erneut Subtraktionen durch. Dieser Vorgang kann so lange fortgesetzt werden, bis die gewünschte Wavelet-Ebene erreicht ist. Solche Differenzen haben einige Eigenschaften klassischer Wavelets und können für die Analyse von Finanzzeitreihen verwendet werden.

Als Anfangswelle kann eine beliebige Zahlengruppe verwendet werden, zum Beispiel 1, 2, 1 oder 1, 1, 1. In diesem Fall sollten die Verhältnisse der ursprünglichen Welle nicht symmetrisch zum Zentrum der Welle sein. Es wird nichts Schlimmes passieren, wenn die ursprüngliche Welle als 3, 2, 1 dargestellt wird. Wir können auch negative Zahlen verwenden.

Da die Summe der Verhältnisse aller erhaltenen Differenzen gleich 0 ist, stellen sie sofort fertige Oszillatoren dar.

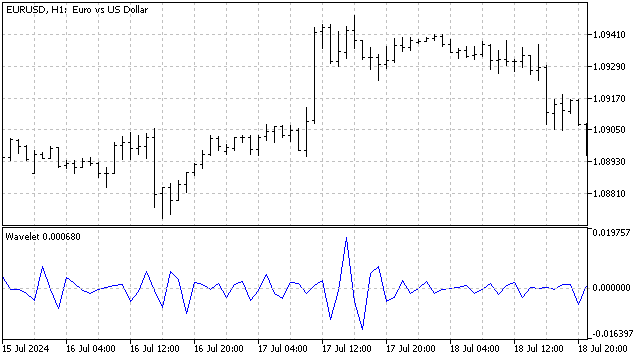
Der Nachteil dieser Unterschiede ist, dass wir uns nicht einmal vorstellen können, wie das Ergebnis bei Verwendung einer bestimmten Ausgangswelle aussehen wird.

Der Hauptvorteil dieser Unterschiede besteht darin, dass wir mit ihrer Hilfe das ursprüngliche Signal wiederherstellen können. Wir kennen zum Beispiel die Werte der 1. und 2. Differenz. Wenn wir die 1. Differenz vom aktuellen Wert der Zeitreihe abziehen, erhalten wir den vorherigen Wert der Reihe. Wenn man diese beiden Werte und die 2. Differenz kennt, erhält man den nächsten Wert der Reihe, und so weiter.

Diese Eigenschaft ermöglicht es uns, nach ähnlichen Bereichen in der Geschichte zu suchen. Wenn die Unterschiede zwischen den verschiedenen Niveaus annähernd gleich groß sind, haben wir ähnliche Preisbewegungen.

Schlussfolgerung

Es ist wichtig, daran zu denken, dass der Markt in der Regel keinen vorhersehbaren Zyklen folgt. Selbst wenn wir eine Art Zyklus beobachten, besteht immer die Gefahr, dass sich das Muster ändert. Es gibt Wellen, aber ihr Verhalten muss noch eingehender untersucht werden. In jedem Fall kann das Verständnis der Marktzyklen ein nützliches Instrument im Arsenal eines jeden Händlers sein. Durch die Erforschung von Zyklen können wir neue Wege und Mittel für die technische Analyse finden.

Die folgenden Programme sind dem Artikel beigefügt:

Name	Typ	Eigenschaften
Dot Mapping	Skript	Anzeigearten Logistik Zufällig Integriert - SerieOrder of integration Preis - reale Preise Linear - linearer Trend Sinus - Zyklus SinusTrend - Zyklus + Trend Sinus3 - Summe von drei Zyklen Nachdem das Skript seine Arbeit beendet hat, werden die Bilder im Ordner „Files“ gespeichert.
Slutsky cycles	Indikator	Verarbeitet alle in Market Watch verfügbaren Symbole
Slutsky MA	Indikator	iPeriode - Periodenlänge des Indikators Glättung
Second Difference	Indikator	Probenahme - Häufigkeit der Probenahme
scr Wavelet	Skript	Darstellung der Wavelet-Verhältnisse InpWave - Liste der Verhältnisse der ursprünglichen Welle. Ratios - durch Komma getrennte ganze Zahlen Lvl - gewünschte Wavelet-Ebene
Wavelet	Indikator	Verwendung der Wavelets als Oszillator InpWave - Liste der Verhältnisse der ursprünglichen Welle. Verhältnisse - durch Komma getrennte ganze Zahlen Lvl - gewünschte Wavelet-Ebene