Mecanismos de gating em aprendizado por ensemble

Os métodos de gating ajustam dinamicamente a influência de modelos individuais com base em informações contextuais por meio do uso de variáveis de gate. Essas variáveis atuam como mecanismos supervisórios, ponderando estrategicamente as saídas dos modelos para alcançar um desempenho preditivo superior em comparação a qualquer modelo individual.

Diferentemente dos métodos tradicionais de ensemble que se baseiam em média, votação ou empilhamento, o gating utiliza explicitamente variáveis de gate para a combinação de modelos. Essa abordagem é particularmente valiosa em cenários com desempenho de modelos flutuante, como na previsão financeira, em que tendências econômicas impactam a precisão das previsões. Ao ponderar adaptativamente os modelos com base no contexto, o gating aprimora a precisão e a adaptabilidade em ambientes complexos.

As técnicas de gating geralmente se enquadram em duas categorias: selecionar um único modelo com base nas variáveis de gate ou combinar as saídas de todos os modelos com pesos dependentes do contexto. A segunda opção costuma ser mais robusta, aproveitando os pontos fortes de múltiplos modelos. As seções a seguir exploram exemplos de ambas as abordagens: especialização preordenada e especialização aprendida.

Especialização preordenada

A especialização preordenada constitui uma forma fundamental de gating, na qual uma única variável atua como fator decisivo na seleção entre dois ou mais modelos especialistas previamente treinados. Essa abordagem particiona efetivamente o espaço de entrada, direcionando as instâncias para o modelo mais adequado com base no valor da variável de gating. Para ilustrar esse conceito, considere um problema de classificação binária representado em um espaço de características bidimensional, com as variáveis A e B. Nesse cenário hipotético, a variável B apresenta poder discriminativo desprezível entre as duas classes, enquanto a variável A demonstra capacidade preditiva moderada, alcançando classificações precisas para algumas instâncias, mas produzindo resultados ambíguos para outras.

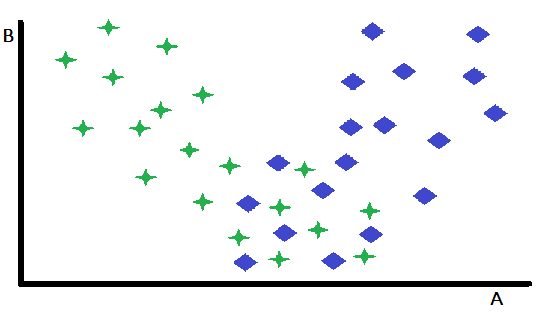
Uma inspeção detalhada de um gráfico de dispersão das características revela que a variável B delimita efetivamente as instâncias para as quais A serve como um classificador robusto daquelas em que seu poder preditivo é reduzido. Especificamente, instâncias caracterizadas por valores elevados de B exibem maior precisão de classificação ao utilizar A como preditor principal. Essa observação sugere uma estratégia natural de particionamento: dividir o conjunto de dados com base em um valor limiar de B. Esse particionamento possibilita o desenvolvimento de dois modelos de classificação distintos: um otimizado para instâncias com valores elevados de B (onde A é um forte preditor) e outro para instâncias com valores baixos de B (onde A pode ser menos confiável).

Embora esse exemplo simplificado demonstre o princípio central, é importante reconhecer que os benefícios de tal particionamento podem ser limitados quando o subconjunto restante de instâncias se mostra inerentemente difícil de classificar. Uma vantagem-chave dessa abordagem reside em sua capacidade de isolar e tratar de forma eficaz as instâncias mais facilmente classificáveis. Essa simplificação também auxilia no desenvolvimento de modelos mais performáticos para o subconjunto restante de dados, mais desafiador. Embora o exemplo recém-descrito tenha se concentrado em uma única variável para esclarecer o conceito, em aplicações práticas a seleção do modelo apropriado pode depender dos valores de múltiplas variáveis, que podem ou não estar incluídas no conjunto principal de preditores utilizados pelos modelos individuais.

Especialização aprendida

A especialização aprendida representa uma abordagem mais sofisticada de gating, na qual a variável de divisão ideal e seu respectivo limiar não são determinados a priori, mas aprendidos a partir dos próprios dados. Embora a inspeção visual de gráficos de dispersão possa ocasionalmente fornecer percepções preliminares sobre possíveis variáveis de divisão e seus limiares, tais abordagens intuitivas frequentemente se mostram insuficientes em aplicações do mundo real.

Na prática, é necessária uma abordagem mais sistemática e orientada por dados. Isso normalmente envolve um processo rigoroso de busca, explorando uma ampla gama de possíveis variáveis de divisão e seus limiares associados. Para cada variável de divisão candidata e limiar, o conjunto de dados é particionado, e modelos separados são treinados e avaliados nos subconjuntos resultantes. Esse processo iterativo de exploração, treinamento e avaliação pode ser computacionalmente exigente, especialmente ao lidar com grandes conjuntos de dados ou modelos complexos. No entanto, os ganhos potenciais no desempenho do modelo frequentemente justificam o aumento do custo computacional.

Além disso, a busca por variáveis de divisão ideais não deve se limitar a um único candidato. Em vez disso, uma avaliação abrangente de múltiplas variáveis potenciais é essencial para identificar a estratégia de gating mais eficaz. Isso exige uma exploração sistemática do espaço de características para identificar variáveis que exibam forte poder preditivo na determinação do modelo ideal para cada subconjunto dos dados. A busca pelas variáveis de gate ideais pode ser realizada empregando redes neurais ou outros algoritmos de aprendizado para determinar a relação entre as entradas e os modelos componentes.

Especialização aprendida utilizando as saídas dos modelos como variáveis de gating

Uma variante da especialização aprendida adota uma abordagem singular para a seleção de modelos ao se basear na análise das previsões geradas por todos os modelos concorrentes. Diferentemente dos métodos de gating que exigem variáveis predefinidas para selecionar um modelo, essa abordagem utiliza as próprias previsões dos modelos como fatores de decisão. Em essência, essa forma de especialização aprendida envolve uma análise em nível meta das saídas dos modelos. Todos os modelos concorrentes são inicialmente acionados para gerar previsões para uma determinada entrada. Subsequentemente, essas previsões são analisadas para determinar o modelo mais confiável para aquela instância específica. Essa abordagem transforma efetivamente as próprias saídas dos modelos em “variáveis de gate” dinâmicas que orientam o processo de seleção.

Um exemplo simplificado pode ser ilustrado em um cenário de classificação binária com dois modelos concorrentes. Quando ambos os modelos concordam quanto ao rótulo da classe, o processo de seleção é direto. No entanto, em casos de discordância, é necessária uma abordagem sistemática para resolver o conflito.

Um método ocasionalmente eficaz, porém primitivo, envolve a análise dos dados de treinamento para identificar a regra de decisão mais confiável para resolver previsões conflitantes. Essa análise requer o exame do desempenho in-sample para determinar qual modelo apresenta maior precisão em cenários específicos de conflito. Por exemplo, se um modelo supera consistentemente um segundo modelo quando ambos discordam, a previsão do primeiro modelo deve ser priorizada.

Essa abordagem orientada por dados permite o desenvolvimento de um conjunto de regras de decisão que otimizam a combinação das saídas dos modelos com base em evidências empíricas.

Existem limitações evidentes na aplicação desse método simples. Se as amostras de treinamento não forem representativas da maioria das instâncias out-of-sample que serão encontradas no uso real, o modelo ensemble resultante será inútil. Metodologias mais sofisticadas, como a discutida em uma seção futura, apresentam maior aplicabilidade e geralmente demonstram desempenho superior em aplicações práticas. Ainda assim, quando é necessário um algoritmo computacionalmente eficiente e rápido, o método apresentado aqui pode se mostrar adequado. Além disso, uma análise aprofundada desse algoritmo simplificado fornece uma base valiosa para a compreensão de conceitos mais avançados.

O código-fonte completo dessa técnica pode ser encontrado no arquivo oracle.mqh, que está anexado ao final deste artigo. O código a seguir é a declaração da classe COracle.

//+------------------------------------------------------------------+
//| Tabulated combination of component model outputs                 |
//+------------------------------------------------------------------+
class COracle
  {
private:
   ulong             m_ncases;
   ulong             m_nin;
   ulong             m_ncats;
   uint              m_nmodels;
   matrix            m_thresh;
   ulong             m_tally[];
public:
                     COracle(void);
                    ~COracle(void);
   bool              fit(matrix &predictors, vector &targets, IModel* &models[],ulong ncats);
   double            predict(vector &inputs,IModel* &models[]);

  };

A classe define dois contêineres principais, m_thresh e m_tally. A matriz m_thresh armazena os limiares de saída que particionam o conjunto de treinamento em subconjuntos de tamanhos iguais, enquanto o array m_tally identifica o modelo ideal para cada um desses subconjuntos. A chamada de fit() constrói um modelo com base nos dados de treinamento fornecidos. A seção inicial desse método é mostrada abaixo.

//+------------------------------------------------------------------+
//| fit an oracle                                                    |
//+------------------------------------------------------------------+
bool COracle::fit(matrix &predictors,vector &targets,IModel *&models[],ulong ncats)
  {
   if(predictors.Rows()!=targets.Size())
     {
      Print(__FUNCTION__," ",__LINE__," invalid inputs ");
      return false;
     }

   m_ncases = predictors.Rows();
   m_nin = predictors.Cols();
   m_nmodels = models.Size();

   m_ncats = ncats;
   ulong nthresh = m_ncats - 1;
   ulong nbins = 1;

   nbins = (ulong)pow(m_ncats,m_nmodels);

   m_thresh = matrix::Zeros(m_nmodels,nthresh);

   ZeroMemory(m_tally);

   if(ArrayResize(m_tally,int(nbins))<0)
     {
      Print(__FUNCTION__," ", __LINE__," error ", GetLastError());
      return false;
     }

   matrix outputs(m_ncases,m_nmodels);
   matrix bins(nbins,m_nmodels);

   bins.Fill(0.0);

   vector inrow;
   for(ulong icase=0;icase<m_ncases; icase++)
     {
      inrow=predictors.Row(icase);
      for(uint imodel =0; imodel<m_nmodels; imodel++)
         outputs[icase][imodel] = models[imodel].forecast(inrow);
     }

   double frac;
   for(uint imodel =0; imodel<m_nmodels; imodel++)
     {
      inrow = outputs.Col(imodel);
      qsortd(0,long(m_ncases-1),inrow);
      for(ulong i = 0; i<nthresh; i++)
        {
         frac = double(i+1)/double(ncats);
         m_thresh[imodel][i] = inrow[ulong(frac*(m_ncases-1))];
        }
     }

O método começa coletando as previsões de cada modelo componente na matriz outputs. A matriz bins é utilizada para contar o número de vezes que cada modelo é o melhor dentro de um bin. Em seguida, para cada coluna da matriz outputs, o número de limiares é determinado encontrando as entradas igualmente espaçadas no vetor de coluna ordenado, inrow. A próxima seção do método fit() progride da seguinte forma.

vector outrow;
   ulong ibin,index, klow, khigh, ibest, k;
   k = 0;
   double diff,best;
   for(ulong icase=0;icase<m_ncases; icase++)
     {
      inrow = predictors.Row(icase);
      outrow = outputs.Row(icase);
      ibin = 0;
      index = 1;
      for(uint imodel =0; imodel<m_nmodels; imodel++)
        {
         if(outrow[imodel] <= m_thresh[imodel][0])
            k = 0;
         else
            if(outrow[imodel] > m_thresh[imodel][nthresh-1])
               k = nthresh;
            else
              {
               klow = 0;
               khigh = nthresh-1;
               while(true)
                 {
                  k = (klow+khigh)/2;
                  if(k == klow)
                    {
                     k = khigh;
                     break;
                    }
                  if(outrow[imodel]<=m_thresh[imodel][k])
                     khigh = k;
                  else
                     klow = k;
                 }
              }
         ibin += k * index;
         index *= ncats;
        }
      best = DBL_MAX;

Para cada amostra no conjunto de dados de treinamento, é determinado o bin correspondente à sua previsão de modelo. Em seguida, é encontrada a previsão, dentre o conjunto de previsões dos modelos componentes, que está mais próxima do valor verdadeiro. Quando encontrada, a combinação correspondente de modelo e bin é incrementada. A seção final do método fit() conclui com o código a seguir.

for(uint imodel =0; imodel<m_nmodels; imodel++)
        {
         diff = fabs(outrow[imodel] - targets[icase]);
         if(diff<best)
           {
            best = diff;
            k = imodel;
           }
        }
      bins[ibin][k]+=1.0;
     }

   for(ibin =0; ibin<nbins; ibin++)
     {
      k = 0;
      ibest = 0;
      for(uint imodel = 0; imodel<m_nmodels; imodel++)
        {
         if(bins[ibin][imodel] > double(ibest))
           {
            ibest = ulong(bins[ibin][imodel]);
            k = ulong(imodel);
           }
        }
      m_tally[ibin] = k;
     }

   return true;
  }

As etapas finais envolvem percorrer a matriz bins para encontrar o modelo que foi selecionado com maior frequência para aquele bin, e os índices desses modelos são armazenados em m_tally. O processo de binning empregado nesta análise utiliza uma estrutura de matriz para categorizar de forma eficiente as amostras de treinamento com base em suas classificações em múltiplos modelos. A matriz pode ser entendida como um vetor que contém outros vetores, com comprimento correspondente ao número de modelos considerados. Cada um armazena a frequência com que cada modelo foi designado como o mais próximo do alvo para a combinação específica de categorias representada pelo bin.

Para ilustrar isso, considere um cenário com três modelos e quatro categorias. Visualize um espaço tridimensional em que cada eixo representa um modelo e é dividido em quatro categorias. Isso resulta em um cubo 4x4x4, em que cada ponto único dentro desse cubo representa uma combinação distinta de atribuições de categorias nos três modelos.

O processo de binning utiliza um par de variáveis de indexação. A primeira desse par referencia diretamente um bin específico ou linha na matriz, correspondendo à combinação única de categorias para uma amostra. A segunda variável de indexação atua como um fator de escala, garantindo que os incrementos naveguem corretamente pelo espaço multidimensional.

Esse esquema de indexação garante que cada incremento no índice da linha posicione corretamente uma amostra no bin apropriado dentro da matriz, capturando de forma eficaz as atribuições conjuntas de categorias em todos os modelos.

O método predict() executa todos os modelos para encontrar o bin ao qual as saídas pertencem. Em seguida, o array m_tally é verificado para identificar qual modelo é mais provável de ser o mais apropriado a ser aplicado à amostra fornecida.

//+------------------------------------------------------------------+
//| make a prediction                                                |
//+------------------------------------------------------------------+
double COracle::predict(vector &inputs,IModel* &models[])
  {
   ulong k, klow, khigh, ibin, index, nthresh ;
   nthresh = m_ncats -1;
   k = 0;
   ibin = 0;
   index = 1;
   vector otk(m_nmodels);

   for(uint imodel = 0; imodel<m_nmodels; imodel++)
     {
      otk[imodel] = models[imodel].forecast(inputs);

      if(otk[imodel]<m_thresh[imodel][0])
         k = 0;
      else
         if(otk[imodel]>m_thresh[imodel][nthresh-1])
            k = nthresh - 1;
         else
           {
            klow=0;
            khigh = nthresh -1 ;
            while(true)
              {
               k = (klow + khigh) / 2;
               if(k == klow)
                 {
                  k = khigh;
                  break;
                 }
               if(otk[imodel] <= m_thresh[imodel][k])
                  khigh = k;
               else
                  klow = k;
              }
           }
      ibin += k*index;
      index *= m_ncats;
     }

   return otk[ulong(m_tally[ibin])];
  }

Testando o código

O script Oracle_Demo.mq5 testa a funcionalidade da classe COracle. Esse programa permite ao usuário configurar vários parâmetros de simulação, incluindo o tamanho do conjunto de dados de treinamento, o número de bins, o número de modelos e um nível de ruído que controla a complexidade da tarefa de previsão. A saída a seguir do script apresenta os resultados obtidos em uma série de cenários envolvendo três modelos com poder preditivo equivalente.

Baixa dificuldade de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 10 amostras.

PF      0       13:59:15.542    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10777835
MQ      0       13:59:15.542    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10777835

Dificuldade moderada de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 10 amostras.

FD      0       14:00:30.967    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38588979
KG      0       14:00:30.967    Oracle_Demo (BTCUSD,D1) Oracle error = 0.38529990

Alta dificuldade de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 10 amostras.

ES      0       14:01:11.874    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.16908710
ND      0       14:01:11.874    Oracle_Demo (BTCUSD,D1) Oracle error = 1.16824689

Baixa dificuldade de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

LQ      0       14:02:57.441    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10706090
NJ      0       14:02:57.441    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10705483

Dificuldade moderada de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

LL      0       14:04:24.070    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.36310507
JO      0       14:04:24.070    Oracle_Demo (BTCUSD,D1) Oracle error = 0.36303485

Alta dificuldade de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

RJ      0       14:06:02.290    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12115161
PM      0       14:06:02.290    Oracle_Demo (BTCUSD,D1) Oracle error = 1.12076456

Baixa dificuldade de previsão, 4 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

FI      0       14:08:24.445    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10681953
FR      0       14:08:24.445    Oracle_Demo (BTCUSD,D1) Oracle error = 0.10681329

Dificuldade moderada de previsão, 4 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

KG      0       14:10:29.012    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.36348921
LP      0       14:10:29.012    Oracle_Demo (BTCUSD,D1) Oracle error = 0.36363647

Alta dificuldade de previsão, 4 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

MR      0       14:12:16.225    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12231642
EE      0       14:12:16.225    Oracle_Demo (BTCUSD,D1) Oracle error = 1.12258202

Experimentos subsequentes incorporaram um quarto modelo, projetado para produzir previsões aleatórias, simulando assim um cenário com um modelo não informativo. Os resultados, apresentados abaixo, demonstram uma alteração significativa no comportamento do sistema.

Baixa dificuldade de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 10 amostras.

GH      0       14:13:47.886    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12971017
MS      0       14:13:47.886    Oracle_Demo (BTCUSD,D1) Oracle error = 0.14153652

Dificuldade moderada de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 10 amostras.

JN      0       14:14:16.985    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.40381512
MI      0       14:14:16.985    Oracle_Demo (BTCUSD,D1) Oracle error = 0.40074764

Alta dificuldade de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 10 amostras.

ND      0       14:14:54.040    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.16720001
OG      0       14:14:54.040    Oracle_Demo (BTCUSD,D1) Oracle error = 1.16304663

Baixa dificuldade de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

QJ      0       14:17:05.521    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12727773
HM      0       14:17:05.521    Oracle_Demo (BTCUSD,D1) Oracle error = 0.17687364

Dificuldade moderada de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

QP      0       14:18:26.976    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38337835
CK      0       14:18:26.976    Oracle_Demo (BTCUSD,D1) Oracle error = 0.39318874

Alta dificuldade de previsão, 2 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

IF      0       14:20:01.925    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.13780482
IQ      0       14:20:01.925    Oracle_Demo (BTCUSD,D1) Oracle error = 1.13878032

Baixa dificuldade de previsão, 4 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

HL      0       14:23:03.090    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12709947
QO      0       14:23:03.090    Oracle_Demo (BTCUSD,D1) Oracle error = 0.11975572

Dificuldade moderada de previsão, 4 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

CR      0       14:25:25.091    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.38314408
CE      0       14:25:25.091    Oracle_Demo (BTCUSD,D1) Oracle error = 0.37892436

Alta dificuldade de previsão, 4 bins e tamanho do conjunto de dados de treinamento de 100 amostras.

GH      0       14:27:50.024    Oracle_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.13828093
CS      0       14:27:50.024    Oracle_Demo (BTCUSD,D1) Oracle error = 1.13422816

A análise de ambos os conjuntos de resultados mostra que, em cenários com baixos níveis de ruído, essa técnica demonstra eficácia excepcional, resultando em uma redução substancial da variância do erro. Por outro lado, em cenários de alto ruído, a técnica não apenas deixa de proporcionar melhorias significativas, como frequentemente leva a um desempenho inferior em comparação ao uso de um único modelo. Esse fenômeno é observado mesmo quando todos os modelos constituintes possuem poder preditivo equivalente, embora as diferenças de desempenho nesses casos sejam reconhecidamente pequenas.

Os testes também revelam que a utilização de quatro bins em vez de dois resultou em diferenças de desempenho inconsistentes e insignificantes. Esse resultado não é surpreendente, dado que ou todos os modelos exibem poder preditivo comparável ou um modelo produz consistentemente previsões inúteis. A principal função desse algoritmo, no contexto atual, é identificar e descartar modelos não informativos quando eles estão presentes. No entanto, é concebível que existam cenários em que um número maior de categorias se mostre benéfico.

Ensembles de regressão geral com gating

Esta seção apresenta uma técnica amplamente aplicável para a combinação de modelos que utiliza variáveis de gating. O método é inspirado em conceitos de Redes Neurais de Regressão Geral (GRNN) e permite que uma ou mais variáveis atuem como gates dinâmicos, modulando a influência de cada modelo contribuinte. Em contraste com métodos de gating anteriores, que exigem a seleção de um único modelo para produzir a saída final, o gating de regressão geral integra as saídas de todos os modelos constituintes ao ponderar de forma ótima cada um com base nas variáveis de gate. Essas variáveis de gating podem incluir valores externos medidos, bem como as saídas dos modelos individuais. Essa abordagem é denominada método de regressão geral com gating.

A implementação desse método requer pelo menos dois modelos componentes treinados e um conjunto de dados separado para o treinamento do ensemble inspirado em GRNN. O conjunto de dados de treinamento deve conter uma ou mais variáveis de gate, previsões dos modelos componentes e os valores-alvo correspondentes. Notavelmente, também é possível designar determinadas saídas dos modelos componentes como variáveis de gate, ampliando ainda mais a flexibilidade da abordagem.

Uma Rede Neural de Regressão Geral (GRNN) é um tipo de rede neural artificial projetada para tarefas de regressão, que envolvem a previsão de saídas contínuas. A GRNN opera com base nos princípios de estimação de densidade por kernel e utiliza uma abordagem de aprendizado baseada em memória. Ela consiste em quatro camadas: entrada, padrão, soma e saída.

A camada de entrada recebe as variáveis preditoras, que são passadas para a camada de padrão, onde cada neurônio representa uma amostra de treinamento e calcula a similaridade entre a entrada e os dados de treinamento utilizando uma função de base radial. A camada de soma agrega as saídas ponderadas da camada de padrão, e a camada de saída produz a previsão final ao normalizar a soma dos pesos.

A GRNN é particularmente vantajosa para modelar relações não lineares, exigindo tempo mínimo de treinamento e adaptando-se automaticamente à distribuição subjacente dos dados.

Nesse contexto, a distância euclidiana ponderada entre uma amostra de teste e uma amostra de treinamento é determinada pelas variáveis de gate. Especificamente, ao avaliar uma amostra de teste, o gate GRNN prioriza as amostras de treinamento cujas variáveis de gate se assemelham mais às da amostra de teste. Ao empregar a GRNN para prever o erro quadrático de um modelo, o erro quadrático previsto para um modelo componente é calculado utilizando a equação abaixo.

Embora existam infinitas maneiras de combinar modelos componentes para produzir uma previsão conjunta, a abordagem mais simples envolve expressar a previsão final como uma combinação linear das saídas dos modelos. Se os modelos componentes exibirem a propriedade desejável de previsões não enviesadas, essa propriedade é preservada apenas se for imposta a condição de que os pesos somem a unidade. Mesmo quando as previsões não são estritamente não enviesadas, essa condição permanece vantajosa na maioria dos cenários. Para uma combinação linear de estimadores não enviesados com erro quadrático médio mínimo, os pesos ideais são proporcionais ao inverso da variância de cada estimador. Ao substituir o erro quadrático previsto pela variância, os pesos podem ser calculados utilizando a fórmula a seguir.

Para gerar uma previsão com gating por GRNN, dados valores apropriados para os pesos sigma, iniciamos estimando o erro de previsão para cada modelo em uma determinada amostra de teste. Subsequentemente, os pesos são calculados, e os modelos componentes são avaliados na amostra de teste. Por fim, as previsões individuais dos modelos componentes são combinadas em uma estimativa final utilizando os pesos calculados.

Determinar valores ideais para os pesos sigma não é uma tarefa simples, pois exige estimação a partir dos dados de treinamento. O método mais eficaz para avaliar a qualidade de um vetor sigma candidato é por meio de validação cruzada. Isso envolve remover uma amostra do conjunto de treinamento para servir como caso de teste, gerar uma previsão com gating por GRNN para essa amostra utilizando o vetor sigma especificado e comparar o valor previsto com o valor verdadeiro. Em seguida, a amostra é retornada ao conjunto de treinamento, e o processo é repetido para todas as amostras do conjunto de dados. O erro quadrático médio ao longo dessas repetições serve como uma medida da qualidade do vetor sigma candidato.

Qualquer algoritmo de otimização sem derivadas pode ser utilizado para determinar o conjunto de pesos sigma que minimiza o erro de validação cruzada. Entre as opções disponíveis, a evolução diferencial é reconhecida por sua robustez e ampla aplicabilidade. No entanto, o método de Powell oferece uma alternativa computacionalmente eficiente, apresentando desempenho satisfatório na maioria das aplicações práticas. Dada sua eficiência, o método de Powell é adotado neste estudo, apesar da superioridade ocasional da evolução diferencial em casos raros que envolvem múltiplos extremos locais.

O arquivo gatedreg.mqh contém o código-fonte da classe CGatedReg, que implementa o método de ensemble com gating inspirado em GRNN descrito acima. A declaração da classe é apresentada abaixo.

//+------------------------------------------------------------------+
//|  GRNN gating model combination                                   |
//+------------------------------------------------------------------+
class CGatedReg:public CPowellsMethod
  {
private:
   ulong             m_nsamples;
   ulong             m_ngates;
   ulong             m_nmodels;
   matrix            m_tset;
   vector            m_sigma;
   vector            m_errvals;
   vector            m_params;

   double            criter(vector &params);
   double            trial(vector &gates, vector &contenders,long i_exclude,long n_exclude);
   virtual double    func(vector &p) {  return criter(p); }
public:
                     CGatedReg(void);
                    ~CGatedReg(void);
   bool              fit(matrix &gates, matrix &contenders,vector &targets);
   double            predict(vector &gates, vector &contenders);
  };

As previsões dos modelos componentes presumem-se pré-computadas e armazenadas em uma matriz. Cada modelo deve ter passado por treinamento prévio para prever a variável dependente. Variáveis de gate (frequentemente uma única variável) serão empregadas para ponderar diferencialmente as contribuições desses modelos componentes na previsão final. O método fit() é responsável por copiar os dados de treinamento necessários e determinar os pesos sigma ideais. A implementação do método é apresentada a seguir.

//+------------------------------------------------------------------+
//| fit a gated grnn model                                           |
//+------------------------------------------------------------------+
bool CGatedReg::fit(matrix &gates,matrix &contenders,vector &targets)
  {
   if(gates.Rows()!=contenders.Rows() || contenders.Rows()!=targets.Size()  || gates.Rows()!=targets.Size())
     {
      Print(__FUNCTION__, " ", __LINE__, " invalid training data ");
      return false;
     }
   m_nsamples = gates.Rows();
   m_ngates = gates.Cols();
   m_nmodels = contenders.Cols();

   m_tset = matrix::Zeros(m_nsamples,m_ngates+m_nmodels+1);
   m_sigma = vector::Zeros(m_ngates);
   m_errvals = vector::Zeros(m_nmodels);

   for(ulong i = 0; i<m_nsamples; i++)
     {
      for(ulong j = 0; j<m_ngates; j++)
         m_tset[i][j] = gates[i][j];
      for(ulong k = 0; k<m_nmodels; k++)
         m_tset[i][m_ngates+k] = contenders[i][k];
      m_tset[i][m_ngates+m_nmodels] = targets[i];
     }

   m_params = vector::Zeros(m_ngates);

   double err =  criter(m_params);
   if(err > 0.0)
      Optimize(m_params);

   criter(m_params);

   return true;

  }

Os dados de treinamento, compreendendo todas as entradas do método fit(), devem ser preservados, pois previsões subsequentes exigem o uso de regressão geral para a previsão intermediária do erro de cada modelo. Além disso, o vetor m_errval será necessário para cada previsão. A técnica de otimização de Powell é utilizada para identificar os pesos sigma ideais. A função objetivo a ser minimizada é definida como o método privado criter().

//+------------------------------------------------------------------+
//|  function criterion                                              |
//+------------------------------------------------------------------+
double CGatedReg::criter(vector &params)
  {
   int i, ngates, nmodels, ncases;
   double  out, diff, error, penalty ;
   vector inputs1,inputs2,row;

   ngates = int(m_ngates); ;
   nmodels = int(m_nmodels) ;
   ncases = int(m_nsamples) ;

   penalty = 0.0 ;
   for(i=0 ; i<ngates ; i++)
     {
      if(params[i] > 8.0)
        {
         m_sigma[i] = exp(8.0) ;
         penalty += 10.0 * (params[i] - 8.0) ;
        }
      else
         if(params[i] < -8.0)
           {
            m_sigma[i] = exp(-8.0) ;
            penalty += 10.0 * (-params[i] - 8.0) ;
           }
         else
            m_sigma[i] = exp(params[i]) ;
     }

   error = 0.0 ;

   for(i=0 ; i<ncases ; i++)
     {
      row = m_tset.Row(i);
      inputs1 = np::sliceVector(row,0,m_ngates);
      inputs2 = np::sliceVector(row,ulong(ngates),ulong(ngates+nmodels));
      out = trial(inputs1, inputs2, long(i), 0) ;
      diff = row[ngates+nmodels] - out ;
      error += diff * diff ;
     }

   return error / double(ncases) + penalty ;

  }

Esse método emprega validação cruzada para avaliar a qualidade de um vetor sigma de teste. Em vez de otimizar diretamente cada sigma, o logaritmo de sigma é otimizado. Isso lineariza o impacto das variações, resultando em maior estabilidade. Para mitigar os problemas associados à superfície de erro de um gate GRNN que apresenta planicidade para valores extremos. A função de critério inicialmente exponencia o parâmetro, impondo ao mesmo tempo um intervalo limitado. Um termo de penalidade é introduzido para incentivar valores de sigma que não sejam extremos. Para cada amostra de treinamento, é feita uma previsão, e essa previsão é comparada com o valor verdadeiro. O erro quadrático é acumulado para servir como critério de erro.

Os elementos de m_errvals são inicializados com zero, para acumular o numerador da equação de erro. O denominador dessa equação não requer computação explícita, pois é cancelado ao se considerar o fator de normalização no denominador da equação dos pesos. Antes de incorporar cada termo à soma, a proximidade sequencial de uma amostra de teste em relação a uma amostra de treinamento é verificada.

Esse método pode ser utilizado para previsão tanto com membros do conjunto de treinamento quanto com amostras totalmente desconhecidas. Ao passar o número de sequência i_exclude de cada amostra de treinamento para a rotina trial(), a validação cruzada pode ser implementada. Um limite de distância, n_exclude, também é passado. Normalmente, isso é definido como zero, excluindo apenas o caso único.

Os leitores devem observar que o algoritmo de validação cruzada apresenta uma limitação séria quando se trata de lidar com conjuntos de treinamento que exibem correlação serial. O que é comum em dados de séries temporais. Isso pode ser tratado excluindo amostras que sejam espacialmente próximas à amostra de treinamento que está sendo testada.

//+------------------------------------------------------------------+
//| trial ( )                                                        |
//+------------------------------------------------------------------+
double CGatedReg::trial(vector &gates, vector &contenders, long i_exclude,long n_exclude)
  {
   int icase, ivar, idist, size, ncases;
   double psum, diff, dist, err, out ;

   m_errvals.Fill(0.0);
   int ngates = int(m_ngates);
   int nmodels = int(m_nmodels);
   size = ngates + nmodels + 1 ;
   ncases = int(m_nsamples);

   for(icase=0 ; icase<ncases ; icase++)
     {

      idist = (int)fabs(int(i_exclude) - icase) ;
      if(ncases - idist < idist)
         idist = ncases - idist ;

      if(idist <= int(n_exclude))
         continue ;

      dist = 0.0 ;

      for(ivar=0 ; ivar<ngates ; ivar++)
        {
         diff = gates[ivar] - m_tset[icase][ivar] ;
         diff /= m_sigma[ivar] ;
         dist += diff * diff ;
        }

      dist = exp(-dist) ;

      for(ivar=0 ; ivar<nmodels ; ivar++)
        {
         err = m_tset[icase][ngates+ivar] - m_tset[icase][ngates+nmodels] ;
         m_errvals[ivar] += dist * err * err ;
        }

     }

   psum = 0.0 ;
   for(ivar=0 ; ivar<nmodels ; ivar++)
     {
      if(m_errvals[ivar] > 1.e-30)
         m_errvals[ivar] = 1.0 / m_errvals[ivar] ;
      else
         m_errvals[ivar] = 1.e30 ;
      psum += m_errvals[ivar] ;
     }

   for(ivar=0 ; ivar<nmodels ; ivar++)
      m_errvals[ivar] /= psum ;

   out = 0.0 ;
   for(ivar=0 ; ivar<nmodels ; ivar++)
      out += m_errvals[ivar] * contenders[ivar] ;

   return out ;
  }

Se um caso de treinamento passar no teste de exclusão da validação cruzada, a distância euclidiana ponderada entre os dois casos é calculada. Essa distância é exponenciada para uso no cálculo do erro de previsão de cada modelo componente. Subsequentemente, para cada modelo, o erro de previsão é determinado. A etapa final envolve a utilização da equação de pesos dos modelos para combinar as saídas de cada modelo concorrente em uma única previsão. Isso constitui o valor de retorno da função.

//+------------------------------------------------------------------+
//|  infer                                                           |
//+------------------------------------------------------------------+
double CGatedReg::predict(vector &gates,vector &contenders)
  {
   return trial(gates,contenders,-1,0);
  }

Testando um ensemble GRNN com gating

O script Gating_Demo.mqh oferece uma comparação abrangente de quatro estratégias distintas de gating. Cada estratégia atende a um propósito específico ao demonstrar diferentes aspectos da seleção e combinação de modelos. A seguir, apresenta-se uma breve visão geral das quatro estratégias:

• Previsões dos componentes como variáveis de gating: essa abordagem utiliza diretamente as previsões dos modelos componentes individuais como variáveis de gating, permitindo uma comparação direta com o método de referência (classe COracle). Ela testa o efeito de usar as próprias saídas dos modelos como fatores de decisão na seleção de modelos.

• Gating por variáveis originais: nessa estratégia, as variáveis de entrada originais (aquelas usadas pelos modelos componentes) servem como variáveis de gating. Como essas variáveis não foram projetadas para atuar como sinais de gating eficazes, essa abordagem ajuda a demonstrar o impacto de variáveis de gating fracas ou irrelevantes no desempenho do modelo.

• Gating aleatório: essa estratégia emprega números gerados aleatoriamente como variáveis de gating, simulando um cenário em que não há variáveis de gating informativas disponíveis. Ela serve como uma linha de base para mostrar a queda de desempenho ao utilizar sinais completamente não informativos.

• Gating baseado em razão: nessa abordagem, o logaritmo da razão entre os erros de previsão do primeiro e do segundo modelos é utilizado como variável de gating. Embora esse método seja irrealista em um cenário do mundo real (já que o erro verdadeiro de previsão dos modelos geralmente é desconhecido), ele serve como um cenário idealizado para dois modelos. Para múltiplos modelos, ele fornece informações de gating parciais, mas ainda valiosas.

Essas quatro estratégias foram projetadas para testar várias condições de desempenho e oferecer percepções sobre os pontos fortes e as limitações de diferentes técnicas de gating para aprendizado por ensemble. O script avalia como cada estratégia de gating impacta a precisão geral das previsões e a variância do erro, possibilitando uma compreensão mais clara da eficácia do mecanismo de gating GRNN.

Três modelos, 100 amostras e baixa dificuldade de previsão.

EK      0       14:36:33.869    Gating_Demo (BTCUSD,D1)  1000    replications completed.
GL      0       14:36:33.869    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.10790466
JP      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Component error = 0.10790458
DF      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Original error = 0.10790458
HM      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Random error = 0.10790458
DJ      0       14:36:33.869    Gating_Demo (BTCUSD,D1) Ratio error = 0.10790458

Três modelos, 100 amostras e alta dificuldade de previsão.

GF      0       14:40:57.600    Gating_Demo (BTCUSD,D1)  1000    replications completed.
LQ      0       14:40:57.600    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.12143040
FE      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Component error = 1.11991444
GQ      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Original error = 1.11991445
QI      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Random error = 1.11991443
EO      0       14:40:57.600    Gating_Demo (BTCUSD,D1) Ratio error = 1.11991443

Quatro modelos, 100 amostras e baixa dificuldade de previsão.

IO      0       14:42:58.751    Gating_Demo (BTCUSD,D1)  1000    replications completed.
LK      0       14:42:58.751    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 0.12792841
RS      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Component error = 0.11516554
MK      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Original error = 0.11516373
GR      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Random error = 0.11516595
GE      0       14:42:58.751    Gating_Demo (BTCUSD,D1) Ratio error = 0.11516595

Quatro modelos, 100 amostras e alta dificuldade de previsão.

QQ      0       14:45:15.030    Gating_Demo (BTCUSD,D1)  1000    replications completed.
HE      0       14:45:15.030    Gating_Demo (BTCUSD,D1)  ++++++ Mean raw error = 1.14025014
EI      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Component error = 1.13144872
GM      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Original error = 1.13144863
QD      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Random error = 1.13144883
NL      0       14:45:15.030    Gating_Demo (BTCUSD,D1) Ratio error = 1.13144882

A surpreendente melhoria de desempenho obtida por meio do gating aleatório pode ser atribuída à forma como o algoritmo de gating GRNN funciona. Em cenários típicos, seria de se esperar que sinais de gating aleatórios piorassem o desempenho do modelo, pois introduzem ruído e não fornecem informações úteis para a seleção de modelos. No entanto, o mecanismo GRNN baseia-se em distâncias euclidianas ponderadas entre amostras de treinamento e ajusta sua previsão com base em quão semelhante a amostra de teste é às amostras de treinamento.

Nos casos em que o sinal de gating é aleatório, o algoritmo GRNN ainda utiliza a estrutura geral dos dados e dos modelos para calcular uma média ponderada das previsões dos modelos componentes. Como os valores de gating aleatórios não introduzem um viés forte em favor de qualquer modelo específico, o algoritmo pode depender mais fortemente da estrutura inerente dos dados e do desempenho dos modelos individuais, que são treinados para prever bem. O resultado geral pode ser uma combinação de modelos mais robusta, com o gating aleatório atuando efetivamente como um neutralizador, garantindo que nenhum modelo único domine o processo de tomada de decisão.

No caso em que três modelos exibem alta precisão preditiva e um modelo gera previsões aleatórias, a abordagem de gating aleatório pode inadvertidamente atuar como um método de descarte do modelo aleatório, reduzindo sua influência no ensemble. Isso leva a uma situação em que o desempenho do modelo ensemble melhora significativamente, à medida que a influência do modelo aleatório não informativo é minimizada.

Assim, embora o gating aleatório possa não parecer intuitivamente benéfico, o processo de gating GRNN pode explorar a estrutura do conjunto de dados e dos modelos de maneiras que resultam em melhorias inesperadas, especialmente em problemas de previsão “fáceis”, nos quais os modelos já são altamente precisos. Esse comportamento ressalta o poder da técnica de gating GRNN, que, mesmo em situações subótimas, consegue aproveitar o potencial de múltiplos modelos para fornecer previsões aprimoradas ao ponderar efetivamente a contribuição de cada modelo.

O algoritmo estima efetivamente o erro de previsão de cada modelo. Na presença de um modelo com erros de previsão consistentemente elevados, como no caso do modelo de previsões aleatórias, o erro de previsão gerará estimativas de erro consistentemente grandes para esse modelo. O que, por sua vez, resulta no esquema de ponderação do ensemble atribuindo um peso correspondentemente baixo a esse modelo dentro da combinação ponderada.

Essa observação destaca a principal vantagem do gating GRNN. Ele pode identificar e reduzir efetivamente o peso de modelos com fraco desempenho preditivo, mesmo quando as próprias variáveis de gating carecem de poder preditivo inerente. Consequentemente, mesmo em situações em que os sinais de gating fornecem informações limitadas ou inexistentes, o gating GRNN ainda pode produzir melhorias significativas de desempenho, particularmente quando o ensemble inclui modelos com níveis variados de precisão preditiva.

Conclusão

Essas técnicas demonstram a adaptabilidade dos mecanismos de gating no aprimoramento da interpretabilidade e do poder preditivo de algoritmos de aprendizado. A escolha da técnica depende do contexto específico, incluindo a complexidade da tarefa, a natureza dos dados e as restrições computacionais. Frequentemente, uma combinação de métodos, como técnicas de otimização associadas a percepções do domínio, produz os resultados mais eficazes e interpretáveis. Todo o código referenciado no artigo está anexado ao final. A tabela abaixo descreve todos os arquivos-fonte acompanhantes.

Nome do Arquivo	Descrição
MQL5/include/gatedreg.mqh	Contém a definição da classe CGatedReg que implementa um ensemble GRNN com gating
MQL5/include/imodel.mqh	Contém a definição das interfaces que encapsulam um modelo treinado
MQL5/include/minimize.mqh	Fornece a definição do CPowellsMethod, que implementa a minimização de funções utilizando o método de Powell
MQL5/include/multilayerperceptron.mqh	Fornece a definição da classe CMlp, que é uma implementação de um perceptron multicamadas
MQL5/include/np.mqh	Uma coleção de funções auxiliares genéricas para manipulação de vetores e matrizes
MQL5/include/oracle.mqh	Fornece a definição da classe COracle, que permite a seleção de modelos a partir de um conjunto de modelos componentes especialistas
MQL5/include/qsort.mqh	Fornece funções simples para ordenação de vetores
Mql5/scripts/Gating_Demo.mq5	Um script que demonstra a funcionalidade fornecida pela classe CGatedReg
Mql5/scripts/Oracle_Demo.mq5	Outro script que demonstra o uso da classe COracle