Представления частотной области временных рядов: Спектральная функция

Введение

Ценовые котировки, которые мы наблюдаем на графиках, представляют собой данные, разбросанные во времени. Считается, что ценовой ряд находится во временной области. Но это не единственный способ отобразить такую информацию. Отображение данных в разных областях может выявить интересные характеристики ряда, которые могут быть не очевидны при проведении анализа исключительно во временной области. Кроме того, мы обсудим некоторые многообещающие перспективы анализа временных рядов в частотной области с использованием дискретного преобразования Фурье (ДПФ). Мы сосредоточимся на анализе спектральных функций, предоставив практические примеры того, как рассчитать и распознать характеристики временных рядов, выявленные с помощью этого метода анализа. Мы также кратко рассмотрим важные методы предварительной обработки, которые следует использовать перед применением дискретного преобразования Фурье.

Дискретное преобразование Фурье

Прежде чем демонстрировать методы анализа спектральной функции (spectrum analysis), мы сначала должны понять, что такое спектральная функция. Анализ спектральных функций временных рядов относится к обширной теме обработки сигналов. В статье "Технические индикаторы как цифровые фильтры" автор показывает, как любую сложную последовательность можно разбить на обычные синусоидальные и косинусоидальные волны. Это позволяет разбить сложный процесс к простым компонентам. Все это возможно благодаря выбранному представлению в частотной области. Основой представления является набор функций для воспроизведения временного ряда.

Одним из наиболее часто применяемых представлений временных рядов в частотной области является дискретное преобразование Фурье. В качестве основы используются синусоидальные и косинусоидальные волны, которые охватывают один цикл на протяжении всей серии. Его самая ценная характеристика заключается в том, что любой временной ряд, описанный в этой форме, всегда определяется однозначно, то есть никакие два ряда не будут иметь одинаковых представлений в частотной области. Спектральная функция показывает, сколько мощности, или энергии, имеет сигнал на разных частотах. В контексте данных временного ряда спектральная функция предоставляет информацию о распределении энергии по разным частотам, составляющим временной ряд.

Вычисление дискретного преобразования Фурье

Чтобы преобразовать любой ряд в частотную область с помощью ДПФ, используется следующая формула.

Каждый член уравнения представляет собой комплексное число, а x — ряд необработанных данных. Каждый член представляет собой периодический компонент, который повторяется ровно j раз по всему диапазону значений. Быстрое преобразование Фурье — это алгоритм, ускоряющий вычисление дискретных преобразований Фурье. Он рекурсивно разбивает серию пополам, преобразуя каждую половину, а затем объединяя результаты.

Спектральная функция

Применяя некоторые базовые математические методы, мы можем рассчитать количество энергии, обусловленное частотной составляющей. Нанеся комплексное число на декартову плоскость, где действительная часть откладывается по оси X, а мнимая часть - по оси Y, мы можем применить теорему Пифагора, которая гласит, что абсолютное значение равно квадратному корню из суммы квадратов как действительных, так и мнимых частей. Следовательно, энергия, обусловленная определенной частотой, равна квадрату ее абсолютного значения. Мощность рассчитывается путем деления квадрата абсолютного значения функции на квадрат числа значений в ряду временной области.

Но прежде чем мы применим необработанный расчет ДПФ к серии, мы должны пройти несколько шагов предварительной обработки, чтобы получить точную оценку мощности на определенной частоте. Это необходимо, так как ДПФ работает с сегментами данных конечной длины и предполагает, что входной сигнал является периодическим, что может привести к спектральной утечке и другим искажениям, если значения не соответствуют этому предположению. Для смягчения этих проблем применяется оконная обработка данных.

Оконная функция

Окно - умножение временного ряда на оконную функцию, которая представляет собой математическую функцию, присваивающую веса различным точкам временного ряда. Это важный шаг в подготовке данных временных рядов для анализа с использованием дискретного преобразования Фурье.

Когда мы анализируем данные временных рядов с помощью ДПФ, мы делим данные на более мелкие сегменты. Если мы не добавим рамку (в данном случае - оконную функцию) вокруг каждого сегмента, мы можем упустить важную информацию, и наш анализ будет неполным. Окно данных сужает концы временного ряда, уменьшая резкие переходы на границах окна ДПФ. Функция сужения обычно предназначена для плавного сужения сигнала до нуля на краях окна, что уменьшает амплитуду любых спектральных компонентов вблизи края окна.

Каким бы важным ни был этот процесс, он потенциально приводит к искажению или изменению исходной формы данных. Эту проблему можно устранить или свести к минимуму, центрируя серию до применения оконной функции к необработанной серии. Когда временной ряд центрирован, его среднее значение вычитается из каждой точки данных в ряду, в результате чего получается новый ряд с нулевым средним значением.

Доступно множество оконных функций, таких как прямоугольное окно, окно Хэмминга, окно Ханнинга, окно Блэкмана и окно Кайзера, каждая из которых имеет свои уникальные свойства и варианты использования. В этом тексте мы будем использовать окно данных Уэлча (Welch data window).  
    
Окно задается формулой ниже.

Каждое значение исходного временного ряда должно быть умножено на соответствующее m(i).

Чтобы центрировать значения, средневзвешенное значение ряда вычисляется с использованием оконной функции. Затем это среднее значение вычитается из каждой точки ряда перед применением самого окна.

Сглаживание спектральной функции

Дискретный спектр мощности, как правило, трудно интерпретировать, так как обычно имеется множество узких пиков, выступающих повсюду. Чтобы лучше понять, что происходит, может потребоваться некоторое сглаживание. Для этих целей обычно применяется фильтр Савицкого-Голея. Его функция фильтрации определяется двумя параметрами: половинной длиной и степенью полиномов. Половина длины указывает количество значений, смежных (до и после) фильтруемому. Степени указывают степень полинома, который должен соответствовать текущему значению и его соседним значениям.

Класс CSpectrum

В этом разделе мы представим класс, позволяющий легко анализировать ряды в mql5. Одна из основных особенностей класса - метод отрисовки, который упрощает отображение различных спектральных графиков с помощью нескольких строк кода.

Весь класс приведен ниже.

//+------------------------------------------------------------------+
//|                                                     Spectrum.mqh |
//|                        Copyright 2023, MetaQuotes Software Corp. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2023, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#include<Math\Stat\Math.mqh>
#include<Math\Alglib\fasttransforms.mqh>
#include<Graphics\Graphic.mqh>

enum ENUM_SPECTRUM_PLOT
  {
   PLOT_POWER_SPECTRUM=0,//PowerSpectrum
   PLOT_FILTERED_POWER_SPECTRUM,//FilteredPowerSpectrum
   PLOT_CUMULATIVE_SPECTRUM_DEVIATION//CumulativeSpectrumDeviation
  };

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CSpectrumAnalysis
  {
private:
   bool              m_window,m_initialized;
   int               m_n,m_cases;
   complex           m_dft[];
   double            m_real[];
   double            m_win,m_win2;
   double            m_wsq;
   double            m_wsum,m_dsum;
   int               m_window_size,m_poly_order;
   void              savgol(double &data[], double&out[], int window_size, int poly_order);
public:
   //---constructor
                     CSpectrumAnalysis(const bool window,double &in_series[]);
   //---destructor
                    ~CSpectrumAnalysis(void)
     {
      if(m_n)
        {
         ArrayFree(m_dft);
         ArrayFree(m_real);
        }
     }
   bool              PowerSpectrum(double &out_p[]);
   bool              CumulativePowerSpectrum(double & out_cp[]);
   double            CumulativeSpectrumDeviation(double &out_csd[]);
   void              Plot(ENUM_SPECTRUM_PLOT plot_series,int window_size=5, int poly_order=2, color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400);
  };

Чтобы использовать его, пользователь вызывает параметрический конструктор, передавая ему два параметра. Первый параметр указывает, следует ли применять оконную функцию к данным. Следует отметить, что при использовании оконной функции также выполняется центрирование ряда. Второй параметр конструктора — массив, содержащий необработанные значения для анализа.

Преобразование Фурье выполняется в конструкторе, а комплексные значения, связанные со спектром, сохраняются в массиве ДПФ.

void CSpectrumAnalysis::CSpectrumAnalysis(const bool apply_window,double &in_series[])
  {
   int n=ArraySize(in_series);

   m_initialized=false;

   if(n<=0)
      return;

   m_cases=(n/2)+1;
   m_n=n;

   m_window=apply_window;

   ArrayResize(m_real,n);

   if(m_window)
     {
      m_wsum=m_dsum=m_wsq=0;
      for(int i=0; i<n; i++)
        {
         m_win=(i-0.5*(n-1))/(0.5*(n+1));
         m_win=1.0-m_win*m_win;
         m_wsum+=m_win;
         m_dsum+=m_win*in_series[i];
         m_wsq+=m_win*m_win;
        }
      m_dsum/=m_wsum;
      m_wsq=1.0/sqrt(n*m_wsq);
     }
   else
     {
      m_dsum=0;
      m_wsq=1.0;
     }


   for(int i=0; i<n; i++)
     {
      if(m_window)
        {
         m_win=(i-0.5*(n-1))/(0.5*(n+1));
         m_win=1.0-m_win*m_win;
        }
      else
         m_win=1.0;
      m_win*=m_wsq;
      m_real[i]=m_win*(in_series[i]-m_dsum);
     }
   CFastFourierTransform::FFTR1D(m_real,n,m_dft);

   m_initialized=true;

  }

Для расчета и получения значений спектральной функции, совокупной спектральной функции, а также суммарного отклонения спектра класс предоставляет методы PowerSpectrum(), CumulativePowerSpectrum() и CumulativeSpectrumDeviation() соответственно. Для каждого метода требуется один параметр массива, в который будут скопированы соответствующие значения.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CSpectrumAnalysis::PowerSpectrum(double &out_p[])
  {
   if(!m_initialized)
      return false;

   ArrayResize(out_p,m_cases);

   for(int i=0; i<m_cases; i++)
     {
      out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i && (i<(m_cases-1)))
         out_p[i]*=2;
     }

   return true;
  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
bool CSpectrumAnalysis::CumulativePowerSpectrum(double &out_cp[])
  {
   if(!m_initialized)
      return false;

   double out_p[];

   ArrayResize(out_p,m_cases);
   ArrayResize(out_cp,m_cases);

   for(int i=0; i<m_cases; i++)
     {
      out_p[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i && (i<(m_cases-1)))
         out_p[i]*=2;
     }

   for(int i=0; i<m_cases; i++)
     {
      out_cp[i]=0;
      for(int j=i; j>=1; j--)
         out_cp[i]+=out_p[j];
     }

   ArrayFree(out_p);

   return true;

  }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
double CSpectrumAnalysis::CumulativeSpectrumDeviation(double &out_csd[])
  {
   if(!m_initialized)
      return 0;

   ArrayResize(out_csd,m_cases);

   double sum=0;
   for(int i=0; i<m_cases; i++)
     {
      out_csd[i]=m_dft[i].re*m_dft[i].re + m_dft[i].im*m_dft[i].im;
      if(i==(m_cases-1))
         out_csd[i]*=0.5;
      sum+=out_csd[i];
     }
   double sfac=1.0/sum;
   double nfac=1.0/(m_cases-1);
   double dmax=sum=0;

   for(int i=1; i<m_cases-1; i++)
     {
      sum+=out_csd[i];
      out_csd[i]=sum*sfac - i*nfac;
      if(MathAbs(out_csd[i])>dmax)
         dmax=MathAbs(out_csd[i]);
     }
   out_csd[0]=out_csd[m_cases-1]=0;

   return dmax;
  }

Последний метод, на который стоит обратить внимание, - функция Plot(). С его помощью пользователь может быстро отобразить один график из трех, указанных в перечислении ENUM_SPECTRUM_PLOT. Второй и третий параметры метода Plot() определяют параметры сглаживания, применяемые к фильтру Савицкого-Голея при построении отфильтрованной совокупной спектральной функции. При выборе других графиков эти параметры не действуют. Остальные параметры Plot() управляют цветом линейного графика, временем отображения графика в секундах и размером графика соответственно.

void CSpectrumAnalysis::Plot(ENUM_SPECTRUM_PLOT plot_series,int windowsize=5, int polyorder=2,color line_color=clrBlue, int display_time_seconds=30, int size_x=750, int size_y=400)
  {
   double x[],y[];
   bool calculated=false;

   string header="";

   switch(plot_series)
     {
      case PLOT_POWER_SPECTRUM:
         ArrayResize(x,m_cases);
         calculated=PowerSpectrum(y);
         for(int i=0; i<m_cases; i++)
            x[i]=double(i)/double(m_n);
         header="Power Spectrum";
         break;
      case PLOT_FILTERED_POWER_SPECTRUM:
        {
         double ps[] ;
         calculated=PowerSpectrum(ps);
         savgol(ps,y,windowsize,polyorder);
         ArrayResize(x,ArraySize(y));
         for(int i=0; i<ArraySize(y); i++)
            x[i]=double((i+(windowsize/2))/double(m_n));
         header="Filtered Power Spectrum";
        }
      break;
      case PLOT_CUMULATIVE_SPECTRUM_DEVIATION:
         calculated=CumulativeSpectrumDeviation(y);
         ArrayResize(x,m_cases);
         for(int i=0; i<m_cases; i++)
            x[i]=i;
         header="Cumulative Spectrum Deviation";
         break;
     }

   if(!calculated)
     {
      ArrayFree(x);
      ArrayFree(y);
      return;
     }

   ChartSetInteger(0,CHART_SHOW,false);

   long chart=0;
   string name=EnumToString(plot_series);

   CGraphic graphic;
   if(ObjectFind(chart,name)<0)
      graphic.Create(chart,name,0,0,0,size_x,size_y);
   else
      graphic.Attach(chart,name);
//---
   graphic.BackgroundMain(header);
   graphic.BackgroundMainSize(16);
   graphic.CurveAdd(x,y,ColorToARGB(line_color),CURVE_LINES);
//---
   graphic.CurvePlotAll();
//---
   graphic.Update();
//---
   Sleep(display_time_seconds*1000);
//---
   ChartSetInteger(0,CHART_SHOW,true);
//---
   graphic.Destroy();
//---
   ChartRedraw();
//---

  }

Чтобы облегчить понимание, мы проанализируем спектральные характеристики некоторых гипотетических рядов с определенными характеристиками, а именно, авторегрессионного ряда с одним положительным или отрицательным членом. Серия с ярко выраженной сезонной и трендовой составляющей. Наконец, мы рассмотрим спектральную природу случайного процесса.

Выявление сезонных закономерностей во временном ряду

Обычно при построении прогностических моделей нам необходимо провести предварительную обработку, прежде чем двигаться дальше. Обычной практикой является удаление любых очевидных признаков, таких как любой тренд или сезонность, прежде чем использовать нейронную сеть для прогнозирования ряда. Одним из способов обнаружения таких особенностей является оценка спектральной функции. Сильные компоненты, определяющие ряд, обычно проявляются в виде широких пиков. Давайте рассмотрим в качестве примера детерминированный ряд, который имеет очевидную сезонную составляющую. Ряд генерируется кодом, показанным ниже.

input bool Add_trend=false;


//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int num_samples = 100; 
   double inputs[];
   ArrayResize(inputs,num_samples);
   MathSrand(2023);
//---
   for(int i=0;i<num_samples;i++)
     {
      inputs[i]=(Add_trend)?i*0.03*-1:0;
      inputs[i]+= cos(2*M_PI*0.1*(i+1)) + sin(2*M_PI*0.4*(i+1)) + (double)rand()/SHORT_MAX;
     } 
//---

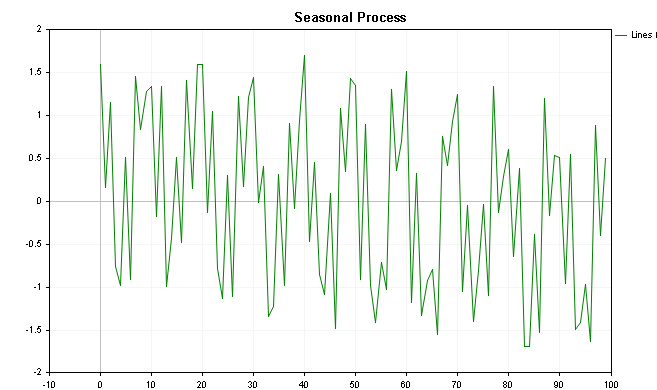
Визуализация этих значений показана на следующих графиках: первый показывает значения с добавленным трендом, а последний показывает график без компонента тренда.

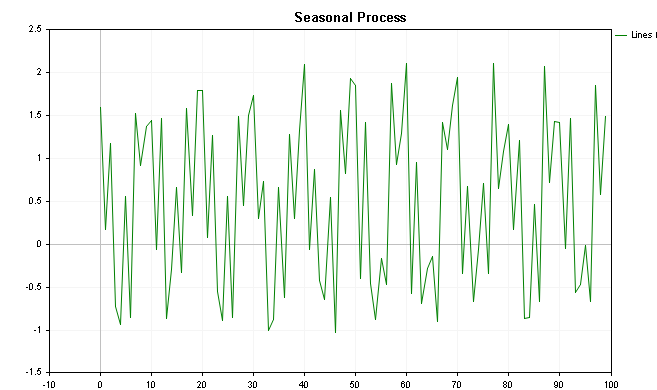
Запустив класс CSpectrum, мы можем визуализировать спектральную функцию ряда, как показано ниже. Мы можем видеть, что спектральная функция четко показывает несколько заметных пиков.

CSpectrumAnalysis sp(true,inputs); 
       
   sp.Plot(PLOT_POWER_SPECTRUM);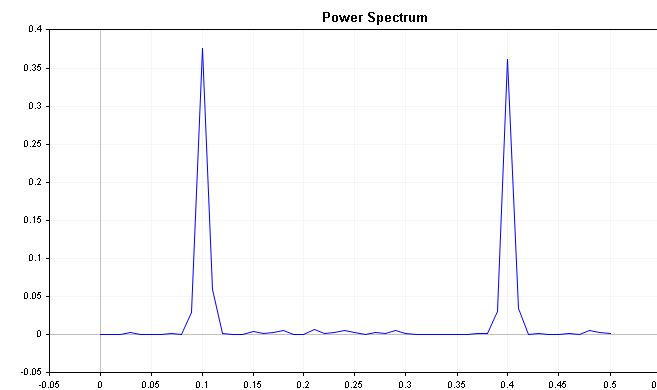 

На графике ясно видно, что на ряд сильно влияют частотные составляющие 0,2 и 0,4 соответственно.

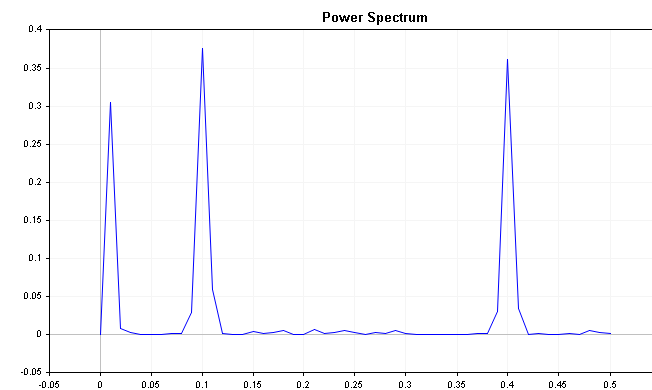
Спектр ряда с небольшим трендом вниз показывает начальный пик наряду с сезонной составляющей. В такой ситуации может быть разумным не только различать ряды, но и применять сезонную привязку. Следует отметить, что наличие таких пиков не всегда является признаком тренда и/или сезонности. Показанный пример имеет небольшой компонент шума, в то время как реальные наборы данных, такие как финансовые ряды, страдают от шума. Сезонность в ряду обычно проявляется в виде очевидного пика на графике спектральной функции.

Определение порядка авторегрессионной (AR) модели

Модели авторегрессии обычно используются в анализе временных рядов для прогнозирования будущих значений ряда на основе его прошлых значений. Порядок модели AR определяет, сколько прошлых значений используется для прогнозирования следующего значения. Один из методов определения соответствующего порядка для модели AR состоит в том, чтобы изучить спектральную функцию временного ряда.

Как правило, спектральная функция затухает по мере увеличения частоты. Например, временной ряд, определяемый краткосрочным положительным членом авторегрессии, будет иметь большую часть своей спектральной энергии, сконцентрированной на низких частотах, в то время как ряд с краткосрочным отрицательным членом авторегрессии сместит свою спектральную энергию в сторону высоких частот.
Посмотрим, как это выглядит на практике, используя другой детерминированный ряд, определяемый положительной или отрицательной авторегрессионной составляющей. Код для создания ряда показан ниже.

double inputs[300];
   ArrayInitialize(inputs,0);

   MathSrand(2023);

   for(int i=1; i<ArraySize(inputs); i++)
     {
      inputs[i]= 0.0;
      
          switch(Coeff_Mult)
             {
              case positive:
               inputs[i]+= 0.9*inputs[i-1];
               break;
              case negative:
               inputs[i]+= -1*0.9*inputs[i-1];
               break;   
             }
             
      inputs[i]+=(double)rand() / double(SHORT_MAX);
     }

Когда ряд определяется положительной авторегрессией, спектральная функция показывает, что большая часть энергии сосредоточена на низких частотах, а мощность на более высоких частотах уменьшается по мере продвижения по шкале значений.

Сравнение с графиком авторегрессионного ряда с отрицательным членом показывает, что мощность увеличивается при дискретизации более высоких частот. Опять же, это простой пример, но он демонстрирует важные характеристики, которые можно применять при построении авторегрессионных моделей.

Изучение спектра распределения ошибок для оценки эффективности модели прогнозирования

Наконец, мы можем использовать спектральную функцию распределения ошибок модели прогнозирования, чтобы оценить, насколько хорошо она моделирует процесс. Для этого мы сначала подбираем модель прогнозирования к данным временных рядов и вычисляем остатки или ошибки (разницу между прогнозируемыми и фактическими значениями).

Далее мы исследуем спектральную функцию распределения ошибок. Хорошая модель прогнозирования будет иметь остаточные значения, представляющие собой белый шум, а это означает, что спектральная функция распределения ошибок должна быть относительно плоской на всех частотах. Выраженные пики в спектральной функции на любой частоте предполагают, что модель прогнозирования не захватывает всю информацию в данных временных рядов, и может потребоваться дополнительная настройка. Проблема в том, что в действительности спектральная функция белого шума обычно не такая плоская, как ожидается. Просто посмотрите на спектр ряда белого шума, сгенерированного кодом ниже.

int num_samples = 500;
   double inputs[];
   MathSrand(2023);
   ArrayResize(inputs,num_samples);
   
   for (int i = 0; i < num_samples; i++) 
    {
        inputs[i] = ((double)rand() / SHORT_MAX) * 32767 - 32767/2;
    }

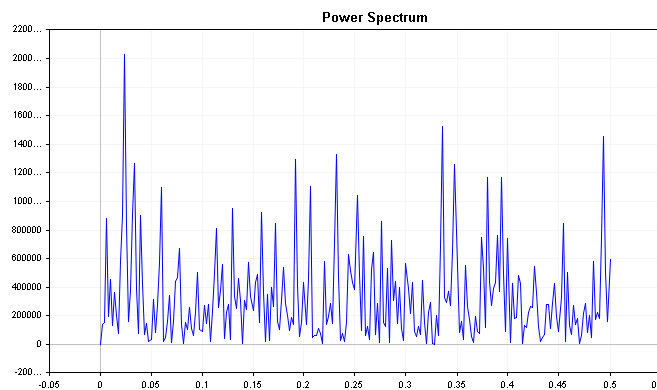
Чтобы получить более четкое представление о частотных компонентах, мы можем использовать совокупную спектральную функцию.

Теоретически, если временной ряд представляет собой белый шум, все спектральные члены будут равны, поэтому ожидается, что график совокупной спектральной функции будет прямым. В частности, доля общей мощности, учитываемая для каждого отдельного члена, должна быть равна доле общего числа накопленных терминов. Математически это означает, что совокупная мощность белого шума имеет детерминированное ожидание. Уравнение, определяющее совокупную мощность для каждой выбранной полосы частот, показано ниже.

 
Если спектральная функция показывает высокую концентрацию энергии на низких или высоких частотах, мы увидим отклонения от теоретической формы волны белого шума. Используя этот факт, мы можем вычислить отклонение между наблюдаемым и теоретическим совокупными спектрами, что дает совокупное отклонение спектра.

Этот ряд может раскрыть важную информацию о временном ряде. Например, если спектральная энергия смещена влево, отклонение начнется около нуля и будет медленно увеличиваться, пока не сойдется намного позже. И наоборот, если спектральная энергия сдвинута вправо, отклонение сразу упадет до отрицательных значений, а затем медленно вернется к нулю с течением времени. Белый шум будет давать значения отклонения, которые изменяются намного меньше относительно нуля.

Графики ниже показывают совокупное отклонение спектра положительных и отрицательных процессов AR(1), определенных ранее. Сравните их с графиком совокупного спектра белого шума, обратите внимание на более четкие различия.

 

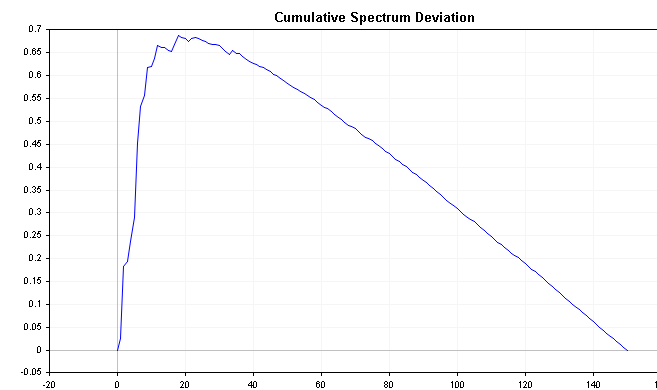
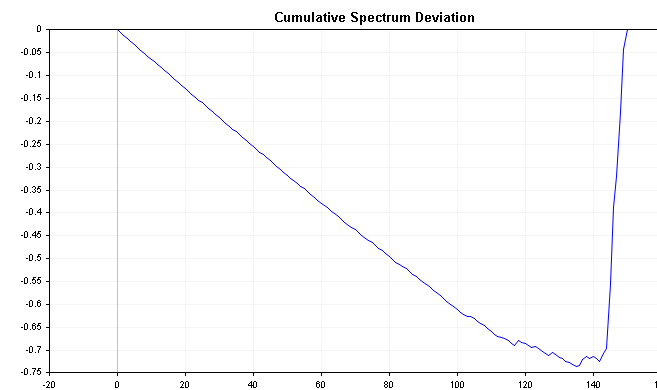
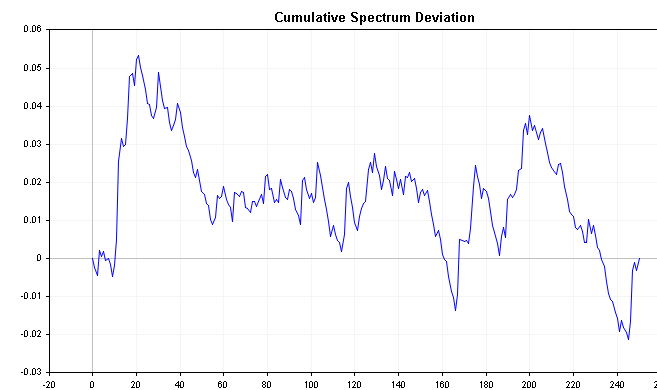
Известно, что распределение максимальной абсолютной величины всех отклонений следует распределению Колмогорова-Смирнова. Применяя приведенную ниже формулу, мы можем напрямую проверить гипотезу о том, что временной ряд представляет собой белый шум. Эта формула вычисляет D-статистику ряда.

q определяет степени свободы, если ДПФ применяется к реальному временному ряду, q =n/2-1. Если перед ДПФ применяется окно данных Уэлча, q необходимо умножить на 0.72, чтобы компенсировать потерю информации, вызванную работой с окнами. Альфа — это уровень значимости, обычно в процентах. Чтобы проверить гипотезу белого шума, получите максимальную разность или отклонение и сравните ее с D-статистикой.

В классе CSpectrum мы можем получить максимальную разницу, определяемую вычислением совокупного отклонения спектра, вызвав метод CumulativeSpectrumDeviation().

Заключение

Основное внимание в статье было уделено широко известному ДПФ для оценки спектральной функции временного ряда. Однако существует альтернативный метод, называемый принципом максимальной энтропии (МЭ), который иногда превосходит ДПФ. Спектр МЭ позволяет увеличивать очень узкие элементы, сглаживая области с низкой спектральной энергией, позволяя добиться всестороннего отображения. Однако метод МЭ имеет тенденцию обнаруживать пики энергии с высоким спектром, даже если они не существуют, что делает его непригодным для использования в одиночку. Поэтому я рекомендую всегда использовать спектр ДПФ в качестве подтверждения.

В заключение, анализ спектральной функции данных временных рядов может дать ценную информацию о различных аспектах анализа временных рядов, таких как определение порядка модели AR, установление необходимости сезонных различий в качестве шага предварительной обработки и изучение производительности модели прогнозирования.

Название файла	Описание
mql5files\include\Spectrum.mqh	Определение класса CSpectrum
mql5files\scripts\OrderOneARProcess.mql5	Скрипт генерирует авторегрессионный временной ряд и применяет класс CSpectrum
mql5files\scripts\SeasonalProcess.mql5	Скрипт генерирует временной ряд с сезонностью и применяет класс CSpectrum
mql5files\scripts\WhiteNoise.mql5	Скрипт генерирует временной ряд белого шума и применяет класс CSpectrum