Modelos polinomiais no trading

Introdução

A eficácia no trading depende fortemente dos métodos de análise dos dados de mercado. Um desses métodos são os polinômios ortogonais. Esses polinômios são funções matemáticas que permitem resolver uma série de tarefas relacionadas ao trading.

Os polinômios ortogonais mais conhecidos são os de Legendre, Chebyshev, Laguerre e Hermite. Cada um desses polinômios possui propriedades únicas que permitem seu uso para resolver diferentes problemas. Aqui estão algumas formas principais de utilizá-los:

• Modelagem de séries temporais. Os polinômios ortogonais podem ser usados para descrever séries temporais. Seu uso pode ajudar na identificação de tendências e outros padrões.
• Regressão. Os polinômios ortogonais podem ser aplicados na análise de regressão. Seu uso melhora a qualidade do modelo e o torna mais interpretável.
• Previsão. Os polinômios ortogonais podem ser usados para construir previsões, por exemplo, sobre qual será o preço se as tendências atuais se mantiverem.

Vamos ver como os polinômios ortogonais podem ser aplicados na prática.

Polinômios ortogonais e indicadores

Toda a essência da análise técnica se resume a identificar padrões no movimento dos preços. Mas séries temporais financeiras geralmente contêm ruídos que ocultam esses padrões. Vamos ver como os polinômios ortogonais podem ser usados em condições de mercado.

A ideia principal é que esses polinômios podem ser usados para decompor sinais complexos em componentes mais simples. Essa decomposição permite filtrar os ruídos e identificar tendências.

Como exemplo, usarei polinômios de Legendre, e criarei com eles um indicador suavizador. A fórmula geral desses polinômios e o domínio de definição são dados pelas seguintes expressões:

Usarei polinômios até o 9º grau. Isso é suficiente para suavização, e o uso de polinômios de grau mais alto pode adicionar ruídos e ocultar as principais tendências no movimento de preços. As fórmulas dos polinômios que usarei estão apresentadas na tabela.

n	polinômios de Legendre
0	1
1	x
2	(3*x^2-1)/2
3	(5*x^3-3*x)/2
4	(35*x^4-30*x^2+3)/8
5	(63*x^5-70*x^3+15*x)/8
6	(231*x^6-315*x^4+105*x^2-5)/16
7	(429*x^7-693*x^5+315*x^3-35*x)/16
8	(6435*x^8-12012*x^6+6930*x^4-1260*x^2+35)/128
9	(12155*x^9-25740*x^7+18018*x^5-4620*x^3+315*x)/128

Antes de tudo, preciso converter os índices de preço para o domínio de definição desses polinômios. Para isso, para cada índice i, aplico uma função de deslocamento:

Depois disso, calculo os valores de todos os polinômios de interesse para cada valor de x[i]. Para dar um exemplo, calcularei o valor do polinômio de 2º grau com período igual a 3:

Agora preciso aplicar uma correção para a natureza discreta dos dados. A soma dos valores dos polinômios de grau 1 em diante deve ser igual a zero. Para atender a essa condição, preciso calcular uma correção:

Com essa correção, ajusto os valores do polinômio:

Agora começa a parte mais interessante. Qualquer série temporal pode ser decomposta como a soma de polinômios, cada um com um determinado peso:

Os próprios pesos podem ser calculados da seguinte forma:

Parece confuso e um pouco assustador. Mas na verdade é simples. Vamos pegar o polinômio de grau 0 com período N. Seus valores em todos os pontos são iguais a 1. E seu peso será:

Essa é a fórmula da SMA. Os pesos dos polinômios de grau superior são equivalentes a certos osciladores com coeficientes especialmente ajustados. Ou seja, pode-se dizer que os polinômios ortogonais são uma SMA com alguns ajustes engenhosamente calculados. Os polinômios de Legendre são muito resistentes a ruídos e lidam muito bem com tarefas de filtragem. Por exemplo, o polinômio de Legendre de 1º grau tem esta aparência.

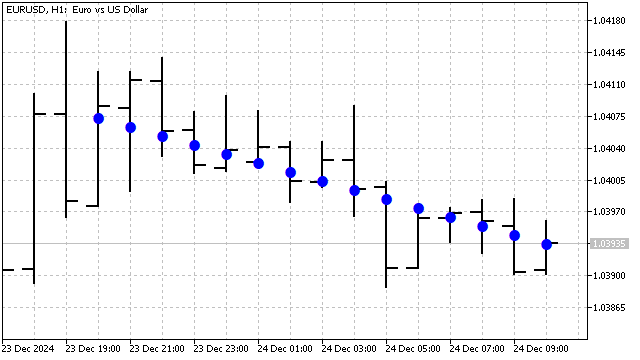
Além dos polinômios de Legendre, para destacar tendências e suavizar curvas, também se podem usar polinômios de Chebyshev. Existem dois tipos desses polinômios. Eles diferem entre si no comportamento nas extremidades. A principal vantagem desses polinômios está na sua sensibilidade a mudanças bruscas de preço. A fórmula desses polinômios é muito simples:

n	polinômios do 1º tipo	polinômios do 2º tipo
0	1	1
1	x	2*x
2	2*x^2-1	4*x^2-1
3	4*x^3-3*x	8*x^3-4*x
4	8*x^4-8*x^2+1	16*x^4-12*x^2+1
5	16*x^5-20*x^3+5*x	32*x^5-32*x^3+6*x
6	32*x^6-48*x^4+18*x^2-1	64*x^6-80*x^4+24*x^2-1
7	64*x^7-112*x^5+56*x^3-7*x	128*x^7-192*x^5+80*x^3-8*x
8	128*x^8-256*x^6+160*x^4-32*x^2+1	256*x^8-448*x^6+240*x^4-40*x^2+1
9	256*x^9-576*x^7+432*x^5-120*x^3+9*x	512*x^9-1024*x^7+672*x^5-160*x^3+10*x

E assim se apresenta a suavização com o polinômio de Chebyshev de 3º grau,

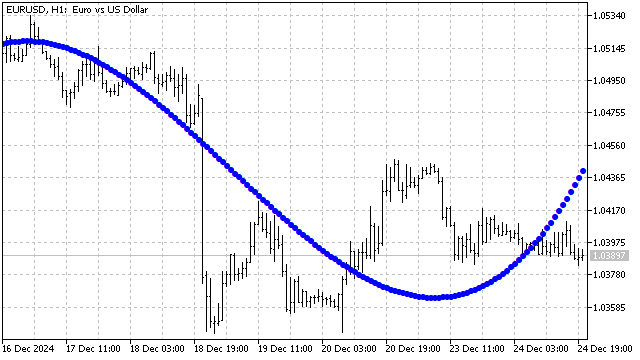
Até agora, consideramos polinômios com domínio de definição entre +/-1, mas existem polinômios com outros domínios. Por exemplo, o polinômio de Laguerre é definido para todos os valores não negativos do argumento. Sua fórmula é assim:

n	polinômio de Laguerre
0	1
1	-x+1
2	(x^2-4*x+2)/2
3	(-x^3+9*x^2-18*x+6)/6
4	(x^4-16*x^3+72*x^2-96*x+24)/24
5	(-x^5+25*x^4-200*x^3+600*x^2-600*x+120)/120
6	(x^6-36*x^5+450*x^4-2400*x^3+5400*x^2-4320*x+720)/720
7	(-x^7+49*x^6-882*x^5+7350*x^4-29400*x^3+52920*x^2-35280*x+5040)/5040
8	(x^8-64*x^7+1568*x^6-18816*x^5+117600*x^4-376320*x^3+564480*x^2-322560*x+40320)/40320
9	(-x^9+81*x^8-2592*x^7+42336*x^6-381024*x^5+1905120*x^4-5080320*x^3+6531840*x^2-3265920*x+362880)/362880

E a função de deslocamento para seu argumento é a seguinte:

Essa transformação faz com que o comportamento do polinômio de Laguerre dependa não apenas do grau, mas também do seu período. Esse polinômio é sensível às mudanças mais recentes de preço. Por exemplo, assim se apresenta o polinômio de Laguerre de 5º grau no gráfico:

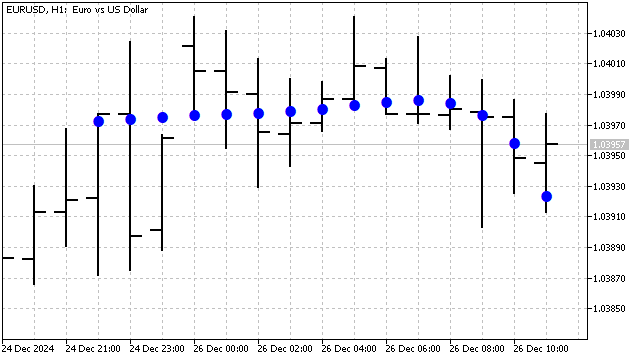
Outro exemplo interessante de ortogonalidade são os polinômios de Hermite. Esses polinômios são aplicados em várias áreas da matemática e da física. Esses polinômios são definidos para quaisquer valores do argumento, e sua fórmula é assim:

n	polinômios de Hermite
0	1
1	x
2	x^2-1
3	x^3-3*x
4	x^4-6*x^2+3
5	x^5-10*x^3+15*x
6	x^6-15*x^4+45*x^2-15
7	x^7-21*x^5+105*x^3-105*x
8	x^8-28*x^6+210*x^4-420*x^2+105
9	x^9-36*x^7+378*x^5-1260*x^3+945*x

A função de deslocamento centraliza os valores do preço:

Como resultado, obtivemos um filtro suavizador cuja eficácia depende do grau do polinômio e de seu período.

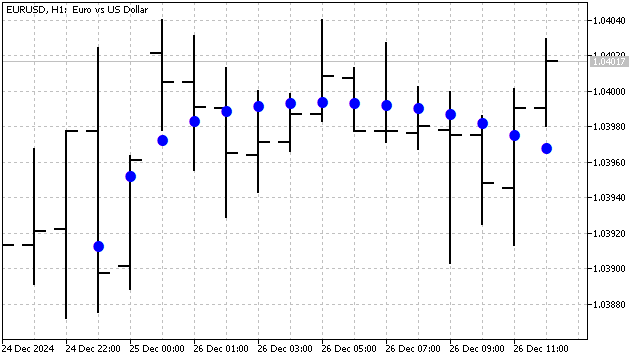
Analisamos os principais polinômios ortogonais clássicos. Mas também é possível criar sua própria versão desses polinômios. Por exemplo, um polinômio que combine as qualidades dos polinômios de Chebyshev e Hermite é definido pela fórmula:

n	polinômios de Chebyshev-Hermite
0	1
1	2*x
2	4*x^2-2
3	8*x^3-12*x
4	16*x^4-48*x^2+12
5	32*x^5-160*x^3+120*x
6	64*x^6-480*x^4+720*x^2-120
7	128*x^7-1344*x^5+3360*x^3-1680*x
8	256*x^8-3584*x^6+13440*x^4-13440*x^2+1680
9	512*x^9-9216*x^7+48384*x^5-80640*x^3+30240*x

Esse polinômio é sensível a tendências não lineares, como as quadráticas, cúbicas e outras. Assim se apresenta o polinômio de Chebyshev–Hermite de 9º grau no gráfico:

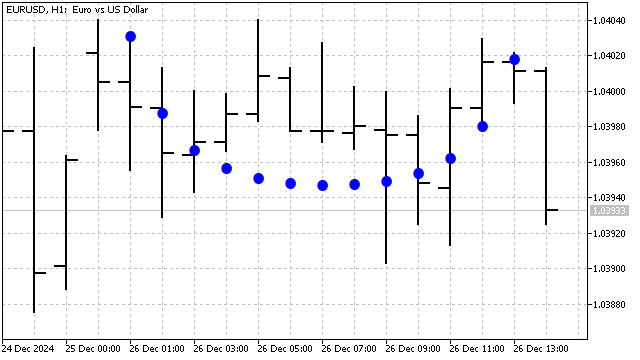
Há várias vantagens em usar polinômios ortogonais.

• Estabilidade e eliminação de correlação. A ortogonalidade dos polinômios garante sua resistência às mudanças nos parâmetros do modelo. Cada polinômio é independente dos demais, o que permite modelar e estudar cada componente da série temporal separadamente.
• Interpretabilidade. Cada polinômio ortogonal representa um modelo de comportamento do preço. Os coeficientes de peso dos polinômios permitem destacar os modelos mais relevantes e focar neles.
• Adaptabilidade e eficiência. Os polinômios ortogonais se ajustam aos valores específicos da série temporal. O surgimento de novos preços altera os coeficientes de peso, fazendo com que o modelo polinomial se adapte ao estado atual do mercado. A utilização de polinômios não lineares torna essa adaptação eficaz.

A única particularidade dos polinômios ortogonais que pode ser considerada uma desvantagem é que esses polinômios processam todos os preços dentro do polinômio. Em outras palavras, o indicador construído com esses polinômios “desenha”. Do meu ponto de vista, essa característica não é um defeito, mas apenas indica que o indicador encontra a melhor aproximação conforme chegam novos dados.

O uso de polinômios ortogonais impõe algumas limitações. O período do indicador deve ser maior que o grau do polinômio. Para fins práticos, podemos nos limitar a um polinômio de 3º grau. Um indicador assim combina uma SMA, uma tendência linear e duas parábolas: uma quadrática e outra cúbica. Isso é suficiente para suavizar situações bastante complexas. Mas, ao aumentar o período do indicador, também se pode aumentar o grau do polinômio.

Agora, vamos analisar alguns exemplos de aplicação dos polinômios ortogonais no trading.

Estratégias de trading

Com base nos polinômios ortogonais, os traders podem criar várias estratégias de trading. Por exemplo, com regressão polinomial baseada nesses polinômios, o trader pode não apenas analisar movimentos passados do preço, mas também construir um modelo capaz de se adaptar às mudanças atuais do mercado.

Como exemplo, vamos considerar algumas estratégias de trading baseadas em desvios da média.

Analisemos a estratégia mais simples, em que as posições são abertas quando o preço cruza a SMA. Substituímos a média móvel por um polinômio ortogonal e mantemos as regras de abertura e fechamento de posições:

• Quando o preço cruza o polinômio de baixo para cima, deve-se abrir uma posição de compra (buy) e fechar a posição de venda (sell).
• Quando o preço cruza o polinômio de cima para baixo, deve-se abrir uma posição de venda (sell) e fechar a posição de compra (buy).

Apesar da simplicidade, essa estratégia é perfeitamente funcional.

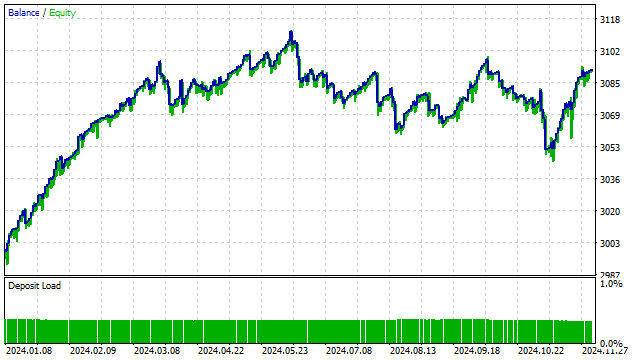
Vamos agora complicar um pouco essa estratégia e substituir o preço pelo valor de algum polinômio. Ou seja, teremos um análogo da estratégia de cruzamento de duas SMA. O resultado é um tanto previsível: entre todas as possibilidades, o otimizador de estratégias preferiu os polinômios ortogonais.

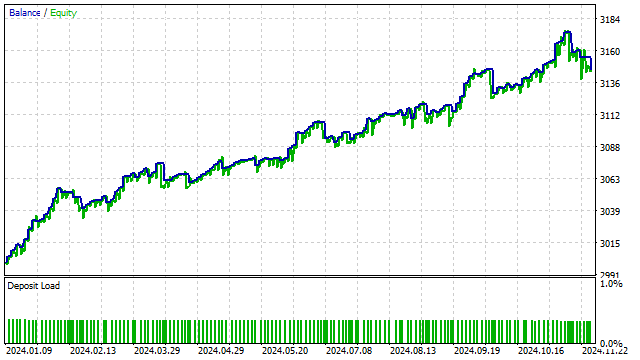
Modelos polinomiais também podem ser usados em estratégias mais complexas. Se a estratégia utiliza algum indicador, pode-se tentar substituí-lo por polinômios ortogonais. Essa substituição pode melhorar a estratégia.

Como exemplo, tomarei o indicador Commodity Channel Index (CCI). A fórmula clássica desse indicador é a seguinte:

Fiz uma pequena modificação nesse indicador. Como já mencionei: a SMA é um polinômio de 0º grau. Em vez da SMA, vou usar um polinômio ortogonal de qualquer grau. Consequentemente, o desvio absoluto médio será calculado em relação a esse polinômio. O indicador ficou assim:

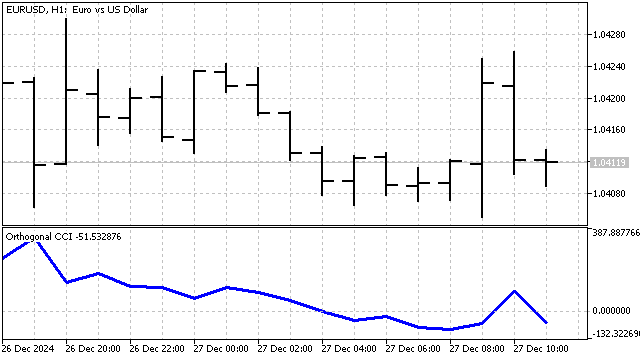
A estratégia de trading será semelhante à clássica:

• abrir uma posição de compra (buy) se o indicador estiver abaixo de um nível definido e continuar caindo;
• abrir uma posição de venda (sell) se o indicador estiver acima de um nível definido e continuar subindo;
• fechamento de posições mediante sinal contrário.

O resultado do teste dessa estratégia com um polinômio de 3º grau:

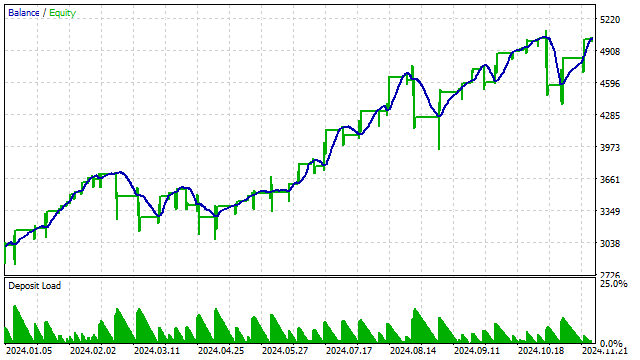
Com base em polinômios ortogonais, também é possível construir outros indicadores. Por exemplo, decidi criar um análogo do RSI. A ideia é simples: primeiro construo um polinômio e depois conto quantos preços ficaram acima desse polinômio. Com base nesse número, tiro conclusões sobre sobrecompra ou sobrevenda.

Com base nesse indicador, crio uma estratégia simples:

• abrir posição se o indicador atingir o nível de sobrecompra ou sobrevenda;
• fechar posições se o indicador estiver no centro.

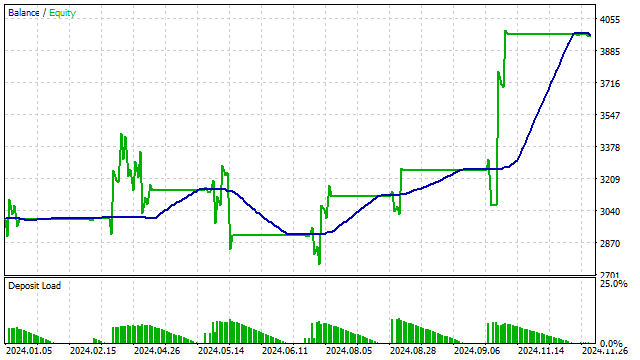
Além disso, os polinômios ortogonais podem ser integrados a vários algoritmos de aprendizado de máquina. A flexibilidade das funções polinomiais permite que algoritmos de machine learning identifiquem dependências complexas nos dados. 

Por exemplo, os polinômios podem ser usados para gerar novas características a partir dos dados brutos. Os polinômios ortogonais oferecem estimativas independentes de diferentes componentes da série temporal. Graças a essa propriedade, eles podem reduzir o sobreajuste. Isso pode melhorar a qualidade dos dados de treinamento e aprimorar o desempenho dos modelos.

Pegue qualquer rede neural e alimente-a com os valores dos coeficientes de peso dos polinômios ortogonais. Mas, nesse caso, será necessário construir o sistema completo de polinômios: iniciando pelo polinômio de 1º grau e terminando no N-1, onde N é o número de preços processados.

Considerações finais

Os polinômios ortogonais são uma ferramenta poderosa para a análise de séries temporais financeiras. Eles proporcionam diversas vantagens e permitem avaliar as mudanças no mercado. O uso de polinômios ortogonais em estratégias de trading pode aumentar sua eficácia e melhorar os resultados no trading.

Na elaboração deste artigo, foram usados os seguintes programas.

Nome	Tipo	Descrição
Orthogonal polynomials	indicador	modela polinômios ortogonais no gráfico Type - tipo de polinômio iPeriod - período do polinômio (mínimo 2) N - grau do polinômio, valores permitidos de 0 a 9 Shift - deslocamento do indicador
EA Orthogonal polynomials	Expert Advisor	executa uma estratégia de trading baseada no cruzamento entre o preço e o polinômio
EA Orthogonal polynomials 2	Expert Advisor	executa uma estratégia baseada no cruzamento de dois polinômios
Orthogonal CCI	indicador	CCI no qual se pode usar polinômios ortogonais em vez de SMA
EA Orthogonal CCI	Expert Advisor	executa uma estratégia com base na versão ortogonal do CCI
Orthogonal RSI	indicador	detecta sobrecompra/sobrevenda usando polinômios ortogonais
EA Orthogonal RSI	Expert Advisor	executa uma estratégia com base na versão ortogonal do RSI