
Neuronale Netze leicht gemacht (Teil 92): Adaptive Vorhersage im Frequenz- und Zeitbereich
Einführung
Zeit- und Frequenzbereich sind zwei grundlegende Darstellungen, die zur Analyse von Zeitreihendaten verwendet werden. Im Zeitbereich konzentriert sich die Analyse auf Amplitudenänderungen im Zeitverlauf, wodurch lokale Abhängigkeiten und Transienten innerhalb des Signals identifiziert werden können. Im Gegensatz dazu zielt die Analyse im Frequenzbereich darauf ab, Zeitreihen anhand ihrer Frequenzkomponenten darzustellen, was einen Einblick in die globalen Abhängigkeiten und spektralen Merkmale der Daten ermöglicht. Die Kombination der Vorteile beider Bereiche ist ein vielversprechender Ansatz, um das Problem der Vermischung verschiedener periodischer Muster in Echtzeit-Zeitreihen zu lösen. Das Problem dabei ist, wie man die Vorteile des Zeit- und des Frequenzbereichs effektiv kombinieren kann.
Im Vergleich zu den Errungenschaften im Zeitbereich gibt es im Frequenzbereich noch viele unerforschte Bereiche. In den letzten Artikeln haben wir einige Beispiele für die Verwendung des Frequenzbereichs zur besseren Handhabung globaler Zeitreihenabhängigkeiten gesehen. Die direkte Vorhersage im Frequenzbereich ermöglicht die Nutzung von mehr Spektralinformationen zur Verbesserung der Genauigkeit von Zeitreihenvorhersagen. Es gibt jedoch einige Probleme im Zusammenhang mit der direkten Vorhersage des Spektrums im Frequenzbereich. Eines dieser Probleme ist die potenzielle Diskrepanz in den Frequenzmerkmalen zwischen dem Spektrum bekannter Daten, die analysiert werden, und dem vollständigen Spektrum der untersuchten Zeitreihe, die sich aus der Verwendung der Diskreten Fourier-Transformation (DFT) ergibt. Diese Diskrepanz macht es schwierig, Informationen über bestimmte Frequenzen im gesamten Spektrum der Quelldaten genau darzustellen, was zu Ungenauigkeiten bei der Vorhersage führt.
Ein weiteres Problem ist, wie man effizient Informationen über Häufigkeitskombinationen extrahieren kann. Die Extraktion von Spektralmerkmalen ist eine schwierige Aufgabe, da die harmonischen Reihen, die in Gruppen innerhalb des Spektrums auftreten, eine erhebliche Menge an Informationen enthalten.
Der Artikel „ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting“ schlägt die Methode ATFNet als Lösung für die oben genannten Probleme vor. Es umfasst Zeit- und Frequenzbereichsmodule zur gleichzeitigen Verarbeitung lokaler und globaler Abhängigkeiten. Darüber hinaus wird ein neuer Gewichtungsmechanismus vorgestellt, der die Gewichte zwischen den beiden Modulen dynamisch verteilt.
Die Autoren der Methode schlugen eine Energiegewichtung dominanter harmonischer Reihen vor, die in der Lage ist, geeignete Gewichtungen für Module im Zeit- und Frequenzbereich zu generieren, die auf dem Grad der Periodizität der Originaldaten basieren. Dadurch können wir die Vorteile beider Bereiche bei der Arbeit mit Zeitreihen mit unterschiedlichen periodischen Mustern effektiv nutzen.
Darüber hinaus führen die Autoren der Methode eine erweiterte DFT ein, um das Spektrum der diskreten Frequenzen der Originaldaten und der vollständigen Zeitreihe anzugleichen, was die Genauigkeit der Darstellung bestimmter Frequenzen erhöht.
Die Autoren der Methode implementieren den Aufmerksamkeitsmechanismus in den Frequenzbereich und schlagen komplexe, spektrale Aufmerksamkeit (CSA) vor. Mit diesem Ansatz können Informationen aus verschiedenen Kombinationen von Frequenzantworten gesammelt werden, was eine effektive Möglichkeit darstellt, die Aufmerksamkeit auf Darstellungen im Frequenzbereich zu lenken.
Der Artikel stellt die Ergebnisse von Experimenten mit acht realen Datensätzen vor, denen zufolge ATFNet vielversprechende Ergebnisse zeigt und andere moderne Zeitreihenvorhersagemethoden bei vielen Datensätzen übertrifft.
1. Der Algorithmus ATFNet
Die Autoren der ATFNet-Methode verwenden ein kanalunabhängiges Schema, das es ermöglicht, die Vermischung von Spektren aus verschiedenen Kanälen zu verhindern. Da die Kanäle unterschiedliche globale Muster aufweisen können, kann sich das Mischen ihrer Spektren negativ auf die Leistung des Modells auswirken.
Der Block T verarbeitet univariate Eingangszeitreihen direkt im Zeitbereich. Das Ergebnis ist die Ausgabe eines bestimmten Vorhersagewerts für zukünftige Werte der analysierten Zeitreihe.
Die Autoren der Methode verwenden die erweiterte diskrete Fourier-Transformation (DFT), um die ursprünglichen univariaten Zeitreihendaten in den Frequenzbereich zu transformieren und ein erweitertes Frequenzspektrum zu erzeugen. Das Spektrum wird dann mit Hilfe der inversen DFT (iDFT) zurück in den Zeitbereich transformiert. Als Ergebnis liefert der Block F vorhergesagte Werte der Zeitreihe auf der Grundlage der Frequenzmerkmale.
Die Vorhersageergebnisse der Blöcke T und F werden unter Verwendung adaptiver Gewichte kombiniert, um das Endergebnis der vorhergesagten Werte der analysierten Zeitreihen zu erhalten. Diese Gewichte werden auf der Grundlage der Energiegewichtung der Harmonische Reihe bestimmt.
Im Allgemeinen kann der Algorithmus wie folgt dargestellt werden:
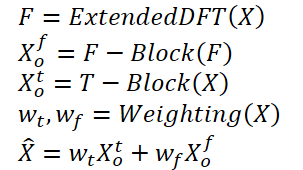
Die Verwendung einer herkömmlichen DFT kann zu einer Nichtübereinstimmung der Frequenzen zwischen den Spektren der ursprünglichen Daten und der gesamten analysierten Reihe führen. Daher haben Prognosemodelle, die auf der Analyse eines kleinen Blocks von Ausgangsdaten basieren, möglicherweise keinen Zugang zu vollständigen und genauen Informationen über die Häufigkeitsmerkmale der gesamten analysierten Zeitreihe. Dies führt zu weniger genauen Prognosen bei der Erstellung der vollständigen Zeitreihen.
Um dieses Problem zu lösen, schlagen die Autoren der Methode eine erweiterte DFT vor, die die durch die Länge der analysierten Quelldaten auferlegte Beschränkung überwindet. Auf diese Weise erhalten wir das ursprüngliche Spektrum, das der DFT-Frequenzgruppe der vollständigen Reihe entspricht. Konkret ersetzen die Autoren der Methode ATFNet die ursprüngliche komplexe Exponentialbasis durch die DFT-Basis der vollständigen Reihe:
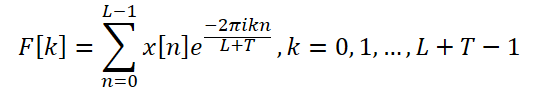
So erhält man ein Spektrum von Frequenzmerkmalen der Länge L + T, das mit dem DFT-Spektrum der gesamten analysierten Reihe (Anfangs- und Prognosedaten) übereinstimmt. Für Echtzeitreihen ist die konjugierte Symmetrie des Ausgangsspektrums eine wichtige Eigenschaft der DFT. Mit dieser Eigenschaft können wir die Rechenkosten senken, indem wir nur die erste Hälfte des Frequenzspektrums der Originaldaten berücksichtigen, da die zweite Hälfte redundante Informationen liefert.
Die Architektur des Blocks F basiert auf dem Transformer Encoder, bei dem alle Parameter komplexe Werte haben. Alle Berechnungen im F-Blockwerden im Feld der komplexen Zahlen durchgeführt.
Darüber hinaus verwenden die Autoren der Methode RevIN um das ursprüngliche Spektrum der Frequenzmerkmale F zu bearbeiten. Obwohl RevIN ursprünglich entwickelt wurde, um Verteilungsverschiebungen im Zeitbereich zu eliminieren, fanden die Autoren der Methode heraus, dass sie auch bei der Verarbeitung von Spektren im Frequenzbereich effektiv ist. Mit diesem Ansatz können Spektren von Reihen mit unterschiedlichen globalen Merkmalen in eine vergleichbare Verteilung umgewandelt werden. Vor der Analyse werden die Frequenzmerkmale F normalisiert. Nach der Verarbeitung der Daten fügen wir die statistischen Merkmale der Häufigkeitsverteilung wieder hinzu.
Da es nur wenige zeitliche Abhängigkeiten im Frequenzbereichsspektrum gibt, verwenden die Autoren der Methode keine Positionskodierung im Block F.
Außerdem verwendeten die Autoren der Methode einen modifizierten, mehrköpfigen Aufmerksamkeitsmechanismus. Für jeden Kopf (head) h = 1, 2, ..., H wird das integrierte Spektrum FF mittels trainierter Projektionen auf die Spektrumsmessung projiziert. Danach wird für jeden Kopf ein komplexes Skalarprodukt der Aufmerksamkeit erstellt.
ATFNet verwendet auch die Schichten von LayerNorm und FeedForward mit Restverbindungen, ähnlich wie Transformer, die auf den Bereich der komplexen Zahlen erweitert werden.
Nach den Encoderschichten M werden die Ergebnisse der Aufmerksamkeitsblockarbeit linear auf den Horizont der vollständigen Serie projiziert. Die erhaltenen Frequenzmerkmale werden mit Hilfe der iDFT in den Zeitbereich projiziert. Die letzten Punkte T (Teil der Prognose) werden als Endergebnis des Blocks F akzeptiert.
Es ist anzumerken, dass der Block F die vollständige Architektur eines komplexen neuronalen Netzes (CVNN) verwendet.
Der Block T ist für die Erfassung lokaler Abhängigkeiten in Zeitreihen zuständig, die im Zeitbereich leichter zu verarbeiten sind. In diesem Block verwenden die Autoren die uns bereits bekannte Methode der Zeitreihensegmentierung. PatchTST ist eine intuitive und effiziente Methode zur Erfassung lokaler Abhängigkeiten in Zeitreihen. Außerdem wird RevIN eingesetzt, um das Problem der Verzerrung der Verteilung zu lösen.
Periodische Zeitreihen weisen durchweg mindestens eine harmonische Gruppe in ihrem Frequenzspektrum auf, wobei die dominante, harmonische Gruppe die höchste Konzentration an spektraler Energie aufweist. Umgekehrt ist dieses Merkmal im Spektrum nicht-periodischer Zeitreihen, wo die Energieverteilung gleichmäßiger ist, selten zu beobachten. Die Autoren der Methode ATFNet zeigen, dass der Grad der Energiekonzentration innerhalb der dominanten harmonischen Reihen im Frequenzspektrum die Periodizität der Zeitreihe widerspiegeln kann. Das Verhältnis zwischen der Energie der dominanten harmonischen Reihe und der Gesamtenergie des Spektrums kann als Maß für die quantitative Bewertung der Energiekonzentration dienen. Wenn eine Zeitreihe eine ausgeprägtere periodische Struktur aufweist, kann sie intuitiv in Komponenten zerlegt werden. Daher weist eine solche Zeitreihe eine höhere Energiekonzentration innerhalb der dominanten harmonischen Reihe auf.
Auf der Grundlage dieser Eigenschaft verwenden die Autoren von ATFNet den Energieanteil der dominanten harmonischen Reihe als Indikator für die quantitative Bewertung des Periodizitätsgrades der Zeitreihe. Um die dominante harmonische Reihe zu ermitteln, ist die wichtigste Aufgabe die Bestimmung der Grundfrequenz. Hier gibt es verschiedene Ansätze, die genutzt werden können:
- Eine naive Methode, die die Frequenz mit dem höchsten Amplitudenwert als Grundfrequenz identifiziert.
- Algorithmen zur Bestimmung der Frequenz eines Signals auf der Grundlage von Regeln.
- Algorithmen zur Bestimmung der Frequenz eines Signals auf der Grundlage von Daten.
Der ATFNet-Algorithmus ermöglicht es uns, jeden beliebigen Ansatz zur Bestimmung der Grundfrequenz zu verwenden. Die Autoren der Methode berücksichtigen diese Komponente zusammen mit ihrer harmonischen Reihe und berechnen die Gesamtenergie Eh. Anschließend werden die Gewichte des Blocks F durch Berechnung des Verhältnisses zwischen der Energie der dominanten Frequenz und der Gesamtenergie des Spektrums ermittelt.
In dem Papier führten die Autoren der Methode eine Reihe von Experimenten durch, um die Wirksamkeit verschiedener Methoden zur Bestimmung der dominanten Frequenz zu bewerten. Sie kamen zu dem Schluss, dass die naive Methode in Bezug auf das Verhältnis zwischen der Genauigkeit der Ergebnisse und den Kosten der Berechnungen führend ist. Es zeigt eine vorbildliche Genauigkeit bei einer Mehrzahl von realen Zeitreihendaten und hält gleichzeitig die Rechenkosten niedrig.
Umgekehrt werden alternative Ansätze durch das Problem der Berechnungskomplexität behindert. Darüber hinaus erfordern datengesteuerte Methoden beschriftete Stufendaten, die oft schwer zu beschaffen sind, was ein ernsthaftes Hindernis für ihre praktische Anwendung darstellt. Daher verwenden die Autoren der ATFNet-Methode in ihren Experimenten standardmäßig eine naive Methode zur Erkennung der Grundfrequenz.
Die originelle Visualisierung der AFTNet-Methode ist unten dargestellt.
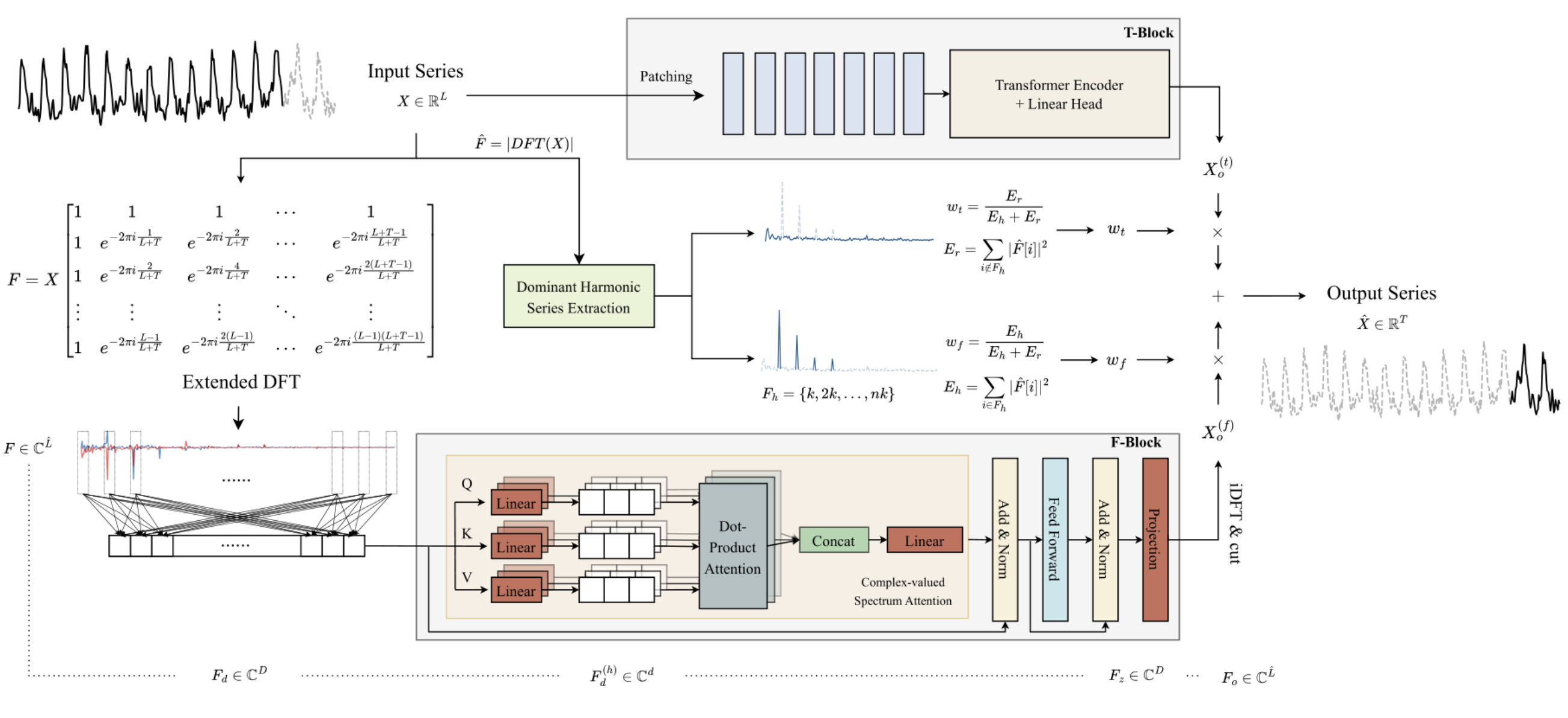
2. Durchführung von Grundoperationen mit komplexen Zahlen
In früheren Artikeln haben wir bereits ein wenig über komplexe Zahlen gesprochen. Sie eignen sich gut zur Beschreibung des Spektrums von Frequenzmerkmalen. Wir verwenden den Realteil, um die Signalamplitude darzustellen, und den Imaginärteil, um die Phasenverschiebung darzustellen. Nachdem wir jedoch von der DFT ein Signal in komplexer Form erhalten hatten, arbeiteten wir getrennt mit dem Real- und Imaginärteil. Anschließend haben wir die so gewonnenen Frequenzmerkmale mit Hilfe der iDFT in den Zeitbereich transformiert.
Obwohl der Ansatz, Real- und Imaginärteil als getrennte Einheiten zu analysieren, einfach zu implementieren ist, ist dieser Ansatz nicht optimal. Die ATFNet-Autoren untersuchen ausführlich beide Ansätze zur Verarbeitung komplexer Zahlen und kommen zu dem Schluss, dass die Analyse der Real- und Imaginärteile als separate Einheiten zu einem Informationsverlust führt. Um die vorgeschlagene Methode zu implementieren, müssen wir daher den Aufmerksamkeitsblock für die Arbeit mit komplexen Zahlen modifizieren.
Leider unterstützt OpenCL keine komplexen Zahlen. Daher müssen wir die Grundoperationen der komplexen Algebra selbst implementieren.
Wie bereits oben erwähnt, besteht eine komplexe Zahl aus einem Realteil und einem Imaginärteil:
![]()
wobei a ist der Realteil,
b ist der Imaginärteil,
i ist die imaginäre Einheit.
Um die komplexe Zahl auf der Seite von OpenCL zu speichern, ist es praktisch, einen Vektor mit 2 Elementen float2 zu verwenden.
Addition und Subtraktion komplexer Zahlen bilden fast vollständig die in Vektoroperationen von OpenCL implementierten Operationen nach. Deshalb werden wir sie jetzt nicht diskutieren.
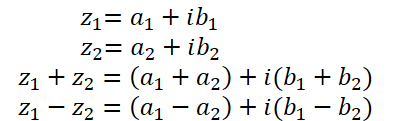
Die Multiplikation komplexer Zahlen ist jedoch ein wenig komplizierter.
![]()
Um diese Operation zu implementieren, erstellen wir die Funktion ComplexMul im OpenCL-Programm.
float2 ComplexMul(const float2 a, const float2 b) { float2 result = 0; result.x = a.x * b.x - a.y * b.y; result.y = a.x * b.y + a.y * b.x; return result; }
Die Funktion nimmt zwei float2-Vektoren als Parameter und gibt das Ergebnis im gleichen Format zurück. Auf diese Weise schaffen wir etwas, das den korrekten Operationen mit komplexen Variablen sehr ähnlich ist.
Die Division von komplexen Zahlen hat eine komplexere Form:
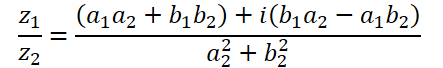
Um diesen Vorgang durchzuführen, erstellen wir die Funktion ComplexDiv.
float2 ComplexDiv(const float2 a, const float2 b) { float2 result = 0; float z = pow(b.x, 2) + pow(b.y, 2); if(z > 0) { result.x = (a.x * b.x + a.y * b.y) / z; result.y = (a.y * b.x - a.x * b.y) / z; } return result; }
Der Absolutwert einer komplexen Zahl ist eine reelle Zahl, die die Energie der Frequenzkomponente angibt:
![]()
Wir wollen dies in der Funktion ComplexAbs umsetzen.
float ComplexAbs(float2 a) { return sqrt(pow(a.x, 2) + pow(a.y, 2)); }
Die Formel für die Extraktion der Quadratwurzel einer komplexen Zahl ist etwas komplizierter:
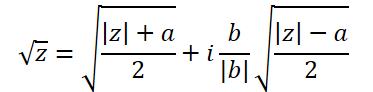
Um sie zu implementieren, erstellen wir eine weitere Funktion, ComplexSqrt.
float2 ComplexSqrt(float2 a)
{
float2 result = 0;
float z = ComplexAbs(a);
result.x = sqrt((z + a.x) / 2);
result.y = sqrt((z - a.x) / 2);
if(a.y < 0)
result.y *= (-1);
//---
return result;
}
Bei der Implementierung des Selbstaufmerksamkeits-Algorithmus normalisieren wir die Abhängigkeitskoeffizienten mit der Funktion SoftMax. Um sie im Bereich der komplexen Zahlen zu implementieren, benötigen wir den Exponenten der komplexen Zahl:
![]()
Im Code implementieren wir die Funktion wie folgt:
float2 ComplexExp(float2 a)
{
float2 result = exp(clamp(a.x, -20.0f, 20.0f));
result.x *= cos(a.y);
result.y *= sin(a.y);
return result;
}3. Komplexe Aufmerksamkeitsschicht
Wir haben die vorbereitenden Arbeiten durchgeführt und grundlegende mathematische Operationen mit komplexen Zahlen eingeführt. Nun gehen wir zum nächsten Schritt über, in dem wir mit Hilfe der Mathematik der komplexen Zahlen eine neuronale Schichtklasse der Aufmerksamkeit erstellen: CNeuronComplexMLMHAttention.
Wir erstellen die neue Klasse auf der Grundlage einer ähnlichen Aufmerksamkeitsschicht für reelle Werte CNeuronMLMHAttentionOCL. Der Vorteil dieses Ansatzes ist, dass wir die bereits vorhandene und vorkonfigurierte Top-Level-Funktionalität maximal wiederverwenden können. Wir müssen also nur die Methoden auf der unteren Ebene neu definieren, um mit komplexen Werten arbeiten zu können. Die Struktur der neuen Klasse ist unten dargestellt.
class CNeuronComplexMLMHAttention : public CNeuronMLMHAttentionOCL { protected: virtual bool ConvolutionForward(CBufferFloat *weights, CBufferFloat *inputs, CBufferFloat *outputs, uint window, uint window_out, ENUM_ACTIVATION activ, uint step = 0); virtual bool AttentionScore(CBufferFloat *qkv, CBufferFloat *scores, bool mask = false); virtual bool AttentionOut(CBufferFloat *qkv, CBufferFloat *scores, CBufferFloat *out); virtual bool ConvolutuionUpdateWeights(CBufferFloat *weights, CBufferFloat *gradient, CBufferFloat *inputs, CBufferFloat *momentum1, CBufferFloat *momentum2, uint window, uint window_out, uint step = 0); virtual bool ConvolutionInputGradients(CBufferFloat *weights, CBufferFloat *gradient, CBufferFloat *inputs, CBufferFloat *inp_gradient, uint window, uint window_out, uint activ, uint shift_out = 0, uint step = 0); virtual bool AttentionInsideGradients(CBufferFloat *qkv, CBufferFloat *qkv_g, CBufferFloat *scores, CBufferFloat *gradient); virtual bool SumAndNormilize(CBufferFloat *tensor1, CBufferFloat *tensor2, CBufferFloat *out, int dimension, bool normilize = true, int shift_in1 = 0, int shift_in2 = 0, int shift_out = 0, float multiplyer = 0.5f); public: CNeuronComplexMLMHAttention(void) {}; ~CNeuronComplexMLMHAttention(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronComplexMLMHAttentionOCL; } };
Das Bemerkenswerte an der Struktur der neuen Klasse ist, dass sie kein einziges internes Objekt oder eine Variable deklariert. Bei der Implementierung der Funktionalität werden wir geerbte Objekte und Variablen verwenden.
Außerdem deklariert die Klassenstruktur nur das Überschreiben von Methoden im protected Block. Alle Methoden wurden zuvor in der übergeordneten Klasse deklariert. Es gibt jedoch keine Methoden für hochrangige und Vorwärts- und Rückwärtsdurchgänge (feedForward, calcInputGradients und updateInputWeights), in denen wir normalerweise den Klassenalgorithmus aufbauen. Das liegt daran, dass wir die Reihenfolge der Aktionen des Algorithmus der übergeordneten Klasse vollständig beibehalten. Um jedoch mit komplexen Werten zu arbeiten, müssen wir die Größe der Datenpuffer verdoppeln, da der Imaginärteil des komplexen Wertes zu jedem realen Wert addiert wird. Darüber hinaus müssen wir die Mathematik der komplexen Zahlen in den Algorithmus integrieren. Wie Sie wissen, führen wir fast alle mathematischen Operationen auf der Seite von OpenCL durch. Daher müssen wir nicht nur die Methoden der unteren Ebenen neu definieren, sondern auch Änderungen an den Programmkernen OpenCL vornehmen.
3.1 Methode zur Initialisierung von Klassen
Die Arbeit einer jeden Klasse beginnt mit ihrer Initialisierung. Wie bereits erwähnt, deklarieren wir in unserer neuen Klasse keine verschachtelten Objekte oder Variablen. Aus diesem Grund sind der Konstruktor und der Destruktor leer. Die Initialisierung von geerbten Objekten wird in der Methode Init durchgeführt. Wie üblich erhalten wir in den Parametern dieser Methode vom Aufrufer die wichtigsten Konstanten, die die Architektur der Klasse definieren. Wie Sie sehen können, ist die Struktur der Methodenparameter die gleiche wie in der ähnlichen Methode der übergeordneten Klasse. Dies ist nicht überraschend. Denn wir behalten den grundlegenden Aufmerksamkeitsalgorithmus und die Struktur der übergeordneten Klasse vollständig bei. Wir werden jedoch die Methode selbst komplett neu schreiben.
bool CNeuronComplexMLMHAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * window * units_count, optimization_type, batch)) return false;
Im Methodenkörper rufen wir wie üblich die Initialisierungsmethode der übergeordneten Klasse auf. Bitte beachten Sie die folgenden beiden Punkte:
- Wir rufen die Initialisierungsmethode nicht von der direkten Elternklasse CNeuronMLMHAttentionOCL auf, sondern von der Basisklasse der neuronalen Schicht CNeuronBaseOCL. Der Grund dafür ist, dass die Initialisierung von verschachtelten Objekten der CNeuronMLMHAttentionOCL Klasse nicht benötigt wird, da wir alle Puffer mit größerer Größe neu definieren müssen, um komplexe Zahlen speichern zu können.
- Beim Aufruf der Methode der übergeordneten Klasse wird die Schichtgröße um das Zweifache erhöht. Das liegt daran, dass wir erwarten, dass die Ebenenoperation komplexe Werte ergibt.
Stellen Sie sicher, dass Sie das logische Ergebnis der Operationen der übergeordneten Klassenmethode überprüfen.
Nach erfolgreicher Initialisierung der von der Basisklasse der neuronalen Schicht geerbten Objekte speichern wir die wichtigsten Parameter der Architektur der erstellten Schicht.
iWindow = window; iWindowKey = fmax(window_key, 1); iUnits = units_count; iHeads = fmax(heads, 1); iLayers = fmax(layers, 1);
Im nächsten Schritt berechnen wir die Größen aller Puffer, die wir anlegen. Wir müssen komplexe Werte speichern. Daher werden alle Puffer im Vergleich zur Elternklasse um den Faktor 2 erhöht.
uint num = 2 * 3 * iWindowKey * iHeads * iUnits; //Size of QKV tensor uint qkv_weights = 2 * 3 * (iWindow + 1) * iWindowKey * iHeads; //Size of weights' matrix of QKV tenzor uint scores = 2 * iUnits * iUnits * iHeads; //Size of Score tensor uint mh_out = 2 * iWindowKey * iHeads * iUnits; //Size of multi-heads self-attention uint out = 2 * iWindow * iUnits; //Size of our tensore uint w0 = 2 * (iWindowKey + 1) * iHeads * iWindow; //Size W0 tensor uint ff_1 = 2 * 4 * (iWindow + 1) * iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2 = 2 * (4 * iWindow + 1) * iWindow; //Size of weights' matrix 2-nd feed forward layer
Dann organisieren wir eine Schleife entsprechend der Anzahl der erstellten verschachtelten Aufmerksamkeitsebenen. In seinem Hauptteil werden die verschachtelten Objekte initialisiert.
for(uint i = 0; i < iLayers; i++) { CBufferFloat *temp = NULL;
Hier erstellen wir zunächst eine verschachtelte Schleife von 2 Iterationen, in der wir Objekte zur Aufzeichnung der Daten des Vorwärtsdurchgangs und der entsprechenden Fehlergradienten initialisieren.
for(int d = 0; d < 2; d++) { //--- Initilize QKV tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Tensors.Add(temp)) return false;
Zunächst erstellen wir einen verketteten Puffer mit den Entitäten Query, Key and Value (Abfrage, Schlüssel und Wert). Als Nächstes benötigen wir nach dem Selbstaufmerksamkeits-Algorithmus (self-attention) einen Puffer, um die Matrix der Abhängigkeitskoeffizienten zu schreiben.
//--- Initialize scores temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(scores, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!S_Tensors.Add(temp)) return false;
Der folgende Puffer speichert die Ergebnisse der mehrköpfigen Aufmerksamkeit:
//--- Initialize multi-heads attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(mh_out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!AO_Tensors.Add(temp)) return false;
Wir werden dann die Größe auf den Eingangspegel reduzieren.
//--- Initialize attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
Auf den Aufmerksamkeitsblock folgt der Block des Vorwärtsdurchgangs, der aus 2 vollständig verbundenen Schichten besteht:
//--- Initialize Feed Forward 1 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(4 * out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 2 if(i == iLayers - 1) { if(!FF_Tensors.Add(d == 0 ? Output : Gradient)) return false; continue; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; }
Wir haben Puffer initialisiert, um die Ergebnisse des Vorwärtsdurchlaufs und die entsprechenden Fehlergradienten zu speichern. Zur Durchführung der Operationen benötigen wir jedoch lernbare Gewichtungsparameter. Zunächst füllen wir die Matrix der erlernbaren Parameter aus, um die Entitäten Query, Key and Value zu erzeugen:
//--- Initilize QKV weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(qkv_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < qkv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
Dann erzeugen wir die Parameter der mehrköpfigen Aufmerksamkeits-Dimensionalitätsreduktionsschicht:
//--- Initilize Weights0 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w = 0; w < w0; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Fügen wir die Parameter des Vorwärtsdurchgangs-Blocks hinzu:
//--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w = 0; w < ff_1; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; k = (float)(1 / sqrt(4 * iWindow + 1)); for(uint w = 0; w < ff_2; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
Während des Trainings der Modellparameter benötigen wir Puffer, um die Trainingsmomente aufzuzeichnen. Die Anzahl solcher Puffer hängt von der verwendeten Parameter-Lernmethode ab.
for(int d = 0; d < (optimization == SGD ? 1 : 2); d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(qkv_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(w0, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_1, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_2, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; } } //--- return true; }
Achten Sie darauf, das Ergebnis jeder Iteration dieser Methode zu überprüfen, da während des Trainings und des Betriebs des Modells das Fehlen auch nur eines der erforderlichen Puffer zu einem kritischen Fehler führen kann.
Nach der Initialisierung aller verschachtelten Objekte beenden wir die Methode und geben den logischen Wert der durchgeführten Operationen an den Aufrufer zurück.
3.2 Vorwärtsdurchgang
Nach der Initialisierung der Klasse fahren wir mit der Organisation des Vorwärtsdurchgangs (Feed-Forward-Pass) fort. Auch wenn wir den High-Level-Algorithmus von der übergeordneten Klasse erben, müssen wir noch einige Arbeit mit den Feed-Forward-Methoden auf der unteren Ebene erledigen. Wir ordnen die Vorgänge in der Reihenfolge des Selbstaufmerksamkeit-Algorithmus an.
Die Eingabedaten der Ebene werden zunächst in die Entitäten Query, Key and Value umgewandelt. Um sie in der übergeordneten Klasse zu erzeugen, haben wir den Kernel des Vorwärtsdurchgangs der Faltungsschicht verwendet. In dieser Implementierung werden wir den gleichen Ansatz verfolgen. Um mit komplexen Variablen zu arbeiten, müssen wir außerdem einen neuen Kernel namens FeedForwardComplexConv auf der Seite von OpenCL erstellen.
In den Kernel-Parametern übergeben wir Zeiger auf 3 Datenpuffer: die Matrix der Trainingsparameter, die Eingabedaten und einen Puffer zum Schreiben der Ergebnisse.
__kernel void FeedForwardComplexConv(__global float2 *matrix_w, __global float2 *matrix_i, __global float2 *matrix_o, int inputs, int step, int window_in, int activation ) { size_t i = get_global_id(0); size_t out = get_global_id(1); size_t w_out = get_global_size(1);
Beachten Sie, dass wir auf der Seite des Hauptprogramms immer noch Datenpuffer vom Typ Float verwenden, die jedoch größer sind. Im Kernel auf der Programmseite OpenCL geben wir den Typ float2 für Datenpuffer an. Dies ist genau die Art von Daten, die wir oben bei der Erstellung von Funktionen mit komplexen Variablen verwendet haben.
Im Hauptteil der Methode wird der aktuelle Thread im zweidimensionalen Aufgabenraum identifiziert. Die erste Dimension bezeichnet das Element in der Ergebnisfolge, die zweite Dimension den verwendeten Filter. In unserem Fall gibt sie die Position im verketteten Vektor der Entitäten an, die ein Element der zu analysierenden Sequenz beschreiben.
Anhand der erhaltenen Daten wird der Offset in den Datenpuffern bestimmt:
int w_in = window_in; int shift_out = w_out * i; int shift_in = step * i; int shift = (w_in + 1) * out; int stop = (w_in <= (inputs - shift_in) ? w_in : (inputs - shift_in));
Als Nächstes erstellen wir eine Schleife, um das Produkt der Vektoren zu berechnen:
float2 sum = matrix_w[shift + w_in]; for(int k = 0; k <= stop; k ++) sum += ComplexMul(matrix_i[shift_in + k], matrix_w[shift + k]);
Beachten Sie, dass wir zur Berechnung des Produkts von 2 komplexen Größen die oben erstellte Funktion ComplexMul verwenden. Wir verwenden grundlegende Vektoroperationen, um Werte zu addieren.
Da wir außerdem den Vektortyp float2 für Datenpuffer deklariert haben, können wir auf sie wie auf normale Fließkomma-Datenpuffer ohne Offset-Anpassung zugreifen. Bei jeder Operation werden zwei Elemente aus dem Puffer extrahiert: der Real- und der Imaginärteil der komplexen Zahl.
Als Nächstes überprüfen wir den berechneten Wert. Im Falle eines Variablenüberlaufs wird der Wert auf 0 gesetzt:
if(isnan(sum.x) || isnan(sum.y) || isinf(sum.x) || isinf(sum.y)) sum = (float2)0;
Jetzt müssen wir nur noch die Aktivierungsfunktion berechnen und den Wert im Ergebnispuffer speichern.
switch(activation) { case 0: sum = ComplexTanh(sum); break; case 1: sum = ComplexDiv((float2)(1, 0), (float2)(1, 0) + ComplexExp(-sum)); break; case 2: if(sum.x < 0) sum.x *= 0.01f; if(sum.y < 0) sum.y *= 0.01f; break; default: break; } matrix_o[out + shift_out] = sum; }
Um den oben erstellten Kernel auf der Seite des Hauptprogramms aufzurufen, wird die Methode CNeuronComplexMLMHAttention::ConvolutionForward überschrieben. Beachten Sie, dass wir die Methode überschreiben, anstatt eine neue Methode zu erstellen. Daher ist es sehr wichtig, dass die vollständige Parameterstruktur der ähnlichen Methode der übergeordneten Klasse erhalten bleibt. Nur wenn wir die Methode überschreiben, können wir diese Methode von der obersten Feed-Forward-Pass-Methode der übergeordneten Klasse aus aufrufen, ohne sie zu ändern.
bool CNeuronComplexMLMHAttention::ConvolutionForward(CBufferFloat *weights, CBufferFloat *inputs, CBufferFloat *outputs, uint window, uint window_out, ENUM_ACTIVATION activ, uint step = 0) { if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(weights) == POINTER_INVALID || CheckPointer(inputs) == POINTER_INVALID || CheckPointer(outputs) == POINTER_INVALID) return false;
Im Hauptteil der Methode wird zunächst die Relevanz der empfangenen Zeiger auf Objekte geprüft. Und dann prüfen wir, ob es Datenpuffer auf der Kontextseite von OpenCL gibt.
if(weights.GetIndex() < 0) return false; if(inputs.GetIndex() < 0) return false; if(outputs.GetIndex() < 0) return false; if(step == 0) step = window;
Nach erfolgreicher Übergabe des Kontrollblocks definieren wir den Aufgabenraum für den Kernel und den Offset darin:
uint global_work_offset[2] = {0, 0}; uint global_work_size[2]; global_work_size[0] = outputs.Total() / (2 * window_out); global_work_size[1] = window_out;
Dann übergeben wir alle notwendigen Parameter an den Kernel, während wir die Ausführung der Operationen kontrollieren:
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_w, weights.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_o, outputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_inputs, (int)(inputs.Total() / 2))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_step, (int)step)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_window_in, (int)window)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffс_window_out, (int)window_out)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_activation - 1, (int)activ)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Danach stellen wir den Kernel in die Ausführungswarteschlange und schließen die Methode ab:
if(!OpenCL.Execute(def_k_FeedForwardComplexConv, 2, global_work_offset, global_work_size)) { string error; CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error); printf("Error of execution kernel %s: %s", __FUNCSIG__, error); return false; } //--- return true; }
Der Algorithmus zur Platzierung der Kernel in der Ausführungswarteschlange ist recht einheitlich. Es kann Unterschiede in der Größe des Aufgabenraums und Variationen mit Variablen geben. Um Ihre Zeit zu sparen und den Umfang des Artikels zu reduzieren, werden wir nicht weiter auf die Kernel-Warteschlangenmethoden eingehen. Der vollständige Code des EAs befindet sich im Anhang. Gehen wir im Detail auf die Algorithmen zur Erstellung dieser Kerne ein.
Wir folgen weiterhin dem Algorithmus der Selbstaufmerksamkeit. Nach der Definition der Entitäten Query, Key and Value geht es an die Definition der Abhängigkeitskoeffizienten. Um die zu definieren, müssen wir die Abfragematrix mit der transponierten Schlüsselmatrix multiplizieren. Die Ergebnismatrix wird mit der Funktion SoftMax normalisiert.
Die beschriebene Funktionsweise wird im Kernel von ComplexMHAttentionScore ausgeführt, der von der Methode CNeuronComplexMLMHAttention::AttentionScore aufgerufen wird.
__kernel void ComplexMHAttentionScore(__global float2 *qkv, __global float2 *score, int dimension, int mask ) { int q = get_global_id(0); int h = get_global_id(1); int units = get_global_size(0); int heads = get_global_size(1);
In den Parametern erhält der Kernel Zeiger auf 2 Datenpuffer. Verketteter Puffer von Entitäten als Eingabe. Und einen Puffer zum Schreiben der Ergebnisse.
Der angegebene Kernel wird in einem zweidimensionalen Aufgabenraum ausgeführt. Die erste Dimension definiert eine Zeile der Query-Matrix, die zweite einen aktiven Aufmerksamkeitskopf. Somit führt jede einzelne Instanz des laufenden Kernels Operationen zur Berechnung einer Zeile der Matrix der Abhängigkeitskoeffizienten innerhalb eines Aufmerksamkeitskopfes durch.
Im Kernelkörper identifizieren wir den aktuellen Thread in beiden Dimensionen des Aufgabenraums und bestimmen die Offsets in den Datenpuffern:
int shift_q = dimension * (h + 3 * q * heads); int shift_s = units * (h + q * heads);
Dann definieren wir den Normalisierungsfaktor für die Daten:
float2 koef = (float2)(sqrt((float)dimension), 0); if(koef.x < 1) koef.x = 1;
Erstellen wir eine Schleife, um die Abhängigkeitskoeffizienten zu berechnen:
float2 sum = 0; for(int k = 0; k < units; k++) { if(mask > 0 && k > q) { score[shift_s + k] = (float2)0; continue; }
An dieser Stelle sei darauf hingewiesen, dass der vorgestellte Algorithmus eine Datenmaskierung vorsieht, die es ermöglicht, den so genannten „Look-ahead“ zu begrenzen. Das Modell analysiert nur die Koeffizienten der Abhängigkeit von früheren Token. Für nachfolgende Token werden die Abhängigkeitskoeffizienten auf 0 gesetzt, damit das Modell während des Trainings keine Informationen „aus der Zukunft“ erhält. Diese Funktionalität wird durch das Flag mask aktiviert, das in den Kernel-Parametern übergeben wird.
Anschließend wird in einer verschachtelten Schleife das nächste Element des Abhängigkeitsvektors durch Multiplikation von 2 Vektoren berechnet.
float2 result = (float2)0; int shift_k = dimension * (h + heads * (3 * k + 1)); for(int i = 0; i < dimension; i++) result += ComplexMul(qkv[shift_q + i], qkv[shift_k + i]);
Wir berechnen den Exponenten für das Ergebnis des Produkts:
result = ComplexExp(ComplexDiv(result, koef));
Es ist notwendig, den Variablenüberlauf zu definieren:
if(isnan(result.x) || isnan(result.y) || isinf(result.x) || isinf(result.y)) result = (float2)0;
Wir schreiben das Ergebnis in den Ergebnispuffer und addieren es zur Gesamtsumme für die anschließende Normalisierung.
score[shift_s + k] = result; sum += result; }
Am Ende des Kernels wird die berechnete Zeile der Matrix der Abhängigkeitskoeffizienten normalisiert:
if(ComplexAbs(sum) > 0) for(int k = 0; k < units; k++) score[shift_s + k] = ComplexDiv(score[shift_s + k], sum); }
Die auf diese Weise erhaltene Score-Matrix der Abhängigkeitskoeffizienten wird zur Berechnung der Ergebnisse des Aufmerksamkeitsblocks verwendet. Hier müssen wir die erhaltene Koeffizientenmatrix mit der Matrix der Entität Value multiplizieren. Diese Arbeit wird im Kernel ComplexMHAttentionOut erledigt. Ähnlich wie der vorherige Kernel arbeitet auch dieser Kernel im gleichen 2-dimensionalen Aufgabenraum.
__kernel void ComplexMHAttentionOut(__global float2 *scores, __global float2 *qkv, __global float2 *out, int dimension ) { int u = get_global_id(0); int units = get_global_size(0); int h = get_global_id(1); int heads = get_global_size(1);
Im Kernelkörper identifizieren wir den aktuellen Thread im Aufgabenraum und bestimmen die Offsets in den Datenpuffern:
int shift_s = units * (h + heads * u); int shift_out = dimension * (h + heads * u);
Danach erstellen wir ein System von verschachtelten Schleifen, um mathematische Operationen zur Multiplikation der Value-Matrix mit den entsprechenden Abhängigkeitskoeffizienten durchzuführen:
for(int d = 0; d < dimension; d++) { float2 result = (float2)0; for(int v = 0; v < units; v++) { int shift_v = dimension * (h + heads * (3 * v + 2)) + d; result += ComplexMul(scores[shift_s + v], qkv[shift_v]); } out[shift_out + d] = result; } }
Das Ergebnis der mehrköpfigen Aufmerksamkeit wird dann zu einem einzigen Tensor zusammengefasst und in seiner Dimension auf die Größe des Eingabedatentensensors reduziert. Dann führen wir die Operationen des Blocks FeedForward durch. Diese Operationen werden mit dem oben beschriebenen Kernel FeedForwardComplexConv durchgeführt. Damit ist die Beschreibung der Kernel-Algorithmen zur Durchführung der Operationen des Vorwärtsdurchgangs abgeschlossen. Sie können den vollständigen Code aller Kernel sowie die Methoden, die sie aufrufen, im Anhang sehen.
3.3 Implementierung des Rückwärtsdurchgangs
Die Funktionsweise des Vorwärtsdurchgangs ist bereit. Als Nächstes werden wir die Algorithmen des Rückwärtsdurchgangs (backpropagation) implementieren. Diese Arbeit ähnelt derjenigen, die oben für den Vorwärtsdurchgang durchgeführt wurde. Wir nutzen die von der übergeordneten Klasse geerbten High-Level-Algorithmen und setzen die Low-Level-Methoden außer Kraft.
Wie bereits erwähnt, werden wir die Algorithmen der Methoden, die Kernel in die Ausführungswarteschlange stellen, nicht berücksichtigen. Sie sind alle gleich. Schenken wir der Analyse der Kernel-Algorithmen auf der Programmseite von OpenCL mehr Aufmerksamkeit.
Der im Vorwärtsdurchgang am häufigsten verwendete Kernel war FeedForwardComplexConv. Dies ist ein universeller Block, den wir in verschiedenen Phasen verwenden. Natürlich beginnen wir die Konstruktion des Rückwärtsdurchgangs-Algorithmen genau mit dem Kernel für die Propagierung des Fehlergradienten durch den angegebenen Block. Wir implementieren diese Funktionalität im Kernel CalcHiddenGradientComplexConv.
__kernel void CalcHiddenGradientComplexConv(__global float2 *matrix_w, __global float2 *matrix_g, __global float2 *matrix_o, __global float2 *matrix_ig, int outputs, int step, int window_in, int window_out, int activation, int shift_out ) { size_t i = get_global_id(0); size_t inputs = get_global_size(0);
Der Kernel läuft in einem eindimensionalen Aufgabenraum entsprechend der Anzahl der Elemente im Eingabedatenpuffer. Jeder einzelne Thread eines bestimmten Kernels sammelt Fehlergradienten von allen Elementen, die von dem analysierten Eingabeelement betroffen sind.
Im Kernelkörper identifizieren wir den aktuellen Thread und bestimmen die Offsets in den Datenpuffern. Wir deklarieren auch die notwendigen lokalen Variablen:
float2 sum = (float2)0; float2 out = matrix_o[shift_out + i]; int start = i - window_in + step; start = max((start - start % step) / step, 0); int stop = (i + step - 1) / step; if(stop > (outputs / window_out)) stop = outputs / window_out;
Danach erstellen wir ein System von Schleifen. In ihrem Körper wird der Gesamtfehlergradient erfasst, wobei der Einfluss des analysierten Elements auf das Gesamtergebnis berücksichtigt wird:
for(int h = 0; h < window_out; h ++) { for(int k = start; k < stop; k++) { int shift_g = k * window_out + h; int shift_w = (stop - k - 1) * step + i % step + h * (window_in + 1); if(shift_g >= outputs || shift_w >= (window_in + 1) * window_out) break; sum += ComplexMul(matrix_g[shift_out + shift_g], matrix_w[shift_w]); } }
Nach dem Verlassen der Schleife wird geprüft, ob die Variable überläuft:
if(isnan(sum.x) || isnan(sum.y) || isinf(sum.x) || isinf(sum.y)) sum = (float2)0;
Wir passen den erhaltenen Fehlergradienten auch durch die Ableitung der Aktivierungsfunktion an:
switch(activation) { case 0: sum = ComplexMul(sum, (float2)1.0f - ComplexMul(out, out)); break; case 1: sum = ComplexMul(sum, ComplexMul(out, (float2)1.0f - out)); break; case 2: if(out.x < 0.0f) sum.x *= 0.01f; if(out.y < 0.0f) sum.y *= 0.01f; break; default: break; } matrix_ig[i] = sum; }
Das Endergebnis wird im Fehlergradientenpuffer der vorherigen Schicht gespeichert.
Als Nächstes betrachten wir den Kernel für die Weitergabe des Fehlergradienten durch den Aufmerksamkeitsblock ComplexMHAttentionGradients. Dieser Kernel stellt einen recht komplexen Algorithmus dar, der je nach Anzahl der Entitäten, für die der Wert des Fehlergradienten bestimmt wird, in drei Blöcke unterteilt werden kann.
__kernel void ComplexMHAttentionGradients(__global float2 *qkv, __global float2 *qkv_g, __global float2 *scores, __global float2 *gradient) { size_t u = get_global_id(0); size_t h = get_global_id(1); size_t d = get_global_id(2); size_t units = get_global_size(0); size_t heads = get_global_size(1); size_t dimension = get_global_size(2);
In diesem Kernel werden eine ganze Reihe von Operationen durchgeführt. Um die Gesamtausführungszeit zu reduzieren, haben wir während des Modelltrainings versucht, die mit der Berechnung der Werte für die einzelnen Variablen verbundenen Operationen zu parallelisieren. Um die Identifizierung von Threads transparent und intuitiv zu gestalten, haben wir für diesen Kernel einen 3-dimensionalen Aufgabenraum geschaffen. Wie bei den Vorwärtsdurchgangsmethoden des Aufmerksamkeitsblock verwenden wir hier das Sequenzelement und den Aufmerksamkeitskopf. Die dritte Dimension des Aufgabenraums wird für die Position des Elements in dem Tensor verwendet, der das Sequenzelement beschreibt. So schreibt jeder einzelne Thread trotz der großen Anzahl von Operationen nur 3 Werte in den Ergebnispuffer. In diesem Fall handelt es sich um einen verketteten Puffer von Fehlergradienten für die Entitäten Query, Key and Value.
Im Kernelkörper identifizieren wir zunächst den Thread im Aufgabenraum und bestimmen die Offsets in den Datenpuffern:
float2 koef = (float2)(sqrt((float)dimension), 0); if(koef.x < 1) koef.x = 1; //--- init const int shift_q = dimension * (heads * 3 * u + h); const int shift_k = dimension * (heads * (3 * u + 1) + h); const int shift_v = dimension * (heads * (3 * u + 2) + h); const int shift_g = dimension * (heads * u + h); int shift_score = h * units; int step_score = units * heads;
Dann bestimmen wir den Fehlergradienten für das analysierte Element der Value-Matrix. Wir multiplizieren eine separate Spalte des Fehlergradiententensors am Ausgang des Aufmerksamkeitsblocks mit der entsprechenden Spalte der Abhängigkeits-Koeffizientenmatrix:
//--- Calculating Value's gradients float2 sum = (float2)0; for(int i = 0; i < units; i++) sum += ComplexMul(gradient[(h + i * heads) * dimension + d], scores[shift_score + u + i * step_score]); qkv_g[shift_v + d] = sum;
Im nächsten Schritt wird der Fehlergradient für das analysierte Element der Query-Entität bestimmt. Diese Einheit hat keinen direkten Einfluss auf das Ergebnis. Es gibt nur einen indirekten Einfluss über die Matrix der Abhängigkeitskoeffizienten. Daher müssen wir zunächst den Fehlergradienten für die entsprechende Zeile der Matrix der Abhängigkeitskoeffizienten finden. Die Normalisierung der Daten mit Hilfe der SoftMax-Funktion verkompliziert den Prozess zusätzlich.
//--- Calculating Query's gradients shift_score = h * units + u * step_score; float2 grad = 0; float2 grad_out = gradient[shift_g + d]; for(int k = 0; k < units; k++) { float2 sc_g = (float2)0; float2 sc = scores[shift_score + k]; for(int v = 0; v < units; v++) sc_g += ComplexMul( ComplexMul(scores[shift_score + v], ComplexMul(qkv[dimension * (heads * (3 * v + 2) + h)], grad_out)), ((float2)(k == v, 0) - sc) );
Der für einen einzelnen Abhängigkeitskoeffizienten gefundene Fehlergradient wird mit dem entsprechenden Element der Matrix der Entity Key multipliziert. Die resultierenden Werte werden addiert, um den Gesamtfehlergradienten zu ermitteln:
grad += ComplexMul(ComplexDiv(sc_g, koef), qkv[dimension * (heads * (3 * k + 1) + h) + d]); }
Wir schreiben den kumulierten Fehlergradienten in den Ergebnispuffer:
qkv_g[shift_q + d] = grad;
In ähnlicher Weise definieren wir den Fehlergradienten der Elemente von der Entität Key, der sich ebenfalls indirekt über die Matrix der Abhängigkeitskoeffizienten auf das Ergebnis auswirkt. Diesmal arbeiten wir jedoch mit einer Spalte der angegebenen Matrix:
//--- Calculating Key's gradients grad = 0; for(int q = 0; q < units; q++) { shift_score = h * units + q * step_score; float2 sc_g = (float2)0; float2 sc = scores[shift_score + u]; float2 grad_out = gradient[dimension * (heads * q + h) + d]; for(int v = 0; v < units; v++) sc_g += ComplexMul( ComplexMul(scores[shift_score + v], ComplexMul(qkv[dimension * (heads * (3 * v + 2) + h)], grad_out)), ((float2)(u == v, 0) - sc) ); grad += ComplexMul(ComplexDiv(sc_g, koef), qkv[dimension * (heads * 3 * q + h) + d]); } qkv_g[shift_k + d] = grad; }
Damit ist die Diskussion über die Konstruktionsalgorithmen des Kernels für den Rückwärtsdurchgang im Rahmen der komplexen Aufmerksamkeitsschichtfunktionalität abgeschlossen. Den vollständigen Code aller Methoden und Kernel der vorgestellten Klasse finden Sie im Anhang.
Schlussfolgerung
In diesem Artikel haben wir die theoretischen Aspekte der ATFNet-Methode erörtert, die Ansätze zur Vorhersage von Zeitreihen sowohl im Frequenz- als auch im Zeitbereich kombiniert.
Im praktischen Teil dieses Artikels haben wir uns intensiv mit der Konstruktion einer Aufmerksamkeitsschicht mit komplexen Operationen beschäftigt. Dies ist jedoch nur ein Objekt des Blocks F der vorgeschlagenen Methode. Im nächsten Artikel werden wir den Algorithmus der ATFNet-Methode weiter ausbauen. Wir werden auch die Ergebnisse seiner Arbeit mit realen Daten sehen.
Referenzen
- ATFNet: Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting
- Andere Artikel aus dieser Reihe
Programme, die im diesem Artikel verwendet werden
| # | Name | Typ | Beschreibung |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | Beispielsammlung EA |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA zum Sammeln von Beispielen mit der Real-ORL-Methode |
| 3 | Study.mq5 | Expert Advisor | Modelltraining EA |
| 4 | StudyEncoder.mq5 | Expert Advisor | Encode Training EA |
| 5 | Test.mq5 | Expert Advisor | Trainings-EA für das Model |
| 6 | Trajectory.mqh | Klassenbibliothek | Struktur der Systemzustandsbeschreibung |
| 7 | NeuroNet.mqh | Klassenbibliothek | Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes |
| 8 | NeuroNet.cl | Code Base | Die Bibliothek des Programmcodes von OpenCL |
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/14996
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Wichtigste Änderungen des Algorithmus für die künstliche kooperative Suche (ACSm)
Wichtigste Änderungen des Algorithmus für die künstliche kooperative Suche (ACSm)
 Entwicklung eines Replay Systems (Teil 51): Die Dinge werden kompliziert (III)
Entwicklung eines Replay Systems (Teil 51): Die Dinge werden kompliziert (III)
 Elemente der Korrelationsanalyse in MQL5: Chi-Quadrat-Test nach Pearson auf Unabhängigkeit und Korrelationsverhältnis
Elemente der Korrelationsanalyse in MQL5: Chi-Quadrat-Test nach Pearson auf Unabhängigkeit und Korrelationsverhältnis
 Neuronale Netze leicht gemacht (Teil 91): Vorhersage durch Frequenzbereiche (Frequency Domain Forecasting, FreDF)
Neuronale Netze leicht gemacht (Teil 91): Vorhersage durch Frequenzbereiche (Frequency Domain Forecasting, FreDF)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuronale Netze sind einfach. Teil 92 😅.
Es ist für jeden zugänglich. Und die Anzahl der Artikel zeigt die Vielseitigkeit und ständige Weiterentwicklung.