
ニューラルネットワークが簡単に(第92回):周波数および時間領域における適応的予測
はじめに
時間領域と周波数領域は、時系列データを分析するために使用される2つの基本的な表現です。時間領域では、分析は時間の経過に伴う振幅の変化に焦点を当て、信号内の局地的依存関係や過渡的な現象を識別することができます。一方、周波数領域の分析は、時系列を周波数成分の観点から表現し、データの大域的依存関係やスペクトル特性に関する洞察を提供することを目的としています。両方の分野の利点を組み合わせることは、リアルタイムの時系列で異なる周期的なパターンが混在する問題に対処するための有望なアプローチとなります。ここでの課題は、時間領域と周波数領域の利点を効果的に組み合わせる方法です。
時間領域での成果と比較すると、周波数領域には未開拓の領域がまだ多くあります。最近の記事では、周波数領域を使用して大域的な時系列の依存関係をより適切に処理する方法が紹介されています。周波数領域での直接予測では、より多くのスペクトル情報を使用することで時系列予測の精度を向上させることができます。しかし、周波数領域での直接スペクトル予測にはいくつかの問題があります。その1つは、分析対象の既知のデータのスペクトルと調査対象の時系列の完全なスペクトルとの間で周波数特性に潜在的な不一致が生じることです。これは、離散フーリエ変換(DFT)を使用した結果として発生する問題です。この不一致により、ソースデータのスペクトル全体にわたって特定の周波数に関する情報を正確に表現することが難しくなり、予測が不正確になる可能性があります。
さらに、周波数の組み合わせに関する情報を効率的に抽出する方法も課題となります。スペクトル内で発生する調和級数には大量の情報が含まれており、スペクトルの特徴を抽出することは難易度が高い作業です。
論文「ATFNet:Adaptive Time-Frequency Ensembled Network for Long-term Time Series Forecasting」では、これらの問題に対する解決策としてATFNet法が提案されています。この方法は、局所的依存関係と大域的依存関係を同時に処理するための時間領域モジュールと周波数領域モジュールを含んでいます。さらに、この論文では、2つのモジュール間で動的に重みを分散させる新しい重み付けメカニズムが紹介されています。
この手法の著者は、優勢な調和級数にエネルギー加重をおこなう手法を提案しました。これにより、元のデータに示された周期性のレベルに基づいて、時間領域と周波数領域のモジュールに適切な加重を生成することが可能となります。これにより、異なる周期パターンを持つ時系列を扱う際に、両分野の利点を効果的に活用することができます。
さらに、この手法の著者は、元のデータと完全な時系列の離散周波数スペクトルを整合させるために拡張DFTを導入し、特定の周波数表現の精度を高めています。
また、周波数領域でアテンションメカニズムを実装し、複素数スペクトルアテンション(CSA: complex spectral attention)という新たなアプローチを提案しています。これにより、さまざまな周波数応答の組み合わせから情報を収集でき、周波数領域表現に対して効果的な注意を向ける手法が提供されます。
この記事では、8つの実際のデータセットを用いた実験結果を紹介しており、ATFNetが有望な結果を示し、多くのデータセットで他の最先端の時系列予測方法よりも優れたパフォーマンスを発揮したことが明らかとなっています。
1. ATFNetアルゴリズム
ATFNet法の著者は、異なるチャネルからのスペクトルの混合を防ぐために、チャネル非依存方式を採用しています。異なる大域的パターンを持つ可能性のあるチャネル間でスペクトルを混ぜ合わせると、モデルのパフォーマンスに悪影響を及ぼす可能性があるためです。
Tブロックでは、入力された単変量時系列データを直接時間領域で処理します。この処理により、解析対象の時系列データの将来の特定の予測値が出力されます。
Fブロックでは、拡張離散フーリエ変換(DFT)を使用して、元の単変量時系列を周波数領域へ変換し、拡張された周波数スペクトルを生成します。このスペクトルは、逆離散フーリエ変換(iDFT)使用して時間領域に戻され、周波数特性に基づいた時系列の予測値を提供します。
TブロックとFブロックでの予測結果は、適応的な重みを用いて組み合わせられ、解析された時系列データの最終的な予測値が得られます。この重みは、優勢な調和級数のエネルギー重みに基づいて計算されます。
一般的に、アルゴリズムは以下のように示すことができます。
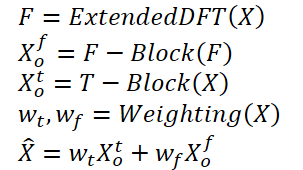
従来のDFTでは、元のデータのスペクトルと解析対象の全時系列の周波数が一致しない場合があり、小規模なデータブロックに基づいて構築された予測モデルでは、時系列全体の周波数特性を完全かつ正確に把握できない可能性があります。この不一致は、モデルの予測精度を低下させる要因となります。
これを解決するため、ATFNetの著者は拡張DFTを提案しました。これにより、分析対象の元データの長さによる制約を克服し、完全な時系列に対応するDFT周波数グループに適合した元のスペクトルを取得できるようになります。具体的には、この手法では元の複素指数基底を、完全な時系列に対応するDFT基底に置き換える手法を採用し、モデルの精度を向上させています。
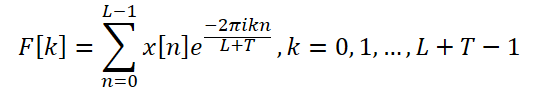
このようにして、長さL + Tの周波数特性スペクトルが得られます。このスペクトルは、完全な分析系列(初期データ + 予測データ)のDFTスペクトルと一致します。リアルタイム系列においては、DFTの重要な特性である出力スペクトルの共役対称性を活用することで、元データの周波数スペクトルの前半部分のみを考慮できます。後半部分は冗長な情報を含むため、これを省略することで計算コストを削減することが可能です。
Fブロックは、すべてのパラメータが複素数値であるTransformerエンコーダを基盤として設計されています。Fブロック内のすべての計算は複素数フィールドでおこなわれます。
また、この手法の著者は元の周波数特性Fのスペクトル処理にRevINを利用しています。RevINはもともと時間領域での分布シフトを排除するために開発された手法ですが、この研究では周波数領域におけるスペクトルの処理にも有効であることが確認されました。このアプローチを使用することで、異なる大域的特性を持つ時系列スペクトルを比較可能な分布へ変換できます。分析の前に、周波数特性Fは正規化され、処理後には元の周波数分布の統計特性が復元されます。
周波数領域スペクトルには時系列依存性がほとんど見られないため、この手法の著者はFブロックでの位置エンコーディングを使用していません。
また、この研究では改良されたマルチヘッドアテンション(multi-head attention)メカニズムが導入されています。各ヘッドh = 1, 2, ..., Hににおいて、埋め込まれたスペクトルFdは訓練済みの投影を通じてスペクトル空間にマッピングされ、その後、各ヘッドで複素スカラー積を用いたアテンション計算が実行されます。
ATFNetではTransformerと同様に、残差接続を持つLayerNorm層およびFeedForward層を使用しており、これらは複素数の領域に拡張されています。
Mエンコーダ層でのアテンションブロックの計算結果は、完全な時系列データにわたる線形投影を通じて得られます。取得された周波数特性はiDFTによって時間領域に逆変換され、予測の一部となる最後のTポイントがFブロックの最終出力として得られます。
なおFブロック全体は複素ニューラルネットワーク(CVNN: complex value neural network)の完全なアーキテクチャを使用して構築されています。
一方で、Tブロックは時間領域で処理しやすい時系列の局地的依存関係を捉える役割を担っています。このブロックでは、PatchTSTのような既存の時系列セグメンテーション手法が利用されています。PatchTSTは時系列の局地的依存関係を効率的にキャプチャでき、さらに分布バイアスの補正にはRevINが用いられています。
周期的な時系列データには、周波数領域スペクトル内に少なくとも1つの高調波グループが存在し、支配的な高調波グループがスペクトルエネルギーの最も高い集中度を示します。一方で、非周期的な時系列のスペクトルではエネルギーが均一に分散しているため、この特性はあまり見られません。ATFNet法の著者は、優勢な調和級数内のエネルギー集中度が時系列の周期性を反映する指標になり得ることを示しています。優勢な調和級数のエネルギーとスペクトル全体のエネルギーの比率が、この集中度の定量的な評価指標として使用されています。直感的には、時系列がより顕著な周期構造を持つ場合、それを構成要素に分解できるため、優勢な調和級数内でのエネルギー集中度が高まります。
この特性に基づき、ATFNetの著者は優勢な調和級数のエネルギー比率を用いて時系列の周期性の度合いを定量的に評価しています。優勢な調和級数を特定するための重要なステップは、基本周波数を決定することです。この決定には以下のような方法があります。
- 最も高い振幅値を持つ周波数を基本周波数とする単純な方法
- ルールベースのピッチ検出アルゴリズム
- データ駆動型のピッチ検出アルゴリズム
ATFNetアルゴリズムでは、基本周波数の決定に任意のアプローチを使用できますが、この方法の著者は、この基本周波数を、その高調波とともに考慮し、それによって得られる合計エネルギーE Ehを計算します。その後、この優位周波数のエネルギーとスペクトル全体のエネルギーの比率を求め、これを基にして Fブロックの重みを決定しています。
この手法の著者らは、一連の実験を通じて、優位周波数を決定するためのさまざまな手法の有効性を評価しました。その結果、計算コストに対する結果の精度の比率では、単純な手法が最良であると結論付けられました。この手法は、低い計算コストを維持しつつ、実際の時系列データセットにおいて優れた精度を発揮することが示されています。
一方で、他のアプローチは計算の複雑さによって制約を受けています。さらに、データ駆動型の手法ではラベル付きのステップデータが必要であり、このデータの取得が難しいことが多く、実用化の障害となります。そのため、ATFNetの著者は、実験において基本周波数の検出に単純な方法をデフォルトで使用しています。
以下に、AFTNet法の元の可視化を示します。
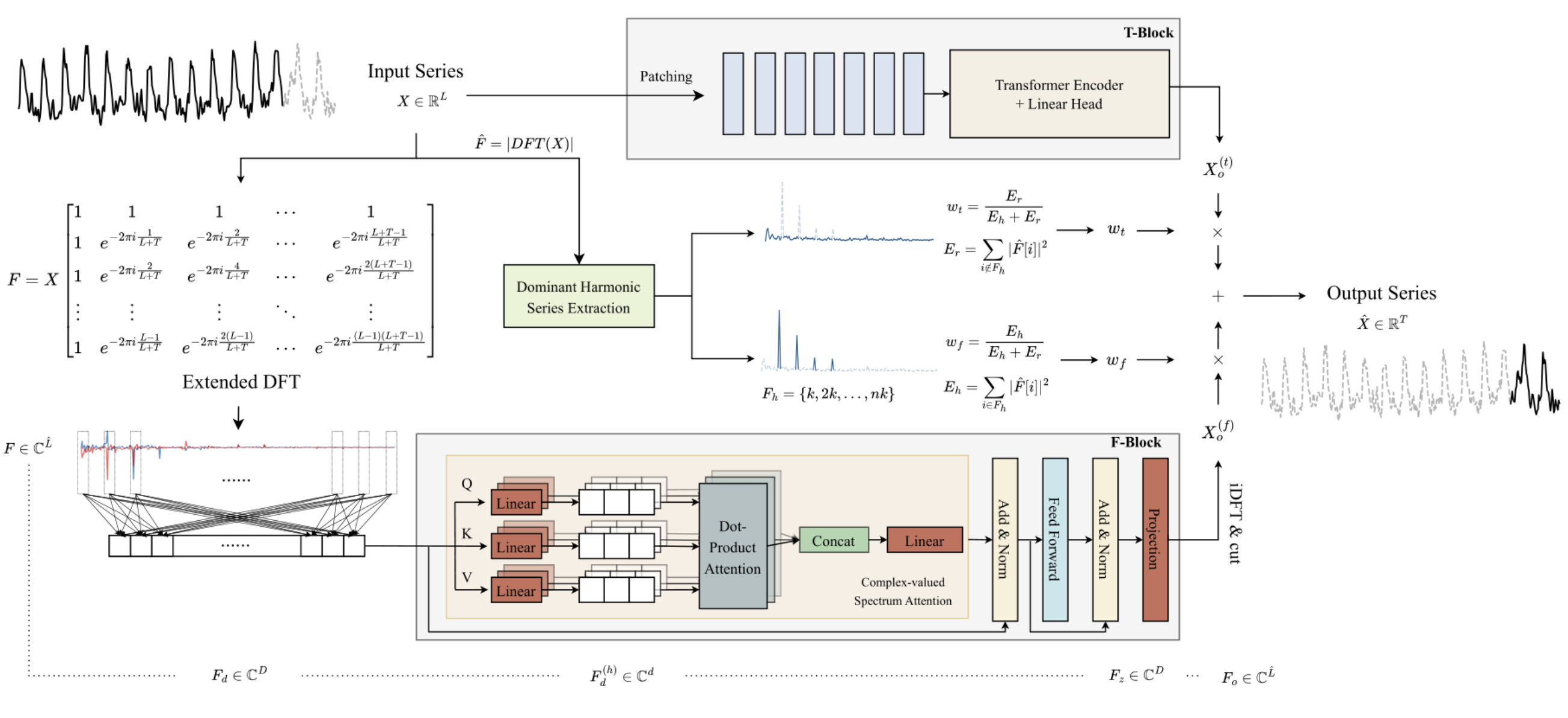
2. 複素数を使った基本操作の実装
以前の記事では、複素数について少し触れました。複素数は、周波数特性のスペクトルを表現するのに非常に便利です。実数部は信号の振幅を示し、虚数部は位相シフトを示します。しかし、DFTを使用して複素形式で信号を受け取る際、実数部と虚数部は別々に処理されました。その後、iDFTを使って、このようにして得られた周波数特性を時間領域に変換しました。
実数部と虚数部を別々に分析するアプローチは実装が容易ですが、最適な方法とは言えません。ATFNetの著者は、複素数を処理するための2つのアプローチを詳細に検討し、実数部と虚数部を別々に扱うと情報が失われるという結論に達しました。そのため、提案された方法を実装するには、複素数として動作するようにアテンションブロックを変更する必要があります。
残念ながら、OpenCLは複素数をサポートしていないため、複素代数の基本的な演算を独自に実装する必要があります。
すでに述べたように、複素数は実数部と虚数部から成り立っています。
![]()
ここでaは実数部
bは虚数部
iは虚数単位
OpenCL側で複素数を保存するには、2要素float2のベクトルを使用すると便利です。
複素数の加算と減算は、OpenCLベクトル演算で実装されているものとほぼ完全に同じであるため、ここでは説明しません。
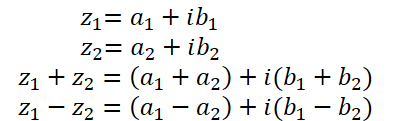
しかし、複素数の乗算はもう少し複雑です。
![]()
この操作を実装するために、OpenCLプログラム内にComplexMul関数を作成します。
float2 ComplexMul(const float2 a, const float2 b) { float2 result = 0; result.x = a.x * b.x - a.y * b.y; result.y = a.x * b.y + a.y * b.x; return result; }
この関数は2つのfloat2ベクトルをパラメータとして受け取り、同じフォーマットで結果を返します。こうすることで、複素数変数を使った正しい操作と非常に似たものを作り出すことができます。
複素数の除算はより複雑な形式になります。
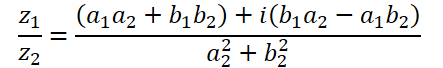
この操作を実行するには、ComplexDiv関数を作成しましょう。
float2 ComplexDiv(const float2 a, const float2 b) { float2 result = 0; float z = pow(b.x, 2) + pow(b.y, 2); if(z > 0) { result.x = (a.x * b.x + a.y * b.y) / z; result.y = (a.y * b.x - a.x * b.y) / z; } return result; }
複素数の絶対値は、周波数成分のエネルギーを示す実数です。
![]()
これをComplexAbs関数に実装してみましょう。
float ComplexAbs(float2 a) { return sqrt(pow(a.x, 2) + pow(a.y, 2)); }
複素数の平方根を求める式は少し複雑です。
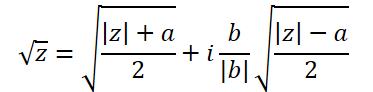
これを実装するには、ComplexSqrtという別の関数を作ってみましょう。
float2 ComplexSqrt(float2 a)
{
float2 result = 0;
float z = ComplexAbs(a);
result.x = sqrt((z + a.x) / 2);
result.y = sqrt((z - a.x) / 2);
if(a.y < 0)
result.y *= (-1);
//---
return result;
}
自己アテンション(Self-Attention)アルゴリズムを実装する際には、SoftMax関数を用いて依存係数を正規化します。複素数の領域で実装するには、複素数の指数表現が必要になります。
![]()
コードでは、この関数を次のように実装しています。
float2 ComplexExp(float2 a)
{
float2 result = exp(clamp(a.x, -20.0f, 20.0f));
result.x *= cos(a.y);
result.y *= sin(a.y);
return result;
}3.複素数アテンション層
準備作業を完了し、複素数を使用した基本的な数学演算を実装しました。次に、複素数数学を使用してアテンションニューラル層クラスCNeuronComplexMLMHAttentionを作成するステップに進みます。
実数値用の同様のアテンション層CNeuronMLMHAttentionOCLに基づいて新しいクラスを作成します。このアプローチの利点は、既存の事前構成されたトップレベルの機能を最大限に活用できることです。複素数値を処理できるようにするには、下位レベルのメソッドを再定義するだけで済みます。この新しいクラスの構造を以下に示します。
class CNeuronComplexMLMHAttention : public CNeuronMLMHAttentionOCL { protected: virtual bool ConvolutionForward(CBufferFloat *weights, CBufferFloat *inputs, CBufferFloat *outputs, uint window, uint window_out, ENUM_ACTIVATION activ, uint step = 0); virtual bool AttentionScore(CBufferFloat *qkv, CBufferFloat *scores, bool mask = false); virtual bool AttentionOut(CBufferFloat *qkv, CBufferFloat *scores, CBufferFloat *out); virtual bool ConvolutuionUpdateWeights(CBufferFloat *weights, CBufferFloat *gradient, CBufferFloat *inputs, CBufferFloat *momentum1, CBufferFloat *momentum2, uint window, uint window_out, uint step = 0); virtual bool ConvolutionInputGradients(CBufferFloat *weights, CBufferFloat *gradient, CBufferFloat *inputs, CBufferFloat *inp_gradient, uint window, uint window_out, uint activ, uint shift_out = 0, uint step = 0); virtual bool AttentionInsideGradients(CBufferFloat *qkv, CBufferFloat *qkv_g, CBufferFloat *scores, CBufferFloat *gradient); virtual bool SumAndNormilize(CBufferFloat *tensor1, CBufferFloat *tensor2, CBufferFloat *out, int dimension, bool normilize = true, int shift_in1 = 0, int shift_in2 = 0, int shift_out = 0, float multiplyer = 0.5f); public: CNeuronComplexMLMHAttention(void) {}; ~CNeuronComplexMLMHAttention(void) {}; virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronComplexMLMHAttentionOCL; } };
この新しいクラスの構造で注目すべき点は、単一の内部オブジェクトや変数を宣言していないことです。機能を実装するプロセスでは、継承されたオブジェクトと変数を使用します。
さらに、クラス構造は、protectedブロック内でのみメソッドのオーバーライドを宣言しています。すべてのメソッドは、親クラスで事前に宣言されていたものです。ただし、通常のクラスアルゴリズムを構築するための高レベルなフィードフォワードメソッドやバックプロパゲーションメソッド(feedForward、calcInputGradients、updateInputWeights)は含まれていません。これは、親クラスアルゴリズムのアクションシーケンスを完全に保持するためです。しかし、複素数値を操作するためには、複素数の虚数部が各実数部に追加される必要があり、そのためデータバッファのサイズを2倍にする必要があります。さらに、アルゴリズムに複素数数学を実装する必要もあります。ご存知の通り、ほとんどの数学演算はOpenCL側で実行されるため、低レベルのメソッドを再定義するだけでなく、OpenCLプログラムのカーネルにも変更を加える必要があります。
3.1 クラスの初期化メソッド
各クラスの作業は、その初期化から始まります。前述のように、新しいクラスではネストされたオブジェクトや変数を宣言しないため、コンストラクタとデストラクタは空です。そのため、コンストラクタとデストラクタは空になっています。継承されたオブジェクトの初期化は、Initメソッドで実行されます。通常どおり、このメソッドのパラメータでは、クラスのアーキテクチャを定義するための主要な定数が呼び出し元から渡されます。ご覧のとおり、メソッドのパラメータ構造は親クラスの同様のメソッドと同じです。これは驚くことではなく、基本的なアテンションアルゴリズムと親クラスの構造を完全に保持しているためです。ただし、メソッド自体は完全に書き直されます。
bool CNeuronComplexMLMHAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint layers, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * window * units_count, optimization_type, batch)) return false;
メソッド本体では、通常通り、親クラスの初期化メソッドを呼び出します。次の2点に注意してください。
- 初期化メソッドは、直接の親CNeuronMLMHAttentionOCLではなく、基本ニューラル層基底クラスCNeuronBaseOCLの初期化メソッドを呼び出します。その理由は、複素数を格納できるようにすべてのバッファのサイズを大きくして再定義する必要があるため、CNeuronMLMHAttentionOCLクラスのネストされたオブジェクトの初期化は必要ないからです。
- 親クラスのメソッドを呼び出すときに、層サイズを2倍に増やします。これは、層の操作の結果が複素数値になることが予想されるためです。
親クラスのメソッドの操作の論理結果を確認してください。
ニューラル層の基本クラスから継承されたオブジェクトを正常に初期化した後、作成された層のアーキテクチャの主なパラメータを保存します。
iWindow = window; iWindowKey = fmax(window_key, 1); iUnits = units_count; iHeads = fmax(heads, 1); iLayers = fmax(layers, 1);
次のステップでは、作成するすべてのバッファのサイズを計算します。複素数値を保存する必要があるため、すべてのバッファは親クラスと比較して2倍に増加します。
uint num = 2 * 3 * iWindowKey * iHeads * iUnits; //Size of QKV tensor uint qkv_weights = 2 * 3 * (iWindow + 1) * iWindowKey * iHeads; //Size of weights' matrix of QKV tenzor uint scores = 2 * iUnits * iUnits * iHeads; //Size of Score tensor uint mh_out = 2 * iWindowKey * iHeads * iUnits; //Size of multi-heads self-attention uint out = 2 * iWindow * iUnits; //Size of our tensore uint w0 = 2 * (iWindowKey + 1) * iHeads * iWindow; //Size W0 tensor uint ff_1 = 2 * 4 * (iWindow + 1) * iWindow; //Size of weights' matrix 1-st feed forward layer uint ff_2 = 2 * (4 * iWindow + 1) * iWindow; //Size of weights' matrix 2-nd feed forward layer
次に、作成されたネストされたアテンション層の数に応じてループを構成します。ループの本体では、ネストされたオブジェクトを初期化します。
for(uint i = 0; i < iLayers; i++) { CBufferFloat *temp = NULL;
ここではまず、2反復のネストされたループを作成し、フィードフォワードパスのデータと対応する誤差勾配を記録するオブジェクトを初期化します。
for(int d = 0; d < 2; d++) { //--- Initilize QKV tensor temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(num, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Tensors.Add(temp)) return false;
まず、Query、Key、Valueエンティティの連結バッファを作成します。次に、自己アテンションアルゴリズムによれば、依存係数の行列を書き込むためのバッファが必要です。
//--- Initialize scores temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(scores, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!S_Tensors.Add(temp)) return false;
次のバッファには、マルチヘッドアテンションの結果が保存されます。
//--- Initialize multi-heads attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(mh_out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!AO_Tensors.Add(temp)) return false;
次に、サイズを入力レベルまで縮小します。
//--- Initialize attention out temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false;
アテンションブロックに、2つの全結合層からなるFeedForwardブロックが続きます。
//--- Initialize Feed Forward 1 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(4 * out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; //--- Initialize Feed Forward 2 if(i == iLayers - 1) { if(!FF_Tensors.Add(d == 0 ? Output : Gradient)) return false; continue; } temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(out, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Tensors.Add(temp)) return false; }
フィードフォワードパスの結果と対応する誤差勾配を保存するためのバッファを初期化しました。ただし、操作を実行するには、学習可能な重みパラメータが必要です。まず、Query、Key、Valueのエンティティを生成するための学習可能なパラメータの行列を入力します。
//--- Initilize QKV weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(qkv_weights)) return false; float k = (float)(1 / sqrt(iWindow + 1)); for(uint w = 0; w < qkv_weights; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false;
次に、マルチヘッドアテンション次元削減層のパラメータを生成します。
//--- Initilize Weights0 temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(w0)) return false; for(uint w = 0; w < w0; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
FeedForwardブロックのパラメータを追加しましょう。
//--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_1)) return false; for(uint w = 0; w < ff_1; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.Reserve(ff_2)) return false; k = (float)(1 / sqrt(4 * iWindow + 1)); for(uint w = 0; w < ff_2; w++) { if(!temp.Add(GenerateWeight() * 2 * k - k)) return false; } if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false;
モデルパラメータの訓練過程では、訓練の瞬間を記録するためのバッファが必要になります。このようなバッファの数は、使用するパラメータ学習方法によって異なります。
for(int d = 0; d < (optimization == SGD ? 1 : 2); d++) { temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(qkv_weights, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!QKV_Weights.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(w0, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; //--- Initilize FF Weights temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_1, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; temp = new CBufferFloat(); if(CheckPointer(temp) == POINTER_INVALID) return false; if(!temp.BufferInit(ff_2, 0)) return false; if(!temp.BufferCreate(OpenCL)) return false; if(!FF_Weights.Add(temp)) return false; } } //--- return true; }
モデルの訓練中および操作中に必要なバッファが1つでも欠けていると重大なエラーにつながるため、このメソッドの各反復の結果を必ず確認してください。
すべてのネストされたオブジェクトを初期化した後、メソッドを終了し、実行された操作の論理値を呼び出し元に返します。
3.2 フィードフォワードパス
クラスの初期化が完了した後は、フィードフォワードパスの構成に進みます。親クラスからは高レベルのアルゴリズムを継承しますが、低レベルのフィードフォワードメソッドにはまだ作業が残っています。自己アテンションアルゴリズムに従って、操作を順序立てて配置します。
層の入力データは、まずQuery、Key、Valueのエンティティに変換されます。これらを親クラスで生成するためには、畳み込み層のフォワードパスカーネルを使用しました。この実装でも、同様のアプローチに従います。さらに、複素数の変数を操作するためには、OpenCLプログラム側で新しいカーネルFeedForwardComplexConvを作成する必要があります。
カーネルのパラメータには、訓練パラメータの行列、入力データ、そして結果を書き込むためのバッファという3つのデータバッファへのポインタを渡します。
__kernel void FeedForwardComplexConv(__global float2 *matrix_w, __global float2 *matrix_i, __global float2 *matrix_o, int inputs, int step, int window_in, int activation ) { size_t i = get_global_id(0); size_t out = get_global_id(1); size_t w_out = get_global_size(1);
メインプログラム側では、引き続きサイズが大きくなったfloat型のデータバッファを使用していることに注意してください。一方、OpenCLプログラム側のカーネルでは、データバッファにfloat2型を指定します。これは、複素数変数の関数を作成する際に、前述のデータ型とまったく同じです。
メソッド本体では、2次元のタスク空間内で現在のスレッドを識別します。最初の次元は結果シーケンス内の要素を示し、2番目の次元は使用するフィルタを示します。この場合、分析対象のシーケンスの1つの要素を記述するエンティティの連結ベクトル内での位置を示しています。
取得したデータに基づいて、データバッファ内のオフセットを決定します。
int w_in = window_in; int shift_out = w_out * i; int shift_in = step * i; int shift = (w_in + 1) * out; int stop = (w_in <= (inputs - shift_in) ? w_in : (inputs - shift_in));
次に、ベクトルの積を計算するループを作成します。
float2 sum = matrix_w[shift + w_in]; for(int k = 0; k <= stop; k ++) sum += ComplexMul(matrix_i[shift_in + k], matrix_w[shift + k]);
2つの複素数の積を計算するには、すでに作成したComplexMul関数を使用します。値を合計する際は、基本的なベクトル演算を利用します。
さらに、データバッファにfloat2ベクトルを宣言したため、オフセット調整なしで通常の浮動小数点データバッファとしてアクセスできます。各操作において、複素数の実数部と虚数部の2つの要素がバッファーから抽出されます。
次に、計算された値をチェックします。もし変数がオーバーフローした場合、その値を0に変更します。
if(isnan(sum.x) || isnan(sum.y) || isinf(sum.x) || isinf(sum.y)) sum = (float2)0;
ここで、活性化関数を計算し、その値を結果バッファに保存するだけです。
switch(activation) { case 0: sum = ComplexTanh(sum); break; case 1: sum = ComplexDiv((float2)(1, 0), (float2)(1, 0) + ComplexExp(-sum)); break; case 2: if(sum.x < 0) sum.x *= 0.01f; if(sum.y < 0) sum.y *= 0.01f; break; default: break; } matrix_o[out + shift_out] = sum; }
メインプログラム側で、前述で作成したカーネルを呼び出すには、CNeuronComplexMLMHAttention::ConvolutionForwardメソッドをオーバーライドします。新しいメソッドを作成するのではなく、既存のメソッドをオーバーライドする点が重要です。これにより、親クラスの同様のメソッドのパラメータ構造をそのまま保持できます。このアプローチを取ることで、親クラスのトップレベルのフィードフォワードパスメソッドから、このメソッドを調整せずに呼び出すことが可能になります。
bool CNeuronComplexMLMHAttention::ConvolutionForward(CBufferFloat *weights, CBufferFloat *inputs, CBufferFloat *outputs, uint window, uint window_out, ENUM_ACTIVATION activ, uint step = 0) { if(CheckPointer(OpenCL) == POINTER_INVALID || CheckPointer(weights) == POINTER_INVALID || CheckPointer(inputs) == POINTER_INVALID || CheckPointer(outputs) == POINTER_INVALID) return false;
メソッドの本体では、まず、受信したポインタのオブジェクトの関連性をチェックします。次に、OpenCLコンテキスト側にデータバッファがあるかどうかをチェックします。
if(weights.GetIndex() < 0) return false; if(inputs.GetIndex() < 0) return false; if(outputs.GetIndex() < 0) return false; if(step == 0) step = window;
制御ブロックを正常に通過した後、カーネルのタスク スペースとその中のオフセットを定義します。
uint global_work_offset[2] = {0, 0}; uint global_work_size[2]; global_work_size[0] = outputs.Total() / (2 * window_out); global_work_size[1] = window_out;
次に、操作の実行を制御しながら、必要なすべてのパラメータをカーネルに渡します。
if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_w, weights.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_i, inputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(def_k_FeedForwardComplexConv, def_k_ffc_matrix_o, outputs.GetIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_inputs, (int)(inputs.Total() / 2))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_step, (int)step)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_window_in, (int)window)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffс_window_out, (int)window_out)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(def_k_FeedForwardComplexConv, def_k_ffc_activation - 1, (int)activ)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
その後、カーネルを実行キューに配置してメソッドを完了します。
if(!OpenCL.Execute(def_k_FeedForwardComplexConv, 2, global_work_offset, global_work_size)) { string error; CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error); printf("Error of execution kernel %s: %s", __FUNCSIG__, error); return false; } //--- return true; }
カーネルを実行キューに配置するアルゴリズムは非常に統一されていますが、タスクスペースのサイズや変数に違いが生じる場合があります。時間の節約と記事のボリュームを減らすために、カーネルのキューイング方法についてはこれ以上詳しく説明しません。完全なコードは添付ファイルに含まれています。それでは、これらのカーネルを構築するアルゴリズムについて詳しく説明します。
自己アテンションアルゴリズムに沿って進み、まずQuery、Key、Valueエンティティを定義した後、次に依存係数を定義します。これを定義するには、Query行列と転置されたKey行列を乗算し、その結果行列をSoftMax関数で正規化します。
この機能はComplexMHAttentionScoreカーネル内で実行され、CNeuronComplexMLMHAttention::AttentionScoreメソッドから呼び出されます。
__kernel void ComplexMHAttentionScore(__global float2 *qkv, __global float2 *score, int dimension, int mask ) { int q = get_global_id(0); int h = get_global_id(1); int units = get_global_size(0); int heads = get_global_size(1);
パラメータとして、カーネルは2つのデータバッファへのポインタを受け取ります。1つはエンティティの連結バッファで、もう1つは結果を書き込むバッファです。
指定されたカーネルは2次元のタスク空間内で実行されます。最初の次元はQuery行列の行を定義し、2番目の次元はアクティブなアテンションヘッドを定義します。つまり、カーネルの各インスタンスでは、1つのアテンションヘッド内の依存係数行を計算する操作が実行されます。
カーネル本体では、タスク空間内の両方の次元で現在のスレッドを識別し、それに基づいてデータバッファ内のオフセットを決定します。
int shift_q = dimension * (h + 3 * q * heads); int shift_s = units * (h + q * heads);
次に、データの正規化係数を定義します。
float2 koef = (float2)(sqrt((float)dimension), 0); if(koef.x < 1) koef.x = 1;
依存係数を計算するループを作成します。
float2 sum = 0; for(int k = 0; k < units; k++) { if(mask > 0 && k > q) { score[shift_s + k] = (float2)0; continue; }
ここで注目すべき点は、提示されたアルゴリズムがデータマスキングを実装しており、いわゆる「先読み」を制限できることです。具体的には、モデルは以前のトークンに対する依存係数のみを計算し、後続のトークンについては依存係数が0に設定されます。これにより、モデルは訓練中に「将来から」情報を受け取ることがありません。この機能は、カーネルのパラメータとして渡されるmaskフラグによって有効化されます。
その後、ネストされたループを用いて、2つのベクトルを乗算し、依存ベクトルの次の要素を計算します。
float2 result = (float2)0; int shift_k = dimension * (h + heads * (3 * k + 1)); for(int i = 0; i < dimension; i++) result += ComplexMul(qkv[shift_q + i], qkv[shift_k + i]);
積の結果に対して指数表現を計算します。
result = ComplexExp(ComplexDiv(result, koef));
変数のオーバーフローを定義します。
if(isnan(result.x) || isnan(result.y) || isinf(result.x) || isinf(result.y)) result = (float2)0;
その結果を結果バッファに書き込み、その後の正規化のために合計に加算します。
score[shift_s + k] = result; sum += result; }
カーネルの最後に、依存係数の行列の計算された行を正規化します。
if(ComplexAbs(sum) > 0) for(int k = 0; k < units; k++) score[shift_s + k] = ComplexDiv(score[shift_s + k], sum); }
このようにして得られた依存係数のScore行列は、アテンションブロックの最終結果を計算するために使用されます。この段階では、得られた係数の行列にValueエンティティの行列を乗算する必要があります。この処理は、ComplexMHAttentionOutカーネルで実行されます。前述のカーネルと同様に、このカーネルも同じ2次元タスク空間内で動作します。
__kernel void ComplexMHAttentionOut(__global float2 *scores, __global float2 *qkv, __global float2 *out, int dimension ) { int u = get_global_id(0); int units = get_global_size(0); int h = get_global_id(1); int heads = get_global_size(1);
カーネル本体では、タスク空間内の現在のスレッドを識別し、データ バッファーへのオフセットを決定します。
int shift_s = units * (h + heads * u); int shift_out = dimension * (h + heads * u);
その後、ネストされたループのシステムを作成し、Value行列に依存係数の対応する行を乗算する数学演算を実行します。
for(int d = 0; d < dimension; d++) { float2 result = (float2)0; for(int v = 0; v < units; v++) { int shift_v = dimension * (h + heads * (3 * v + 2)) + d; result += ComplexMul(scores[shift_s + v], qkv[shift_v]); } out[shift_out + d] = result; } }
マルチヘッドアテンションの結果は単一のテンソルに統合され、その後、入力データテンソルのサイズに合わせて次元が縮小されます。その後、FeedForwardブロックの処理が実行されます。これらの処理は、前述のFeedForwardComplexConvカーネルを使用しておこなわれます。これで、フィードフォワードパス操作を実行するためのカーネルアルゴリズムの説明は完了です。すべてのカーネルの完全なコードと、それらを呼び出すメソッドについては、添付ファイルをご確認ください。
3.3 バックプロパゲーションパスの実装
フィードフォワードパスの機能が準備できた後は、バックプロパゲーションアルゴリズムの実装に進みます。この作業は、フィードフォワードパス同様、親クラスから継承した高レベルのアルゴリズムを活用し、低レベルのメソッドをオーバーライドすることで実現されます。
前述のように、カーネルを実行キューに配置するアルゴリズムに関しては、すでに述べた通りであり、特に新しい内容はありません。したがってOpenCLプログラム側でのカーネルアルゴリズムの詳細な分析に重点を置いて説明します。
フィードフォワードパスで最も多く使用されたカーネルはFeedForwardComplexConvでした。これはさまざまな処理段階で利用される汎用ブロックであり、当然、バックプロパゲーションアルゴリズムでも、誤差勾配をこのブロックを通じて伝播するために使用されます。この機能はCalcHiddenGradientComplexConvカーネルに実装されています。
__kernel void CalcHiddenGradientComplexConv(__global float2 *matrix_w, __global float2 *matrix_g, __global float2 *matrix_o, __global float2 *matrix_ig, int outputs, int step, int window_in, int window_out, int activation, int shift_out ) { size_t i = get_global_id(0); size_t inputs = get_global_size(0);
カーネルは、入力データバッファー内の要素数に基づき、1次元のタスク空間で実行されます。各スレッドは、対象となる入力要素の影響を受けるすべての要素から誤差勾配を収集します。
カーネル本体内では、まず現在のスレッドを識別し、データバッファーへのオフセットを決定します。また、必要なローカル変数も宣言します。
float2 sum = (float2)0; float2 out = matrix_o[shift_out + i]; int start = i - window_in + step; start = max((start - start % step) / step, 0); int stop = (i + step - 1) / step; if(stop > (outputs / window_out)) stop = outputs / window_out;
その後、ループのシステムを作成します。ループ本体では、分析された要素が全体の結果に与える影響を考慮して、合計誤差勾配を収集します。
for(int h = 0; h < window_out; h ++) { for(int k = start; k < stop; k++) { int shift_g = k * window_out + h; int shift_w = (stop - k - 1) * step + i % step + h * (window_in + 1); if(shift_g >= outputs || shift_w >= (window_in + 1) * window_out) break; sum += ComplexMul(matrix_g[shift_out + shift_g], matrix_w[shift_w]); } }
ループを終了した後、変数のオーバーフローをチェックします。
if(isnan(sum.x) || isnan(sum.y) || isinf(sum.x) || isinf(sum.y)) sum = (float2)0;
得られた誤差勾配を活性化関数の導関数によって調整します。
switch(activation) { case 0: sum = ComplexMul(sum, (float2)1.0f - ComplexMul(out, out)); break; case 1: sum = ComplexMul(sum, ComplexMul(out, (float2)1.0f - out)); break; case 2: if(out.x < 0.0f) sum.x *= 0.01f; if(out.y < 0.0f) sum.y *= 0.01f; break; default: break; } matrix_ig[i] = sum; }
最終結果は、前の層の誤差勾配バッファに保存されます。
次に、アテンションブロックComplexMHAttentionGradientsを通じて誤差勾配を伝播するカーネルについて考えます。このカーネルは、誤差勾配値が決定されるエンティティの数に応じて、条件付きで 3 つのブロックに分割できる、非常に複雑なアルゴリズムを提供します。
__kernel void ComplexMHAttentionGradients(__global float2 *qkv, __global float2 *qkv_g, __global float2 *scores, __global float2 *gradient) { size_t u = get_global_id(0); size_t h = get_global_id(1); size_t d = get_global_id(2); size_t units = get_global_size(0); size_t heads = get_global_size(1); size_t dimension = get_global_size(2);
このカーネルでは、非常に多くの操作が実行されます。全体的な実行時間を短縮するために、モデルの訓練プロセス中に個々の変数の値を計算する操作を並列化することを試みました。スレッドの識別を直感的かつ効率的にするために、このカーネル用に3次元のタスク空間を構築しました。アテンションブロックのフィードフォワードパスメソッドと同様に、ここでもシーケンスの要素とアテンションヘッドを活用します。タスク空間の3番目の次元は、シーケンス要素を記述するテンソル内の要素の位置を表します。そのため、操作が多いにもかかわらず、各スレッドは結果バッファに3つの値のみを出力します。これらは、Query、Key、Valueエンティティの誤差勾配の連結バッファです。
カーネル本体では、まずタスク空間内でスレッドを識別し、データバッファへのオフセットを計算します。
float2 koef = (float2)(sqrt((float)dimension), 0); if(koef.x < 1) koef.x = 1; //--- init const int shift_q = dimension * (heads * 3 * u + h); const int shift_k = dimension * (heads * (3 * u + 1) + h); const int shift_v = dimension * (heads * (3 * u + 2) + h); const int shift_g = dimension * (heads * u + h); int shift_score = h * units; int step_score = units * heads;
次に、Value行列の分析された要素に対する誤差勾配を計算します。これは、アテンションブロックの出力における誤差勾配テンソルの対応する列を、依存係数行列の対応する列と乗算することで求めます。
//--- Calculating Value's gradients float2 sum = (float2)0; for(int i = 0; i < units; i++) sum += ComplexMul(gradient[(h + i * heads) * dimension + d], scores[shift_score + u + i * step_score]); qkv_g[shift_v + d] = sum;
次のステップでは、Queryエンティティの分析対象要素に対する誤差勾配を決定します。このエンティティは結果に直接的な影響を与えるわけではなく、依存係数行列を通じて間接的に影響します。そのため、まずは依存係数行列の対応する行における誤差勾配を求める必要があります。さらに、SoftMax関数によるデータの正規化がプロセスを複雑にします。
//--- Calculating Query's gradients shift_score = h * units + u * step_score; float2 grad = 0; float2 grad_out = gradient[shift_g + d]; for(int k = 0; k < units; k++) { float2 sc_g = (float2)0; float2 sc = scores[shift_score + k]; for(int v = 0; v < units; v++) sc_g += ComplexMul( ComplexMul(scores[shift_score + v], ComplexMul(qkv[dimension * (heads * (3 * v + 2) + h)], grad_out)), ((float2)(k == v, 0) - sc) );
単一の依存係数に対して検出された誤差勾配は、Keyエンティティ行列の対応する要素に乗算されます。結果の値は合計され、合計誤差勾配が累積されます。
grad += ComplexMul(ComplexDiv(sc_g, koef), qkv[dimension * (heads * (3 * k + 1) + h) + d]); }
累積誤差勾配を結果バッファに書き込みます。
qkv_g[shift_q + d] = grad;
同様に、Keyエンティティ要素の誤差勾配を定義します。この誤差勾配も、依存係数の行列を通して結果に間接的な影響を与えます。ただし、今回は指定された行列の列を操作します。
//--- Calculating Key's gradients grad = 0; for(int q = 0; q < units; q++) { shift_score = h * units + q * step_score; float2 sc_g = (float2)0; float2 sc = scores[shift_score + u]; float2 grad_out = gradient[dimension * (heads * q + h) + d]; for(int v = 0; v < units; v++) sc_g += ComplexMul( ComplexMul(scores[shift_score + v], ComplexMul(qkv[dimension * (heads * (3 * v + 2) + h)], grad_out)), ((float2)(u == v, 0) - sc) ); grad += ComplexMul(ComplexDiv(sc_g, koef), qkv[dimension * (heads * 3 * q + h) + d]); } qkv_g[shift_k + d] = grad; }
これで、複素数アテンション層機能内のバックプロパゲーション パスカーネル構築アルゴリズムの説明は終了です。提示されたクラスのすべてのメソッドとカーネルの完全なコードは、添付ファイルにあります。
結論
本稿では、ATFNet法の構築における理論的側面について、周波数領域と時間領域の両方で時系列予測をおこなうアプローチを組み合わせた方法を説明しました。
実践的な部分では、アテンション層を構築するための複雑な操作を用いた多くの作業がおこなわれましたが、これは提案された手法のFブロックの1つのオブジェクトに過ぎません。次回の記事では、ATFNetメソッドのアルゴリズム構築を引き続きおこない、実際のデータを使用してその結果を確認する予定です。
参照文献
記事で使用されているプログラム
| # | 名前 | 種類 | 詳細 |
|---|---|---|---|
| 1 | Research.mq5 | EA | コレクションEAの例 |
| 2 | ResearchRealORL.mq5 | EA | Real-ORL法による事例収集のためのEA |
| 3 | Study.mq5 | EA | モデル訓練EA |
| 4 | StudyEncoder.mq5 | EA | エンコード訓練EA |
| 5 | Test.mq5 | EA | モデルをテストするEA |
| 6 | Trajectory.mqh | クラスライブラリ | システム状態記述の構造体 |
| 7 | NeuroNet.mqh | クラスライブラリ | ニューラルネットワークを作成するためのクラスのライブラリ |
| 8 | NeuroNet.cl | コードベース | OpenCLプログラムコードライブラリ |
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/14996
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 最も注目すべき人工協調探索アルゴリズムの修正(ACSm)
最も注目すべき人工協調探索アルゴリズムの修正(ACSm)
 リプレイシステムの開発(第51回):物事は複雑になる(III)
リプレイシステムの開発(第51回):物事は複雑になる(III)
 MQL5における相関分析の要素:ピアソンのカイ二乗検定による独立性と相関比
MQL5における相関分析の要素:ピアソンのカイ二乗検定による独立性と相関比
 ニューラルネットワークが簡単に(第91回):周波数領域予測(FreDF)
ニューラルネットワークが簡単に(第91回):周波数領域予測(FreDF)
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
ニューラルネットワークは簡単です。その92 😅。
誰でもアクセスできる。そして、記事の多さが汎用性の高さと絶え間ない発展を示している。