
Redes neurais: Da teoria à prática
Introdução
Atualmente, todo negociador já deve ter ouvido falar sobre redes neurais e sabe como é interessante utilizá-las. A maioria acredita que as pessoas que sabem lidar com redes neurais são algum tipo de super-humano. Neste artigo, tentaremos explicar a arquitetura da rede neural, descrever as suas aplicações e apresentar exemplos de uso prático.
O conceito de redes neurais
As redes neurais artificiais são uma das áreas de pesquisa de inteligência artificial que é baseada em tentativas de simular o sistema nervoso humano no que se refere a sua capacidade de aprender e de se adaptar, o que deve permitir que seja construída uma simulação muito simplificada da operação do cérebro humano.
Curiosamente, as redes neurais artificiais são constituídas de neurônios artificiais.
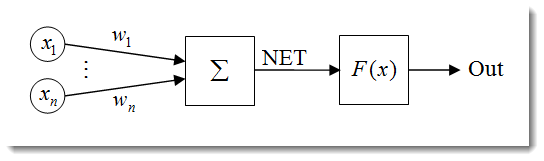
Figura 1. Modelo de neurônio artificial
A estrutura de um neurônio pode ser representada como uma composição das seguintes unidades:
- Entradas
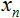 ;
; - Pesos
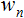 ;
; - Função de transferência
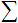 e entrada de rede
e entrada de rede  ;
; - Função de ativação
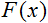 ;
; - Saída
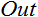 .
.
As redes neurais apresentam diversas propriedades, dentre as quais a mais importante é a capacidade de aprendizagem. O processo de aprendizagem resume-se à mudança dos pesos ![]() .
.

![]() aqui está a entrada de rede do neurônio.
aqui está a entrada de rede do neurônio.
![]()
A entrada de rede é então transformada na saída através da função de ativação, a qual abordaremos posteriormente. Essencialmente, uma rede neural pode ser vista como uma "caixa preta" que recebe sinais como entradas e gera o resultado de saída.
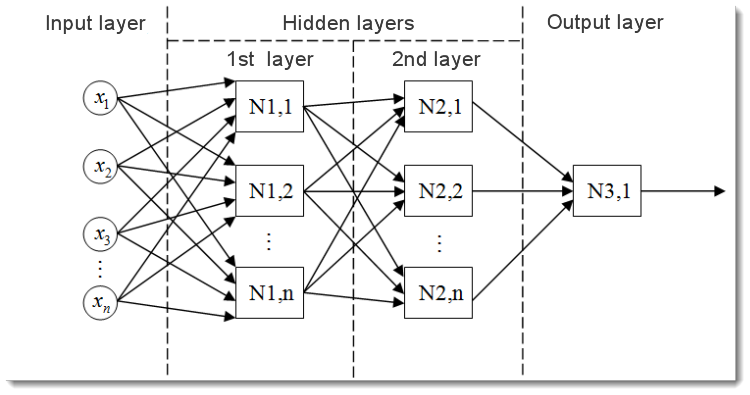
Figura 2. Modelo de uma rede neural multicamadas
Este é o aspecto de uma rede neural multicamadas. Ela compreende:
- A camada de entrada, que serve para distribuir os dados ao longo da rede e não realiza nenhum cálculo. As saídas dessa camada transmitem sinais às entradas da próxima camada (escondida ou de saída);
- A camada de saída, que geralmente contém um neurônio (ou, às vezes, mais de um) que gera a saída de toda a rede neural. O sinal fundamenta toda a lógica de controle futura do EA;
- As camadas escondidas, que são camadas de neurônios padrão que transmitem sinais da camada de entrada à camada de saída. A sua entrada é a saída da camada anterior, enquanto que a sua saída serve como entrada da próxima camada.
O exemplo apresentado mostra uma rede neural com duas camadas escondidas. Entretanto, poderá haver redes neurais com mais camadas escondidas.
Normalização de dados de entrada
A normalização de dados de entrada é o processo pelo qual todos os dados são normalizados, ou seja, reduzido aos limites [0,1] ou [-1,1]. Caso a normalização não seja realizada, os dados de entrada terão um efeito adicional sobre o neurônio, levando a decisões erradas. Em outras palavras, como é possível comprar valores de diferentes ordens de magnitude?
A fórmula de normalização, em sua forma padrão, é a seguinte:
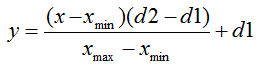
em que:
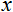 - valor a ser normalizado;
- valor a ser normalizado;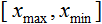 - variação do valor de х;
- variação do valor de х;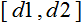 - limite ao qual o valor de x será reduzido.
- limite ao qual o valor de x será reduzido.
Explicaremos com um exemplo:
Suponha que temos n dados de entrada do limite [0,10], então ![]() = 0 e
= 0 e ![]() = 10. Reduziremos os dados ao limite [0,1], então
= 10. Reduziremos os dados ao limite [0,1], então ![]() = 0 e
= 0 e ![]() = 1. Agora que encaixamos os valores na fórmula, podemos calcular valores normalizados para qualquer x a partir de n dados de entrada.
= 1. Agora que encaixamos os valores na fórmula, podemos calcular valores normalizados para qualquer x a partir de n dados de entrada.
Este é o seu aspecto, quando implementada em MQL5:
double d1=0.0; double d2=1.0; double x_min=iMA_buf[ArrayMinimum(iMA_buf)]; double x_max=iMA_buf[ArrayMaximum(iMA_buf)]; for(int i=0;i<ArraySize(iMA_buf);i++) { inputs[i]=(((iMA_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; }
Primeiramente, especificamos os limites superior e inferior do valor de saída e, em seguida, obtemos os valores mínimo e máximo do indicador (não se copia dados do indicador, mas poderá ser, por exemplo, os 10 últimos valores). Por fim, normalizamos cada elemento de entrada (valores de indicador em barras diferentes) e armazenamos os resultados em uma série para uso posterior.
Funções de ativação
A função de ativação é uma função que calcula a saída de um neurônio. A entrada que ela recebe representa a soma de todos os produtos das entradas e seus respectivos pesos (doravante denominada "soma ponderada"):
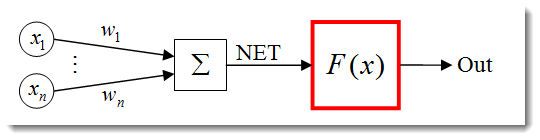
Figura 3. Modelo de neurônio artificial com função de ativação em destaque
A fórmula da função de ativação, em sua forma padrão, é a seguinte:
![]()
em que:
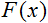 é a função de ativação;
é a função de ativação;-
 é a soma ponderada obtida na primeira etapa do cálculo da saída de de um neurônio;
é a soma ponderada obtida na primeira etapa do cálculo da saída de de um neurônio; 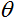 é um valor limite da função de ativação. é apenas utilizado para a função de limite rígido e é igual a zero em outras funções.
é um valor limite da função de ativação. é apenas utilizado para a função de limite rígido e é igual a zero em outras funções.
Os principais tipos de função de ativação são:
-
A função de passo de unidade ou função de limite rígido.
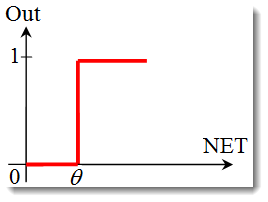
A função é descrita pela seguinte fórmula:
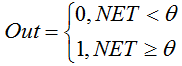
Se a soma ponderada é menor que o valor especificado, a função de ativação resulta em zero. Caso a soma for maior, a função de ativação resulta em um. -
Função sigmoide.
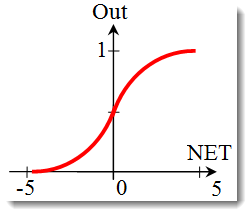
A fórmula que descreve a função sigmoide é a seguinte:
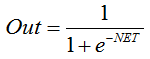
é geralmente utilizada em redes neurais multicamadas e em outras redes com sinais contínuos. A suavidade e continuidade da função são propriedades muito positivas. -
A tangente hiperbólica.
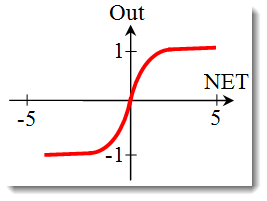
Fórmula:
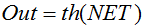 ou
ou 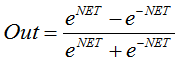
também é usada com frequência em redes com sinais contínuos. Ela é peculiar, visto que pode resultar em valores negativos.
Alteração da forma da função de ativação
Na seção anterior, abordamos os tipos de funções de ativação. Entretanto, há outro aspecto importante a ser considerado - a inclinação da função (exceto para a função de limite rígido). Vamos analisar a função sigmoide mais de perto:
Observando o gráfico da função, é possível perceber facilmente que ela é suave ao longo do período [-5,5]. Suponha que tenhamos uma rede de apenas um neurônio com 10 entradas e uma saída. Agora vamos tentar calcular o valor superior e inferior da variável ![]() . Cada entrada obterá um valor normalizado (como já mencionado em Normalização de dados de entrada), por exemplo, do intervalo [-1,1].
. Cada entrada obterá um valor normalizado (como já mencionado em Normalização de dados de entrada), por exemplo, do intervalo [-1,1].
Usaremos os valores de entrada negativos, visto que a função é diferenciável mesmo em relação a um argumento negativo. Os pesos também serão selecionados dentro do mesmo intervalo. Com todas as combinações possíveis de entradas e pesos, obteremos os valores extremos ![]() no período [-10,10] como:
no período [-10,10] como:

Em MQL5, a fórmula terá o seguinte aspecto:
for(int n=0; n<10; n++) { NET+=Xn*Wn; }
Agora precisamos representar a função de ativação no período, conforme identificado. Vamos usar a função sigmoide como exemplo. A forma mais fácil de fazer isso é utilizando o Excel.
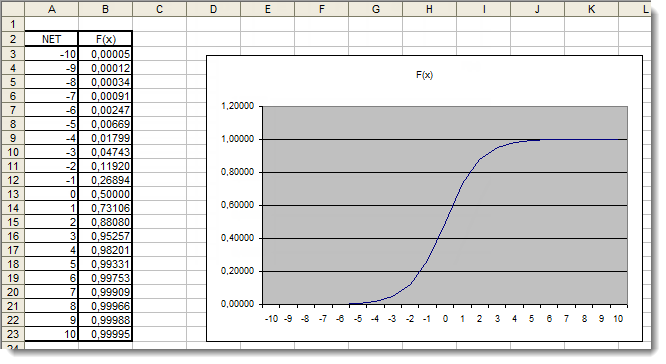
Figura 4. Gráfico da função sigmoide no Excel
Aqui, podemos ver claramente que os valores do argumento que estão fora do período [-5,5] não têm efeito algum sobre os resultados. Isso sugere que o período de valores está incompleto. Vamos tentar consertar isso. Ao argumento, adicionaremos um coeficiente adicional d, o qual permitirá aumentarmos o limite de valores.
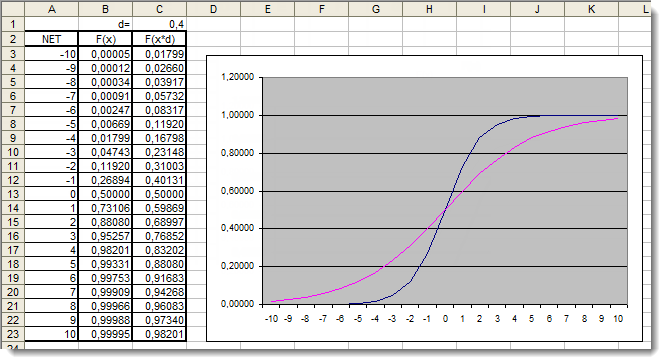
Figura 5. Gráfico da função sigmoide com coeficiente adicional aplicado no Excel
Vamos observar os gráficos novamente. Adicionamos um coeficiente d=0,4 que alterou a forma da função. A comparação dos valores da tabela sugere que eles estão agora mais uniformemente distribuídos. Assim, os resultados podem ser expressos da seguinte forma:
for(int n=0; n<10; n++) { NET+=Xn*Wn; } NET*=0.4;
Agora, vamos analisar a função de ativação tangente hiperbólica. Passando pela teoria abordada na análise da função anterior, chegamos imediatamente à aplicação prática. Aqui, a única diferença é que a saída poderá estar dentro do período [-1,1]. A soma ponderada também pode obter valores dentro do período [-10,10].
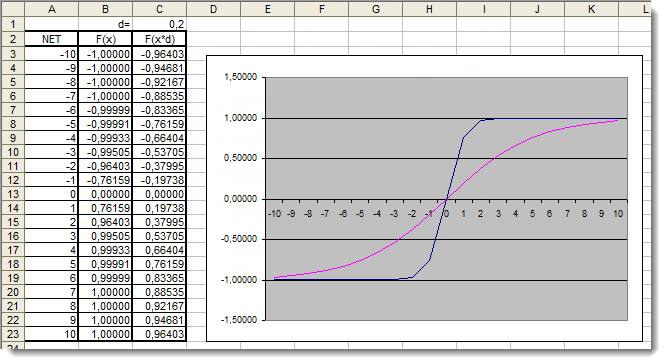
Figura 6. Gráfico da função tangente hiperbólica com coeficiente adicional aplicado no Excel
O gráfico mostra que a forma da função melhorou devido ao uso do coeficiente d=0,2 adicional. Assim, os resultados podem ser expressos da seguinte forma:
for(int n=0;n<10;n++) { NET+=Xn*Wn; } NET*=0.2;
Dessa forma, você pode alterar e melhorar a forma de qualquer função de ativação.
Aplicação
Agora, vamos passar à aplicação prática. Primeiramente, tentaremos implementar o cálculo da entrada de rede do neurônio, seguido pela adição da função de ativação. Vamos lembrar a fórmula para cálculo da entrada de rede do neurônio:

double NET; double x[3]; double w[3]; int OnInit() { x[0]=0.1; // set the input value х1 x[1]=0.8; // set the input value х2 x[2]=0.5; // set the input value х3 w[0]=0.5; // set the weight value w1 w[1]=0.6; // set the weight value w2 w[2]=0.3; // set the weight value w3 for(int n=0;n<3;n++) { NET+=x[n]*w[n]; // add the weighted net input values together } }
Vamos analisá-lo:
- Começamos declarando uma variável para armazenar a entrada de rede do neurônio
 e duas séries: entradas
e duas séries: entradas 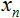 e pesos
e pesos 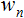 ;
; - Essas variáveis foram declaradas logo no início, fora de todas as funções, para que tenham uma abrangência global (para que sejam acessíveis de qualquer local no programa);
- Na função de inicialização OnInit() (pode, na verdade, ser qualquer outra função), preenchemos a série de entradas e a série de pesos;
- A isso seguiu o circuito de soma, n<3, visto que temos apenas três entradas e três pesos respectivos;
- Em seguida, adicionamos os valores ponderados de entrada e os armazenamos na variável
 .
.
Dessa forma, a primeira tarefa foi finalizada - obtivemos a soma. Agora é a vez da função de ativação. Você encontrará abaixo os códigos para calcular as funções de ativação analisadas na seção Funções de ativação.
A função de passo de unidade ou função de limite rígido
double Out; if(NET>=x) Out=1; else Out=0;
Função sigmoide
double Out = 1/(1+exp(-NET));
Função tangente hiperbólica
double Out = (exp(NET)-exp(-NET))/(exp(NET)+exp(-NET));
Juntando tudo
Para tornar a implementação mais fácil, usaremos uma rede formada por um único neurônio. é certamente um pouco forçado chamá-la de rede, mas isso é importante para compreendermos o princípio. Afinal, uma rede neural multicamadas é formada pelos mesmos neurônios em que a saída da camada de neurônios anterior serve como a entrada para a próxima camada.
Utilizaremos uma versão levemente modificada do Expert Advisor desenvolvido e apresentado no artigo "Inicialização rápida ou guia rápido para iniciantes". Assim, por exemplo, substituiremos o indicador de tendência Média Móvel pelo oscilador índice de Força Relativa. As informações sobre os parâmetros do indicador e suas sequências podem ser encontrados na ajuda integrada.
//+------------------------------------------------------------------+ //| neuro-example.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| http://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "http://www.mql5.com" #property version "1.00" //+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ #include <Trade\Trade.mqh> //include the library for execution of trades #include <Trade\PositionInfo.mqh> //include the library for obtaining information on positions //--- weight values input double w0=0.5; input double w1=0.5; input double w2=0.5; input double w3=0.5; input double w4=0.5; input double w5=0.5; input double w6=0.5; input double w7=0.5; input double w8=0.5; input double w9=0.5; int iRSI_handle; // variable for storing the indicator handle double iRSI_buf[]; // dynamic array for storing indicator values double inputs[10]; // array for storing inputs double weight[10]; // array for storing weights double out; // variable for storing the output of the neuron string my_symbol; // variable for storing the symbol ENUM_TIMEFRAMES my_timeframe; // variable for storing the time frame double lot_size; // variable for storing the minimum lot size of the transaction to be performed CTrade m_Trade; // entity for execution of trades CPositionInfo m_Position; // entity for obtaining information on positions //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ int OnInit() { //--- save the current chart symbol for further operation of the EA on this very symbol my_symbol=Symbol(); //--- save the current time frame of the chart for further operation of the EA on this very time frame my_timeframe=PERIOD_CURRENT; //--- save the minimum lot of the transaction to be performed lot_size=SymbolInfoDouble(my_symbol,SYMBOL_VOLUME_MIN); //--- apply the indicator and get its handle iRSI_handle=iRSI(my_symbol,my_timeframe,14,PRICE_CLOSE); //--- check the availability of the indicator handle if(iRSI_handle==INVALID_HANDLE) { //--- no handle obtained, print the error message into the log file, complete handling the error Print("Failed to get the indicator handle"); return(-1); } //--- add the indicator to the price chart ChartIndicatorAdd(ChartID(),0,iRSI_handle); //--- set the iRSI_buf array indexing as time series ArraySetAsSeries(iRSI_buf,true); //--- place weights into the array weight[0]=w0; weight[1]=w1; weight[2]=w2; weight[3]=w3; weight[4]=w4; weight[5]=w5; weight[6]=w6; weight[7]=w7; weight[8]=w8; weight[9]=w9; //--- return 0, initialization complete return(0); } //+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- delete the indicator handle and deallocate the memory space it occupies IndicatorRelease(iRSI_handle); //--- free the iRSI_buf dynamic array of data ArrayFree(iRSI_buf); } //+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- variable for storing the results of working with the indicator buffer int err1=0; //--- copy data from the indicator array to the iRSI_buf dynamic array for further work with them err1=CopyBuffer(iRSI_handle,0,1,10,iRSI_buf); //--- in case of errors, print the relevant error message into the log file and exit the function if(err1<0) { Print("Failed to copy data from the indicator buffer"); return; } //--- double d1=0.0; //lower limit of the normalization range double d2=1.0; //upper limit of the normalization range double x_min=iRSI_buf[ArrayMinimum(iRSI_buf)]; //minimum value over the range double x_max=iRSI_buf[ArrayMaximum(iRSI_buf)]; //maximum value over the range //--- In the loop, fill in the array of inputs with the pre-normalized indicator values for(int i=0;i<ArraySize(inputs);i++) { inputs[i]=(((iRSI_buf[i]-x_min)*(d2-d1))/(x_max-x_min))+d1; } //--- store the neuron calculation result in the out variable out=CalculateNeuron(inputs,weight); //--- if the output value of the neuron is less than 0.5 if(out<0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Sell position, then close it if(m_Position.PositionType()==POSITION_TYPE_SELL) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Buy position, then exit if(m_Position.PositionType()==POSITION_TYPE_BUY) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Buy(lot_size,my_symbol); } //--- if the output value of the neuron is equal to or greater than 0.5 if(out>=0.5) { //--- if the position for this symbol already exists if(m_Position.Select(my_symbol)) { //--- and this is a Buy position, then close it if(m_Position.PositionType()==POSITION_TYPE_BUY) m_Trade.PositionClose(my_symbol); //--- or else, if this is a Sell position, then exit if(m_Position.PositionType()==POSITION_TYPE_SELL) return; } //--- if we got here, it means there is no position; then we open it m_Trade.Sell(lot_size,my_symbol); } } //+------------------------------------------------------------------+ //| Neuron calculation function | //+------------------------------------------------------------------+ double CalculateNeuron(double &x[],double &w[]) { //--- variable for storing the weighted sum of inputs double NET=0.0; //--- Using a loop we obtain the weighted sum of inputs based on the number of inputs for(int n=0;n<ArraySize(x);n++) { NET+=x[n]*w[n]; } //--- multiply the weighted sum of inputs by the additional coefficient NET*=0.4; //--- send the weighted sum of inputs to the activation function and return its value return(ActivateNeuron(NET)); } //+------------------------------------------------------------------+ //| Activation function | //+------------------------------------------------------------------+ double ActivateNeuron(double x) { //--- variable for storing the activation function results double Out; //--- sigmoid Out=1/(1+exp(-x)); //--- return the activation function value return(Out); } //+------------------------------------------------------------------+
Primeiro de tudo, precisamos treinar a nossa rede. Vamos otimizar os pesos.
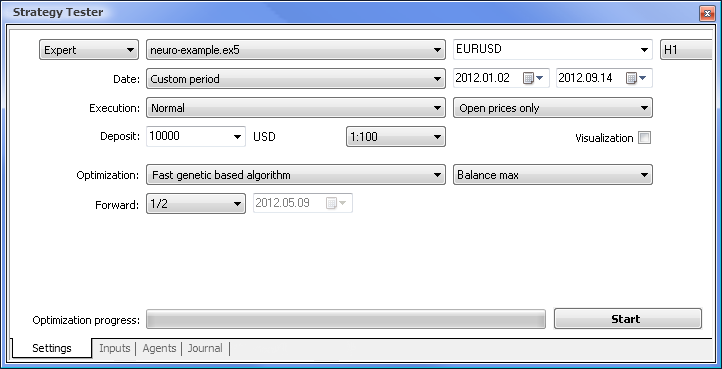
Figura 7. Provador de estratégia com o conjunto de parâmetros requerido
Executaremos a otimização utilizando os seguintes parâmetros:
- Data - por exemplo, desde o começo do ano. Quanto maior o período, menor a ocorrência de ajuste de curvas e melhor o resultado.
- Execução - normal, apenas preços Open. Não há sentido em realizar o teste no modo "Cada tick" visto que o nosso Expert Advisor apenas obtém os últimos 10 valores do indicador, com exceção do valor atual.
- Otimização pode ser configurada para ser executada utilizando o algoritmo completo lento. A otimização genética, entretanto, terá resultados mais rápidos, o que é particularmente útil durante a avaliação de um algoritmo. Caso o resultado seja satisfatório, você também pode tentar utilizar o algoritmo completo lento para resultados mais precisos.
- Progressão de 1/2 e mais permite que você avalie por quanto tempo o seu EA pode gerar os resultados obtidos até a próxima otimização.
- Período de tempo e Par de moeda podem ser configurados de acordo com a sua preferência.
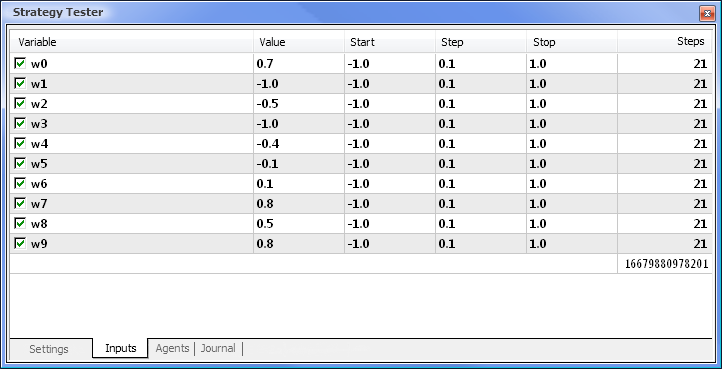
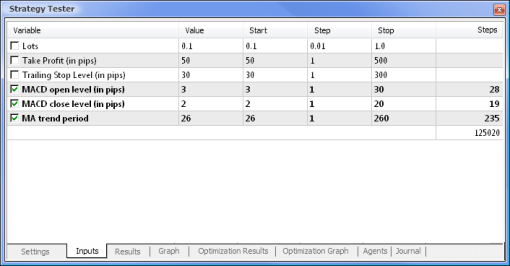
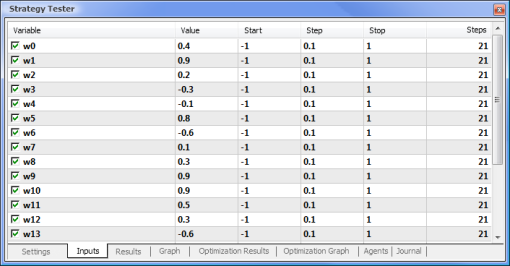
Figura 8. Configuração dos parâmetros e seus respectivos períodos a serem otimizados
A otimização será executada em relação a todos os pesos e seus limites. Inicie a otimização retornando à aba Configurações e clicando no botão Iniciar.
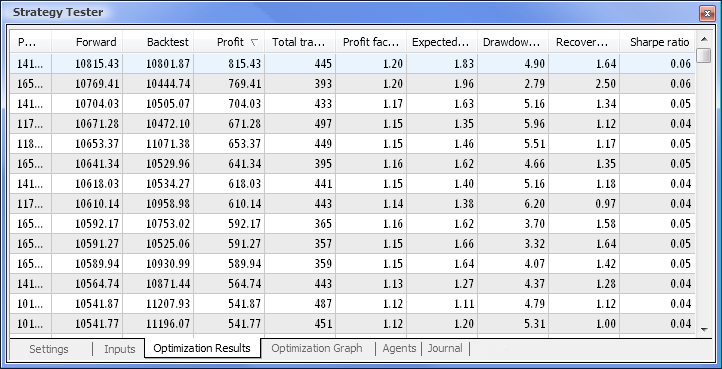
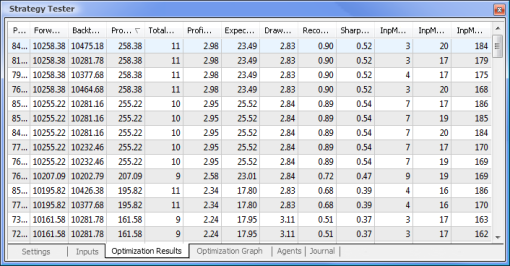
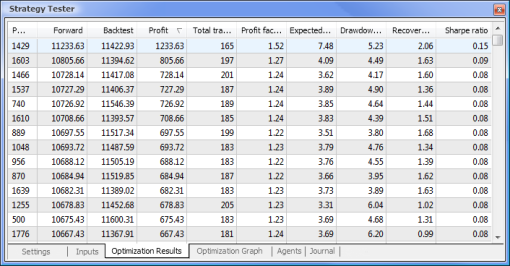
Figura 9. Dados obtidos após a otimização
Após a finalização da otimização, selecionamos a aprovação com o valor de lucro máximo (para organizar por um dos parâmetros, clique no título da coluna relevante) na aba de Resultados de otimização. Você então poderá avaliar outros parâmetros e selecionar a aprovação desejada, se necessário.
Um clique duplo na aprovação requerida inicia o teste dos resultados que são exibidos nas abas Resultados e Gráfico.
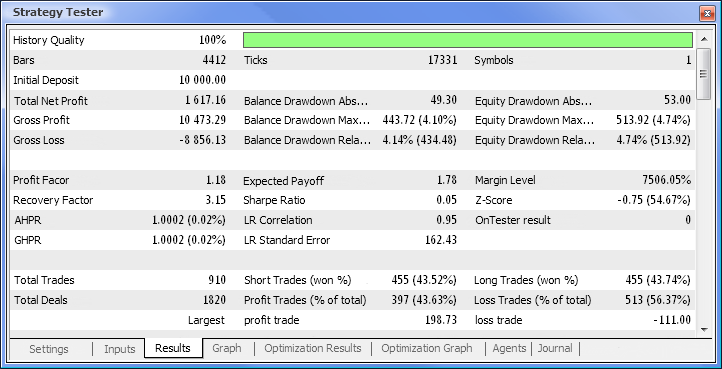
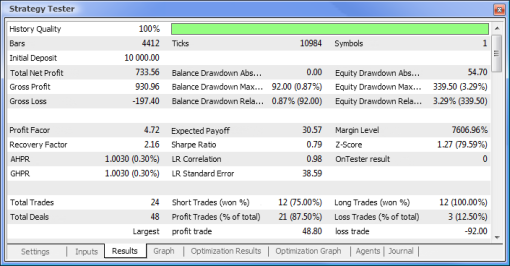
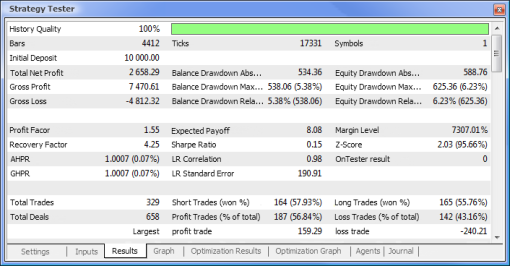
Figura 10. Relatório de teste
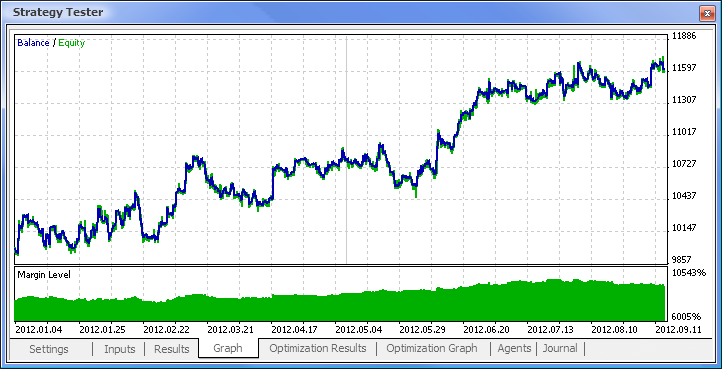
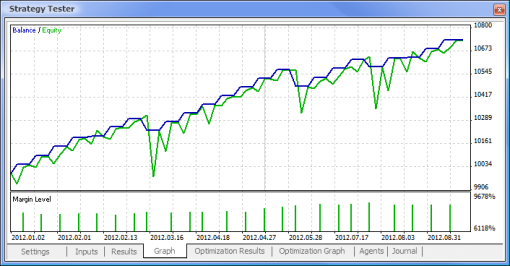
Figura 11. Gráfico de balanço
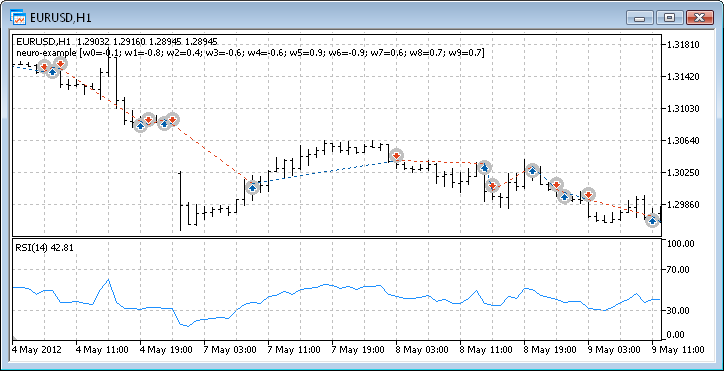
Figura 12. Desempenho de negociação do Expert Advisor
Finalmente obtivemos os resultados e, para início, eles não são nada maus. Leve em consideração que apenas tínhamos um neurônio. O exemplo apresentado é claramente primitivo, mas devemos admitir que mesmo ele pode proporcionar lucros.
Vantagens das redes neurais
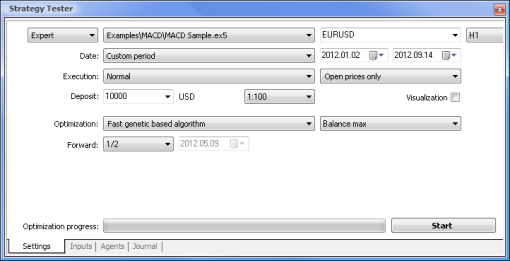
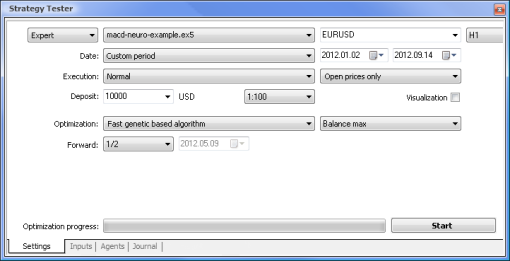
Agora vamos tentar comparar um EA baseado na lógica padrão com um EA baseado em rede neural. Compararemos os resultados de otimização e teste do Expert Advisor MACD de exemplo que vem integrado ao terminal com os resultados do EA de rede neural com base no MACD.
Os valores de Take Profit (obter lucro) e Trailing Stop (limite móvel) não serão envolvidos na otimização visto que eles não existem no EA baseado em rede neural. Os dois Expert Advisors que serão testados estão baseados no MACD com os seguintes parâmetros:
- Período da média móvel rápida: 12;
- Período da média móvel lenta: 26;
- Período de cálculo da média da diferença: 9;
- Tipo de preço: preço de fechamento.
Você também pode configurar o par de moedas e período de tempo requeridos, mas, em nosso caso, não faremos alterações - EURUSD e H1, respectivamente. O período de teste é o mesmo nos dois casos: desde o começo do ano, utilizando preços de abertura.
| Amostra MACD | macd-neuro-example |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
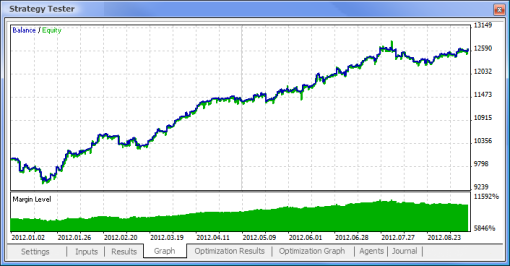 |
Agora vamos comparar os parâmetros-chave dos Expert Advisors testados:
| Parâmetro | Amostra MACD | macd-neuro-example |
|---|---|---|
| Lucro líquido total | 733,56 | 2 658,29 |
| Balanço de redução absoluta | 0,00 | 534,36 |
| Redução de participação máxima | 339,50 (3.29%) | 625,36 (6.23%) |
| Fator de lucro | 4,72 | 1,55 |
| Fator de recuperação | 2,16 | 4,25 |
| Lucro esperado | 30,57 | 8,08 |
| índice de Sharpe | 0,79 | 0,15 |
| Total de negociações | 24 | 329 |
| Total de acordos | 48 | 658 |
| Lucro de negociações (% do total) | 21 (87.50%) | 187 (56.84%) |
| Lucro médio de negociação | 44,33 | 39,95 |
| Média de ganhos consecutivos | 5 | 2 |
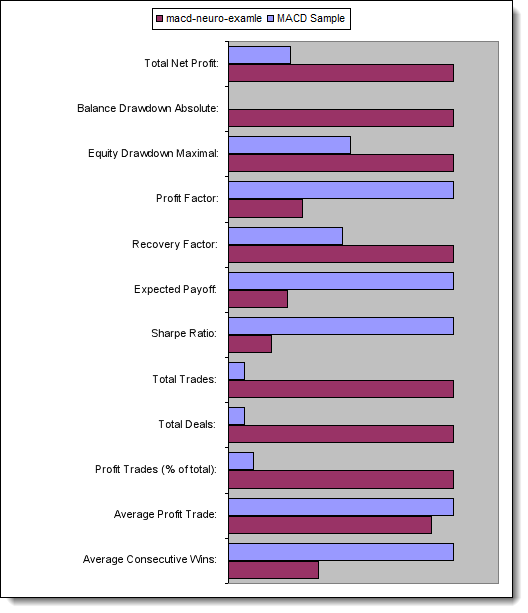
Figura 13. Comparação dos parâmetros-chave
Conclusão
Este artigo abordou os principais pontos que você precisa saber para projetar EAs utilizando redes neurais. Ele apresentou a estrutura de um neurônio e a arquitetura da rede neural, destacou as funções de ativação e os métodos para alteração da forma da função de ativação, bem como o processo de otimização e normalização de dados de entrada. Além disso, comparamos um EA baseado na lógica padrão com um EA baseado em rede neural.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/497
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Como comprar um robô negociação, no Mercado MetaTrader, e instalá-lo?
Como comprar um robô negociação, no Mercado MetaTrader, e instalá-lo?
 Estratégia de Carry Trade estatístico
Estratégia de Carry Trade estatístico
 Como preparar cotações do MetaTrader 5 para outros aplicativos
Como preparar cotações do MetaTrader 5 para outros aplicativos
 Explorar as classes de estratégia de negociação da biblioteca padrão - Personalização de estratégias
Explorar as classes de estratégia de negociação da biblioteca padrão - Personalização de estratégias
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
abre apenas uma negociação no backtest
Uma pergunta importante:
O RSI N valores passados está definido como 14 (N=14).
O número de entradas é 10 (valores anteriores).
Há algum problema? Parece que os resultados do ML podem ser instáveis?
Por favor, responda: ....
Agradecimentos
Uma pergunta importante:
Os N valores anteriores do RSI estão definidos como 14 (N=14).
O número de entradas é 10 (valores anteriores).
Há algum problema? Parece que os resultados do ML podem ser instáveis?
Por favor, responda: ....
Agradecimentos
14 é o período para calcular o indicador RSI. A entrada é de 10 valores do buffer RSI.