OpenCL：パラレルワールドへの橋渡し

はじめに

本稿はOpenCLまたはOpen Computing Languageでのプログラミングについての短編出版シリーズの第一号です。OpenCLのサポート提供に先立ち、最近の形式の MetaTrader 5 プラットフォームにより 直接、すなわちそのまま使用し、 計算スピードアップのマルチコアプロセッサーのメリットを享受することはできませんでした。

明らかに開発者はターミナルがマルチスレッドであり、「それぞれの EA／スクリプトが個別のスレッドを実行する」を際限なく繰り返すことができましたが、プログラマーは以下のシンプルなループ（これはπ 値 = 3.14159265...を計算するコードです）の比較的簡単なパラレル実行の機会を与えられませんでした。

long num_steps = 1000000000;
double step = 1.0 / num_steps;
double x, pi, sum = 0.0;
 
for (long i = 0; i<num_steps; i++)
{
   x = (i + 0.5)*step;
   sum += 4.0/(1.0 + x*x);
}
pi = sum*step;

ただ、18か月前『記事』セクションに『MetaTrader 5での並列計算』 という題名の興味深い内容が出ました。しかし方法が創意あふれるにもかかわらずそれはいくらか不自然な印象を受けます。- 上記のループ内計算速度を上げるために書かれたプログラム階層全体（Expert Advisor と2つのインディケータ）が 過ぎたるは及ばざるがごとし、だったのです。

OpenMPをサポートする計画はない またOMP を追加することでコンパイラーのかなりな再プログラミングが必要になることはすでにわかっております。まったく、プログラマーがなにも考えなくてよい安価で簡単なソリュ―ションはどこにもないものです。

in МQL5におけるOpenCLのネイティブ サポートの 発表 はそのためたいへん歓迎されるニュースでした。同じニューススレッドの22ページからスタートしてMetaDriverは CPU および GPUにおける実装の違いを判定することのできるポスティング スクリプトを始めました。OpenCL は数々の興味を喚起しました。

本稿の著者はまず処理には関わりませんでした。：かなり安価なコンピュータの構成（Pentium G840/8 Gb DDR-III 1333/No ビデオカード）は OpenCLを効果的に使用できないようでした。

それでもAMD APP SDKのインストールに続き AMDによって開発された特別なソフトウェア、個別のビデオカードが使用可能ならば他によって実行されるMetaDriverによって提案された最初のスクリプトが著者のコンピュータで問題なく実行され、一つのプロセッサコアの標準スクリプトランタイム に比較するとかなりなスピードアップ、およそ25倍の速さを見せました。その後、Intel OpenCL Runtime がサポートチームの助けを借りてインストールに成功したことで、同じスクリプトのランタイムスピードアップは75におよびました。

ixbt.comが提供しているフォーラムや資料をよく調査してみるとIvy Bridgeプロセッサ以上でのみインテルのIntegrated Graphics Processor (IGP) はOpenCL 1.1をサポートしていることが判りました。結果、上記構成のPCにおけるスピードアップは IGP とは関係なく、この特別なケースでのOpenCL プログラムコードは х86 コア CPUでのみ実行されました。

著者が ixbtの専門家とスピードアップの数値を共有したとき、彼らは即座にいっせいに このすべてはソース言語（MQL5）のしっかりした最適化の結果であると答えました。OpenCL の専門家コミュニティでは С++ 言語（もちろんマルチコアプロセッサと SSEx ベクトルを使用して）での正しい最適化はOpenCL のエミュレーションにおいて数十パーセントのゲインという最良結果で可能であり、最悪のケースでは損失も可能です。すなわちデータを渡す際かなり高い消費（時間の）のため、ということは周知の事実なのです。

よって別の仮定：純粋なOpenCLエミュレーションにおけるMetaTrader 5での「魔法のような」スピードアップ数値は OpenCL 自体の『かっこよさ』のせいにせずに適切に取り扱われる必要があります。С++ 言語でよく最適化されたプログラムを超えるGPUの強い利点はかなり力強い 個別のビデオカードを使用することによってのみ獲得できます。それはいくつかのアルゴリズムにおけるその計算能力がいかなる最新のCPUの能力も凌駕しているからです。

ターミナル開発者はそれらはまだ適切に最適化されていないと述べます。かれらもまた以下の最適化で数倍というスピードアップの程度についてのヒントを投げかけました。OpenCLにおけるすべてのスピードアップ数値は同じ「数倍」に相当するレベルで失われます。ただしそれでもまだ1よりかなり大きなものです。

それはわれわれが進めていく OpenCL 言語（みなさんのビデオカードが OpenCL 1.1 をサポートしていなかったり、単にそれがなかったとしても）を学習するよい理由です。しかしまず基本について述べます。 - Open CL および適切なハードウェアをサポートするソフトウェアについて、です。

. 基本のソフトウェアとハードウェア

1.1.AMD

適切なソフトウェアは非営利産業企業体メンバーである AMD、 Intel、 NVidiaによって製造されます - 異機種環境において計算に関連する異なる言語仕様を開発するKhronos グループです。

Khronos Groupのオフィシャルウェブサイトに有用な資料をいくつか見つけることができます。たとえば以下です。

• OpenCL 1.1 仕様
• OpenCL 1.1 資料

こういったドキュメントは OpenCL については端末でヘルプ情報がまだ提供されていないため（短い OpenCL APIの概要のみ提供されています。）OpenCLを学習する仮定で非常によく利用されます。三社とも（AMD、Intel、NVidia）ビデオハードウェアの供給者で、それぞれ独自の OpenCL ランタイム実装および個別のソフトウェア開発キット - SDKを持っています。ビデオカード選択の特性に入っていきます。ここでは AMD 製品を例にとります。

お手持ちの AMD ビデオカードがあまり古いものでない（最初の発売は2009～2010年またはそれ以降）なら、ことは簡単です - すぐ作業にとりかかるにはそのビデオカードドライバーをアップデートするだけで十分です。OpenCL と互換性のあるビデオカードリストはここです。一方、Radeon HD 4850 (4870)のようにそのときはひじょうに良いビデオカードは OpenCLを扱う際には問題です。

まだ AMD ビデオカードは持っていないが一つ入手してもよいと思っているならまず仕様を見てください。ここにひじょうに包括的な 最新AMD ビデオカード仕様一覧 があります。われわれにとって最も重要なのは以下です。

• 搭載メモリ — ローカルメモリ量大きいほど良いです。通常1 GB で十分です。

• コアクロック — コア処理フリクエンシーこれも明らかです。：GPU マルチプロセッサの処理頻度が高いほど良いです。650-700 MHz でよいでしょう。

• [メモリ] タイプ — ビデオメモリタイプメモリは理想的に速い必要があります。すなわち GDDR5. メモリバンド幅は2倍劣りますが GDDR3 でもよいでしょう。

• [メモリ] クロック (Eff.) - ビデオメモリの処理（効果的）頻度。厳密にはこのパラメータは前の項目と密接に関連しています。TechnicallyThe GDDR5 処理効果頻度は平均 GDDR3の二倍高くなっています。「より高い」メモリタイプはより高い頻度で動作するという事実とは関係はなく、メモリによって使用されるデータ送信数によります。すなわちそれはメモリバンド幅に関連があるのです。

• [メモリ] バス - バスデータ幅。 最低 256 ビットが賢明です。

• MBW — メモリバンド幅。このパラメータは上記3つのビデオメモリパラメータの組合せです。高いほど良いです。

• Config Core (SPU:TMU(TF):ROP) — GPU コアユニットのコンフィギュレーション。 われわれにとって重要なもの、すなわちノングラフィック計算にとって、は最初の数です。1024:64:32 記載ではわれわれは数値1024（統一されたストリームプロセッサまたはシェーダーの番号）が必要であることを意味します。明らかに高いほど良いです。

• 処理パワー — 理論上の浮動小数型計算のパフォーマンス（FP32 （シングルプレシジョン）／ FP64 （ダブルプレシジョン）。 仕様書テーブルにはつねに FP32（ビデオカードはすべてシングルプレシジョン計算を処理することができます。）に対応する値が含まれています。 これは FP64の場合とは大きく異なります。ビデオカードがダブルプレシジョンをサポートしていないからです。 GPU計算にダブルプレシジョン（ダブルタイプ）がまったく必要ではないと確信しているなら二番目のパラメータは注意を払わなくてもよいでしょう。ただどんな場合でもこのパラメータが高いほど良いです。

• TDP — Thermal デザインパワー。これは簡単に言うとビデオカードが最も困難な計算において 浪費する最大パワーです。お手持ちの Expert Advisor が頻繁にGPUにアクセスするならビデオカードは多くのパワーを費やす（ペイオフするなら悪くありません。）だけでなくひじょうにうるさくなります。
  

ここから二番目のケースです。：ビデオカードがない、または既存のビデオカードが OpenCL 1.1 をサポートしていないが AMD プロセッサは持っている。ここからランタイムから離れていて SDK、Kernel Analyzer 、 Profilerを持つAMD APP SDKをダウンロードすることができます。AMD APP SDKをインストールしたら、プロセッサは OpenCL デバイスとして認識されます。そしてフル機能の OpenCL アプリケーションを CPUのエミュレーションモードで開発することができます。

AMDと反対にSDKの主要な特徴はインテルプロセッサと互換性があることです。（インテル CPUで開発するとき、AMDプロセッサでつい最近利用可能になったSSE4.1、SSE4.2、AVX インストラクションセットをサポートする能力があるためネイティブ SDK がより効果的であったとしても）。

1.2. インテル

インテルプロセッサで作業をする前に Intel OpenCL SDK/Runtimeをダウンロードするとよいでしょう。

以下の点を指摘します。

• CPU（OpenCLエミュレーションモード）だけ使用して OpenCLアプリケーションを開発しようとするなら、インテルCPUグラフィックカーネルはSandy Bridgeおよびそれ以前のプロセッサに対してOpenCL 1.1をサポートしていないことを知っておく必要があります。Ivy Bridgeプロセッサのみサポートしていますが、 超パワフルなインテル HD 4000 統合グラフィックユニットに対してもほとんど違いはありません。Ivy Bridgeより古いプロセッサに対しては、これはMQL5環境でのスピードアップが使用されている SS(S)Ex ベクトルインストラクションによることを意味しています。それでもそれはまだすばらしいように思われます。

• OpenCL SDKをインストールした後、以下のように改定するため登録入力 HKEY_LOCAL_MACHINE\SOFTWARE\Khronos\OpenCL\Vendorsが要求されます。：置換 IntelOpenCL64.dll in the Name column with intelocl.dll 。MetaTrader 5をリブートし起動します。これでCPU はOpenCL 1.1 デバイスとして認識されます。

正直、インテルの OpenCL サポートに関する問題はすべて解決されたとは言えません。そこで将来ターミナル開発者に解決してもらいたい点がいくつかあります。基本的にだれもみなさんのためにカーネルコードエラー（OpenCLカーネルはGPU上で実行されるプログラムです。）に注意を払わないことが問題です。これは MQL5 コンパイラではありません。コンパイラはただカーネルの大きなラインを取得し、それを実行しようとするだけです。たとえば、カーネルで使用されるいくつかの内部変数 хを宣言しなかったとしたら、カーネルはまだ厳密に実行され、エラーを伴いalbeit

ただし端末内で出るすべてのエラーは、関数CLKernelCreate() および CLProgramCreate()に対してAPI OpenCL上のヘルプで述べられている数十のエラーよりも少なくなります。言語シンタックスはひじょうにC言語のシンタックスに似ています。ベクトル関数とデータタイプで強化されています（実際この言語は1999年に ANSI С 規格として採用されたC99です。）

本稿の著者がOpenCLについてのコードをデバッグするのに使用しているのはインテル OpenCL SDK オフラインコンパイラです。それは MetaEditorでやみくも にエラーを探すよりはずっと便利です。将来的に状況が良い方に変われば良いのですが。

1.3. NVidia

残念ながら著者は本テーマにおいての情報を探しませんでした。とはいうものの、一般的推奨は同じです。新しいNVidia ビデオカード用ドライバーは自動的に OpenCLをサポートします。

基本的に本稿著者はNVidia ビデオカードに対して反論はありませんが、情報検索、フォーラム議論から得た知識を基にした結論は次のようなものです。：ノングラフィカル計算に対してAMD ビデオカードは価格／パフォーマンス比率という点で NVidia ビデオカードよりもより最適に思える。

ではプログラミングに進みます。

2. OpenCLを使用した最初のMQL5プログラム

われわれの最初のひじょうにシンプルなプログラムを作成するためにそのようなタスクを定義する必要があります。例としておおよそ 3.14159265 に等しいπ値の計算を使用することは並列プログラミングコースではいつも行われることです。

このため、以下の式が使用されます（著者は以前にこの特殊な式に出くわしたことはありませんが、それは真のようです）。

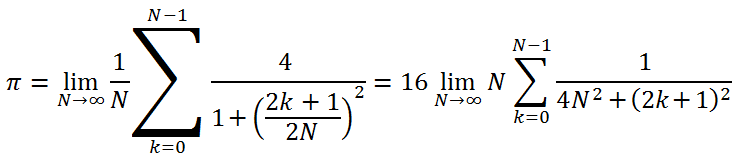
小数点以下 12 位まで正確な値を計算したいと思います。基本的にそのような精度は約100万ループ取得可能ですが、この数字では OpenCL での計算の恩恵を判定できません。GPU 上の計算が短くなりすぎるからです。

GPGPU プログラミングコースは GPU タスク継続時間が最低 20 ミリ秒となるように計算量を選択することを提案しています。われわれの場合、この制限を GetTickCount() 関数の有意なエラーのために100ミリ秒に比べもっと高く設定する必要があります。

下記はこの計算が実装されている MQL5 プログラムです。

//+------------------------------------------------------------------+
//|                                                           pi.mq5 |
//+------------------------------------------------------------------+
#property copyright "Copyright (c) 2012, Mthmt"
#property link      "https://www.mql5.com"

long     _num_steps        = 1000000000;
long     _divisor          = 40000;
double   _step             = 1.0 / _num_steps;
long     _intrnCnt         = _num_steps / _divisor;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart()
  {
   uint start,stop;
   double x,pi,sum=0.0;

   start=GetTickCount();
//--- first option - direct calculation
   for(long i=0; i<_num_steps; i++)
     {
      x=(i+0.5)*_step;
      sum+=4.0/(1.+x*x);
     }
   pi=sum*_step;
   stop=GetTickCount();

   Print("The value of PI is "+DoubleToString(pi,12));
   Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds");

//--- calculate using the second option
   start=GetTickCount();
   sum=0.;
   long divisor=40000;
   long internalCnt=_num_steps/divisor;
   double partsum=0.;
   for(long i=0; i<divisor; i++)
     {
      partsum=0.;
      for(long j=i*internalCnt; j<(i+1)*internalCnt; j++)
        {
         x=(j+0.5)*_step;
         partsum+=4.0/(1.+x*x);
        }
      sum+=partsum;
     }
   pi=sum*_step;
   stop=GetTickCount();

   Print("The value of PI is "+DoubleToString(pi,12));
   Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds");
   Print("_______________________________________________");
   return(0);
  }
//+------------------------------------------------------------------+

コンパイルしこのスクリプトを実行します。そこで以下を取得します。

2012.05.03 02:02:23    pi (EURUSD,H1)    The time to calculate PI was 8.783 seconds
2012.05.03 02:02:23    pi (EURUSD,H1)    The value of PI is 3.141592653590
2012.05.03 02:02:15    pi (EURUSD,H1)    The time to calculate PI was 7.940 seconds
2012.05.03 02:02:15    pi (EURUSD,H1)    The value of PI is 3.141592653590

π値 ~ 3.14159265 は少しだけ異なる2とおりの方法で計算されます。

最初の方法は OpenMP、 Intel TPP、Intel MKL、その他といったマルチスレッドライブラリの能力を示すためにほとんど古典的とされるものです。

二番目の方法はダブルループと同じ形式の計算です。計算全体は10億ループで構成されており、各プロックが内部ループを作成する25000の「基本」ループを実行します。）外部ループ（そこにはそれが4万個あります）の大きなブロックに分割されます。

この計算が 10-15%少し遅めに実行されるのが判ります。しかしOpenCLに変換する際、基本として使用していくのはこの特殊な計算です。メモリの一領域から別の領域にデータ移転が行われるとき使われる時間とカーネルで実行されるそのような計算の間の合理的妥協を行うカーネル（GPUによって実行される基本の計算タスク）選択が主な理由です。よって現在タスクに関わりカーネルはおおざっぱに言うと二番目の計算アルゴリズムの内部ループです。

OpenCLを使用し値を計算します。プログラムコード全体の次には OpenCLにバインディングするホスト言語(MQL5) の関数特性についての短いコメントが続きます。しかしまず、OpenCLのコーディングに干渉する典型的な『障害』 に関わる数点を強調したいと思います。

1. カーネルはカーネル外で宣言される変数を見ません。それはグローバル半数 _stepおよび _intrnCnt がカーネルコード冒頭で再び宣言される必要があることを意味します（以下を参照ください）。そしてそれぞれの値はカーネルコードで適切に読まれるストリングに変換される必要があります。ただし、これは最近ひじょうに有用であると証明された OpenCLにおけるプログラミングの特殊性です。 C言語には元々ないベクトルデータタイプを作成するときなど。
   
   
2. 合理的な数量でカーネルにできるだけ多くの計算を与えてみます。既存ハードウェアのこのコードでカーネルはひじょうに速いのでこのコードにとってこれはあまり重要ではありません。しかしこの要因はパワー個別のビデオカードが使用されていたら計算スピードアップに役立ちます。

以下は OpenCL カーネルを使ったスクリプトコードです。

//+------------------------------------------------------------------+
//|                                                 OCL_pi_float.mq5 |
//+------------------------------------------------------------------+
#property copyright "Copyright (c) 2012, Mthmt"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs;

input int _device=0;        /// OpenCL device number (0, I have CPU)

#define  _num_steps        1000000000 
#define  _divisor          40000
#define  _step             1.0 / _num_steps
#define  _intrnCnt         _num_steps / _divisor

string d2s(double arg,int dig) { return DoubleToString(arg,dig); }
string i2s(int arg)            { return IntegerToString(arg); }

const string clSrc=
                   "#define _step "+d2s(_step,12)+"                   \r\n"
                   "#define _intrnCnt "+i2s(_intrnCnt)+"             \r\n"
                   "                                                   \r\n"
                   "__kernel void pi( __global float *out )            \r\n"   // type float
                   "{                                                  \r\n"
                   "  int i = get_global_id( 0 );                      \r\n"
                   "  float partsum = 0.0;                             \r\n"   // type float
                   "  float x = 0.0;                                   \r\n"   // type float
                   "  long from = i * _intrnCnt;                       \r\n"
                   "  long to = from + _intrnCnt;                      \r\n"
                   "  for( long j = from; j < to; j ++ )               \r\n"
                   "  {                                                \r\n"
                   "     x = ( j + 0.5 ) * _step;                      \r\n"
                   "     partsum += 4.0 / ( 1. + x * x );              \r\n"
                   "  }                                                \r\n"
                   "  out[ i ] = partsum;                              \r\n"
                   "}                                                  \r\n";
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart()
  {
   Print("FLOAT: _step = "+d2s(_step,12)+"; _intrnCnt = "+i2s(_intrnCnt));
   int clCtx=CLContextCreate(_device);

   int clPrg = CLProgramCreate( clCtx, clSrc );
   int clKrn = CLKernelCreate( clPrg, "pi" );

   uint st=GetTickCount();

   int clMem=CLBufferCreate(clCtx,_divisor*sizeof(float),CL_MEM_READ_WRITE); // type float
   CLSetKernelArgMem(clKrn,0,clMem);

   const uint offs[ 1 ]  = { 0 };
   const uint works[ 1 ] = { _divisor };
   bool ex=CLExecute(clKrn,1,offs,works);
//--- Print( "CL program executed: " + ex );

   float buf[];                                          // type float
   ArrayResize(buf,_divisor);
   uint read=CLBufferRead(clMem,buf);
   Print("read = "+i2s(read)+" elements");

   float sum=0.0;                                        // type float
   for(int cnt=0; cnt<_divisor; cnt++) sum+=buf[cnt];
   float pi=float(sum*_step);                            // type float

   Print("pi = "+d2s(pi,12));

   CLBufferFree(clMem);
   CLKernelFree(clKrn);
   CLProgramFree(clPrg);
   CLContextFree(clCtx);

   double gone=(GetTickCount()-st)/1000.;
   Print("OpenCl: gone = "+d2s(gone,3)+" sec.");
   Print("________________________");

   return(0);
  }
//+------------------------------------------------------------------+

スクリプトコードに関するより詳細な説明は後に行います。

同時にコンパイルしプログラムを起動すると以下のようになります。

2012.05.03 02:20:20    OCl_pi_float (EURUSD,H1)    ________________________
2012.05.03 02:20:20    OCl_pi_float (EURUSD,H1)    OpenCl: gone = 5.538 sec.
2012.05.03 02:20:20    OCl_pi_float (EURUSD,H1)    pi = 3.141622066498
2012.05.03 02:20:20    OCl_pi_float (EURUSD,H1)    read = 40000 elements
2012.05.03 02:20:15    OCl_pi_float (EURUSD,H1)    FLOAT: _step = 0.000000001000; _intrnCnt = 25000

ご覧のようにランタイムは少し短くなりました。がこれでは満足ではありません。：π値 ~ 3.14159265 は小数点以下3桁まで正確なのは明らかです。そのような計算の粗さは実計算では、カーネルは要求される少数点以下12位までの精度を明らかにした回る浮動小数型を使用します。

According to MQL5 ドキュメンテーションによると浮動小数型の精度はたった7有効桁数までしか正確でないのです。一方ダブルタイプ数値の精度は 15有効桁数までとなっています。

よって実データタイプは「より正確」にする必要があります。上記コードでは、浮動小数型をダブルタイプと置き換える必要のある行をコメント ///type floatでマークしています。同じインプットデータを使用してコンパイルしたあと、以下を得ます。（ソースコードを持つ新しいファイル - OCL_pi_double.mq5）

2012.05.03 03:25:35    OCL_pi_double (EURUSD,H1)    ________________________
2012.05.03 03:25:35    OCL_pi_double (EURUSD,H1)    OpenCl: gone = 12.480 sec.
2012.05.03 03:25:35    OCL_pi_double (EURUSD,H1)    pi = 3.141592653590
2012.05.03 03:25:35    OCL_pi_double (EURUSD,H1)    read = 40000 elements
2012.05.03 03:25:23    OCL_pi_double (EURUSD,H1)    DOUBLE: _step = 0.000000001000; _intrnCnt = 25000

ランタイムは大幅に増え、OpenCLのないソースコードの時間さえ超えています（8.783 秒）。

「ダブルタイプが計算を遅くしたのは間違いない」- そう思われることでしょう。実験を行い、それぞれ入力パラメータ_divisorを40000 から 40000000に変えていきます。

2012.05.03 03:26:55    OCL_pi_double (EURUSD,H1)    ________________________
2012.05.03 03:26:55    OCL_pi_double (EURUSD,H1)    OpenCl: gone = 5.070 sec.
2012.05.03 03:26:55    OCL_pi_double (EURUSD,H1)    pi = 3.141592653590
2012.05.03 03:26:55    OCL_pi_double (EURUSD,H1)    read = 40000000 elements
2012.05.03 03:26:50    OCL_pi_double (EURUSD,H1)    DOUBLE: _step = 0.000000001000; _intrnCnt = 25

それは正確性を低下させず、ランタイムは浮動小数型のケースよりわずかに短くなっています。しかし整数型を long から int に変え、前の値 _divisor = 40000を復元すると、カーネルのランタイムは半分減ります。

2012.05.16 00:22:46     OCL_pi_double (EURUSD,H1)       ________________________
2012.05.16 00:22:46     OCL_pi_double (EURUSD,H1)       OpenCl: gone = 2.262 sec.
2012.05.16 00:22:46     OCL_pi_double (EURUSD,H1)       pi = 3.141592653590
2012.05.16 00:22:46     OCL_pi_double (EURUSD,H1)       read = 40000 elements
2012.05.16 00:22:44     OCL_pi_double (EURUSD,H1)       DOUBLE: _step = 0.000000001000; _intrnCnt = 25000

常に覚えておくべきことがあります。：かなり「長い」が「軽い」ループ（たとえばそれぞれあまり多くの計算をしないループで構成されるループ）ループがあると、データタイプを「重い」もの（long タイプ - 8 バイト）から「軽い」もの（int タイプ- 4 バイト）に替えるだけでカーネルのランタイムは 激減します。

少しプログラミングの実験は中断し、カーネルコードを全体的に「バインディング」する意味に注目し、いましていることを理解するようにします。カーネルコードの「バインディング」によってOpenCL APIすなわちコマンドシステムがカーネルがホストプログラムと通信することを可能にする（この場合、MQL5のプログラム）ことを意味します。

3. OpenCL API 関数

3.1. コンテクストの作成

以下で与えられたコマンドはコンテクストを作成します。すなわちOpenCL オブジェクトとリソースを管理する環境です。

int clCtx = CLContextCreate( _device );

まず、プラットフォームモデルについて少し述べます。

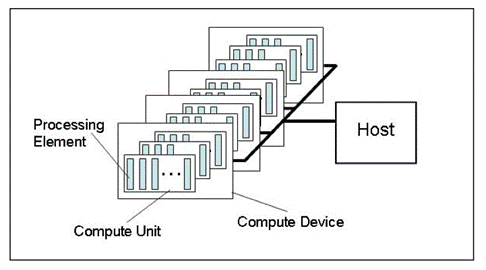
図1　計算プラットフォームの抽象モデル

図では計算プラットフォームの抽象モデルが示されています。ビデオカードに連携するハードウェアのストラクチャをあまり詳細に述べていませんが、現実にかなり近く一般的考えをよく表しています。

ホストとはプログラム実行処理全体を制御する主要な CPU を言います。それはいくつかの OpenCL デバイス（計算デバイス）を認識することができます。 多くの場合、トレーダーがシステムユニットで利用可能な計算用ビデオカードを持っている場合、ビデオカードはデバイスとみなされます。（デュアルプロセッサビデオカードは2デバイスとみなされます！その上、ホストper se,すなわち CPU はつねに OpenCL デバイスとみなされます。各デバイスはプラットフォーム内で独自の番号を持ちます。

CPU の場合 х86 コア（インテル CPU「仮想」コア、ハイパースレッディングを介して作成される「コア」を含みます）に対応するそれぞれのデバイ内に複数の「計算ユニット」があります。；記事 GPU 計算の観点からビデオカードに対してこれらは SIMD エンジン、そなわち SIMD コアまたはミニプロセッサです。AMD/ATI Radeon Architectural Features. パワフルなビデオカードは一般的に 20 SIMD コアを持ちます。

各 SIMD コアにはストリームプロセッサが含まれています。たとえば Radeon HD 5870 ビデオカードには各SIMD エンジンに16ストリームプロセッサがあります。

最後にそれぞれのストリームプロセッサは4または5の処理エレメントを持ちます。同じカードでは ALUです。

ハードウェア用グラフィックのベンダーが使用する用語は初心者にとってはかなり混乱を招くものだということに注意が必要です。人気の高い OpenCLについてのフォーラムスレッドで一般的に使用される"bees"が何を意味するか必ずしも明確ではありません。それでもなお、近代的ビデオカードのスレッド数、計算の同時スレッドはひじょうに大きなものです。たとえば Radeon HD 5870ビデオカードで推測されるスレッド数は 5,000です。

以下の図にはこのビデオカードの技術仕様が表示されています。

図2　Radeon HD 5870 GPU の特徴

以下で指定されるすべて（OpenCL リソース）は CLContextCreate() 関数によって作成されるコンテクストに関連付けられている必要があります。

• OpenCL デバイス。計算に使用されるハードウェア

• プログラムオブジェクト。カーネルを実行するプログラムコード。

• カーネル。デバイスで実行される関数。

• メモリオブジェクト。デバイスによって操作されるデータ（たとえばバッファ、 2D または 3D画像）

• コマンドキュー（現在実装しているターミナル言語は個別の APIを提供しません。）

作成されるコンテクストは以下でアタッチされるデバイスを持つ空のフィールドとして説明することができます。T

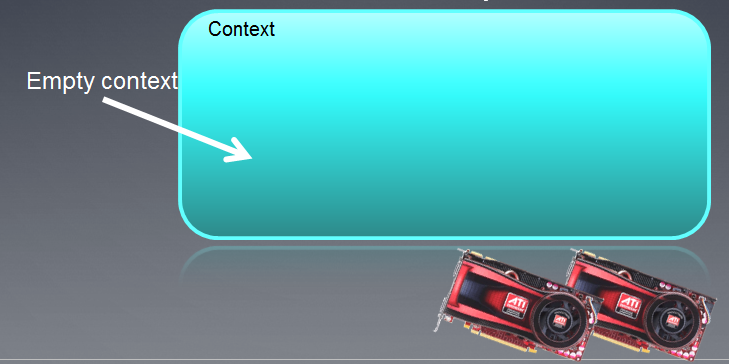
図3　OpenCL コンテクスト

関数の実行後はコンテクストフィールドは空になっています。

MQL5 におけるOpenCLコンテクストは1件のデバイスのみに連携します。

3.2. プログラム作成

int clPrg = CLProgramCreate( clCtx, clSrc );

CLProgramCreate() 関数はリソース "OpenCL program"を作成します。

オブジェクトThe object "Program" は実際、OpenCL カーネル（これは次項でお話します。）コレクションですが MetaQuotes 実装では、OpenCL プログラムにはカーネルは1つしかないのは明らかです。オブジェクト "Program"の作成にはソースコード（ここではclSrc）がストリングに読み込まれることを確認する必要があります。

今回の場合は clSrc がすでにグローバル変数として宣言されているためそれは必要ありません。

下の図は前に作成されたコンテクストの一部であるプログラムを表示しています。

図4　プログラムはコンテクストの一部です。

プログラムがコンパイルに失敗したら、開発者はコンパイラのアウトプットでデータへのリクエストを個別に起動する必要があります。フル機能の OpenCL API は API 関数 clGetProgramBuildInfo() を持ち、それを呼んだあとコンパイラのアウトプットでストリングが返されます。

現バージョン (b.642) は、カーネルコード修正についての情報をもっともつ OpenCL デベロッパーを提供するためのOpenCL APIにはインクルードする価値があるこの関数をサポートしていません。

デバイス（ビデオカード）からの"Tongues" は明らかに API レベルのMQL5ではサポートされないコマンドキューです。

3.3. カーネルの作成

CLKernelCreate() 関数は OpenCL リソース "Kernel"を作成します。

int clKrn = CLKernelCreate( clPrg, "pi" );

カーネルは OpenCL デバイスで実行されるプログラムで宣言される関数です。

われわれの場合、それは名前が"pi"の pi() 関数です。オブジェクト "kernel" は対応する引数を伴うカーネルの関数です。この関数の二番目の引数はプログラム内の関数名に正確にしたがった関数 name です。

図5　カーネル

オブジェクト "kernel" はカーネルとして宣言される一つの同じ関数に対して異なる引数を設定するとき必要なだけ使用することができます。

ここで関数 CLSetKernelArg() および CLSetKernelArgMem() ど移動する必要がありますが、まずデバイスのメモリに格納されているオブジェクトについてお話します。

3.4. メモリオブジェクト

まず、GPUで処理されるあらゆる「大きい」オブジェクトは最初に GPU 自体のメモリに作成、またはホストメモリ (RAM)から移動する必要があります。「大きい」オブジェクトは、バッファ（一次元配列）また二次元あるいは三次元の画像（2D または 3D）のいずれかを意味します。

バッファは個別の隣接するバッファエレメントを持つ大きいメモリ領域です。これらはシンプルデータタイプ（char、double、float、longなど）または複合データタイプ（ストラクチャ、ユニオンなど）のいずれかです。個別のバッファエレメントは直接アクセス、読み出し、書き込み可能です。

現時点では画像は観ません。それは特殊なデータタイプだからです。OpenCLに関するスレッドの最初のページにある ターミナル開発者から提供されるコードは開発者は画像使用に取り組まないことを示しています。

紹介されているコードではバッファを作成する関数は以下のようなものです。

int clMem = CLBufferCreate( clCtx,  _divisor * sizeof( double ), CL_MEM_READ_WRITE );

最初のパラメータはT OpenCL バッファがリソースとして 関連付けられたコンテクストハンドルです。二番目のパラメータはバッファに割り当てられたメモリです。三番目のパラメータはこのオブジェクトで何ができるのか示しています。返される値は OpenCL バッファへのハンドル（問題なく作成されれば）、または1（作成がエラーのため失敗であれば）です。

この場合、バッファはGPUのメモリ、すなわち OpenCL デバイスに直接作成されました。この関数を使わず RAM に作成された場合、下記で説明されるように OpenCL デバイスメモリ (GPU) に移動する必要があります。

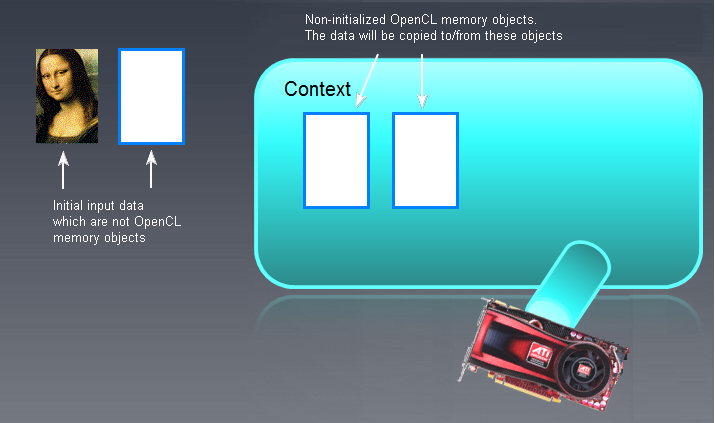
図6　OpenCL メモリオブジェクト

OpenCL メモリオブジェクトではない入力／出力バッファ（画像である必要はありません。モナリザがここで表示されているのは単に説明目的です！）は左に表示されます。空の初期化されていない OpenCL メモリオブジェクトはメインのコンテクストフィールドの右に表示されます。初期データ「モナリザ」は個別に OpenCL コンテクストフィールドに移動され OpenCL プログラムにより出力されるなんらかが左側、RAMに戻される必要があります。

以下はOpenCL でホスト／OpenCLデバイスから／へデータコピーのために使用される語です。

• ホストからデバイスメモリへのデータコピーは書き込み （CLBufferWrite() 関数）と呼ばれます。
• デバイスメモリからホストへのデータコピーは読み出し（CLBufferRead() 関数）と呼ばれます。

書き込みコマンド（ホスト ->デバイス）はデータによってメモリオブジェクトを初期化し、同時にオブジェクトをデバイスメモリにセットします。

デバイスで利用可能なメモリオブジェクトの有効期限はデバイスに対応するハードウェアベンダーによるので OpenCL 仕様では指定されていないことを覚えておきます。そのためメモリオブジェクト作成の際は注意が必要です。

メモリオブジェクトが初期化され、デバイスに書き込まれたら、このような絵が表示されます。

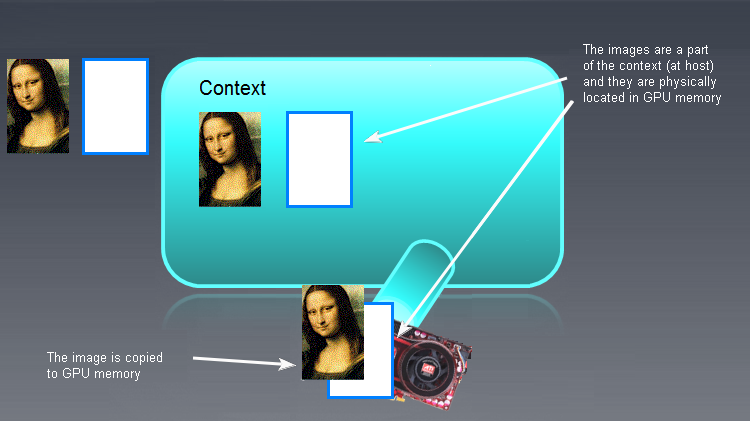
図7　メモリオブジェクト OpenCL の初期化結果

カーネルのパラメータを設定する関数に話を進めていきます。

3.5. カーネルのパラメータ設定

CLSetKernelArgMem( clKrn, 0, clMem );

CLSetKernelArgMem() 関数は前に作成したバッファをカーネルのゼロパラメータと定義します。

カーネルコードで同じパラメータを見ると、それは以下のようなものです。

__kernel void pi( __global float *out )

カーネルではそれは API 関数 CLBufferCreate()で作成されるのと同じタイプのout[ ] 配列です。

ノンバッファパラメータを設定する似た関数があります。

bool  CLSetKernelArg( int   kernel,          // handle to the kernel of the OpenCL program
                       uint  arg_index,       // OpenCL function argument number
                      void  arg_value );     // function argument value

たとえばカーネルの二番目のパラメータとしていくつかダブル x0 を設定しようとすると、まずそれを宣言しMQL5 プログラム内で初期化する必要があります。

double x0 = -2;

そうして関数が呼ばれることとなります。（MQL5コードで）

CLSetKernelArg( cl_krn, 1, x0 );

上記操作後、絵は以下のようになります。

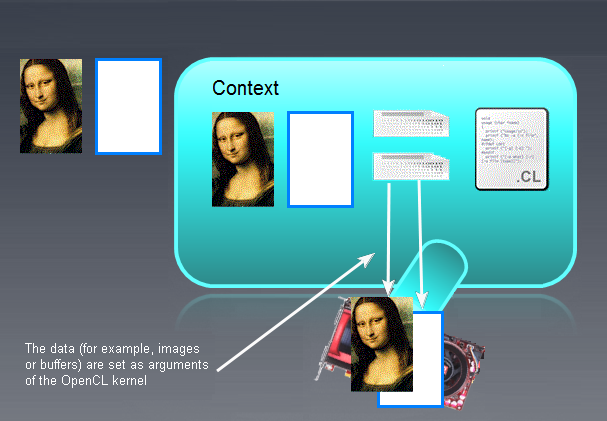
図8　カーネルのパラメータ設定結果

3.6. プログラムの実行

bool ex = CLExecute( clKrn, 1, offs, works );

著者は OpenCL 仕様にこの関数の直接の類似体は見つけていません。この関数は与えられたパラメータでカーネル clKrnを実行します。最後のパラメータ 'works' は計算タスクの計算ごとに実行されるタスク数を設定します。関数は SPMD (Single Program Multiple Data) 原則を表しています。：関数を一度呼びだすと works パラメータ値に等しい地震のパラメータを数値で持つカーネルインスタンスを作成します。；これらカーネルインスタンスは伝統的な考え方から言えば 同時にしかし、 AMD 用語で言うところの異なるストリームコア上で実行されます。

OpenCL の一般性は言語がコード実行に関与するハードウェアの構造にあるのではないという事実にあります。：プログラマーは OpenCL プログラムを適切に実行するためハードウェアの仕様を知る必要はありません。それでもプログラムは実行されるのです。またコードの有効性を高める（たとえばスピード）これら仕様を知ることは強く推奨されます。

たとえばこのコードは個別のビデオカードのない著者のハードウェアでちゃんと実行されます。著者はすべてのエミュレーションが行われる CPU そのもののストラクチャについてはあいまいな考えしか持っていません。

さて、OpenCL プログラムはついに実行され、これでホストプログラムでその結果を利用することができるのです。 

3.7. 出力データの読み取り

以下はデバイスからのホストプログラム読みとりの一部です。

float buf[  ]; 
ArrayResize( buf, _divisor );                                                   
uint read = CLBufferRead( clMem, buf );

OpenCL でのデータ読み取りはこのデータをデバイスからホストへコピーすることだということを思い出してください。この3行がその方法を示しています。メインプログラムで読み取られたOpenCL バッファと同じタイプのbuf[] バッファを宣言し、関数を呼ぶだけです。ホストプログラム（ここではMQL5言語）で作成されたバッファタイプはカーネルのバッファタイプとは異っても、そのサイズは正確に一致している必要があります。

これでデータはホストメモリにコピーされ、メインプログラム内、すなわちMQL5でのプログラムで完全に利用可能です。

OpenCLデバイス上で必要な計算をすべて行った後、メモリはすべてのオブジェクトから解放する必要があります。 freed

3.8. すべての OpenCL オブジェクトの破壊

これは以下のコマンドによって行われます。

CLBufferFree( clMem );
CLKernelFree( clKrn );
CLProgramFree( clPrg );
CLContextFree( clCtx );

このシリーズの関数の主な特殊性はオブジェクトが作成手順と逆の手順でオブジェクトを破壊することです。

それではカーネルコード自体を簡単に見ていきます。

3.9. カーネル

ご覧のようにカーネルコードは全体的に複数ストリングが構成する単一の長いストリングです。

カーネルヘッダは標準関数のように見えます。

__kernel void pi( __global float *out )

カーネルヘッダにはいくつか要件があります。

• 戻り値タイプは常に voidです。
• 指定子 __kernel は下線の文字を2つ含む必要はありません。それは kernelと同様です。
• 引数が一つの配列（バッファ）である場合、それは参照によってのみ渡されます。メモリ指定子 __global (or global) はこのバッファがデバイスのグローバルメモリに格納されることを意味します。
• シンプルデータタイプの引数は値で渡されます。

カーネル本体はいずれにしても C言語の標準コードとは異なります。

重要：ストリング

int i = get_global_id( 0 ); 

上記は i がセル内の計算結果を決めるGPU 内部の計算対称セル番号であることを意味します。この結果はのちにアウトプット配列（この場合、out[]）に書き込まれます。GPU メモリから CPU メモリに配列が読み出されたら、ホストプログラムでその値が足し算されます。

OpenCL プログラムコードには2個以上の関数があるかもしれないおとに留意が必要です。たとえば、シンプルな inline 関数は pi() 関数の外側にあり、「メイン」のカーネル関数 pi()内部で呼ばれることが可能です。このケースはのちに考察します。

これで MetaQuotes の実装におけるOpenCL APIの知識を少し得ました。実験を続けていくことができます。本稿で著者はランタイムを最大まで最適化することができるようになるハードウェア詳細は掘り下げる予定をしていませんでした。今の主要なタスクは OpenCL でそのようはプログラミングのきっかけを提供することです。

言い換えればコードはかなり繊細です。なぜならハードウェア仕様は考慮しないからです。naive同時に、それはまったく一般的でどのようなハードウェアでも実行可能なはずです。 - CPU、AMD によるIGP（CPUに統合されたGPU）、AMD / NVidiaによる個別ビデオカード

ベクトルデータタイプを使用した繊細な最適化をもっと考察する前に、まずそれらを知る必要があります。

4. ベクトルデータタイプ

ベクトルデータタイプは C99とは別にそれを設定するOpenCLに指定のタイプです。この中には (u)charN、(u)shortN、(u)intN、(u)longN、floatNのどのタイプもあり、ここでは N = {2|3|4|8|16}です。

こういったタイプは内蔵コンパイラが別の並列計算を行うことを知った（または推測される）場合に使用されることになっています。これはかならずというわけではないことに注意が必要です。カーネルコードが値 N でだけ異なる場合や、その他すべての点（著者はそれを見ることができました。）で同じ場合でも、です。

以下は内蔵 データタイプです：

表1　 OpenCLの内蔵ベクトルデータタイプ

このタイプはあらゆるデバイスでサポートされています。このタイプはそれぞれカーネルとホストプログラムの間で通信するためAPI の対応タイプを持ちます。これは現時点では MQL5 実装に提供されていませんが、それは大きな問題ではありません。 

また別のタイプもありますが、それらを使用するためには明確に指定することが必要です。どのデバイスでもサポートされているわけではないからです。

表2　 OpenCLのその他の内蔵データタイプ

さらに、OpenCLでサポートされるため確保されたデータタイプがあります。言語仕様にはそれらのきわめて長いリストがあります。

ベクトルタイプの定数または変数を宣言するにはシンプルで直感的ルールに従います。

以下にいくつか例を示します。

float4 f = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f);
uint4  u = ( uint4  ) ( 1 );             /// u is converted to a vector (1, 1, 1, 1).
float4 f = ( float4 ) ( ( float2 )( 1.0f, 2.0f ), ( float2 )( 3.0f, 4.0f ) );
float4 f = ( float4 ) ( 1.0f, ( float2 )( 2.0f, 3.0f ), 4.0f );
float4 f = ( float4 ) ( 1.0f, 2.0f );   /// error

ご覧のように右側のデータタイプを左側に宣言された変数 "width" （ここでは4です）と一致させ、まとめるだけでよいのです。唯一の例外は、スカラーからスカラーに等しい成分を持つベクトルへの変換（2行目）です。

それぞれのベクトルデータタイプに 対してベクトル成分をアドレス指定するシンプルなメカニズムがあります。一方でそれらはベクトル（配列）で、もう一方でそれらはストラクチャです。たとえば幅2の最初のベクトル成分（float2 uなど）は u.x とアドレス指定され、二番目のものはu.yです。

ベクトル long3 u タイプへの三番目の成分は u.x、u.y, u.zです。

ベクトル float4 u タイプのベクトルにはそれに応じて.xyzw、すなわち u.x,、u.y、u.z、u.wです。

float2 pos;
pos.x = 1.0f; // valid
pos.z = 1.0f; // invalid because pos.z does not exist

float3 pos;
pos.z = 1.0f; // valid
pos.w = 1.0f; // invalid because pos.w does not exist

一度に複数成分を選択することもでき、それらの順序を変えることもできます。（グループ記述）

float4 c;
c.xyzw = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f );
c.z = 1.0f;
c.xy =  ( float2 ) ( 3.0f, 4.0f );
c.xyz = ( float3 ) ( 3.0f, 4.0f, 5.0f );

float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f );
float4 swiz= pos.wzyx;                          // swiz = ( 4.0f, 3.0f, 2.0f, 1.0f )
float4 dup = pos.xxyy;                          // dup = ( 1.0f, 1.0f, 2.0f, 2.0f )

成分グループ記述、すなわち複数成分の仕様は代入文の左側にきます。(i.e. l-value)

float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f );
pos.xw     = ( float2 ) ( 5.0f, 6.0f );            // pos = ( 5.0f, 2.0f, 3.0f, 6.0f )
pos.wx     = ( float2 ) ( 7.0f, 8.0f );            // pos = ( 8.0f, 2.0f, 3.0f, 7.0f )
pos.xyz    = ( float3 ) ( 3.0f, 5.0f, 9.0f );      // pos = ( 3.0f, 5.0f, 9.0f, 4.0f )
pos.xx     = ( float2 ) ( 3.0f, 4.0f );           // invalid as 'x' is used twice
pos.xy     = ( float4 ) (1.0f, 2.0f, 3.0f, 4.0f ); // mismatch between float2 and float4

float4 a, b, c, d;

float16 x;
x = ( float16 ) ( a, b, c, d );
x = ( float16 ) ( a.xxxx, b.xyz, c.xyz, d.xyz, a.yzw );
x = ( float16 ) ( a.xxxxxxx, b.xyz, c.xyz, d.xyz );  // invalid as the component a.xxxxxxx is not a valid vector type

個別の成分は別の記述を使用してアクセス可能です。- グループ記述の16真数の1ケタまたは数ケタ前に挿入する文字 s （または S）です。

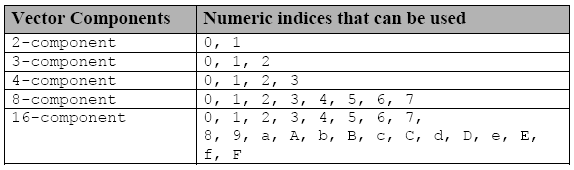
表3　ベクトルデータタイプの個別成分にアクセスするために使用される指数

ベクトル変数を f と宣言する場合

float8 f;

f.s0 はベクトルの第一成分で、f.s7 は8番目の成分です。

同様に 16次元ベクトル vector x を宣言すると

float16 x;

x.sa（またはx.sA） はベクトル x の11番目の成分で、x.sf （または x.sF）は16番目の成分です。<br0/>

数値 indices （.s0123456789abcdef）と文字記述（.xyzw）は同じ指示子においてグループ成分記述と混ぜることはできません。

float4 f, a;
a = f.x12w;             // invalid as numeric indices are intermixed with the letter notations .xyzw
a.xyzw = f.s0123;       // valid

そして最後に、.lo、.hi、.even、.oddを使ってベクトルタイプ成分を操作する方法がまだ別にあります。

これら接尾辞は以下のように使用します。

• .lo は与えられたベクトルの下半分を参照します。
• .hi は与えられたベクトルの上半分を参照します。
• .even は与えられたベクトルのすべての成分を参照します。
• .odd は与えられたベクトルの奇数成分を参照します。

例：

float4 vf;
float2 low  = vf.lo;           // vf.xy
float2 high = vf.hi;           // vf.zw
float2 even = vf.even;         // vf.xz
float2 odd  = vf.odd;          // vf.yw

この記述はスカラー（非ベクトルデータタイプ）まで繰り返し使用可能です。

float8 u = (float8) ( 1.0f, 2.0f, 3.0f, 4.0f, 5.0f, 6.0f, 7.0f, 8.0f );
float2 s = u.lo.lo;                              //  ( 1.0f, 2.0f )
float2 t = u.hi.lo;                              //  ( 5.0f, 6.0f )
float2 q = u.even.lo;                            //  ( 1.0f, 3.0f )
float  r = u.odd.lo.hi;                           //  4.0f

3個のベクタータイプ成分に関して状況はわずかに複雑です。：厳密にはそれは4個の成分を持つベクトルタイプです。4個目の成分は未定義です。

float3 vf   = (float3) (1.0f, 2.0f, 3.0f);
float2 low  = vf.lo;                             // ( 1.0f, 2.0f );
float2 high = vf.hi;                             // ( 3.0f, undefined );

算術の簡単なルール (+, -, *, /)

指定された産出処理はすべて同じ次元のベクトルに対して定義され、成分に関して処理されます。

float4  d   = (float4) ( 1.0f, 2.0f, 3.0f, 4.0f );
float4  w   = (float4) ( 5.0f, 8.0f, 10.0f, -1.0f );
float4  _sum = d + w;                             // ( 6.0f, 10.0f, 13.0f, 3.0f )
float4  _mul = d * w;                             // ( 5.0f, 16.0f, 30.0f, -4.0f )
float4  _div = w / d;                             // ( 5.0f,  4.0f, 3.333333f, -0.25f )

唯一の例外は、オペランドの一つがスカラーでその他がベクトルの場合です。この場合には、スカラータイプはスカラーそれ自体がベクトルオペランドとして同次元のベクトルに変換される一方でベクトルで宣言されたデータタイプに型変換されます。これに算術処理が続きます。関係演算子についても同じことが言えます (<, >, <=, >=)。

そこから派生して、本項で示した最初の表に挙げられている内蔵データタイプを作成することのできるC99 ネイティブデータタイプ（たとえば配列struct、union、他）もまた OpenCL 言語でサポートされています。

そして最後です。計算を抽出するためにGPU を使いたければ、当然ダブルデータタイプとその結果 doubleNを使用する必要があります。

このため、行を挿入します。

#pragma OPENCL EXTENSION cl_khr_fp64 : enable 

位置はカーネルコードの冒頭部分です。

この情報はすでに続く事柄を理解するには十分です。疑問がある場合は OpenCL 1.1 仕様書を参照ください。

5. ベクトルデータタイプを持つカーネルの実装

きわめて正直に話すと、著者はベクトルタイプのワーキングコードを即座に書けなかったのです。

当初、著者はカーネルでベクトルデータタイプ、たとえばdouble8が宣言されればすぐに勝手にすべてが動作するだろうとの考えで、言語仕様を読むのにあまり注意を払いませんでした。その上double8ベクトル配列として ただ一つの配列を宣言しようとしたのも失敗しました。

効果的にカーネルをベクトル化し、本当のスピードアップを達成するのにこれはまったく十分ではないと気づくまでしばらくかかりました。データはすばやくインプットしアウトプットすることだけではなくすばやく計算することをを要求しているため、ベクトル配列の出力結果で問題は解決されません。この事実に気づくことで処理のスピードアップをし、有効性を高めました。そしてついにずっと速いコードを作成することができたのです。

しかしそれでけではありません。カーネルコードが書かれている間、その上でほとんどやみくもにデバッグを行うことができました。エラー検索はベクトルデータ使用によりたいへん困難になりました。この標準的なメッセージからどのような建設的情報を得ることができるのでしょうか。

ERR_OPENCL_INVALID_HANDLE - OpenCL プログラムに対して無効なハンドル 

または以下です。

ERR_OPENCL_KERNEL_CREATE -  OpenCL オブジェクト作成中の内部エラー

?

これで SDKを再ソートする必要がありました。この場合、著者にとってハードウェア構成が利用可能であるとすると、それはたまたまインテルOpenCL SDK （CPUs/GPUs 向けにインテル以外ではSDK も適切なオフラインコンパイラを含んでいます。）に提供されているインテル OpenCL SDK オフライン コンパイラ（32 ビット）でした。 これは ホスト APIにバインディングすることなくカーネルコードをデバッグすることが可能なので便利です。

MQL5 コードで使用されている形式でなく、代わりに外部クオート文字と "\r\n"（キャリッジリターン文字） を持たない形式で、コンパイラウィンドウにただカーネルコードを挿入し、そこのギア型の「ビルド」ボタンを押すだけです。

そうすると「ビルドログ」ウィンドウが「ビルド」の手順とその進捗情報を表示します。

図9　インテル OpenCL SDK オフィスコンプライヤにてのプログラムコンパイル

クオート文字なしでカーネルコードを取得するために、カーネルコードをファイルWriteCLProgram()に出力するホスト言語(MQL5)シンプルなプログラムを各のが有用です。それにはもうホストプログラムコードもインクルードされています。

コンパイラのメッセージは必ずしも解りやすいとは限りませんが、それらは MQL5 が現時点でもたらすよりもはるかに多量の情報を提供してくれます。エラーはすぐにコンパイラウィンドウで修正され、ひとたびエラーがなくなったことを確認すると、修正は MetaEditor内のカーネルコードに送信されます。

最後です。著者の最初の考えは、単一のグローバルパラメータ「チャンネル数」を設定する方法にてベクトル double4、 double8、 double16 と連携するベクトル化されたコードを作成する、というものでした。なんらかの理由でトークン結合オペレータ ## がカーネルコードと連携しなくなってしまうというつらい数日の後、これは最終的に達成されました。

この間、著者はそれぞれがそのディメンション；4、8、16に適した3つのカーネルコードを持つスクリプトのワーキングコードを問題なく作成していました。この中間コードは本稿では提供していませんが、みなさんがあまり問題を抱えずカーネルコードを書きたいと思われる場合に備えてお話する価値はあると思います。このスクリプト実装のコード (OCL_pi_double_several_simple_kernels.mq5) は本稿末尾の以下に添付しています。

そして以下がベクトル化されたカーネルです。

"/// enable extensions with doubles                                                          \r\n"
"#pragma OPENCL EXTENSION cl_khr_fp64 : enable                                               \r\n"
"#define _ITERATIONS "        + i2s( _intrnCnt ) + "                                     \r\n"
"#define _STEP "             + d2s( _step, 12 )  + "                                     \r\n"     
"#define _CH "               + i2s( _ch )       + "                                     \r\n"
"#define _DOUBLETYPE double"   + i2s( _ch )       + "                                     \r\n"   
"                                                                                            \r\n"
"/// extensions for 4-, 8- and 16- scalar products                                           \r\n"     
"#define dot4( a, b )         dot( a, b )                                                    \r\n"
"                                                                                            \r\n"
"inline double dot8( double8 a, double8 b )                                                  \r\n"
"{                                                                                           \r\n"     
"     return dot4( a.lo, b.lo ) + dot4( a.hi, b.hi );                                        \r\n"
"}                                                                                           \r\n"
"                                                                                            \r\n"      
"inline double dot16( double16 a, double16 b )                                               \r\n"     
"{                                                                                           \r\n"     
"     double16 c  = a * b;                                                                   \r\n" 
"     double4 _1  = ( double4 ) ( 1., 1., 1., 1. );                                          \r\n" 
"     return dot4( c.lo.lo + c.lo.hi + c.hi.lo  + c.hi.hi, _1 );                             \r\n" 
"}                                                                                           \r\n"     
"                                                                                            \r\n"
"__kernel void pi( __global double *out )                                                    \r\n"
"{                                                                                           \r\n"
"  int i = get_global_id( 0 );                                                               \r\n"
"                                                                                            \r\n"
"  /// define vector constants                                                               \r\n"     
"  double16 v16  = ( double16 ) ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 );    \r\n"
"  double8  v8   = v16.lo;                                                                   \r\n"
"  double4  v4   = v16.lo.lo;                                                                \r\n"
"  double2  v2   = v16.lo.lo.lo;                                                             \r\n"          
"                                                                                            \r\n"    
"  /// all vector-related with the calculated type                                           \r\n"
"  _DOUBLETYPE in;                                                                           \r\n"    
"  _DOUBLETYPE xVect;                                                                        \r\n"
"  _DOUBLETYPE sumVect          = ( _DOUBLETYPE ) ( 0.0 );                                   \r\n"
"  _DOUBLETYPE doubleOneVect    = ( _DOUBLETYPE ) ( 1.0 );                                   \r\n"
"  _DOUBLETYPE doubleCHVect     = ( _DOUBLETYPE ) ( _CH + 0. );                              \r\n"
"  _DOUBLETYPE doubleSTEPVect   = ( _DOUBLETYPE ) ( _STEP );                                 \r\n"
"                                                                                            \r\n"    
"  for( long j = 0; j < _ITERATIONS; j ++ )                                                  \r\n"
"  {                                                                                         \r\n"
"     in =  v" + i2s( _ch ) + " + doubleCHVect * ( i * _ITERATIONS + j );                  \r\n"           
"     xVect = ( in + 0.5 ) * doubleSTEPVect;                                                 \r\n"
"     sumVect += 4.0 / ( xVect * xVect + 1. );                                               \r\n"
"  }                                                                                         \r\n"
"  out[ i ] = dot" + i2s( _ch ) + "(  sumVect, doubleOneVect );                            \r\n"
"}                                                                                           \r\n";   

外部ホストプログラムはあまり変更していません。変更箇所は「ベクトル化チャネル」番号を設定する新しいグローバル定数_ch と _intrnCntが _ch 倍小さくなったことです。それが著者がホストプログラムコードをここで提供しないでおこうと思った理由です。それは本稿末尾に添付したスクリプトファイル (OCL_pi_double_parallel_straight.mq5)にあります。

ご覧のように、カーネルpi()の「主要な」関数から離れて、ここに2つの inline 関数があります。ベクトル dotN( a, b ) のスカラー結果を判断する関数と、1つのマクロ置換です。これらはOpenCLのdot()関数内でディメンションが4を超えないベクトルに従って定義されていることで使用されます。

dot()関数を再定義する dot4() マクロは、計算されたnameを持つdotN() 関数を呼ぶのに便利なだめだけにあります。

"  out[ i ] = dot" + i2s( _ch ) + "(  sumVect, doubleOneVect );                              \r\n"

指数4なしで dot() 関数を通常の形式で使用すると、ここに示されるように簡単にそれを呼ぶことができました。そのと _ch = 4 （ベクトル化チャネルの数が4）

この行はそのようなカーネルはホストプログラムでストリングとして扱われる特定のカーネルの有用な機能を説明しています。：われわれ関数に対してだけでなくデータタイプに対しても 計算された カーネル内の識別子を使用することができます。

このカーネルを持つホストプログラムの全貌は以下に添付しています。 (OCL_pi_double_parallel_straight.mq5).

「幅」16 ( _ch = 16 )のベクトルを持つスクリプトを実行すると以下を得ます。

2012.05.15 00:15:47     OCL_pi_double2_parallel_straight (EURUSD,H1)    ==================================================
2012.05.15 00:15:47     OCL_pi_double2_parallel_straight (EURUSD,H1)    CPUtime / GPUtime = 4.130
2012.05.15 00:15:47     OCL_pi_double2_parallel_straight (EURUSD,H1)    SMARTER: The time to calculate PI was 8.830 seconds
2012.05.15 00:15:47     OCL_pi_double2_parallel_straight (EURUSD,H1)    SMARTER: The value of PI is 3.141592653590
2012.05.15 00:15:38     OCL_pi_double2_parallel_straight (EURUSD,H1)    DULL: The time to calculate PI was 8.002 seconds
2012.05.15 00:15:38     OCL_pi_double2_parallel_straight (EURUSD,H1)    DULL: The value of PI is 3.141592653590
2012.05.15 00:15:30     OCL_pi_double2_parallel_straight (EURUSD,H1)    OPENCL: gone = 2.138 sec.
2012.05.15 00:15:30     OCL_pi_double2_parallel_straight (EURUSD,H1)    OPENCL: pi = 3.141592653590
2012.05.15 00:15:30     OCL_pi_double2_parallel_straight (EURUSD,H1)    read = 20000 elements
2012.05.15 00:15:28     OCL_pi_double2_parallel_straight (EURUSD,H1)    CLProgramCreate: unknown error.
2012.05.15 00:15:28     OCL_pi_double2_parallel_straight (EURUSD,H1)    DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125
2012.05.15 00:15:28     OCL_pi_double2_parallel_straight (EURUSD,H1)    ==================================================

ベクトルデータタイプを使用した最適化さえカーネルを速めないことが判ります。

ただ、同じコードを GPUで実行すれば、スピードゲインは再びずっと大きくなります。

MetaDriver（ビデオカード- HIS Radeon HD 6930, CPU - AMD Phenom II x6 1100T）により提供される情報によると、同じコードは以下の結果を導きます。

2012.05.14 11:36:07     OCL_pi_double2_parallel_straight (AUDNZD,M5)    ==================================================
2012.05.14 11:36:07     OCL_pi_double2_parallel_straight (AUDNZD,M5)    CPUtime / GPUtime = 84.983
2012.05.14 11:36:07     OCL_pi_double2_parallel_straight (AUDNZD,M5)    SMARTER: The time to calculate PI was 14.617 seconds
2012.05.14 11:36:07     OCL_pi_double2_parallel_straight (AUDNZD,M5)    SMARTER: The value of PI is 3.141592653590
2012.05.14 11:35:52     OCL_pi_double2_parallel_straight (AUDNZD,M5)    DULL: The time to calculate PI was 14.040 seconds
2012.05.14 11:35:52     OCL_pi_double2_parallel_straight (AUDNZD,M5)    DULL: The value of PI is 3.141592653590
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    OPENCL: gone = 0.172 sec.
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    OPENCL: pi = 3.141592653590
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    read = 20000 elements
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    CLProgramCreate: unknown error.
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    ==================================================

6. 最後の仕上げ

ここにもう一つ別のカーネルがあります。（それは以下に添付した OCL_pi_double_several_simple_kernels.mq5 ファイルにありますが、ここでは表示されていません。）

このスクリプトは一時的に「単一」カーネルを書くことから離れ、異なるベクトルディメンション（4, 8, 16, 32）について4つのシンプルなカーネルを書くことを考えていた時に著者にあった考えの実装です。

"#pragma OPENCL EXTENSION cl_khr_fp64 : enable                                               \r\n"
"#define _ITERATIONS " + i2s( _itInKern ) + "                                             \r\n"
"#define _STEP "      + d2s( _step, 12 ) + "                                              \r\n"
"                                                                                            \r\n"
"typedef struct                                                                              \r\n"
"{                                                                                           \r\n"
"  double16    lo;                                                                           \r\n"
"  double16    hi;                                                                           \r\n"
"} double32;                                                                                 \r\n"
"                                                                                            \r\n"
"inline double32 convert2double32( double a )                                                \r\n"        
"{                                                                                           \r\n"
"  double32 b;                                                                               \r\n"    
"    b.lo = ( double16 )( a );                                                               \r\n"
"    b.hi = ( double16 )( a );                                                               \r\n"
"    return b;                                                                               \r\n"
"}                                                                                           \r\n"
"                                                                                            \r\n"
"inline double dot32( double32 a, double32 b )                                               \r\n"     
"{                                                                                           \r\n"     
"     double32 c;                                                                            \r\n" 
"     c.lo = a.lo * b.lo;                                                                    \r\n" 
"     c.hi = a.hi * b.hi;                                                                    \r\n" 
"     double4 _1  = ( double4 ) ( 1., 1., 1., 1. );                                          \r\n" 
"     return dot( c.lo.lo.lo + c.lo.lo.hi + c.lo.hi.lo  + c.lo.hi.hi +                       \r\n" 
"                 c.hi.lo.lo + c.hi.lo.hi + c.hi.hi.lo  + c.hi.hi.hi, _1 );                  \r\n" 
"}                                                                                           \r\n"     
"                                                                                            \r\n"
"__kernel void pi( __global double *out )                                                    \r\n"
"{                                                                                           \r\n"
"  int i = get_global_id( 0 );                                                               \r\n"
"                                                                                            \r\n"
"  /// define vector constants                                                               \r\n"
"  double32 _v32;                                                                            \r\n"
"  _v32.lo = ( double16 ) (  0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,                          \r\n"
"                            8.,  9., 10., 11., 12., 13., 14., 15. );                        \r\n"
"  _v32.hi = ( double16 ) ( 16., 17., 18., 19., 20., 21., 22., 23.,                          \r\n"
"                           24., 25., 26., 27., 28., 29., 30., 31. );                        \r\n"
"                                                                                            \r\n"
"  /// all vector-related with undefined type                                                \r\n"
"  double32 xVect;                                                                           \r\n"
"  double32 sumVect           = convert2double32( 0.0 );                                     \r\n"
"  double32 double1Vect       = convert2double32( 1.0 );                                     \r\n"
"                                                                                            \r\n"
"  double32 in;                                                                              \r\n"
" /// work only with 16-vectors in the loop!                                                 \r\n"
"  for( long j = 0; j < _ITERATIONS; j ++ )                                                  \r\n"
"  {                                                                                         \r\n"
"     in.lo = _v32.lo + 32. * ( i * _ITERATIONS + j );                                       \r\n"
"     in.hi = _v32.hi + 32. * ( i * _ITERATIONS + j );                                       \r\n"
"     xVect.lo = ( in.lo  + 0.5 ) * _STEP;                                                   \r\n"
"     xVect.hi = ( in.hi  + 0.5 ) * _STEP;                                                   \r\n"
"     sumVect.lo += 4. / ( xVect.lo * xVect.lo + 1. );                                       \r\n"
"     sumVect.hi += 4. / ( xVect.hi * xVect.hi + 1. );                                       \r\n"                             
"  }                                                                                         \r\n"
"  out[ i ] = dot32( sumVect, double1Vect );                                                 \r\n"
"}                                                                                           \r\n";    

このカーネルはディメンション 32のベクトルを実装しています。新しいベクトルタイプと数個の必要なインライン関数はカーネルの主要関数外に定義されます。それ以外（そしてここが重要です！）、メインループ内のすべての計算は故意に標準ベクトルデータタイプのみで作成され、非標準タイプはループ外で処理されています。このことでコード実行時間がかなりスピードアップします。

ここでの計算では、このカーネルは幅16のベクトル使用時よりも遅いようには見えませんが、それでもずっと速いわけではありません。

MetaDriverにより提供される情報によると、このカーネル t (_ch=32) を伴うスクリプトは以下の結果を導きます。

2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: gone = 0.156 sec.
2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: pi = 3.141592653590
2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) read = 10000 elements
2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) CLProgramCreate: unknown error or no error.
2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) GetLastError returned .. 0
2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) DOUBLE2: _step = 0.000000001000; _itInKern = 3125; vectorization channels - 32
2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) =================================================================

概要およびまとめ

著者は完全に OpenCL リソース表示のため選択されたタスクはこの言語の典型ではないことを理解しています。

テキストを手にとりここに揚げるため大きな行列をかけ算する標準的な例 を不正コピーする方がずっと簡単だったかもしれません。そういう例は明らかに印象的なことでしょう。ただ、大きな行列のかけ算を要求する金融計算に取り組んでいる mql5.com フォーラムのユーザーは多くいるのでしょうか？きわめて疑わしいものです。著者は自身の例を選び、途中で遭遇する問題を自分で解決したいと思いました。同時に他の人と自身の経験を共有しようと思いました。もちろんフォーラムユーザーの皆さんがご判断することです。

OpenCL エミュレーションの有効性ゲイン （そのままの CPUで） はMetaDriverのスクリプトを使用して取得する何百、何千というものに比べるときわめて小さなものだと解りました。しかし適切な GPUでは、CPU AMDを用いたCPUにおけるランタイムが多少長いことを無視したとしても、それは少なくとも1エミュレーションよりは大きな指標です。OpenCL はまだ学習の 価値があります 計算スピードのゲインがそんなに大きかったとしてもです！

次回の記事ではハードウェア上にOpenCLの抽象モデルを表示する特殊性に関連した問題を取り上げるつもりです。こういった事柄の知識はかなり計算スピードアップを可能にすることもあります。

ひじょうに価値あるプログラミングおよび最適化ヒントのパフォーマンスに関し MetaDriver に、また OpenCL SDKを使用することの可能性に関し サポートチームに特別な謝辞を述べたいと思います。

添付ファイル内容：

• pi.mq5 - 2とおりの "pi" 値計算を行うpureMQL5のスクリプト
• OCl_pi_float.mq5 - 浮動小数型で実計算を行う OpenCL カーネルを持ちたスクリプトの最初の実装
• OCL_pi_double.mq5 - 同上。実計算にダブルタイプを使用。
• OCL_pi_double_several_simple_kernels.mq5 - さまざまなベクトル幅（4、8、16、32）に対する複数の指定カーネルを使用したスクリプト
• OCL_pi_double_parallel_straight.mq5 - いくつかのベクトル「幅」 （4、8、16）に対する単一カーネルを使用したスクリプト