OpenCL: A ponte para mundos paralelos

Introdução

Esse artigo é o primeiro de uma curta série de publicações sobre programação na OpenCL, ou Linguagem de cálculo aberta. A plataforma do MetaTrader 5 está na sua forma atual, antes de fornecer suporte para a OpenCL, não permitia diretamente, ou seja, de forma nativa usar e desfrutar das vantagens de processadores de multi-core (múltiplos núcleos) para acelerar cálculos.

Obviamente, os desenvolvedores poderiam repetir incessantemente que o terminal é multitarefa e que "todo o EA/script é executado em um segmento separado", mas o codificador não teve uma oportunidade para uma execução paralela relativamente fácil do seguinte loop simples (isto é um código para calcular o valor de pi = 3,14159265...):

long num_steps = 1000000000;
double step = 1.0 / num_steps;
double x, pi, sum = 0.0;
 
for (long i = 0; i<num_steps; i++)
{
   x = (i + 0.5)*step;
   sum += 4.0/(1.0 + x*x);
}
pi = sum*step;

No entanto, já há 18 meses atrás, um trabalho muito interessante intitulado "Cálculos paralelos em MetaTrader 5" apareceu na seção "Artigos". E ainda ... tem-se a impressão de que, apesar da ingenuidade da abordagem, é de alguma forma, pouco natural - uma hierarquia inteira de programa (o Expert Advisor e dois indicadores), escritos para acelerar os cálculos no loop acima teriam sido uma coisa muito boa.

Nós já sabemos que não há planos para o suporte de OpenMP e estamos cientes do fato de que a adição de OMP requer uma reprogramação drástica do compilador. Infelizmente, não haverá solução barata e fácil para um programador, onde nenhum pensamento é necessário.

O anúncio do suporte nativo para OpenCL em МQL5 foi, portanto, uma notícia muito bem-vinda. A partir da página 22 do mesmo segmento de notícias, o MetaDriver começou a postar scripts que permitem avaliar a diferença entre a implementação em CPU e GPU. A OpenCL despertou enorme interesse.

O autor deste artigo primeiro optou por não fazer parte desse processo: a configuração do computador muito inferior (Pentium G840/ 8 Gb DDR-III 1333/ sem placa de vídeo) não pareceu proporcionar um uso eficaz da OpenCL.

No entanto, após a instalação da AMD APP SDK, um software especializado desenvolvido pela AMD, o primeiro roteiro proposto por MetaDriver que havia sido executado por outras pessoas somente se uma placa de vídeo discreta estava disponível, foi executado com êxito no computador do autor e demonstrou um aumento de velocidade que estava longe de ser insignificante em comparação com um tempo de execução de script padrão em um núcleo do processador, sendo cerca de 25 vezes mais rápido. Mais tarde, a aceleração do mesmo tempo de execução de script chegou a 75, devido a Intel OpenCL Runtime ser instalada com sucesso, com a ajuda da equipe de suporte.

Tendo estudado cuidadosamente o fórum e os materiais providos pelo ixbt.com, o autor descobriu que o processador de gráfico integrado (JGP) da Intel suporta a OpenCL 1.1, apenas iniciando com processadores Ivy Bridge e superiores. Consequentemente, a aceleração alcançada no PC com a configuração acima não poderia ter nada a ver com o IGP e o código do programa OpenCL, neste caso particular foi executado apenas em CPU núcleo х86.

Quando o autor compartilhou as figuras de aceleração com iXBT especialistas, eles responderam imediatamente e de uma só vez que tudo isso foi resultado de uma considerável sub-otimização da fonte de linguagem (MQL5). Na comunidade de profissionais da OpenCL, é um fato conhecido que uma otimização correta de um código fonte em C++ (claro, sujeito ao uso de um processador multi-core e instruções de vetor SSEX) podem em seu melhor resultado em um ganho de várias porcentagens de dezena na simulação de OpenCL; na pior das hipóteses, você pode até mesmo perder, por exemplo, devido a gastos extremamente altos (de tempo) ao transmitir dados.

Assim - uma outra suposição: figuras de aceleração 'milagrosas' em MetaTrader 5 na simulação pura da OpenCL devem ser tratadas de forma adequada, sem ser atribuída à "frieza"da própria OpenCL. Uma vantagem realmente forte da GPU durante um programa bem otimizado em С++ só pode ser adquirida através de uma placa de vídeo discreta muito poderosa desde que as suas capacidades de cálculo em alguns algoritmos esteja muito além das capacidades de qualquer CPU moderna.

Os desenvolvedores do terminal declararam que ele ainda não foi devidamente otimizado. Eles também deixaram escapar uma pista sobre o grau de aceleração que será aumentado em várias vezes após a otimização. Todos os valores de aceleração na OpenCL serão reduzidos em conformidade com as mesmas "várias vezes". No entanto, eles ainda vão ser consideravelmente maiores do que a unidade.

é um bom motivo para aprender a linguagem OpenCL (mesmo que sua placa de vídeo não suporte OpenCL 1.1 ou simplesmente que não a tenha) com o qual vamos prosseguir. Mas, primeiro, deixe-me dizer algumas palavras sobre a base essencial - o software que suporta a Open CL e o hardware apropriado.

1. Software essencial e hardware

1.1.AMD

O software apropriado é produzido pela AMD, Intel e NVidea, os membros do consórcio industrial sem fins lucrativos - o Khronos Group que desenvolve diferentes linguagens específicas em relação aos cálculos em ambientes heterogêneos.

Alguns materiais úteis podem ser encontrados no site oficial do Khronos Group, por exemplo:

• A especificação da OpenCL 1.1,
• Referência OpenCL 1.1.

Estes documentos terão que ser usados muitas vezes no processo de aprendizagem da OpenCL, pois o terminal ainda não oferece informações de ajuda sobre a OpenCL (há apenas um breve resumo da OpenCL API). Todas as três empresas (AMD, Intel e NVidia) são fornecedoras de hardware de vídeo e cada uma delas tem sua própria implementação de OpenCL Runtime e respectivos kits de desenvolvimento de software - SDK. Vamos para as peculiaridades de escolher placas de vídeo, tendo os produtos da AMD como um exemplo.

Se a sua placa de vídeo AMD não for muito antiga (lançada em produção em 2009-2010 ou posterior), vai ser bastante simples - uma atualização do driver da placa de vídeo deve ser o suficiente para começar a trabalhar imediatamente. Uma lista das placas de vídeo compatíveis com a OpenCL pode ser encontrada aqui. Por outro lado, mesmo uma placa de vídeo que é muito boa para a época, como a Radeon HD 4850 (4870), não lhe poupará o trabalho ao lidar com a OpenCL.

Se você ainda não tiver uma placa de vídeo AMD, mas pensa em obter uma, dê uma olhada para nas suas especificações primeiro. Aqui você pode ver uma Tabela de especificação de placas de vídeo AMDbastante abrangentes. As mais importantes para nós são as seguintes:

• Memória On-board - a quantidade de memória local. Quanto maior é, melhor. 1GB normalmente seria suficiente.

• Core Clock - operação da frequência do núcleo. Também está claro: quanto maior a frequência de operação de multiprocessadores da GPU, melhor. 650-700 MHz não é nem um pouco ruim.

• Tipo de [Memória] - Tipo de memória de vídeo. A memória deve, idealmente, ser rápida, ou seja, GDDR5. Mas a GDDR3 também seria ótima, embora cerca de duas vezes pior em termos de largura de banda de memória.

• [Memória] Clock (Eff.) - Operação (efetiva) de frequência de memória de vídeo. Tecnicamente, este parâmetro está estreitamente relacionado com o anterior. A frequência efetiva de operação da GDDR5 é duas vezes maior que a frequência da GDDR3. Não tem nada a ver com o fato de que tipos de memórias "mais elevadas" trabalhem em frequências mais altas, mas é devido ao número de canais de transferência de dados utilizados pela memória. Em outras palavras, tem a ver com largura de banda da memória.

• Barramento [Memória] - largura de dados de barramento. é aconselhável que seja no mínimo de 256 bit.

• MBW - largura da banda de memória. Esse parâmetro é na verdade uma combinação dos três parâmetros de memórias de vídeo acima. Quanto mais alta, melhor.

• Configuração do núcleo (SPU:TMU(TF):ROP) - Configuração de unidades de núcleo da GPU. O que é importante para nós, isto é, para os cálculos não-gráficos, é o primeiro número. 1024:64:32 declarado significaria que precisamos do número 1024 (o número de processadores de transmissão unificado ou shaders). Obviamente, quanto mais alto, melhor.

• Poder de processamento - desempenho teórico em cálculos de ponto flutuante (FP32 (precisão simples) / FP64 (precisão dupla). Considerando que as tabelas de especificação sempre contem um valor correspondente a FP32 (todas as placas de vídeo podem lidar com cálculos de precisão simples), este está longe de ser o caso com o FP64 a precisão dupla não é suportado por todas as placas de vídeo. Se você está certo que você precisará de precisão dupla (tipo duplo) em cálculos da GPU, você pode ignorar o segundo parâmetro. Mas qualquer que seja o caso, quanto mais alto for este parâmetro, melhor será.

• TDP - Potência do projeto térmico. Isto é, falando a grosso modo, que a potência máxima da placa de vídeo se dissipa nos cálculos mais difíceis. Se o seu Expert Advisor estará frequentemente acessando a GPU, a placa de vídeo não só irá consumir uma grande quantidade de energia (o que não é ruim, se valer à pena), mas também será muito barulhenta.
  

Agora, o segundo caso: não há placa de vídeo ou a placa de vídeo existente não suporta a OpenCL 1.1, mas você tem um processador AMD. Aqui você pode baixar o AMD APP SDK que além do tempo de execução também contém SDK, Analisador de núcleo e Profiler. Após a instalação do AMD APP SDK, o processador deve ser reconhecido como um dispositivo da OpenCL. E você será capaz de desenvolver aplicações totalmente caracterizadas em modo de simulação da CPU.

A principal característica do SDK, em oposição a AMD, é que ele também é compatível com os processadores Intel (embora, ao desenvolver na CPU da Intel, o SDK nativo seja ainda significativamente mais eficiente, uma vez que é capaz de suportar os conjuntos de instrução SSE4.1, SSE4.2 e AVX que apenas recentemente se tornaram disponíveis em processadores AMD).

1,2. Intel

Antes de começar a trabalhar nos processadores Intel, é aconselhável baixar o Intel OpenCL SDK/Runtime.

Devemos destacar o seguinte:

• Se você pretende desenvolver aplicações OpenCL usando apenas CPU (modo de simulação OpenCL), você deve saber que o núcleo de gráficos da CPU Intel não suporta OpenCL 1.1 para processadores mais antigos que e inclusive o Sandy Bridge. Este suporte está disponível apenas com processadores Ivy Bridge, mas dificilmente fará qualquer diferença, mesmo para as unidades gráficas integradas Intel HD 4000 ultra poderosas. Para os processadores mais antigos que o Ivy Bridge, isso significaria que a aceleração alcançada no ambiente MQL5 é apenas devido às instruções de vetor SS (S)EX usadas. No entanto, também parece ser significativa.

• Após a instalação do Intel OpenCL SDK, a entrada de registro HKEY_LOCAL_MACHINE\SOFTWARE\Khronos\OpenCL\Vendors é necessária que seja alterada do seguinte modo: substituir IntelOpenCL64.dll na coluna Nome porintelocl.dll . Em seguida, reinicie e inicie o MetaTrader 5. A CPU agora é reconhecida como um dispositivo OpenCL 1.1.

Para ser sincero, a questão sobre o suporte OpenCL da Intel ainda não foi totalmente resolvido, então devemos esperar alguns esclarecimentos dos desenvolvedores do terminal no futuro. Basicamente, a questão é que ninguém vai prestar atenção em erros de código do núcleo (núcleo OpenCL é um programa executado na GPU) para você - isso não é o compilador MQL5. O compilador apenas levará tudo em uma grande linha inteira do núcleo e tentará executá-lo. Se, por exemplo, você não declarar alguma variável interna х usada no núcleo, o núcleo ainda será tecnicamente executado, embora com erros.

No entanto, todos os erros que você obterá no terminal se reduzem para menos que uma dúzia em relação a tais descritos na Ajuda no API OpenCL para as funções CLKernelCreate() e CLProgramCreate(). A sintaxe da linguagem é muito semelhante à C melhorada, com funções vetoriais e tipos de dados (na verdade, esta linguagem é C99, que foi adotado como padrão ANSI С em 1999).

é o compilador offline Intel OpenCL SDK que o autor deste artigo utiliza para depurar o código para a OpenCL, que é muito mais conveniente do que procurar cegamente erros do núcleo do MetaEditor. Esperemos que, no futuro, a situação mude para melhor.

1,3. NVidia

Infelizmente, o autor não busca informações sobre este assunto. As recomendações gerais, no entanto, permanecem as mesmas. Drivers para as novas placas de vídeo NVidia automaticamente suportam OpenCL.

Basicamente, o autor do artigo não tem nada contra placas de vídeo NVidia, mas a conclusão com base no conhecimento adquirido a partir da procura de informações e discussões do fórum é a seguinte: para os cálculos não-gráficos, placas de vídeo da AMD parecem ser mais ideais em termos da relação preço/desempenho do que as placas de vídeo da NVIDIA.

Vamos agora proceder à programação.

2. O primeiro programa MQL5 usando OpenCL

Para ser capaz de desenvolver o nosso primeiro e, muito simples, programa é preciso definir a tarefa como tal. Isso deve ter se tornado habitual em cursos de programação paralela, usar o cálculo do valor de pi que é aproximadamente igual a 3,14159265 como um exemplo.

Para este propósito, a seguinte fórmula é usada (o autor nunca se deparou com esta fórmula especial antes, mas parece ser verdadeira):

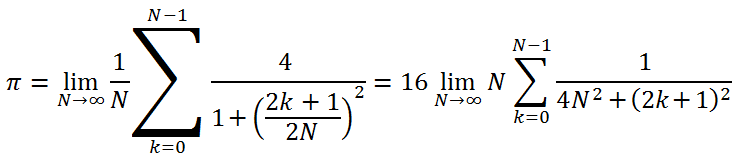
Queremos calcular o valor exato até 12 casas decimais. Basicamente, tal precisão pode ser obtida com cerca de 1 milhão de repetições, mas esse número não nos permitirá avaliar o benefício de cálculos na OpenCL, pois a duração de cálculos na GPU fica muito curta.

Cursos de programação GPGPU sugerem selecionar a quantidade de cálculos de modo que a duração da tarefa da GPU seja de pelo menos 20 milissegundos. No nosso caso, esse limite deve ser ajustado mais alto devido a um erro significativo da função GetTickCount() comparável a 100 ms.

Abaixo está o programa MQL5 onde esse cálculo é implementado:

//+------------------------------------------------------------------+
//|                                                           pi.mq5 |
//+------------------------------------------------------------------+
#property copyright "Copyright (c) 2012, Mthmt"
#property link      "https://www.mql5.com"

long     _num_steps        = 1000000000;
long     _divisor          = 40000;
double   _step             = 1.0 / _num_steps;
long     _intrnCnt         = _num_steps / _divisor;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart()
  {
   uint start,stop;
   double x,pi,sum=0.0;

   start=GetTickCount();
//--- first option - direct calculation
   for(long i=0; i<_num_steps; i++)
     {
      x=(i+0.5)*_step;
      sum+=4.0/(1.+x*x);
     }
   pi=sum*_step;
   stop=GetTickCount();

   Print("The value of PI is "+DoubleToString(pi,12));
   Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds");

//--- calculate using the second option
   start=GetTickCount();
   sum=0.;
   long divisor=40000;
   long internalCnt=_num_steps/divisor;
   double partsum=0.;
   for(long i=0; i<divisor; i++)
     {
      partsum=0.;
      for(long j=i*internalCnt; j<(i+1)*internalCnt; j++)
        {
         x=(j+0.5)*_step;
         partsum+=4.0/(1.+x*x);
        }
      sum+=partsum;
     }
   pi=sum*_step;
   stop=GetTickCount();

   Print("The value of PI is "+DoubleToString(pi,12));
   Print("The time to calculate PI was "+DoubleToString(( stop-start)/1000.0,3)+" seconds");
   Print("_______________________________________________");
   return(0);
  }
//+------------------------------------------------------------------+

Tendo compilado e executado esse script, nós obtemos:

2012.05.03 02:02:23    pi (EURUSD,H1)    The time to calculate PI was 8.783 seconds
2012.05.03 02:02:23    pi (EURUSD,H1)    The value of PI is 3.141592653590
2012.05.03 02:02:15    pi (EURUSD,H1)    The time to calculate PI was 7.940 seconds
2012.05.03 02:02:15    pi (EURUSD,H1)    The value of PI is 3.141592653590

O valor de pi ~ 3,14159265 é calculado de duas formas um pouco diferentes.

A primeira pode ser quase considerada um método clássico para a demonstração das capacidades de bibliotecas multitarefas, como OpenMP, Intel TPP, Intel MKL e outras.

A segunda é o mesmo cálculo na forma de um loop duplo. O cálculo inteiro que consiste em 1 bilhão de repetições é dividido em grandes blocos de loops externos (há 40.000 deles lá) onde cada bloco executa 25.000 repetições "básicas" que compõem o loop interno.

Você pode ver que esse cálculo é executado um pouco mais lento, por 10-15%. Mas é este cálculo específico que vamos usar como base para a conversão à OpenCL. A principal razão é o núcleo (a tarefa de cálculo básica executado na GPU) seleção que realizaria um compromisso razoável entre o tempo gasto com a transferência de dados de uma área da memória para outra e, como tal, os cálculos de execução no núcleo. Assim, em termos da tarefa atual, o núcleo será, falando em grosso modo, o loop interno do segundo algoritmo de cálculo.

Vamos agora calcular o valor usando a OpenCL. Um código completo do programa será seguido de breves comentários sobre as características de funções da linguagem anfitrião (MQL5) de ligação à OpenCL. Mas, primeiro, eu gostaria de destacar alguns pontos relacionados com "obstáculos" típicos que possam interferir com codificação na OpenCL:

1. O núcleo não vê variáveis ​​declaradas fora do núcleo. é por isso que as variáveis ​​globais _step e _intrnCnt tiveram que ser declaradas novamente no início do código do núcleo (ver abaixo). E seus respectivos valores tiveram de ser transformados em sequências para serem lidos corretamente no código do núcleo. No entanto, essa peculiaridade de programação em OpenCL se revelou muito útil mais tarde, por exemplo, ao fazer tipos de dados de vetor que são nativamente ausentes de C.
   
   
2. Tente dar o maior número de cálculos para o núcleo quanto possível, mantendo o seu número razoável. Isso não é muito crítico para este código, pois, o núcleo não é muito rápido neste código no hardware existente. Mas este fator o ajudará a acelerar os cálculos se uma poderosa placa de vídeo discreta é usada.

Então, aqui está o código de script com o núcleo OpenCL:

//+------------------------------------------------------------------+
//|                                                 OCL_pi_float.mq5 |
//+------------------------------------------------------------------+
#property copyright "Copyright (c) 2012, Mthmt"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs;

input int _device=0;        /// OpenCL device number (0, I have CPU)

#define  _num_steps        1000000000 
#define  _divisor          40000
#define  _step             1.0 / _num_steps
#define  _intrnCnt         _num_steps / _divisor

string d2s(double arg,int dig) { return DoubleToString(arg,dig); }
string i2s(int arg)            { return IntegerToString(arg); }

const string clSrc=
                   "#define _step "+d2s(_step,12)+"                   \r\n"
                   "#define _intrnCnt "+i2s(_intrnCnt)+"             \r\n"
                   "                                                   \r\n"
                   "__kernel void pi( __global float *out )            \r\n"   // type float
                   "{                                                  \r\n"
                   "  int i = get_global_id( 0 );                      \r\n"
                   "  float partsum = 0.0;                             \r\n"   // type float
                   "  float x = 0.0;                                   \r\n"   // type float
                   "  long from = i * _intrnCnt;                       \r\n"
                   "  long to = from + _intrnCnt;                      \r\n"
                   "  for( long j = from; j < to; j ++ )               \r\n"
                   "  {                                                \r\n"
                   "     x = ( j + 0.5 ) * _step;                      \r\n"
                   "     partsum += 4.0 / ( 1. + x * x );              \r\n"
                   "  }                                                \r\n"
                   "  out[ i ] = partsum;                              \r\n"
                   "}                                                  \r\n";
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
int OnStart()
  {
   Print("FLOAT: _step = "+d2s(_step,12)+"; _intrnCnt = "+i2s(_intrnCnt));
   int clCtx=CLContextCreate(_device);

   int clPrg = CLProgramCreate( clCtx, clSrc );
   int clKrn = CLKernelCreate( clPrg, "pi" );

   uint st=GetTickCount();

   int clMem=CLBufferCreate(clCtx,_divisor*sizeof(float),CL_MEM_READ_WRITE); // type float
   CLSetKernelArgMem(clKrn,0,clMem);

   const uint offs[ 1 ]  = { 0 };
   const uint works[ 1 ] = { _divisor };
   bool ex=CLExecute(clKrn,1,offs,works);
//--- Print( "CL program executed: " + ex );

   float buf[];                                          // type float
   ArrayResize(buf,_divisor);
   uint read=CLBufferRead(clMem,buf);
   Print("read = "+i2s(read)+" elements");

   float sum=0.0;                                        // type float
   for(int cnt=0; cnt<_divisor; cnt++) sum+=buf[cnt];
   float pi=float(sum*_step);                            // type float

   Print("pi = "+d2s(pi,12));

   CLBufferFree(clMem);
   CLKernelFree(clKrn);
   CLProgramFree(clPrg);
   CLContextFree(clCtx);

   double gone=(GetTickCount()-st)/1000.;
   Print("OpenCl: gone = "+d2s(gone,3)+" sec.");
   Print("________________________");

   return(0);
  }
//+------------------------------------------------------------------+

Uma explicação mais detalhada sobre o código de script será dada um pouco mais tarde.

Nesse meio tempo, compile e inicie o programa para obter o seguinte:

2012.05.03 02:20:20    OCl_pi_float (EURUSD,H1)    ________________________
2012.05.03 02:20:20    OCl_pi_float (EURUSD,H1)    OpenCl: gone = 5.538 sec.
2012.05.03 02:20:20    OCl_pi_float (EURUSD,H1)    pi = 3.141622066498
2012.05.03 02:20:20    OCl_pi_float (EURUSD,H1)    read = 40000 elements
2012.05.03 02:20:15    OCl_pi_float (EURUSD,H1)    FLOAT: _step = 0.000000001000; _intrnCnt = 25000

Como se pode ver, o tempo de execução foi ligeiramente reduzido. Mas isso não é suficiente para nos deixar felizes: o valor de pi ~ 3,14159265 é, obviamente, preciso apenas até o 3º dígito depois do ponto decimal. Tal rugosidade dos cálculos é devido ao fato de que em cálculos reais o núcleo usa números de tipo flutuante cuja exatidão é claramente inferior à precisão exigida de 12 casas decimais.

De acordo com a Documentação MQL5, a precisão de um número de tipo flutuante só é precisa para 7 números significativos. Embora a precisão de um número do tipo duplo tem precisão de 15 números significativos.

Portanto, precisamos tornar tipos de dados reais "mais precisos". No código acima, as linhas onde o tipo flutuante deve ser substituído pelo o tipo duplo são marcadas com o comentário ///tipo flutuante. Após a compilação usando os mesmos dados de entrada, temos o seguinte (novo arquivo com o código fonte - OCL_pi_double.mq5):

2012.05.03 03:25:35    OCL_pi_double (EURUSD,H1)    ________________________
2012.05.03 03:25:35    OCL_pi_double (EURUSD,H1)    OpenCl: gone = 12.480 sec.
2012.05.03 03:25:35    OCL_pi_double (EURUSD,H1)    pi = 3.141592653590
2012.05.03 03:25:35    OCL_pi_double (EURUSD,H1)    read = 40000 elements
2012.05.03 03:25:23    OCL_pi_double (EURUSD,H1)    DOUBLE: _step = 0.000000001000; _intrnCnt = 25000

O tempo de execução aumentou significativamente e até mesmo ultrapassou o tempo do código-fonte sem a OpenCL (8,783 seg.)

"é claramente o tipo duplo que retarda os cálculos", - você pensaria. No entanto, vamos experimentar e alterar substancialmente o parâmetro de entrada _divisor de 40.000 para 40000000:

2012.05.03 03:26:55    OCL_pi_double (EURUSD,H1)    ________________________
2012.05.03 03:26:55    OCL_pi_double (EURUSD,H1)    OpenCl: gone = 5.070 sec.
2012.05.03 03:26:55    OCL_pi_double (EURUSD,H1)    pi = 3.141592653590
2012.05.03 03:26:55    OCL_pi_double (EURUSD,H1)    read = 40000000 elements
2012.05.03 03:26:50    OCL_pi_double (EURUSD,H1)    DOUBLE: _step = 0.000000001000; _intrnCnt = 25

Não prejudicou a precisão e o tempo de execução ficou até um pouco mais curto do que no caso do tipo flutuante. Mas se simplesmente mudarmos todos os tipos inteiros, de tempo para int e restaurar o valor anterior do _divisor = 40000, o tempo de execução do núcleo diminuirá em mais da metade:

2012.05.16 00:22:46     OCL_pi_double (EURUSD,H1)       ________________________
2012.05.16 00:22:46     OCL_pi_double (EURUSD,H1)       OpenCl: gone = 2.262 sec.
2012.05.16 00:22:46     OCL_pi_double (EURUSD,H1)       pi = 3.141592653590
2012.05.16 00:22:46     OCL_pi_double (EURUSD,H1)       read = 40000 elements
2012.05.16 00:22:44     OCL_pi_double (EURUSD,H1)       DOUBLE: _step = 0.000000001000; _intrnCnt = 25000

Você deve sempre lembrar: se há um loop bem "longo", mas "leve" (ou seja, um ciclo que consista em uma série de repetições, cada uma delas não têm muita aritmética), uma simples mudança em tipos de dados de "pesados" (tipo longo - 8 bytes) para os "leves" (int - 4 bytes) pode diminuir drasticamente o tempo de execução do núcleo.

Vamos agora parar nossas experiências de programação por um curto tempo e focar no significado de toda a "ligação" do código do núcleo para obter alguma compreensão do que estamos fazendo. Por código do núcleo "ligação" nós queremos dizer provisoriamente OpenCL API, por exemplo, um sistema de comandos que permitem ao núcleo se comunicar com o programa anfitrião (neste caso, com o programa em MQL5).

3. Funções API OpenCL

3,1. Criação de um contexto

Um comando dado abaixo cria contexto, ou seja, um ambiente para o gerenciamento de objetos e recursos OpenCL.

int clCtx = CLContextCreate( _device );

Primeiro, algumas palavras sobre o modelo de plataforma.

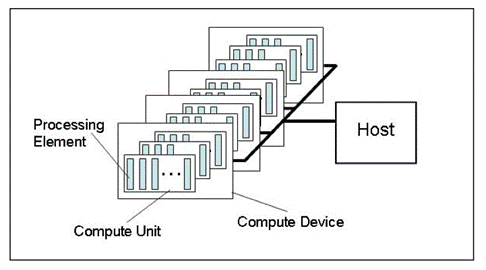
Fig. 1. Modelo abstrato de uma plataforma de cálculo

A figura mostra um modelo abstrato de uma plataforma de computação. Não é uma descrição muito detalhada da estrutura do hardware com relação a placa de vídeo, mas é bastante próximo da realidade e dá uma boa ideia geral.

O host (anfitrião) é a principal CPU que controla todo o processo de execução do programa. Ele pode reconhecer alguns dispositivos OpenCL (dispositivos de computação). Na maioria dos casos, quando um operador tem uma placa de vídeo para os cálculos disponíveis na unidade do sistema, uma placa de vídeo é considerada como um dispositivo (uma placa de vídeo dual-processador será considerada como dois dispositivos!). Além disso, o anfitrião, por si só, por exemplo, a CPU é sempre considerada como um dispositivo OpenCL. Cada dispositivo tem seu número exclusivo dentro da plataforma.

Existem várias unidades de computação em todos os dispositivos que em caso com a CPU correspondem a núcleos х86 (incluindo os núcleos "virtuais" da CPU Intel, ou seja, "núcleos" criados via hiperprocessamento), para uma placa de vídeo, estes seriam os SIMD Engines, ou seja, núcleos SIMD ou mini-processadores em termos do artigo computação GPU. Características arquitetônicas AMD/ATI Radeon. Placas de vídeo poderosas normalmente têm cerca de 20 núcleos SIMD.

Cada núcleo SIMD contém processadores de fluxo, por exemplo a placa de vídeo Radeon HD 5870 tem 16 processadores de fluxo em cada Engine SIMD.

Finalmente, cada processador de fluxo tem quatro ou cinco elementos de processamento, ou seja, ALU, na mesma placa.

Note que a terminologia utilizada por todos os grandes fornecedores de gráficos para hardware é bastante confuso, especialmente para iniciantes. Nem sempre é evidente o que se entende por "bees" tão comumente usados em um tópico do fórum popular sobre OpenCL. No entanto, o número de segmentos, ou seja, segmentos simultâneos de cálculos, em placas de vídeo modernas é muito grande. Por exemplo o número estimado de segmentos na placa de vídeo Radeon HD 5870 é mais de 5 mil.

A figura abaixo mostra as especificações técnicas padrão desta placa de vídeo.

Fig. 2. Recursos da GPU Radeon 5870

Tudo especificado mais abaixo (os recursos OpenCL) devem necessariamente serem associados com o contexto criado pela função CLContextCreate():

• Dispositivos OpenCL, ou seja, hardware usado em cálculos;

• Objetos de programa, ou seja, o código do programa executando o núcleo;

• Núcleos, isto é as funções executadas nos dispositivos;

• Objetos de memória, ou seja, dados (por exemplo, buffers, em imagens 2D e 3D) manipulados pelo dispositivo;

• Filas de comando (atual implementação da linguagem do terminal não prevê um respectivo API).

O contexto criado pode ser ilustrado como um campo vazio com dispositivos conectados à ele abaixo.

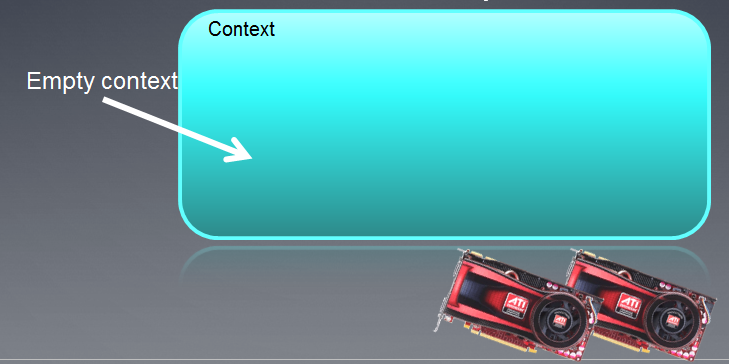
Fig. 3. Contexto OpenCL

Seguinte à execução da função, o campo de contexto está atualmente vazio.

Deve ser notado que no contexto OpenCL no MQL5 se trabalha com um único dispositivo.

3,2. Criando um programa

int clPrg = CLProgramCreate( clCtx, clSrc );

A função CLProgramCreate() cria o recurso "programa OpenCL".

O objeto "Programa" é na verdade uma coleção de núcleos OpenCL (que vai ser discutida na próxima cláusula), mas na implementação do MetaQuotes, aparentemente, só pode haver um núcleo no programa OpenCL. A fim de criar o objeto "Programa" , você deve garantir que o código-fonte (aqui - clSrc) é lido em uma sequência.

No nosso caso, não é necessário, como a sequência de clSrc já foi declarada como uma variável global:

A figura abaixo mostra o programa, sendo uma parte do contexto criada anteriormente.

Fig. 4. Programa é uma parte do contexto

Se o programa falhou para compilar, o desenvolvedor deve iniciar de forma independente um pedido de dados à saída do compilador. Um API da OpenCL inteiramente caracterizado tem a função API clGetProgramBuildInfo() após chamar uma sequência que é devolvida à saída do compilador.

A versão atual (b.642) não suporta esta função, o que provavelmente deve valer à pena ser incluído na OpenCL API para fornecer um desenvolvedor OpenCL com mais informações sobre a correção do código de núcleo.

"Línguas" provenientes dos dispositivos (placas de vídeo) são filas de comando que, aparentemente, não vão ser suportadas em MQL5 no nível API.

3,3. Criação de um núcleo

A função CLKernelCreate() cria um "Núcleo" fonte OpenCL .

int clKrn = CLKernelCreate( clPrg, "pi" );

Núcleo é uma função declarada no programa que é executada no dispositivo OpenCL.

No nosso caso, é a função pi() com o nome de "pi". O objeto "núcleo" é a função do núcleo, juntamente com os respectivos argumentos. O segundo argumento nesta função é o nome da função que deve ser exatamente de acordo com o nome da função dentro do programa.

Fig. 5. Núcleo

"Núcleo" de objetos podem ser usados quantas vezes forem necessários ao definir argumentos diferentes para uma ou mesma função declarada assim como o núcleo.

Devemos agora passar para as funções CLSetKernelArg() e CLSetKernelArgMem(), mas vamos primeiro dizer algumas palavras sobre os objetos armazenados nas memórias dos dispositivos.

3,4. Objetos da Memória

Em primeiro lugar, devemos entender que qualquer "grande" objeto processado na GPU deve primeiro ser criado na memória da própria GPU ou movidos da memória do anfitrião (RAM). Por um objeto "grande" queremos dizer qualquer buffer ( de matriz unidimensional) ou uma imagem que pode ser de duas ou três dimensões (2D ou 3D).

Um buffer é uma grande área de memória que contém elementos buffer adjacentes separados. Estes podem ser tipos simples de dados (char, duplo, flutuante, longo, etc.) ou tipos de dados complexos (estruturas, uniões, etc.) Elementos de buffer separados podem ser acessados ​​diretamente, lidos e escritos.

Não vamos olhar para as imagens no momento, pois é um tipo de dado peculiar. O código fornecido pelos desenvolvedores do terminal na primeira página do tópico sobre OpenCL sugere que os desenvolvedores não se engajaram no uso de imagens.

No código introduzido, a função de criar o buffer parece ser a seguinte:

int clMem = CLBufferCreate( clCtx,  _divisor * sizeof( double ), CL_MEM_READ_WRITE );

O primeiro parâmetro é um identificador de contexto com o qual o buffer OpenCL é associado como um recurso, o segundo parâmetro é a memória alocada para o buffer, o terceiro parâmetro mostra o que pode ser feito com este objeto. O valor retornado é um identificador para o buffer OpenCL (se criado com sucesso) ou -1 (se a criação falhou devido a um erro).

No nosso caso, o buffer foi criado diretamente na memória da GPU, ou seja, no dispositivo OpenCL. Se ele foi criado na memória RAM sem usar esta função, deve ser transferido para a memória do dispositivo OpenCL (GPU), como ilustrado abaixo:

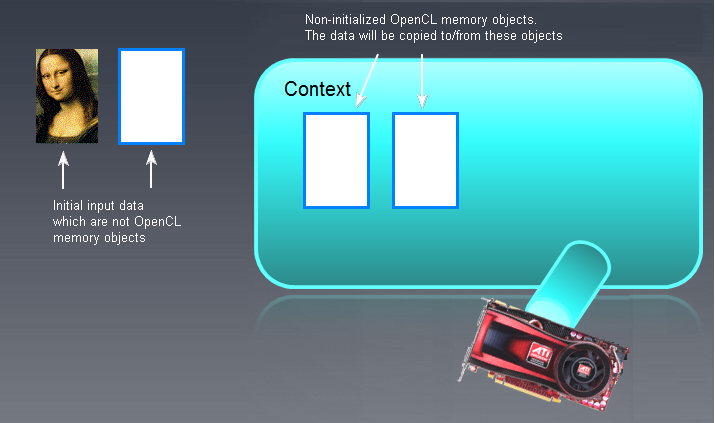
Fig. 6. Objetos da memória OpenCL

Buffers de entrada/saída (não necessariamente imagens - a Mona Lisa está aqui apenas para fins ilustrativos!) que não são objetos da memória OpenCL que são mostrados à esquerda. Objetos de memória OpenCL vazios, não inicializados são exibidos mais à direita, no campo contexto principal. Os dados iniciais "Mona Lisa" serão posteriormente movidos para o campo de contexto OpenCL e tudo o que é produzido pelo programa OpenCL terá que ser movido de volta para a esquerda, ou seja, para a RAM.

Os termos utilizados na OpenCL para copiar dados de/no dispositivo anfitrião/OpenCL são os seguintes:

• A cópia de dados de anfitrião para a memória do dispositivo é chamada escrever ( funçãoCLBufferWrite());
• A cópia dos dados da memória do dispositivo para a memória do anfitrião é chamada de leitura (funçãoCLBufferRead(), ver abaixo).

O comando de escrita (anfitrião -> dispositivo) inicializa um objeto de memória por dados e ao mesmo tempo coloca o objeto na memória do dispositivo.

Tenha em mente que a validade dos objetos de memória disponível no dispositivo não é especificado nas especificações OpenCL, uma vez que depende do fornecedor de hardware correspondente ao dispositivo. Portanto, tenha cuidado ao criar objetos de memória.

Depois que os objetos de memória foram inicializados e gravados para os dispositivos, a imagem parece ser algo como isto:

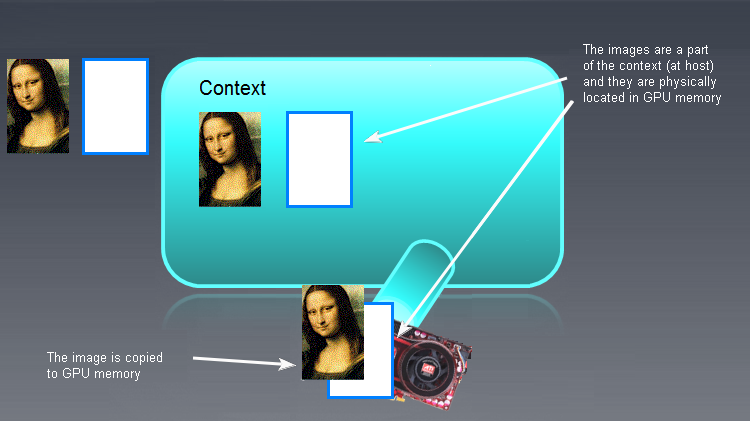
Fig. 7. Resultado da inicialização dos objetos de memória OpenCL

Podemos agora avançar para as funções que definem os parâmetros do núcleo.

3,5. Definição de parâmetros do núcleo

CLSetKernelArgMem( clKrn, 0, clMem );

A função CLSetKernelArgMem() define o buffer criado anteriormente como parâmetro zero do núcleo.

Se dermos agora uma olhada no mesmo parâmetro no código do núcleo, podemos ver que ele aparece da seguinte forma:

__kernel void pi( __global float *out )

No núcleo, é a matriz fora[ ] que tem o mesmo tipo como criado pela função API CLBufferCreate().

Há uma função semelhante para definir os parâmetros de não buffer:

bool  CLSetKernelArg( int   kernel,          // handle to the kernel of the OpenCL program
                       uint  arg_index,       // OpenCL function argument number
                      void  arg_value );     // function argument value

Se, por exemplo, nós decidirmos definir algumas duplas x0 como um segundo parâmetro do núcleo, ele primeiro precisa ser declarado e inicializado no programa MQL5:

double x0 = -2;

e a função, então, precisará ser chamada (também no código MQL5):

CLSetKernelArg( cl_krn, 1, x0 );

Após as manipulações acima, a imagem será a seguinte:

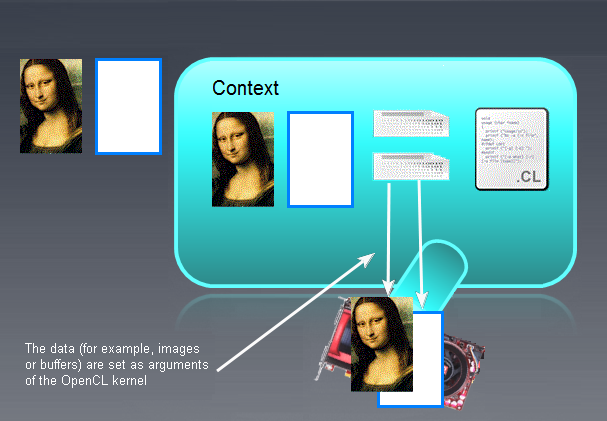
Fig. 8. Resultados dos parâmetros de configuração do núcleo

3.6. Execução do programa

bool ex = CLExecute( clKrn, 1, offs, works );

O autor não encontrou um análogo direto desta função na especificação OpenCL. A função executa o núcleo clKrn com os parâmetros dados. O último parâmetro "funcionar" define o número de tarefas a serem executadas por cada cálculo da tarefa de cálculo. A função demonstra o princípio SPMD (Dados múltiplos de programa único): uma chamada da função cria instâncias de núcleo com os seus próprios parâmetros no número igual ao valor do parâmetro funcionar; essas instâncias de núcleo são, convencionalmente falando, executadas simultaneamente, mas em diferentes núcleos de fluxo, em termos de AMD.

A generalidade da OpenCL consiste no fato de que a linguagem não é ligada à infraestrutura de hardware subjacente envolvida na execução de código: o codificador não tem que saber as especificações de hardware para executar corretamente um programa OpenCL. Isso ainda será executado. No entanto, é fortemente aconselhável conhecer estas especificações para melhorar a eficiência do código (por exemplo, velocidade).

Por exemplo, esse código é executado muito bem no hardware do autor sem uma placa de vídeo discreta. Dito isso, o autor tem uma ideia muito vaga da estrutura da própria CPU, onde toda a simulação está ocorrendo.

Assim, o programa OpenCL foi finalmente executado, e podemos agora fazer uso de seus resultados no programa anfitrião.

3.7. Leitura de dados de saída

Abaixo está um fragmento dos dados de leitura do programa anfitrião a partir do dispositivo:

float buf[  ]; 
ArrayResize( buf, _divisor );                                                   
uint read = CLBufferRead( clMem, buf );

Lembre-se que dados de leitura em OpenCL é copiar esses dados a partir do dispositivo para o anfitrião. Estas três linhas mostram como isso é feito. Bastará declarar o buffer buf[] do mesmo tipo que o buffer de leitura OpenCL no programa principal e chamar a função. O tipo de buffer criado no programa anfitrião (aqui - na linguagem MQL5) pode ser diferente do tipo de buffer no núcleo, mas seus tamanhos devem ter uma correspondência exata.

Os dados já foram copiados na memória do anfitrião e estão totalmente disponíveis para nós dentro do programa principal, por exemplo, no programa em MQL5.

Depois que todos os cálculos necessários no dispositivo OpenCL forem feitos, a memória deve ser liberada de todos os objetos.

3,8. Destruição de todos os objetos OpenCL

Isso é feito utilizando os seguintes comandos:

CLBufferFree( clMem );
CLKernelFree( clKrn );
CLProgramFree( clPrg );
CLContextFree( clCtx );

A principal peculiaridade dessas séries de funções é que os objetos devem ser destruídos na ordem inversa à ordem de sua criação.

Vamos agora dar uma olhada rápida no próprio código do núcleo.

3,9. Núcleo

Como pode ser visto todo o código do núcleo é uma única sequência longa que consiste em várias sequências.

O cabeçalho do núcleo é parecido com uma função padrão:

__kernel void pi( __global float *out )

Existem alguns requisitos para o cabeçalho do núcleo:

• O tipo de um valor retornado é sempre vazio;
• O especificador __núcleo não tem que incluir dois caracteres sublinhados, pode também ser núcleo;
• Se um argumento for uma matriz (buffer), ele é passado apenas por referência. Especificador de memória __global (ou global) significa que este buffer é armazenado na memória global do dispositivo.
• Argumentos de tipos de dados simples são transmitidos pelo valor.

O corpo do núcleo não é de forma alguma diferente do código padrão em C.

Importante: a sequência:

int i = get_global_id( 0 ); 

significa que i é um número de uma célula computacional dentro da GPU, que determina o resultado do cálculo dentro dessa célula. Este resultado é ainda escrito para a matriz de saída (no nosso caso, fora[]) após que seus valores sejam somados no programa anfitrião depois da leitura da matriz da memória da GPU para a memória da CPU.

Deve ser notado que pode haver mais do que uma função no código do programa da OpenCL. Por exemplo uma função em linha, simples, situada fora da função pi() pode ser chamada dentro da "principal" função do núcleo pi(). Este caso será considerado mais adiante.

Agora que nós nos familiarizar rapidamente com OpenCL API na implementação MetaQuotes, podemos continuar a experimentar. Neste artigo, o autor não pretende ir fundo em detalhes de hardware que permitam otimizar o tempo de execução para o seu máximo. A principal tarefa no momento é fornecer um ponto de partida para a programação em OpenCL como tal.

Em outras palavras, o código é um pouco ingênuo, pois não leva em conta as especificações de hardware. Ao mesmo tempo, é bastante geral para que pudesse ser executado em qualquer hardware - CPU, IGP pela AMD (GPU integrado na CPU) ou uma placa de vídeo discreta pela AMD/NVidia.

Antes de considerar novas otimizações ingênuas usando tipos de dados vetoriais, vamos primeiro ter que nos familiarizarmos com eles.

4. Tipos de dados vetoriais

Tipos de dados vetoriais são os tipos específicos à OpenCL, afastando-a do C99. Entre eles estão todos os tipos de (u)CharN, (u)shortN, (u)INTN, (u)longN, floatN, onde N = {2|3|4|8|16}.

Estes tipos são supostamente usados quando sabemos (ou supomos) que o compilador embutido gerenciarão adicionalmente cálculos paralelos. Precisamos observar aqui que isso nem sempre é o caso, mesmo se os códigos do núcleo diferem apenas no valor de N e são idênticos em todos os outros aspectos (o autor pode ver por si mesmo).

Abaixo está a lista de tipos de dados embutidos:

Tabela 1. Tipos de dados vetoriais embutidos no OpenCL

Estes tipos são suportados por qualquer dispositivo. Cada um destes tipos tem um tipo correspondente de API para a comunicação entre o núcleo e o programa anfitrião. Isso não está previsto na implementação MQL5 atual, mas não é um grande negócio.

Existem também outros tipos, mas eles devem ser explicitamente especificadas, a fim de serem utilizados, já que não são suportados por todos os dispositivos:

Tabela 2. Outros tipos de dados embutidos no OpenCL

Além disso, existem tipos de dados reservados que ainda estão a ser suportados na OpenCL. Há uma lista bastante longa deles na Especificação de linguagem.

Para declarar uma constante ou uma variável do tipo vetor, você deve seguir as regras simples e intuitivas.

Alguns exemplos são apresentados a seguir:

float4 f = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f);
uint4  u = ( uint4  ) ( 1 );             /// u is converted to a vector (1, 1, 1, 1).
float4 f = ( float4 ) ( ( float2 )( 1.0f, 2.0f ), ( float2 )( 3.0f, 4.0f ) );
float4 f = ( float4 ) ( 1.0f, ( float2 )( 2.0f, 3.0f ), 4.0f );
float4 f = ( float4 ) ( 1.0f, 2.0f );   /// error

Como pode ser visto, é suficiente para combinar com os tipos de dados à direita, simultaneamente, com a "largura" da variável declarada na esquerda (aqui, é igual a 4). A única exceção é a conversão de um escalar a um vetor com os componentes iguais ao escalar (linha 2).

Há um simples mecanismo de endereçar componentes do vetor para cada tipo de dados de vetor. Por um lado, eles são vetores (matrizes), enquanto, por outro, são estruturas. Assim, por exemplo, o primeiro componente de vetores tendo largura de 2 (por exemplo, float2 u) pode ser tratado como u.x e o segundo como u.y

Os três componentes de um vetor de tipo long3 u será: u.x, u.y, u.z.

Para um vetor de tipo float4 u, estes serão, portanto, .xyzw, ou seja, u.x, u.y, u.z, u.w.

float2 pos;
pos.x = 1.0f; // valid
pos.z = 1.0f; // invalid because pos.z does not exist

float3 pos;
pos.z = 1.0f; // valid
pos.w = 1.0f; // invalid because pos.w does not exist

Você pode selecionar vários componentes de uma só vez e até permutá-los (notação de grupo):

float4 c;
c.xyzw = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f );
c.z = 1.0f;
c.xy =  ( float2 ) ( 3.0f, 4.0f );
c.xyz = ( float3 ) ( 3.0f, 4.0f, 5.0f );

float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f );
float4 swiz= pos.wzyx;                          // swiz = ( 4.0f, 3.0f, 2.0f, 1.0f )
float4 dup = pos.xxyy;                          // dup = ( 1.0f, 1.0f, 2.0f, 2.0f )

A notação de grupo de componentes, por exemplo, a especificação de vários componentes, pode ocorrer no lado esquerdo da declaração de atribuição (ex. l-value):

float4 pos = ( float4 ) ( 1.0f, 2.0f, 3.0f, 4.0f );
pos.xw     = ( float2 ) ( 5.0f, 6.0f );            // pos = ( 5.0f, 2.0f, 3.0f, 6.0f )
pos.wx     = ( float2 ) ( 7.0f, 8.0f );            // pos = ( 8.0f, 2.0f, 3.0f, 7.0f )
pos.xyz    = ( float3 ) ( 3.0f, 5.0f, 9.0f );      // pos = ( 3.0f, 5.0f, 9.0f, 4.0f )
pos.xx     = ( float2 ) ( 3.0f, 4.0f );           // invalid as 'x' is used twice
pos.xy     = ( float4 ) (1.0f, 2.0f, 3.0f, 4.0f ); // mismatch between float2 and float4

float4 a, b, c, d;

float16 x;
x = ( float16 ) ( a, b, c, d );
x = ( float16 ) ( a.xxxx, b.xyz, c.xyz, d.xyz, a.yzw );
x = ( float16 ) ( a.xxxxxxx, b.xyz, c.xyz, d.xyz );  // invalid as the component a.xxxxxxx is not a valid vector type

Os componentes individuais podem ser acessados ​​usando outra notação - a letra s (ou S), que é inserida antes de um dígito hexadecimal ou vários dígitos em uma notação de grupo:

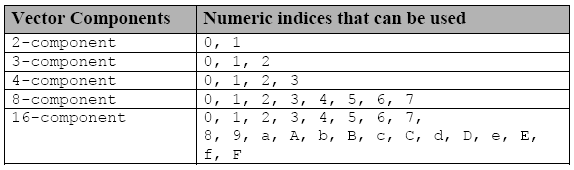
Tabela 3. índices que são usados ​​para acessar os componentes individuais de tipos de dados vetoriais

Se você declarar uma variável de vetor f

float8 f;

então f.s0 é o primeiro componente do vetor e f.s7 é o oitavo componente.

Da mesma forma, se declararmos um vetor 16-dimensional x,

float16 x;

então x.sa (ou x.sA) é o componente 11 do vetor x e x.sf (ou x.sF) refere-se ao componente 16 do vetor x.

índices numéricos (.s0123456789abcdef) e notações de letra (.xyzw) não podem ser misturados no mesmo identificador com a notação de grupo de componentes:

float4 f, a;
a = f.x12w;             // invalid as numeric indices are intermixed with the letter notations .xyzw
a.xyzw = f.s0123;       // valid

E, finalmente, há ainda uma outra forma de manipular componentes do tipo vetor usando .lo, .hi, .even, .odd.

Estes sufixos são usados como a seguir:

• .lo refere-se à metade inferior de um dado vetor;
• .hi refere-se à parte superior de um dado vetor;
• .even refere-se a todos os mesmo componentes de um vetor;
• .odd refere-se a todos os componentes ímpares de um vetor.

Por exemplo:

float4 vf;
float2 low  = vf.lo;           // vf.xy
float2 high = vf.hi;           // vf.zw
float2 even = vf.even;         // vf.xz
float2 odd  = vf.odd;          // vf.yw

Esta notação pode ser usada repetidamente, até que um escalar (tipo de dados não-vetorial) apareça.

float8 u = (float8) ( 1.0f, 2.0f, 3.0f, 4.0f, 5.0f, 6.0f, 7.0f, 8.0f );
float2 s = u.lo.lo;                              //  ( 1.0f, 2.0f )
float2 t = u.hi.lo;                              //  ( 5.0f, 6.0f )
float2 q = u.even.lo;                            //  ( 1.0f, 3.0f )
float  r = u.odd.lo.hi;                           //  4.0f

A situação é um pouco mais complicada em um tipo de vetor de 3 componentes: tecnicamente, é um tipo de vetor de 4 componentes com o valor do quarto componente indefinido.

float3 vf   = (float3) (1.0f, 2.0f, 3.0f);
float2 low  = vf.lo;                             // ( 1.0f, 2.0f );
float2 high = vf.hi;                             // ( 3.0f, undefined );

Regras breves de aritmética (+, -, *, /).

Todas as operações aritméticas especificadas são definidas por vetores da mesma dimensão e são feitas em componentes sábios.

float4  d   = (float4) ( 1.0f, 2.0f, 3.0f, 4.0f );
float4  w   = (float4) ( 5.0f, 8.0f, 10.0f, -1.0f );
float4  _sum = d + w;                             // ( 6.0f, 10.0f, 13.0f, 3.0f )
float4  _mul = d * w;                             // ( 5.0f, 16.0f, 30.0f, -4.0f )
float4  _div = w / d;                             // ( 5.0f,  4.0f, 3.333333f, -0.25f )

A única exceção é quando um dos operandos é um escalar e o outro é um vetor. Neste caso, o tipo escalar é convertido para o tipo de dados declarados no vetor, enquanto o próprio escalar é convertido a um vetor com a mesma dimensão que o operando vetor. Isto é seguido por uma operação aritmética. O mesmo é verdadeiro para os operadores relacionais (, =).

Tipos de dados nativos C99, derivados (por exemplo, estruturas, união, matrizes e outros) que podem ser feitos até dos tipos de dados embutidos listados na primeira tabela desta seção também são suportados na linguagem OpenCL.

E a última coisa: se você quiser usar a GPU para cálculos exatos, você inevitavelmente terá que usar o tipo de dados duplo e, consequentemente, doubleN.

Para isso, basta inserir a linha:

#pragma OPENCL EXTENSION cl_khr_fp64 : enable 

No começo do código do núcleo.

Esta informação já deveria ser suficiente para entender muito do que se segue. Se você tiver alguma dúvida, consulte a Especificação OpenCL 1.1.

5. A Implementação do núcleo com tipos de dados vetoriais

Para ser honesto, o autor não conseguiu escrever um código funcional com tipos de dados vetoriais fora de mão.

No início, o autor não prestou muita atenção na leitura da especificação da linguagem pensando que tudo iria dar certo por si só assim que um tipo de dados de vetor, por exemplo, double8 fosse declarado dentro do núcleo. Além disso, a tentativa do autor de declarar apenas uma matriz de saída como uma matriz de vetores double8 também falhou.

Demorou um tempo para perceber que isto é absolutamente não suficiente para vetorizar efetivamente o núcleo e alcançar aceleração real. O problema não será resolvido pela saída de resultados na matriz de vetores, pois os dados não requerem apenas rapidez para entrada e saída, mas também serem calculados rapidamente. A realização deste fato acelerou o processo de aumento da sua eficiência, possibilitando finalmente desenvolver um código muito mais rápido.

Mas há mais do que isso. Enquanto o código do núcleo definido acima pode ser depurado quase cegamente, à procura de erros tornou-se bastante difícil, devido ao uso de dados vetoriais. Que informação construtiva podemos obter a partir desta mensagem padrão:

ERR_OPENCL_INVALID_HANDLE - invalid handle to the OpenCL program 

ou dessa

ERR_OPENCL_KERNEL_CREATE - internal error while creating an OpenCL object

?

Por isso, o autor teve que recorrer ao SDK. Neste caso, dada a configuração de hardware disponível ao autor, resultou-se de compilador offline SDK OpenCL Intel (32 bit) fornecido pela Intel OpenCL SDK (para CPUs/GPUs além da Intel, SDK também deve conter compiladores off-line relevantes). é conveniente, pois permite a depuração do código do núcleo, sem ligação ao API anfitrião.

Basta inserir o código do núcleo na janela do compilador, embora não na forma usada no código MQL5 mas sem caracteres de cotas externas e "\r\n" (caracteres de tecla similares à Enter) e pressionar o botão Construir com um ícone de roda veloz nele.

Ao fazê-lo, a janela de log de Construir exibirá informações sobre o processo de construção e seu progresso:

Fig. 9. Compilação de programa no compilador offline SDK OpenCL Intel

A fim de obter o código do núcleo, sem caracteres de cota, seria útil escrever um programa simples na linguagem do anfitrião (MQL5) que iria gerar o código do núcleo em um arquivo - WriteCLProgram(). Isso agora está incluso no código de programa anfitrião.

Mensagens do compilador nem sempre são muito claras, mas oferecem muito mais informações do que o MQL5 atualmente pode. Os erros podem ser corrigidos imediatamente na janela do compilador e uma vez que você tenha certeza que não há mais deles, as correções podem ser transferidas para o código do núcleo em MetaEditor.

E a última coisa. A ideia inicial do autor era desenvolver um código vetorizado capaz de trabalhar com vetores double4, double8 e double16 por meio da configuração de um parâmetro global único "número de canais". Isso acabou por ser realizado, após alguns dias tendo problemas com operador de token- pasting ## que, por alguma razão, estava se recusando a trabalhar dentro do código do núcleo.

Durante este tempo, o autor desenvolveu com sucesso um código de trabalho do script com três códigos núcleo, cada um dos quais é adequado para a sua dimensão - 4, 8 ou 16. Este código intermediário não será fornecido no artigo, mas valeu à pena mencionar, no caso você pode desejar escrever um código do núcleo sem ter muito problema. O código de implementação de script (OCL_pi_double_several_simple_kernels.mq5) está anexado abaixo da extremidade do artigo.

E aqui está o código do núcleo vetorizado:

"/// enable extensions with doubles                                                          \r\n"
"#pragma OPENCL EXTENSION cl_khr_fp64 : enable                                               \r\n"
"#define _ITERATIONS "        + i2s( _intrnCnt ) + "                                     \r\n"
"#define _STEP "             + d2s( _step, 12 )  + "                                     \r\n"     
"#define _CH "               + i2s( _ch )       + "                                     \r\n"
"#define _DOUBLETYPE double"   + i2s( _ch )       + "                                     \r\n"   
"                                                                                            \r\n"
"/// extensions for 4-, 8- and 16- scalar products                                           \r\n"     
"#define dot4( a, b )         dot( a, b )                                                    \r\n"
"                                                                                            \r\n"
"inline double dot8( double8 a, double8 b )                                                  \r\n"
"{                                                                                           \r\n"     
"     return dot4( a.lo, b.lo ) + dot4( a.hi, b.hi );                                        \r\n"
"}                                                                                           \r\n"
"                                                                                            \r\n"      
"inline double dot16( double16 a, double16 b )                                               \r\n"     
"{                                                                                           \r\n"     
"     double16 c  = a * b;                                                                   \r\n" 
"     double4 _1  = ( double4 ) ( 1., 1., 1., 1. );                                          \r\n" 
"     return dot4( c.lo.lo + c.lo.hi + c.hi.lo  + c.hi.hi, _1 );                             \r\n" 
"}                                                                                           \r\n"     
"                                                                                            \r\n"
"__kernel void pi( __global double *out )                                                    \r\n"
"{                                                                                           \r\n"
"  int i = get_global_id( 0 );                                                               \r\n"
"                                                                                            \r\n"
"  /// define vector constants                                                               \r\n"     
"  double16 v16  = ( double16 ) ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 );    \r\n"
"  double8  v8   = v16.lo;                                                                   \r\n"
"  double4  v4   = v16.lo.lo;                                                                \r\n"
"  double2  v2   = v16.lo.lo.lo;                                                             \r\n"          
"                                                                                            \r\n"    
"  /// all vector-related with the calculated type                                           \r\n"
"  _DOUBLETYPE in;                                                                           \r\n"    
"  _DOUBLETYPE xVect;                                                                        \r\n"
"  _DOUBLETYPE sumVect          = ( _DOUBLETYPE ) ( 0.0 );                                   \r\n"
"  _DOUBLETYPE doubleOneVect    = ( _DOUBLETYPE ) ( 1.0 );                                   \r\n"
"  _DOUBLETYPE doubleCHVect     = ( _DOUBLETYPE ) ( _CH + 0. );                              \r\n"
"  _DOUBLETYPE doubleSTEPVect   = ( _DOUBLETYPE ) ( _STEP );                                 \r\n"
"                                                                                            \r\n"    
"  for( long j = 0; j < _ITERATIONS; j ++ )                                                  \r\n"
"  {                                                                                         \r\n"
"     in =  v" + i2s( _ch ) + " + doubleCHVect * ( i * _ITERATIONS + j );                  \r\n"           
"     xVect = ( in + 0.5 ) * doubleSTEPVect;                                                 \r\n"
"     sumVect += 4.0 / ( xVect * xVect + 1. );                                               \r\n"
"  }                                                                                         \r\n"
"  out[ i ] = dot" + i2s( _ch ) + "(  sumVect, doubleOneVect );                            \r\n"
"}                                                                                           \r\n";   

O programa de anfitrião externo não mudou muito, exceto pela nova constante global _ch que define o número de "canais" de vetorização e a constante global _intrnCnt que se tornou _ch vezes menor. é por isso que o autor decidiu não mostrar o código do programa de anfitrião aqui. Ele pode ser encontrado no script do arquivo anexado abaixo do final do artigo (OCL_pi_double_parallel_straight.mq5).

Como pode ser visto, além da função "principal" de pi do núcleo(), temos agora duas funções em linha que determinam produto escalar dos vetores dotN(a, b ) e uma substituição macro. Estas funções estão envolvidas devido ao fato de que a função dot() em OpenCL é definida no que diz respeito a vetores, cuja dimensão não excede a 4.

A dot4() macro que redefine a função dot() está lá apenas para a conveniência de chamar a função dotN() com o nome calculado:

"  out[ i ] = dot" + i2s( _ch ) + "(  sumVect, doubleOneVect );                              \r\n"

Se tivéssemos usado a função dot() na sua forma habitual, sem índice 4, não seriamos capaz de chamá-la tão facilmente como é mostrado aqui, quando _ch = 4 (número de canais de vetorização sendo igual a 4).

Esta linha ilustra uma outra característica útil do formulário específico do núcleo sob o fato de que o núcleo como tal é tratado no âmbito do programa anfitrião como uma sequência: podemos usar identificadores calculados no núcleo, não só para funções, mas também para tipos de dados!

O código do programa anfitrião completo com este núcleo está anexado abaixo (OCL_pi_double_parallel_straight.mq5).

Executando o script com a "largura" de vetor sendo 16 (_ch = 16 ), temos o seguinte:

2012.05.15 00:15:47     OCL_pi_double2_parallel_straight (EURUSD,H1)    ==================================================
2012.05.15 00:15:47     OCL_pi_double2_parallel_straight (EURUSD,H1)    CPUtime / GPUtime = 4.130
2012.05.15 00:15:47     OCL_pi_double2_parallel_straight (EURUSD,H1)    SMARTER: The time to calculate PI was 8.830 seconds
2012.05.15 00:15:47     OCL_pi_double2_parallel_straight (EURUSD,H1)    SMARTER: The value of PI is 3.141592653590
2012.05.15 00:15:38     OCL_pi_double2_parallel_straight (EURUSD,H1)    DULL: The time to calculate PI was 8.002 seconds
2012.05.15 00:15:38     OCL_pi_double2_parallel_straight (EURUSD,H1)    DULL: The value of PI is 3.141592653590
2012.05.15 00:15:30     OCL_pi_double2_parallel_straight (EURUSD,H1)    OPENCL: gone = 2.138 sec.
2012.05.15 00:15:30     OCL_pi_double2_parallel_straight (EURUSD,H1)    OPENCL: pi = 3.141592653590
2012.05.15 00:15:30     OCL_pi_double2_parallel_straight (EURUSD,H1)    read = 20000 elements
2012.05.15 00:15:28     OCL_pi_double2_parallel_straight (EURUSD,H1)    CLProgramCreate: unknown error.
2012.05.15 00:15:28     OCL_pi_double2_parallel_straight (EURUSD,H1)    DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125
2012.05.15 00:15:28     OCL_pi_double2_parallel_straight (EURUSD,H1)    ==================================================

Você pode ver que até mesmo a otimização que usa tipos de dados vetoriais não tornou o núcleo mais rápido.

Mas se você executar o mesmo código em GPU, o ganho de velocidade será muito mais considerável.

De acordo com as informações fornecidas pelo MetaDriver (placa de vídeo - HIS Radeon HD 6930, CPU - AMD Phenom II x6 1100T), o mesmo código produz os seguintes resultados:

2012.05.14 11:36:07     OCL_pi_double2_parallel_straight (AUDNZD,M5)    ==================================================
2012.05.14 11:36:07     OCL_pi_double2_parallel_straight (AUDNZD,M5)    CPUtime / GPUtime = 84.983
2012.05.14 11:36:07     OCL_pi_double2_parallel_straight (AUDNZD,M5)    SMARTER: The time to calculate PI was 14.617 seconds
2012.05.14 11:36:07     OCL_pi_double2_parallel_straight (AUDNZD,M5)    SMARTER: The value of PI is 3.141592653590
2012.05.14 11:35:52     OCL_pi_double2_parallel_straight (AUDNZD,M5)    DULL: The time to calculate PI was 14.040 seconds
2012.05.14 11:35:52     OCL_pi_double2_parallel_straight (AUDNZD,M5)    DULL: The value of PI is 3.141592653590
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    OPENCL: gone = 0.172 sec.
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    OPENCL: pi = 3.141592653590
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    read = 20000 elements
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    CLProgramCreate: unknown error.
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    DOUBLE2: _step = 0.000000001000; _intrnCnt = 3125
2012.05.14 11:35:38     OCL_pi_double2_parallel_straight (AUDNZD,M5)    ==================================================

6. O toque final

Aqui está outro núcleo (que pode ser encontrado no arquivo abaixo em anexo OCL_pi_double_several_simple_kernels.mq5, do qual, entretanto, não está demonstrado aqui).

O script é uma implementação da ideia que o autor tinha quando abandonou temporariamente uma tentativa de escrever um "único" núcleo e pensei em escrever quatro núcleos simples para diferentes dimensões de vetor (4, 8, 16, 32), :

"#pragma OPENCL EXTENSION cl_khr_fp64 : enable                                               \r\n"
"#define _ITERATIONS " + i2s( _itInKern ) + "                                             \r\n"
"#define _STEP "      + d2s( _step, 12 ) + "                                              \r\n"
"                                                                                            \r\n"
"typedef struct                                                                              \r\n"
"{                                                                                           \r\n"
"  double16    lo;                                                                           \r\n"
"  double16    hi;                                                                           \r\n"
"} double32;                                                                                 \r\n"
"                                                                                            \r\n"
"inline double32 convert2double32( double a )                                                \r\n"        
"{                                                                                           \r\n"
"  double32 b;                                                                               \r\n"    
"    b.lo = ( double16 )( a );                                                               \r\n"
"    b.hi = ( double16 )( a );                                                               \r\n"
"    return b;                                                                               \r\n"
"}                                                                                           \r\n"
"                                                                                            \r\n"
"inline double dot32( double32 a, double32 b )                                               \r\n"     
"{                                                                                           \r\n"     
"     double32 c;                                                                            \r\n" 
"     c.lo = a.lo * b.lo;                                                                    \r\n" 
"     c.hi = a.hi * b.hi;                                                                    \r\n" 
"     double4 _1  = ( double4 ) ( 1., 1., 1., 1. );                                          \r\n" 
"     return dot( c.lo.lo.lo + c.lo.lo.hi + c.lo.hi.lo  + c.lo.hi.hi +                       \r\n" 
"                 c.hi.lo.lo + c.hi.lo.hi + c.hi.hi.lo  + c.hi.hi.hi, _1 );                  \r\n" 
"}                                                                                           \r\n"     
"                                                                                            \r\n"
"__kernel void pi( __global double *out )                                                    \r\n"
"{                                                                                           \r\n"
"  int i = get_global_id( 0 );                                                               \r\n"
"                                                                                            \r\n"
"  /// define vector constants                                                               \r\n"
"  double32 _v32;                                                                            \r\n"
"  _v32.lo = ( double16 ) (  0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,                          \r\n"
"                            8.,  9., 10., 11., 12., 13., 14., 15. );                        \r\n"
"  _v32.hi = ( double16 ) ( 16., 17., 18., 19., 20., 21., 22., 23.,                          \r\n"
"                           24., 25., 26., 27., 28., 29., 30., 31. );                        \r\n"
"                                                                                            \r\n"
"  /// all vector-related with undefined type                                                \r\n"
"  double32 xVect;                                                                           \r\n"
"  double32 sumVect           = convert2double32( 0.0 );                                     \r\n"
"  double32 double1Vect       = convert2double32( 1.0 );                                     \r\n"
"                                                                                            \r\n"
"  double32 in;                                                                              \r\n"
" /// work only with 16-vectors in the loop!                                                 \r\n"
"  for( long j = 0; j < _ITERATIONS; j ++ )                                                  \r\n"
"  {                                                                                         \r\n"
"     in.lo = _v32.lo + 32. * ( i * _ITERATIONS + j );                                       \r\n"
"     in.hi = _v32.hi + 32. * ( i * _ITERATIONS + j );                                       \r\n"
"     xVect.lo = ( in.lo  + 0.5 ) * _STEP;                                                   \r\n"
"     xVect.hi = ( in.hi  + 0.5 ) * _STEP;                                                   \r\n"
"     sumVect.lo += 4. / ( xVect.lo * xVect.lo + 1. );                                       \r\n"
"     sumVect.hi += 4. / ( xVect.hi * xVect.hi + 1. );                                       \r\n"                             
"  }                                                                                         \r\n"
"  out[ i ] = dot32( sumVect, double1Vect );                                                 \r\n"
"}                                                                                           \r\n";    

Este mesmo núcleo implementa dimensão de vetor 32. O novo tipo de vetor e algumas funções necessárias alinhadas são definidos fora da função principal do núcleo. Além disso (e isso é importante!), todos os cálculos dentro do loop principal são feitos intencionalmente apenas com tipos de dados de vetor padrão; tipos não-padrão são tratados fora do loop. Isto permite acelerar substancialmente o tempo de execução do código.

No nosso cálculo, este núcleo não parece ser mais lento do que quando usado para vetores com uma largura de 16, mas não é muito mais rápido também.

De acordo com as informações fornecidas pelo MetaDriver, o script com este núcleo (_ch =32) produz os seguintes resultados:

2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: gone = 0.156 sec.
2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) OPENCL: pi = 3.141592653590
2012.05.14 12:05:33 OCL_pi_double32-01 (AUDNZD,M5) read = 10000 elements
2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) CLProgramCreate: unknown error or no error.
2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) GetLastError returned .. 0
2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) DOUBLE2: _step = 0.000000001000; _itInKern = 3125; vectorization channels - 32
2012.05.14 12:05:32 OCL_pi_double32-01 (AUDNZD,M5) =================================================================

Resumo e conclusões

O autor compreende perfeitamente que a tarefa escolhida para a demonstração dos recursos OpenCL não é bem típico desta linguagem.

Teria sido muito mais fácil pegar um livro didático e copiar um exemplo padrão de multiplicação de grandes matrizes para postá-lo aqui. Esse exemplo seria, obviamente, impressionante. No entanto, existem muitos usuários do fórum mql5.com que estão envolvidos em cálculos financeiros que requerem a multiplicação de grandes matrizes? é bastante duvidoso. O autor desejava escolher seu próprio exemplo e superar todas as dificuldades encontradas no caminho por conta própria, enquanto ao mesmo tempo tentava compartilhar sua experiência com os outros. Claro, vocês são os únicos a julgar, caros usuários do fórum.

O ganho de eficiência em simulação OpenCL (na CPU "exposta") acabou por ser muito pequeno em comparação com centenas e até milhares obtidos usando scripts do MetaDriver. Mas em uma GPU adequada, será pelo menos uma ordem de magnitude maior do que a simulação, mesmo se ignorarmos um pouco mais de tempo de execução na CPU com CPU AMD. A OpenCL ainda vale à pena aprender, mesmo que o ganho em velocidade de cálculo seja assim tão grande!

O próximo artigo do autor é esperado endereçar questões relacionadas às peculiaridades de exibir modelos abstratos OpenCL em hardware real. O conhecimento destas coisas, por vezes, permite acelerar ainda mais os cálculos de forma considerável.

O autor gostaria de expressar seus agradecimentos especiais ao MetaDriver por muito valiosos de programação e otimização de desempenho e dicas para a equipe de suporte para a própria possibilidade de usar Intel OpenCL SDK.

Conteúdo dos arquivos anexados:

• pi.mq5 - um script em MQL5 puro com duas formas de calcular o valor de "pi";
• OCl_pi_float.mq5 - a primeira implementação do script com o núcleo OpenCL envolvendo cálculos reais com o tipo flutuante;
• OCL_pi_double.mq5 - o mesmo, envolvendo apenas cálculos reais com o tipo de duplo;
• OCL_pi_double_several_simple_kernels.mq5 - um script com vários núcleos específicos para várias "larguras" de vetores ( 4, 8 , 16, 32);
• OCL_pi_double_parallel_straight.mq5 - um script com um único núcleo para alguma "largura" de vetor ( 4, 8, 16).