誤った考え、パート２統計は、偽りの科学か、暴落するなくてはならない歴史です。

はじめに

この記事の見出しの最初の部分は、SergNF によって, 2008年4月17日14:04に 投稿されたものです。https://www.mql5.com/ru/forum/108164. 最も厳格な数学でさえも実際的なアプリケーションなしで魅力的な公式を用いて行うことにした”研究者”によって、偽りの科学に変わってしまいます。

その引用元の著者の懐疑主義は、明白です。この理由はかなり明らかです；統計的なメソッドに客観的な現実、つまり金融上の出来事に適用とする試みは、不十分なデータや、確率分布やプロセスの非定常性に直面し、虚しく失敗してしまっているのです。どの既存のマーケットモデルも現実に十分に適切なものであると認識はされていません。そして、たとえもし統計的な規則性を発見しようとしたとしても、それらの使用の結果はその規則性の抽出性に用いた努力にそぐわないです。

この記事では、そのような金融上の出来事ではなく、主観的な意見を記述し、トレーダーがどのようにこれらを防ごうとしたか、トレーダーシステムについて記述します。トレーディング結果の統計的な規則性の抽出は、むしろ大変面白い作業です。時折、このプロセスのそのモデルに関する結論が導かれ、これらがトレーディングシステムに適用されます。

数学に親しくない方に対してこの複雑さについて謝りたいと思いますが、それが確実のこの記事のコンテンツの避けられない内容となります。私の過去の記事の最後に述べられている約束は、まだ満たされていません。なので、調査を始めましょう。

この記事では、幾何学的なMMで損失を出すものを利益を出すものに変える資産管理のルール、"lot=0.1"を持つ利益を出す戦略を示す人工的な例を構築し、負けトレードは現実にないものを使用しました：P L P L P L P L P L P L ... 最初の疑問は「なぜそのような”規則的な”ものを分析するのか？」というものです。

負けトレード：簡単な概要

この理由はシンプルです：それは My First "Grail"という記事で明記されています。:

同時に、負け注文は利益を生むものの中でどのように分散されているかを予想できません。この分散は、ランダムな性質を持つものです。.

A.利益と損失の理想的な分散は、全体のトレーディング歴史の中で単一の分散になるでしょう。

P P P L P P P L P P P L P P P L P P P L P P P L P P P L ...

しかしながら、そのような分散は必ずしも理想的であるという保証はありません。ただし、長い連続的な損失は遅かれ早かれ高い確率で起こりうるものです。

B. 以下は、実際のトレーディング中に利益のある 非単一的な分散の起こりうる状況の例です。

P P P P P P P P P P P P P P P L L L L P P P L P P P L ...

５つの連続する損失は、上記で示されています。それ以上は続きません。この場合、勝ちと負け注文の比率は、3 : 1で維持されていることに注意してください。

従って、勝ちと負けトレードの”規則的な”互い違いの発生は、最小ドローダウン（そして、最大リカバリー要因）の観点から理想的です。そして、もし以前の記事にように、この理想的なケースにてさえ（利益と損失を出すトレードの互い違い）そのシステムは幾何学的なMMにて利益と損失を出す取引の数学的な予想値損失を出すものに変わります。

注：勝ち負けトレードの比率は、14:9に等しくなります。最小のドローダウンを持つためにどのようにトレードを分散すべきでしょうか？これは、たとえもしMMルール"lot=0.1"であることを考慮し、その連続が最適のものであることを示そうとしたとしても、簡単な問題ではありません。その損失取引が全体の中で”均一に”分散される必要があることは明らかで、以下のようになります：

P L P L P P L P P L P P L P L P L P P L P P L...

これは、23のトレード、そのうちの14トレードが利益を出すものからなる”初歩的なひと続きのトレード”です。その後、これが繰り返されます。例えば以下のものよりも両方のMMタイプにおいてより低いドローダウンを持つことは明らかです；

P P P P P P P P P P P P P P L L L L L L L L L…

それは、幾何学的なMMの場合特に明らかです（その理由はこちらの記事で説明されています). しかし、そのような一連の負け取引（"losing cluster"）は無制限なものです。これを理解するには、確率理論の基礎を再度確認しましょう。しかし、まずはいくつかの用語を定義しましょう。

専門用語

この記事はBenoullliシリーズや様々な確率分布の視覚化するヒストグラムと関連する用語を含みます。それらを混ぜ合わせないよう、用語を定義しましょう。..:

1. 全トレードは、単純にここではシリーズ.と呼ばれます。この用語は、実際のテスト結果の処理中に取得されたシリーズと、一致するBernoulliシリーズの生成中に総合的に取得されたシリーズ両方をさします。もしそのシリーズの長さが示される必要があれば、以下のように示します: 3457-series (3457トレードを持つシリーズ).
2. 一つのシリーズの中で同じサインを持つ連続するトレード（勝ち、負けトレードか、"成功"、”失敗”など）はここでは クラスターと呼ばれます。もしその長さが示さるとすれば、例えば、7-cluster (7つの長さのクラスター)と呼ばれます。
3. たくさんのシリーズ（ここでは総合的なシリーズをさします）は、シリーズの配列と呼ばれます。その数はまた以下のように記されます: 5049-seriesの65000-array (65000 Bernoulliシリーズ、それぞれ5049トレードの長さ).
4. ヒストグラムを構築する際に時折いくつかの特定のシリーズだけではなく、シリーズの全配列に属するクラスターを考慮する必要があります。そのヒストグラム名は、分散が視覚化されるそのパラメーターに一致します。"各3174の長さの5000シリーズの配列での４の長さを持つクラスタの分散を示すヒストグラム"を記述する代わりに以下を記載します: "4-clusters in 5000-array of 3174-series».

Bernoulliスキーム：基礎

一連のイベントが考慮されるたくさんの実際的な作業が以下のスキームに縮小されます：

• 各イベントが二つの結果のみを持ちます - "成功"と"失敗"です ("勝ち" と"負け"). ”成功”の確率はpで、”失敗”の確率は q = 1-pです。
• そのイベント結果の確率は、先んずる過去のイベントには依存しません。

これは、Bernoulli スキーム (またBernoulli trials)と呼ばれます。上記の定義の２番目の基準が確かなものであれば、色付けされたものはBernoulliスキームと考えられます。

その作成者は、これが多くのトレーディングに当てはまると考えています。こちらがいくつかの間接的な証拠です:

• MM最適化にてシステムZアカウントを適用しようとした人の意見に沿ったシステムZアカウントに関する情報は、特定の トレードの確率を計算しようとする際、 – たとえ勝ちの確率が90%以上だったとしても - 役に立ちません;
• 様々なマーチンゲールのスキームの効果はまた0に等しく、むしろマイナスのもので、許容しがたいドローダウンに繋がります。

そのため、トレーディングシステムの大半において、一連のトレードがBernoulliスキームの基準に一致すると受け入れることが論理的でしょう。そのような仮説は深い結果に繋がります。

Bernoulliスキームにおけるnシリーズのうちのk回の勝ち確率における古典的な公式 (損失を出すトレードも参照できます) は以下です (勝ちの確率はpに等しいです):

この公式は、そのシリーズのいくつかのパラメーターや、勝ちの回数を示しますが、これらの勝ちがいかに等しく分散されるかについては示さず、起こりうる確率の長さについては何も知ることはありません。Bernoulliシリーズの起こりうる損失のクラスターの長さの検索は、ずっと難しい作業です：そのソリューションは、Feller [1]によって記述されています。以下は、テストシリーズの長さの数学的推測やp（勝ち確率）とq （負け確率） 、r (勝ちクラスターの長さ)としてセットされたパラメーターを持つ分散のための公式になります - Bernoulliスキームにマッチするテストを持つと仮定します。rの長さの勝ちシリーズにおいてリターン時間の予想と分散は、以下に等しくなります。

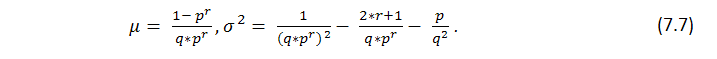
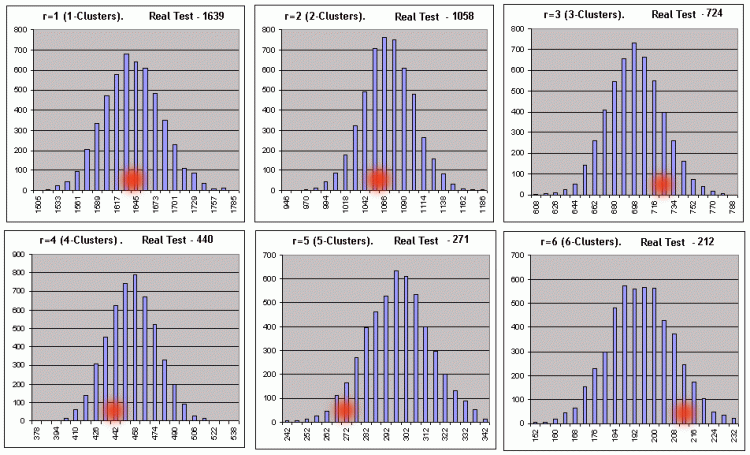
大きいnとともに、nテストにて取得されたrシリーズの数は、おおよそ標準の分散を持ち、非均衡の確率が固定されています。

傾向

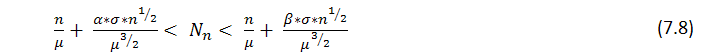
そのテーブルは、典型的なリターン時間の数のための数学的な予想を記載しています。

シリーズの長さ,r	p = 0.6	p=0.5 (coin)	p=1/6 (dice)
5	30.7 秒	1 分	2.6 時間
10	6.9 分	34.1 分.	28.0 ヶ月
15	1.5時間	18.2時間	18 098年
20	19 時間	25.3日	140.7分hunn年

表1. 勝ちトレードのシリーズにおける平均的なリターン時間（１秒につき１テストが実行されます）

結論1: もし(7.7)を損失に適用し、最初の公式からrを表す場合、テストの長さに依存する最長の損失クラスタは、長さにおいて無制限です。というのも、対数の法則で拡大するためです。そのようなトレーディング戦略の特徴のためにスカルピング戦略の結果は特に厳しいです。

結論2:制限、熟慮ある減速、テストシリーズの長さに依存するその損失クラスタの超過は、そのトレーディングシステムはがBernoulliスキームを満たさない事実を指摘します。例えば、もし

n, p, qその実際の損失の最大のクラスタは５の長さであり、"Bernoulli scheme"仮説に沿って計算された同じ長さは15であり、これはトレード結果が依存する イベントのようではないので、 非"Bernoulli scheme"であると想定できます。.

結論3: もしその"Bernoulli scheme" 仮説が正しければ、そのような戦略はp, q = 1-pに等しく一致する確率を持つ非対称のコインを賭すするスキームと異なりません。

それでは、この観点からいくつかの”おもしろい”戦略を分析してみましょう。

スカルピング: "Lucky", パート１

全て、もしくは全てのスカルピングシステムは、たくさんの共通の特徴を所有しています。

• SL is much more than TP (typical values – 20 and 2; the point values correspond to the 4-digit quotes of EURUSD);
• pは、 q以上の確率です (利益を出すトレードの確率は、80%以上で、時折99%です);
• トレード数は、かなり多く、一年間で1万に達します。

３番目のポイント、これが取引センターで可能か否かにとどまりません。このトピックはフォーラムだけでなく、 SK.という上記で言及された記事にて議論されています。 取引所は、スリッページや際価格設定によってトレーダーを妨害せず、MODE_STOPLEVELであることなどを想定します。

スカルピングトレーディングシステム（TS）を作成したトレーダーは、負け取引の頻度において時折失敗しています。この錯覚のルーツは、クロージング価格のWienerの特徴と、Brownian移動のEinstein公式の本当の特徴関する考えに遡ります："もしSL=20, TP=2を設定すれば、ストップロス発生の確率は (20/2)^2=100で、TPヒットの確率よりも100倍低くなります；従って、そのようなTSは利益が生まれるものになります。この考えの妄想性は、このプロセスがWienerプロセスではなく、一致する確率は100倍以下で異なるという事実にあります!

この場合、スカルピングトレーディング戦略がこのプロセスのランダムな特異性を用い、またいくつかの取引所で受けいれられる濾過作用の特異性を用いようとするため、"Bernoulli scheme" 仮説はかなり利益を生むものです。

それでは、 "Lucky" (https://www.mql5.com/ja/code/7464)という名前で知られるトレーディング戦略のパラメーターを取得しましょう。元の形では（同じセクションではLucky_new.mq4)このEAは、利益を生むポイントの数学的な推測に伴う数百回のトレードのオープンを受け入れる取引所はほとんどないため、おもちゃでしかありません。しかし、わずかにコードを修正し、より厳格な条件をTPレベルにセットし、かなり満足のいくバランス/資産カーブを得ることができます。修正されたEAのコード（同時にオープンされたトレードの数、この場合１に等しいものに対する制限を考慮します：以下の説明をご覧ください）は、この記事に貼り付けられました。

このEAの主な利点は、莫大な数のトレードを実行し、統計学のための十分な素材を提供します - これは後ほど証明されます。その仮説を保証、もしくは論破する証拠を発見することのみに焦点が当てられています：”そのトレード結果は、Bernoulliスキームに一致します”マーケットの動きの非ランダムな特性に関して議論したい人のために、価格の動きは常にランダムではないと述べておきます。マーケットをコインのトスに集約する気はなく、トレード結果の統計にのみ興味があります。さらに、外部パラメーターのいくつかのセットは、述べられた仮説をチェックするために意図的に"負け"として選択されます。

こちらがその最初のテストの結果になります；

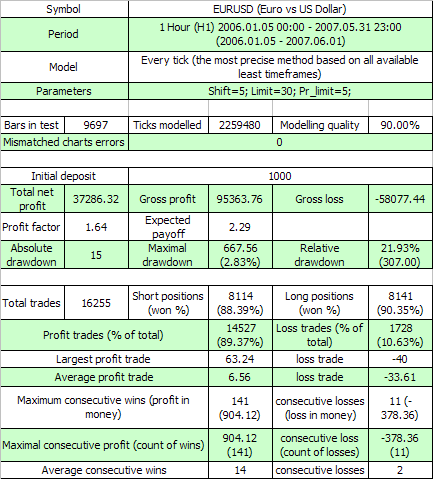
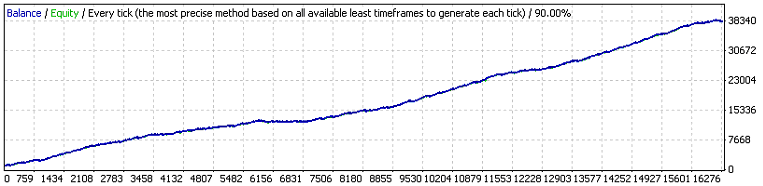
最初の外部変数は、元のコードの中で同じ意味を持ち、３つ目は利益の値で、注文が利食いイベントを開始させるために超える必要のある値です。(7.7)によると、損失11クラスターを満たすために必要なその最小のテストシリーズの数学的な予想を推定しましょう (p=0.8937, q=0.1063, r_loss=11):

N_loss = 1 / (p * q^r_loss) – 1 / p ~ 57 140 275 804

こちらが. 利益を出す141-clusterを満たすためのテストシリーズの長さの計算の類似した推定です。

N_profit = 1 / (q * p^r_profit) – 1 / q ~ 71 685 085

... ご存知の通り、シリーズの実際の長さは16255トレードに等しく、100億や1000万ではありません。そのような実際のシリーズの長さの超過は、このTSのためにBernoulliスキーム仮説は直接動作しないことの印です。おそらく、こちらが考慮していなかった要因の影響です。

Bernoulli スキーム；興味深い結果

以下のような要因があります：エキスパートアドバイザー(EA)は、一度に１トレード以上もオープンすることができます：200つのトレードの中で、連続で6トレードをオープンしました。その”掛け算の要因”は、おそらく予想されていたものと比較して増大したクラスターの長さに影響を与えています：もしそのマーケットが量的に同質であれば、そのEAは各ティックにてたくさんのトレードをオープンし始めます。しかしながら、その特徴により、またストップロスと比較して小さいサイズの利食いとフラットな市場により、それらの多くは利益を出してクローズされます。一方で、もし強い動きが始まれば、そのEAは一方向性のトレードをたくさんマーケットの動きとは別の芳香でオープンします - そして、最終的にそれらの多くは損失としてクローズされます。

シンプルな計算を行いましょう。. . 以前のパラグラフから全テストシリーズの長さの計算のために両方の公式を取得します。r_loss_real, r_profit_realは、最大の勝ち・負けクラスターの実際の長さです。取得された N_xxxx 値はむしろ大きく、２番目の用語(1/p と 1/q) を切り落とすことは、これらの等式を項目別に分けた場合、何もエラーを起こしません。:

N_loss / N_profit = q * p ^ r_profit_real / ( p * q ^ r_loss_real ) =

p ^ ( r_profit_real – 1) / q ^ (r_loss_real – 1)

対数を見つけ、単純化しましょう:

ln( N_loss / N_profit ) = ( r_profit_real – 1 ) * ln( p ) - ( r_loss_real – 1 ) * ln( q )

もしそのテストがBernoulliスキームによって支配され、最長のクラスターの長さや、pや q両方がそこまで小さくなければ、 N_lossと N_profit値は、おおよそ等しくなるはずです。そのため、興味深い相関関係を得ることができます:

( r_profit_real – 1 ) / ( r_loss_real – 1 ) * ln( p ) / ln( q ) ~ 1 (*)

別の方法で書き直した場合:

p ^ ( r_profit_real – 1 ) ~ q ^ ( r_loss_real – 1 )

相関関係の意味(*) は明らかになります: Bernoulli TS ( pやq確率が低くなく、長いテストシリーズ) にて、二つのクラスター（”勝ち”と”負け”）は等しくなります。実際、この原則は同様に Bernoulliではないその他のTSに適用できますが、その相関関係の形式はBernoulliスキームにおいて特定のものです。この相関関係は"bernoullity"のためのTSテストということができます。.

スカルピング: "Lucky", パート2

掛け算の要因を除外しましょう：同時にオープンされる注文の数に対する制限を１に設定してください。注文の数が同じ期間に数回減少する一方で、テストの範囲を拡大し、2004年1月1日から2008年4月4日に設定します。以下は、結果といくつかの計算の表です（BSは、"Bernoulli scheme"の省略した形です）；最初の”+”は勝ちクラスターのBernoulliスキームへの良い一致を示し、負けクラスターの二つ目の"-"は、論破された仮説を示し、"The system satisfies the BS", "0"はその正確性に対する疑問を意味します）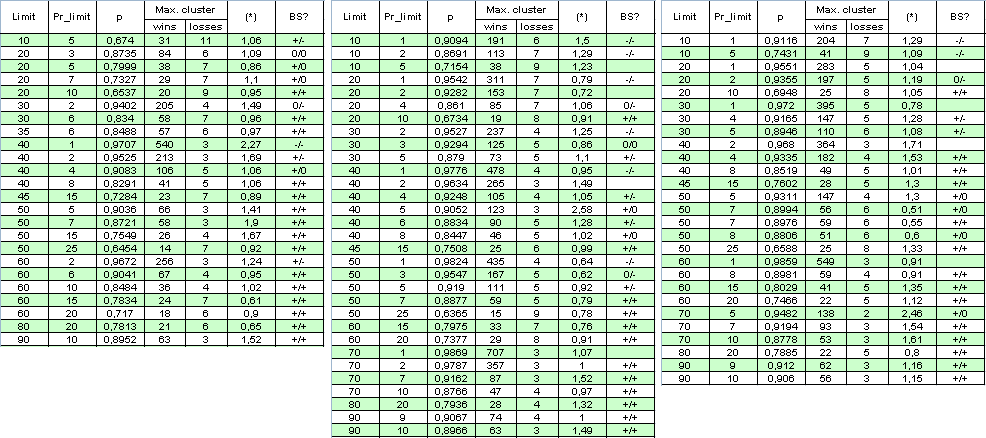

その著者は、すべてを理解する上でのテーブルの大きいサイズに対して謝りの意を示しています。そのパラメーターは、１に近づいた際にそのシステムがBernoulliスキームへ参照されなくなるため、そのシステムの"bernoullity"を決定するには十分ではないようです。

P.S. 乗数が１から逸脱しているにもかかわらず、その値は依然１に近いです。例えば、もしLimit = 40 and Pr_limit = 1である場合、以下を持ちます；

( * ) = ( 478 - 1 ) / ( 4 - 1 ) * ln( 0.9776 ) / ln( 0.0224 ) ~

477 / 3 * ( -0.02265 ) / ( - 3.7987 ) ~ 0.95

この事実は別の推測を許容します；たとえそのシステムのBerunoullity仮説が保留になった場合でも、そのトレードの依存性は勝ち、負けトレードにおいてほぼ同じです。

Berunoulliスキームに対するトレーディングシステムの一致の基準

スクリプトのオペレーションの詳細

テスト結果をどのように確実に二つのBernoulliスキームと”非Bernoulliスキーム”のグループに分けることができるでしょうか？いくつかのメソッドを試すことができますが、私の意見では、最もシンプルなものは以下です：もしテスト中に発見されたものと一致するパラメータを持つBernoulliシリーズをたくさん生成すれば、クラスターの長さの確率分布関数（p.d.f）はおおよそ変更されずに残ります。この事実は明らかに勝ち確率の不変性とトレードの独立性に関する想定に由来します。

不幸にも、長さに基づく勝ち/負けクラスターの分布の理論的な関数を私は知りません。上記にて、勝ち確率と長さに依存するテストシリーズの勝ちクラスタ数. の計算の推定を可能にする公式をいくつか記載しています（7.8 をご覧ください）このために、Feller ([1]) はクラスターの所属する再発のイベントの理論に従う特別なメソッドを提供しています。一見、このメソッドは”勝ちシリーズ”の用語のトレーダーの理解にそぐわないようですが、このメソッドは理論自体を単純化し、"r-cluster registration"イベントの特定が([1], page 302):

将来のBernoulliテストの勝ちシリーズに依存しなくなります。 rの長さの勝ちシリーズ"という用語は様々なメソッドによって定義されます。これらの連続的なk値が長さの0か1か2のシリーズどれを保持するとみなされるかどうかの質問は、利便性に関する質問であり、様々な目的のために様々な示し方を受け入れます。しかし、もし再発のイベントの理論を適用しようとすれば、rの長さのシリーズの意味は、シリーズの後にそのプロセスが毎回再度開始されるように定義されなければなりません。以下の定義を受け入れるということになります: WとLのnの連続は、r の長さのシリーズを多く所持し、 r とW からなるサブシーケンスを保持します。Bernoulliテストのシーケンスにおいて、n-番目のテストの結果として、新しいシリーズが生まれた場合、nの数を持つテストにこのシリーズが現れると言えます。

従って、WWW|WL|WWW|WWWのシーケンスにて、長さ3の3つのシリーズがあり、3番目、8番目、11番目のテストに現れます；同じシーケンスは長さ2の5つのシリーズを持ちます；2番目、4番目、7番目、11番目のテストに現れます。この定義は固定された長さのシリーズは再発のイベントになるため、その理論を単純化します。2*rが二つのシリーズとしてみなされるという条件にて、少なくともr 連続の勝ちで作成されたシーケンスの数に等しくなります。

一方で、(WWWWLWWWWWW) における勝ちクラスターの数（Fellerによると"Win series"）は以下の通りです；まず、勝ち4クラスター、一回の負けのあと、勝ち６クラスター。Fellerによるとあるようですが、長さ1、2、3、と５の完全なクラスターはありません。[1] からのこの抽出は、その問題の難しさを示すためだけにこちらに記載されています。従って、たくさんのBernoulliシリーズを生成し、それらの中にトレーダによるそれらの理解に一致するシリーズを発見します。（損失にて終了する15回連続の勝ちは1クラスターの15の記載や、3クラスターの5つの記載ではありませんが、15クラスターの１の記載です。）"bernoullity"のシリーズのチェックのために、1000Bernoulliシリーズは十分です。

この考えによると、まずスクリプトは一つの配列に実際のトレードの結果のシーケンスをアップロードし、MS Excelにクラスターの長さのヒストグラムを描画するデータを取得するように記述されました。このスクリプトは、MS Excelにヒストグラムを作成するためのデータを準備し、Bernoulliシリーズを生成する関数を保持します。スクリプトコードをこの記事に挿入しません；代わりにそのコードのコメントを提示します。そのスクリプトは以下に添付されています。そのテスターのレポートファイルは、まずexperts\files\Sequences\というディレクトリに配置され、その名前は外部スクリプトパラメーターに移動されなければなりません。

始めに、テスターレポートファイルに基づき、 readIntoArray()関数の助けにより、トトレードのバイナリの結果 (1 or -1)が グローバル配列res[]に挿入されます。そのオペレーションを理解するために、小さい配列を用いてその説明を図示しましょう。この関数の処理は最終的に以下の配列 _res[]に至ります (トレード数、つまり、シリーズの長さは50です):

1,1,-1,-1,1,1,1,1,1,-1,1,1,1,1,1,1,1,-1,1,1,-1,-1,-1,-1,1,1,1,-1,1,1,1,1,-1,1,-1,1,-1,-1,-1,1, 1,-1,1,1,1,1,1,1,1,1

その後、関数 formClustersArray( int results[], int& sequences[], int& h, int nr ) は、クラスターの長さを計算し、損益を定義するグローバルパラメータ whatに依存し、 シリーズの長さをsequences[] (実際はグローバル配列 seq[])に記述します。この配列のクラスターの数を数えてみましょう:

2,-2,5,-1,7,-1,2,-4,3,-1,4,-1,1,-1,1,-3,2,-1,8

マイナスの値は、負けクラスターを言及します。その数の絶対値すべての合計は、シリーズの長さ、50に等しいことは明らかです。損失、_what = -1に興味があると想定します。それでは、その配列 _seq[]は、マイナスの値のみ保存しますが、"プラス"のサインとともに保存します；

2,1,1,4,1,1,1,3,1

その後、 配列seq[]が配列histogramReal[]を構築することを目的に処理されます。1-、2-、3-クラスターの量を計算し、その配列に記述する必要があります。結果として、配列 _histogramReal[] は、以下の値を保持します:

6,1,1,1

これは、我々のシリーズは６つの負けの１クラスターと1負けの２クラスター、1損失の３つのクラスターと、１の負けの４つのクラスターを保持することを意味します。さらに、後者の配列はアウトプットファイルに記述されます。Bernoulliスキームによると、テストの統合的なシリーズの類似するヒストグラムに記述する必要があるため、このファイルは閉じられません。

”統合物”を形成する際に、重要な関数はBernoulliスキームによるシングルテストのジェネレーターです。このシンプルなコードにもかかわらず、それはよく動作します；セグメント[0, 32767] の結果の規則的な配分の歪みに影響する"エッジ効果"は観測されていまえん。

// generates a single Bernoulli test (+-1 with different probabilities)
int genBernTest( double probab )
{
   int rnd = MathRand();
   if( rnd < probab * 32767 ) return(  _what );
   else                       return( -_what );
}

MathSrand( GetTickCount() )の一回の呼び出しの後、この関数はテスト期間のテストの回数 (testsTotal)分使用されます。そして、生成されたBernoulliシリーズを持った際に、その結果はクラスターを数え、"ヒストグラム"を構築する関数によって処理されます。これらのアクションは、一つのテストに一致する一つのヒストグラムの生成（関数genSynthHistogr( int& h, int nr ) )に繋がります。. そして、最終的に最後の関数がループにて呼ばれ、結果内でBernoulliシリーズの配列が生成され、それらのためのヒストグラムが形成され、アウトプットファイルに記述されます。

このファイルをMS Excelでこのファイルを開き、必要なダイアグラムを作成し、Bernoulliスキームにそのシステムの一致性に関する結論を導くことができます。そのファイルにおける数は以下の意味を持ちます（5クラスターなどのデータはここでは記載しません）:

テストシリーズなし	最大クラスターの長さ	１クラスターの数	２クラスターの数	３クラスターの数	４クラスターの数
1	9	1639	1058	724	440
0	11	1649	1044	688	478
1	8	1681	1093	675	458
2	13	1628	1067	701	461
3	7	1616	1039	726	474
4	12	1601	1054	699	465

そのファイルの最初の行は、実際のテストの結果を示しており、その下の行は、0から始まる番号を持つ総合テストシリーズに一致します。

そして、最後の段階 - Bernoulliスキームへの一致に関する実際のテスト結果の推定：総合Bernoulliシリーズから一致するカラムが必要な長さのクラスタのヒストグラムを構築するために選択されます。例えば、勝ち1クラスター数量分布を構築するため、３番目のカラム（1649, 1681, 1628, 1616, 1601…）を取得する必要があります：そのような数字の合計は、統合Bernoulliシリーズの量に等しいです。勝ち3クラスターにおいて、4番目のカラム (1044, 1093, 1067, 1039, 1054…）を取得します。

そのようなヒストグラムは、Bulashev [7]に記述されるそのメソッドに沿って構築され、実際のテストの数の統合シリーズの平均の推定に等しいかに関するZero仮説をチェックします。Zero仮説における重要性のレベルは、0.05に等しいです（おおよそ二つの標準偏差を指します）

最初の結果

パラメーター3, 20, 10のLuckyテスト結果のスクリプトを始めてみましょう。スクリプトパラメーター: _what = 1 (profitable clusters), globalSeriesQty = 5000. 大きいテーブルのパラメーターは１に等しく、つまり、そのスクリプトのオペレーションの結果はBernoulliスキームへの一致を示します。クラスターの長さ1-6におけるZero仮説を直接のチェックに一致するファイルの記録のみを示します（わずかにより簡単に認識するためテーブルに組み込みました。）:

// The first line of the file is results of the real test made in the tester. 最初の二つは、シリーズの数と最大クラスターの長さです。

1,20,1639,1058,724,440,271,212,137,91,62,30,26,22,5,7,1,4,1,0,1,1,

…

// End of file (partially):

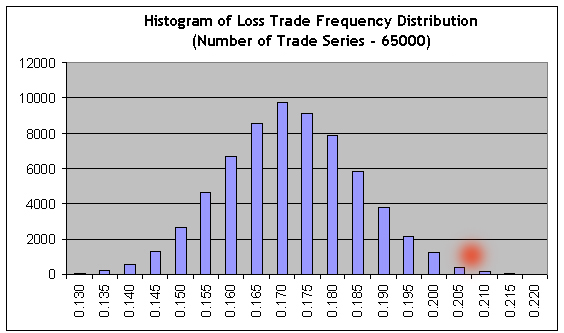
6つの二線の図表は、それぞれ上方の線がヒストグラムインターバルの左の値に一致し、Bernoulliシリーズの数は下方のものと一致します。それにおいては、特定の長さのクラスターの数がこれらのインターバルの中にあります。以下に同じものが視覚的に示されています（利益を出すBernoulliシリーズのr-clusterは、5000です）

赤色のスポットの横座標は、実際のテストにて取得されたクラスターの数に一致します。負けクラスタにおける同じスクリプト(_what = -1)は、同じパラメーターにて良い全体図を示します：[7]の推奨に沿って計算されたインターバルの数がデータのスプレッドを超え始めるとすぐに、インターバルの設定された数のヒストグラムの構築は不可能になります。しかし、そのスクリプトのレポートの０は、必要なすべてのパラメーターがヒストグラムなしに計算できるため、何も怖いものはありません。3-、7-clusterのみにおけるパラメーターにて、その０仮説は否認されました。Bernoulliシステムにテストされたシステムを参照するための主な基準として、あいまいな種類の基準が選択されました。負けクラスターにおけるスクリプトのオペレーション結果の例に関する意思決定の原則を考えてみましょう:

平均の評価との実際のテストの違い = -0.37 SD (standard deviation)

平均の評価との実際のテストの違い = 0.95 SD

平均の評価との実際のテストの違い = -2.04 SD

平均の評価との実際のテストの違い = -0.45 SD

平均の評価との実際のテストの違い = 0.36 SD

平均の評価との実際のテストの違い = 1.13 SD

平均の評価との実際のテストの違い = 3.27 SD

平均の評価との実際のテストの違い = 0.11 SD

平均の評価との実際のテストの違い = 0.46 SD

平均の評価との実際のテストの違い = -0.47 SD

こちらが主な基準です：

• もしその平均が1.5を超えない場合（ここでは0.96）
• 数字の平均は1.2以上ではありません。
• 外層の数（2SD以上の違いに一致します) は、それら合計の量の20%を超えません。

そのシステムは"surely bernoullian"とみなされます。もしその一致した重要な数字が2、1.5と30%であれば、そのシステムは間違いなく"bernoullian"です。もしその数字がこれらの境界を越えれば、その仮説は否認されます。その逸脱は主要な一つのサインによって決められるものであるべきではないので、２番目のポイントが合理的なものであると考えます。

Bernoulliスキームへの一致性の統計的な基準は私にはわからないので、そのような基準を考える必要があります。そのような即席の決定基準の結果は、スクリプトオペレーションレポートファイルに提示されています。興味もった読者の方はより良い決定基準を作成しても良いと思います。

このケースにおいて、 3, 20, 10のパラメーターを持つLucky システムは、Bernoulliスキーム、つまり、そのなくてはならないスキームと同調します。

それでは最悪のケースの一つを見、1000に等しいBernoulliシリーズの数にて同じ計算してみましょう： Luckyのパラメーターは5, 10, 1です。勝ち1クラスターを考えてみましょう:

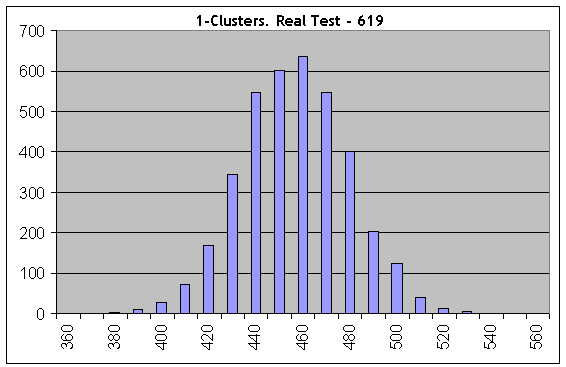
最初のヒストグラムでさえ、すべては完全に異なっています：実際のテスト結果（619 1-cluster）はテストシリーズの同じ長さや同じ勝ち確率の合成物に適合しません。従って、そのトレードは独立したものではありません。

大きい図表のその他のパラメーターでの類似したテストはBernoulliスキームは例外というよりもルールであるという結論を下しました。加えて、トレードのいくつかのグループにおいて（例えば”勝ちトレード”）そのBernoulliスキームは満たされ、その他のグループにおいては満たされません。これはこの記事にて後ほど紹介する予定の役に立つ情報を取得するためのこのモデルの使用を妨害しません。そして、最後：決定基準は不十分な量の統計データのために負けクラスターにあまり依存できませんが、全体の様相を得るためのみにそのスクリプトをそれらに適用しました。

"Universum" System: Bernoulli Scheme Again!

"Universum"という全く異なるシステムを見てみましょう；そのソースはhttps://www.mql5.com/ja/code/7999にて投稿されています。その開発者はそのシステムは形成されたバーにて動作し、そのためすべてのティックのテストは必要ではありません。そのシステムが2000.01.01 - 2008.04.04の期間におけるトレードの統計を得る開始残高が$10Mにセットされました。最初にオープンされたロットは0.1です。実際に三つの変化されたパラメーターはp, tp, slです。掛け算はないので、これは簡単です: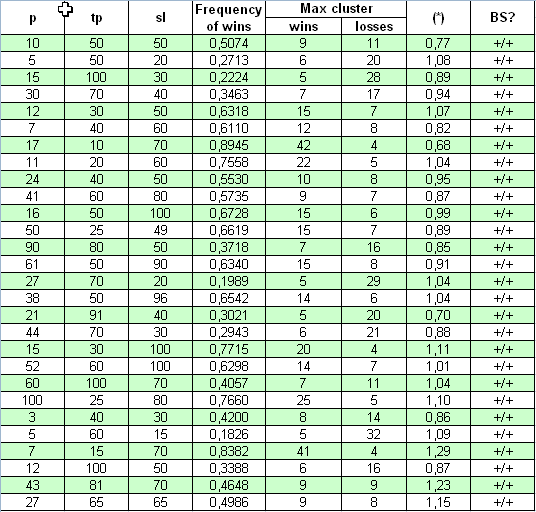

１の(*) パラメーターの準拠は以前のケースよりも良いものです：(*) 値はわずかに異なります。決定基準によるチェックは、かなり広いパラメーターの範囲にて、このTSはBernoulliスキームに従います。

予備的なまとめ

Ralph Vince [4] は、Bernoulliスキームへの一致をチェックするテストシリーズの異なる手続きを提供しています。これはZ-scoreの計算で、特別な相関関係におけるトレード結果のテストです。その手続きは上記で記したものよりも重要な結果を提示しているとは思えません。提示された決定基準は実証を伴う必要があります。さらに、以前述べた通り、最大クラスターの短い長さでのこのチェックの信頼性は高くはありません Lucky_ これらは普通負けシリーズテストです). しかし、私の意見は、この決定基準はより広範囲な計算を必要としますが、Bernoulliスキームとの適応性という観点でテストシリーズの特定の特徴をカバーする方が良いと思います。この疑問はさらなる研究が必要で、まだわかっていません。

ただ、期待は証明されました：外部パラメーターの異なるセットにて、そのトレードシリーズはBernoulliスキームに一致し、Bernoulliスキームからの逸脱は常に価格設定フィルタリングプロセスの特徴であり、Pr_limitの小さい値を持つシステムに固有の規則の統合的な利用に由来します。これは特にLucky_checkの結果を記している大きい図表にて明らかです。

Vinceは、もし系列相関のチェックやZ-scoreのテストがトレード間の依存を明らかにすれば、そのシステムはやや最適なもので、その依存性はTSに含まれ、テスト結果にて依存性を低下させ、TS 最適化を向上させる必要があります。従って、二つのシステムのテスト結果を置いて、その"Universum"システムはLuckyシステムよりもより最適なものであると認める必要があります。しかし、これは Universumにて使用されているMMを正当化しません。

そのシステムのBernoullityをどのように使用すべきでしょうか？

1. 今何がわかっているでしょうか？

少なくとも1と-1で示されているトレード結果のシーケンスは、Bernoulliのものであると前もって知り、このプロセスの適切なモデルを取得します。Brownian運動の修正ですので、このプロセスに関して十分知っています。P. Samuelson は、金融理論と実践([6]にて幾何学的なBrownian運動を紹介しました:

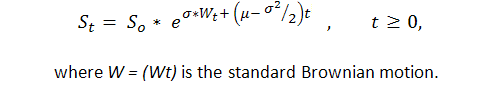
標準のBrownian運動の理論的な研究結果を 残高カーブに適用します。しかし、Brownian運動理論は、かなり複雑で、数学の教育を受けた少数の人にのみ理解できるものです。

２番目のアプローチは、高度な理論的計算を避け、Bernoulliシリーズの直線的プログラム生成を行い、これらを "testing MM 0.1 lot"における残高カーブに変換することです。ここでは勝ち・負けトレードの平均的な値と勝ち頻度pのみを知る必要があります。そのような数百ものシリーズ(例えば、Bernoulliシリーズの1000の配列) は、Bernoulliスキームと同調する戦略がどのようなことをできるのかについてよい理解を与えてくれます。

そのような総合的なテストがめんどくさいPardoテスト（[5]）の良い代替物になることを理解することが重要です：もしZero仮説の正当性を確認できれば、[5]で記載されている一歩進んだ分析によって提示されたものとは異なるシステムに関する十分な情報を提供します。もちろん、その残高カーブは実際のテストによって取得されたカーブとはかなり異なります。

***********

そのようなテストは数分間で一つのコンピューターで実行されるので、一般的にそのようなアプローチの実装を妨害するものは何もありません；結果として、分析されうる広範囲な情報を取得できます。不幸にも、この記事はすべての結果を記載していません。Lucky_で、パラメーターが4, 70, 10であり、その図表と同じテスト期間におけるチャートがいくつかあります。Bernoulliスキームの生成は、上記のスクリプトで実行されるものよりもずっと簡単です；MS Excelの手段で十分です

0.1でのテスト:

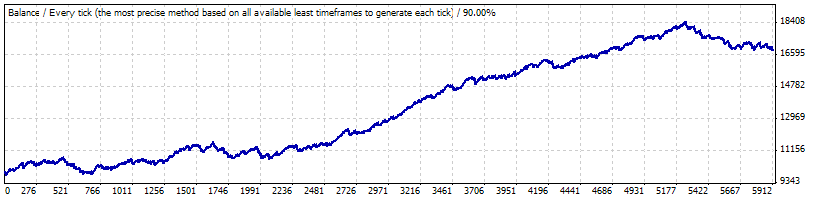
そのレポートからの以下のパラメーターは重要です；Bernoulliシリーズやバランス変化カーブにシリーズを変換する際にそれらを設定します：

勝ちトレードの頻度(p)	0.8765
勝ちトレード平均.	11.71
負けトレード平均	-73.73
トレード合計	5904

バランスカーブは、Bernoulliシリーズに基づいて変化します：

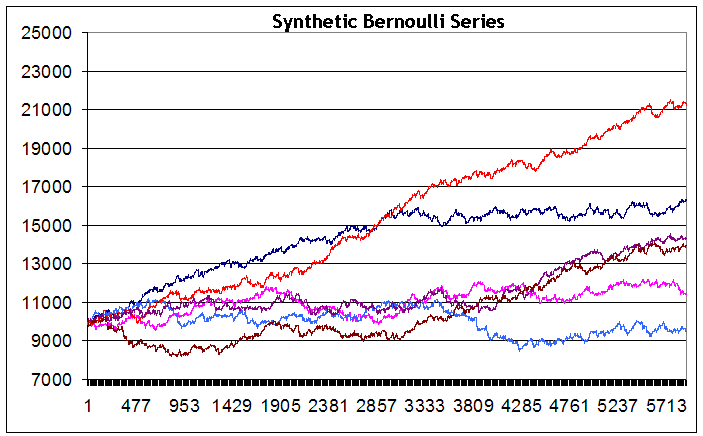
シリーズは同一の入力データで生成されたにもかかわらず、そのテスト期間終了時の残高の結果はシリーズごとで小さい損失から多大な利益など違いが生まれます。確実に減少する残高のシリーズを生成することができなかったと認めなければなりません。おそらく、たくさんのシリーズにて、これは実現可能でしょう。しかし、そのようなケースはこの戦略の典型的なものでありません。さらに、どのシリーズにおいても2500ポイント以上のドローダウンはありません。

Bernoulliスキームに同調する戦略のパラメーターの評価に関連する結果を考察しましょう。

2. レポート値を超える最大負けクラスターの評価（"black swan"）

システムのBernoullityの証拠を受け取り、現実的に実際のトレーディングと同様の量にて待機する負けクラスターの最大の長さを評価できます。ここで、Bernoulliシリーズを生成でき、本当の"black swan"([2,3])の確率を推定でき、それはテスト期間で起こっていないので、テスト結果のみに基づいて確率を推定できないイベントです。それは、必要な統計を集めることのできる確率理論モデルです。

4,50,7のパラメーターを持つすべて同じのLucky_ システムのトレーディング結果を用います:

そのレポートによると、最大負けクラスターの長さは5に等しいです。たくさんのBernoulliシリーズを-1に等しいパラメーター _whatでセットし、テスターレポートにスクリプトを適用します。. 最長の線を見つけましょう（最初の番号は、Bernoulliシリーズの#で、２番目は最大クラスターの長さ、そして、それぞれの長さのクラスタの数です。）:

26001 9 1030 136 13 4 0 0 0 0 1

最大負けクラスターの長さは、5よりも長くなります。（ここでは９です）！たぶんこれはかなり珍しいイベントかもしれません。確かに、とても珍しいものです；65,000シリーズ外で満たされ、その実際のテストでの外見は、消滅しかかっていると考えられ、”エルゴード性仮説”を考慮します。しかし、この頻度の推定はとても信頼できないものです；従って、それには頼ることはできません；このシリーズは例えば20Bernoulliシリーズにおいて発生します。結果として、もし信頼性の推定基準について知らなければ、この推定がかなり高い確率を持っていると考察していたでしょう。

”エルゴード性仮説”は以下の通りです: ”統合的なテストスペース”でのイベントの確率は（いそのイベントの適切なモデルに基づきます）実際のトレーディング、タイムスペースにおける同じイベントの確率に等しいです - 実際のテストでのトレード数がモデルテストにおいてと等しいと仮定しています。それはもちろん実際のテストでのトレード結果のシーケンスはBernoulli スキームのように定常的です。たくさんのトレードにて、非定常性の唯一の源はいわゆる普通の法則に沿って分散された"win drift"であるため、これはあまり正しくはありません。

以下は、Bernoulliシリーズの65000配列の負けクラスターの数の図表です。

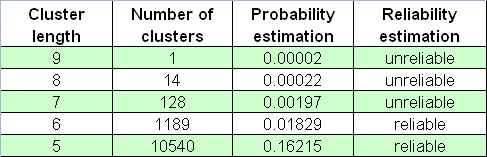
期待しない時にちょうど来る"black swans"を忘れてはいけません。

上記の計算とは対照的に、"black swan"の反対の特徴、つまり、増大する長さの勝ちクラスタにおける推定を使用できます。実際のテストは最大勝ちクラスタの長さが59に等しいことを示します。65,000モデルシリーズの類似したモデリングを持ち、スクリプトレポートの最長の線を再度見つけます。

44118 153 115 117 111 87 70 71 52 51 50 40 36 42 42 34 20 32 15 20 20 13 10 11 12 8 5 7 3 5 4 2 2 6 7 0 2 1 2 1 1 5 0 0 1 0 0 0 0 0 0 1 0 0 2 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1

これはモデルシリーズ #44118で、153トレードに等しい最大勝ちクラスタの長さで、実際のテストでの最大クラスタよりもおおよそ2.6倍の長さです。しかし、統計的に重要なクラスタ頻度の推定は約80やそれより低い値から取得され、80は59よりもかなり大きい値です。勝ちクラスタにおける1/2の注文の分移転（配分関数が確率密度配分関数下の領域で二等分にその配分が分かれる0.5の値を取得する際のクラスタの長さ）は、おおよそ62で、50よりも少し低い値です。Bernoulliシリーズ配列での最大クラスタの長さの配分におけるヒストグラムは、参照ためこちらに含まれています。

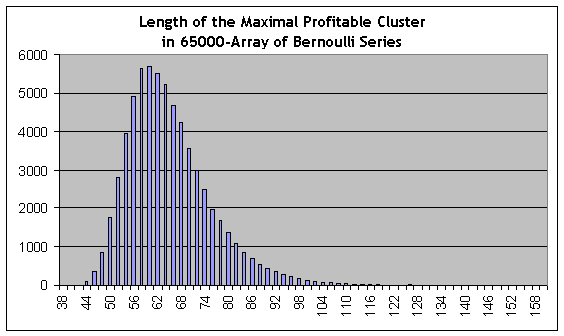
もちろん、その"black swan"という用語は計算不可能な確率のイベントであるため、あまり注意深く使用されていません。しかし経験的なデータのみで判断し、理論モデルを何も使用せず、統計的に負け6クラスタか勝ち80クラスタの確率、つまり、レポートにないイベントに関する信頼できる結論を導くことはできません。

3. "Failure drift": 経験的頻度からの失敗確率の好まざる逸脱
機器へのアプローチ、試み１

Bernoullliスキームによるそのシリーズでの大量のテストにて、失敗頻度f はわずかに失敗確率q とは異なり、"正しい"正規分布に従います；Laplace理論は依然効果的です。にもかかわらず、fは変化し、かなり小さい数学的なトレードの期待値の戦略で利ざやを稼ぐために、そのような変化はかなり重要で、全体のテストインターバルにおいてそのシステムを負けシステムに変化させてしまいます。そのような変化の確率の統計的予想においてそのツールは、もしBernoulliスキームが動作しているという証拠があれば、十分です。

不幸にも、そのEA Lucky_ は、固定の時間での１トレードでの可能性において限られていますが、多すぎる統計情報を提示します。

これは間違っていますが、ロシア語の原文が公開されて理解できるようになりました：ただ、本物らしくするためそのままに残しています。- Mathemat.

真面目な戦略開発者のためにこれはルールというよりも例外です。というのも数百、数十のトレードを含むテスト結果に基づく曲がりくねった結論を導く必要があるためです。統計量の増大はGauss配分の幅の低下につながり、その中央値からの逸脱の確率を低下させます。

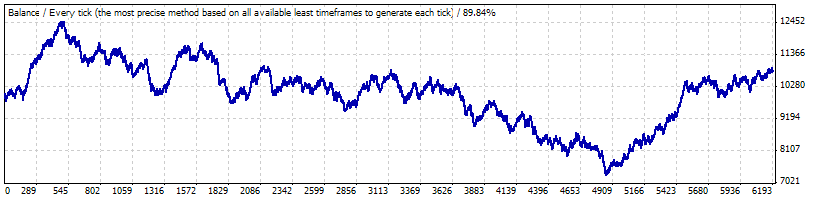
例として、ロット0.1の4, 80, 20の全く好ましくないパラメータにおける Lucky_ を考えてみましょう。全時間のインターバル ("interval A")にて – 2004年1月1日から2008年4月4日 (EURUSD H1)までの期間においてテストを行いました。こちらは、そのレポートにより提示されたバランスチャートです:

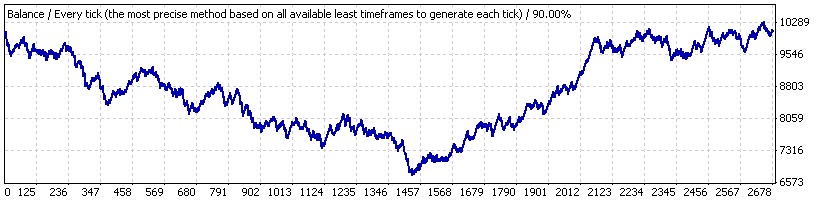
これにはあまり驚きません。スクリプトのトレードシーケンスをチェックしたのち（1000モデルBernoulliシリーズ)、全トレードシリーズは、Bernoulliスキームに勝ち・負けクラスタ両方において一致していると考えられます。

平均トレードのパラメーターに注目してみましょう。

平均勝ちトレード

21.71

負けトレード

-83.32

それでは、2005.10.21から2007.06.07までの短期間 ("interval B")においてEAをテストし、その戦略は安定的な成長を見せると想定します。このチャートは以下です：

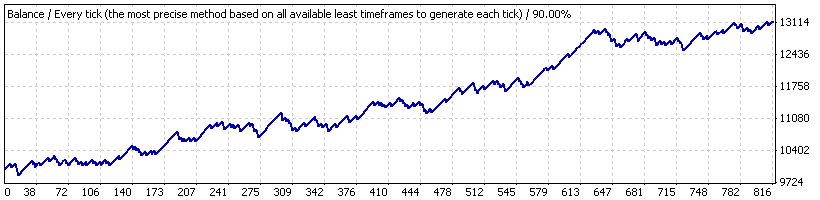
こちらが平均トレードの結果です。

平均勝ちトレード

21.69

負けトレード

-82.94

平均して、そのトレードはわずかに変化しました; 従って、それらはだいたい不変であると考えられ、また、テスト期間において戦略の利益性には関連しません。. 実際、そのトレードは外部パラメーターによって設定された特定の利益・損失レベルに達したのちにクローズされます。

２番目のBernoullityのチェックは再度Bernoulliスキームとの順応を確認します。大量のBernoulliシリーズのスクリプトを短期間のテスト時間（interval B）に適用し、65000 Bernoulliモデルシリーズの結果をMS Excelにインポートし、勝ちトレード比率の配分のヒストグラムを作成します。:

無利益である場合、勝ちと負けの頻度は、それらの平均値に逆比例します: r = 21.69/82.94 = 0.2615. 負けトレードの頻度は、 f = r / ( 1+r ) = 0.2073に等しいはずです。この値は、その右の下部に位置し、右方のバーの合計は、すべてのヒストグラムのバーの合計の0.3%、利益なし/負け確率はおおよそ0.003です。おおよそ、同じ値はLaplace理論の直接的な使用にて取得されます。

Danish Kingdomはどこかおかしく思います：インターバルAのレポートデータは、Aの最初半分、成長インターバル前にて、その残高は同じ速さで低下し、その低下期間はトレードの数分Bよりも長いです。もしおよそインターバルBのテストデータに基づき、低下バランスの同じインターバルの確率を推定すると、確率はかなり小さくなります（境界頻度fはより右に移動します）。そして、これは事件データとは矛盾しているようです。

おそらく、その問題はインターバルBに一致する確率を持つ長いシリーズのトレードが大きい逸脱であるということです；1999年1月から2008年5月の初めまでのテストは、この戦略が勝ちでも負けでもないことを示します：

トレードの数学的予想は、0.17でしかなく、負けトレードの自然な頻度は以前計算されたf (0.2073)に等しく、0.2054にもなります。

稀なイベントの統計に基づく確率の推定（インターバルBにおける負けトレードの頻度は0.1706に等しく、2.8Σにおけるものと異なります）は、あまり信頼できません。しかし、確実に本当の頻度はわかりません。ただ、"failure drift"の考えは利益をもたらすのでしょうか？

4. "Failure drift": Short-Term "Shock"ドローダウンの確率の推定
ツールへのアプローチ、試み2

明らかに、もし配分の”尾”に一致する極端なターゲットではなく、妥当なものを設定すれば、可能です。インターバルBにおけるテスト結果があるとします；これはBernoulliスキームであることを確信しており、その数学的勝ち、負けトレードの予想は、その残高に現在起こっていることには依存しません。とても楽観的な負け確率の推定に基づいて、ショートですが、深い””shock”ドローダウンの確率を推定してみましょう。そのようなドローダウンは、トレーダーは”マーケットが変わった”などという不思議なフレーズを言い始めるので、トレーダーへの心理的な効果は絶大です。

Laplace理論は、その公式にふくまれている n*p*qは小さく、約10くらいか低くなるので、大きい助けにはなりません。（これは複数のトレードに一致します。）この計算の基盤にある考えは、ショートトレードシリーズにて、その負けの頻度は”本当の”ものと大きく変わり、つまり、その確率から異なります：負け頻度の分配は、少数のテストのために幅広く広がります。

短い期間のドローダウンの推定は、負けクラスタの最大の長さの推定という問題とは異なるものです。というのも、ドローダウンは負けトレードのみからは成り立たないためです。好ましい負け頻度 0.1706での長さ40の65000シリーズを生成するためのスクリプトを用い、Approaching Apparatus, Attempt No. 1のようなヒストグラムを構築します。

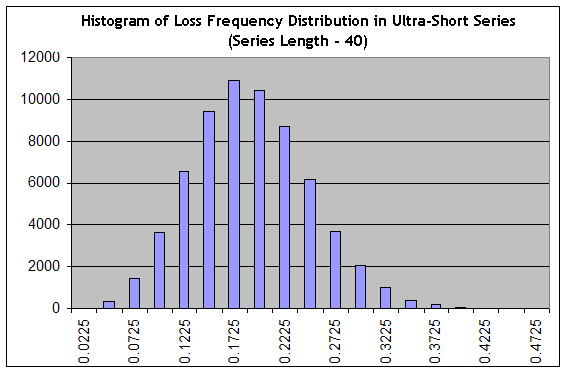
そのセットアップはかなり変化しました：鋭いものから、その配分はなだらかなものに変化し、つまり、”関連した幅”が増大しました。40-longシリーズにて、利益のないトレーディングから（負けトレードの頻度が0.1975に等しく、平均トレードが0.25ポイント得ます）鋭い負けトレード（負けトレード頻度0.3000にて、このシリーズのトレードの計算は、）. 0.7*20-0.3*80=-10 ポイントになります)の範囲で取得する確率は、"0.2225"のカラムのカラムの合計に等しくカラムの総合計の34パーセントほどの右側になります。すべて同じく、その配分の頂点は"楽観的な"頻度の0.1706になるため、これは楽観的な推定です。

確率分布とトレーディングのスペース、実際の時間のスペースの架け橋を配置するエルゴード性仮説を思い出し、少なくともトレーディング時間の34%にて、そのシステムは平均して勝ちか負けのどちらにもなりません。この数字は、[4]のデータと相関関係にあり、それによると、Bernoulliシステムはすべてのトレーディング時刻の35から55%のドローダウンになります。

ショックドローダウンを満たす実際の確率は、どれほど魅力的に見えても初期の好ましい頻度にあまり強く依存しないという事実に注意してください。これは、そのシステムの特徴的な要素で、それはBernoulliyに関連し、このイベントは平均勝ち・負けトレードの結果の向上した比率によってのみ平滑化できます。

ウルトラショートシリーズの生成に基づいたこれらの推定は、テストインターバルにて複数のトレードのみで利益を出すシステムのテスト結果をふるいにかけることができます：トレードの数学的な予想にもかかわらず、そのような少数のトレードにて、その"shock"ドローダウンは、そのシステムがBernoullity性を持つ場合、避けられないものです。

まとめ

"Mechanical Trading Systems"と呼ばれる論理的な構成を構築したいという事実にもかかわらず、どれほどのランダム性を孕んでいるのか、テスト結果で出くわさないものも含めて時折気づきません。

バイナリの表記法により示された連続したトレードの結果（”成功”か”失敗”）として、Bernoulliスキームとよく順応し、特に違いはありません。もちろん、これは、利益を出すシステムが不可能であるという意味ではありません：特定の戦略はたとえBernoulliスキームと順応していたとしても利益を出すこともあります。これは、もし勝ちトレードの確率と計算の両方が. 負けトレードのものよりも安定して高ければ、その戦略は利益を出すことができるという考えに由来します。

すくなくとも数学が少しでも理解できる読者の方は、たとえ決定的ではなくともモデルの利点を理解する必要があります。実際の統計的な自称に適しているそのモデルの主な価値は、その神秘 -つまり、乏しい実験的なデータから取得できない情報に関しての貴重な知識を取得することができるということです。この場合、Bernoulliスキームは、確率分布の"thick-tailness" がなく、その生成が極端にシンプルであるために、とても価値があります。

難しい質問にてこの記事を終えましょう；大半のTSの分析部分は、役に立たず、主な努力は効果的な資産管理メソッドにて調査される必要があります。("Analytics is nothing, money management is all!"),